人教版初中八年级数学上册专题角的相关计算和证明讲义及答案
人教版八年级上册数学11.2 与三角形有关的角(解析版)

11.2与三角形有关的角知识要点:1.三角形内角和定理:三角形三个内角的和等于180︒.(1)三角形内角和定理适用于任意三角形.(2)任何一个三角形中,至少有两个锐角,最多有一个钝角或直角.2.直角三角形的性质与判定(1)性质:直角三角形的两个锐角互余.在Rt ABC∠+∠=︒.A BC△中,90∠=︒,则90(2)判定:有两个角互余的三角形是直角三角形.3.三角形的外角三角形内角的一边与另一边的反向延长线组成的角,叫做三角形的外角.4.三角形外角的性质(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于与它不相邻的任意一个内角.一、单选题1.一个三角形三个内角的度数之比是2:3:4,这个三角形一定是()A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形【答案】C【解析】设一份为k∘,则三个内角的度数分别为2k°,3k°,4k.根据三角形内角和定理可知2k°+3k°+4k°=180°,所以2k°=40°,3k°=60°,4k°=80°.即这个三角形是锐角三角形。
故选:C2.已知三角形两个内角的差等于第三个内角,则它是()A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形【答案】C【解析】依题意得∠A-∠B=∠C,即∠A=∠B+∠C,又∠A+∠B+∠C=180°,∴∠A=90°,∴三角形为直角三角形,故选C.3.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为()A.100°B.120°C.140°D.160°【答案】B【解析】∵∠A=2(∠B+∠C),∠A+∠B+∠C=180°∴∠A=2(180°-∠A)解得∠A=120°,故选B.4.下列条件:(1)∠A=25°,∠B=65°;(2)3∠A=2∠B=∠C;(3)∠A=5∠B;(4)2∠A=3∠B=4∠C中,其中能确定△ABC是直角三角形的条件有()A.1个B.2个C.3个D.4个【解析】(1)∵∠A=25°,∠B=65°,∴∠A+∠B=25°+65°=90°,又∵∠A+∠B+∠C=180°,∴∠C=180°-(∠A+∠B)=180°-90°=90°,∴△ABC是直角三角形;(2)∵3∠A=2∠B=∠C,∴∠A=13∠C,∠B=12∠C,∵∠A+∠B+∠C=180°∴13∠C+12∠C+∠C=116∠C=180°∴∠C≠90°∴△ABC不是直角三角形;(3)∵∠A=5∠B∴无法计算内角的度数,因此无法判定△ABC的形状;(4)∵2∠A=3∠B=4∠C,∴∠A=2∠C,∠B=43∠C,又∵∠A+∠B+∠C=180°,∴2∠C+43∠C+∠C=133∠C=180°,∴∠C=54090 13≠︒∴△ABC不是直角三角形.故选A.5.已知三角形的一个内角是另一个内角的23,是第三个内角的45,则这个三角形各内角的度数分别为()A.60°,90°,75°B.48°,72°,60°C.48°,32°,38°D.40°,50°,90°【答案】B【解析】设第一个内角的度数为x,∵三角形的一个内角是另一个内角的23,是第三个内角的45,∴另一个内角的度数为32x,第三个内角为54x,∴x+32x+54x=180°,解得x=48°,∴三个内角分别为48°,72°,60°故选B.6.如图有四条互相不平行的直线l1、l2、l3、l4所截出的七个角,关于这七个角的度数关系,下列结论正确的是()A.∠2=∠4+∠7B.∠3=∠1+∠7C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°【答案】B【解析】A、∵∠2=∠10+∠9,∠10=∠7,∠9≠∠4,∴∠2=∠4+∠7不成立,故本选项错误;B、∵∠3=∠8+∠10,∠8=∠1,∠10=∠7,∴∠3=∠1+∠7,故本选项正确;C、∠4=∠8+∠6,∠8=∠1,∴∠4=∠1+∠6,∴无法说明∠1+∠4+∠6=180°,故本选项错误;D、根据多边形的外角和定理,∠2+∠4+∠5=360°,∵l3、l4不平行,∴∠3≠∠4,∴∠2+∠3+∠5=360°不成立,故本选项错误.故选B.7.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=()A.80°B.70°C.60°D.90°【答案】A【解析】∵AB∥CD,∠1=45°,∴∠C=∠1=45°.∵∠2=35°,∴∠3=∠2+∠C=35°+45°=80°.故选A.8.如图,∠BDC=98°,∠C=38°,∠A=37°,则∠B的度数是()A.33°B.23°C.27°D.37°【答案】B【解析】如图,延长CD交AB于E,∵∠C=38°,∠A=37°,∴∠1=∠C+∠A=38°+37°=75°,∵∠BDC=98°,∴∠B=∠BDC-∠1=98°-75°=23°.故选:B.9.如图所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,若∠1=70°,∠2=30°,则∠3的度数为()A.30°B.40°C.45°D.50°【答案】B【解析】∵CE平分∠ACD,∴∠1=∠ECF,∵FG∥CE,∴∠F=∠ECF,∵∠FCD=∠3+∠BAC,∠BAC=∠2+∠F,∴∠FCD=∠3+∠2+∠F,∴∠1+∠ECF=∠3+∠2+∠F,∴∠2+∠3=∠1,又∵∠1=70°,∠2=30°,∴∠3=70°-30°=40°,故选B.10.如图,在△ABC中,∠BAC=90︒,AD⊥BC于D,则图中互余的角有A.2对B.3对C.4对D.5对【答案】C【解析】∵∠BAC=90°∴∠B+∠C=90°①;∠BAD+∠CAD=90°②;又∵AD⊥BC,∴∠BDA=∠CDA=90°,∴∠B+∠BAD=90°③;∠C+∠CAD=90°④。
人教版八年级数学上册第十二章《全等三角形的综合、角平分线》讲义(带答案)

第7 讲全等三角形的综合、角平分线第一部分知识梳理知识点一:全等三角形的综合⑴ 平移全等型知识点二:角平分线的性质⑴、角平分线上的点到角的两边的距离相等;⑵、到角的两边距离相等的点在角的平分线上.它们具有互逆性.角平分线是天然的、涉及对称的模型,一般情况下,有下列三种作辅助线的方式:1.由角平分线上的一点向角的两边作垂线,2.过角平分线上的一点作角平分线的垂线,从而形成等腰三角形,3.OA OB ,这种对称的图形应用得也较为普遍,知识点三:角平分线的作法角平分线的作法(尺规作图)①以点O为圆心,任意长为半径画弧,交OA、OB于C、D 两点;②分别以C、D 为圆心,大于CD长为半径画弧,两弧交于点P;③过点P 作射线OP,射线OP即为所求.第二部分考点精讲精练考点1、三角形全等综合1、全等三角形实际应用1、如图,要测量河两岸相对的两点A、B 间的距离,先在过B点的AB的垂线L 上取两点C、D,使CD=BC,再在过 D 点的垂线上取点E,使A、C、E在一条直线上,ED=AB这时,测ED的长就得AB得长,判定△ ACB≌△ECD的理由是()A. SASB. ASAC. SSS D .AAS2、如图,小强利用全等三角形的知识测量池塘两端M、N 的距离,如果△PQO≌△ NMO,则只需测出其长度的线段是(B )A.PO B.PQ C.MO D.MQ2)1)3、如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的点 B 处打开,墙壁厚是35cm,点B与点O的垂直距离AB长是20cm,在点O处作一直线平行于地面,在直线上截取OC=35cm,过C作OC的垂线,在垂线上截取CD=20cm,连接OD,然后,沿着D0 的方向打孔,结果钻头正好从点 B 处打出.这是什么道理?4、1805 年,法军在拿破仑的率领下与德军在莱茵河畔激战.德军在莱茵河北岸Q处,如图所示,因不知河宽,法军大炮很难瞄准敌营.聪明的拿破仑站在南岸的点O 处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面德国军营Q处,然后他一步一步后退,一直退到自己的视线恰好落在他刚刚站立的点0 处,让士兵丈量他所站立位置B与0点的距离,并下令按照这个距离炮轰德军.试问:法军能命中目标吗?请说明理由.用帽舌边缘视线法还可以怎样测量,也能测出河岸两边的距离吗?5、某校七年级学生到野外活动,为测量一池塘两端A,B 的距离,甲、乙、丙三位同学分别设计出如下几种方案:甲:如图① ,先在平地取一个可直接到达A,B 的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的长即为A,B 的距离.乙:如图② ,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离.丙:如图③ ,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠ BDC=∠BDA,这时只要测出BC的长即为A,B 的距离.(1)以上三位同学所设计的方案,可行的有____ ;(2)请你选择一可行的方案,说说它可行的理由.2、证两次全等相关问题1、已知: 如图,AB=AE,BC=ED ∠, B= ∠E,AF ⊥ CD,F 为垂足, 求证:CF=DF.3、如图, AB=AD ,BC=DE ,且 BA ⊥AC ,DA ⊥AE ,你能证明 AM=AN 吗?2、已知:如图, AB=CD ,BC=DA ,AE=CF .求证: BF=DE .EC⊥BF.2、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC 于F,若BD=AD,DE=DC。
专题五几何证明人教版八年级数学(上册)-【完整版】

∴△DAB≌△CBA(AAS). ∴BD=AC. ∴AD=BC. 在△ADC和△BCD中,
∴△ADC≌△BCD(SSS). ∴∠CDA=∠DCB.
四、 证明线段垂直
15. 如图,点 C 在线段 AB 上,AD∥EB,AC=BE,
AD=BC,CF 平分∠DCE.求证:CF⊥DE.
∵F为CE的中点, ∴AF平分∠EAC. ∴AF⊥CE.即∠AFC=90°. 又∠FAC+∠ACE=180°-∠AFC=90°, ∠DAC=∠ACE, ∴∠DAC+∠FAC=90°. 即∠DAF=90°. ∴AF⊥AD.
五、 证明等边三角形
20. 如图,在△ABC 中,D 为 AC 边上一点,DE⊥AB
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
在△ACM和△DCN中,
∴△ACM≌△DCN(ASA). ∴CM=CN. 又∠DCN=60°, ∴△CMN为等边三角形.
专题五 几何证明人教版八年级数学上册-精 品课件p pt(实 用版)
证明:∵△ABC≌△EDC, ∴BC=DC,∠ACB=∠DCE.
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS). ∴∠FBC=∠HDC. 在△FBC和△FDK中, ∵∠FBC=∠HDC,∠BFC=∠DFK, ∴∠DKF=∠ACB.
14. 如图,AC 与 BD 相交于点 O,∠DBA=∠CAB, ∠1=∠2. 求证:∠CDA=∠DCB.
点 F,连接 BE. 求证:BE⊥AF.
证明:∵AD∥BC, ∴∠DAE=∠F,∠ADE=∠FCE.
在△ADE和△FCE中,
部编版人教初中数学八年级上册《角的相关计算和证明 专题突破讲义(含答案)》最新精品优秀

前言:该专题突破讲义由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的专题突破讲义助力考生查漏补缺,在原有基础上更进一步。
(最新精品专题突破讲义)角的相关计算和证明(讲义)➢课前预习背默我们到目前学习过的定理:(1)平行线:判定:①_______________,两直线平行;②_______________,两直线平行;③_______________,两直线平行.性质:①两直线平行,_______________;②两直线平行,_______________;③两直线平行,_______________.(2)余角、补角、对顶角:同角(等角)的余角__________;同角(等角)的补角________;对顶角_ _______.(3)三角形:三角形的内角和等于_______;直角三角形两锐角________;三角形的外角等于______________________________.➢知识点睛在证明的过程中,由平行想到____________、____________、____________;由垂直想到__________________、____________________;由外角想到________________________________________.➢精讲精练1. 如图,AB ∥EF ∥CD ,∠ABC =45°,∠CEF =155°,则∠BCE =_________.FE D CBA 2. 如图,在△ABC 中,∠B =60°,∠A =40°,DC 平分∠ACB 交AB 于点D ,过点D 作DE ∥BC 交AC 于点E ,则∠EDC =_____.ED C B A G F EDC B A第2题图 第3题图3. 如图,在正方形ABCD 中,∠ADC =∠DCB =90°,G 是BC 边上一点,连接D G ,AE ⊥DG 于点E ,CF ⊥DG 于点F .若∠DAE =25°,则∠GCF =_________.4. 如图,在Rt △ABC 中,∠BAC =90°,∠C =45°,在Rt △AFG 中,∠G =90°,∠FAG =45°,∠CAG =20°,则∠AEB =_______,∠ADC =________.GF E DC B A G F E DC A第4题图 第5题图。
人教版 八年级数学 多边形及其内角和讲义 (含解析)
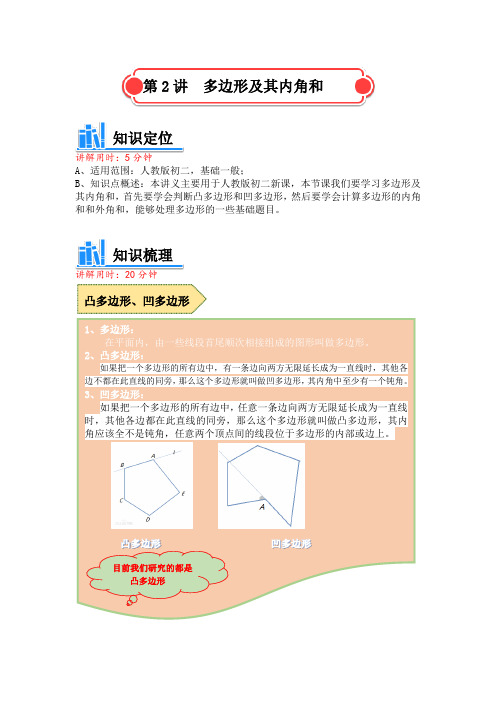
第2讲多边形及其内角和知识定位讲解用时:5分钟A、适用范围:人教版初二,基础一般;B、知识点概述:本讲义主要用于人教版初二新课,本节课我们要学习多边形及其内角和,首先要学会判断凸多边形和凹多边形,然后要学会计算多边形的内角和和外角和,能够处理多边形的一些基础题目。
知识梳理讲解用时:20分钟凸多边形、凹多边形1、多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
2、凸多边形:如果把一个多边形的所有边中,有一条边向两方无限延长成为一直线时,其他各边不都在此直线的同旁,那么这个多边形就叫做凹多边形,其内角中至少有一个钝角。
3、凹多边形:如果把一个多边形的所有边中,任意一条边向两方无限延长成为一直线时,其他各边都在此直线的同旁,那么这个多边形就叫做凸多边形,其内角应该全不是钝角,任意两个顶点间的线段位于多边形的内部或边上。
目前我们研究的都是凸多边形1、多边形的内角:多边形相邻两边组成的角叫做它的内角。
2、多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
3、多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
4、正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
从同一个顶点引出对角线的条数:0 1 2 3 n-3 (n≥3)分割出三角形的个数:0 2 3 4 n-2 (n≥3)多边形内角和:180° 360° 540° 720° (n-2)·180°课堂精讲精练【例题1】设四边形内角和等于,五边形外角和等于,则与之间的关系是( ) A.B.C.D.【答案】B【解析】四边形的内角和是360°,多边形的内角和也是360°.解:多边形边数为,则内角和为,四边形内角和,多边形外角和为, 五边形外角和, 因此. 故正确答案为:.讲解用时:2分钟解题思路:此题比较简单,熟记多边形的内角和和外角和公式做题即可. 教学建议:掌握多边形的内角和和外角和公式,灵活做题.难度: 3 适应场景:当堂例题 例题来源:无 年份:2018【练习1.1】下列图形中,多边形有( )总结:1、多边形对角线的条数:(1)从n 边形的一个顶点出发可以引(n-3)条对角线,把多边形分词(n-2)个三角形。
人教版八年级上册第2讲 与三角形有关的角讲义

第2讲与三角形有关的角三角形内角和定理(1)定理:三角形三个内角的和等于180°.(2)证明方法:证法多样,主要是运用平行线知识把三个角转移成一个平角,从而得到内角和是180°。
①如图所示,过C作CM∥AB,将求∠A+∠B+∠ACB转化为求∠1+∠2+∠ACB,②过A点作DE∥BC,把求∠BAC+∠B+∠C转化为求∠BAC+∠DAB+∠EAC.(3)理解与延伸:①一个三角形中最多只有一个钝角或直角;②一个三角形中最少有一个角不小于60°;③直角三角形两锐角互余;④等边三角形每个角都是60°.(4)作用:求角度,尤其是三角形中的角度计算。
【例1-1】填空:(1)在△AB C中,若∠A=80°,∠C=20°,则∠B=__________°;(2)若∠A=80°,∠B=∠C,则∠C=__________°;(3)已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠B=________°,∠C=_________°.【例1-2】如图,在△ABC中,∠CAB=∠B=2∠C,AD是∠BAC的平分线,求∠ADC 的度数.【例1-3】如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数。
【例1-4】若等腰三角形的一内角为40°,则顶角为( )A. 40°B. 100°C. 70°或40°D.40°或100°直角三角形的性质与判定(1)直角三角形的性质:直角三角形的两个锐角互余.如图所示,在Rt △ABC 中,如果∠C =90°,那么∠A +∠B =90°.【例2-1】 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是 ( ). A .43° B .47° C .30° D .60°【例2-2】 如图所示,AB ∥CD ,直线EF 分别交AB ,CD 于点E ,F ,∠BEF 的平分线与∠DFE 的平分线相交于点P ,求证:△EPF 是直角三角形.判定:有两个角互余的三角形是直角三角形。
人教版八年级数学上册与三角形有关的角复习及习题11.2解析答案教案

人教版八年级数学11.2复习及习题11.2教案备课人:备课日期:年月日四、习题指导复习巩固1.求下列图形中x的值:【解析】利用三角形的内角和定理列出方程求解。
2.(1)一个三角形最多有几个直角,为什么?(2)一个三角形最多有几个钝角,为什么?(3)直角三角形的外角可以是锐角吗?为什么?【解析】一个三角形只能有一个直角或一个钝角,因为有两个直角或钝角时,三个内角的和就超过了180°。
因为三角形的一个顶点处的外角和相邻的内角互为补角,而直角三角形的内角是一个直角和两个锐角,所以它的外角就只能是直角或钝角,不可以是锐角。
3.△ABC中,∠B=∠A+ 10°,∠C=∠B+10°。
求△ABC各角的度数。
【解析】可设∠A为x°,根据内角和定理列方程解答。
4.如图,AD⊥BC,∠1=∠2,∠C=65°。
求∠BAC的度数。
【解析】根据锐角三角形两个内角互余,分别求出∠1和∠DAC,求其和即得∠BAC的度数。
综合运用5.如图,AB∥CD,∠A=40°,∠D=45°.求∠1和∠2的度数.【解析】根据平行线的性质得∠2=∠A=40°。
根据三角形的外角等于与它不相邻的两个内角的和,得∠1=∠D+∠2=85°.【答案】∠2=40°,∠1=85°.6.如图,AB∥CD,∠A=45°,∠C=∠E,求∠C的度数.【解析】记AE与CD的交点为F。
∵AB∥CD,∴∠DFE=∠A=45°.F∵∠DFE是△CEF的外角,∠C=∠E,∴ 2∠C=∠DFE=45°.∴∠C==22.5°.7.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数.【解析】根据方位角和平行线的性质,得∠ABC=80°-45°=35°,∠BAC=45°+15°=60°。
人教版八年级数学上册三角形的内角和定理

三角形的内角和定理人教八上初中数学试卷金戈铁骑整理制作11-4一、学习目标理解“三角形的内角和等于180°”及证明过程;证明“三角形内角和定理”,体会证明中辅助线的作用,尝试用多种方法证明三角形内角和定理;运用三角形内角和定理解决问题.二、知识回顾拼拼看,将任意一个三角形的三个内角拼合在一起会形成什么角?三、新知讲解1.三角形内角和定理定理三角形三个内角的和等于180°符号语言在△ABC中,∠A+∠B+∠C=180°图示2.三角形内角和定理的证明已知:如图,已知△ABC,求证:∠A+∠B+∠C=180°.〖方法1〗证明:过A点作DE∥BC,∵DE∥BC,(已作)∴∠DAB=∠B,∠EAC=∠C,(两直线平行,内错角相等)∵∠DAB+∠BAC+∠EAC=180°,(平角=180°)∴∠BAC+∠B+∠C=180°,(等量代换)〖方法2〗证明:作BC的延长线CD,过点C作射线CE∥BA.∵CE∥BA,∴∠B=∠ECD(两直线平行,同位角相等),∠A=∠ACE(两直线平行,内错角相等),∵∠BCA+∠ACE+∠ECD=180°,(平角=180°)∴∠A+∠B+∠ACB=180°.(等量代换)3.三角形内角和定理的应用(1)已知三角形的两个内角,利用三角形内角和定理可求第三个角;(2)已知各角之间的关系,利用三角形内角和定理可求各角.四、典例探究扫一扫,有惊喜哦!1.三角形的内角和定理【例1】(2014春•靖江市校级月考)若一个三角形的三个内角之比为3:4:5,则它的最大内角的度数是()A.80°B.75°C.90°D.108°总结:给出三角形三个内角的比求内角度数时,通常要设未知数,通过列方程求解.【例2】(2014•重庆校级模拟)如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=45°,则∠A的度数为()A.65°B.75°C.85°D.95°总结:关于三角形与平行线结合的问题,求解时,先从平行线的性质入手,把有关角转化到三角形中,再利用三角形的内角和定理求解.【例3】(2014秋•太和县期末)如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP 平分∠ACB,则∠BPC的大小是()A.100°B.110°C.115°D.120°总结:三角形中两内角平分线相交组成的角等于90°与第三个内角一半的和.练1.(2015•重庆模拟)在△ABC中,已知∠A=4∠B=104°,则∠C的度数是()A.50°B.45°C.40°D.30°练2.(2014秋•安庆期中)在△ABC中,∠A、∠B、∠C的度数之比为3:4:5,那么△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形练3.(2014春•通川区校级期中)如图,已知△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.2.三角形内角和定理的实际应用【例4】如图,一轮船由B处向C处航行,在B处测得C处在B的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,若轮船行驶到C处时测得∠BAC=55°,那么从C处看A,B两处的视角∠ACB是多少度?总结:1.“三角形的内角和为180°”是隐含条件,在实际应用中必不可少.2.在有关方位角的计算中,常常构造三角形,在三角形中计算角的度数.练4.(2010•石家庄二模)如图所示是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处夹角∠BCD为________度.一、选择题1.(2014•江北区模拟)在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()A.90°B.94°C.98°D.108°2.(2014春•合川区校级期中)已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.正三角形3.(2014春•江阴市校级期中)如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=()A.50°B.40°C.70°D.35°4.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C 的度数为()A.30°B.40°C.50°D.60°二、填空题5.(2014秋•宁津县校级月考)在△ABC中,∠A:∠B:∠C=2:3:4,则∠A=,∠C=.6.(2014•徐州二模)如图,AB∥CD,AD和BC相交于点O,∠A=35°,∠AOB=75°,则∠C=.7.(2013春•苏州期末)如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=.三、解答题8.(2014春•庐江县期末)如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.9.(2012春•中山区期中)已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.10.(2011春•宣威市校级月考)如图所示,已知图①五角星ABCDE,将图①中的A点向下移动得到图②,将图①中的C点向上移动得图③,对于五角星及五角星的变形图,∠A+∠B+∠C+∠D+∠E 的和为多少度?并选择一图加以说明.典例探究答案:【例1】(2014春•靖江市校级月考)若一个三角形的三个内角之比为3:4:5,则它的最大内角的度数是()A.80°B.75°C.90°D.108°分析:设三角形的三个内角的度数分别为3x、4x、5x,根据三角形内角和定理得到3x+4x+5x=180°,然后解方程求出x后计算5x即可.解答:解:设三角形的三个内角的度数分别为3x、4x、5x,所以3x+4x+5x=180°,解得x=15°,所以5x=75°.故选B.点评:本题考查了三角形内角和定理,即三角形内角和是180°.【例2】(2014•重庆校级模拟)如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=45°,则∠A的度数为()A.65°B.75°C.85°D.95°分析:根据平行线的性质可得∠C=∠AED=45°,再利用三角形内角和为180°可以计算出∠A的度数.解答:解:∵DE∥BC,∴∠C=∠AED=45°,∴∠A=180°﹣∠B﹣∠C=180°﹣45°﹣60°=75°,故选:B.点评:此题主要考查了三角形内角和定理,即三角形内角和为180°.【例3】(2014秋•太和县期末)如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是()A.100°B.110°C.115°D.120°分析:根据三角形内角和定理计算.解答:解:∵∠ABC=50°,∠ACB=80°,且BP平分∠ABC,CP平分∠ACB,∴∠PBC=25°,∠PCB=40°,∴∠BPC=115°.故选C.点评:此题主要考查了三角形的内角和定理:三角形的内角和为180°.练1.(2015•重庆模拟)在△ABC中,已知∠A=4∠B=104°,则∠C的度数是()A.50°B.45°C.40°D.30°分析:根据已知条件求出∠B的度数,再根据三角形的内角和等于180°列式计算即可得解.解答:解:∵4∠B=104°,∴∠B=26°,∴∠C=180°﹣∠A﹣∠B=180°﹣104°﹣26°=50°.故选A.点评:本题考查了三角形的内角和定理,是基础题,求出∠B的度数,然后列出∠C的表达式是解题的关键.练2.(2014秋•安庆期中)在△ABC中,∠A、∠B、∠C的度数之比为3:4:5,那么△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形分析:已知三角形三个内角的度数之比,可以设一份为k°,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.解答:解:设一份为k°,则三个内角的度数分别为3k°,4k°,5k°.则3k°+4k°+5k°=180°,解得k°=15°,∴5k°=75°,3k°=45°,4k°=60°,所以这个三角形是锐角三角形,故选A.点评:此题主要考查三角形的按边分类,直接根据三角形三个内角的度数比来判断是解题的关键.练3.(2014春•通川区校级期中)如图,已知△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.分析:由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE﹣∠BAD=10°.解答:解:在△ABC中,∵∠BAC=180°﹣∠B﹣∠C=70°,∵AE是∠BAC的平分线,∴∠BAE=∠CAE=35°.又∵AD是BC边上的高,∴∠ADB=90°,∵在△ABD中∠BAD=90°﹣∠B=25°,∴∠DAE=∠BAE﹣∠BAD=10°.点评:本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理,一定要熟稔于心.【例4】如图,一轮船由B处向C处航行,在B处测得处在B的北偏东75°方向上,在海岛上的观察所A测得B在A的南偏西30°方向上,若轮船行驶到C处时测得∠BAC=55°,那么从C处看A,B两处的视角∠ACB是多少度?分析:根据方位角就可求得BA与正北方向的夹角,即可得到∠ABC,在△ABC中,根据三角形内角和定理即可求得∠ACB的度数.解答:解:∵∠BAE=30°,∴∠ABD=30°,∴∠ABC=∠DBC-∠ABD=75°-30°=45°.在△ABC中,根据三角形内角和定理得到:∠ACB=180°-45°-55°=80°,即从C处看A,B两处的视角∠ACB是80°.点评:本题主要考查了方位角的定义,以及三角形的内角和定理.练4.(2010•石家庄二模)如图所示是小李绘制的某大桥断裂的现场草图,若∠1=38°,∠2=23°,则桥面断裂处夹角∠BCD为_____度.分析:连接BD,根据对顶角相等得到∠1=∠4=38°,∠2=∠3=23°,然后根据三角形内角和定理进行计算即可.解答:解:连接BD,如图,∵∠1=∠4=38°,∠2=∠3=23°,∴∠BCD=180°-∠4-∠3=180°-23°-38°=119°.故答案为:119.点评:本题考查了三角形内角和定理:三角形的内角和为180°.也考查了对顶角相等.课后小测答案:一、选择题1.(2014•江北区模拟)在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()A.90°B.94°C.98°D.108°解:如图所示:∵∠A=3∠C=54°,∴∠C=18°,∴∠B的度数是:180°﹣∠A﹣∠C=108°.故选:D.2.(2014春•合川区校级期中)已知△ABC中,∠A=20°,∠B=∠C,那么三角形△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.正三角形解:∵∠A=20°,∴∠B=∠C=(180°﹣20°)=80°,∴三角形△ABC是锐角三角形.故选A.3.(2014春•江阴市校级期中)如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=()A.50°B.40°C.70°D.35°解:∵BE、CF都是△ABC的角平分线,∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣2(∠DBC+∠BCD)∵∠BDC=180°﹣(∠DBC+∠BCD),∴∠A=180°﹣2(180°﹣∠BDC)∴∠BDC=90°+∠A,∴∠A=2(110°﹣90°)=40°.故选B.4.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为()A.30°B.40°C.50°D.60°解:∵△ABC中,∠A=100°,∠B=40°,∴∠C=180°-∠A-∠B=180°-100°-40°=40°.故选B.二、填空题5.(2014秋•宁津县校级月考)在△ABC中,∠A:∠B:∠C=2:3:4,则∠A=,∠C=.解:设∠A=2x°,则∠B=3x°,∠C=4x°,∵∠A+∠B+∠C=180°,即:2x°+3x°+4x°=180°,解得:x=20∴∠A=40°,则∠B=60°,∠C=80°,故答案为:40°、80°6.(2014•徐州二模)如图,AB∥CD,AD和BC相交于点O,∠A=35°,∠AOB=75°,则∠C=.解:∵∠A=35°,∠AOB=75°,∠A+∠B+∠C=180°,∴∠B=180°﹣35°﹣75°=70°.又∵AB∥CD,∴∠C=∠B=70°.7.(2013春•苏州期末)如图,CD、CE分别是△ABC的高和角平分线,∠A=30°,∠B=60°,则∠DCE=.解:∵∠A=30°,∠B=60°,∴∠ACB=180°﹣∠A﹣∠B=90°,∵CD、CE分别是△ABC的高和角平分线,∴∠BCE=∠ACB=45°,∠BDC=90°,∴∠BCD=90°﹣∠B=30°,∴∠DCE=∠BCE﹣∠BCD=45°﹣30°=15°.故答案为:15°.三、解答题8.(2014春•庐江县期末)如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.解:∵∠DAB=70°,AC平分∠DAB,∴∠DAC=35°,又∵∠1=35°,∴∠D=180°﹣(∠1+∠DAC)=180°﹣(35°+35°)=110°.9.(2012春•中山区期中)已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.解:∵AB∥CD,AE平分∠BAC,CE平分∠ACD,又∠BAC+∠DCA=180°⇒∠CAE+∠ACE=(∠BAC+∠DCA)=90°,∠E=180°﹣(∠CAE+∠ACE)=90°,∴∠E=90°.10.(2011春•宣威市校级月考)如图所示,已知图①五角星ABCDE,将图①中的A点向下移动得到图②,将图①中的C点向上移动得图③,对于五角星及五角星的变形图,∠A+∠B+∠C+∠D+∠E的和为多少度?并选择一图加以说明.解:∠A+∠B+∠C+∠D+∠E=180°,图①:∵∠A+∠D=∠BNM,∠E+∠C=∠BMN,(三角形的外角等于与它不相邻的两个内角的和),又∵∠B+∠BNM+∠BMN=180∴∠A+∠B+∠C+∠D+∠E=180°.图②:延长AD交BE于点F,再根据三角形外角的性质解答;③同①,∵∠A+∠C=∠1,∠B+∠E=∠2,∠1+∠2+∠D=180°,∴∠A+∠B+∠C+∠D+∠E=180°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角的相关计算和证明(讲义)
课前预习
背默我们到目前学习过的定理: (1)平行线: 判定:
①_______________,两直线平行; ②_______________,两直线平行; ③_______________,两直线平行. 性质:
①两直线平行,_______________; ②两直线平行,_______________; ③两直线平行,_______________. (2)余角、补角、对顶角:
同角(等角)的余角__________;同角(等角)的补角________;对顶角________. (3)三角形:
三角形的内角和等于_______; 直角三角形两锐角________;
三角形的外角等于______________________________.
知识点睛
在证明的过程中,
由平行想到____________、____________、____________; 由垂直想到__________________、____________________; 由外角想到________________________________________.
精讲精练
1. 如图,AB ∥EF ∥CD ,∠ABC =45°,∠CEF =155°,则
∠BCE =_________.
F E
D C
B
A
2. 如图,在△ABC 中,∠B =60°,∠A =40°,DC 平分∠ACB 交AB 于点D ,过点D
作DE ∥BC 交AC 于点E ,则∠EDC =_____.
E
D
B
A
G F
E
D
C
B
A
第2题图第3题图
3. 如图,在正方形ABCD 中,∠ADC =∠DCB =90°,G 是BC 边上一点,连接DG ,
AE ⊥DG 于点E ,CF ⊥DG 于点F .若 ∠DAE =25°,则∠GCF =_________.
4. 如图,在Rt △ABC 中,∠BAC =90°,∠C =45°,在Rt △AFG 中,∠G =90°,∠FAG =45°,
∠CAG =20°,则∠AEB =_______,∠ADC =________.
G
F
E D
C
B
A
G F
E
D
C
A
第4题图第5题图
5. 如图,ED ⊥AB 于点D ,EF ∥AC ,∠A =35°,则∠DEF =______.
6. 如图,在△ABC 中,∠B =60°,P 为BC 上一点,且∠1=∠2,则∠APD =________.
21
P
D
C
B
A
7. 如图,E ,F 分别在AB ,CD 上,EC ⊥AF ,垂足为点O ,
∠1+∠C =90°,∠2=∠D .求证:AB ∥CD .
2
1
O E B
A
8. 如图,在△ABC 中,∠B =35°,∠C =75°,AD ⊥BC 于D ,AE 平分∠BAC ,求∠
EAD 的度数.
9. 如图,直线AD 分别与直线BF ,EG 相交于点C ,D .若
∠D=∠A+∠B ,∠BFE =75°,∠G =35°,求∠EFG 的度数.
F
E
D
C
B
A
E D
C
A
10.如图,BP平分∠ABC,CP平分△ABC的外角∠ACE.
求证:∠A=2∠P.
证明:如图,设∠PBC=α,∠PCE=β
∵BP平分∠ABC (_____________________)
∴∠ABC=2∠PBC=2α(_____________________)
∵CP平分∠ACE (_____________________)
∴∠ACE=______=_______ (_____________________)
∵∠ACE是△ABC的一个外角(_____________________)∴∠ACE =∠ABC+∠A (_____________________)
∴_____=_____+∠A (_____________________)∵∠PCE是△BCP的一个外角(_____________________)∴___________________(_____________________)
∴β=______+_______(_____________________)
∴2β=2α+2∠P(_____________________)
∴∠A=2∠P (_____________________)
11.已知:如图,在△ABC中,BD平分∠ABC,CD平分∠ACB.
求证:
1
90
2
D A
∠=︒+∠.A
B C
D
C
B
A
【参考答案】
课前预习
(1)同位角相等;内错角相等;同旁内角互补.
同位角相等;内错角相等;同旁内角互补.
(2)相等;相等;相等.
(3)180°;互余;与它不相邻的两个内角的和.
知识点睛
同位角、内错角、同旁内角;
直角三角形两锐角互余,同角(等角)的余角相等;
三角形的外角等于与它不相邻的两个内角的和. 精讲精练 1. 20° 2. 40° 3.
25°
4. 65°,70°
5. 125°
6. 60°
7. 证明:如图,
2
1
O E F
D C
B
A
∵EC ⊥AF (已知)
∴∠COF =90°(垂直的定义)
∴∠C +∠2=90°(直角三角形两锐角互余) ∵∠1+∠C =90°(已知) ∴∠1=∠2(同角的余角相等) ∵∠2=∠D (已知) ∴∠1=∠D (等量代换)
∴AB ∥CD (内错角相等,两直线平行) 8. 解:如图,
E D C A
在△ABC 中,∠B =35°,∠C =75°(已知)
∴∠BAC =180°-∠B -∠C
=180°-35°-75°
=70°(三角形的内角和等于180°)
∵AE 平分∠BAC (已知)
∴∠BAE =1
2
∠BAC
=1
2
×70°
=35°(角平分线的定义)
∵∠AED是△ABE的一个外角(外角的定义)
∴∠AED=∠B+∠BAE
=35°+35°
=70°(三角形的外角等于与它不相邻的两个内角
的和)
∵AD⊥BC(已知)
∴∠ADE=90°(垂直的定义)
∴∠AED+∠EAD=90°(直角三角形两锐角互余)
∴∠EAD=90°-∠AED
=90°-70°
=20°(等式的性质)
9.解:如图,
∵∠ACF是△ABC的一个外角(外角的定义)
∴∠ACF=∠A+∠B(三角形的外角等于与它不相邻的两个内角的和)
∵∠D=∠A+∠B(已知)
∴∠ACF=∠D(等量代换)
∴BF∥DG(同位角相等,两直线平行)
∴∠BFE=∠FEG(两直线平行,内错角相等)
∵∠BFE=75°(已知)
∴∠FEG=75°(等量代换)
在△FEG中,∠FEG=75°,∠G=35°(已知)
∴∠EFG=180°-∠FEG-∠G
=180°-75°-35°
=70°(三角形的内角和等于180°)
10.证明:如图,设∠PBC=α,∠PCE=β
∵BP平分∠ABC (已知)
∴∠ABC=2∠PBC=2α(角平分线的定义)
∵CP平分∠ACE (已知)
∴∠ACE=2∠PCE=2β(角平分线的定义)
∵∠ACE是△ABC的一个外角(外角的定义)
∴∠ACE=∠ABC+∠A (三角形的外角等于与它不相邻的两个内角的和)∴2β=2α+∠A (等量代换)
∵∠PCE是△BCP的一个外角(外角的定义)
∴∠PCE=∠PBC+∠P(三角形的外角等于与它不相邻的两个内角的和)
∴β=α+∠P(等量代换)
∴2β=2α+2∠P(等式的性质)
∴∠A=2∠P (等式的性质)
11.证明:如图,设∠DBC=α,∠DCB=β
∵BD平分∠ABC(已知)
∴∠ABC=2∠DBC=2α(角平分线的定义)
∵CD平分∠ACB(已知)
∴∠ACB=2∠DCB=2β(角平分线的定义)
∵∠ABC+∠ACB+∠A=180°(三角形的内角和等于180°)∴2α+2β+∠A=180° (等量代换)
∴
1
90
2
∠A
αβ
++=︒(等式的性质)
∵∠DBC+∠DCB+∠D=180°(三角形的内角和等于180°)∴α+β+∠D=180°(等量代换)
∴
1
90
2
D A
∠=︒+∠(等式的性质)。
