实验四 电压源与电流源的等效变换
电压源与电流源的等效变换实验报告

电压源与电流源的等效变换实验报告示例文章篇一:《电压源与电流源的等效变换实验报告》嘿!同学们,今天我要跟你们讲讲我做的那个超级有趣又有点难搞的电压源与电流源的等效变换实验!实验开始前,老师把我们分成了小组,我和我的好朋友小明、小红一组。
我们一到实验室,就看到桌子上摆满了各种各样的仪器,有电源、电阻、电流表、电压表,就像一个神秘的宝库等着我们去探索。
我们先按照老师的指导连接电路。
这可不像搭积木那么简单!我们小心翼翼地摆弄着电线,生怕接错了。
我一边弄一边嘟囔:“这电线怎么这么不听话,老跟我作对!”小明在旁边笑着说:“别着急,咱们慢慢来,肯定能成功!”好不容易把电路接好了,接下来就是测量数据啦。
当我打开电源开关的那一刻,心里紧张得要命,就像揣了一只小兔子,砰砰直跳。
我眼睛紧紧盯着电流表和电压表,生怕错过了任何一个数字。
可是,第一次测量的数据好像不太对劲。
“哎呀,这是怎么回事?”我忍不住叫了起来。
小红安慰我说:“别慌,咱们再检查检查电路是不是哪里出问题了。
”于是,我们又仔仔细细地检查了一遍电路,发现原来是有一个电阻接错了位置。
重新调整好之后,再次测量,这次的数据终于正常啦!我们高兴得差点跳起来。
在实验过程中,我们发现电压源和电流源就像两个性格不同的小伙伴。
电压源就像一个大力士,总是能提供稳定的力量(电压);而电流源呢,则像一个短跑健将,能迅速地输出强大的电流。
我们不断地改变电阻的大小,观察着电流和电压的变化,就好像在指挥一场精彩的表演。
有时候电流会突然增大,就像火箭一样飙升;有时候电压又会突然下降,就像泄了气的皮球。
这感觉太神奇啦!经过多次测量和计算,我们终于得出了结论:在一定条件下,电压源和电流源是可以等效变换的。
这就好比一个人可以换不同的衣服,但本质还是那个人。
这次实验让我深刻地理解了电压源和电流源的概念,也让我明白了做实验要有耐心,要细心,更要有团队合作精神。
不然,一个人可搞不定这么复杂的实验!同学们,你们说,科学实验是不是特别有趣,特别能让人长知识?我觉得呀,只要我们勇于探索,就能在科学的海洋里发现更多的宝藏!示例文章篇二:哎呀呀!今天我要跟你们讲讲我们做的那个超级有趣的电压源与电流源的等效变换实验!一进实验室,我就看到桌子上摆满了各种各样的仪器,我的心都激动得怦怦直跳啦!老师在前面给我们讲解实验步骤的时候,我眼睛都不敢眨一下,生怕错过了什么重要的信息。
电路分析实验报告
电压源与电流源的等效变换一、实验目的1、 加深理解电压源、电流源的概念。
加深理解电压源、电流源的概念。
2、 掌握电源外特性的测试方法。
掌握电源外特性的测试方法。
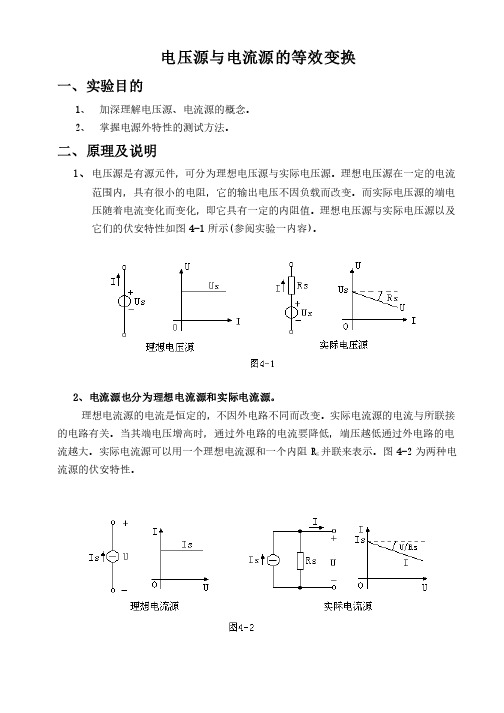
二、原理及说明1、 电压源是有源元件,电压源是有源元件,可分为理想电压源与实际电压源。
可分为理想电压源与实际电压源。
可分为理想电压源与实际电压源。
理想电压源在一定的电流理想电压源在一定的电流范围内,具有很小的电阻,它的输出电压不因负载而改变。
而实际电压源的端电压随着电流变化而变化,压随着电流变化而变化,即它具有一定的内阻值。
即它具有一定的内阻值。
即它具有一定的内阻值。
理想电压源与实际电压源以及理想电压源与实际电压源以及它们的伏安特性如图4-1所示所示((参阅实验一内容参阅实验一内容))。
2、电流源也分为理想电流源和实际电流源。
理想电流源的电流是恒定的,理想电流源的电流是恒定的,不因外电路不同而改变。
不因外电路不同而改变。
不因外电路不同而改变。
实际电流源的电流与所联接实际电流源的电流与所联接的电路有关。
当其端电压增高时,通过外电路的电流要降低,端压越低通过外电路的电流越大。
实际电流源可以用一个理想电流源和一个内阻R S 并联来表示。
图4-2为两种电流源的伏安特性。
流源的伏安特性。
3、电源的等效变换一个实际电源,尤其外部特性来讲,可以看成为一个电压源,也可看成为一个电流源。
两者是等效的,其中I S =U S /R S 或或 U S =I S R S图4-3为等效变换电路,由式中可以看出它可以很方便地把一个参数为U s 和R s 的电压源变换为一个参数为I s 和R S 的等效电流源。
同时可知理想电压源与理想电流源两者之间不存在等效变换的条件。
之间不存在等效变换的条件。
三、仪器设备电工实验装置电工实验装置 : DG011 DG011、、 DG053 DG053 、、 DY04 DY04 、、 DYO31四、实验内容1、理想电流源的伏安特性1)1) 按图4-4(a)4-4(a)接线,毫安表接线使用电流插孔,接线,毫安表接线使用电流插孔,接线,毫安表接线使用电流插孔,R R L 使用1K Ω电位器。
电路实验4电压源与电流源的等效变换

实验四电压源与电流源的等效变换一、实验目的1.通过实验加深对电流源及其外特性的认识;2.掌握电流源和电压源进行等效变换的条件。
二、原理电压源是给外电路提供电压的电源,电压源分理想电压源和实际电压源。
理想电压源的输出电压为恒定值,不随外接负载变化。
理想电压源的电路模型及其伏安特性如图4-1所示。
图4-1实际电压源的输出电压随外接负载变化。
负载的阻值越大,电压源的输出电压越高,当负载的阻值达到无穷大时,实际电压源的输出电压达到最大值。
实际电压源可以用一个理想电压源与一个内阻的串联的电路模型表示。
其伏安特性曲线如果4-2所示。
图4-2电流源是除电压源以外的另一种形式的电源,它可以产生电流提供给外电路。
电流源可以分为理想电流源和实际电流源。
理想电流源可以向外电路提供一个恒值电流,不论外电路电阻的大小如何,其伏安特性曲线如图4-3所示。
图4-3实际电流源当其端电压增加时,通过外电路的电流并非恒定值而是减小。
端电压越高,电流下降得越多;相反,端电压越低通过外电路的电流越大,当端电压为零时,流过外电路的电流最大。
实际电流源的电路模型及伏安特性曲线如图4-4所示。
图4-4某些器件的伏安特性具有近似理想电流源的性质,如硅光电池,晶体三极管输出特性等。
本实验中的电流源是用晶体管来实现的。
图4-5给出了晶体三极管在共基极连接时,集电极电流和集电极与集极间的电压关系曲线。
图4-5一个实际的电源,就其外部特性而言,既可以看成是一个电压源,也可以看成是一个电流源。
其具体说明如下图所示。
图4-6三、实验仪器和器材1.直流可调电压0~30V板2.+15直流稳压电源和200mA恒流源3.电阻4.电位器5.三极管6.交直流电压电流表/电流表7.标准型导线8.标准型短接桥9.九孔实验方板四、实验内容及步骤1.测绘理想电压源的伏安特性曲线按图4-7所示连接电路。
将图中的电压源调至US=15V,负载电阻R为电阻箱。
调整电阻箱阻值,测量负载电阻R两端的电压U、流过负载电阻R的电流I。
实验四 电压源与电流源的等效变换

实验四 电压源与电流源的等效变换一、实验目的1.掌握电压源与电流源外特性的测试方法。
2.验证电压源与电流源等效变换的条件。
二、原理说明1.能向外电路输送定值电压的装置被称为电压源。
理想电压源的内阻为零,其输出电压值与流过它的电流的大小和方向无关,即不随负载电流而变;流过它的电流是由定值电压和外电路共同决定的。
它的外特性即伏安特性U =f(I)是一条平行于I 轴的直线。
而具有一定内阻值的非理想电压源,其端电压不再如理想电压源一样总是恒定值了,而是随负载电流的增加而有所下降。
一个质量高的直流稳压电源,具有很小的内阻,故在一定的电流范围内,可将它视为一个理想的电压源。
非理想电压源的电路模型是由理想电压源Us 和内阻Rs 串联构成的,如图4-1所示,其输出电压U =Us —I Rs2.能向外电路输送定值电流的装置被称为电流源。
理想电流源的内阻为无穷大,其输出电流与其端电压无关,即不随负载电压而变;电流源两端的电压值是由定值电流Is 和外电路共同决定的。
它的伏安特性I =f(U)是一条平行于U 轴的直线。
对于非理想的电流源,因其内阻值不是无穷大,输出电流不再是恒定值,而是随负载端电压的增加有所下降。
一个质量高的恒流源其内阻值做得很大,在一定的电压范围内,可将它视为一个理想的电流源。
非理想电流源的电路模型是由理想电流源Is 和内阻Rs 并联构成的,如图4-2 所示,其输出电流I=LR Rs IsRs .3.一个实际的电源,就其外部特性而言,即可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个理想的电压源Us 与一个电阻Ro 相串联的组合来表示;若视为电流源,则可用一个理想电流源Is 与一电导g o 相并联的给合来表示,若它们向同样大小的负载提供同样大小的电流和端电压,则称这两个电源是等效的,即具有相同的外特性。
一个非理想电压源与一个非理想电流源等效变换的条件为Is =Us / Ro , g o =1 / Ro 或 Us =Is / g o , Ro =1 / g o 序号名 称型号与规格数量备 注图4-1 电压源的电路模型 图4-2电流源的电路模型1 可调直流稳压电源0-30V 1 RTDG-12 可调直流恒流源0-500mA 1 RTDG-13 直流数字电压表 1 RTT014 直流数字毫安表 1 RTT015 万用表MF-30 1 另备6 电阻器51Ω,1kΩ,200Ω各1 RTDG-087 可调电阻箱0-99999.9Ω 1 RTDG-08四、实验内容与步骤1.测定直流稳压电源(理想)与非理想电压源的外特性(1)按图4-1接线,令内阻Rs=0,直流稳压电源Es作为理想电压源,调Us=6V,改变负载电阻R L,令其阻值由大至小变化,将电压表和电流表的读数记入表4-1中。
等效变换实验报告

一、实验目的1. 理解并掌握等效变换的基本概念和原理。
2. 通过实际操作,验证电压源与电流源等效变换的条件。
3. 学会使用实验仪器进行电源外特性的测试。
4. 增强对电路分析方法的理解和应用能力。
二、实验原理等效变换是指在电路分析中,将复杂的电路简化为等效的简单电路,使得简化后的电路与原电路在某些方面具有相同的电性能。
常见的等效变换包括电压源与内阻的等效电压源、电流源与内阻的等效电流源等。
电压源与电流源的等效变换条件如下:- 电压源(Us)与内阻(Rs)串联可以等效为一个电流源(Is)与内阻(Rs)并联。
- 电流源(Is)与内阻(Rs)并联可以等效为一个电压源(Us)与内阻(Rs)串联。
等效变换的公式为:- 对于电压源与内阻的等效变换:Is = Us / Rs- 对于电流源与内阻的等效变换:Us = Is Rs三、实验器材1. 直流稳压电源1台2. 直流恒流源1台3. 直流数字电压表1块4. 直流数字电流表1块5. 可调电阻箱1个6. 电阻器若干7. 电线若干四、实验步骤1. 按照实验电路图连接电路,将直流稳压电源或直流恒流源作为电源接入电路。
2. 使用电压表和电流表测量电路中各个元件的电压和电流值。
3. 根据测得的电压和电流值,计算电路的等效电压源或等效电流源。
4. 将计算得到的等效电压源或等效电流源接入电路,再次测量电路中各个元件的电压和电流值。
5. 比较两次测量结果,验证等效变换的正确性。
五、实验数据及结果分析1. 实验一:电压源与内阻的等效变换- 实验电路:将直流稳压电源接入电路,测量电路中各个元件的电压和电流值。
- 等效变换:根据测得的电压和电流值,计算等效电流源。
- 实验结果:将计算得到的等效电流源接入电路,测量电路中各个元件的电压和电流值,与原电路结果基本一致。
2. 实验二:电流源与内阻的等效变换- 实验电路:将直流恒流源接入电路,测量电路中各个元件的电压和电流值。
- 等效变换:根据测得的电压和电流值,计算等效电压源。
电压源和电流源的等效变换

1.5电压源和电流源的等效变换实际使用的电源,按其外特性,可分为电压源和电流源。
当一个电压源和一个电流源能够为同一个负载提供相同的电压、电流和功率时,这两个电源对该负载来说是等效的,可以互相置换,这种置换称为等效变换。
下面来讨论电压源和电流源的等效变换。
1.5.1 电压源在电路分析课程中,将能够向外电路提供电压的器件称为电压源。
如,电池,发电机等均是电压源。
在物理学中,电池表示成电动势E和内阻R相串联的电路模型,电池是一个典型的电压源,所以,电压源也可表示成电动势和内阻相串联的电路模型。
为了利用KVL的方便,对电压源特性进行标定时,通常不使用电动势E,而改用电压源所能输出的恒压值US,如图1-30(a)所示虚线框内部的电路。
图中电压源旁的箭头为US的参考方向。
注意: US 和E是不同性质的两个物理量,US是描述电压源所能输出的恒值电压,该值的大小与E相等,设定的参考方向与E相反。
当电压源与负载电阻RL相连时,根据KVL可得描述电压源外特性的函数式。
描述理想化电压源外特性的函数式是(1-57)由式1-57可见,理想化电压源的外特性曲线是直线,如图1-30(b)所示,图1-30(b)又称为电压源伏(U)-安(A)特性曲线。
图1-30(b)纵轴上的点,为电压源输出电流等于0的情况,相当于电压源处在开路的状态下。
当电压源开路时,电压源的输出电压U就等于US ,所以,US的值等于电压源的开路电压。
图1=30(b)横轴上的点,为电压源输出电压等于0的情况,相当于电压源处在短路的状态下(实际上这是不允许的),电压源输出电流为IS ,所以,IS称为短路电流。
计算短路电流的表达式为(1-58)U=f(I)曲线的斜率为R0,R越小,斜率越小,直线越平坦。
当R=0时,电源外特性曲线是一条平行与I轴的直线。
具有这种外特性曲线的电压源输出电压保持恒定值US,这种电压源称为理想电压源,简称恒压源。
将图1-30(a)虚线框内部电路的电阻R去掉,剩下的电路就是恒压源电路的模型。
实验四电压源与电流源的等效变换

实验四电压源与电流源的等效变换一、实验目的1. 了解电路等效原理;2. 学会电路变换的方法;4. 探究电路等效变化对电路参数的影响。
二、实验原理电路等效原理是指在电路中,若有两个电路具有相同的端点电压和电流,则这两个电路等效。
电路等效原理使得电路分析的计算变得更加简洁、直观。
电路变换是指通过等效变换,将电路简化为更为简单的电路,从而使得电路分析更加简单和直观。
电路变换的方法主要有:(1)串、并联变换在串联电路中,把两个元件并联起来等效,即两个电阻并联后其电阻之和等于两者串联之和的倒数,即$${{1}\over{R_{eq}}}={{1}\over{R_1}}+{{1}\over{R_2}}$$$$R_{eq}=R_1+R_2$$(2)电压、电流源相互转换电压源可以理解为将电荷推动到某个位置的装置,而电流源可以理解为将电荷注入到电路中的装置。
因此,电压源和电流源可以通过等效变换来相互转换。
将电压源等效为电流源,其电流为$$I={{U}\over{R}}$$$$U=IR$$三、实验内容(1)将如图1所示的两个电阻串联,求其等效电阻。
(3)搭建如图3所示的串、并联电路,在不改变总电阻的条件下,将其等效为只含一个电阻的电路。
(2)将如图5所示的电流源等效为电压源。
四、实验器材数字万用表、电阻箱、实验台、导线等。
五、实验步骤(1)按照图1,搭建两个电阻串联的电路,分别测量两个电阻的值。
(2)通过串联电路等效公式计算出等效电阻。
(6)通过等效变换,将其等效为只含一个电阻的电路。
(5)按照图6,搭建电路,将其中的电压源等效为电流源,并测量电流的值。
六、实验数据处理(1)电路1中的电阻为10 Ω,电路2中的电阻为15 Ω,故两个电阻串联后的等效电阻为$$R=10+15=25 Ω$$化简得因此,将具有等效作用的两个电阻并联后,电路中的电阻为${{150}\over{7}} Ω$。
(1)电压源的电压为10 V,电阻R的值为10 Ω,故$$U=IR=1\times 15=15 V$$七、误差分析在实际测量时,由于电路和器材的一些不可避免的误差,实验结果可能与理论值存在一些差异。
电路分析-电压源和电流源等效变换

f
Rf
d Pf d Rf
0
时,Rf获最大功率
得 Rf = Ri
U2 Pmax 4Ri
直流电路最大功率传输定理
例2 直流电桥电路
R1
R2
I
R3
R4
US
当
R1 R3 R2 R4
即 R1R4=R2R3 时,I = 0 称R1R4=R2R3为电桥平衡条件。
利用上述关系式,可测量电阻。
二、理想电流源的串、并联 并联: 可等效成一个理想电流源 i S( 注意参考方向).
iS1
iSk …
iSn
iS
n
iS iSk
1
串联: 电流相同的理想电流源才能串联,并且每个电
流源的端电压不能确定。
例1
uS
iS
uS
例2
uS
iS
iS
电压源和电流源的等效变换
一、实际电压源 实际电压源,当它向外电路提供电流时,它的
i
+
uS _
+
u
iS
i +
Ri
_
Gi u _
u = uS – Ri i i = uS/Ri – u/Ri
i = iS – Gi u
等效的条件 iS= uS /Ri , Gi = 1/Ri
由电压源变换为电流源: i
Hale Waihona Puke +uS _
+ 转换
u
Ri
_
由电流源变换为电压源:
i
iS
+
转换
Gi u _
i
iS
+
Gi u _
端电压总是小于其电动势,电流越大端电压越小。
实验四 电压源与电流源的等效变换
实验4电压源与电流源及其等效转换1实验目的(1)了解理想电流源与理想电压源的外特性。
(2)验证电压源与电流源互相进行等效转换的条件。
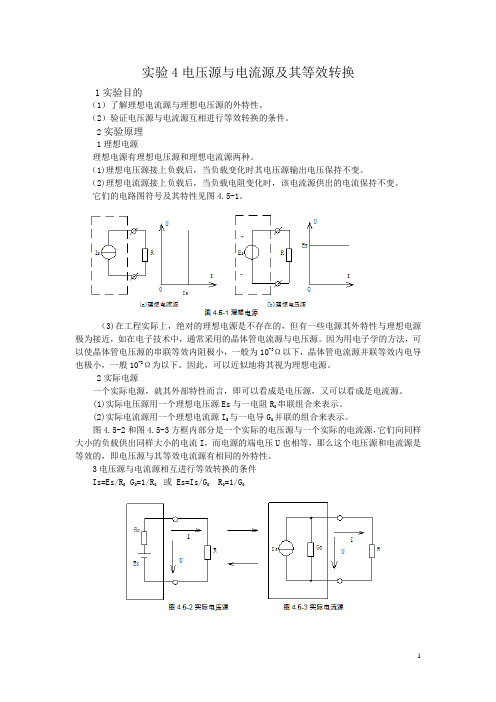
2实验原理1理想电源理想电源有理想电压源和理想电流源两种。
(1)理想电压源接上负载后,当负载变化时其电压源输出电压保持不变。
(2)理想电流源接上负载后,当负载电阻变化时,该电流源供出的电流保持不变。
它们的电路图符号及其特性见图4.5-1。
(3)在工程实际上,绝对的理想电源是不存在的,但有一些电源其外特性与理想电源极为接近,如在电子技术中,通常采用的晶体管电流源与电压源。
因为用电子学的方法,可以使晶体管电压源的串联等效内阻极小,一般为10-3Ω以下,晶体管电流源并联等效内电导也极小,一般10-3Ω为以下。
因此,可以近似地将其视为理想电源。
2实际电源一个实际电源,就其外部特性而言,即可以看成是电压源,又可以看成是电流源。
(1)实际电压源用一个理想电压源Es与一电阻R0串联组合来表示。
(2)实际电流源用一个理想电流源I S与一电导G0并联的组合来表示。
图4.5-2和图4.5-3方框内部分是一个实际的电压源与一个实际的电流源,它们向同样大小的负载供出同样大小的电流I,而电源的端电压U也相等,那么这个电压源和电流源是等效的,即电压源与其等效电流源有相同的外特性。
3电压源与电流源相互进行等效转换的条件Is=Es/R0 G0=1/R0 或 Es=Is/G0 R0=1/G04实验内容及步骤1)测量理想电流源的外特性当负载电阻在一定的范围内变化时(注意必须使电流源两端的电压不超出额定值),电流基本不变,即可将其视为理想电流源。
(1)将一可变电阻R接至稳流源的输出端上,串联接入直流电流表,并联接入直流电压表,即接成图4.5-4的实验电路。
(2)首先置可变电阻R=0,调节直流电流源,使其输出电流I=50mA,测出此时电流源的端电压U和输出电流I记入表4.5-1。
(3)改变电阻电阻R,每改变R值记下U和I,但应使Rmax*I≤20V,此时数据记入表4.5-1,即可得至理想电流源的外特性。
简述电压源与电流源的等效变换方法

电压源与电流源是电路中常见的两种基本元件,它们分别以恒定的电压和恒定的电流来驱动电路。
在电路分析和设计中,经常需要将电压源转换为等效的电流源,或将电流源转换为等效的电压源,以便更方便地进行电路分析和计算。
下面将分别介绍电压源与电流源的等效变换方法。
一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。
根据欧姆定律,电流等于电压除以电阻,即I=V/R。
我们可以将电压源转换为等效的电流源,通过在电压源的正负端并联一个等效电阻,使得该电阻上的电流等于电压源的电压除以电阻值。
2. 转换公式电压源转换为等效电流源的公式为:I=V/R,其中I为等效电流源的输出电流,V为电压源的电压,R为等效电流源的电阻。
3. 举例说明假设有一个5V的电压源,需要将其转换为等效的电流源。
如果我们希望等效电流源的输出电流为1A,那么根据公式I=V/R,可得等效电阻R=V/I=5Ω。
我们可以在电压源的正负端并联一个5Ω的电阻,即可将电压源转换为等效的电流源。
二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。
根据欧姆定律,电压等于电流乘以电阻,即V=IR。
我们可以将电流源转换为等效的电压源,通过在电流源的两端串联一个等效电压源,使得该电压等于电流源的电流乘以电阻值。
2. 转换公式电流源转换为等效电压源的公式为:V=IR,其中V为等效电压源的输出电压,I为电流源的电流,R为等效电压源的电阻。
3. 举例说明假设有一个2A的电流源,需要将其转换为等效的电压源。
如果我们希望等效电压源的输出电压为10V,那么根据公式V=IR,可得等效电阻R=V/I=5Ω。
我们可以在电流源的两端串联一个10V的电压源,并在其正负端串联一个5Ω的电阻,即可将电流源转换为等效的电压源。
电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。
通过合理应用这些方法,可以使得电路分析更加简便和直观,为电路设计提供重要的参考依据。
电压源与电流源的等效变换

一、电压源
3、电压源的串联和并联
1) 电压源的串联
接法: E1=2V;E2=5V;E3=10V, E=? E
E1
E2
E3
总电源电动势E:
E的方向:与
如图可知:E = - E1 - E2 + E3
n
即:
E Ek
E3相同
k 1
表明: 串联电源总电动势为各分电源电动势的代
数和。可用一个电动势E等效(代替)。
(c)
注意事项:
① 电压源和电流源的等效关系只对外电路而言,
对电源内部则是不等效的。
例:当RL= 时,电压源的内阻 r 中无功率损耗, 而电流源的内阻 r 中有功率损耗。
② 等效变换时,两电源的参考方向要一一对应。
+
a
E
– r
IS
b
a–
a
E
r
+ r
IS
b
b
a r
b
③ 理想电压源与理想电流源之间无等效关系。
课堂讨论: 求下列各电路的等效电源
2 +
3 5V–
+a
U 2 5A
(a)
解:
2 + 5V –
(a)
a + U 5A b
+a 3 U
b
(b)a + 3 Ub (b)+a
2 +
+ 2V-
5V-
U b
(c)
+a + 5V U –
b (c)
复习与回顾
一、电压源的串联
1、理想电压源的串联—总电动势等于各分电动势的
电流恒定,电压随负载变化。
电路分析基础实验报告-电压源、电流源及其电源等效变换

XXX 实验室学生实验报告课程名称电路分析基础实验学院XXX专业XXX班级XXX学号XXX姓名XXX辅导教师XXX实验时间:X 年X 月X 日预 习 实 验 报 告1、 实验名称电压源、电流源及其电源等效变换2、实验目的1.掌握建立电源模型的方法。
2.掌握电源外特性的测试方法。
3.加深对电压源和电流源特性的理解。
4.研究电源模型等效变换的条件。
3、实验内容1.电压源和电流源电压源具有端电压保持恒定不变,而输出电流的大小由负载决定的特性。
其外特性,即端电压U 与输出电流I 的关系U = f (I ) 是一条平行于I轴的直线。
实验中使用的恒压源在规定的电流范围内,具有很小的内阻,可以将它视为一个电压源。
电流源具有输出电流保持恒定不变,而端电压的大小由负载决定的特性。
其外特性,即输出电流I 与端电压U 的关系I = f (U ) 是一条平行于U 轴的直线。
实验中使用的恒流源在规定的电流范围内,具有极大的内阻,可以将它视为一个电流源。
2.实际电压源和实际电流源实际上任何电源内部都存在电阻,通常称为内阻。
因而,实际电压源可以用一个内阻R S 和电压源U S 串联表示,其端电压U 随输出电流I 增大而降低。
在实验中,可以用一个小阻值的电阻与恒压源相串联来模拟一个实际电压源。
实际电流源是用一个内阻R S 和电流源I S 并联表示,其输出电流I 随端电压U 增大而减小。
在实验中,可以用一个大阻值的电阻与恒流源相并联来模拟一个实际电流源。
3.实际电压源和实际电流源的等效互换一个实际的电源,就其外部特性而言,既可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个电压源U s 与一个电阻R S 相串联表示;若视为电流源,则可用一个电流源I S 与一个电阻R S 相并联来表示。
若它们向同样大小的负载供出同样大小的电流和端电压,则称这两个电源是等效的,即具有相同的外特性。
实际电压源与实际电流源等效变换的条件为: (1)取实际电压源与实际电流源的内阻均为R S ;(2)已知实际电压源的参数为U s 和R S ,则实际电流源的参数为SS S R UI =和R S ,若已知实际电流源的参数为I s 和R S ,则实际电压源的参数为S S S R I U =和R S 。
参考资料电压源与电流源等效变换实验

(2) 电压表的接线, 一般使用表笔,把红 表笔接至电压表的 “ +” 端 , 黑 表 笔 接 至电压表的“-”端, 测量时将红表笔接至 被测电压的正极,黑 表笔接至负极;
(3) 根据被测电压的 大小,选择适当的电 压表量程,测量中尽 量使指针偏转在2/3 量程以上。
17
电路板
18
电阻箱
19
思考题的参考答案
如晶体三极管。晶体三极管共基极连接,当UBC在一定范围内变化时,集电极电流IC近 乎恒值,可将其视为理想电流源。
• 实际的电源可以用一个理想电流源和一个电阻并联的模型来表示。
I I
I
I’
I
R
IS
IS
R0
IS
IS
R
0
U
理想电流源
0
U
实际电流源
4
• 三、电源的等效变换
• 如果两种电源的参数满足:R0=R0’ E/R0 =Is 则电压源与电流源可以互相转换,而对 外电路不发生任何影响。见图
13
14
晶体管稳压电源
15
直流电流表的使用
(1)应将直流电流表 串联在待测电流的 支路中;
(2) 接线时,必须使 电流从电流表的“+” 端流入,“-”端流 出,不得反接;
(3) 根据被测电流的 大小,选择适当的 电流表量限,测量 中尽量使指针偏转 在;2/3量限以上。
电压源与电流源及其等效变换

一、电压源与电流源及其等效变换理想的电压源就是串联内阻为零的恒压源,理想的电流源就是并联内阻为∞的恒流源。
理想的情况在实践中并不存在,因此用电压源或电流源表示都是可以的。
在什么场合使用电压源或电流源,视需要和方便而定,并没有固定地说必须用哪一种。
3、电压源与电流源的等效变换变换的原则:不论是使用电压源模型还是电流源模型,在负载上电压、电流都应该完全相同。
电压源与电流源之间作等效变换时,传统的推导过程如下:Ua=E -Ia*Ra ,Ub=(Is-Ib)*Rb由于Ia=Ib ,Ua=Ub ,所以,E -Ia*Ra=(Is-Ib)*Rb ,展开与替换后即:E -Ia*Ra=Is*Rb -Ia*Rb推导至此,传统方法就认为上面等式左右两边的分项各自相等,即E= Is*Rb ,Ia*Ra= Ia*Rb ,进而Ra=Rb 。
这应该很牵强,怎么能说A —B=C —D ,就一定会有A=B ,C=D ?我使用一种更直观、更好理解的方式推导如下:负载上电压、电流完全相同,实际上就是两种模型下的电流-电压曲线完全相同(重叠)。
电压源与电流源模型下的电流-电压曲线如下图所示:由于Ua=Ub ,Ia=Ib ,所以①、E= Is*Rb ;②、Is=E/Ra (亦即E=Is*Ra )。
综合①和②,由电源源转换为电流源时:Rb=Ra ,Is= E/Ra由电流源转换为电压源时:Ra=Rb ,E= Is*Rb负载 RL + _ 负载 RL + _ 0 电流 电压 电压源模型的电流-电压曲线: Ua=E -I*Ra Ia=0,Ua=E Ia=E/Ra ,Ua=0 0 电流 电压 电流源模型的电流-电压曲线: Ub=(Is-Ib)*Rb Ib=0,Ub=Is*RbIb=Is ,Ub=0。
电压源与电流源的等效变换实验报告总结

电压源与电流源的等效变换实验报告总结电压源与电流源的等效变换实验报告总结电压源与电流源的等效变换实验报告总结篇一:实验一电压源与电流源的等效变换实验一电压源与电流源的等效变换学号: 132021520 姓名:XXX 班级:13通信X班指导老师:X老师实验组号:5 实验地点:1实203 实验日期:201X年5月18日一、实验目的和要求:1(掌握电源外特性的测试方法;2(验证电压源与电流源等效变换的条件。
二、实验仪器:一、可调直流稳压电源 1台二、直流恒流源 1台三、直流数字电压表 1只四、直流数字毫安表 1只五、电阻器 1个三、实验原理:1、一个直流稳压电源在一定的电流范围内,具有很小的内阻,故在实用中,常将它视为一个理想的电压源,即其输出电压不随负载电流而变,其外特性,即其伏安特性U=f(I)是一条平行于I轴的直线。
一个恒流源在使用中,在一定的电压范围内,可视为一个理想的电流源,即其输出电流不随负载的改变而改变。
2(一个实际的电压源(或电流源),其端电压(或输出电压)不可能不随负载而变,因它具有一定的内组值。
故在实验中,用一个小阻值的电阻(或大电阻)与稳压源(或恒流源)相串联(或并联)来模拟一个电压源(或电流源)的情况。
3(一个实际的电源,就其外部特性而言,既可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个理想的电压源ES与一个电导g相并联的组合来表示,若它们向同样大小的负载供出同样大小的电流和端电压,则称这两个电源是等效的,即具有相同的外特性。
一个电压源与一个电流源等效变换条件为第 1 页共 4 页Is? 或 Es1 g= RR Es? 如下图6-1所示:Is1 R= g0g0四、实验内容:1(测定电压源的外特性(1)按图6-2(a)接线,ES为+6V直流稳压电源,调节R,令其阻值由大至小变化,记录两表的读数图6-2(a) 图6-2(b)(2)按图6-2(b)接线,虚线框可模拟为一个实际的电压源,调节R阻值,记录两表读数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 电压源与电流源的等效变换
一、实验目的
1.掌握电压源与电流源外特性的测试方法。
2.验证电压源与电流源等效变换的条件。
二、原理说明
1.能向外电路输送定值电压的装置被称为电压源。
理想电压源的内阻为零,其输出电压值与流过它的电流的大小和方向无关,即不随负载电流而变;流过它的电流是由定值电压和外电路共同决定的。
它的外特性即伏安特性U =f(I)是一条平行于I 轴的直线。
而具有一定内阻值的非理想电压源,其端电压不再如理想电压源一样总是恒定值了,而是随负载电流的增加而有所下降。
一个质量高的直流稳压电源,具有很小的内阻,故在一定的电流范围内,可将它视为一个理想的电压源。
非理想电压源的电路模型是由理想电压源Us 和内阻Rs 串联构成的,如图4-1所示,其输出电压
U =Us —I Rs
2.能向外电路输送定值电流的装置被称为电流源。
理想电流源的内阻为无穷大,其输出电流与其端电压无关,即不随负载电压而变;电流源两端的电压值是由定值电流Is 和外电路共同决定的。
它的伏安特性I =f(U)是一条平行于U 轴的直线。
对于非理想的电流源,因其内阻值不是无穷大,输出电
流不再是恒定值,而是随负载端电压的增加
有所下降。
一个质量高的恒流源其内阻值做得很大,在一定的电压范围内,可将它视为一个理想的电流源。
非理想电流源的电路模型是由理想电流源Is 和内阻Rs 并联构成的,如图4-2 所示,其输出电流
I=
L
R Rs Is
Rs .
3.一个实际的电源,就其外部特性而言,即可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个理想的电压源Us 与一个电阻Ro 相串联的组
合来表示;若视为电流源,则可用一个理想电流源Is 与一电导g o 相并联的给合来表示,
若
它们向同样大小的负载提供同样大小的电流和端电压,则称这两个电源是等效的,即具
图4-1 电压源的电路模型 图4-2电流源的电路模型
有相同的外特性。
一个非理想电压源与一个非理想电流源等效变换的条件为
Is =Us / Ro, g o=1 / Ro
或 Us =Is / g o, Ro=1 / g o
序号名称型号与规格数量备注
1可调直流稳压电源0-30V1RTDG-1
2可调直流恒流源0-500mA1RTDG-1
3直流数字电压表1RTT01
4直流数字毫安表1RTT01
5万用表MF-301另备
6电阻器51Ω,1kΩ,200Ω各 1RTDG-08
7可调电阻箱0-99999.9Ω1RTDG-08
1.测定直流稳压电源(理想)与非理想电压源的外特性
(1)按图4-1接线,令内阻Rs=0,直流稳压电源Es作为理想电压源,调Us=6V,改变负载电阻R L,令其阻值由大至小变化,将电压表和电流表的读数记入表4-1中。
(2)按图4-1接线,选51Ω电阻器作为内阻Rs与直流稳压电源Es串联接入电路,模拟一个实际的电压源,调节负载电阻R L由大至小变化,读取电压表和电流表的数据,并记入表4-1中。
负载
内阻
R L(Ω)∞200015001000800500300200
Rs=0U(v) I(Ma)
Rs=51ΩU’(v) I’(mA)
2.测定电流源的外特性
按图4-2接线,Is为直流恒流源,调节其输出为5mA,令Rs分别为1KΩ和∞,调节可变电阻箱R L(从0至5000Ω),测出这两种情况下的电压表和电流表的读数,并记入表4-2中。
表4-2 电流源的外特性
负载
内阻
R L(Ω)0200400600800100020005000
R s=1KΩI’(Ma) U’(v)
Rs=∞I(mA) U(v)
3.测定电源等效变换的条件
图4-3 电源等效变换
按图4-3线路接线,首先读取7-3(a)线路两表的读数,然后调节7-3(b)线路中恒流源Is(取R’s=Rs),令两表的读数与7-3(a)时的数值相等,记录Is之值,验证等效变换条件的正确性。
实际电压源实际电流源
R s(Ω)R L(Ω)U(V)I(mA)Us(V)R’s(
Ω)
R’L
(Ω)
I’(mA
)
U’(V)Is(
Ω)
五、实验注意事项
1.在测电压源外特性时,不要忘记测空载时的电压值,改变负载电阻时,不可使电压源短路。
2.在测电流源外特性时,不要忘记测短路时的电流值,改变负载电阻时,不可使电流源开路。
3.换接线路时,必须关闭电源开关。
4.直流仪表的接入应注意极性与量程。
六、预习思考题
1.直流稳压电源的输出端为什么不允许短路?直流恒流源的输出端为什么不允许开路?
2.电压源与电流源的外特性为什么呈下降变化趋势,稳压源和恒流源的输出在任何负载下是否保持恒值?
七、实验报告
1.根据实验数据绘出电源的四条外特性曲线,并总结、归纳各类电源的特性。
2.从实验结果,验证电源等效变换的条件。
3.本次实验的收获与体会。
如有侵权请联系告知删除,感谢你们的配合!
如有侵权请联系告知删除,感谢你们的配合!。
