不规则四边形面积计算方式
不规则图形的面积计算
不规则图形的面积计算在图形面积计算时,经常会到一些无法直接求或不规则的图形,这时我们需要转换解题思维,根据图形的基本关系,运用分解、平移、旋转、割补、添辅助线等方法来思考。
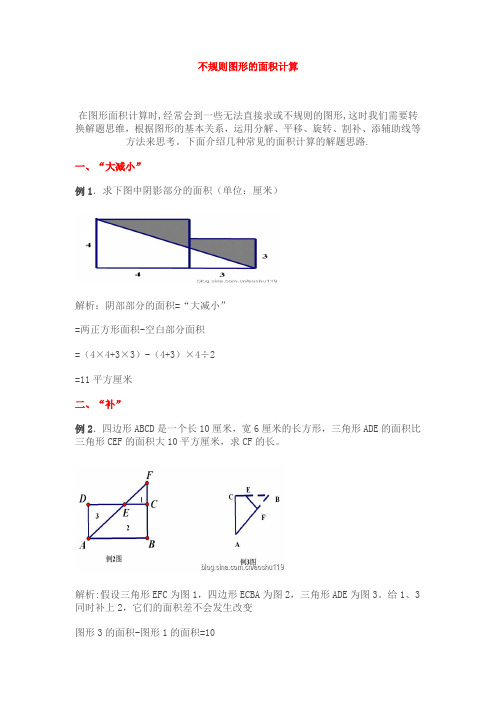
下面介绍几种常见的面积计算的解题思路.一、“大减小”例1.求下图中阴影部分的面积(单位:厘米)解析:阴部部分的面积=“大减小”=两正方形面积-空白部分面积=(4×4+3×3)-(4+3)×4÷2=11平方厘米二、“补”例2.四边形ABCD是一个长10厘米,宽6厘米的长方形,三角形ADE的面积比三角形CEF的面积大10平方厘米,求CF的长。
解析:假设三角形EFC为图1,四边形ECBA为图2,三角形ADE为图3。
给1、3同时补上2,它们的面积差不会发生改变图形3的面积-图形1的面积=10(图形3+图形2)-(图形1+图形2)=即长方形ABCD的面积-三角形ABF的面积=10那么,三角形ABF的面积=60-10=50=AB×BF÷2可算出 BF=10厘米,所以CF=10-6=4厘米例3.如图,四边形ACEF中,角ACE=角EFA=90°,角CAF=45°,AC=8厘米,EF=2厘米,求四边形ACEF的面积解析:分别延长AF、CE,交于B点在三角形ABC中,很明显,它是个等腰直角三角形,面积=8×8÷2=32平方厘米在三角形EFB中,很明显,它也是一个等腰直角三角形,面积=2×2÷2=2平方厘米所以,S四边形ACEF=S△ABC-S△EFB=32-2=30平方厘米三、“移”例4.如图所示(1图),四边形ABCD是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求路的面积。
解析:小路是曲折的,不规则图形,可用采用“移”的思路来解决把图1下面空白部分往上、往左移,使它与上面空白部分连接在一起,就成了图2中的空白部分,是一个长方形,长是20-2=18米,宽是14-2=12米,这个长方形的面积=18×12=216平方米,小路的面积=大长方形的面积-空白长方形的面积=20×14-216=64平方米例5.如图,AE=ED,AF=FC,已知三角形ABC的面积是100平方厘米,求阴影部分的面积解析:由于两阴影部分不在一起,我们可以考虑用“移”的思维把阴影变成一个整体。
任意四边形的面积公式

任意四边形的面积公式
四边形是形状较为常见的几何图形,它由四条线段构成,可以是正四边形(即所有的边都相等),也可以是不规则四边形(即边的长度不相等),下面主要讨论正四边形。
正四边形的面积公式如下:
S=a^2·cot(π/4)
其中,a表示正四边形的边长,S表示正四边形的面积,cot(π/4)表示正四边形的倾斜角的余切值。
上式中,余切值是通过计算正四边形倾斜角的正切值来求得的,由正四边形特性可知,正四边形倾斜角的角度为45度,因此上式中,cot (π/4)的值为1,即cot(π/4)=1
因此,正四边形的面积公式可以简化为:
S=a^2
即,正四边形的面积等于它的边长平方。
另外,由于近似原理,不规则四边形的面积也可以通过正四边形的面积公式求得,即把不规则四边形的面积看做由几个完全相等或者近乎相等的正四边形组成,把这些正四边形的面积加起来就可以求出不规则四边形的面积,即:
S=S1+S2+S3+…
s1,s2,s3…分别表示不规则四边形中各个正四边形的面积,也就是每个正四边形的边长平方。
以上就是正四边形及不规则四边形的面积公式。
不规则四边形的面积计算公式

不规则四边形的面积计算公式
不规则四边形的面积计算公式可以分为两种情况进行计算:根据边长和对角线
的长度,以及根据顶点坐标的方法。
第一种情况,当已知不规则四边形的边长和对角线的长度时,可以使用以下公
式计算面积:
面积= 0.5 * d1 * d2 * sinθ
其中,d1和d2分别是不规则四边形的对角线的长度,θ是对角线d1和d2之
间的夹角,sin表示求正弦值。
第二种情况,当已知不规则四边形的顶点坐标时,可以使用以下公式计算面积:
面积 = 0.5 * |(x1y2 + x2y3 + ... + xn-1yn + xny1) - (x2y1 + x3y2 + ... + xnyn-1 +
x1yn)|
其中,(x1, y1), (x2, y2), ..., (xn, yn)是不规则四边形的顶点坐标,| | 表示取绝对值。
需要注意的是,以上两种公式适用于不规则四边形,即四边形的边长和角度均
不相等的情况。
如果是规则四边形,即四边形的边长和角度均相等,则可以使用其他简化的公式计算面积。
希望以上解答对您有帮助,如果还有其他问题,请随时向我提问。
不规则四边形的面积计算公式

不规则四边形的面积计算公式【原创版】目录1.引言:介绍不规则四边形的概念和计算面积的必要性2.公式推导:详述不规则四边形面积计算公式的推导过程3.公式应用:介绍如何使用公式计算不规则四边形的面积4.结论:总结不规则四边形面积计算公式的重要性和应用场景正文一、引言不规则四边形是指四边形的四条边长和四个内角不都是直角,或者虽然四个内角都是直角,但四条边长不固定,无法通过简单的几何变换得到矩形或平行四边形的四边形。
在实际生活中,我们常常会遇到需要计算不规则四边形面积的情况,如土地测绘、城市规划等领域。
因此,探讨不规则四边形的面积计算公式具有重要的实际意义。
二、公式推导为了计算不规则四边形的面积,我们可以将其分割成无数个小三角形,然后将这些小三角形的面积求和。
设不规则四边形 ABCD 的顶点 A、B、C、D 的坐标分别为 A(x1, y1)、B(x2, y1)、C(x2, y2) 和 D(x1, y2),那么可以将四边形分割成两个三角形 ABC 和 ACD。
三角形 ABC 的面积计算公式为:S1 = 0.5 * |x1 * (y2 - y1) + x2 * (y1 - y2) + y1 * (x2 - x1) - y2 * (x1 - x2)|,其中|...|表示绝对值。
同理,三角形 ACD 的面积计算公式为:S2 = 0.5 * |x1 * (y2 - y1) - x2 * (y1 - y2) + y1 * (x2 + x1) - y2 * (x1 + x2)|。
因此,不规则四边形 ABCD 的面积计算公式为:S = S1 + S2 = 0.5 *|x1 * (y2 - y1) + x2 * (y1 - y2) + y1 * (x2 - x1) - y2 * (x1 - x2)| + 0.5 * |x1 * (y2 - y1) - x2 * (y1 - y2) + y1 * (x2 + x1) - y2 * (x1 + x2)|。
求不规则四边形的面积

面积类:求不规则四边形的面积:求不规则四边形的面积.txt题目:如图,腰长为6cm的等腰Rt△FED和腰长为9cm的等腰Rt△ABC部分重叠在一起,且BE=1cm,求阴影部分的面积。
逐步提示:1、观察图形可知,阴影面积为一不规则的多边形面积,要求此面积,考虑常用的求不规则多边形面积的方法:割补法、和差法、等积代换法等等,看看哪种方法更为合适。
2、本题适用和差法,我们已经知道BE,根据等腰直角三角形的性质可容易求得CK、BD、AD的值,求得这些值,你能求得哪些三角形的面积呢?和阴影面积有关系的三角形有哪些?3、如果能求得△ABC的面积,再求得△ADG和△CHK的面积,那么阴影面积就可以求得,△ADG的面积相信你可以容易求得,看看△CHK的面积怎样求?4、已知∠C=∠A =∠F =45°,你能否推出∠CHK=90°呢?如果可以得出△CHK是等腰直角三角形,那么通过CK=8即可求出它的腰了,那么面积也可得出了,至此阴影的面积你可以求得了吧!解后反思:1、此题属于求解不规则多边形的面积的题目。
观察图形可知,我们可以求出和阴影面积有关的三角形的面积,从而能够利用和差法方便求出原不规则多边形的面积。
2、求面积有以下几种方法:(1)补形法:计算某个图形的面积,如果它的面积难以直接求出,那么就设法把它补成面积较容易计算的图形;(2)分割法:把应求部分的图形分割成若干份规则的图形,求它们的面积和;(3)求差法:若图形A由图形B和图形C组成,且其中图形B为阴影部分,则B的面积=A的面积-C的面积。
本题就是采用方法(3),希望同学们深刻理解。
巩固练习:LMZT4-P134-8如图,在长方形ABCD中,AB=3,BC=2,E为BC的中点,F在AB上,且BF=2AF,则四边形AFEC的面积为________.。
不规则四边形面积怎么算

不规则四边形面积怎么算
不规则四边形面积计算方式如下:
1、不规则四边形的面积,等于四边形不相邻两边中点的连线长乘以另两边的任一中点到该连线距离的2倍。
2、顺次连接任意四边形上的中点所得四边形叫中点四边形,中点四边形都是平行四边形。
菱形的中点四边形是矩形,矩形中点四边形是菱形,等腰梯形的中点四边形是菱形,正方形中点四边形就是正方形。
四边形的分类
四边形有正方形、矩形、平行四边形、菱形、梯形等等。
由不在同一直线上的不交叉的四条线段依次首尾相接围成的封闭的平面图
形或立体图形叫四边形。
由不在同一直线上的四条线段依次首尾相接围成的封闭的平面
图形或立体图形叫四边形,由凸四边形和凹四边形组成。
顺次连接任意四边形上的中点所得四边形叫中点四边形,中点四边形都是平行四边形。
菱形的中点四边形是矩形,矩形中点四边形是菱形,等腰梯形的中点四边形是菱形,正方形中点四边形就是正方形。
四边形有正方形、矩形、平行四边形、菱形、梯形等等。
不规则平行四边形面积公式

不规则平行四边形面积公式在咱们学习数学的这个大旅程中,不规则平行四边形可是个有点调皮的家伙。
那今天咱们就来好好聊聊它的面积公式。
先给大家讲讲我之前遇到的一件有趣的事儿。
有一次我去公园散步,看到园林工人正在规划一片草地。
那片草地的形状就像是一个不规则的平行四边形。
我好奇地凑过去问工人师傅,这怎么计算面积呀?师傅笑着说:“这可难不倒我们,虽然形状不规则,但咱们有办法!”咱们回到数学知识上来哈。
要计算不规则平行四边形的面积,常用的方法就是把它转化成我们熟悉的图形。
比如说,通过作辅助线,将其分割或者补成一个矩形或者三角形。
就拿分割来说吧,假如有一个不规则的平行四边形 ABCD,我们可以从 A 点向对边作一条垂线 AE,把它分割成一个直角三角形 ABE 和一个规则的平行四边形 AECD。
然后分别计算这两个图形的面积,再相加就得到了原来不规则平行四边形的面积。
那如果是补形呢?假设还是这个不规则平行四边形 ABCD,我们在它的一侧补上一个三角形,使得整体变成一个矩形。
然后用矩形的面积减去补上的三角形的面积,也能得出不规则平行四边形的面积。
在实际解题的时候,大家可一定要仔细观察图形的特点,选择最合适的方法。
别着急,多思考,就像我们解决生活中的难题一样,耐心总会有办法的。
再举个例子吧,比如说有个不规则平行四边形,它的两条邻边分别是 5 厘米和 8 厘米,夹角是 60 度。
这时候我们就可以过一个顶点作高,利用三角函数求出高的长度,然后用底乘以高就能算出面积啦。
大家在计算面积的时候,可别马虎哟。
一定要把长度单位搞清楚,面积单位可别弄错啦。
而且要认真计算每一步,不然就像盖房子地基没打好,后面可就全乱套了。
其实呀,数学中的这些知识就像我们生活中的工具,学会了就能解决好多问题。
就像那个园林工人师傅,他们用数学知识把公园规划得美美的。
我们学会了不规则平行四边形的面积公式,也能在很多地方派上用场呢。
总之,不规则平行四边形的面积计算虽然有点小挑战,但只要我们掌握了方法,多练习,就一定能轻松应对,让数学成为我们的好朋友,帮助我们解决更多的难题!。
四边形面积求法

四边形面积求法四边形作为几何学中最基本的图形之一,广泛应用于各个领域。
无论是在建筑设计中,还是在地理测量中,准确计算四边形的面积都至关重要。
本文将介绍常见的四边形类型,并逐一介绍它们的面积求法。
一、矩形的面积求法矩形是最简单的四边形之一,它的四条边两两平行且长度相等。
计算矩形面积的公式为:面积 = 长 ×宽。
其中,长代表矩形的长边的长度,宽代表矩形的短边的长度。
例如,一个矩形的长边长度为8米,短边长度为4米,则它的面积为32平方米。
二、正方形的面积求法正方形是一种特殊的矩形,它的四条边长度相等且两两平行。
正方形的面积求法与矩形相同,即面积 = 边长 ×边长。
例如,一个正方形的边长为5米,则它的面积为25平方米。
三、平行四边形的面积求法平行四边形是指具有两组对边平行的四边形。
计算平行四边形面积的公式为:面积 = 底边长 ×高。
其中,底边长代表平行四边形的底边的长度,高代表从底边到对边的垂直距离。
例如,一个平行四边形的底边长为6米,高为3米,则它的面积为18平方米。
四、梯形的面积求法梯形是一种具有两组平行边的四边形,其中一组较短的平行边称为上底,另一组较长的平行边称为下底。
计算梯形面积的公式为:面积 = (上底 + 下底) ×高 / 2。
其中,上底和下底代表梯形的两个平行边的长度,高代表从上底到下底的垂直距离。
例如,一个梯形的上底长为5米,下底长为8米,高为4米,则它的面积为26平方米。
五、不规则四边形的面积求法不规则四边形是指没有平行边或者长度不相等的四边形。
计算不规则四边形面积的方法有多种,其中一种常用的方法是将不规则四边形分割为多个规则四边形,然后逐个计算面积并求和。
例如,将一个不规则四边形划分为两个三角形和一个梯形,然后分别计算这些图形的面积,最后将它们相加,得到不规则四边形的面积。
总结四边形作为几何学中常见的图形,求解其面积的方法多种多样。
从简单的矩形到复杂的不规则四边形,每种四边形的面积求法都有其特点和适用范围。
2019年中考数学求不规则四边形面积的两种方法

2019年中考数学求不规则四边形面积的两种方法对于不规则图形面积的计算问题,一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出组合图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:(平方厘米)2.相加、相减求面积:这种方法是将组合图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出该图形的面积。
例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:5×5+4×4=41(平方厘米)三个空白三角形的面积和:(5+4)×5&pide;2+4×4&pide;2+5×(5-4)&pide;2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)除了以上这两种方法,还有其他的几种方法,同学们不妨了解了解。
3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米。
已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米。
平行四边形ABCD的面积:8×6&pide;2+8=32(平方厘米)4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
例4:下图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2平方厘米,CD的长是多少?解答:结合已知条件看图,很难有思路,连接DA,就可以发现:三角形ABE比三角形CDE的面积大2平方厘米,分别加上三角形DAE得到的三角形ABD比三角形CDA的面积大2平方厘米。
几何中的四边形的面积计算方法

几何中的四边形的面积计算方法四边形是几何学中常见的图形,它由四条线段组成,而其面积的计算方法则有一定的规律和原理。
本文将介绍四边形的不同类型以及计算它们面积的方法。
一、矩形的面积计算方法矩形是一种特殊的四边形,它的对边长度相等且相对平行。
矩形的面积计算方法十分简单,只需将矩形的长度与宽度相乘即可。
设矩形的长度为a,宽度为b,则其面积S等于S = a * b。
二、正方形的面积计算方法正方形也是一种特殊的矩形,其四条边相等且相对平行。
与矩形类似,正方形的面积计算方法也是将边长相乘。
设正方形的边长为a,则其面积S等于S = a * a,或记作S = a^2。
三、平行四边形的面积计算方法平行四边形是指具有相对平行的对边的四边形。
计算平行四边形的面积需要知道两个重要信息:底边的长度和高的长度。
设平行四边形的底边长度为a,高的长度为h,则其面积S等于S = a * h。
四、梯形的面积计算方法梯形是指有两边平行但另外两边不平行的四边形。
计算梯形的面积也需要知道两个关键信息:上底边的长度、下底边的长度和高的长度。
设梯形的上底长度为a,下底长度为b,高为h,则其面积S等于S = (a + b) * h / 2。
五、菱形的面积计算方法菱形是指所有边线相等的四边形,其特点是对角线不相等但互相垂直。
计算菱形的面积需要知道两条对角线的长度。
设菱形的对角线长度分别为d1和d2,则其面积S等于S = (d1 * d2) / 2。
六、不规则四边形的面积计算方法对于不规则四边形,也称为任意四边形,其面积计算稍微复杂一些。
一种常见的方法是将不规则四边形分割为多个三角形或梯形,然后计算每个部分的面积,最后将它们累加得到整个四边形的面积。
综上所述,不同类型的四边形有不同的面积计算方法。
矩形、正方形、平行四边形、梯形、菱形和任意四边形的面积计算原理分别为“长度乘以宽度”、“边长的平方”、“底边乘以高”、“上底加下底再乘以高除以2”、“对角线相乘再除以2”以及“分割为多个三角形或梯形并累加各部分面积”。
不规则矩形面积计算

不规则矩形面积计算
不规则矩形面积计算是一项重要的几何计算技能。
不规则矩形是一种四边形,其中相邻两边长度不同,且对角线长度不相等。
计算不规则矩形的面积需要测量其两条对角线的长度,然后将其乘以一半。
这个公式可以表示为:面积 = 1/2 ×对角线1 ×对角线2。
在实际应用中,可以使用直尺或测量仪等工具来测量不规则矩形的对角线长度,然后应用公式计算出面积。
掌握不规则矩形面积计算技能对于许多领域非常重要,如建筑和土木工程等。
- 1 -。
不规则四边形对角线定理

不规则四边形对角线定理
不规则四边形对角线定理是:边形一条对角线平分另一对角线,则过其交点的两条直线,以四边交点(邻边)的连线,与被平分的对角线的两个交点到对角线焦点距离相等。
不规则四边形的面积,等于四边形不相邻两边中点的连线长乘以另两边的任一中点到该连线距离的2倍。
因为四边形不具有稳定性,所以仅仅知道四条边的长度是无法算出面积的,必须知道一个角的度数。
由四条不在同一条直线上的线段首尾相连依次围成的封闭的平面图形或立体图形称为四边形,它由一个凸四边形和一个凹四边形组成。
将任意四边形的中点依次连接得到的四边形称为中点四边形,所有中点四边形都是平行四边形。
菱形的中点四边形是长方形,长方形的中点四边形是菱形,等腰梯形的中点四边形是菱形,正方形的中点四边形是正方形。
不规则四边形面积计算方式如下:
1.不规则四边形的面积等于四边形两条不相邻边的中点连线长度乘以从其他两条边的任意中点到连线距离的两倍。
2.将任意四边形的中点依次连接得到的四边形称为中点四边形,所有中点四边形都是平行四边形。
菱形的中点四边形是长方形,长方形的中点四边形是菱形,等腰梯形的中点四边形是菱形,正方形的中点四边形是正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不规则四边形面积计算方式
摘要:
I.引言
- 介绍不规则四边形的概念
- 提出问题:如何计算不规则四边形的面积
II.不规则四边形面积计算方法
- 方法一:海伦公式
- 方法二:分割成规则图形
III.计算步骤与示例
- 使用海伦公式计算不规则四边形面积的步骤
- 使用分割成规则图形的方法计算不规则四边形面积的步骤
- 示例:计算一个不规则四边形的面积
IV.结论
- 总结两种计算方法
- 指出方法的优缺点
正文:
I.引言
不规则四边形是指四边形的边长和角度不满足规则条件的四边形。
在数学和实际生活中,我们经常需要计算不规则四边形的面积。
那么,如何计算不规则四边形的面积呢?
II.不规则四边形面积计算方法
方法一:海伦公式
海伦公式是一种计算任意三角形面积的公式,它可以通过计算不规则四边形对角线的长度和夹角来求得不规则四边形的面积。
具体步骤如下:
1.计算不规则四边形对角线的长度。
2.计算对角线夹角。
3.应用海伦公式计算面积。
方法二:分割成规则图形
如果将不规则四边形分割成若干个规则图形(如三角形或矩形),则可以分别计算每个图形的面积,然后将它们加起来得到不规则四边形的面积。
具体步骤如下:
1.将不规则四边形分割成规则图形。
2.计算每个规则图形的面积。
3.将所有规则图形的面积加起来得到不规则四边形的面积。
III.计算步骤与示例
示例:计算一个不规则四边形的面积
假设有一个不规则四边形,其边长分别为3、5、8 和10,夹角分别为45°、90°和45°。
我们可以使用海伦公式和分割成规则图形的方法来计算其面积。
