第8章__回归正交试验设计
正交试验设计法简介

正交试验设计法简介一、本文概述正交试验设计法是一种高效、系统的试验设计方法,广泛应用于科学研究、工程实践以及日常生产中的优化问题。
本文将对正交试验设计法的基本概念、原理、应用及其优势进行详细介绍,旨在帮助读者更好地理解和应用这一实用的试验设计方法。
正交试验设计法基于数理统计和正交表的理论,通过合理安排试验因素与水平,以较少的试验次数获得丰富的试验信息。
该方法的核心在于利用正交表的正交性,使得各试验因素之间互不干扰,从而能够准确地评估各因素对试验结果的影响程度。
本文将从正交试验设计法的基本原理出发,阐述其在实际应用中的操作步骤和方法。
通过具体案例的分析,展示正交试验设计法在解决实际问题中的优势和应用价值。
本文还将对正交试验设计法的局限性和改进方向进行探讨,以期为读者提供更为全面、深入的了解。
二、正交试验设计法的基本原理正交试验设计法是一种以数理统计和正交性原理为基础的高效试验设计方法。
其基本原理在于,通过选择一组具有代表性的试验点,即正交表中的行,来全面、均衡地考察多个因素在不同水平下的试验效果。
这种方法能够在保证试验全面性的大大减少试验次数,提高试验效率。
正交试验设计法主要基于两个核心原理:正交性原理和代表性原理。
正交性原理指的是在试验设计中,各因素之间应相互独立,互不影响,从而确保试验结果的准确性和可靠性。
代表性原理则是指在选择试验点时,应确保每个试验点都能代表一定的因素水平组合,以便全面考察各因素对试验结果的影响。
正交表是正交试验设计法的核心工具,它是一种具有特定结构的表格,用于安排试验因素和水平。
正交表具有均衡分散和整齐可比的特点,能够确保每个试验点都具有一定的代表性,并且各因素之间保持正交性。
通过正交表,可以方便地安排试验,并对试验结果进行分析和比较。
正交试验设计法的应用范围广泛,适用于多因素、多水平的试验场景。
它不仅可以用于新产品的开发和优化,还可以用于工艺改进、质量控制等领域。
通过正交试验设计法,可以更加高效地找出最优的参数组合,提高产品的性能和质量,降低生产成本,为企业带来更大的经济效益。
回归正交试验设计PPT精品文档

Orthogonal Regression Design
1
正交设计:优方案只能限制在已定的水平上,而不是一定 试验范围内的最优方案
回归正交设计(orthogonal regression design) : ➢ 可以在因素的试验范围内选择适当的试验点 ➢ 用较少的试验建立回归方程 ➢ 能解决试验优化问题 ➢ 不适合非数量性因素
2
8.1 一次回归正交试验设计及结果分析
建立试验指标(y)与m个试验因素x1,x2,…,xm之间的 一次回归方程
例:m=3时,一次回归方程: y=a+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3
➢ 其中x1,x2,x3表示3个因素;x1x2,x1x3,x2x3表示交互作用 ➢ 若不考虑交互作用,为三元一次线形回归方程:
8
(4)试验方案的确定 表头设计 : ➢ 可参考正交设计的表头设
计方法 ➢ 交互作用列的编码等于表
中对应两因素列编码的乘 积 零水平试验(中心试验 )
9
8.1.2 一次回归方程的建立
总试验次数为n : n=mc+m0
➢ mc:二水平试验次数 ➢ m0:零水平试验次数 一次回归方程系数的计算: ➢ 常数项:a ➢ 一次项系数:bj ➢ 交互项系数: bjk
14
例8-1: (1)因素水平编码
15
(2)正交表的选择和试验方案的确定
16
(3)回归方程的建立 ➢ m0=0,n=mc=8 ➢ 计算表 ➢ 计算各回归系数 ➢ 写出y与规范变量zj的回归方程 ➢ 根据偏回归系数绝对值大小,确定因素和交互作用主次 ➢ 根据偏回归系数正负,得到各因素对试验指标的影响方向 (4)方差分析 (5)回归方程的回代:得到试验指标y与自然变量xj的回归
回归正交试验设计

回归正交试验设计一、概述(1)回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式,用于描述自变量与因变量之间的函数关系。
它的主要缺点是毫不关心试验数据如何取得,这样,不仅盲目地增加了试验次数,而且试验数据还往往不能提供充分的信息。
因此,有些工作者将经典的回归分析方法描述成:“这是撒大网,捉小鱼,有时还捉不到鱼”。
所以说,回归分析只是被动地处理试验数据,并且回归系数之间存在相关关系,若从回归方程中剔除某个不显著因素时,需重新计算回归系数,耗费大量的时间。
正交试验设计的主要优点是科学地安排试验过程,用最少的试验次数获得最全面的试验信息,并对试验结果进行科学分析(如方差分析),从而得到最佳试验条件,但是它的主要缺点是试验结果无法用一个经验公式来表达,从而不便于考察试验条件改变后,试验指标将作如何变化。
(2)回归正交试验设计回归正交试验设计,实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法,它利用正交试验设计法的“正交性”特点,有计划、有目的、科学合理地在正交表上安排试验,并将试验结果用一个明确的函数表达式即回归方程来表示,从而达到既减少试验次数、又能迅速地建立经验公式的目的。
根据回归模型的次数,回归正交试验设计又分为一次回归试验设计和二次回归试验设计。
二、一次回归正交试验设计(一)一次回归正交试验设计的概念一次回归设计研究的是一个因素z (或多个因素z 1,z 2,……)与试验指标y 之间的线性关系。
当只研究一个因素时,其线性回归模型:y =β0+β1z +e (1)其回归方程为:z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数,e 是随机误差,是一组相互独立、且服从正态分布N(0,σ2)的随机变量。
可以证明,∧0β、∧1β和∧y 是β0、β1和y 的无偏估计,即E(∧0β)=β0,E(∧1β)=β1,E(∧y )=y一次回归正交试验设计是通过编码公式x =f(z) −− 即变量变换,将式(2)变为:x b b y 10+=∧(3)且使试验方案具有正交性,即使得编码因素X的各水平之和为零:∑==mi ix1(4)式中m 是因素x 的水平数。
8第八章_回归正交试验设计

16
7.1.3 回归分析对数据的处理由被动变主动 古典的回归分析方法只是被动地处理已有的试验数据,对 试验的安排不提任何要求,对如何提高回归方程的精度研究 很少。 后果: (1)盲目增加试验次数,而这些试验结果还不能提供充分 的信息,以致在许多多因子试验问题中达不到试验目的。 (2)对模型的合适性有时无法检验,因为在被动处理数据 时在同一试验点上不一定存在重复试验数据。 为了适应寻求最佳工艺、最佳配方、建立生产过程的数学 模型等的需要,人们就要求以较少的试验次数建立精度较高 的回归方程。
ˆ b0 b1 x1 bp x p y 今后称 A X X 为正规方程组的系数矩阵, B X Y 为正规 1 方程组的常数项向量,C X X 为相关矩阵。 在模型(7.1.5)下,有
b ~ N ( , 2 ( X X ) 1 )
2015-1-9 试验设计与数据处理 9
( xi1 , xi 2 ,, xip , yi ), i 1,2,, n
假定回归模型为:
yi 0 1 xi1 p xip i,i 1,2,, n 2 各 iid ~ N ( 0 , ) i (7.1.5)
2015-1-9
试验设计与数据处理
i 1 i 1 i 1
ˆi )2 ( y ˆ i y) 2 S E S R ST ( yi y ) 2 ( yi y
其中
ˆi )2 S E ( yi y
ˆ i y) 2 S R ( y
i
为残差平方和,自由度为 为回归平方和,自由度为
2015-1-9 试验设计与数据处理 15
当H0j为真时,有 Fj ~ F (1, f E ) 。 给定的显著性水平 ,当 Fj F1 (1, f E ) 时拒绝假设H0j,即认 为 j 显著不为零,否则可以将对应的变量从回归方程中删除。 注:当有不显著的系数时,一般情况下一次只能删除一个F 值最小的变量,重新计算回归系数,再重新检验。通常要到余 下的系数都显著时为止。
第8章回归正交试验设计

②二次项的中心化 对二次项的每个编码进行中心化处理 :
(二次项编码)-(二次项编码算术平均值)
z ji
'
z
j
2 i
1 n
n i 1
z
j
2 i
二元二次回归正交组合设计编码表
试验号
z1
1
1
z2
z1 z2
z12
1
1
1
2
1
-1
-1
1
3
-1
1
-1
1
4
-1
-1
1
1
5
1
0
0
1
6
-1
0
0
1
7
0
1
0
0
8
0
-1
0
1.414
1.483
3 1.147 1.353
1.471
1.547
4 1.210 1.414
1.525
1.607
5 1.267 1.471
1.575
1.664
6 1.320 1.525
1.623
1.719
7 1.369 1.575
1.668
1.771
8 1.414 1.623
1.711
1.820
9 1.457 1.668
bkj
i 1 n
(zk z j )i2
i 1
二次项偏回归系数bjj :
n
(
z
' ji
)
yi
b jj
i 1 n
(
z
' ji
)
2
i 1
⑤回归方程显著性检验
卫生统计学第八章正交试验方差分析

WENKU DESIGN
正交试验设计定义与原理
正交试验设计定义
正交试验设计是研究多因素多水平的一种设计方法,它是根 据正交性从全面试验中挑选出部分有代表性的点进行试验, 这些有代表性的点具备了“均匀分散,齐整可比”的特点。
正交试验设计原理
正交试验设计是利用正交表来安排与分析多因素试验的一种 设计方法。它是由试验因素的全部水平组合中,挑选部分有 代表性的水平组合进行试验的,通过对这部分试验结果的分 析,了解全面试验的情况。
THANKS
感谢观看
REPORTINGΒιβλιοθήκη https://VS
正交表特点
每列中不同数字出现的次数相等;任意两 列中数字的排列方式齐全而且均衡。
正交试验设计步骤
挑因素,选水平
根据试验的目的和专业知识,挑选出与考察指标有关的因素。对选出的因素要分清主次,合理安排。 选取的水平数应根据实际情况而定,过少会导致结果不准确,过多则可能数据分布的规律性较差,代 表性差;
通过建立线性模型来描述各因素 与结果之间的关系,从而进行方 差分析和参数估计。
PART 03
正交试验方差分析步骤
REPORTING
WENKU DESIGN
数据整理与描述性统计
整理试验数据
按照试验因素和水平整理数据,列出试验指标的观察值。
计算总均值和总变异
计算所有观察值的总和、均值、离差平方和等描述性统计量。
选正交表,进行表头设计
根据确定的列数(C)与水平数(t)选择相应的正交表。选择的原则是首先满足列数,其次是水平数。若 有2个或2个以上正交表满足条件时则应选取行数最少的一个;
正交试验设计步骤
明确试验方案,进行试验;
实验五回归正交试验设计(Excel)

j 1
一次回归正交试验的结果分析
I. 建立回归方程
第一步:计算各列的SSj值
n
n
SS j d j zi2j dkj (zik zij )2
i 1
i 1
第二步:计算各列的Bj值
n
n
B0 yi Bj zkj yk
i 1
i 1
n
Bkj zik zij yi i 1
第三步:计算各列的回归系数bj值
二次回归组合设计结果分析
第一步,计算Bj,dj
n
B0 yi i 1
n
d j zi2j i 1
n
n
B j zij yi Bkj zik zij yi
i 1
i 1
n
B jj
z
' ij
yi
k 1
n
dkj (zik zij )2 i 1
n
d jj (zi'j )2 i 1
第二步,计算bj
b0
B0 n
bj
Bj dj
bkj
Bkj dkj
b jj
B jj d jj
II. 回归方程显著性检验
第一步: 计算各列回归系数的偏回归平方和 ( U j)
U j B2j / d j Ukj Bk2j / dkj U jj B2jj / d jj
第二步: 计算总变异均方、剩余的均方、回归均方
p
p
内容:
一次回归正交试验设计
yˆ b0 b1x1 b2 x2... bp xp
p
p1 p
或 yˆ b0 bj x j
bkj xk x j
j 1
k 1 jk 1
二次回归正交试验设计
第八章回归正交试验设计

8回归正交试验设计本章要点:主要讲述了一次回归正交试验设计、二次回归正交试验设计的原理、基本方法和统计分析步骤,并针对不同类型的回归正交试验给出了相应的计算案例。
重点:回归正交试验设计的方法,统计过程中方程的建立以及显著性分析检验。
难点:二次回归组合设计正交性的实现及其统计分析。
8.1 回归正交试验设计简介产品质量通常受多因素的综合影响,试验效应既包括因素的主效应,也包括因素间的交互作用,因此,在产品研究中总希望安排足够多的研究因素以使试验效应有充分的试验论据。
但因素和水平的增加造成试验规模庞大,特别是对于多指标分析的试验往往由于分析困难而无法实施。
线性反应试验一般是研究一个因素多水平的试验设计,面体反应试验是研究两个因素多水平的的试验设计。
当试验因素超过3个的多水平试验时,由于采用组合处理,处理数目等于因素水平间的乘积,它随因素的增加呈几何级数增加。
例如,一个3因素4水平的试验,总共有43=64个试验处理,而4因素5水平的试验就有54=625个处理,由于处理数目太大,不仅增加了试验误差,而且由于受试材和条件的限制,这对产品研究来说是难以实施的。
正交试验设计方法在产品工艺改进、新产品的试制中得到了广泛的应用,它能够利用较少的处理安排较多的试验因素,获得较佳的试验结果。
但是正交设计不能在一定的试验范围内,根据数据样本,去确定变量间的相关关系及相应的回归方程。
如果试验传统的回归分析,又只能被动地去处理由试验所得到的数据,而对试验的设计安排几乎不提出任何要求。
这样不仅盲目地增加了试验次数,而且由数据所分析出的结果还往往不能提供充分的信息,造成在多因素试验的分析中,由于设计的缺陷而达不到预期的试验目的。
因而回归正交试验设计应运而生。
回归正交试验设计是将试验安排与数据的回归分析结合起来考虑。
在试验中,通过适当地安排试验点,使得在每个试验点上获得的数据含有最大的信息,并且各自变量(因素)向量间满足正交性以便于回归分析。
第八章-回归的正交设计教程文件

§2 一次回归正交设计及统计分析
(3)选择适合的2水平正交表进行设计。
在应用2水平正交表进行回归设计时,需以“-1”代换 表中的“2”,以“+1”代换表中的“1”,并增加“0”水 平。这种变换的目的是为了适应对因素水平进行编码的需要, 代换后正交表中的“+1”和“-1”不仅表示因素水平的不 同状态,而且表示因素水平数量变化的大小。原正交表经过 上述代换,其交互作用列可以直接从表中相应几列对应元素 相乘而得到。因此原正交表的交互作用列表也就不用了,这 一点较原正交表使用更为方便。
§2 一次回归正交设计及统计分析
(1)确定试验因素的变化范围。
根据试验研究的目的和要求确定试验因素数 ,并在此基 础上拟定出每个因素Zj的变化范围。回归正交试验设计的因 素一般都大于3个,但也不能太多,否则处理过多,方案难 以实施。
各试验因素取值最高的那个水平称为上水平,以Z2j表示; 取值最低的那个水平称为下水平,以Z1j 表示;两者之算术平 均数称为零水平,以Z0j表示,
因此,在对供试因素 Zj 各水平进行了以上的编码以后,就 把试验结果 y 对供试因素各水平 Zi1,Zi2 , … , Zim 的回归问题转 化为在编码空间试验结果 y 对编码值 xi1,xi2 , … , xim 的回归问 题。
今后,不论是一次回归设计还是二次回归设计,我们都先 将各因素进行编码,再去求试验指标 y 对 x1,x2 , … , xm 的回归方程,这种方法在试验设计中是经常被采用的。
因素 1 2 3 4 5 6 7 8 9 … N
§2 一次回归正交设计及统计分析
表13-2 3元一次回归正交设计试验方案
x1 (Z1) 1 (17) 1 (17) 1 (17) 1 (17)
x2 ( Z2 ) 1 (22.6) 1 (22.6) -1 (9.4) -1 (9.4)
正交试验设计

正交试验设计
正交试验设计(Orthogonal experimental design)是一种常用于科学实验设计的方法。
它是统计学中一种重要的试验设计方法,通过选择合适的正交表将试验因素进行组合,以达到最大程度地减少误差和提高效率的目的。
正交实验设计最常见的类型是正交数组设计(Orthogonal array design),通过正交表将试验因素的各个水平进行组合,以实
现均匀分布和互不干扰的目的。
这种设计方法可以帮助确定影响结果的主要因素,找出最优的处理条件,并提高试验的可信度和重复性。
正交试验设计的特点之一是可以通过相对较少的实验次数得出准确的结果。
它通过最小化不相关的因素,使试验结果更易于解释和分析,并避免重复实验浪费资源和时间。
正交试验设计还可以通过分析试验结果和误差分布,确定主要影响因素的重要性和交互作用的效应。
通过建立数学模型和进行回归分析,可以进一步优化试验结果,并提高产品的质量和效率。
正交试验设计广泛应用于工程、制造、化学、医药等领域。
它可以帮助确定最佳工艺参数、产品配方、药物剂量等,并优化生产过程、提高产品质量和效率。
它还可以用于新产品开发、工艺改进、质量控制等方面。
正交试验设计的成功关键一是正确选择试验因素和水平,确保
能够覆盖全部可能的条件。
另外,正确解读试验结果、分析影响因素的相对重要性和相互作用也是至关重要的。
总之,正交试验设计是一种有效的实验设计方法,可以在较短的时间内得出准确的结果,并提供优化产品和工艺的参考依据。
它具有广泛的应用前景,并在工程和科学研究中发挥着重要的作用。
工程试验设计 回归正交试验设计

第一节 一次回归正交设计一 正交设计和回归设计的特点1 正交设计的特点正交设计是一种很实用的试验设计方法,它利用较少的试验次数获得较好的试验结果;但是通过正交设计得到的优方案只是局限在确定的水平组合中,而不是一定试验范围内的最优方案。
2 回归设计回归分析是一种有效的数据处理方法,通过所确定的回归方程,可对试验结果进行预测和控制;但是,它只能对试验数据进行被动的分析和处理,不涉及对试验设计的要求。
如果把两者的优势统一起来,不仅有合理的试验设计和较少的试验次数,还能建立有效的数学模型,这就是回归正交设计方法。
二 一次回归正交设计基本方法一次回归正交设计就是利用回归正交设计原理,建立试验指标y 与m 个因素x 1、x 2、…、x m 之间的一次回归方程:)(ˆ1k j x x b x b a yjk j k kj mj j j ≠++=∑∑<=(k=1,2,…,m ) 如果不考虑交互作用,则一次回归方程为m m x b x b x b a y++++=...ˆ2211 一次回归正交设计的基本步骤如下:1 确定因素的变化范围根据指标y ,确定需要考察的m 个因素x j (j=1,2,…,m ),并确定每个因素的取值范围。
设:x j 的变化范围为[x j 1,x j 2],分别称x j 1和x j 2为因素x j 的下水平和上水平,并将其算术平均值称为零水平,即2210j j j x x x +=上水平与零水平之差或零水平与下水平之差称为x j 的变化间距j ∆,即2121002j j j j j j j x x x x x x -=-=-=∆例如,某试验中温度的变化范围为30-90℃,则其上水平为x j 2=90℃,x j 1=30℃,零水平x j 0=60℃,变化间距△j =30℃。
2 因素水平的编码编码(coding )就是将x j 的各水平进行线性变换,即jj j j x x z ∆-=式中,z j ——x j 的编码。
正交回归设计(2)

2.检验一次方程的合适性 为了了解是否存在因子间的交互作用,是否有因子的高次效 应,在中心点进行了m=5次试验,结果为: 40.3,40.5,40.7,40.2,40.6 5 其平均值为 y 0 40.46 ,偏差平方和为 S0 ( y0i y0 ) 2 0.172 , i 1 其自由度=4。 采用方法1中的检验统计量t作检验。 ˆ 0 40.425, y 0 40.46 , 现在 y
最后再将编码式
2 206 .23 14 .338 x 2 21 .818 x12 35.868 x 2
x1
F 250 A 3.5 ,x2 109 1.74
代入,即可得y关于F,A的二次回归方程: ˆ 86.5547 1.0497 F 0.0018 F 2 82.9291 A 11.8470 A 2 y 为延长寿命,可以将回归方程对F与A分别求导,并令 其为零以解出最佳水平组合为F=291.58,A=3.50,在该水 平组合下,平均寿命的估计是211.6。
2 2
0 0 0 0
0 0
这里mc=4,2p=4,则n=mc+2p+m0=8+m0,再记
h 4 2 2
f 4 2 4
那么
n 0 0 X X 0 h h 0 0 h 0 0 h 0 0 0 0 0 0 0 0 0 h 0 0 0 f mc h 0 0 0 mc f
1 1 1 1 1 1 1 1 1 X 1 1 0 1 0 1 0 1 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 2 2 0 0
《试验设计及最优化》课程教学大纲

“DesignofExperimentaland Optimization” mainly teaches the methods and skills of experimental design and data processing. It is a fundamental professional course that provides practical and scientific knowledge of experimental design and data processing skills for personnel engaged in scientific research, engineering experiments, and engineering design in the fields of chemical engineering and material science.
试验设计及最优化
课程名称
中文
试验设计及最优化
课程编号
0005200105
英文
DesignofExperimentaland Optimization
开课单位
化学化工学院
考核方式
考试
学时
32
学分
2
课程术学位硕士生、专业学位硕士生、非全日制专业学位硕士生
课程简介(中文):
《试验设计及最优化》主要讲授试验设计与数据处理的方法和技能,是一门为从事化工、材料等方面的科学研究、工程实验以及工程设计等工作的研究人员提供相应的试验设计与数据处理知识与技能的基础性专业课程。
教材及主要参考书目:
李云雁,胡传荣编,《试验设计与数据处理》第三版,化学工业出版社,2017.9
试验优化设计-第八章(2013)

p
p
p
2 j
z
j 1
p
j
1
ˆ y
b
j 1
p
j
x j bhj xh x j
h j
ˆ a0 a j z j ahj zh z j a jj z y
j 1 j h j 1
p
p
p
2 j
ˆ y
b x b
j j j 1 h j
正交(比率设计) 混料D最优 混料旋转设计
5、追求优良设计
§3 单形重心设计
一、单形:顶点数与坐标空间维数相等的凸图形
正三角形,正四面体形,p 维单形即(p-1)维单纯形。
单形 单纯形 相同点 多维空间的凸图形 多维空间的凸图形 ①顶点数与坐标维 ①顶点数仅比空间 数相等 维数多一
不同点
ns p
第八章 混料回归设计
§1 混料试验
一、混料
定义:是指若干种不同成分的混合或合成。
例:1°材料:由铁、镍、铜和铬四种元素组成的不锈 钢,由镁,硝酸钠、硝酸锶和固定剂组成的闪光剂; 2°食品工业:吃喝; 3°建筑材料:水泥,混凝土,粘接剂; 4°能源:由不同成分组成的固态、液态和气态的燃料;
5°工厂中不同品种,不同合格率的产品总体,不同 型号,不同完好率的设备总体; 6°资金、人员、材料、设备的分配问题。
j i
(x j , N )
(z j , N )
X1
X2
① ② ③ ④ ⑤ ⑥ ⑦
1 2 3 4
5
6 7
1 0 0 1 0 0.2 0.6 0 0 1 0.2 0.4 1/2 1/2 0 0.3 0.5 1/2 0 1/2 0.4 0.4 0 1/2 1/2 0.2 0.5 1/3 1/3 1/3 0.27 0.47
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明
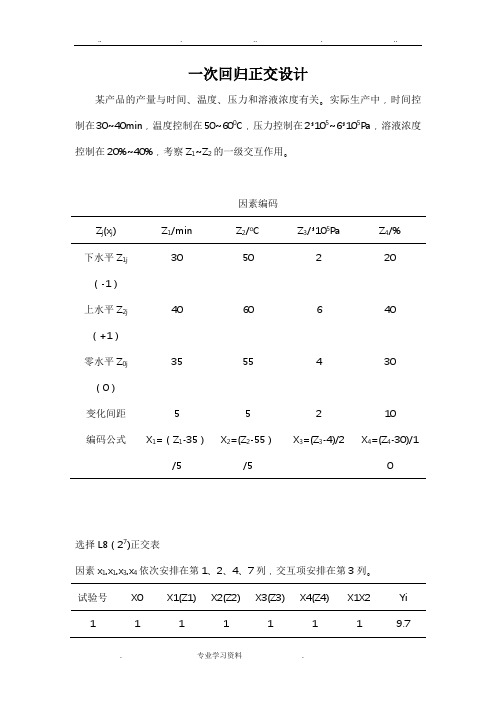
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
JMP试验设计

JMP试验设计1.试验设计方法及其在国内的应用 (2)2.试验设计(DOE)就在你身边试验设计(DOE)就在你身边 (7)3.初识试验设计(DOE) (12)4.多因子试验设计(DOE)的魅力 (18)5.用DOE方法最优化质量因子配置 (25)6.顾此不失彼的DOE (32)7.试验设计(DOE)五部曲 (38)8.稳健参数设计的新方法 (44)9.JMP的试验设计优势——为什么用JMP做试验设计 (49)试验设计方法及其在国内的应用随着改革开放的深入,以市场经济为代表的西方先进文明及其方法论越来越多被国内企业界所接纳。
在质量管理、产品(医药,化工产品,食品,高科技产品,国防等)研发、流程改进等领域,统计方法越来越多成为企业运营的标准配置。
试验设计作为质量管理领域相对复杂、高级的统计方法应用,也开始在国内被逐渐接受,推广。
其实试验设计对于我国学术界来说并不陌生。
比如均匀设计,均匀设计是中国统计学家方开泰教授(下图左)和中科院院士王元首创,是处理多因素多水平试验设计的卓有成效的试验技术,可用较少的试验次数,完成复杂的科研课题开发和研究。
国内一些大学的数学系和统计系近年来已经逐渐开始开设专门的试验设计课程,比如清华大学,电子科技大学、复旦大学等高校。
国内一些行业领先的企业,比如中石化,华为科技,中石油,宝钢等企业,也开始在质量管理和产品研发、工艺改进等领域采用DOE方法。
尽管DOE越来越多的被国内产、学、研领域所接受,但是我们还是看到,国内对于DOE的研究和推广仍旧停留在比较浅的层次。
以上述企业为例,中石化下属的石化科学研究院和上海石化研究院应该是我国石油化工研究领域的王牌单位了,不过不管是北京的石科院,还是上海石化研究院,在油品研发、工艺改进、质量管理等领域,对于DOE的使用还仅仅停留在部分因子和正交设计层面。
笔者在网络上查询到电子科技大学的DOE课程目录如下:教材目录:第一章正交试验基本方法第二章正交试验结果的统计分析——方差分析法第三章多指标问题及正交表在试验设计中的灵活运用第四章Ltu(tq)型正交表的构造第五章2k和3k因子设计第六章优选法基础第七章回归分析法第八章正交多项式回归设计第九章均匀设计法第十章单纯形优化法第十一章鲍威尔优化法及应用第十二章三次设计第十三章稳定性设计目前业界常用的高端试验设计方法比如定制设计,筛选设计,空间填充设计等高级试验设计方法(Advanced DOE),无论在国内的统计教学、科研还是在产业界的应用,都还比较少见,但已有逐步扩大趋势.西方企业对于DOE的应用早已大规模开始,比如美国航天、航空设计的顶尖单位,乔治亚宇航设计中心,在开发导弹、战斗机等美国绝密武器系统的时候,无一例外的使用了定制设计(Customer Design)。
回归正交试验设计

规范变量z 规范变量 j 上星号臂γ 上星号臂 上水平1 上水平 零水平0 零水平 下水平-1 下水平- 下星号臂- 下星号臂-γ 变化间距 变化间距 j
②确定合适的二次回归正交组合设计 参考表8-22 参考表
正交表的选用 因素数m 因素数 2 3 4(1/2实施) ( 实施 实施) 4 5(1/2实施) ( 实施 实施) 5 选用正交表 L4(23) L8(27) L8(27) L16(215) L16(215) L32(231) 表头设计 1,2列 , 列 1,2,4列 , , 列 1,2,4,7列 , , , 列 1,2,4,8列 , , , 列 1,2,4,8,15列 , , , , 列 1,2,4,8,16列 , , , , 列 mc 22= 4 23= 8
(3)回归方程的建立 ) m0=0,n=mc=8 , = 计算表 计算各回归系数 写出y与规范变量 写出 与规范变量zj的回归方程 与规范变量 根据偏回归系数绝对值大小, 根据偏回归系数绝对值大小,确定因素和交互作用主次 根据偏回归系数正负, 根据偏回归系数正负,得到各因素对试验指标的影响方向 (4)方差分析 ) 与自然变量x (5)回归方程的回代:得到试验指标 与自然变量 j的回归 )回归方程的回代:得到试验指标y与自然变量 方程
1 m0 SSe1 = ∑ ( y0i y 0 ) 2 = ∑ y0i2 (∑ y0i ) 2 m0 i =1 i =1 i =1
m0
m0
重复试验误差的自由度: 重复试验误差的自由度: ②回归方程失拟部分: 回归方程失拟部分: 失拟平方和 :
df e1 = m0 1
SS Lf = SST SS R SS e1 = SS e SS e1
回归平方和 : SS R = ∑ SS 一次项 + ∑ SS 交互项 残差平方和 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1.2 一次回归方程的建立
总试验次数为n : n=mc+m0
➢ mc:二水平试验次数 ➢ m0:零水平试验次数
一次回归方程系数的计算:
➢ 常数项:a ➢ 一次项系数:bj ➢ 交互项系数: bjk
方差分析表
F0.01(1,2)=98.49 F0.05(1,2)=18.51
F0.01(5,2)=99.30 F0.05(5,2)=19.30
差异 SS
df MS
F
源
z1
0.000761 1 0.000761 12.27
z2
0.009113 1 0.009113 146.98
z3
0.000265 1 0.000265 4.27
z12 0.000181 1 0.000181 2.92
Z13 0.000421 1 0.000421 6.79 回归 0.010741 5 0.002148 34.65
残差 0.000123 2 0.000062
总和 0.010864 7
显著性
** *
新的方差分析表
F0.05(1,6)=5.99 F0.01(1,6)=13.74
例:m=3时,一次回归方程: y=a+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3
➢ 其中x1,x2,x3表示3个因素;x1x2,x1x3,x2x3表示交 互作用
➢ 若不考虑交互作用,为三元一次线形回归方程:
y=a+b1x1+b2x2+b3x3
8.1.1 一次回归正交设计的基本方法
(2)因素水平的编码
编码(coding):将因素xj的各水平进行线性变
换:
zj
xj xj0 j
➢ zj:因素xj的编码 ,称为规范变量 ➢ xj:自然变量 ➢ 上水平xj2的编码 :zj2=1 ➢ 下水平xj1的编码:zj1=-1 ➢ 零水平xj0的编码:zj0=0
编码目的:
使每因素的每水平在编码空间是“平等”的, 规范变量zj的取值范围都是[1,-1]内变化,不 会受到自然变量xj的单位和取值大小的影响。 编码能将试验结果y与因素xj(j=1,2,…, m)各水平之间的回归问题,转换成试验结果 y与编码值zj之间的回归问题,从而大大简化了 回归计算量。
(1)确定因素的变化范围 以因素xj为例:
设xj 的变化范围为[xj1, xj2] xj1为xj的下水平 xj2为xj的上水平 xj0为xj的零水平: xj0= (xj1+ xj2)/2 因素xj的变化间距 Δj:
➢ Δj=上水平- 零水平=xj2-xj0 ➢ Δj= (xj2 - xj1)/2
8.1.1 一次回归正交设计的基本方法
失拟性检验:为了检验一次回归方程在整 个研究范围内的拟合情况
失拟性检验步骤:
设m0次零水平试验结果为y01,y02,…,y0m0
①重复试验误差:
平方和:SSe1
m0
( y0i
i1
y0)2
m0 i1
y0i2
1 m0
(
m0 i1
y0i )2
重复试验误差的自由度:dfe1 m0 1
差异源 SS 回归(z2) 0.009113 残差e 0.001751 总和 0.010864
df MS 1 0.009113 6 0.000292 7
F 31.21
显著性 **
(5)最终的回归方程
y=0.50475+0.03375z2 z2=(x2-2100)/300 y=0.50475+0.03375 ×(x2-2100)/300 整理后得:
0.010741
SSe SST SSR 0.010864 0.010741 0.000123
(4)方差分析
dfT=n-1=8-1=7 df1=df2=df3=1 df12=df13=1 dfR=df1+df2+df3+df12+df13=1+1+1+1+1=5 dfe=dfT-dfR=7-5=2 MS1=SS1/df1=0.000761 MS2=SS2/df2=0.009113 MS3=SS3/df3=0.000265 MS12=SS12/df12=0.000181 MS13=SS13/df13=0.000421 MSR=SSR/dfR=0.010741/5=0.002148 MSe=SSe/dfe=0.000123/2=0.000062 F1=MS1/MSe=0.000761/0.000062=12.27 F2=MS2/MSe=0.009113/0.000062=146.98 F3=MS3/MSe=0.000265/0.000062=4.27 F12=MS12/MSe=0.000181/0.000062=2.92 F13=MS13/MSe=0.000421/0.000062=6.79 FR=MSR/MSe=0.002148/0.000062=34.65
第8章 回归正交 试验设计
本章问题的提出
正交设计:优方案只能限制在已定的水平上,而不 是一定试验范围内的最优方案
回归分析可通过所确立的回归方程 ,对试验结果 进行预测和优化,但回归分析只能对试验数据进行 被动的处理和分析,不涉及对试验设计的要求。
回归正交设计可将两者结合起来。它可以在因素的 试验范围内选择适当的试验点,用较少的试验建立 一个精度高、统计性质好的回归方程,并能解决试 验优化问题。
-
-0.554
0.554
3
1 -1 -1 1 1 0.480 0.230400 0.480 0.480 0.480 0.480 0.480
4
1 -1 -1 -1 -1 0.472 0.222784 0.472 -0.472 -0.472
-
-0.472
0.472
5 -1 1 -1 1 -1 -0.516 0.266256 -0.516 -0.516 0.516 0.516 -0.516
④F检验: 回归方程显著性检验
偏回归系数显著性检验 :
➢ 判断因素或交互作用对试验的影响程度 ➢ 经检验不显著的因素或交互作用应归入
残差,重新检验
➢ 可直接从回归方程中剔除这些一次和交 互项
例8-1:p.126~129
例8-1 用石墨炉原子吸收分光光度计测定食 品中的铅,为提高测定灵敏度,希望吸光度(y) 大。为提高吸光度,讨论了x1(灰化温度/℃), x2(原子化温度/℃)和 x3 (灯电流/mA)三个因素 对吸光度的影响,并考虑交互作用x1x2 , x1x3 。已知x1=300~700℃, x2= 1800~2400℃,x3=8~10mA。试通过回归正 交试验确定吸光度与三个因素之间的函数关系 式。
例8-1:p.126~129 (1)因素水平编码
编码
上水平(1) 下水平(-1) 零水平(0) 变化间距Δj
因素xj
x1(灰化温度 x2(原子化温 x3 (灯电流
/℃)
度/℃)
/mA)
700
2400
10
300
1800
8
500
2100
9
200
300
1
(2)正交表的选择和试验方案的确定
(3)回归方程的建立 依题意 m0=0,n=mc=8
回归平方和 :
SSR SS一次项 SS交互项
残差平方和 :SSe SST SSR
②自由度
dfT=n―1 各种偏回归平方和的自由度=1 回归平方和的自由度 :
dfR df一次项 df交互项
残差自由度:
dfe dfT dfR
③均方
z2i yi
i 1
mc
n
0.270 0.03375
8
b3
n
z3i yi
i 1
mc
0.046 0.00575 8
b12
(z1z2 )i yi
i 1
mc
0.038
0.00475
8
b13
n
(z1z2 )i yi
i1
mc
0.058 0.00725 8
试
z1 z2 z1z2 z3 z1
y
验
z3
号
y2
z1y z2y z3y (z1z2 (z1z2)y
)y
1
1 1 1 1 1 0.552 0.304704 0.552 0.552 0.552 0.552 0.552
2
1 1 1 -1 -1 0.554 0.306919 0.554 0.554 -0.554
(3)一次回归正交设计表
将二水平的正交表中“2”用“-1”代换 ,例:
回归正交设计表的特点:
➢任一列编码的和为0 ➢任两列编码的乘积之和等于0
说明经转换后的正交表同样具有正交 性。
(4)试验方案的确定
表头设计 :
➢ 可参考正交设计的表 头设计方法
➢ 交互作用列的编码等 于表中对应两因素列 编码的乘积
y=0.2685+0.0001125x2
(2)有零水平试验时
目的:进行回归方程的失拟性(lack of fit) 检验 (要求m0≥2 )
前面所提的对回归方程进行的显著性检验, 只能说明相对残差平方和而言,各因素对 试验结果的影响是否显著。即使所建立的 回归方程是显著的, 也只反映了回归方程 在试验点与试验结果拟合得较好,不能说 明在整个研究范围内回归方程都与实测值 有好的拟合。
(3)回归方程的建立
➢ 写出y与规范变量zj的回归方程
