人教版八年级数学上册第十一章三角形测试题.doc
八年级数学上册试题 第十一章 三角形章节测试卷--人教版(含详解)

第十一章《三角形》章节测试卷一.选择题(共12小题,满分48分,每小题4分)1.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是( )A.直角三角形B.锐角三角形C.钝角三角形D.正三角形2.下面四个图形中,线段BD是△ABC的高的是( )A.B.C.D.3.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )A.1根B.2根C.3根D.4根4.能把一个任意三角形分成面积相等的两部分是( )A.以上都可以B.高C.中线D.角平分线5.长度分别为3,8,x的三条线段能组成一个三角形,x的值可以是( )A.4B.5C.6D.116.如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )A.90°B.20°C.45°D.70°7.如图所示,∠1=∠2=150°,则∠3=( )A.30°B.150°C.120°D.60°8.如图,在△ABC中,AB=2021,AC=2018,AD为中线,则△ABD与△ACD的周长之差为( )A.1B.2C.3D.49.若一个多边形的每个内角都等于150°,则这个多边形的边数是( )A.10B.11C.12D.1310.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.90°B.135°C.270°D.315°11.△ABC的两边是方程组{x+2y=104x+3y=20的解,第三边长为奇数.符合条件的三角形有( )A.1个B.2个C.3个D.4个12.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )A.∠A+∠D﹣45°B.12(∠A+∠D)+45°C.180°-(∠A+∠D)D.12∠A+12∠D二.填空题(共4小题,满分16分,每小题4分)13.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1= °.14.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A= .15.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠AFD的度数为 .16.如图,D,E,F分别是△ABC的边AB,BC,AC上的中点,连接AE,BF,CD交于点G,AG:GE=2:1,△ABC的面积为6,设△BDG的面积为S1,△CGF的面积为S2,则S1+S2= .三.解答题(共8小题,满分86分)17.已知一个多边形的内角和是外角和的三倍,则这个多边形是几边形?18.如图,∠ABC=∠FEC=∠ADC=90°.(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 ;(3)若AB=2.4cm,CD=2cm,AE=3cm,求△AEC的面积及CE的长.19.如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数;(2)∠AEF的度数.20.已知一等腰三角形的两边长x,y满足方程组{3x−y=55x+2y=23求此等腰三角形的周长.21.一个零件的形状如图,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=149°,就判断这个零件不合格,运用三角形的有关知识说出零件不合格的理由.22.如图1所示,将一副三角板的直角顶点重合在点O处.(1)∠AOD ∠BOC;(填“>”“<”“=”)(2)若将三角尺按图2的位置摆放,∠AOC和∠BOD在数量上有何关系?说明理由;(3)在图2中,已知∠BOC与∠AOC的度数比为m:n,当a6m b11与a n+1b2n﹣11是同类项时,求∠BOD的度数.23.问题1现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系是 研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是 研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.问题2研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .24.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)如图2(∠B<∠C),试说明∠DAE与∠B、∠C的数量关系;(3)拓展:如图3,四边形ABDC中,AE是∠BAC的角平分线,DA是∠BDC的角平分线,猜想:∠DAE与∠B、∠C的数量关系是否改变.说明理由.答案一.选择题1.【解答】解:∵△ABC中,∠A=20°,∠B=70°,∴∠C=180°﹣20°﹣70°=90°,∴△ABC是直角三角形.故选:A.2.【解答】解:由图可得,线段BD是△ABC的高的图是D选项.故选:D.3.【解答】解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.故选:B.4.【解答】解:三角形的中线把三角形分成等底同高的两个三角形,面积相等,所以,能把一个任意三角形分成面积相等的两部分是中线.故选:C.5.【解答】解:8﹣3<x<8+3,5<x<11,只有选项C符合题意.故选:C.6.【解答】解:∵∠BAC=90°,∴∠DAC+∠BAD=90°,∵AD是△ABC的高,∴∠ADB=∠BAD+∠B=90°,∴∠DAC=∠B=20°,故选:B.7.【解答】解:∵∠1=∠2=150°,∴∠ABC=∠BAC=180°﹣150°=30°,∴∠3=∠ABC+∠BAC=60°.故选:D.8.【解答】解:∵AD为中线,∴DB=DC,∴△ABD与△ACD的周长之差为:(AB+AD+BD)﹣(AD+DC+AC)=AB+AD+BD﹣AD﹣DC﹣AC=AB﹣AC=2021﹣2018=3,故选:C.9.【解答】解:由题意可得:180°•(n﹣2)=150°•n,解得n=12.故多边形是12边形.故选:C.10.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.故选:C.11.【解答】解:方程组{x+2y=104x+3y=20的解为:{x=2 y=4,∵△ABC的两边是方程组{x+2y=104x+3y=20的解,第三边长为奇数,∴2<第三边长<6,1∴第三边长可以为:3,5.∴这样的三角形有2个.故选:B.12.【解答】解:∵四边形的内角和=360°,∴∠ABC+∠BCD=360°﹣(∠A+∠D),∵∠ABC与∠BCD的平分线的交点E恰好在AD边上,∴2∠EBC=∠ABC,2∠ECB=∠BCD,∴∠EBC+∠ECB=12(∠ABC+∠BCD)=12×[360°−(∠A+∠D)],∴∠BEC=180°﹣(∠EBC+∠ECB)=180°−12×[360°−(∠A+∠D)]=12(∠A+∠D),故选:D.二.填空题13.【解答】解:∵∠A=60°,∠C=50°,∴∠ABC=180°﹣∠A﹣∠C=180°﹣60°﹣50°=70°,∴∠1=∠ABC﹣∠D=50°﹣20°=50°.故答案为:50.14.【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABC=2∠ABP,∠ACM=2∠ACP,又∵∠ABP=20°,∠ACP=50°,∴∠ABC=2×20°=40°,∠ACM=2×50°=100°,∴∠A=∠ACM﹣∠ABC=60°,故答案为60°.15.【解答】解:∵∠B=40°,∠C=30°,∴∠BAC=110°,由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∵DE∥AB,∴∠BAE=∠E=30°,∴∠CAD=40°,∴∠ADC=180°﹣∠CAD﹣∠C=110°,∴∠AFD=110°﹣40°=70°,故答案为:70°.16.【解答】解:∵D,E,F分别是△ABC的边AB,BC,AC上的中点,∴AD=DB,AF=CF,∴△BDG的面积=△ADG的面积,△CFG的面积=△AGF的面积,∴设△BDG的面积为S1,△CGF的面积为S2,则S1+S2=四边形ADGF的面积,∵△ABC的面积为6,AG:GE=2:1,∴四边形ADGF的面积=23×12×6=2,∴S1+S2=2,故答案为:2三.解答题17.解:设这个多边形为n边形,n边形的内角和为:(n﹣2)×180°,n边形的外角和为:360°,根据题意得:(n﹣2)×180°=3×360°,解得:n=8,答:这个多边形是八边形.18.解:(1)在△ABC中,BC边上的高是线段AB;故答案为线段AB;(2)在△AEC中,AE边上的高是线段CD;故答案为线段CD;(3)∵S△AEC=12×AE×CD=12×CE×AB,∴CE=AE⋅CDAB= 2.5(cm).19.解:(1)∵DF⊥AB,∴∠B=90°﹣∠D=48°,∵∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠B=83°;(2)∵DF⊥AB,∴∠AFD=90°,∴∠AEF=90°﹣∠A=55°.20.解:解方程组组{3x−y=55x+2y=23得{x=3 y=4,所以,等腰三角形的两边长为3,4.若腰长为3,底边长为4,由3+3=6>4知,三角形的周长为10.若腰长为4,底边长为3,则三角形的周长为11.所以,这个等腰三角形的周长为10或11.21.解:延长CD交AB于点E,∵∠BEC是△ACE的一个外角,∴∠BEC=∠A+∠C=90°+21°=111°,同理,∠BDC=∠BEC+∠B=111°+32°=143°,而检验工人量得∠BDC=149°,所以零件不合格.22.解:(1)∵∠AOB=∠COD=90°,∴∠AOB+∠BOD=∠COD+∠BOD,即∠AOD=∠BOC.故答案为:=;(2)∵∠AOB=∠COD=90°,∴∠AOC+∠BOD=180°.故∠AOC和∠BOD在数量上的关系为:∠AOC+∠BOD=180°;(3)∵a6m b11与a n+1b2n﹣11是同类项,∴{6m=n+111=2n−11,解得{m=2n=11,∵∠BOC与∠AOC的度数比为m:n,11﹣2=9,∴∠BOC=90°×2=20°,11−2∴∠BOD=90°﹣20°=70°.故∠BOD的度数是70°.23.解:(1)如图1,∠1=2∠A,理由是:由折叠得:∠A=∠DA′A,∵∠1=∠A+∠DA′A,∴∠1=2∠A;故答案为:∠1=2∠A;(2)如图2,猜想:∠1+∠2=2∠A,理由是:由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,∵∠ADB+∠AEC=360°,∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;故答案为:∠1+∠2=2∠A;(3)如图3,∠2﹣∠1=2∠A,理由是:∵∠2=∠AFE+∠A,∠AFE=∠A′+∠1,∴∠2=∠A′+∠A+∠1,∵∠A=∠A′,∴∠2=2∠A+∠1,∴∠2﹣∠1=2∠A;(4)如图4,由折叠得:∠BMN=∠B′MN,∠ANM=∠A′NM,∵∠DNA+∠BMC=360°,∴∠1+∠2=360°﹣2∠BMN﹣2∠ANM,∵∠BMN+∠ANM=360°﹣∠A﹣∠B,∴∠1+∠2=360°﹣2(360°﹣∠A﹣∠B)=2(∠A+∠B)﹣360°,故答案为:∠1+∠2=2(∠A+∠B)﹣360°.24.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°,∵AD是∠BAC的角平分线,∠BAC=40°,∴∠CAD=∠BAD=12∵AE是△ABC的高,∴∠AEC=90°,∵∠C=60°,∴∠CAE=90°﹣60°=30°,∴∠DAE=∠CAD﹣∠CAE=10°;(2)∵∠BAC+∠B+∠C=180°,∴∠BAC =180°﹣∠B ﹣∠C ,∵AD 是∠BAC 的角平分线,∴∠CAD =∠BAD =12∠BAC ,∵AE 是△ABC 的高,∴∠AEC =90°,∴∠CAE =90°﹣∠C ,∴∠DAE =∠CAD ﹣∠CAE =12∠BAC ﹣(90°﹣∠C )=12(180°﹣∠B ﹣∠C )﹣90°+∠C =12∠C −12∠B ,即∠DAE =12∠C −12∠B ; (3)不变,理由:连接BC 交AD 于F ,过点A 作AM ⊥BC 于M ,过点D 作DN ⊥BC 于N ,∵AE 是∠BAC 的角平分线,AM 是高,∴∠EAM =12(∠ACB ﹣∠ABC ),同理,∠ADN =12(∠BCD ﹣∠CBD ),∵∠AFM =∠DFN ,∠AMF =∠DNF =90°,∴∠MAD =∠ADN ,∴∠DAE =∠EAM+∠MAD =∠EAM+∠ADN =12(∠ACB ﹣∠ABC )+12(∠BCD ﹣∠CBD )=12(∠ACD ﹣∠ABD ).。
20212022学年人教版八年级数学上册第十一章三角形单元测试卷含答案.docx
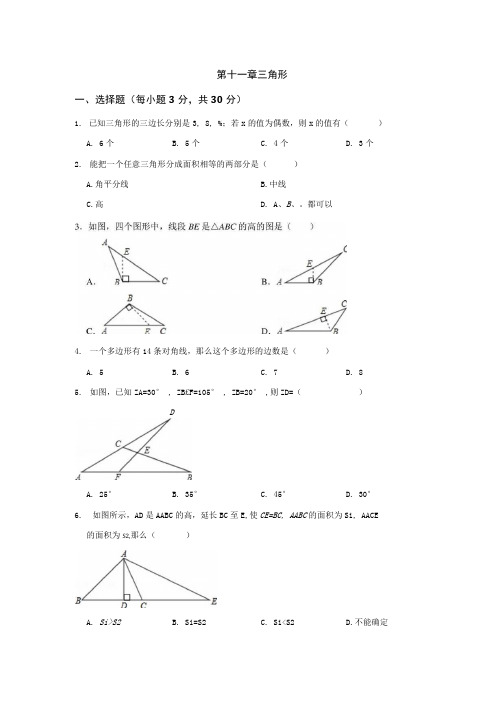
第十一章三角形一、选择题(每小题3分,共30分)1.已知三角形的三边长分别是3, 8, %;若x的值为偶数,则x的值有()A. 6个B. 5个C. 4个D. 3个2.能把一个任意三角形分成面积相等的两部分是()A.角平分线B.中线C.高D. A、B、。
都可以4.一个多边形有14条对角线,那么这个多边形的边数是()A. 5B. 6C. 7D. 85.如图,已知ZA=30° , ZB£F=105° , ZB=20° ,则ZD=()DA. 25°B. 35°C. 45°D. 30°6.如图所示,AD是AABC的高,延长BC至E,使CE=BC, AABC的面积为Si, AACE的面积为S2,那么()A. Si>S2B. Si=S2C. Si<S2D.不能确定7.下列图形中具有稳定性有()9. 下列判断:①三角形的三个内角中最多有一个钝角,②三角形的三个内角中至少有两个 锐角,③有两个内角为50°和20°的三角形一定是钝角三角形,④直角三角形中两锐角 的和为90° ,其中判断正确的有( )10. 如图所不,Z1+Z2+Z3+匕4=()二、填空题(每小题3分,共18分)11. 若一个两边相等的三角形的两边分别是4cm 和9cm,则其周长是 .12. 一个多边形的每一个内角都相等,且比它的一个外角大100° ,则边数〃= 13. 如图△ABC 中,AB=AC, AD=AE, ZBAD=40° ,则ZEDC=.14. 如图所不,/ 1+N2+匕3+匕4+匕5+匕6=(1) (2) A. 2个8.在△ABC 中,若ZA=ZC=AZB,3A. 30°B. 36°C. 72°D. 108°A. 1个B. 2个C. 3个D. 4个C. 480°D. 540°D. 5个则匕A 的度数为()⑶ (4)B. 3个15. AABC 中,ZA=40° ,高BE 、CF 所在直线交于点。
完整版人教版八年级上册数学第十一章 三角形含答案

人教版八年级上册数学第十一章三角形含答案一、单选题(共15题,共计45分)1、下列几种形状的瓷砖中,只用一种不能够铺满地面的是()A.正三角形;B.正四边形;C.正五边形;D.正六边形.2、如图,D,E分别是的边AB、BC上的点,,若,则的值为()A. B. C. D.3、如图,是的角平分线,,则与的面积比为().A. B. C. D.4、如图,AD∥BC,若△ABC面积是15,则△DBC的面积是()A.12B.13C.14D.155、如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=()A.180°B.360°C.540°D.720°6、三角形两边的长分别是8和6,第三边的长是一元二次方程的一个实数根,则该三角形的周长是()A.20B.20或24C.26D.287、如图,在△ABC中,∠C=80°,D为AC上可移动的点,则x可能是()A.5B.10C.20D.258、以下列各组线段为边,能组成三角形的是()A.1cm,2cm,3cmB.15cm,8cm,6cmC.10cm,4cm,7cm D.3cm,3cm,7cm9、如图,在边长为a的正六边形内有两个小三角形,相关数据如图所示.若图中阴影部分的面积为S1,两个空白三角形的面积为S2.则=()A.3B.4C.5D.610、下列长度的三条线段可以组成三角形的是()A.1,2,4B.5,6,11C.3,3,3D.4,8,1211、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形的形状是()A.锐角三角形;B.直角三角形;C.钝角三角形;D.等腰三角形.12、已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是()A.a 2﹣b 2=c 2B.∠A﹣∠B=∠CC.∠A:∠B:∠C=3:4:5 D.a:b:c=7:24:2513、已知如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠OAD=()A.95°B.85°C.75°D.65°14、如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转角(0°< <180°)至△A′B′C,使得点A′恰好落在AB边上,则等于().A.150°B.90°C.60°D.30°15、如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为()A.相等B.互补C.相等或互补D.无法确定二、填空题(共10题,共计30分)16、设△ABC三边为a、b、c,其中a、b满足|a+b﹣6|+(a﹣b+4)2=0,则第三边c的取值范围________.17、若一个n边形的边数增加一倍,则内角和将增加________18、一个三角形有两边长为3和6,第三边的长是方程x2﹣6x+8=0的根,则这个三角形的周长等于________.19、一副三角板如图所示叠放在一起,则图中∠ABC=________20、如图,在△ABC中,M、N分别是AB、AC上的点,MN∥BC,若S△MBC :S△CMN=3:1,则S△AMN :S△ABC=________.21、一个凸多边形的内角和是其外角和的2倍,则这个多边形是________边形.22、一个多边形截去一个角后,形成的另一个多边形后的内角和为720°,那么原多边形的边数为________.23、若为三角形三边,化简________.24、已知如图ABC中,AD为BC边上的中线,AB=6,AC=8,则ABD与ACD的面积之差为________.25、如图,∠C=90°,∠A=30°,BD为角平分线,则SABD :S△CBD=________.三、解答题(共5题,共计25分)26、求出下列图中x的值。
人教版数学八年级上第11章三角形全章测试含答案

第11章 三角形 全章测试一、选择题(每题3分,共30分)1. 以下列各组长度的线段为边,能构成三角形的是 ( )A .7,3,4B .5,6,12C .3,4,5D .1,2,3 2. 等腰三角形的一个外角是80°,则其底角是( )A .100°B .100°或40°C .40°D .80 3.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )A .1260°B .1080°C .1620°D .360°4.用一批完全相同的多边形地砖铺地面,不能进行镶嵌的是( ) A.正三角形 B.正方形 C.正六边形 D.正八边形5.下列说法正确的是( )A.三角形的角平分线、中线及高都在三角形内B.直角三角形的高只有一条.C.三角形至少有一条高在形内D.钝角三角形的三条高都在形外. 6.一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( ) A .5 B .6 C .7 D .8 7.在下图中,正确画出AC 边上高的是( ).EBAC C A BCA BCA BE EE(A ) (B ) (C ) (D ) 8.如图所示,∠A 、∠1、∠2的大小关系是( ) A. ∠A >∠1>∠2 B. ∠2>∠1>∠A C. ∠A >∠2>∠1 D. ∠2>∠A >∠19. 给出下列命题:⑴三角形的一个外角一定大于它的一个内角.⑵若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形 ⑶三角形的最小内角不能大于60°⑷三角形的一个外角等于和它不相邻的两个内角的和 其中真命题的个数是 ( )(A )1个 (B )2个 (C )3个 (D )4个10.如图1,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )A .∠A=∠1+∠2B .2∠A=∠1+∠2C .3∠A=2∠1+∠2D .3∠A=2(∠1+∠2)E DA CB二、填空题(每题3分,共30分)11.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是 . 12.已知等腰三角形的两边长是5cm 和11cm ,则它的周长是 _______13.一个等腰三角形的周长为18,已知一边长为5,则其他两边长为 ____________. 14.已知一个三角形的三条边长为2、7、x ,则x 的取值范围是 _______. 15.如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E 的度数为 . 16.如图,∠A +∠B +∠C +∠D +∠E +∠F= .17.在△ABC 中,在△ABC 中,∠A-∠B=∠B-∠C =15°则∠A 、∠B 、∠C 分别为 .18.如图,在△ABC 中,两条角平分线BD 和CE 相交于点O ,若∠BOC=116°,那么∠A 的度数是_______。
人教版初中数学八年级上册第十一单元《三角形》综合测试卷(解析版)

⼈教版初中数学八年级上册第⼗⼀单元《三⾓形》综合测试卷(解析版)⼀⼆三四总分⼀、选择题(每题3分,共30分)(共10题;共30分)1.(3分)(2023八上·双鸭⼭期中)下列各图中,正确画出△ABC中AC边上的⾼的是( )A.B.C.D.2.(3分)(2023七上·沭阳⽉考)⼀块矩形草坪的⻓比宽多10米,它的周⻓是132米,求宽x所列的⽅程是( )A.x+10=132B.2x+10=132C.22x+10=132D.2x−10=132 3.(3分)(2020七上·庆云⽉考)代数式|x−2|+3的最⼩值是( )A.0B.2C.3D.54.(3分)(2020八上·余⼲⽉考)在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC为( )A.等腰三⾓形B.锐⾓三⾓形C.直⾓三⾓形D.钝⾓三⾓形5.(3分)(2023七下·承德期末)下列四个选项中,∠1与∠2互为邻补⾓的是( )A.B.C.D.6.(3分)(2024八上·合江期末)根据图中的数据,可得∠B的度数为( )A .40°B .50°C .60°D .70°7.(3分)(2022七上·晋州期中)已知射线OC 在∠AOB 的内部,下列4个表述中:①∠AOC =12∠AOB ;②∠AOC =∠BOC ;③∠AOB =2∠BOC ;④∠AOC +∠BOC =∠AOB ,能表⽰射线OC 是∠AOB 的⾓平分线的有( )A .1个B .2个C .3个D .4个8.(3分)(2022八上·港南期中)下列图形具有稳定性的是( )A .B .C .D .9.(3分)(2021九下·曹县期中)如图,在平⾯直⾓坐标系中,点 A 1 , A 2 , A 3 ,…, A n 在 x 轴上,点 B 1 , B 2 ,…, B n 在直线 y 上,若点 A 1 的坐标为 (1,0) ,且 △A 1B 1A 2 , △A 2B 2A 3 ,…, △A n B n A n +1 都是等边三⾓形,从左到右的⼩三⾓形(阴影部分)的⾯积分别记为 S 1 , S 2 ,.., S n ,则 S n 可表⽰为( )A .22B .22n −C .22n −D .22n −10.(3分)(2021八上·诸暨⽉考)如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与CE 交于G ,若∠BDC =130°,∠BGC =100°,则∠A 的度数为( )A .60°B .70°C .80°D .90°⼆、填空题(每题3分,共15分)(共5题;共15分)11.(3分)过⼗边形的⼀个顶点可作对⾓线的条数为m,则m的值为 .12.(3分)(2024七下·⽞武期中)如图1,点D在△ABC边BC上,我们知道若BDCD=ab,则S△ABDS△ACD=ab;反之亦然.如图2,BE是△ABC的中线,点F在边AB上,BE、CF相交于点O,若AFBF =m,则OEOB= .13.(3分)(2024七下·⻄安期中)已知三⾓形两边的⻓分别为1cm,5cm,第三边⻓为整数,则第三边的⻓为 .14.(3分)(2024七下·淮阴期中)如图,在△ABC中,点D是边BC的中点,点E是AC边上⼀点,AD和BE交于点O,CE=14AC,△ABC的⾯积是2024,若把△ABO的⾯积记为S1,把四边形CDOE的⾯积记为S 2,则S1−S2的值为 .15.(3分)(2018八上·武汉⽉考)图中x的值为 .三、解答题(共7题,共65分)(共7题;共65分)16.(10分)(2018八上·潘集期中)某零件如图所⽰,按规定∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=146°,就断定这个零件不合格,你能说出其中的道理吗?17.(5分)(2023八上·鹿寨期中)已知⼀个多边形中,每个内⾓都相等,并且每个外⾓等于与它相,求这个多边形的边数及内⾓和.邻的内⾓的1818.(5分)(2023八上·城厢开学考)已知:△ABC中,图①中∠B、∠C的平分线相交于M,图②中∠B、∠C的外⾓平分线相交于N,(1)(1分)若∠A=80°,∠BMC= °,∠BNC= ° .(2)(1分)若∠A=β,试⽤β表⽰∠BMC和∠BNC19.(11分)(2016八上·肇庆期末)⼀个零件的形状如图所⽰,按规定∠A=90º,∠C=25º,∠B=25º,检验员已量得∠BDC=150º,请问:这个零件合格吗?说明理由。
2023-2024学年人教版八年级数学上册第11章三角形 单元同步达标测试题(含答案)

2023年秋人教版八年级数学上册《第11章三角形》同步达标测试题一、单选题(满分40分)1.下列长度的三条线段能组成三角形的是()A.4cm,5cm,9cm B.5cm,5cm,11cmC.8cm,9cm,15cm D.7cm,12cm,20cm2.正十二边形的外角和为( )A.30°B.150°C.360°D.1800°3.如图,在△ABC中,BC边上的高为()A.线段AD B.线段BF C.线段BE D.线段CG4.如图,有一个与水平地面成20°角的斜坡,现要在斜坡上竖起一根与水平地面垂直的电线杆,电线杆与斜坡所夹的角∠1的度数为()A.50°B.60°C.70°D.80°5.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,就是平面图形的镶嵌.只用下面一种图形能够进行平面镶嵌的是()A.正三角形B.正五边形C.正八边形D.正十二边形6.如图,在△ABC中,D是BC中点,E是AD中点,连结BE、CE,若△ABC的面积为20,则△BCE的面积为()A.5B.10C.15D.187.将一副直角三角板如图放置,已知∠E=60°,∠C=45°,EF∥BC,则∠BND的大小为()A.100°B.105°C.110°D.115°8.如图,∠B=20°,∠C=60°,AD平分∠BAC,AE⊥BC,则∠DAE度数是()A.30°B.25°C.20°D.15°10.一个多边形的内角和是外角和的14.如图,在△ABC中,D为AC边的中点,积为4,则△BFC的面积为.15.如图,在△ABC中,∠ABC∠A的度数为____________.16.图①是一盏可折叠台灯,图为固定支撑杆,∠A是∠B的两倍,灯体旋转到CD′位置(图②中虚线所示∠BCD−∠DCD′=120°,则∠DCD三、解答题(满分40分)17.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是多少?18.如图,在ΔABC中,AD是高,∠DAC=10°,AE是ΔABC外角∠MAC的平分线,交BC 的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB和∠E的度数.19.画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将△ABC向左平移5格,再向下平移1格.请在图中画出平移后的△A′B′C′;(2)利用网格在图中画出△ABC的中线CD,高线AE;(3)△A′B′C′的面积为__________;(4)在图中能使S△ABC=S△PBC的格点P的个数有__________个(点P异于A).20.如图,已知∠1=∠BDC,∠2+∠3=180°.(1)求证:AD∥EC;(2)若CE⊥AE于点E,∠F=50°,求∠ADF的度数.21.如图,已知△ABC中,点D、E分别在边AB、AC上,点F在BE上.(1)若∠ADE=∠ABC,(2)若D、E、F分别是△ABC的面积.(1)如图1,这是一个五角星,则(2)如图2,将五角星截去一个角后多出一个角,求参考答案∵电线杆与水平地面垂直,∴∠2=90°,∴∠1=∠3=180°−20°−90°故答案为:三角形具有稳定性.10.解:由题意,得:(n−2)180°=2×360°,解得:n=6;∴这个多边形的边数为6;故答案为:611.解:∵a+b>c,b−a<c,c+b>a,∴a+b−c>0,b−a−c<0,c−a+b>0,∴|a+b−c|+|b−a−c|+|c−a+b|=a+b−c+a+c−b+c−a+b=a+b+c故答案为:a+b+c.12.解:由折叠的性质得∠ADE=∠ADC=110°,∵∠ADB=180°−∠ADC=70°,∴∠BDE=110°−∠ADB=110°−70°=40°,∵DE∥AB,∴∠B=∠BDE=40°.故答案为:40.13.解:∵AB∥CD,∠B+∠D=70°,∴∠B=∠HGD,∵∠EHF是△HGD的一个外角,∴∠EHF=∠HGD+∠D,∴∠EHF=∠B+∠D=70°,∵∠1+∠2+∠EHF=180°,∴∠1+∠2=180°−∠EHF=110°.∵CD∥OE,∴OA⊥CD,∵AO⊥OE,D′G⊥AB,∴∠AGC=∠AFC=90°,在四边形AFCG中,∠AGC+∠GCF+∠AFC(4)如图,利用等高模型,在图中能使S△ABC=S△PBC的格点P在直线m,n上(除点A 外),总共有21个;故答案为21.20.(1)证明:∵∠1=∠BDC,∴AB∥CD,∴∠2=∠ADC,∵∠2+∠3=180°,∴∠ADC+∠3=180°,∴AD∥CE;(2)解:∵CE⊥AE,∴∠CEF=90°,由(1)知AD∥CE,∴∠DAF=∠CEF=90°,在△AFD中,∠F=50°∴∠ADF=180°−90°−50°=40°.21.(1)证明:∵∠ADE=∠ABC,∴DE∥BC,∴∠AED=C,∵∠EDF=∠C,∴∠EDF=∠AED,∴DF∥AC;(2)解:∵点F是BE中点,∴S△DEF=S△DBF,设S△DEF=S△DBF=x,∵D是AB中点,∴S△ADE=S△BDE=2x,∵E是AC中点,∴S△ABE=S△CBE=4x,S△CEF=2x,=3x∴S四边形DECF∵S=9,四边形DECF∴3x=9,x=3,∴S△ABC=2S△ABE=8x=24.22. 解:(1)如图,由三角形的外角性质,得∠A+∠C=∠1,∠B+∠D=∠2,∵∠2+∠1+∠E=180°∴∠A+∠B+∠C+∠D+∠E=180°,故答案为:180°;(2)如图,延长CA与DG相较于点H,∠CAG和∠AGD是△HAG的两个外角,则∠CAG=∠H+∠AGH,∠AGD=∠H+∠HAG,∴∠CAG+∠AGD=∠H+∠HGA+∠H+∠HAG=∠H+180°,∴∠GAC+∠B+∠C+∠D+∠E+∠AGD=180°+180°=360°,故∠A+∠B+∠C+∠D+∠E+∠G的度数为360°.(3)由(2)知,每截去图1中的一个角,剩余角的度数会增加180°,图1中,∠A+∠B+∠C+∠D+∠E=180°,在题图3中,去掉五个角后,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J =180°+5×180°=1080°.。
人教版八年级数学上册第十一章《三角形》单元测试题及答案

人教版八年级数学上册第十一章《三角形》单元测试题及答案一、选择题(每题4分,共40分)1. 在三角形ABC中,a = 3cm,b = 4cm,c = 5cm,那么这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定2. 如果一个三角形的两边长分别是5和10,那么第三边的长度可能是()A. 3B. 6C. 11D. 153. 三角形的一个外角等于与它不相邻的两个内角的和,那么这个外角的度数是()A. 90°B. 120°C. 180°D. 无法确定4. 在三角形ABC中,∠A = 50°,∠B = 60°,那么∠C 的度数是()A. 70°B. 80°C. 90°D. 100°5. 如果一个三角形的两边长分别是8和15,那么第三边的长度可能是()A. 7B. 10C. 17D. 206. 一个等腰三角形的底边长是8cm,腰长是10cm,那么这个三角形的周长是()A. 36cmB. 40cmC. 44cmD. 48cm7. 在三角形ABC中,∠A = 30°,∠B = 45°,那么∠C 的度数是()A. 75°B. 85°C. 90°D. 95°8. 如果一个三角形的两边长分别是6和9,那么第三边的长度可能是()A. 3B. 6C. 12D. 159. 一个等边三角形的周长是15cm,那么这个三角形的边长是()A. 3cmB. 4cmC. 5cmD. 6cm10. 在三角形ABC中,∠A = 40°,∠B = 70°,那么∠C的度数是()A. 20°B. 30°C. 50°D. 60°二、填空题(每题4分,共40分)11. 在三角形ABC中,a = 5cm,b = 7cm,c = 9cm,那么这个三角形的面积是_________。
2021年人教版数学八年级上册 第十一章《三角形》测试卷(十一).doc

2021年人教版数学八年级上册第十一章《三角形》测试卷(十一)姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、单项选择题。
(每小题1分,共10分)1.在如图所示的图形中,三角形有()A. 4个B. 5个C. 6个D. 7个2.在△ABC中,若三条边长均为整数,周长为11,且有一条边长为4,则这个三角形最长边可能取值的最大值是()A. 7B. 6C. 5D. 43.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为()A. 2B. 3C. 5D. 134.若一个三角形的两条边长分别为3和8,而第三条边长为奇数,则第三条边长为()A. 5或7B. 7C. 9D. 7或95.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()评卷人得分A. 三角形的稳定性B. 两点之间线段最短C. 两点确定一条直线D. 垂线段最短6.如图,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于()A. 120°B. 115°C. 110°D. 105°7.一副三角尺有两个直角三角形,如图叠放在一起,则∠α的度数是()A. 165°B. 120°C. 150°D. 135°8.一副三角板如图叠放在一起,则图中∠a的度数为()A. 75°B. 60°C. 65°D. 55°9.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是()A. 110°B. 108°C. 105°D. 100°10.如果一个多边形的内角和是其外角和的一半,那么这个多边形是()A. 六边形B. 五边形C. 四边形D. 三角形二、填空题。
人教版八年级数学上册第十一章《三角形》考试卷(含答案)
人教版八年级数学上册第十一章《三角形》考试卷(含答案)一、选择题(共10小题)1. 如图,窗户打开后,用窗钩AB可将其固定,所运用的几何原理是( )A. 两点之间线段最短B. 三角形两边之和大于第三边C. 三角形的稳定性D. 两点确定一条直线2. 下列各组数中,能作为一个三角形三边长的是( )A. 1,1,2B. 1,2,4C. 2,3,5D. 2,3,43. 如图,AB∥CD,AC,BD相交于点E,若∠DEC=100∘,∠C=40∘,则∠B的度数是( )A. 30∘B. 40∘C. 50∘D. 60∘4. 一个正多边形的每个内角的度数都等于相邻外角的度数,则该正多边形的边数是( )A. 3B. 4C. 6D. 125. 把一把直尺与一块三角板如图放置,若∠1=45∘,则∠2的度数为( )A. 115∘B. 120∘C. 145∘D. 135∘6. 如图,∠C,∠1,∠2之间的大小关系是( )A. ∠1<∠2<∠CB. ∠2>∠1>∠CC. ∠C>∠1>∠2D. ∠1>∠2>∠C7. 已知一个多边形的内角和是1080∘,则这个多边形是( )A. 六边形B. 七边形C. 八边形D. 九边形8. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4cm2,则S阴影等于( )A. 2cm2B. 1cm2C. 12cm2 D. 14cm29. 在△ABC中,如果∠A:∠B:∠C=1:2:3,那么△ABC的形状是( )A. 直角三角形B. 锐角三角形C. 等腰三角形D. 等腰直角三角形10. 如图,在△ABC中,点D是∠ABC和∠ACB的平分线的交点,∠A=80∘,∠ABD=30∘,则∠DCB的度数为( )A. 25∘B. 20∘C. 15∘D. 10∘二、填空题(共8小题)11. 三角形中,其中两条边长分别为4cm和7cm,则第三边c的长度的取值范围是.12. 一副三角板按如图所示摆放,则α的度数为.13. 如图,在△ABC中,∠C=90∘,∠A=20∘,BD为∠ABC的平分线,则∠BDC=.14. 如图,在△ABC中,∠ABC=∠C,∠A=40∘,BD⊥AC于点D,则∠DBC=度.15. 一个多边形截去一个角(截线不过顶点)后,形成的多边形的内角和是2520∘,则原多边形的边数是.16. 将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为.17. 如图,在△ABC中,∠ACB=90∘,∠A=50∘.如果将△ABC沿着CD所在直线翻折,使点A溶在边CB上Aʹ处,那么∠AʹDB=.18. 已知,如图1,在△ABC,∠ABC、∠ACB的角平分线交于点O,则∠BOC=90∘+12∠A=1 2×180∘+12∠A.如图2,在△ABC中,∠ABC、∠ACB的两条三等分角线分别对应交于O1、O2,则∠BO1C=23×180∘+13∠A,∠BO2C=13×180∘+23∠A.根据以上阅读理解,你能猜想(n等分时,内部有n−1个点)(用n的代数式表示)∠BO1C=.三、解答题(共6小题)19. 如图所示,已知AD,AE分别是△ABC高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90∘.试求:(1)AD的长;(2)△ABE的面积;(3)△ACE与△ABE的周长的差.20. 请回答下列问题.(1)如图(1),BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,请说明∠BDC与∠A∠A.之间的等量关系是∠BDC=90∘+12(2)如图(2),BD,CD是△ABC的两个外角的平分线,请你探究∠BDC与∠A之间有怎样的等量关系.(3)如图(3),BD,CD分别是△ABC的一个内角的平分线与一个外角的平分线,试探究∠BDC与∠A之间的等量关系.21. 在△ABC中,CD是AB边上的中线,如果△BCD的周长比△ACD的周长多3cm,且AC=4cm,求边BC的长.22. 如图,在△ABC中,∠BAC=45∘,AD是∠BAC的角平分线,BE是边AC上的高,AD,BE相交于点O,求∠AOB的度数.23. 如图,在△ABC中,AD是∠BAC的角平分线,BE是边AC上的高,AD,BE相交于点O,如果∠AOE=67.5∘,求∠ABE的度数.24. 如图,在△ABC中,已知∠BAC=86∘,BD平分∠ABC,CD∥AB,∠ACB=34∘,求∠D的度数.参考答案1. C2. D【解析】A选项:1+1=2,故不能作为三角形三边长;B选项:1+2=3<4,故不能作为三角形三边长;C选项:2+3=5,故不能作为三角形三边长;D选项:2+3=5>4,故能作为三角形三边长.3. B4. B【解析】正多边形的每个内角的度数都等于相邻外角的度数,则外角的度数为90∘,360÷90∘=4,则正多边形的边数是4.5. D【解析】易知∠2=∠1+90∘,∵∠1=45∘,∴∠2=45∘+90∘=135∘.6. D7. C【解析】设这个多边形是n边形,由题意知,(n−2)×180∘=1080∘,所以n=8,所以该多边形的边数是八边形.8. B【解析】S阴影=12S△BCE=14S△ABC=1cm2.9. A10. B【解析】∵BD平分∠ABC,∴∠ABC=2∠ABD=2×30∘=60∘,∴∠ACB=180∘−∠A−∠ABC=180∘−80∘−60∘=40∘,∵CD平分∠ACB,∴∠DCB=12∠ACB=12×40∘=20∘.11. 3cm<c<11cm【解析】三角形两边的和大于第三边,两边的差小于第三边,由题意得7−4<c<7+4,即3<c<11.12. 105∘13. 55∘14. 2015. 15【解析】设截去一个角后的多边形的边数为n,于是(n−2)⋅180∘=2520∘,解得n=16.一个多边形截去一个角(截线不过顶点)后边数增加1,所以原多边形有15条边.16. 105∘17. 10∘18. n−1n ×180∘+1n∠A【解析】根据题中所给的信息,总结可得:∠BO1C=n−1n ×180∘+1n∠A,故答案为:∠BO1C=n−1n ×180∘+1n∠A.19. (1)∵∠BAC=90∘,AD是边BC上的高,∴12AB⋅AC=12BC⋅AD,∴AD=AB⋅ACBC =6×810=4.8(cm),即AD的长为4.8cm.(2)∵△ABC是直角三角形,∠BAC=90∘,AB=6cm,AC=8cm,∴S△ABC=12AB⋅AC=12×6×8=24(cm2),又∵AE是△ABC的中线,∴BE=EC,∴12BE⋅AD=12EC⋅AD,即S△ABE=S△AEC,∴S△ABE=12S△ABC=12(cm2),∴△ABE的面积是12cm2.(3)∵AE为BC边上的中线,∴BE=CE,∴△ACE的周长−△ABE的周长=AC+AE+CE−(AB+BE+AE)=AC−AB=8−6=2(cm),即△ACE与△ABE的周长的差是2cm.20. (1)略.∠A.(2)∠BDC=90∘−12∠A(3)∠BDC=1221. 因为CD是△ABC的中线,所以AD=BD.因为C△ACD=AC+AD+CD,C△BCD=BC+BD+CD,所以(BC+BD+CD)−(AC+AD+CD)=3.所以BC−AC=4.因为AC=3cm,所以BC=7cm.22. ∠AOB=112.5∘.23. ∵AD是∠BAC的角平分线(已知),∠BAC(角平分线的意义),∴∠BAD=∠CAD=12∵BE是边AC上的高(己知),∴∠BEA=90∘(垂直的意义),∵∠AOE+∠CAD+∠BEA=180∘(三角形的内角和180∘),且∠AOE=67.5∘(已知),∴∠CAD=22.5∘(等式性质),∴∠BAD=22.5∘(等量代换),∵∠AOE=∠ABE+∠BAD(三角形的一个外角等于与它不相邻的两个内角之和),∴∠ABE=45∘(等式性质).24. 因为∠BAC=86∘,∠ACB=34∘,所以∠ABC=180∘−86∘−34∘=60∘,因为BD平分∠ABC,∠ABC=30∘,所以∠ABD=12因为CD∥AB,所以∠D=∠ABD=30∘.。
八年级数学上册第十一章《三角形》测试题-人教版(含答案)

八年级数学上册第十一章《三角形》测试题-人教版(含答案)一、选择题(30分)1.下列说法错误的是()A.三角形的角平分线把三角形分成面积相等的两部分B.三角形的三条中线相交于一点C.直角三角形的三条高交于三角形的直角顶点处D.钝角三角形的三条高所在直线的交点在三角形的外部2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是()A.①②③B.①③④C.①④D.①②④3.如果线段AB=3cm,BC=1cm,那么A,C两点的距离d的长度为()A.4cm B.2cm C.4cm或2cm D.小于或等于4cm,且大于或等于2cm4.如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=()A.40°B.50°C.60°D.70°5.如图,△ABC中,BD,BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE,∠F, ②2∠BEF,∠BAF,∠C,③∠F,∠BAC,∠C,④∠BGH,∠ABE,∠C,其中正确个数是()A.4个B.3个C.2个D.1个6.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2016°,则n等于()A.11B.12C.13D.147.如图,直线AB,CD被BC所截,若AB,CD,,1,45°,,2,35°,则∠3,( )A.80°B.70°C.60°D.90°8.如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为()A.∠AHE>∠CHG B.∠AHE<∠CHG C.∠AHE=∠CHG D.不一定9.若a,b,c是△ABC的三边的长,则化简|a,b,c|,|b,c,a|,|a,b,c|的结果是()A.a,b,c B.,a,3b,c C.a,b,c D.2b,2c10.已知正多边形的一个外角等于40,那么这个正多边形的边数为()A.6B.7C.8D.9二、填空题(15分)11.如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.12.设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x,150°时,对应的和谐数对有一个,它为(10,20);当x,66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________,13.根据如图所示的已知角的度数,求出其中∠α的度数为______.14.在图中过点P任意画一条直线,最多可以得到____________个三角形.15.如图,点O是△ABC的两条角平分线的交点,若△BOC=118°,则△A的大小是。
人教版八年级上册数学第11章三角形单元测试卷2(Word版,含答案)

人教版八年级上册数学第11章三角形单元测试卷2一.选择题(本大题共10小题,每小题3分,共30分)1.下列图形中具有稳定性的是( )A.正三角形B.平行四边形C.正五边形D.正六边形2.下列每组数能摆出三角形的是( )A.1,2,3B. 3,4,4C. 5,5,11D. 3,5,93.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为()A.2B.3C.5D.64.下列说法正确的是()A.三角形的三条中线交于一点B.三角形的三条高都在三角形内部C.三角形不一定具有稳定性D.三角形的角平分线可能在三角形的内部或外部5.如图,直线AB∥CD,且AC∥CB于点C,若∥BAC=35°,则∥BCD的度数为()A.65°B.55°C.45°D.35°6.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B是()A.45°B.55°C.65°D.75°7.如图,若∥A=70°,∥B=40°,∥C=32°,则∥BDC=()A.102°B.110°C.142°D.148°8.如图,在∥ABC中,AD为BC边上的中线,若AB=5 cm,AC=3 cm,则∥ABD的周长比∥ACD 的周长多( )A.5 cmB.3 cmC.8 cmD.2 cm9.将一个四边形截去一个角后,它不可能是()A.六边形B.五边形C.四边形D.三角形10.如图,四边形ABCD中,∥1、∥2、∥3分别为四边形ABCD的外角.判断下列大小关系何者正确.()A.∥1+∥3=∥ABC+∥DB.∥1+∥3<∥ABC+∥DC.∥1+∥2+∥3=360°D.∥1+∥2+∥3>360°二.填空题(本大题共5小题,每小题3分,共15分)11.一个三角形的两边长分别是2和4,若第三边的长为偶数,则第三边的长是.12.一个多边形的每一个外角都等于45°,则这个多边形的内角和为度.13.如图,H若是△ABC三条高AD,BE,CF的交点,则△BHA中边BH上的高是.14.一个多边形的每个内角都为144°,则它的边数是15.如图,∠1,∠2,∠3的大小关系是.三.解答题(一):(本大题共3小题,每小题8分,共24分)16.如图所示,已知△ABC,过点A画△ABC的角平分线AD、中线AE和高线AF.17.如图所示,在∥ABC中,∥A=50°,∥B=70°,∥ACB的平分线交AB于点D,DE∥BC交AC 于点E,求∥BDC,∥EDC的度数.18.如图所示,在△ABC中,AE是角平分线,AD是高,∠BAC=80°,∠EAD=10°,求∠B 的度数四.解答题(二):(本大题共3小题,每小题9分,共27分)19.如图所示,CE是∥ABC的一个外角∥ACD的平分线,且EF∥BC交AB于点F,∥A=60°,∥CEF =50°,求∥B的度数.20.如图所示,已知AD是∥ABC的边BC上的中线.(1)作出∥ABD的边BD上的高;(2)若∥ABC的面积为10,求∥ADC的面积;(3)若∥ABD的面积为6,且BD边上的高为3,求BC的长.21.如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12 cm与15 cm 两部分,求三角形各边长.五.解答题(三):(本大题共2小题,每小题12分,共24分)22.在四边形ABCD中,∠A=140°,∠D=80°.(1)如图①,若∠B=∠C,求∠C的度数;(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.23.(1)如图①,求∠A+∠C+∠G+∠E+∠F的度数;(2)若将图①中的每个角都截去,如图②,则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=1080° .参考答案一.选择题(本大题共10小题,每小题3分,共30分)1.下列图形中具有稳定性的是( A)A.正三角形B.平行四边形C.正五边形D.正六边形2.下列每组数能摆出三角形的是( B)A.1,2,3B. 3,4,4C. 5,5,11D. 3,5,93.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为(C)A.2B.3C.5D.64.下列说法正确的是(A)A.三角形的三条中线交于一点B.三角形的三条高都在三角形内部C.三角形不一定具有稳定性D.三角形的角平分线可能在三角形的内部或外部5.如图,直线AB∥CD,且AC∥CB于点C,若∥BAC=35°,则∥BCD的度数为(B)A.65°B.55°C.45°D.35°6.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B是(C)A.45°B.55°C.65°D.75°7.如图,若∥A=70°,∥B=40°,∥C=32°,则∥BDC=(C)A.102°B.110°C.142°D.148°8.如图,在∥ABC中,AD为BC边上的中线,若AB=5 cm,AC=3 cm,则∥ABD的周长比∥ACD 的周长多( D)A.5 cmB.3 cmC.8 cmD.2 cm9.将一个四边形截去一个角后,它不可能是(A)A.六边形B.五边形C.四边形D.三角形10.如图,四边形ABCD中,∥1、∥2、∥3分别为四边形ABCD的外角.判断下列大小关系何者正确.(A)A.∥1+∥3=∥ABC+∥DB.∥1+∥3<∥ABC+∥DC.∥1+∥2+∥3=360°D.∥1+∥2+∥3>360°二.填空题(本大题共5小题,每小题3分,共15分)11.一个三角形的两边长分别是2和4,若第三边的长为偶数,则第三边的长是4.12.一个多边形的每一个外角都等于45°,则这个多边形的内角和为1080度.13.如图,H若是△ABC三条高AD,BE,CF的交点,则△BHA中边BH上的高是AE.14.一个多边形的每个内角都为144°,则它的边数是1015.如图,∠1,∠2,∠3的大小关系是∠1<∠2<∠3.三.解答题(一):(本大题共3小题,每小题8分,共24分)16.如图所示,已知△ABC,过点A画△ABC的角平分线AD、中线AE和高线AF.17.如图所示,在∥ABC中,∥A=50°,∥B=70°,∥ACB的平分线交AB于点D,DE∥BC交AC 于点E,求∥BDC,∥EDC的度数.解:∠ACB =180°-∠A -∠B =180°-50°-70°=60°.∵CD 平分∠ACB ,∴∠BCD =12∠ACB =12×60°=30°.∴∠BDC =180°-∠B -∠BCD =180°-70°-30°=80°.∵DE ∥BC ,∴∠EDC =∠BCD =30°.18.如图所示,在△ABC 中,AE 是角平分线,AD 是高,∠BAC =80°,∠EAD =10°,求∠B 的度数解:∵AD 是高,∴∠ADC =90°,∵AE 是角平分线,∠BAC =80°,∴∠CAE =12∠BAC =40°, ∵∠EAD =10°,∴∠CAD =30°,∴∠C =60°,∴∠B =180°﹣∠BAC ﹣∠C =40°四.解答题(二):(本大题共3小题,每小题9分,共27分)19.如图所示,CE 是∥ABC 的一个外角∥ACD 的平分线,且EF∥BC 交AB 于点F ,∥A =60°,∥CEF =50°,求∥B 的度数.解:∵EF∥BC,∴∠ECD=∠CEF=50°.∵CE平分∠ACD,∴∠ACD=2∠ECD=100°.∴∠ACB=180°-∠ACD=80°.∴∠B=180°-(∠A+∠ACB)=180°-(60°+80°)=40°.20.如图所示,已知AD是∥ABC的边BC上的中线.(1)作出∥ABD的边BD上的高;(2)若∥ABC的面积为10,求∥ADC的面积;(3)若∥ABD的面积为6,且BD边上的高为3,求BC的长.(1)如图所示,虚线即为所求.×10=5.(2)∥AD是∥ABC的边BC上的中线,∥ABC的面积为10,∥∥ADC的面积=12(3)∥AD是∥ABC的边BC上的中线,∥BD=CD,∥∥ABD的面积为6,∥∥ABC的面积为12,∥BD边上的高为3,∥BC=12×2÷3=8.21.如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12 cm与15 cm 两部分,求三角形各边长.解:∵DB为△ABC的中线,∴AD=CD.设AD=CD=x,则AB=AC=2x.当x+2x=12,BC+x=15时,解得x=4,BC=11.此时△ABC的三边长为AB=AC=8,BC=11.当x+2x=15,BC+x=12时,解得x=5,BC=7.此时△ABC的三边长为AB=AC=10,BC=7.五.解答题(三):(本大题共2小题,每小题12分,共24分)22.在四边形ABCD中,∠A=140°,∠D=80°.(1)如图①,若∠B=∠C,求∠C的度数;(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.解:(1)∵∠A +∠B +∠C +∠D =360°,∠B =∠C ,∴∠B =∠C =360°-∠A -∠D 2=360°-140°-80°2=70°.(2)∵BE ∥AD ,∴∠BEC =∠D =80°,∠ABE =180°-∠A =180°-140°=40°.又∵BE 平分∠ABC ,∴∠EBC =∠ABE =40°.∴∠C =180°-∠EBC -∠BEC =180°-40°-80°=60°.23.(1)如图①,求∠A +∠C +∠G +∠E +∠F 的度数;(2)若将图①中的每个角都截去,如图②,则∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠M +∠N = 1080° .解:(1)∵∠A +∠G =∠DMF ,∠C +∠E =∠MDF ,△DFM 中,∠F +∠DMF +∠MDF =180°,∴∠A +∠C +∠G +∠E +∠F =180°.。
2022-2023学年人教版八年级数学上册第11章三角形 单元达标测试题 (word版含答案)

2022-2023学年人教版八年级数学上册《第11章三角形》单元达标测试题(附答案)一.选择题(共8小题,满分40分)1.已知一个三角形的两边长分别为6和3,则这个三角形的第三边长可能是()A.3B.6C.9D.102.一个多边形的每个外角都是45°,则这个多边形的边数为()A.八B.九C.十D.七3.如图,在△ABC中,AF平分∠BAC交BC于点F、BE平分∠ABC交AC于点E,AF与BE相交于点O,AD是BC边上的高,若∠C=50°,BE⊥AC,则∠DAF的度数为()A.10°B.12°C.15°D.20°4.如图,在△CEF中,∠E=78°,∠F=47°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()A.45°B.47°C.55°D.78°5.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=()A.15°B.25°C.30°D.45°6.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是()A.三角形具有稳定性B.三角形内角和等于180°C.两点之间线段最短D.同位角相等,两直线平行拉杆7.下列各组图形中,BD是△ABC的高的图形是()A.B.C.D.8.如图,在三角形ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①AH⊥EF;②∠ABF=∠EFB;③AC∥BE;④∠E=∠ABE.其中正确的结论有()A.4个B.3个C.2个D.1个二.填空题(共8小题,满分40分)9.已知三角形的两边a和b的长分别为3和8,则第三边c的范围为.10.若一个正多边形的内角和与它的外角和之和是1260°,则这个正多边形的边数是.11.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为°.12.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD 折叠后,点C落到点E处,若∠BAE=50°,则∠DAC的度数为°.13.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=70°,∠C =40°,则∠DAE的度数为.14.在锐角△ABC中,将∠a的顶点P放置在BC边上,使∠a的两边分别与边AB,AC交于点E,F(点E不与B点重合,点F不与点C重合,且点E,F均不与点A重合).(1)当∠BAC=40°,∠a=60°时,∠BEP+∠CFP=°;(2)直接写出∠BEP,∠CFP,∠BAC,∠a之间的数量关系.15.在△ABC中,AB<AC,BC边上的中线AD将△ABC分成的两个新三角形的周长差为5cm,AB与AC的和为13cm,则AC的长为.16.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与F A交于点E,则∠E的度数为.三.解答题(共5小题,满分40分)17.如图所示,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E.(1)若∠C=60°,∠BAC=80°,求∠ADB的度数;(2)若∠BED=60°,求∠C的度数.18.如图,在四边形ABCD中,∠D+∠ABC=180°,BE平分∠ABC交CD于点E,连接.(1)若∠C=∠1,求证:∠CBE=∠AED.(2)若∠C=80°,∠D=124°,求∠CEB的度数.19.如图,在△ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,AD∥EF,∠1+∠2=180°.(1)说明:AB∥DG;(2)若DG是∠ADC的平分线,∠2=3∠B+40°,求∠B的度数.20.在三角形ABC中,点D在线段AC上,DE∥BC交AB于点E,点F在线段AB上(点F不与点A,E,B重合),连接DF,过点F作FG⊥FD交射线CB于点G.(1)如图1,点F在线段BE上.①用等式表示∠EDF与∠BGF的数量关系,并说明理由;②如图,求证:∠ABC+∠BFG﹣∠EDF=90°;(2)当点F在线段AE上时,依题意,在图2中补全图形,请直接用等式表示∠EDF与∠BGF的数量关系,不需证明.21.在△ABC中,(1)如图1,BP、CP为∠ABC和∠ACB的角平分线,求∠P与∠A之间的关系?(2)如图2,BP、CP为∠ABC和∠ACE的角平分线,求∠P与∠A之间的关系?(3)如图3,BP、CP为∠CBD和∠BCE的角平分线,求∠P与∠A之间的关系?(请选择其中一道小题写出详细过程)参考答案一.选择题(共8小题,满分40分)1.解:根据三角形的三边关系得,第三边长应大于6﹣3=3,而小于6+3=9,答案中,只有B符合题意.故选:B.2.解:∵360÷45=8(边),∴多边形的边数为八,故选:A.3.解:∵BE⊥AC,BE平分∠ABC,∴∠AEB=∠CEB=90°,∠ABE=∠CBE,∵BE=BE,∴△ABE≌△CBE(ASA),∴∠BAC=∠C=50°,∴∠ABC=190°﹣∠BAC﹣∠C=80°,∵AF平分∠BAC,∴∠BAF=∠BAC=25°,∵BE⊥AC,∴∠ADB=90°,∴∠BAD=10°∴∠DAF=∠BAF﹣∠DAB=15°,故选:C.4.解:延长EC交AB于点H,如图所示:∵∠E=78°,∠F=47°,∴∠ECF=180°﹣∠E﹣∠F=55°,∵AB∥CF,AD∥CE,∴∠BHE=∠ECF=55°,∠BHE=∠A,∴∠A=55°.故选:C.5.解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,∴∠DCE=∠ACE,∠DBC=∠ABC,又∵∠D=∠DCE﹣∠DBC,∠A=∠ACE﹣∠ABC,∴∠D=∠A=25°.故选:B.6.解:人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做的道理是三角形具有稳定性.故选:A.7.解:根据三角形高的定义可知,只有选项B中的线段BD是△ABC的高,故选:B.8.解:∵AH⊥BC,EF∥BC,∴AH⊥EF,故①正确;∵BF平分∠ABC,∴∠ABF=∠CBF,∵EF∥BC,∴∠EFB=∠CBF,∴∠ABF=∠EFB,故②正确;∵BE⊥BF,而AC与BF不一定垂直,∴BE∥AC不一定成立,故③错误;∵BE⊥BF,∴∠E和∠EFB互余,∠ABE和∠ABF互余,而∠EFB=∠ABF,∴∠E=∠ABE,故④正确.故选:B.二.填空题(共8小题,满分40分)9.解:由题意可得8﹣3<c<8+3,∴5<c<11.故答案为:5<c<11.10.解:设正多边形的边数为n,则180×(n﹣2)+360°=1260°,∴n=7,∴这个正多边形的边数是七.故答案为:七.11.解:∵∠B=50°,∠CEB=∠ADB﹣90°,∴∠EHD=180°﹣50°=130°,又∵∠EHD=∠AHC,∴∠AHC=130°,故答案为:130.12.解:∵∠B=40°,∠C=30°,∴∠BAC=110°,∵∠BAE=50°,∴∠CAE=60°,∵△ADC沿直线AD折叠得到△ADE,∴∠CAD=∠EAD=30°,故答案为:30.13.解:∵∠B=70°,∠C=40°,∴∠BAC=70°,∵AD是BC边上的高,∴∠CAD=50°,∵AE是∠BAC的平分线,∴∠CAE=∠BAC=35°,∴∠DAE=∠CAD﹣∠CAE=15°.故答案为:15°.14.解:(1)如图,连接AP,∵∠BEP=∠EAP+∠EP A,∠CFP=∠F AP+∠FP A,∴∠BEP+∠CFP=∠EAP+∠EP A+∠F AP+∠FP A,即∠BEP+∠CFP=∠BAC+∠EPF,∴∠BEP+∠CFP=∠BAC+∠α=40°+60°=100°,故答案为:100°;(2)∠BEP+∠CFP=∠BAC+∠α,理由如下:∵∠BEP=∠EAP+∠EP A,∠CFP=∠F AP+∠FP A,∴∠BEP+∠CFP=∠EAP+∠EP A+∠F AP+∠FP A,即∠BEP+∠CFP=∠BAC+∠EPF,∴∠BEP+∠CFP=∠BAC+∠α.15.解:∵AD是△ABC的中线,∴BD=CD,∵AB<AC,两个新三角形的周长差为5cm,∴(AC+AD+CD)﹣(AB+AD+BD)=5cm,∴AC﹣AB=5cm,∵AB+AC=13cm,∴AC=9cm,故答案为:9cm.16.解:∵BE平分∠ABC,∴∠ABE=.∵AF平分外角∠BAD,∴∠F AB=.又∵∠BAD=∠C+∠ABC=90°+∠ABC,∴∠F AB=.又∵∠F AB=∠E+∠ABE,∴∠E=∠F AB﹣∠ABE=45°+﹣=45°.故答案为:45°.三.解答题(共5小题,满分40分)17.解:(1)∵AD平分∠BAC,∠BAC=80°,∴∠DAC=∠BAC=40°,∵∠ADB是△ADC的外角,∠C=60°,∴∠ADB=∠C+∠DAC=100°;(2)∵∠BED是△ABE的外角,∠BED=60°,∴∠BAD+∠ABE=∠BED=60°,∵AD平分∠BAC,BE平分∠ABC,∴∠BAC=2∠BAD,∠ABC=2∠ABE,∴∠BAC+∠ABC=2(∠BAD+∠ABE)=120°,∵∠BAC+∠ABC+∠C=180°,∴∠C=180°﹣(∠BAC+∠ABC)=60°.18.(1)证明:∵∠C+∠CBE+∠CEB=180°,∠AED+∠1+∠CEB=180°,∠C=∠1,∴∠CBE=∠AED;(2)解:∵∠D+∠ABC=180°,∠D=124°,∴∠ABC=56°,∵BE平分∠ABC,∴∠CBE=∠ABC=28°,∵∠C+∠CBE+∠CEB=180°,∠C=80°,∴∠CEB=72°.19.证明:(1)由题意可知,∠BEF=∠1,∠BFE=∠ADB,∴∠BEF+∠BFE=∠1+ADB,∴180°﹣(∠BEF+∠BFE)=180°﹣(∠1+ADB),即∠B=∠GDC,∴AB∥DG.解:(2)∵DG是∠ADC的平分线,且AB∥DG,∴∠1=∠DGC=∠B,∵∠2=3∠B+40°,∴180°﹣∠1=3∠B+40°,∴180°﹣∠B=3∠B+40°,∴∠B=35°.20.(1)①解:结论:∠EDF+∠BGF=90°.理由:如图1中,过点F作FH∥BC交AC于点H.∵ED∥BC,∴ED∥FH.∴∠EDF=∠1.∵FH∥BC,∴∠BGF=∠2.∵FG⊥FD,∴∠DFG=90°.∴∠1+∠2=90°.∴∠EDF+∠BGF=90°.②证明:过点F作FH∥BC交AC于点H.如图2,∴∠ABC=∠AFH.∴∠ABC=∠1+∠3.∴∠3=∠ABC﹣∠1.∵∠EDF=∠1,∴∠3=∠ABC﹣∠EDF.∵FG⊥FD,∴∠DFG=90°.∴∠BFG+∠3=90°.∴∠3=90°﹣∠BFG.∴90°﹣∠BFG=∠ABC﹣∠EDF.∴∠ABC+∠BFG﹣∠EDF=90°.(2)解:结论:∠BGF﹣∠EDF=90°.理由:设DE交FG于J.如图3,∵DE∥BC,∴∠BGF=∠FJE,∵∠FJE=∠DEJ+∠EDF,∠DEJ=90°,∴∠BGF﹣∠EDF=90°.当点G在CB的延长线上时,同法可证∠EDF+∠BGF=90°,如图3,21.解:(1)∵BP、CP为∠ABC和∠ACB的角平分线,∴∠CBP=,∠BCP=.∴∠CBP+∠CBP=.∵∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A.∴∠PBC+∠PCB=.∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣=90°+.(2)∵∠P+∠PBC=∠PCD,∴∠P=∠PCD﹣∠PBC.∵BP、CP为∠ABC和∠ACE的角平分线,∴∠PCD=,∠PBC=.∴∠P==.(3)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,∴∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.∵BP、CP为∠CBD和∠BCE的角平分线,∴∠CBP=,∠BCP=.∴=.∴∠P=180°﹣(∠CBP+∠BCP)=180°﹣=90°﹣.。
八年级数学上册《第十一章 三角形》单元测试卷-带答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷-带答案(人教版)一、单选题1.下列语句正确的是()A.三角形的角平分线、中线和高都在三角形内B.直角三角形的高只有一条C.三角形的高至少有一条在三角形内D.钝角三角形的三条高都在三角形外2.正多边形的每一个外角都等于45°,则这个多边形的边数是()A.6 B.7 C.8 D.93.已知三角形的两边长分别是4、7,则第三边长a的取值范围是()A.3<a<11 B.3≤a≤11 C.a>3 D.a<114.如图,∠1+∠2+∠3+∠4+∠5+∠6=()A.180°B.270°C.360°D.不能确定5.如图,在△ABC中AB=AC,点D是B C延长线上一点,且∠BAC=2∠CAD已知BC=4,AD= 7则△ACD的面积为()A.7 B.14 C.21 D.286.如图,D,E是△ABC中BC边上的点,且BD=DE=EC,那么()A.S1<S2<S3B.S1>S2>S3C.S1=S2=S3D.S2<S1<S37.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为()A.180°B.270°C.360°D.720°8.如图,将三角尺的直角顶点放在直尺的一边上∠1=30°,∠2=50°则∠3的度数等于()A.20°B.30°C.50°D.80°二、填空题9.在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC的度数是.10.正多边形的每一个内角比相邻的外角大90°,则这个多边形的边数是11.已知△ABC的三个内角的度数之比∠A:∠B:∠C=1:3:5则∠B=度,∠C=度.12.如图,已知AB//DE,∠ABC=70°,∠CDE=140°则∠BCD=.13.如图,△ABC中,点D在BC上且BD=2DC,点E是AC中点,已知△CDE面积为2,那么△ABC的面积为.14.如图所示,在△ABC中∠A=66°,点I是三条角平分线的交点,则∠BIC的大小为三、解答题15.将长度为24的一根铝丝折成各边均为正整数的三角形,这个三角形的三边分别记为a、b、c,且a≤b≤c,请写出满足题意的a、b、c.16.已知:如图,△ABC的两条高线BD、CE相交于H点∠A=56°求∠BHC的度数.17.探索归纳:(1)如图1,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( ) A.90°B.135°C.270°D.315°(2)如图2,已知△ABC中∠A=40°,剪去∠A后成四边形,则∠1+∠2=(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.18.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.19.如图,六边形ABCDEF的内角都相等,CF∥AB.(1)求∠FCD的度数;(2)求证:AF∥CD.20.如图,已知直线AB,CD,AC上的点M,N,E满足ME⊥NE,∠AME+∠CNE=90°,∠ACD的平分线CG 交MN于G,作射线GF∥AB.(1)直线AB与CD平行吗?为什么?(2)若∠CAB=66°,求∠CGF的度数.参考答案1.C2.C3.A4.C5.A6.C7.C8.A9.115°10.811.60;10012.30°13.1214.123°15.解答:∵a+b+c=24,且a+b>c,a≤b≤c,∴8≤c≤11,即c=8,9,10,11,故可得(a,b,c)共12组:当c=11时,有:2,11,11; 3,10,11;4,9,11;5,8,1;6,7,11.当c=10时,有:4,10,10;5,9,10;6,8,10;7,7,10.当c=9时,有: 6,9,9;7,8,9.当c=8时,有:8,8,8.16.∵BD⊥AC,CE⊥AB∴∠AEH=∠ADH=90°在四边形AEHD中,∠AEH=∠ADH=90°,∠A=56°∴∠EHD=360°-∠AEH-∠ADH-∠A=360°-90°-90°-56°=124°∵∠BHC与∠EHD是对顶角∴∠BHC=∠EHD=124°.17.(1)C(2)220°(3)∠1+∠2=180°+∠A(4)∵△EFP是由△EFA折叠得到的∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°﹣2∠AFE,∠2=180°﹣2∠AEF∴∠1+∠2=360°﹣2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°﹣∠A∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A.18.解:∵DE=EB∴设∠BDE=∠ABD=x∴∠AED=∠BDE+∠ABD=2x∵AD=DE∴∠AED=∠A=2x∴∠BDC=∠A+∠ABD=3x∵BD=BC∴∠C=∠BDC=3x∵AB=AC∴∠ABC=∠C=3x在△ABC中,3x+3x+2x=180°解得x=22.5°∴∠A=2x=22.5°×2=45°.19.(1)解:∵六边形ABCDEF的内角相等∴∠B=∠A=∠BCD=120°∵CF∥AB∴∠B+∠BCF=180°∴∠BCF=60°∴∠FCD=60°(2)解:∵∠AFC=360°﹣120°﹣120°﹣60°=60°∴∠AFC=∠FCD∴AF∥CD20.(1)解:平行,理由如下:∵ ME⊥NE,即∠MEN=90°∴∠AEM+∠CEN=90°又∵∠AME+∠CNE=90°∴∠A+∠ECN=180°+180°-(∠AEM+∠CEN+∠AME+∠CNE) =360°-90°×2=180°∴ AB∥CD.(2)解:∵GF∥AB, AB∥CD∴GF∥CD∴∠GNC=∠FGN∴∠CGF=∠CGN+∠FGN=∠CGN+GNC=180°-∠GCN∵AB∥CD,∠CAB=66°∴∠ACD=180°-∠CAB=180°-66°=114°∴CG 平分∠ACD∠ACD=57°∴∠GCN=12∴∠CGF=180°-∠GCN=180°-57°=123°。
人教版八年级数学上册第十一章三角形单元测试卷(含答案).doc

第 11 章三角形单元测试题(考试时长:120 分钟满分:120分)一、选择题(每小题 3 分,共30 分)1 .下列各图中,正确画出△ABC 中 AC 边上的高的是()A.①B.②C.③D.④2 .已知等腰三角形的周长为16 ,且一边长为3,则腰长为()A.3B.10C. 6.5D. 3或6.53 .在三边互不相等的三角形中,最长边的长为a,最长的中线的长为m,最长的高线的长为h,则()A .a> m> hB . a> h> m C. m > a> h D . h> m > a4 .已知一个三角形的三边长均为整数,若其中仅有一条边长为5,且它不是最短边,也不是最长边,则满足条件的三角形共有()A.10个B.8个C.6个D.4个5 .三角形中,最大角α的取值范围是()A .0°<α< 90°B . 60 °<α< 180 °C . 60°≤α< 90°D . 60°≤α< 180°6 .如图,∠ABD ,∠ ACD 的角平分线交于点P,若∠A=50 °,∠ D=10 °,则∠ P 的度数为()A.15°B.20°C. 25°D. 30°第6题第9题7 .在一个三角形的内部有一个点,这个点到三角形三边的距离相等,这个点是()A .角平分线的交点B .中线的交点C.高线的交点 D .中垂线的交点8 .已知∠ 1=48 °,∠ 2 的两边分别与∠ 1 的两边垂直,则∠2= ()A .48°B. 132 °C. 42°D . 48 °或132°9 .如图,∠ 1+∠ 2+∠3+∠4+ ∠5+∠6+∠7= ()度.A .450 B. 540 C. 630 D. 72010 .小明在加一多边形的角的和时,不小心把一个角多加了一次,结果为1500 °,则小明多加的那个角的大小为()A.60°B. 80°C. 100 °D. 120°二、填空题(每小题 3 分,共 18 分)11 .在△ ABC 中,∠ B 、∠ C 的平分线相交于点O ,若∠ A=40 °,则∠ BOC= 度.12 .三角形有两边的长为2cm 和 6cm,第三边的长为xcm ,则 x 的范围是;若第三边为奇数,则周长为.13 .三边都不相等且都是整数,周长为24 的三角形有个.14 .若 a, b , c 为三角形的三边长,化简|a﹣ b ﹣ c|+|a ﹣ c+b|+|a+b+c| 等于.15 .如图所示,平面镜I 、 II 的夹角是15 °,光线从平面镜I 上 O 点出发,照射到平面镜II 上的 A 点,再经 II 反射到 B 点,再经 C 点反射到 D 点,接着沿原线路反射回去,则∠ a 的大小为度.第15题第16 题16 .如图,在△∠CHD = ABC中,∠.ACB=60 °,∠BAC=75 °,AD ⊥BC于D, BE ⊥AC于E,AD与BE 交于H ,则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章三角形检测题(人教新课标八年级上)
班级 姓名 分数
一、选择题(每题3分,共33分)
1、等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为( )
A.150°
B.80°
C.50°或80°
D.70° 2.下面四个图形中,线段BE 是⊿ABC 的高的图是( )
3.已知三角形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作 为第三边的是 ( ) A .13cm B .6cm C .5cm D .4cm 4.三角形一个外角小于与它相邻的内角,这个三角形是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .不能确定 5.如图,在直角三角形ABC 中,AC ≠AB ,AD 是斜边上的高, DE ⊥AC ,DF ⊥AB ,垂足分别为E 、F ,则图中与∠C (∠C 除外)相等的角的个数是( )
A 、3个
B 、4个
C 、5个
D 、6个 6.下面说法正确的是个数有( )
①如果三角形三个内角的比是1∶2∶3,那么这个三角形是直角三角形; ②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角
形是直角三角形;④如果∠A=∠B=2
1
∠C ,那么△ABC 是直角三角形;⑤若三角
形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在∆ABC 中,若∠A +∠B=∠C ,则此三角形是直角三角形。
A 、3个
B 、4个
C 、5个
D 、6个
7.五角星的顶点为A 、B 、C 、D 、E ,∠A +∠B +∠C +∠D +∠E 的度数为( )
A 、90°
B 、180°
C 、270°
D 、360°
8.如图,将一副三角板叠放在一起,使直角的顶点重合
于O ,则∠AOC+∠DOB=( )
A 、900
B 、1200
C 、1600
D 、1800
9、一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A 、4
B 、5
C 、6
D 、7
10、过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形
的边数是( ) A 、8 B 、9 C 、10 D 、11 11、n 边形的每个外角都为24°,则边数n 为( ) A 、13 B 、14 C 、15 D 、16
二、填空题(每题3分,共33分)
12.如图,一面小红旗其中∠A=60°, ∠B=30°,则∠BCD= 。
13、一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是____________。
14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE 是 度。
15.如图,∠
1=_____.
16.若三角形三个内角度数的比为2:3:4,则相应的外角比是 .
17.如图,⊿ABC 中,∠A = 40°,∠B = 72°,CE 平分∠ACB ,CD ⊥AB 于D , DF ⊥CE ,则∠CDF = 度。
18.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形, 那么a 的取值范围是 19.如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内 角的2倍,则此三角形各内角的度数是___________ 。
20.如图,△ABC 中,∠A=1000,BI 、CI 分别平分∠ABC ,∠ACB ,则∠BIC= , 若BM 、CM 分别是∠ABC ,∠ACB 的外角平分线,则∠M= 21.如图∆ABC 中,AD 是BC 上的中线,BE 是∆ABD 中AD 边上的中线,若∆ABC 的面积是24,则∆ABE 的面积是________。
22、从10边形的一个顶点画所有的对角线,一共能画 条
第2题图 第5题图 C B A 第12题图 A B C D E
第14题图 第15题图
第17题图 A B C D
E 第21题图 1 2 B
A E C D M
I
第20题
三、解答题(共33分)
24.(本题6分)在△ABC 中,∠B=3∠A, ∠C=5∠A,求△ABC 的三个内角度数
25、 如图,在△ABC 中,∠BAC 是钝角,完成下列画图. (6分) (1)∠BAC 的平分线AD ; (2)AC 边上的中线BE ; (3)AC 边上的高BF ;
26.如图,在△ABC 中, AD ⊥BC 于D ,AE 平分∠DAC ,∠BAC=800,∠B=600; 求∠AEC 的度数.(7分)
27.(7分)有人说,自己的步子大,一步能走三米多,你相信吗?用你学过的数学知识说明理由。
28、(7分)如图,∠1=20°,∠2=25°,∠A=35°,求∠BDC 的度数。
【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】
C B
A A
B C
D
1
2。
