万有引力PPT课件
合集下载
万有引力定律完美版课件

07
总结与展望
Chapter
课件内容回顾与总结
万有引力定律的表述和数学公式
01
详细阐述了万有引力定律的定义、公式和适用范围,使学生全
面理解该定律。
引力常量的测定及意义
02
介绍了引力常量的历史背景、测定方法和在科学研究中的重要
性,加深了学生对引力常量的认识。
万有引力定律在天体运动中的应用
03
通过实例分析了万有引力定律在天体对万有引力定律的验 证不仅加深了我们对宇宙的认识和理解, 同时也为未来的空间探测和科学研究提 供了重要的理论支持和技术手段。
广义相对论对万有引力定律修正与发展
广义相对论简介
广义相对论是爱因斯坦在1915年提出 的一种描述引力的理论,它认为引力是 由物质和能量在时空中弯曲而产生的几 何效应。这一理论对万有引力定律进行 了修正和发展,为我们提供了更深刻、 更全面的引力理论。
了学生运用该定律解决实际问题的能力。
万有引力定律在科学和技术中重要性
天文学领域
万有引力定律为天文学提供了基础理论支持,是研究天体运动和 宇宙演化的关键。
航天工程领域
万有引力定律是航天工程设计和实施的重要依据,如卫星轨道计 算、太空探测等。
其他领域
万有引力定律还对地理学、地质学等其他领域产生了深远影响, 推动了相关学科的发展。
公式
F=G(m1m2)/r^2,其中F为两物体之
间的引力,m1和m2分别为两物体的
质量,r为两物体之间的距离,G为万
有引力常数。
科学家牛顿与万有引力定律
牛顿的生平与成就 牛顿是英国著名的物理学家、数学家和天文学家,他在物 理学领域取得了举世瞩目的成就,其中最为著名的就是万 有引力定律。
7.2万有引力定律的应用课件(共25张PPT)

力的作用是相互的,行星与太阳的引 力也应与太阳的质量m太成正比。
F m太 r2
G与太阳、行星都没有关
F
m太m r2
F=G
m太m r2
r
系。太阳与行星间引力的
方向沿着二者的连线。
1 行星与太阳间的引力
行星与太阳的引力与行星的质量成正比,
与太阳的质量成正比,与太阳与行星间距离的 二次方成反比
牛顿 (1643—1727) 英国著名的物理学家
ห้องสมุดไป่ตู้
使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点 的力,这个力应该就是太阳对它的引力
我们跟从牛顿发现万有引力定律的过程来研究行星与太阳间的引力。
太阳与行星的物理模型
太阳
行星
a
简化
理想化模型
行星
太阳 r
• (1)匀速圆周运动模型:
由于行星绕太阳做椭圆运动的轨迹的两个焦点靠得很近,行星的运动轨迹非常 接近圆,所以将行星的运动看成匀速圆周运动。
注意:在分析一般物体受力时,物体间的万有引力一般也可忽略不计。
万有引力定律的推论:
内容:在匀质球壳的空腔内任意位置处,质点受到球
●
壳的万有引力为零。
例 如图所示,r 虽然大于两球的半径,但两球的半径不能忽略,而球的质量分布均 匀,大小分别为m1与m2,则两球间万有引力的大小为 ( )
r1
r2
r
A、
• (2)质点模型:
由于天体间的距离很远,研究天体间的引力时将天体看成质点,即天体的质量 集中在球心上。
1 行星与太阳间的引力
方向:太阳与行星间引力的方向沿着二者的连线。
大小:
m太
m
F=m v2 r
v 2r
《万有引力》课件

《万有引力》PPT课件
欢迎各位同学参加今天的《万有引力》课件。本课件将带你深入了解引力的 奥秘,探索引力在宇宙中的重要作用。
引言
引出物体运动与万有引力的关系。 简单介绍牛顿的万有引力定律。
牛顿的万有引力定律
公式阐述
详细解释引力的计算公式以及其意义。
解释三个要素
通过质量、距离和力这三个要素解释引力的影响。
万有引力的应用
行星运动定律
探索行星如何绕太阳运动,并 解释如何借助引力保 持稳定的轨道运行。
地心引力
探索地心引力如何影响我们的 生活和地球的运动。
万有引力的历史和发展
1 牛顿发现万有引力定律的经过
深入探索牛顿是如何发现万有引力这一伟大定律的。
2 以及后来发生的变化和发展
了解其他科学家对万有引力理论的补充和扩展。
结论
总结并归纳万有引力的基本规律,强调其在宇宙中的重要性。 展望未来:万有引力在宇宙探索中的应用前景。
结束语
感谢各位同学聆听,期待与大家分享和交流对于《万有引力》的疑问和见解。
欢迎各位同学参加今天的《万有引力》课件。本课件将带你深入了解引力的 奥秘,探索引力在宇宙中的重要作用。
引言
引出物体运动与万有引力的关系。 简单介绍牛顿的万有引力定律。
牛顿的万有引力定律
公式阐述
详细解释引力的计算公式以及其意义。
解释三个要素
通过质量、距离和力这三个要素解释引力的影响。
万有引力的应用
行星运动定律
探索行星如何绕太阳运动,并 解释如何借助引力保 持稳定的轨道运行。
地心引力
探索地心引力如何影响我们的 生活和地球的运动。
万有引力的历史和发展
1 牛顿发现万有引力定律的经过
深入探索牛顿是如何发现万有引力这一伟大定律的。
2 以及后来发生的变化和发展
了解其他科学家对万有引力理论的补充和扩展。
结论
总结并归纳万有引力的基本规律,强调其在宇宙中的重要性。 展望未来:万有引力在宇宙探索中的应用前景。
结束语
感谢各位同学聆听,期待与大家分享和交流对于《万有引力》的疑问和见解。
《万有引力定律 》课件

02
详细描述
万有引力是一种自然现象,存在于任何两个物体之间,无论它们的质 量大小、距离远近,都存在相互吸引的力。这个力的大小与两个物体 的质量成正比,与它们之间的距离的平方成反比。
万有引力定律的公式
总结词
万有引力定律的公式是F=G(m1m2)/r^2。
详细描述
万有引力定律的公式是描述两个物体之间相互吸引的力的数学表达式。其中,F 表示两物体之间的万有引力,G是自然界的常量,m1和m2分别表示两个物体的 质量,r表示它们之间的距离。
现代科学的万有引力推导方法
广义相对论
在现代科学中,爱因斯坦的广义 相对论提供了另一种理解万有引 力的方式。它描述了质量如何弯 曲空间和时间,从而产生引力。
量子力学
尽管量子力学与万有引力理论在一 些基本原则上存在冲突,但它也为 理解宇宙的基本结构提供了框架。
宇宙学模型
现代宇宙学模型,如大爆炸理论和 暗物质模型,都基于万有引力定律 ,帮助我们理解宇宙的起源和演化 。
地球重力的计算
总结词
地球重力是万有引力定律在地球表面的具体表现,通过计算地球重力,可以了解地球的质量、赤道半 径、地球自转角速度等重要参数。
详细描述
地球重力是指地球对地球表面物体的吸引力,它是万有引力的一个分力。通过测量地球表面不同位置 的重力加速度,结合地球的几何参数,可以计算出地球的质量、赤道半径、地球自转角速度等重要参 数,这些参数对于地球科学、气象学、海洋学等领域的研究具有重要意义。
05
万有引力定律的影响
对科学发展的影响
01
02
03
促进天文学发展
万有引力定律解释了天体 运动规律,为天文学的发 展奠定了基础。
推动物理学进步
《万有引力》课件

行星轨道偏心率
行星轨道的偏心率表示轨 道形状的离心率,偏心率 为0表示轨道为圆形,偏心 率为1表示轨道为椭圆形。
04
万有引力与生活
万有引力对地球的影响
维持地球自转
万有引力提供向心力,使地球能 够保持稳定的自转。
维持地球轨道
万有引力使地球能够沿椭圆轨道绕 太阳运行,保持稳定。
形成气候
万有引力影响大气层的分布和运动 ,形成不同气候带和天气系统。
03
万有引力与天体运动
天体运动的规律
01
02
03
地球自转
地球绕自身轴线旋转一周 ,周期为24小时,形成昼 夜交替现象。
地球公转
地球绕太阳旋转一周,周 期为一年,形成四季交替 现象。
天体轨道
天体按照椭圆、抛物线或 双曲线等轨道运动,遵循 开普勒三定律。
月球与地球的相互作用
月球引潮力
月球引潮力引起地球潮汐现象,对地 球上的海洋、湖泊、河流等产生周期 性涨落。
VS
万有引力
万有引力是指任何两个物体之间相互吸引 的力。根据牛顿的万有引力定律,这个力 与两个物体的质量成正比,与它们之间的 距离的平方成反比。万有引力是宇宙中最 重要的力之一,它对天体运动和宇宙演化 起着重要作用。
探索宇宙的未知领域
宇宙微波背景辐射
宇宙微波背景辐射是指充溢于整个宇宙的微 波辐射,它是宇宙大爆炸后留下的余辉。通 过对宇宙微波背景辐射的研究,科学家们可 以了解宇宙早期的状态和演化过程。
暗能量
暗能量是一种充溢于空间的能量,它占据了宇宙中大部分的能量密度。暗能量的作用机制也尚不清楚 ,但它对宇宙的加速膨胀起着关键作用。科学家们正在研究暗能量的性质和作用机制,以揭示宇宙加 速膨胀的奥秘。
《高一物理万有引力》课件

雷达测距
向月球或更远的天体发射雷达信 号,通过测量信号的往返时间可 以精确计算出天体与地球之间的 距离。
计算天体的质量
环绕天体运动
通过测量环绕天体的运动轨道和周期 ,利用万有引力定律可以计算出中心 天体的质量。
重力加速度法
在地球上测量不同纬度处的重力加速 度,结合地球半径和地球质量,可以 推算出其他天体的质量。
详细描述
牛顿出生于1643年,他是一位英国物 理学家、数学家、天文学家和哲学家 。他在科学领域做出了卓越的贡献, 其中最著名的就是万有引力定律。
万有引力定律的发现过程
总结词
万有引力定律的发现过程是一个漫长而复杂的过程,涉及到许多科学家和他们的研究成 果。从开普勒行星运动三定律,到牛顿万有引力定律的提出,人类对宇宙的理解不断深
宇宙的起源与万有引力
大爆炸理论
大爆炸理论认为宇宙起源于一个极度高温和高密度的状态,被称为 大爆炸。在此之前,物理定律可能不再适用。
宇宙的演化
根据大爆炸理论,宇宙经历了急剧的扩张和冷却过程。万有引力在 宇宙演化中起着重要作用,它影响了星系的形成和宇宙的扩张速度 。
宇宙的未来
由于宇宙的加速扩张,未来宇宙的命运仍不确定。万有引力与宇宙的 其他基本力之间的关系仍需进一步研究。
助人类理解宇宙的运行规律。
天文观测
通过研究万有引力,人类能够更准 确地预测天体的位置和运动轨迹, 提高天文观测的精度。
宇宙演化
万有引力还影响了宇宙的演化过程 ,通过对它的研究,人类可以更深 入地了解宇宙的起源和演化历程。
对人类生活的影响
地球自转
航天工程
地球自转是由于地球自身受到的万有 引力作用,这种自转导致了昼夜交替 的现象,影响人类的生活节奏。
向月球或更远的天体发射雷达信 号,通过测量信号的往返时间可 以精确计算出天体与地球之间的 距离。
计算天体的质量
环绕天体运动
通过测量环绕天体的运动轨道和周期 ,利用万有引力定律可以计算出中心 天体的质量。
重力加速度法
在地球上测量不同纬度处的重力加速 度,结合地球半径和地球质量,可以 推算出其他天体的质量。
详细描述
牛顿出生于1643年,他是一位英国物 理学家、数学家、天文学家和哲学家 。他在科学领域做出了卓越的贡献, 其中最著名的就是万有引力定律。
万有引力定律的发现过程
总结词
万有引力定律的发现过程是一个漫长而复杂的过程,涉及到许多科学家和他们的研究成 果。从开普勒行星运动三定律,到牛顿万有引力定律的提出,人类对宇宙的理解不断深
宇宙的起源与万有引力
大爆炸理论
大爆炸理论认为宇宙起源于一个极度高温和高密度的状态,被称为 大爆炸。在此之前,物理定律可能不再适用。
宇宙的演化
根据大爆炸理论,宇宙经历了急剧的扩张和冷却过程。万有引力在 宇宙演化中起着重要作用,它影响了星系的形成和宇宙的扩张速度 。
宇宙的未来
由于宇宙的加速扩张,未来宇宙的命运仍不确定。万有引力与宇宙的 其他基本力之间的关系仍需进一步研究。
助人类理解宇宙的运行规律。
天文观测
通过研究万有引力,人类能够更准 确地预测天体的位置和运动轨迹, 提高天文观测的精度。
宇宙演化
万有引力还影响了宇宙的演化过程 ,通过对它的研究,人类可以更深 入地了解宇宙的起源和演化历程。
对人类生活的影响
地球自转
航天工程
地球自转是由于地球自身受到的万有 引力作用,这种自转导致了昼夜交替 的现象,影响人类的生活节奏。
高中物理竞赛讲座课件:万有引力-(共80张PPT)

dt t x
xdu uvdt udx
(dx vdt)
积分得
ux C
u v0l / x
mv l F x
2 2 0 3
F 2m uf
m u2 x
利用以上结论还容易证明,把表面从距离l推近到距离x 时所 做的功等于球的动能的增加
例.在水平桌面上有一卷质量为m 、长为l的链条,其一 端用手以恒速v竖直向上提起(如图所示),当提起的 长度为x时, (1) 求手的提力为多少?做功多少? (2) 链条获得的机械能为多少? (3) 比较以上功与机械能变化是否相等,你能解释吗?
v
x
解: 取提起的这一段链条为研究对象,它受到的合力为
手的提力与这一段自身的重力之和,即
F mgx/ l
链条在dt时间内,一段长度为dx=vdt的链条由静止加速到 v,其动量的增量为 dm vm
vdm v
vm dx l
dx
dx
l
dx
( F mgx / l )dt
竞赛题与常规考题的区别:
1. 考察的问题原型相同,但是综合性或复杂性更强 对策:熟悉各种原型问题。 2. 在试题的入手上设置障碍,让人难以下手,实际上还是 对应于一些基本的物理原型。 对策:识破题目的障眼法,找到原型。 3. 题目的物理过程较多,有的是同一个物理原型的反复运用, 加上各种物理情形的讨论, 有的是多个不同物理原型的综合。 对策:养成严谨的思维习惯。对于讨论题,常规考题设置了 一些简化假设(比如没有摩擦,2004复赛第七题在碰撞停 止之前水平速度一直向右等等)。不要想当然,问问自 己,有几种可能?都要考虑进去。
简谐振动,能量守恒 (不要把v 当成发射速度)
1 2 1 1 1 1 2 2 m v m v1 kA2 m v1 m u2 2 2 2 2 2 2 2 3 M m 2 2 2 v1 v u 1u M m
xdu uvdt udx
(dx vdt)
积分得
ux C
u v0l / x
mv l F x
2 2 0 3
F 2m uf
m u2 x
利用以上结论还容易证明,把表面从距离l推近到距离x 时所 做的功等于球的动能的增加
例.在水平桌面上有一卷质量为m 、长为l的链条,其一 端用手以恒速v竖直向上提起(如图所示),当提起的 长度为x时, (1) 求手的提力为多少?做功多少? (2) 链条获得的机械能为多少? (3) 比较以上功与机械能变化是否相等,你能解释吗?
v
x
解: 取提起的这一段链条为研究对象,它受到的合力为
手的提力与这一段自身的重力之和,即
F mgx/ l
链条在dt时间内,一段长度为dx=vdt的链条由静止加速到 v,其动量的增量为 dm vm
vdm v
vm dx l
dx
dx
l
dx
( F mgx / l )dt
竞赛题与常规考题的区别:
1. 考察的问题原型相同,但是综合性或复杂性更强 对策:熟悉各种原型问题。 2. 在试题的入手上设置障碍,让人难以下手,实际上还是 对应于一些基本的物理原型。 对策:识破题目的障眼法,找到原型。 3. 题目的物理过程较多,有的是同一个物理原型的反复运用, 加上各种物理情形的讨论, 有的是多个不同物理原型的综合。 对策:养成严谨的思维习惯。对于讨论题,常规考题设置了 一些简化假设(比如没有摩擦,2004复赛第七题在碰撞停 止之前水平速度一直向右等等)。不要想当然,问问自 己,有几种可能?都要考虑进去。
简谐振动,能量守恒 (不要把v 当成发射速度)
1 2 1 1 1 1 2 2 m v m v1 kA2 m v1 m u2 2 2 2 2 2 2 2 3 M m 2 2 2 v1 v u 1u M m
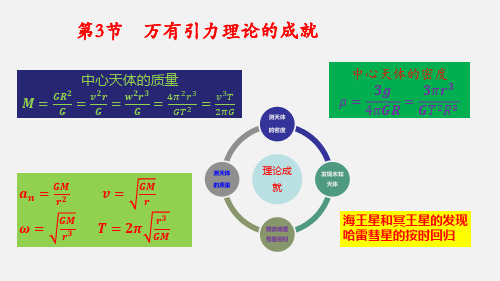
7.3万有引力理论的成就课件(22张PPT)
G
m1m 2
2r 、G m1m 2 =m (2πf)2r ,r +r =L,
=m
(2πf)
1
1
2
2
1 2
L2
L2
2 2 3
4
f L ,故选项A错误,选项B正确;
联立解得:m1+m2=
G
v1=2πfr1、v2=2πfr2解得v1+v2=2πfL,故选项C正确;
各自的自转角速度无法估算,故选项D错误。 【正确答案】BC
1、英国亚当斯和法国勒维耶。根据天
哈雷依据万有引力定律,发现 1531 年、
王星的观测资料,利用万有引力定律
1607 年和 1682 年出现的这三颗彗星轨
计算出这颗“新”行星的轨道。德国
道看起来如出一辙,他大胆预言,这三
的伽勒在勒维耶预言的位置附近发现
次出现的彗星是同一颗星,周期约为 76
了这颗行星,人们称其为“笔尖下发
)
【典例6】宇航员站在某星球的一个斜坡上,以初速度v0水平扔出一个小球,经过时
间t小球落在斜坡上,经测量斜坡倾角为 θ,星球半径为R,引力常量为G,求星球的
质量。
【解析】小球位移偏向角为θ:
v0
tan
ϴ
y
x
g
2v0 tan
t
G
Mm
mg
R2
2v0 R 2 tan
M
Gt
专题:双星题型
定点做周期相同的匀速圆周运动。根据宇宙大爆炸理论,双星间的距离在缓
慢增加,设双星仍做匀速圆周运动,则下列说法正确的是(
)
A.双星相互间的万有引力增大
B.双星做圆周运动的周期增大
m1m 2
2r 、G m1m 2 =m (2πf)2r ,r +r =L,
=m
(2πf)
1
1
2
2
1 2
L2
L2
2 2 3
4
f L ,故选项A错误,选项B正确;
联立解得:m1+m2=
G
v1=2πfr1、v2=2πfr2解得v1+v2=2πfL,故选项C正确;
各自的自转角速度无法估算,故选项D错误。 【正确答案】BC
1、英国亚当斯和法国勒维耶。根据天
哈雷依据万有引力定律,发现 1531 年、
王星的观测资料,利用万有引力定律
1607 年和 1682 年出现的这三颗彗星轨
计算出这颗“新”行星的轨道。德国
道看起来如出一辙,他大胆预言,这三
的伽勒在勒维耶预言的位置附近发现
次出现的彗星是同一颗星,周期约为 76
了这颗行星,人们称其为“笔尖下发
)
【典例6】宇航员站在某星球的一个斜坡上,以初速度v0水平扔出一个小球,经过时
间t小球落在斜坡上,经测量斜坡倾角为 θ,星球半径为R,引力常量为G,求星球的
质量。
【解析】小球位移偏向角为θ:
v0
tan
ϴ
y
x
g
2v0 tan
t
G
Mm
mg
R2
2v0 R 2 tan
M
Gt
专题:双星题型
定点做周期相同的匀速圆周运动。根据宇宙大爆炸理论,双星间的距离在缓
慢增加,设双星仍做匀速圆周运动,则下列说法正确的是(
)
A.双星相互间的万有引力增大
B.双星做圆周运动的周期增大
万有引力定律ppt课件

量子引力理论 尝试将万有引力定律与量子力学相结合,发展出 量子引力理论,如弦论、圈量子引力等。
3
修改引力理论
通过对万有引力定律进行修正,以适应不同尺度 和环境下的引力现象,如MOND理论、f(R)重力 理论等。
未来研究方向和前景展望
深入研究暗物质与暗能量 揭示暗物质和暗能量的本质,以及它 们与万有引力的关系。
定律的公式
• F=(G×m1×m2)/r^2。两个可看作质点的物体之间的万有引力,可以用以下公式计算:F=(G×m1×m2)/r^2,即 万有引力 等于引力常量乘以两物体质量的乘积除以它们距离的平方。其中G代表引力常量,其值约为6.67×10的负11次方单位, N·m2/kg2。为英国物理学家、化学家亨利·卡文迪许通过扭秤实验测得。
定律中各物理量的含义
• G为引力常量,m1和m2分别为两个物体的质量,r为两个物 体间的距离。万有引力定律公式适用于质点间的相互作用, 在宏观物体间由于距离远大于物体本身的大小,所以通常把 物体看做质点,此时该公式适用。而当两个物体间的距离小 于物体本身的大小时,此公式就不适用了。
03
CATALOGUE
相对论揭示了时间、空间、物质 和能量之间的深刻联系,为原子 能、宇宙学、粒子物理等领域的
研究提供了理论基础。
相对论的提出和发展对于推动现 代科学技术的进步具有不可估量
的作用。
06
CATALOGUE
万有引力定律的挑战和发展前景
定律面临的挑战和问题
弱引力问题
01
在极弱引力环境下,万有引力定律的预测与观测结果存在偏差。
卫星轨道设计
万有引力定律是卫星轨道设计的 基础,通过计算地球对卫星的引 力,可以确定卫星的轨道参数。
太空探测任务
3
修改引力理论
通过对万有引力定律进行修正,以适应不同尺度 和环境下的引力现象,如MOND理论、f(R)重力 理论等。
未来研究方向和前景展望
深入研究暗物质与暗能量 揭示暗物质和暗能量的本质,以及它 们与万有引力的关系。
定律的公式
• F=(G×m1×m2)/r^2。两个可看作质点的物体之间的万有引力,可以用以下公式计算:F=(G×m1×m2)/r^2,即 万有引力 等于引力常量乘以两物体质量的乘积除以它们距离的平方。其中G代表引力常量,其值约为6.67×10的负11次方单位, N·m2/kg2。为英国物理学家、化学家亨利·卡文迪许通过扭秤实验测得。
定律中各物理量的含义
• G为引力常量,m1和m2分别为两个物体的质量,r为两个物 体间的距离。万有引力定律公式适用于质点间的相互作用, 在宏观物体间由于距离远大于物体本身的大小,所以通常把 物体看做质点,此时该公式适用。而当两个物体间的距离小 于物体本身的大小时,此公式就不适用了。
03
CATALOGUE
相对论揭示了时间、空间、物质 和能量之间的深刻联系,为原子 能、宇宙学、粒子物理等领域的
研究提供了理论基础。
相对论的提出和发展对于推动现 代科学技术的进步具有不可估量
的作用。
06
CATALOGUE
万有引力定律的挑战和发展前景
定律面临的挑战和问题
弱引力问题
01
在极弱引力环境下,万有引力定律的预测与观测结果存在偏差。
卫星轨道设计
万有引力定律是卫星轨道设计的 基础,通过计算地球对卫星的引 力,可以确定卫星的轨道参数。
太空探测任务
万有引力定律ppt课件

星的质量m成正比,与r2成反比。
m
F 2
r
2.行星对太阳的引力
m
F 2
r
行
星
F
F′
太
阳
M
F 2
r
'
太阳和行星的引力是相互的,行星和太阳的地
位对等的,太阳对行星的引力与行星质量成正
比,由类比法可得行星对太阳的引力与太阳的
质量成正比。
m
F 2
r
类 牛
比
法 三
M
F 2
r
牛三
Mm
F 2
r
Mm
当时,已能准确测量的量有:(即事实)地球表面附近的重力加速度:
g = 9.8m/s2,地球半径:
R = 6.4×106m,月亮的公转周期:T =27.3天
≈2.36×106s,月亮轨道半径: r =3.8×108m≈ 60R
2
4
r
2
a r
T
a 2.69 10 3 m / s 2
1
该就是太阳对它的引力。
知识点二:行星与太阳间的引力
行星
行星
太阳
太阳
a
r
简化
(1)匀速圆周运动模型:
行星绕太阳做椭圆运动的轨迹的两个焦点靠得很近,行星的运动轨迹非常接
近圆,所以将行星的运动看成以太阳为圆心的匀速圆周运动。
(2)太阳对行星的引力提供行星做圆周运动的向心力。
1.太阳对行星的引力
行星绕太阳的运动看做匀速圆周运动,行
F=G 2
r
'
F 和F ′是一对作用力和反作用力,所以F的大小既
和太阳质量M成正比、也和行星质量m成正比。
m
F 2
r
2.行星对太阳的引力
m
F 2
r
行
星
F
F′
太
阳
M
F 2
r
'
太阳和行星的引力是相互的,行星和太阳的地
位对等的,太阳对行星的引力与行星质量成正
比,由类比法可得行星对太阳的引力与太阳的
质量成正比。
m
F 2
r
类 牛
比
法 三
M
F 2
r
牛三
Mm
F 2
r
Mm
当时,已能准确测量的量有:(即事实)地球表面附近的重力加速度:
g = 9.8m/s2,地球半径:
R = 6.4×106m,月亮的公转周期:T =27.3天
≈2.36×106s,月亮轨道半径: r =3.8×108m≈ 60R
2
4
r
2
a r
T
a 2.69 10 3 m / s 2
1
该就是太阳对它的引力。
知识点二:行星与太阳间的引力
行星
行星
太阳
太阳
a
r
简化
(1)匀速圆周运动模型:
行星绕太阳做椭圆运动的轨迹的两个焦点靠得很近,行星的运动轨迹非常接
近圆,所以将行星的运动看成以太阳为圆心的匀速圆周运动。
(2)太阳对行星的引力提供行星做圆周运动的向心力。
1.太阳对行星的引力
行星绕太阳的运动看做匀速圆周运动,行
F=G 2
r
'
F 和F ′是一对作用力和反作用力,所以F的大小既
和太阳质量M成正比、也和行星质量m成正比。
《万有引力定律》PPT课件

(因物体不再受地球自转影响!)
mg h
G
Mm (R地 h)2
②重力随高度的增大而减小。
对于质量为m1和质量为m2的两个物体间的万有引力
的表达式F=Gmr1m2 2,下列说法正确的是
()
• A.公式中的G是引力常量,它是由实验 得出的,而不是人为规定的
• B.当两个物体间的距离r趋于零时,万有 引力趋于无穷大
(4)特殊性:两个物体之间的万有引力只与它 们本身的质量和它们间的距离有关,而与所 在空间的性质无关,也与周围是否存在其他 物体无关。
三、万有引力与重力之间的关系
1.在地球表面,重力只是万有引力 的一个分力.
F mg G Mm r2
①重力随纬度的减小而减小。 g赤 g极
2.在地球高空,重力就是万有引力.
B.
G
m1m2 r12
D. G m1m2
(r r1 r2 ) 2
r1
r2
r
图7-9
它在数值上等于质量都是1kg的物体相距1m时的相 互作用力。
4.万有引力定律公式的适用条件
(1) F G m1m2 适用于计算两个质点间相互作用. r2
(2)两个质量分布均匀的球体间的相互作用,可 用公式计算,其中r是两个球体球心的距离。
(3)一个均匀球体与球外一个质点间的万有引力, 可用公式计算,其中r是球心到质点间的距离。
有椭圆的一个焦点上。
第二定律:
开普勒
行星和太阳的连线,在相等的时间内
(面积定律) 扫过相同的面积。
同一颗行星在近 日点的速率大于 远日点的速率.
第三定律: 行星绕太阳公转的周期的平方和轨道半 (周期定律) 长轴的立方成正比
注:1)K与行星无关, 只与“中心天体”--太阳质量有关。
mg h
G
Mm (R地 h)2
②重力随高度的增大而减小。
对于质量为m1和质量为m2的两个物体间的万有引力
的表达式F=Gmr1m2 2,下列说法正确的是
()
• A.公式中的G是引力常量,它是由实验 得出的,而不是人为规定的
• B.当两个物体间的距离r趋于零时,万有 引力趋于无穷大
(4)特殊性:两个物体之间的万有引力只与它 们本身的质量和它们间的距离有关,而与所 在空间的性质无关,也与周围是否存在其他 物体无关。
三、万有引力与重力之间的关系
1.在地球表面,重力只是万有引力 的一个分力.
F mg G Mm r2
①重力随纬度的减小而减小。 g赤 g极
2.在地球高空,重力就是万有引力.
B.
G
m1m2 r12
D. G m1m2
(r r1 r2 ) 2
r1
r2
r
图7-9
它在数值上等于质量都是1kg的物体相距1m时的相 互作用力。
4.万有引力定律公式的适用条件
(1) F G m1m2 适用于计算两个质点间相互作用. r2
(2)两个质量分布均匀的球体间的相互作用,可 用公式计算,其中r是两个球体球心的距离。
(3)一个均匀球体与球外一个质点间的万有引力, 可用公式计算,其中r是球心到质点间的距离。
有椭圆的一个焦点上。
第二定律:
开普勒
行星和太阳的连线,在相等的时间内
(面积定律) 扫过相同的面积。
同一颗行星在近 日点的速率大于 远日点的速率.
第三定律: 行星绕太阳公转的周期的平方和轨道半 (周期定律) 长轴的立方成正比
注:1)K与行星无关, 只与“中心天体”--太阳质量有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这样就能比较精确地测量 金属丝的扭转。
2020年10月2日
9
万有引力定律在天文学上的应用
1.天体质量的计算 应用万有引力定律可以计算天体的质量.基 本思路是:根据行星(或卫星)运动的情 况,求出行星(或卫星)的向心加速度, 而向心力是由万有引力提供的,这样,列 出方程即可求得中心天体(太阳或行星) 的质量.
2020年10月2日
2
万有引力定律的发现
牛顿在前人研究的基础 上,凭借他超凡的数学 能力证明了:如果太阳 和行星间的引力与距离 的二次方成反比,则行 星的轨迹是椭圆.并且 阐述了普遍意义下的万 有引力定律。
2020年10月2日
3
万有引力定律的发现
结论:行星和太阳之间的引力跟行星的质量成正比, 跟行星到太阳的距离的二次方成反比.
汇报人:XXX 汇报日期:20XX年10月10日
13
同理,根据月球绕地球运转的轨道半径和周期,可 以计算出地球的质量是5.89×1024 kg。
2020年10月2日
12
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
2020年10月2日
4
万有引力定律的发现
牛顿认为,既然这个引力与行星的质量成正 比,当然也应该和太阳的质量成正比.因此, 如果用m′表示太阳的质量,那么有
•G是一个常量,对任何行星都是相同的.
2020年10月2日
5
万有引力定律
自然界中任何两个物体都是相互吸引的,引力 的大小跟这两个物体的质量的乘积成正比,跟 它们的距离的二次方成反比. 如果用m1和m2表示两个物体的质量,用r表示 它们的距离,那么,万有引力定律可以用下面的 公式来表示:
第五章 匀速圆周运动
D.天体运动 万有引力
2020年10月日
1
对天体运动认识的发展
开普勒认为,行星绕太阳运动,一定是受到了来 自太阳的类似于磁力的作用。 法国物理学家笛卡儿(1596-1650)认为行星的 运动是因为在行星的周围有旋转的物质(以太) 作用在行星上,使得行星围绕太阳运动。 牛顿同时代的一些科学家,如胡克、哈雷等对这 一问题的认识则更进一步.胡克等人认为,行星围 绕太阳运动是因为受到了太阳对它的引力,甚至 证明了如果行星的轨道是圆形的,它所受的引力 的大小跟行星到太阳的距离的二次方成反比.但是 他们无法证明在椭圆轨道下,引力也遵循同样的 规律,更没能严格地证明这种引力的一般规律。
2020年10月2日
6
万有引力定律
式中质量的单位用kg,距离的单位用m,力的单 位用N。G为常数,叫做引力常量,适用于任何 两个物体,它在数值上等于两个质量都是1kg的 物体相距1m时的相互作用力。
通常取G=6.67×10-11N·m2/kg2 万有引力定律中两个物体的距离,对于相距很远 因而可以看作质点的物体,就是指两个质点的距 离;对于均匀的球体,指的是两个球心的距离。
2020年10月2日
7
引力常量的测定
1789年,即在牛顿发现万有引力定律一百多年以后, 英国物理学家卡文迪许(1731-1810),巧妙地 利用扭秤装置,第一次在实验室里比较准确地测出 了引力常量.
2020年10月2日
8
卡文迪许扭秤实验
卡文迪许扭秤的主要部分 是一个轻而坚固的T型架, 倒挂在一根金属丝的下端。 T形架水平部分的两端各 装一个质量是m的小球, T形架的竖直部分装一面 小平面镜M,它能把射来 的光线反射到刻度尺上,
2020年10月2日
10
1.天体质量的计算
假设m′是太阳的质量,m是某个行星的质量,r是 它们之间的距离,T是行星公转的周期,那么行 星做匀速圆周运动所需的向心力为
2020年10月2日
11
1.天体质量的计算
地球绕太阳公转的轨道半径是1.50×1011m, 公转的周期是3.16×1O7s, 所以太阳的质量为
2020年10月2日
9
万有引力定律在天文学上的应用
1.天体质量的计算 应用万有引力定律可以计算天体的质量.基 本思路是:根据行星(或卫星)运动的情 况,求出行星(或卫星)的向心加速度, 而向心力是由万有引力提供的,这样,列 出方程即可求得中心天体(太阳或行星) 的质量.
2020年10月2日
2
万有引力定律的发现
牛顿在前人研究的基础 上,凭借他超凡的数学 能力证明了:如果太阳 和行星间的引力与距离 的二次方成反比,则行 星的轨迹是椭圆.并且 阐述了普遍意义下的万 有引力定律。
2020年10月2日
3
万有引力定律的发现
结论:行星和太阳之间的引力跟行星的质量成正比, 跟行星到太阳的距离的二次方成反比.
汇报人:XXX 汇报日期:20XX年10月10日
13
同理,根据月球绕地球运转的轨道半径和周期,可 以计算出地球的质量是5.89×1024 kg。
2020年10月2日
12
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
2020年10月2日
4
万有引力定律的发现
牛顿认为,既然这个引力与行星的质量成正 比,当然也应该和太阳的质量成正比.因此, 如果用m′表示太阳的质量,那么有
•G是一个常量,对任何行星都是相同的.
2020年10月2日
5
万有引力定律
自然界中任何两个物体都是相互吸引的,引力 的大小跟这两个物体的质量的乘积成正比,跟 它们的距离的二次方成反比. 如果用m1和m2表示两个物体的质量,用r表示 它们的距离,那么,万有引力定律可以用下面的 公式来表示:
第五章 匀速圆周运动
D.天体运动 万有引力
2020年10月日
1
对天体运动认识的发展
开普勒认为,行星绕太阳运动,一定是受到了来 自太阳的类似于磁力的作用。 法国物理学家笛卡儿(1596-1650)认为行星的 运动是因为在行星的周围有旋转的物质(以太) 作用在行星上,使得行星围绕太阳运动。 牛顿同时代的一些科学家,如胡克、哈雷等对这 一问题的认识则更进一步.胡克等人认为,行星围 绕太阳运动是因为受到了太阳对它的引力,甚至 证明了如果行星的轨道是圆形的,它所受的引力 的大小跟行星到太阳的距离的二次方成反比.但是 他们无法证明在椭圆轨道下,引力也遵循同样的 规律,更没能严格地证明这种引力的一般规律。
2020年10月2日
6
万有引力定律
式中质量的单位用kg,距离的单位用m,力的单 位用N。G为常数,叫做引力常量,适用于任何 两个物体,它在数值上等于两个质量都是1kg的 物体相距1m时的相互作用力。
通常取G=6.67×10-11N·m2/kg2 万有引力定律中两个物体的距离,对于相距很远 因而可以看作质点的物体,就是指两个质点的距 离;对于均匀的球体,指的是两个球心的距离。
2020年10月2日
7
引力常量的测定
1789年,即在牛顿发现万有引力定律一百多年以后, 英国物理学家卡文迪许(1731-1810),巧妙地 利用扭秤装置,第一次在实验室里比较准确地测出 了引力常量.
2020年10月2日
8
卡文迪许扭秤实验
卡文迪许扭秤的主要部分 是一个轻而坚固的T型架, 倒挂在一根金属丝的下端。 T形架水平部分的两端各 装一个质量是m的小球, T形架的竖直部分装一面 小平面镜M,它能把射来 的光线反射到刻度尺上,
2020年10月2日
10
1.天体质量的计算
假设m′是太阳的质量,m是某个行星的质量,r是 它们之间的距离,T是行星公转的周期,那么行 星做匀速圆周运动所需的向心力为
2020年10月2日
11
1.天体质量的计算
地球绕太阳公转的轨道半径是1.50×1011m, 公转的周期是3.16×1O7s, 所以太阳的质量为
