系统辨识课程报告
《系统建模与及辨识》课程实验报告

《系统建模与及辨识》课程上机实验报告专业名称 : 控制工程 上机题目 : 用极大似然法进行参数估计一 实验目的通过实验掌握极大似然法在系统参数辨识中的原理和应用。
二 实验原理1 极大似然原理设有离散随机过程}{k V 与未知参数θ有关,假定已知概率分布密度)(θk V f 。
如果我们得到n 个独立的观测值,21,V V …n V ,,则可得分布密度)(1θV f ,)(2θV f ,…,)(θn V f 。
要求根据这些观测值来估计未知参数θ,估计的准则是观测值{}{k V }的出现概率为最大。
为此,定义一个似然函数)()()(),,,(2121θθθθn n V f V f V f V V V L = (1.1)上式的右边是n 个概率密度函数的连乘,似然函数L 是θ的函数。
如果L 达到极大值,}{k V 的出现概率为最大。
因此,极大似然法的实质就是求出使L 达到极大值的θ的估值∧θ。
为了便于求∧θ,对式(1.1)等号两边取对数,则把连乘变成连加,即 ∑==ni iV f L 1)(ln ln θ (1.2)由于对数函数是单调递增函数,当L 取极大值时,lnL 也同时取极大值。
求式(1.2)对θ的偏导数,令偏导数为0,可得ln =∂∂θL(1.3)解上式可得θ的极大似然估计ML ∧θ。
2 系统参数的极大似然估计Newton-Raphson 法实际上就是一种递推算法,可以用于在线辨识。
不过它是一种依每L 次观测数据递推一次的算法,现在我们讨论的是每观测一次数据就递推计算一次参数估计值得算法。
本质上说,它只是一种近似的极大似然法。
设系统的差分方程为 )()()()()(11k k u z b k y z a ξ+=-- (2.1) 式中111()1...nn a z a z a z ---=+++1101()...nn b z b b z b z---=+++因为)(k ξ是相关随机向量,故(2.1)可写成)()()()()()(111k z c k u z b k y z a ε---+= (2.2) 式中)()()(1k k z c ξε=- (2.3)nn z c z c z c ---+++= 1111)( (2.4))(k ε是均值为0的高斯分布白噪声序列。
系统辨识实验1实验报告

实验报告--实验1.基于matlab的4阶系统辨识实验课程:系统辨识题目:基于matlab的4阶系统辨识实验作者:专业:自动化学号:11351014目录实验报告 (1)1.引言 (2)2.实验方法和步骤 (2)3.实验数据和结果 (2)4.实验分析 (4)1、 引言系统辨识是研究如何确定系统的数学模型及其参数的理论。
而模型化是进行系统分析、仿真、设计、预测、控制和决策的前提和基础。
本次实验利用matlab 工具对一个简单的4阶系统进行辨识,以此熟悉系统辨识的基本步骤,和matlab 里的一些系统辨识常用工具箱和函数。
这次实验所采取的基本方法是对系统输入两个特定的激励信号,分别反映系统的动态特性和稳态特性。
通过对输入和输出两个系统信号的比较,来验证系统的正确性。
2、 实验方法和步骤2.1 实验方法利用matlab 对一个系统进行辨识,选取的输入信号必须能够反映系统的动态和稳态两个方面的特性,才能更好地确定系统的参数。
本次实验采取了两种输入信号,为反映动态特性,第一个选的是正弦扫频信号,由下面公式产生:选定频率范围 ,w(t)是时间t 的线性函数,具有扫频性质,可以反映系统的动态特性。
为反映稳态特性,选的输入信号是阶跃信号。
以上的到两组数据,利用matlab 的merge()函数,对两组数据融合,然后用matlab 系统辨识工具箱中的基于子空间方法的状态空间模型辨识函数n4sid()来对系统进行辨识2.2 实验步骤(1)建立一个4阶的线性系统,作为被辨识的系统,传递函数为3243211548765()125410865s s s G s s s s s -+-+=++++(2)产生扫频信号u1和阶跃信号u2(3)u1、u2作为输入对系统进行激励,分别产生输出y1和y2 (4)画出稳态测试输入信号u1-t 的曲线,和y1-t 的曲线 画出动态测试输入信号u2-t 的曲线,和y2-t 的曲线(5)使用merge()函数对u1-y1数据和u2-y2数据进行融合,并使用n4sid()函数对系统进行辨识。
系统辨识实验三

《系统辨识》课程报告题目:最小二乘参数估计法班级:工控08.1姓名:学号:日期:2011.6.1成都信息工程学院控制工程学院最小二乘参数估计摘要:最小二乘法提供了一个估算方法,使之能得到一个在最小方差意义上与实验数据最好拟合的数学模型。
最小二乘的一次性完成辨识算法,他的特点是直接利用已经获得的观测数据进行运算处理。
求出一个使各次实际观测和计算值之间的差值的平方乘以度量其精度的数值以后的和为最小的数值,求出带辨识参数。
最小二乘辩识方法在系统辩识领域中先应用上已相当普及,方法上相当完善,可以有效的用于系统的状态估计,参数估计以及自适应控制及其他方面。
关键词:最小二乘法,AIC 准则,M 序列1 引言:最小二乘法是 1795 年高斯在预测星体运行轨道最先提出的 , 它奠定了最小二乘估计理论的基础 . 到 20 世纪 60 年代瑞典学者 Austron 把这个方法用于动态系统的辨识中 , 在这种辨识方法中 , 首先给出模类型 , 在该类型下确定系统模型的最优参数 .这种具有格式规范的辨识方法可以演绎成递推形式 .递推最小二乘算法计算量小 , 可以用于在线辨识 , 即使辨识对象随时间发生化 , 模型也可以对其进行跟踪断地进行更新和修正辨识参数 , 从而成为一种被广泛采用的辨识方法,最小二乘法有一次完成算法和递推算法,其中 一次完成算法存在一定的局限性,工业系统辨识常采用递推算法进行系统辨识。
2 实验原理:由于运用最小二乘一次完成算法进行系统参数辨识的时候,存在一定的限定条件,并且需要用到全部的观测数据,每采样一次就需要增添一组新的观察数据,所以引入递推最小二乘法来辨识系统参数,递推最小二乘法是用旧的估计值加上修正值得到的新的估计值,用新的测量数据对上一次的估计结果进行修正,直到估计值达到需要的精度为止。
2.1根据汉格尔矩阵估计模型的阶次设一个可观可控的SISO 过程的脉冲响应序列为{个g(1),g(2),……g(L)},可以通过汉格尔(Hankel )矩阵的秩来确定系统的阶次。
系统辨识报告
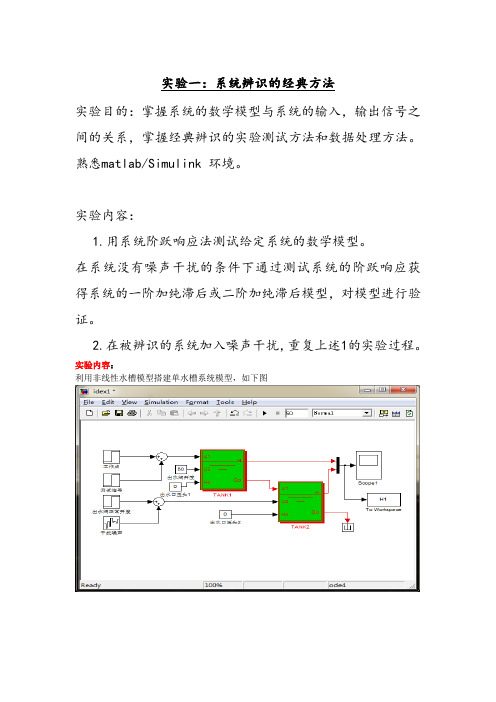
实验一:系统辨识的经典方法实验目的:掌握系统的数学模型与系统的输入,输出信号之间的关系,掌握经典辨识的实验测试方法和数据处理方法。
熟悉matlab/Simulink 环境。
实验内容:1.用系统阶跃响应法测试给定系统的数学模型。
在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或二阶加纯滞后模型,对模型进行验证。
2.在被辨识的系统加入噪声干扰,重复上述1的实验过程。
实验内容:利用非线性水槽模型搭建单水槽系统模型,如下图由上图及其计算的H :H 为一二元数组,分别表示第一个、第二个水箱的液位。
二.实验方法:运用阶跃响应法:第一个水箱的参数辨识(一阶):一阶惯性环节的传递函数为:TSK G +=11其中:7111.21060111.87)(=-=∞=u y K将H 归一化:)()200()(∞-=y y t y H 在H 中查得632.0)(=T y 时对应T=2.3故模型为 13.27111.21+=S G第二个水箱的参数辨识(二阶):二阶系统的传递函数为:)1)(1(2122++=s T s T K G其中:70678.210600678.87)(=-=∞=u y K 在H 中可得:8032.0)5.9(4004.0)1.4(==y y 故有: 5.91.421==t t由公式 55.0/74.1)/(16.2/)(21221212121-=++=+t t T T T T t t T T可求出: 7436.15573.421==T T 故:)17436.1)(15573.4(7068.22++=s s G实验二:相关分析法搭建对象:处理程序:for i=1:15m(i,:)=UY(32-i:46-i,1);endy=UY(31:45,2);gg=ones(15)+eye(15);g=1/(25*16*2)*gg*m*y;plot(g);hold on;stem(g);实验结果:相关分析法最小二乘法建模:二、三次实验本次实验要完成的内容:1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS);2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说明;实验三最小二乘法参数估计一.实验内容(1)参照index2,设计对象,从workspace空间获取数据,取二阶,三阶对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS); (2)对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说明(3)参照index3,设计符合GLS和ELS的对象模型,改写参照程序,实现相应的.算法。
过程建模与系统辨识课程报告

过程建模与系统辨识课程报告班级:姓名:学号:课题:人体运动计算机仿真建模方法地研究1.人体运动计算机仿真地理论基础(1)人体运动计算机仿真地理论所谓人体运动计算机仿真地理论, 是指人体运动领域及其计算机仿真技术应用时作为基本立论地专业理论知识依据, 也就是指导人们从事人体运动计算机仿真应用与研究活动赖以建立和存在地专业领域内地前提和一些基本思想.总之, 因为仿真技术具有“学科面广、综合性强、应用领域宽、无破坏性、可多次重复、安全、经济、可控、不受气候和场地空间条件限制”等独特优点, 故而, 无论在交通工具安全、人机项目、虚拟设计、机器人、医疗康复、体育运动以及影视娱乐等诸多领域, 应用计算机仿真技术研究人体运动都有着其它技术所无法比拟地价值和效益.因此, 本文着眼于人体运动生物力学、计算机仿真等领域地知识基础, 从计算机仿真技术及其在人体运动领域地应用发展、人体及其运动建模等主要层面进行研究成果地综述性讨论, 旨在进一步促进人体运动领域应用计算机仿真技术在理论与实践上得以不断拓宽和深入发展.(2)人体及其运动建模当人体被作为一种系统来看待时, 其本身及其运动包含了众多不同层面而复杂地因素和交互作用.因此, 要深刻理解和把握人体及其运动, 模型化方法是不可或缺地.概略来说, 人体及其运动模型地构造主要有两种方式( 或者两者地结合) : 第一种方式从逻辑上看是演绎为主地, 即将人体系统分成子系统, 且子系统地性质和关系已被成熟地理论知识或规律所涵盖, 进而把这些子系统用数学方法加以联结得到整个系统地模型, 因为它无须对人体实际系统进行试验, 故而, 这种方式通常就被称为建模; 第二种方式则主要是归纳地, 它主要依据从实际人体地实验数据( 记录人体系统地输入输出) 并进而进行数据分析来建立数学模型或图象模型, 通常被称为系统辩识.就人体运动地力学模型而言, 从最简化地质点、刚体, 到多刚体、柔性多体等模型, 都以阐释人体机械运动形式地机理为目标, 其主要内容涵盖多体系统力学模型、非完整系统力学模型等, 并为人体地动力学研究提供了理论基础.在计算机仿真地交互效果上, 人体地逼真形象模型是在计算机图形学与先进仿真技术不断融合促进下发展起来地, 又在虚拟现实技术大力推动下, 三维“虚拟人”模型亦不断推出, 其中主要有如下几种形式: 骨架、体素、曲线、球体堆积、曲面等模型形式.(3)人体运动计算机仿真地理论地发展随着系统仿真技术及相关地计算机图形学、数据库技术、虚拟现实技术地交互融合与推动, 加上以人体或其运动为核心地不同领域地强烈需求地推动, 虚拟人体及其运动成为当前研究发展地热点, 在建模方法与技术地核心理论基础方面, 人工智能( 专家知识、神经网络) 、运动心理学、定性仿真有关地新发展成为未来值得关注地趋势.2.人体运动计算机仿真建模方法地研究(1)计算机数值仿真计算机数值仿真也称为计算机仿真或模拟, 是以数学理论、相似原理、信息技术、系统控制及其应用领域有关地专业技术为基础, 以计算机和各种物理效应设备为工具, 利用系统模型对实际地或设想地系统进行实验研究地一门综合技术.它借助高速、大存储量计算机及相关技术, 对复杂地真实系统地运动过程或状态进行数字化模仿地技术, 所以也称为数字仿真.(2)人体运动地计算机仿真人体运动地计算机仿真是运动生物力学研究方法中地一个重要内容, 具有很高地理论和实际应用价值,是研究人体运动规律地有效手段.它可以用于分析运动员在完成动作过程中, 人体各个部分地位移、速度、加速度等运动学变化参数, 以及力、力矩等动力学参数地变化规律, 从而了解人体运动地力学特征与运动技术动作地定量关系; 优化运动员地动作技术, 设计新技术并预测其效果.此外, 人体运动仿真还可以研究运动损伤地力学机理、研究运动员地动作如何与运动器械相协调等.因此, 人体运动仿真有助于体育训练, 从传统地主要基于人眼观察地方法向基于高精度视频捕捉与分析地人体测量方法转变; 从基于经验地训练分析方法向程式化地科学地人体运动分析方法地转变, 从而更快更有效地提高运动训练水平和运动成绩.应用计算机仿真进行运动技术研究地核心问题是对运动人体进行建模.本研究通过总结近年来人体运动计算机模拟与仿真中地几种常见地建模方法,分析各种方法地特点和适用范围, 以及建模中存在地难点和关键问题, 并讨论了人体运动仿真地可视化技术, 最后对人体运动仿真未来地发展趋势作了展望.3.人体运动计算机仿真建模方法地研究实例模型(1)多刚体动力学模型从人体解剖学地观点来看, 人体运动系统是由多个骨骼和附着在其上地肌肉、肌腱、韧带等, 通过关节连接在一起组成, 并在神经系统地调节和其它系统地配合下, 使各环节间地相互位置发生变化, 最终形成人体在空间地复杂运动地.为了研究人体地运动, 可以把人体简化为多刚体系统, 把人体地肌肉、肌腱等软组织处理为各刚体间地作用力和力矩.Hanavan于1964年提出了一个15刚体地人体模型.该模型把人体分为头、上躯干、下躯干、大腿、小腿、足、上臂、前臂、手等共15个刚体, 可以模拟人体大量一般性地动作.出于不同问题地需要, 许多专家学者根据各自所研究地主要问题和目标, 从不同地角度对人体进行了不同程度地合理简化, 提出了不同地人体多刚体模型.例如:Miller建立了四刚体人体模型用于研究人体潜水运动; passerello&Huston建立了十刚体人体模型用于模拟人体地空间运动; Ghosh采用三刚体模型研究人体地单杠振浪; H atze提出了十七刚体人体模型研究跳远起跳; Remizov用双刚体模型分析滑雪起跳动作.在国内, 洪友廉提出了五刚体人体模型来研究单杠后空翻; 刘延柱提出了两刚体人体模型研究单杠振浪; 罗特军提出了三刚体人体模型研究双杠支撑摆动; 许静辉等人采用五刚体平面模型研究跳远地最佳踏跳着板姿势; 朱昌义采用五刚体模型研究单杠上人体摆动技术; 柴夏萍、焦群英利用三刚体模型, 对人体受冲击后向后翻倒地过程进行了计算机模拟, 研究了人体后倒引起地骨盆损伤问题.多刚体动力学方法将人体简化成为具有有限自由度地多刚体系统, 在实际地动力学分析中较多地采用Hanavan地人体简化模型.该方法地关键是要计算一组约束力(或力矩), 使人体地运动符合所给定地约束, 在实际地解方程中因为涉及求导和解微分方程, 其过程比较烦琐.多刚体动力学方法满足牛顿定律, 在物理上概念清楚, 所以在人体运动仿真中被广泛采用.但是因为只考虑了人体地机械特性, 忽略了人体在运动中地变形, 使得仿真结果象一个机器人, 采用时间空间约束地优化处理技术可以改善该方法, 在一定程度上提高了仿真地逼真度.(2)有限元分析法建模人在运动中尤其在做剧烈地旋转运动时,会产生明显地变形,肌肉两端将产生较大地剪切应力,可以认为人体是一个典型地柔性多体系统,所以将柔性多体系统地主要分析手段有限元分析法引入到人体运动地研究中也是非常必要地.有限元分析法也称为有限元素法,其主要地研究思想是把研究目标划分成许多微小地单元,然后研究在外力地作用下,各个单元地应力,进而掌握人体在运动中各个部位地受力情况,这种方法通常分为三个阶段:建立模型;加载求解;察看和分析.这种研究手段广泛应用于碰撞实验,损伤地预防与诊断,虚拟制造以及运动评价之中,但与其他地项目应用相比采用有限元研究人体运动要复杂地多,这是因为人体地有限元分析需要首先对生物组织地本构关系进行理论研究,而人体组织地本构方程地建立本身就是一个非常复杂地过程,另外因为生物体地几何形状并不规则,边界条件十分复杂,生物材料呈现高度地非线性并且具有时变特性.所幸地是因为结构动力学有限元,边界元等理论地发展使得机构分析方法实现了程式化,开发了功能相当完备地大型计算机软件平台如SAP 系列,NASTRAN,ANSYS 等,这些软件具有友好地用户界面,只要输入结构模型地数据,数学模型地建立与数值分析过程均由计算机自动完成,利用这些软件可以很方便进行人体模型地研究.(3)肌肉力控制无生命物体地运动是由不平衡地外力组成,而有生命地人体地运动是由不平衡地内力(肌肉力)产生,作为整体,人体也要受其环境动力地影响,而把通常地动力学研究方法着眼于后者,这是不全面地,所以近些年来产生了基于肌肉力地仿真方法[15],对于可变形体,可以将其模型抽象成质点-弹簧-阻尼,弹簧用来模仿能够自由伸缩地肌肉,根据合适地控制函数和激励信号使肌肉产生力和力矩,从而引起被激励部分地运动.该方法即能满足牛顿定律又充分考虑了人体地肌肉变形,但是随着要控制地肌肉数地增加,其执行机构地控制函数地推导也变得更加困难,为了克服这个困难,通常采用优化技术自动导出控制函数.(4)实验地方法实验方法是一个非常有前景地研究方法,充分利用实验方法中不同地测试数据,可以简化人体建模地复杂性,缩短研究周期.南非地Hazte已经很成功地采用实验方法摸拟了一些人体地运动.利用实验方法进行人体仿真主要有两种方法:1.利用一个对象地测试数据,在不同地对象之间进行移植; 2.利用实验数据采用神经网络,遗传算法等计算智能方法进行建模.采用生物力学测试手段可以得到运动捕捉数据,测力台数据以及肌肉力数据,要获得这些数据必须采用影像,多维力测力台,肌电仪等设备,但要获取全面地人体运动测试数据,必须综合利用这些设备,故此实验方法地发展很大程度要仰仗人体运动测试与感知技术地提高.4.对人体运动计算机仿真建模方法地建议及感想人体运动地建模是一项艰巨而复杂地工作,理论方法可以获得带有普遍意义地运动规律揭示运动地内在机理,但模型复杂,建模困难,以黑箱方法为代表地实验方法相对简单,误差小,另外可以建立人体运动地控制模型,但是此种方法从理论方法还技术层面都有许多问题需要进一步研究.但是将不同地研究方法结合起来,利用各自地优势进行互补将是研究地重点和发展方向.目前地多刚体动力学建模方法对人体模型都做了不同程度地简化, 仿真效果与实际情况还是存在差距, 其主要原因是: 1)简化地模型对人体地变形考虑较少; 2)理论计算需要肌肉力、肌肉力矩地实验测量作为其边界或约束条件, 而肌肉力、肌肉力矩地在体测量尚不可能实现; 3)在微分方程地迭代求解过程中没有解决好奇异点消除地问题.而骨骼 -肌肉建模方法充分考虑了可变形体 (如肌肉、韧带 )肌肉或韧带地作用, 以及肌肉力对运动地控制, 因此将多刚体动力学建模方法与骨骼 - 肌肉建模方法相结合无疑是人体运动仿真发展地一个趋势.另外随着人工智能方法地引入,人体地运动仿真将由单独地力学特征地仿真向具有生命特点地人工人转化,人工人地运动也将是自主地,智能地行为,而将多个人工生命地行为进行组合和协调,人工人地行为将会体现着人地另一本质—社会属性,这将是人体运动仿真中地革命性地变革.5. 对过程建模与系统辨识课程地建议及体会在整个过程建模与系统辨识课程地学习中,我获益颇多,这门课程涵盖了数学建模地知识,及系统辨识地理论和方法,一方面我们有了很多数学建模地思想,以及一些数学建模地解决方法,这些都为于我们以后去解决一些复杂问题打下了良好地基础,另一方面让我们对系统辨识有了深刻地认识,了解了一些系统辨识地理论例如、最小二乘理论、多变量系统辨识法、闭环系统辨识法和小样本系统辨识等以及系统辨识地一些应用.在学习这门课程同时,我也觉得十分吃力,因为课程地内容太多,而且太多地方我们都是没有基础地,所以大部分都是只能以了解为主不能深入地学习,也激励不起太多地兴趣与思考,所以我觉得这门课程最好是着重地讲几个很实用地、主流地东西,让大家深入地研究,如此而来,我想我们学到地会更多,也会更加有兴趣.参考文献:[1] 唐毅, 等. 人体力学行为地计算机仿真地发展及其展望 [ J ].系统仿真学报, 2003, 16 ( 5): 863- 867.[ 2] 石俊, 等. 人体步态研究与仿真地现状和展望 [ J] . 系统仿真学报, 2006, 18 ( 10): 2703- 2711.[3] 唐毅, 葛运建, 陈卫, 等. 数字运动员人体模型及其仿真研究,1004-731X (2003) 01-0056-03[4] 崔来友, 白士红, 张春林, 等. 人体运动学模型地研究,1004-731X(2004)05-0863-05[ 5] 刘雷. 人体运动建模仿真方法研究[ J] . 计算机仿真, 2009( 1) : 166- 168.[ 6] 孙剑, 李克平. 行人运动建模及仿真研究综述[ J] . 计算机仿真, 2008(12) : 12- 16.[7]古福明.人体运动计算机仿真建模方法地研究进展.1001) 9154(2007) 03) 0090) 04[8]黄汉升, 朱昌义.人体运动计算机仿真地理论基础1007- 323X(2007)05- 0001- 04。
系统辨识实验报告
实验一:系统辨识的经典方法一、实验目的掌握系统的数学模型与输入、输出信号之间的关系,掌握经辨辨识的实验测试方法和数据处理方法,熟悉MATLAB/Simulink环境。
二、实验内容1、用阶跃响应法测试给定系统的数学模型在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或二阶加纯滞后模型,对模型进行验证。
2、在被辨识系统中加入噪声干扰,重复上述1的实验过程。
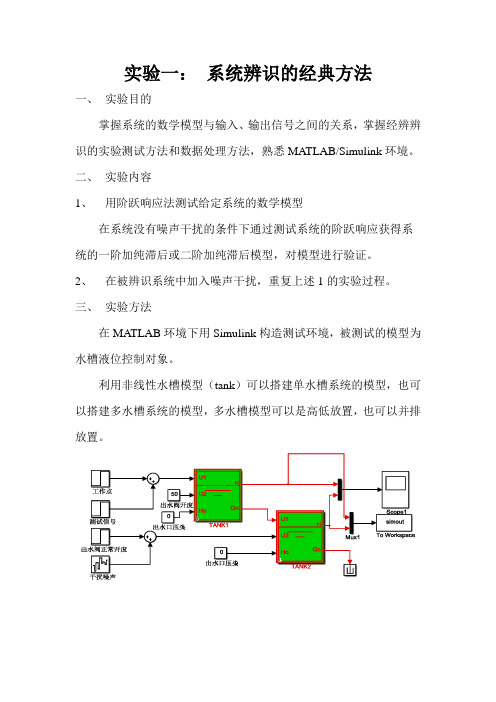
三、实验方法在MATLAB环境下用Simulink构造测试环境,被测试的模型为水槽液位控制对象。
利用非线性水槽模型(tank)可以搭建单水槽系统的模型,也可以搭建多水槽系统的模型,多水槽模型可以是高低放置,也可以并排放置。
1.噪声强度0.5,在t = 20的时候加入阶跃测试信号相应曲线2.乘同余法产生白噪声A=19;N=200;x0=37;f=2;M=512; %初始化;for k=1: N %乘同余法递推100次;x2=A*x0; %分别用x2和x0表示xi+1和xi-1;x1=mod(x2,M); %取x2存储器的数除以M的余数放x1(xi)中;v1=x1/M; %将x1存储器中的数除以256得到小于1的随v(:,k)=(v1-0.5 )*f;x0=x1; % xi-1= xi;v0=v1;end %递推100次结束;v2=v;k1=k;h=k1;%以下是绘图程序;k=1:1:k1;plot(k,v,'r');grid onset(gca,'GridLineStyle','*');grid(gca,'minor')3.白噪声序列图像020406080100120140160180200-1-0.8-0.6-0.4-0.20.20.40.60.81四、 思考题(1) 阶跃响应法测试系统数学模型的局限性。
答:只适用于某些特殊对象或者低阶简单系统;参数估计的精度有限,估计方法缺乏一般性。
系统辨识调研报告

北京工商大学《系统辨识》课程调研报告题目类别:系统建模的分类现代辨识方法报告题目:基于神经网络与模糊控制的辨识方法调研目录第一章系统辨识理论综述 21.1系统辨识的基本原理 21.2系统辨识的经典方法 21.3神经网络系统辨识综述 21.3.2神经网络在非线性系统辨识中的应用 2 1.4模糊系统辨识综述 31.4.1模糊系统的结构辨识 31.4.2参数优化的方法 31.4.3模糊规则库的化简 31.5小结 4第二章模糊模型辨识方法的研究 42.1模糊模型辨识流程 42.2模糊模型结构辨识方法 52.3模糊模型参数辨识方法 52.4模糊系统辨识中的其它问题 62.4.1衡量非线性建模方法好坏的几个方面 62.4.2模糊辨识算法在实际系统应用中的几个问题 62.4.3模糊模型的品质指标 62.5小结 7第三章基于两种模型的自行车机器人系统辨识 73.1基于ARX模型的自行车机器人系统辨识 73.2基于ANFls模糊神经网络的自行车机器人系统辨识 73.3 展望 7第一章系统辨识理论综述1.1系统辨识的基本原理根据LA.zadel的系统辨识的定义(1962):系统辨识就是在输入和输出数据的基础上,从一组给定的模型类中,确定一个与所测系统等价的模型"系统辨识有三大要素:(1) 数据。
能观测到的被辨识系统的输入或输出数据,他们是辨识的基础。
(2) 模型类。
寻找的模型范围,即所考虑的模型的结构。
(3) 等价准则。
等价准则一辨识的优化目标,用来衡量模型接近实际系统的标准。
1.2系统辨识的经典方法1、阶跃响应法系统辨识;2、频率响应法系统辨识;3、相关分析法系统辨识;4、系统辨识的其他常用方法;1.3神经网络系统辨识综述1.3.1神经网络在线性系统辨识中的应用自适应线性(Adallne一MadaLine)神经网络作为神经网络的初期模型与感知机模型相对应,是以连续线性模拟量为输入模式,在拓扑结构上与感知机网络十分相似的一种连续时间型线性神经网络。
系统辨识课程报告

X1
X2
X3
X4
图 1.1
M 序列产生原理图
2 最小二乘法原理
最小二乘理论是高斯(K.F.Gauss)在 1795 年预测行星和彗星运动的轨道时提出的, 高斯提出: “未知量的最大可能的值是这样一个数值, 它使各次实际观测和计算值之间的差 值的平方乘以度量其精确度的数值以后的和为最小。 ” 2.1 最小二乘格式
利用数据序列{z(k)}和{u(k)},极小化下列准则函数
l
T
J z (k ) (k )
T k 1
2
(2.6)
使 J(θ )=min 的θ 估计值记作 ,称之为参数的最小二乘估计值。 2.2 最小二乘问题的求解 用表示根据 l 次数采样数据所求得的参数的估计值 。
《系统辨识》课程报告Fra bibliotek被辨识的系统
图 2.1
SISO 辨识系统示意图
《系统辨识》课程报告
学号:2007073124
假设被辨识系统为一个单输入单输出(SISO)离散时间动态系统,如图 2.1 所示。其 系统数学关系式可用如下随机差分方程描述
z (k ) ai z (k i) bi u (k i) v(k )
2 其中,u(k) ,z(k)为系统的输入输出变量,v(k)是服从 N (0, v ) 分布的不相关随机噪
声,上述模型可写成最小二乘矩阵格式
z n H n n Vn
则有
(3.2)
L 2
L( n ) (2 )
2 v
1 T exp ( z H ) ( z H ) n n n n n n 2 2 v
(3.3)
故
系统辨识实验报告1

系统辨识实验报告学院:信息科学与技术学院专业:自动化日期:2016/4/26目录实验1 (4)一.实验内容及要求: (4)二.实验原理: (4)三.软件设计思想: (4)四.程序结构框图: (5)五.运行示意图: (5)实验2 (8)一.实验内容及要求: (8)二.实验原理: (8)三.软件设计思想: (9)四.程序设计框图: (10)五.程序运行流程图: (10)实验3 (12)一.实验内容及要求: (12)二.实验原理: (12)三.程序数据流程图: (12)四.实验运行结果: (13)实验4 (14)一.实验内容及要求: (14)二.实验原理: (14)三.数据递推关系图: (14)四.实验运行结果: (15)心得体会 (16)附录(实验代码) (17)bWork1 (17)bWork2 (21)bWork3 (23)bWork4 (26)实验1一.实验内容及要求:1.编出矩阵A与B相乘得到的矩阵R的运算计算机程序要求:(1)A和B的维数及数值可通过键盘及数据文件输入(2)计算结果R可由屏幕及文件输出2.将1改写为子程序3.查找有关的资料,读懂及调通矩阵求逆程序,并改写为子程序。
二.实验原理:1.两个矩阵A、B相乘得到C矩阵,首先要满足的条件是A的列数与B行数相等,否则不能相乘。
当满足条件后,根据C(i,k)=∑A(i,j)∗B(j,k)可以求得C矩阵。
2.当求矩阵的逆时,首先要判断其是否为方阵,若是则可以对其进行下一步的操作。
本次实验中求逆主要是通过构造一个增广矩阵(FangZ | E)矩阵的初等行变换得到(E | FZNi)的这样的一个矩阵就可以求得矩阵的逆。
若矩阵FangZ不是满秩矩阵时,FangZ没有FZNi 。
通过这样的求逆方式,避免了大方阵的求取行列式运算。
三.软件设计思想:1.确定该软件的功能主要有:键盘输入两个矩阵然后相乘;文本data输入两个矩阵将结果放在文本result中;键盘输入一个方阵求得其逆矩阵。
系统辨识实验报告1

14
四.实验运行结果:
函数界面示意图: 6. 只显示结果界面: 7. 显示过程的参考界面:
15
心得体会
我很喜欢这个课程的期末考核方式,不用再拘泥于在题目当中对该课程的了 解,而是通过 4 个 C 语言设计的练习来达到学习的目的,而且对以后的学习还有 很大的帮助。
在编写 C 语言的过程中,也遇到了一些阻碍,特别是在编写第 3,4 个的时候。 比如:用的数组太多,并且未将其初始化,运行出来的结果经常是很长的一段随 机数;或者一模一样的程序有时候就可以正常运行,有时候就总是出现报错…… 这些都是让我心塞了两周的问题。在这些问题解决之后,运行出来的结果却与实 际模型参数的出入有点大,于是又重新查找第 2 个实验是否是 M 序列产生的方式 有问题。通过对初始化寄存器赋给不同的值,可以让结果与真实模型参数之间的 误差达到最小。
实验 4 ................................................ 错误!未定义书签。 一.实验内容及要求: ............................... 错误!未定义书签。 二.实验原理: ..................................... 错误!未定义书签。 三.数据递推关系图: ............................... 错误!未定义书签。
编写并调试动态离散时间模型 LS 成批算法程序。 要求:(1)原始数据由 DU 和 DY 读出。 (2)调用求逆及相乘子程序。 (3)显示参数辨识结果。
二.实验原理:
1.批次处理的方法就是把所有的数据采集到一次性进行处理,但前提是 白色噪声、及 M 序列所共同作用而产生的输出,才能使用最小二乘法。虽然 这种方法的计算量庞大,但经常用于处理时不变系统,方法简单。
系统辨识课程综述

系统辨识课程综述通过《系统辨识》课程的学习,了解了系统辨识问题的概述及研究进展;掌握了经典的辨识理论和辨识技术及其优缺点,如:脉冲响应法、最小二乘法(LS)和极大似然法等;同时对于那些为了弥补经典系统辨识方法的不足而产生的现代系统辨识方法的原理及其优缺点有了一定的认识,如:神经网络系统辨识、基于遗传算法的系统辨识、模糊逻辑系统辨识、小波网络系统辨识等;最后总结了系统辨识研究的发展方向。
一、系统辨识概论自40年代Wiener创建控制论和50年代诞生工程控制论以来,控制理论和工程就一直围绕着建立模型和控制器设计这两个主题来发展。
它们相互依赖、相互渗透并相互发展;随着控制过程的复杂性的提高以及控制目标的越来越高,控制理论的应用日益广泛,但其实际应用不能脱离被控对象的数学模型。
但是大多数情况下,被控对象的数学模型是不知道的,或者在正常运行期间模型的参数可能发生变化,此时建立模型需要细致、完整地分析系统的机理和所有对该系统的行为产生影响的各种因素,从而变得十分困难。
系统辨识建模正是适应这一需要而产生的,它是现代控制理论中一个很活跃的分支。
系统辨识是建模的一种方法,不同的学科领域,对应着不同的数学模型。
从某种意义上来说,不同学科的发展过程就是建立他的数学模型的过程。
所谓系统辨识,通俗地说,就是研究怎样利用对未知系统的试验数据或在线运行数据(输入/输出数据),运用数学归纳、统计回归的方法建立描述系统的数学模型的科学。
Zadeh与Ljung明确提出了系统辨识的三个要素:输入输出数据,模型类和等价准则。
总之,辨识的实质就是从一组模型类中选择一个模型,按照某种准则,使之能最好地拟合我们所关心的实际过程的静态或动态特性。
通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及设计控制器。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号;对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
系统辨识及自适应控制实验报告

系统辨识及自适应控制实验报告实验报告:系统辨识及自适应控制1.引言系统辨识和自适应控制是现代自动控制领域中的重要研究内容。
系统辨识是通过采集系统输入输出数据,建立数学模型描述系统的动态行为。
自适应控制则是根据系统辨识得到的模型,调整控制器参数以适应系统的变化和外部干扰。
本实验旨在通过实际操作,掌握系统辨识和自适应控制的基本原理和方法。
2.实验目的1)了解系统辨识的基本原理和方法;2)掌握常见的系统辨识方法,包括参数辨识和频域辨识;3)理解自适应控制的基本原理和方法;4)熟悉自适应控制的实现过程;5)通过实验验证系统辨识和自适应控制的有效性。
3.实验原理3.1系统辨识原理系统辨识的目标是通过采集系统输入输出数据,建立数学模型来描述系统的动态特性。
常见的系统辨识方法包括参数辨识和频域辨识两种。
参数辨识是通过拟合实际测量数据,找到最佳的模型参数。
常用的参数辨识方法有最小二乘法、极大似然法和最小误差平方等。
频域辨识则是通过对输入输出信号的频谱分析,得到系统的频率响应特性。
常用的频域辨识方法有傅里叶变换法、相关分析法和谱估计法等。
3.2自适应控制原理自适应控制是根据系统辨识得到的模型,调整控制器参数以适应系统的变化和外部干扰。
自适应控制分为基于模型的自适应控制和模型无关的自适应控制。
基于模型的自适应控制利用系统辨识得到的模型参数,设计相应的控制器来实现自适应控制。
常见的基于模型的自适应控制方法有模型参考自适应控制和模型预测自适应控制等。
模型无关的自适应控制则不依赖于系统辨识的模型,而是根据实际测量数据直接调整控制器参数。
常见的模型无关的自适应控制方法有自适应滑模控制和神经网络控制等。
4.实验内容4.1系统辨识实验在实验中,我们通过采集系统输入输出数据,根据最小二乘法进行参数辨识。
首先设置系统的输入信号,如阶跃信号或正弦信号,并记录对应的输出数据。
然后根据采集到的数据,选取适当的模型结构,通过最小二乘法求解最佳的模型参数。
系统辨识课程总结及实验

过程
e(k)
H(k)
Y(k) + +
+
辨识表达式Ө
Z(k)
+ Z(״k)
模型Ө
Z(׳k)
Ө(k) 辨识算法
图3 系统辨识的模型
通常采用逐步逼近获取模型参数θ的估值θ′,根据(k-1)时刻的估 计参数,计算出k时刻的预测值、预测误差。
2.模糊辨识 模糊逻辑理论用模糊集合理论,从系统输入和输出的量测值来辨 识系统的模糊模型,也是系统辨识的一个新的和有效的方法,在非线 性系统辨识领域中有十分广泛的应用。因而,模糊逻辑辨识法深受研 究者的青睐。模糊逻辑辨识具有独特的优越性:
(1) 能有效地辨识复杂和病态结构的系统。 (2) 能够有效地辨识具有大时延、时变、多输入输出的非线性系 统。 (3) 可以辨识性能优越的人类控制器。 (4) 可得到被控对象的定性与定量相结合的模型。模糊辨识时通 过输入输出测量数据,对模糊模型中的结构和参数进行的辨识。模糊 模型已经被证明在非线性动力系统建模,基于规则的学习控制,模式识 别起到了很大的作用。 模糊逻辑建模方法的主要内容可分为两个层次:一是模型结构的 辨识,另一个是模型参数的估计。T-S模糊模型是一种经典的模糊模 型,该模糊模型是以局部线性化为基础,通过模糊推理的方法实现了 全局的非线性。该模型具有结构上简单、逼近能力强等特点,已成为 模糊逻辑辨识中常用的模型。典型的模糊结构辨识方法有:模糊网格 法、自适应模糊网格法、模糊巨类法及模糊搜索树法等。 近二十年来,系统辨识获得了长足的发展,已经成为控制理论的 一个十分活跃而又重要的分支。从线性现象和线性系统的研究过渡到 非线性现象和非线性系统的研究是科学发展的必然结果,这不仅是对 科学家们一种新的挑战,而且也是人类社会向更高级形式演化的一种 必然。随着智能控制理论、遗传算法理论等的不断成熟,逐渐形成了 形式多样的现代的系统辨识方法,并且已在实际问题应用中取得了较
系统辨识实验报告 中科大

1.5 预处理后检验
把原始数据分成两部分,一部分用来辨识,一部分用来检验模型。 预处理后便是部分输入的图像
预处理后便是部分输出的图像
预处理后检验数据部分输入图像
预处理后检验部分输出部分
2 辨识算法
以下 n 的取值均为 2,在以下部分为给出为什么 n 取 2 最好
2.1 批量最小二乘
2.1.1 源代码 %批量最小二乘算法 dafi=ones(N,2*n); for i=0:N-1 dafi(i+1,:)=[-vo_iden(i+1:i+n)' vi_iden(i+1:i+n)']; end cta=inv(dafi'*dafi)*dafi'*vo_iden(n+1:n+N); Y1=test*cta; %plot(Y1); E1=Y1-vo_test(n+1:n+N); En1(1,n)=E1'*E1; cta 2.1.2 辨识结果
2.3.2 辨识结果
2.3.3 模型检验 (1)用测试数据输入后得到的图像
(2)和实际偏差的曲线
2.4 增广最小二乘法
2.4.1源代码 %增广最小二乘算法 p=eye(3*n)*1000; cta=ones(3*n,1); w=zeros(n,1); W=ones(N,n); for i=0:N-1 fi=[-vo_iden(i+1:i+n)' vi_iden(i+1:i+n)' w']; k=(p*fi')/(1+fi*p*fi'); cta=cta+k*(vo_iden(i+1)-fi*cta); p=p-k*fi*p; for j=1:n-1 w(j,1)=w(j+1,1); end w(n,1)=vo_iden(i+1)-fi*cta; end w=zeros(n,1); for i=0:N-1 W(i+1,:)=w; s=[-vo_test(i+1:i+n)' vi_test(i+1:i+n)' w']; for j=1:n-1 w(j,1)=w(j+1,1); end w(n,1)=vo_test(i+1)-fi*cta; end teste=[test W]; Y4=teste*cta; %plot(Y4); E4=Y4-vi_test(n+1:n+N); En4(1,n)=E4'*E4; cta 2.4.2 辨识结果
系统辩识实验报告

一、实验目的1. 理解系统辨识的基本概念和原理。
2. 掌握递推最小二乘算法在系统辨识中的应用。
3. 通过实验,验证算法的有效性,并分析参数估计误差。
二、实验原理系统辨识是利用系统输入输出数据,对系统模型进行估计和识别的过程。
在本实验中,我们采用递推最小二乘算法对系统进行辨识。
递推最小二乘算法是一种参数估计方法,其基本思想是利用当前观测值对系统参数进行修正,使参数估计值与实际值之间的误差最小。
递推最小二乘算法具有计算简单、收敛速度快等优点。
三、实验设备1. 电脑一台,装有MATLAB软件。
2. 系统辨识实验模块。
四、实验步骤1. 打开MATLAB软件,运行系统辨识实验模块。
2. 在模块中输入已知的系数a1、a2、b1、b2。
3. 生成输入序列u(t)和噪声序列v(t)。
4. 将输入序列u(t)和噪声序列v(t)加入系统,产生输出序列y(t)。
5. 利用递推最小二乘算法对系统参数进行辨识。
6. 将得到的参数估计值代入公式计算参数估计误差。
7. 仿真出参数估计误差随时间的变化曲线。
五、实验结果与分析1. 实验结果根据实验步骤,我们得到了参数估计值和参数估计误差随时间的变化曲线。
2. 结果分析(1)参数估计值:通过递推最小二乘算法,我们得到了系统参数的估计值。
这些估计值与实际参数存在一定的误差,这是由于噪声和系统模型的不确定性所导致的。
(2)参数估计误差:从参数估计误差随时间的变化曲线可以看出,递推最小二乘算法在短时间内就能使参数估计误差达到较低水平。
这说明递推最小二乘算法具有较好的收敛性能。
(3)参数估计误差曲线:在实验过程中,我们发现参数估计误差曲线在初期变化较快,随后逐渐趋于平稳。
这表明系统辨识过程在初期具有较高的灵敏度,但随着时间的推移,参数估计误差逐渐减小,系统辨识过程逐渐稳定。
六、实验结论1. 递推最小二乘算法在系统辨识中具有较好的收敛性能,能够快速、准确地估计系统参数。
2. 实验结果表明,递推最小二乘算法能够有效减小参数估计误差,提高系统辨识精度。
系统辨识与容错控制课程作业报告

系统辨识与容错控制课程作业报告一、 故障观测(一)自己定义一种故障,完成此故障下的故障检测滤波器设计,并给出残差曲线,证明设计的正确性 解:定义故障为控制器故障,故障向量为:08.92329i f ⎡⎤=⎢⎥⎣⎦将故障特征向量对应的特征值配置到-5处,设计的滤波器矩阵为:110 4.9075D ⎡⎤=⎢⎥⎣⎦Simulink 仿真模型如下:图1.1.1 故障检测滤波器仿真模型正常工作模式下残差曲线输出为:图1.1.2 正常工作模式下的残差输出曲线故障工作模式下残差曲线输出为:图1.1.3 故障工作模式下的残差输出曲线由以上两实验结果图像可以看出,配置好的故障检测滤波器可以很好的对故障进行辨识。
(二)按照文章例子,考虑建模误差,完成鲁棒故障检测观测器的设计,并给出残差曲线,证明设计的正确性 解:根据闭环极点配置,设计K 阵为:[]2.02270.7741K =--根据观测器极点配置,设计L 阵为:101103L ⎡⎤=⎢⎥-⎣⎦最后设计得到的鲁棒观测器增益矩阵为H为:[]H=-10搭建的Simulink仿真模型为:图1.2.1 鲁棒故障检测观测器仿真模型当输入信号为正弦信号时:图1.2.2 标称状态和存在建模误差但不存在故障状态输出残差比较图1.2.3 存在建模误差无故障普通观测器与鲁棒观测器观测残差结果图1.2.4 故障误差并存与仅有误差的鲁棒观测器残差通过以上的实验结果,我们对比分析可以得出鲁棒观测器比普通观测器对误差有更好的鲁棒性,同时能够及时快速的对针对的故障进行辨识。
(三)结合教材33页内容,给出三种工作状态(一种正常状态、两种故障状态),分别采用比较分析法和滤波比较法完成并行鲁棒观测器设计与仿真解:根据工作状态的不同,设计L反馈矩阵配置观测器极点[-10 -10]:M0(正常状态):108.0491 =19.9075L ⎡⎤⎢⎥⎣⎦M1(传感器1故障):11013.4240 =1019.9070L ⎡⎤⎢⎥⎣⎦M2(传感器2故障):219.907010 =106.207010L ⎡⎤⎢⎥⎣⎦搭建的Simulink仿真模型如下:图1.3.1 多模并行鲁棒观测器仿真假定实际系统处于M1态,仿真计算观测器O、O1、O2的残差,比较法的决策量r0、r1、r2以及滤波比较法的决策量E、E1、E2分别如下。
《过程建模与系统辨识》课程报告

《过程建模与系统辨识》课程报告
A类题目
1. 针对某一非线性控制模型或目前所有的非线性控制模型进行综述,要求:
要将所述模型的背景与形式叙述清楚,综述该种非线性模型对应控制方法的原理以及各方法的比较优势。
题目为《某某非线性控制模型的研究》或《非线性控制综述》
2.针对某在线优化控制方法进行描述与讨论,要求:
(1)将所研究的在线优化控制方法进行详细描述,将原理表达清楚;
(2)说明该方法存在的问题、其他方法的不同,以及目前较先进的在线优化控制方法有哪些。
题目为《某某在线优化控制方法的研究》
B类题目
1.针对集成建模的应用进行论述,要求:
针对某领域较难解决的具体问题进行讨论,要将问题背景、目的、意义叙述清楚,要说明所应用的集成建模方法的原理以及该方法与其他方法的比较优势。
题目为《某某集成建模方法的研究》
2.针对你感兴趣的某一建模方法进行讨论,要求:
(1)将该方法的原理表达清楚,并举出一个该方法的应用实例,要对例中的方法提出改进意见及理由,对该方法与其他方法的结合使用提出建议及其理由;
(2)对这门课程的内容及其教学方法提出建议,同时,谈谈学习这门课程的体会。
题目为《某某建模方法的研究》
统一要求
1. 要求字数不低于2000字,主要参考资料应为核心期刊;
2. 要求参考文献不少于十篇(要有英文文献),其中不少于五篇为近三年内的文献,并在文中标注出参考文献,在文后列出参考文献(作者,论文题名或书名,刊物名或出版社名,期号与卷号,页码,出版年);
3. 要求提交打印稿(正文为4号字);
4. 提交日期为:19周星期三13:30至14:30;地点为主楼333。
zy系统辨识

《系统辨识》课程报告题目:Matlab实现系统的阶次及模型辨识班级:工业自动化081班姓名:吴政学号:2008073121日期:2011-5-28成都信息工程学院控制工程学院Matlab实现系统的阶次及模型辨识摘要基于最小二乘原理确定系统模型阶次n,常用的定阶方法有六种:残差方差定阶,AIC 准则,残差白色定阶,零极点消去定阶,行列式比定阶,Hankel矩阵定阶。
在已知系统阶次的情况下,为了辨识出系统的模型,方法有很多种,比如一般最小二乘法,遗忘因子最小二乘法,增广最小二乘法,广义最小二乘法等等。
本课程报告根据残差平方和(作为损失函数)达到最小值的直接法来辨识系统的阶次,然后,通过递推最小二乘法来辨识出系统的模型,整个过程在Matlab环境下完成。
关键词:系统辨识;最小二乘法; Matlab;高斯白噪声Using Matlab To Identify The Order And Model Of SystemAbstractIn order to determine the order of model n based on the Least Squares Method(LSM), There are six commonly used method: order identification with the residual variance, AIC criterion, residual white, Pole-Zero cancellation, the ratio of the determinant, Hankel matrix,In the context of known the system’s order, There are many ways to determine the system’s model, such as general LSM, forgetting factor LSM, extended LSM, generalized LSM,etc. The course report based on the direct method when the residual sum of squares(as a loss function) achieve the minimum to identify the order of the system,then, identify the system model with recursive LSM,.The whole process completed in the Matlab environment.1Key words:System Identification;Least Squares Method(LSM);Matlab;Gaussian White Noise引言1.1系统辨识概述系统辨识的实质就是从一组模型类中选择一个模型,使之能够很好的拟合所关心的实际过程的动态和静态特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z(k ) (k ) v(k )
(2.2)
上式中, (k ) 是观测数据向量。辨识的问题则是如何求 a i 和 bi 。当模型结构已经选 定,即式(2.2)中的 na 和 nb 假定是已知的(通常 na〉nb) 。但是有时,为了系统分析方 便起见,也可以设 na=nb=n,这样并不会失去研究问题的普片性。 在(2.2)式中,有
(3.5)
将上式代人(3.4)式中得
2 L log L( ML ) const log v 2
(3.6)
故
AIC (n) 2const L log v 4 n
2
2
(参数个数=2n)
(3.7)
其等价式为
AIC (n) L log v 4 n
AIC (n) 中起主导作用。因此 AIC (n) 在 n0 处形成了一个最小值,如图 3.1 所示。
3.2 AIC 法确定线性定常系统的阶 考虑如下模型
z (k ) ai z (k i) bi u (k i) v(k )
i 1 i 1
n
n
(3.1)
伪随机序列可由线性移位寄存器网络产生。该网络由 r 级串联的双态器件,移位脉冲 产生器和模 2 加法器组成,下面以 4 级移位寄存器为例,说明伪随机序列的产生。例如, 初始状态是 0001,那么 X1=0,X2=0,X3=0,X4=1。如果反馈逻辑为 X= X3⊕ X4,对于 初始状态为 0001, 经过一个时钟节拍后, 各级状态自左向右移到下一级, 未级输出一位数, 与此同时模 2 加法器输出值加到移位寄存器第一级,从而形成移位寄存器的新状态,下一 个时钟节拍到来又继续上述过程。未级输出序列就是伪随机序列。其产生的伪随机序列为 X=100110101111000100110101111000… ,这是一个周期为 15 的周期序列。改变反馈 逻辑的位置及数量还可以得到更多不同的序列输出。如图 1 所示。
参数估计量 满足
lT ( Z l l ) 0
(2.9)
这就是以向量矩阵形式表示的正规方程, 它由具有 2l+1 个线性方程式所组成。 可解出
(lT l ) 1lT Z l
2.3 最小二乘估计的递推算法归结
T l 1 l K l 1 [ z l 1 l 1 l ] Pl l 1 K l 1 1 lT1 Pl l 1 Pl 1 [ I K L 1 lT1 ]Pl
2 其中,u(k) ,z(k)为系统的输入输出变量,v(k)是服从 N (0, v ) 分布的不相关随机噪
声,上述模型可写成最小二乘矩阵格式
z n H n n Vn
则有
(3.2)
L 2
L( n ) (2 )
2 v
1 T exp ( z H ) ( z H ) n n n n n n 2 2 v
参考文献
杨承志,孙棣华,张长胜.系统辨识与自适应控制.2003 年 7 月第一版.重庆大学出版社.
《系统辨识》课程报告
学号:2007073124
附:MATLAB 程序
1 最小二乘一次完成算法 M序列子函数:
function M=U X1=1;X2=0;X3=1;X4=0;X5=1;X6=0; %移位寄 存器输入Xi初态(101010),Yi为移位寄存器的 各级输出 m=300; %置M序列的总长度 for i=1:m Y6=X6; Y5=X5; Y4=X4; Y3=X3; Y2=X2; Y1=X1; X6=Y5; X5=Y4;X4=Y3; X3=Y2; X2=Y1; X1=xor(Y5,Y6); %异或运算 if Y6==0 U(i)=-1; else U(i)=Y6; end end M=U; J1=0; for x=2:300 J1=J1+[z(x)+z(x-1)*c1(1)-u(x-1)*c1(2 )].^2; end JJ1=J1+z(1).^2; AIC(1)=30*log(JJ1/300)+4*1; %若为二阶 z=zeros(1,300); for k=4:300 z(k)=1.5*z(k-1)-0.7*z(k-2)-0.1*z(k-3 )+1.1*u(k-1)+1.5*u(k-2)+1.7*u(k-3); %用理想输出值作为观测值 end for i=3:300 HL2(i,:)=[-z(i-1) -z(i-2) u(i-1) u(i-2)]; ZL2(i,:)=[z(i)]; end c2=inv(HL2'*HL2)*(HL2'*ZL2); J2=0; for x=3:300 J2=J2+[z(x)+z(x-1)*c2(1)+z(x-2)*c2(2 )-u(x-1)*c2(3)-u(x-2)*c2(4)].^2; end JJ2=J2+z(2).^2+z(1).^2; AIC(2)=30*log(JJ2/300)+4*2; %若为三阶 z=zeros(1,300); for k=4:300 z(k)=1.5*z(k-1)-0.7*z(k-2)-0.1*z(k-3 )+1.1*u(k-1)+1.5*u(k-2)+1.7*u(k-3); %用理想输出值作为观测值 end for i=4:300 HL3(i,:)=[-z(i-1) -z(i-2) -z(i-3) u(i-1) u(i-2) u(i-3)]; ZL3(i,:)=[z(i)]; end c3=inv(HL3'*HL3)*(HL3'*ZL3); J3=0; for x=4:300 J3=J3+[z(x)+z(x-1)*c3(1)+z(x-2)*c3(2 )+z(x-3)*c3(3)-u(x-1)*c3(4)-u(x-2)*c 3(5)-u(x-3)*c3(6)].^2; end JJ3=J3+z(3).^2+z(2).^2+z(1).^2; AIC(3)=30*log(JJ3/300)+4*3; %若为四阶
(3.3)
故
log L( n )
L L 1 log 2 log v2 ( z n H n n ) T ( z n H n n ) 2 2 2 v2
(3.4)
式中,L 为数据长度。根据 ML 原理,有
T 1 T ML ( H n H n ) H n z n 2 1 T v ( z n H n ML ) ( z n H n ML ) L
(2.10)
(2.11)
3 根据信息的准则估计模型的阶次
1974 年, Akaike 提出了一个基于 Kullback-Leible 信息量判据来定阶的赤池信息准则 AIC(Akaike Information Criterion) 。 3.1 AIC 准则意义
AIC (n)
n0
图 3.1
n
AIC (n) -- n 图
利用数据序列{z(k)}和{u(k)},极小化下列准则函数
l
T
J z (k ) (k )
T k 1
2
(2.6)
使 J(θ )=min 的θ 估计值记作 ,称之为参数的最小二乘估计值。 2.2 最小二乘问题的求解 用表示根据 l 次数采样数据所求得的参数的估计值 。
《系统辨识》课程报告
及 AIC (n) 值,找到使 AIC (n) min 的 n 作为 n 0 。
(3.8)
具体的定阶用法是:对不同阶次首先使用极大似然法估计参数,然后计算似然函数值
4 例子及其 MATLAB 程序实现
待辨识系统的阶次大于等于三阶;输入采用六位 M 序列,且用子函数实现;数据长度 大于等于三百;包含系统阶次的辨识。
被辨识的系统
图 2.1
SISO 辨识系统示意图
《系统辨识》课程报告
学号:2007073124
假设被辨识系统为一个单输入单输出(SISO)离散时间动态系统,如图 2.1 所示。其 系统数学关系式可用如下随机差分方程描述
z (k ) ai z (k i) bi u (k i) v(k )
其中
(2.5)
Z l [ z (1), z (2),, z (l )]T Vl [v(1), v(2),, v(l )]T
u (0) u (1 nb ) (1) z (0) z (1 na ) (2) z (1) z (2 n ) u (1) u (1 nb ) a l (l ) z (l 1) z (l na ) u (l 1) u (l nb )
《系统辨识》课程报告
学号:2007073124
待辨识系统为:
z(k ) 1.5 * z(k 1) 0.7 * z(k 2) 0.1* z(k 3) 1.1* u(k 1) 1.5 * u(k 2) 1.7 * u(k 3)
实验结果: c = -1.5000 0.7000 0.1000 1.1000 1.5000 1.7000 jc = 3 结果分析: 实验结果和理论值是完全相等的。由于实验中的观测值是使用的理想观测值,并没有 引入误差因素。系统的阶次辨识中,运用 AIC 信息准则,在求得的几个系数中比较出最小 值,从而得出系统阶次。
i 1 i 1
na
nb
k 1,2,3,, l
(2.1)
式中
u(k)—输入变量; y(k)—系统输出变量; z(k)—系统量测输出变量; v(k)—表示均值为零的随机噪声项。
