线段的垂直平分线的性质和判定练习题
线段垂直平分线的性质定理及其逆定理练习题

线段垂直平分线的性质定理及其逆定理练习题1. 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是()A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°2.如图:Rt△ABC中,∠C=90°,DE是AB的垂直平分线,∠CAD:∠DAB=2:1,则∠B的度数为()A.20° B.22.5° C.25° D.30°3.如图,在Rt△ABC中,∠ACB=90°,BC的中垂线交斜边AB于D,图中相等的线段有()A.1组 B.2组 C.3组 D.4组4.(2002•哈尔滨)如图,到△ABC的三个顶点距离相等的点是△ABC的() A.三边垂直平分线的交点 B.三条角平分线的交点C.三条高的交点 D.三边中线的交点5. 线段AB外有两点C,D(在AB同侧)使CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB=()A.80° B.90° C.100° D.110°6. 如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在()的垂直平分线上.A.AB B.AC C.BC D.不能确定7.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有()A.1个 B.2个 C.3个 D.4个8. 已知M,N是线段AB的垂直平分线上任意两点,则∠MAN和∠MBN之间的关系是.9. 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.10.如图,△ABC中,边AB的垂直平分线交AC于E,△ABC和△BEC的周长分别是24和14,则。
专题1.4 线段的垂直平分线的判定与性质【九大题型】(举一反三)(北师大版)(原卷版)

专题1.4 线段的垂直平分线的判定与性质【九大题型】【北师大版】【题型1 利用线段垂直平分线的性质求长度】 (1)【题型2 利用线段垂直平分线的性质求最值】 (2)【题型3 利用线段垂直平分线的性质求角度】 (3)【题型4 利用线段垂直平分线的性质探究角度之间的关系】 (4)【题型5 利用线段垂直平分线的性质证明】 (5)【题型6 线段垂直平分线的判定】 (7)【题型7 尺规作线段垂直平分线】 (8)【题型8 线段垂直平分线的判定与性质的综合运用】 (9)【题型9 线段垂直平分线的实际应用】 (10)【知识点1线段垂直平分线的性质】线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.【题型1利用线段垂直平分线的性质求长度】【例1】(2023春·辽宁阜新·八年级统考期末)如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若△ABC的周长是20,AB=4,AC=7,则△AEF的周长为()A.4B.7C.9D.11【变式1-1】(2023春·四川成都·八年级校考期中)如图,△ABC中,∠ABC的角平分线BD和AC边的中垂线DE交于点D,DM⊥BA的延长线于点M,DN⊥BC于点N.若AB=3,BC=7,则AM的长为.【变式1-2】(2023春·福建福州·八年级校考期中)如图,ΔABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.如果AB=5,AC=3,则AE=.【变式1-3】(2023春·辽宁丹东·八年级校考期中)如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为11cm,分别连接OA、OB、OC,若△OBC的周长为23cm,则OA的长为.【题型2利用线段垂直平分线的性质求最值】【例2】(2023春·甘肃陇南·八年级统考期末)如图,在△ABC中,AB=5,AC=7,BC=10,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是.【变式2-1】(2023春·江西九江·八年级统考开学考试)如图,在△ABC中,AC=4,BC边上的垂直平分线分别交BC、AB于点D、E,若△AEC的周长是11,则直线DE上任意一点到A、C距离和最小为( )A.28B.18C.10D.7【变式2-2】(2023春·山东济南·八年级统考期中)如图,在△ABC 中,AB =AC ,分别以点A 、B 为圆心,以适当的长为半径作弧,两弧分别交于E ,F ,作直线EF ,D 为BC 的中点,M 为直线EF 上任意一点.若BC =2,△ABC 面积为3,则BM +MD 长度的最小值等于 .【变式2-3】(2023春·山东青岛·八年级校考期末)如图,在△ABC 中,∠A =54°,∠C =76°,D 为AB 中点,点P 在AC 上从C 向A 运动;同时,点Q 在BC 上从B 向C 运动,当∠PDQ =时,△PDQ 的周长最小.【题型3 利用线段垂直平分线的性质求角度】【例3】(2023春·福建宁德·八年级统考期中)如图,在△ABC 中,点M ,N 为AC 边上的两点,AM =NM ,BM ⊥AC ,ND ⊥BC 于点D ,且NM =ND ,若∠A =α,则∠C =( )A .32αB .90°−12αC .120°−αD .2α−90°【变式3-1】(2023春·安徽池州·八年级统考开学考试)如图,△ABC 中,BD 平分∠ABC ,BC 的中垂线交BC 于点E ,交BD 于点F ,连接CF .若∠A =60°,∠ACF =48°,则∠ABC 的度数为 .【变式3-2】(2023春·四川甘孜·八年级统考期末)如图,在△ABC 中,∠B =32°,∠BAC 的平分线AD 交BC 于点D ,若DE 垂直平分AB ,求∠C 的度数.【变式3-3】(2023春·河北保定·八年级统考期中)如图,在△ABC 中,AI 平分∠BAC ,BI 平分∠ABC ,点O 是AC 、BC 的垂直平分线的交点,连接AO 、BO ,若∠AOB =α,则∠AIB 的大小为( )A .αB .14α+90°C .12α+90°D .180°−12α【题型4 利用线段垂直平分线的性质探究角度、线段之间的关系】【例4】(2023春·福建三明·八年级统考期末)如图,四边形ABCD 是长方形,E 是边CD 的中点,连接AE 并延长交边BC 的延长线于F ,过点E 作AF 的垂线交边BC 于M ,连接AM .(1)请说明 ΔADE ≌ ΔFCE ;(2)试说明AM = BC + MC ;(3)设S △AEM = S 1,S △ECM = S 2,S △ABM = S 3,试探究S 1,S 2,S 3三者之间的等量关系,并说明理由.【变式4-1】(2023春·陕西西安·八年级西安市铁一中学校考期末)△ABC 的两边AB 、AC 的中垂线交于边BC 上的P 点,则线段PA 和BC 的关系正确的是( )A .PA <12BCB .PA =12BC C .PA >12BCD .PA ≥12BC 【变式4-2】(2023春·河南平顶山·八年级统考期末)如图,OF 是∠MON 的平分线,点A 在射线OM 上,P ,Q 是直线ON 上的两动点,点Q 在点P 的右侧,且PQ =OA ,作线段OQ 的垂直平分线,分别交直线OF ,ON 于点B ,点C ,连接AB ,P B .(1)如图1,请指出AB 与PB 的数量关系,并说明理由.(2)如图2,当P ,Q 两点都在射线ON 的反向延长线上时,线段AB ,PB 是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由.【变式4-3】(2023春·山东日照·八年级统考期末)如图1,在直角△ABC 中,∠C=90°,分别作∠CAB 的平分线AP 和AB 的垂直平分线DP ,交点为P .(1)如图2,若点P 正好落在BC 边上.①求∠B 的度数;②求证:BC=3PC .(2)如图3,若点C 、P 、D 恰好在一条直线上,线段AD 、PD 、BC 之间的数量关系是否满足AD +PD=BC ?若满足,请给出证明;若不满足,请说明理由.【题型5 利用线段垂直平分线的性质证明】【例5】(2023春·陕西榆林·八年级校考期末)如图,在四边形ABDC 中,AD 所在直线垂直平分线段BC ,过点C作CF∥BD交AB于点F,延长AB,CD交于点E.求证:(1)CB平分∠ECF;(2)∠ACF=∠E.【变式5-1】(2023春·重庆綦江·八年级校联考期中)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM丄AB与M,DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.【变式5-2】(2023春·陕西咸阳·八年级统考期末)如图,在Rt△ABC中,∠ACB=90°,点E、F在AB上,连接CE,CF,且CF=BF.已知∠A=50°,∠ACE=30°,试证明∠CFE=∠CEF.【变式5-3】(2023春·福建龙岩·八年级校考开学考试)已知(如图),在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,交AB于点E,连结EF.(1)求证:BG=CF.(2)试判断BE+CF与EF的大小关系,并说明理由.【知识点2线段垂直平分线的判定】到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,(这样的点需要找两个)【题型6线段垂直平分线的判定】【例6】(2023春·吉林长春·八年级长春外国语学校校考期中)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.(1)求证:AD垂直平分EF;(2)若AB=3,AC=2,△ABC的面积是4,则DE=.【变式6-1】(2023春·陕西宝鸡·八年级统考期中)如图所示,已知AD⊥BC于点D,BD=DC,AB+BD=DE,求证:点C在AE的垂直平分线上.【变式6-2】(2023春·四川成都·八年级统考期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BE 平分∠ABC交AC于点E,交CD于点F,过点E作EG∥CD,交AB于点G,连接CG.(1)求证:∠A+∠AEG=90°;(2)求证:EC=EG;(3)若CG=4,BE=5,求四边形BCEG的面积.【变式6-3】(2023春·陕西汉中·八年级统考期末)如图,AD与BC相交于点O,AB=CD,∠ABC=∠CDA,EB=ED,连接OE,BD,求证;OE垂直平分BD.【题型7尺规作线段垂直平分线】【例7】(2023春·山东威海·八年级统考期末)如图,在△ABC中,AB=AC,请用尺规作图法在AC上求作一点M,使MC+MB=AC,并连接MB.(保留作图痕迹,不写作法)【变式7-1】(2023春·湖南郴州·八年级统考期末)如图,在△ABC中,AB=AC=5,BC=8.(1)尺规作图:作边AC的垂直平分线交BC于点D,连接AD(要求:保留作图痕迹,不必写作法和证明);(2)在(1)作出的图形中,求△ABD的周长.【变式7-2】(2023春·广东深圳·八年级深圳市福田区上步中学校考期中)如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC,则下列选项正确的()A.B.C.D.【变式7-3】(2023春·上海闵行·八年级校考期中)如图,点P在∠AOB外,点Q在边OA上,按要求画图,写出作图结论,并填空.(1)过点P分别画PE⊥OA,PF⊥OB,垂足分别是E、F.(2)连接PQ,用尺规作线段PQ的垂直平分线MN.(3)过P、Q两点分别作OA、OB的平行线交于点G;若∠AOB=120°,则∠G=______________.【题型8线段垂直平分线的判定与性质的综合运用】【例8】(2023春·广东河源·八年级校考期中)如图:在△ABC中,点D是BC的中点,点E,F分别在AB,AC 边上,且DE⊥DF.(1)猜想:EF BE+CF(填上“<”、“=”或“>”);(2)证明你的猜想.【变式8-1】(2023春·福建福州·八年级统考期末)如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.(1)求证:∠ACB=∠ACD;(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.①连接PE,交AM于点N,证明AM垂直平分PE;②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.【变式8-2】(2023春·河北唐山·八年级统考期中)如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①∠FCD=45°;②AE=EC;③S△ABF:S△AFC=AD:FD;④若BF=2EC,则BC=AB.正确的结论序号是()A.①②B.①②④C.②③④D.①③④【题型9线段垂直平分线的实际应用】【例9】(2023春·河南平顶山·八年级统考期末)(1)图1是小正方形的边长均为1的方格纸,请你涂出一个图形(所有顶点都在格点上),使其满足如下条件:①图形的面积为7;②图形是轴对称图形.(2)如图2,一条笔直的公路MN同一侧有两个村庄A和B,现准备在公路MN上修一个公共汽车站点P,使站点P到两个村庄A和B的距离相等.请你用尺规作图找出点P的位置,不写作法,保留作图痕迹.【变式9-1】(2023春·河北秦皇岛·八年级校考开学考试)元旦联欢会上,3名同学分别站在△ABC三个顶点的位置上.游戏时,要求在他们中间放一个凳子,该先坐到子上谁获胜,为使游戏公平,则凳子应放置。
八年级数学重点题型强化训练05 线段垂直平分线专题(解析版)

八年级数学重点题型强化训练5——线段垂直平分线专题第1题第2题【分析】本题考查的是线段垂直平分线的性质:熟记:线段垂直平分线上的点到这条线段两个端点的距离第3题可证BEF CED ≌△△,可得EF =BC 的中点,第5题第6题第7题第8题 第9题【答案】B 【分析】利用全等三角形的判定以及垂直平分线的性质得出OBC Ð,以及40,OBC OCB Ð=Ð=°,再利用翻折变换的性质得出,CEF FEO =Ð进而求出即可.50,BAC BAC Ð=°ÐQ 12OAB CAO \Ð=Ð=25OAB ABO Ð=Ð=∵在等腰ABC V 中,DG Q 是BC 的垂直平分线,BD CD \=,AD Q 是BAC Ð的平分线,DE DF \=,在Rt BDE △和Rt CDF △中,C .60°D 【分析】先根据线段垂直平分线的性质得到BE CE =,则AC EC =,再根据等腰三角形的性质和三角形内,接着利用三角形外角性质计算出EBC Ð=Ð的度数.故选:C .题型2:线段垂直平分线的判定11.如图,AD AC =,BD BC =,则下列判断一定正确的是( )A .AB 垂直平分CDB .CD 垂直平分ABC .CD 平分ACB ÐD .以上都不正确第11题第12题【答案】A【分析】根据线段垂直平分线的判定求解即可.【详解】解:∵AD AC =,BD BC =,∴点A 、B 在线段CD 的垂直平分线上,即AB 垂直平分CD ,故选:A .12.如图,ABC AB AC BC >>V ,,边AB 上存在一点P ,使得PA PC AB +=.下列描述正确的是( )A .P 是AC 的垂直平分线与AB 的交点B .P 是ACB Ð的平分线与AB 的交点C .P 是BC 的垂直平分线与AB 的交点D .P 是AB 的中点【答案】C【分析】根据线段垂直平分线的判定解答即可.【详解】解:PA PC AB PA BP AB +=+=Q ,,PC BP \=,∴P 是BC 的垂直平分线与AB 的交点.故选:C .13.如图,将长方形纸片沿AC 折叠后点B 落在点E 处,则下列关于线段BE 与AC 的关系描述正确的是( )A .AC BE =B .AC 和BE 相互垂直平分C .AC BE ^且AC BE=D .AC BE ^且AC 平分BE【答案】D 【分析】只要证明AC 是线段BE 的垂直平分线即可解决问题.【详解】解:ACE QV 是由ACB △翻折得到,AE AB \=,CB CE =,AC EB \^,AC 平分EB ,故选:D .14.如图,已知:AB AC =,MB MC =.求证:直线AM 是线段BC 的垂直平分线.下面是小彬的证明过程,则正确的选项是( )证明:∵AB AC=∴点A 在线段BC 的垂直平分线上①∵MB MC=∴点M 在线段BC 的垂直平分线上②∴直线AM 是线段BC 的垂直平分线③A .①处的依据是:线段垂直平分线上的点与这条线段两个端点的距离相等B .②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上C .③处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上D .以上说法都不对【答案】B【分析】根据垂直平分线的判定方法逐项判断即可.【详解】解:①处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故A 选项错误,不合题意;②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故B 选项正确,符合题意;③处的依据是:两点确定一条直线;故C 选项错误,不合题意;综上可知,选项D 错误,不合题意;故选B .15.下列说法错误的是( )A .若点P 是线段AB 的垂直平分线上的点,则PA PB=B .若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线C .若PA PB =,则点P 在线段AB 的垂直平分线上D .若PA PB =,则过点P 的直线是线段AB 的垂直平分线【答案】D【分析】根据线段垂直平分线的判定方法,即可一一判定.【详解】解:A.若点P 是线段AB 的垂直平分线上的点,则PA PB =,故该说法正确,不符合题意;B.若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线,故该说法正确,不符合题意;C.若PA PB =,则点P 在线段AB 的垂直平分线上,故该说法正确,不符合题意;D.若PA PB =,则过点P 的直线不一定是线段AB 的垂直平分线,故该说法错误,符合题意;故选:D .16.如图,AD 是ABC V 的角平分线,交BC 于D ,DE DF 、分别是ABD △和ACD V 的高,分别交AB AC 、于E 、F ,连接EF 交AD 于G .下列结论:①AD 垂直平分EF ;②EF 垂直平分AD ;③AED AFD V V ≌;④当BAC Ð为60°时,AEF △是等边三角形,其中正确的结论的个数为( )A .4个B .3个C .2个D .1个第16题第17题【答案】B 【分析】根据角平分线性质求出DE DF =,证AED AFD V V ≌,推出AE AF =,再逐个判断即可.【详解】解:∵AD 是ABC V 的角平分线,DE DF 、分别是ABD △和ACD V 的高,∴DE DF =,90AED AFD Ð=Ð=°,在Rt AED △和Rt AFD △中,AD AD DE DF =ìí=î,∴()Rt Rt HL AED AFD ≌△△,故③正确;∴AE AF =,∴AD 垂直平分EF ,①正确;②错误;∵60BAC Ð=°,且AE AF =,∴AEF △是等边三角形,④正确.综上,①③④正确,共3个.故选:B .17.如图,在△ABC 中,AD 是△ABC 的角平分线,点E 、F 分别是AD 、AB 上的动点,若∠BAC =50°,当BE +EF 的值最小时,∠AEB 的度数为( )A .105°B .115°C .120°D .130°【答案】B【分析】过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,证明AD 垂直平分BB ′,推出BE =BE ′,由三角形三边关系可知,BE EF B E EF B F B F ¢¢¢¢+=+³³,即BE +EF 的值最小为B F ¢¢,通过证明△ABE ′≌△AB ′E ′,推出∠AE ′B =AE ′B ′,因此利用三角形外角的性质求出AE ′B ′即可.【详解】解:过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,如图:此时BE +EF 最小.∵AD 是△ABC 的角平分线,∠BAC =50°,∴∠BAD =∠B ′AD =25°,∵BB ′⊥AD ,∴∠AGB =∠AGB ′=90°,在△ABG 和△AB ′G 中,BAG B AG AG AGAGB AGB Ð=Ðìï=íïТ=Ðî¢,∴△ABG ≌△AB ′G (ASA ),∴BG =B ′G , AB =AB ′,∴AD 垂直平分BB ′,∴BE =BE ′,在△ABE ′和△AB ′E ′中,BE BE AE AE AB AB ¢¢¢¢ìï=íï=î=,∴△ABE ′≌△AB ′E ′(SSS ),∴∠AE ′B =AE ′B ′,∵AE ′B ′=∠BAD + AF ′E ′=25°+90°=115°,∴∠AE ′B =115°.即当BE +EF 的值最小时,∠AEB 的度数为115°.故选B .18.如图,点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,连接OP ,CD .若PC PD =,则下列结论不一定成立的是( )A .AOP BOPÐ=ÐB .OPC OPD Ð=ÐC .PO 垂直平分CD D .PD CD=【答案】D【分析】根据角平线的判定定理可判断A ,证明Rt COP Rt DOP V V ≌,可判断B ,根据Rt COP Rt DOP V V ≌,可得OC =OD ,进而可判断C ,根据等边三角形的定义,可判断D .【详解】解:∵点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,PC PD =,∴OP 是∠AOB 的平分线,即AOP BOP Ð=Ð,故A 成立,不符合题意;∵OP =OP ,AOP BOP Ð=Ð,第19第20题=,利用ASA Ð,再根据E是CD的中点可求出ECECF=,结合已知可得BE的垂直平分线,根据线段垂直AE EF=+,进而即可求解.即可证得AB BC AD故答案为:70.题型3:与线段垂直平分线相关的尺规作图21.如图,在ABC V 直线MN ,交BC A .9【答案】B 【分析】由题意可得MN ADC C AC BC =+V ,求解即可.【详解】解:由题意可得,A.3B 【答案】B【分析】利用基本作图得到V的周长为20再利用ABC【详解】解:由作法得DE \==,,DA DB AE BEA .①③B .①④C .②④D .③④【答案】B 【分析】依次对各个图形的作图痕迹进行分析即可.【详解】 由图①知AD AC =,AB AD >,AB AC \>,故图①能说明AB AC >;由图②知射线BD 是ABC Ð的平分线,不能说明AB AC >;由图③知CD AB ^,不能说明AB AC >;由图④知DE 是BC 的垂直平分线,DB DC \=.ADC QV 中AD DC AC +>,AD DB AC \+>,即AB AC >.故图④能说明AB AC >.故选:B24.如图所示,在Rt ABC △中,90C Ð=°,以B 为圆心,以任意长度为半径作弧,与BA ,BC 分别交于A.20°B.36【答案】C【分析】由作图可知:BO为=,再根据等腰三角形的性质得AD BD和定理即可求出AÐ的度数.【详解】解:由作图可知:平分EAC Ð;③AC CD =;④ABC S V C .①③DA .只有甲的答案正确B .甲和乙的答案合在一起才正确C .甲和丙的答案合在一起才正确D .甲乙丙的答案合在一起才正确【答案】D 【分析】分四种情况讨论:当APB Ð为锐角时,当APB Ð为钝角时,当APB Ð为直角时,当135APB Ð=°时,分别画出图形,求出x 与y 的关系,即可得出答案.【详解】解:当APB Ð为锐角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∴90PAD APD Ð+Ð=°,即90x y +=;当APB Ð为钝角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∵APB Ð为ADP △的外角,∴APB ADP DAP Ð=Ð+Ð,∴90x y =+,即90x y -=;当APB Ð为直角时,如图所示:此时直线n 与PA 重合,∴此时直线n 与PA 所夹的角为0°,即90x y +=或90x y -=;当135APB Ð=°时,如图所示:18013545DPA Ð=°-°=°,∵AD BP ^,∴90ADP Ð=°,∴904545DAP Ð=°-°=°,∴45135180DAP APB Ð+Ð=°+°=即180x y +=;1AB 的长为半径作弧,两弧相交于AM ;的长为半径作弧,与BC 边相交于点N ,连接C.9AC,根据中垂线的定义和性质找到相等的边,进而由AC,A .15B .16C .18D .20【答案】A 【分析】根据题意得到MN 是线段AB 的垂直平分线,进而得到点D 是AB 的中点,根据三角形的面积公式计算,得到答案.【详解】解:由尺规作图可知,MN 是线段AB 的垂直平分线,\点D 是AB 的中点,ACD BCD S S \=△△,ADE CDE CDB S S S \+=V V V ,Q CDB △的面积为12,ADE V 的面积为9,1293CDE CDB ADE S S S \=-=-=V V V ,\四边形EDBC 的面积为:12315CDE CDB EDBC S S S =+=+=V V 四边形,故选:A .30.如图,在ABC V 中,根据尺规作图痕迹,下列说法不一定正确的是( ).A .AF BF=B .90AFD FBC Ð+Ð=°C .DF AB^D .BAF CAFÐ=Ð【答案】D 【分析】由图中尺规作图痕迹可知,BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线,结合角平分线的定义和垂直平分线的性质逐项分析即可.【详解】解:由图中尺规作图痕迹可知, BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线.上求作点D ,使;,若点D 在边上,在上求作点E ,使.)作BC 的垂直平分线与BC 的交点即为所求;)如图:由题意得,只要作12BDE ABC S S △△=即可,由第(1)问得,12ABP ABC S S △△=,只要作BC ABD ACD S S =V V AB BC BDE ADEC S S △四边形=作BC 的垂直平分线与BC 交于D 点,BD CD \=,ABD QV 与ACD V 高相同,ABD ACD S S \=V V .如图1:点D 即为所求;(2)如图:由题意得,只要作12BDE ABC S S △△=即可,作BC 的垂直平分线交BC 于P 点,由第(1)问得,12ABP ABC S S △△=,故只要作BDE ABP S S △△=即可,连接D 、P ,要使得BDE ABP S S △△=,只要作根据“夹在平行线之间的垂线段相等”,即,高相等,如图2:点E 即为所求.32.如图,在中,点E 在上且.(1)请用尺规作图的方法在边上确定点D ,使得;(保留作图痕迹,不写作法)(2)在(1)的条件下,若的周长为,求的长.【分析】(1)线段AB 的垂直平分线与BC 边的交点即为所求;(2)根据线段垂直平分线的性质,通过等量代换求解.【详解】(1)解:如图所示,线段AB 的垂直平分线与BC 边交于点D ,点D 即为所求;(2)解:Q ADE V 的周长为12cm ,\12AD AE DE ++=,Q BD AD =,AE CE =,\12BC BD CE DE AD AE DE =++=++=,即BC 的长为12cm .题型4:与线段垂直平分线相关的计算与证明33.如图,在ABC V 中,AB 、AC 边的垂直平分线相交于点O ,分别交BC 边于点M 、N ,连接AM ,AN .(1)若AMN V 的周长为6,求BC 的长;(2)若30B Ð=°,25C Ð=°,求MAN Ð的度数;(3)若MON a Ð=,请用a 表示MAN Ð的度数(直接写出即可).ABC V BC AE CE =BC BD AD =ADE V 12cm BC【答案】(1)6(2)70°(3)1802MAN aÐ=°-【分析】(1)由垂直平分线的性质可得,AM BM AN CN ==,再由BC AM MN AN =++可得结论;(2)由垂直平分线的性质可得30,30,B BAM C CAN Ð=Ð=°Ð=Ð=°,再根据三角形内角和定理可得结论;(3)根据三角形内角和定理可得()1802MAN B C Ð=°-Ð+Ð,再由四边形内角和定理可得180B C MAN O Ð+Ð=°-Ð-Ð,代入求解即可【详解】(1),OM ON Q 分别是AB 、AC 边的垂直平分线,,,AM BM AN CN \==6AM MN AN ++=Q 6BM MN CN \++=,即6BC =(2),,AM BM AN CN ==Q 30,25,BAM B CAN C \Ð=Ð=°Ð=Ð=°180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CANÐ=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°18022180605070MAN B C \Ð=°-Ð-Ð=°-°-°=°(3)如图,180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CAN Ð=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°()1802MAN B C \Ð=°-Ð+Ð,,OM ON Q 分别是AB 、AC 边的垂直平分线,90AEO AFO \Ð=Ð=360AEO EAF AFO FOE \Ð+Ð+Ð+Ð=°180EAF O \Ð+Ð=°180,BAF MAN CAN O \Ð+Ð+Ð+Ð=°180,B C MAN O \Ð+Ð+Ð+Ð=°180B C MAN O\Ð+Ð=°-Ð-Ð()()180********MAN B C MAN O \Ð=°-Ð+Ð=°-°-Ð-Ð\解得,1802MAN aÐ=°-34.如图,在Rt ABC △中,45,90,ACB BAC AB AC Ð=°Ð=°=,点D 是AB 的中点,AF CD ^于H 交BC 于F ,BE AC ∥交AF 的延长线于E .求证:BC 垂直且平分DE .【答案】见解析【分析】根据全等三角形的判定证明(ASA)ABE CAD ≌V V ,在再证明(SAS)DBP EBP ≌V V 即可解决问题;【详解】证明:由题意可知,9090DAH ADH ACH ADH ÐÐÐÐ+=°+=°,,∴DAH ACH ÐÐ=,∵90BAC Ð=°,BE AC ∥,∴90CAD ABE ÐÐ==°.又∵AB CA =,∴在ABE V 与CAD V 中,DAH ACH AB AC CAD ABE Ð=Ðìï=íïÐ=Ðî,∴(ASA)ABE CAD ≌V V .∴AD BE =,又∵AD BD =,∴BD BE =,在Rt ABC V 中,45,90,ACB BAC AB AC ÐÐ=°=°=,故45ABC Ð=°.∵90ABE Ð=°,∴904545EBF Ð=°-°=°,∴(SAS)DBP EBP ≌V V ,∴DP EP =,∴BC 垂直且平分DE .35.如图,ABC V 中,AD 平分BAG Ð,DG 垂直平分BC ,DE AB ^于E ,DF AC ^于F .(1)求证:BE CF =;(2)如果9AB =,5AC =,求BE 的长.【答案】(1)见解析;(2)2BE =.【分析】(1)由DG 垂直平分BC 可得DB DC =,由AD 平分BAG Ð, DE AB ^,DF AC ^,可得DE DF =,90DEB DFC Ð=Ð=°,从而证得()Rt Rt HL DBE DCF V V ≌,得证BE CF =;(2)易证()Rt Rt HL ADE ADF ≌△△,得到AE AF =,又BE CF =,因此2AB AE BE AF BE AC CF AC BE =+=+=+=+,代入即可解答.【详解】(1)连接DB ,DC ,∵DG 垂直平分BC ,∴DB DC =,∵AD 平分BAG Ð,DE AB ^,DF AC ^,∴DE DF =,90DEB DFC Ð=Ð=°,∴在Rt DBE V 和Rt DCF V 中DB DC DE DF=ìí=î∴()Rt Rt HL DBE DCF V V ≌,∴BE CF =.(2)∵DE AB ^,DF AC ^,∴在Rt ADE △和Rt ADF V 中AD AD DE DF=ìí=î∴()Rt Rt HL ADE ADF ≌△△,∴AE AF=∵BE CF=∴2AB AE BE AF BE AC CF AC BE =+=+=+=+,∵9AB =,5AC =,∴952BE =+,∴2BE =.36.如图,AB AC >,BAC Ð的平分线与BC 边的垂直平分线GD 相交于点D ,过点D 作DE AB ^于点E ,DF AC ^于点F ,求证:BE CF =.【答案】见解析【分析】连接DC ,根据GD 是BC 边的垂直平分线,得到DC DB =,根据AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,得到DE DF =,根据DE DF DB DC =ìí=î,得到()HL DEB DFC V V ≌即可得证.【详解】如图,连接DC ,∵GD 是BC 边的垂直平分线,∴DC DB =,∵AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,∴DE DF =,∵DE DF DB DC =ìí=î,∴()HL DEB DFC V V ≌∴BE CF =.37.如图,在ABC V 中,BAC Ð的平分线与BC 的中垂线DE 交于点E ,过点E 作AC 边的垂线,垂足N ,过点E 作AB 延长线的垂线,垂足为M .(1)求证:BM CN =;(2)若2AB =,8AC =,求BM 的长.【分析】(1)连接BE ,CE ,由题意易得BE CE =,EM EN =,进而可证Rt Rt BME CNE ≌V V ,然后问题得解;(2)由(1)得:EM EN =,进而可证Rt Rt AME ANE ≌V V ,则有AB BM AC CN +=-,然后根据线段的和差关系可求解.【详解】(1)证明:连接BE ,CE ,DE Q 是BC 的垂直平分线,BE CE \=,AE Q 是BAC Ð的平分线,EM AB ^,EN AC ^,EM EN \=,在Rt BME △和Rt CNE △中,BE CE EM EN=ìí=î()Rt Rt BME CNE HL \V V ≌,BM CN \=;(2)由(1)得:EM EN =,在Rt AME △和Rt ANE △中,AE AE EM EN=ìí=îRt Rt AME ANE \≌V V ,请根据所给教材内容,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.定理应用:V中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,已知)如图②,在ABC的周长为20,则BC的长为__________.∵AB AC AD BC ^=,,的周长为7,可得∴19712AB BE +=-=,∴6AB BE ==;(2)∵30ABC Ð=°,45C Ð=°,∴1803045105BAC Ð=°-°-°=°,在BAD V 和BED V 中,BA BE BD BD DA DE =ìï=íï=î,∴()SSS BAD BED V V ≌,∴105BED BAC Ð=Ð=°,∴1054560CDE BED C Ð=Ð-Ð=°-°=°.40.如图,在ABC V 中,点E 在AB 上,点D 在BC 上,BD BE =,BAD BCE Ð=Ð,AD 与CE 相交于F .(1)求证:AF CF =;(2)连接,试判断与的位置关系,并说明理由.【分析】(1)根据全等三角形的判定与性质,可得BA BC =,BDA BEC Ð=Ð,根据补角的性质,可得FDC FEA Ð=Ð,根据全等三角形的判定与性质,可得答案.(2)由AB CB =,AF CF =可得点B ,F 在AC 的垂直平分线,即可得出结论【详解】(1)在BAD V 和BCE V 中,∵B B BAD BCE BD BE Ð=ÐìïÐ=Ðíï=î,∴BAD V ≌BCE V ,∴AB CB =,BF BF AC与点A 重合,则 , .,四边形的直角沿直线l 折叠后(如图2),点B 落在四边形的边与AB 相交于点F ,猜想OF 、EF 、AB 三者数量关系,并证明.若折叠后点D 恰为AB 的中点(如图3),求的度数;45°,8数量关系为:AB OF EF =+;证明见解析q ==a OABC OCB ÐOABC q∴E O D FO D Ð=Ð.由折叠可得FOD EOC EOD q Ð=Ð=Ð=,∴390COA q Ð==°,∴30q =°.。
《线段的垂直平分线的性质和判定定理》课后习题-八年级上册数学青岛版

《线段的垂直平分线》评测练习
1、已知线段AB及一点P,且PA=PB=3cm,则点P一定在线段AB的上。
2、如果P是线段AB垂直平分线上的一点,PB=6cm,那么PA= cm。
3、如图,△ABC中,∠C AB=120º,AB,AC的垂直平分线分别交B C于点E、F,则∠EAF等于()
A.40ºB.50º C.60ºD.80º
4、已知:△ABC中,边AB,AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
5、⑴作一个钝角三角形,利用尺规作这个三角形三条边的垂直平分线;
⑵作直角三角形和锐角三角形,利用尺规作三角形三条边的垂直平分线;
⑶你发现三角形三条边的垂直平分线与三角形的形状有怎样的位置关系?
6、将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为()
A.60°B.75° C.90° D.95°
7、如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
8、如图,有A、B、C三个村庄,要在这三个村庄附近建一个卫生所,建在何处能使三个村庄的居民去往此处所走路程相同?请在图中标出。
A
C
B。
线段的垂直平分线的性质和判定精选优秀练习

13.1.2 线段的垂直平分线的性质第1课时线段的垂直平分线的性质和判定一、选择题(共8小题)1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,CD边垂直平分线的交点,连接EC;则∠AEC等于()F,:第1题图第2题图第5题图第6题图第7题图第8题图B二、填空题(共10小题)9.到线段AB两个端点距离相等的点的轨迹是_________ .10.如图,有A、B、C三个居民小区是位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在_________ .11.在阿拉伯数字中,有且仅有一条对称轴的数字是____________.12、如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= _________ 度.13、如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,则△ABD的周长为_________ cm.14.如图,已知在△ABC中,AB=AC=10,DE垂直平分AB,垂足为E,DE交AC于D,若△BDC的周长为16,则BC= _________ .15.如图,在△ABC中,∠B=30°,直线CD垂直平分AB,则∠ACD的度数为_________ .16.已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于_________ .17.如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E,BC=6,△CDB的周长为15,则AC= _________ .18.如图,△ABC中,AB=AC,∠A=40°,AC的垂直平分线分别交AB,AC于D,E两点,连接CD.则∠BCD=_________ 度.第10题图第12题图第13题图第14题图第15题图第16题图第17题图第18题图三、解答题(共5小题)19.如图,四边形ABCD中,AC垂直平分BD于点O.(1)图中有多少对全等三角形?请把它们都写出来;(2)任选(1)中的一对全等三角形加以证明.20.如图,在△AB C中,AB=AC,D是AB的中点,且DE⊥AB,△BCE的周长为8cm,且AC﹣BC=2cm,求AB、BC的长.21.如图,已知:在ABC中,AB、BC边上的垂直平分线相交于点P.求证:点P在AC的垂直平分线上.22.如图,△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.求证:AD垂直平分EF.23.如图,已知∠C=∠D=90°,AC与BD交于O,AC=BD.(1)求证:BC=AD;(2)求证:点O在线段AB的垂直平分线上.13.1.2 线段的垂直平分线的性质一、选择题(共8小题)1.B 2.A 3.A 4.A 5.C 6.C 7.A 8.A二.填空题(共10小题)9. 线段AB的中垂线;10. 三边垂直平分线的交点处;11. 3;12. 50;3. 13 ;14. 615. 60°;16. 8 ;17. 9 ;18.35°三.解答题(共5小题)19.(1)解:图中有三对全等三角形:△AOB≌△AOD,△COB≌△COD,△ABC≌△ADC;(2)证明△ABC≌△AD C.证明:∵AC垂直平分BD,∴AB=AD,CB=CD(中垂线的性质),又∵AC=AC,∴△ABC≌△ADC.20. 解:∵△ABC中,AB=AC,D是AB的中点,且DE⊥AB,∴AE=BE,∵△BCE的周长为8cm,即BE+CE+BC=8cm,∴AC+BC=8cm…①,∵AC﹣BC=2cm…②,①+②得,2AC=10cm,即AC=5cm,故AB=5cm;①﹣②得,2BC=6cm,BC=3cm.故AB=5cm、BC=3cm.21.证明:∵P在AB、BC的垂直平分线上∴AP=BP,BP=CP∴AP=CP,∴P点在AC的垂直平分线上.22.证:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,∠AED=∠AFD=90°,在Rt△AED和Rt△AFD中∴Rt△AED≌Rt△AFD(HL),∴AE=AF,∵AD是∠BAC的平分线,∴AD垂直平分EF(三线合一)23. 证明:(1)∵∠C=∠D=90°,∴在Rt△ACB和Rt△BDA中,,∴Rt△ACB≌Rt△BDA,∴AD=BC;(2)∵Rt△ACB≌Rt△BDA,∴∠CAB=∠DBA,∴OA=OB,∴点O在线段AB的垂直平分线上.。
垂直平分线的性质第1课时线段的垂直平分线的性质和判定练习新版新人教版含答案
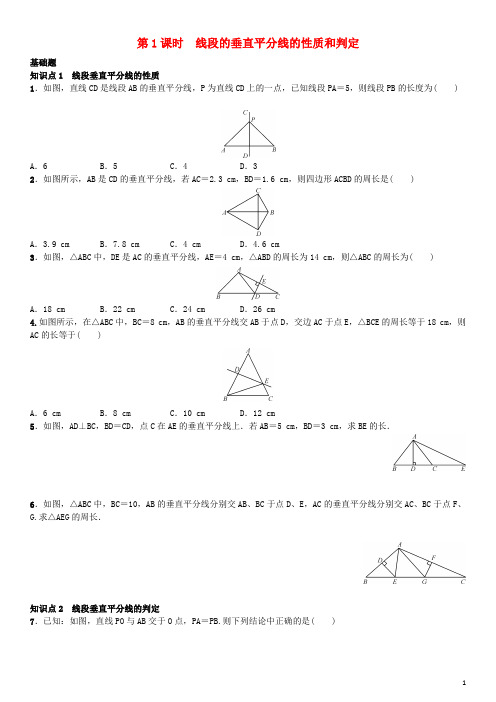
第1课时线段的垂直平分线的性质和判定基础题知识点1 线段垂直平分线的性质1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )A.6 B.5 C.4 D.32.如图所示,AB是CD的垂直平分线,若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是( )A.3.9 cm B.7.8 cm C.4 cm D.4.6 cm3.如图,△ABC中,DE是AC的垂直平分线,AE=4 cm,△ABD的周长为14 cm,则△ABC的周长为( )A.18 cm B.22 cm C.24 cm D.26 cm4.如图所示,在△ABC中,BC=8 cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18 cm,则AC的长等于( )A.6 cm B.8 cm C.10 cm D.12 cm5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5 cm,BD=3 cm,求BE的长.6.如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.知识点2 线段垂直平分线的判定7.已知:如图,直线PO与AB交于O点,PA=PB.则下列结论中正确的是( )A.AO=BOB.PO⊥ABC.PO是AB的垂直平分线D.P点在AB的垂直平分线上8.如图所示,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.知识点3 经过直线外一点作已知直线的垂线9.如图,已知钝角△ABC,其中∠A是钝角,求作AC边上的高BH.中档题10.(临沂中考)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC11.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB∶∠CAE=3∶1,则∠C等于( )A.28°B.25°C.22.5° D.20°12.已知:如图,AC是线段BD的垂直平分线,E是AC上的一点,则图中全等的三角形共有( )A.3对B.4对C.5对D.6对13.在锐角△ABC内一点P,满足PA=PB=PC,则点P是△ABC( )A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点14.如图,在△ABC中,AB=AC,AB的垂直平分线交AB,AC于点D,E,△BCE的周长是8,AB-BC=2,则△ABC 的周长是( )A.13 B.12 C.11 D.1015.如图所示,直线MN是线段AB的对称轴,点C在MN外,CA与MN相交于点D,如果CA+CB=8 cm,那么△BCD 的周长等于________cm.16.如图,△ABC中,边AB,BC的垂直平分线交于点P,且AP=5,那么PC=________.17.已知直线l与线段AB交于点O,点P在直线l上,且AP=PB,下列结论:①OA=OB;②PO⊥AB;③∠APO=∠BPO;④点P在线段AB的垂直平分线上,其中正确的有________.18.如图,四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A,连接AC,求证:点A在CD的垂直平分线上.综合题19.如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC 交AC于点G.求证:(1)BF =CG ;(2)AF =12(AB +AC).参考答案1.B 2.B 3.B 4.C 5.∵AD⊥BC,BD =CD ,∴AB =AC.∵点C 在AE 的垂直平分线上,∴AC =CE.∵AB=5 cm ,BD =3 cm ,∴CE =5 cm ,CD =3 cm.∴BE =BD +DC +CE =11 cm. 6.∵DE 是AB 的垂直平分线,∴AE =BE.同理:AG =CG.∴△AEG 的周长为AE +AG +EG =BE +CG +EG =BC =10.7.D 8.相等.连接BC ,∵AB =AC ,∴点A 在线段BC 的垂直平分线上.同理:D 点也在线段BC 的垂直平分线上.∵两点确定一条直线,∴AD 是线段BC 的垂直平分线.∵E 是AD 延长线上的一点,∴BE =CE. 9.图略 10.C 11.A 12.D 13.D 14.A 15.816.5 17.④ 18.证明:∵MN 垂直平分BC ,∴AB =AC.∵AB=AD ,∴AC =AD.∴点A 在CD 的垂直平分线上. 19.证明:(1)连接BE 、CE.∵AE 平分∠BAC,EF ⊥AB ,EG ⊥AC ,∴EF =EG.∵DE 垂直平分BC ,∴EB =EC.在Rt △EFB 和Rt △EGC 中,⎩⎪⎨⎪⎧EF =EG ,EB =EC ,∴Rt △EFB ≌Rt △EGC(HL).∴BF=CG.(2)∵BF=CG ,∴AB +AC =AB +BF +AG =AF +AG.又易证Rt △AEF ≌Rt △AEG(HL),∴AF =AG.∴AF=12(AB +AC).。
专项1.5 线段垂直平分线的性质与判定(解析版)

2020—2021八年级下学期专项冲刺卷(北师大版)专项1.5线段垂直平分线的性质与判定姓名:___________考号:___________分数:___________(考试时间:100分钟满分:120分)一、选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在△ABC中,∠ACD=20°,∠B=45°,BC的垂直平分线分别交AB、BC 于点D、E,则∠A的度数是()A.60°B.65°C.70°D.75°【答案】C解:∵DE垂直平分BC,∴DB=DC,∴∠BCD=∠B=45°,∵∠ACD=20°,∴∠ACD=65°,∴∠A=180°﹣∠B﹣∠ACD=180°﹣45°﹣65°=70°,故选:C.2.如图,线段AB,DE的垂直平分线交于C,∠ABC=∠EDC=74°,∠EBD=118°.则∠AEB=()A.72°B.74°C.86°D.88°【答案】C连结CE,∵线段AB,DE的垂直平分线交于C,∴CA=CB,CE=CD,∴∠CAB=∠ABC=∠CED=∠EDC=74º,∴∠ACB=∠ECD=32º,∴∠ACE=∠ACB-∠ECB=∠ECD-∠ECB=∠BCD,∴△CAE≌△CBD(SAS),∴∠CEA=∠CDB,∵∠EBD=118°,∴∠BED+∠BDE=180º-∠EBD=62º,∴∠CEB+∠CDB=180º-∠ECD-∠BED-∠BDE=180º-32º-62º=86º,∴∠AEB=∠AEC+∠CEB=∠BDC+∠CEB=86º,故选择:C.3.如图,在ABC 中,AB AC =,36A ∠=︒,AC 的垂直平分线交AB 于E ,D 为垂足,连接EC ,若3CE =,则BC 等于( )A .2B .3C .4D .5【答案】B ∵AB AC =,36A ∠=︒,∴∠B=∠ACB=72︒,∵DE 垂直平分AC ,∴AE=CE ,∴∠ACE=36A ∠=︒,∴∠BEC=2∠A=72︒,∴∠B=∠BEC ,∴BC=3CE =,故选:B .4.如图,已知在Rt △ABC 中,∠ABC =90°,点D 是BC 边的中点,分别以B .C 为圆心,大于线段BC 长度一半的长为半径画弧,两弧在直线BC 上方的交点为P ,直线PD 交AC 于点E ,连接BE ,则下列结论:①ED ⊥BC ;②∠A =∠EBA ;③EB 平分∠AED ;④EB =EC 中,其中正确的结论有( )A .4个B .3个C .2个D .1个【答案】B由作法得DE 垂直平分BC ,即ED ⊥BC ,所以①正确;∴EB =EC ,所以④正确;∴∠EBC =∠C ,∵∠A +∠C =90°,∠EBA +∠EBC =90°,∴∠A =∠EBA ,所以②正确;∵点D 是BC 边的中点,∴DE 为△ABC 的中位线,∴DE =12AB ,DE ∥AB , ∴∠ABE =∠BED ,只有当∠A =60°时,∠ABE =∠AEB ,BE 平分∠AED ,所以③不一定正确.故选:B .5.如图,等腰ABC 中,10AB AC ==,16BC =,ABD △是等边三角形,点P 是BAC ∠的角平分线上一动点,连接PC 、PD ,则PC PD +的最小值为( )A .8B .10C .12D .16【答案】B 解:如图,连接BP ,∵点P 是∠BAC 的角平分线上一动点,AB=AC ,∴AP 垂直平分BC ,∴CP=BP ,∴PD+PC=PD+PB ,∴当B,P,D在在同一直线上时,BP+PD的最小值为线段BD长,又∵△ABD是等边三角形,AB=BD=10,∴PD+PC的最小值为10,故选:B.6.如图,在ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于12BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若5AB=,7AC=,则ABD△的周长为()A.10B.11C.12D.13【答案】C解:由作图知,MN是线段BC的垂直平分线,∴BD=CD,∴AD+BD=AD+CD=AC=7∵AB=5,∴ABD△的周长=AB+BD+AD=AB+AC=5+7=12,故选:C.7.如图,在ABC∆中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又BEG∆的周长为16,且1GE=,则AC的长为()A.16B.15C.14D.13【答案】C DE 是AB 边的垂直平分线,EB EA ∴=, FG 是BC 边的垂直平分线,GB GC ∴=,BEG ∆的周长为16,16GB GE EB ∴++=,16AE GE GC ∴++=,16AC GE GE ∴++=,1GE =,16214AC ∴=-=,故选:C .8.如图,ABC 中,AB 4.5cm =,AC 6.5cm =,BC 的垂直平分线l 与AC 相交于点D ,则ABD 的周长为( )A .10cmB .11cmC .12cmD .13cm【答案】B 解:∵BC 的垂直平分线l 与AC 相交于点D ,∴DB DC =,∴ABD 的周长()AB AD DB AB AD DC AB AC 4.5 6.511cm =++=++=+=+=.故选:B .9.如图,在Rt △ABC 中,∠C =90°,DE 是斜边AB 的垂直平分线,与BC 相交于点D 连接AD ,若AC =5,△ACD 的周长为17,则斜边AB 的长为( )A .11B .12C .13D .14 【答案】C解:DE 是AB 的垂直平分线,DA DB ∴=,ACD ∆的周长为17,17AC CD AD ∴++=,17AC CD DB AC BC ∴++=+=,5AC =,17512BC ∴=-=,由勾股定理得,13AB =,故选:C . 10.如图,在△ABC 中,∠BAC =100°,MP 和NQ 分别垂直平分AB 和AC ,则∠P AQ 的度数是( )A .20°B .30°C .40°D .80°【答案】A ∵MP 和NQ 分别垂直平分AB 和AC∴BP=PA ,CQ=QA ,∴∠BAP=∠B ,∠CAQ=∠C ,∵180B BAC C ∠+∠+∠=︒又∵∠BAC=100°∴18010080B C ∠+∠=︒-︒=︒∴80BAP CAQ ∠+∠=︒∴1008020PAQ BAC BAP CAQ ∠=∠-∠-∠=︒-︒=︒故选A .11.如图,在ABC 中,5AB =,7AC =,9BC =,DE 垂直平分BC ,点P 为直线DE 上的任一点,则ABP △的周长的最小值是( )A .12B .13C .14D .15【答案】A 解:∵ED 垂直平分BC ,∴B 、C 关于ED 对称,∴当P 和D 重合时,AP+BP 的值最小,最小值等于AC 的长,∵AB=5,AC=7,∴△ABP 周长的最小值是AB+AC=5+7=12.故选:A .12.如图,在ABC 中,DE 是AC 的垂直平分线,12cm AB =,10cm BC =,则BCD △的周长为( )A .22cmB .16cmC .26cmD .25cm【答案】A 解:∵DE 垂直平分AC ,∴CD=AD ,又AB=12,BC=10,∴△BCD 的周长为BD+DC+BC=AD+DB+BC=AB+BC=12+10=22,故选:A .二、填空题(本大题共6小题,每小题3分,共18分)13.如图,在四边形ABCD 中,130DAB ∠=︒,90D B ∠=∠=︒,点M ,N 分别是CD ,BC 上两个动点,当AMN 的周长最小时,AMN ANM ∠+∠的度数为_________.【答案】100°解:如图,作点A 关于BC 的对称点A′,关于CD 的对称点A″,连接A′A″与BC 、CD 的交点即为所求的点M 、N ,∵∠BAD=130°,∠B=∠D=90°,∴∠A′+∠A″=180°-∠130°=50°,由轴对称的性质得:A′N= AN ,A″M=AM∴∠A′=∠A′AN ,∠A″=∠A″AM ,∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.故答案为:100°14.如图,在ABC 中,AB AC =,120A ∠=︒,AB 的垂直平分线分别交AB ,BC 于D ,E ,3BE =,则EC 的长为_____.【答案】6解:连接AE ,∵ AB=AC ,∵A=120︒ , ∵ ∵B=∵C=()1180120302︒-︒=︒, ∵ED 垂直平分AB ,∵AE=BE ,∵EAD=30︒ ,∵BE=3, ∵DE=1322BE =∵BD ==∵AB=AC=2BD=∵ ∵A=120︒ ,∵ ∵EAC=90︒ ,∵6CE ==,故答案为:6.15.如图,DF 垂直平分AB ,EG 垂直平分AC ,若110BAC ∠=︒,则DAE =∠__________°.【答案】40︒解:∵在△ABC 中,∠BAC=110°,∴∠B+∠C=180°﹣110°=70°,∵DF 垂直平分AB ,EG 垂直平分AC ,∴AD=BD ,AE=CE ,∴∠B=∠BAD ,∠C=∠CAE ,∴∠BAD+∠CAE=70°,∴∠ADE=∠BAC ﹣(∠BAD+∠CAE )=110°﹣70°=40°,故答案为:40°.16.如图,在ABC 中,点D 是BC 上一动点,BD ,CD 的垂直平分线分别交AB ,AC 于点E ,F ,在点D 的运动过程中,EDF ∠与A ∠的大小关系是EDF ∠______A ∠(填“>”“=”或“<”).【答案】=解:∵BD 、CD 的垂直平分线分别交AB 、AC 于点E 、F ,∴EB=ED ,FD=FC ,∴∠EDB=∠B ,∠FDC=∠C ,∴∠EDB+∠FDC=∠B+∠C ,∵∠EDF=180°-(∠EDB+∠FDC ),∠A=180°-(∠B+∠C ),∴∠EDF=∠A .故答案为:=.17.如图,点P 是AOB ∠外的一点,点M ,N 分别是AOB ∠两边上的点,点P 关于OA 的对称点Q 恰好落在线段MN 上,点P 关于OB 的对称点R 落在MN 的延长线上.若3PM cm =,4PN cm =, 5.5MN cm =,则线段QR 的长为__.【答案】6.5cm 解:点P 关于OA 的对称点Q 恰好落在线段MN 上,OA ∴垂直平分PQ ,3QM PM cm ∴==,5.53 2.5()QN MN QM cm ∴=-=-=,点P 关于OB 的对称点R 落在MN 的延长线上,OB ∴垂直平分PR ,4RN PN cm ∴==,2.54 6.5()QR QN RN cm ∴=+=+=.故答案为:6.5cm .18.如图,在ABC 中,ACB ∠的平分线CD 与BC 的垂直平分线交于点D.连接BD ,若A 65∠=︒,ABD 16∠=︒,则BDC ∠的度数为______.︒【答案】114解:ACB ∠的平分线CD 与BC 的垂直平分线交于点D ,BD CD ∴=,ACD BCD ∠=∠,DBC BCD ACD ∠∠∠∴==,A 65∠=︒,ABD 16∠=︒,ACD BCD DBC 180A ABD 99∠∠∠∠∠∴++=︒--=︒,ACD BCD DBC 33∠∠∠∴===︒,BDC 114∠∴=︒,故答案为114.三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程) 19.如图,已知等腰三角形ABC 中,AB=AC ,点D ,E 分别在边AB 、AC 上,且AD=AE ,连接BE 、CD ,交于点F .(1)判断∠ABE 与∠ACD 的数量关系,并说明理由;(2)求证:过点A 、F 的直线垂直平分线段BC .【答案】(1)∠ABE=∠ACD ,理由见解析;(2)见解析.(1)ABE ACD ∠=∠理由:在△ABE 和△ACD 中∵ AB AC A A AD AE ⎧=∠=∠=⎪⎨⎪⎩∴△ABE ≌△ACD (SAS )∴ABE ACD ∠=∠(2) ∵AB AC =,∴A ABC CB =∠∠.又∵ABE ACD ∠=∠,∴ FBC FCB ∠=∠,∴ FB FC =.又∵AB AC =,∴点A 、F 均在线段BC 的垂直平分线上,即直线AF 垂直平分线段BC .20.如图1,在△ABC 中,AB =AC ,∠BAC =30°,点D 是△ABC 内一点,DB =DC ,∠DCB =30°,点E 是BD 延长线上一点,AE =AB .(1)直接写出∠ADE 的度数 ;(2)求证:DE =AD +DC ;(3)作BP 平分∠ABE ,EF ⊥BP ,垂足为F ,(如图2),若EF =3,求BP 的长.【答案】(1)60︒;(2)证明见解析;(3)6.解:(1)∵△ABC 中,AB=AC ,∠BAC=30°,∴∠ABC=∠ACB=18030752,∵DB=DC ,∠DCB=30°,∴∠DBC=∠DCB=30°,∴∠ABD=∠ABC -∠DBC=45°,∵AB=AC ,DB=DC ,∴AD 所在直线垂直平分BC ,∴AD 平分∠BAC ,∴∠BAD=12∠BAC=15°, ∴∠ADE=∠ABD+∠BAD=60°;故答案为:60.︒(2)如图1,在线段DE 上截取DM=AD ,连接AM ,∵∠ADE=60°,DM=AD ,∴△ADM 是等边三角形,∴∠ADB=∠AME=120°∵AE=AB ,∴∠ABD=∠E ,在△ABD 和△AEM 中,ADB AME ABD EAB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△AEM (AAS ),∴BD=ME ,∵BD=CD ,∴CD=ME ,∵DE=DM+ME ,∴DE=AD+CD ;(3)延长EF 交BA 的延长线与点N ,由(2)及图1得△ABD≌△AEM,△ADM是等边三角形,1560MAE BAD DAM∠=∠=︒∠=︒,,90BAE BAD DAM MAE∴∠=∠+∠+∠=︒,EF⊥BP,90BAE PFE∴∠=∠=︒,,APB FPE∠=∠∴∠ABF=∠NEA,又AB=AE,∴Rt△ANE≌Rt△APB(AAS),∴BP=EN,∵BF既是△BEN的角平分线又是高,,N BEN∴∠=∠∴BF是△BEN的中线,即:1,2EF EN=3EF=,6.BP EN∴==21.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB(1)若∠ABC=65°,则∠NMA的度数为(2)若AB=10cm,△MBC的周长是18cm①求BC的长度②若点P为直线MN上一点,则△PBC周长的最小值为cm【答案】(1)40°;(2)①8cm;②18解:(1)∵AB=AC,∴∠ABC=∠C∵∠ABC=65°,∴∠C=65°,∴∠A=50°,∵MN是AB的垂直平分线,∴∠ANM=90°,∴∠NMA=90°-50°=40°;(2)∠∠MN是线段AB的垂直平分线,∠AM=MB.∠∠MBC的周长是18cm ,AB=10cm,∠BM+MC+BC=AM+MC+BC=AC+BC=AB+BC=18cm ,∠BC=18-AB=18-10=8cm;②∵MN是线段AB的垂直平分线,∴点A和点B关于直线MN对称,∴当点P与点M重合时,∠PBC周长的值最小,∴∠PBC的周长的最小值为18cm.22.如图,在ABC中,边AB的垂直平分线1l交BC于点D,边AC的垂直平分线2l交BC 于点E,1l与2l相交于点O,连接AD,AE,ADE的周长为12cm.(1)求BC 的长;(2)分别连接OA ,OB ,OC ,若OA 的长为8cm ,求OBC 的周长.【答案】(1)12cm ;(2)28cm .解:(1)∵1l 垂直平分AB ,∴DB DA =,同理EA EC =.∠ADE 的周长为12cm ,∴12DA DE EA cm ++=,∴12BC BD DE EC DA DE EA cm =++=++=,即BC 的长为12cm .(2)如图,连接OA ,OB ,OC .∵1l 垂直平分AB ,∴OB OA =,同理OA OC =.∵OA 的长为8cm ,8OA OB OC cm ===.由(1)可知,12BC cm =,∴OBC 的周长为()881228OB OC BC cm ++=++=.23.如图,在ABC 中,60B ∠=︒,22.5C ∠=︒,AC 的垂直平分线交BC 于点D ,CD =,AE BC ⊥ 于点E ,求BE 的长.连接AD ,∵AC 的垂直平分线交BC 于点D ,∴DA=CD =,∴∠DAC=22.5C ∠=︒,∴∠ADE=45°,∵AE BC ⊥ 于点E ,∴∆ADE 是等腰直角三角形,∴AE=DA ,在直角∆ABE 中,60B ∠=︒,∴∠BAE=30°,∴设BE=x ,则AB=2x ,∴,=3,解得:∴24.如图,△ABC 中,BC 的垂直平分线DE 分别交AB 、BC 于点D 、E ,且BD 2﹣DA 2=AC 2.(1)求证:∠A =90°;(2)若AB =8,AD :BD =3:5,求AC 的长.【答案】(1)见解析;(2)4(1)证明:连接CD ,∵BC 的垂直平分线DE 分别交AB 、BC 于点D 、E ,∴CD =DB ,∵BD 2﹣DA 2=AC 2,∴CD 2﹣DA 2=AC 2,∴CD 2=AD 2+AC 2,∴△ACD 是直角三角形,且∠A =90°;(2)解:∵AB =8,AD :BD =3:5,∴AD =3,BD =5,∴CD =BD =5,∴在Rt ACD △中,4AC ==.。
垂直平分线的性质与判定练习题

1/3垂直平分线(一)的性质·练习1、如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于 ( ) A .6cm B .8cm C .10cm D .12cm 2、如图,在Rt ABC△中,90ACB D E ∠=,,分别为AC AB ,的中点,连DE CE ,.下列结论中不一定正确的是 ( )A .ED BC ∥B .ED AC ⊥C .ACE BCE ∠=∠D .AE CE =3、△ABC 中,∠C=90°,AB 的垂直平分线交直线BC 于D ,若∠BAD -∠DAC=22.5°,则∠B 等于 ( )A.37.5°B.67.5°C.37.5°或67.5°D.无法确定4、如图,在△ABC 中,AC 的垂直平分线交AC 于E ,交BC 于D ,△ABD 的周长是12 cm ,AC=5cm ,则AB+BD+AD= cm ;AB+BD+DC= cm ;△ABC 的周长是 cm 。
4题 5题5、如图,在Rt △ABC 中,∠C=90°,∠B=15°,DE 是AB 的垂直平分线,垂足为D ,交BC 于E ,BE=5,则AE=__________,∠AEC=__________,AC=__________ 。
6、在△ABC 中,∠C =90°,用直尺和圆规在AC 上作点P ,使P 到A 、B 的距离相等(保留作图痕迹,不写作法和证明).7、如右图,在△ABC 中,AB=AC , BC=12,∠BAC =120°,AB 的垂直平分线交BC 边于点E , AC 的垂直平分线交BC 边于点N 。
(1) 求△AEN 的周长。
(2) 求∠EAN 的度数。
(3) 判断△AEN 的形状。
ABCDE MN2/38、如图,已知AOB ∠和AOB ∠内两点M 、N 画一点P 使它到AOB ∠的两边距离相等,且到点M 和N 的距离相等。
线段垂直平分线的性质和判定(分层作业)(解析版)

13.1.2线段垂直平分线的性质和判定夯实基础篇一、单选题:1.如图,△AB C中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC 的周长是()A.8B.10C.12D.14【答案】B【知识点】线段垂直平分线的性质【解析】【解答】设边AB的垂直平分线交AB于点E,∵ED是AB的垂直平分线,∴AD=BD,∵△BDC的周长=DB+BC+CD,∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10.故答案为:B.【分析】本题考查了线段垂直平分线的性质,三角形周长的计算,掌握转化思想的应用是解题的关键.2.如图,在△AB C中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠AC B.若BE=2,则AE的长为()AB.1C D.2【答案】B【知识点】角平分线的性质;线段垂直平分线的性质;含30°角的直角三角形【解析】【解答】解:∵在△AB C中,∠B=30°,BC的垂直平分线交AB于E,BE=2,∴BE=CE=2,∴∠B=∠DCE=30°,∵CE平分∠ACB,∴∠ACB=2∠DCE=60°,∠ACE=∠DCE=30°,∴∠A=180°﹣∠B﹣∠ACB=90°.在Rt△CAE中,∵∠A=90°,∠ACE=30°,CE=2,∴AE=12CE=1.故选B.【分析】先根据线段垂直平分线的性质得出BE=CE=2,故可得出∠B=∠DCE=30°,再由角平分线定义得出∠ACB=2∠DCE=60°,∠ACE=∠DCE=30°,利用三角形内角和定理求出∠A=180°﹣∠B﹣∠ACB=90°,然后在Rt△CAE中根据30°角所对的直角边等于斜边的一半得出AE=12CE=1.3.如图所示,在△AB C中,∠ACB=90°,分别以点A,B为圆心,大于12AB长为半径画弧,两弧交于点M,N,作直线MN分别交AB,AC于点D,E,连结CD,BE.下列结论中,错误的是()A.AD=CD B.BE>CDC.∠BEC=∠BDC D.BE平分∠CBD【答案】D【知识点】三角形的外角性质;线段垂直平分线的性质【解析】【解答】解:由作图可得,DE是AB的垂直平分线,∴AE=BE,AD=BD,∴点D为AB的中点.∵∠ACB=90°,点D为AB的中点,∴CD为Rt△ABC的边AB上的中线,∴CD=AD=BD,故A选项正确;∵DE⊥AB,∴Rt△ADE中,AE>A D.∵AE>AD。
垂直平分线和角平分线典型题

知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.图1图2经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( )A .6cmB .8cmC .10cmD .12cm课堂笔记:针对性练习::1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点 E ,如果△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果∠A=28 度,那么∠EBC 是例2. 已知: AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
线段垂直平分线

线段垂直平分线1、想一想:什么叫线段的垂直平分线?性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。
已知 MN ⊥AB ,AC=BC , 求证:PA=PB逆命题:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上例、如图,在△ABC 中,∠B =22.50,∠C =600,AB 的垂直平分线交BC 于点D ,BD =26,AE ⊥BC 于点E ,求EC 的长。
第3题图 E FD CB A例:如图,直线MN 和DE 分别是线段AB 、BC的垂直平分线,它们交于P 点,请问PA 和PC 相等吗?练习:1,如图、在三角形ABC 中,AB=AC=8, AD=5,∠A=40°,AB 的垂直平分线交AC 于D 。
则(1)∠ABD= (2) ∠DBC= (3)AE= (4)BD=2、三角形内一点到三角形三边的距离都相等,则这一点一定是三角形什么的交点A .三边中垂线B .三条中线C .三条高D .三内角平分线3如右图,在△ABC 中,分别作AB 边、BC 边的垂直平分线,两线相交于点P ,分别交AB 边、 BC 边于点E 、F 。
∵点P 是AB 边垂直平线上的一点,∴ = ( ). 同理可得,点P 是BC 边垂直平线上的一点,∴ = ( ). ∴ = (等量代换).∴ (到一条线段两个端点距离相等的点,在这条线段的 ) ∴AB 、BC 、AC 的垂直平分线 。
4、在△ABC,PM,QN 分别垂直平分AB,AC ,若BC=10cm 则△APQ 的周长=_____ cm5,如下图△ABC 中,AC=16,DE 为AB 的垂直平分线, △BCE 的周长为26,求BC 的长。
8如图,已知在△ABC 中,AB =AC ,∠B =300,AB 的垂直平分线EF 交AB 于点E ,交BC 于点F ,求证:CF =2BF 。
例题图1 F EC B A例 用尺规作已知线段垂直平分线1用尺规作线段的垂直平分线。
线段垂直平分线的性质定理及其逆定理练习题

线段垂直平分线的性质定理及其逆定理练习题1. 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是()A.ED=CD B.∠DAC=∠B C.∠C>2∠B D.∠B+∠ADE=90°考点:线段垂直平分线的性质.分析:根据线段垂直平分线的性质得等腰三角形ADB,运用等腰三角形的性质得出尽量多的结论,与各选项进行比对,答案可得.解答:解:∵DE是线段AB的垂直平分线,∴AD=BD.∴∠B=∠BAD,∠ADE=∠BDE.∴∠B+∠ADE=90°其它选项无法证明其是正确的.故选D点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.利用角的等量代换是正确解答本题的关键.2.如图:Rt△ABC中,∠C=90°,DE是AB的垂直平分线,∠CAD:∠DAB=2:1,则∠B的度数为()A.20° B.22.5° C.25° D.30°考点:线段垂直平分线的性质.分析:由DE是AB的垂直平分线,利用线段的垂直平分线的性质得∠B=∠BAD,结合∠CAD:∠DAB=2:1与直角三角形两锐角互余,可以得到答案.解答:解:在Rt△ABC中∵DE是AB的垂直平分线∴∠B=∠BAD∵∠CAD:∠DAB=2:1∴4∠B=90°∴∠B=22.5°故选B点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.由已知条件得出4∠B=90°是正确解答本题的关键.3.如图,在Rt△ABC中,∠ACB=90°,BC的中垂线交斜边AB于D,图中相等的线段有()A.1组 B.2组 C.3组 D.4组考点:线段垂直平分线的性质.分析:由已知条件易得CD=BD,CE=BE,还可得到∠B=∠BCD,找各自的余角,于是得到∠A=∠ACD,得到AD=CD,可得AD=BD答案可得.解答:解:∵BC的中垂线交斜边AB于D,CD=BD,CE=BE,∴∠B=∠BCD,又∠A+∠B=90°,∠BCD+∠ACD=90°∴∠A=∠ACD,∴AD=CD∴AD=BD共4组.故选D.点评:此题主要考查线段的垂直平分线的性质等几何知识:线段的垂直平分线上的点到线段的两个端点的距离相等.利用等角的余角相等是正确解答本题的关键.4.(2002•哈尔滨)如图,到△ABC的三个顶点距离相等的点是△ABC的()A.三边垂直平分线的交点 B.三条角平分线的交点C.三条高的交点 D.三边中线的交点考点:线段垂直平分线的性质.分析:根据线段垂直平分线的性质(三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等)可得到△ABC的三个顶点距离相等的点是三边垂直平分线的交点.解答:解:△ABC的三个顶点距离相等的点是三边垂直平分线的交点.故选A.点评:本题考查的是线段垂直平分线的性质(三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等).5. 线段AB外有两点C,D(在AB同侧)使CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB=()A.80° B.90° C.100° D.110°考点:线段垂直平分线的性质.分析:由已知条件易得CD的连线垂直平分AB,然后利用三角形外角的知识可得答案.解答:解:∵CA=CB,DA=DB,∴CD垂直平分AB且垂足为M.∵∠ADB=80°,∠CAD=10°,∴∠ACM=50°,∴∠ACB=100°.故选C点评:此题主要考查线段的垂直平分线的性质等和三角形的外角等于不相邻的两内角和.由已知得到CD垂直平分AB是解答本题的关键.6. 如图,点D在△ABC的边BC上,且BC=BD+AD,则点D在()的垂直平分线上.A.AB B.AC C.BC D.不能确定考点:线段垂直平分线的性质.分析:由已知条件BC=BD+AD及图形知BC=BD+CD知AD=CD,根据线段垂直平分线的性质可判断出答案.解答:解:∵BC=BD+AD=BD+CD∴AD=CD∴点D在AC的垂直平分线上.故选B.点评:此题主要考查线段垂直平分线的性质的逆定理:和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.得到AD=CD是正确解答本题的关键.7.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有()A.1个 B.2个 C.3个 D.4个考点:线段垂直平分线的性质.分析:仔细阅读各已知条件,结合线段垂直平分线定理及逆定理对每一个小问题进行判断,其中④是错误的,过点E的直线有无数条,有且仅有一条垂直平分线段AB,所以原说法是错误的.解答:解:根据线段垂直平分线的性质定理及逆定理,①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB,符合性质定理,是正确的;②若PA=PB,EA=EB,则直线PE垂直平分线段AB,符合逆定理,是正确的;③若PA=PB,则点P必是线段AB的垂直平分线上的点,符合逆定理,是正确的;④若EA=EB,则过点E的直线垂直平分线段AB,不符合逆定理,是错误的;所以正确的是①②③三个.故选C.点评:此题主要考查线段垂直平分线的性质定理及逆定理:(1)线段垂直平分线上的点和这条线段的两个端点的距离相等;(2)和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.做题时要注意对每一个小题都要认真验证,不重不漏.8. 已知M,N是线段AB的垂直平分线上任意两点,则∠MAN和∠MBN之间的关系是.考点:线段垂直平分线的性质.分析:根据垂直平分线的性质转化为等腰三角形的问题,再进行两角大小的运算.解答:解:图1中,因为MN垂直平分AB所以MA=MB,NA=NB则∠MAO=∠MBO,∠NAO=∠NBO于是∠MAO+∠NAO=∠MBO+∠NBO即∠MAN=∠MBN.同理,图2中,∠MAO-∠NAO=∠MBO-∠NBO即∠MAN=∠MBN.点评:主要考查线段垂直平分线的性质和等边对等角,注意两种情况都要考虑是正确解答本题的关键.9. 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.考点:线段垂直平分线的性质.专题:探究型.分析:先根据等腰三角形的性质及三角形内角和定理求出∠ABC及∠ACB的度数,再根据线段垂直平分线的性质求出∠ABD 的度数即可进行解答.解答:解:∵AB=AC ,∴∠ABC=∠ACB702401802180=-=∠-=A ,∵MN 的垂直平分AB ,∴DA=DB , ∴∠A=∠ABD=40°,∴∠DBC=∠ABC-∠ABD=70°-40°=30°.故答案为:30°.点评:本题考查的是线段垂直平分线的性质,即线段垂直平分线上的点到线段两端的距离相等.10.如图, △ABC 中,边AB 的垂直平分线交AC 于E ,△ABC 和△BEC 的周长分别是24和14,则 。
线段的垂直平分线的性质与判定练习题课件

16.如图,在△ABC中,AB,AC的垂直平分线分别交BC于D,E, 垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长; (2)若∠BAC=100°,求∠DAE的度数.
解:(1)∵DM垂直平分AB,EN垂直平分AC,∴AD=BD,AE=EC,又 ∵AD+DE+AE=10,∴BD+DE+EC=10,即BC=10
5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5 cm,BD=3 cm,求BE的长.
解:11 cm
知识点2:线段垂直平分线的判定 6.如图,AC=AD,BC=BD,则有( A ) A.AB垂直平分CD B.CD垂直平分AB C.AB与CD互相垂直平分 D.CD平分∠ACB
7.(2016·毕节)到三角形三个顶点的距离都相等的点是这个三角形的( D ) A.三条高的交点 B.三条角平分线的交点 C.三条中线的交点 D.三条边的垂直平分线的交点
A.3.9 cm B.7.8 cm C.4 cm D.4.6 cm
3.(2016·随州)如图,△ABC中,AB=5,AC=6,BC=4,边AB 的垂直平分线交AC于点D,则△BDC的周长是( C )
A.8 B.9 C.10 D.11
4.如图,在△ABC中,AB=AC,AB的垂直平分线DE交AB于E,交 AC于D,若BD+DC=8 cm,则AB=_8___ cm.
知识点1:线段垂直平分线的性质 1.如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一 定成立的是( C ) A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC
2.如图,AB是CD的垂直平分线,若AC=2.3 cm,BD=1.6 cm,则四 边形ACBD的周长是( B )
八年级数学线段的垂直平分线的性质和判定(人教版)(基础)(含答案)

线段的垂直平分线的性质和判定(人教版)(基础)一、单选题(共11道,每道9分)1.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的一条直线垂直平分线段AB.其中不正确的个数有( )A.1个B.2个C.3个D.4个答案:A解题思路:根据线段垂直平分线的性质定理和判定定理,①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB,符合性质定理,是正确的;②若PA=PB,EA=EB,则直线PE垂直平分线段AB,符合判定定理,是正确的;③若PA=PB,则点P必是线段AB的垂直平分线上的点,符合判定定理,是正确的;④若EA=EB,则点E在AB垂直平分线上,但是平面内过一点的直线有无数条,不能确定是垂直平分线,所以错误;综上④错误,故选A试题难度:三颗星知识点:略2.如图,AC=AD,BC=BD,则有( )A.CD垂直平分ABB.AB垂直平分CDC.AB与CD互相垂直平分D.CD平分∠ACB答案:B解题思路:AC=AD,根据到线段两个端点距离相等的点在这条线段的垂直平分线上,所以A在CD的垂直平分线上;BC=BD,所以B在CD的垂直平分线上.两点确定一条直线,则AB垂直平分CD.故选B.试题难度:三颗星知识点:略3.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,下列结论不一定成立的是( )A.DE=CEB.OE平分∠DECC.OE垂直平分CDD.CD垂直平分OE答案:D解题思路:A:因为OE平分∠AOB,EC⊥OA,ED⊥OB,所以DE=CE成立;B:由题可知∠DOE=∠COE,∠ODE=∠OCE=90°,可证△DOE≌△COE(AAS)所以∠OED=∠OEC,故OE平分∠DEC成立;C:由选项A,B可知DE=CE,OD=OC,所以点E和点O分别在线段CD的垂直平分线上,所以OE垂直平分CD成立;D:点C和点D均不在线段OE的垂直平分线上,所以CD垂直平分OE不成立;故选D试题难度:三颗星知识点:略4.平面内,过直线外一点作已知直线的垂线最终都转化为下列哪一种基本作图( )A.作一个角等于已知角B.作一条线段等于已知线段C.作已知角的角平分线D.作已知线段的垂直平分线答案:D解题思路:过直线外一点作已知直线的垂线可以先在直线上作一条线段,使直线外的一点在这条线段的垂直平分线上,再作这条线段的垂直平分线.故选D.试题难度:三颗星知识点:略5.如图1,已知A为直线MN外一点,求作直线AB,使AB⊥MN.如图2用尺规作图作出直线AB,下列叙述:①任取一点P;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.其中错误的是( )A.①B.②C.③D.④答案:A解题思路:过点A作直线AB,使AB⊥MN的作法为:①任取一点P,使点P和点A位于直线MN的异侧;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.要保证以AP为半径的弧与直线MN有交点,点P与点A应位于直线MN异侧,①错误.故选A.试题难度:三颗星知识点:略6.如图1,已知线段MN,在MN上求作一点O,使OM=ON.如图2用尺规作图作出了点O,下列作图语言叙述正确的是( )A.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.B.分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.C.以点M为圆心,任意长为半径作弧,再以点N为圆心,大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.D.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB,直线AB即为所求.答案:B解题思路:在MN上求作一点O,使OM=ON可以转化为作线段MN的垂直平分线,与MN的交点即为点O.正确作法为:分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求;要找到MN垂直平分线上的两点,需要保证以相同长为半径作弧,且两弧有交点,所以此半径应大于,故选项A,C,D错误.故选B.试题难度:三颗星知识点:略7.如图,以C为圆心,以大于点C到AB的距离为半径作弧交AB于点D,E,再以D,E为圆心,以大于DE为半径作弧,两弧交于点F,作射线CF,则( )A.CF平分∠ACBB.CF垂直平分DEC.CF平分ABD.CF垂直平分AB答案:B解题思路:由题意可知,点C到D,E两点的距离相等,点F到D,E两点的距离相等,所以点C和点F 均在线段DE的垂直平分线上,所以CF垂直平分DE;故选B试题难度:三颗星知识点:略8.如图,某地由于居民增多,要在公路边增加一个公共汽车站,A,B是路边两个新建小区,要使两个小区到车站的路程一样长,这个公共汽车站C应建在( )A.点A到l的垂线与l的交点处B.线段AB的垂直平分线上任意某点处C.线段AB的垂直平分线和l的交点处D.点B到l的垂线与l的交点处答案:C解题思路:由题意可得,点C到A,B两点的距离相等,所以C在AB的垂直平分线上,因为C在l上,所以这个公共汽车站C应建在线段AB的垂直平分线和l的交点处.故选C试题难度:三颗星知识点:略9.如图,某公园的三个出口A,B,C构成△ABC,想要在公园内修建一个公共厕所,要求到三个出口距离都相等,则公共厕所应该在( )A.三条边的垂直平分线的交点B.三个角的角平分线的交点C.三角形三条高的交点D.三角形三条中线的交点答案:A解题思路:∵公共厕所到出口A,B的距离相等∴公共厕所在线段AB的垂直平分线上,同理,公共厕所在线段BC的垂直平分线上所以,公共厕所应该在三条边的垂直平分线的交点故选A试题难度:三颗星知识点:略10.电信部门要在S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )A.∠COD的平分线上任意某点处B.线段AB的垂直平分线上任意某点处C.∠COD的平分线和线段AB的交点处D.∠COD的平分线和线段AB垂直平分线的交点处答案:D解题思路:由题意可得,发射塔到两个城镇A,B的距离相等,所以发射塔要建在AB的垂直平分线上,又因为发射塔到两条高速公路OC,OD的距离也相等,所以发射塔要建在∠COD的平分线上,所以发射塔应建在线段AB垂直平分线和∠COD的平分线的交点处;故选D试题难度:三颗星知识点:略11.如图,△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB,下列描述正确的是( )A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点答案:B解题思路:因为PA+PB=AB,要使PA+PC=AB即PB=PC,即点P在BC的垂直平分线上所以点P为线段BC的垂直平分线与AB的交点故选B试题难度:三颗星知识点:略。
《线段的垂直平分线的性质和判定》基础训练1

课时2 线段的垂直平分线的性质过基础知识点1 线段的垂直平分线的性质1.[2021湖南湘潭中考]如图,在RtΔABC中,∠C = 90°,BD平分∠ABC交AC 于点D,DE垂直平分AB,垂足为E点,请任意写出一组相等的线段________.2.如图,四边形ABCD中,对角线AC垂直平分BD,垂足为E,下列结论不一定成立的是()=AD 平分∠BCD=BD D.ΔBEC≌ΔDEC3.如图,已知线段AB,BC的垂直平分线,l1,l2交于点M,则线段AM,CM的大小关系是( )>CM =CM<CM D.无法确定4.[2021湖北孝感大悟期中]如图,在ΔABC中,BC=8,AB的垂直平分线交BC 于点D,AC的垂直平分线交BC于点E,则ΔADE的周长等于_______.5. 如图,在△ABC中,边BC的垂直平分线与AC交于点E,与BC交于点D,已知AB=6,△ABE的周长是16,求AC的长.6.[2021湖北黄冈英才学校期中]如图,在△ABE中,AD⊥BE于点D,C是BE 上一点,BD=DC,且点C在AE的垂直平分线上,若ΔABC的周长为22,求DE 的长.知识点2 线段的垂直平分线的判定7.如图,已知AC=AD,BC=BD,则( )垂直平分CD 垂直平分AB与CD互相垂直平分 D.以上都不正确8.如图,BC=10,BD=6,AD=4,则点D在线段______的垂直平分线上.9.如图,在ΔABC中,AB=AC,O是ΔABC内一点,且OB=OC.求证:AO⊥BC.10.如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点.求证:DF所在直线是AB的垂直平分线.参考答案过基础=BE(或DC=DE或BE=EA或DB=DA)【解析】由角平分线的性质定理,知DC=DE.易证ΔBCD≌ΔBED,所以BC=BE.由线段的垂直平分线的性质,知DB=DA,EB=EA..【解析】∵对角线AC垂直平分BD,∴AB=AD,BC=DC,BE=DE,故A正确;在RtΔBEC和RtΔDEC中,∵BE=DE,BC=DC,∴RtΔBEC≌RtΔDEC,∴∠BCE=∠DCE,即CA平分∠BCD,故B,D正确.故选C.【解析】连接BM.∵L1和L2分别是线段AB,BC的垂直平分线,∴AM=BM, CM=BM,∴AM=CM.故选B.【解析】∵点D在AB的垂直平分线上,∴AD=DB.∵点E在AC的垂直平分线上,∴EA=EC,∴ΔADE的周长为AD+AE+ED=BD+EC+DE=BC=8.5.【解析】点E在BC的垂直平分线上,∴EB=EC.∴ΔABE的周长为AB+BE+AE=AB+EC+AE=AB+AC=6+AC=16,∴AC=10.6.【解析】∵BD=DC,AD丄BE,∴AB=AC.∵点C在AE的垂直平分线上,∴AC=CE.∵ΔABC的周长是22,∴AC+AB+BD+CD=22,∴AC+CD=11,∴DE=CD+CE=CD+AC=11.【解析】∵AC=AD,BC=BD,∴点A,B在线段CD的垂直平分线上,∴AB 垂直平分CD.故选A.【解析】∵BC=10,BD=6,∴CD=BC-BD=10-6=4.又AD=4,∴CD=AD,∴点D 在线段AC的垂直平分线上.9.【解析】∵AB=AC,∴点A在BC的垂直平分线上.∵OB=OC,∴点O在BC的垂直平分线上.∴AO是BC的垂直平分线,∴AO⊥BC.10.【解析】如图,连接AD.∵DE垂直平分AC,∴AD=DC,∵点D是BC的中点,∴BD=CD,∴AD=BD.∵F是BA的中点,∴AF=BF,在ΔADF和ΔBDF中,有AF=BF,DF=DF,AD=BD∴ΔADF≌ΔBDF,∠AFD=∠BFD.又∠AFD+∠BFD=180°,∴∠AFD=∠BFD=90°,∴DF⊥AB,∴DF所在直线是AB的垂直平分线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
△ ABD≌△ACD , ∴ AB = AC = 5 cm.∵点 C 在 AE 的垂直平分线上 ,
∴CE=AC=5 cm,∴BE=BC+CE=11 cm
知识点2:线段的垂直平分线的判定 6.如图,AC=AD,BC=BD,则有( A.AB垂直平分CD A)
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
7.在锐角△ABC内有一点P,满足PA=PB=PC,则点P是△ABC( A.三边垂直平分线的交点 B.三条角平分线的交点
)A
C.三条高的交点
D.三边中线的交点
8 . 如图 , 点 D 在三角形 ABC 的 BC 边上 , 且 BC = BD + AD , 则点 D 在 AC 的垂直平分线上. _______
分线,即点D在线段AB的垂直平分线上
16.如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于 点P,过点P分别作PN⊥AB于点N,PM⊥AC于点M.求证:BN=CM. 解:连接PB,PC,由角的平分线的性质证PN=PM,由线段垂直平分线 的性质证PB=PC,从而由HL证Rt△PNB≌Rt△PMC,∴BN=CM
即DG⊥EF,∴DG垂直平分EF
方法技能: 1.利用线段的垂直平分线的性质可证明两线段相等 ,应用时要注意:一是 点必须在垂直平分线上,二是距离指的是点到线段两端点的距离. 2.利用线段的垂直平分线的判定可证明垂直关系和线段相等关系.
易错提示:
对线段的垂直平分线的判定理解不透彻而出错.
Hale Waihona Puke 解:BH即为所求,如图:11.如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不
一定成立的是(
C)
A.AB=AD B.CA平分∠BCD
C.AB=BD D.△BEC≌△DEC
12.如图,∠MON内有一点P,PP1,PP2分别被OM,ON垂直平分,P1P2
与OM,ON分别交于点A,B.若P1P2=10 cm,则△PAB的周长为(
解:∵DE垂直平分BC,∴BD=CD,∴△ACD的周长=AD+AC+CD=
AB+AC=14 cm,又∵AB-AC=2 cm,可得AB=8 cm,AC=6 cm
15 . 如图 , 在 Rt△ABC 中 , ∠ C = 90° , AB = 2AC , AD 为∠ BAC 的平 分线.求证:点D在线段AB的垂直平分线上. 解:过点 D 作 DE⊥AB 于点 E , 由 AAS 可证△ ACD≌△AED , ∴ AC = AE.∵AB=2AC=BE+AE,∴BE=AE=AC,∴DE是线段AB的垂直平
A.6 cm B.8 cm C.10 cm D.12 cm
) C
13.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,PE =3 cm,则点P到直线AB的距离是____ 3 cm.
14.如图,已知AB比AC长2 cm,BC的垂直平分线交AB于D,交BC于E,
△ACD的周长是14 cm,求AB和AC的长.
9.如图,AB=AC,DB=DC,E是AD延长线上的一点,则BE是否与CE相 等?试说明理由. 解:BE=CE.理由:连接BC,∵AB=AC,DB=DC,∴A,D都在线段BC 的垂直平分线上,即AD垂直平分BC,∴BE=CE
知识点3:经过直线外一点作已知直线的垂线 10.如图,已知钝角△ABC,其中∠A是钝角,求作AC边上的高BH.(尺规 作图,保留作图痕迹,不写过程)
4.如图,线段AB的垂直平分线与 BC的垂直平分线的交点 M恰好在 AC
上,且AC=16 cm,则点B到点M的距离为________ . 8 cm
5 . 如图 , AD⊥BC , BD = CD , 点 C 在 AE 的垂直平分线上.若 AB = 5
cm,BD=3 cm,求BE的长.
解:∵ BD = CD , ∴ BC = 2BD = 6 cm , 又∵ AD⊥BC , ∴由 SAS 可证
17.如图,在△ABC中,∠B=∠C,点D,E,F分别在三边上,且BE =CD,BD=CF,G为EF的中点.求证:DG垂直平分EF. 解:连接 DE , DF , 由 SAS 证△ BED≌△CDF , ∴ DE = DF , 又∵ GE = GF , GD = GD , ∴△ GED≌△GFD(SSS) , ∴∠ EGD =∠ FGD = 90° ,
第十三章
13.1 13.1.2
轴对称
轴对称
线段的垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
知识点1:线段的垂直平分线的性质 1.如图,直线CD是线段AB的垂直平分线,P为直线CD上一点,已知线 段PA=5,则线段PB的长度为( A.6 B.5 C.4 D.3 ) B
2.如图,∠C=90°,AB的垂直平分线交BC于D,连接AD,若∠CAD =20°,则∠B等于( ) C
A.20° B.30° C.35° D.40°
3.(教材P65习题6变式)如图,△ABC的周长为30 cm,把△ABC的边AC
对折 , 使顶点 C 和点 A 重合 , 折痕交 BC 边于点 D , 交 AC 边于点 E , 若
△ABD的周长是22 cm,则AE的长为( C )
A.2 cm B.3 cm C.4 cm D.5 cm
