负阻抗变换器和回转器
16.6 回转器和负阻抗变换器
本节介绍两种特殊的二端口器件: 本节介绍两种特殊的二端口器件:
回转器和负阻抗变换器
一、回转器
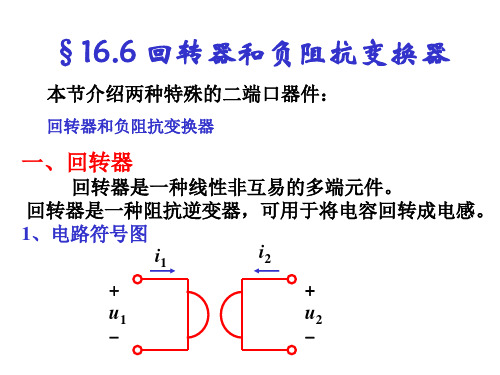
回转器是一种线性非互易的多端元件。 回转器是一种线性非互易的多端元件。 回转器是一种阻抗逆变器,可用于将电容回转成电感。 回转器是一种阻抗逆变器,可用于将电容回转成电感。 1、电路符号图 、 i2 i1 + u1 + u2 -
0 − r Z= r 0 0 g Y== - r i2 u2 = r i1 或 i1 = g u2 i2 = -g u1
u1i1+u2i2= - r i2 i1 + r i1 i2 = 0
理想回转器既不消耗功率又不发出功率, 理想回转器既不消耗功率又不发出功率,它 是一个无源线性元件 无源线性元件。 是一个无源线性元件。且互易定理不适用于回转 器。
4、回转器的应用 、 回转器具有把一个端口上的电流 回转” “回转”为另一端口上的电压或相反过 程的性质。 程的性质。 应用这一性质回转器可以把一个电 容回转为一个电感, 容回转为一个电感, 这在微电子器件中为用易于集成的 电容来实现难于集成的电感提供了可能 来实现难于集成的电感 电容来实现难于集成的电感提供了可能 性。
0 U 2 − I 1 2
4、负阻抗的实现(以电流反向型为例) 、负阻抗的实现 I1 + U1 NIC I2
Z2
U1 1 0 U 2 I = 0 − k − I 2 + 1
U2 U2 = - Z2I2
U1 ( s ) U 2 (s) = 输入阻抗 Zin= I1 ( s ) kI 2 ( s )
电容回转为电感. 若C=1µF,r = 50k ,则L=2500H.电容回转为电感 , 电容回转为电感
电路教案第16章 二端口网络

本章重点:1. 两端口的参数和方程2. 两端口的等效电路3. 两端口的转移函数16.1 二端口网络在工程实际中,研究信号及能量的传输和信号变换时,经常碰到如下两端口电路——三极管、传输线、变压器、放大器、滤波器,如图。
1. 端口(前面已介绍概念的复习)端口由一对端钮构成,且满足如下端口条件:从一个端钮流入的电流等于从另一个端钮流出的电流。
2. 二端口●当一个电路与外部电路通过两个端口连接时称此电路为二端口网络。
(如上图例)注意强调:二端口网络与四端网络的关系——都为四个引脚,但两端口网络每两个引出端表现为成对特性,电流方向相反、大小相等;四端网络则四个引出端的电流可以是完全不同的,无论大小还是方向。
●二端口的两个端口间若有外部连接,则会破坏原二端口的端口条件。
如上图放大器,最外端的四个端口构成一个二端口网络,而内部部分的四个引脚表现的特性是四端网络。
3. 研究二端口网络的意义●两端口的分析方法易推广应用于n端口网络;●大网络可以分割成许多子网络(两端口)进行分析;●仅研究端口特性时,可以用二端口网络的电路模型进行研究。
4. 分析方法●分析前提:讨论初始条件为零的线性无源二端口网络;●找出两个端口的电压、电流关系的独立网络方程,这些方程通过一些参数来表示。
16.2 二端口的方程和参数在本章讨论仅限于如下内容:1. 讨论范围:线性R、L、C、M与线性受控源,不含独立源。
2. 端口电压、电流的参考方向如图。
针对上图,可以看到:⏹ 端口物理量4个:i1、i2、u1、u2⏹ 端口电压电流有六种不同的方程来表示,即可用六套(三组)参数描述二端口网络。
2121u u i i ⇔;2211i u i u ⇔;2121u i i u ⇔;1. Y 参数和方程● Y 参数方程(Y → 短路导纳参数) 采用相量形式(正弦稳态)。
将两个端口各施加一电压源,则端口电流可视为电压源单独作用时产生的电流之和。
即:⎪⎩⎪⎨⎧+=+=22212122121111U Y U Y I U Y U Y I写成矩阵形式为:⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡212221121121U U Y Y Y Y I I Y 参数矩阵:⎥⎦⎤⎢⎣⎡=22211211Y Y Y Y ][Y 注意:Y 参数值由内部元件参数及连接关系决定。
14.5回转器和负阻抗变换器

+
u1
+
u2 C
u1 ri 2 u2 ri 1 du2 i 2 C dt
du2 u1 ri 2 rC dt di1 di1 2 r C L dt dt
Lr C
2
从端口1看,u1, i1关系为一等效电感关系,L= r2C. 若 r =50k, C =1F 则 等效电感 L=2500H ! (3) 回转器不消耗功率(能量),也不储能。是线性无源元件。
u1 1 i1 0
0 u2 i k 2
T 参数矩阵
(2) 阻抗变换器关系 (以INIC为例)
I1
+ U1
I2
INIC
+ U2
ZL
U 1 U 2 I 1 kI 2 U2 ZL I2
U1 U 2 Ua Uc U1 Uc I1 R1 R1 U2 Uc I2 R2
R1 I 1 R2 I 2 R2 I I1 2 R1
R1
I1
+ U1
a b
+
c R2
I2
+ U2
U 1 U 2 R2 k R2 R1 I1 I2 R1 0 1 U1 U2 R2 I1 0 R I 2 1
电流反向型
负阻抗变换器
R1
I1
i1 i2
+ u1
UNIC
电压反向型
+ u2
u1 ku2 i1 i 2
u1 k i1 0
14.6 回转器和负阻抗转换器

14.6 回转器和负阻抗转换器
回转器和负阻抗变换器都是一种线性的、非互易的多端元件,
可以用晶体管电路或运算放大器实现。
1、回转器
将一个端口的电流(或电压)回转为另一个端口的电压
(或电流)的多端器件。
第 1 页
回转电阻r (回转电导g) i r(g)
112200u i r u i r -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥
⎢⎥⎣
⎦⎣⎦⎣⎦00r r -⎡⎤
=⎢⎥⎣⎦
Z 1221
Z Z ≠(1)回转器的基本特性
1)回转器是非互易的线性二端口元件
1221
u ri u ri =-⎧⎨
=⎩Z 参数方程
Z 参数
第 3 页
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
112221120
u i u i ri i ri i +=-+=任一瞬间输入回转器的功率为:2)理想回转器是不储能、不耗能的无源二端口元件。
(2)回转器的等效电路
u 2
i 2i 1u 1-++
-
+
+--ri 1ri 2
u 2
i 2
i 1u 1
-
++-gu 1
gu 2
1221
i gu i gu =⎧⎨
=-⎩1221
u ri u ri =-⎧⎨
=⎩第 4 页
逆变性:把阻抗逆变为导纳L
把电容逆变为电感
NIC 端口的电压和电流关系
电流反向型
电压反向型
NIC
U U 电压反向型
电流反向型
NIC
1in (=1.5+电流反向型
的输入阻抗。
负阻抗变换器和回转器的设计

负阻抗变换器和回转器的设计摘要 本文简要介绍了负阻抗变换器(NIC )和回转器的原理,通过实验研究NIC 的性能,并应用NIC 性能作为负内阻电源研究其输出特性,还将这负电阻应用到R LC 串联电路中, 从中观察到除过阻尼、临界阻尼、负阻尼外的无阻尼等幅振荡和总电阻小于零的负阻尼发散震荡;并且利用负阻抗变换器实现回转器,进而利用回转器将电容回转成模拟纯电感,还利用模拟的电感组成RLC 并联谐振电路。
关键字 负阻抗变换器 运算放大器 二端口网络 回转器 回转电导 模拟电感 并联谐振1.负阻抗变换器的原理负转换器是一种二端口网络,通常,把一端口处的U 1和I 1称为输入电压和输入电流,而把另一端口’处的U 2和-I 2称为输出电压和输出电流。
U 1、I 1和U 2、I 2的指定参考方向如下图中所示。
根据输入电压和电流与输出电压和电流的相互关系,负阻抗变换器可分为电流反向型(INIC)和电压反向型(VNIC)两种, 电路图分别如下图的(a )(b )所示:图中U 1和I 1称为输入电压和输入电流, U 2和-I 2称为输出电压和输出电流。
U 1、I 1和U 2、I 2的指定参考方向如图1-1、1-2中所示。
根据输入电压和电流与输出电压和电流的相互关系,负阻抗变换器可分为电流反向型(INIC)和电压反向型(VNIC)两种,对于INIC ,有U 1 =U 2 ;I 1=( 1K -)(2I -)式中K 1为正的实常数,称为电流增益。
由上式可见,输出电压与输入电压相同,但实际输出电流-I 2不仅大小与输入电流I 1不同(为I 1的1/ K 1倍)而且方向也相反。
换言之,当输入电流的实际方向与它的参考方向一致时,输出电流的实际方向与它的参考方向相反(即和I 2的参考方向相同)。
对于VNIC ,有U 1= 2K - U 2 ; I 1 = 2I -式中K 2是正的实常数,称为电压增益。
由上式可见,输出电流-I 2与输入电流I 1相同,但输出电压U 2不仅大小与输入电压U 1不同(为U 1的1/K 2倍)而且方向也相反。
回转器与负阻抗变换器的仿真分析

第19卷第3期2003年9月天 津 理 工 学 院 学 报JOURNA L OF TIAN JIN INSTITUTE OF TECHN OLOG Y V ol.19N o.3Sep.2003 文章编号:100422261(2003)0320086203回转器与负阻抗变换器的仿真分析Ξ徐 伟1,马 韬2,徐钦民1(1.天津理工学院自动化与能源工程学院,天津300191;2.天津大学机械工程学院,天津300072)摘 要:回转器和负阻坑变换器是两个具有实用意义的器件,通过电路仿真标准工具PSPICE6.2的“软教学”、“软实验”和“软设计”,丰富了理论教学内容,填补了实验教学的空白,使理论环节与实践环节进一步紧密地结合起来.关键词:回转器;负阻抗变换器;仿真;PSPICE 中图分类号:TP39 文献标识码:AEmulating analysis of circle round device andnegative impedance converterX U Wei 1,MA T ao 2,X U Qin 2min 1(1.C ollege of Automation and Energy S ource Eng.,T ianjin Institute of T echnology ,T ianjin 300191,China ;2.School of Mechanical Engineering ,T ianjin University ,T ianjin 300072,China )Abstract :C ircle round device and negative im pedance converter are tw o devices of having pragmatic meaning.Through“soft teaching ”,“soft test ”,and “soft desigh ”of circuit emulating criterion tool PSPICE6.2,they enrich the content intheory teaching ,fu fil the gaps in test teaching ,make theory link and practice link m ore inseparable in a further combi 2nation.K eyw ords :circle round device ;negative im pedance converter ;emulating ;PSPICE 回转器和负阻抗变换器是电路理论中具有实用价值的两个器件,邱关源所编第四版《电路》教材中只给出其符号,对其端口处伏安关系进行了理论推导[1].实践教学中,由于受到实验设备等硬件设施及学时的限制也将其搁置一边,学生不知其组成、没有直观地感性认识,认识上的模糊,影响了对其应用方面的开发,如何填补理论教学和实践教学的不足,如何将理论与实际紧密结合,在有限的学时内给学生以更大的信息量,电路仿真软件PSPICE 的使用[2],使这一问题得到了很好的解决.1 回转器的仿真分析及应用 由于回转器能使容性负载和感性负载互为逆变,而用电容器来模拟电感器是其重要应用之一,为用易于集成的电容来实现难于集成的电感提供了可能性,特别是在模拟大电感量和低损耗的电感器方面,具有很高的实用价值.针对教材中给出的回转器符号及推导出的功能,调用PSPICE6.2,在Schematice 环境中绘制出由运算放大器构成的回转器电路,如图1.负载为图1 回转器电路Fig.1 Circle round deviceΞ收稿日期:2002212231 第一作者:徐 伟(1956— ),女,副教授一个3mF 的电容器,然后选择Analysis 菜单中“Set up ”项,选择“瞬态分析”类型,完成相应的设置后,进入Analysis 菜单中Simulate 项进行仿真,其结果如图2.图2 回转器1端伏安关系Fig.2 Circle round device 1extremityvoltage 2current characteristic图3 用等效电感器作高通滤波器电路Fig.3 H igh 2p ass filter systemcircuit图4 高通滤波器幅频特性Fig.4 H igh 2p ass filter system amplitude andfrequency ch aracteristic 显见,回转器入端(1端)电压超前于电流90°,呈纯电感性质,其等效电感值L eq =U m /I m ω≈3.18(H ).图3是用图1构成的等效电感器组成高通滤波器的应用电路,图4为其幅频特性. 同理,回转器还可以构成低通、带通滤波电路、R LC 谐振电路等等.2 负阻抗变换器的仿真分析及应用 负阻抗变换器能够起逆变阻抗的作用,即具有把一个正阻抗变为负阻抗的本领,分电流反向型和电压反向型.针对教材中给出的负阻抗变换器的符号及推导出的功能,以电流反向型、负载为一个1kΩ的纯电阻元件、输入电压为正弦激励情况为例,调用PSPICE 6.2,同上述回转器的绘制、设置、分析步骤,得到其电路如图5、图6的仿真结果.图5 负阻抗变换器电路Fig.5 N egative imped ance convertercircuit图6 负阻抗变换器1端伏安特性Fig.6 N egative imped ance conveter 1extremityvoltage 2current ch aracteristic・78・ 2003年9月 徐 伟,等:回转器与负阻抗变换器的仿真分析 显见,输入电流与输入电压反相,从而证明该电路确实是一个负阻抗变换器,它将一个正电阻变换成了一个负电阻,等效阻值为R eq=-U m/I m≈-100(Ω).图7是以该等效负电阻去低消R LC串联二阶零输入响应电路中R7值(其中:u c3(0+)=0.1V),以获得无阻尼等幅振荡的应用电路,图8是其电容电压等幅振荡情况. 同理,负阻抗变换器还可以构成回转器、构成一个具有负内阻的电压源等.图7 R LC串联无阻尼等幅振荡电路Fig.7 R LC series not resistance equiamplitudevibrationcircu图8 Uc等幅振荡波形Fig.8 Equiamplitude vibration circu U c w aveform3 结 论 通过电路仿真工具PSPICE的使用,将理性认识与感性认识、理论与实际紧密地结合在一起,丰富了理论教学内容,弥补了实验手段不足,在有限的学时内,给学以生动的、更多的信息,开拓了学生的视野,激发了学生的学习兴趣,收效十分显著.参 考 文 献:[1] 邱关源.电路[M].北京:高等教育出版社,1999.[2] 徐 伟,张晓光.电路分析和模拟技术[M].香港:现代知识出版社,2002.・88・天 津 理 工 学 院 学 报 第19卷 第3期 。
负阻抗变换器和回转器的设计

负阻抗变换器和回转器的设计摘要本论文详细地推导了利用运算放大器实现的负阻抗变换器和回转器的原理,并根据原理设完成了负阻抗变换器和回转器的设计以及实验验证和分析,实验过程是通过利用Multisim 软件进行的电路仿真,并在本章中给出了实验方法和具体的实验数据以及仿真过程中的真实截图,实验中的数据通过表格的方式给出,并绘制了曲线图。
关键词 运算放大器 负阻抗变换器 回转器引言 负阻抗是电路理论中的一个重要基本概念,在工程实践中有广泛的应用。
负阻的产生除某些非线性元件在某个电压或电流的范围内具有负阻特性外一般都由一个有源双口网络来形成一个等效的线性负阻抗。
该网络由线性集成电路或晶体管等元件组成,这样的网络称作负阻抗变换器。
回转器有把一个端口上的电流“回转”为另一端口上的电压或相反过程的性质。
正是由于这一性质,使回转器具有把一个电容( 电感)回转为一个电感( 电容)的本领。
用电容元件来模 拟电感器是回转器的主要应用之一,特别是模拟大电感量和低损耗的电感器。
正文1. 设计要求(1)用运算放大器设计一个负阻抗变换器电路,研究其端口关系。
(2)用运算放大器设计一个回转器电路。
1)推导其基本方程。
2)测量其回转参数g ,验证其满足基本方程。
3)将负载电容“回转”成一个电感量为0.1~1H 的模拟纯电感,用实验的方法验证该模拟量的电感特性及电感量准确性,并于理论值进行比较。
2. 设计原理(1)用运算放大器组成电流倒置型负阻抗变换器的原理。
Z L+-U 2z i.+-.U .1.(b)+-(a )图1 电流倒置型负阻抗变换器图1(a )虚线框所示的电路是一个用运算放大器组成的电流倒置型负阻抗变换器,(b )、(c)为其等效电路及电路符号。
由于运放“+”端和“—”端之间为虚短路,且运放的输出阻抗为无穷大,故有:Up Un = 即 12U U =而运放的输出电压0U 为:0131242U U I R U I R -=-= 得: 3142I R I R = 又因: 13I I =,24I I = 得:1122I R I R = 根据图6-4-2-1所示的2U 与2I 的参考方向可知:22LU I Z =-因此电路的输入阻抗:12121221L L in U U R Z Z KZ R I R I R =-===- 12R K R =称为电流增益负阻抗变换器的电压电流及阻抗关系如下:21U U =,21I KI =,L in Z KZ =-,以上关系既是负阻抗变换器的T 参数方程。
回转器的设计实验报告

姓名:赵玲学号: 1010200219回转器的设计摘要:回转器是理想回转器的简称,是一种新型的双口元件。
其特性表现为它能将一端口上的电压(或电流)“回转”为另一端口上的电流(或电压)。
本文利用运算放大器实现负阻抗变换器电路,进而利用负阻抗变换器实现回转器。
通过在multisim11.0仿真软件中的模拟,验证了回转参数满足的基本方程以及回转器将负载电容“回转”为电感量的准确性。
关键字:回转器回转参数模拟电感正文:一、实验装置及设备装置双路稳压电源函数发生器交流毫伏表数字示波器有源电路实验板二、实验内容1、用运算放大器设计一个回转器电路并推导其基本方程(a)基本原理:①回转器示意图如图1-1,回转器端口量之间的关系:I1=gU2 I2=-gU1 或 U1=rI2 U2=-rI1式中g和r(r=1/g)分别为回转电导和回转电阻,简称回转常数。
用矩阵形式表示为: =⎥⎦⎤⎢⎣⎡I2I1⎢⎣⎡-g 0⎥⎦⎤0g ⎥⎦⎤⎢⎣⎡U2U1 或 =⎥⎦⎤⎢⎣⎡U2U1⎢⎣⎡r 0⎥⎦⎤0-r ⎥⎦⎤⎢⎣⎡I2I1 ②回转器电路图如图1-2所示:图 1-1图 1-2(b )实验的仿真电路图如下图所示:①实验步骤:电路图中:R1=R2=R3=R4=R5=R6=R7=R8=1kΩ,改变R8和一端的电压U1,测量一端电流I1、另一端电压U2和电流I2,并记录在表格中。
②仿真截图:V1=1.000 R8=1KΩ:R8=2KΩV2=2.000 R8=1KΩR8=2KΩ③由电路图知-13S10.01-⨯-=理g,R8/k ΏV1/VI1/mAU2/VI2/mAg测/1-S(g=I1/U2)g理/1-S%100|-|⨯理理测ggg1 1.000 1.00-1.0001.00-1.00310-⨯-1.00310-⨯2 1.000 1.999-1.9991.00-1.00410-⨯1 2.000 2.00-2.0002.00-1.00410-⨯2 2.0003.963-3.9631.982-1.00410-⨯④结果分析:由表格知,所测的回转参数的值与理论上回转器的回转参数值吻合,从而验正了回转参数满足了基本方程。
16.6 回转器和负阻抗变换器

I1
I2 NIC
Z2
+ U1 -
+ U2 -
因此,NIC具有把一个正阻抗变为负阻抗的本领,
1 1 当2-2’接上R、L、C时,在1-1’将变为 k R、 k L、 kC
负阻抗变换器为电路设计中实现 负R、L、C提供了可能性
第16章结束
+ U2 -
负阻抗变换器的两种类型
式中k为一个正的实常数
3、负阻抗变换器的两种类型 ①电流反向型 + U1 -
I1
I2
NIC
U1 1 0 U 2 I 0 k I 2 1
②电压反向型
+ U2 -
U1 k 0 U 2 I 0 1 I 2 1
4、负阻抗的实现(以电流反向型为例) I1 I2 NIC
Z2
+ U1 -
U1 1 0 U 2 I 0 k I 2 + 1
U2 U2 = - Z2I2
U1 ( s ) U 2 (s) 输入阻抗 Zin= I1 ( s ) kI 2 ( s )
§16.6 回转器和负阻抗变换器
本节介绍两种特殊的二端口器件:
回转器和负阻抗变换器
一、回转器(gyrator)
回转器是一种线性非互易的多端元件。 回转器是一种阻抗逆变器,可用于将电容回转成电感。 1、电路符号图 i2 i1 + u1 + u2 -
2、理想回转器的端口电压和电流方程
u1 = - r i2 u2 = r i1 或 i1 = g u2 i2 = -g u1
2 0 2
应用:主要是电感和电容的互换
电工电子综合实验报告-负阻抗变换器和回转器

电工电子综合实验报告——负阻抗变换器和回转器的设计一、摘要本文提出了利用运算放大器实现:(1)负阻抗变换器(NIC)的电路(2)回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大;②输入电阻为无穷大;③输出电阻为零的特性。
而它在线性工作区的两个特性:“虚短”及“虚短”使得它有了广泛的应用。
如比例器、加法器、减法器、积分器等。
本文中则是实现了简单的负阻抗变换器和回转器。
2、负阻抗变换器(NIC)是一种二端口器件,是电路理论中的一个重要的基本概念,在工程实践中也有广泛的应用。
它一般由一个有源二端网络形成一个等值的线性负阻抗。
该网络可由线性集成电路或晶体管等元器件组成。
3、回转器是一种二端口网络元件,可用含晶体管或运算放大器的电路来实现。
它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。
也就是说它具有把一个端口的电压(或电流)“回转”成另一端口电流(或电压)的能力。
它的一个重要用途就是将电容“回转”成电感,或反之。
三、正文(一)实验材料与设备装置本实验采用的是虚拟的方法,所使用的软件为Multisim7。
(二)实验过程1、用运放设计一负阻抗变换器(NIC)电路⑴电流反向型负阻抗变换器(INIC)(图1—1)图1—1 INIC电路INIC的端口特性可用T参数描述为:U1 1 0 U2 ,其中 1 0= T=I1 0 -1/k I2 0 -1 /k当有负载Zl时,11’端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2.即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
⑵电压反向型负阻抗变换器(VINC)(图1—2)图1—2 VNIC电路VNIC的端口特性可用T参数描述为:U1 -k 0 U2 ,其中-k 0= T=I1 0 1 I2 0 1当有负载Zl时,11’端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2.即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
电工电子综合实验报告材料-负阻抗变换器和回转器

电工电子综合实验报告——负阻抗变换器和回转器的设计一、摘要本文提出了利用运算放大器实现:(1)负阻抗变换器(NIC)的电路(2)回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大;②输入电阻为无穷大;③输出电阻为零的特性。
而它在线性工作区的两个特性:“虚短”及“虚短”使得它有了广泛的应用。
如比例器、加法器、减法器、积分器等。
本文中则是实现了简单的负阻抗变换器和回转器。
2、负阻抗变换器(NIC)是一种二端口器件,是电路理论中的一个重要的基本概念,在工程实践中也有广泛的应用。
它一般由一个有源二端网络形成一个等值的线性负阻抗。
该网络可由线性集成电路或晶体管等元器件组成。
3、回转器是一种二端口网络元件,可用含晶体管或运算放大器的电路来实现。
它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。
也就是说它具有把一个端口的电压(或电流)“回转”成另一端口电流(或电压)的能力。
它的一个重要用途就是将电容“回转”成电感,或反之。
三、正文(一)实验材料与设备装置本实验采用的是虚拟的方法,所使用的软件为Multisim7。
(二)实验过程1、用运放设计一负阻抗变换器(NIC)电路⑴电流反向型负阻抗变换器(INIC)(图1—1)图1—1 INIC电路INIC的端口特性可用T参数描述为:U1 1 0 U2 ,其中 1 0= T=I1 0 -1/k I2 0 -1 /k当有负载Zl时,11’端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2.即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
⑵电压反向型负阻抗变换器(VINC)(图1—2)图1—2 VNIC电路VNIC的端口特性可用T参数描述为:U1 -k 0 U2 ,其中-k 0= T=I1 0 1 I2 0 1当有负载Zl时,11’端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2.即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
实验二十七负阻抗变换器的研究

实验二十七负阻抗变换器的研究1实验目的1.加深对负阻抗概念的认识,掌握对含有负阻抗器件电路的分析方法。
2.了解负阻抗变换器的工作原理及其运放实现。
3.掌握负阻抗变换器的各种测试方法。
2实验器材1.QY-DT01电源控制屏2.直流稳压电源3.函数信号发生器4.QY-DG05通用电路实验模块5.QY-DG14受控源/回转器/负阻抗变换器实验模块6.示波器3实验原理1.负阻抗是电路理论中一个重要基本概念,在工程实践中广泛的应用。
负阻抗的产生除某些线性元件(如燧道二极管)在某个电压或电流的范围内具有负阻特性外,一般都由一个有源双口网络来形成一个等值的线性负阻抗。
该网络由线性集成电路或晶体管等元件组成,这样的网络称作负阻抗变换器(NIC)。
按有源网络输入电压和电流与输出电压和电流的关系,可分为电流倒置型和电压倒置型两种(INIC及VNIC),电路模型如图1 所示。
图1负阻抗变换器电路模型理想情况下,两种负阻抗变换器的电压、电流变换关系为:(1) 对于INIC 型:12U U = , 21I KI = (K 为正的常实数电流增益) (公式1)(2) 对于VNIC 型: 211U K U =- , 21I I =- (K 1为电压增益) (公式2)由(公式1)可见,输入电压1U 经传输后等于输出电压2U ,大小和极性均未改变,但电流1I 经传输后变为2KI ,即大小和方向都变了,故名电流倒置型;由式(公式2)可见,经传输后,21I I =-,但电压的大小和正负极性都变了,故名电压倒置型。
2. 阻抗变换作用今在NIC 的输出端接以阻抗Z L ,如图26-2所示,则其输入阻抗可由(式1)求得:1221112121()i L U U U Z Z K I K I K I ====---或由(式2)可得122212i L U K U Z K Z I I -===--图2阻抗变换原理图可见Z i 为Z L 的(-1/K 1)倍或(-K 2)倍,即把正阻抗Z L 变换成了负阻抗,亦即能把R ,L ,C 元件分别变换为-R/K 1,L /K 1,C/K 1(或-K 2R ,-K 2L ,-K 2C ),故名负阻抗变换器。
电工 负阻抗变换和回转器的研究

有关负抗阻变换器和回转器的研究(一)负阻抗变换器1.实验目的1.了解负阻抗变换器(NIC)的原理.2. 通过实验研究NIC 的性能,并应用NIC 性能作为负内阻电源研究其输出特性,还将这负电阻应用到R LC 串联电路中,从中观察到除过阻尼、临界阻尼、负阻尼外的无阻尼等幅振荡和总电阻小于零的负阻尼发散震荡. 2.总体设计方案 1.负阻抗变换器的原理负转换器是一种二端口网络,通常,把一端口处的U 1和I 1称为输入电压和输入电流,而把另一端口处的U 2和-I 2称为输出电压和输出电流。
U 1、I 1和U 2、I 2的指定参考方向如下图中所示。
根据输入电压和电流与输出电压和电流的相互关系,负阻抗变换器可分为电流反向型(INIC)和电压反向型(VNIC)两种, 电路图分别如下图的(a )(b )所示:图中U 1和I 1称为输入电压和输入电流,U 2和-I 2称为输出电压和输出电流。
U 1、I 1和U 2、I 2的指定参考方向如图1-1、1-2中所示。
根据输入电压和电流与输出电压和电流的相互关系,负阻抗变换器可分为电流反向型(INIC)和电压反向型(VNIC)两种,对于INIC ,有U 1 =U 2 ;I 1=( 1K -)(2I -)式中K 1为正的实常数,称为电流增益。
由上式可见,输出电压与输入电压相同,但实际输出电流-I 2不仅大小与输入电流I 1不同(为I 1的1/ K 1倍)而且方向也相反。
换言之,当输入电流的实际方向与它的参考方向一致时,输出电流的实际方向与它的参考方向相反(即和I 2的参考方向相同)。
对于VNIC ,有U 1= 2K - U 2 ;I 1 = 2I -式中K 2是正的实常数,称为电压增益。
由上式可见,输出电流-I 2与输入电流I 1相同,但输出电压U 2不仅大小与输入电压U 1不同(为U 1的1/K 2倍)而且方向也相反。
若在NIC 的输出端口2—2’接上负载Z L ,则有U 2= -I 2Z L 。
16章自看内容

L[输 量 出 ] H(s) = L [输 量 入 ]
+ U1 (s) –
I1 (s)
I2 (s)
N0
+ U2(s) –
1.无端接二端口 1.无端接二端口 输出端口没有接负载 输入激励无内阻 2.有端接二端口 2.有端接二端口 输出端口接有负载 输入激励有内阻 单端接二端口 双端接二端口
-----输出端开路或短路 输出端开路或短路 -----电源为理想电源 电源为理想电源
u1 = −ku2 i = −i 1 2
1 0 [T] = 0 − k 负阻抗变换的性质 ② 负阻抗变换的性质
& & U1 U2 Zi = = & & I1 kI2
− k 0 或 [T] = 0 1 . I1 + . NIC 1 U1 = − ZL −
k
I2 .+ U2 −
16自看) 16-4 二端口的转移函数 (自看)
16- 二端口的转移函数(自看) 16-4 二端口的转移函数(自看)
二端口常为完成某种功能起着连接两部分电路 的作用,这种功能一般通过转移函数描述。 的作用,这种功能一般通过转移函数描述。
二端口转移函数 说明
用拉氏变换形式表示的输出量与输入量的之比
I 1. 单一激励下,转移函数就是网络函数; 单一激励下,转移函数就是网络函数; + U N 2. 转移函数又称传递函数; 转移函数又称传递函数; − 3. 分析前提:无源二端口,动态元件零状态。 分析前提:无源二端口,动态元件零状态。
I1
.
I2 +. U2 ZL
.
-
+. U1
-
& & U1 − rI2 r2 Zi = = = & & I1 U2 / r ZL
14.5回转器和负阻抗变换器.
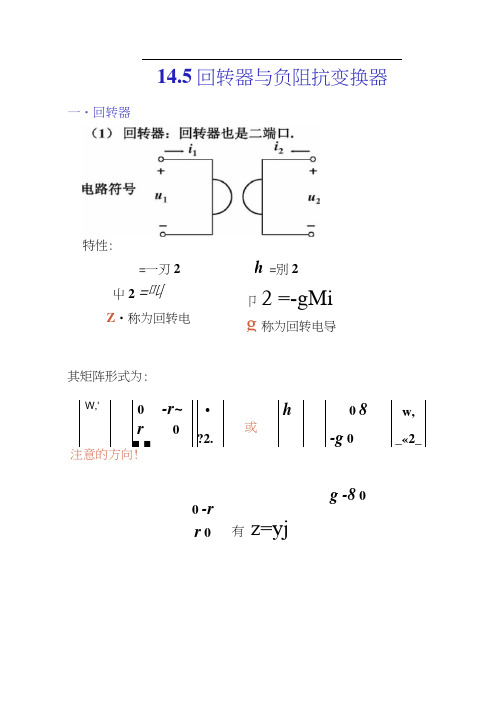
14.5回转器与负阻抗变换器一・回转器其矩阵形式为:W,'0 -r~•h0 8w, r0■ ■?2.或-g 0 _«2_ 注意的方向!g -8 0有z=yj=一刃2=叫屮2Z•称为回转电卩2 =-gMig称为回转电导0 -rr 0特性:h =別2(2)回转器可以把一个端口的电流(或电压)回转成另一个 端口的电压(或电流)。
电感。
:从端口丄看,叭畀]关系为一等效电感关系,L= r^C. 若 z-=5«kn,C=lpF 则等效电感L=250«H I(3)回转器不消耗功率(能量),也不储能。
是线性无源元件。
(4)回转器是非互易元件。
因此利用回转器可以把电容回转成 ii 一负阻抗变换器(1)电压反向型负阻抗变换器和电流反向型负阻抗变换器M, =—kU2'-kO'■ uJ2电压反向型7i =一匚•0 1 _°2T参数矩阵(3)电流反向型叮1()■M J一k_-^2_卩参数矩阵(2)阻抗变换器关系(以INIC 为例)丄O — + O —5=5A* m —Z/O-+INIC2-----O + «2 —OINIC(1) INIC 变换器(Z)6=^2-i,=ki,Z=—ZiZ ⑶代入⑴得e=-Z』2⑷除以⑵得5 二-Z 丿2 A “2即入端阻抗Z, =--z,k'丨亠INIC ■ 2+a -----------当时,Zj=—Z|^ Zf与Zi.差一负号。
实现了负阻抗的变换!2(3)(4)电路举例:人O ----- 1 --- + a + t>cU, b輕 2u -uR2RJi = R2I2IO — +O+ 0cR A ---- o +工sU\=57,ri 01■■ "1/ = 0R.1L 1」&■2」2电流反向型 负阻抗变换器则 即占为一负电阻。
当输出端口接阻抗z 时6=—Z ,2++* I O ------------+ a U,b Q代入后得若Z=R,。
1-10__阻抗变换器和阻抗逆变器

n2 Z L ( s)
− k1 k 2 Z L ( s )
1 Z L r2
r1 r2
NII
1 1 r2
− r1 1
− r1 r2
1 Z L ( s)
故它同时具有阻抗逆变和将参数反号的作用。 故它同时具有阻抗逆变和将参数反号的作用。
表1-1 阻抗变换器和阻抗逆变器
第2端口接ZL(s) 时 第1端口的输入 阻抗
元件
传输参数矩阵T
n 0
+ − k1 0
PIC
0 1 n
0 − 1 + k2
0 u1 =1 i1 r2
− r1 0
u2 − i 2
如果在负阻抗逆变器的第2端口接以阻抗 如果在负阻抗逆变器的第 端口接以阻抗ZL(s),则第 端口接以阻抗 ) 则第1 端口的输入阻抗为
1 Z(s)= − r1 r2 1 Z ( s) L
1-10-2 阻抗逆变器 回转器是一种正阻抗逆变器,它是无源、 回转器是一种正阻抗逆变器,它是无源、无损二端口 电阻元件。 电阻元件。
0 u1 =1 i1 r2
r1 0
u2 − i 2
回转器可以用受控源实现,也可用运算放大器和电阻 回转器可以用受控源实现, 实现, 实现, 负阻抗逆变器的元件特性用传输参数矩阵表示为
负阻抗变换器的阻抗变换作用是:将阻抗变换至 倍 负阻抗变换器的阻抗变换作用是:将阻抗变换至k倍 并反号。即所谓“负阻抗变换”作用。在有源网络综 并反号。即所谓“负阻抗变换”作用。 合中,可利用NIC的这一性质实现负值的电阻、电感 合中,可利用 的这一性质实现负值的电阻、 的这一性质实现负值的电阻 或电容。 或电容。 负阻抗变换器是有源二端口电阻元件。 负阻抗变换器是有源二端口电阻元件。 负阻抗变换器可用受控源实现, 负阻抗变换器可用受控源实现,也可用运算放大器和 电阻元件实现。 电阻元件实现。
回转器与负阻抗变换器的设计

回转器与负阻抗变换器的设计回转器和负阻抗变换器的设计是电路设计的任务之一,它们的重要性不可低估。
它们被用来对电压和电流进行变换,从而改变一个系统的电气特性。
这篇文章将回转器和负阻抗变换器的设计进行简单介绍,以便于理解这两种变换器的原理及其应用。
回转器是一种特殊的能量转换器,它可以把直流能量转换成交流能量。
它一般由两个电感组成,连接在一起,中间接收到一个外部交流电源,当电流通过第一个电感的最大的时候,会产生磁场从正一方到负一方,从而把电能转换到另一个电极上。
由于回转器的简单、紧凑和可靠的性能,它被用在电动机驱动系统、放大器电源、电抗器控制系统等等。
负阻抗变换器是一种电力变换器,用来在电力系统中改变电压水平和可以输出快速反应电流。
它通常由一个电容器和一个控制回路组成,电容器可以存储和释放电荷,而控制回路则可以控制电容器的行为。
它的特点是反应迅速,可以快速改变电压,有助于调节电力系统的电压水平和负面反馈控制。
它主要应用于甲烷气体压缩机、燃料电池电源等系统。
回转器和负阻抗变换器的设计需要考虑到不少因素,例如电感、电源、控制、电容等,根据不同系统的不同要求,需要经过精心设计来确保它们的工业性能。
此外,如果需要更高效的能量传输和反应,还需要考虑它们的其他变换器,如带反馈的驱动器、高压变换器等。
综上所述,回转器和负阻抗变换器是电路设计的重要组成部分,它们可以用来调整系统的输入和输出,改善系统效率、可靠性和生态友好性。
使用合理的回转器和负阻抗变换器设计,可以在很短的时间内完成能源变换,同时保持系统的安全和稳定性,从而提高电力系统的整体性能。
负阻抗变换器和回转器1

负阻抗变换器和回转器设计运算放大器的应用摘要抗变换器和回转器是两个具有实用意义的器件。
本文从理论和仿真分析两方面研究负阻抗变换器的性能并得到一些实用的结论。
并且对负阻抗进行了详细的分类讨论,从不同角度分析了负阻抗变换器的实现。
进而讨论如何用两个负阻抗变换器实现回转器,以及讨论回转器在实现模拟电感上的应用。
关键词运算放大器;复阻抗变换器;回转器;模拟电感;姓名:赖森锋学号:0804210127引言近代电路理论和电工电子技术的发展,在实践中又研究了许多种新型元件,例如负阻抗变换器(negative-impedance convertor,NIC)和回转器,负阻抗变换器(NIC)是一种二端口器件,是电路理论中的一个重要的基本概念,在工程实践中也有广泛的应用。
负阻抗变换器(NIC)一般由一个有源双口网络形成一个等值的线性负阻抗。
该网络由线性集成电路或晶体管等元件组成。
负阻抗变换器可分为电流反相型(INIC)和电压反相型(VNIC)。
通过此次研究与设计,了解负阻抗变换器的原理及其运算放大器的实现,加深对负电阻(阻抗)特性的认识。
同时研究INIC和VNIC接法的开路稳定性及短路稳定性。
它们不但在理论上,而且在实践上都有很重要的意义。
负阻抗变换器能够起逆变阻抗的作用,即具有把一个正阻抗变为负阻抗的本领,分电流反向型和电压反向型。
回转器能回转阻抗的特性,广泛用于大规模集成电路。
因为在一个极小的单晶片上制造尺寸小且无损耗的电感元件非常困难,但电容元件却易于制作,利用回转器将电容元件回转为电感元件,即能实现上述要求。
本文首先研究了负阻抗变换器的一些基本性质,然后介绍如何利用负阻抗变换器实现回转器,进而指出其应用。
正文一.负阻抗变换器的电路理论工程中常有一些非线性元件在一定的工作区域呈现负阻抗的特性(如隧道二极管等),可以利用运算放大器二端口网络可以形成一个等效的线性负阻抗,而这种由有源元件组成的网络称作负阻抗变换器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
负阻抗变换器和回转器一、摘要本文提出了利用运算放大器实现:(1)负阻抗变换器(NIC)的电路(2)回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大;②输入电阻为无穷大;③输出电阻为零的特性。
而它在线性工作区的两个特性:“虚短”及“虚短”使得它有了广泛的应用。
如比例器、加法器、减法器、积分器等。
本文中则是实现了简单的负阻抗变换器和回转器。
2、负阻抗变换器(NIC)是一种二端口器件,是电路理论中的一个重要的基本概念,在工程实践中也有广泛的应用。
它一般由一个有源二端网络形成一个等值的线性负阻抗。
该网络可由线性集成电路或晶体管等元器件组成。
3、回转器是一种二端口网络元件,可用含晶体管或运算放大器的电路来实现。
它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。
也就是说它具有把一个端口的电压(或电流)“回转”成另一端口电流(或电压)的能力。
它的一个重要用途就是将电容“回转”成电感,或反之。
三、正文(一)实验材料与设备装置本实验采用的是虚拟的方法,所使用的软件为Multisim7。
(二)实验过程1、用运放设计一负阻抗变换器(NIC)电路⑴电流反向型负阻抗变换器(INIC)(图11 INIC电路INIC的端口特性可用T参数描述为:U11 0 U2 ,其中1 0 = T= I1 01 /k 当有负载Zl时,11’ 端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2、即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
⑵电压反向型负阻抗变换器(VINC)(图12 VNIC电路VNIC的端口特性可用T参数描述为:U1k 0 = T= I1 01 I2 01当有负载Zl时,11’ 端口看进去的端口阻抗Z=U1/I1=kU2/I2,即为Z=-kZ2、即若22’接电阻R时,端口阻抗为-kR;接电感时,端口阻抗为-kL;接电容时,端口阻抗为-kC。
总结:利用NIC电路可实现负电阻、负电容及负电感。
⑶实验电路INIC的开路稳定(OCS)及短路稳定(SCS)性的研究① OCS研究:改变OCS端口的阻值,观察T矩阵中参数k的变化情况。
实验线路参见图11a。
其中SCS端口接入7V直流电源,元件R1=1000欧,R2=2000欧,R3为可调。
则K理论值为0、5。
图11a 电流反相型阻抗变换器实验电路a(INIC)表11aR3U/VIR=U/IK=-R/R3OCS端口接入小电阻临界状况507、0000、028A5007、0000、028A10007、0000、028A10017、000-0、014A-50010507、000-0、013A-538、4OCS端口接入大电阻1600、07、000-8、753mA-799、70、49981800、07、000-7、780mA-899、70、49982000、07、000-7、002mA-999、70、49982200、07、000-6、365mA-1099、70、49992400、07、000-5、835mA-1199、60、4998从表中数据我们不难发现当OCS端口接入的电阻值小于1000欧时,电路并不满足上面推导的T矩阵关系式,而接入大于1000欧的电阻时,电路趋于稳定,而实验测得的参数k=0、4998的误差为0、4‰,这说明该电路能很好的满足T矩阵关系式。
即OCS端口只允许接高阻抗负载,即满足开路稳定。
② SCS 研究:改变SCS端口的阻值,观察T矩阵中参数k的变化情况。
实验线路参见图11b。
其中SCS端口接入7V直流电源,元件R1=1000欧,R2=2000欧,R3=3000欧,R4可调。
则K理论值为0、5。
图11b 电流反相型阻抗变换器实验电路b(INIC)表11bR4U/VIR=U/IK=-R/R3SCS端口接入小电阻107、047-4、699mA-1499、7 0、4999307、143-4、763mA-1499、70、4999507、241-4、828mA-1499、80、4999707、342-4、897mA-1499、30、4998907、446-4、966mA-1499、40、4998临界状况SCS端口接入大电阻66712、593-8、397mA-1499、7668-4、2130、017A-247、8800-5、4430、016A1000-6、9970、014A1200-8、2960、013A从表中数据我们不难发现当SCS端口接入的电阻值大于667欧时,电路并不满足上面推导的T矩阵关系式,而接入小于667欧的电阻时,电路趋于稳定,而实验测得的参数k=0、49986的误差为0、28‰,这说明该电路能很好的满足T矩阵关系式。
即SCS端口只允许接低阻抗负载,即满足短路稳定。
⑷实验电路VNIC的开路稳定(OCS)及短路稳定(SCS)性的研究①OCS 研究:改变OCS端口的阻值,观察T矩阵中参数k的变化情况。
实验线路参见图11a。
其中OCS端口接入8V直流电源,元件R1=1欧,R2=0、5欧,R3为可调。
则K理论值为2。
图11a 电压反相型阻抗变换器实验电路a(VNIC)表11aR3U/VIR=U/IK=-R/R3临界状况1n8、00014、500GA1u8、000-4、004MA1、9980uOCS端口接入大电阻1000、08、000-4、000mA-2000、02、00001200、08、000-3、332mA-2401、02、00081400、08、000-2、858mA-2799、21、99941600、08、000-2、503mA-3196、21、99761800、08、000-2、222mA-3600、42、0002经过多次实验,我发现当OCS端口接入的电阻值小于1u欧时,电路才并不满足上面推导的T矩阵关系式,而接入大于1u欧的电阻时,电路趋于稳定,而实验测得的参数k=1、9996的误差为0、2‰,这说明该电路能很好的满足T矩阵关系式。
对于这个电路,它对大电阻的要求并不高,只需大于1u欧的电阻的电阻就可。
② SCS研究:改变SCS端口的阻值,观察T矩阵中参数k的变化情况。
实验线路参见图11b。
其中SCS端口接入8V直流电源,元件R1=1欧,R2=0、5欧,R3=3000欧,R4可调。
则K理论值为2。
图11b 电压反相型阻抗变换器实验电路b (VNIC)表11bR4U/VIR=U/IK=-R/R3SCS端口接入小电阻10、08、013-1、336mA-5981、999330、08、040-1、341mA-5995、61、998550、08、067-1、345mA-5997、81、999370、08、094-1、350mA-5995、61、998590、08、121-1、354mA-5997、81、9993临界状况接入大电阻26 30、014、056-2、316mA-6069、12614、060-2、315mA-6073、42637、0-5、5635、149mA-1080、44000、0-8、5164、418mA-1927、6从表中数据我们不难发现当SCS端口接入的电阻值大于2637欧时,电路并不满足上面推导的T矩阵关系式,而接入小于2637欧的电阻时,电路趋于稳定,而实验测得的参数k=1、99898的误差为0、5‰,这说明该电路能很好的满足T矩阵关系式。
即SCS端口只允许接低阻抗负载,即满足短路稳定。
总结以上四组数据可知,用集成运放组成的NIC,为稳定工作,必须保证运放的负反馈强于正反馈。
OCS正是只容许接高阻抗负载的端口,为开路稳定端;SCS正是只容许接低阻抗负载的端口,为短路稳定端。
2、用运放设计一个回转器电路⑴设计如图21回转器电路参数见图示。
回转器电压电流关系式的推导过程如下:其中g=1/R、很显然,此方程为回转器(与图22。
元件参数为:电阻R1-R7和R9全取1000欧,电源电压3V,频率1000赫兹,R8为可调电阻。
则理论值g=1/R8=0、001。
图23 将电容回转成电感电路表2-3f/Hz1001xx0140150155160I/mA3、6053、7433、8473、9213、9693、9954、0004、002f/Hz165170180190200210220230I/mA3、9993、9793、9573、9403、9003、8533、8013、745特别的,我还测得了f0=159、155Hz时,I=4、002mA为了得到直观的I变化趋势,作图2-3-1。
图2-3-1 I-f图从图中我们可以读出I取最大值时所对应的频率为160Hz,误差为0、5﹪,这说明了设计的电路的确将电容回转成了一个纯电感。
四、总结本次实验中我研究的侧重点为①电路中参数的选择②实验数据的测量及处理。
在电路元件参数的选择方面,需要我们对电路的原理及运行方式和特性有熟练的掌握,否则无法选出能够测得较准数据电路元件。
如在NIC电路之中,T矩阵参数的有几种表达方式,为了减少可能出现的误差,我选择了本文中的矩阵方式,在测量过程中我们只需测一个参数即k即可,如此很是方便快捷。
不仅如此,实验中电路里的电源也有一定的要求。
一开始做这个实验时我选择的电源过大,测出的数据跳动性很大,在选择了小一些的电源之后,实验数据稳定了很多。
在实验数据的测量及处理方面,主要的难点在NIC电路中端口SCS和OCS研究上。
在此,我选择了控制变量法的研究方法。
控制了电路中的变量之后,研究也变得方便了很多。
而测量出SCS和OCS端口的临界电阻也需要很大的耐心,不断重复测量。
在回转电路中,如何证明电容回转后形成了一个电感是另一个难点。
在老师的提示下,我选择了LC谐振中的串联谐振。
而我们已经在平时做过研究LC谐振的电路实验,在这里可以说是学以致用。
总的来说,这次的电路虚拟实验给了我受益匪浅。
我不仅学到了书本里没有的知识如负阻抗变换器,而且懂得了书本里面放大器的实际应用和回转器的构成等。
五、参考文献老师提供的有关负阻抗的课件一份、上海交大实验负阻抗的研究课件、网上的一些资料。
