相似三角形模型分析大全(非常全面-经典)

相似三角形经典模型总结与例题分类

相似三角形经典模型总结与例题分类相似三角形经典模型总结在相似三角形中，有一些经典的模型，包括平移型、平行型、旋转180°型、翻折180°型、一般型、特殊型、斜交型、双垂直型等。

这些模型可以帮助我们更好地理解和解决相似三角形的问题。

其中，平移型、平行型、翻折180°型、斜交型和双垂直型都是比较常见的模型。

在解决相似三角形的问题时，可以根据具体情况选择相应的模型进行分析。

以下是一些例题，可以帮助我们更好地理解相似三角形的模型和应用。

例1：如图，EE1∥FF1∥MM1，若AE=EF=FM=MB，则S△.例2：如图，AD∥EF∥MN∥BC，若AD=9，BC=18，.例3：已知，P为平行四边形ABCD对角线，AC上一点，过点P的直线与AD，BC，CD的延长线，AB的延长线分别相交于点E，F，G，H。

则PEPH=PFPG。

例4：已知：在△ABC中，D为AB中点，E为AC上一点，且AE=2，BE、CD相交于点F。

则ABF=2EFD。

例5：已知：在△ABC中，AD=11AB，延长BC到F，使CF=BC，连接FD交AC于点E。

则①DE=EF②AE=2CE。

例6：已知：D，E为三角形ABC中AB、BC边上的点，连接DE并延长交AC的延长线于点F，例7：如图，已知XXX，若AB=a，CD=b，EF=c，则a/b=c/(a+c)。

例8：如图，S△.例9：如图，四边形ABCD中，∠B=∠D=90°，M是AC上一点，ME⊥AD于点E，MF⊥BC于点F。

则MF/ME+1=BD/AC。

例10：如图，在△ABC中，D是AC边的中点，过D作直线EF交AB于E，交BC的延长线于F。

则AE·BF=BE·CF。

BCF：在线段AB上取一点C，以AC、CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB，AE交CD于点P，BD交CE于点Q，证明CP=CQ。

解法：首先，由等腰三角形的性质可知，∠XXX∠CEB，∠ACD=∠BCD，因此△ADC≌△CEB，从而AP=BP，AQ=CQ。

相似三角形常见模型(总结)

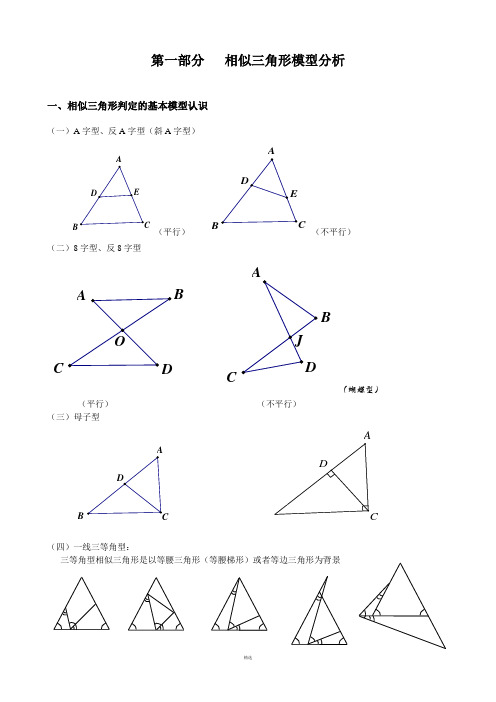
第一部分相似三角形模型分析一、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GBCEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD是Rt△ABC中∠A的平分线，∠C=90°，EF是AD的垂直平分线交AD于M，EF、BC的延长线交于一点N。

求证：(1)△AME∽△NMD; (2)ND2=NC·NB3、已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。

求证：EB·DF=AE·DB4.在∆ABC中，AB=AC，高AD与BE交于H，EF BC⊥，垂足为F，延长AD到G，使DG=EF，M是AH的中点。

求证：∠=︒GBM905．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt△ABC中，∠C=90°，BC=2，AC=4，P是斜边AB上的一个动点，PD⊥AB，交边AC 于点D（点D与点A、C都不重合），E是射线DC上一点，且∠EPD=∠A．设A、P两点的距离为x，△BEP的面积为y．（1）求证：AE=2PE；（2）求y关于x的函数解析式，并写出它的定义域；（3）当△BEP与△ABC相似时，求△BEP的面积．ABPD E（第25题图）GMFEHDCBADC双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高求证：（1）△ABD ∽△ACE ；（2）△ADE ∽△ABC ；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=62，求：点B 到直线AC 的距离。

相似三角形模型分析大全(非常全面,经典)

相似三角形模型分析大全一、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．ACDEB相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

求证：∠=︒GBM 90GMF EHDCBA5．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt △ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC 于点D （点D 与点A 、C 都不重合），E 是射线DCB上一点，且∠EPD=∠A．设A、P两点的距离为x，△BEP的面积为y．（1）求证：AE=2PE；（2）求y关于x的函数解析式，并写出它的定义域；（3）当△BEP与△ABC相似时，求△BEP的面积．双垂型1、如图，在△ABC中，∠A=60°，BD、CE分别是AC、AB上的高求证：（1）△ABD∽△ACE；（2）△ADE∽△ABC；(3)BC=2ED2、如图，已知锐角△ABC，AD、CE分别是BC、AB边上的高，△ABC和△BDE的面积分别是27和3，DE=62，求：点B到直线AC的距离。

相似三角形模型总结

相似三角形模型总结相似三角形是中学数学中常见的一个概念。

相似三角形有着非常重要的应用，尤其在建筑、地图、航空等领域中被广泛地运用。

在这篇文章中，我将对相似三角形的模型及其应用进行总结。

一、相似三角形的定义相似三角形是指形状相似而大小不同的两个或多个三角形。

它们的对应角度相等，对应边的比例相等。

根据这个定义，我们可以推出相似三角形的判定定理：若两个三角形对应角度分别相等，则它们是相似的。

二、重心模型重心模型是一种抽象的几何模型，它是在研究固体对象的重心和转动惯量时得出的。

对于任意三角形 ABC，以其三条边的中点为顶点，连上互相垂直的直线，将它们相交于 G 点。

这里 G 点称为三角形 ABC 的重心，它与每个中点连成的线段相等。

同时，可以证明如果一个点在三角形内部且到三边距离的乘积等于其到三条中线距离的乘积，则该点一定是三角形的重心。

三、海龟图模型海龟图模型是一个很著名的相似三角形应用模型，它是由美国数学家T. N. Thiele 提出的。

在海龟图中，一个三角形符号代表前进一步，一个圆点符号则代表不动。

当这个图形以相似的规律继续扩展时，就能在图形中看到似乎随机且自相似的模式。

在实际操作中，我们可以将这个模型用于分形的制作和操作中，实现较好的效果。

四、印章模型印章模型是相似三角形的另一种应用模型。

在制作印章时，多会使用到相似三角形的概念。

根据相似三角形的定义，我们可以通过相似三角形来制造缩小复制的图案。

具体来说，我们可以通过将大三角形分割为单位面积相等的若干小三角形，然后根据相似的规律进行缩小，就可以得到与大三角形相似而更小的三角形。

五、三角剖分模型三角剖分模型是相似三角形的一种实际应用模型。

在三角剖分中，我们会把一个多边形分解为多个三角形，这些三角形可以保持相似性，这比将多边形分解成其它形状的图形更容易实现。

总结在本文中，我们总结了几种相似三角形的应用模型，这些模型不仅具有学术研究的意义，更能够应用于实际的生产和生活中。

(完整版)相似三角形经典模型总结及例题分类.doc

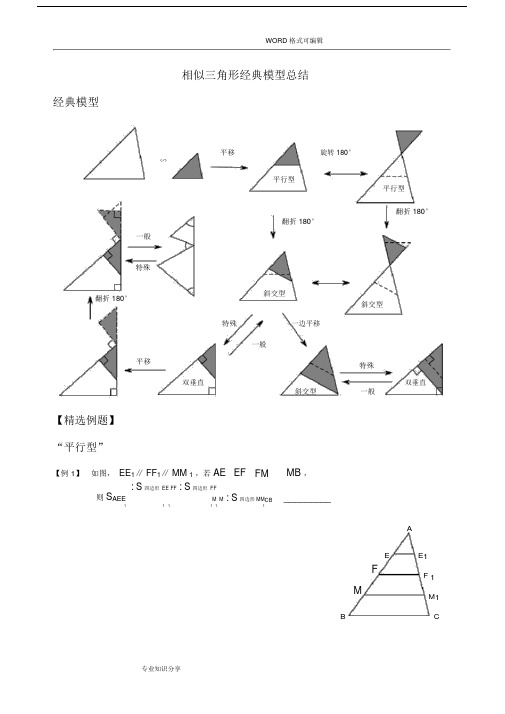
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图，EE1∥FF1∥MM1，若AE EF FM MB ，则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图，AD∥EF∥MN∥BC，若AD 9，BC 18 ， AE:EM :MB 2:3:4,则EF _____ ， MN _____A DE FMNB C【例 3】已知，P为平行四边形ABCD 对角线， AC 上一点，过点P 的直线与 AD ， BC ， CD 的延长线， AB 的延长线分别相交于点 E ， F ， G ， H求证： PE PHPF PGG D CE PFA B H【例 4】已知：在ABC 中， D 为 AB 中点， E 为 AC 上一点，且AE2, BE、 CD相交于点 F ，求BF的值ECEF ADF EB C【例 5】已知：在ABC 中， AD 1AB，延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证：① DE EF ② AE 2CEADEB专业知识分享【例 6】已知：D，E为三角形ABC 中 AB 、BC 边上的点，连接 DE 并延长交 AC 的延长线于点 F ，BD: DE AB: AC求证：CEF 为等腰三角形ACDEB F【例7】如图，已知 AB / / EF / /CD ，若 AB a ， CD b ， EF c ，求证：11 1 .c a bACEB F D【例 8】如图，找出S ABD、 S BED、 S BCD之间的关系，并证明你的结论.CAEB F D【例 9】如图，四边形ABCD中，B D90M是AC上一点，ME AD于点EMF BC，，于点 F 求证：MFME 1AB CDDEMA CFB【例 10】如图，在ABC 中， D 是 AC 边的中点，过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证： AE BF BE CFAEDBC F 【例 11】如图，在线段AB 上，取一点 C ，以 AC ， CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB， AE交 CD于点 P， BD交 CE于点Q,求证： CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中，求作一个正方形DEFG，使 D， E落在 BC边上， F ， G分别落在AC , AB 边上，作法如下：ABC 两边上的正方形D'E'F 'G'如图，第一步：画一个有三个顶点落在第二步：连接 BF ' 并延长交 AC 于点 F第三步：过 F 点作 FE BC ,垂足为点 E第四步：过 F 点作 FG∥BC 交 AB 于点 G第五步：过 G 点作 GD BC ，垂足为点 D四边形 DEFG 即为所求作的正方形问题：⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中，如果BC 6 3，ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理：E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况： B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C ， E'， F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD ， AD ∥BC ，对角线AC 、 BD 互相垂直，则①证明： AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ，以点 O 为旋转中心，逆时针旋转度（090 ），问上面的结论是否成立，请说明理由DAOB C【例 15】（全国初中数学联赛武汉选拔赛试题）如图，四边形ABCD 和 BEFG 均为正方形，求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图，ABC 中， D 在 AB 上，且 DE∥BC 交 AC 于 E ， F 在 AD 上，且 AD2AF AB ，求证：AEF :ACDAFD EB C【例 17】如图，等边三角形ABC中，D，E分别在BC，AB上，且CE BE ，AD ，CE 相交于 M ，求证 : EAM : ECAAEMB DC AGF BE【例 18】如图，四边形ABCD 的对角线相交于点O ，BAC CDB ,求证：DAC CBDADOB C【例 19】如图，设ABBCCA，则 1 2 吗？AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中， AD ， CE 分别为 BC ， AB 边上的高，ABC 和BDE 的面积分别等于 18和 2 ， DE 2，求 AC 边上的高AEB D C【例 21】如图，在等边ABC 的边 BC 上取点 D ，使BD 1，作CH AD，H为垂足，连结BH。

相似三角形常见模型(总结)1

相似三角形第一部分相似三角形模型分析一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）BDE（平行）BDE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行）（不平行）（三）母子型BDD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：ADC 二、相似三角形判定的变化模型旋转型：由A字型旋转得到。

8字型拓展CB EDA共享性GABEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD中，AD∥BC，对角线AC、BD交于点O，BE∥CD交CA延长线于E．求证：OEOAOC⋅=2．例2：已知：如图，△ABC中，点E在中线AD上, ABCDEB∠=∠．求证：（1）DADEDB⋅=2；（2）DACDCE∠=∠．例3：已知：如图，等腰△ABC中，AB＝AC，AD⊥BC于D，CG∥AB，BG分别交AD、AC于E、F．求证：EGEFBE⋅=2．相关练习：1、如图，已知AD为△ABC的角平分线，EF为AD的垂直平分线．求证：FCFBFD⋅=2．A CDEBGMF EHDCBA2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

求证：∠=︒GBM 905．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt △ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC 于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高求证：（1）△ABD ∽△ACE ；（2）△ADE ∽△ABC ；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=62，求：点B 到直线AC 的距离。

模型05 相似三角形中的常见五种基本模型(解析版)

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型例题精讲考点一、A字相似模型【例1】．如图，在△ABC中，∠A＝78°，AB＝4，AC＝6，将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确．D、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误；故选：C．变式训练【变式1-1】．如图，在△ABC中，DE∥BC，AH⊥BC于点H，与DE交于点G．若，则＝．解：∵，∴，∵DE∥BC，∴△ADE∽△ABC，∴，故答案为．【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝__________.解：如图，过C点作CP∥AB，交DE于P，∵PC∥AE，∴△AEM∽△CPM，∴＝，∵M是AC的中点，∴AM＝CM，∴PC＝AE，∵AE＝AB，∴CP＝AB，∴CP＝BE，∵CP∥BE，∴△DCP∽△DBE，∴＝＝，∴BD＝3CD，∴BC＝2CD，即＝2．【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．解：（1）∵AD＝9，BD＝7，AC＝12，∴AB＝AD+BD＝16，∵＝＝，＝＝，∴＝，∵∠BAC＝∠CAD，∴△ACD∽△ABC；（2）由（1）可知，△ACD∽△ABC，∴∠ABE＝∠ACF，∵AE平分∠BAC，∴∠BAE＝∠CAF，∴△ABE∽△ACF，∴＝，即＝，∴AE＝＝．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值解：∵AG∥BD，∴△AFG∽△BFD，∴＝，∵，∴CD＝BD，∴，∵AG∥BD，∴△AEG∽△CED，∴．变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．解：A、∵AB∥CD，∴＝，故本选项不符合题目要求；B、∵AE∥DF，∴△CEG∞△CDH，∴＝，∴＝，∵AB∥CD，∴＝，∴＝，∴＝，∴＝，故本选项不符合题目要求；∵AB∥CD，AE∥DF，∴四边形AEDF是平行四边形，∴AF＝DE，∵AE∥DF，∴，∴＝，故本选项不符合题目要求；D、∵AE∥DF，∴△BFH∞△BAG，∴，故本选项符合题目要求；故选：D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14解：如图，∵四边形ABCD是平行四边形，∵EA∥BC，∴△AEF∽△CBF，∵AE＝DE＝AD，CB＝AD，∴＝＝＝＝，∴AF＝AC，EF＝BF，＝S△ABC，∴S△ABF＝S△ABF＝×S△ABC＝S△ABC，∴S△AEF＝2，∵S△AEF＝6S△AEF＝6×2＝12，故选：C．∴S△ABC【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝1：2．解：如图，∵在△ADC中，∠A＝60°，CD⊥AB于点D，∴∠ACD＝30°，∴＝．又∵在△ABE中，∠A＝60°，BE⊥AC于E，∴∠ABE＝30°，∴＝，∴＝．又∵∠A＝∠A，∴△ADE∽△ACB，∴DE：BC＝AD：AC＝1：2．故答案是：1：2．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．13.5解：∵点D和E分别是边AB和AC的中点，∴O点为△ABC的重心，∴OB＝2OE，＝2S△DOE＝2×1＝2，∴S△BOD＝3，∴S△BDE∵AD＝BD，＝2S△BDE＝6，∴S△ABE∵AE＝CE，＝2S△ABE＝2×6＝12．故选C．∴S△ABC变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，＝1，则S△ABC＝24．若S△EFG解：方法一：∵DE是△ABC的中位线，∴D、E分别为AB、BC的中点，如图过D作DM∥BC交AG于点M，∵DM∥BC，∴∠DMF＝∠EGF，∵点F为DE的中点，∴DF＝EF，在△DMF和△EGF中，，∴△DMF≌△EGF（AAS），＝S△EGF＝1，GF＝FM，DM＝GE，∴S△DMF∵点D为AB的中点，且DM∥BC，∴AM＝MG，∴FM＝AM，＝2S△DMF＝2，∴S△ADM∵DM为△ABG的中位线，∴＝，＝4S△ADM＝4×2＝8，∴S△ABG＝S△ABG﹣S△ADM＝8﹣2＝6，∴S梯形DMGB＝S梯形DMGB＝6，∴S△BDE∵DE是△ABC的中位线，＝4S△BDE＝4×6＝24，∴S△ABC方法二：连接AE，∵DE是△ABC的中位线，∴DE∥AC，DE＝AC，∵F是DE的中点，∴＝，∴＝＝，＝1，∵S△EFG＝16，∴S△ACG∵EF∥AC，∴＝＝，∴＝＝，＝S△ACG＝4，∴S△AEG＝S△ACG﹣S△AEG＝12，∴S△ACE＝2S△ACE＝24，故答案为：24．∴S△ABC【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF ＝2．（1）求EB的长；（2）求FG的长．解：（1）∵EG∥AD，∴△BAD∽△BEF，∴＝，即＝，∴EB＝3．（2）∵EG∥∥BC，∴△AEG∽△ABC，∴＝，即＝，∴EG＝，∴FG＝EG﹣EF＝．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；：S△EBC：S△ECD．（2）求S△ABE（1）证明：∵AB∥CD，∴＝＝，∵，∴＝，∴EF∥CD，∴AB∥EF．（2）解：设△ABE的面积为m．∵AB∥CD，∴△ABE∽△CDE，∴＝（）2＝，＝4m，∴S△CDE∵＝＝，＝2m，∴S△BEC：S△EBC：S△ECD＝m：2m：4m＝1：2：4．∴S△ABE模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．证明：（1）∵△PCD是等边三角形，∴∠PCD＝∠PDC＝∠CPD＝60°，∴∠ACP＝∠PDB＝120°，∵∠APB＝120°，∴∠APC+∠BPD＝60°，∵∠CAP+∠APC＝60°∴∠BPD＝∠CAP，∴△ACP∽△PDB；（2）由（1）得△ACP∽△PDB，∴，∵△PCD是等边三角形，∴PC＝PD＝CD，∴，∴CD2＝AC•BD．变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．解：在△ABP和△ACB中，∠BAP＝∠CAB，∴当∠ABP＝∠C时，满足两组角对应相等，可判断△ABP∽△ACB，故A正确；当∠APB＝∠ABC时，满足两组角对应相等，可判断△ABP∽△ACB，故B正确；当时，满足两边对应成比例且夹角相等，可判断△ABP∽△ACB，故C正确；当时，其夹角不相等，则不能判断△ABP∽△ACB，故D不正确；故选：D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2解：∵∠ABC+∠BDC＝180°，∠ADB+∠BDC＝180°，∴∠ADB＝∠ABC，∵∠A＝∠A，∴△ABC∽△ADB，∴，∵AD＝2，CD＝4，∴，∴AB2＝12，∴AB＝2或﹣2（不合题意，舍去），故选：D．【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则PA+PB的最小值为2．解：设⊙O半径为r，OP＝r＝BC＝2，OB＝r＝2，取OB的中点I，连接PI，∴OI＝IB＝，∵，，∴，∠O是公共角，∴△BOP∽△POI，∴，∴PI＝PB，∴AP+PB＝AP+PI，∴当A、P、I在一条直线上时，AP+PB最小，作IE⊥AB于E，∵∠ABO＝45°，∴IE＝BE＝BI＝1，∴AE＝AB﹣BE＝3，∴AI＝＝，∴AP+PB最小值＝AI＝，∵PA+PB＝（PA+PB），∴PA+PB的最小值是AI＝＝2．故答案是2．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．解：连接OA、OD，∵△ABC与△DEF均为等边三角形，O为BC、EF的中点，∴AO⊥BC，DO⊥EF，∠EDO＝30°，∠BAO＝30°，∴OD：OE＝OA：OB＝：1，∵∠DOE+∠EOA＝∠BOA+∠EOA即∠DOA＝∠EOB，∴△DOA∽△EOB，∴OD：OE＝OA：OB＝AD：BE＝：1＝，故答案为：．变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．证明：（1）∵∠BAC＝∠DAE，∠ABC＝∠ADE．∴△BAC∽△DAE；（2）∵△BAC∽△DAE，∴，∴，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．解：如图，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴＝，∵AC＝，∴BM＝3，在Rt△ABM中，AM＝＝＝，∴AD＝AM＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k的式子表示）解：如图中，∵AE⊥BC，BE＝EC，∴AB＝AC，将△ABD绕点A逆时针旋转得到△ACG，连接DG．则BD＝CG，∵∠BAD＝∠CAG，∴∠BAC＝∠DAG，∵AB＝AC，AD＝AG，∴∠ABC＝∠ACB＝∠ADG＝∠AGD，∴△ABC∽△ADG，∵AD＝kAB，∴DG＝kBC＝4k，∵∠BAE+∠ABC＝90°，∠BAE＝∠ADC，∴∠ADG+∠ADC＝90°，∴∠GDC＝90°，∴CG＝＝．∴BD＝CG＝，故答案为：．实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．解：A、∵EF∥AB，∴＝，∵DE∥BC，∴＝，∴＝，故A正确，B、易知△ADE∽△EFC，∴＝，∴＝，故B正确．C、∵△CEF∽△CAB，∴＝，∴＝，故C正确．D、∵DE∥BC，∴＝，显然DE≠CF，故D错误．故选：D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：解：∵AD∥BC，∴∠ACB＝∠DAC又∵∠B＝∠ACD＝90°，∴△CBA∽△ACD＝＝＝，∵＝（）2＝∴△ABC与△DCA的面积比为4：9．故选：C．3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC ∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC解：∵AH＝8，HG＝5，GD＝4，∴AD＝8+5+4＝17，∵四边形ABCD为菱形，∴BC＝CD＝AD＝17，∵AE∥HC，AD∥BC，∴四边形AECH为平行四边形，∴CE＝AH＝8，∴BE＝BC﹣CE＝17﹣8＝9，∵HC∥GF，∴＝，即＝，解得：DF＝，∴FC＝17﹣＝，∵＞9＞8＞，∴CF长度最长，故选：A．4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP 交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．18解：如图，延长BQ交射线EF于M，∵E、F分别是AB、AC的中点，∴EF∥BC，∴∠M＝∠CBM，∵BQ是∠CBP的平分线，∴∠PBM＝∠CBM，∴∠M＝∠PBM，∴BP＝PM，∴EP+BP＝EP+PM＝EM，∵CQ＝CE，∴EQ＝2CQ，由EF∥BC得，△MEQ∽△BCQ，∴＝2，∴EM＝2BC＝2×6＝12，即EP+BP＝12．故选：C．5．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．解：过D作DE⊥BC于E，则BE＝AD＝2，DE＝2，设B′C＝BC＝x，则DC＝x，∴DC2＝DE2+EC2，即2x2＝28+（x﹣2）2，解得：x＝4（负值舍去），∴BC＝4，AC＝，∵将△ABC绕点C顺时针方向旋转后得△A′B′C，∴∠DB′C＝∠ABC＝90°，B′C＝BC，A′C＝AC，∠A′CA＝∠B′CB，∴∴△A′CA∽△B′CB，∴，即∴AA′＝，故选：A．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝6．解：∵∠A＝∠A，∠ACP＝∠B，∴△ACP∽△ABC，∴AC2＝AP•AB，即AB＝AC2÷AP＝16÷2＝8，∴BP＝AB﹣AP＝6．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD 于点F，如果△AEF的面积是4，那么△BCE的面积是36．解：∵在▱ABCD中，AO＝AC，∵点E是OA的中点，∴AE＝CE，∵AD∥BC，∴△AFE∽△CBE，∴＝＝，＝4，＝（）2＝，∵S△AEF＝36，故答案为36．∴S△BCE8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为8．解：连接BG并延长交AC于H，∵G为ABC的重心，∴＝2，∵DE∥AC，DF∥BC，∴四边形DECF是平行四边形，∴CE＝DF＝4，∵GE∥CH，∴△BEG∽△CBH，∴＝2，∴BE＝8，故答案为：8．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．解：∵将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，∴BD＝AB，BC＝BE，∠ABD＝∠CBE，∠DEB＝∠ACB，∴∠D＝∠BAC＝∠BAD＝（180°﹣∠ABD），∴∠BEC＝（180°﹣∠CBE），∴∠D＝∠BEC，∵∠ABC＝∠DBE＝90°，∴∠DEB+∠BEC＝90°，∴∠AEC＝90°，∵∠AGB＝∠EGC，∴∠ACE＝∠ABE，∵在Rt△ABC中，AB＝3，BC＝4，∴AC＝DE＝5，过B作BH⊥DE于H，则DH＝AH，BD2＝DH•DE，∴DH＝＝，∴AD＝，∴AE＝DE﹣AD＝，∴sin∠ABE＝sin∠ACE＝＝＝，故答案为：．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．解：（1）∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝30°，在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，∴CD＝2，在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，∴BC＝6，∴BD＝BC﹣CD＝4，∵DE∥CA，∴，∴DE＝4；（2）如图，∵点M是线段AD的中点，∴DM＝AM，∵DE∥CA，∴，∴DF＝AG，∵DE∥CA，∴，∴，∵BD＝4，BC＝6，DF＝AG，∴．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC 于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．解：（1）∵四边形ABCD是菱形，∴AD＝CD，∠DAF＝∠DCE，又∵∠ADE＝∠CDF，∴∠ADE﹣∠EDF＝∠CDF﹣∠EDF，∴∠ADF＝∠CDE，在△ADF和△CDE中，，∴△ADF≌△CDE，∴CE＝AF．（2）∵四边形ABCD是菱形，∴AB＝BC，由（1）得：CE＝AF＝2，∴BE＝BF，设BE＝BF＝x，∵＝，AF＝2，∴，解得x＝，∴BE＝BF＝，∵＝，且CE＝AF，∴＝＝，∵∠CMD＝∠AMF，∠DCM＝∠AMF，∴△AMF∽△CMD，∴，∴＝，且∠ACB＝∠ACB∴△ABC∽△MEC∴∠CAB＝∠CME＝∠ACB∴ME＝CE＝212．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝1；②求的值．（1）证明：如图①，∵△ABC∽△ADE，∴∠BAC＝∠DAE，＝，∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，＝，∴∠BAD＝∠CAE，∴△ABD∽△ACE．（2）解：①如图②，∵∠DAE＝90°，∠ADE＝30°，∴DE＝2AE，∴AD＝＝＝AE，∵＝，∴AD＝BD，∴AE＝BD，∴＝1，故答案为：1．②如图②，连接CE，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE，∴△BAC∽△CAE，∴＝，∴＝，∵∠BAD＝∠CAE＝90°﹣∠CAD，∴△BAD∽△CAE，∴∠ABC＝∠ACE，∴∠ADE＝∠ACE，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴＝，由①得AD＝AE，AD＝BD，∴＝＝，∴BD＝CE，∴AD＝×CE＝3CE，∴＝3，∴＝3，∴的值是3．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．（1）证明：如图1，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝90°，∴∠ABD＝∠ADB＝45°，∴∠ABN＝∠MBE＝45°，∠BME＝∠ABD+∠BAM＝45°+∠BAM，∵∠EAF＝45°，∴∠BAN＝∠EAF+∠BAM＝45°+∠BAM，∴∠BAN＝∠BME，∴△ABN∽△MBE．（2）证明：如图1，将△ADN绕点A顺时针旋转90°得到△ABH，连接MH，∴∠BAH＝∠DAN，AH＝AN，HB＝ND，∵∠MAN＝∠EAF＝45°，∴∠MAH＝∠BAH+∠BAM＝∠DAN+∠BAM＝45°，∴∠MAH＝∠MAN，∵AM＝AM，∴△MAH≌△MAN（SAS），∴MH＝MN，∵∠ABH＝∠ADN＝45°，∴∠MBH＝∠ABD+∠ABH＝90°，∴BM2+HB2＝MH2，∴BM2+ND2＝MN2．（3）解：①如图2，将△ADF绕点A顺时针旋转90°得到△ABK，∴AK＝AF，∠BAK＝∠DAF，BK＝DF，∠ABK＝∠ADF＝90°，∴∠ABK+∠ABE＝180°，∴点K、点B、点E在同一条直线上，∵∠EAK＝∠BAE+∠BAK＝∠BAE+∠DAF＝45°，∴∠EAK＝∠EAFM，∵AE＝AE，∴△EAK≌△EAF（SAS），∴EK＝EF，∴BE+DF＝BE+BK＝EK＝EF，∵CB＝CD＝AB＝4，∴CE+EF+CF＝CE+BE+DF+CF＝CB+CD＝4+4＝8，∴△CEF的周长是8．②如图2，∵F是CD的中点，∴CF＝DF＝CD＝2，∵∠C＝90°，∴CF2+EF2＝CE2，∵EF＝BE+DF＝BE+2，CE＝CB﹣BE＝4﹣BE，∴22+（4﹣BE）2＝（BE+2）2，解得BE＝，∴EF＝+2＝，∵∠MBE＝∠MAN＝45°，∠BME＝∠AMN，∴△BME∽△AMN，∴＝，∴＝，∴∠AMB＝∠NME，∴△AMB∽△NME，∴∠NEM＝∠ABM＝45°，∴∠ENF＝∠MAN+∠NEM＝90°，∵G是EF的中点，∴NG＝EF＝×＝，故答案为：．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB ＝4，AC＝2，直接写出AD的长．问题背景证明：∵△ABC∽△ADE，∴，∠BAC＝∠DAE，∴∠BAD＝∠CAE，，∴△ABD∽△ACE；尝试应用解：如图1，连接EC，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，∴△ABC∽△ADE，由（1）知△ABD∽△ACE，∴，∠ACE＝∠ABD＝∠ADE，在Rt△ADE中，∠ADE＝30°，∴，∴＝3．∵∠ADF＝∠ECF，∠AFD＝∠EFC，∴△ADF∽△ECF，∴＝3．拓展创新解：如图2，过点A作AB的垂线，过点D作AD的垂线，两垂线交于点M，连接BM，∵∠BAD＝30°，∴∠DAM＝60°，∴∠AMD＝30°，∴∠AMD＝∠DBC，又∵∠ADM＝∠BDC＝90°，∴△BDC∽△MDA，∴，又∠BDC＝∠MDA，∴∠BDC+∠CDM＝∠ADM+∠CDM，即∠BDM＝∠CDA，∴△BDM∽△CDA，∴，∵AC＝2，∴BM＝2＝6，∴在Rt△ABM中，AM＝＝＝2，∴AD＝．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG ⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．解：（1）①猜想：BG ⊥DE ，BG ＝DE ；故答案为：BG ＝DE ，BG ⊥DE ；②结论成立．理由：如图2中，∵四边形ABCD 和四边形CEFG 是正方形，∴BC ＝DC ，CG ＝CE ，∠BCD ＝∠ECG ＝90°，∴∠BCG ＝∠DCE ，∴△BCG ≌△DCE （SAS ），∴BG ＝DE ，∠CBG ＝∠CDE ，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG ⊥DE ．（2）∵AB ＝a ，BC ＝b ，CE ＝ka ，CG ＝kb ，∴＝＝，又∵∠BCG ＝∠DCE ，∴△BCG ∽△DCE ，∴∠CBG ＝∠CDE ，＝＝，又∵∠CBG +∠BHC ＝90°，∴∠CDE +∠DHG ＝90°，∴BG⊥DE．故答案为：＝，BG⊥DE．（3）连接BE、DG．根据题意，得AB＝4，BC＝3，CE＝2，CG＝1.5，∵BG⊥DE，∠BCD＝∠ECG＝90°∴BE2+DG2＝BO2+OE2+DO2+OG2＝BC2+CD2+CE2+CG2＝9+16+2.25+4＝．。

相似三角形模型专题精品

5
A
E
B
F
D
C
练2. 如图在 ABCD中，E是BC上一点， BE：EC=1：2，AE与BD相交于F，则 BF：FD=_______，S △ADF : S △EBF =______
1:3
1:9
9:1
练3. 如图,在▱ABCD中，AB=4,BC=6,∠ABC, ∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( ) A. 2:3 B. 4:9 C. 1:4 D. 1:9
6. 过∆ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和E，求证：AE：ED=2AF：FB。
C
A
B
F
D
E
G
已知：AB∥CD,连接AD,CB相交于点E.过E点作EF平行于线段AB，与线段AC相交于点F。求：的值。
8字型反8字型（蝴蝶型）相似三角形判定的基本模型二（平行）（不平行）
迁移拓展知识提升
P
（3）当t=2秒时，连接AP、PQ,将∠APQ逆时针旋转，使角的两边与AB、AD、AC分别交于点E、N、F，连接EF.若AN=1,求S△EPF.
注意运用转化的数学思想
迁移拓展知识提升
（4）以OS为一边在∠SOC内作∠SOT,使 ∠SOT = ∠BDC,OT边交BC的延长线于点T, 若BT=4.8,求AK的长。
例：如图，在ABC中，∠C=90°，AC=4，BC=3，PQ∥AB，点P在AC上（与点A、C不重合），点Q在BC上。试问：在AB上是否存在点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长。
P
Q
M3
A
B
C

相似三角形”A“字模型(含详细问题详解)-经典

教师辅导教案授课日期：年月日授课课时：课时ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）． 4．相似三角形周长的比等于相似比． ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++． 5．相似三角形面积的比等于相似比的平方．ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．二、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似． 4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．三、相似证明中的基本模型A 字形图①A 字型，DE//BC ;结论：AD AE DEAB AC BC==，【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（）已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，求证：△ADE∽△DBF．证明：①又∵DF∥AC，②∵DE∥BC，③∴∠A=∠BDF，④∴∠ADE=∠B，∴△ADE∽△DBF．A．③②④① B．②④①③ C．③①④② D．②③④①【解答】证明：②∵DE∥BC，④∴∠ADE=∠B，①又∵DF∥AC，③∴∠A=∠BDF，∴△ADE∽△DBF．故选：B．【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t= 4.8或秒时，△CPQ与△ABC相似．【解答】解：CP和CB是对应边时，△CPQ∽△CBA，所以，，即，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，，即，解得t=．综上所述，当t=4.8或时，△CPQ与△CBA相似．故答案为4.8或．图②反A字型，∠ADE=∠B或∠1=∠B结论：AE AD DE==AC AB BC【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B【解答】解：∵∠DAE=∠CAB，∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；当=即=时，△ABC∽△AED．故选：A．【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．【解答】解：∵∠A=∠A，∠ACP=∠B，∴△ACP∽△ABC；∵，∠A=∠A，∴△ACP与△ABC；故答案为：B；．【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽△ABC．其中D、E分别对应B、C．（填一个条件）．【解答】解：当∠ADE=∠B，∵∠EAD=∠CAB，∴△ADE∽△ABC．故答案为∠ADE=∠B．【练习2】如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．求证：△ADE∽△ACB．【解答】证明：∵AD=5，DB=7，AE=6，EC=4，∴AB=5+7=12，AC=6+4=10，∴====，∴=，又∵∠A=∠A，∴△ADE∽△ACB．【练习3】如图，AB=AC，∠A=36°，BD是∠ABC的角平分线，求证：△ABC∽△BCD．【解答】证明：∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，∵BD是角平分线，∴∠ABD=∠DBC=36°，∴∠A=∠CBD，又∵∠C=∠C，∴△ABC∽△BCD．【练习4】已知：如图，△ABC中，∠ACD=∠B，求证：△ABC∽△ACD．【解答】证明：∵∠ACD=∠B，∠A=∠A，∴△ABC∽△ACD．【练习5】如图，已知AD•AC=AB•AE．求证：△ADE∽△ABC．【解答】证明：∵AD•AC=AE•AB，∴=在△ABC与△ADE 中∵=，∠A=∠A，∴△ABC∽△ADE．【练习6】已知：如图，在△ABC中，D，E分别为AB、AC边上的点，且AD=AE，连接DE．若AC=4，AB=5．求证：△ADE∽△ACB．【解答】证明：∵AC=3，AB=5，AD=，∴，∵∠A=∠A，∴△ADE∽△ACB．图③双A字型【例4】如图，在△ABC中，D，E分别是AB，AC上的点，∠AED=∠ABC，∠BAC 的平分线AF交DE于点G，交BC于点F．（1）试写出图中所有的相似三角形，并说明理由（2）若=，求的值．【解答】解：（1）∵∠AED=∠ABC，∠EAD=∠BAC，∴△ABC∽△AED．∵∠AED=∠ABC，∠EAG=∠BAF，∴△AEG∽△ABF．∵∠EDG=∠ACF，∠DAG=∠CAF，∴△ADG∽△ACF．（2）∵=，∴=，∵△ADG∽△ACF，∴==．【练习1】如图，在△ABC中，D、E分别是AB、AC上的点，AE=4，AB=6，AD：AC=2：3，△ABC的角平分线AF交DE于点G，交BC于点F．（1）请你直接写出图中所有的相似三角形；（2）求AG与GF的比．【解答】解：（1）△ADG∽△ACF，△AGE∽△AFB，△ADE∽△ACB；（2）∵==，=，∴=，又∵∠DAE=∠CAB，∴△ADE∽△ACB，∴∠ADG=∠C，∵AF为角平分线，∴∠DAG=∠FAE∴△ADG ∽△ACF ， ∴==，∴=2．图④内含正方形A 字形，结论AH a aAH BC-=（a 为正方形边长）【例5】如图，△ABC ，是一张锐角三角形的硬纸片，AD 是边BC 上的高，BC=40cm ，AD=30cm ，从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ，使它的一边EF 在BC 上，顶点G 、H 分别在AC ，AB 上，AD 与HG 的交点为M ．（1）求证：=；（2）求这个矩形EFGH 的周长；（3）是否存在一个实数a ，当HE=a 时从三角形硬纸片上剪下的矩形面积最大？若存在，试求出a ；若不存在，请说明理由．【解答】（1）证明：∵四边形HEFG 为矩形， ∴HG ∥EF ，而AD ⊥BC ， ∴AM ⊥BC ，。

相似三角形常见模型[总结]

相似三角形常见模型[总结]相似三角形常见模型相似三角形是初中数学中一个重要的概念，也是解题过程中常见的模型。

通过研究和总结相似三角形的常见模型，可以帮助我们更好地理解和应用这个概念。

本文将从角度相似、边长比例和投影相似三个方面进行内容阐述。

一、角度相似在相似三角形中，角度是最直观的相似特征。

如果两个三角形的对应角相等，那么它们就是相似三角形。

根据这一特性，我们可以应用以下模型：1. AA相似模型当两个三角形中角的对应边分别相等时，这两个三角形相似。

这个模型常用于证明和构造相似三角形。

例如，在已知一个角相等的情况下，可以通过构造等腰三角形来证明相似。

2. AAA相似模型当两个三角形的三个角分别相等时，这两个三角形相似。

这个模型常用于解题中，当我们已知两个三角形的三个角分别相等时，可以得出它们是相似三角形的结论。

二、边长比例在相似三角形中，边长的比例关系也是常见的模型。

如果两个三角形的对应边的比值相等，那么它们是相似三角形。

根据这一特性，我们可以应用以下模型：1. 直角三角形边长模型在一个直角三角形中，由勾股定理可知，两直角边的平方和等于斜边的平方。

如果两个直角三角形斜边的比例相等，那么它们是相似的。

这个模型常用于解决与直角三角形相关的问题。

2. 形状类似三角形边长模型当两个三角形形状相似时，它们的对应边长之比也相等。

例如，当一个等边三角形与一个正三角形形状相似时，它们的对应边长比例为1:2。

这个模型常用于解决与形状类似三角形相关的问题。

三、投影相似在相似三角形中，投影的相似关系也是一种常见的模型。

当两个三角形的两直角边分别成比例时，它们是相似三角形。

根据这一特性，我们可以应用以下模型：1. 倒影相似模型当两个直角三角形的一条直角边与另一个直角三角形的斜边成比例时，它们是相似的。

这个模型常用于解决与倒影相似三角形相关的问题。

2. 旁影相似模型当两个直角三角形的一条直角边与另一个直角三角形的直角边成比例时，它们是相似的。

相似三角形”A“字模型(含详细答案解析)~经典

教师辅导教案授课日期：年月日授课课时：课时ABC △与A B C '''△相似，AD 是ABC △中BAC ∠的角平分线，A D ''是A B C '''△中B A C '''∠的角平分线，则有AB BC AC AD k A B B C A C A D ====''''''''（k 为相似比）． 4．相似三角形周长的比等于相似比． ABC △与A B C '''△相似，则有AB BC ACk A B B C A C ===''''''（k 为相似比）．应用比例的等比性质有AB BC AC AB BC ACk A B B C A C A B B C A C++====''''''''''''++． 5．相似三角形面积的比等于相似比的平方．ABC △与A B C '''△相似，AH 是ABC △中BC 边上的高线，A H ''是A B C '''△中B C ''边上的高线，则有AB BC AC AH k A B B C A C A H ====''''''''（k 为相似比）．进而可得21212ABC A B C BC AHS BC AH k S B C A H B C A H '''⋅⋅==⋅=''''''''⋅⋅△△．二、相似三角形的判定1．平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 2．如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．可简单说成：两角对应相等，两个三角形相似．3．如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似． 4．如果一个三角形的三条边与另一个三角形的你对应成比例，那么这两个三角形相似．可简单地说成：三边对应成比例，两个三角形相似．5．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．6．直角三角形被斜边上的高分成的两个直角三角形相似（常用但要证明）7．如果一个等腰三角形和另一个等腰三角形的顶角相等或一对底角相等，那么这两个等腰三角形相似；如果它们的腰和底对应成比例，那么这两个等腰三角形也相似．三、相似证明中的基本模型A 字形图①A 字型，DE//BC ;结论：AD AE DEAB AC BC==，【例1】李老师在编写下面这个题目的答案时，不小心打乱了解答过程的顺序，你能帮他调整过来吗？证明步骤正确的顺序是（）已知：如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，DF ∥AC ，求证：△ADE∽△DBF．证明：①又∵DF∥AC，②∵DE∥BC，③∴∠A=∠BDF，④∴∠ADE=∠B，∴△ADE∽△DBF．A．③②④① B．②④①③ C．③①④② D．②③④①【解答】证明：②∵DE∥BC，④∴∠ADE=∠B，①又∵DF∥AC，③∴∠A=∠BDF，∴△ADE∽△DBF．故选：B．【练1】如图，在△ABC中，∠ACB=90°，BC=16cm，AC=12cm，点P从点B出发，以2cm/秒的速度向点C移动，同时点Q从点C出发，以1cm/秒的速度向点A移动，设运动时间为t秒，当t=秒时，△CPQ与△ABC相似．【解答】解：CP和CB是对应边时，△CPQ∽△CBA，所以，，即，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，，即，解得t=．时，△CPQ与△CBA相似．．图②反A字型，∠ADE=∠ B或∠1=∠B结论：AE AD DE==AC AB BC【例2】如同，在△ABC中，点D，E分别在边AB，AC上，下列条件中不能判断△ABC∽△AED的是（）A．=B．=C．∠ADE=∠C D．∠AED=∠B【解答】解：∵∠DAE=∠CAB，∴当∠AED=∠B或∠ADE=∠C时，△ABC∽△AED；当=即=时，△ABC∽△AED．故选：A．【例3】如图，P是△ABC的边AB上的一点．（不与A、B重合）当∠ACP=∠ B 时，△APC与△ABC是否相似；当AC、AP、AB满足时，△ACP与△ABC相似．【解答】解：∵∠A=∠A，∠ACP=∠B，∴△ACP∽△ABC；∵，∠A=∠A，∴△ACP与△ABC；故答案为：B；．【练习1】如图，D、E为△ABC的边AC、AB上的点，当∠ADE=∠B 时，△ADE∽△ABC．其中D、E分别对应B、C．（填一个条件）．【解答】解：当∠ADE=∠B，∵∠EAD=∠CAB，相似三角形全章节教案和练习比例线段一，线段的比定义：在同一长度单位下，两条线段的长度的比叫做这两条线段的比。

(完整版)相似三角形模型分析大全(非常全面-经典)

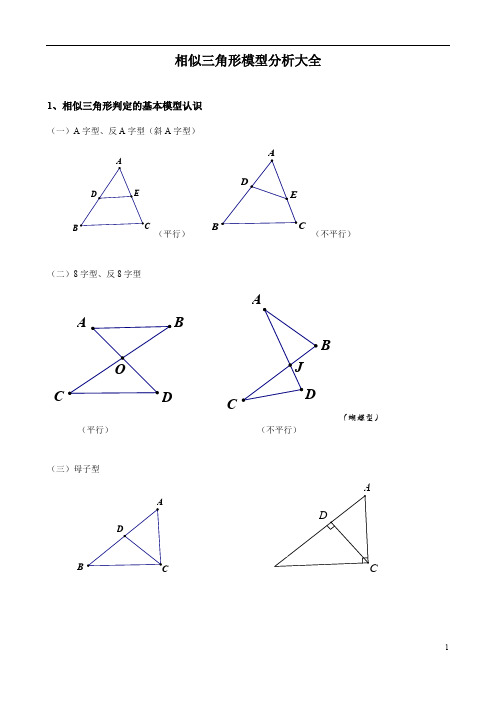
相似三角形模型分析大全1、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）B（平行）B（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（6）双垂型：2、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展B一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：．OE OA OC ⋅=2例2：已知：如图，△ABC 中，点E 在中线AD 上, ．ABC DEB ∠=∠求证：（1）；（2）．DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：．EG EF BE ⋅=2相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：．FC FB FD ⋅=22、已知：AD 是Rt△ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME∽△NMD; (2)ND =NC·NB23、已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，E是AC上一点，CF⊥BE于F。

求证：EB·DF=AE·DB⊥，垂足为F，延长AD到G，使DG=EF，M是AH的中点。

4.在∆ABC中，AB=AC，高AD与BE交于H，EF BCGBM90求证：∠=︒5．（本题满分14分，第（1）小题满分4分，第（2）、（3）小题满分各5分）已知：如图，在Rt△ABC 中，∠C =90°，BC =2，AC =4，P 是斜边AB 上的一个动点，PD ⊥AB ，交边AC于点D （点D 与点A 、C 都不重合），E 是射线DC 上一点，且∠EPD =∠A ．设A 、P 两点的距离为x ，△BEP 的面积为y ．（1）求证：AE =2PE ；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）当△BEP 与△ABC 相似时，求△BEP 的面积．双垂型1、如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高A（第25题图）求证：（1）△ABD∽△ACE；（2）△ADE∽△ABC；(3)BC=2ED2、如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=6，求：点B 到直线AC 的距离。

初中数学相似三角形的8大模型

相似三角形是几何中重要的证明模型之一，是全等三角形的推广。

全等三角形可以被理解为相似比为1的相似三角形。

相似三角形其实是一套定理的集合，它主要描述了相似三角形是几何中两个三角形中，边、角的关系。

0 1 模型1：A字型相似
0 2 模型2:“8”字型相似
0 3 模型3：三平行倒数和模型
0 4 模型4：一线三等角
0 5 模型5：半角形似（两个字母型相似）
0 6 模型6：旋转型相似
0 7 模型7：与圆有关的简单相似
0 8 模型8：阿氏圆
知识需知：
阿波罗尼斯圆:在平面上给定两点A、B，设点P在同一平面上且满足PB/PA= λ ，当 λ ＞ 0 且 λ ≠ 1 时，P点的轨迹就是一个圆，称之为阿波罗尼斯圆（ λ
=1 时P点的轨迹为线段AB是的中垂线）。

相似三角形是几何中重要的模型之一，从历年中考考情来看，相似三角形的应用广泛。

在选择题中，直接应用相似三角形的性质，考察线段或面积比，分值4分，题型简单。

但它其实更多的是作为一种计算工具，在图形的翻折中，利用相似可以更快更简单求解；利用圆中的相似，快速求得线段或角度；在压轴大题二次函数中，利用相似可以简化模型，减少计算量，节约做题时间。

由此可看出相似三角形的重要性。

因此，笔者编写初中常见的八大相似模型，从最简单的“A”字、“8”字相似，到旋转型、半角型相似，从易到难，大家可以有选择性的进行学习。

“喜欢我到什么程度？”绿子问。

“整个世界的老虎全部融化成黄油。

” ——村上春树《挪威的森林》。

相似三角形的九大模型

相似三角形的九大模型相似三角形是几何学中一类重要的图形，它具有一些独特的性质和模型。

这些模型可以用来解决各种实际问题，从简单的长度关系到复杂的空间结构。

本文将介绍相似三角形的九大模型，并给出相应的例子和应用场景。

相似三角形是指两个三角形形状相同，大小成比例。

相似三角形的对应边成比例，对应角相等。

相似三角形还有一些其他的性质，例如，相似三角形的中线、角平分线、高的比等于它们的相似比。

平行线模型：两个三角形分别在两条平行线上，它们的对应边平行且成比例。

这种模型经常用于解决一些与长度和角度相关的问题。

共顶点模型：两个三角形有一个共同的顶点，且它们的对应边成比例。

这种模型常用于证明两个三角形相似，以及求解一些角度问题。

角平分线模型：一个三角形的角平分线将这个三角形分成两个小的相似三角形。

这种模型可以用于证明两个三角形相似，以及求解一些角度问题。

平行四边形模型：一个平行四边形被它的两条对角线分成四个小的相似三角形。

这种模型可以用于解决一些与面积和长度相关的问题。

位似模型：一个相似变换将一个三角形映射到另一个三角形，这种变换称为位似变换。

这种模型可以用于解决一些与长度、角度和面积相关的问题。

旋转模型：一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与角度和长度相关的问题。

镜像模型：一个三角形沿一条直线翻折后得到另一个三角形，这两个三角形是相似的。

这种模型可以用于解决一些与长度和角度相关的问题。

传递模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分相似。

这种模型可以用于解决一些与长度和角度相关的问题。

扩展模型：如果一个三角形与另一个三角形相似，那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。

这种模型可以用于解决一些与长度和角度相关的问题。

相似三角形的九创作者是几何学中一类重要的模型，它们具有广泛的应用价值。

相似三角形模型分析和典型例题讲解大全good

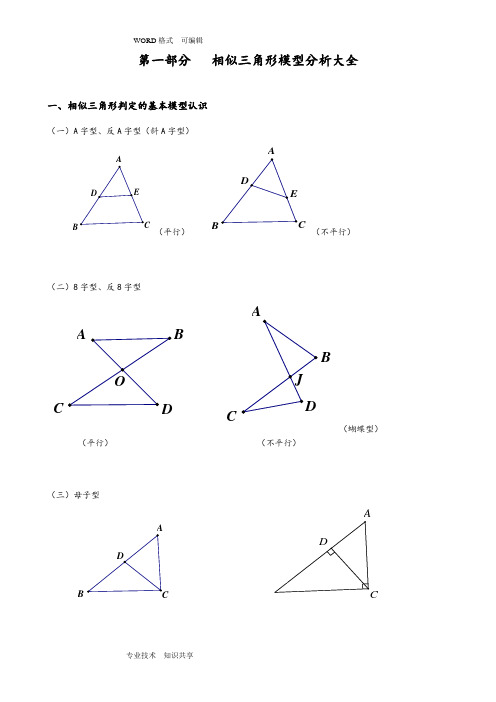
第一部分相似三角形模型分析大全一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CBA DE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行）（不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。

8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ．求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。

求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。

求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。

相似三角形模型分析大全(非常全面-经典)

相似三角形 经典模型总结与例题分类

相似三角形常见模型(总结)

相似三角形模型分析大全(非常全面,经典)

相似三角形模型总结

(完整版)相似三角形经典模型总结及例题分类.doc

相似三角形常见模型(总结)1

模型05 相似三角形中的常见五种基本模型(解析版)

相似三角形模型专题精品

相似三角形”A“字模型(含详细问题详解)-经典

相似三角形常见模型[总结]

相似三角形”A“字模型(含详细答案解析)~经典

(完整版)相似三角形模型分析大全(非常全面-经典)

初中数学 相似三角形的8大模型

相似三角形的九大模型

相似三角形模型分析和典型例题讲解大全good

相似三角形经典模型总结与例题分类

初中数学相似三角形的8大模型