相似三角形经典模型总结与例题分类(超全)
相似三角形经典模型总结.docx
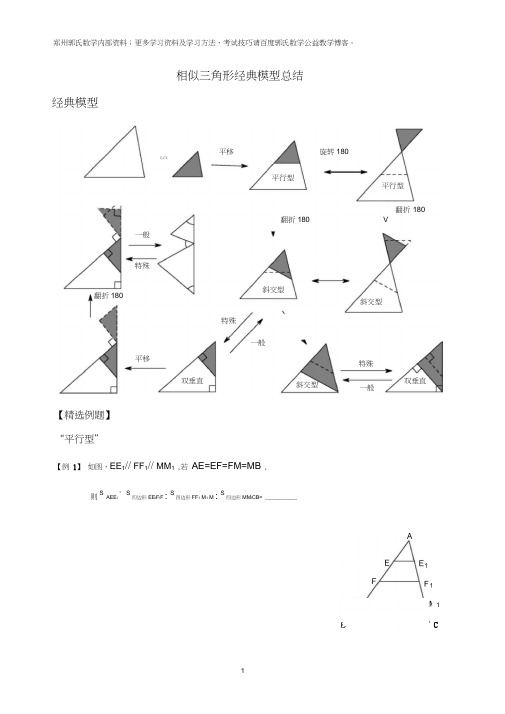
相似三角形经典模型总结经典模型【精选例题】“平行型”【例1】如图,EE1// FF1// MM1,若AE=EF=FM=MB ,则S AEE I : S四边形EE I F l F : S四边形FF1 M1 M : S四边形MM I CB= ___________翻折180°翻折180°V平行型斜交型斜交型平行型斜交型双垂直双垂直特殊平移翻折180°一般平移旋转180°一般一般特殊特殊1C【例 2】 如图,AD// EF MIN BC 若 AD =9 , BC =18 , AE :EM :M^ 2:3: 4,则EF= _____ , MN= ______长线,AB 的延长线分别相交于点 E , F , G , H求证:PE PH PF 一 PG【例4】已知:在 ABC 中,D 为AB 中点,BF求的值EFAEE为AC上一点,且EC =2,BE、CD相交于点AF ,D.FEBC1已知:在 ABC 中,AB=3AD 延长BC 到F ,使CF BC ,连接FD 交AC 于点E 3【例3】 已知,P 为平行四边形 ABCD 对角线,AC 上一点,过点P 的直线与AD , BC , CD 的延【例引 N C求证:①DE=EF②AE =2CE【例6】 已知:D ,E 为三角形 ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,BD: DE =AB: AC求证::CEF 为等腰三角形【例 7】如图,已知 AB //EF //CD ,若 AB = a , CD =b , EF=C ,求证:2 =IICab【例8】 如图,找出S ABD 、S B ED、S B CD之间的关系,并证明你的结论【例9】 如图,四边形ABCD 中,∙ B =∕D =90 ,M 是AC 上一点,ME _ AD 于点E ,MF _ BC 于点F求证:MF ME=1AB CDC【例10】如图,在ABC中,D是AC边的中点,过D作直线EF交AB于E,交BC的延长线于F 求证:AEBF=BECF【例11】如图,在线段AB上,取一点C ,以AC,CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB,AE交CD于点P,BD交CE于点Q,求证:CP =CQ【例12】阅读并解答问题.在给定的锐角三角形ABC中,求作一个正方形DEFG ,使D,E落在BC边上,F , G分别落在AC , AB边上,作法如下:第一步:画一个有三个顶点落在ABC两边上的正方形D'E'F'G'如图,第二步:连接BF'并延长交AC于点F第三步:过F点作FE _ BC ,垂足为点E 第四步:过F点作FG // BC交AB于点G第五步:过G点作GD _ BC ,垂足为点D四边形DEFG即为所求作的正方形问题:⑴证明上述所作的四边形DEFG为正方形⑵在ABC中,如果BC = 6 ∙、、3 , ABC =45 , ∙ BAC = 75 ,求上述正方形DEFG的边长B D' E' D“平行旋转型”图形梳理:特殊情况:B、E'、F'共线C , E', F'共线【例13】已知梯形ABCD , AD // BC ,对角线AC、BD互相垂直,则1.证明:AD2 BC2 = AB2 CD2二AEF旋转到色AE ' F' 己AEF旋转到乙AE 'F'IAEF 旋转到Λ.AE ' F' AAEF旋转到八AE ' F' LAEF旋转至U匕AE ' F' -A AEF旋转至U A AE ' F'^AEF旋转至U匚AE ' F' ^AEF旋转至AE ' F'2.当 AOD ,以点0为旋转中心,逆时针旋转 二度(0 ' 90 ),问上面的结论是否成立,请说明理 由“斜交型”【例15】如图,∙ABC 中,D 在AB 上,且DE // BC 交AC 于E , F 在AD 上,且AD 2=AF AB , 求证:AEFL ACD【例16】如图,四边形 ABCD 的对角线相交于点 0 , ∙ BAC- CDB ,求证:∙ DAC- CBD【例14】(全国初中数学联赛武汉选拔赛试题)如图,四边形AG : DF : CE= ____________ .ABCD 和BEFG 均为正方形,求GFBEDCDB CAB BC CA【例17】如图,设-AB =-B C =CA ,则.仁.2吗?AD DE EA等于18和2,DE =2 ,求AC 边上的高BD 1【例19】如图,在等边 ABC 的边BC 上取点D ,使BD=丄,作CH -AD ,H 为垂足,连结BH 。
相似三角形经典模型总结及例题分类

相似三角形经典模型总结经典模型【精选例题】 “平行型”【例 1】 如图,EEJ / FFJ / MM 1,若 AE=EF=FM=MB ,贝V S.A E ® : S 四边形EE 1F 1F : S 四边形FF 1M 1M : S 四边形MM QB 二翻折180°翻折180°V平行型斜交型斜交型平行型斜交型双垂直双垂直特殊平移翻折180°一般平移旋转180°一般一般特殊特殊C1[例2】如图,AD// EF M/N BC若AD =9 , BC =18 , AE :EM :MB = 2:3: 4,则EF = _____ , MN = ______长线,AB的延长线分别相交于点E,F,G,H求证:PE PH PF 一PG【例3】已知, P为平行四边形ABCD对角线,AC上一点,过点P的直线与AD , BC , CD的延【例4】已知:在ABC中,D为AB中点, 求目匸的值EF E为AC上一点,且Ah2,BE、CD相交于点F ,NCWORD整理版1 1【例引已知:在ABC中,AD AB,延长BC到F,使CF BC ,连接FD交AC于点E2 3AE =2CE求证: ① DE 二EF ②【例6】已知:D , E为三角形ABC中AB、BC边上的点,连接DE并延长交AC的延长线于点F , BD: DE 二AB:AC求证::CEF为等腰三角形【例7】如图,已知AB//EF / /CD,若AB =a,CD = b,EF = c,求证:1 =——cab【例8】如图,找出S.ABD、S BED、S.BCD之间的关系,并证明你的结论【例9】如图,四边形ABCD中,B=/D =90,M是AC上一点,ME _ AD于点E , MF _ BC于占JF 求证: MF ME ,1AB CDC【例10】如图,在ABC中,D是AC边的中点,过D作直线EF交AB于E,交BC的延长线于F 求证:AE BF 二BE CF【例11】如图,在线段AB上,取一点C,以AC,CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB,AE交CD于点P,BD交CE于点Q,求证:CP =CQ【例12】阅读并解答问题.在给定的锐角三角形ABC中,求作一个正方形DEFG,使D,E落在BC边上,F , G分别落在AC , AB边上,作法如下:第一步:画一个有三个顶点落在ABC两边上的正方形D'E'F'G'如图,第二步:连接BF'并延长交AC于点F第三步:过F点作FE _ BC ,垂足为点E 第四步:过F点作FG // BC交AB于点G 第五步:过G点作GD _ BC,垂足为点D 四边形DEFG即为所求作的正方形问题:⑴证明上述所作的四边形DEFG为正方形⑵在ABC中,如果BC =6「3 , ABC =45 , • BAC = 75 ,求上述正方形DEFG的边长B D' E' D E C“平行旋转型”图形梳理:C , E', F'共线【例13】已知梯形ABCD , AD // BC,对角线AC、BD互相垂直,则①证明:AD2 BC2二AB2 CD2色AEF旋转到公AE 一AEF旋转到一AE ' F' AAEF旋转到至AE ''二AEF旋转到二AE 'F' △AEF旋转至U色AE ' F'△AEF旋转至U色AE ' F' △AEF旋转至U色AE ' F'【例14】当 MOD ,以点O 为旋转中心,逆时针旋转 日度(0£日<90),问上面的结论是否成立,请 说明理由D【例15】(全国初中数学联赛武汉选拔赛试题)如图,四边形AG : DF : CE = ___________ .“斜交型”【例16】如图,.:ABC 中,D 在AB 上,且DE // BC 交AC 于E , F 在AD 上,且AD^AF AB , 求证:AEF L ACD【例17】如图,等边三角形 ABC 中,D , E 分别在BC , AB 上,且CE 二BE , AD , CE 相交于M , 求证:EAM L ECAABCD 和BEFG 均为正方形,求GFBEDCD【例18】如图,四边形 ABCD 的对角线相交于点 O , . BAC — CDB ,求证:.DAC = . CBDAB BC CA【例佃】如图,设伴二CA ,则.仁.2吗?AD DE EA等于18和2,DE =2,求AC 边上的高BD 1【例21】如图,在等边 ABC 的边BC 上取点D ,使 ,作CH _AD ,H 为垂足,连结BH 。
(完整版)相似三角形模型分析大全(精).doc

(完整版)相似三角形模型分析大全(精).doc第一部分相似三角形知识要点大全知识点 1. .相似图形的含义把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读:(1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.(2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.(3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.例1.放大镜中的正方形与原正方形具有怎样的关系呢?分析:要注意镜中的正方形与原正方形的形状没有改变.解:是相似图形。
因为它们的形状相同,大小不一定相同.例2.下列各组图形:①两个平行四边形;②两个圆;③两个矩形;④有一个内角80°的两个等腰三角形;⑤两个正五边形;⑥有一个内角是100°的两个等腰三角形,其中一定是相似图形的是_________( 填序号 ) .解析:根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,而平行四边形、矩形、等腰三角形都属于形状不唯一的图形,而圆、正多边形、顶角为100°的等腰三角形的形状不唯一,它们都相似.答案:②⑤⑥.知识点 2.比例线段对于四条线段 a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a c(或a:b=c:d )那么这四条线段叫做成比例线段,简称比例线段.bd解读:( 1)四条线段 a,b,c,d成比例,记作a c(或 a:b=c:d ),不能写成其他形式,即比例线段b d有顺序性.( 2)在比例式a c(或 a:b=c:d )中,比例的项为 a,b,c,d,其中 a,d 为比例外项, b,c 为比例内项, dbd是第四比例项.( 3)如果比例内项是相同的线段,即a bb或 a:b=b:c ,那么线段 b 叫做线段和的比例中项。
c(4) 通常四条线段a,b,c,d 的单位应一致,但有时为了计算方便,a 和b 统一为一个单位,c 和d 统一为另一个单位也可以,因为整体表示两个比相等.例 3.已知线段 a=2cm, b=6mm, 求 a. b分析:求a即求与长度的比,与的单位不同,先统一单位,再求比.b例 4.已知 a,b,c,d成比例,且 a=6cm,b=3dm,d= 3dm ,求 c 的长度.2分析:由 a,b,c,d成比例,写出比例式a:b=c:d ,再把所给各线段a,b,,d统一单位后代入求c .知识点 3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读:(1)正确理解相似多边形的定义,明确“对应”关系.(2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.例 5.若四边形 ABCD 的四边长分别是 4, 6,8, 10,与四边形 ABCD 相似的四边形 A 1B 1C 1D 1 的最大边长为 30,则四边形 A 1B 1C 1D 1 的最小边长是多少?分析:四边形 ABCD 与四边形 A 1B 1C 1D 1 相似,且它们的相似比为对应的最大边长的比,即为1,再根据相似3多边形对应边成比例的性质,利用方程思想求出最小边的长.知识点 4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读:( 1)相似三角形是相似多边形中的一种;(2)应结合相似多边形的性质来理解相似三角形;(3)相似三角形应满足形状一样,但大小可以不同;( 4)相似用“∽”表示,读作“相似于” ;( 5)相似三角形的对应边之比叫做相似比.注意:①相似比是有顺序的,比如△ABC ∽△ A 1B 1C 1,相似比为 k, 若△ A 1B 1C 1∽△ABC ,则相似比为1。
(完整版)相似三角形经典模型总结及例题分类.doc
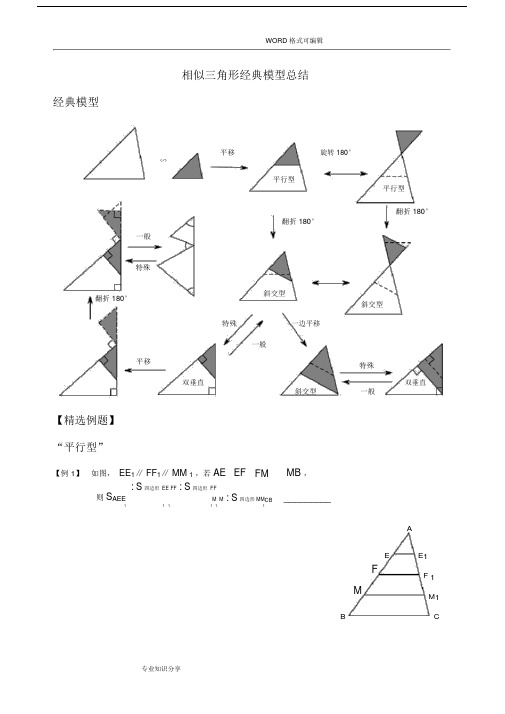
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB ,则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____A DE FMNB C【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H求证: PE PHPF PGG D CE PFA B H【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且AE2, BE、 CD相交于点 F ,求BF的值ECEF ADF EB C【例 5】已知:在ABC 中, AD 1AB,延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证:① DE EF ② AE 2CEADEB专业知识分享【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC求证:CEF 为等腰三角形ACDEB F【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:11 1 .c a bACEB F D【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论.CAEB F D【例 9】如图,四边形ABCD中,B D90M是AC上一点,ME AD于点EMF BC,,于点 F 求证:MFME 1AB CDDEMA CFB【例 10】如图,在ABC 中, D 是 AC 边的中点,过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证: AE BF BE CFAEDBC F 【例 11】如图,在线段AB 上,取一点 C ,以 AC , CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB, AE交 CD于点 P, BD交 CE于点Q,求证: CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中,求作一个正方形DEFG,使 D, E落在 BC边上, F , G分别落在AC , AB 边上,作法如下:ABC 两边上的正方形D'E'F 'G'如图,第一步:画一个有三个顶点落在第二步:连接 BF ' 并延长交 AC 于点 F第三步:过 F 点作 FE BC ,垂足为点 E第四步:过 F 点作 FG∥BC 交 AB 于点 G第五步:过 G 点作 GD BC ,垂足为点 D四边形 DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中,如果BC 6 3,ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理:E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况: B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C , E', F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD , AD ∥BC ,对角线AC 、 BD 互相垂直,则①证明: AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ,以点 O 为旋转中心,逆时针旋转度(090 ),问上面的结论是否成立,请说明理由DAOB C【例 15】(全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和 BEFG 均为正方形,求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图,ABC 中, D 在 AB 上,且 DE∥BC 交 AC 于 E , F 在 AD 上,且 AD2AF AB ,求证:AEF :ACDAFD EB C【例 17】如图,等边三角形ABC中,D,E分别在BC,AB上,且CE BE ,AD ,CE 相交于 M ,求证 : EAM : ECAAEMB DC AGF BE【例 18】如图,四边形ABCD 的对角线相交于点O ,BAC CDB ,求证:DAC CBDADOB C【例 19】如图,设ABBCCA,则 1 2 吗?AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中, AD , CE 分别为 BC , AB 边上的高,ABC 和BDE 的面积分别等于 18和 2 , DE 2,求 AC 边上的高AEB D C【例 21】如图,在等边ABC 的边 BC 上取点 D ,使BD 1,作CH AD,H为垂足,连结BH。
(完整版)相似三角形基本知识点+经典例题(完美打印版)

相似三角形知识点与经典题型知识点1 有关相似形的概念(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形.(2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多 边形.相似多边形对应边长度的比叫做相似比(相似系数).知识点2 比例线段的相关概念(1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:ad c b=.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项, a 、c 叫比例前项,b 、d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
(3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB.即AC BC AB AC ==简记为:12长短==全长注:黄金三角形:顶角是360的等腰三角形。
黄金矩形:宽与长的比等于黄金数的矩形知识点3 比例的性质(注意性质立的条件:分母不能为0)(1) 基本性质:①bc ad d c b a =⇔=::;②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb db a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项 (3)反比性质(把比的前项、后项交换): a c b d b da c=⇔=.(4)合、分比性质:a c abcd b d b d±±=⇔=.注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间发生同样和差变化比例仍成立.如:⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc dc b a b a c cd a a b d c b a 等等.(5)等比性质:如果)0(≠++++====n f d b nm f e d c b a ΛΛ,那么b an f d b m e c a =++++++++ΛΛ.注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . 知识点4 比例线段的有关定理1.三角形中平行线分线段成比例定理:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.由DE ∥BC 可得:ACAEAB AD EA EC AD BD EC AE DB AD ===或或注:①重要结论:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边......与原三角形三边......对应成比例.②三角形中平行线分线段成比例定理的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边.此定理给出了一种证明两直线平行方法,即:利用比例式证平行线.③平行线的应用:在证明有关比例线段时,辅助线往往做平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.2.平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例. 已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等.注:平行线分线段成比例定理的推论:平行线等分线段定理:两条直线被三条平行线所截,如果在其中一条上截得的线段相等,那么在另一条上截得的线段也相等。
中考中相似三角形的常见模型及典型例题

B
C
(2)对应边比: AD AE DE AC AB BC
例 1 如图,梯形ABCD中,AD//BC,对角线AC、BD交于点O,BE//CD
交CA延长线于E.求证:OC2 OA OE
E
AD//BC BE//CD
A
D
.O
B
AO OD OC OB OC OD OE OB
C
AO OC OC OE
(1)内角平分线定理: AB BD AC CD
(2)证明:作平行线构造A字型相似
E A
△BAD∽△BEC
B
DC
【模型3】角平分线型
【三角形两边之比等于其夹角的外角平分线外分对边之比】
(1)外角平分线定理: AB BD AC CD
F A E
(2)证明:作平行线构造A字型相似
B
C
D
例 6 阅读与计算,请阅读以下材料,并完成相应的问题:
【二级形态】三垂直模型→K型相似
E
F
△BED∽△CDF
E
F
BD C
BD
C
【模型5】一线三等角相似
【二级形态】三垂直模型→K型相似
△BED∽△CDF
E E
PE
R
BD
F
F
F
M
C
C
BD
C
Q BD
T
☆基本结论1: △BED∽△CDF,将图中相似三角形进行平移仍相似 ☆基本结论2: 矩形内两垂直线段之比等于矩形边长之比:DE PQ ☆基本结论3: 特别地,当矩形PQTR为正方形时,DE=MFM. F QT
(3)求线段的比;
(4)证明线段的等积式。
【模型1】“A”字型&“8”字型
(完整版)相似三角形模型分析大全(精).doc

第一部分相似三角形知识要点大全知识点 1. .相似图形的含义把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读 :( 1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.( 2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.( 3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.例 1.放大镜中的正方形与原正方形具有怎样的关系呢?分析:要注意镜中的正方形与原正方形的形状没有改变. 解:是相似图形。
因为它们的形状相同,大小不一定相同.例 2.下列各组图形:①两个平行四边形;②两个圆;③两个矩形;④有一个内角 80°的两个等腰三角形;⑤两个正五边形;⑥有一个内角是 100°的两个等腰三角形,其中一定是相似图形的是_________( 填序号 ) .解析:根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,而平行四边形、矩形、等腰三角形都属于形状不唯一的图形, 而圆、正多边形、 顶角为 100°的等腰三角形的形状不唯一, 它们都相似. 答案:②⑤⑥.知识点 2.比例线段对于四条线段 a,b,c,d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a c(或a:b=c:d )那么这四条线段叫做成比例线段,简称比例线段.bd解读 :( 1)四条线段 a,b,c,d成比例,记作a c(或 a:b=c:d ),不能写成其他形式,即比例线段b d有顺序性.( 2)在比例式a c(或 a:b=c:d )中,比例的项为 a,b,c,d,其中 a,d 为比例外项, b,c 为比例内项, dbd是第四比例项.( 3)如果比例内项是相同的线段,即a bb或 a:b=b:c ,那么线段 b 叫做线段和的比例中项。
c(4) 通常四条线段 a,b,c,d 的单位应一致,但有时为了计算方便, a 和 b 统一为一个单位,c 和d 统一为另一个单位也可以,因为整体表示两个比相等.例 3.已知线段 a=2cm, b=6mm, 求 a. b分析:求a即求与长度的比,与的单位不同,先统一单位,再求比.b例 4.已知 a,b,c,d成比例,且 a=6cm,b=3dm,d= 3dm ,求 c 的长度.2分析:由 a,b,c,d成比例,写出比例式a:b=c:d ,再把所给各线段a,b,,d统一单位后代入求c .知识点 3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读 :( 1)正确理解相似多边形的定义,明确“对应”关系. ( 2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.例 5.若四边形 ABCD 的四边长分别是 4, 6,8, 10,与四边形 ABCD 相似的四边形 A 1B 1C 1D 1 的最大边长为 30,则四边形 A 1B 1C 1D 1 的最小边长是多少?分析:四边形 ABCD 与四边形 A 1B 1C 1D 1 相似,且它们的相似比为对应的最大边长的比,即为1,再根据相似3多边形对应边成比例的性质,利用方程思想求出最小边的长. 知识点 4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读 :( 1)相似三角形是相似多边形中的一种;( 2)应结合相似多边形的性质来理解相似三角形; ( 3)相似三角形应满足形状一样,但大小可以不同; ( 4)相似用“∽”表示,读作“相似于” ;( 5)相似三角形的对应边之比叫做相似比.注意 :①相似比是有顺序的,比如△ABC ∽△ A 1B 1C 1,相似比为 k, 若△ A 1B 1C 1∽△ABC ,则相似比为1。
相似三角形常见模型(总结)1

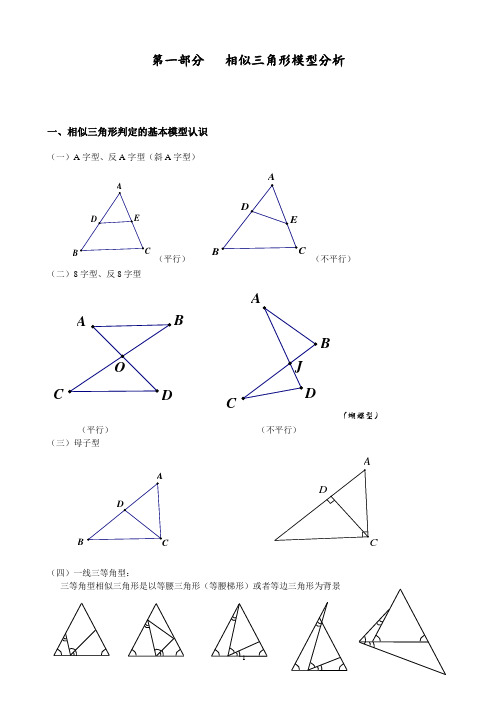
相似三角形第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)BDE(平行)BDE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行) (三)母子型BDD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:ADC 二、相似三角形判定的变化模型旋转型:由A字型旋转得到。
8字型拓展CB EDA共享性GABEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.求证:OEOAOC⋅=2.例2:已知:如图,△ABC中,点E在中线AD上, ABCDEB∠=∠.求证:(1)DADEDB⋅=2;(2)DACDCE∠=∠.例3:已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:EGEFBE⋅=2.相关练习:1、如图,已知AD为△ABC的角平分线,EF为AD的垂直平分线.求证:FCFBFD⋅=2.A CDEBGMF EHDCBA2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
求证:∠=︒GBM 905.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt △ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域; (3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高 求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=62,求:点B 到直线AC 的距离。
相似三角形经典模型总结和例题分类
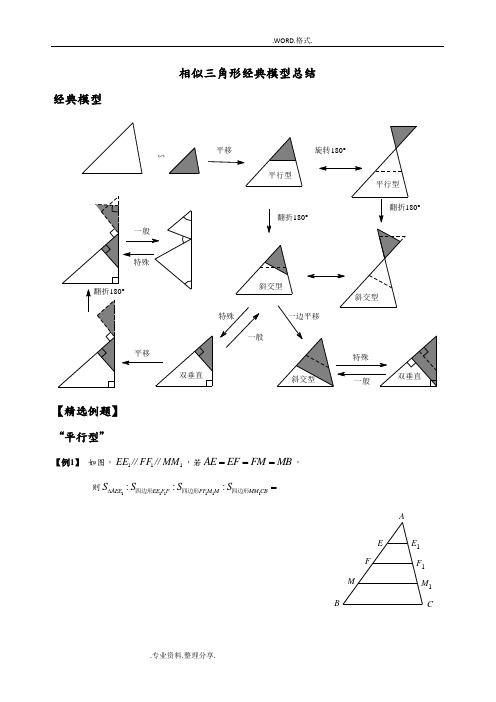
相似三角形经典模型总结经典模型【精选例题】 “平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形M 1F 1E 1M E F A BC【例2】 如图,A D E F M N B C ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =M N A BCD E F【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG=PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC=,BE 、CD 相交于点F ,求BFEF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE =ABCDFEFE DCBA【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC =求证:CEF ∆为等腰三角形FEDCBA【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= ABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长G'F'E'D'ABCDEFG“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’F'CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEFACD ∆∆F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆M E DC B A【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDE【例21】 如图,在等边ABC ∆的边BC 上取点D ,使21=CD BD ,作C H A D ⊥,H 为垂足,连结BH 。
最新相似三角形-经典模型总结与例题分类

相似三角形经典模型总结经典模型【精选例题】 “平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形M 1F 1E 1M E F A BC【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =M N A BCD E F【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG=PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC=,BE 、CD 相交于点F ,求BFEF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE =ABCDFEFE DCBA【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC =求证:CEF ∆为等腰三角形FEDCBA【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= ABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长G'F'E'D'ABCDEFG“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEF ACD ∆∆:F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆:M E D C B A【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDE【例21】 如图,在等边ABC ∆的边BC 上取点D ,使21=CD BD ,作CH AD ⊥,H 为垂足,连结BH 。
相似三角形典型模型及例题

:相似三角形判定的基本模型(一)A字型、反A字型(斜A字型)(平行)(不平行)(二)8字型、反8字型(蝴蝶型)(不平行)(三)母子型(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:(五)一线三直角型:三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
(六)双垂型:二:相似三角形判定的变化模型8字型拓展旋转型:由A字型旋转得到一线三等角的变形一线三直角的变形2:相似三角形典型例题(1)母子型相似三角形例1:如图,梯形ABCDh AD// BC对角线AC BD交于点O, BE// CD交CA延长线于E.求证:OC2=OA OE .例2:已知:如图,△ ABC中,点E在中线AD上, . DEB =/ABC .求证:(1) DB2二DE DA ;(2) . DCE 二DAC .例 3:已知:如图,等腰△ ABC中, AB= AC ADL BC于D, CG/ AB BG分别交AD AC于E、F. 求证:BE2=EF EG .1、如图,已知AD^^ ABC的角平分线,EF为AD的垂直平分线.求证:FD2二FB FC .2、已知:AD是Rt△ ABC中/A的平分线,/ C=90 , EF是AD的垂直平分线交 AD于 M EF、BC的延长线交于一点No 求证:⑴△ AM0A NMD; (2)ND 2=NC- NB3、已知:如图,在△ ABC中,/ ACB=90 , CDL AB于 D, E是 AC上一点,CF丄 BE于 F。
相似三角形模型分析大全(精)

第一部分相似三角形知识要点大全知识点1..相似图形的含义把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读:(1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.(2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.(3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.例1.放大镜中的正方形与原正方形具有怎样的关系呢?分析:要注意镜中的正方形与原正方形的形状没有改变.解:是相似图形。
因为它们的形状相同,大小不一定相同.例2.下列各组图形:①两个平行四边形;②两个圆;③两个矩形;④有一个内角80°的两个等腰三角形;⑤两个正五边形;⑥有一个内角是100°的两个等腰三角形,其中一定是相似图形的是_________(填序号).解析:根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,而平行四边形、矩形、等腰三角形都属于形状不唯一的图形,而圆、正多边形、顶角为100°的等腰三角形的形状不唯一,它们都相似.答案:②⑤⑥.知识点2.比例线段对于四条线段a,b,c,d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即a cb d=(或a:b=c:d)那么这四条线段叫做成比例线段,简称比例线段.解读:(1)四条线段a,b,c,d成比例,记作a cb d=(或a:b=c:d),不能写成其他形式,即比例线段有顺序性.(2)在比例式a cb d=(或a:b=c:d)中,比例的项为a,b,c,d,其中a,d为比例外项,b,c为比例内项,d是第四比例项.(3)如果比例内项是相同的线段,即a bb c=或a:b=b:c,那么线段b叫做线段和的比例中项。
(4)通常四条线段a,b,c,d的单位应一致,但有时为了计算方便,a和b统一为一个单位,c和d统一为另一个单位也可以,因为整体表示两个比相等.例3.已知线段a=2cm, b=6mm, 求ab.分析:求ab即求与长度的比,与的单位不同,先统一单位,再求比.例4.已知a,b,c,d成比例,且a=6cm,b=3dm,d=32dm,求c的长度.分析:由a,b,c,d成比例,写出比例式a:b=c:d,再把所给各线段a,b,,d统一单位后代入求c.知识点3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读:(1)正确理解相似多边形的定义,明确“对应”关系.(2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.例5.若四边形ABCD的四边长分别是4,6,8,10,与四边形ABCD相似的四边形A1B1C1D1的最大边长为30,则四边形A1B1C1D1的最小边长是多少?分析:四边形ABCD与四边形A1B1C1D1相似,且它们的相似比为对应的最大边长的比,即为13,再根据相似多边形对应边成比例的性质,利用方程思想求出最小边的长. 知识点4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读:(1)相似三角形是相似多边形中的一种; (2)应结合相似多边形的性质来理解相似三角形; (3)相似三角形应满足形状一样,但大小可以不同; (4)相似用“∽”表示,读作“相似于”; (5)相似三角形的对应边之比叫做相似比.注意:①相似比是有顺序的,比如△ABC ∽△A 1B 1C 1,相似比为k,若△A 1B 1C 1∽△ABC ,则相似比为1k。
(完整版)相似三角形模型分析大全(非常全面-经典)
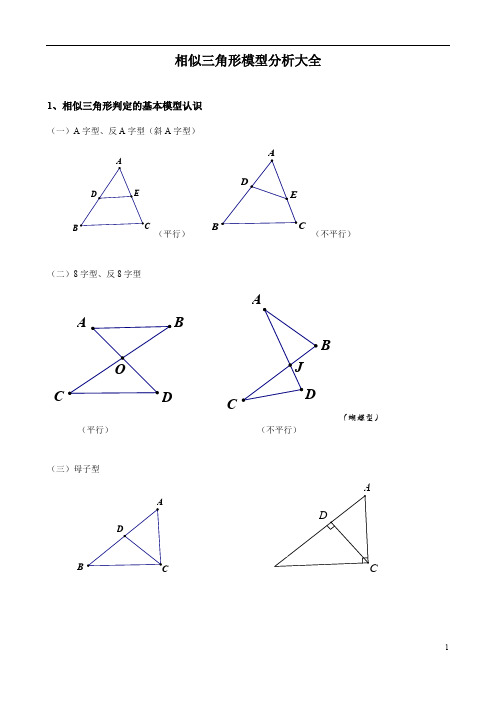
相似三角形模型分析大全1、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)B(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(6)双垂型:2、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展B一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:.OE OA OC ⋅=2例2:已知:如图,△ABC 中,点E 在中线AD 上, .ABC DEB ∠=∠求证:(1); (2).DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:.EG EF BE ⋅=2相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:.FC FB FD ⋅=22、已知:AD 是Rt△ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME∽△NMD; (2)ND =NC·NB23、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EB·DF=AE·DB⊥,垂足为F,延长AD到G,使DG=EF,M是AH的中点。
4.在∆ABC中,AB=AC,高AD与BE交于H,EF BCGBM90求证:∠=︒5.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域;(3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高A(第25题图)求证:(1)△ABD∽△ACE;(2)△ADE∽△ABC;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=6,求:点B 到直线AC 的距离。
相似三角形常见模型( 总结 )
第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)ABCDE(平行)CBA DE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行) (三)母子型ABCDCAD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:CAD二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC D E B2、已知:AD是Rt△ABC中∠A的平分线,∠C=90°,EF是AD的垂直平分线交AD于M,EF、BC的延长线交于一点N。
求证:(1)△AME∽△NMD; (2)ND2=NC·NB3、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EB·DF=AE·DB4.在∆ABC中,AB=AC,高AD与BE交于H,EF BC⊥,垂足为F,延长AD到G,使DG=EF,M是AH的中点。
求证:∠=︒GBM905.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,P是斜边AB上的一个动点,PD⊥AB,交边AC 于点D(点D与点A、C都不重合),E是射线DC上一点,且∠EPD=∠A.设A、P两点的距离为x,△BEP的面积为y.(1)求证:AE=2PE;(2)求y关于x的函数解析式,并写出它的定义域;(3)当△BEP与△ABC相似时,求△BEP的面积.A CBPD E(第25题图)GMFEHDCBAEDCAB双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高 求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=62,求:点B 到直线AC 的距离。
相似三角形模型大全

相似三角形模型大全第一部分相似三角形模型分析大全相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)B(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:双垂型:D相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:OE OA OC ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高 求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;共享型相似三角形1、△ABC是等边三角形,D、B、C、E在一条直线上,∠DAE=120 ,已知BD=1,CE=3,,求等边三角形的边长.D例:如图,等边△ABC 中,边长为6,D 是BC 上动点,∠EDF=60° (1)求证:△BDE ∽△CFD(2)当BD=1,FC=3时,求BE练习:1、如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠. (1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域; (3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.CAD B EFABCDE例、已知矩形ABCD 中,CD=2,AD=3,点P 是AD 上的一个动点,且和点A,D 不重合,过点P 作CP PE ⊥,交边AB 于点E,设y AE x PD ==,,求y 关于x 的函数关系式,并写出x 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形经典模型总结经典模型【精选例题】“平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG= M 1F 1E 1M E FA BCM N A BCD E F PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC =,BE 、CD 相交于点F , 求BF EF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E求证:①DE EF = ②2AE CE =【例6】 已知:D ,E 为三角形ABC 中AB 、BC边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC = 求证:CEF ∆为等腰三角形【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+. FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= FE DCB AABCDFEFEDCBAABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则G'F'E'D'AB CDEFG①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEFACD ∆∆F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDEM E DC B A【例21】如图,在等边ABC∆的边BC上取点D,使21=CDBD,作CH AD⊥,H为垂足,连结BH。
求证:DBH DAB∠=∠【例22】已知:在正三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD CE=,直线CD 与AE相交于点F求证:①DC AE=,②2AD DC DF=⋅AB CDEF“斜交特殊型”(隐含三垂直)【例23】已知,如图,ABC∆中,AD BC⊥于点D,DE AC⊥于点E,DF AB⊥于点F,求证:AEF B∠=∠AB CDEF【例24】已知:如图,CE是直角三角形斜边AB上的高,在EC的延长线上任取一点P,连结AP,BG ⊥AP,垂足为G,交CE于D,求证:DEPECE⋅=2。
GPABCDE【例25】 如图,E 、G 、F 、H 分别是矩形ABCD 四条边上的点,EF GH ⊥,若2AB =,3BC =,则:EF GH 等于( )A. 2:3B. 3:2C. 4:9D.无法确定ABCD E FG H【例26】 如图,已知:正方形ABCD 中,点M 、N 分别在AB 、BC 上,且BM BN =,BP MC⊥于点P求证:DP NP ⊥PAB CDMN【例27】 如图,Rt ABC ∆中,90BAC ∠=︒,2AB AC ==,点D 在BC 上运动(不经过B ,C ),过点D 作45ADE ∠=︒,DE 交AC 于E①图中有无与ABD ∆一定相似的三角形,若有,请指出来并加以证明②设BD x =,AE y =,求y 与x 的函数关系,并写出其定义域; ③若ADE ∆恰为等腰三角形,求AE 的长EDCBA相似三角形的判定与性质综合运用经典题型考点一:相似三角形的判定与性质:例1、如图,△PCD是等边三角形,A、C、D、B在同一直线上,且∠APB=120°.求证:⑴△PAC∽△BPD;⑵ CD2 =AC·BD.例2、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC 上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE;(2)设BD=x,AE=y,求y关于x函数关系式及自变量x值范围,并求出当x为何值时AE取得最小值?(3)在AC上是否存在点E,使得△ADE为等腰三角形?若存在,求AE的长;若不存在,请说明理由?例3、如图所示,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B:1)求证:△ADF∽△DEC;2)若AB=4,33AD,AE=3,求AF的长。
考点二:射影定理:例4、如图,在RtΔABC中,∠ACB=90°,CD⊥AB于D,CD=4cm,AD=8cm,求AC、BC及BD的长。
例5、如图,已知正方形ABCD,E是AB的中点,F是AD上的一点,且AF=14AD,EG⊥CF于点G,(1)求证:△AEF∽△BCE;(2)试说明:EG2=CG·FG.例6、已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连结AF和CE.(1)求证:四边形AFCE是菱形;(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.AB CDFAB CDEFG考点三:相似之共线线段的比例问题:例7、已知如图,P 为平行四边形ABCD 的对角线AC 上一点,过P 的直线与AD 、BC 、CD 的延长线、AB 的延长线分别相交于点E 、F 、G 、H.求证:PGPH PF PE例8、如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于点E ,交BA 的延长线于点F .(1)求证:PC 2=PE •PF ;(2)若菱形边长为8,PE=2,EF=6,求FB 的长.例9、如图,CD 是Rt △ABC 斜边上的高,E 为AC 的中点,ED 交CB 的延长线于F .求证:BD •CF=CD •DF .例10、如图:已知在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD=CE ,直线CD 与AE相交于点F.(1)求证:DC=AE;(2)求证:AD2=DC•DF.例11、如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.(1)找出与△ABH相似的三角形,并证明;(2)若E是BC中点,BC=2AB,AB=2,求EM的长.例12、如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证:(1)AE=CG;(2)AN•DN=CN•MN.例13、如图,在Rt△ABC中,CD是斜边AB上的高,点M在CD上,DH⊥BM且与AC的延长线交于点E.求证:(1)△AED∽△CBM;(2)AE•CM=AC•CD.例14、如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.(1)求证:FD2=FB•FC;(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.例15、如图,四边形ABCD、CDEF、EFGH都是正方形.(1)⊿ACF与⊿ACG相似吗?说说你的理由.(2)求∠1+∠2的度数.考点四:相似三角形的实际应用:例16、如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.(1)若这个矩形是正方形,那么边长是多少?(2)若这个矩形的长PQ是宽PN的2倍,则边长是多少?例17、已知左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。
