高考模拟卷二(答案)

合集下载

2024年高考地理第二次模拟考试卷及答案解析(江西卷)

2024年高考地理第二次模拟考试卷及答案解析（江西卷）第Ⅰ卷一、选择题：本题共16小题，每小题3分，共48分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

自20世纪80年代起，江苏南部的沈巷村因周边工业区的扩展而逐渐变为城中村，居民开始出租空闲房间和摆摊经营。

随着富裕村民陆续外迁，租户则成为照看房屋与商铺的“二房东”。

下图示意20世纪80年代至今，沈巷村布局与经营组织自发演变的三个阶段。

完成1-3题。

1．从阶段Ⅰ到阶段Ⅰ，沈巷村出租屋空间变化的主要驱动力是（）A．交通线路增多B．外来人口流入C．老旧民房改造D．生态村居建设2．与阶段Ⅰ相比，阶段Ⅰ流动摊贩与商铺数量的变化说明经营者考虑更多的是（）A．提高交易价格B．降低经营成本C．方便组织经营D．方便村居管理3．从20世纪80年代至今，沈巷村民居经营组织方式的自发演变有利于（）Ⅰ实现村居成员协同共建Ⅰ完善当地基础设施建设Ⅰ形成经济利益共享模式Ⅰ带动地方特色产业发展A．ⅠⅠB．ⅠⅠC．ⅠⅠD．ⅠⅠ【答案】1．B 2．C 3．B【解析】1．由图可知，从阶段Ⅰ到阶段Ⅰ，村民出租的空闲房间和摆摊点位增多，整个沈巷村出租屋空间变化主要是因为周边工业区的发展，由于工业活动增多，外来人口流入增多，对空闲房间的需求增多，B正确。

从阶段Ⅰ到阶段Ⅰ，交通线路变化不大，A错误。

并无材料表示该村进行了老旧民房改造，且老居民房改造并不是出租屋空间变化的主要原因，C错误。

并无材料表示该村进行了生态乡村建设，且生态乡村建设对出租屋空间变化影响小，D错误。

综上所述，故选B。

2．据图可知，阶段Ⅰ流动摊贩数量减少，商铺数量增加，经营者提高交易价格不利于商品的竞争，A错误；经营者需要缴纳商铺的租金，经营成本提高，B错误；商铺利于组织经营，提高经营者的运营效率和竞争力,实现持续发展和创造利润，C正确；方便村居管理不是经营者主要考虑的因素，D错误。

故选C。

3．结合材料可知，80年代至今沈巷村民居经营组织方式的自发演变有利于实现村居成员协同共建，有利于形成经济利益共享模式，ⅠⅠ正确；当地基础设施建设与政府规划调整有关，与沈巷村民居经营组织方式的自发演变无关，Ⅰ错误；沈巷村民居经营组织方式的自发演变无法带动地方特色产业发展，Ⅰ错误。

广西2024年高考语文模拟试卷及答案2

广西2024年高考语文模拟试卷及答案35分）现代文阅读I材料一：虚与实，既是一个哲学宇宙观问题，又是一种艺术实践的尺度。

宋人范晞文在《对床夜语》中说：“不以虚为虚，而以实为虚，化景物为情思，从首至尾，自然如行云流水，此其难也。

”以虚为虚，就会陷入纯粹的虚无主义；以实为实，就会机械僵化，全无生气；唯有化实为虚，才能产生无穷的意味。

虚实相生是中国古代诗歌创作的重要艺术手段，这种“诗笔”移植到唐传奇的写作中，首要的贡献就是创造了众多个性鲜明、栩栩如生的人物形象。

唐传奇在塑造人物时，通常是截取人物的几个重要生活片段，而把另外一些内容、事件省略，留下大量空白，让读者通过想象自己去填充。

化实为虚，由虚入实。

如沈既济《任氏传》描写任氏，仅有“容色姝丽”四字正面叙写任氏之美，并无具体的描摹刻画，但其美貌却如在目前，原因就在于作者全从侧面烘托，从虚处着笔，写郑六一见钟情、不能自己，“见之惊悦，策其驴，忽先之，忽后之，将挑而未敢”。

更为精彩的是，韦崟派遣家僮秘密察看之后两人的一段对话，先问之“容若何”，家僮答之“奇怪也！天下未尝见之矣”。

简单的一问一答，任氏的绝美之姿已经跃然纸上。

接着又不厌其烦地拿出其他佳丽进行对比，特别是吴王之第六女，“秾艳如神仙，中表素推第一”，但即便如此美貌，与任氏比起来，仍“非其伦也”。

所有这些铺叙，没有一处正面描摹，全从虚处落笔，由虚入实，这正是诗歌意象创造中的虚实相生之法。

再比如裴铏的《昆仑奴》，虽然磨勒是小说的主人公，但是读者读完全篇，对其所知仍然甚少，他究竟从哪里来，如何具有这样超常的本领，最后又怎样生活等等，这些问题小说中都没有交代，但人物的形象却因此而具有了巨大的张力，那些空白点召唤着读者的参与，每一个读者都可以用自己的审美经验来填补这些空白，而正是阅读接受过程中审美意象的再生成，赋予了小说更深沉的审美意蕴。

像《柳毅传》《莺莺传》《无双传》《虬髯客传》等作品，在人物形象的塑造上，也都充分运用了虚实相生之法，使人物形象生动饱满，具有强大的艺术感染力。

2024届浙江高考信息技术模拟卷(二)+答案解析

浙江省普通高等学校招生信息技术考试模拟卷（二）一、选择题1.下列有关数据、信息和知识的说法不正确的是（）A．信息是用来消除随机不确定性的东西B．牛顿的名言“站在巨人的肩膀上”说明知识是可以继承和传递的C．“结绳记事”方法中那些大小不一、数量不同的绳结是信息D．当人们用 3.14乘以半径的平方来计算圆的面积时，这就是知识2.在网络订票系统中，顾客平板电脑的作用是（）A．对售票机信息进行管理B．对前置机信息进行管理C．对订票系统进行用户信息管理D．数据加工、计算3.“智慧校园”项目让师生的学习与生活更加方便和智能，以下不属于人工智能在“智慧校园”中应用的是（）A．进入校园时，测温终端快速对进入人员进行体温检测和口罩佩戴侦测B．就餐时，同学们通过面部识别，“刷脸”消费C．感应到手靠近时，洗手台水龙头自动出水D．下课了，老师说：“小沃，小沃，关机！”智慧黑板便自动关机4.2019年1月，全国首个“互联网医院”APP在浙江省上线。

该系统利用互联网技术，打破了传统医疗模式的地域限制和时间限制，为患者提供包括在线医生问诊、远程影像诊断、线上药品购买等多项医疗服务。

为保护该系统的数据安全，下列行为恰当的是（）A．关闭服务器自动更新功能B．传播未经授权的医疗数据C．定期备份系统服务器数据D．为所有用户分配相同的权限5.下列关于网络说法不正确的是（）A．网络是由数据通信系统以及网络软件和网络协议三部分组成B．移动通信的实质是利用无线电波来传递信息C．网络互联设备，主要包括调制解调器、路由器和交换机等D．网络资源共享指网络中的软件、硬件、数据资源的共享6.2012年我国研制出首款国产商用8核处理器“龙芯3B”，主频达到1GHz。

1GHz等于（）A．1000MB B．1024MB C．1024MHz D．1000MHz7.某四位二进制数1■01，其中有一位模糊不清，则可能与此二进制数等值的十进制数是（）A．15或2B．2或3C．26或18D．9或138.有树结构的示意图如图所示，下列关于该树的描述正确的是（）A．该树的度为6B．该树的叶子节点数量是7C．节点I、J互为兄弟节点D．该树的深度为59.存在栈st，其元素入栈顺序为a，b，c，d，e，f，已知最后出栈的元素依次为c，f，则其出栈顺序不可能为（）A．a，b，d，e，c，f B．b，a，e，d，c，f C．b，e，a，d，c，f D．a，b，e，d，c，f有程序段如下：s=[0]*10;a=[6,3,2,4,2,1,5]n=len(a);top=0;s[top]=a[0]for i in range(1,n):while top!=-1and a[i]%2==s[top]%2:top-=1top+=1s[top]=a[i]while top!=-1:print(s[top],end='')top-=1程序运行后，输出结果是（）A．2426B．513C．1236D．523610.算法部分流程图如图所示。

_语文丨2023届高考模拟调研卷(二)语文试卷及答案

绝密★启用前2023年普通高等学校招生全国统一考试模拟试题语文（二）本试卷共8页，23小题，满分150分。

考试用时150分钟。

注意事项：1.答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名、准考证号、考场号和座位号填写在答题纸上。

将条形码横贴在答题纸“贴条形码区”。

2.作答选择题时，选出每小题答案后，用2B铅笔在答题纸上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题纸各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.考生必须保持答题纸的整洁。

考试结束后，将试卷和答题纸一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，17分）阅读下面的文字，完成1～5题。

材料一：日前，四川广汉三星堆遗址考古传来捷报，在以往丰硕的发掘成果的基础上，此次祭祀区发掘1834平方米，新发现的6座坑出土编号文物近13000件，其中相对完整的文物3155件。

大量新出土文物以无可辩驳的事实澄清了以往古代巴蜀研究的一些迷失，进一步勾勒了中华先民早年突破地理疆域限制，在多民族交流融合中开拓前行的壮阔历史画卷。

相对于中原广袤平原，巴蜀偏于一隅，向来以山高水远著称。

过去学术界流行的看法是，诸如四川这样的巴蜀地区，文化多半是封闭的，与中原文化没有什么实质联系。

如顾颉刚的《古代巴蜀与中原的关系说及其批判》认为：“当时的蜀国本和中原没有什么关系，直到春秋战国间才同秦国起了交涉……不幸历代人士为秦汉的大一统思想所陶冶，认为古代也是一模一样的，终不肯说这一块土地上的文化在古代独立发展，偏要设法把它和中原的历史混同搅和起来，于是处处勉强拍合，成为一大堆乱丝。

”三星堆大规模考古发现证明，自新石器时代晚期，至少是晚期之末起。

巴蜀地区与中原间就打破隔绝，开始往来交流，有时还是比较畅通的频繁交流。

2024年高考物理第二次模拟考试卷及答案解析(江西、广西、黑龙江、吉林卷)

2024年高考物理第二次模拟考试卷及答案解析（江西、广西、黑龙江、吉林卷）一、选择题：本题共10小题，共46分。

在每小题给出的四个选项中，第1~7题只有一项符合题目要求，每小题4分，第8~10题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

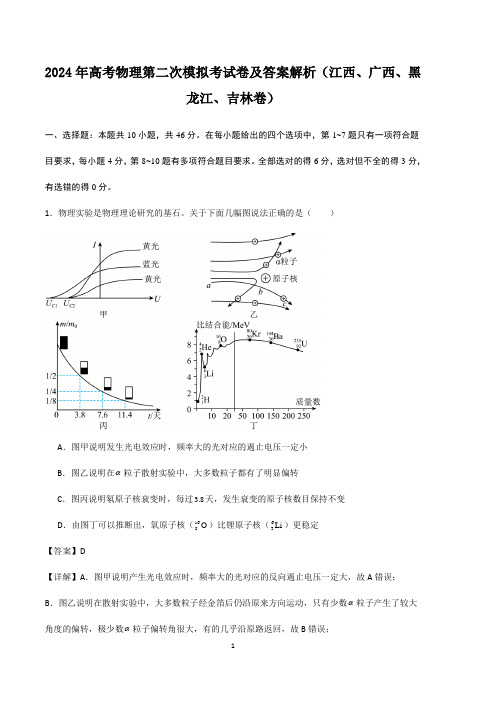
1．物理实验是物理理论研究的基石。

关于下面几幅图说法正确的是（）A．图甲说明发生光电效应时，频率大的光对应的遏止电压一定小B．图乙说明在α粒子散射实验中，大多数粒子都有了明显偏转C．图丙说明氡原子核衰变时，每过3.8天，发生衰变的原子核数目保持不变D．由图丁可以推断出，氧原子核（168O）比锂原子核（63Li）更稳定【答案】D【详解】A．图甲说明产生光电效应时，频率大的光对应的反向遏止电压一定大，故A错误；B．图乙说明在散射实验中，大多数粒子经金箔后仍沿原来方向运动，只有少数α粒子产生了较大角度的偏转，极少数α粒子偏转角很大，有的几乎沿原路返回，故B错误；C ．图丙说明氡原子核衰变时的规律是，每过3.8天，原子核发生衰变的数量下降一半，原子核发生衰变的概率不变，故C 错误；D ．由图丁可知，质量数中等的原子核比结合能最大，原子核越稳定，图中氧的原子核（188O ）是比锂的原子核（43Li ）更接近中等质量数的原子核，所以氧的原子核（188O ）比锂的原子核（43Li ）更稳定，故D 正确。

故选D 。

2．一台空调外机用两个三脚架固定在外墙上，如图所示，空调外机的重心在支架水平横梁AO 和斜梁BO 连接点O 的正上方，横梁对O 点的作用力沿OA 方向、大小为1F ，斜梁对O 点的作用力沿BO 方向、大小为2F ，如果把斜梁加长一点，仍保持OA 水平且连接点O 的位置不变，则（）A ．1F 不变B ．1F 增大C ．2FD ．减小2F 不变【答案】C【详解】设斜梁OB 与竖直方向夹角为θ，则1tan F mg θ=2cos mgF θ=如果把斜梁加长一点，仍保持OA 水平，则θ减小，则F 1减小，F 2减小。

天津市2024年高考语文模拟试卷及答案2

天津市2024年高考语文模拟试卷及答案阅读下面一段文字，完成下面小题。

“青白黄赤黑，东西中南北；五色的经纬，织出山与水。

”2023央视兔年春晚，《满庭芳·国色》以曲为韵、以舞为语，织就出一场华美的视觉盛宴。

“满庭芳”是词牌名，清徐筑《词苑丛谈》认为，该词牌取自唐柳宗元“满庭芳草积”的诗句，后代诸多文人都曾依此词牌写下（）的诗句，苏轼在《满庭芳·蜗角虚名》中云：“江南好，千钟美酒，一曲满庭芳”；李清照在《满庭芳·小阁藏春》中写下：“难言处，良宵淡月，疏影尚风流”。

《满庭芳·国色》分寻色、舞色、唱色三个段落，五种民族乐器与五种颜色、五位顶尖舞者相互对应、配合，将人间绝色吟之以曲，绘之以舞。

桃红迎水袖、凝脂搭折扇、细叶载油伞、群青合翎子、沉香配宝剑……婀娜轻盈而又刚健有力的舞姿，动而不惊、静而不郁，表明了刚柔并济的中国艺术辩证法，凸显着生生不息的大国气象。

节目将四十多种中国颜色的名称作为歌词配以国风旋律，让世界认识了那些充满独特东方审美情趣的中国色彩——苍烟落照、香炉紫烟、东方既白、藕丝秋半。

世间至艳不过五彩，人间至美不过国色。

这些色彩（）了千年的审美和智慧，如沧海遗珠，在历经岁月的洗礼之后变得更加（）。

国色出圈，文化破壁。

中华传统文化是无尽的宝藏，如何将传统文化和当代技术完美结合，让青灯古卷重焕光彩，则成为历史留给我们的课题。

1．依次填入选文括号内的词语，最恰当的一项是（）A．脍炙人口凝结熠熠生辉B．名噪一时凝聚熠熠生辉C．脍炙人口凝结琳琅满目D．名噪一时凝聚琳琅满目2．选文中画横线的句子有语病，修改最恰当的一项是（）A．婀娜轻盈而又刚健有力的舞姿，动而不惊、静而不郁，表明了刚柔并济的中国艺术辩证法，诠释着生生不息的大国气象。

B．刚健有力而又婀娜轻盈的舞姿，动而不惊、静而不郁，体现了刚柔并济的中国艺术辩证法，彰显着生生不息的大国气象。

C．刚健有力而又婀娜轻盈的舞姿，动而不惊、静而不郁，表明了刚柔并济的中国艺术辩证法，彰显着生生不息的大国气象。

2024年全国高考仿真模拟卷二语文

模拟卷二：一、现代文阅读（共9分，每小题3分）（一）阅读下面的文字，完成1-3题。

《庄子》在春秋战国时期的特殊地位及其成因是多方面的。

首先，儒、墨、道三家思想相互融合，相互影响，为《庄子》的创作提供了良好的社会环境。

其次，《庄子》作者所处的时代，百家争鸣，思想活跃，为其提供了丰富的素材和灵感。

此外，《庄子》的创作还受到当时文化背景的影响，如儒家经典的影响、楚辞的熏陶等。

1. 下列对《庄子》在春秋战国时期特殊地位的表述，不正确的一项是（）A. 《庄子》的创作受到了当时文化背景的影响。

B. 《庄子》的创作受到了当时社会环境的影响。

C. 《庄子》的创作受到了儒家经典的影响。

D. 《庄子》的创作受到了百家争鸣的影响。

2. 下列对原文的理解和分析，不正确的一项是（）A. 儒、墨、道三家思想相互融合，相互影响，为《庄子》的创作提供了良好的社会环境。

B. 《庄子》作者所处的时代，思想活跃，为其提供了丰富的素材和灵感。

C. 儒家经典对《庄子》的创作产生了重要影响。

D. 楚辞的熏陶对《庄子》的创作起到了决定性的作用。

3. 根据原文信息，下列推断正确的一项是（）A. 《庄子》作为经典著作的地位会一直延续到当今社会。

B. 当时的社会环境影响了《庄子》作者的创作思想。

C. 只要社会环境稳定，就不会有百家争鸣的现象出现。

D. 思想文化的交流与融合对后世的文化发展具有积极作用。

二、古代诗文阅读（共36分）（二）阅读下面的文言文，完成4-7题。

魏武侯时，吴起为西河守，以法家之治使秦人不敢东乡。

而公叔痤任痤以国事而相魏，未任而卒。

公叔痤病且死，谓魏惠王曰：“……夫吴起，布衣也，贤贤君王之用不贤者也。

举而委国，必有单(一义不可测)患害周章之变矣。

又况非魏氏之徙者乎?魏氏子孙必有构患于王之腹中者矣。

”其人用矣其言中矣然惠王不用其言遂举兵而加吴起于是公叔痤病甚强生告吴起曰若诸侯亡者必起之忧矣也。

起遂辞疾而去魏惠王恨焉及惠王薨，秦休蜀兵五万守蒲津须要烧取上林之木武侯亦以朝过如旧令人骂公叔曰诸侯受寡人之恩自斗不已复增五万给半归了言起则阴告门下曰昔吴起出敝兵绝阵也魏武侯忿之欲斩之而行欲舍之又疑之乃大置酒延群臣而谋曰吴起今者教秦攻魏寡人甚爱起可杀不可留何也群臣莫敢应者武侯曰公叔常言此谋者吾今用之矣公叔曰君之谋过矣夫君人者示之以利而观其心若德我以示之以害则必趋害而就利吴起非贪于魏者也君以利见之则往矣今君弃其主而从其利则臣不识也武侯曰善吾则以公叔之计行矣遂杀吴起及公叔辞曰臣之于君也尽节而已矣虽得罪也不恨也武侯大悦曰噫吾之得公叔也犹飞鸿得树焉。

2025年高考(新高考)模拟试卷英语试题(二)(含听力音频和答案)

2025届仿真模拟★第02套2025年普通高等学校招生全国统一考试英语注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

英语听力高三模拟第2025-02套.mp4第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。

1．Where does the conversation probably take place?A. In a supermarket.B. In the post office.C. In the street. 2．What did Carl do?A. He designed a medal.B. He fixed a TV set.C. He took a test.3．What does the man do?A. He’s a tailor.B. He’s a waiter.C. He’s a shop assistant. 4．When will the flight arrive?A. At 18:20.B. At 18:35.C. At 18:50.5．How can the man improve his article?A. By deleting unnecessary words.B. By adding a couple of points.C. By correcting grammar mistakes.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

高考模拟卷(二)备战2024年高考地理阶段性模拟仿真冲刺卷(山东专用)试题含答案解析

备战2024年高考地理阶段性模拟仿真冲刺卷（山东专用）高考模拟卷（二）（本卷共19小题，满分100分，考试用时90分钟）第I卷（选择题）一、单项选择题:本题共15小题,每小题3分,共45分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

近年来屋顶光伏发电发展迅速，但在具体安装中，工程要考虑屋顶坡度、前后排光伏板的距离、建筑物遮挡及自然地理环境等多个影响因素。

下图示意辽宁省西部某处厂房房屋的屋顶光伏板安装结构，完成下面小题。

1．该地光伏板的最低点距离屋面的高度（H）不宜过高或过低，主要考虑的自然因素是（）A．最大降水量B．最大积雪深度C．最大太阳高度角D．最大风速2．为保证最佳发电效果，若图示屋面倾角α变小，则安装倾角θ和光伏板间的距离L应（）A．θ不变，L变大B．θ变小，L变大C．θ不变，L变小D．θ变小，L变小在空气中水汽含量不变，保持气压一定的情况下，空气因冷却而达到饱和时的温度，称为露点温度。

其数值越大，反映空气中水汽含量越大。

一般情况下，温度相同时湿空气要比干空气密度小。

两个温度相近的干、湿气团相遇所形成的锋，称为干线。

下图为我国河套平原及其附近地区6月某日14时主要气象要素分布形势示意图。

完成下面小题。

3．与乙、丙气团相比，甲气团的物理性质是（）A．暖湿B．冷湿C．暖干D．冷干4．最易出现扬沙天气的地点是（）A．甲B．乙C．丙D．丁疏勒河从祁连山流出，形成昌马洪积-冲积扇，河流则潜行至冲积扇边缘出露（古称冥水），之后西行。

党河则是疏勒河的最大支流。

月牙泉原为党河的一部分，是河流改道后留下的一部分河湾。

月牙泉水深仅五米，是一处天然淡水湖泊。

读图，完成下面小题5．冥水（）A．在土层薄的冲积扇边缘流出成河B．落差大，河流的汇水速度快C．夏季蒸发旺盛，形成季节性断流D．是地下溶洞中流动的地下水6．党河（）A．春季流量最大，冬季流量最小B．流量季节变化小，泥沙多C．为内流河，主要是冰雪融水补给D．干流基本为西北流向东南7．月牙泉是淡水湖的主要原因是其（）A．周边沙土中的含盐率很低B．有地下径流进出，可平衡盐分C．没有径流注入和带入盐分D．常受党河洪水侵袭，带走盐分冬克玛底河是长江上游通天河的二级支流，流域内的河谷为平坦开阔的稀疏草地，地表植被矮，多在5～10cm，根系深度主要集中于0～40cm。

2023年全国新高考仿真模拟卷(二)数学试题(含答案解析)

2023年全国新高考仿真模拟卷（二）数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合{}2|log 1A x x =<，{}2|20B x x x =--<，则B A =ð（）A ．（﹣∞，2）B ．（﹣1，0]C ．（﹣1，2）D ．（﹣1，0）2．已知复数11i z =+，22i z a =+，若12z z ⋅为纯虚数，则实数a 的值为（）A ．1-B ．1C ．2-D ．23．函数()f x 为R 上的奇函数，当0x >时，()lg f x x x =-，则()100f -=（）A ．98B ．98-C ．90D ．90-4．小陈和小李是某公司的两名员工，在每个工作日小陈和小李加班的概率分别为13和14，且两人同时加班的概率为16，则某个工作日，在小李加班的条件下，小陈也加班的概率为（）A ．112B ．12C ．23D ．345．若22cos 1sin 26παα⎛⎫-=+ ⎪⎝⎭，则tan 2α的值为（）A ．B C ．2D ．2+6．如图所示，在ABC 中，2B A =，点D 在线段AB 上，且满足23AD BD =，ACD BCD ∠=∠，则cos A 等于（）A ．23B ．34C ．35D ．457．已知等比数列{}n a 的前n 项和为n S ，若1220a a +=，398S =，且2n a S a ≤≤+，则实数a 的取值范围是（）A ．1,02⎡⎤-⎢⎥⎣⎦B ．13,24⎡⎤-⎢⎥⎣⎦C ．33,42⎡⎤⎢⎥⎣⎦D ．30,2⎡⎤⎢⎥⎣⎦8．已知x ∈R ，符号[]x 表示不超过x 的最大整数，若函数()[]()0x f x a x x=-≠有且仅有2个零点，则实数a 的取值范围是（）A ．23,34⎛⎤ ⎥⎝⎦B ．3,22⎡⎫⎪⎢⎣⎭C ．2,23⎛⎫ ⎪⎝⎭D ．233,2342⎛⎤⎡⎫ ⎪⎢⎝⎦⎣⎭二、多选题9．体育王老师记录了16名小学生某周课外体育运动的时长（单位：h ），记录如下表．运动时长456789运动人数122452则这16名小学生该周课外体育运动时长的（）A ．众数为8B ．中位数为6.5C ．平均数为7D ．标准差为210．已知,αβ是空间两个不同的平面，,m n 是空间两条不同的直线，则给出的下列说法中正确的是（）A ．//m α，//n β，且//m n ，则//αβB ．//m α，//n β，且m n ⊥，则αβ⊥C ．m α⊥，n β⊥，且//m n ，则//αβD ．m α⊥，n β⊥，且m n ⊥，则αβ⊥11．设1F ，2F 分别为椭圆221259x y+=的左、右焦点，P 为椭圆上第一象限内任意一点，1PF k ，2PF k 表示直线1PF ，2PF 的斜率，则下列说法正确的是（）A ．存在点P ，使得17PF =成立B ．存在点P ，使得1290F PF ∠=︒成立C ．存在点P ，使得217PF PF k k =成立D ．存在点P ，使得127PF PF ⋅=成立12．设函数()sin 2sin cos xf x x x=+，则（）A ．()f x 的一个周期为πB ．()f x 在ππ,44⎛⎫- ⎪⎝⎭上单调递增C ．()f x 在π3π,44⎛⎫- ⎪⎝⎭D ．()f x 图象的一条对称轴为直线π4x =三、填空题13．在平行四边形OACB 中，E 是AC 的中点，F 是BC 边上的点，且3BC BF =，若OC mOE nOF =+，其中m ，n ∈R ，则m n +的值为______．14．请写出与曲线()sin f x x =在()0,0处具有相同切线的另一个函数：______．15．Rt ABC △中，其边长分别为3，4，5，分别以它的边所在直线为旋转轴，旋转一周所形成的几何体的体积之和为______．16．已知1F ，2F 分别为双曲线22221x ya b-=（0a >，0b >）的左、右焦点，P 为双曲线右支上任意一点，若212PF PF 的最小值为2c，c ，则该双曲线的离心率是______．四、解答题17．设数列{}n a 的首项为1，前n 项和为n S ，且对*n ∀∈N ，kn n a S b n c +=⋅+恒成立，其中b ，k ，c 均为常数．(1)当0b =时，求数列{}n a 的通项公式；(2)当1k =时，若数列{}n a 为等差数列，求b ，c 的值．18．已知ABC 的内角,,A B C 的对边分别为,,a b c ，B 为钝角．若ABC 的面积为S ，且()2224bS a b c a =+-．(1)证明：2B A π=+；(2)求sin sin A C +的最大值．19．某校团委针对“学生性别和喜欢课外阅读”是否有关做了一次不记名调查，其中被调查的全体学生中，女生人数占总人数的13．调查结果显示，男生中有16的人喜欢课外阅读，女生中有23的人喜欢课外阅读．(1)以频率视为概率，若从该校全体学生中随机抽取2名男生和2名女生，求其中恰有2人喜欢课外阅读的概率；(2)若有95%的把握认为喜欢课外阅读和性别有关，求被调查的男生至少有多少人？附：()20P k χ≥0.0500.0100k 3.8416.635()()()()()22n ad bc a b c d a c b d χ-=++++，n a b c d =+++．20．如图，在多面体ABCDE 中，已知ABC ，ACD ，BCE 均为等边三角形，平面ACD ⊥平面ABC ，平面BCE ⊥平面ABC ，H 为AB 的中点．(1)判断DE 与平面ABC 的位置关系，并加以证明；(2)求直线DH 与平面ACE 所成角的正弦值．21．已知点M 是抛物线()2:20C x py p =>的对称轴与准线的交点，过M 作抛物线的一条切线，切点为P ，且满足2PM =．(1)求抛物线C 的方程；(2)过()1,1A -作斜率为2的直线与抛物线C 相交于点B ，点()0,T t ()0t >，直线AT 与BT 分别交抛物线C 于点E ，F ，设直线EF 的斜率为k ，是否存在常数λ，使得t k λ=？若存在，求出λ值；若不存在，请说明理由．22．已知函数()()22ln xf x x a a x=--∈R ．(1)求函数()f x 的极值；(2)当11a <时，若函数()f x 有两个零点()1212,x x x x >．①证明：12ln ln x x -<②证明：1201x x <<．参考答案：1．B【分析】解对数不等式化简集合A ，解一元二次不等式化简集合B ，根据补集运算可得结果.【详解】∵集合{}{}2|log 1|02A x x x x =<=<<，{}{}2|20|12B x x x x x =--<=-<<，∴{}|10B A x x =-<≤ð，故选：B.【点睛】本题主要考查了对数与二次不等式的求解以及集合的补集运算.属于基础题.2．D【分析】求出12z z ⋅的代数形式，然后根据其实部为零，虚部不为零列式计算即可.【详解】复数11i z =+，22i z a =+，∴()()()121i 2i 22i z z a a a ⋅=++=-++，12z z ⋅为纯虚数，20a ∴-=且20a +≠，2a ∴=.故选：D.3．A【分析】直接利用函数奇偶性及0x >时的解析式计算即可.【详解】因为函数()f x 为R 上的奇函数，所以()()100100f f -=-，又当0x >时，()lg f x x x =-，所以()()()100100lg10010098f f -=-=--=.故选：A.4．C【分析】根据题意结合条件概率公式运算求解.【详解】记“小李加班”为事件A ，“小陈加班”为事件B ，则()()()111,,436P A P B P AB ===，故在小李加班的条件下，小陈也加班的概率为()()()2|3P AB P B A P A ==.故选：C.5．D【分析】先利用倍角公式降次，再利用两角和的公式展开后转化为用tan 2α表示的等式，然后解方程即可.【详解】22cos 1sin 26παα⎛⎫-=+ ⎪⎝⎭ 1cos 21sin 23παα⎛⎫∴+-=+ ⎪⎝⎭，1cos 22sin 222ααα∴+=，又cos 20α≠，则12tan 22αα=，解得tan 22α=.故选：D.6．B【分析】根据三角形的边角关系，结合角平分线定理、二倍角公式、正弦定理即可求得cos A 的值.【详解】在ABC 中，角,,A B C 对应的边分别为,,a b c ，又点D 在线段AB 上，且满足23AD BD =，所以332,555AD AB c BD c ===，又ACD BCD ∠=∠，由角平分线定理可得AC BC AD BD =，所以3255b ac c =，则32b a =，又2B A =，所以sin sin 22sin cos B A A A ==，则sin cos 2sin BA A=，由正弦定理得3sin 32cos 2sin 224aB b A A a a ====.故选：B.7．B【分析】设等比数列{}n a 的公比为q ，由1220a a +=，398S =，列方程求出1,a q ，进而可求出n S ，结合指数函数的性质求出n S 的最大、小值，列不等式组即可求出a 的取值范围【详解】解：设等比数列{}n a 的公比为q ，因为1220a a +=，398S =，所以121(12)09(1)8a q a q q +=⎧⎪⎨++=⎪⎩，解得131,22a q ==-，所以31111,2221112111,22nnn n nn S n ⎡⎤⎧⎛⎫⎛⎫--⎢⎥+ ⎪⎪ ⎪⎝⎭⎢⎥⎪⎝⎭⎛⎫⎣⎦==--=⎨ ⎪⎛⎫⎝⎭⎛⎫⎪-- ⎪- ⎪⎪⎝⎭⎝⎭⎩为奇数为偶数，当x 为正整数且奇数时，函数1()12xy =+单调递减，当x 为正整数且偶数时，函数1()12xy =-+单调递增，所以1n =时，n S 取得最大值32，当2n =时，n S 取得最小值34，所以34322a a ⎧≤⎪⎪⎨⎪+≥⎪⎩，解得1324a -≤≤.故选：B.8．D【分析】设()[]x g x x=，根据已知作出()g x 的草图，分析已知函数()[]()0x fx ax x=-≠有且仅有2个零点，则[]x a x=有且仅有2个解，即可得出答案.【详解】函数()[]()0x f x a x x=-≠有且仅有2个零点，则[]x a x=有且仅有2个解，设()[],1,00,01nx n x n n g x xxx ⎧≤<+≠⎪==⎨⎪≤<⎩，根据符号[]x 作出()g x的草图如下：则2334a <≤或322a ≤<，故选：D.9．AC【分析】根据表格数据计算得到众数，中位数，平均数和标准差即可判断结果【详解】由题意，这组运动时长数据中8出现了5次，其余数出现次数小于5次，故众数为8，A 正确；将16小学生的运动时长从小到大排列为：4,5,5,6,6,7,7,7,7,8,8,8,8,8,9,9，则中位数为7772+=，故B 错误；计算平均数为142526475829716⨯+⨯+⨯+⨯+⨯+⨯=，故C 正确；方差为()()()()()()2222222147257267477587297216s ⎡⎤=-+⨯-+⨯-+⨯-+⨯-+⨯-=⎣⎦，所以标准差为s ==D 错误.故选：AC 10．CD【分析】利用空间线面、面面平行、垂直的性质定理和判定定理分别分析四个命题，即可得到正确答案.【详解】A 选项，若//m α，//n β，且//m n ，则,αβ可能相交或平行，故A 错误；B 选项，若//m α，//n β，且m n ⊥，则,αβ可能相交，也可能平行，故B 错误；C 选项，若m α⊥，//m n ，则n α⊥，又n β⊥，则//αβ；即C 正确；D 选项，若m α⊥，m n ⊥，则//n α或n ⊂α；又n β⊥，根据面面垂直的判定定理可得：αβ⊥，即D 正确.故选：CD.11．ABD【分析】根据椭圆的性质逐项进行分析即可判断.【详解】由椭圆方程221259x y +=可得：5,3a b ==，4c ==，对于A ，由椭圆的性质可得：129a c PF a c =-≤≤+=，又因为点P 在第一象限内，所以159a PF a c =<<+=，所以存在点P ，使得17PF =成立，故选项A 正确；对于B ，设点00(,)P x y ，因为12(4,0),(4,0)F F -，所以100(4,)PF x y =--- ，200(4,)PF x y =--，则2222212000009161616972525PF PF x y x x x ⋅=-+=-+-=- ，因为005x <<，所以20025x ≤≤，所以2120167(7,9)25PF PF x ⋅=-∈- ，所以存在点P ，使得120PF PF ⋅=，则1290F PF ∠=︒成立，故选项B 正确；对于C ，因为1004PF y k x =+，2004PF y k x =-，若217PF PF k k =，则00(316)0x y +=，因为点00(,)P x y 在第一象限内，所以000,0y x >>，则00(316)0x y +=可化为：03160x +=，解得：01603x =-<不成立，所以不存在点P ，使得217PF PF k k =成立，故选项C 错误；对于D ，由选项B 的分析可知：2120167(7,9)25PF PF x ⋅=-∈- ，所以存在点P ，使得127PF PF ⋅=成立，故选项D 正确，故选：ABD.12．BD【分析】利用诱导公式化简可得()()πf x f x +=-，可判断选项A ；利用换元法和函数的单调性，可判断选项B 和C ；利用诱导公式化简可得()π2f x f x ⎛⎫-= ⎪⎝⎭，可判断选项D ．【详解】对A ：()()()()()()sin 2πsin 22πsin 2πsin πcos πsin cos sin cos x x xf x f x x x x xx x+++===-=-+++--+，故π不是()f x 的周期，A 错误；对B ：令πsin cos 4t x x x ⎛⎫=+=+ ⎪⎝⎭，则2sin 22sin cos 1x x x t ==-，则211t y t t t-==-，∵ππ,44x ⎛⎫∈- ⎪⎝⎭，则()πππ0,,sin 0,1424x x ⎛⎫⎛⎫+∈+∈ ⎪ ⎪⎝⎭⎝⎭，∴π4t x ⎛⎫=+ ⎪⎝⎭在π0,2⎛⎫ ⎪⎝⎭上单调递增，且(π0,4t x ⎛⎫=+∈ ⎪⎝⎭，又∵1y t t =-在()0,∞+上单调递增，故()f x 在ππ,44⎛⎫- ⎪⎝⎭上单调递增，B 正确；对C ：∵π3π,44⎛⎫- ⎪⎝⎭，则()π0,π4x +∈，∴(]πsin 0,14x ⎛⎫+∈ ⎪⎝⎭，则(π0,4t x ⎛⎫=+∈ ⎪⎝⎭，又∵1y tt =-在(上单调递增，且|2x y ，∴1y t t =-在(上最大值为2，即()f x 在π3π,44⎛⎫- ⎝⎭，C 错误；对D ：()()πsin 2sin π2πsin 22ππ2cos sin sin cos sin cos 22x x x f x f x x x x xx x ⎛⎫- ⎪-⎛⎫⎝⎭-=== ⎪++⎛⎫⎛⎫⎝⎭-+- ⎪ ⎪⎝⎭⎝⎭，故()f x 图象的一条对称轴为直线π4x =，D 正确.故选：BD.【点睛】结论点睛：若()()f m x f n x +=-，则()f x 关于直线2m nx +=对称，特别地()()2f x f a x =-，则()f x 关于直线x a =对称；若()()2f m x f n x b ++-=，则()f x 关于点,2m n b +⎛⎫⎪⎝⎭对称，特别地()()20f x f a x +-=，则()f x 关于点(),0a 对称.13．75##1.4【分析】先以{},OA OB 为基底向量求,OE OF uu u r uuu r，联立求解可得6362,5555OA OE OB OF OE =-=-uu r uu u r uuu r uu u r uuu r uu u r ，再结合OC OA OB =+，代入运算即可得答案.【详解】由题意可得：11,23OE OA AE OA OB OF OB BF OB OA =+=+=+=+uu u r uu r uu u r uu r uu u r uuu r uu u r uu u r uu u r uu r，联立1213OE OA OB OF OB OA ⎧=+⎪⎪⎨⎪=+⎪⎩，解得63556255OA OE OB OF OE ⎧=-⎪⎪⎨⎪=-⎪⎩ ，∵636243555555OC OA OB OE OF OF OE OE OF ⎛⎫⎛⎫=+=-+-=+ ⎪ ⎪⎝⎭⎝⎭uuu r uu r uu u r uu u r uuu r uuu r uu u r uu u r uuu r ，则43,55m n ==，故75m n +=.故答案为：75.14．3y x x =+（答案不唯一）【分析】利用导数的几何意义可求得在()0,0处的切线斜率，由此可得切线方程；若两曲线在原点处具有相同切线，只需满足过点()0,0且在0x =处的导数值1y '=即可，由此可得曲线方程.【详解】sin y x = 的导函数为cos y x '=，又sin y x =过原点，sin y x ∴=在原点()0,0处的切线斜率cos 01k ==，sin y x ∴=在原点()0,0处的切线方程为y x =；所求曲线只需满足过点()0,0且在0x =处的导数值1y '=即可，如3y x x =+，231y x '=+ ，又3y x x =+过原点，3y x x ∴=+在原点处的切线斜率1k =，3y x x ∴=+在原点()0,0处的切线方程为y x =.故答案为:3y x x =+（答案不唯一）.15．188π5【分析】分类讨论旋转轴所在的直线，结合锥体的体积公式运算求解.【详解】由题意不妨设：3,4,5AB AC BC ===，边BC 上的高为h ，则1122AB AC BC h ⨯=⨯，可得125AB AC h BC ⨯==，若以边AB 所在直线为旋转轴，则所形成的几何体为圆锥，其底面半径14r =，高为3AB =，故此时圆锥的体积为2113π416π3V =⨯⨯⨯=；若以边AC 所在直线为旋转轴，则所形成的几何体为圆锥，其底面半径23r =，高为4AC =，故此时圆锥的体积为2214π312π3V =⨯⨯⨯=；若以边BC 所在直线为旋转轴，则所形成的几何体为两个共底面的圆锥，其底面半径3125r h ==，高为12,h h ，且125h h BC +==，故所得几何体的体积为()22223132312311111248πππ5ππ333355V h r h r h h r ⎛⎫=⨯⨯+⨯⨯=+⨯⨯=⨯⨯⨯= ⎪⎝⎭；故体积之和为4818816π12πππ55++=.故答案为：188π5.16．22+【分析】设2PF m =，则m c a ≥-，根据双曲线的定义12PF m a =+，故221244PF a m a PF m=++，分2a c a ≥-与2a c a <-讨论，结合“对勾”函数的性质可求出离心率.【详解】设2PF m =，则m c a ≥-，由双曲线的定义知122PF PF a -=，∴12PF m a =+，()22212244PF m a a m a PF mm+==++，当2a c a ≥-，即13a c ≥时，221244PF a m a PF m =++84823a a c c ≥=>>，不符合题意；当2a c a <-，即3ce a=>时，244a y m a m=++在[),m c a ∈-+∞上单调递增，所以当m c a =-时212PF PF 取得最小值，故2442a c a a c c a-++=-，化简得2240c ac a --=，即2410e e --=，解得2e =（舍）或2e =3e >.综上所述，该双曲线的离心率是2故答案为:2.17．(1)1*1,2n n a n -⎛⎫=∈ ⎪⎝⎭N (2)1b =，1c =【分析】（1）根据1n n n a S S -=-，结合已知等式得出112n n a a -=，即可得出数列{}n a 是以首项为1，公比为12的等比数列，即可得出数列{}n a 的通项公式；（2）利用关系式得出1a 、2a 、3a ，再根据等差中项列式，即可得出答案.【详解】（1）令1n =，则11a S b c +=+，即12a b c =+，11a = ，0b =，2c ∴=，则2nn a S +=，即2n n S a =-，当2n ≥时，()1122n n n n n a S S a a --=-=---，化简得112n n a a -=，而11a =，则数列{}n a 是以首项为1，公比为12的等比数列，则数列{}n a 的通项公式1*1,2n n a n -⎛⎫=∈ ⎪⎝⎭N ，（2）当1k =时，n n a S nb c +=+，令1n =，则11a S b c +=+，则12a b c =+，11a = ，2b c ∴+=，令2n =，则222a S b c +=+，则2122a b c a =+-，2b c += ，11a =，221a b ∴=+，令3n =，则333a S b c +=+，则31223a b c a a =+--，2b c += ，11a =，212b a +=，33144b a ∴=+，数列{}n a 为等差数列，2132a a a ∴=+，即311144b b +=++，解得1b =，则21c b =-=.18．(1)证明见解析(2)98【分析】（1）利用余弦定理及面积公式将条件变形得cos sin A B =，再利用诱导公式及三角函数的性质可证明结论；（2）利用（1）的结论及三角公式，将sin sin A C +转化为关于cos B 的二次函数，然后配方可以求最值.【详解】（1）由余弦定理222cos 2b c a A bc+-=得2222cos bc A b c a =+-，4412cos sin 2bS b bc A ac B a a ∴==⨯，cos sin A B ∴=，cos cos 2πA B ⎛⎫∴=- ⎪⎝⎭，B 为钝角，则,2πA B -均为锐角，2B A π∴-=，即2B A π=+；（2）2ππsin sin sin sin cos cos 22cos cos 122A C B B B B B B B ⎛⎫⎛⎫+=-++-=--=--+ ⎪ ⎪⎝⎭⎝⎭，令cos B t =，B 为钝角，则()1,0t ∈-，2219sin sin 21248A C t t t ⎛⎫∴+=--+=-++ ⎪⎝⎭，当14t =-，即1cos 4B =-时，sin sin A C +取最大值，且为98.19．(1)47108；(2)12.【分析】（1）由相互独立事件同时发生的概率，可得结论；（2）设出男生人数，列出22⨯列联表，根据2 3.841χ≥及,,236x x x均为整数即可求解.【详解】（1）从该校全体学生中随机抽取2名男生和2名女生，记其中恰有2人喜欢课外阅读为事件A ，则()222211221152151247C C 63636633108P A ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⨯⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.（2）设被调查的男生人数为x ,则被调查的女生人数为2x，则22⨯列联表为：喜欢课外阅读不喜欢课外阅读合计男生6x56x x 女生3x 6x 2x 合计2x x32x若有95%的把握认为喜欢课外阅读和性别有关，则2 3.841χ≥，即223526663 3.84122x x x x x x xx x χ⎛⎫⋅-⋅ ⎪⎝⎭≥≥⋅⋅⋅，则 3.841810.2433x ⨯≥≈，因为,,236x x x均为整数，所以被调查的男生至少有12人.20．(1)DE ∥平面ABC ，证明见解析；5【分析】（1）分别取,AC BC 的中点,O P ，连接,,DO EP OP ，EP DO ∥且EP DO =，再利用线面平行的判定定理，即可得到答案；（2）连接BO ，则易知BO ⊥平面ACD ，以O 为坐标原点，分别以,,OD OA OB 的方向为,,x y z 轴的正方向，建立如图所示的空间直角坐标系O xyz -，求出向量1,22DH ⎛= ⎝⎭uuu r 及平面ACE 的法向量()1,0,2m =-，代入夹角公式，即可得到答案；【详解】（1）DE ∥平面ABC ，理由如下：分别取,AC BC 的中点,O P ，连接,,DO EP OP ，因为AD CD =，所以DO AC ⊥，又平面ACD ⊥平面ABC ，平面ACD 平面ABC AC =，DO ⊂平面ACD ，所以DO ⊥平面ABC ，同理EP ⊥平面ABC ，所以EP DO ∥，又因为,ACD BCE 是全等的正三角形，所以EP DO =，所以四边形DOPE 是平行四边形，所以DE OP ∥，因为ED ⊄平面ABC ，OP ⊂平面ABC ，所以ED ∥平面ABC ；（2）连接BO ，则易知BO ⊥平面ACD ，以O 为坐标原点，分别以,,OD OA OB的方向为,,x y z轴的正方向，建立如图所示的空间直角坐标系O xyz -，令2AC =.则()()())110,0,0,0,1,0,0,1,0,,0,,0,22O A C D H P ⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，1,2DE OP E ⎫=∴-⎪⎪⎭所以()310,2,0,,2222AC AE DH ⎫⎛⎫=-=-=⎪ ⎪⎪ ⎪⎭⎝⎭，设平面ACE 的法向量为(),,m x y z =，所以·0·0m AC m AE ⎧=⎪⎨=⎪⎩，所以203022y y -=⎧⎪-+=则0y =，取2z =，1x ∴=-，则()1,0,2m =-，所以cos ,DH m DH m DH m ===设直线DH 与平面ACE 所成的角为θ，则sin cos ,DH m θ==21．(1)2x y =(2)存在，32λ=【分析】（1）利用导数求得切线方程2002x x y x p p =-，根据切线方程过点0,2p M ⎛⎫-⎪⎝⎭求得220x p =，再结合两点间距离公式运算求解；（2）根据题意联立方程求点B 的坐标，再分别求直线,AT BT 的方程和,E F 的坐标，代入斜率公式运算求解即可.【详解】（1）∵抛物线()2:20C x py p =>，则20,,22p x M y p ⎛⎫-= ⎪⎝⎭，∴x y p'=，设20,2x P x p ⎛⎫ ⎪⎝⎭，则在点P 处的切线斜率0x k p =，故在点P 处的切线方程为()20002x x y x x p p -=-，即2002x x y x p p =-，∵切线过点0,2p M ⎛⎫- ⎪⎝⎭，则2022x p p -=-，解得220x p =，则2PM ===，解得12p =，故抛物线C 的方程为2x y =.（2）存在，32λ=，理由如下：由题意可得：直线AB 的方程为()121y x -=+，即23y x =+，联立方程223y x x y=+⎧⎨=⎩，解得11x y =-⎧⎨=⎩或39x y =⎧⎨=⎩，即直线AB 与抛物线的交点坐标为()()1,1,3,9A B -，∵直线AT 的斜率1k t =-，故其方程为()1y t x t =-+，联立方程()21y t x t x y⎧=-+⎨=⎩，解得11x y =-⎧⎨=⎩或2x ty t =⎧⎨=⎩，即点()2,E t t，又∵直线BT 的斜率93tk -=，故其方程为93t y x t -=+，联立方程293t y x t x y -⎧=+⎪⎨⎪=⎩，解得11x y =-⎧⎨=⎩或239t x t y ⎧=-⎪⎪⎨⎪=⎪⎩，即点2,39t t F ⎛⎫- ⎪⎝⎭，故直线EF 的斜率为222933t t k t t t λ-===+，则32λ=.【点睛】存在性问题求解的思路及策略（1）思路：先假设存在，推证满足条件的结论，若结论正确则存在；若结论不正确则不存在．（2）策略：①当条件和结论不唯一时要分类讨论；②当给出结论而要推导出存在的条件时，先假设成立，再推出条件；③当条件和结论都不知，按常规法解题很难时，可先由特殊情况探究，再推广到一般情况．22．(1)()f x 有极小值()11f a =-，无极大值(2)①证明见详解；②证明见详解【分析】（1）求导，利用导数判断原函数的单调性，进而可求极值；（2）对①：根据分析可得12ln ln x x -<12ln 0t t t-->，构建()12ln g x x x x =--，利用导数证明；对②：令11m x =，整理可得()112ln f m m m m m m ⎛⎫⎛⎫=+-- ⎪⎪⎝⎭⎝⎭，结合()g x 的单调性证明()0f m <，再结合()f x 的单调性即可证明.【详解】（1）由题意可得：()()()3222ln 121ln 2x x x f x x x x +='--=-，∵()3ln 1F x x x =+-在()0,∞+上单调递增，且()10F =，∴当01x <<时，()0F x <，当1x >时，()0F x >，即当01x <<时，()0f x '<，当1x >时，()0f x ¢>，故()f x 在()0,1上单调递减，在()1,+∞上单调递增，可得()f x 有极小值()11f a =-，无极大值.（2）若函数()f x 有两个零点()1212,x x x x >，则()110f a =-<，解得1a >，当111a <<时，则()()2422424e e 4e 0,e e 0ef a f a --=-+>=-->，结合()f x 的单调性可知：()f x 在()0,1，()1,+∞内均只有一个零点，则2101x x <<<，构建()12ln g x x x x =--，则()()22212110x g x x x x-'=-+=≥当0x >时恒成立，故()g x 在()0,∞+上单调递增，①令1t =>，则12ln ln x x -<1121ln x x x x -，等价于221ln t t t-<，等价于12ln 0t t t-->，∵()g x 在()1,+∞上单调递增，则()()10g t g >=，即12ln 0t t t-->，故12ln ln x x -<②若函数()f x 有两个零点()1212,x x x x >，令()110,1m x =∈，即11x m=，则()21212ln1112ln 01m f x f a a m m m m m m⎛⎫⎛⎫==--=-+= ⎪ ⎪⎝⎭⎝⎭，可得212ln a m m m =+，故()2222ln 12ln 112ln 2ln m mf m m a m m m m m m m m m m m ⎛⎫⎛⎫⎛⎫=--=--+=+-- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，由()0,1m ∈，则10m m+>，∵()g x 在()0,1上单调递增，则()()10g m g <=，即12ln 0m m m--<，∴()112ln 0f m m m m m m ⎛⎫⎛⎫=+--< ⎪⎪⎝⎭⎝⎭当()0,1m ∈时恒成立，又∵()f x 在()0,1上单调递减，且()()20f m f x <=，∴2m x >，即211x x >，故1201x x <<.【点睛】方法点睛：利用导数证明不等式的基本步骤（1）作差或变形．（2）构造新的函数h (x )．（3）利用导数研究h (x )的单调性或最值．（4）根据单调性及最值，得到所证不等式．特别地：当作差或变形构造的新函数不能利用导数求解时，一般转化为分别求左、右两端两个函数的最值问题．。

2024年天津市高考模拟英语试卷试题及答案详解二(精校打印)

2024年天津市高考模拟英语试卷试题及答案详解本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分，共130分，考试时间100分钟。

第Ⅰ卷1至8页，第Ⅱ卷9至10页。

答题时，将第Ⅰ卷的答案填涂在答题卡上，将第Ⅱ卷答案填写在答题卡上。

祝各位考生考试顺利!第Ⅰ卷(选择题共95分)注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号用2B铅笔涂写在答题卡上。

2.选出答案后，用2B铅笔把答题卡上的对应题目的答案涂黑。

第一部分：英语知识运用(共两节，满分45分)第一节：单项填空(共15小题;每小题1分，满分15分)从A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

1．—Candy’s new skirt looks funny on her．—________It looks fine to me．A．Who cares?B．You are telling me.C．What’s wrong?D．I wouldn’t say that.2．—Peter can’t concentrate on his work recently.—Yes,that might________why he made a big mistake in preparing for the meeting.A．allow for B．apply for C．account for D．call for3．The TV series Flight to You has received a lot of positive________from the audience.A．reviews B．previews C．revisions D．proposals4．Scientists have found that imagination is generated in the right side of the brain;________,the left side of the brain is thought to be“logical”.A．in other words B．in consequence C．in a word D．in contrast5．As is known to all,one way for people to prevent COVID-19is to open the windows to allow the airto________.A．calculate B．circulate C．investigate D．accelerate6．—Have you ever been to Tibet?—Actually,I________there for two years and then left for home when my father was ill.A．had worked B．has worked C．worked D．was working34．A．bright B．polite C．dark D．quiet35．A．pill B．example C．order D．instruction第二部分：阅读理解(共20小题;每小题 2.5分，满分50分)阅读下列短文，从每题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

新高考语文模拟试卷2(附答案)

新高考语文模拟试卷2（附答案）一、现代文阅读（35 分）（一）现代文阅读Ⅰ（本题共5 小题，19 分）阅读下面的文字，完成1～5 题。

材料一：科技创新是推动经济发展的核心动力。

在当今全球化的时代，科技创新的竞争日益激烈。

各国纷纷加大对科技创新的投入，以提升自身的竞争力。

科技创新不仅能够创造新的产品和服务，还能够提高生产效率，降低成本，推动产业升级。

例如，人工智能、大数据、云计算等新兴技术的发展，正在深刻改变着各个行业的发展模式。

同时，科技创新也能够促进社会的进步和发展。

例如，医疗技术的创新可以提高疾病的诊断和治疗水平，改善人们的健康状况；环保技术的创新可以减少环境污染，保护生态环境。

然而，科技创新也面临着一些挑战。

例如，科技创新需要大量的资金和人才投入，而且创新的过程充满了不确定性和风险。

此外，科技创新也可能带来一些社会问题，例如失业、贫富差距扩大等。

材料二：文化创新是推动文化发展的重要动力。

文化创新可以为文化产业的发展提供新的内容和形式，促进文化产业的繁荣。

同时，文化创新也可以丰富人们的精神文化生活，提高人们的文化素养。

文化创新需要在继承传统文化的基础上进行。

传统文化是一个国家和民族的精神财富，它蕴含着丰富的智慧和价值。

只有在继承传统文化的基础上进行创新，才能够使文化创新具有深厚的根基和底蕴。

此外，文化创新也需要借鉴和吸收其他国家和民族的优秀文化成果。

不同国家和民族的文化都有其独特的魅力和价值，通过借鉴和吸收其他国家和民族的优秀文化成果，可以丰富和拓展本国文化的内涵和形式。

1.下列对材料相关内容的理解和分析，正确的一项是（3 分）A.科技创新和文化创新都是推动经济发展的核心动力。

B.科技创新能够创造新的产品和服务，提高生产效率，推动产业升级。

C.文化创新可以为文化产业的发展提供新的内容和形式，促进文化产业的繁荣，因此文化创新比科技创新更重要。

D.科技创新和文化创新都面临着一些挑战，其中科技创新面临的挑战更大。

2023年普通高等学校招生全国统一考试新高考仿真模拟卷数学(二)答案

2023年普通高等学校招生全国统一考试·仿真模拟卷数学（二）一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1.已知集合{}2A x x x=≤，(){}2log1B x y x ==-，则A B ⋃=（）A.[)1,+∞B.[)0,∞+C.（0，1）D.[]0,1【答案】B 【解析】【分析】分别化简集合,A B ，根据并集的定义求解.【详解】{}2A x x x=≤ ∴不等式2x x ≤的解集是集合A又因为(){}21001,01x x x x x A x x ≤⇒-≤⇒≤≤∴=≤≤又(){}2log 1x y x =- ，所以满足函数()2log 1y x =-中x 的范围就是集合B所以{}1011x x B x x ->⇒>∴=>所以{}{}{}[)01100,A B x x x x x x ∞⋃=≤≤⋃>=≥=+故选：B2.已知复数()()2i 1i z a =+-为纯虚数，则实数=a （）A.12-B.23-C.2D.2-【答案】D 【解析】【分析】根据复数乘法计算方法化简复数，结合纯虚数的概念求值即可.【详解】()()()2i 22i 1i i 2i 2i 2a a a a z a ==-++++---=，因为复数z 为纯虚数，所以2020a a -≠⎧⎨+=⎩，即2a =-.故选：D3.在正方形ABCD 中，M 是BC 的中点．若AC m = ，AM n = ，则BD =（）A.43m n -B.43m n+ C.34m n -D.34m n+【答案】C 【解析】【分析】作图，根据图像和向量的关系，得到2()22BC AC AM m n =-=-和AB AC BC =- 222m m n n m =-+=-，进而利用BD BC CD BC AB =+=- ，可得答案.【详解】如图，AC m =，AM n =，且在正方形ABCD 中，AB DC=12AC AM MC BC -==，2()22BC AC AM m n ∴=-=- ， AC AB BC =+，AB AC BC ∴=- 222m m n n m =-+=- ，∴BD BC CD BC AB =+=-= 22234m n n m m n--+=- 故选：C4.已知40.5=a ，5log 0.4b =，0.5log 0.4c =，则a ，b ，c 的大小关系是（）A.b a c >>B.a c b >>C.c a b >>D.a b c>>【答案】C 【解析】【分析】利用指数函数，对数函数单调性，找出中间值0,1，使其和,,a b c 比较即可.【详解】根据指数函数单调性和值域，0.5x y =在R 上递减，结合指数函数的值域可知，()()400,0.50,10.5a ∈==；根据对数函数的单调性，5log y x =在(0,)+∞上递增，则55log 0.4log 10b =<=，0.5log y x =在(0,)+∞上递减，故0.50.5log 0.4log 0.51c =>=，即10c a b >>>>，C 选项正确.故选：C5.端午佳节，人们有包粽子和吃粽子的习俗．四川流行四角状的粽子，其形状可以看成一个正四面体．广东流行粽子里放蛋黄，现需要在四角状粽子内部放入一个蛋黄，蛋黄的形状近似地看成球，当这个蛋黄的表面积是9π时，则该正四面体的高的最小值为（）A.4 B.6C.8D.10【答案】B 【解析】【分析】根据题意分析可知，当该正四面体的内切球的半径为32时，该正四面体的高最小，再根据该正四面体积列式可求出结果.【详解】由球的表面积为9π，可知球的半径为32，依题意可知，当该正四面体的内切球的半径为32时，该正四面体的高最小，设该正四面体的棱长为a 3a =，根据该正四面体积的可得2163334a a ⨯⨯=21334324a ⨯⨯⨯，解得a =.所以该正四面体的高的最小值为66633a =⨯=.故选：B6.现有一组数据0，l ，2，3，4，5，6，7，若将这组数据随机删去两个数，则剩下数据的平均数大于4的概率为（）A.514 B.314C.27D.17【答案】D 【解析】【分析】先得到删去的两个数之和为4时，此时剩下的数据的平均数为4，从而得到要想这组数据随机删去两个数，剩下数据的平均数大于4，则删去的两个数之和要小于4，利用列举法得到其情况，结合组合知识求出这组数据随机删去两个数总共的情况，求出概率.【详解】0，l ，2，3，4，5，6，7删去的两个数之和为4时，此时剩下的数据的平均数为284482-=-，所以要想这组数据随机删去两个数，剩下数据的平均数大于4，则删去的两个数之和要小于4，有()()()()0,1,0,2,0,3,1,2四种情况符合要求，将这组数据随机删去两个数，共有28C 28=种情况所以将这组数据随机删去两个数，剩下数据的平均数大于4的概率为41287=.故选：D7.在棱长为3的正方体1111ABCD A B C D -中，O 为AC 与BD 的交点，P 为11AD 上一点，且112A P PD =，则过A ，P ，O 三点的平面截正方体所得截面的周长为（）A. B.C.+D.+【答案】D 【解析】【分析】根据正方体的性质结合条件作出过A ，P ，O 三点的平面截正方体所得截面，再求周长即得.【详解】因为112A P PD =，即11113D P A D = ，取11113D H D C =uuuu r uuuu r，连接11,,PH HC A C ，则11//HP AC ，又11//AC AC ，所以//HP AC ，所以,,,,A O C H P 共面，即过A ，P ，O 三点的正方体的截面为ACHP ，由题可知APCH ===，PH =，11A C =，所以过A ，P ，O 三点的平面截正方体所得截面的周长为+.故选：D.8.不等式15e ln 1-≥+x a xx x对任意(1,)x ∈+∞恒成立，则实数a 的取值范围是（）A.(,1e]-∞- B.(2,2e⎤-∞-⎦C.(,4]-∞- D.(,3]-∞-【答案】C 【解析】【分析】分离参数，将15e ln 1-≥+x a x x x 变为41e ,1ln x x xa x x---≤>，然后构造函数，即将不等式恒成立问题转化为求函数的最值问题，利用导数判断函数的单调性，求最值即可.【详解】由不等式15e ln 1-≥+x a xx x 对任意(1,)x ∈+∞恒成立，此时ln 0x >，可得41e ,1ln x x xa x x---≤>恒成立，令41e ,1ln x x x y x x ---=>，从而问题变为求函数41e ,1ln x x x y x x---=>的最小值或范围问题；令1()e x g x x -=-，则1()e 1x g x -'=-，当1x <时，1()e 10x g x -'=-<，当1x >时，1()e 10x g x -'=->，故1()e (1)0x g x x g -=-≥=，即1e x x -≥，所以4411ln 4ln 1e e e e 4ln x x x x x x x x ------=⋅=≥-，()*，当且仅当4ln 1x x -=时取等号，令()4ln 1h x x x =--，则44()1x h x x x-'=-=，当4x <时，()0h x '<，当>4x 时，()0h x '>，故min ()(4)34ln 40h x h ==-<，且当x →+∞时，()4ln 1h x x x =--也会取到正值，即4ln 1x x -=在1x >时有根，即()*等号成立，所以41e 4ln 4ln x x x x x x x---≥--=-，则41e 4ln x x xx---≥-，故4a ≤-，故选：C【点睛】本题考查了不等式的恒成立问题，解法一般是分离参数，构造函数，将恒成立问题转化为求函数最值或范围问题，解答的关键是在于将不等式或函数式进行合理的变式，这里需要根据式子的具体特点进行有针对性的变形，需要一定的技巧.二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9.在平面直角坐标系中，圆C 的方程为22210x y y +--=，若直线1y x =-上存在一点M ，使过点M 所作的圆的两条切线相互垂直，则点M 的纵坐标为（）A.1B.C.1- D.【答案】AC 【解析】【分析】首先可根据圆的方程得出圆心与半径，然后根据题意得出点M 、圆心以及两个切点构成正方形，最后根据2MC =以及两点间距离公式即可得出结果.【详解】22210x y y +--=化为标准方程为：()2212x y +-=，圆心()0,1C ，，因为过点M 所作的圆的两条切线相互垂直，所以点M 、圆心以及两个切点构成正方形，2MC =，因为M 在直线1y x =-上，所以可设(),1M a a -，则()22224MCa a =+-=，解得：2a =或0a =，所以()2,1M 或()0,1M -，故点M 的纵坐标为1或1-.故选：AC.10.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象如图所示，若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象，则m 的值可以是（）A.π4B.π3C.4π3D.9π4【答案】AD 【解析】【分析】根据函数图象可确定A 和最小正周期T ，由此可得ω，结合π26f ⎛⎫= ⎪⎝⎭可求得ϕ，从而得到()(),f x g x 的解析式，根据()()f x m g x -=可构造方程求得()ππ4m k k =-∈Z ，由此可得m 可能的取值.【详解】由图象可知：2A =，最小正周期5ππ4π126T ⎛⎫=⨯-=⎪⎝⎭，2π2T ω∴==，ππ2sin 263f ϕ⎛⎫⎛⎫∴=+= ⎪ ⎪⎝⎭⎝⎭，()ππ2π32k k ϕ∴+=+∈Z ，解得：()π2π6k k ϕ=+∈Z ，又π2ϕ<，π6ϕ∴=，()π2sin 26f x x ⎛⎫∴=+ ⎪⎝⎭，()π2sin 23g x x ⎛⎫=- ⎪⎝⎭，()()π2sin 226f x m x m g x ⎛⎫-=-+= ⎪⎝⎭ ，()ππ22π63m k k ∴-+=-+∈Z ，解得：()ππ4m k k =-∈Z ，当0k =时，π4m =；当2k =-时，9π4m =.故选：AD.11.大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理，数列中的每一项都代表太极衍生过程．已知大衍数列{}n a 满足10a =，11,,,n n na n n a a n n +++⎧=⎨+⎩为奇数为偶数，则（）A.34a =B.221n n a a n +=++C.221,,2,2n n n a n n ⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数D.数列(){}1nn a -的前2n 项和的最小值为2【答案】ACD 【解析】【分析】当2n k =时，2122k k a a k +=+,当21n k =-时，2212k k a a k -=+,联立可得21214k k a a k +--=，利用累加法可得22122k a k k +=+，从而可求得221,2,2n n n a n n ⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数，在逐项判断即可.【详解】令k *∈N 且1k ≥，当2n k =时，2122k k a a k +=+①；当21n k =-时，221212112k k k a a k a k --=+-+=+②，由①②联立得21214k k a a k +--=.所以315321214,8,,4k k a a a a a a k +--=-=-= ，累加可得()22112114844222k k k k a a a k k k+++-==+++=⨯=+ .令21k n +=(3n ≥且为奇数)，得212n n a -=.当1n =时10a =满足上式，所以当n 为奇数时，212n n a -=.当n 为奇数时，()21112n nn aa n ++=++=，所以22n n a =，其中n 为偶数.所以221,2,2n n n a n n ⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数，故C 正确.所以233142a -==，故A 正确.当n 为偶数时，()22222222n nn n aa n ++-=-=+，故B 错误.因为()()222212211222n n n n a a n ----=-=，所以(){}1nna -的前2n 项和21234212nn nSa a a a a a -=-+-++-+()()121222212n n n nn +=⨯+⨯++⨯=⨯=+ ，令()1n c n n =+，因为数列{}n c 是递增数列，所以{}n c 的最小项为1122c =⨯=，故数列(){}1nna -的前2n 项和的最小值为2，故D 正确.故选:ACD.【点睛】数列求和的方法技巧(1)倒序相加：用于等差数列、与二项式系数、对称性相关联的数列的求和．(2)错位相减：用于等差数列与等比数列的积数列的求和．(3)分组求和：用于若干个等差或等比数列的和或差数列的求和．12.已知抛物线()220y px p =>的准线为:2l x =-，焦点为F ，点(),P P P x y 是抛物线上的动点，直线1l 的方程为220x y -+=，过点P 分别作PA l ⊥，垂足为A ，1PB l ⊥，垂足为B ，则（）A.点F 到直线1l 的距离为655B.2p x +=C.221p px y ++的最小值为1 D.PA PB +的最小值为655【答案】ABD 【解析】【分析】对于A ，用点到直线的距离公式即可判断；对于B ，利用抛物线的定义即可判断；对于C ，利用基本不等式即可判断；对于D ，利用抛物线的定义可得到PA PB PF PB BF +=+≥，接着求出BF 的最小值即可【详解】由抛物线()220y px p =>的准线为:2l x =-可得抛物线方程为28y x =，焦点为()2,0F ，对于A ，点F 到直线1l的距离为655d ==，故A 正确；对于B ，因为(),P P P x y 在抛物线上，所以利用抛物线的定义可得2P PF x =+，即2p x +=，故B 正确；对于C ，因为(),P P P x y 在抛物线上，所以28,0p p p y x x =≥，所以211221144111818888p p p pp p p p x x x x y x x x +=+=+=+++++1788≥=，当且仅当38p x =时，取等号，故C 错误；对于D ，由抛物线的定义可得PA PF =，故PA PB PF PB BF +=+≥，当且仅当,,P B F 三点共线时，取等号，此时1BF l ⊥，由选项A 可得点F 到直线1l的距离为5d =，故PA PB +的最小值为655，故D正确，故选：ABD三、填空题：本题共4小题，每小题5分，共20分．13.已知sin 3cos 0αα+=，则tan 2α=______．【答案】34##0.75【解析】【分析】利用已知等式可求得tan α，由二倍角正切公式可求得结果.【详解】由sin 3cos 0αα+=得：sin 3cos αα=-，sin tan 3cos ααα∴==-，22tan 63tan 21tan 194ααα-∴===--.故答案为：34.14.函数()()ln 211f x x x =++-的图象在点()()0,0f 处的切线方程是______．【答案】310x y --=【解析】【分析】求导函数，可得切线斜率，求出切点坐标，运用点斜式方程，即可求出函数()f x 的图象在点()()0,0f 处的切线方程.【详解】()()ln 211f x x x =++-，∴2()121f x x '=++，则(0)213f '=+=，又()ln 201(0)011f =⨯++-=-Q ，∴切点为()0,1-，∴函数()()ln 211f x x x =++-的图象在点()0,1-处的切线方程是()130,y x +=-即310x y --=.故答案为：310x y --=.15.2名老师带着8名学生去参加数学建模比赛，先要选4人站成一排拍照，且2名老师同时参加拍照时两人不能相邻．则2名老师至少有1人参加拍照的排列方法有______种．（用数字作答）【答案】3024【解析】【分析】分两种情况讨论：①若只有1名老师参与拍照；②若2名老师都拍照.利用计数原理、插空法结合分类加法计数原理可求得结果.【详解】分以下两种情况讨论：①若只有1名老师参与拍照，则只选3名学生拍照，此时共有134284C C A 2688=种排列方法；②若2名老师都拍照，则只选2名学生拍照，先将学生排序，然后将2名老师插入2名学生所形成的空位中，此时，共有222823C A A 336=种排列方法.综上所述，共有26883363024+=种排列方法.故答案为：3024.16.已知A ，B 是双曲线22:124x y C -=上的两个动点，动点P 满足0AP AB += ，O 为坐标原点，直线OA 与直线OB 斜率之积为2，若平面内存在两定点1F 、2F ，使得12PF PF -为定值，则该定值为______．【答案】【解析】【分析】设()()1122(,),,,,P x y A x y B x y ,根据0AP AB += 得到122x x x =-，122y y y =-，根据点A ,B 在双曲线22124x y -=上则22212212416,248y x y x -=-=，代入计算得22220x y -=，根据双曲线定义即可得到12PF PF -为定值.【详解】设()()1122(,),,,,P x y A x y B x y ,则由0AP AB += ,得()()()112121,,0,0x x y y x x y y --+--=，则122x x x =-，122y y y =-，点A ,B 在双曲线22124x y -=上,222211221,12424x y x y ∴-=-=，则22212212416,248y x y x -=-=()()222212122222x y x x y y ∴-=---()()()2222121212121212828442042x x x x y y y y x x y y =+--+-=--，设,OA OB k k 分别为直线OA ,OB 的斜率,根据题意,可知2OA OBk k ⋅=,即12122y y x x ⋅=，121220y y x x ∴-=22220x y ∴-=，即2211020x y -=P ∴在双曲线2211020x y -=上,设该双曲线的左、右焦点分别为12,F F ，由双曲线定义可知||12||||PF PF -为定值，该定值为.故答案为：.四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.在ABC 中，角,,A B C 的对边分别是,,a b c ，()()()0a c a c b b a -++-=．（1）求C ；（2）若c =ABC 的面积是2，求ABC 的周长．【答案】（1）π3.（2）.【解析】【分析】（1）将()()()0a c a c b b a -++-=化为222a b c ab +-=，由余弦定理即可求得角C .（2）根据三角形面积求得2ab =，再利用余弦定理求得3a b +=，即可求得答案.【小问1详解】由题意在ABC 中，()()()0a c a c b b a -++-=，即222a b c ab +-=，故2221cos 22a b c C ab +-==，由于(0,π)C ∈，所以π3C =.【小问2详解】由题意ABC 的面积是32，π3C =，即133sin ,2242ABC S ab C ab ab ===∴= ，由c =2222cos c a b ab C =+-得2223()6,3a b ab a b a b =+-=+-∴+=，故ABC 的周长为a b c ++=.18.已知数列{}n a 满足，()*1232311112222n n a a a a n n +++⋅⋅⋅+=∈N ．（1）求数列{}n a 的通项公式；（2）若()21n n b n a =-，记n S 为数列{}n b 的前n 项和，求n S ，并证明：当2n ≥时，6n S >．【答案】（1）2nn a =（2）()12326n n S n +=-+【解析】【分析】(1)利用递推式相减得出2n n a =，并验证首项符合通项，最后得出答案；(2)错位相减法求前n 项和【小问1详解】1232311112222n n a a a a n ++++= ，①则()12312311111122222n n a a a a n n --++++=-≥ ，②①-②得11(2)2n n a n =≥，则2(2)n n a n =≥，当n =1时，由①得1112a =，∴1122a ==，∴2n n a =.【小问2详解】易得()212nn b n =-，()123123512222n n S n =⋅+⋅+∴+-⋅+ ，①()21341232522212n n S n +=⋅+⋅+⋅+∴+- ，②②-①得()()34112122222n n n S n ++=--++++- ()()21228212n n n +++=----()12326n n +=-+，故()12326n n S n +=-+，当2n ≥时，()12320n n +->6n S ∴>19.如图，四棱锥P ABCD -中，平面APD ⊥平面ABCD ，APD △为正三角形，底面ABCD 为等腰梯形，AB //CD ，224AB CD BC ===．（1）求证：BD ⊥平面APD ；（2）若点F 为线段PB 上靠近点P 的三等分点，求二面角F AD P --的大小．【答案】（1）证明见解析；（2）π4【解析】【分析】（1）先用几何关系证明π3A ∠=，然后根据余弦定理求出BD ，结合勾股定理可得BD AD ⊥，最后利用面面垂直的性质定理证明；（2）过P 作PG AD ⊥，垂足为G ，结合面面垂直的性质先说明可以在G 处为原点建系，然后利用空间向量求二面角的大小.【小问1详解】取AB 中点E ，连接CE ，根据梯形性质和2AB CD =可知，CD //AE ，且CD AE =，于是四边形ADCE 为平行四边形，故2CE AD BE CB ====，则CEB 为等边三角形，故π3A CEB ∠=∠=，在ABD △中，由余弦定理，222π2cos 1648123BD AB AD AB AD =+-⨯⨯=+-=，故BD =，注意到22212416BD AD AB +=+==，由勾股定理，π2ADB ∠=，即BD AD ⊥，由平面APD ⊥平面ABCD ，平面APD 平面ABCD AD =，BD ⊂平面ABCD ，根据面面垂直的性质定理可得，BD ⊥平面APD .【小问2详解】过P 作PG AD ⊥，垂足为G ，连接EG ，由平面APD ⊥平面ABCD ，平面APD 平面ABCD AD =，PG ⊂平面PAD ，根据面面垂直的性质定理，PG ⊥平面ABCD ，APD △为正三角形，PG AD ⊥，故AG GD =（三线合一），由AE EB =和中位线性质，GE //BD ，由（1）知，BD ⊥平面APD ，故GE ⊥平面APD ，于是,,GA GE GP 两两垂直，故以G 为原点，,,GA GE GP 所在直线分别为,,x y z 轴，建立如图所示的空间直角坐标系.由（1）知，BD ⊥平面APD ，又BD //y 轴，故可取(0,1,0)m =为平面APD的法向量，又P，(B -，根据题意，2BF FP = ，设(,,)F x y z，则()()1,2,,x y z x y z +-=--，解得12323,,333F ⎛- ⎝⎭，又(1,0,0)A ，(1,0,0)D -，(2,0,0)DA = ，42323,,333FA ⎛=-- ⎝⎭ ，设平面FAD 的法向量(,,)n a b c = ，由00n DA n FA ⎧⋅=⎪⎨⋅=⎪⎩ ，即0423230333a a =⎧⎪⎨--=⎪⎩，于是(0,1,1)n =- 为平面FAD 的法向量，故2cos ,2m n m n m n⋅=== ，二面角大小的范围是[]0,π，结合图形可知是锐二面角，故二面角F AD P --的大小为π420.为落实体育总局和教育部发布的《关于深化体教融合，促进青少年健康发展的意见》，某校组织学生参加100米短跑训练．在某次短跑测试中，抽取100名女生作为样本，统计她们的成绩（单位：秒），整理得到如图所示的频率分布直方图（每组区间包含左端点，不包含右端点）．（1）估计样本中女生短跑成绩的平均数；（同一组的数据用该组区间的中点值为代表）（2）由频率分布直方图，可以认为该校女生的短跑成绩X 服从正态分布()2,N μσ，其中μ近似为女生短跑平均成绩x ，2σ近似为样本方差2s ，经计算得，2 6.92s =，若从该校女生中随机抽取10人，记其中短跑成绩在[]12.14,22.66以外的人数为Y ，求()1P Y ≥．2.63≈，随机变量X 服从正态分布()2,N μσ，则()0.6827P X μσμσ-<≤+=，()220.9545P X μσμσ-<<+=，()330.9974P X μσμσ-<<+=，100.68270.0220≈，100.95450.6277≈，100.99740.9743≈．【答案】（1）17.4（2）0.3723【解析】【分析】(1)结合频率分布直方图中求平均数公式,即可求解.(2)根据已知条件,可知，217.4, 6.92μσ==，即可求出212.14,222.66μσμσ-=+=，结合正态分布的对称性以及二项分布的概率公式,即可求解.【小问1详解】估计样本中女生短跑成绩的平均数为:()120.02140.06160.14180.18200.05220.03240.02217.4⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯=；【小问2详解】该校女生短跑成绩X 服从正态分布()17.4,6.92N ,由题可知217.4, 6.92μσ==， 2.63σ=≈，则212.14,222.66μσμσ-=+=，故该校女生短跑成绩在[]12.14,22.66以外的概率为：1(12.1422.66)10.95450.0455P X -≤≤=-=，由题意可得,~(10,0.0455)Y B ,10(1)1(0)10.954510.62770.3723P Y P Y ≥=-==-≈-=.21.已知椭圆()2222:10x y C a b a b +=>>的左焦点为F ，右顶点为A ，离心率为22，B 为椭圆C 上一动点，FAB 面积的最大值为212+．（1）求椭圆C 的方程；（2）经过F 且不垂直于坐标轴的直线l 与C 交于M ，N 两点，x 轴上点P 满足PM PN =，若MN FP λ=，求λ的值．【答案】（1）2212x y +=；（2）λ=.【解析】【分析】（1）由题意可得22c e a ==，121()22a c b ++=，再结合222a b c =+可求出,a b ，从而可求出椭圆的方程；（2）由题意设直线MN 为1x ty =-（0t ≠），1122(,),(,)M x y N x y ，设0(,0)P x ，将直线方程代入椭圆方程中化简利用根与系数的关系，然后由PM PN =可得0212x t =-+，再根据MN FP λ=可求得结果.【小问1详解】因为椭圆的离心率为2，所以2c e a ==，因为FAB面积的最大值为12+，所以121()22a cb ++=，因为222a bc =+，所以解得1a b c ===，所以椭圆C 的方程为2212x y +=；【小问2详解】(1,0)F -，设直线MN 为1x ty =-（0t ≠），1122(,),(,)M x y N x y ，不妨设12y y >，设0(,0)P x ，由22112x ty x y =-⎧⎪⎨+=⎪⎩，得22(2)210t y ty +--=，则12122221,22t y y y y t t -+==++，所以12y y -==，因为PM PN =，所以2222101202()()x x y x x y -+=-+，所以222212102012220x x x x x x y y --++-=，所以12120121212()()2()()()0x x x x x x x y y y y +---+-+=，所以12120121212(11)()2()()()0ty ty ty ty x ty ty y y y y -+----+-+=，因为120y y -≠，所以12012(2)2()0t ty ty x t y y +--++=，所以20222222022t t t x t t t ⎛⎫--+= ⎪++⎝⎭，所以20222222022t x t t --+=++，解得0212x t =-+，因为MN FP λ=，所以222MN FP λ=，0λ>，所以222212120()()(1)x x y y x λ-+-=+，222212120()()(1)ty ty y y x λ-+-=+2222120(1)()(1)t y y x λ+-=+，所以22222222288(1)(1)(2)(2)t t t t t λ+++=++，化简得28λ=，解得λ=±，因为0λ>，所以λ=22.已知函数()()1ln R 1x f x x m m x -=-⋅∈+．（1）当1m =时，判断函数()f x 的单调性；（2）当1x >时，()0f x >恒成立，求实数m 的取值范围．【答案】（1）()f x 在()0,∞+上是单调递增的（2）2m ≤【解析】【分析】（1）对()f x 求导，从而确实()f x '为正及()f x 的单调性；（2）令()()()1(m )ln 1R x x x m x g =+--∈，然后分2m ≤和m>2两种情况讨论()g x 的单调性及最值，即可得答案.【小问1详解】当1m =时，()1ln 1x f x x x -=-+，定义域为()0,∞+()()()()()2222212111121x x x f x x x x x x x +-+'=-==+++，所以()0f x ¢>，所以()f x 在()0,∞+上是单调递增的.【小问2详解】当1x >时，()()1ln R 1x f x x m m x -=-⋅∈+，()0f x >等价于()()()()1ln 1g m x x x m x R =+--∈，则()0g x >，1g ()ln 1x x m x '=++-，令()1ln 1m h x x x =++-，则22111()x h x x x x-'=-=，当1x >时，()0h x '>，则()g x '在()1,+∞上是单调递增的，则()(1)2g x g m ''>=-①当2m ≤时，()0g x '>，()g x 在()1,+∞上是单调递增的，所以()(1)0g x g >=，满足题意．②当m>2时，(1)20g m '=-<，(e )e 1e 10m m m g m m --'=++-=+>，所以0(1,e )mx ∃∈，使00()g x '=，因为()g x '在()1,+∞上是单调递增的所以当0(1,)x x ∈时，()0g x '<，所以()g x 在0(1,)x 上是单调递减的，又(1)0g =，即得当0(1,)x x ∈时，()(1)0g x g <=，不满足题意．综上①②可知：实数m 的取值范围2m ≤.。

2024届高考考前原创仿真求质模拟卷02(适用于新高考全国Ⅰ卷地区)(含答案)

2024届高考考前原创仿真求质模拟卷02（适用于新高考全国Ⅰ卷地区）一、现代文阅读：本大题共9小题，共60分。

阅读下面的文字，完成下列小题。

材料一：唐宋时期，不少诗人对诗歌写作行为本身进行观照，并将其呈现在诗歌文本中——诗歌写作行为本身成了被书写的对象。

在陈与义、陆游的诗中，我们可以看到其对于诗歌写作本身更细致、频繁的书写，“题诗”“成诗”“寻诗”“哦诗”等有关诗歌写作的表达大量出现，有意寻诗、出声吟哦的诗人形象也越发明晰，这表明：宋诗对诗歌写作本身的呈现更为深细，写作者对自我作为诗人的身份有了更清晰的意识。

“题诗”“成诗”在陈与义的诗中承载了丰富内涵。

“鹳鹤忽双起，吾诗还欲成”“洒面风吹作飞雨，老夫诗到此间成”两例清晰展示出外部环境怎样激起了诗人内心的波澜，眼前转瞬即逝的景致如何被诗人捕捉到进而成为诗歌的一部分。

而“成诗”的过程往往具有实时性、不可复制性。

有道是“有诗还忘记”“忽有好诗生眼底，安排句法已难寻”，诗人内心感知到的诗意、诗人在语言表达上的疏离，都清晰呈现在诗中。

他在《对酒》中的“新诗满眼不能裁，鸟度云移落酒杯”，同样感叹着自己在语言表达上的窘迫。

诗人也常常自发外出“寻诗”。

“柳林横绝野，藜杖去寻诗”（《游八关寺后池上》），诗人专门拄着藜杖寻诗：“醒来推户寻诗去，乔木峥嵘明月中”（《寻诗两绝句》），半夜从酒醉中醒来的诗人特意推开门，在明月乔木中寻诗。

场景本身就是诗意的来源，诗人在呈现出诗意产生的特定情境之后便结束了诗篇，不再述说此刻的感受。

这类似前引“鹳鹤忽双起，吾诗还欲成”：诗人看似只是记录实时景象，然而诗情恰恰渗透在眼前所见之中，诗歌写作也在此刻完成。

不同的是，“寻诗”更能体现寻找、访求的过程性和目的性，在这一表达中，“诗”仿佛成了触手可及的实体；作者自认与读者对何为“诗”有着高度默契，只需呈现特定场景，读者便可心领神会。

这种将“诗”客体化的过程，体现出诗歌已成为诗人日常生活中随时可见的一部分，同时，诗人的主体身份在诗歌中也呈现得愈发明晰。

2024年全国普通高中九省联考仿真模拟数学试题(二)(含答案)

2024年高考仿真模拟数试题（二）试卷+答案注意事项：]．答卷前，考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需要改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．A ．1B ．3C ．6D ．1或33．设等差数列{}n a 的前n 项和为n S ，若3510a a +=−，642S =−，则10S =（） A ．12B ．10C ．16D ．20A ．32种B ．128种C ．64种D ．256种5．在某次数学探究活动中，小明先将一副三角板按照图1的方式进行拼接，然后他又将三角板ABC 折起，使得二面角A BC D −−为直二面角，得图2所示四面体ABCD ．小明对四面体ABCD 中的直线、平面的位置关系作出了如下的判断：①CD ⊥平面ABC ；②AB ⊥平面ACD ；③平面ABD ⊥平面ACD ；④平面ABD ⊥平面BCD ．其中判断正确的个数是（）A ．1B ．2C ．3D ．4A ．[]3,3−B ．[]3,5C ．[]1,9D ．[]3,7二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．三、填空题：本题共3小题，每小题5分，共15分．为；此时棱柱的高为 .14．已知正实数,,,a b c d 满足210a ab −+=，221c d +=，则当22()()a c b d −+−取得最小值时，ab = ．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．2024年高考仿真模拟数试题（二）试卷+答案（题型同九省联考，共19个题）注意事项：]．答卷前，考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需要改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．A．1 B．3 C．6 D．1或3A．12B．10C．16D．20A．32种B．128种C．64种D．256种答案 C解析若甲、乙都去，剩下的5人每个人都可以选择去或不去，有52种去法；若甲、乙都不去，剩下的5人每个人都可以选择去或不去，有52种去法．故一共有55+=种去法．故选C.22645．在某次数学探究活动中，小明先将一副三角板按照图1的方式进行拼接，然后他又将三角板ABC折起，使得二面角A BC D −−为直二面角，得图2所示四面体ABCD ．小明对四面体ABCD 中的直线、平面的位置关系作出了如下的判断：①CD ⊥平面ABC ；②AB ⊥平面ACD ；③平面ABD ⊥平面ACD ；④平面ABD ⊥平面BCD ．其中判断正确的个数是（）A ．1B ．2C ．3D ．4A ．[]3,3−B ．[]3,5C ．[]1,9D ．[]3,7二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．答案 AD解析对A ：令1x =，0y =，则()()()21210f f f =，因为()11f =−，所以()01f =，故A 正确；对B ：令0x =得：()()()()20f y f y f f y +−=，结合()01f =可得()()f y f y =−，所以()f x 为偶函数，故B 错误；对C ：令1y =可得：()()()()1121f x f x f x f ++−=，因为()11f =−，三、填空题：本题共3小题，每小题5分，共15分．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．≤.……………17分综上，不存在正实数M，使得对任意的正整数n，都有n a M。

2024年全国高考仿真模拟卷(二)语文

2024年全国高考仿真模拟卷(二)语文一、现代文阅读（2024·仿真模拟）阅读下面的文字，完成问题。

商周时期数量巨大、内容丰富的青铜器铭文，体现了中华文明独特的书写文化。

相比于其他文献，铭文能基本反映书写的原貌，因而对研究中国早期社会的历史、文化、思想等，有着重要的价值。

商周铜器铭文的书写之所以如此繁盛，除了物质条件的进步与社会需求等因素外，思想、情感层面的追求也是一个重要原因。

用文字进行书写是人类文明进步史上的大事，因为它代表着思想、情感的传播可以灾破时空的限制。

《墨子兼爱（下）》提到，今人不与“先圣六王”同时，却能了解其德行，“以其所书于竹帛，镂于金石，琢于盘盂，传遗后世子孙者知之”。

可见，古人早已认识到书写之于思想传承、文明演进的价值。

而在“传遗后世子孙”方面，铜器铭文（即所谓“金石”“盘盂”）更有着无可比拟的优势。

当古人认识到生命的有限性之后，青铜材质所具有的永存性，便寄托了他们对“永恒”的希冀，或者说是对生命“不朽”价值的追寻。

中国早期关于生命价值的体认，最有代表性的便是“三不朽”说。

《左传•襄公二十四年》记载晋范宣子与鲁叔孙豹讨论何谓“死而不朽”。

范宣子认为，自己家族自古至今皆有官职，这便是不朽。

但叔孙豹认为这只是“世禄”，并非不朽，真正的不朽应如鲁国臧文仲“既没，其言立”，即死后其言论仍能流传后世。

进而他便论述了“三不朽”的观念：“约闻之：‘大上有立德，其次有立功，其次有立言。

’虽久不废，此之谓不朽。

”即当时人们认为要在有限的生命中追求德、功、言三者的树立与传承，这样才能实现人生的崇高价值。

此种“生命价值观”后为儒家所继承并发扬，构成了中华文明的重要思想底色。

当然，“三不朽”的价值观并非《左传》所创，它应来自更久远的传承，并有逐步演化的过程，这一点便可从铜器铭文的发展中找到线索。

最早的铜器铭文非常简单，有的仅由一个或数个名词组成，稍复杂的也仅是一个主谓句。

商代晚期才有长篇铭文，其主要进步是能完整叙述一连串事件且有清晰的因果联系。