昆明理工大学理论力学练习册答案(第七章后)
昆明理工大学工程力学习题册答案

昆明理工大学工程力学习题册答案一、选择题1. 在平面力系中,力对点的矩的常用单位是(A)A. N·mB. N/mC. N·sD. N·m^2答案:A2. 平面汇交力系的平衡方程是(C)A. Fx=0, Fy=0, M=0B. Fx=0, Fy=0C. Fx=0, Fy=0, M=0(其中M为力矩)D. Fx=0, Fy=0, M≠0答案:C3. 在空间力系中,力的投影与原力的关系是(B)A. 投影等于原力B. 投影小于等于原力C. 投影大于原力D. 投影与原力无关答案:B二、填空题1. 力对物体的作用效果包括______和______。
答案:使物体发生形变,使物体产生运动2. 平面力系中的合力可以用______和______来确定。
答案:力的大小,力的方向3. 在平面力系中,力矩的计算公式为______。
答案:M=F×d(其中F为力,d为力臂)三、计算题1. 已知:力F=10N,作用点距离A点4cm,求力F 对A点的力矩。
解:力矩的计算公式为M=F×d,其中d为力臂,即作用点到力作用点的距离。
本题中,d=4cm=0.04m。
所以,M=10N×0.04m=0.4N·m。
答案:0.4N·m2. 平面汇交力系中,已知F1=20N,F2=30N,F3=40N,求该力系的合力。
解:首先,将F1和F2合成,得到合力F12。
F12的大小为F12=√(F1^2+F2^2+2F1F2cosθ),其中θ为F1和F2之间的夹角。
假设F1和F2之间的夹角为60°,则F12=√(20^2+30^2+2×20×30×cos60°)=√(400+900+ 1200×0.5)=√(2000)=44.72N。
然后,将F12与F3合成,得到合力F123。
F123的大小为F123=√(F12^2+F3^2+2F12F3cosθ),其中θ为F12和F3之间的夹角。
昆明理工大学理论力学B练习册题解答
(∨)
1.1.17凡是两端用铰链连接的直杆都是二力杆。(×)
1.1.18如图1.1所示三铰拱,受力F,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。(×)
二、填空题
1.2.1力对物体的作用效应一般分为外效应和内效应。
三、受力图
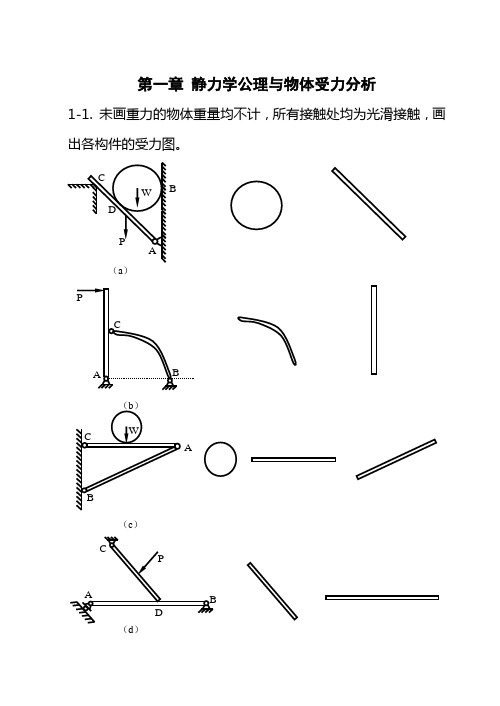
1.3.1画出各物体的受力图。下列各图中所有接触均处于光滑面,各物体的自重除图中已标出的外,其余均略去不计。
1.3.2画出下列各物体系中各指定研究对象的受力图。接触面为光滑,各物自重除图中已画出的外均不计。
第二章 平面力系(汇交力系与平面偶系)
一、 是非判断题
2.1.1当刚体受三个不平行的力作用时,只要这三个力的作用线汇交于同一点,则刚体一定处于平衡状态。(×)
2.1.1一个任意力系的合力矢是主矢。(×)
2.1.2某平面任意力系向A、B两点简化的主矩皆为零,即MA=MB=0,此力系简化的最终结果为:
A、可能简化为一个力。(∨)
B、可能简化为一个力偶。(×)
C、可能平衡。(∨)
2.1.3若平面平行力系平衡,可以列出三个独立的平衡方程。(1个)(×)
2.1.4平面任意力系的三个独立平衡方程不能全部采用投影方程。(∨)
322板abcd由六根杆支承如图所示受任意已知力系而处于平衡为保证所列的每个方f1fcd三计算题331在图示力系中f1100nf2300nf3200n各力作用线位置如图所示求力系cos3002002002003453n100131001005f?rx300cos03f0xmx?rz01300f2cos300300100132496cos30003100131002001001056n02f1sin02100010z03f2sio3f3cos03300332如图所示的空间构架由三根杆件组成在my20030020010013200032003453i2496j1056k1005179nm1003664nm200032005179i3664j10359knm若各杆自重不计求各杆的内力
昆明理工大学理论力学B练习册题+解答
第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学第7章答案

x′
a
n A
sin
θ
−
aAτ
cosθ= NhomakorabeaaBx
cos
θ
−
aBy
sin
θ
aAτ
=
−aBx
+
(a
n A
+ aBy )tgθ
=
−1cm/s 2
α OA
=
a
τ A
/ OA
=
−(1/ 40)rad/s2
7.13 滚压机构的滚子沿水平面作纯滚动如图示 曲柄 OA 长 r 连杆 AB 长 l 滚子 半径为 R 若曲柄以匀角速度 ω 绕固定轴 O 转动 计算连杆 AB 和滚子的角加速度
向
v A
垂直于
OA
杆
因此瞬心为 C
不难看出 C 点相对
AB 杆和定系的位置可分别以 (2r, ϕ) 和 (r,2ϕ) 表示 则动 定瞬心迹线分别是半径为 2r 和 r 的圆
7.9 图示反平行四边形机构中 AB = CD = 2a AC = BD = 2c a > c 求杆 BD
的动瞬心轨迹和定瞬心轨迹
b
杆速度瞬心在 点 vC = 0
∴ ωBC = vB / a = ω ωCD = 0
基点
aCτ = aBn + aCτ B + aCnB
x′ acτ cos θ = −aBn − aCnB
Q cos θ = sin ϕ = 7 / 4
aBn = ω2a
aCnB = ω2a
∴ aCτ = −8ω2a / 7
上二式中消去 ψ 得 (ρsin ϕ)2 + (2c − ρ cos ϕ)2 = (2a − ρ)2
理论力学课后习题答案 第7章 质点动力学

习题7-2图习题7-3图习题7-1图(a) g m NF s F a(b)θs F N F gm a 第7章 质点动力学7-1 图示滑水运动员刚接触跳台斜面时,具有平行于斜面方向的速度40.2km/h ,忽略摩擦,并假设他一经接触跳台后,牵引绳就不再对运动员有作用力。
试求滑水运动员从飞离斜面到再落水时的水平长度。
解:接触跳台时 171136001024030..v =⨯=m/s 设运动员在斜面上无机械能损失7688442892171122020....gh v v =⨯⨯-=-=m/s 1418.cos v v x ==θm/s, 2563.sin v v y ==θm/s 5410221.g v h y ==m 33201.gv t y ==s 220121)(gt h h =+780.08.9)44.2541.0(2)(2012=+=+=g h h t s112.121=+=t t t s0591*******...t v x x =⨯==m7-2 图示消防人员为了扑灭高21m 仓库屋顶平台上的火灾,把水龙头置于离仓库墙基15m 、距地面高1m 处,如图所示。
水柱的初速度250=υm/s ,若欲使水柱正好能越过屋顶边缘到达屋顶平台,且不计空气阻力,试问水龙头的仰角α应为多少?水柱射到屋顶平台上的水平距离s 为多少? 解:(1) αcos v t 0115=(1) 2021sin 2110=-⋅gt t v α (2) (1)代入(2),得01.44cos sin 375cos 5002=+-ααα ααα22cos 1cos 3751.44cos 500-=+ 081.1944cos 96525cos 39062524=+-αα 22497.0cos 2=α, ︒=685.61α(2) gv t αsin 02=(到最高点所经过时间) 26.232)15cos (20=⨯-⋅=t v S αm7-3 图示三角形物块置于光滑水平面上,并以水平等加速度a 向右运动。
理论力学 第六版部分习题答案 第七章
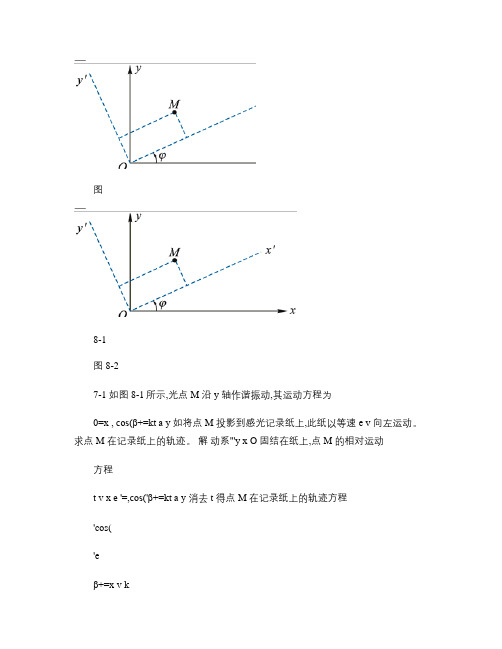
图8-1图8-27-1 如图8-1所示,光点M 沿y 轴作谐振动,其运动方程为0=x , cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解动系'''y x O 固结在纸上,点M 的相对运动方程t v x e '=,cos('β+=kt a y 消去t 得点M 在记录纸上的轨迹方程'cos('eβ+=x v ka y 7-2 如图8-2所示,点M 在平面''y Ox 中运动,运动方程为cos 1(40't x −=,t y sin 40'= 式中t 以s 计,'x 和'y 以mm 计。
平面''y Ox 又绕垂直于该平面的轴O 转动,转动方程为rad t =ϕ,式中角ϕ为动系的'x 轴与定系的x 轴间的交角。
求点M 的相对轨迹和绝对轨迹。
解由点M 的相对运动方程可改写为t yt x sin 40cos 140''=−=⎟⎟⎠⎞⎜⎜⎝⎛−上2式两边平方后相加,得点M 的相对轨迹方程 1600'40'(22=+−y x 由题得点M 的坐标变换关系式ϕϕsin 'cos 'y x x −= ϕϕcos 'sin 'y x y +=将t =ϕ和相对运动方程代入,消去t 得点M 的绝对轨迹方程160040(22=++y x7-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成°=60β角,如图8-3a 所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
′′v(a (b图8-3解水轮机工作轮入口处的1滴水为动点M ,动系固结于工作轮,定系固结于机架/地面(一般定系可不别说明,默认为固结于机架,下同;牵连运动为定轴转动,相对运动与叶片曲面相切,速度分析如图8-3b 所示,设θ为r v 与'x 轴的夹角。
昆明理工大学理论力学B练习册题+解答

第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学1-7章答案【精选】

习题7-1图Oυ(a)υυ(b)习题7-3图第7章 点的复合运动7-1 图示车A 沿半径R 的圆弧轨道运动,其速度为v A 。
车B 沿直线轨道行驶,其速度为v B 。
试问坐在车A 中的观察者所看到车B 的相对速度v B /A ,与坐在车B 中的观察者看到车A 的相对速度v A /B ,是否有B A A B //v v -=?(试用矢量三角形加以分析。
)答:B A A B //v v -≠1.以A 为动系,B 为动点,此时绝对运动:直线;相对运动:平面曲线;牵连运动:定轴转动。
为了定量举例,设R OB 3=,v v v B A ==,则v v 3e =∴ ⎩⎨⎧︒==6021/θv v A B2.以B 为动系,A 为动点。
牵连运动为:平移;绝对运动:圆周运动;相对运动:平面曲线。
此时⎪⎩⎪⎨⎧︒==4522/θv v B A ∴ B A A B //v v -≠7-3 图示记录装置中的鼓轮以等角速度0ω转动,鼓轮的半径为r 。
自动记录笔连接在沿铅垂方向并按)sin(1t a y ω=规律运动的构件上。
试求记录笔在纸带上所画曲线的方程。
解:t r x 0ω= (1) )sin(1t a y ω=(2)由(1)0ωr xt =代入(2),得)sin(01r xa y ωω=7-5 图示铰接四边形机构中,O 1A = O 2B = 100mm ,O 1O 2 = AB ,杆O 1A 以等角速度ω= 2rad/s 绕轴O 1转动。
AB 杆上有一套筒C ,此套筒与杆CD 相铰接,机构的各部件都在同一铅垂面内。
试求当ϕ= ︒60,CD 杆的速度和加速度。
解:1.动点:C (CD 上),动系:AB ,绝对:直线,相对:直线,牵连:平移。
2.r e a v v v +=(图a ) v e = v A01.02121.0cos e a =⨯⨯==ϕv v m/s (↑)3. r e a a a a +=(图b )4.021.022e =⨯==ωr a m/s 2 346.030cos e a =︒=a a m/s 2(↑)习题7-5图习题7-7图习题7-9图υ(a) (b)(a)7-7 图示瓦特离心调速器以角速度ω绕铅垂轴转动。
理论力学第7章答案
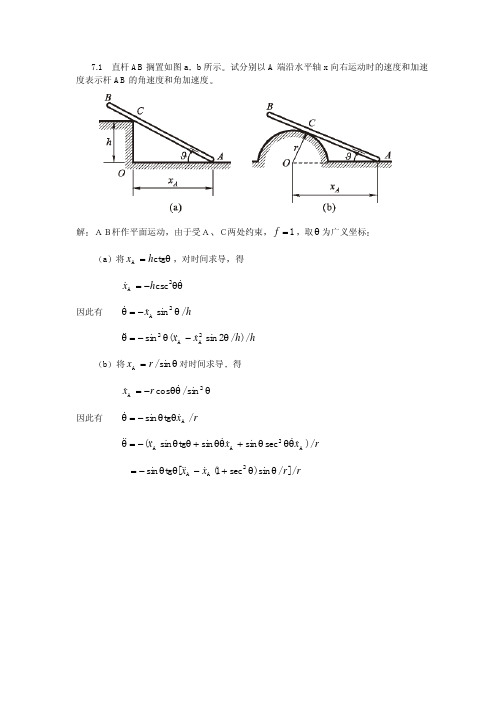
7.1 直杆AB 搁置如图a b 所示试分别以A 端沿水平轴x 向右运动时的速度和加速度表示杆AB 的角速度和角加速度解杆作平面运动由于受两处约束1=f 取θ为广义坐标a 将θ=ctg A h x 对时间求导得θθ−=&&2A csc h x因此有h x /sin 2A θ−=θ&&hh x x /)/2sin (sin 2A A 2θ−θ−=θ&&&&&b 将θ=sin /A r x 对时间求导得θθθ−=2A sin /cos &&r x因此有r x /tg sin A &&θθ−=θr x x x/)sec sin sin tg sin (A 2A A &&&&&&&&θθθ+θθ+θθ−=θr r x x/]/sin )sec 1([tg sin 2A A θθ+−θθ−=&&&7.2 试证明直杆AB 搁置如图a b 所示杆AB 运动时杆上点C 的速度沿杆AB其大小等于θcos A v解基点CA A C v v v +=a x ′0sin sinA CA A x C =θ+θ=−θ=′&&CA xv v v y ′θ=′cos A y C v v 证毕b x ′0sin sinA CA A x C =θ+θ=+θ=′&&CA x v v v y ′θ=′cos A y C v v 证毕7.3 滚压机构的滚子沿水平面作纯滚动如图示曲柄OA 长r 连杆AB 长l 滚子半径为R 若曲柄以匀角速度ω绕固定轴O 转动试求任意时刻θ=∠AOB 连杆AB和滚子的角速度解本机构自由度14233=×−×=f 除θ外取多余坐标ϕ两者间有约束方程ϕ=θsin sin l r 1矢量法基点BA A B v v v +=)(A r v ω=)sin()sin()sin(B 2A 2BA ϕ+θ=ϕ−=θ−ππv v v ϕθ=cos cos A BA v v ϕθω==ωcos cos BA AB l r l vϕϕ+θ=cos )sin(A B v v ϕϕ+θω==ωcos )sin(B B R r R v分析法将式1对时间求导得ϕθω=ϕθθ=ϕcos cos cos cos l r r &&对ϕ+θ=cos cos B l r x 对时间求导得ϕϕ+θω−=ϕϕ−θθ−=)sin(sin sin B r l r x&&&因此ϕϕ+θω=−=ωcos )sin(/B B R r R x&7.4 一放大机构中ABCD 为一平行四边形B 为OC 的中点D 为CE 的中点设图示位置点A 的速度如图示求点E 的速度解平行四边形机构在任意时有BC//ADAB//CD 因此1AD BC ωωω==2CD AB ωωω==A 基点ABB A v v v +=基点ECC E v v v +=Q OB OC 2=BACE 2=∴B11C 22v v =×=×=OB OC ωωAB22EC 22v v =×=×=BA CE ωω可导出AE 2v v =7.5 一自动卸货大卡车的升降机构如图示图中BFBE =l AC =在此瞬时活塞在处于水平的液压缸中的速度为v 求车厢转动的角速度解利用速度投影定理杆vv =o 60cosF vv 2F =v v v 2F E ==杆v v v ==o 60cosE D 因此lv AD v 2D ==ω7.6 画出图示机构中作平面运动的杆件在图示位置的速度瞬心7.7 图示拱桥上受到1F 和2F 两力作用若给出的三拱桥的支座C 若突然坍塌试求此瞬时GBJ 和ICJ 两部分的速度瞬心解GBI 构件瞬心为ICJ 构件瞬心在无穷远7.8 杆AB 可在作定轴转动的套筒O ′内滑动如图示其A 端与曲柄OA 铰接已知r O O OA =′=求杆的动瞬心轨迹和定瞬心轨迹解AB 杆作平面运动杆上与O 相重合之点速度O ′v 沿杆方向A v 垂直于OA 杆因此瞬心为C 不难看出C 点相对AB 杆和定系的位置可分别以),2(ϕr 和)2,(ϕr 表示则动定瞬心迹线分别是半径为r 2和r 的圆7.9 图示反平行四边形机构中a CD AB 2==c BD AC 2==c a >求杆BD的动瞬心轨迹和定瞬心轨迹解BD 杆的瞬心为AB 与CD 的交点P 容易证明三角形APC和DPB 全等因此瞬心P 点相对BD 杆和定系的位置均可用),(ϕρ表示在三角形APC 中有DPAP ==ρ 0sin )2(sin =ψρ−−ϕρa ca 2cos )2(cos =ψρ−+ϕρ上二式中消去ψ得222)2()cos 2()sin (ρ−=ϕρ−+ϕρa c 可导出如下椭圆方程]cos )/(1[]/)[(22ϕ−−=ρa c a c a 因此动定瞬心迹线均为椭圆7.11 三根连杆AB BC 和CD 用铰链相连组成一四连杆机构AD 可视作固定不动的连杆已知a BC AB ==a CD 2=杆AD 以匀角速度ω转动求图示两位置杆CD的角速度和角加速度解a 杆作瞬时平动0BC =ωBC v v =∴2/2/C CD ω==ωa v 基点ττ+=+CBn B n C C a a a a∴0C =τa 0CD =αb 杆速度瞬心在点0=C v ∴ω==ωa v /B BC 0CD =ω基点nCBCB n B C a a a a ++=ττx ′n CBn B c cos a a a −−=θτQ 4/7sin cos =ϕ=θaa 2n B ω=aa 2n CB ω=∴7/82C a a ω−=τ7/742/2C CD ω−==ατa a7.12 平面机构如图示已知CD//EG B 为杆DG 的中点O A B C D E G 均为铰链cm 20==EG CD cm 50=DG cm 40=OA 在图示位置杆CD 铅垂OA//CD cm/s20A =v 水平向左B 的加速度沿水平方向的分量2Bx cm/s10=a3.0tan =θ试用平面运动基点法求此瞬时 1杆CD 和杆OA 的角速度2B 的加速度沿铅垂方向的分量3杆OA 的角加速度解杆做瞬时平动AB =ωBA v v = rad/s 5.0/A OA ==ωOA v22OA nA cm/s10=ω=OA a 某点ττ++=+ABBy Bx A n A a a a a ax ′θ−θ=θ−θτsin cos cos sinBy Bx A nA a a a a 2By n A Bx A cm/s 1tg )(−=θ++−=τa a a a 2A OA rad/s )40/1(/−==ατOA a7.13 滚压机构的滚子沿水平面作纯滚动如图示曲柄OA 长r 连杆AB 长l 滚子半径为R 若曲柄以匀角速度ω绕固定轴O 转动计算连杆AB 和滚子的角加速度解矢量法基点nBABA n A B a a a a ++=τyϕ+ϕ−θ−=τsin cos sin 0n BA BA n A a a aϕω−ϕ=ϕθω−ϕϕ=τtg )(cos /)sin sin (2222BA &&l r l a x ′nBAn A B )cos(cos a a a +ϕ+θ=ϕϕϕ+ϕ+θω=cos /])cos([22B &l r a ∴ϕω−ϕ==ατtg )(/22BA AB &l a ϕϕ+ϕ+θω==αcos /])cos([/22B B R l r R a &分析法ϕω−ϕ=ϕϕθω+ϕθω−=ϕ=αtg )(cos /sin cos cos /sin 2222AB &&&l r l r ϕϕϕϕ+θω+ϕϕ+ωϕ+θω=ω=α2B B cos /sin )sin(cos /))(cos(R r R r &&&ϕϕ+ϕ+θω=cos /])cos([22R l r &7.14 半径为r 的圆盘在水平面上作直线纯滚子如图示其中心O 的速度O v 常量杆AB 长l 其B 端用铰链与圆盘边缘相连接求在水平面上运动的A 端的速度和加速度以转角ϕ表示之解本机构自由度1=f θ和ϕ有约束方程)cos 1(sin ϕ−=θr l )1(矢量法圆盘的瞬心为点杆的瞬心为点因此)2/sin(2)/(O O B ϕ==v BP r v v θϕϕ==ωcos /)2/cos()2/sin(2/O l v CB v B AB θϕ=cos /sin O l v ]2cos /)2/sin()[cos /sin (O ϕϕ+θθϕ=ω=l l v CA v AB A )2/sin()2/sin(2)cos /(O ϕϕ+θθ=v ]cos /)cos(1[O θϕ+θ−=v 基点nBO BO O B a a a a ++=τO =a τBOa基点nAB ABB A a a a a ++=τx ′nABB A )2cos(cos a a a +θ−ϕ−π=θ∴θϕ+θϕ+θ=3222A cos sin cos )sin(l v r v a O O 分析法将式1对时间求导得θϕ=θcos /sin Ol v &因为θ−ϕ−=cos sin O A l r x x 对时间求导得)cos /sin (sin cos O O O A A θϕθ+ϕ−==l v l v v xv &]cos /)cos(1[O θϕ+θ−=v θθθϕ+θ−θϕ+θϕ+θ==2O A A cos /sin )cos(cos /))(sin(&&&&v va θϕ+θϕ+θ=322O 2O cos sin cos )sin(l v r v7.15 半径为10cm 的轮B 由曲柄OA 和连杆AB 带动在半径为40cm 的固定轮上作纯滚动设OA 长10cm AB 长40cm OA 匀角速转动角速度rad/s 10=ω求在图示位置轮B 滚动的角速度和角加速度解矢量法杆作瞬时平动AB =ωω==r v v A Brad/s10/B B =ω==ωr v cmr 10=基点ττ+=+BA n A n B Ba a a ax ′α−=β−βτsin sin cos nA nB B a a a ∴75/154tg )5/(2222B ω−=βω−ω−=τr r r r a 2rad/s 7.2075/154/2B B −=ω−==ατr a 分析法设的坐标分别为A x A y BxB y 此瞬时0A =x r y =A rx 15B =0B =y 则有22A B 2A B )4()()(r y y x x =−+−将上式求导得0))(())((A B A B A B A B =−−+−−y y y y x xx x &&&&0))(()())(()(A B A B 2A B A B A B 2A B =−−+−+−−+−y y y y y y x x x x x x &&&&&&&&&&&&将0B A ==y y&&2A ω−=r y&&r x y 5/2B B &&&−=及0A =x&&等代入上二式得ω−==r x xB A &&75/1542B ω=r x&&因此导出rad/s 10/B B =−=ωr x &2B B rad/s 7.20/−=−=αr x&&7.16 半径为r 的两轮用长l 杆A O 2相连如图示前轮1O 匀速滚动轮心的速度为v求在图示位置后轮2O 滚动的角加速度解矢量法1O 轮纯滚动vv v 221O A ==A O 2杆瞬时平动v v v 2A O 2==0A O 2=ω2O 轮纯滚动rv r v /2/22O O ==ω基点1O n AOAOO A1a a a a ++=τ1O =a 0AO =τa2O 基点n AO A O AO 221a a a a ++=τx ′ϕ−=ϕsin cosA O2a a rv a /tg 2O 2ϕ−=222O O //22r l r v r a −−==α分析法A O 2杆长l ,故22O A 2O A )()(22l y y x x =−+−则有0))(())((2222O A O A O A O A =−−+−−y y y y x xx x &&&&0))(()())(()(222222O A O A 2O A O A O A 2O A =−−+−+−−+−y y y y y y x x x x x x &&&&&&&&&&&&将0B A ==y y&&r v y/2A −=&&02O =y&&0A =x&&代入上二式得v x x2A O2==&&222O /2r l v x−−=&&于是导出r v r x /2/22O O ==ω&222O O //22r l r v r x −−==α&&7.17 圆柱体C 在固定的半圆柱D 上纯滚动一杆AB 一端与圆柱体中心铰接另一端与滑块A 铰接在图示瞬时滑块A 的速度m/s3=v 加速度2m/s2=a 求此瞬时圆柱体C 的角速度和角加速度解B基点ABAA B v v v +=o o o 105sin 15sin 60sin ABA B v v v ==m/s 70.2B =v m/s80.0BA =v∴rad/s8.15.1/B C ==ωvrad/s1.08/BA AB ==ωv nBABA AnBBa a a a a ++=+ττ5.4/2B v 82AB ⋅ωx ′n BA A n B B 30cos 15sin 15cos a a a a +=−τo o o2B m/s 31.2=τa 2B C rad/s 54.15.1/==ατa7.18 一杆AB 一端与小齿轮中心A 铰接另一端与圆盘D 的边缘B 点铰接如图示若圆盘D 以匀角速度ω转动杆AB 长m5.0求此瞬时小齿轮在齿圈上滚动的角速度和角加速度解杆的速度瞬心即齿圈的圆心因此ω=−=ω)3/4()25.3/(B AB vω=ω=)3/16(4B A v ω==ω3.51/A A &v基点nABABnBnA Aa a a a a ++=+ττ4/2A v 22⋅ωABAB ωx ′n AB n B n A A45cos cos sin a a a a +=β+β−τo 在三角形中AB)45sin(5.1sin 445sin β+=β=o o 解得o377.15=β)m 10(92.41−=AB 于是有2A 45.12ω−=τa 2A45.121/ω−==ατa A7.19 直杆CD 在C 点处与齿轮B 铰接在图示瞬时杆CD 的速度为0=v 加速度2mm/s 600=a 求此瞬时齿条A 的加速度解(1)令齿轮轮心O, 以C 为基点有τOC C O a a a += 0Ox =a 0Oy =a 所以0O =a (2)τPOP a a =2CP m/s 8.0==OP OCa a 齿条加速度 )/(8.02P s m a a ==7.20 上题中若速度改为mm/s75=v 加速度不变求齿条A 的加速度解轮心O 为速度瞬心rad/s 1C==OCv ωnOCOC C O a a a a ++=τ2C rad/s 875600/===OC a αnPOPO O P a a a a ++=τ2O τPO Px m/s 725.0075.08.0=−=−=a a a 所以2Px A m/s725.0==a a7.21 图示动齿轮O ′由曲柄O O ′带动在定齿轮O 上滚动已知曲柄的角速度为ω计算齿轮相对曲柄的角速度解方法一ω−=′)(21O r r v ω−==ω′)1/(/212O r r r v a齿轮O ′动系O O ′杆er a ωωω+=ω=ω−−ω=ω)/()(21a r r r 方法二齿轮O ′瞬心位于O ′连线外侧因此因此r ω必与ω=ωe 反向由e r /ωω=′O C CO 得ω=ω)/(21r r r7.22 图示行星齿轮系中轮I 固定轮II 由曲柄AB 带动轮III 又由轮II 带动已知曲柄的角速度为ω角加速度为零求轮III 相对曲柄AB 的角速度和角加速度设轮II 轮III 半径相同解设轮 半径为r 则rAB 2=ω=r v B 2ω==ω2/B 2r vω=ω=r r v 422P ω==ω4/P 3r v轮 动系杆er a ωωω+=∴ω=ω−ω=ω34r 03=ω=ω=α&&r r7.23 图示传速器由以下齿轮组成半径cm 401=r 的定齿轮半径各为cm 202=r 和cm 303=r 的相连的行星齿轮以及半径cm 904=r 的内啮合齿轮主动轴转速min /r 18001=n 带动行星齿轮在定齿轮上滚动并通过内啮合齿轮使从动轴转动试求从动轴每分钟的转速2n 解A 点作圆周运动a21A )(n r r v +=齿轮2在定齿轮1上纯滚动r v A /2=ω齿轮3与齿轮2有相同角速度23ω=ω基点BAA B v v v +=b 4n r 33ωr a232133A B )/1)((n r r r r r v v ++=ω+=∴rpm3000/)/1)((/4a 23214b =++==r n r r r r r v n B rpm 转数分e r杆OA 作顺时针纯滚动圆盘半径为r 3r =OP 求圆盘中心B 的速度解方法一因r ω与e ω反向圆盘的瞬心在连线外侧由e r //ωω=CP CO 可得rCP =圆盘动系杆e r a ω+ω=ωω=ω3a∴ω=ω=r r v 232a B 方法二基点BPP B v v v +=Q ω=ω=r r v 33e P ω=ω=r r v 3a BP∴ω=+=r v v v 23)(2/12BP 2P B 方法三动系杆er a v v v +=Q ω=ω=r r v 4r r ω=ω=r r v 1010e e∴ω=β−+=r v v v v v 23)cos 2(2/1e r 2e 2r ae r杆OA 作顺时针纯滚动圆盘半径为r 3r =OP 试求圆盘与杆OA 的接触点P 的加速度解圆盘上动系杆kr n e e P a a a a a +++=τe r α323e r ω2rr ωQ 0=r v x ′2n e x P 3ω−=−=′r a ay ′222r e y P 13)4(3ω=ω+ω−=+=τ′r r r a a a7.27 图中直杆AB 表示齿条圆轮O 表示齿轮当齿条的一端运动时带动半径为cm 5的齿轮绕轴O 转动今设A 端以cm/s 30的速度向右匀速运动求图示位置齿条AB 及齿轮O 的角速度和角加速度解AB 杆瞬心为点rad/s3/AB ==ωPA v AABC ω=PC vrad/s3/AB C O =ω==ωCO v 矢量法圆盘动系杆ABr O ωωω+=rad/s6r =ωAB r O ααα+=ABO r α+α=α圆盘上动系杆ke r O a a a a ++=杆上O ′基点nOAOA A e a a a a ++=τ由于0O =a 0A =a 由以上二式得k n OA OA r =+++τa a a ar αr AB αOA 2AB ωOA r AB 2v ωrr ω=r v x ′060cos 30cos k n OA OA =−+−τa a a o o 2AB rad/s 39−=αy ′060sin 30sin n OA OA =−−τo o a a a r 2O rad/s 39=α分析法设ϕ为广义坐标)2/(ctg ϕ=r x A 将上式求导得2/)2/(csc 2ϕϕ−=&r v A可导出rad/s 3|/)2/(sin 2602A −=ϕ−=ϕ=ϕo &r v 260A rad/s 39|/sin =ϕϕ−=ϕ=ϕo &&&r v 因为为杆瞬心ϕ==cos /A A C v PA PC v v则有rad/s3|/cos /60A C O =ϕ==ω=ϕo r v r v 260A O rad/s 39|/sin =ϕϕ−=α=ϕo &r v7.28 一机构在图示位置时OB OA ⊥点C 位于AB 的中点已知rOA =r AB 4=求当杆OA 以匀角速度ω转动时杆CD 的速度和加速度解杆瞬时平动A C v v =′0AB =ω基点nBA BA n A B a a a a ++=τ0n BA =ay β+−=τcos 0BA n A a a 15/4/2BA AB ω==ατr a杆上动系杆e r a v v v +=15/CD ωr v = k e r a a a a a ++=0k =a杆上C ′基点nCA CA n A e a a a a ++=τ0n CA =a导出τ++=CAn A r a a a a a x ′τββCAn A a a a −=cos cos CD 15AB /r r r a 22CD 7cos /2ωαεω=−=7.29 套筒C 上装有一销轴可在半径为1m 的圆槽内滑动当滑块A 以匀速m/s 5.0=v 向右上方运动而杆DA 以匀角速度2rad/s =θ&转动时求图示瞬时套筒C 在杆AD 上滑动的速度和加速度图示位置o90=θ解动系杆e r a v v v += 1k e r n a a a a a a a ++=+τ 2杆C ′点基点CA A e v v v += 3nCA CA a e a a a a ++=τ 4由13得CA A r a v v v v ++=θ=&AC CA v m/s 8=a v m/s4r =v由24得kn CA r n a a a a a a a ++=+τ1/2a v 2θAC r2v θ&y oo o 30sin 30cos 30cos k n CA r n a a a a a −−−=−∴m/s6.5330tg 30cos /k n CA n r =−−=o o a a a a a7.30 图示一机构在某瞬时的位置此时ω=ωOA 0OA =αω=l v CD 0CD =a求杆AB 的角速度和角加速度解动系杆e r a v v v += 1k e r a a a a a ++=0a =a 2杆上P 点基点A P A e v v v +=3nPA PA na e a a a a ++=τ4由13得PAe r a v v v v ++=CD v OA ωl AB 2ωl x ′PAA a 45cos 45cos v v v +=−o o ω−=+ω−==ωl v l l v 2/)(2/CD OA PA AB y ′o o 45cos 45cos A r a v v v −=ω=l v 2r由24得0k nPA PA nA r =++++τa a a a a 2OA ωl AB 2αl 2AB 2ωl r AB 2v ω x ′045cosk PA nA =−+τa a a o 222PA AB 5.222/2/ω−=ω−ω−==ατl l l l a7.31 两个半径为cm 20=r 中心距离保持不变的圆盘在地面作纯滚动在其边缘B D 处铰接的连杆BD 上安装一滑块C 杆AC 一端与滑块铰接另一端与一圆盘的中心A 铰接若A 以cm/s 60A =v 匀速水平向左运动求图示位置杆AC 的角速度和滑块C 相对BD 的速度以及杆AC 的角加速度解矢量法圆盘rad/s3/A A ==ωrv 0/A A ==εra基点BAA B v v v +=1n BA BA A B a a a a ++=τ0A =a 0BA =τa2C基点CAA C v v v +=3n CACA A C a a a a ++=τ0A =a4C 动系BD e r C v v v +=B e v v=5e r C a a a +=B e a a=6由135得CA A BA A r v v v v v +=++ yo o 30cos 30sin CA BA v v=rad/s 13/CA AC ==ωr vxo o 30sin 30cos CA BA r v v -v −=cm/s 320r =v 由246得n CA CA n BA r a a a a +=+τy oo o 30sin 30cos 30cos n CA CA BA a a a n −=−τ2CA AC rad/s 3/383/−==ατr a 分析法取θϕ为坐标存在约束方程θ=ϕcos sin 3r r 高丽营对上式连续求导得θθ−=ϕϕ&&sin cos 3θθ−θθ−=ϕϕ−ϕϕ&&&&&&sin cos sin 3cos 322将o 30=ϕ=θrad/s 3/A−=−=θr v &0=θ&&代入得rad/s 1=ϕ&2rad/s 3/38−=ϕ&&令BC =ρ则有θ−ϕ=ρsin cos 3r r 因此cm/s 320|)cos sin 3(30r =θθ+ϕϕ−=ρ==ϕ=θo&&&r v7.32 图示机构中已知杆AB 相对杆OA 的角速度ω=ωr 杆AB 相对杆OA 的角加速度0r =α杆AB 长为l 2l OC =求图示位置杆AB 上点B 的速度和加速度解矢量法杆动系杆OA r AB ω+ω=ωOA r AB ααα+=0r =α动系套筒AB C ω=ωABC αα=e r a v v v +=ea 30cos v v =oω=ω2OA ω=ω=ω3AB Clv v a ω==32/r k n e e r n a a a a a a a a +++=+ττOA 3αl 2OA 3ωl C αl 2C ωl r C 2v ωx ′k e n a a 30sin 30cos a a a a −−=−−ττo o 2OA C 38ω=α=αy ′n e r n a a 30cos 30sin a a a a −−=−τo o 2r 15ω=a动系套筒er a v v v ′+′=′Q r r v v =′e e v v −=′iv l a ω−=′32kn e e r a a a a a a ′+++′=′′τ′其中r r a a =′ττ′−=e e a a n e n e a a −=′kk a a =′xl a a a a a 2e k n e r ax 1530cos )(30sin )(ω−=−′++′−=′τ′′o oy l a a a a a 2e k n e r ay 31130sin )(30cos )(ω−=−′−+′−=′τ′′o o 分析法本题一自由度取θϕ为坐标存在如下约束)sin(sin 3=ϕ+θ−θ对上式连续求导有0))(cos(cos 3=ϕ+θϕ+θ−θθ&&&0))(sin())(cos(cos 3sin ))(cos()sin (cos 322=ϕ+θϕ+θ+ϕ+θϕ+θ−θθ+ϕ+θϕ+θ−θθ−θθ&&&&&&&&&&&&o 30=ϕ=θ时ω=ω=θr &0=α=θr&&代入以上二式得ω=ϕ2&238ω=ϕ&&取为原点点坐标为)cos(2cos 3ϕ+θ+ϕ−=l l x B )sin(2sin 3ϕ+θ+ϕ−=l l y B 对上二式连续求导并代入具体数值解出l l l xB ω−=ϕ+θϕ+θ−ϕϕ=32))(sin(2sin 3&&&&0))(cos(2cos 3=ϕ+θϕ+θ+ϕϕ−=&&&&l l y B )cos (sin 32ϕϕ+ϕϕ=&&&&&l xB l l 2215]))(cos())([sin(2ω−=ϕ+θϕ+θ+ϕ+θϕ+θ−&&&&&&)sin (cos 32ϕϕ−ϕϕ−=&&&&&l y B l l 22311]))(sin())([cos(2ω−=ϕ+θϕ+θ−ϕ+θϕ+θ+&&&&&&。
昆明理工大学理论力学B练习册题解答

1.1.14当软绳受两个等值反向的压力时,可以平衡。(×)
1.1.15静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。(∨)
1.1.16静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
(∨)
1.1.17凡是两端用铰链连接的直杆都是二力杆。(×)
二、填空题
4.2.1考虑摩擦时物体的平衡问题,其特点在于P116(1),(2),(3)。
4.2.2物快重P,放置在粗糙的水平面上,接触处的摩擦系数为fs,要使物块沿水平面向右滑动,可沿OA方向施加拉力F1如图4.1所示,也可沿BO方向施加推力F2如图所示,两种情况比较图(a)所示的情形更省力。
4.2.3材料相同、光洁度相同的平皮带和三角皮带,如图4.2所示,在相同压力F作用下,三角皮带的最大摩擦力大于平皮带的最大摩擦力。
1.1.18如图1.1所示三铰拱,受力F,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。(×)
二、填空题
1.2.1力对物体的作用效应一般分为外效应和内效应。
1.2.2对非自由体的运动所预加的限制条件称为约束;约束力的方向总是与约束所能阻止的物体的运动趋势的方向相反;约束力由主动力引起,且随主动力的改变而改变。
(答案:FB=40kN,FAy=15kN,FC=5kN ,FD=15kN)
2.3.6如图所示组合梁由AC和DC两段铰接构成,起重机放在梁上,已知起重机重P=50kN,重心在铅直线EC上,起重载荷P1=10kN,如不计梁重,求支座A、B和D三处的约束反力。
(答案:FB=100kN,FAy=48.3kN,FD=8.33kN.m)
昆明理工大学理论力学B练习册题+解答

第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
(完整word版)理论力学课后习题及答案解析.docx

理论力学教科书课后习题及解析第一章偶,大小是260Nm,转向是逆时针。
习题 4- 1.求图示平面力系的合成结果,长度单位为m。
习题 4- 3.求下列各图中平行分布力的合力和对于 A 点之矩。
解: (1) 平行力系对 A 点的矩是:解: (1) 取 O 点为简化中心,求平面力系的主矢:取 B 点为简化中心,平行力系的主矢是:求平面力系对O 点的主矩:平行力系对 B 点的主矩是:(2)合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;向 A 点简化的结果是一个力R A和一个力偶M A,且:如图所示;将 R B向下平移一段距离d,使满足:最后简化为一个力R ,大小等于R B。
其几何意义是: R 的大小等于载荷分布的将 R A向右平移一段距离d,使满足:矩形面积,作用点通过矩形的形心。
(2)取 A 点为简化中心,平行力系的主矢是:最后简化为一个力R,大小等于R A。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
平行力系对 A 点的主矩是:列平衡方程:习题 4-4 .求下列各梁和刚架的支座反力,长度单位为m。
解方程组:反力的实际方向如图示。
校核:解: (1) 研究 AB 杆,受力分析,画受力图:结果正确。
(2) 研究 AB 杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:(3) 研究 ABC ,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:列平衡方程:反力的实际方向如图示。
校核:解方程组:结果正确。
反力的实际方向如图示。
校核:结果正确。
习题 4-5 .重物悬挂如图,已知G=1.8kN ,其他重量不计;求铰链 A 的约束反力和杆 BC 所受的力。
列平衡方程:解方程组:解: (1) 研究整体,受力分析(BC 是二力杆),画受力图:反力的实际方向如图示。
列平衡方程:习题 4-8 .图示钻井架,G=177kN ,铅垂荷载P=1350kN ,风荷载 q=1.5kN/m ,水平力 F=50kN ;求支座 A 的约束反力和撑杆CD 所受的力。
昆明理工大学理论力学B练习册题+解答

第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
昆明理工大学理论力学练习册答案(第七章后)

8.2.1刚体的平面运动可以简化为一个___平面图形_____在自身平面内的运动。平面图形的运动可以分解为随基点的__平动__和绕基点的_转动___。其中,__平动______部分为牵连运动,它与基点的选取__有__关;而__转动____部分为相对运动,它与基点的选取_无___关。
8.2.2如图8.1所示,圆轮半径为R,沿固定平面只滚不滑,已知轮心速度为 ,选轮心为基点,则图示瞬时轮缘上M点牵连速度的大小为vO,相对速度的大小为vO,方向在图上标出。
(3)若 则必有 。(∨)
7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。(×)
7.1.10当牵连运动为定轴转动时一定有科氏加速度。(×)
二、填空题
7.2.1牵连点是某瞬时动系上与动点重合的那一点。
7.2.2在ve与vr共线情况下,动点绝对速度的大小为 ,在情况下,动点绝对速度的大小为 ,在一般情况下,若已知ve、vr,应按_________计算va的大小。
中⑤。
①图(a)所示系统动量守恒;②图(b)所示系统动量守恒;
③图(c)所示系统动量守恒;④图示三系统动量均守恒;⑤图示三系统动量均不守恒。
(a) (b) (c)
10.3.3若作用于质点系的外力在某段时间内在固定坐标Ox轴上投影的代数和等于零,则在这段时间内②。
①质点系质心的速度必保持不变;②质点系动量在x轴上的投影保持不变;③质点系质心必静止不动。
四、计算题
7.4.1杆OA长L,由推杆BC通过套筒B推动而在图面内绕点O转动,如图所示。假定推杆的速度为 ,其弯头高为 。试求杆端A的速度的大小(表示为由推杆至点O的距离 的函数)。
7.4.2在图a和b所示的两种机构中,已知 。求图示位置时杆 的角速度。
理论力学习题集昆明理工大学工程力学系

第一章 静力学公理和物体的受力分析一、是非判断题1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( ) 1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( ) 1.4 力的可传性只适用于刚体,不适用于变形体。
( ) 1.5 两点受力的构件都是二力杆。
( ) 1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( ) 1.7 力的平行四边形法则只适用于刚体。
( ) 1.8 凡矢量都可以应用平行四边形法则合成。
( ) 1.9 只要物体平衡,都能应用加减平衡力系公理。
( ) 1.10 凡是平衡力系,它的作用效果都等于零。
( ) 1.11 合力总是比分力大。
( ) 1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( ) 1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ) 1.14 当软绳受两个等值反向的压力时,可以平衡。
( ) 1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ) 1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
1.17 凡是两端用铰链连接的直杆都是二力杆。
( )1.18 如图所示三铰拱,受力F ,F 1作用, 其中F 作用于铰C 的销子上,则AC 、 BC 构件都不是二力构件。
( )二、填空题 1.1 力对物体的作用效应一般分为 效应和 效应。
1.2 对非自由体的运动所预加的限制条件称为 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 ;约束力由 力引起,且随 力的改变而改变。
1.3 图示三铰拱架中,若将作用于构件AC 上的力偶M处的约束力 。
A. 都不变;B. 只有C 处的不改变;C. 都改变;D. 只有C 处的改变。
三、受力图1-1 画出各物体的受力图。
昆明理工大学工程力学习题集册答案解析

第一章静力学基础二、填空题2、1 –F1 sinα1; F1 cosα1; F2 cosα2; F2 sinα2; 0;F3; F4 sinα4; F4 cosα4。
2、2 1200, 0。
2、3 外内。
2、4约束; 相反; 主动主动。
2、53,2、6力偶矩代数值相等(力偶矩得大小相等,转向相同)。
三、选择题3、1(c)。
3、2A。
3、3 D。
3、4D。
3、5 A。
3、6B。
3、7C。
3、8四、计算题4、1(d)(a) (b) (c)4、2五 、受力图 5、15、2(a)(c)ACC AB B(b)A5、3q(c)P 2(1)小球(2)大球(1) AC 杆 (2) CB 杆 (3)整体 (1) (2) (3)整体(d)(1) CD 杆 (2) AB 杆 (3) OA 杆C(i)(1) 滑轮D (2) AB 杆 (3) CD 杆(1) AB 杆 (2) CD 杆 (3)整体B BA B1、1、2 ( × )二、填空题2、1 平衡 。
2、2 分布载荷图形得面积 , 合力矩定理 , 分布载荷图形得形心 。
2、3 平行力系合力得作用点 ; 物体合重力得作用点 ; 物体得几何中心 。
三、计算题3、13、2:解:由(2、10)式:由(2、14)式:BB第三章力系得平衡方程及其应用一、就是非判断题1、1( ∨) ;1、2 ( ×);1、3 ( ∨) ;1、4( ×);1、5 ( ×);1、6 ( ∨)二、填空题2、1力偶矩得代数值相等; 。
2、2力多边形自行封闭; 。
2、3, A、B得连线不垂直x轴。
2、4, A、B、C三点不共线。
2、5(a)、(b)、(c)、(d)。
三、计算题解:取锻锤为研究对象∵力偶只能用力偶平衡,∴F A = F B方向如图。
3、23、33、4(c)CF(d)(b)DF 1q解:取CD 为研究对象3、5取ABC 为研究对象D EP 1解:取EBCD 为研究对象∴杆AC 受压3、6360˚解:取整体为研究对象,设滑轮E 得半径为r 。
理论力学练习册及答案
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影,得:
再取动点杆O1C上C点,动系固连套筒B上,定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影,得:
取 方向投影,得:
第八章 刚体平面运动
8-1.已知图示机构滑块B,沿水平方向按规律SB=0.01t2+0.18t m移动,通过连杆AB带动半径R=0.1 m的轮子沿水平方向只滚不滑。求当t=1 s时,点A和点C在图示位置的速度和加速度。
解:当 时,
由于杆AB作瞬时平动,且P为轮C
的速度瞬心,故有:
8-2.曲柄OA=17 cm,绕定轴O转动的角速度ωOA=12 rad/s,AB=12 cm,BD=44 cm,滑块C、D分别沿着铅垂与水平滑道运动,在图示瞬时OA铅垂,求滑块C与D的速度。
2、研究滑块A运动副,求 ,
3、分别作套筒o运动副、滑块A运动副
加速度图,
4、研究杆BE,作O、A加速度图,
5、分别列O、A点加速度投影式求解
7-7.圆盘半径OA=r,可绕其边缘上一点A转动,从而带动直杆BC绕B点转动,AB=3r,且直杆与圆盘始终相切,当圆盘中心运动到AB连线上时,圆盘转动的角速度为ω,角加速度为ε,求此瞬时直杆BC的角速度和角加速度。
8-5.滑块B、D在铅直导槽中滑动,通过连杆BA及CD与轮子A相连,各连接处都是光滑铰链。轮A放在水平面上,AB=10 cm,CD=13 cm。在图示瞬时,即轮心A至两铅垂导槽的距离均为8 cm时,可在水平面上自由滚动的轮子,其轮心速度νA=30 cm/s,方向水平向右。求此时滑块D的速度。
昆明理工大学理论力学B练习册题+解答

1 / 27第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
昆明理工大学工程力学习题集册答案解析

第一章 静力学基础二、填空题2.1 –F 1 sin α1; F 1 cos α1; F 2 cos α2; F 2 sin α2 ; 0 ;F 3 ; F 4 sin α4; F 4 cos α4。
2.2 1200, 0 。
2.3 外 内 。
2.4 约束 ; 相反 ; 主动 主动 。
2.5 3 ,2.6 力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题 3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.1(d)(a) (b) (c)mmKN F M ⋅-=18030)(mmKN F M ⋅=-=3.2815325)(20mmKN F M ⋅-=25210.)(4.2五 、受力图5.15.2(a)(c)ACCAB B(b)1=)(F M x mN F M y ⋅-=501)(01=)(F M z m N F M x ⋅-=2252)(m N F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M x ⋅=2253)(mN F M y ⋅-=2253)(mN F M z ⋅=2253)(qAM BA(c)P 2(d)5.3(1) 小球 (2) 大球(3) 两个球合在一起P 2P 1ACB(a)(1) AB 杆 (2) CD 杆 (3)整体(1) AC杆(2) CB杆(3)整体(1) AC段梁(2) CD段梁(3)整体第二章 力系的简化一、是非判断题1.1 ( × ) 1.2 ( ∨ ) 1.2 ( × ) 二、填空题2.1 平衡 。
2.2 分布载荷图形的面积 , 合力矩定理 , 分布载荷图形的形心 。
2.3 平行力系合力的作用点 ; 物体合重力的作用点 ; 物体的几何中心 。
三、计算题 3.1F 3F 1ykNX 98340.=⋅⋅⋅=∑kNY 13587.=⋅⋅⋅=∑解:由(2.10)式:kNY X F R 9667822.)()('=+=∑∑(1) CD 杆 (2) AB 杆 (3) OA 杆C(i)(1) 滑轮D (2) AB 杆 (3) CD 杆(j)DDF PPABKIBCF AY AX IY IX KY CID,DF ,BCF 'IX 'I Y DCE,EFFCF ABE.EF AY AX BY BX CAO,CF,A Y ,AXY 0X3.2第三章 力系的平衡方程及其应用一、是非判断题1.1 ( ∨ ) ;1.2 ( × );1.3 ( ∨ ) ;1.4 ( × );1.5 ( × );1.6 ( ∨ )(a)(b)5020.cos '==∑R F Xα8650.cos '==∑R F Y βcmkN FM M i ⋅=⋅⋅⋅==∑58460000.)(kNF F R R 96678.'==cm F M d R7860.'==M=c mmc 086.=mm125.mm1210.由(2.14)式:二、填空题2.1 力偶矩的代数值相等 ; 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 点的合成运动一、是非题7.1.1动点的相对运动为直线运动,牵连运动为直线平动时,动点的绝对运动必为直线运动。
( × ) 7.1.2无论牵连运动为何种运动,点的速度合成定理r e av v v +=都成立。
( ∨ ) 7.1.3某瞬时动点的绝对速度为零,则动点的相对速度和牵连速度也一定为零。
( × ) 7.1.4当牵连运动为平动时,牵连加速度等于牵连速度关于时间的一阶导数。
(∨ ) 7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。
( × ) 7.1.6不论牵连运动为何种运动,关系式a a +a a r e =都成立。
( × ) 7.1.7只要动点的相对运动轨迹是曲线,就一定存在相对切向加速度。
( × )7.1.8在点的合成运动中,判断下述说法是否正确:(1)若r v 为常量,则必有r a =0。
( × ) (2)若e ω为常量,则必有e a =0. ( × ) (3)若e rωv //则必有0=C a 。
( ∨ )7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
( × ) 7.1.10当牵连运动为定轴转动时一定有科氏加速度。
( × )二、 填空题7.2.1 牵连点是某瞬时 动系 上与 动点 重合的那一点。
7.2.2在 v e 与v r 共线 情况下,动点绝对速度的大小为e a v v =大小为22r e a v v v +=,在一般情况下,若已知v e 、v r ,应按v a的大小。
三、选择题:7.3.1 动点的牵连速度是指某瞬时牵连点的速度,它相对的坐标系是( A )。
A 、 定参考系B 、 动参考系C 、 任意参考系7.3.2 在图示机构中,已知t b a s ωsin +=, 且t ωϕ=(其中a 、b 、ω均为常数),杆长为L ,若取小球A 为动点,动系固结于物块B ,定系固结于地面,则小球的牵连速度v e 的大小为( B )。
A 、 ωLB 、 t b ωωcosC 、 t L t b ωωωωcos cos +D 、ωωωL t b +cos四、计算题7.4.1 杆OA 长L ,由推杆BC 通过套筒B 推动而在图面内绕点O 转动,如图所示。
假定推杆的速度为v ,其弯头高为b 。
试求杆端A 的速度的大小(表示为由推杆至点O 的距离x 的函数)。
2学时对完概念题的答案和从最后到第十二章动能定理的讲解7.4.2 在图a 和b 所示的两种机构中,已知s rad mm b O O /3,200121===ω。
求图示位置时杆A O 2的角速度。
7.4.3 图示四连杆平行形机构中,m m 10021==B O A O ,A O 1以等角速度rad/s 2=ω绕1O 轴转动。
杆AB 上有一套筒C ,此筒与滑杆CD 相铰接。
机构的各部件都在同一铅直面内。
求当ο60=ϕ时,杆CD 的速度和加速度。
解:取滑块C 为动点,动系固连在杆AB 上;则动点的绝对运动为铅垂方向的直线运动,相对运动为沿AB 杆的直线运动,牵连运动平动。
re a v v v ρρρ+=)式:由(7-7sm A O v v A e /2.01=⋅==ω其中:解:(a) 取滑块A 为动点,动系固连在杆O 1A上;则动点的绝对运动为绕O 2点的圆周运动,相对运动为沿O 1A 杆的直线运动,牵连运动为绕O 1点的定轴转动。
re a v v v ρρρ+=)式:由(7-7111其中:ωωb A O v e =⋅=030cos /:则e a v v =由几何关系02102230cos 2)30cos 2()30cos 2(/2ωω====b v b v A O v e a a A o )(/24323逆时时s rad =⨯=(b) 取滑块A 为动点,动系固连在杆O 2A 上;则动点的绝对运动为绕O 1点的圆周运动,相对运动为沿O 2A 杆的直线运动,牵连运动为绕O 2点的定轴转动。
re a v v v ρρρ+=)式:由(7-7030cos :则a e v v =由几何关系)逆时(/5.12)2()30cos 2(/1022针s rad b v b v A O v a e e A o =====ωω111其中:ωωb A O v a =⋅=径为R 的半圆形凸轮C 等速u 水平向右运动,带动从动杆AB 沿铅直方向上升,如图所示。
求ο30=ϕ时杆AB如图所示,半径为r 的圆环内充满液体,液体按箭头方向以相对速度v 在环内作匀速运动。
如圆环以等角速1和2处液体的绝对加速度的大小。
7.4.6 图示直角曲杆OBC 绕O 轴转动,使套在其上的小环M 沿固定直杆OA 滑动。
已知:m 1.0=OB ,OB 与BCa t ra re a v v v ρρρ+=u v v e r 332cos /==ϕnr t r e a a a a a ρρρρ++=Ru R v a n r3422==Ru a a n rt r934tan 2=⨯=ϕ)(/1.0cos ↑===s m v v v e a CD ϕ则:re a +=由(137-22214.021.0s m A O a a nA e =⨯=⋅==ω其中:ο60sin 4.0sin ⨯=⋅==ϕe a CD a a a 则:)(346.032.02↑==s m 1、2处的液体为动点,动系固连在圆环上。
则动点的绝对运动为曲线运动,相对运动为沿圆环的匀速圆周运动,牵连运动为绕O 点的匀速定轴转动。
c r e a a a a a ++=)式:20-7由(21其中:ωr a n e =)(a a a a a cn r n e a ++=⇒va c ω21=225ωr a n e =v a c ω22=)(2221111↑++-=++-=v r v r a a a a c n r n e a ωω对1点:将(a )式向y 轴投影得: vr v r a a a a c n r n e x a ωωϕ2sin 222222---=---=2222cos ωϕr a a n e y a -=-=42222222224)2(ωωωr v r v r a a a ya x a a +++=+=∴4222222224)2(2cos ωωωωωαr v r v r v r v r a a a x a +++++-==rv a n r 22=v a n r 21=对2点:将(a )式向x 、y 轴投影得:52cos 51sin ==ϕϕ,422222224)2(2cos ωωωωβr v r v r r a a a y a +++-==垂直,曲杆的角速度 rad/s 5.0=ω,角加速度为零。
求当ο60=ϕ时,小环M 的速度和加速度。
第八章 刚体的平面运动一、是非题8.1.1刚体运动时,若已知刚体内任一点的运动,则可由此确定刚体内其它各点的运动。
( × ) 8.1.2刚体作平面运动时,其上任意一点的轨迹为平面曲线。
( ∨ ) 8.1.3平面图形的速度瞬心只能在图形内。
( × )8.1.4当平面图形上A 、B 两点的速度v A 和v B 同向平行,且AB 的连线不垂直于v A 和v B ,则此时图形作瞬时平动,v v A B =。
( ∨ ) 8.1.5平面图形上A 、B 两点的速度v A 和v B 反向平行的情形是不可能存的。
( × ) 8.1.6已知刚体作瞬时平动,有ω=0,因此必然有0=α。
( × ) 8.1.7刚体作瞬时平动时,刚体上各点的加速度都是相等的。
( × )8.1.8只要角速度不为零,作平面运动的刚体上的各点一定有加速度。
( × )8.1.9刚体作平面运动时,平面图形内两点的速度在任意轴上的投影相等。
( × )二、填空题8.2.1刚体的平面运动可以简化为一个___平面图形_____在自身平面内的运动。
平面图形的运动可以分解为随基点的__平动__和绕基点的_转动___。
其中,__平动______部分为牵连运动,它与基点的选取__有__关;而__转动____部分为相对运动,它与基点的选取_无___关。
8.2.2如图所示,圆轮半径为R ,沿固定平面只滚不滑,已知轮心速度为v O ,选轮心为基点,则图示瞬时轮缘上M 点牵连速度的大小为 v O ,相对速度的大小为 v O ,方向在图上标出。
re a v v v +=)式:由(7-7tBA n BA A B a a a a ++=刚体作平面运动解:取小环M 为动点,动系固连在直角杆OBC 上。
则动点的绝对运动为沿OA 杆的直线运动,相对运动为沿BC 杆的直线运动,牵连运动为绕O 点的定轴转动。
ϕωωcos 其中:OB OM v e ⋅=⋅=)(/1732.031.0则:→=⨯===s m tg v v v e a M ϕsm /1.021.05.0=⨯⨯=)(/2.021.0cos 方向如图s m v v e r =⨯==ϕϕωωcos ,0其中:22OB OM a a n ete ⋅=⋅==r r e c v v a ωω22==将(a )式向x 轴投影得: c n e aa a a ++-=0cos cos ϕϕr a v OB a ωω222+⋅-=⇒)(35.04222→==+⋅-==⇒s m v OB a a r a M Λωω)()式:207由(a a a a a a cr n e t e a +++=-8.2.3边长为L 的等边三角形板在其自身平面内运动。
A 点的速度大小为v A ,沿AC 方向,B 点的速度沿CB ____ ___ _______。
8.2.4如图所示,塔轮沿直线轨道作纯滚动,外轮半径为R ,内轮半径为r ,轮心的速度和加速度为v O 、a O 。
则外轮缘上A 、B 、C 、D 四点的加速度分别为 ____________=A a , ____________=Ba ,___________=Ca , ____________=D a 。
三、选择题8.3.1某瞬时,平面图形(图)上任意两点A 、B 的速度分别为v A 和v B ,则此时该两点连线中点D 的速度为( B )。
A. B A D v v v ρρρ+= B. ()2B A D v v v ρρρ+=C. ()2B A D v v v ρρρ-=D. ()2A B D v v v ρρρ-=8.3.2三角形板DCE 与等长的两杆AD 和BC 铰接如图所示,面内运动。
图示瞬时杆AD 以匀角速度ω转动,则E 度为( A )。
