第三章 多变量回归分析(计量经济学,南开大学)
合集下载
计量经济学中的回归分析方法
计量经济学中的回归分析方法计量经济学是经济学中的一个重要分支，它主要是利用经济数据来进行定量分析。
而对于计量经济学来说，最重要的方法之一就是回归分析。
回归分析方法可以用来寻找变量之间的关系，进而预测未来的趋势和结果。
本文将介绍回归分析方法的基本原理及其在计量经济学中的应用。
回归分析的基本原理回归分析是一种利用数据来寻找变量之间关系的方法，其核心原理是利用多元线性回归模型。
多元线性回归模型可以描述多个自变量与一个因变量之间的关系，如下所示：Y = β0 + β1X1 + β2X2 + … + βkXk + ε其中，Y表示因变量，即需要预测的变量；X1、X2、 (X)表示自变量，即可以通过对它们的变化来预测Y的变化；β0、β1、β2、…、βk表示模型中的系数，它们可以反映每个自变量对因变量的影响；ε表示误差项，即预测结果与真实值之间的差异。
利用回归分析方法，我们可以通过最小化误差项来得到最佳的系数估计值，从而建立一个能够准确预测未来趋势和结果的模型。
回归分析的应用在计量经济学中，回归分析被广泛应用于各个领域。
下面我们以宏观经济学和微观经济学为例，来介绍回归分析在计量经济学中的具体应用。
1. 宏观经济学：用回归分析预测国内生产总值（GDP）国内生产总值是一个国家经济发展的重要指标，因此预测GDP 的变化是宏观经济学研究的重点之一。
在这个领域，回归分析可以用来寻找各种经济因素与GDP之间的关系，进而通过对这些因素的预测来预测GDP的变化。
例如，我们可以通过回归分析来确定投资、消费、进出口等因素与GDP之间的关系，进而利用这些关系来预测未来的GDP变化。
2. 微观经济学：用回归分析估算价格弹性在微观经济学中，回归分析可以用来估算价格弹性。
价格弹性可以衡量消费者对价格变化的敏感度，其计算公式为：价格弹性= %Δ数量÷ %Δ价格例如，如果价格变化1%，相应数量变化1.5%，那么价格弹性就是1.5 ÷ 1 = 1.5。
计量经济学导论
第十六页，编辑于星期三：七点 五十五分。
1995 Robert E. Lucas Jr.
1994 John C. Harsanyi, John F. Nash Jr., Reinhard Selten 1993 Robert W. Fogel, Douglass C. North 1992 Gary S. Becker
Memory of Alfred Nobel 1969
for having developed and applied dynamic models for the analysis of economic processes
Ragnar Frisch Norway
Jan Tinbergen the etherlands
Economic Forecasts. 4rd ed. McGraw-HILL,1998.
[21] Veerbeek M. A Guide to Modern Economertrics.England:John Wiley and Sons Ltd,2000.
第四页，编辑于星期三：七点 五十五分。
1972 John R. Hicks, Kenneth J. Arrow 1971 Simon Kuznets 1970 Paul A. Samuelson
1969 Ragnar Frisch, Jan Tinbergen
第十九页，编辑于星期三：七点 五十五分。
The Bank of Sweden Prize in Economic Sciences in
中级计量经济学 讲课提纲
第一页，编辑于星期三：七点 五十五分。
参考文献
[1] 李子奈 . 计量经济学 (第二版 ). 北京：高等教育出版社， 2005. [2] 于 俊 年 ． 计 量 经 济 学 ( 第 二 版 ). 北 京 ： 对 外 经 济 贸 易 大 学 出 版
1995 Robert E. Lucas Jr.
1994 John C. Harsanyi, John F. Nash Jr., Reinhard Selten 1993 Robert W. Fogel, Douglass C. North 1992 Gary S. Becker
Memory of Alfred Nobel 1969
for having developed and applied dynamic models for the analysis of economic processes
Ragnar Frisch Norway
Jan Tinbergen the etherlands
Economic Forecasts. 4rd ed. McGraw-HILL,1998.
[21] Veerbeek M. A Guide to Modern Economertrics.England:John Wiley and Sons Ltd,2000.
第四页，编辑于星期三：七点 五十五分。
1972 John R. Hicks, Kenneth J. Arrow 1971 Simon Kuznets 1970 Paul A. Samuelson
1969 Ragnar Frisch, Jan Tinbergen
第十九页，编辑于星期三：七点 五十五分。
The Bank of Sweden Prize in Economic Sciences in
中级计量经济学 讲课提纲
第一页，编辑于星期三：七点 五十五分。
参考文献
[1] 李子奈 . 计量经济学 (第二版 ). 北京：高等教育出版社， 2005. [2] 于 俊 年 ． 计 量 经 济 学 ( 第 二 版 ). 北 京 ： 对 外 经 济 贸 易 大 学 出 版
南开大学计量经济学课件回归方程的变量和形式
检验判断1994年之前和之后两段时期消费函数是否产生显著的
差异。
7.2 模型的稳定性检验
2、Chow预测检验
Chow预测检验是先对包含前T1个观察值的子样本 建立模型，然后用这个模型对后T2个观察值的自变量 进行预测，如果实际值与预测值有很大变动，就可以 怀疑模型中存在结构性变化。T1 和T2的相对大小，没 有确定的规则，可能根据如战争、石油危机、经济改 革等明显的转折点来确定，如果不存在这样明显的转 折点，常用的方法是用85%-90%的数据进行估计，剩 余的数据进行检验。
7.2 模型的稳定性检验
1、Chow断点（Breakpoint）检验
实例一：估计C-D函数 log(Y ) 0 1 log(L) 2 log(K )
（1）1929－1967年数据估计如下 log(Y ) 3.938 1.451log(L) 0.384log(K )
R 2 0.9946 , R 2 0.9943 , RSS 0.0434 （2）分1929-1948和1949－1967两段数据估计如下 log(Y ) 4.058 1.617log(L) 0.220log(K )
3、冗余（Redundant)变量检验
检验一部分变量的统计显著性，通过判断方程中一
部分变量系数是否与0没有显著差异，决定是否从方程 中剔除这些变量，检验方法可以通过F检验和似然比 （LR）检验。 冗余变量检验是遗漏变量检验逆过程。
Eviews实现过程：
View－Coefficient Tests－Redundant Variables－
7.2 模型的稳定性检验
1、Chow断点（Breakpoint）检验（邹至庄断点检验） 思想：对每个子样本单独拟合方程，并与对于全部样本 拟合方程进行比较，来观察每个子样本的估计方程是否 有显著差异，判断是否存在结构变化。 零假设：两个子样本拟合的方程无显著差异。即结 构没有发生变化。 如果拒绝零假设，则代表有显著差异，意味着模型 中存在结构变化。
南开计量经济学课件 (3)
以下非线性回归模型是无法用最小二乘法估计参数的。 可采用非线性方法进行估计。估计过程非常复杂和困难，计 算机的出现大大方便了非线性回归模型的估计。专用软件使 这种计算变得非常容易。但本章不是介绍这类模型的估计。
下面介绍几种典型的可以做线性化处理的非线性模型。
(1)多项式函数模型(1)
多项式方程
（第3版教材第90页）
案例4 ：钉螺存活率曲线（file:nonli3）（生长曲线模型）
100
Y 80
60
40
20
T
0
0
2
4
6
8
10
12
案例4：钉螺存活率曲线（file:nonli3）（生长曲线模型）
钉螺存活率样本值与拟合值。
100 Y YF
80
60
40
20
T
0
2
4
6
8
10
12
点预测：当t = 6.5月时
yˆt
101 1 e4.310.76536.5
还原，Lny = Ln(7.33) + 104.5 (1/x) 104.5( 1 )
y 7.33e x
(6) 幂函数模型(全对数模型)
(b > 1)
(b = -1) (b < -1)
(0<b <1)
(0 > b > -1)
yt axt b eut
b取不同值的图形分别见上图。对上式等号两侧同取对数，得
(4) 生长曲线 (logistic) 模型（与教材中的模型稍异，称S曲线）
Y k
Y k
k/2
0
0
(lnb)/a
t
t
下面介绍几种典型的可以做线性化处理的非线性模型。
(1)多项式函数模型(1)
多项式方程
（第3版教材第90页）
案例4 ：钉螺存活率曲线（file:nonli3）（生长曲线模型）
100
Y 80
60
40
20
T
0
0
2
4
6
8
10
12
案例4：钉螺存活率曲线（file:nonli3）（生长曲线模型）
钉螺存活率样本值与拟合值。
100 Y YF
80
60
40
20
T
0
2
4
6
8
10
12
点预测：当t = 6.5月时
yˆt
101 1 e4.310.76536.5
还原，Lny = Ln(7.33) + 104.5 (1/x) 104.5( 1 )
y 7.33e x
(6) 幂函数模型(全对数模型)
(b > 1)
(b = -1) (b < -1)
(0<b <1)
(0 > b > -1)
yt axt b eut
b取不同值的图形分别见上图。对上式等号两侧同取对数，得
(4) 生长曲线 (logistic) 模型（与教材中的模型稍异，称S曲线）
Y k
Y k
k/2
0
0
(lnb)/a
t
t
第三章多变量回归分析(计量经济学南开大学)
根据残差的平方和最小化的原理，解出参数的估计量。 ˆ ˆ X ˆ X )2 ˆ i2 (Yi 残差平方和RSS u 1 2 2i k ki
ˆ 'u u ˆ u ˆ Y Xβ ˆ ˆ Y Xβ u ˆ )' ( Y Xβ ˆ) ˆ i2 u ˆ ' u ( Y Xβ RSS u ˆ ' X' Y β ˆ ' X' Xβ ˆ Y' Y β ˆ ' X' Y Y ' Y 2β
ˆ 2代替 2，则 如果 2未知，以 2 1 ˆ )的估计量为： ˆ（ Var Cov(β X' X）
2 1 1 ˆ 的标准差Se(β ˆ )为 ˆ（ ˆ β X' X） （X' X）
ˆ 的性质： 四、OLS估计量 β
1 、线性 1 ˆ （ β [ X' X） X' ]Y 2、无偏性 ˆ] β E[β 3、最小方差性 ˆ 具有Var (β ˆ )最小。 OLS估计量β
X X X X
2i 2 2i 3i
2i
X X X X
3i 2i 2
3i
3i
X X X X X
ki
X ki X 2i 1 X 22 X 32 X k2 1 X 23 X 33 X 3k
X ki X 3i
ˆ 1 ˆ 2i ki ˆ2 3i ki 3 2 ˆ X ki k
二、 的估计量
2 ˆ u i
ˆ ' X' Y β ˆ ' X' Xβ ˆ ˆ Y' Y 2β u ˆ u ˆ 0 2 X' Y 2 X' Xβ
第二章 双变量回归分析(计量经济学,南开大学)
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
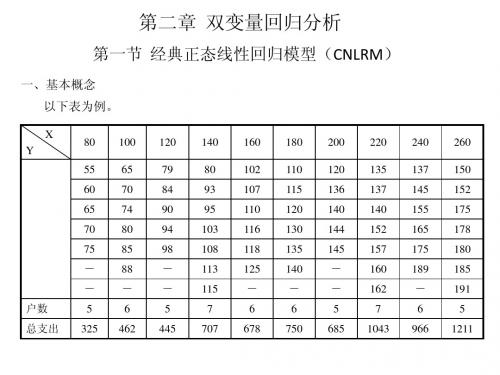
6、样本回归函数（SRF） 由于在大多数情况下，我们只知道变量值得一个样本，要用样本信息的基础 上估计PRF。(表） 样本1
X（收入） Y（支出） 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ： 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差：VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量（Estimator）：一个估计量又称统计量(statistic)，是指一个规则、公式 或方法，以用来根据已知的样本所提供的信息去估计总体参数。在应用中，由估 计量算出的数值称为估计（值）（estimate)。 样本回归函数SRF的随机形式为：
南开大学计量课件多元线性回归异方差问题共43页文档
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
南开大学计量课件多元线性回归异方 问题
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
45、自己的饭量自己知道。——苏联
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
南开大学计量课件多元线性回归异方 问题
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
计量经济学 张晓峒 第三版 南开大学出版社
第四章一、练习题 （一）简答题1、多元线性回归模型的基本假设是什么？试说明在证明最小二乘估计量的无偏性和有效性的过程中，哪些基本假设起了作用？2、多元线性回归模型与一元线性回归模型有哪些区别？3、某地区通过一个样本容量为722的调查数据得到劳动力受教育的一个回归方程为fedu medu sibs edu 210.0131.0094.036.10++-=R 2=0.214式中，edu 为劳动力受教育年数，sibs 为该劳动力家庭中兄弟姐妹的个数，medu 与fedu 分别为母亲与父亲受到教育的年数。
问（1）若medu 与fedu 保持不变，为了使预测的受教育水平减少一年，需要sibs 增加多少？（2）请对medu 的系数给予适当的解释。
（3）如果两个劳动力都没有兄弟姐妹，但其中一个的父母受教育的年数为12年，另一个的父母受教育的年数为16年，则两人受教育的年数预期相差多少？ 4、以企业研发支出（R&D ）占销售额的比重为被解释变量（Y ），以企业销售额（X1）与利润占销售额的比重（X2）为解释变量，一个有32容量的样本企业的估计结果如下：099.0)046.0()22.0()37.1(05.0)log(32.0472.0221=++=R X X Y其中括号中为系数估计值的标准差。
（1）解释log(X1)的系数。
如果X1增加10%，估计Y 会变化多少个百分点？这在经济上是一个很大的影响吗？（2）针对R&D 强度随销售额的增加而提高这一备择假设，检验它不虽X1而变化的假设。
分别在5%和10%的显著性水平上进行这个检验。
（3）利润占销售额的比重X2对R&D 强度Y 是否在统计上有显著的影响？ 5、什么是正规方程组？分别用非矩阵形式和矩阵形式写出模型：i ki k i i i u x x x y +++++=ββββ 22110，n i ,,2,1 =的正规方程组，及其推导过程。
6、假设要求你建立一个计量经济模型来说明在学校跑道上慢跑一英里或一英里以上的人数，以便决定是否修建第二条跑道以满足所有的锻炼者。
南开大学计量多元线性回归异方差问题
和为
2
wi2
2
i
wi2
yi b0b1xi
获得的估计量就是加权最小二乘估计量。对于多元线性回
归模型y=Xβ＋u，令权数序列wi =1/i ，W为N×N对角矩 阵，对角线上为wi ，其他元素为0。则变换后的模型为
Wy WX Wu
（一）加权最小二乘法
方差未知的情形 （1）误差方差与xi成比例
（3）其他的与自变量xi的加权形式f(xi)
f xi r0 r1xi
（一）加权最小二乘法
方差未知的情形
Var
(
)
i
2 i
2
r
0
r
1x
i
y i
b0
b1xi
r0 r1xi r0 r1xi r0 r1xi
i
r0 r1xi
Var
i
1 Var
r 0 r1xi r 0 r1xi
下这个回归的R平方Ru22 。
4、检验零假设是
H0 :1 2 k 0
对方程（2）进行F检验，或计算LM统计量进行检验。
LM
n
•
R2 u2
~
2 k
（三）戈里瑟检验
1、通常拟合
e
和
X
之间的回归模型：
j
e
X
l j
根据图形中的分布选择
l 1,1或 1 2
2、再检验零假设 ＝0（不存在异方差）。如果零假设
纠正异方差性的一个可行程序
（1）将y对x1, x2,…xk做回归并得到残差u; （2）将残差进行平方，然后再取自然对数而得到log(u2); （3）做log(u2)对x1, x2,…xk的回归并得到拟合值g； （4）求拟合值的指数：h=exp(g) （5）以1/h为权数用WLS来估计方程。
四计量经济学多变量回归分析模型
i 1
n
2
Min[Yi ( 0 1 X 1i ... p X pi )]
i 1
n
^
^
^
2
• 根据最 小二乘原 理，参数 估计值应 该是右列 方程组的 解
ˆ 0 ˆ 1 ˆ 2 ˆ k
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki Ki
2 ˆ Q e (Yi Yi ) i 1 2 i i 1 n n
i=1,2…n
其 中
ˆ ˆ X ˆ X ˆ X )) (Yi ( 0 1 1i 2 2i k ki
1 Y1 X 1n Y2 Y X kn n
0 1 β 2 k
X 11 X 12 X 1n
X 21 X X kn n ( k 1 )
( k 1 )1
1 μ 2 n n 1
用来估计总体回归函数的样本回归函数为：
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki ki
ˆ ˆ X ˆ X ˆ X e 其随机表示式: Yi 0 1 1i 2 2i ki ki i
ei称为残差或剩余项(residuals)，可看成 是总体回归函数中随机扰动项i的近似替代。
表示：各变量X值固定时Y的平均响应。
j也被称为偏回归系数，表示在其他解释变
量保持不变的情况下，X j每变化1个单位时，Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响。
n
2
Min[Yi ( 0 1 X 1i ... p X pi )]
i 1
n
^
^
^
2
• 根据最 小二乘原 理，参数 估计值应 该是右列 方程组的 解
ˆ 0 ˆ 1 ˆ 2 ˆ k
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki Ki
2 ˆ Q e (Yi Yi ) i 1 2 i i 1 n n
i=1,2…n
其 中
ˆ ˆ X ˆ X ˆ X )) (Yi ( 0 1 1i 2 2i k ki
1 Y1 X 1n Y2 Y X kn n
0 1 β 2 k
X 11 X 12 X 1n
X 21 X X kn n ( k 1 )
( k 1 )1
1 μ 2 n n 1
用来估计总体回归函数的样本回归函数为：
ˆ ˆ X ˆ X ˆ X ˆ Y i 0 1 1i 2 2i ki ki
ˆ ˆ X ˆ X ˆ X e 其随机表示式: Yi 0 1 1i 2 2i ki ki i
ei称为残差或剩余项(residuals)，可看成 是总体回归函数中随机扰动项i的近似替代。
表示：各变量X值固定时Y的平均响应。
j也被称为偏回归系数，表示在其他解释变
量保持不变的情况下，X j每变化1个单位时，Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”（不含其他变量）影响。
庞浩 计量经济学3第三章 多元线性回归模型
4
2.样本回归函数SRF
条件均 值形式
ˆ ˆ X ˆ Y i 1 2 i
ˆ ˆ X ˆ X ˆ X ˆ Y i 1 2 2i 3 3i k ki
ˆ ˆ X e Yi 1 2 i i
个别值 ˆ ˆ X ˆ X ˆ X e 形式 Yi 1 2 2i 3 3i k ki i
16
X e 0
多元线性回归模型参数的 最小二乘估计
ˆ e Y X
ˆ X e X Y X X
X e 0
ˆ X Y X X
ˆ ( X X )1 X Y
17
二、参数最小二乘估计的性质
在古典假定下，多元线性回归模型的最小二乘估 计式是最佳线性无偏估计（BLUE）。 1.线性 参数的最小二乘估计式是被解释变量Yi的线性 组合。 ˆ ( X X )1 X Y
X 31 X k 1 1 X 32 X k 2 2 X 3 n X kn nk k k 1
Y X U
8
总体回归函数与样本回归函数 的矩阵形式
总体回归函数 条件期 望形式
E (Y ) X Y X U
20
三、参数最小二乘估计的分布
依据线性，参数的最小二乘估计是被解 1 ˆ ( X X ) X Y 释变量Y 的线性函数
i
Yi 1 2 X 2i 3 X 3i k X ki ui
ui ~ N (0, ) (i 1,2,, n) ˆ ( j 1,2,, k ) 服从正态分布
9
三、多元线性回归模型的古典假定
u1 Eu1 0 u Eu 0 2 2 E (U ) E E ( ui ) 0 un Eun 0 n1 2.同方差和无自相关假定
2.样本回归函数SRF
条件均 值形式
ˆ ˆ X ˆ Y i 1 2 i
ˆ ˆ X ˆ X ˆ X ˆ Y i 1 2 2i 3 3i k ki
ˆ ˆ X e Yi 1 2 i i
个别值 ˆ ˆ X ˆ X ˆ X e 形式 Yi 1 2 2i 3 3i k ki i
16
X e 0
多元线性回归模型参数的 最小二乘估计
ˆ e Y X
ˆ X e X Y X X
X e 0
ˆ X Y X X
ˆ ( X X )1 X Y
17
二、参数最小二乘估计的性质
在古典假定下，多元线性回归模型的最小二乘估 计式是最佳线性无偏估计（BLUE）。 1.线性 参数的最小二乘估计式是被解释变量Yi的线性 组合。 ˆ ( X X )1 X Y
X 31 X k 1 1 X 32 X k 2 2 X 3 n X kn nk k k 1
Y X U
8
总体回归函数与样本回归函数 的矩阵形式
总体回归函数 条件期 望形式
E (Y ) X Y X U
20
三、参数最小二乘估计的分布
依据线性，参数的最小二乘估计是被解 1 ˆ ( X X ) X Y 释变量Y 的线性函数
i
Yi 1 2 X 2i 3 X 3i k X ki ui
ui ~ N (0, ) (i 1,2,, n) ˆ ( j 1,2,, k ) 服从正态分布
9
三、多元线性回归模型的古典假定
u1 Eu1 0 u Eu 0 2 2 E (U ) E E ( ui ) 0 un Eun 0 n1 2.同方差和无自相关假定
最新南开大学《计量经济学》案例分析
南开大学《计量经济学》案例分析南开大学《计量经济学》案例分析案例一：用回归模型预测木材剩余物（file:b1c3）伊春林区位于黑龙江省东北部。
全区有森林面积218.9732万公顷，木材蓄积量为2.324602亿m3。
森林覆盖率为62.5%，是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m3。
按此速度44年之后，1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式，保护森林生态环境。
为缓解森林资源危机，并解决部分职工就业问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产品，如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面，利用一元线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表1.1。
散点图见图1.1。
观测点近似服从线性关系。
建立一元线性回归模型如下：y t = β0 + β1 x t + u t表1.1 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t（万m3）年木材采伐量x t（万m3）乌伊岭26.13 61.4 东风23.49 48.3 新青21.97 51.8 红星11.53 35.9 五营7.18 17.8 上甘岭 6.80 17.0 友好18.43 55.0 翠峦11.69 32.7 乌马河 6.80 17.0 美溪9.69 27.3 大丰7.99 21.5 南岔12.15 35.5 带岭 6.80 17.0 朗乡17.20 50.0 桃山9.50 30.0 双丰 5.52 13.8 合计202.87 532.00图1.1 年剩余物y t和年木材采伐量x t散点图图1.2 EViews输出结果EViews估计结果见图1.2。
在已建立Eviews数据文件的基础上，进行OLS估计的操作步骤如下：打开工作文件，从主菜单上点击Quick键，选Estimate Equation 功能。
南开大学经济学院历年本科计量经济学期末试卷及答案解析汇编
3
答案勘误表
2002 年第一学期计量经济学期末开卷试题答案
第一大题，第 1 小题： 第二空答案是 118.634 应改为 118.6377； 第三空答案是 0.0384 应改为 0.04034 第五大题，第 1 小题： 因为是对 Dyt 建模，所以答案应从 ARIMA 模型改为 ARMA 模型 第五大题，第 3 小题： ˆ1996 带入有 误，原答 案代入的 是 1997 年的-0.00127，应该代入 1996 年 的 u 0.00179， 并且题目要求是求 Dyt 值，答案求的是 yt 值，由于题目没有给出 y1997 ， 所以 y1998 是求不出来的
Prob. 0.0044 0.0000 7.430699 1.021834 -6.336402 -6.237663 14074.12 0.00000
1．在空白处填上相应的数字（共 4 处） （计算过程中保留 4 位小数） （8 分） 2．根据输出结果，写出回归模型的表达式。 （5 分）
3．给定检验水平α=0.05， 检验上述回归模型的临界值 t0.025=_______， F0.05=_______； 说明估计参数与回归模型是否显著?（6 分）
四、给出结构模型（共 20 分）
Ct=α0 +α1Yt+α2Ct-1+ u1t It=β0+β1Yt+β2Yt-1+β3rt+ u2t Yt=Ct+It+Gt
其中 C—总消费，I—总投资，Y—总收入，r—利率，G—政府支出 1．写出模型中的内生变量、外生变量、预定变量。 （5 分）
2．讨论联立方程模型的识别问题。 （10 分）
ˆ =e 0 3． A 4．因为使用的样本为横截面数据，随机误差项可能存在异方差；变量 L 和 K 之间可能存在 较严重的多重共线性。
南开大学《计量经济学》复习资料
回答如下问题。 （1）对模型残差进行 DW 检验。 （检验水平 0.05，临界值：DL=1.26，DU =1.44） = 。 （2）如果存在一阶自相关，写出广义差分变量计算公式。 （3）根据如下 Dgdp 对 Dinvest 回归结果，写出模型估计式，并表示成 Dgdp 的自回归分布滞 后形式。
【答】 （1）DW = 0.9 < DL = 1.26，所以模型残差存在一阶正自相关。 （4 分） （2）GYt = Dgdpt - 0.55 Dgdpt-1， GXt = Dinvestt - 0.55 Dinvestt-1 （4 分） （3）模型的回归结果为： （8 分）
43.9376 41.9222 35.4311 41.9222/ 737
（3 分） （3 分）
5
（5） 、0.0318 - 0.0973 = -0.0655
2．根据计算机输出结果，写出一元回归模型表达式。 【答】 NER = 0.0972 + 0.0035 RATE
（4 分） 。
(9.2) (6.0) R2 = 0.046, T = 739 3．你认为上述回归式用考虑自相关问题吗？ 不必考虑自相关 （2 分） 4．异方差的 White 检验式估计结果如下，
(2003) (1998)
【答】 （1） 1997 年的东南亚金融危机和 2003 年的非典分别导致外国入境旅游人数出现下降。 4 分） （ （2）设定的模型是： Lnyt 0 1t 2 D1 3 D2 ut 其中： D2 1 0
2003年 其他年份
， D1 1
本科《计量经济学》课程期末复习
1．闭卷考试. 2．熟知EViews输出结果和所要求掌握的内容要 点，不考计算机操作。 3．重点考试内容已经发给同学们了(复习大纲) 4. 数学推导会考一些, 所以同学们在复习第二和 第三章的时候一定要花一些时间 5. 考试的重点和往年类似,所以同学们一定要对 往年的试卷作出熟练的理解 6. 大家复习辛苦了!
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
（4）判断： t t (n k )， 则接受H 0 , 参数 i显著异于0 2 若 t t (n k )， 则拒绝H 0 , 接受H1 , 参数 i不显著异于0
i 非负，则可做单侧检验，比较 t 与tα。 如果根据理论或常识，
若 t t (n k )， 则接受H 0 , 参数 i不显著异于0 t t (n k )， 则拒绝H 0 , 接受H1 , 参数 i显著异于0
2 ˆ ˆ ˆ ˆ X X X X X X X kiYi 1 ki 2 ki 2i k ki 3i k ki
写成矩阵形式： n X 2i 2 X 2i X 2i X 3i X 3i X 2 i X X ki X 2i ki 1 1 1 X 21 X 22 X 23 X 31 X 32 X 33 X k1 X k 2 X 3k
第三节 拟合优度检验：
一、判定系数R2：
总平方和： TSS y i2 (Yi Y ) Yi 2 2 YiY nY
2
Y' Y nY 2 残差平方和：
ˆ ' X' Y ˆ i2 u ˆ 'u ˆ Y' Y β RSS u 回归平方和： ESS TSS ESS Y' Y nY
u2
u12 u u un 2 1 u u n 1
u1u 2
2 u2
unu2
u1u n u 2u n 2 un
2
0 0
2
0
0 0 2 I 0 2
同方差性；无序列相关。
3、 X为非随机的
ˆ ' X' Y) /(k 1) (Y' Y β
ˆ ' X' Y nY 2 ) /(n k ) (β
2
RSS
TSS
n-k
2
2
i
n-1
判定系数：
二、校正的R2 ：
2 ˆ ESS β ' X ' y n Y R2 TSS Y' Y nY 2
由R2的计算式可看出， R2 随解释变量的增加而可能提高（不可能降 低）： ˆ ' X ' y nY 2 ESS β 2 R TSS Y' Y nY 2 2 ˆ u RSS i 1 1 2 TSS y i ˆi2则可能随着解释变量的增加 yi2与解释变量X的个数无关，而 u
或：
Y Xβ u
Y为因变量观测值列向量
在
Y Xβ u
X为数据矩阵。 中， β 为待估计参数列向量 u为随机扰动项列向量
二、多 变量线性回归模型的基本假定
1 、 E u 0
随机干扰项的期望值为0。
u1 u 2、 E uu' 2 u1 u n 2 0 0 0 0 0 0
原假设H 0 : i 0 备择假设H 1 : i 0
如果接受H0 ，则变量Xi 对因变量没有影响，而接受H1，则说明变 量Xi 对因变量有显著影响。
检验步骤：
(1)选择显著水平，如 0.05。 ˆ i （2）计算统计量： t ˆ) Se(
i
（3）查t分布表，找出t ( n k )。
二、 的估计量
2 ˆ u i
ˆ ' X' Y β ˆ ' X' Xβ ˆ ˆ Y ' Y 2β u ˆ u ˆ 0 2 X' Y 2 X' Xβ
2
i
ˆ 'u ˆ u ˆ nk nk ˆ为的无偏估计量：E[ ˆ ] 。
ˆ 的方差-协方差矩阵 三、 β
2
ˆ ' X' y β ˆ ' X' Y nY Y' Y β
2
方差分析表（ ANOVA) 平方和 ESS
ˆ Y ˆ ) Y' Y β ˆ ' X' Y (Y i
ˆ ' X ' Y nY ˆ β u (Y Y ) Y' Y nY
2 2
i
df k-1
均方差
而减少（至少不会下降），因而，不同的SRF，得到的R2 就可能不同。 必须消除这种因素，使R2 即能说明被解释的离差与总离差之间的关系， 2 又能说明自由度的数目。定义校正的样本决定系数 R ： ESS /(n k ) n 1 2 2 R 1 1 (1 R ) TSS /(n 1) nk
1
ˆ2 ˆ) Se(Y
三、R2 与 R 2的性质
0 R 2 1, R 2 R2 ,
0 R2 1 当k 时，R 2 R 2
第四节 显著性检验
一、单参数的显著性检验：
ˆ ~ N ( , 2 ( X' X) 1 ) 根据假定，u ~ N (0, 2 I)，因此 ˆ代替，则统计量 以 ˆ i t i ~ t (n k ) ˆ Se( i ) ˆ 是否显著不为0。 ˆ 的显著性， 即在一定显著水平下， 检验 i i
2
二、回归的总显著性检验： 检验回归系数全部为零的可能性。
原假设H 0 : 1 2 k 0 备择假设H 1 : i (i 1,2, , k )不同时为零
方差分析表（ ANOVA) 平方和
ˆ Y ˆ ) Y' Y β ˆ ' X' Y ESS (Y i
SRF :
ˆ ˆ X ˆ X ˆ X u ˆi Yi 1 2 2i 3 3i k ki ˆ u ˆ 或 Y Xβ
ˆ 和u ˆ 分别为回归系数的OLS估计量的列向量和残差列向量。 其中β
第二节 多变量回归模型的OLS估计
一、参数估计
SRF :
ˆ ˆ X ˆ X ˆ X u ˆi Yi 1 2 2i 3 3i k ki
ˆ 2代替 2，则 如果 2未知，以 2 1 ˆ )的估计量为： ˆ（ Var Cov(β X' X）
2 1 1 ˆ 的标准差Se(β ˆ )为 ˆ（ ˆ β X' X） （X' X）
四、OLS估计量 β ˆ 的性质：
1 、线性 1 ˆ （ β [ X' X） X' ]Y 2、无偏性 ˆ] β E[β 3、最小方差性 ˆ 具有Var(β ˆ )最小。 OLS 估计量β
R 2 /(k 1) 可得到F (1 R 2 ) /(n k )
显然，R2 越大，F越大，当R2 =1时，F 无限大。
选择显著水平α ，计算F统计量的值，与F分布表中的临界值进行比 较： F F ( k 1, n k )， 则接受H 0 , 不显著 若 F F ( k 1, n k )， 则拒绝H 0 , 接受H 1 , 显著
X X X X
3i 2i 2
3i
3i
X X X X X
ki
X
ki
X 3i
ˆ 1 ˆ 2i ki ˆ2 3i ki 3 2 ˆ X ki k
2
df k-1 n-k
2
2
均方差
ˆ ' X' Y) /(k 1) (Y' Y β
ˆ ' X' Y nY 2 ) /(n k ) (β
RSS TSS
ˆ ' X ' Y nY ˆ β u (Y Y ) Y' Y nY
2
i
2
i
n-1
如果假定：1 2 k 0，则统计量 ˆ ' X' Y nY 2 ) /(k 1) ESS /(k 1) (β F ~ F ( k 1, n k ) ˆ RSS /(n k ) ( Y ' Y β ' X' Y ) /(n k ) ESS ESS /(k 1) 根据R 2 ，F , TSS ESS RSS TSS RSS /(n k )
i
根据残差的平方和最小化的原理，解出参数的估计量。 ˆ ˆ X ˆ X )2 ˆ 2 (Yi 残差平方和RSS u 1 2 2i k ki
ˆ 'u u ˆ u ˆ Y Xβ ˆ ˆ Y Xβ u ˆ )' ( Y Xβ ˆ) ˆ i2 u ˆ ' u ( Y Xβ RSS u ˆ ' X' Y β ˆ ' X' Xβ ˆ Y' Y β ˆ ' X' Y Y ' Y 2β
PRF :
Yi 1 2 X 2i 3 X 3i k X ki ui , i 1,2,, k
Y1 1 X 21 Y2 1 X 22 Y 1 X 2n n
X 31 X k 1 1 u1 X 32 X k 2 2 u2 X 3n X kn n u n
4、 r（X） k
无多重共线性，即Xi (i = 2,3, …,k )之间不存在线性关系： 不存在不全为零的一组数：1 , 2 , k , 使： 1 X 1i 2 X 2 i , k X ki 0
成立。
5、 u ~ N (0, 2 I )
随机干扰项服从正态分布。
（4）判断： t t (n k )， 则接受H 0 , 参数 i显著异于0 2 若 t t (n k )， 则拒绝H 0 , 接受H1 , 参数 i不显著异于0
i 非负，则可做单侧检验，比较 t 与tα。 如果根据理论或常识，
若 t t (n k )， 则接受H 0 , 参数 i不显著异于0 t t (n k )， 则拒绝H 0 , 接受H1 , 参数 i显著异于0
2 ˆ ˆ ˆ ˆ X X X X X X X kiYi 1 ki 2 ki 2i k ki 3i k ki
写成矩阵形式： n X 2i 2 X 2i X 2i X 3i X 3i X 2 i X X ki X 2i ki 1 1 1 X 21 X 22 X 23 X 31 X 32 X 33 X k1 X k 2 X 3k
第三节 拟合优度检验：
一、判定系数R2：
总平方和： TSS y i2 (Yi Y ) Yi 2 2 YiY nY
2
Y' Y nY 2 残差平方和：
ˆ ' X' Y ˆ i2 u ˆ 'u ˆ Y' Y β RSS u 回归平方和： ESS TSS ESS Y' Y nY
u2
u12 u u un 2 1 u u n 1
u1u 2
2 u2
unu2
u1u n u 2u n 2 un
2
0 0
2
0
0 0 2 I 0 2
同方差性；无序列相关。
3、 X为非随机的
ˆ ' X' Y) /(k 1) (Y' Y β
ˆ ' X' Y nY 2 ) /(n k ) (β
2
RSS
TSS
n-k
2
2
i
n-1
判定系数：
二、校正的R2 ：
2 ˆ ESS β ' X ' y n Y R2 TSS Y' Y nY 2
由R2的计算式可看出， R2 随解释变量的增加而可能提高（不可能降 低）： ˆ ' X ' y nY 2 ESS β 2 R TSS Y' Y nY 2 2 ˆ u RSS i 1 1 2 TSS y i ˆi2则可能随着解释变量的增加 yi2与解释变量X的个数无关，而 u
或：
Y Xβ u
Y为因变量观测值列向量
在
Y Xβ u
X为数据矩阵。 中， β 为待估计参数列向量 u为随机扰动项列向量
二、多 变量线性回归模型的基本假定
1 、 E u 0
随机干扰项的期望值为0。
u1 u 2、 E uu' 2 u1 u n 2 0 0 0 0 0 0
原假设H 0 : i 0 备择假设H 1 : i 0
如果接受H0 ，则变量Xi 对因变量没有影响，而接受H1，则说明变 量Xi 对因变量有显著影响。
检验步骤：
(1)选择显著水平，如 0.05。 ˆ i （2）计算统计量： t ˆ) Se(
i
（3）查t分布表，找出t ( n k )。
二、 的估计量
2 ˆ u i
ˆ ' X' Y β ˆ ' X' Xβ ˆ ˆ Y ' Y 2β u ˆ u ˆ 0 2 X' Y 2 X' Xβ
2
i
ˆ 'u ˆ u ˆ nk nk ˆ为的无偏估计量：E[ ˆ ] 。
ˆ 的方差-协方差矩阵 三、 β
2
ˆ ' X' y β ˆ ' X' Y nY Y' Y β
2
方差分析表（ ANOVA) 平方和 ESS
ˆ Y ˆ ) Y' Y β ˆ ' X' Y (Y i
ˆ ' X ' Y nY ˆ β u (Y Y ) Y' Y nY
2 2
i
df k-1
均方差
而减少（至少不会下降），因而，不同的SRF，得到的R2 就可能不同。 必须消除这种因素，使R2 即能说明被解释的离差与总离差之间的关系， 2 又能说明自由度的数目。定义校正的样本决定系数 R ： ESS /(n k ) n 1 2 2 R 1 1 (1 R ) TSS /(n 1) nk
1
ˆ2 ˆ) Se(Y
三、R2 与 R 2的性质
0 R 2 1, R 2 R2 ,
0 R2 1 当k 时，R 2 R 2
第四节 显著性检验
一、单参数的显著性检验：
ˆ ~ N ( , 2 ( X' X) 1 ) 根据假定，u ~ N (0, 2 I)，因此 ˆ代替，则统计量 以 ˆ i t i ~ t (n k ) ˆ Se( i ) ˆ 是否显著不为0。 ˆ 的显著性， 即在一定显著水平下， 检验 i i
2
二、回归的总显著性检验： 检验回归系数全部为零的可能性。
原假设H 0 : 1 2 k 0 备择假设H 1 : i (i 1,2, , k )不同时为零
方差分析表（ ANOVA) 平方和
ˆ Y ˆ ) Y' Y β ˆ ' X' Y ESS (Y i
SRF :
ˆ ˆ X ˆ X ˆ X u ˆi Yi 1 2 2i 3 3i k ki ˆ u ˆ 或 Y Xβ
ˆ 和u ˆ 分别为回归系数的OLS估计量的列向量和残差列向量。 其中β
第二节 多变量回归模型的OLS估计
一、参数估计
SRF :
ˆ ˆ X ˆ X ˆ X u ˆi Yi 1 2 2i 3 3i k ki
ˆ 2代替 2，则 如果 2未知，以 2 1 ˆ )的估计量为： ˆ（ Var Cov(β X' X）
2 1 1 ˆ 的标准差Se(β ˆ )为 ˆ（ ˆ β X' X） （X' X）
四、OLS估计量 β ˆ 的性质：
1 、线性 1 ˆ （ β [ X' X） X' ]Y 2、无偏性 ˆ] β E[β 3、最小方差性 ˆ 具有Var(β ˆ )最小。 OLS 估计量β
R 2 /(k 1) 可得到F (1 R 2 ) /(n k )
显然，R2 越大，F越大，当R2 =1时，F 无限大。
选择显著水平α ，计算F统计量的值，与F分布表中的临界值进行比 较： F F ( k 1, n k )， 则接受H 0 , 不显著 若 F F ( k 1, n k )， 则拒绝H 0 , 接受H 1 , 显著
X X X X
3i 2i 2
3i
3i
X X X X X
ki
X
ki
X 3i
ˆ 1 ˆ 2i ki ˆ2 3i ki 3 2 ˆ X ki k
2
df k-1 n-k
2
2
均方差
ˆ ' X' Y) /(k 1) (Y' Y β
ˆ ' X' Y nY 2 ) /(n k ) (β
RSS TSS
ˆ ' X ' Y nY ˆ β u (Y Y ) Y' Y nY
2
i
2
i
n-1
如果假定：1 2 k 0，则统计量 ˆ ' X' Y nY 2 ) /(k 1) ESS /(k 1) (β F ~ F ( k 1, n k ) ˆ RSS /(n k ) ( Y ' Y β ' X' Y ) /(n k ) ESS ESS /(k 1) 根据R 2 ，F , TSS ESS RSS TSS RSS /(n k )
i
根据残差的平方和最小化的原理，解出参数的估计量。 ˆ ˆ X ˆ X )2 ˆ 2 (Yi 残差平方和RSS u 1 2 2i k ki
ˆ 'u u ˆ u ˆ Y Xβ ˆ ˆ Y Xβ u ˆ )' ( Y Xβ ˆ) ˆ i2 u ˆ ' u ( Y Xβ RSS u ˆ ' X' Y β ˆ ' X' Xβ ˆ Y' Y β ˆ ' X' Y Y ' Y 2β
PRF :
Yi 1 2 X 2i 3 X 3i k X ki ui , i 1,2,, k
Y1 1 X 21 Y2 1 X 22 Y 1 X 2n n
X 31 X k 1 1 u1 X 32 X k 2 2 u2 X 3n X kn n u n
4、 r（X） k
无多重共线性，即Xi (i = 2,3, …,k )之间不存在线性关系： 不存在不全为零的一组数：1 , 2 , k , 使： 1 X 1i 2 X 2 i , k X ki 0
成立。
5、 u ~ N (0, 2 I )
随机干扰项服从正态分布。