工程力学最新完全试题(卷)(含有答案)
《工程力学》考试复习题库(含答案)

《工程力学》考试复习题库(含答案)一、选择题1. 工程力学是研究()A. 材料力学性能B. 力的作用和物体运动规律C. 结构的计算和分析D. 机器的设计与制造答案:B2. 在静力学中,力的作用效果取决于()A. 力的大小B. 力的方向C. 力的作用点D. A、B、C均正确答案:D3. 平面汇交力系的平衡条件是()A. 力的代数和为零B. 力矩的代数和为零C. 力的投影和为零D. 力的投影和为零且力矩的代数和为零答案:D4. 拉伸或压缩时,杆件横截面上的正应力等于()A. 拉力或压力B. 拉力或压力除以横截面面积C. 拉力或压力乘以横截面面积D. 拉力或压力除以杆件长度答案:B5. 材料在屈服阶段之前,正应力和应变的关系符合()A. 胡克定律B. 比例极限C. 屈服强度D. 断裂强度答案:A二、填空题1. 工程力学中的基本单位有()、()、()。
答案:米、千克、秒2. 二力平衡条件是:作用在同一个物体上的两个力,必须()、()、()。
答案:大小相等、方向相反、作用在同一直线上3. 材料的弹性模量表示材料在弹性范围内抵抗()的能力。
答案:变形4. 在剪切力作用下,杆件横截面沿剪切面发生的变形称为()。
答案:剪切变形5. 梁的挠度是指梁在受力后产生的()方向的位移。
答案:垂直三、判断题1. 力偶的作用效果只与力偶矩大小有关,与力偶作用点位置无关。
()答案:正确2. 在拉伸或压缩过程中,杆件的横截面面积始终保持不变。
()答案:正确3. 材料的屈服强度越高,其抗断裂能力越强。
()答案:错误4. 在受弯构件中,中性轴是弯矩等于零的轴线。
()答案:错误5. 梁的挠度曲线是梁的轴线在受力后的实际位置。
()答案:正确四、计算题1. 一根直径为10mm的圆形杆,受到轴向拉力1000N的作用。
求杆件的伸长量。
答案:杆件的伸长量约为0.005mm。
2. 一根简支梁,受到均布载荷q=2kN/m的作用,跨度l=4m。
求梁的最大挠度。
工程力学本科试题及答案

工程力学本科试题及答案一、选择题(每题5分,共40分)1. 在下列关于力的说法中,正确的是()A. 力是矢量,有大小和方向,但没有作用点B. 力是标量,只有大小,没有方向C. 力是矢量,有大小和方向,作用点在力的作用线上D. 力是标量,只有大小,作用点在力的作用线上答案:C2. 在平面汇交力系中,力的分解方法通常有()A. 正交分解法B. 平行四边形法C. 力的三角形法D. A、B和C都是答案:D3. 下列关于力矩的说法中,正确的是()A. 力矩是标量,没有方向B. 力矩是矢量,有大小和方向C. 力矩是矢量,只有大小D. 力矩是标量,只有方向答案:B4. 在下列关于约束的说法中,错误的是()A. 约束是限制物体运动的条件B. 约束可以是主动约束,也可以是被动约束C. 约束可以是固定约束,也可以是移动约束D. 约束不能是力的作用答案:D5. 下列关于静定和超静定结构的说法中,正确的是()A. 静定结构的未知反力个数等于约束个数B. 超静定结构的未知反力个数小于约束个数C. 静定结构的未知反力个数小于约束个数D. 超静定结构的未知反力个数等于约束个数答案:A6. 在下列关于应力与应变的关系中,正确的是()A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成非线性关系答案:A7. 下列关于材料力学性能的说法中,错误的是()A. 弹性模量越大,材料越硬B. 泊松比越大,材料越脆C. 延伸率越大,材料塑性越好D. 断面收缩率越大,材料韧性越好答案:B8. 在下列关于梁的弯曲的说法中,正确的是()A. 梁的弯曲应力与梁的长度成正比B. 梁的弯曲应力与梁的截面惯性矩成反比C. 梁的弯曲应力与梁的弹性模量无关D. 梁的弯曲应力与梁的截面形状无关答案:B二、填空题(每题10分,共40分)9. 平面汇交力系中,力的分解方法有__________和__________。
答案:正交分解法、平行四边形法10. 材料力学性能指标主要有__________、__________、__________和__________。
工程力学知识考试试卷含答案

工程力学知识考试试卷含答案一、选择题(每题3分,共30分)1. 下列哪个选项不是工程力学的基本分析方法?A. 矢量分析法B. 动力学分析法C. 静力学分析法D. 量子力学分析法答案:D2. 下列哪个物理量不属于力的基本属性?A. 大小B. 方向C. 作用点D. 颜色答案:D3. 平面汇交力系的平衡条件是:A. 力的合力为零B. 力矩的合力为零C. 力的投影为零D. 力的合力与力矩的合力为零答案:D4. 下列哪个杆件不属于受拉杆?A. 拉杆B. 压杆C. 梁杆D. 柔性杆答案:B5. 下列哪个选项不是梁的内力?A. 弯矩B. 剪力C. 轴力D. 扭矩答案:C6. 下列哪个选项不是弹性力学的分支?A. 材料力学B. 结构力学C. 动力学D. 流体力学答案:D7. 在静力学中,下列哪个力系是平衡力系?A. 非平面力系B. 平面力系C. 空间力系D. 汇交力系答案:B8. 下列哪个选项不是力的单位?A. 牛顿B. 千克力C. 磅力D. 瓦特答案:D9. 下列哪个选项是弹性体?A. 刚体B. 柔性体C. 超弹性体D. 塑性体答案:B10. 在材料力学中,下列哪个选项是描述材料强度性能的指标?A. 弹性模量B. 屈服极限C. 断裂极限D. 延伸率答案:C二、填空题(每题3分,共30分)1. 工程力学的两大基本分析方法为________和________。
答案:矢量分析法,动力学分析法2. 平面汇交力系的平衡条件为________。
答案:力的合力与力矩的合力为零3. 梁的内力包括________、________和________。
答案:弯矩,剪力,轴力4. 材料力学的三大基本假设为________、________和________。
答案:连续性假设,均匀性假设,各向同性假设5. 在弹性力学中,应力与________有关,应变与________有关。
答案:应变,应力三、判断题(每题3分,共30分)1. 力是矢量,具有大小和方向。
(完整版)工程力学最新完全试题(含有答案)汇总

(完整版)⼯程⼒学最新完全试题(含有答案)汇总模拟试题7参考解答测7-1 多项选择题(共4个⼩题)测7-1-1(4分)图为低碳钢试件的拉伸实验的应⼒应变图形。
在以下结论中, A B D 是正确的。
A .加载到B 点前卸载,当应⼒消失为零时,应变也消失为零。
B .加载到C 点卸载,当应⼒消失为零时,应变并不消失为零。
C .加载到C 点卸载,再次加载,构件的屈服强度提⾼了。
D .在C 点处卸载的卸载曲线,与在D 点处卸载的卸载曲线⼏乎是平⾏的。
E .在C 点处卸载的残余应变,与在D 点处卸载的残余应变⼏乎是相等的。
测7-1-2(3分)下列各种情况中,重物均可以在梁上沿⽔平⽅向⾃由移动。
重物所处的位置已经使所在的梁具有最⼤弯矩的情况有 BC D 。
测7-1-3(3分)圆轴扭转时,其表⾯各点所处于的应⼒状态属于 B D 。
A .单向应⼒状态B .双向应⼒状态C .三向应⼒状态D .纯剪应⼒状态测7-1-4(4分)在下列措施中, A B D 将明显地影响压杆失稳临界荷载。
A .改变杆件的长度B .改变杆件两端的约束形式C .在不改变横截⾯两个主惯性矩的前提下改变横截⾯形状ABCD 测 7-1-2 图测 7-1-1 图D .在不改变横截⾯形状的前提下改变横截⾯尺⼨E .在杆件上沿垂直于轴线⽅向上开孔测7-2 填空题(共4个⼩题)测7-2-1(3分)直径为d 的圆轴两端承受转矩m 的作⽤⽽产⽣扭转变形,材料的泊松⽐为ν,其危险点的第⼀强度理论的相当应⼒ =eq1σ 3π16dm,第⼆强度理论的相当应⼒=eq2σ)(ν+1π163d m,第三强度理论的相当应⼒ =eq3σ3π32d m。
测7-2-2(2分)承受均布荷载q 的悬臂梁的长度为L ,其横截⾯是宽度为b ,⾼度为h的矩形,该梁横截⾯上的最⼤弯曲切应⼒为 bhqL23 。
测7-2-3(4分)题图中左、右两杆的抗拉刚度分别是EA 和EA 20,则A 点的竖向位移为EAPa 22。
工程力学考试题及答案

工程力学考试题及答案第一部分:选择题(共40分,每题2分,共20小题)1.以下哪个是工程力学的基本概念?A.质量B.速度C.功率D.电流答案:A 质量2.以下哪个是工程力学的单位?A.米B.牛顿C.度D.秒答案:B 牛顿3.下列哪个是牛顿第一定律?A.质体静止B.速度恒定C.加速度不断变化D.物体受到力时才会运动答案:B 速度恒定4.物体所受的外力大小等于物体运动状态发生改变时的惯性力,这是牛顿的哪个定律?A.一定律B.二定律C.三定律D.四定律答案:B 二定律5.哪个是工程力学中动力学的研究对象?A.平衡结构B.静力学C.运动结构D.变形结构答案:C 运动结构第二部分:填空题(共30分,每空2分,共15空)1.牛顿的第一定律也叫_______定律。
答案:惯性定律2.________是测量物体运动速度的物理量。
答案:速度3.牛顿的第三定律也叫________定律。
答案:作用与反作用定律4._______是测量物体运动加速度的物理量。
答案:加速度5._______是测量物体质量大小的物理量。
答案:质量第三部分:简答题(共30分,每题10分,共3题)1.简述牛顿的三大定律。
答案:牛顿的第一定律是运动物体保持匀速直线运动或静止状态,直至受到外力的作用;牛顿的第二定律是物体所受的合力等于物体质量乘以加速度;牛顿的第三定律是每个作用力都有一个等大相反方向的反作用力。
2.什么是动力学学?答案:动力学是力及物体的相互作用,研究物体的运动状态和运动规律。
3.简述质量和重力的区别。
答案:质量是物体所拥有的物质量大小;重力是地球对物体的吸引力,是一种力的作用。
以上就是工程力学考试题及答案,希望可以帮助大家更好地理解和掌握工程力学知识。
祝大家考试顺利!。
工程力学试题及答案

工程力学试题及答案一、选择题(每题5分,共25分)1. 在下列力学分支中,主要研究刚体运动的规律和力的作用效应的是()A. 材料力学B. 理论力学C. 弹性力学D. 流体力学答案:B2. 在下列力系中,属于平面力系的是()A. 空间力系B. 平面汇交力系C. 平面平行力系D. 空间平行力系答案:C3. 刚体在空间中绕定点转动的运动称为()A. 平面运动B. 定轴转动C. 一般运动D. 点的运动答案:B4. 在下列静力学公理中,错误的是()A. 力的平行四边形法则B. 力的分解与合成法则C. 二力平衡公理D. 力的独立性公理答案:D5. 在下列弹性体中,属于脆性材料的是()A. 钢材B. 铸铁C. 铝材D. 塑料答案:B二、填空题(每题5分,共25分)6. 在平面力系中,力矩的量纲是______。
答案:力×长度7. 刚体绕定点转动的角速度与______成正比。
答案:转动半径8. 材料力学中,将材料内部各点的应力与应变之间的关系称为______。
答案:应力应变关系9. 在静力学中,二力平衡公理表明,作用在刚体上的两个力,如果它们的大小相等、方向相反且作用线______,则该刚体处于平衡状态。
答案:重合10. 弹性体在外力作用下,内部各点的应力与应变之间的关系遵循______。
答案:胡克定律三、判断题(每题5分,共25分)11. 刚体在空间中的运动可以分解为平动和绕定点转动。
()答案:正确12. 平面力系的平衡方程可以推广到空间力系。
()答案:错误13. 在材料力学中,胡克定律适用于弹性材料的线性范围。
()答案:正确14. 刚体绕定点转动的角速度越大,其线速度也越大。
()答案:错误15. 在静力学中,力的分解与合成法则表明,一个力可以分解为两个或多个力的合力。
()答案:错误四、计算题(每题25分,共100分)16. 如下图所示,一个质量为10kg的物体受到一个水平力F 的作用,沿着水平面运动。
2023年工程力学试题及答案

2023年工程力学试题及答案一、选择题(每题3分,共30分)1. 下列哪项不是工程力学的研究内容?A. 结构分析B. 材料力学性质C. 工程经济分析D. 流体力学答案:C2. 在静力学中,一个物体处于平衡状态的必要和充分条件是合力:A. 为零B. 大于物体重量C. 小于物体重量D. 不确定答案:A3. 根据胡克定律,弹簧的变形量与作用力成正比,这个比例系数称为:A. 弹性模量B. 泊松比C. 剪切模量D. 弹簧常数答案:D4. 在材料力学中,下列哪项不是基本的力学性能指标?A. 屈服强度B. 抗拉强度C. 硬度D. 密度答案:D5. 流体静力学中,流体的压力随深度的增加而:A. 增加B. 减少C. 保持不变D. 先增加后减少答案:A6. 根据能量守恒定律,下列哪项描述是错误的?A. 能量可以被创造B. 能量可以从一种形式转换为另一种形式C. 能量的总量在封闭系统中保持不变D. 能量转换具有方向性答案:A7. 在工程力学中,下列哪项不是常见的结构失效模式?A. 断裂B. 屈服C. 腐蚀D. 塑性变形答案:C8. 根据牛顿第三定律,作用力和反作用力:A. 大小相等,方向相反B. 大小不等,方向相反C. 大小相等,方向相同D. 大小不等,方向相同答案:A9. 在结构力学中,桁架结构的特点是:A. 所有杆件只承受拉力或压力B. 所有杆件只承受弯矩C. 部分杆件承受弯矩,部分杆件承受拉力或压力D. 所有杆件只承受剪力答案:A10. 下列哪项不是影响材料疲劳寿命的因素?A. 应力幅度B. 循环次数C. 材料的弹性模量D. 应力集中答案:C二、填空题(每题2分,共20分)11. 工程力学中的三大基本力学问题是:__________、__________、__________。
答案:静力学,动力学,材料力学12. 理想流体的连续性方程表明,在无源和汇的情况下,单位时间内流过任意截面的流体质量是________的。
工程力学试题及答案

工程力学试题及答案一、选择题1. 工程力学是研究物体力学性质以及力的作用等内容的学科。
以下哪个不属于工程力学的内容?A) 动力学 B) 静力学 C) 电力学 D) 材料力学答案:C) 电力学2. 向外的作用力称为正向作用力,相反的称为反向作用力。
以下哪个不属于正向作用力?A) 拉力 B) 推力 C) 重力 D) 弹性力答案:C) 重力3. 在平衡状态下,物体所受合力和合力矩都为零。
以下哪个条件不属于平衡状态的条件?A) 合力为零 B) 合力矩为零 C) 速度为零 D) 加速度为零答案:D) 加速度为零4. 动力学研究物体受力作用下的运动情况。
以下哪个不属于动力学的内容?A) 速度 B) 位移 C) 质量 D) 面积答案:D) 面积5. 力的合成物理量是指由两个或多个力合成的结果的量。
以下哪个不属于力的合成物理量?A) 力的合力 B) 力的合力矩 C) 力的合速度 D) 力的合加速度答案:C) 力的合速度二、填空题1. 根据牛顿运动定律第一定律的原理,物体只有在受到外力作用时才会产生加速度,即F=ma中的______。
答案:a (加速度)2. 质点在匀变速直线运动中,每单位时间内的路程与时间的比值称为质点的______。
答案:速度3. 物体受到的合外力为零时,物体处于______状态。
答案:平衡4. 刚体绕固定轴的转动,受力矩的大小等于______乘以物体上的力臂。
答案:力5. 物体在受力作用下产生的质心加速度与作用在物体上的合外力成______。
答案:正比三、计算题1. 一个质点从静止开始沿直线做匀加速直线运动,它在3秒内的位移为12米,求它的加速度大小。
答案:已知:位移s = 12米,时间t = 3秒,初速度v0 = 0加速度a = ?根据运动学公式:s = v0t + (1/2)at^2代入已知数据:12 = 0*t + (1/2)*a*3^2化简方程:36 = (1/2)*a*9解方程得:a = 8 m/s^22. 一个质点以2 m/s^2 的加速度做匀变速直线运动,经过5秒后速度变为12 m/s,请计算这段时间内的位移。
工程力学试卷及答案完整版

工程力学试卷及答案完整版工程力学试卷及答案工程力学》试卷及答案一、填空题(每空1分,共22分)1、力的三要素是力的大小、方向、作用点。
用符号表示力的单位是N或KN。
2、力偶的三要素是力偶矩的大小、转向和作用面方位。
用符号表示力偶矩的单位为N·m或___·m。
3、常见的约束类型有柔性约束、光滑接触面约束、光滑铰链约束和固定端约束。
4、作用于一个刚体上的二力,使刚体保持平衡状态的充要条件是两个力大小相等、方向相反、作用线相同。
5、平面汇交力系平衡的充要条件是该力系的合力等于零。
6、平面任意力系的平衡条件为∑Fix=0,∑Fiy=0和∑M(F)=0.7、当平面任意力系有合力时,合力对作用面内任意点的矩,等于力系中各力对同一点之矩的代数和。
8、空间力系根据力的作用线不同可分为空间汇交力系、空间平行力系和空间任意力系。
9、力在空间坐标轴上的投影有两种运算方法,即直接投影法和二次投影法。
10、工程中二力杆需满足三个条件,即自重不计、两端均用铰链连接和不受其他力的作用。
二、判断题:(对的画“√”,错的画“×”)(每题2分,共20分)1、力的可传性定理,只适用于刚体。
(√)3、力的大小等于零或力的作用线通过矩心时,力矩等于零(√)4、力偶无合力,且力偶只能用力偶来等效。
(√)5、共线力系是平面汇交力系的特殊情况,但汇交点不能确定。
(√)7、平面汇交力系的合力一定等于各分力的矢量和。
(√)8、力使物体运动状态发生变化的效应称力的外效应。
(√)10、同一平面内作用线汇交于一点的三个力一定平衡。
(×)三、选择题(每题2分,共20分)1、平衡是指物体相对于地球保持静止或作匀速直线运动状态。
2、力的平行四边形公理说明,共点二力的合力等于两个分力的矢量和。
3、静力学研究对象主要是物体的平衡状态。
4、某刚体上作用了三个力,这三个力汇交于一点且互不平行。
根据这个条件,可以确定刚体处于平衡状态。
(完整版)工程力学试题及答案

工程力学试题及答案一、填空题(每空1分,共16分)1.物体的平衡是指物体相对于地面__________或作________运动的状态。
2.平面汇交力系平衡的必要与充分条件是:_____。
该力系中各力构成的力多边形____。
3.一物块重600N,放在不光滑的平面上,摩擦系数f=0.3,在左侧有一推力150N,物块有向右滑动的趋势。
F max=__________,所以此物块处于静止状态,而其F=__________。
4.刚体在作平动过程中,其上各点的__________相同,每一瞬时,各点具有__________的速度和加速度。
5.AB杆质量为m,长为L,曲柄O1A、O2B质量不计,且O1A=O2B=R,O1O2=L,当φ=60°时,O1A杆绕O1轴转动,角速度ω为常量,则该瞬时AB杆应加的惯性力大小为__________,方向为__________ 。
6.使材料丧失正常工作能力的应力称为极限应力。
工程上一般把__________作为塑性材料的极限应力;对于脆性材料,则把________作为极限应力。
7.__________面称为主平面。
主平面上的正应力称为______________。
8.当圆环匀速转动时,环内的动应力只与材料的密度ρ和_____________有关,而与__________无关。
二、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共18分)1.某简支梁AB受载荷如图所示,现分别用R A、R B表示支座A、B处的约束反力,则它们的关系为( )。
A.R A<R BB.R A>R BC.R A=R BD.无法比较2.材料不同的两物块A和B叠放在水平面上,已知物块A重0.5kN,物块B重0.2kN,物块A、B间的摩擦系数f1=0.25,物块B与地面间的摩擦系数f2=0.2,拉动B物块所需要的最小力为( )。
A.0.14kNB.0.265kNC.0.213kND.0.237kN3.在无阻共振曲线中,当激振力频率等于系统的固有频率时,振幅B趋近于( )。
(完整)工程力学试卷和答案

1. 表示扭转变形程度的量(B ).A. 是扭转角ψ,不是单位长度扭转角θB. 是单位长度扭转角θ,不是扭转角ψC。
是扭转角ψ和单位长度扭转角θD. 不是扭转角ψ和单位长度扭转角θ满分:5 分2. 平面汇交力系平衡的充分且必要的几何条件是(A).A. 力多边形自行封闭B。
所有力共线C。
所有力相交满分:5 分3。
梁的挠度是(B )。
A。
横截面上任意一点沿梁轴线垂直方向的线位移B. 横截面形心沿梁轴垂直方向的线位移C. 横截面形心沿梁轴方向的线位移D。
横截面形心的位移满分:5 分4。
理想均匀直杆与轴向压力P=Pcr时处于直线平衡状态。
当其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆(C )。
A. 弯曲变形消失,恢复直线形状B. 弯曲变形减小,不能恢复直线形状C. 微弯变形状态不变D。
弯曲变形继续增大满分:5 分5。
一圆轴用碳钢制作,校核其扭转角时,发现单位长度扭转角超过了许用值。
为保证此轴的扭转刚度,采用哪种措施最有效(C )。
A。
改用合金钢材料B。
增加表面光洁度C。
增加轴的直径满分:5 分6. 当平面力系的主矢不等于零,主矩等于零时,此力系合成为(A)。
A。
合力B。
合力偶C。
力螺旋满分:5 分7. 一拉伸钢杆,弹性模量E=200GPa,比例极限为200MPa,今测得其轴向应变ε=0。
0015,则横截面上的正应力(C )。
A. σ=Eε=300MPaB. σ>300MPaC. 200MPa<σ<300MPaD. σ<200MPa满分:5 分8. 作用在刚体上的三个力使刚体处于平衡状态,则这三个力必然(C)。
A. 相交B. 共线C. 共面满分:5 分9。
在下列有关压杆临界应力σcr的结论中,( A)是正确的。
A。
细长杆的σcr值与杆的材料无关B。
中长杆的σcr值与杆的柔度无关C. 中长杆的σcr值与杆的材料无关D. 粗短杆的σcr值与杆的柔度无关满分:5 分10。
关于平面力系的主矢和主矩,以下表述中正确的是(A)。
工程力学考试题及答案

工程力学考试题及答案一、单项选择题(每题2分,共20分)1. 工程力学中,下列哪一项不是力学的基本概念?A. 力B. 位移C. 速度D. 功答案:C2. 在静力学中,物体处于平衡状态的必要条件是:A. 合力为零B. 合力矩为零C. 合力和合力矩都为零D. 只有合力为零答案:C3. 材料力学中,下列哪一项不是基本假设?A. 均匀性假设B. 连续性假设C. 各向异性假设D. 小变形假设答案:C4. 梁在弯曲时,下列哪一项是正确的?A. 梁上任意截面的弯矩相等B. 梁上任意截面的剪力相等C. 梁上任意截面的弯矩和剪力都相等D. 梁上任意截面的弯矩和剪力都不相等答案:D5. 在拉伸和压缩实验中,下列哪一项不是材料的基本力学性能?A. 弹性模量B. 屈服强度C. 疲劳强度D. 抗拉强度答案:C6. 材料力学中,下列哪一项不是应力集中的影响因素?A. 几何形状B. 材料性质C. 加载方式D. 温度变化答案:D7. 在扭转实验中,圆轴的扭转角与下列哪一项无关?A. 扭矩B. 材料的剪切模量C. 轴的极惯性矩D. 轴的长度答案:D8. 材料力学中,下列哪一项不是梁的弯曲变形的基本形式?A. 纯弯曲B. 偏心弯曲C. 剪切弯曲D. 复合弯曲答案:C9. 在受压构件中,下列哪一项不是影响稳定性的因素?A. 截面形状B. 材料性质C. 长度D. 温度答案:D10. 材料力学中,下列哪一项不是疲劳破坏的特点?A. 循环加载B. 低应力水平C. 局部应力集中D. 无明显塑性变形答案:D二、填空题(每题2分,共20分)1. 牛顿第二定律表明,物体的加速度与作用在其上的合力成正比,与物体的质量成反比,其数学表达式为:_______。
答案:F=ma2. 材料力学中的应力定义为:单位面积上的_______。
答案:力3. 梁的挠度是指梁在受载后的_______。
答案:垂直位移4. 材料的弹性模量是描述材料_______的物理量。
答案:弹性变形5. 材料力学中,梁的剪力图是表示梁上任意截面处_______的图形。
工程力学完全试题(含有答案)
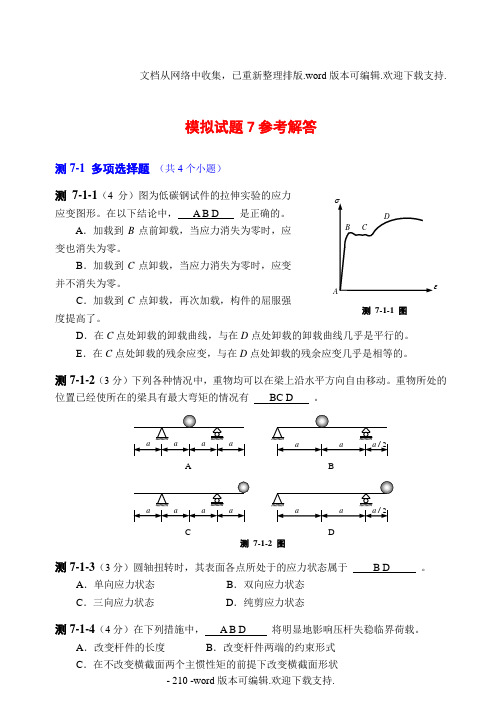
模拟试题7参考解答测7-1 多项选择题 (共4个小题)测7-1-1(4分)图为低碳钢试件的拉伸实验的应力应变图形。
在以下结论中, A B D 是正确的。
A .加载到B 点前卸载,当应力消失为零时,应变也消失为零。
B .加载到C 点卸载,当应力消失为零时,应变并不消失为零。
C .加载到C 点卸载,再次加载,构件的屈服强度提高了。
D .在C 点处卸载的卸载曲线,与在D 点处卸载的卸载曲线几乎是平行的。
E .在C 点处卸载的残余应变,与在D 点处卸载的残余应变几乎是相等的。
测7-1-2(3分)下列各种情况中,重物均可以在梁上沿水平方向自由移动。
重物所处的位置已经使所在的梁具有最大弯矩的情况有 BC D 。
测7-1-3(3分)圆轴扭转时,其表面各点所处于的应力状态属于 B D 。
A .单向应力状态B .双向应力状态C .三向应力状态D .纯剪应力状态测7-1-4(4分)在下列措施中, A B D 将明显地影响压杆失稳临界荷载。
A .改变杆件的长度B .改变杆件两端的约束形式C .在不改变横截面两个主惯性矩的前提下改变横截面形状ABCD 测 7-1-2 图测 7-1-1 图D .在不改变横截面形状的前提下改变横截面尺寸E .在杆件上沿垂直于轴线方向上开孔测7-2 填空题(共4个小题)测7-2-1(3分) 直径为d 的圆轴两端承受转矩m 的作用而产生扭转变形,材料的泊松比为ν,其危险点的第一强度理论的相当应力 =eq1σ 3π16dm,第二强度理论的相当应力=eq2σ)(ν+1π163d m,第三强度理论的相当应力 =eq3σ3π32d m。
测7-2-2(2分)承受均布荷载q 的悬臂梁的长度为L ,其横截面是宽度为b ,高度为h的矩形,该梁横截面上的最大弯曲切应力为 bhqL23 。
测7-2-3(4分)题图中左、右两杆的抗拉刚度分别是EA 和EA 20,则A 点的竖向位移为EAPa 22。
测7-2-4(6分)图示单元体所有应力分量均为MPa 50,材料的弹性模量GPa 210=E ,泊松比25.0=ν。
工程力学考试题及答案

工程力学考试题及答案一、单项选择题(每题2分,共20分)1. 以下哪项不是材料力学的研究对象?A. 材料的强度B. 材料的硬度C. 材料的弹性D. 材料的塑性答案:B2. 应力的定义是:A. 单位面积上的内力B. 单位体积上的内力C. 单位长度上的内力D. 单位质量上的内力答案:A3. 在拉伸试验中,材料的弹性极限是指:A. 材料发生永久变形的应力B. 材料发生断裂的应力C. 材料应力与应变成正比的应力D. 材料应力达到最大值的应力答案:C4. 以下哪项不是梁的弯曲变形的基本形式?A. 平面弯曲B. 扭转C. 轴向拉伸D. 剪切答案:C5. 梁在纯弯曲时,横截面上的正应力分布规律是:A. 线性分布B. 抛物线分布C. 指数分布D. 对数分布答案:B6. 根据能量守恒定律,以下哪种情况下结构的稳定性最好?A. 势能最小B. 动能最大C. 势能最大D. 动能最小答案:A7. 以下哪项不是影响材料疲劳寿命的因素?A. 材料的表面粗糙度B. 材料的硬度C. 材料的塑性D. 材料的弹性模量答案:D8. 以下哪项不是结构动力学的研究内容?A. 自由振动B. 受迫振动C. 热传导D. 随机振动答案:C9. 以下哪项不是结构静力分析的基本假设?A. 材料是连续的B. 材料是各向同性的C. 材料是完全弹性的D. 材料是完全塑性的答案:D10. 以下哪项不是结构稳定性分析的主要内容?A. 失稳的类型B. 失稳的条件C. 失稳的预防措施D. 材料的疲劳寿命答案:D二、填空题(每题2分,共20分)11. 材料力学中,材料的______是指材料在外力作用下抵抗变形的能力。
答案:弹性12. 材料力学中,材料的______是指材料在外力作用下抵抗断裂的能力。
答案:强度13. 材料力学中,材料的______是指材料在外力作用下抵抗永久变形的能力。
答案:塑性14. 在梁的弯曲理论中,中性轴是梁横截面上正应力为______的直线。
工程力学本科试题及答案

工程力学本科试题及答案一、单项选择题(每题2分,共20分)1. 力学中的基本假设是()。
A. 质点B. 刚体C. 弹性体D. 塑性体答案:B2. 材料力学中,下列哪一项不是基本假设?()。
A. 均匀性B. 各向同性C. 连续性D. 非线性答案:D3. 应力是()。
A. 内力B. 外力C. 内力与面积的比值D. 外力与面积的比值答案:C4. 应变是()。
A. 内力B. 外力C. 位移与长度的比值D. 位移与面积的比值答案:C5. 材料力学中,下列哪一项不是基本变形?()。
A. 拉伸B. 压缩C. 剪切D. 扭转答案:D6. 根据胡克定律,应力与应变的关系是()。
A. 线性B. 非线性C. 抛物线D. 指数答案:A7. 材料的弹性模量E是()。
A. 应力B. 应变C. 应力与应变的比值D. 位移与力的比值答案:C8. 材料的泊松比ν是()。
A. 纵向应变与横向应变的比值B. 横向应变与纵向应变的比值C. 应力与应变的比值D. 位移与长度的比值答案:A9. 在拉伸试验中,材料的屈服强度是指()。
A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生永久变形的应力答案:A10. 材料的疲劳强度是指()。
A. 材料在循环加载下发生断裂的应力B. 材料在单次加载下发生断裂的应力C. 材料在循环加载下发生塑性变形的应力D. 材料在单次加载下发生塑性变形的应力答案:A二、填空题(每题2分,共20分)11. 力的三要素包括力的大小、方向和作用点。
答案:大小、方向、作用点12. 力矩是力与力臂的乘积。
答案:乘积13. 力偶是一对大小相等、方向相反、作用线平行的力。
答案:力14. 材料力学中的强度条件是指构件在受力时不发生破坏。
答案:破坏15. 材料力学中的刚度条件是指构件在受力时不发生过大的变形。
答案:变形16. 材料力学中的稳定性条件是指构件在受力时不发生失稳。
17. 材料力学中的应力集中是指在构件的某些局部区域,应力值远大于应力。
工程力学考试题及答案

工程力学考试题及答案一、单项选择题(每题2分,共20分)1. 以下哪项是工程力学中研究的主要对象?A. 材料B. 结构C. 力D. 以上都是答案:D2. 静力学中,平衡状态是指物体所受的合力为:A. 非零B. 零C. 任意值D. 不可确定答案:B3. 材料力学中,弹性模量是描述材料的哪种性质?A. 强度B. 硬度C. 弹性D. 塑性答案:C4. 根据牛顿第三定律,作用力和反作用力的大小关系是:A. 相等B. 不相等C. 相反D. 无法确定答案:A5. 在梁的弯曲问题中,梁的弯曲刚度与以下哪项无关?A. 梁的截面形状B. 梁的长度C. 梁的材料D. 梁的截面尺寸答案:B6. 应力集中是指在材料的哪些部位应力会显著增大?A. 光滑表面B. 无缺陷区域C. 几何突变处D. 均匀受力区域答案:C7. 动载荷是指:A. 静止不动的载荷B. 随时间变化的载荷C. 随空间变化的载荷D. 均匀分布的载荷答案:B8. 能量守恒定律在工程力学中的应用主要体现在:A. 热力学B. 动力学C. 静力学D. 流体力学答案:B9. 以下哪种材料可以认为是理想弹性体?A. 橡胶B. 钢铁C. 玻璃D. 木材答案:B10. 塑性变形是指材料在外力作用下发生变形后,去掉外力后:A. 不能恢复原状B. 完全恢复原状C. 部分恢复原状D. 无法确定答案:A二、填空题(每空1分,共20分)1. 物体在受到三个力的作用下,若这三个力的合力为零,则物体处于______状态。
答案:平衡2. 材料力学中,梁的挠度是指梁在受力后与______之间的最大垂直距离。
答案:原始直线3. 材料在拉伸过程中,其应力与应变的关系曲线称为______曲线。
答案:应力-应变4. 根据胡克定律,弹簧的变形量与施加在其上的力成正比,其比例系数称为______。
答案:弹簧常数5. 在材料力学中,材料的屈服强度是指材料在______状态下的最大应力。
答案:塑性变形6. 动载荷引起的振动通常需要考虑______效应。
工程力学课程试题库及参考答案

工程力学课程试题库及参考答案试题一:选择题1. 下列哪个选项不是力的基本性质?A. 力是物体间相互作用的体现B. 力是矢量C. 力不能离开物体单独存在D. 力的大小可以无限大答案:D2. 在静力学中,下列哪个条件是物体平衡的必要和充分条件?A. 力的合力为零B. 力矩的合力为零C. 力的合力为零,且力矩的合力为零D. 力的合力不为零,力矩的合力为零答案:C3. 下列哪个力系是平面力系?A. 空间力系B. 静力力系C. 汇聚力系D. 平面汇聚力系答案:D试题二:填空题1. 在工程力学中,力的单位是______,符号为______。
答案:牛顿,N2. 物体在力的作用下发生形变,这种形变称为______。
答案:弹性形变3. 在平面力系中,力矩的合力等于______。
答案:零试题三:判断题1. 力的平行四边形法则表明,两个力的合力等于这两个力的矢量和。
()答案:正确2. 在空间力系中,力的合力一定等于零。
()答案:错误3. 拉伸试验中,当拉力达到最大值时,试件一定会断裂。
()答案:错误试题四:计算题1. 已知一物体质量为10kg,在水平方向受到两个力的作用,分别为20N和30N,且两个力的作用线与水平方向的夹角分别为30°和60°。
求物体的合力及合力方向。
答案:合力约为45.8N,合力方向约为39.8°。
2. 一简支梁受到均布载荷的作用,载荷大小为20N/m,梁长2m,求梁的中点处的弯矩。
答案:40N·m3. 一圆形截面轴受到扭矩的作用,扭矩大小为100N·m,轴的直径为20mm,求轴的扭转应力。
答案:约为39.8MPa二、工程力学课程参考答案1. 选择题参考答案:(1)D(2)C(3)D2. 填空题参考答案:(1)牛顿,N(2)弹性形变(3)零3. 判断题参考答案:(1)正确(2)错误(3)错误4. 计算题参考答案:(1)合力约为45.8N,合力方向约为39.8°。
工程力学试题及答案(全)

工程力学试题及答案(全)一、选择题(每题2分,共20分)1. 在静力学中,力的基本要素包括以下哪几项?A. 力的大小B. 力的方向C. 力的作用点D. 力的作用时间答案:ABC2. 下列关于约束反力的说法,正确的是:A. 约束反力总是与物体运动方向相反B. 约束反力总是与物体受到的主动力相等C. 约束反力总是垂直于约束面D. 约束反力的大小和方向与物体的运动状态有关答案:C3. 在平面汇交力系中,力的投影是指:A. 力在坐标轴上的分量B. 力在坐标平面上的投影长度C. 力在物体表面上的投影长度D. 力在坐标系中的位置答案:B4. 平面力偶的作用效果取决于以下哪个因素?A. 力偶的大小B. 力偶的方向C. 力偶的作用点D. 力偶的转向答案:A5. 下列关于功的说法,正确的是:A. 功是力与物体位移的乘积B. 功是力与物体位移在同一方向上的投影的乘积C. 功是力与物体位移的乘积再乘以2D. 功是力与物体位移的乘积再除以2答案:B二、填空题(每题3分,共30分)6. 在静力学中,力的单位是______,符号为______。
答案:牛顿,N7. 二力平衡的条件是:作用在同一物体上的两个力,大小______,方向______,作用线______。
答案:相等,相反,共线8. 力矩的符号是______,力矩的单位是______。
答案:M,N·m9. 平面汇交力系平衡的充要条件是:各力在x轴上的投影之和______,各力在y轴上的投影之和______,各力对任意点的力矩之和______。
答案:等于零,等于零,等于零10. 功的计算公式是______,符号为______。
答案:W = F·S,W三、判断题(每题2分,共20分)11. 力偶的作用效果与力偶的大小、方向和作用点有关。
()答案:错误12. 在平面力偶系中,力偶的转向改变,其作用效果不变。
()答案:正确13. 功的正负取决于力与位移的方向关系,当力与位移同向时,功为正。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 210 -模拟试题7参考解答测7-1 多项选择题 (共4个小题)测7-1-1(4分)图为低碳钢试件的拉伸实验的应力应变图形。
在以下结论中, A B D 是正确的。
A .加载到B 点前卸载,当应力消失为零时,应变也消失为零。
B .加载到C 点卸载,当应力消失为零时,应变并不消失为零。
C .加载到C 点卸载,再次加载,构件的屈服强度提高了。
D .在C 点处卸载的卸载曲线,与在D 点处卸载的卸载曲线几乎是平行的。
E .在C 点处卸载的残余应变,与在D 点处卸载的残余应变几乎是相等的。
测7-1-2(3分)下列各种情况中,重物均可以在梁上沿水平方向自由移动。
重物所处的位置已经使所在的梁具有最大弯矩的情况有 BC D 。
测7-1-3(3分)圆轴扭转时,其表面各点所处于的应力状态属于 B D 。
A .单向应力状态B .双向应力状态C .三向应力状态D .纯剪应力状态测7-1-4(4分)在下列措施中, A B D 将明显地影响压杆失稳临界荷载。
A .改变杆件的长度B .改变杆件两端的约束形式C .在不改变横截面两个主惯性矩的前提下改变横截面形状ABCD 测 7-1-2 图测 7-1-1 图. 下载可编辑 .D .在不改变横截面形状的前提下改变横截面尺寸E .在杆件上沿垂直于轴线方向上开孔测7-2 填空题(共4个小题)测7-2-1(3分) 直径为d 的圆轴两端承受转矩m 的作用而产生扭转变形,材料的泊松比为ν,其危险点的第一强度理论的相当应力 =eq1σ 3π16dm,第二强度理论的相当应力=eq2σ)(ν+1π163dm,第三强度理论的相当应力 =eq3σ3π32d m。
测7-2-2(2分)承受均布荷载q 的悬臂梁的长度为L ,其横截面是宽度为b ,高度为h的矩形,该梁横截面上的最大弯曲切应力为 bhqL23 。
测7-2-3(4分)题图中左、右两杆的抗拉刚度分别是EA 和EA 20,则A 点的竖向位移为EAPa 22。
测7-2-4(6分)图示单元体所有应力分量均为MPa 50,材料的弹性模量GPa 210=E ,泊松比25.0=ν。
应将应变片贴在与x 轴成 45 度的方向上,才能得到最大拉应变读数;在此方向上的正应变=αε 476 με,切应变 =αγ 0 。
测7-3 计算题 ( 共5个小题 )测7-3-1 (14分)图示水平刚性梁由杆 ① 和杆 ② 悬挂。
两杆材料和横截面面积相同。
m 5.1=L ,m 2=a ,m 1=b 。
由于制造误差,杆 ①的长度做短了mm 5.1=δ。
材料常数 GPa 200=E ,试求装配后杆 ① 和杆 ② 横截面上的应力。
解:设 ①、② 号杆分别承受拉力N1F 和N2F ,则有平衡条件: b F a F N2N1221=。
测 7-2-4 图测 7-2-3 图测 7-3-1 图- 212 -物理条件: EALF N11=δ,EA L F N222=δ。
协调条件: δδδ=+212ba。
可解得 Lb a EAb F )24(2222N1+=δ, L b a EAab F )24(222N2+=δ。
故有 Lb a Eb )24(2222(1)+=δσ, L b a Eab )24(222(2)+=δσ。
代入数据可得MPa 16.2)1(=σ,MPa 45.9)2(=σ。
测7-3-2 (12分)如图结构中kN 5=F ,螺栓许用切应力MPa 110][=τ,刚架变形很小,试根据切应力强度设计螺栓尺寸d 。
解:螺栓群承受竖直向下的力,每个螺栓相应的剪力(方向向下)N 125041==F Q 。
记 mm 500=L ,则螺栓群承受转矩 FL T =。
记 m m 601=r ,m m 1802=r ,根据图(a) 可知,上下两个螺栓与中间两个螺柱所受的力的比例为 312=r r。
记上下两个螺栓所受这部份剪力为2Q ,则有FL Qr Q r =⋅+3222122, 故有 )3(23122r r FL Q +=N 6250)601803(250050003=+⨯⨯⨯⨯=。
故有总剪力N 77.637362501250222221=+=+=Q Q Q 。
由Q d ≥][π412τ 可得 ][π4τQ d ≥mm 59.8110π77.63734=⨯⨯=, 取 mm 9=d 。
(a)测 7-3-2 图 120120120. 下载可编辑 .测7-3-3(15分)如图的结构中,立柱是外径 mm 80=D ,外径之比 8.0=α 的空心圆杆,m 2=H 。
板面尺寸 m 1=b ,m 5.1=h 。
板面承受的最大风压为 Pa 200=q 。
不计立柱和板面自重,用第四强度理论求立柱中危险点的应力。
解:立柱承受弯扭组合变形。
板面所受合力 N 3005.11200=⨯⨯==qbh F 。
弯矩 ⎪⎭⎫ ⎝⎛+=2h H F Mm m N 10825.0)7502000(3006⋅⨯=+⨯=。
扭矩 ⎪⎭⎫⎝⎛+=22D b F Tm m N 10162.0)40500(3006⋅⨯=+⨯=。
第四强度理论相当应力 2243eq475.0)1(π32T M D +-=ασ MPa 2.28162.075.0825.0)8.01(80π103222436=⨯+⨯-⨯⨯⨯=。
测7-3-4(20分)在如图的结构中,(1) 求C 点处的位移;(2) 画出结构的剪力图和弯矩图。
解:解除C 点处的约束而代之以约束力R ,如图(a),EI Ra EI a R w l 3423233-=⋅-=)(EIa R F w r 33)(--=协调条件EI Ra EI a R F 343)(33-=--,F R 51=。
故 EIFa EI Fa w C 15453433-=⋅-= ()↓。
由此可得结构剪力图和弯矩图。
测 7-3-4 图F R(a)测7-3-3 图5- 214 -测7-3-5(10分)图示结构中,AB 杆为边长为a 的正方形截面,BC 为直径为d 的圆杆,两杆材料相同,且皆为细长杆。
已知A 端固定,B 、C 为球铰。
为使两杆同时失稳,直径d 与边长a 之比应为多少? 解:左端部份的临界荷载()221crl 7.0πL EI F =,右端部份的临界荷载 2222cr πLEI F =。
两杆同时失稳,有 2cr 1cr F F =, 故有2149.0I I =。
即44π64112490d a =⨯., a a d 36.1π1249.0644=⨯⨯=。
故有 36.1=ad。
测 7-3-5 图. 下载可编辑 .模拟试题8参考解答测8-1 填空题 (共3个小题)测8-1-1(6分)某试件材料的弹性模量 E 为GPa 25,泊松比为0.25,则这种材料的剪切弹性模量G 为 10 GPa 。
若试件直径为mm 40,该试件拉伸到轴向应变为 4108-⨯ 时相应的拉伸应力为 20 MPa ,直径缩短了 0.008mm 。
测8-1-2(4分)图示等截面直杆,杆长为a 3,材料的抗拉刚度为EA ,受力如图。
杆中点横截面的铅垂位移为()↓EAPa。
测8-1-3(4分)为了使如图的抗弯刚度为EI 的悬臂梁轴线变形成为半径为R 的圆弧(R 远大于梁的长度),可在梁 的自由端处加上一个大小为 REI的力偶矩。
测8-2 计算题 ( 共6个小题 )测8-2-1(15分)画出图示外伸梁的剪力、弯矩图。
解:∑=0A m , 023222=-⋅+⋅-⋅-qa a R a qa a qa B , qa R B 37=, ∑=0Bm , 022232=-⋅+⋅+⋅-qa a qa a qa a R A , qa R A 32=。
由此可得如下剪力图和弯矩图。
测 8-1-2 图3测 8-2-1 图测 8-1-3 图- 216 -测8-2-2(16分)在上题中,梁的横截面形状如图,m /kN 5=q ,m 5.1=a ,求梁中横截面上最大的拉应力。
解:先求截面形心位置,以下边沿为基准,有25200250150100252002)20025(501502⨯⨯+⨯⨯⨯⨯++⨯⨯=y mm 57.153=。
m m 439657153502001..)(=-+=y 。
再求截面关于形心轴(即中性轴)的惯性矩232543965015050150121).(-⨯⨯+⨯⨯=I ⎥⎦⎤⎢⎣⎡-⨯⨯+⨯⨯⨯+231005715320025200251212).( 71010153298293⨯⨯+=)..(48mm 100191⨯=.。
在BC 区段上侧有最大拉应力mm N 1025.21500522722⋅⨯=⨯⨯==qa M BC ,Iy M BC 1=σMPa 3.2110019.143.961025.287=⨯⨯⨯=。
在A 截面下侧有最大拉应力 mm N 1075.0150053232722⋅⨯=⨯⨯==qa M A , Iy M A 2=σMPa 3.1110019.157.1531075.087=⨯⨯⨯=。
故最大拉应力在BC 区段上侧,MPa 3.21max =σ。
2525测 8-2-2 图. 下载可编辑 .测8-2-3(15分)阶梯形圆轴直径分别为 m m 401=d ,m m 702=d ,轴上装有三个皮带轮,如图所示。
已知由轮B 输入的功率为 kW 303=P ,轮A 输出的功率为kW 131=P ,轴作匀速转动,转速 r/min 200=n ,材料的许用切应力 MPa 60][=τ,GPa 80=G ,许用扭转角 m /2][︒=θ。
不考虑皮带轮厚度的影响,试校核轴的强度和刚度。
解: 首先作阶梯轴的扭矩图,如图所示。
(1) 强度校核m N 621300129549954911⋅=⨯=⨯=n P m , m N 812200)1330(9549954922⋅=-⨯=⨯=n P m 。
根据平衡条件,有m N 1433m N )812621(213⋅=⋅+=+=m m m ,AD 段最大切应力为MPa 60][MPa 49.440π1062116π1633311P111=<=⨯⨯⨯===ττd m W T 。
AC 段的最大工作切应力小于许用切应力,满足强度要求。
DC 段的扭矩与AD 段的相同,但其直径比AD 段的大,所以DC 段也满足强度要求。
CB 段上最大切应力为MPa 60][MPa 21.370π10143316π1633323P222=<=⨯⨯⨯===ττd m W T 。
故CB 段的最大工作切应力小于许用切应力,满足强度要求。
(2) 刚度校核AD 段的最大单位长度扭转角为15433411P11mm 10089.340π10801062132π32--⨯=⨯⨯⨯⨯⨯===d G m GI T θ m /2][/m 77.1︒=<︒=θ。
