初中数学:二元一次方程组的几种简便解法
二元一次方程组的解法

二元一次方程组的解法
数学一直注重学习的连贯性,如果小学的思维基础没打好,学习初中数学就会有些吃力。
有些同学就会问二元一次方程组的解法。
下面是由小编为大家整理的“二元一次方程组的解法”,仅供参考,欢迎大家阅读。
二元一次方程组的解法
代入消元法。
我们先把第一个方程看成只有一个未知数(另一个字母看成已知数),通过移项去括号等把它写成字母等于的形式。
然后我们把第二个方程里面的那个字母换成刚才我们得到的代数式,这样我们就得到了一个一元一次方程。
把这个一元一次方程解出来,得到其中一个未知数的值。
代入到方程组中其中一个方程,就得到了一个未知数的值,到这里,方程组就被我们解出来了。
加减消元法。
得到一个二元一次方程组,我们通过乘以一个数,想办法把两个方程中其中相对应的一个未知数的系数化为相同相反的数。
然后让这两个式子做差或和,便可以消去一个未知数,得到一个一元一次方程,以下步骤和代入消元法里面的一样。
拓展阅读:二元一次方程组的解有几个
一个二元一次方程表示一条直线,一般情况是相交的,是一个解,平行时候无解,重合时候有无数解。
二元一次方程是指含有两个未知数(例如x和y),并且所含未知数的项的次数都是1的方程。
两个结合在一起的共含有两个未知数的一次方程叫二元一次方程组。
每个方程可化简为ax+by=c的形式。
如果一个方程含有两个未知数,并且所含未知数的次数都为1,这样的整式方程叫做二元一次方程。
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
利用数的整除特性结合代入排除的方法去求解。
第二节 二元一次方程组的解法(含答案)...七年级数学 学而思
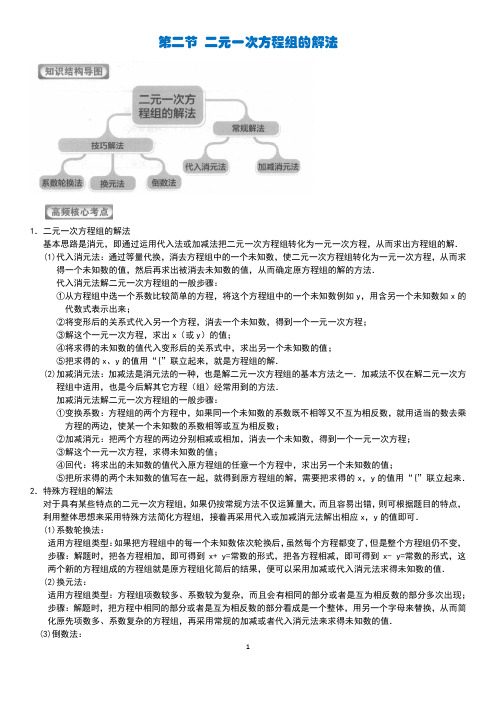
第二节二元一次方程组的解法1.二元一次方程组的解法基本思路是消元,即通过运用代入法或加减法把二元一次方程组转化为一元一次方程,从而求出方程组的解. (1)代入消元法:通过等量代换,消去方程组中的一个未知数,使二元一次方程组转化为一元一次方程,从而求得一个未知数的值,然后再求出被消去未知数的值,从而确定原方程组的解的方法.代入消元法解二元一次方程组的一般步骤:①从方程组中选一个系数比较简单的方程,将这个方程组中的一个未知数例如y,用含另一个未知数如x的代数式表示出来;②将变形后的关系式代入另一个方程,消去一个未知数,得到一个一元一次方程;③解这个一元一次方程,求出x(或y)的值;④将求得的未知数的值代入变形后的关系式中,求出另一个未知数的值;⑤把求得的x、y的值用“{”联立起来,就是方程组的解.(2)加减消元法:加减法是消元法的一种,也是解二元一次方程组的基本方法之一.加减法不仅在解二元一次方程组中适用,也是今后解其它方程(组)经常用到的方法.加减消元法解二元一次方程组的一般步骤:①变换系数:方程组的两个方程中,如果同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数;②加减消元:把两个方程的两边分别相减或相加,消去一个未知数,得到一个一元一次方程;③解这个一元一次方程,求得未知数的值;④回代:将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数的值;⑤把所求得的两个未知数的值写在一起,就得到原方程组的解,需要把求得的x,y的值用“{”联立起来.2.特殊方程组的解法对于具有某些特点的二元一次方程组,如果仍按常规方法不仅运算量大,而且容易出错,则可根据题目的特点,利用整体思想来采用特殊方法简化方程组,接着再采用代入或加减消元法解出相应x,y的值即可.(1)系数轮换法:适用方程组类型:如果把方程组中的每一个未知数依次轮换后,虽然每个方程都变了,但是整个方程组仍不变,步骤:解题时,把各方程相加,即可得到x+ y=常数的形式,把各方程相减,即可得到x- y=常数的形式,这两个新的方程组成的方程组就是原方程组化简后的结果,便可以采用加减或代入消元法求得未知数的值.(2)换元法:适用方程组类型:方程组项数较多、系数较为复杂,而且会有相同的部分或者是互为相反数的部分多次出现;步骤:解题时,把方程中相同的部分或者是互为相反数的部分看成是一个整体,用另一个字母来替换,从而简化原先项数多、系数复杂的方程组,再采用常规的加减或者代入消元法来求得未知数的值.(3)倒数法:适合方程组类型:方程中出现分母是和的形式,分子是积的形式⋅+yx xy步骤:解题时,采用倒数法变换成分子是和、分母是积的形式,xyyx +然后进行拆分,利用加减或者代入或者换元法来解出x ,y 的值.1.代入消元方法的选择①运用代入法时,将一个方程变形后,必须代入另一个 方程,否则就会 得出“0=0”的形式,求不出未知数的值;②当方程组中有一个方程的一个未知数的系数是1或一1时,用代入法较简便. 2.加减消元方法的选择①一般选择系数绝对值最小的未知数消元;②当某一未知数的系数互为相反数时,用加法消元;当某一未知数的系数相 等时,用减法消元;③某一未知数系数成倍数关系时,直接使其系数互为相反数或相等,再用 加减消元求解;④当相同的未知数的系数都不相同时,找出某一个未知数的系数的最小公倍数,同时对两个方程进行变形,转化为系数的绝对值相同的方程,再用加减消元求解,例1.如果关于x ,y 的方程组⎩⎨⎧-=-=+223a y x y x 的解是负数,则a 的取值范围是( )54.<<-a A 5.>a B 4.-<a C D .无解检测1.(浙江绍兴期末)已知关于x ,y 的方程组⎩⎨⎧-=-=-,52253a y x ay x 若x ,y 的值互为相反数,则a 的值为( )5.-A 5.B 20.-C 20.D例2.(四川南江县期末)已知,0)112(|32|2=+++--y x y x 则( )⎩⎨⎧==12.y x A ⎩⎨⎧-==30.y x B ⎩⎨⎧-=-=51.y x C ⎩⎨⎧-=-=72.y x D检测2.(山东滨州期末)已知,0|72|)12(2=-++--y x y x 则=-y x 3( )3.A 1.B 6.-C 8.D例3.(湖北黄冈期末)若y x h y xb a ba -+--332243是同类项,则b a -的值是( )0.A 1.B 2.C 3.D检测3.若y x nm +243与n m y x -5是同类项,则m .n 的值分别是( ) 3,2.A 1,2.B 0,2.C 2,1.D例4.(湖南衡阳县一模)解方程组:⎩⎨⎧=+=+,604320122016604120162012y x y x 则yx yx -+值是3.A 3.-B 6.C 6.-D检测4.(1)(江苏海门市期末)如果实数x ,y 满足方程组⎩⎨⎧=+=+,4222y x y x 那么=+y x(2)(安徽泗县校级模拟)关于x ,y 的二元一次方程组⎩⎨⎧-=+-=+22132y x k y x 的解满足y x +,1=则k=例5.(河北古冶区一模)已知a ,b 满足方程组⎩⎨⎧=-=+,283b a b a 则=+b a2.A3.B4.C5.D检测5.(1)(河北模拟)已知e 、f 满足方程组⎩⎨⎧=-=--,6223e f f e 则f e +2的值为( )2.A 4.B 6.C 8.D(2)(广东广州中考)已知a .b 满足方程组⎩⎨⎧=-=+,43125b a b a 则b a +的值为第二节 二元一次方程组的解法(建议用时:35分钟)实战演练1.用加减法解方程组⎩⎨⎧-=-=+15y x y x 中,消x 用 法,消y 用 法( )A.加,加 B .加,减 C .减,加 D .减,减2.若用代入法解方程组⎩⎨⎧+==,12332y x yx 以下各式代入正确的是( )1)32(23.+=x x A 1)32(23.+=y x B1)23(23.+=x x C 1623.+⋅=x x x D3.若,0|52||12|=--+--y x y x 则x+y 的值为( )4.A5.B6.C7.D4.已知:|32|++y x 与2)2(y x +互为相反数,则=-y x ( )7.A 5.B 3.C 1.D5.(山东临清市期末)已知方程组⎩⎨⎧=+=-my x y x 24中x ,y 相加为0,则m 的值为( )2.A 2.-B 0.C 4.D6.(河北石家庄校级模拟)若方程组⎩⎨⎧=++=+my x m y x 32253的解x 与y 互为相反数,则m 的值为( )2.-A 0.B 2.C 4.D7.若方程组⎩⎨⎧=+=+16156653y x y x &的解也是方程103=+ky x 的解,则( )6.=k A 10.=k B 9.=k C 101.=k D 8.若3243y x b a +与ba y x -634的和是单项式,则=+b a ( ) 3.-A 0.B 3.C 6.D9.按如图8 -2—1所示的运算程序,能使输出结果为3的x ,y 的值是( )128--2,5.-==y x A ⋅-==3,3.y x B 2,.4.=-=y x C 9,3.-=-=y x D10.(山东临沂中考)已知x ,y 满足方程组⎩⎨⎧=+=+,4252y x y x 则y x -的值为( )⎩⎨⎧==12.11y x 是方程组⎩⎨⎧=-=+04by ax by ax 的解,那么=+-))((b a b a 12.已知方程组⎩⎨⎧-=+=-123225m y x my x 的解x ,y 互为相反数,则m=13.(江苏常州期末)若关于x ,y ,的二元一次方程组⎩⎨⎧=+-=+22132y x a y x 的解满足x+ y=l ,则a 的值为14.三个同学对问题“若方程组⎪⎩⎪⎨⎧=+=+222111c y b x a c y b x a 的解是⎩⎨⎧==,43y x 求方程组⎪⎩⎪⎨⎧=+=+222111523523c y b x a c y b x a 的解.”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”,参考他们的讨论,你认为这个题目的解应该是 .15.(“信利杯”竞赛题)已知:a ,b ,c 三个数满足,31=+b a ab ,41=+c b bc ,51=+a c ca 则ca bc ab abc++的值为 16.(重庆校级自主招生)解方程组:⎩⎨⎧=+=+200320042005200620052004y x y x17.解方程组:⎪⎩⎪⎨⎧-=-=-+-421621y x y x18.已知方程组⎩⎨⎧+=---=+ay x ay x 317的解中,x 为非正数,y 为负数.(1)求a 的取值范围; (2)化简.|2||3|++-a a19.(江苏张家港市期末)已知关于x ,y 的方程组⎩⎨⎧+=+=+12242m y x my x (实数m 是常数).(1)若x+y=1,求实数m 的值;(2)若,51≤-≤-y x 求m 的取值范围; (3)在(2)的条件下,化简:.|32||2|-++m m20.(黑龙江讷河市校级期末)已知二元一次方程组⎩⎨⎧+=-+=+1593a y x a y x 的解x ,y 均是正数.(1)求a 的取值范围; (2)化简.|4||54|--+a a拓展创新21.解方程组:⎩⎨⎧==+44y -3x 23y x 2拓展1.解方程组:⎪⎪⎩⎪⎪⎨⎧=-=+443232y x y x 拓展2.解方程组:⎪⎪⎩⎪⎪⎨⎧=-=+41432132x y xy x y xy极限挑战22.(全国初中数学竞赛)若,0634=--z y x ),0(072=/=-+xyz z y x 则式子222222103225z y x z y x ---+的值等于( )21.-A219.-B 15.-C 13.-D课堂答案培优答案。
初中二元一次方程知识归纳

初中二元一次方程知识归纳二元一次方程是初中解方程的重要知识点,求解二元一次方程首先要明白其基础内容。
以下是店铺分享给大家的初中二元一次方程知识,希望可以帮到你!初中二元一次方程知识一.二元一次方程(组)的相关概念1.二元一次方程:含有两个未知数并且未知项的次数是1的方程叫做二元一次方程。
2.二元一次方程组:二元一次方程组两个二元—次方程合在一起就组成了一个二元一次方程组。
3.二元一次方程的解集:(1)二元一次方程的解适合一个二元一次方程的每一对未知数的值.叫做这个二元一次方程的一个解。
(2)二元一次方程的解集对于任何一个二元一次方程,令其中一个未知数取任意二个值,都能求出与它对应的另一个未知数的值.因此,任何一个二元一次方程都有无数多个解.由这些解组成的集合,叫做这个二元一次方程的解集。
4.二元一次方程组的解:二元一次方程组可化为使方程组中的各个方程的左、右两边都相等的未知数的值,叫做方程组的解。
二.利用消元法解二元一次方程组解二元(三元)一次方程组的一般方法是代入消元法和加减消元法。
1.解法:(1) 代入消元法是将方程组中的其中一个方程的未知数用含有另一个未知数的代数式表示,并代入到另一个方程中去,消去另一个未知数,得到一个解。
代入消元法简称代入法。
(2)加减消元法利用等式的性质使方程组中两个方程中的某一个未知数前的系数的绝对值相等,然后把两个方程相加或相减,以消去这个未知数,使方程只含有一个未知数而得以求解。
这种解二元一次方程组的方法叫做加减消元法,简称加减法。
用加减法消元的一般步骤为:①在二元一次方程组中,若有同一个未知数的系数相同(或互为相反数),则可直接相减(或相加),消去一个未知数;②在二元一次方程组中,若不存在①中的情况,可选择一个适当的数去乘方程的两边,使其中一个未知数的系数相同(或互为相反数),再把方程两边分别相减(或相加),消去一个未知数,得到一元一次方程;③解这个一元一次方程;④将求出的一元一次方程的解代入原方程组系数比较简单的方程,求另一个未知数的值;⑤把求得的两个未知数的值用大括号联立起来,这就是二元一次方程组的解。
2017-2018学年人教版七年级数学下册(广东专版)高分突破讲练:(四) 二元一次方程组
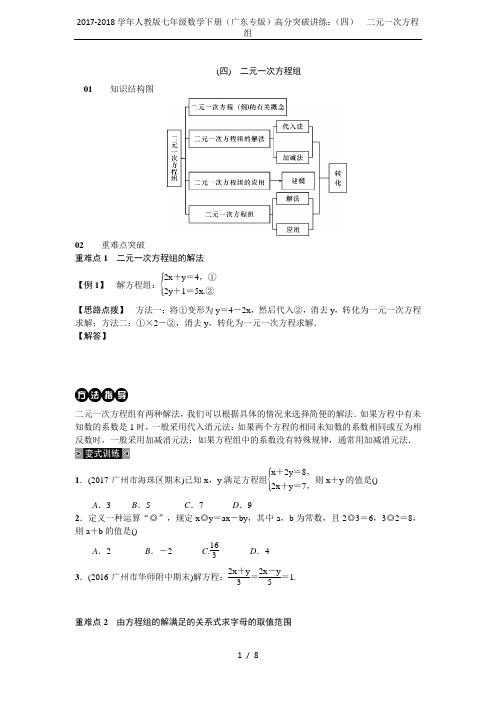
(四) 二元一次方程组01 知识结构图02 重难点突破重难点1 二元一次方程组的解法【例1】 解方程组:⎩⎪⎨⎪⎧2x +y =4,①2y +1=5x.②【思路点拨】 方法一:将①变形为y =4-2x ,然后代入②,消去y ,转化为一元一次方程求解;方法二:①×2-②,消去y ,转化为一元一次方程求解. 【解答】二元一次方程组有两种解法,我们可以根据具体的情况来选择简便的解法.如果方程中有未知数的系数是1时,一般采用代入消元法;如果两个方程的相同未知数的系数相同或互为相反数时,一般采用加减消元法;如果方程组中的系数没有特殊规律,通常用加减消元法.1.(2017·广州市海珠区期末)已知x ,y 满足方程组⎩⎪⎨⎪⎧x +2y =8,2x +y =7,则x +y 的值是()A .3B .5C .7D .92.定义一种运算“◎”,规定x ◎y =ax -by ,其中a ,b 为常数,且2◎3=6,3◎2=8,则a +b 的值是()A .2B .-2C .163D .43.(2016·广州市华师附中期末)解方程:2x +y 3=2x -y5=1.重难点2 由方程组的解满足的关系式求字母的取值范围【例2】 若二元一次方程组⎩⎪⎨⎪⎧2x +3y =k -3,x -2y =2k +1的解互为相反数,则k 的值为()A .58B .85C .165D .-85【思路点拨】 先解方程组,得到⎩⎨⎧x =8k -37,y =-3k -57,再根据方程组的解互为相反数,得到关于k 的一元一次方程,求解方程即可得到k 的值.由方程组的解满足的关系式求字母的取值范围的解题步骤一般是:①先解方程组,用含未知数的值表示方程组的解;②根据方程组的解满足的关系式列方程或不等式;③解方程或不等式即可得到字母的取值范围.4.二元一次方程组⎩⎪⎨⎪⎧3x +2y =10,kx +(k +2)y =6的解x ,y 的值相等,则k 的值为()A .12B .1C .2D .525.若关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧x +y =k ,2x -y =8k 的解也是二元一次方程3x +2y =10的解,则k 的值为()A .1B .-2C .2D .46.若关于x ,y 的二元一次方程组⎩⎪⎨⎪⎧3x +y =1+a ,①x +3y =3②的解,满足x +y<2,则a 的取值范围为()A .a<4B .a>4C .a<-4D .a>-4重难点3 二元一次方程组的应用【例3】 某中学拟组织九年级师生去黄山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5 000元.”小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.” 根据以上对话,解答下列问题:(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元? 【思路点拨】 (1)根据题目给出的条件得出的等量关系是60座客车每辆每天的租金-45座客车每辆每天的租金=200元,4辆60座一天的租金+2辆45座的一天的租金=5 000元,由此可列出方程组求解;(2)可根据“我们九年级师生租用5辆60座和1辆45座的客车正好坐满”以及(1)的结果来求出答案. 【解答】列方程解决实际问题的解题步骤是:1.审题:弄清已知量和未知量;2.设未知数,并根据相等关系列出符合题意的方程; 3.解这个方程;4.验根并作答:检验方程的根是否符合题意,并写出完整的答案.7.从甲地到乙地的路有一段上坡,一段下坡.如果上坡平均每分钟走50米,下坡平均每分钟走100米,那么从甲地走到乙地需要25分钟,从乙地走到甲地需要20分钟.甲地到乙地上坡与下坡的路程各是多少?03 备考集训一、选择题(每小题3分,共30分)1.下列方程组中,是二元一次方程组的是()A .⎩⎪⎨⎪⎧2x +y =-1y +z =2B .⎩⎪⎨⎪⎧5x -3y =3y =2+3xC .⎩⎪⎨⎪⎧x -5y =1xy =2D .⎩⎪⎨⎪⎧3x -y =7x 2+y =1 2.下列各选项中,是二元一次方程x -5y =2的一个解的是()A .⎩⎪⎨⎪⎧x =3y =1B .⎩⎪⎨⎪⎧x =0y =2 C .⎩⎪⎨⎪⎧x =2y =0D .⎩⎪⎨⎪⎧x =3y =-13.方程组⎩⎪⎨⎪⎧3x -y =2,①3x +2y =11 ②的最优解法是()A .由①,得y =3x -2,再代入②B .由②,得3x =11-2y ,再代入①C .由②-①,消去xD .由①×2+②,消去y 4.方程组⎩⎪⎨⎪⎧2x +y =4,x +3z =1,x +y +z =7的解是()A .⎩⎪⎨⎪⎧x =2y =2z =1B .⎩⎪⎨⎪⎧x =2y =1z =1C .⎩⎪⎨⎪⎧x =-2y =8z =1D .⎩⎪⎨⎪⎧x =2y =2z =25.由方程组⎩⎪⎨⎪⎧x +m =4,y -3=m 可得出x 与y 的关系是()A .x +y =1B .x +y =-1C .x +y =7D .x +y =-76.(2017·舟山)若二元一次方程组⎩⎪⎨⎪⎧x +y =3,3x -5y =4的解为⎩⎪⎨⎪⎧x =a ,y =b ,则a -b =()A .1B .3C .-14D .747.(2017·广州市南沙区期末)甲、乙两人骑自行车比赛,若甲先骑30分钟,则乙出发后50分钟可追上甲.设甲、乙每小时分别骑x 千米、y 千米,则可列方程()A .30x =50yB .12x =(12+56)y C .(30+50)x =50yD .(12+56)x=56y 8.(2017·柳州期末)若方程组⎩⎪⎨⎪⎧ax +y =5,x +by =-1解为⎩⎪⎨⎪⎧x =2,y =1,则点P(a ,b)所在的象限为() A .第一象限 B .第二象限 C .第三象限 D .第四象限9.已知关于x ,y 的方程组⎩⎪⎨⎪⎧3x -5y =2a ,x -2y =a -5,若x ,y 的值互为相反数,则a 的值为()A .-5B .5C .-20D .2010.(2017·黑龙江)某企业决定投资不超过20万元建造A ,B 两种类型的温室大棚.经测算,投资A 种类型的大棚6万元/个、B 种类型的大棚7万元/个,那么建造方案有()A .2种B .3种C .4种D .5种 二、填空题(每小题4分,共20分)11.写出一个解为⎩⎪⎨⎪⎧x =1,y =-2的二元一次方程组:____________________________________.12.(2017·枣庄)已知⎩⎪⎨⎪⎧x =2,y =-3是方程组⎩⎪⎨⎪⎧ax +by =2,bx +ay =3的解,则a 2-b 2=________.13.如果4x a+2b -5-2y 3a-b -3=8是二元一次方程,那么a -b =________.14.(2017·玉林市陆川县期末)小东将书折过来,该角顶点A 落在F 处,BC 为折痕,如图所示,若DB 平分∠FBE ,∠DBE 比∠CBA 大30°,设∠CBA 和∠DBE 分别为x °,y °,那么可求出这两个角的度数的方程组是__________________. 15.定义运算“*”,规定x*y =ax 2+by ,其中a ,b 为常数,且1*2=5,2*1=6,则2*3=________. 三、解答题(共50分) 16.(12分)解方程组:(1)⎩⎪⎨⎪⎧3x -2y =-1,①x +3y =7;②(2)⎩⎪⎨⎪⎧3x +2y =5,①2x +5y =7;②(3)⎩⎪⎨⎪⎧4(x -y -1)=3(1-y )-2,x 2+y 3=2.17.(12分)4月23日“世界读书日”期间,玲玲和小雨通过某图书微信群网购图书,请根据他们的微信聊天对话,求出每本《英汉词典》和《读者》杂志的单价.18.(12分)已知方程组⎩⎪⎨⎪⎧5x +y =3,ax +5y =4与方程组⎩⎪⎨⎪⎧x -2y =5,5x +by =1有相同的解,求a ,b 的值.19.(14分)“五一”节期间,步步高超市进行兑换活动,亮亮妈妈的积分卡里有7 000分,她看了看兑换方法后(见表),兑换了两种礼品共5件并刚好用完积分,请你求出亮亮妈妈的兑换方法.(四) 二元一次方程组例1 方法一:由①,得y =4-2x.③把③代入②,得2(4-2x)+1=5x.解得x =1.把x =1代入③,得y =2.∴原方程组的解为⎩⎪⎨⎪⎧x =1,y =2.方法二:①×2,得4x +2y =8.③③-②,得4x -1=8-5x.解得x =1.把x =1代入②,得y =2.∴原方程组的解为⎩⎪⎨⎪⎧x =1,y =2.例2 B例3 (1)设平安客运公司60座和45座的客车每辆每天的租金分别为x 元,y 元.由题意,得⎩⎪⎨⎪⎧x -y =200,4x +2y =5 000.解得⎩⎪⎨⎪⎧x =900,y =700.答:平安客运公司60座和45座的客车每辆每天的租金分别为900元和700元.(2)5×900+1×700=5 200(元).答:九年级师生租车一天共需租金5 200元. 变式训练 1.B 2.A3.由原方程可得⎩⎪⎨⎪⎧2x +y =3,①2x -y =5.②①+②,得4x =8.解得x =2.①-②,得2y =-2.解得y =-1.∴方程组的解为⎩⎪⎨⎪⎧x =2,y =-1.4.A 5.C 6.A7.设甲地到乙地上坡路x 米,下坡路y 米.根据题意,得⎩⎨⎧x 50+y100=25,y 50+x 100=20.解得⎩⎪⎨⎪⎧x =1 000,y =500.答:甲地到乙地上坡路1 000米,下坡路500米. 备考集训1.B 2.C 3.C 4.C 5.C 6.D 7.D 8.D 9.D 10.B11.答案不唯一,如⎩⎪⎨⎪⎧x +y =-1x -y =3 12.1 13.0 14.⎩⎪⎨⎪⎧2x +2y =180y -x =3015.10 16.(1)由②,得x =7-3y.③③代入①,得3(7-3y)-2y =-1.解得y =2.把y =2代入③,得x =7-3y =1.∴原方程组的解是⎩⎪⎨⎪⎧x =1,y =2.(2)①×2-②×3,得-11y =-11,解得y =1.将y =1代入①,得x =1.∴原方程组的解是⎩⎪⎨⎪⎧x =1,y =1.(3)原方程组可化为:⎩⎪⎨⎪⎧4x -y =5,①3x +2y =12.②①×2+②,得11x =22.解得x =2.将x =2代入①,得y =3.∴原方程组的解是⎩⎪⎨⎪⎧x =2,y =3.17.设每本《汉英词典》和《读者》杂志的单价分别为x ,y 元,根据题意,得⎩⎪⎨⎪⎧10x +4y +5=349,2x +12y +5=141.解得⎩⎪⎨⎪⎧x =32,y =6.答:每本《汉英词典》和《读者》杂志的单价分别为32元和6元.18.解方程组⎩⎪⎨⎪⎧5x +y =3,x -2y =5.得⎩⎪⎨⎪⎧x =1,y =-2.将⎩⎪⎨⎪⎧x =1,y =-2代入ax +5y =4,得a =14.将⎩⎪⎨⎪⎧x =1,y =-2代入5x+by =1,得b =2.19.设亮亮妈妈兑换了x 个电茶壶和y 个书包.由题意,得⎩⎪⎨⎪⎧2 000x +1 000y =7 000,x +y =5.解得⎩⎪⎨⎪⎧x =2,y =3.或设亮亮妈妈兑换了a 个榨汁机和b 个书包.由题意,得⎩⎪⎨⎪⎧3 000a +1 000b =7 000,a +b =5.解得⎩⎪⎨⎪⎧a =1,b =4.由题知,7 000分兑换不了5个榨汁机和电茶壶,故只有上述两种情况.答:亮亮妈妈兑换了2个电茶壶和3个书包或1个榨汁机和4个书包.。
初中七年级数学二元一次方程的解法

二元一次方程的解法•二元一次方程的解:使二元一次方程左、右两边的值相等的一对未知数的值,叫做二元一次方程的一个解。
1.消元解法“消元”是解二元一次方程组的基本思路。
所谓“消元”就是减少未知数的个数,使多元方程最终转化为一元多次方程再解出未知数。
这种将方程组中的未知数个数由多化少,逐一解决的解法,叫做消元解法。
代入消元法(1)概念:将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程组的解.。
这种解方程组的方法叫做代入消元法,简称代入法。
(2)代入法解二元一次方程组的步骤①选取一个系数较简单的二元一次方程变形,用含有一个未知数的代数式表示另一个未知数;②将变形后的方程代入另一个方程中,消去一个未知数,得到一个一元一次方程(在代入时,要注意不能代入原方程,只能代入另一个没有变形的方程中,以达到消元的目的);③解这个一元一次方程,求出未知数的值;④将求得的未知数的值代入①中变形后的方程中,求出另一个未知数的值;⑤用“{”联立两个未知数的值,就是方程组的解;⑥最后检验(代入原方程组中进行检验,方程是否满足左边=右边)。
2.加减消元法(1)概念:当方程中两个方程的某一未知数的系数相等或互为相反数时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法,简称加减法.(2)加减法解二元一次方程组的步骤①利用等式的基本性质,将原方程组中某个未知数的系数化成相等或相反数的形式;②再利用等式的基本性质将变形后的两个方程相加或相减,消去一个未知数,得到一个一元一次方程(一定要将方程的两边都乘以同一个数,切忌只乘以一边,然后若未知数系数相等则用减法,若未知数系数互为相反数,则用加法);③解这个一元一次方程,求出未知数的值;④将求得的未知数的值代入原方程组中的任何一个方程中,求出另一个未知数的值;⑤用“{”联立两个未知数的值,就是方程组的解;⑥最后检验求得的结果是否正确(代入原方程组中进行检验,方程是否满足左边=右边)。
七年级数学下册期末复习(四) 二元一次方程组(含答案)

期末复习(四) 二元一次方程组考点一 二元一次方程(组)的解的概念【例1】已知2,1x y ==⎧⎨⎩是二元一次方程组8,1mx ny nx my +=-=⎧⎨⎩的解,则2m-n 的算术平方根为( ) A.4 B.2D.±2【解析】把2,1x y ==⎧⎨⎩代入方程组8,1mx ny nx my +=-=⎧⎨⎩得28,2 1.m n n m +=-=⎧⎨⎩解得3,2.m n ==⎧⎨⎩ 所以2m-n=4,4的算术平方根为2.故选B.【方法归纳】方程(组)的解一定满足原方程(组),所以将已知解代入含有字母的原方程(组),得到的等式一定成立,从而转化为一个关于所求字母的新方程(组),解这个方程(组)即可求得待求字母的值.1.若方程组,ax y b x by a+=-=⎧⎨⎩的解是1,1.x y ==⎧⎨⎩求(a+b)2-(a-b)(a+b)的值.考点二 二元一次方程组的解法【例2】解方程组:128.x y x y =++=⎧⎨⎩,①② 【分析】可以直接把①代入②,消去未知数x ,转化成一元一次方程求解.也可以由①变形为x-y=1,再用加减消元法求解.【解答】方法一:将①代入到②中,得2(y+1)+y=8.解得y=2.所以x=3.因此原方程组的解为3,2.x y ==⎧⎨⎩方法二:1,28.x y x y =++=⎧⎨⎩①②对①进行移项,得x-y=1.③②+③得3x=9.解得x=3.将x=3代入①中,得y=2.所以原方程组的解为3,2.x y ==⎧⎨⎩【方法归纳】二元一次方程组有两种解法,我们可以根据具体的情况来选择简便的解法.如果方程中有未知数的系数是1时,一般采用代入消元法;如果两个方程的相同未知数的系数相同或互为相反数时,一般采用加减消元法;如果方程组中的系数没有特殊规律,通常用加减消元法.2.方程组 25,7213x y x y +=--=⎧⎨⎩的解是__________. 3.解方程组:3419,4.x y x y +=-=⎧⎨⎩①②考点三 由解的关系求方程组中字母的取值范围【例3】若关于x 、y 的二元一次方程组31,33x y a x y +=++=⎧⎨⎩①②的解满足x+y<2,则a 的取值范围为( )A.a<4B.a>4C.a<-4D.a>-4【分析】本题运用整体思想,把二元一次方程组中两个方程相加,得到x 、y 的关系,再根据x+y<2,求得本题答案;也可以按常规方法求出二元一次方程组的解,再由x+y<2求出a 的取值范围,但计算量大.【解答】由①+②,得4x+4y=4+a,x+y=1+4a ,由x+y<2,得1+4a <2,解得a<4.故选A. 【方法归纳】通过观察两个方程,运用整体思想解题,这是中考中常用的解题方法.4.已知x 、y 满足方程组25,24,x y x y +=+=⎧⎨⎩则x-y 的值为__________.考点四 二元一次方程组的应用【例4】某中学拟组织九年级师生去黄山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5 000元.”小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”根据以上对话,解答下列问题:(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?【分析】(1)根据题目给出的条件得出的等量关系是60座客车每辆每天的租金-45座客车每辆每天的租金=200元,4辆60座一天的租金+2辆45座的一天的租金=5 000元;由此可列出方程组求解;(2)可根据“我们九年级师生租用5辆60座和1辆45座的客车正好坐满”以及(1)的结果来求出答案.【解答】(1)设平安公司60座和45座客车每辆每天的租金分别为x 元,y 元.由题意,得200,425000.x y x y -=+=⎧⎨⎩解得900,700.x y ==⎧⎨⎩答:平安客运公司60座和45座的客车每辆每天的租金分别为900元和700元.(2)5×900+1×700=5 200(元).答:九年级师生租车一天共需资金5 200元.【方法归纳】列方程解决实际问题的解题步骤是:1.审题:弄清已知量和未知量;2.列未知数,并根据相等关系列出符合题意的方程;3.解这个方程;4.验根并作答:检验方程的根是否符合题意,并写出完整的答.5.如图是一个正方体的展开图,标注了字母“a ”的面是正方体的正面.如果正方体相对两个面上的代数式的值相等,求x,y 的值.6.在某次亚运会中,志愿者们手上、脖子上的丝巾非常美丽.车间70名工人承接了制作丝巾的任务,已知每人每天平均生产手上的丝巾1 800条或者脖子的丝巾1 200条,一条脖子上的丝巾要配两条手上的丝巾.为了使每天生产的丝巾刚好配套,应分配多少名工人生产脖子上的丝巾,多少名工人生产手上的丝巾?复习测试一、选择题(每小题3分,共30分)1.下列方程组中,是二元一次方程组的是( )A.212x y y z +=-+=⎧⎨⎩B.53323x y y x -==+⎧⎨⎩C.512x y xy -==⎧⎨⎩D.2371x y x y -=+=⎧⎨⎩2.方程2x+y=9的正整数解有( )A.1组B.2组C.3组D.4组3.方程组32,3211x y x y -=+=⎧⎨⎩①②的最优解法是( )A.由①得y=3x-2,再代入②B.由②得3x=11-2y ,再代入①C.由②-①,消去xD.由①×2+②,消去y4.已知21x y ==⎧⎨⎩,是方程组4,0ax by ax by +=--=⎧⎨⎩的解,那么a ,b 的值分别为( )A.1,2B.1,-2C.-1,2D.-1,-25.A 、B 两地相距6 km ,甲、乙两人从A 、B 两地同时出发,若同向而行,甲3 h 可追上乙;若相向而行,1 h 相遇,求甲、乙两人的速度各是多少?若设甲的速度为x km/h ,乙的速度为y km/h ,则得方程组为( )A.6336x y x y +=+=⎧⎨⎩B.636x y x y +=-=⎧⎨⎩C.6336x y x y -=+=⎧⎨⎩D.6336x y x y +=-=⎧⎨⎩6.足球比赛的记分为:胜一场得3分,平一场得1分,负一场得0分,一队打了14场比赛,负5场,共得19分,那么这个队胜了( )A.3场B.4场C.5场D.6场7.已知a 、b 满足方程组22,26,a b a b -=+=⎧⎨⎩则3a+b 的值为( ) A.8 B.4 C.-4 D.-88.方程组24,31,7x y x z x y z +=+=++=⎧⎪⎨⎪⎩的解是( )A.221x y z ===⎧⎪⎨⎪⎩B.211x y z ===⎧⎪⎨⎪⎩C.281x y z ⎧=-==⎪⎨⎪⎩D.222 xyz===⎧⎪⎨⎪⎩9.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,已知一个螺栓配套两个螺帽,应该如何分配工人才能使生产的螺栓和螺帽刚好配套?则生产螺栓和生产螺帽的人数分别为( )A.50人,40人B.30人,60人C.40人,50人D.60人,30人10.甲、乙二人收入之比为4∶3,支出之比为8∶5,一年间两人各存5 000元(设两人剩余的钱都存入银行),则甲、乙两人年收入分别为( )A.15 000元,12 000元B.12 000元,15 000元C.15 000元,11 250元D.11 250元,15 000元二、填空题(每小题4分,共20分)11.已知a、b12.已知2,1xy==⎧⎨⎩是二元一次方程组7,1mx nynx my+=-=⎧⎨⎩的解,则m+3n的立方根为__________.13.孔明同学在解方程组,2y kx by x=+=-⎧⎨⎩的过程中,错把b看成了6,他其余的解题过程没有出错,解得此方程组的解为1,2,xy=-=⎧⎨⎩又已知3k+b=1,则b的正确值应该是__________.14.已知|x-8y|+2(4y-1)2+|8z-3x|=0,则x=__________,y=__________,z=__________.15.一个两位数的十位数字与个位数字的和为8,若把这个两位数加上18,正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数,则原来的两位数为__________.三、解答题(共50分)16.(10分)解方程组:(1)251x yx y+=-⎧=⎨⎩,①;②(2)1151.x y zy z xz x y+-=+-=+-⎪⎨=⎧⎪⎩,①,②③17.(8分)(2013·吉林)吉林人参是保健佳品.某特产商店销售甲、乙两种保鲜人参,甲种人参每棵100元,乙种人参每棵70元.王叔叔用1 200元在此特产商店购买这两种人参共15棵,求王叔叔购买每种人参的棵数.18.(9分)已知方程组53,54x yax y+=+=⎧⎨⎩与方程组25,51x yx by-=+=⎧⎨⎩有相同的解,求a,b的值.19.(11分)食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?20.(12分)某商场计划拨款9万元从厂家购进50台电冰箱,已知该厂家生产三种不同型号的电冰箱,出厂价分别为:甲种每台1 500元,乙种每台2 100元,丙种每台2 500元.(1)某商场同时购进其中两种不同型号电冰箱共50台,用去9万元,请你研究一下商场的进货方案;(2)该商场销售一台甲种电冰箱可获利150元,销售一台乙种电冰箱可获利200元,销售一台丙种电冰箱可获利250元,在同时购进两种不同型号的方案中,为使销售时获利最多,你选择哪种进货方案?参考答案变式练习1.把1,1x y ==⎧⎨⎩代入方程组,ax y b x by a +=-=⎧⎨⎩,得1,1.a b b a +=-=⎧⎨⎩整理,得1,1.a b a b -=-+=⎧⎨⎩ ∴(a+b)2-(a-b)(a+b)=12-(-1)×1=2.2.13x y ==-⎧⎨⎩, 3.由②,得x=4+y.③把③代入①,得3(4+y)+4y=19.解得y=1.把y=1代入③,得x=4+1=5.∴原方程组的解为51.x y ==⎧⎨⎩, 4.15.根据题意,得25,5 1.x y x y -=-=+⎧⎨⎩解得3,1.x y ==⎧⎨⎩ 6.设应分配x 名工人生产脖子上的丝巾,y 名工人生产手上的丝巾,由题意得 70,120021800.x y x y +=⨯=⎧⎨⎩解得30,40.x y ==⎧⎨⎩答:应分配30名工人生产脖子上的丝巾,40名工人生产手上的丝巾. 复习测试1.B2.D3.C4.D5.D6.C7.A8.C9.C 10.C11.6 12.2 13.-11 14.2 14 3415.35 16.(1)①+②,得3x=6.解得x=2.把x=2代入②,得y=1.所以原方程组的解为21.x y ==⎧⎨⎩, (2)①+②+③,得x+y+z=17.④④-①,得2z=6,即z=3.④-②,得2x=12,即x=6.④-③,得2y=16,即y=8.所以原方程组的解是683.x y z ⎧⎪=⎩==⎪⎨,,17.设王叔叔购买甲种人参x 棵,乙种人参y 棵.根据题意,得151********.x y x y +=+=⎧⎨⎩,解得510.x y =⎩=⎧⎨, 答:王叔叔购买甲种人参5棵,乙种人参10棵.18.解方程组53,25x y x y +=-=⎧⎨⎩,得1,2.x y ==-⎧⎨⎩ 将x=1,y=-2代入ax+5y=4,得a=14.将x=1,y=-2代入5x+by=1,得b=2.19.设A 饮料生产了x 瓶,B 饮料生产了y 瓶,依题意得100,23270.x y x y +=+=⎧⎨⎩解得30,70.x y ==⎧⎨⎩ 答:A 饮料生产了30瓶,B 饮料生产了70瓶.20.(1)①设购进甲种电冰箱x 台,购进乙种电冰箱y 台,根据题意,得50,1500210090000.x y x y +=+=⎧⎨⎩解得25,25.x y ==⎧⎨⎩ 故第一种进货方案是购甲、乙两种型号的电冰箱各25台.②设购进甲种电冰箱x 台,购进丙种电冰箱z 台,根据题意,得50,1500250090000.x z x z +=+=⎧⎨⎩解得35,15.x z ==⎧⎨⎩ 故第二种进货方案是购进甲种电冰箱35台,丙种电冰箱15台. ③设购进乙种电冰箱y 台,购进丙种电冰箱z 台,根据题意,得 50,2100250090000.y z y z +=+=⎧⎨⎩解得87.5,37.5.y z ==-⎧⎨⎩不合题意,舍去. 故此种方案不可行.(2)上述的第一种方案可获利:150×25+200×25=8 750(元),第二种方案可获利:150×35+250×15=9 000(元),因为8 750<9 000,故应选择第二种进货方案,即购进甲种电冰箱35台,乙种电冰箱15台.。
二元一次方程组的解法公式

二元一次方程组的解法公式二元一次方程组是代数方程的一种形式,包括两个未知数和两个方程。
解决二元一次方程组的最常见方法是使用消元法或代入法。
这篇文章将探讨二元一次方程组的解法公式和步骤。
什么是二元一次方程组?二元一次方程组通常具有以下一般形式:$$ \\begin{cases} ax + by = c \\\\ dx + ey = f \\end{cases} $$其中a,b,c,d,e,f是已知的数字,x,y是未知数。
解决这个方程组的目标是找到满足两个方程同时成立的x和y的值。
消元法消元法是解决二元一次方程组的常用方法。
其基本思想是通过一系列加减乘除等操作,将一个方程的某个未知数的系数调整成与另一个方程对应未知数的系数相等或相反数。
然后两个方程相加或相减,从而消去一个未知数,再代入得到另一个未知数的值。
步骤1.选择一个未知数进行消元,通常选择系数较小的未知数。
2.通过加减乘除等运算,让两个方程中这个未知数的系数相等或相反数。
3.将两个方程相加或相减,得到只含有另一个未知数的新方程。
4.解出另一个未知数的值。
5.将求得的未知数的值代入原方程中,计算出另一个未知数的值。
代入法代入法是另一种解决二元一次方程组的方法。
其基本思想是通过将一个方程的一个未知数用另一个方程中的未知数表示出来,再代入到另一个方程中,从而得到只含有一个未知数的方程。
步骤1.从一个方程中解出一个未知数,通常选择较容易解出的未知数。
2.将解出的未知数代入另一个方程中,得到只含有一个未知数的新方程。
3.解出这个未知数的值。
4.将求得的未知数的值代入原方程中,计算出另一个未知数的值。
总结二元一次方程组的解法公式主要包括消元法和代入法。
在解决方程组时,选择合适的方法和正确的步骤至关重要。
消元法适合系数比较简单的情况,而代入法则适合单一方程较容易解出某个未知数的情况。
通过熟练掌握这两种方法,我们可以快速准确地求解二元一次方程组,解决实际的数学问题。
七年级下册数学7.2二元一次方程组的解法

2015.湖北荆州中考.7分 解方程组:
① ②
※多种解法
这个方程可以用整体代 入法解出,但是程序繁 琐,有没有更好一点的、 更简便的方法来解这个 方程呢?请想一想。
① ②
解法
解:②×3-①得11y=22,即y=2(3分) 把y=2代入②得x=1…………法)
那么我们再看一例:
2015.乐山中考.5分
①
解方程组:
②
解法
①
②
解:由①,得2x=5+3y③ 将③代入②,得2(5+3y)-5y=7,解得y=3. 将y=-3代入①,得2x+9=5,解得x=-2. 所以:
注意:
整体代入消元法适用 于方程中含有未知数 项的系数有倍数关系 的方程组。
来看一例:
根据题意:得x+4-3x=1 (3分) 解,得:x=1.5,∴x+4=5.5. (5分)
再看一题:
2015.湖北娄底中考.9分
出租车起步价所包含的路程为0—1.5km,超过 1.5km的部分按每千米另收费。 刘说:“我乘出租车从市政府到娄底汽车站走了 4.5千米,付车费10.5元。” 李说:“我乘出租车从市政府到娄底火车站走了 6.5千米,付车费14.5元。” 问:(1)出租车的起步价是多少;超过一点五千米 后每千米收费多少元? (2)小张乘出租车从市政府到娄底南站地铁走 了5.5千米,应付车费多少元?
解二元一次方程基本步骤(代入法)
解二元一次方程的基本思路是“消元”——把 “二元”转化成“一元”。用代入法解二元一次 方程组的基本步骤: 第一步:选择其中一个方程,用含有一个未知数 的代数式表示另一个未知数; 第二步:把得到的表达式代入另一个方程中,化 这个方程为一元一次方程; 第三步:解这个一元一次方程; 第四步:将方程的解代入第一步得到的表达式中, 求出另一个未知数的值; 第五步:确定方程组的解。
初中数学【二元一次方程组的解法——加减消元法】课件

知数的数值。
3.把解得的一个未知数的 值代入原方程中的任意一个方程,
解得另一个未知数的值。
4.把解得的两个未知数的,并列写在花括号,得到原方程
组的解。
拓展提升
解方程组
+ −
+ =6
2
3
①
2(x+y)-3x+3y=24
②
引导:将较为复杂的方程组先化简转化为一般形式,然后用代入法或
③ - ④, 得 26v=13
解这个一元一次方程,得v=
1
2
1
2
将v= 代入方程①,得5u+1=-9
解得
u=-2∴Βιβλιοθήκη 程组的解为u=-2v=
1
2
课堂总结
用加减消元法解二元一次方程组的一般步骤:
1.在一个或两个方程的两边分别乘以一个适当的数,使两
个方程中某一个未知数的系数绝对值相等。
2.绝对值相等的未知数的系数符号相反时,将两个方程相
二元一次方程组的解法——加减消元法
知识回顾
解二元一次方程组的根本方法—— “消元”
消元本质: 通过消掉一个未知数,将二元转化为
一元。
情景导航
x+y=7300 ①
解方程组
y-x=6100
②
“加减消元法”
“化归思想”
观察这个方程组的系数特点,你还能想出其它办法来消元吗?
整体思路:
法1:①式与②式x前面的系数互为相反数,利用等式的基本性质,将两式相加,就能消
的这种解法叫做加减消元法,简称加减法。
典例分析
5u+2v=-9 ①
解方程组
人教版初中七年级数学下册第八单元《二元一次方程组》(含答案解析)

一、选择题1.小明的妈妈在菜市场买回2斤萝卜、1斤排骨共花了41.4元,而两个月前买同重量的这两样菜只要36元,与两个月前相比,这次萝卜的单价下降了10%,但排骨单价却上涨了20%,设两个月前买的萝卜和排骨的单价分别为x 元/斤,y 元/斤,则可列方程为( ) A .()()2362110%120%41.4x y x y +=⎧⎨⨯-++=⎩ B .()()241.42110%120%36x y x y +=⎧⎨⨯-++=⎩C .()()241.4110%2120%36x y x y +=⎧⎨-+⨯+=⎩ D .()()236110%2120%41.4x y x y +=⎧⎨-+⨯+=⎩ A 解析:A【分析】 根据题目中设的两个月前的萝卜和排骨的单价,先列出两个月前的式子236x y +=,再根据降价和涨价列出现在的式子()()2110%120%41.4x y ⨯-++=,得到方程组.【详解】解:两个月前买菜的情况列式:236x y +=,现在萝卜的价格下降了10%,就是()110%x -,排骨的价格上涨了20%,就是()120%y +,那么这次买菜的情况列式:()()2110%120%41.4x y ⨯-++=,∴方程组可以列为()()2362110%120%41.4x y x y +=⎧⎨⨯-++=⎩. 故选:A .【点睛】本题考查二元一次方程组的应用,解题的关键是根据题意找到等量关系列出方程组. 2.若x ,y 均为正整数,且2x +1·4y =128,则x +y 的值为( )A .3B .5C .4或5D .3或4或5C解析:C【解析】∵2x +1·4y =128,27=128,∴x +1+2y =7,即x +2y =6.∵x ,y 均为正整数, ∴22x y =⎧⎨=⎩或41x y =⎧⎨=⎩ ∴x +y =4或5.3.解方程组232261s t s t +=⎧⎨-=-⎩①②时,①—②,得( )A .31t -= .B .33t -=C .93t =D .91t = C解析:C【分析】运用加减消元法求解即可.【详解】 解:解方程组232261s t s t +=⎧⎨-=-⎩①②时,①-②,得3t-(-6t)=2-(-1), 即,9t=3,故选:C .【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.4.下列方程中是二元一次方程的是( )A .(2)(3)0x y +-=B .-1x y =C .132x y=+ D .5xy = B 解析:B【分析】含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程.【详解】解:(2)(3)0x y +-=化简得3260xy x y -+-=,最高次是2次,故A 选项错误; -1x y =是二元一次方程,故B 选项正确;132x y=+不是整式方程,故C 选项错误; 5xy =最高次是2次,故D 选项错误.故选:B【点睛】本题主要考查的是二元一次方程的概念,正确的掌握二元一次方程的概念是解题的关键. 5.古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x 只,树有y 棵,由题意可列方程组( )A .3551y x y x +=⎧⎨-=⎩B .3551y x y x -=⎧⎨=-⎩C .15355x y y x ⎧+=⎪⎨⎪=-⎩D .5315x y x y -⎧=⎪⎪⎨⎪=-⎪⎩ D 解析:D根据“三个坐一棵,五个地上落;五个坐一棵,闲了一棵树”,即可得出关于x,y的二元一次方程组,此题得解.【详解】解:设乌鸦有x只,树有y棵,依题意,得:5315xyxy-⎧=⎪⎪⎨⎪=-⎪⎩.故选:D.【点睛】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.6.某校七年级1班学生为了参加学校文化评比买了22张彩色的卡纸制作如下图形(每个图形由两个三角形和一个圆形组成),已知一张彩色卡纸可以剪5个三角形,或3个圆形,要使圆形和三角形正好配套,需要剪三角形的卡纸有x张,剪圆形的卡纸有y张,可列式为()A.2256x yx y+=⎧⎨=⎩B.2265x yx y+=⎧⎨=⎩C.22310x yx y+=⎧⎨=⎩D.22103x yx y+=⎧⎨=⎩A解析:A【分析】设需要剪三角形的卡纸有x张,剪圆形的卡纸有y张,根据彩色卡纸的总张数为22张其剪出三角形的数量为圆的2倍,即可得出关于x、y的二元一次方程组,此题得解.【详解】设需要剪三角形的卡纸有x张,剪圆形的卡纸有y张,根据题意得:22 56x yx y+=⎧⎨=⎩.【点睛】此题考查由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.7.已知关于x 、y 的二元一次方程组356310x y x ky +=⎧⎨+=⎩给出下列结论:①当5k =时,此方程组无解;②若此方程组的解也是方程61516x y +=的解,则10k =;③无论整数k 取何值,此方程组一定无整数解(x 、y 均为整数),其中正确的是( )A .①②③B .①③C .②③D .①②A解析:A【分析】根据二元一次方程组的解法逐个判断即可.【详解】 当5k =时,方程组为3563510x y x y +=⎧⎨+=⎩,此时方程组无解 ∴结论①正确由题意,解方程组35661516x y x y +=⎧⎨+=⎩得:2345x y ⎧=⎪⎪⎨⎪=⎪⎩把23x =,45y =代入310x ky +=得2431035k ⨯+= 解得10k =,则结论②正确 解方程组356310x y x ky +=⎧⎨+=⎩得:20231545x k y k ⎧=-⎪⎪-⎨⎪=⎪-⎩又k 为整数 x 、y 不能均为整数∴结论③正确综上,正确的结论是①②③故选:A .【点睛】本题考查了二元一次方程组的解与解法,掌握二元一次方程组的解法是解题关键. 8.把方程23x y -=改写成用含x 的式子表示y 的形式,正确的是( )A .23x y =+B .32y x +=C .23y x =-D .32y x =- C解析:C将x 看做常数移项求出y 即可得.【详解】由2x-y=3知2x-3=y ,即y=2x-3,故选C .【点睛】此题考查了解二元一次方程,解题的关键是将x 看做已知数求出y .9.已知方程组2325x y x y +=⎧⎨-=⎩,则39x y +的值为( ) A .2-B .2C .6-D .6C解析:C【分析】方程组两方程相减求出x+3y 的值,进而即可求得3x+9y 的值.【详解】 2325x y x y +=⎧⎨-=⎩①②, ①-②得:32x y +=-,∴()39336x y x y +=+=-,故选:C .【点睛】本题考查了求代数式的值以及解二元一次方程组,解二元一次方程组利用了消元的思想,消元的方法有:代入消元法与加减消元法.灵活运用整体代入法是解题的关键.10.方程组320x y x y +=⎧⎨-=⎩的解是( ) A .11x y =⎧⎨=⎩B .12x y =⎧⎨=⎩C .21x y =⎧⎨=⎩D .30x y =⎧⎨=⎩ B 解析:B【分析】二元一次方程组的求解方法有两种:(1)加减消元法;(2)代入消元法,此题用加减消元法求解更为简便;【详解】 ∵320x y x y +=⎧⎨-=⎩①② , ①+②得:3x=3,即x=1,把x=1代入①得:y=2,则方程组的解为12x y =⎧⎨=⎩,【点睛】本题考查了二元一次方程组的解法,正确利用加减消元法求解是解题的关键.二、填空题11.重庆某快递公司规定:寄件不超过1kg 的部分按起步价计费,超过1kg 不足2kg ,按照2kg 收费;超过2kg 不足3kg 按照3kg 收费,以此类推.某产家分别寄快递到重庆市内和北京,其中,寄往重庆市内的起步价为a 元,超过部分b 元/kg ;寄往北京的起步价为()7a +元,超过部分()4b +元/kg .已知一个寄往重庆市内的快件,质量为2kg ,收费13元;一个寄往北京的快件,质量为4.5kg ,收费42元.如果一个寄往北京的快件,质量为2.8kg ,应收费______元.30【分析】根据分别寄快递到上海和北京的快递质量和费用即可得出关于ab 的二元一次方程组解之然后根据28kg 按照3kg 收费即可得出应收费【详解】解:依题意得:解得寄往北京市快件重28kg 按照3kg 收费解析:30【分析】根据分别寄快递到上海和北京的快递质量和费用,即可得出关于a ,b 的二元一次方程组,解之,然后根据2.8kg 按照3kg 收费即可得出应收费.【详解】解:依题意,得:137(51)(4)42a b a b +=⎧⎨++-+=⎩, 解得112a b =⎧⎨=⎩, 寄往北京市快件重2.8kg 按照3kg 收费,应收费:7(31)(4)1172(24)30a b ++-+=++⨯+=元,故答案为:30.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.12.甲、乙两筐苹果各有若干千克,从甲筐拿出20%到乙筐后,又从乙筐拿出25%到甲筐,这时甲、乙两筐苹果的质量相等,则原来乙筐的苹果质量是甲筐的__________ % .140【分析】设甲乙两筐苹果各有先求出从甲筐拿出20到乙筐后甲乙两筐分别为再求出从乙筐拿出25到甲筐后甲乙两筐分别为:列方程求出x 与y 的关系即可【详解】设甲乙两筐苹果各有从甲筐拿出20到乙筐后甲乙两 解析:140【分析】设甲、乙两筐苹果各有x 、kg y ,先求出从甲筐拿出20%到乙筐后,甲、乙两筐分别为80%x ,20%y x +,再求出从乙筐拿出25%到甲筐后,甲、乙两筐分别为:171204x y +,33420y x +,列方程17133204420x y y x +=+,求出x 与y 的关系即可. 【详解】设甲、乙两筐苹果各有x 、kg y ,从甲筐拿出20%到乙筐后,甲、乙两筐分别为80%x ,20%y x +,从乙筐拿出25%到甲筐后,甲、乙两筐分别为:()17180%25%20%204x y x x y +⨯+=+, ()3375%20%420y x y x ⨯+=+, 由题可得:17133204420x y y x +=+, 解得75y x =, 75y x =, 则原来乙筐苹果质量为甲筐的:7100%100%140%5y x ⨯=⨯=. 故答案为:140.【点睛】本题考查循环倒液类型问题,掌握循环倒液类型问题的解法,抓住经过两次循环两者质量相等构造等式(或方程)解决问题是关键. 13.若1,3x y =-⎧⎨=⎩是关于x ,y 的二元一次方程组5,x y m x my n +=⎧⎨-=⎩的解,则n 的值为______.5【分析】将代入方程组求解即可【详解】将代入方程组得解得故答案为:5【点睛】此题考查二元一次方程组的解解二元一次方程组正确计算是解题的关键 解析:5【分析】将13x y =-⎧⎨=⎩代入方程组求解即可. 【详解】 将13x y =-⎧⎨=⎩代入方程组5x y m x my n +=⎧⎨-=⎩,得 213m m n =-⎧⎨--=⎩解得25m n =-⎧⎨=⎩, 故答案为:5.【点睛】此题考查二元一次方程组的解,解二元一次方程组,正确计算是解题的关键.14.已知37m m n x y +-与653x y 是同类项,则m n -=_______.【分析】先根据同类项的定义可得mn 的值再代入计算即可得【详解】由题意得:解得则故答案为:【点睛】本题考查了同类项二元一次方程组的应用熟练掌握同类项的定义是解题关键解析:1-【分析】先根据同类项的定义可得m 、n 的值,再代入计算即可得.【详解】由题意得:365m m n =⎧⎨+=⎩, 解得23m n =⎧⎨=⎩, 则231m n -=-=-,故答案为:1-.【点睛】本题考查了同类项、二元一次方程组的应用,熟练掌握同类项的定义是解题关键. 15.为落实习总书记“绿水青山就是金山银山”的发展理念,我区府部门决定由甲、乙、丙三个工程队负责完成一条总工作量为a 的公园改造的施工任务.经过一段时间,甲、乙、丙三个工程队完成的工程量之比是3:4:5为更合理的分任务,经测算,将剩余工程量的916交给了丙队,其余工程量由甲、乙两个工程队共同完成,乙工程队再工作一段时间后因另有任务先离开.工程结束时发现,丙队完成的工程量占总工程量的1940,甲、乙两队完成其余工程的工程量之比为4:3.则乙队完成的工程量与总工程量之比是:______.【分析】设一开始甲乙丙三个工程队完成的工程量为b 则剩余工程量为a-b 然后表示出丙队完成的工程量根据丙队完成的工程量占总工程量的列出等式从而得到a 与b 的数量关系再表示出乙队完成的工程量把a 与b 的数量关解析:11:40.【分析】设一开始甲、乙、丙三个工程队完成的工程量为b ,则剩余工程量为a-b ,然后表示出丙队完成的工程量,根据丙队完成的工程量占总工程量的1940列出等式,从而得到a 与b 的数量关系,再表示出乙队完成的工程量,把a 与b 的数量关系代入计算即可.【详解】解:设一开始甲、乙、丙三个工程队完成的工程量为b ,则剩余工程量为a-b ,∴丙队完成的工程量为()951612a b b -+, ∴()9519161240a b b a -+=, 解得,35b a =, 乙队一开始完成的工程量为412b ,后来完成的工程量为()()73316716a b a b -⨯=-, ∴乙队完成的工程量为()43433311121612516540b a b a a a a ⎛⎫+-=⨯+-= ⎪⎝⎭, ∴乙队完成的工程量与总工程量之比是11:40.故答案是:11:40.【点睛】本题考查工程问题,考查学生分析解决问题的能力,正确求出一开始完成的工程量与总工程量的数量关系是关键.16.“九九重阳节, 浓浓敬老情”,今年某花店在重阳节推出“松鹤长春”“欢乐远长”“健康长寿”三种花束.“松鹤长春”花束中有8枝百合,16 枝康乃馨;“欢乐远长”花束中有6枝百合,16枝康乃馨,2枝剑兰;“健康长寿”花束中有4枝百合,12枝康乃馨,2枝剑兰.已知百合花每枝1元,康乃馨每枝34元,剑兰每枝5元,重阳节当天销售这三种花束共2549元,其中百合花的销售额为458元,则剑兰的销售量为________枝.【分析】设松鹤长春欢乐远长健康长寿三种花束的销量分别为:(单位:束)再分别求解一束松鹤长春欢乐远长健康长寿的单价根据重阳节当天销售这三种花束共2549元其中百合花的销售额为458元列方程组再求解剑兰解析:216.【分析】设“松鹤长春”“欢乐远长”“健康长寿”三种花束的销量分别为:,,x y z (单位:束),再分别求解一束“松鹤长春”“欢乐远长”“健康长寿”的单价,根据重阳节当天销售这三种花束共2549元,其中百合花的销售额为458元,列方程组,再求解剑兰的销量:22y z +,即可得到答案.【详解】解:设“松鹤长春”“欢乐远长”“健康长寿”三种花束的销量分别为:,,x y z (单位:束), 由题意可得:一束“松鹤长春”的单价为:318+16=204⨯⨯(元), 一束“欢乐远长”花束的单价为:316+16+52=284⨯⨯⨯(元), 一束“健康长寿”花束的单价为:314+12+25=234⨯⨯⨯(元),8644582028232549x y z x y z ++=⎧∴⎨++=⎩①② ②2⨯-①5⨯得:40564640302050982290,x y z x y z ++---=-26262808,y z ∴+=108,y z ∴+=22216,y z ∴+=即剑兰的销量为:216枝.故答案为:216.【点睛】本题考查的是三元一次方程组的应用,利用整体法求解方程组中的量是解题的关键. 17.一个两位数,交换个位与十位的数字之后,新得到的两位数比原数小63,则原来的两位数是________________.81或92【分析】结合题意设原来的两位数十位数字为x 个位数字为y 根据新得到的两位数比原数小63进行分析即可得到答案【详解】设原来的两位数十位数字为x 个位数字为y 根据题意得:∴∵一个两位数交换个位与十解析:81或92【分析】结合题意,设原来的两位数,十位数字为x ,个位数字为y ,根据新得到的两位数比原数小63进行分析,即可得到答案.【详解】设原来的两位数,十位数字为x ,个位数字为y根据题意得:()101063x y y x +-+=∴7x y -=∵一个两位数,交换个位与十位的数字之后,新得到的两位数比原数小63∴6x >当7x =时,0y =,即原两位数为:70,新得到的为:7,不是两位数,故不符合题意; 当8x =时,1y =,即原两位数为:81,新得到的为:18;当9x =时,2y =,即原两位数为:92,新得到的为:29;故答案为:81或92.【点睛】本题考查了二元一次方程的应用;解题的关键是熟练掌握用代数式表示两位数,从而完成求解.18.已知,方程12230a b x y -+-+=是关于,x y 的二元一次方程,则a b +=________.1【分析】利用二元一次方程的定义得出关于的方程解方程并代入代数式即可【详解】∵方程是关于的二元一次方程∴解得∴故答案为:1【点睛】本题考查了二元一次方程的定义熟练掌握二元一次方程的定义是解本题的关键【分析】利用二元一次方程的定义得出关于a ,b 的方程,解方程并代入代数式即可.【详解】∵方程12230a b x y -+-+=是关于x ,y 的二元一次方程,∴11a -=,21b +=,解得2a =,1b =-,∴211a b +=-=.故答案为:1.【点睛】本题考查了二元一次方程的定义,熟练掌握二元一次方程的定义是解本题的关键. 19.若方程2(3)31a a x y --+=是关于x ,y 的二元一次方程,则a 的值为_____.-3【分析】根据二元一次方程的定义:含有两个未知数并且含有未知数的项的次数都是1像这样的方程叫做二元一次方程可得|a|-2=1且a-3≠0再解即可【详解】解:由题得解得a=-3故答案为:-3【点睛】解析:-3【分析】根据二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程可得|a|-2=1,且a-3≠0,再解即可.【详解】 解:由题得,2130a a ⎧-⎨-≠⎩= , 解得a=-3,故答案为:-3.【点睛】本题考查了二元一次方程的定义.二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的最高次数为一次;(3)方程是整式方程.20.如果关于x ,y 的二元一次方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是62x y =⎧⎨=⎩,则关于x ,y 的二元一次方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解是______.【分析】先将所求的方程组变形为然后根据题意可得进一步即可求出答案【详解】解:由方程组可得∵关于xy 的二元一次方程组的解是∴解得故答案为【点睛】本题考查了二元一次方程组的解法正确理解题意合理变形得出是解析:105x y =⎧⎨=⎩先将所求的方程组变形为11122232553255a b c a b c x y x y ⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭⎧+=⎪⎪⎨⎪+=⎪⎩,然后根据题意可得365225x y ⎧=⎪⎪⎨⎪=⎪⎩,进一步即可求出答案.【详解】解: 由方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩可得11122232553255a b c a b c x y x y ⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭⎧+=⎪⎪⎨⎪+=⎪⎩, ∵关于x ,y 的二元一次方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是62x y =⎧⎨=⎩, ∴365225x y ⎧=⎪⎪⎨⎪=⎪⎩,解得105x y =⎧⎨=⎩, 故答案为105x y =⎧⎨=⎩. 【点睛】 本题考查了二元一次方程组的解法,正确理解题意、合理变形、得出365225x y ⎧=⎪⎪⎨⎪=⎪⎩是解本题的关键.三、解答题21.某水果店有甲,乙两种水果,它们的单价分别为a 元/千克,b 元/千克.若购买甲种水果5千克,乙种水果2千克,共花费25元,购买甲种水果3千克,乙种水果4千克,共花费29元.(1)求a 和b 的值;(2)甲种水果涨价m 元/千克(02)m <<,乙种水果单价不变,小明花了45元购买了两种水果10千克,那么购买甲种水果多少千克?(用含m 的代数式表示).解析:(1)a 的值为3,b 的值为5;(2)52m- 【分析】(1)根据等量关系:购买甲5千克,乙2千克,共花费25元;购买甲3千克,乙4千克,共花费29元;列出方程组求解即可;(2)可设购买甲种糖果x 千克,则购买乙种糖果(10-x )千克,根据花了45元,列出方程即可求解;【详解】解:(1)依题意有52253429a b a b +=⎧⎨+=⎩,解得35a b =⎧⎨=⎩. 故a 的值为3,b 的值为5;(2)设购买甲种水果x 千克,则购买乙种水果(10)x -千克,依题意有:(3)5(10)45m x x ++-=, 解得:52x m=-; 故购买甲种水果52m-千克. 【点睛】 本题考查了二元一次方程组的应用,解题的关键是找准等量关系,正确列出二元一次方程组.22.解方程组:()()41622358x y x y ⎧+=-⎪⎨-=-⎪⎩①② 解析:9412x y ⎧=-⎪⎪⎨⎪=-⎪⎩【分析】将原方程化简整理后再运用加减消元法求解即可.【详解】解:原方程组可化为233,252,x y x y -=-⎧⎨-=-⎩③④③-④,得21y =-, 12y , 将12y 代入③,得94x =-. 所以原方程组的解是9,41.2x y ⎧=-⎪⎪⎨⎪=-⎪⎩. 【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.23.(1)解方程组:21035x yx y+=⎧⎨-=⎩;(2)解不等式组:2(1)35423xxx+-<⎧⎪-⎨-≥⎪⎩.解析:(1)81xy=⎧⎨=⎩;(2) 13x≤<.【分析】(1)利用加减消元法,先消去x,求得y,后代入求得x,从而得到方程组的解;(2)分别求得不等式组中每一个不等式的解集,再确定出公共部分即可.【详解】(1)由21035x yx y+=⎧⎨-=⎩①②,①-②,得5y=5,解得y=1;把y=1代入①,解得x=8,所以原方程组的解为=81 xy⎧⎨=⎩.(2)由2(1)35423xxx+-<⎧⎪⎨--≥⎪⎩①②,解不等式①得 x<3;解不等式②得x≥1;所以原不等式组的解集为1≤x<3.【点睛】(1)考查了二元一次方程组的解法,熟练掌握加减消元法是解题的关键;(2)考查了一元一次不等式组的解法,熟练求解,利用数形结合思想,灵活确定解集是解题的关键.24.萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:(1)写出用含x、y的整式表示地面总面积;(2)已知客厅面积是厨房面积的4倍,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?解析:(1)6218x y ++;(2)3600元【分析】(1)根据长方形的面积=长×宽,表示各部分的面积,于是可表示出总面积.(2)根据已知客厅面积是厨房面积的4倍,且地面总面积是卫生间面积的15倍,列出方程组求解,可求出总面积,再根据单价可求出铺地砖的总费用.【详解】解:(1)卧室的长=2+2=4,厨房的长=6-3=3,∴地面的总面积为:3×4+2y+2×3+6x=6x+2y+18.(2)由题意得64236218152x x y y =⨯⨯⎧⎨++=⨯⎩解得:41.5x y =⎧⎨=⎩∴地面总面积为:S=6x+2y+18=45(m 2),∴铺地砖的总费用为:45×80=3600(元).答:那么铺地砖的总费用为3600元.【点睛】本题考查二元一次方程组的应用,关键是能根据等量关系列出方程组.25.若在一个两位正整数 N 的个位数字与十位数字之间添上数字 2 ,组成一个新的三位数,我们称这个三位数为 N 的“诚勤数”,如 34 的“诚勤数”为 324 ;若将一个两位正整数 M 加 2 后得到一个新数,我们称这个新数为 M 的“立达数”,如 34 的“立达数”为 36. (1)求证:对任意一个两位正整数 A ,其“诚勤数”与“立达数”之差能被 6 整除;(2)若一个两位正整数 B 的“立达数”的各位数字之和是 B 的各位数字之和的一半,求 B 的值.解析:(1)见解析;(2) B 的值为68或59.【分析】(1)设A 的十位数字为a ,个位数字为b ,其“诚勤数”为100a+20+b 、“立达数”为10a+b+2,作差整理即可得;(2)设B=10a+b ,1≤a≤9,0≤b≤9(B 加上2后各数字之和变小,说明个位发生了进位),根据““立达数”的各位数字之和是B 的各位数字之和的一半”列出关于a 、b 的方程,求解可得.【详解】解:(1)设A的十位数字为a,个位数字为b,则A=10a+b,它的“诚勤数”为100a+20+b,它的“立达数”为10a+b+2,∴100a+20+b-(10a+b+2)=90a+18=6(15a+3),∵a为整数,∴15a+3是整数,则“诚勤数”与“立达数”之差能被6整除;(2)设B=10m+n,1≤m≤9,0≤n≤9(B加上2后各数字之和变小,说明个位发生了进位),∴B+2=10m+n+2,则B的“立达数”为10(m+1)+(n+2-10),∴m+1+n+2﹣10=12(m+n),整理,得m+n=14,∵1≤m≤9,0≤n≤9,∴m8n6=⎧⎨=⎩、m6n8=⎧⎨=⎩、m9n5=⎧⎨=⎩、m5n9=⎧⎨=⎩、m7n7=⎧⎨=⎩,经检验:77、86和95不符合题意,舍去,∴所求两位数为68或59.【点睛】本题主要考查了数字问题,根据题意表示出A、B两数的“立达数”、“诚勤数”及其变化是解题的关键.26.列方程解应用题:为让同学们幸福成长,年级准备组织师生秋游.关于租车问题:若只租45座的客车若干辆,则刚好坐满;若只租60座的客车,则可少租4辆,且余30个座位.(1)若只租45座的客车,求需要多少辆车?(2)已知一辆45座的客车租金每天2500元,一辆60座的客车租金每天3000元,若可以同时租用这两种类型的客车,则两种客车分别租多少辆最省钱?解析:(1) 18辆;(2) 租45座的客车2辆,租60座客车最省钱.【分析】(1)设单租45座客车x辆,则参加春游的师生总人数为45x人,根据人数与客车的数量关系建立方程求出其解即可;(2)等量关系为:45座客车能坐的人数+60座客车能坐的人数=秋游的师生总人数,选取正整数解,比较即可.【详解】解:(1)设单租45座客车x辆,则参加春游的师生总人数为45x人.根据题意,得45x=60(x−4)−30,解得:x=18.答:只租45座的客车,需要18辆车;(2)解:45×18=810(人)设租45座客车x 辆,60座客车y 辆.根据题意得:45x +60y =810.∵x ,y 均为正整数,∴x =2,y =12;或x=6,y=9;或x=10,y=6;或 x=14,y=3.2500×2+3000×12=41000(元)2500×6+3000×9=42000(元)2500×10+3000×6=43000(元)2500×14+3000×3=44000(元)∵41000﹤42000﹤43000﹤44000∴租45座的客车2辆,租60座客车12辆最省钱.【点睛】本题主要考查了用一元一次方程及二元一次方程解决实际问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系.27.解方程组:(1)379x y x y +=⎧⎨=-⎩; (2)5217345x y x y -=⎧⎨+=⎩. 解析:(1)54x y =-⎧⎨=⎩;(2)31x y =⎧⎨=-⎩【分析】(1)利用代入消元法即可解方程求解;(2)利用加减消元法①×2+②得出x 的值,进而代入②求出y 的值即可.【详解】解:()3719x y x y +=⎧⎨=-⎩,①,② 把②代入①,得937y y -+=,解得4y =,把4y =代入②,得495x =-=-,所以方程组的解为54.x y =-⎧⎨=⎩, ()52172345x y x y -=⎧⎨+=⎩,①,② ①2⨯+②,得103345x x +=+,解得3x =,把3x =代入②,得945y +=,解得1y =-,所以方程组的解为31.x y =⎧⎨=-⎩, 【点睛】本题考查解二元一次方程组,熟练掌握代入消元法和加减消元法解二元一次方程组是解题的关键.28.把y ax b =+(其中a 、b 是常数,x 、y 是未知数)这样的方程称为“雅系二元一次方程”当y x =时,“雅系二元一次方程y ax b =+”中x 的值称为“雅系二元一次方程”的“完美值”.例如:当y x =时,雅系二元一次方程”34y x =-化为34x x =-,其“完美值”为2x =.(1)求“雅系二元一次方程”56y x =-+的“完美值”;(2)3x =是“雅系二元一次方程”3y x m =+的“完美值”,求m 的值;(3)“雅系二元一次方程”1y kx =+(0k ≠,k 是常数)存在“完美值”吗?若存在,请求出其“完美值”,若不存在,请说明理由.解析:(1)x =1;(2)m =﹣6;(3)当k =1时,不存在“完美值”,当k≠1,k≠0时,存在“完美值”x =11k - 【分析】(1)由已知得到式子x=-5x+6,求出x 即可;(2)由已知可得x=3x+m ,将x=3代入即可求m ;(3)假设存在,得到x=kx+1,所以(1-k )x=1,当k=1时,不存在“完美值”,当k≠1,k≠0时,存在“完美值”x=11k -. 【详解】(1)由已知可得,x =-5x+6,解得x =1,∴“雅系二元一次方程”y =-5x+6的“完美值”为x =1;(2)由已知可得x =3x+m ,x =3,∴m =﹣6;(3)若“雅系二元一次方程”y =kx+1(k≠0,k 是常数)存在“完美值”,则有x =kx+1,∴(1﹣k )x =1,当k =1时,不存在“完美值”,当k≠1,k≠0时,存在“完美值”x =11k-. 【点睛】本题考查新定义,能够理解题意,将所求问题转化为一元一次方程求解是关键.。
二元一次方程组的解法步骤

二元一次方程组的解法步骤
引言
在代数学中,二元一次方程组是一种包含两个未知数的线性方程组。
解二元一次方程组是代数中的基本问题之一,下面将介绍解二元一次方程组的步骤。
步骤一:消元法
首先,我们需要对二元一次方程组中的两个方程进行消元操作。
消元法可以让我们得到一个只含有一个未知数的方程,从而简化计算过程。
步骤二:整理方程
经过消元操作后,我们得到一个简化的方程,接下来需要整理方程,将未知数的系数移到方程的一侧,常数移到另一侧,使方程变成标准形式。
步骤三:代入法
在得到整理后的方程之后,我们可以使用代入法来求解未知数的值。
通过将一个方程中的一个未知数用另一个未知数表示,然后代入另一个方程中,可以得到未知数的解。
步骤四:检验解
最后一步是对求得的解进行检验。
将解代入原方程组中,检验是否满足原方程组两个方程中的所有条件,如果满足,则表示求解正确。
结论
通过以上四个步骤,我们可以解出二元一次方程组的未知数的值。
二元一次方程组是代数学中常见的问题,掌握解题步骤对培养逻辑思维能力有很大帮助。
希望以上内容能够帮助您更好地理解二元一次方程组的解法步骤。
初中数学二元一次解法公式知识点

二元一次方程解法公式(一)代入消元法(1)概念:将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程组的解.这种解方程组的方法叫做代入消元法,简称代入法.(2)代入法解二元一次方程组的步骤①选取一个系数较简单的二元一次方程变形,用含有一个未知数的代数式表示另一个未知数;②将变形后的方程代入另一个方程中,消去一个未知数,得到一个一元一次方程(在代入时,要注意不能代入原方程,只能代入另一个没有变形的方程中,以达到消元的目的.);③解这个一元一次方程,求出未知数的值;④将求得的未知数的值代入①中变形后的方程中,求出另一个未知数的值;⑤用“{”联立两个未知数的值,就是方程组的解;⑥最后检验(代入原方程组中进行检验,方程是否满足左边=右边).例题:{x-y=3①{3x-8y=4②由①得x=y+3③③代入②得3(y+3)-8y=4y=1把y=1带入③得x=4则:这个二元一次方程组的解二)加减消元法(1)概念:当方程中两个方程的某一未知数的系数相等或互为相反数时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法,简称加减法.(2)加减法解二元一次方程组的步骤①利用等式的基本性质,将原方程组中某个未知数的系数化成相等或相反数的形式;②再利用等式的基本性质将变形后的两个方程相加或相减,消去一个未知数,得到一个一元一次方程(一定要将方程的两边都乘以同一个数,切忌只乘以一边,然后若未知数系数相等则用减法,若未知数系数互为相反数,则用加法);③解这个一元一次方程,求出未知数的值;④将求得的未知数的值代入原方程组中的任何一个方程中,求出另一个未知数的值;⑤用“{”联立两个未知数的值,就是方程组的解;⑥最后检验求得的结果是否正确(代入原方程组中进行检验,方程是否满足左边=右边)。
(完整版)二元一次方程组的常见解法

二元一次方程组的常见解法二元一次方程组中含有两个未知数,所以解二元一次方程组的主要思路就是消元,即消去一个未知数,使其转化为一元一次方程,这样就可以先解出一个未知数,然后设法求另一个未知数.常见的消元方法有两种:代入消元法和加减消元法.一、代入法即由二元一次方程中的一个方程变形,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程中,实现消元,进而求解.一般情况下用代入法解方程组时,选择变形的方程要尽可能的简单,表示的代数式也要尽可能的简单,以利于计算.2x+5y=-21①例1、解方程组x+3y=8 ②解由②得:x=8-3y ③把③代入①得2(8-3y)+5y=-21解得:y=37把y=37代入③得:x=8-3×37=-103x=-103所以这个方程组的解是y=37二、整体代入法当方程组中的两个方程存在整数倍数关系时,用代入法解可将整数倍数关系数中较小的一个变形,用另一个字母代数式表示它后代入另一个方程.3x-4y=9①例2、解方程组9x-10y=3②解由①得3x=4y+9 ③把③代入②得3(4y+9)-10y=3解得y=-12把y=-12代入③得3x=4×(-12)+9解得x=-13x=-13所以方程组的解是y=-12三、加减消元法即方程组中两个二元一次方程中的同一个未知数的系数相等时,让两个方程相减.如果方程组中两个二元一次方程中的同一个未知数的系数互为相反数时则让两个方程相减.消去一个未知数,得到一个一元一次方程,这种方法叫加减消元法.2x+3y=14 ①例3、解方程组4x-5y=6②解由①×2得4x+6y=28 ③③-②得:11y=22解得y=2把y=2代入②得4x-5×2=6解得x=4x=4所以方程组的解为y=2四、整体运用加减法即当两个二元一次方程中的某一部分完全相同或符号相反时,可以把这两个方程两边相加或相减,把相同的部分整体消去.3(x+2)+(y-1)=4 ①例4 解方程组3(x+2)+(1-y)=2 ②解①-②得(y-1)-(1-y)=4-2整理得2y=4解得y=2把y=2 代入①得3(x+2)+(2-1)=4整理得3x+7=4解得x=-1x=-1所以方程组的解为y=2解二元一次方程组的主要方法有代入法和消元法,因为方程的形式是多种多样的.所以在解方程中一定要仔细观察方程中各部分以及各个未知数和它们的系数之间的关系的找到最简便的解题方法.。
二元一次方程组的解的公式

二元一次方程组的解的公式
对于二元一次方程组,我们可以使用消元法或代入法来求解。
消元法:
将两个方程相加,得到一个新方程,这个新方程的右边为0。
将新方程两边同时除以未知数的系数,得到一个新方程,这个新方程的右边为0。
解这个新方程,即可得到一个未知数的值。
将这个未知数的值代入原方程组中的任意一个方程,即可得到另一个未知数的值。
代入法:
从第一个方程中解出一个未知数,得到这个未知数的值。
将这个未知数的值代入第二个方程中,得到另一个未知数的值。
例如,对于方程组:
3x + 2y = 18
5x - y = 3
我们可以使用消元法来求解:
解得: [{x: 24/13, y: 81/13}]
图像法:将二元一次方程组转化为一元一次方程,通过求解一元一次
方程得到答案。
拉格朗日插值法:利用拉格朗日插值多项式求解二元一次方程组。
牛顿插值法:利用牛顿插值多项式求解二元一次方程组。
最小二乘法:利用最小二乘法求解二元一次方程组。
反代法:将二元一次方程组的两个方程相减,得到一个新的方程。
再将这个新的方程代入其中一个方程中,即可得到另一个未知数的值。
参数法:将二元一次方程组的两个方程都转化为含有同一个参数的方程,通过求解参数得到答案。
联立解法:将二元一次方程组的两个方程联立起来,构成一个新的方程组,然后解这个新的方程组得到答案。
矩阵法:将二元一次方程组转化为矩阵形式,通过求解矩阵得到答案。
二元一次方程组的解法步骤

二元一次方程组的解法步骤二元一次方程组的解法步骤第 1 篇代入消元法(1)等量代换:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数(例如y),用另一个未知数(如x)的代数式表示出来,即将方程写成y=ax+b的形式;(2)代入消元:将y=ax+b代入另一个方程中,消去y,得到一个关于x的一元一次方程;(3)解这个一元一次方程,求出x的值;(4)回代:把求得的x的值代入y=ax+b中求出y的值,从而得出方程组的解;(5)把这个方程组的解写成x=c y=d的形式。
换元法解一些复杂的问题,常用到换元法,即对结构比较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),则能使复杂的问题简单化,明朗化。
该方法在减少多项式项数,降低多项式结构复杂程度等方面能起到独到作用。
加减消元法(1)变换系数:利用等式的基本性质,把一个方程或者两个方程的两边都乘以适当的数,使两个方程里的某一个未知数的系数互为相反数或相等;(2)加减消元:把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;(3)解这个一元一次方程,求得一个未知数的值;(4)回代:将求出的未知数的值代入原方程组的任何一个方程中,求出另一个未知数的值;(5)把这个方程组的解写成x=c y=d的形式。
二元一次方程组的解法步骤第 2 篇教学目的1、使学生巩固等式与方程的概念。
2、使学生掌握等式的*质和灵活掌握一元一次方程的解法,培养学生求解方程的计算能力。
教学分析重点:熟练掌握一元一次方程的解法。
难点:灵活地运用一元一次方程的解法步骤,计算简化而准确。
突破:多练习,多比较,多思考。
教学过程一、复习1、什么是一元一次方程?一元一次方程的标准形式是什么?它的解是什么?2、等式的*质是什么?(要求说出应注意的两点)3、解一元一次方程的基本步骤是什么?以解方程-2x+=为例,说明解一元一次方程的基本步骤与注意点,并口头检验。
二、新授1、已知方程(n+1)x|n|=1是关于x的一元一次方程,求n 的值。
初一二元一次方程组的解法

二元一次方程组的解法考点名称:二元一次方程组的解法二元一次方程组的解:使二元一次方程组的两个方程都成立的一对未知数的值,叫做方程组的解,即其解是一对数。
二元一次方程组解的情况:一般地,使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
求方程组的解的过程,叫做解方程组。
一般来说,一个二元一次方程有无数个解,而二元一次方程组的解有以下三种情况:1、有一组解。
如方程组:x+y=5①6x+13y=89②x=-24/7y=59/7 为方程组的解2、有无数组解。
如方程组:x+y=6①2x+2y=12②因为这两个方程实际上是一个方程(亦称作“方程有两个相等的实数根”),所以此类方程组有无数组解。
3、无解。
如方程组:x+y=4①2x+2y=10②,因为方程②化简后为x+y=5这与方程①相矛盾,所以此类方程组无解。
可以通过系数之比来判断二元一次方程组的解的情况,如下列关于x,y的二元一次方程组:ax+by=cdx+ey=f当a/d≠b/e 时,该方程组有一组解。
当a/d=b/e=c/f 时,该方程组有无数组解。
当a/d=b/e≠c/f 时,该方程组无解。
二元一次方程组的解法:解方程的依据—等式性质1.a=b←→a+c=b+c2.a=b←→ac=bc (c>0)一、消元法1)代入消元法用代入消元法的一般步骤是:①选一个系数比较简单的方程进行变形,变成 y = ax +b 或x = ay + b的形式;②将y = ax + b 或 x = ay + b代入另一个方程,消去一个未知数,从而将另一个方程变成一元一次方程;③解这个一元一次方程,求出 x 或 y 值;④将已求出的 x 或 y 值代入方程组中的任意一个方程(y = ax +b 或 x = ay + b),求出另一个未知数;⑤把求得的两个未知数的值用大括号联立起来,这就是二元一次方程的解。
例:解方程组:x+y=5①{6x+13y=89②解:由①得x=5-y③把③代入②,得6(5-y)+13y=89即 y=59/7把y=59/7代入③,得x=5-59/7即 x=-24/7∴ x=-24/7y=59/7 为方程组的解我们把这种通过“代入”消去一个未知数,从而求出方程组的解的方法叫做代入消元法,简称代入法。
初中数学 二元一次方程组及其解法

二元一次方程组及其解法一、二元一次方程的概念1.二元一次方程:含有两个未知数,并且含未知数的项的最高次数是1的整式方程,叫做二元一次方程.二元一次方程的一般形式为:ax by c ++=0(,)a b ≠0≠0.【例】x y +2=5,x y 2=3,x y 3=-2,x y 2+3+6=0等都是二元一次方程. 2.二元一次方程的判定: 必须同时满足四个条件:(1)含有两个未知数——“二元”;(2)未知数项的最高次数为1——“一次”; (3)方程两边都是整式——整式方程; (4)未知数的系数不能为0.【例】x y +=1,()y x 1=+82,x y 3-1=2-5,x y 4=3等都是二元一次方程;y x 4+=5,x y z 2+3=,x y 21+=02,x x 2+3=-5等都不是二元一次方程. 3.二元一次方程的解:使二元一次方程左、右两边的值相等的两个未知数的值,叫做二元一次方程的解.【注】任何一个二元一次方程都有无数个解.【例】x y =1⎧⎨=2⎩和x y =3⎧⎨=1⎩是方程x y +2=5的解,可以看出x y +2=5有无数个解.二、二元一次方程组的概念和解法1.二元一次方程组:由几个一次方程组成并含有两个未知数的方程组,叫做二元一次方程组.【注意】(1)二元一次方程组不一定由几个二元一次方程合在一起.(2)方程可以超过两个.【例】x x y 2=6⎧⎨3-=1⎩,x x y 2=6⎧⎨3-=1⎩,x y x y =2⎧⎪=3⎨⎪+=4⎩等都是二元一次方程组.2.二元一次方程组的解:使二元一次方程组的几个方程左、右两边都相等的两个未知数的值(即几个方程的公共解),叫做二元一次方程组的解.【例】x x y 2=6⎧⎨3-=1⎩的解是x y =3⎧⎨=8⎩.3.二元一次方程组解的情况:一般情况下,一个二元一次方程组只有唯一一组解;但在特殊情况下,二元一次方程组也可能无解或有无数组解.【例】方程组x y x y +=1⎧⎨2+2=2⎩有无数组解,方程组x y x y +=2⎧⎨2+2=2⎩和x y x y =2⎧⎪=3⎨⎪+=4⎩无解.4.二元一次方程组的基本解法(1)代入消元法:①从方程组中选一个系数比较简单的方程,将该方程中的一个未知数用含另一未知数的式子表示出来,例如y ax b =+;②把y ax b =+代入另一个方程中,消去y ,得到一个关于x 的一元一次方程;③解这个一元一次方程,求出x 的值; ④把求得的x 的值代回y ax b =+中,求出y 的值,从而得出方程组的解;⑤把这个方程组的解写成x my n =⎧⎨=⎩的形式.解方程组:19,x y x y 3+4=⎧⎨-=4.⎩解:19,x y x y 3+4=⎧⎨-=4.⎩①②由②,得x y =4+,③ 把③代入①,()y y 34++4=19, ∴y y 12+3+4=19,得y =1. 把y =1代入③,得x =4+1=5.∴方程组的解为5x y =⎧⎨=1.⎩,(2)加减消元法:①把一个方程或者两个方程的两边都乘以适当的数,使两个方程里的某一个未知数的系数相反或相等;②把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;③解这个一元一次方程,求出一个未知数的值;④把求得的未知数的值代入原方程组中,求出另一个未知数的值,从而得出方程组的解;⑤把这个方程组的解写成x my n=⎧⎨=⎩的形式.解方程组:x y x y +2=1⎧⎨3-2=11⎩解:x y x y +2=1⎧⎨3-2=11⎩①②①+②,得x 4=12,解得:x =3.将x =3代入①,得y 3+2=1, 解得y =-1.∴方程组的解是x y =3⎧⎨=-1⎩.5.解方程组的三大解题思想(1)消元思想;(2)整体思想;(3)换元思想.(1)在下列方程中,①x 4+5=1;②x y 3-2=1;③x y1+=1;④xy y +=14;⑤x y =;⑥()y x 1=+82,其中是二元一次方程的是__________.(填序号)(2)已知方程||n m x y m -1-1+2=是关于x 、y 的二元一次方程,则m =_____,n =______.(3)若已知方程()()()k x k x k y k 22-1++1+-7=+2,当k =______时,方程为一元一次方程,当k =_______时,方程为二元一次方程.【解析】(1)②⑤⑥;(2)m =0或2,n =2.(3)-1,1.模块一 二元一次方程的概念例题1(1)已知x y =1⎧⎨=-1⎩是方程x ay 2-=3的一个解,那么a 的值是_________.(2)若x ky k =2⎧⎨=-3⎩是二元一次方程x y 2-=14的解,则k 的值是_________.【解析】(1)1;(2)2.(1)下列方程组中,是二元一次方程组的是( )A .x y y 2+=1⎧⎪1⎨=-1⎪⎩ B .x xy 2=1⎧⎨=-1⎩ C .x y y z 2+=1⎧⎨-=-1⎩D .x y =1⎧⎨=-1⎩(2)已知x y =-4⎧⎨=3⎩是方程组ax y x by +=-1⎧⎨-=2⎩的解,则()a b 6+=______.(3)已知x y =2⎧⎨=1⎩是二元一次方程组ax by bx ay +=1⎧⎨+=2⎩的解,则a b -的值为______.【解析】(1)D ;(2)由题意得a =1,b =-2,a b +=1,∴()a b 6+=1.(3)把解代入方程组得a b b a 2+=1⎧⎨2+=2⎩①②,①-②得a b -=-1.(1)用代入消元法解方程组:x y x y 3+4=2⎧⎨2-=5⎩.(2)用加减消元法解方程组:x y x y 4+3=5⎧⎨-2=4⎩.例题2模块二二元一次方程组的概念和解法例题3例题4【解析】(1)由题意得,x yx y3+4=2⎧⎨2-=5⎩①②由②,得y x=2-5,③把③代入①,得()x x3+42-5=2,∴x x3+8-20=2,得x11=22,解得x=2.把x=2代入③,得y=-1.∴方程组的解为xy=2,⎧⎨=-1.⎩(2)由题意得,x yx y4+3=5⎧⎨-2=4⎩①②①×2+②×3,得x x8+3=10+12,∴x11=22,解得x=2.将x=2代入①,得y8+3=5,解得y=-1.∴方程组的解为xy=2,⎧⎨=-1.⎩【提示】展示解二元一次方程组的基本解法.用合适的方法解下列二元一次方程组:(1)()()()x yy x3-1=+5⎧⎨5-1=3+5⎩(2)()()()x yx y+1=5+2⎧⎨32-5-43+4=5⎩(3)()()x y yx y4--1=31--2⎧⎪⎨+=2⎪23⎩(4)m n n mnm+-⎧-=2⎪⎪34⎨⎪4+=14⎪3⎩(5)x yx y3-22-1⎧+=2⎪⎪45⎨3+23+1⎪-=0⎪45⎩(6)...x yx y112⎧+=⎪535⎨⎪05-03=02⎩【解析】(1)由题意得,x yx y3-=8⎧⎨3-5=-20⎩①②①-②,得y4=28,解得y=7.将y=7代入①,得x3-7=8,解得x=5.∴方程组的解为xy=5⎧⎨=7⎩.(2)由题意得,x yx y-5=9⎧⎨-2=6⎩①②②-①,得y3=-3,解得y=-1.将y=-1代入①,得x+5=9,解得x=4.∴方程组的解为xy=4⎧⎨=-1⎩.(3)xy=2⎧⎨=3⎩.(4)mn18⎧=⎪⎪5⎨6⎪=-⎪5⎩.(5)xy=2⎧⎨=3⎩.(6)xy14⎧=⎪⎪17⎨12⎪=⎪17⎩.例题5【提示】练习解二元一次方程组的一般步骤:(1)去分母,去括号,最好转化为各项系数为整数的二元一次方程组; (2)多观察,系数为1±时优先使用代入消元法,其次才是加减消元法.解方程组:(1)x y x y 23+17=63⎧⎨17+23=57⎩(2)x y x y 2011-2013=4023⎧⎨2013-2011=4025⎩【解析】(1)两方程相加,得:x y 40+40=120,即x y +=3 ①两方程相减,得:x y 6-6=6,即x y -=1 ② ①+②得:x 2=4,解得x =2,①-②得:y 2=2,解得y =1,∴方程组的解为:x y =2⎧⎨=1⎩.(2)x y 3⎧=⎪⎪2⎨1⎪=-⎪⎩2.【提示】系数对称的二元一次方程组的特殊解法.(1)若方程组.a b a b 2-3=13⎧⎨3+5=309⎩的解是..a b =83⎧⎨=12⎩,则方程组()()()().x y x y 2+2-3-1=13⎧⎨3+2+5-1=309⎩的解是( )A ...x y =63⎧⎨=22⎩B ...x y =83⎧⎨=12⎩C ...x y =103⎧⎨=22⎩D ...x y =103⎧⎨=02⎩(2)用适当的方法解下列方程组:()()x y x y x y x y 3+-2-=-1⎧⎪⎨+-+=1⎪⎩24.【解析】(1)A .比较两个方程组可知..x a y b +2==83⎧⎨-1==12⎩,解得..x y =63⎧⎨=22⎩.(2)令x y u +=,x y v -=,则u v u v 3-2=-1⎧⎪⎨+=1⎪⎩24,解得u v =1⎧⎨=2⎩,即x y x y +=1⎧⎨-=2⎩,解得x y 3⎧=⎪⎪2⎨1⎪=-⎪⎩2.【提示】整体换元法.例题6例题7解方程组:(1)x y z x y z x y z +-=0⎧⎪2-3+2=5⎨⎪+2+=13⎩ (2)x y z x y z x y z 2+3+=16⎧⎪-+2=-1⎨⎪+2-=5⎩【解析】(1)由题意得,x y z x y z x y z +-=0⎧⎪2-3+2=5⎨⎪+2+=13⎩①②③由①,得y z x =-,④把④代入②和③, 得x z x z 5-=5⎧⎨-+3=13⎩,解得x z =2⎧⎨=5⎩. 把x z =2⎧⎨=5⎩代入④得,y =3.∴方程组的解为x y z =2⎧⎪=3⎨⎪=5⎩.(2)由题意得,x y z x y z x y z 2+3+=16⎧⎪-+2=-1⎨⎪+2-=5⎩①②③③①+得,④x y 3+5=21, 2③②⨯+得,⑤x y 3+3=9,④﹣⑤得y 2=12,y =6,将y =6代入⑤得,x 3=-9,x =-3,将x =-3,y =6代入①得,()z =16-2⨯-3-3⨯6=4, ∴方程组的解为x y z =-3⎧⎪=6⎨⎪=4⎩.【提示】三元一次方程组的基本解法:(1)通过消元把三元一次方程组转化为二元一次方程组; (2)解二元一次方程组.模块三 多元一次方程组的解法例题8(1) x y zx y z ⎧==⎪234⎨⎪5+2-3=8⎩ (2) x y z x y z x y z 2++=2⎧⎪+2+=4⎨⎪++2=6⎩【解析】(1)令x y zk ===234,即x k =2,y k =3,z k =4, 代入②可求得k =2,所以x y z =4⎧⎪=6⎨⎪=8⎩.(2)①+②+③得x y z ++=3,用①、②、③分别减去此式得x y z =-1⎧⎪=1⎨⎪=3⎩.【提示】三元一次方程组的特殊解法:(1)连比设k 型;(2)对称轮换型,整体相加.解方程组:(1)pq p q pq p q1⎧=⎪+5⎪⎨1⎪=⎪-3⎩ (2)xyx y yz y z zx z x ⎧=1⎪+⎪⎪=2⎨+⎪⎪=3⎪+⎩【解析】(1)原方程组可化为p q q p 11⎧+=5⎪⎪⎨11⎪-=3⎪⎩,解得q p 1⎧=4⎪⎪⎨1⎪=1⎪⎩,∴q p 1⎧=⎪4⎨⎪=1⎩.(2)原方程组可化为,解得,∴.【提示】均为可以转化为二元一次方程组或者三元一次方程组的分式方程.11111121113x y y z z x ⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩151217121112x y z ⎧=⎪⎪⎪=⎨⎪⎪=-⎪⎩12512712x y z ⎧=⎪⎪⎪=⎨⎪⎪⎪=-⎩例题9非常挑战(1)已知二元一次方程x y--1=023,下列用含x 的代数式表示y 正确的是( ). A .y x 3=-12 B .y x 3=+12 C .y x 3=-32 D .y x 3=+32(2)下列方程属于二元一次方程的是( )A .x y +=1B .xy +5=4C .y x 23-8=D .x y1+=2(3)已知方程||||()()a b a x b y -1-4-2-+5=3是关于x 、y 的二元一次方程,则a =________,b =__________.【解析】(1)C ;(2)A ;(3)根据题意可得:a -2≠0,b +5≠0,||a -1=1,||b -4=1,所以a =-2,b =5.(1)下列不是二元一次方程组的是( )A .x y =2⎧⎨=-1⎩B .m n n m =2+3⎧⎨3-=4⎩C .x y y z +=2⎧⎨+=3⎩D .(())a a b a b 4+2=5⎧⎨2-+1=2+-3⎩(2)二元一次方程ax by +=6有两组解是x y =2⎧⎨=-2⎩与x y =-1⎧⎨=-8⎩,求a 、b 的值.【解析】(1)C .(2)将两组解分别代入ax by +=6,可得a b a b 2-2=6⎧⎨--8=6⎩,解得a b =2⎧⎨=-1⎩.复习巩固演练1演练2解方程组:(1)m n m n 3+2=2⎧⎨5-4=7⎩(2)()()()()y x x y 3-1=4-4⎧⎨5-1=3+5⎩(3)()()y x x y y x -1⎧-=3⎪2⎨⎪2-+32-=-6⎩ (4)x y x y +1+2⎧=⎪⎪34⎨-3-31⎪-=⎪4312⎩【解析】(1)m n =1⎧⎪⎨1=-⎪⎩2. (2)x y =7⎧⎨=5⎩. (3)x y =2⎧⎨=-1⎩. (4)x y =2⎧⎨=2⎩.解下列方程组:(1)x y x y 21+23=243⎧⎨23+21=241⎩ (2)x y x y 2014+2013=2012⎧⎨2012+2011=2010⎩(3)x y x yx y x y 2+32-3⎧+=7⎪⎪43⎨2+32-3⎪+=8⎪32⎩【解析】(1)x y =5⎧⎨=6⎩.(2)x y =-1⎧⎨=2⎩.(3)设x y a 2+3=,x y b 2-3=,则原方程组可变为,,a ba b ⎧+=7⎪⎪43⎨⎪+=8⎪32⎩整理,得,,a b a b 3+4=84⎧⎨2+3=48⎩解得,.a b =60⎧⎨=-24⎩∴,,x y x y 2+3=60⎧⎨2-3=-24⎩解得,,x y =9⎧⎨=14⎩ ∴原方程组的解为,.x y =9⎧⎨=14⎩演练3演练4解方程组:(1)x z z y x y z -=4⎧⎪-2=-1⎨⎪+-=-1⎩(2)::::::x y z u x y z u =1234⎧⎨9+7+3+2=200⎩(3) x y z y z x z x y +-=11⎧⎪+-=3⎨⎪+-=1⎩(4)mn m n mn m n 1⎧=⎪⎪3+213⎨1⎪=⎪2+312⎩【解析】(1)x y z =-7⎧⎪=-5⎨⎪=-11⎩.(2)设x k =,y k =2,z k =3,u k =4,所以有k k k k 9+14+9+8=200, 即k =5,故x y z u =5⎧⎪=10⎪⎨=15⎪⎪=20⎩.(3)①+②+③得:x y z ++=15,分别去减①、②、③式可得:x y z =6⎧⎪=7⎨⎪=2⎩.(4)m n 1⎧=⎪⎪2⎨1⎪=⎪3⎩.演练5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学:二元一次方程组的几种简便解法
1、整体代入法
整体代入法是用含未知数的表达式代入方程进行消元.有些方程组并不一定能直接应用这种解法,不过,我们可以创造条件进行整体代入.
解析:这道题中的系数较繁,按常规方法去解比较麻烦.我们可以先将②式有目的地进行变形,再将①式中的看成一个整体代入求解.
由②式可得.
化简,得.③
将①代入③,得.解得,代入①可得.
故方程组的解为
2、换元法
换元法就是设出一个辅助未知数,分别用含有这个未知数的代数式表示原方程组中未知数的值,把二元一次方程组转化为一元一次方程组进行求解.换元有一定的技巧性.有代数式整体换元,还有设比值换元等多种方法,下面举例说明.
解析:我们可以分别尝试整体换元和设比值换元.
方法1:设,则.代入②,得.解得.
从而可得方程组的解为
方法2:设.
由①得,所以.③
由②得.④
③÷④,得.
解得.从而可得
3、直接加减法
直接加减法有别于课本中的加减消元法,它通过将方程组中的方程相加减后把较繁的题目转化得相对简单.
解析:若用一般方法去解这个方程组,其复杂程度可想而知,我们采用直接加减法.
①+②,得,即.③
①-②,得.④
由③④可得
4、消常数项法
解析:可将两式消去常数项,直接得到与的关系式,而后代入消元.
①-②,得,即.
将代入②,得,即.
从而可得
5、相乘保留法
解析:去分母时,如果把两数相乘得出结果,不仅数值变大,而且给下面的解题过程带来麻烦,所以有时我们暂时保留相乘的形式.
由①,得.③
由②,得.④
④-③,得.
从而可得
6、科学记数法
当方程组中出现比较大的数字时,可用科学记数法简写.
例6、解方程组
解析:这个数比较大,可用科学记数法写成.
由②,可得.③
将①代入③,得.
从而可得
7、系数化整法
若方程组中含有小数系数,一般要将小数系数化为整数,便于运算.
解析:利用等式的性质,把①式变形为.③
利用分子、分母相除,把②式变形为.④
③-④,得.
从而可得
8、对称法
例8、解方程组
解析:这个方程组是对称方程组,其特点是把某一个方程中的互换即可得到另一个方程.
由对称性可知,则可得
解得
9、拆数法
例9、解方程组
解析:我们可以有目的地将常数项进行变形,通过观察得出方程组的解.
原方程组可变形为
从而可得。
