第09章线性回归计算
多元线性回归的计算模型

多元线性回归的计算模型多元线性回归模型的数学表示可以表示为:Y=β0+β1X1+β2X2+...+βkXk+ε,其中Y表示因变量,Xi表示第i个自变量,βi表示第i个自变量的回归系数(即自变量对因变量的影响),ε表示误差项。
1.每个自变量与因变量之间是线性关系。
2.自变量之间相互独立,即不存在多重共线性。
3.误差项ε服从正态分布。
4.误差项ε具有同方差性,即方差相等。
5.误差项ε之间相互独立。
为了估计多元线性回归模型的回归系数,常常使用最小二乘法。
最小二乘法的目标是使得由回归方程预测的值与实际值之间的残差平方和最小化。
具体步骤如下:1.收集数据。
需要收集因变量和多个自变量的数据,并确保数据之间的正确对应关系。
2.建立模型。
根据实际问题和理论知识,确定多元线性回归模型的形式。
3.估计回归系数。
利用最小二乘法估计回归系数,使得预测值与实际值之间的残差平方和最小化。
4.假设检验。
对模型的回归系数进行假设检验,判断自变量对因变量是否显著。
5. 模型评价。
使用统计指标如决定系数(R2)、调整决定系数(adjusted R2)、标准误差(standard error)等对模型进行评价。
6.模型应用与预测。
通过多元线性回归模型,可以对新的自变量值进行预测,并进行决策和提出建议。
多元线性回归模型的计算可以利用统计软件进行,例如R、Python中的statsmodels库、scikit-learn库等。
这些软件包提供了多元线性回归模型的函数和方法,可以方便地进行模型的估计和评价。
在计算过程中,需要注意检验模型的假设前提是否满足,如果不满足可能会影响到模型的可靠性和解释性。
总而言之,多元线性回归模型是一种常用的预测模型,可以分析多个自变量对因变量的影响。
通过最小二乘法估计回归系数,并进行假设检验和模型评价,可以得到一个可靠的模型,并进行预测和决策。
线性回归算法原理

线性回归算法原理
线性回归是一种预测模型,用于建立自变量(输入)与因变量(输出)之间的线性关系。
其原理基于最小二乘法,通过拟合一条最优直线来描述数据点的分布趋势。
线性回归假设自变量与因变量之间存在线性关系,可以表示为
y = β0 + β1x + ε,其中 y 是因变量,x 是自变量,β0 和β1 是
回归系数,ε 是随机误差项。
回归系数的求解过程是通过最小化残差平方和来实现的,即找到使得∑(yi - β0 - β1xi)² 最小化的β0 和β1。
求解过程主要利用了最小二乘法,该方法通过对误差的平方和进行求导,使得导数等于零得到回归系数的估计值。
对于简单线性回归来说,只有一个自变量,回归方程可以表示为y = β0 + β1x + ε。
而对于多元线性回归,有多个自变量,回归方程可以表示为y = β0 + β1x1 + β2x2 + ... + βnxn + ε。
线性回归模型在实际应用中具有广泛的适用性,特别是在预测和预测分析领域。
它可以用来解决许多实际问题,如房价预测、销售量预测、趋势分析等。
《统计分析与SPSS应用第五版》课后练习答案第9章.docx

《统计分析与SPSS 的应用(第五版)》(薛薇)课后练习答案第9章SPSS 的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成 绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别 针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
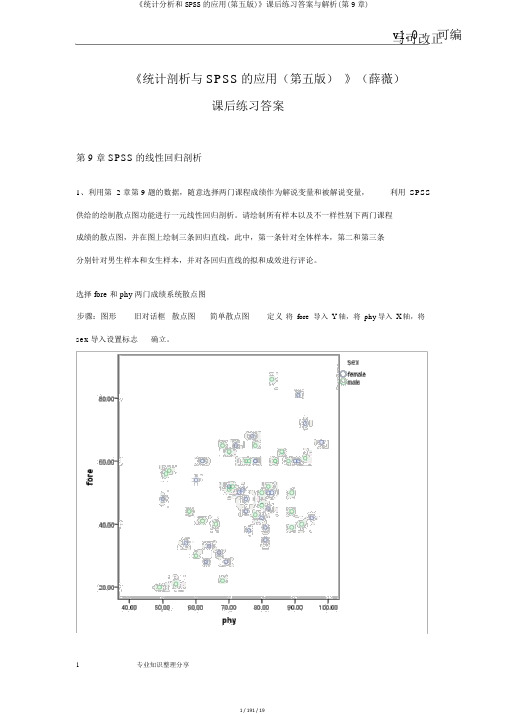
选择fore 和phy 两门成绩体系散点图步骤:图形 旧对话框 散点图 简单散点图 定义 将fore 导入Y 轴,将phy 导入X 轴,将 sex 导入设置标记确定。
OO O O O O OOOO O ODOOO08。
OOO OOD O °。
O°O O O O° OO ° OO °O Oo O°O OO °80.00-40.00-20.00-接下来在SPSS输出查看器中,双击上图,打开图表编辑sex O female O male60.00-40.00 50.00 60.00 70.00 80.00 90.00 100.00phy在图表编辑器中,选择“元素”菜单选择总计拟合线选择线性应用再选择元素菜单点击子组拟合线选择线性应用。
40.00 50.00 60.00 70.00 80.00 90.00 100.00分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
(09)第9章 一元线性回归(2011年)

变量之间是否存在关系? 如果存在,它们之间是什么样的关系? 变量之间的关系强度如何? 样本所反映的变量之间的关系能否代表总体 变量之间的关系?
9-9 *
9.1 变量间的关系 9.1.1 变量间是什么样的关系?
统计学 STATIS TICS
函数关系
(第四版) 1. 是一一对应的确定关系 2. 设有两个变量 x 和 y ,变量 y y 随变量 x 一起变化,并完 全依赖于 x ,当变量 x 取某 个数值时, y 依确定的关系 取相应的值,则称 y 是 x 的 函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量 x 3. 各观测点落在一条线上
y 是 x 的线性函数(部分)加上误差项 线性部分反映了由于 x 的变化而引起的 y 的变化 误差项 是随机变量 反映了除 x 和 y 之间的线性关系之外的随机因素 对 y 的影响 是不能由 x 和 y 之间的线性关系所解释的变异性 0 和 1 称为模型的参数
9 - 30 *
统 计 学 数据分析 (方法与案例)
作者 贾俊平
统计学 STATIS TICS
(第四版)
统计名言
不要过于教条地对待研究的结果, 尤其当数据的质量受到怀疑时。
——Damodar N.Gujarati
9-2 *
第 9 章 一元线性回归
9.1 9.2 9.3 9.4 变量间关系的度量 一元线性回归的估计和检验 利用回归方程进行预测 用残差检验模型的假定
9-7
*
第 9 章 一元线性回归
9.1 变量间的关系
9.1.1 变量间是什么样的关系? 9.1.2 用散点图描述相关关系 9.1.3 用相关系数度量关系强度
练习6-9

返回同步训练列表同步训练四(第6-9章)同步训练习题属于辅助性学习资源,不计入过程性考核的成绩,请学员根据自己的学习情况安排时间学习。
一、填空题1. 设总体X~N(0,1),x1,x2,…,xn为来自该总体的样本,则统计量的抽样分布为___。
隐藏答案【答案】x2(n)【解析】教材137页表6-4~ x2(n)【知识点】第六章正态总体的抽样分布2. 设X1,X2…,Xn是来自总体N(μ,σ2)的样本,则2~____(标出参数)。
隐藏答案【答案】x2(n-1)【解析】教材140页定理6-4【知识点】第六章正态总体的抽样分布3. 设总体X~N(1,σ2),x1,x2,…,xn为来自该总体的样本,,则___。
隐藏答案【答案】1【解析】记住公式=1【知识点】第六章样本均值4. 当随机变量F~F(m,n)时,对给定的若F~F(10,5),则P{F<}= ___。
隐藏答案【答案】0.95【解析】首先F分布的性质,教材138页的图6-5下边【知识点】第六章 F 分布性质和分位数的定义5. 设总体X服从正态分布N(μ1,σ2),总体Y服从正态分布N(μ2,σ2),X1,X2,…,Xn和Y 1,Y2,…,Ym分别是来自总体X和Y的简单随机样本,则E=___。
隐藏答案【答案】σ2【解析】定理6-2和期望的性质。
E【知识点】第六章期望性质和样本方差的期望6. 设总体X具有区间[0,θ]上的均匀分布(θ>0),x1,x2,…,xn是来自该总体的样本,则θ的矩估计=___。
隐藏答案【答案】【解析】根据重要随机变量的期望和方差,知道所以根据矩估计的方法有=【知识点】第七章矩估计法7. 设总体X的概率密度为,x1,x2,…,xn为总体X的一个样本,则未知参数α的矩估计=___。
隐藏答案【答案】【解析】教材149页例7-8的(2)【知识点】第七章矩估计法8. 设总体X~N(μ,σ2),x1,x2,x3为来自X的样本,则当常数a=___时,是未知参数μ的无偏估计。
第09章 线性回归模型的异方差问题

ˆ y = a + bx
∑
ˆ ) 2 = m in (y − y
2
ˆ 由∑ ( y − y ) = min ,有 ∑ ( y − a − bx ) = min, 分别对函数中 a、 b求偏导数,并令其为零 ,有 2∑ ( y − a − bx )(− 1) = 0 2∑ ( y − a − bx )(− x ) = 0
14
(0.0019)
安徽大学经济学院
计量经济学讲义
9.2 异方差的性质-方程回归结果图
15
安徽大学经济学院
计量经济学讲义
9.2 异方差的性质-残差与观察值(销售额)关系图
16
安徽大学经济学院
计量经济学讲义
9.2 异方差的性质
从残差图可以看出:残差的绝对值随着销售额的 增加而增加。 尽管残差ei与扰动项ui是两个不同的概念,根据ei 的变化并不能断言ui的方差也是变化的。但是,实践 u 中很难观察到ui,只能利用检验ei的变动来推断ui的 变化。 问题:如何理解残差ei与扰动项ui两个概念的差 别?
7
安徽大学经济学院
计量经济学讲义
一元线性回归分析-回归的假定条件
假定3 给定X,扰动误差项u的数学期望或均值为0, 即E(u|X)= 0。 Y
+u +u -u -u -u
+u
E(Y|X)=α+β*X
0
X
8
安徽大学经济学院
计量经济学讲义
一元线性回归分析-回归的假定条件
假定4 误差扰动项u的方差为常数,即Var(u)=σ2,称 之为同方差(homoscedasticity) 同方差的含义:每个Y值以相同的方差分布在其均值周 围,即Y偏离其均值的程度相同。 Y
总结:线性回归分析的基本步骤

线性回归分析的基本步骤步骤一、建立模型知识点:1、总体回归模型、总体回归方程、样本回归模型、样本回归方程①总体回归模型:研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。
Y X Uβ=+特点:由于随机误差项U 的存在,使得Y 和X 不在一条直线/平面上。
例1:某镇共有60个家庭,经普查,60个家庭的每周收入(X )与每周消费(Y )数据如下:每周收入(X )每周消费支出(Y )805560657075 100657074808588 1207984909498 140809395103108113115160102107110116118125 180110115120130135140 200120136140144145 220135137140152157160162240137145155165175189 260150152175178180185191作出其散点图如下:②总体回归方程(线):由于假定,因此因变量的均值与自变0EU =量总处于一条直线上,这条直线就称为总体回归线(方()|E Y X X β=程)。
总体回归方程的求法:以例1的数据为例1)对第一个X i ,求出E (Y |X i )。
每周收入(X )每周消费支出(Y )E (Y |X i )805560657075 65100657074808588 771207984909498 89140809395103108113115101160102107110116118125 113180110115120130135140 125200120136140144145 137220135137140152157160162149240137145155165175189 161260150152175178180185191173由于()01|i i i E Y X X ββ=+,因此任意带入两个X i 和其对应的E (Y |X i )值,即可求出01ββ一,并进而得到总体回归方程。
计量经济学课后答案——张龙版

计量经济学第一次作业第二章P858.用SPSS软件对10名同学的成绩数据进行录入,分析得r=,这说明学生的课堂练习和期终考试有密切的关系,一般平时练习成绩较高者,期终成绩也高。
9.(1)一元线性回归模型如下:Y i=ß0+ß1X i+u i其中,Yi 表示财政收入,Xi表示国民生产总值,ui为随机扰动项,ß0 ß1为待估参数。
由Eviews软件得散点图如下图:(2)Ýi=+SÊ:t:R2=0.958316 F= df=28斜率ß1=表示国民生产总值每增加1亿元,财政收入增加亿元。
(3)可决系数R2=表示在财政收入Y的总变差中由模型作出的解释部分占%,即有%由国民生产总值来解释,同时说明样本回归模型对样本数据的拟合程度较高。
R2=ESS/(ESS+RSS)ESS=RSS*R2/(1-R2)=+08)*=+08F=(n-2)ESS/RSS,ESS=F*RSS/(n-2)=*E09(4)SÊ(ß0)= SÊ(ß1)=ß1的95%的置信区间是:[ß(28)S Ê(ß1),ß1+(28)S Ê(ß1)] 代入数值得: [即:[,]同理可得,ß0的95%置信区间为[,] (5)①原假设H 0:ß0=0 备择假设:H 1:ß0≠0则ß0的t 值为:t 0=当ɑ=时t ɑ/2(28)=|t 0|=>t ɑ/2(28)= 故拒绝原假设H 0,表明模型应保留截距项。
②原假设H 0:ß1=0 备择假设:H 1:ß1≠0当ɑ=时t ɑ/2(28)= 因为|t 1|=>t ɑ/2(28)=故拒绝原假设H 0表明国民生产总值的变动对国家财政收入有显著影响.计量经济学第二次作业第二章9.(10) 、建立X 与t 的趋势模型,其回归分析结果如下:Dependent Variable: X Method: Least Squares Date: 04/19/10 Time: 22:03 Sample: 1978 2008Included observations: 31Dependent Variable: Y Method: Least Squares Date: 04/10/10 Time: 17:31 Sample: 1978 2007Included observations: 30VariableCoefficien t Std. Error t-StatisticProb.C XR-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid +08 Schwarz criterionLog likelihood F-statistic Durbin-Watson statProb(F-statistic)VariableCoefficien t Std. Error t-StatisticProb.T CR-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid +10 Schwarz criterionLog likelihood F-statistic Durbin-Watson statProb(F-statistic)令t=2008,其预测结果X=再根据X 对Y 进行预测,其预测结果为Y= X 2008= Y 2008=(S Ê(e 0))2—(S Ê(Y0))2=ó2 所以S Ê(e 0)= 在95%的置信度下,Y 2008的预测区间为: [Y 0-t α/2S Ê(e 0),Y 0+t α/2S Ê(e 0)]=[,]第三章P124,6. 该家庭在衣着用品方面的开支(Y )对总开支(X 1)以及衣着用品价格(X 2)的最小二乘估计结果如下:Dependent Variable: Y Method: Least Squares Date: 04/20/10 Time: 09:24 Sample: 1991 2000Included observations: 10VariableCoefficien t Std. Error t-StatisticProb.C X1 X2R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid Schwarz criterion Log likelihoodF-statisticDurbin-Watson stat Prob(F-statistic)12- 3.755455 + 0.183866 + 0.301746 i i i Y X X = :SE (2.679575) (0.028973) (0.167644) :t (-1.401511) (6.346071) (1.799923) :P (0.2038) (0.0004) (0.1149) 20.960616R = 2 0.949364R = :F (85.36888) ():(0.000012)P F :(2.725104)DW 7df =在=5%α的显著性水平下,对解释变量的估计参数1ˆβ、2ˆβ进行检验: 0111:0,:0H H ββ=≠,1{ 6.346071}0.0004<=0.05P t t α>==,1t 落入拒绝域,接受备择假设1H ,1ˆβ不显著为0,即就单独而言,总开支(X 1)对衣着用品方面的开支(Y )影响显著。
第09章 具有结构变化特征的回归模型(第三版)

点后进行分段回归;门限回归以被解释变量的滞后项、解释
变量或者其他变量作为门限,不仅对于区制的划分更为科学, 而且对于不同区制内被解释变量差异化影响因素的解释更为
合理,最重要的是打破了间断点回归模型中仅以时间作为门
限变量的限制;在门限回归模型的基础上,转换回归模型研 究了不同区制之间的转换概率等特征,这对于预测而言是一 种重要的参考。
间断点,这时存在 m+1 个区制( Regime )。我们定义间断点是接下 来出现的状态的第一个时点,并设定T0 = 1,Tm+1 = T。对于第 j 个区
制,观测值为
y T j , y T j 1 , , y T j 1 1
例如,当m=1,即存在1个间断点时,这时存在2个区制,整个 样本分为2部分,假设第1个区制中包含前19个观测值,第2个区制 的观测值从第20个到样本末端,则第20个观测值是间断点,记T1 =20。
(9.1.4)
10
考虑所有可能的存在m个间断点的情形,选择使得 (9.1.4)式最小化的间断点集合和相应的系数估计值。注 意,需要比较的模型随着m和T的增加而快速增加,因此, 需要有效的计算方法进行优化。 Bai and Perron(1998)描述了检验的一般情形,检验 多个区制下 j 是否相等。检验的原假设H0:没有结构变化, 备选假设H1:存在 l 个间断点,采用F统计量检验原假设。 F统计量的一般形式是:
3
在宏观经济分析中,一些经济变量的运行中存在着区制
转换(Regime Switch,RS)问题,在线性模型的基础上,加 入区制变动的非线性特征,将样本划分为不同区制,并引入被 解释变量的滞后项、自相关误差项等构建动态马尔科夫区制转 换模型,可以准确并完整地体现这一特征。
spss-09生物统计回归研究报告

416703. 023 74190. 155
599428. 778 70913. 206
F 9.064
5.685
5.617
8.453
逐步回归方程的方差分析表
Sig. .017a
.034b
.035c
.014d
生物统计
Coefficients a
Unstandardized Coef f icients
生物统计
例9.3 随机抽测10名女中学生的体重(x1)、胸围(x2)、胸围呼吸差(x3)、 肺活量(y),数据如表。试做 y 对诸 xi 的多元线性回归分析。
学生 号
x1
x2
x3
y
1 35 69 0. 7 1600
2 40 74 2. 5 2600
3 40 64 2. 0 2100
4 42 74 3. 0 2650
生物统计
第九章 回归
生物统计
【例9.1】在四川白鹅的生产性能研究中, 得到如下一组关于雏鹅重(g)与70日龄重(g) 的数据,试建立70日龄重(y)与雏鹅重(x)的 直线回归方程。
生物统计
表9-1 四川白鹅雏鹅重与70日龄重测定结果 (单位:g)
生物统计
生物统计
利用SPSS实现直线回归:
SPSS操作步骤: Analyze Regression Linear
新样本数据如上表所示。再作新数据散点图见右上图,已呈现直线关
联, 作直线回归分析得:
Y= 19. 7451 + 7. 7771 X 经检验该直线回归方程有意义。做反变换得曲线回归方程:
y= 19. 7451 + 7. 7771 lnx
贾俊平统计学第十二章 多元线性回归_09

12 - 32
Excel 输出结果的分析
SPSS共线性诊断
• • 自变量间的相关系数矩阵,观察是否存在自变量的相关系数非 常高。一般,相关系数>0.9将会存在共线性问题;相关系数在 0.8以上可能有问题 容忍度(Tolerance):容忍度即以每个自变量作为应变量对其 他自变量进行回归分析时得到的残差比例,大小用1减决定系 数来表示。该指标越小,说明该自变量被其余自变量预测的越 精确,共线性可能就越严重。陈希孺根据经验得出:如果某个 自变量的容忍度小于0.1,则可能存在共线性问题严重 方差膨胀因子(Variance inflation factor,VIF):实际上是容忍 度的倒数,VIF越大,说明共线性问题可能越严重 特征根(Eigenvalue):实际上是对自变量进行主成分分析, 如果相当多维度的特征根约等于0,则可能有较严重的共线性 条件指数(Condition Index):当某些维度的该指标数值大于 30时,可能存在共线性 12 - 33
12 - 35
多重共线性
(例题分析 例题分析) 例题分析
1. tα/2(25-2)=2.0687,所有统计量 α/2(25-2)=2.0687 ,所有统计量t>t 所以均拒绝原假设, 说明这4个自变量两两之间 , 所以均拒绝原假设 , 说明这 个自变量两两之间 都有显著的相关关系 由表Excel输出的结果可知 , 回归模型的线性关系 输出的结果可知, 由表 输出的结果可知 显著(Significance-F= 1.03539E-06<α=0.05)。 而 显著 = α 。 回 归 系 数 检 验 时 却 有 3 个 没 有 通 过 t 检 验 (PValue=0.074935 、 0.862853 、 0.067030>α=0.05) α 。这也暗示了模型中存在多重共线性 固定资产投资额的回归系数为负号(-0.029193) , 固定资产投资额的回归系数为负号 与预期的不一致
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)
v1.0 可编写可改正《统计剖析与SPSS的应用(第五版)》(薛薇)课后练习答案第 9 章 SPSS的线性回归剖析1、利用第 2 章第 9 题的数据,随意选择两门课程成绩作为解说变量和被解说变量,利用SPSS供给的绘制散点图功能进行一元线性回归剖析。
请绘制所有样本以及不一样性别下两门课程成绩的散点图,并在图上绘制三条回归直线,此中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和成效进行评论。
选择 fore 和phy 两门成绩系统散点图步骤:图形旧对话框散点图简单散点图定义将fore导入Y轴,将phy导入X轴,将sex 导入设置标志确立。
v1.0可编写可改正接下来在 SPSS输出查察器中,双击上图,翻开图表编写在图表编写器中,选择“元素” 菜单选择总计拟合线选择线性应用再选择元素菜单点击子组拟合线选择线性应用。
v1.0可编写可改正剖析:如上图所示,经过散点图,被解说变量y( 即:fore) 与解说变量 phy有必定的线性关系。
但回归直线的拟合成效都不是很好。
2、请说明线性回归剖析与有关剖析的关系是如何的有关剖析是回归剖析的基础和前提,回归剖析则是有关剖析的深入和持续。
有关剖析需要依靠回归剖析来表现变量之间数目有关的详细形式,而回归剖析则需要依赖有关剖析来表现变量之间数目变化的有关程度。
只有当变量之间存在高度有关时,进行回归剖析追求其有关的详细形式才存心义。
假如在没有对变量之间能否有关以及有关方向和程度做出正确判断之前,就进行回归剖析,很简单造成“虚假回归”。
与此同时,有关剖析只研究变量之间有关的方向和程度,不可以推测变量之间互相关系的详细形式,也没法从一个变量的变化来推测另一个变量的变化状况,所以,在详细应用过程中,只有把有关剖析和回归剖析联合起来,才能达到研究和剖析的目的。
v1.0可编写可改正线性回归剖析是有关性回归剖析的一种,研究的是一个变量的增添或减少会不会惹起另一个变量的增添或减少。
《贾俊平 统计学 考研真题 含复试 与典型习题详解 第6版 》读书笔记PPT模板思维导图下载

内容简介
第1章 导论
1.2 课后习题详 解
1.1 复习笔记
1.3 典型习题详 解
第2章 数据的搜集
2.2 课后习题详 解
2.1 复习笔记
2.3 典型习题详 解
第3章 数据的图表展示
3.2 课后习题详 解
3.1 复习笔记
3.3 典型习题详 解
第4章 数据的概括性度量
4.2 课后习题详 解
4.1 复习笔记
4.3 典型习题详 解
第5章 概率与概率分布
5.2 课后习题详 解
5.1 复习笔记
5.3 典型习题详 解
第6章 统计量及其抽样分布
6.2 课后习题详 解
6.1 复习笔记
6.3 典型习题详 解
第7章 参数估计
7.2 课后习题详 解
7.1 复习笔记
7.3 典型习题详 解
第8章 假设检验
8.2 课后习题详 解
8.1 复习笔记
8.3 典型习题详 解
第9章 分类数据分析
9.2 课后习题详 解
9.1 复习笔记
9.3 典型习题详 解
第10章 方差分析
10.2 课后习题 详解
10.1 复习笔记
10.3 典型习题 详解
第11章 一元线性回归
11.2 课后习题 详解
11.1 复习笔记
11.3 典型习题 详解
第12章 多元线性回归
12.2 课后习题 详解
12.1 复习笔记
12.3 典型习题 详解
第13章 时间序列分析和预测
13.2 课后习题 详解
13.1 复习笔记
13.3 典型习题 详解
第14章 指数
14.2 课后习题 详解
14.1 复习笔记
09第九章 定量预测法PPT

St
(1)
ˆ xt 1 St 1 (t 1 2,,n),yt 1 St ,3,
(1)
(1)
式中:t (1) ——第t 期的一次平滑值,上标(1)表示一次指数平滑; S ——第t-1期的一次平滑值; (1) St 1 ——第t期的实际值; xt ——第t-1期的预测值; ˆ yt 1 ——平滑系数,取值范围为[0,1]。
表9-23 某企业1—11月份销售量统计表
1 2 3 4 5 6 7 8 9 10 11
2009年月份
销售量(台)
180
160
170
220
250
260
280
300
310
320
350
年份 表9-9 某物业公司2001~2009年的营业额状况(单位:万元) 2001 2002 2003 2004 2005 2006 2007 2008 2009
营业额
80
100
200
280
350
380
450
500
550
解:第一步,利用已有时间序列数据通过 Excel绘制散点图
ˆ 第二步,设直线预测模型为 yt a bt , 确定参数a、b。 第三步,根据直线预测模型,将时间外推 到2010年和2011年,求预测值。
2000 450
2001 500
2002 620
2003 2004 680 750
2005 710
2006 680
2007 640
2008 600
解:第一步:明确预测目标,确定因变量 与自变量。 第二步:进行相关分析,确定相关方向和 相关程度。
Stata实验指导、统计分析与应用chap09

▪ 此命令语句中mfx表示对回归之后的模型计算解释变量的 边际效应,其中options内容如下表所示:
精选课件
9
▪ 本实验中,在进行logit模型回归估计后,在Stata 命令窗口中输入如下命令:
▪ mfx ▪ 此命令计算模型回归之后,解释变量取值在样本
精选课件
14
▪ 本实验中,在以上工作后,在命令窗口中 输入如下命令绘制ROC曲线图
▪ lroc
▪ 因为准确率就是曲线下面的面积,读此图 可以看到ROC曲线是完全在45度直线上面, 所以准确率高于错误率,即准确率大于0.5。 此图曲线下方面积=0.7806,就是预测的准 确率是0.7806。
精选课件
▪ 本实验用此数据来以female和age为解释变量, brand为被解释变量,brand的取值是离散的,且 有三个取值,应建立多值选择模型进行相关分析。
精选课件
27
▪ 二实验操作指导 ▪ 1.选择合理模型 ▪ 在Stata中将数据按照某个或某几个变量进行分类
并按这个变量获得其频数分布的命令如下: ▪ tab varlist ▪ 其中varlist表示按照其分类的变量或者变量组合。 ▪ 在本实验中,打开数据文件并将数据按brand取
▪ 结果显示LR检验的结果是接受原假设,即模型不 存在异方差问题。所以回归不应使用异方差回归 模型,可以直接应用probit模型进行估计。
精选课件
24
实验9-2:多值选择模型
▪ 一 实验基本原理 ▪ 1.多值选择模型 ▪ 有时候人们面临的选择是多个的,比如交通选择,入读大
学的选择等等。假设个体可以选择的y=1,2,3,…,J ,其中J 是正整数。当研究的被解释变量是这样多值离散的,建立 的模型就是多值选择模型,而当J=2时,就是上节所说的 probit或者logit模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SSR 回归均方 MSR 1
(9-10)
误差均方
SSE MSE n2
(9-11)
第九章
一元线性回归
9.4 样本确定系数与样本相关系数
9.4.1 样本确定系数
SSR SSTO SSE SSE r 1 SSTO SSTO SSTO
2
(9-12)
注:Y的总变差中能被X解释的那部分所占的比率
i 1 i 1
n
n
2
2 ( X X ) i i 1 n
所以,b1服从 N ( 1 , n
2
)
i 1
( X i X )2
第九章
一元线性回归
9.5.2 F 检验
在一元线性回归中,为了检验Y对于X线性 关系的统计显著性,对β1进行F检验
1)提出假设:H0:β1=0,H1:β1≠0。
(1) 线性特性 由(9-5)得
b1 i 1
( X i X )(Yi Y )
i 1
n
(Xi
n
i 1
n
( X i X )Yi ( X i X )2
n
X )2
i 1
令
Ci
Xi X
则
(X
i 1
n
i
X )2
b1 Ci Yi
i 1
n
表明b1是Yi 的线性组合
第九章
一元线性回归
9.3 总平方和分解
9.3.1 总平方和分解
ˆ Y ˆ Y Yi Y Yi Y i i
(Y
i 1
n
n
i
ˆ )(Y ˆ Y) 0 Y i i
(Yi Y )
i 1
2
2 ˆ ˆ ( Y Y ) ( Y Y ) i i i 2 i 1 i 1
X Y
i 1 i n i 1
n
i
2
( X i )( Yi ) n ( X i ) 2 n
(9-5)
Xi
b0 Y b1 X
(9-6 )
第九章
一元线性回归
9.2.5 最小二乘估计量b0,b1的特性
线性性 b0,b1的特性 无偏性
第九章
一元线性回归
9.2.5 最小二乘估计量b0,b1的特性
SSR
2) 构造并计算统计量:
F
fR fE
SSE
3)查F分布临界值表,得临界值 F (1, n 2)
F F (1, n 2) 接受H0,认为Y与 4)比较: X不存在一元线性关系。
第九章
一元线性回归
9.5.2 F 检验
若F> F (1, n 2) 拒绝H0,认为Y与X存在一元线性关系。
第九章
一元线性回归
9.5 一元线性回归显著性检验
在回归函数E(Y)=β0+β1X中,如果β1=0,则对于X的一切水 平E(Y)=β0,说明Y的变化与X的变化无关,因而,我们不能 通过X去预测Y。所以,对模型Yi=β0+β1Xi+εi 检验β1=0是 否成立,等价于检验Y与X之间是否存在线性关系。
第九章
±0.8~1
±0.5~0.8 ±0.3~0.5 ±0~0.3
第九章
r的取值情况
一元线性回归
9.4.2 样本相关系数
情况一
图9-6
第九章
一元线性回归
9.4.2 样本相关系数
情况二
图9-7
第九章
一元线性回归
9.4.2 样本相关系数
情况三
图9-8
第九章
一元线性回归
9.4.2 样本相关系数
情况四
图9-9
第九章
一元线性回归
9.2.5 最小二乘估计量b0,b1的特性
b0 k i Yi
同理,可得
i 1
n
1 k i Ci X n
b0 是Yi 线 性组合
第九章
(2) 无偏性
一元线性回归
9.2.5 最小二乘估计量b0,b1的特性
可以证明b0和b1分别是β0 和β1的无偏估计 (过程比较繁琐,参照第五章内容 有兴趣大家自己证明。)
一元线性回归
9.5.1 b1的抽样分布
为了检验β1=0是否成立,需要构造一 个合适的统计量,因此,首先讨论b1 的抽样分布。
第九章
一元线性回归
9.5.1 b1的抽样分布
b1是观测值Yi的线 性组合 b1也服从正态分布 Yi服从正态分布且 相互独立
第九章
一元线性回归
9.5.1 b1的抽样分布
以下可以证明
第九章
一元线性回归
9.1.2 回归分析
回归分析(Regression Analysis)
就是应用统计方法,对大量的观测数据进行整 理、分析和研究,从而得出反映事物内部规律 性的一些结论(数学模型)。
第九章
9.2
一元线性回归
一元线性回归模型
• 9.2.1 统计关系的特征
因变量Y随自变量X有规律的变化,而统 计关系直线描述了这一变化的趋势。 观测点散布在统计关系直线的周围,此 种情况说明Y的变化除了受自变量X 影响以外,还受其他因素的影响。 因此试图建立这样一个回归模型,通过对此模型 所作的一些假设,可以体现出上述统计关系所刻划的特征。
Yi=β0+β1Xi+εi (i=1,2,···,n)
其中,(X i,Yi)表示(X,Y)的第i个观测值,β0 , β1 为参数,β0+β1Xi为反映统计关系直线的分量, ε i为反映在统计关系直线周围散布的随机分量 ε i~N (0,σ2)。
第九章
一元线性回归
9.2.3 一元线性回归模型
对于任意Xi值有:
第九章
一元线性回归
样本的全部观察值都落在 所拟和的回归直线上 SSE=0,
9.4.1 样本确定系数
r2=1
r2的取值范围
0 r2 1
当X与Y无关,Y的变差完 全由于随机因素引起, 此时,SSR=0 r2=0
第九章
一元线性回归
9.4.2 样本相关系数
样本相关系数
r r
2
r
(X
i 1 n i 1
r (n 2)
第九章
一元线性回归
9.5.4 利用样本相关系数进行统计检验
若
4)比较 若
r r
,接受H0
r r
,拒绝H0
第九章
例题
一元线性回归
• 某市欲对货运总量与工业总产值的数量关系进行研究, 以便通过工业总产值预测货运总量。现将2001-2010年 的数据,列入下表:
货运总量(亿吨) 2.8 2.9 3.2 3.2 3.4 3.2 3.3 3.7 3.9 4.2
第九章
一元线性回归
9.2.4 一元线性回归方程
Yi =β0 +β1 Xi +εi β0和β1均未知 根据样本数据 对β0 和β1 进行估计
β0和β1的估计
值为b0和b1
建立一元线性回归方程
ˆ b b X Y 0 1
第九章
一元线性回归
9.2.4 一元线性回归方程
一般而言,所求的b0和b1应能使每个样本观测点(X i,Y i) 与回归直线之间的偏差尽可能小,即使观察值与拟 合值的误差平方和Q达到最小。
若
4)比较
t t / 2 (n 2)
,接受H0
若
t t / 2 (n 2)
,拒绝H0
第九章
一元线性回归
9.5.4 利用样本相关系数进行统计检验
步 骤: 1)提出假设
H0:ρ =0 H1 :ρ 0
ρ是总体Y 与X的线性 相关系数
2)计算简单相关系数r
3)查相关系数临界值表
得临界值
第九章
一元线性回归
9.3.1 总平方和分解
( Yi ) 2
i 1 n
SSTO Yi
2 i 1
n
n
SSR b1 [ X i
2 2 i 1
n( X i ) 2i 1 Nhomakorabean
n
]
SSE=SSTO-SSR
第九章
一元线性回归
9.3.2 自由度的分解
n
SSTO
i 1
(Yi Y ) 0
表9-1 方差分析表
第九章
步 骤: 1)提出假设
一元线性回归
9.5.3 t 检验
H0 : H1 :
b1 t s (b1 )
1 0 1 0
s (b1 ) MSE
2)构造并计算统计量
(X
i
X )2
3)查t分布临界值表
得临界值 t / 2 (n 2)
第九章
一元线性回归
9.5.3 t 检验
nb0 b1 X i Yi
n
n
令偏导数为0
i 1
i 1
解方程
b0 X i b1 X i X i Yi
2 i 1 i 1 i 1
n
n
n
第九章
一元线性回归
(X
i 1 n i 1 n
9.2.4 一元线性回归方程
b1
i
X )(Yi Y )
2 ( X X ) i
第九章
一元线性回归
回归分析适合研究哪类问题? 回归方程的显著性检验适合什么情况? 回归系数的显著性检验适合什么情况?
第九章
一元线性回归
9.1 回归分析的基本概念
• 9.1.1 因变量(Y)与自变量(X)之间的关系 根据因变量与自变量之间的关系不同,可以分为两种类型: 函数关系
