光与原子相互作用
原子与光子相互作用——基本过程和应用

原子与光子相互作用——基本过程和应用以原子与光子相互作用——基本过程和应用为题,本文将介绍原子与光子相互作用的基本过程以及在科学研究和技术应用中的重要性。
原子与光子相互作用是指原子与光子之间发生能量交换的过程。
光子是光的基本单位,也是电磁辐射的量子。
原子是物质的基本单位,由原子核和绕核运动的电子组成。
原子与光子的相互作用是量子力学的重要研究内容之一,对于解释光的各种现象和开发相关技术具有重要意义。
原子与光子的相互作用可以通过吸收、发射和散射等过程来实现。
吸收是指原子吸收光子的能量,使得原子的能级发生变化。
发射是指原子从一个能级跃迁到另一个能级,释放出一个光子。
散射是指光子与原子碰撞后改变方向并传递能量。
在吸收过程中,原子吸收光子的能量,使得电子从低能级跃迁到高能级。
这个过程符合能量守恒定律,光子的能量等于电子跃迁前后的能级差。
吸收光谱是研究原子和分子结构的重要手段之一,通过测量吸收光谱可以获得物质的能级结构和能级间的跃迁规律。
在发射过程中,原子从高能级跃迁到低能级,释放出一个光子。
发射光谱是研究物质发光性质的重要手段之一,通过测量发射光谱可以得到物质的能级结构和能级间的跃迁规律。
散射是光子与原子碰撞后改变方向并传递能量的过程。
根据散射的性质可以分为弹性散射和非弹性散射。
弹性散射是指光子与原子碰撞后仅改变方向而能量不发生变化。
非弹性散射是指光子与原子碰撞后除了改变方向外,还发生能量转移。
散射光谱是研究物质的结构和动力学过程的重要手段之一,通过测量散射光谱可以得到物质的结构信息和粒子运动的规律。
原子与光子相互作用在科学研究和技术应用中具有广泛的应用价值。
在科学研究方面,原子与光子相互作用是研究光谱学、量子力学和原子物理等领域的基础。
通过研究原子与光子的相互作用,可以深入了解物质的结构和性质,推动科学的发展。
在技术应用方面,原子与光子相互作用在光通信、光电子器件、激光技术、光谱分析等领域发挥着重要作用。
光子操控原子运动

光子操控原子运动光子操控原子运动是一项研究光与原子相互作用的前沿科学技术,在量子信息处理、量子计算与量子模拟等领域具有巨大的应用潜力。
本文将探讨光子操控原子运动的原理、技术和应用。
一、光子操控原子运动的原理光子操控原子运动的原理是基于光与原子的相互作用。
光子具有粒子性和波动性,而原子又是微观粒子,其运动状态由它的动量和位置确定。
通过调节光的频率、强度和相位等参数,可以改变光子对原子的力学作用,进而操控原子的运动状态。
在光子操控原子运动的研究中,最常用的方法是利用光子的动量传递。
当一个原子受到光子的照射时,光子会将动量转移给原子,使其产生运动。
这种光子动量传递的机制可以用来实现原子的操控、运动的置换和陷阱效应等。
二、光子操控原子运动的技术实现1. 光强调制技术:通过改变激光的强度分布,可以产生光强梯度,从而对原子的运动状态施加力。
例如,利用高斯光束在径向和轴向上的梯度场分布,可以形成一个光阱,将原子限制在特定的空间区域内。
2. 相位控制技术:调节激光的相位可以改变光的传播方向和散射角度,从而对原子运动的轨迹进行精确控制。
例如,利用光晶格技术,可以产生一个周期性的势场,将原子束分离成不同路径,实现原子的定向和分波导。
3. 实时反馈控制技术:通过精确测量原子的运动状态,并及时给出控制反馈信号,可以实现对原子运动的实时调控。
这种技术可以用于制备特定的原子量子态、调节原子自旋的耦合以及实现量子信息处理等应用。
三、光子操控原子运动的应用1. 量子计算与通信:光子操控原子运动的技术可以用于实现量子比特的操作和量子门的构建,进而实现量子计算和量子通信。
通过光子与原子之间的交互,可以实现远程量子纠缠、量子隐形传态和量子密码学等任务。
2. 量子模拟与精密测量:光子操控原子运动的技术可以用于模拟量子系统的行为,研究原子、分子和固体材料的基本性质。
此外,通过对光子与原子相互作用的精确测量,可以实现精密测量、时钟校准和引力探测等应用。
光与原子相互作用

上式与前式相比较,得 上式与前式相比较,
8πh ν 3 A21 ⋅ hν = , hν ν ν 3 c k T kT e −1 B12e − B21
要使上式两端对任何h 之值都成立 相应系数必须相等. 要使上式两端对任何 ν/kT之值都成立 相应系数必须相等 之值都成立,相应系数必须相等
即
B12 = B21,
8πhν 3 8πhν 3 A21 = B = B21. 12 3 3 c c
上面两关系式叫做爱因斯坦关系式 虽然是在热平 上面两关系式叫做爱因斯坦关系式,虽然是在热平 爱因斯坦关系式 衡条件下推出的,但它对普遍情况仍是适用的 但它对普遍情况仍是适用的. 衡条件下推出的 但它对普遍情况仍是适用的 是单位时间粒子由E 能级上的几率, B12 是单位时间粒子由 1能级跃迁到 E2能级上的几率 是单位时间粒子由E 能级跃迁到E 能级上的几率. B21 是单位时间粒子由 2能级跃迁到 1能级上的几率
原子的能级寿命与原子的结构有关,一般激发态能级寿命 原子的能级寿命与原子的结构有关 , 一般激发态能级寿命 寿命达10 秒的能级状态 称亚稳态. 秒的能级状态,称亚稳态 τ~10-8s,寿命达 -3~1秒的能级状态 称亚稳态 寿命达
实际上由于碰撞或其他外界干扰,原子能级的寿命要比自然 实际上由于碰撞或其他外界干扰 原子能级的寿命要比自然 寿命(10 小几个数量级 小几个数量级. 寿命 -8s)小几个数量级
dN 21 ( ) 受激辐射 = B21 ρ (ν ) N 2 , dt
dN12 ( )受激吸收 = B12 ρ (ν ) N1. dt
称为爱因斯坦系数. A21 , B21 , B12 称为爱因斯坦系数
在热平衡状态下, 两能级之间,单位时间受激吸收的光子 在热平衡状态下 两能级之间 单位时间受激吸收的光子 数应等于受激发射和自发发射的光子数.因此 数应等于受激发射和自发发射的光子数 因此
激光与原子相互作用的研究

激光与原子相互作用的研究在物理学领域里一直是一个备受关注的领域。
激光是一种高度相干的光束,它的波长短,光强高,使用它可以在原子尺度上对精细细节进行探索。
早在上世纪70年代,科学家们就开始对进行实验。
这项研究目前已经成为了现代物理学中最重要的研究领域之一。
起源于研究激光与分子相互作用的实验。
在这项实验中,科学家们使分子通过一个激光束,并观察它们在光束中运动的方式。
结果显示,分子在光束中表现出了原本不会表现的非常规运动方式。
这项实验开创了激光与原子相互作用的新方向。
后来科学家们又发现,激光与原子相互作用可用于制造高质量的光学设备,提高光学设备的精度和效率。
实验中广泛使用的激光类型是光电子激光,这种激光有着极高的能量和波长,可以在原子尺度上探测精细的细节。
激光与原子相互作用可使原子发生一系列的改变,例如电离、激发和碰撞等。
科学家通过观察这些变化,可以研究原子的基本性质和结构,并且利用这些基本信息来设计制造新的材料和设备。
除了在原子和分子的基础物理方面有很多应用,同时还能够为行星科学、生物物理学和化学领域提供许多应用。
例如,科学家们利用激光束的高分辨率来研究分子的反应动力学,发现了许多新的反应方式;同时,还可以应用激光光谱技术来研究地球大气层和行星大气层中的化学反应,并且还可以应用激光技术来监测和处理人类组织中的肿瘤。
在过去的几十年中,一直在不断的发展。
除了使用传统的实验方法外,科学家们还利用超高速激光脉冲来研究分子中的电子和原子之间的相互作用。
此外,还有更高级的研究方法,例如量子力学、量子计算和原子陷阱等,这些方法为提供了更加复杂的体系。
总体来说,已经成为现代物理学、化学和生物学领域中最重要的研究领域之一。
不仅可以为我们提供高分辨率、高效率的分子成像技术,而且还可以为我们开发出新型的药物、光学材料和新型高分辨率光学设备等。
虽然这项研究需要运用复杂的实验技术和科学理论,但它却为我们提供了一个探究自然界基本规律的契机。
光子与原子相互作用
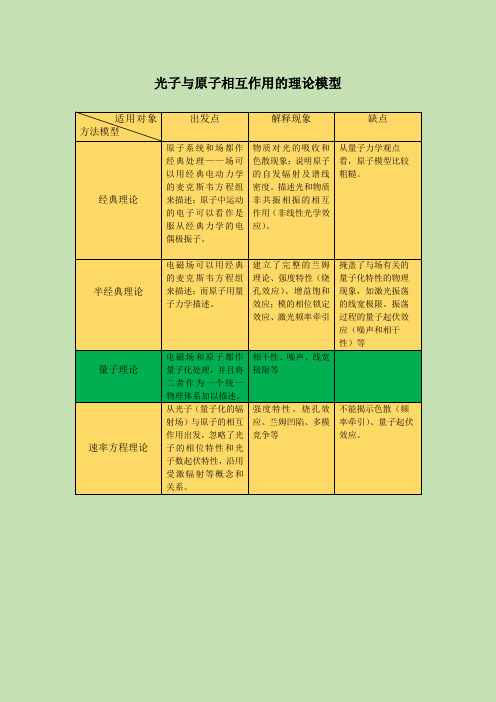
光子与原子相互作用的理论模型适用对象
方法模型
出发点解释现象缺点
经典理论原子系统和场都作
经典处理——场可
以用经典电动力学
的麦克斯韦方程组
来描述;原子中运动
的电子可以看作是
服从经典力学的电
偶极振子。
物质对光的吸收和
色散现象;说明原子
的自发辐射及谱线
密度。
描述光和物质
非共振相振的相互
作用(非线性光学效
应)。
从量子力学观点看,
原子模型比较粗糙。
半经典理论电磁场可以用经典
的麦克斯韦方程组
来描述;而原子用量
子力学描述。
建立了完整的兰姆
理论、强度特性(烧
孔效应)、增益饱和
效应;模的相位锁定
效应、激光频率牵引
掩盖了与场有关的
量子化特性的物理
现象,如激光振荡的
线宽极限。
振荡过程
的量子起伏效应(噪
声和相干性)等
量子理论电磁场和原子都作
量子化处理,并且将
二者作为一个统一
物理体系加以描述。
相干性、噪声、线宽
极限等
速率方程理论从光子(量子化的辐
射场)与原子的相互
作用出发,忽略了光
子的相位特性和光
子数起伏特性,沿用
受激辐射等概念和
关系。
强度特性、烧孔效
应、兰姆凹陷、多模
竞争等
不能揭示色散(频率
牵引)、量子起伏效
应。
研究激光与原子的相互作用

研究激光与原子的相互作用激光与原子的相互作用是当代光学研究领域的重要课题。
激光具有高激光能量和高相干性的特点,而原子则是微观世界中最基本的构成单位之一。
研究激光与原子的相互作用不仅有助于深入了解光与物质的相互作用机制,还为光学技术的发展提供了新的思路和方法。
在激光与原子的相互作用中,最常见的现象是光子与原子之间的相互相互作用。
当激光照射到原子上时,光子会与原子的电子发生相互作用,从而引起原子能级的变化。
这种相互作用通常可以通过光谱学技术进行观测和研究。
通过研究光谱线的强度、频率和形状等参数的变化,可以得到原子内部结构和原子能级的信息,从而揭示原子与激光之间的相互作用机制。
激光与原子的相互作用不仅存在于光谱学中,还广泛应用于光谱分析、激光离子化、激光冷却等研究领域。
例如,在激光谱学中,研究激光与原子的相互作用可以用来确定物质的组成和结构,为化学分析提供重要的手段。
在激光离子化研究中,激光与原子的相互作用可以使原子离子化,从而产生带电的离子,为原子和分子的研究提供了新的途径。
而在激光冷却领域,激光与原子的相互作用可以通过反馈机制使原子的动能减小,从而实现原子的冷却和捕获,为制备玻色-爱因斯坦凝聚等低温物理现象提供了重要的手段。
除了光子与原子的相互作用之外,激光与原子之间还存在一种更为微弱且复杂的相互作用,即光子与原子核之间的相互作用。
光子与原子核的相互作用是量子电动力学的一个重要研究课题,对理解原子核的结构和性质具有重要意义。
通过研究激光与原子核的相互作用,可以揭示原子核内部的奇特结构和核力的本质。
此外,光子和原子核的相互作用也是激光核物理研究的重要内容,可以通过激光诱导的核反应来实现对核物质的精确操控和研究。
总之,研究激光与原子的相互作用是光学领域中的重要课题,对深入了解光与物质的相互作用机制具有重要意义。
通过研究光子与原子之间的相互作用,可以揭示原子的内部结构和能级的变化规律,为光谱学和化学分析提供了重要的手段。
原子结构知识:原子和分子光吸收和发射

原子结构知识:原子和分子光吸收和发射原子和分子光吸收和发射光是电磁波,可以表达为波动或粒子,它与物质的相互作用是光学研究的重要课题之一。
在光与物质相互作用中,发生了两个最基本的过程:吸收和发射。
吸收是指原子或分子从光中得到能量,发射则是原子或分子向外辐射能量。
本文将着重介绍原子结构怎样影响光吸收和发射的过程。
原子结构原子是构成物质的基本单位,它包含了原子核和电子云。
原子核是由质子和中子组成的,中心核电荷Z决定了原子的化学性质。
电子云是由电子构成的,处于高能级的电子能吸收光的能量,跃迁到更高的能级,处于低能级的电子则能把能量发射出来,跃迁到更低的能级。
光与原子的交互作用可分为三种类型:弹性散射、非弹性散射和吸收。
其中弹性散射是光与原子的相互作用中最简单的一种,比如太阳光散射。
但是,非弹性散射和吸收过程中均会引起电子能级的改变,从而导致能量的释放或吸收,这两种过程的重点是电子的跃迁。
光吸收当处于低能级的电子吸收光能量时,它跃迁到高能级,形成了一个激发态。
激发态是一种相对不稳定的状态,因为电子更倾向于处于低能级,因此激发态电子会在短时间内返回到基态,同时放出与吸收光子的能量相等的光子,即发生光释放。
光吸收和发射是由电子跃迁引起的,跃迁中电子的能量变化被表示为△E=hυ,其中h为普朗克常数,υ为光的频率。
原子中电子从低能量级跃迁到高能量级时,需要吸收光子能量,即光能必须等于跃迁能量才能被吸收;电子从高能量级跃迁到低能量级时,释放出等于跃迁能量hυ的光能。
因此,同一物质对不同波长的光的吸收和发射能力是不同的,这就是光谱现象。
吸收光谱是物质对不同波长光的吸收强度与波长的关系图,发射光谱是物质在受激条件下产生光的强度随波长的变化关系图。
由于每个物质的原子结构都是独特的,因此它们的吸收光谱和发射光谱也是独特的,是物质特性的重要指标。
分子光吸收和发射相较于原子,分子的能级比较复杂,包括振动能级和转动能级。
因此,分子对光的吸收和发射表现出与原子不同的特性。
光与原子相互作用

光与原子相互作用首先,当一个原子与光相互作用时,光的能量可以被吸收或辐射出来。
当一个光子与一个处于低能级的原子相互作用时,如果光子的能量与原子的能级差相匹配,原子可以吸收光子的能量,并跃迁到一个高能级。
这个跃迁的能级差决定了吸收光的波长,并且符合玻尔的频率条件。
相反地,当一个处于高能级的原子与一个光子相互作用时,如果光子的能量足以覆盖两个能级之间的能级差,原子可以从高能级跃迁到低能级,并通过辐射出来的光子来释放能量。
这种辐射过程被称为自发辐射。
其次,原子吸收和辐射光子的过程可以通过诸如共振和非共振的机制来实现。
共振是指光子与原子的能级结构之间有一个准确的匹配,使吸收和辐射过程能够以最大概率发生。
这样的共振通常是由光的频率与原子跃迁之间的共振频率相匹配来实现的。
非共振则是指光的频率要远离原子的共振频率,吸收和辐射的几率相对较小。
非共振通常发生在原子能级差异较大或光子频率较低的情况下。
光和原子的相互作用还涉及其他一些重要的过程,例如受激辐射和受激吸收。
受激辐射是指当一个原子在一个激发态被一个光子激发后,它可以通过释放一个与入射光子完全相同频率和相位的光子来回到基态。
这可以在光子的刺激下发生,因此称为受激辐射。
类似地,受激吸收是指当一个原子处于一个能级上的粒子受到入射光子的作用后,它可以从该能级跃迁到一个高能级,这取决于入射光子的能量和原子的能级结构。
除了单个原子与光子的相互作用外,多个原子的团簇也可以与光子相互作用。
这种团簇中的原子通常相互紧密地排列在一起,形成了一种特殊的结构。
团簇与光子相互作用时,团簇的结构和性质可能会发生显著变化。
例如,当光与金属团簇相互作用时,金属团簇的电子可以在光子作用下发生共振激发,产生类似于固体材料的能带结构。
这种光与团簇的相互作用在催化剂和纳米器件等领域中具有重要的应用潜力。
总之,光与原子的相互作用是一个复杂而多样的过程,涉及到能级结构、波长匹配、共振、受激辐射、受激吸收等多个方面。
光的相互作用与原子物质的激发态

光的相互作用与原子物质的激发态光是一种电磁波,它在与物质相互作用的过程中,能够引起原子和分子的电子跃迁,从而激发物质的激发态。
光的相互作用与原子物质的激发态之间存在着密切的联系和相互影响。
在本文中,我们将探讨光的相互作用与原子物质的激发态的相关性,并介绍一些光与物质相互作用的实际应用。
光与原子物质的相互作用是通过光的电磁场与原子的电子云之间的相互作用来实现的。
当光通过物质时,光的电磁场会与物质中的电子云发生相互作用,使电子云发生振动。
这种振动会导致电子从一个能级跃迁到另一个能级,从而激发物质的激发态。
原子的激发态可以分为离散能级和连续能带两种。
离散能级是指原子在特定能量下的能级,而连续能带则是指原子在一定范围内的能量。
光的相互作用可以使原子从一个离散能级跃迁到另一个离散能级,也可以使原子在连续能带中发生跃迁。
光的相互作用与原子物质的激发态在许多领域都有着广泛的应用。
其中一个重要的应用是激光技术。
激光是一种高度聚焦的、具有高能量密度的光束,它可以通过光与物质的相互作用来实现对物质的激发。
激光在医学、材料加工、通信等领域都有着重要的应用。
另一个重要的应用是光谱学。
光谱学是研究物质与光的相互作用的学科,它可以通过测量物质对不同波长的光的吸收、散射或发射来研究物质的性质。
通过光谱学的研究,我们可以了解物质的结构、组成和性质,对于化学、物理等科学领域的研究起着重要的作用。
此外,光的相互作用还可以用于光学传感器的制造。
光学传感器是一种利用光与物质相互作用的原理来检测和测量环境中的物理量或化学物质的设备。
通过光的相互作用,光学传感器可以实现对温度、压力、湿度、气体浓度等参数的测量。
光学传感器在环境监测、医学诊断、工业生产等领域都有着广泛的应用。
总之,光的相互作用与原子物质的激发态之间存在着紧密的联系和相互影响。
光的相互作用可以引起原子和分子的电子跃迁,从而激发物质的激发态。
这种相互作用在激光技术、光谱学和光学传感器等领域都有着重要的应用。
光波与原子相互作用

光波与二能级原子的相互作用 ——半径典理论一般情况下只考虑原子的二能级体系与光波的相互作用,光波与原子体系的哈密顿量,E r e H H ˆˆˆ0−=,这里使用了偶极子近似和偶极子尺寸远小于光波波长的条件。
而没有受光波作用时,原子体系的哈密顿量0ˆˆH H =,本征能量和函数为2121ϕϕ、、、E E ,满足能量本征方程和薛定谔方程,)()(ˆ0x E x H jj j ϕϕ=,2,1=j (4-20) ⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡∂∂−−t E i j tE i j jj e x H e x t h h )(ˆ)(0ϕϕ,2,1=j (4-21) 在没有光波作用时,原子的波函数可以表示为 t E it E iex c ex c t x hh21)()(),(2211−−+=ϕϕψ (4-22)这种情况下,c 1、c 2是与时间无关的常数,也就是说此时原子处于稳定的状态,及处于两个本征态的几率是稳定的。
当光波与原子作用时,原子的状态将随时间变化,那么处于某个本征态的几率也随时间变化,c 1、c 2将是时间的函数,而由于量子力学假设所用的微观系统都按薛定谔方程演化,所以原子的态函数, ),()ˆˆ(),(0t x E r e H t x ti ψψ−=∂∂h(4-23) 那么利用(4-20)和(4-21),从(4-23)得到,⎥⎦⎤⎢⎣⎡+−=⎥⎦⎤⎢⎣⎡+∂∂−−−−t Ei t E i t E i t Ei e x t c e x t c E r e H e x t c e x t c t i h h hh h 2121)()()()()ˆˆ()()()()(221102211ϕϕϕϕ⎥⎦⎤⎢⎣⎡+−⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡++∂∂+∂∂−−−−−−−−t E i t Ei t E i t E i t Ei t E i t E i t E i ex t c e x t c E r e ex t c e x t c H e x t c E e x t c E e x t c t i ex t c t i hhhhh hh h h h 21212121)()()()(ˆ)()()()(ˆ)()()()()()()()(2211221102221112211ϕϕϕϕϕϕϕϕν = (E 212⎥⎦⎤⎢⎣⎡+−=∂∂+∂∂−−−−t Ei t E i Ei t E i e x t c e x t c E r e e x t c ti ex t c t i h h h hh h 2121)()()()(ˆ)()()()(22112211ϕϕϕϕ (4-24) 分别将t E iex h1)(*1ϕ、t E iex h2)(*2ϕ乘上(4-24)并积分,利用本征函数的正交性和光波,ij j i dx δϕϕ=∫* (4-25))(21)cos(2100t i t i e e E t E E ωωω+==− (4-26)得到,⎪⎩⎪⎨⎧+=∂∂+=∂∂∆∆−22221121221111)()()()()()(V t c e V t c t c ti eV t c V t c t c t i ti ti ωωh h (4-26)这里h12E E −=∆ω,ij t i t i j i t i t i ij V e e dx re e eE V ~)(ˆ)(21*0ωωωωϕϕ+=+−=−−∫,dx reE V j i ij ϕϕ∫−=ˆ21~*0,*2112~~~V V V == 由本征函数的奇偶对称性,得到 0~~22112211====V V V V , 那么(4-26)式得到,⎪⎩⎪⎨⎧+=+=∂∂+=+=∂∂∆+∆−−−∆∆−∆+−−∆−][~)()(~)()(][~)()(~)()()()(2112112)()(1221221ti t i t i t i t i ti t i t i t i t i e e V t c e e e V t c t c ti e e V t c e e e V t c t c ti ωωωωωωωωωωωωωωh h (4-27) 另外,这里考虑旋转波近似,忽略高频变化项ti e)(ωω∆+、ti e)(ωω∆+−,那么(4-27)式变为⎪⎩⎪⎨⎧=+=∂∂=+=∂∂∆−−−∆∆−−∆−t i ti t i t i t i ti t i t i e V t c e e e V t c t c ti e V t c e e e V t c t c t i )(*1212112)(1221221~)()(~)()(~)()(~)()(ωωωωωωωωωωh h (4-28) 由(4-28)得到,⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡Ω−Ω−=⎥⎦⎤⎢⎣⎡∆−−∆−21)(*12)(122100c c e i e i c c dt d ti t i ωωωω (4-29)∫∫−==Ωdx r eE V 1*201212ˆ21~ϕϕh h,记为 C M C dtd= (4-30) 作旋转变换,⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡∆−−∆−212)(2)(2100a ae e c c t i t i ωωωω (4-31) 记为 A R C = (4-32) (4-32)代入(4-30)得到,A R dt d R R M R A dt d ⎥⎦⎤⎢⎣⎡−=−−11 (4-33) 矩阵 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆−−Ω−Ω−∆−=⎥⎦⎤⎢⎣⎡−−−2)(2)(*121211ωωωωi i i i R dt d RR M R (4-34)那么方程(4-34)的通解为222212)(214)(ωωωωλ∆−+Ω±=∆−+Ω±=±ii i (4-35)所对应的本征矢量为,⎥⎦⎤⎢⎣⎡Ω+Ω=±2/)(2/22δδm A , (4-36) 这里∫∫−=Ω=Ωdx r eE 1*2012ˆ2ϕϕh,ωωδ∆−=,方程 (4-33) 的通解为,⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡Ω++Ω+−ΩΩ=Ω+−Ω+Ω+−Ω+212/222/222/2/222222222/)(2/)(2/2/)(a a e e e e t A t i t i t i t i δδδδδδδδ (4-37) 如果知道t=0时原子的状态,即知道⎥⎦⎤⎢⎣⎡==)0()0()0(21c c t C (4-38) 利用(4-32)和(4-37),我们可以得到(4-37)的两个未知系数,并得到)(t C 的通解和演化矩阵, ⎥⎦⎤⎢⎣⎡=)0()0()()(21c c t T t C (4-39) ()()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛Ω+Ω+−Ω+Ω+Ω+Ω−Ω+Ω+Ω−⎟⎟⎠⎞⎜⎜⎝⎛Ω+Ω++Ω+=−−22222122212/2221222/2221222/22222122212/]sin[]cos[]sin[]sin[]sin[]cos[)(δδδδδδδδδδδδδδδδt i t e t i e t i e t i t e t T tt i tt i tt i tt i当光波与两能级共振时,0=δ,那么此时演化矩阵变为,⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)0()0())()(2121c c t T t c t c⎥⎦⎤⎢⎣⎡ΩΩ−Ω−Ω=]cos[]sin[]sin[]cos[)(112121t t i t i t t T 即得到,⎩⎨⎧Ω+Ω−=Ω−Ω=]cos[)0(]sin[)0()(]sin[)0(]cos[)0()(21221122122111t c t ic t c t ic t c t c (4-39) 那么处于能级E 1和E 2的几率分别为,⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡−ΩΩ+Ω+Ω=⎥⎥⎦⎤⎢⎢⎣⎡−ΩΩ+Ω+Ω=)]0()0()0()0(][cos[]sin[][sin )0(][cos )0()()]0()0()0()0(][cos[]sin[][sin )0(][cos )0()(*21*122121212212122222*12*212121212222122121c c c c t t i t c t c t c c c c c t t i t c t c t c (4-40) 如果原子一开始处于低能级E 1,即0)0(,1)0(21==c c ,那么上式(4-40)变为⎪⎩⎪⎨⎧Ω=Ω=][sin )(][cos )(2122221221t t c t t c (4-41) Ω称为拉比(Rabi )频率,它表示光波与原子作用的强度,它正比于偶极子和光场强度。
原子与光子相互作用——基本过程和应用

原子与光子相互作用——基本过程和应用
原子和光子是微观粒子世界中最基本的单位,它们之间的相互作用是物理学研究的重
要内容之一。
原子与光子相互作用的基本过程包括:吸收、散射、自发辐射和受激辐射等。
这些过程在物理、化学、生物学、信息科学等领域都有着广泛的应用。
吸收是指原子吸收光子能量,跃迁到一个高能级状态。
当原子处于高能级状态时,它
会发生辐射或与其他原子或分子发生碰撞并失去能量,重新回到低能级状态。
吸收现象是
光电子学中的基础,在能量传输、光谱学等领域都有着广泛的应用。
例如,太阳能电池和
半导体激光都是基于光子吸收的机理。
散射是指光子与原子之间的相互作用,将光子散发到不同的方向。
这种现象在医疗成像、光学通讯等领域有着广泛应用。
例如,计算机断层扫描(CT)和磁共振成像(MRI)都是利用散射现象来定位病变部位。
自发辐射是指原子在激发态自发地发射辐射,回到基态。
这种现象在激光、荧光灯等
领域有着广泛应用。
例如,在激光系统中,粒子在激发态通过受激辐射和自发辐射的相互
作用,发生多次辐射和受激辐射,最终放出高强度的单色光。
受激辐射是指原子在受到外部能量的激发后,受到一个外部光子的刺激而发射出同相
干的辐射,此时发射的光子具有与刺激光子相同的频率、方向和极化状态。
受激辐射有着
广泛的应用,如激光器、单光子发生器等工业、科研等领域。
总之,原子与光子相互作用的基本过程是物理学中的基础和关键。
它们在社会和经济
发展,特别是在光电子学、信息科学等领域的应用中发挥着重要作用。
光子与原子相互作用的基本原理和现象解析

光子与原子相互作用的基本原理和现象解析光子与原子相互作用是量子力学中一个重要的研究领域,也是光谱学和量子计算等领域的基础。
本文将解析光子与原子相互作用的基本原理和现象,以帮助读者更好地理解这一领域。
光子是光的基本组成单位,它是量子力学中描述光波粒性的概念。
光子具有能量和动量,并遵循能量守恒和动量守恒的定律。
与光子相互作用的原子系统可以分为两个主要的情况:一是自由原子,二是束缚原子。
自由原子指的是原子处于无外界场的自由状态,束缚原子指的是原子受到某种外界场的束缚状态,比如原子在晶格中。
当光子与自由原子相互作用时,可以发生光电效应、康普顿散射和光背散射等现象。
其中最典型的是光电效应,即光子的能量高于一定能量阈值时,光子会被吸收,电子被激发并跃迁到连续能量态。
这种现象在实际应用中被广泛利用,例如用于光电转换装置。
康普顿散射是指当光子与自由电子碰撞时,光子的能量和动量会被散射,同时电子也发生散射。
光背散射是指当光子与自由原子或分子作用时,光子的能量和动量会被激发并发生散射。
对于束缚原子,光子与原子的相互作用可以导致原子的激发、退激发和光吸收等现象。
这种相互作用可以用来研究物质的结构和性质,例如原子光谱学中的拉曼光谱和拉曼散射等。
当光子与束缚原子相互作用时,光子的能量与原子的能级差相匹配时,光子会被吸收,从而激发原子跃迁到更高的能级。
当光子的能量与原子的能级差不匹配时,光子被散射,原子退激发到低能级。
另外,光子与原子相互作用还可以导致光的干涉、衍射和散射等现象。
光的干涉和衍射是光和原子之间相互作用的结果,通过它们可以研究光的波动性和原子的结构。
例如Young实验中的双缝干涉实验证明了光的波动性,而原子的Beugung 实验则证实了原子的波动性。
光的散射是指入射光在与原子碰撞后发生方向变化和能量损失的现象,其中最著名的是拉曼散射。
拉曼散射是指光子与原子或分子之间发生能量、动量和频率的交互转移,从而导致散射光的频移和强度变化。
光与二能级原子的相互作用

光与二能级原子的相互作用二能级原子与光场的相互作用是最基本的模型,如图1为二能级原子与光场的相互作用。
图1二能级原子与光场的相互作用如图1所示,频率为v 的单模光场与二能级原子系统相互作用。
不考虑外界因素的影响,分析光场与原子相互作用。
其中,m 表示激发态,n 表示基态,原子在上下能态之间作简谐振荡,其中拉比频率为Ω,原子跃迁频率为ω,探测光的失谐量为v -=∆ω,激发态到基态的自发辐射衰减率为Γ,相干衰减率为()2/n m γγγ+=,二能级的电偶极矩矩阵元为n r m e mn =℘。
该系统的总哈密顿量由自由哈密顿0H 和光与原子相互作用的哈密顿1H 。
系统的总哈密顿量为10H H H +=。
nn m m H n m ωω +=0(3.1.2)m n e n m e H ivt ivt *122Ω-Ω-=- (3.1.3)根据考虑耗散作用的密度矩阵方程:[]{}ρρρ,21,Γ--=H i ()()∑∑Γ-Γ---=k kj kj kj ik k kj kj kj ik ij H H i ρρρρρ21 (3.1.4)利用可以得到:()()mm nn ivt mn mn mn nm ivt mn ivt nn nn mn ivt nm ivt mm mm e i i e i e i e i e i ρρργωρρρρρρρρρ-Ω++=Ω-Ω+Γ=Ω-Ω+Γ-=---22222**1 (3.1.5)做慢变振幅近似有:ivt mnmn e -=ρρ~,mm mm ρρ~=,nn nn ρρ~=()()mm nn mn mn nm mn nn nn mn nm mm mm i i i i i i ρρργρρρρρρρρρ~~2~~~2~2~~~2~2~~**1-Ω+-∆=Ω-Ω+Γ=Ω-Ω+Γ-= (3.1.6)由系统封闭条件:1~~=+nnmm ρρ令方程左边倒数部分为零,求解可得:()()()()()()[]222222222222222/2/~/2/~/2/~∆+Ω+Γ∆-ΓΩ=∆+Ω+Γ∆+Ω+Γ=∆+Ω+Γ∆+Ω=γγγργγγγργγγγρi i mn nn mm (3.1.7)由极化强度关系:[]..~..210c c e c c e E P ivt mn nm ivt +℘=+=--ρχε(3.1.8)Ω℘=''+'= 02~2ερχχχmnmn N i (3.1.9)由此得到探测光极化率的实部χ'和虚部χ'',它们分别表示色散和吸收()()()()mm nn mn mm nn mn N N ρργεγχρργεχ~~~~22022202-∆+℘=''-∆+∆℘=' (3.1.10)其中,令0~,1~==mm nn ρρ,原子数密度为N ,真空介电常数为0ε,绘制出探测光的吸收和色散随其失谐量变化的曲线,如图2所示。
双模光场与三能级原子的相互作用哈密顿量

双模光场与三能级原子的相互作用哈密顿量概述1. 光场与原子的相互作用是量子光学和原子物理中的重要研究领域。
双模光场是一种特殊的光场,其光子分布可以描述为两个不同的模式之间的转换。
而三能级原子是一种具有三个能级的原子系统,其能级结构的复杂性使得与光场的相互作用具有一定的特殊性。
本文将着重讨论双模光场与三能级原子的相互作用哈密顿量的推导和性质分析。
双模光场的描述2. 根据量子光学理论,双模光场可以由两个模式下的产生和湮灭算符$a_1, a_2, a_1^{\dagger}, a_2^{\dagger}$来描述。
在相干态的定义下,双模光场的描述可以通过其密度矩阵$\hat{\rho}$和期望值$\langle \hat{A} \rangle$来进行。
3. 双模光场与三能级原子的相互作用可以通过相互作用哈密顿量进行描述,该哈密顿量可以表示为$H_{int} = -\vec{d} \cdot \vec{E}$,其中$\vec{d}$为偶极子算符,$\vec{E}$为电场。
在考虑双模光场的情况下,我们可以将相互作用哈密顿量表示为$H_{int} = \sum_{i=1,2} g_i (a_i e^{-i\omega_i t} + a_i^{\dagger} e^{i\omega_i t})\vec{d}\cdot \vec{E}_i$,其中$g_i$为相互作用强度,$\omega_i$为频率,$\vec{E}_i$为电场。
三能级原子的描述4. 三能级原子由三个能级组成,分别为基态$|1\rangle$,第一激发态$|2\rangle$和上带态$|3\rangle$。
在外场作用下,原子之间可以发生跃迁,这些跃迁可以由跃迁矩阵元$V_{ij}$来描述。
在光学腔中,原子的跃迁可以受到光场的影响,从而导致原子的能级结构发生变化。
相互作用哈密顿量的推导5. 要描述双模光场与三能级原子的相互作用,我们需要推导相互作用哈密顿量。
波尔频率条件

波尔频率条件
波尔频率条件是指在光子与原子相互作用时,光子的频率必须与原子的能级差相等。
这个条件是由丹麦物理学家尼尔斯·波尔在1913年提出的,是量子力学中重要的基本原理之一。
一、光子与原子相互作用
当一个光子与一个原子相互作用时,有两种可能性:光子被吸收或者被发射。
如果光子被吸收,其能量将被传递给原子,使得原子处于一个更高的能级。
如果光子被发射,则原子会向低能级跃迁,并释放出一个新的光子。
二、能级差
在量子力学中,原子可以处于不同的能级上。
当一个电子从一个较高的能级跃迁到较低的能级时,它会释放出一定能量的光子。
这个能量就等于两个能级之间的差值。
三、波尔频率条件
波尔发现,在光电效应中,只有当入射光线的频率大于某个临界值时
才会发生电离现象。
他认为这个现象可以推广到其他领域中。
因此他提出了波尔频率条件:只有当光子的频率与原子能级差相等时,光子才能被吸收或发射。
四、波尔频率条件的实际应用
波尔频率条件是量子力学中非常重要的一个原理。
它被广泛应用于各个领域,如激光技术、核磁共振、光谱学等。
在激光技术中,波尔频率条件决定了激光器的工作方式。
在核磁共振中,波尔频率条件可以帮助科学家们确定样品中不同分子的结构和组成。
在光谱学中,波尔频率条件可以帮助科学家们研究物质的性质和结构。
五、总结
总之,波尔频率条件是量子力学中非常重要的一个原理。
它决定了光子与原子之间相互作用的方式,并被广泛应用于各个领域。
对于理解量子力学以及相关领域中的现象和技术都有着重要意义。
光子与原子相互作用的基本原理

光子与原子相互作用的基本原理光子是光的基本单位,是一种电磁波粒子。
而原子是物质的基本单位,包含了质子、中子和电子等粒子。
光子与原子之间的相互作用是光学和量子力学的基础,对于理解光的传播和物质的性质具有重要意义。
本文将从光子的产生、传播以及与原子的相互作用等方面,探讨光子与原子相互作用的基本原理。
一、光子的产生与传播光子的产生源于原子的能级跃迁。
当原子处于高能级时,电子可以吸收能量而跃迁到更高的能级,此时原子吸收了光子。
而当原子处于激发态时,电子可以从高能级跃迁到低能级,释放出能量,此时原子发射了光子。
这种能级跃迁过程是光子产生的基本机制。
光子的传播遵循电磁波的性质。
光的传播是通过电磁场的变化而实现的,电磁场的变化导致电场和磁场的相互作用,从而形成电磁波。
光子作为电磁波的载体,具有波粒二象性,既可以看作是电磁波的一部分,也可以看作是能量量子的载体。
光子在真空中传播的速度是光速,这是由于光子没有质量,所以能以最大速度传播。
二、光子与原子的相互作用光子与原子的相互作用是光学和量子力学的基础。
在光学中,光子与原子的相互作用可以解释光的吸收、散射和透射等现象。
在量子力学中,光子与原子的相互作用可以解释原子的激发和退激发过程,以及光的干涉和衍射等现象。
光子与原子之间的相互作用可以通过电磁场的相互作用来描述。
当光子与原子相互作用时,光子的电场和原子的电荷分布发生相互作用,从而引起原子的激发或退激发。
这种相互作用可以通过电偶极子的概念来描述,即光子的电场与原子的电偶极矩之间的相互作用。
除了电偶极子相互作用外,光子与原子之间还存在其他形式的相互作用。
例如,当光子的频率与原子的共振频率相匹配时,会出现共振吸收现象。
此外,光子还可以使原子的电子发生跃迁,从而改变原子的能级结构。
这些相互作用过程在光学和量子力学中都有广泛的应用。
三、光子与原子相互作用的应用光子与原子相互作用的基本原理在许多领域都有重要应用。
在光学中,光子与原子的相互作用可以用于光谱分析、激光技术和光通信等方面。
原子结构知识:原子结构与光子的相互作用

原子结构知识:原子结构与光子的相互作用原子结构是物理学研究的一个重要领域,其中包括原子内部结构的组成、电子的能级分布及其与光子的相互作用等内容。
在这篇文章中,我们将重点探讨原子结构与光子的相互作用。
光子是一种电磁波,它具有波动和粒子性质。
与原子的相互作用主要表现在光子的能量与电子能级之间的匹配上。
当光子的能量与原子中某个电子跃迁所需能量相等时,电子会吸收光子并被激发到更高的能级上。
反之,电子从高能级向低能级跃迁时会发射光子。
这种现象称为光电效应。
在理论上,计算原子的吸收和发射光谱可以通过量子力学中的矩阵元理论解释。
计算过程中需要考虑原子内部电子的能级分布和跃迁的概率等因素。
这种计算方法在实际应用中被广泛使用,可以用来计算各种物质的光谱和电子能级结构等等。
除了光电效应外,光子还可以通过其他方式与原子相互作用。
例如,当光子与原子碰撞时,光子的能量和角动量可以传递给原子,使得原子内部发生能级跃迁或外部电子发生电离等现象。
这种相互作用在化学、材料科学等领域中的应用广泛,例如在激光加工、原子与离子束技术等方面都有着重要的应用。
最近几十年来,随着光学、物理学、化学等领域科学技术的发展,人们对原子内部结构和与光子的相互作用越来越深入地了解并加以应用。
例如,人们通过调控光子的能量和波长来控制原子的光谱,实现原子的操纵和控制,从而创造新型材料和纳米结构。
这种研究为材料科学、计算机科学、生物医学等领域的发展带来了巨大的贡献。
总之,原子结构与光子的相互作用是一个非常重要的物理学研究领域,它不仅涉及到物质的基本性质,还对现代科技的发展有着广泛的应用。
随着科技的不断进步,我们可以预期在未来的研究中,原子与光子的相互作用将起到更重要的作用,并在许多领域中发挥巨大的作用。
量子光学 第一部分《原子与光场的相互作用》

(1)
i
(t ) H (t ) t
(2)
方程中的哈密顿量可以表示为
H H 0 H1
(3)
1
原子与光场的相互作用
H 0 和 H 1 分别为没有微扰和相互作用的哈密顿量, 利用它的完备性关系 a a b b 1 ,
我们可以把 H 0 表示为
H 0 =( a a b b ) H 0 ( a a b b )
wyp8514@
原子与光场的相互作用
第一章
两能级原子与光场相互作用的简单求解
原子的结构本身是非常复杂的, 一般是由一系列分立的能级组成, 且大部分能级是简并 的,为了研究原子与光场相互作用,我们将假设原子只有两个非简并的能级,让与光场相互 作用,我们通过不同的方法进行简单求解,得出相关性质与结论。
a b a =(
b b a b a ) E (t )
(5)
这里ab ba e a x b 是电偶极矩阵元, E (t ) 为原子场的,我们假设在电场中线 性偏振沿 x 轴线,我们可以把场表示为
E (t ) = cos vt
(6)
3.半经典方法求解
3.1 概率幅求解
对系统方程化简求解
a (t ) C b
C
(7)
a ab cos vt H ( cos vt b ba
求解将(7)和(8)代入薛定谔方程(2)可得
(8)
C a i a C a i R e i cos(vt)Cb Cb ib Cb i R e
= a a a b b b (4)
我们在利用了 H 0 a a a 和 H 0 b b b 之间的关系,而哈密顿量 H 1 在原子辐射 场中相互作用可以表示为
光与三能级原子的相互作用

1.1.光与三能级原子的相互作用对于三能级Lambda 型系统,它是最易于实现EIT 的系统。
它有两个低能级属于基态,分别使用强相干场耦合做耦合跃迁与另一个弱相干场探测做探测跃迁。
在有这样的条件下,原子吸收光的两个可能通道之间发生干涉,彼此相消,由于相消干涉,没有共振吸收,导致了EIT 效应的产生。
人们对于这个系统的研究比较成熟,理论的框架也比较完整。
如图3所示,为三能级lambda 型原子系统。
图3频率分别为1v 和1v 的双光场与Lambda 型三能级原子相互作用如图3可见,探测场的频率为1v ,耦合场的频率为2v ,拉比频率为1Ω的探测场作用于能级21↔上,拉比频率为2Ω的耦合场作用于能级31↔,能级32↔之间的跃迁为偶极禁戒,能级1和2之间的电偶极矩矩阵元为12℘,探测场的频率与原子能级21↔间有失谐量为1121v -=∆ω,耦合场的频率与原子能级31↔间有失谐量2132v -=∆ω。
1γ分别为能级1的自发辐射衰减率,2γ为1到2能级的辐射衰减率,3γ为1到3能级的辐射衰减率。
ij γ代表i 到j 能级之间的退相干衰减率。
该系统的总哈密顿量由自由哈密顿0H 和光与原子相互作用的哈密顿1H 。
系统的总哈密顿量为10H H H +=3322113210ωωω ++=H (3.2.1)..1221221211c h e e H t iv t iv +Ω-Ω-=--(3.2.2)由公式3.1.4可以得到密度矩阵方程如下:()()()()()()()()()32112*2323232322313311213131313322112211212121213*131*********12111122212*121112*121111111122121221122112222222222ρρργωρρρρργωρρρρργωρρρργρρρργρρρρρργρtiv t iv t iv t iv t iv t iv tiv t iv tiv t iv tiv t iv t iv t iv e i e i i e ie i i e ie i i e e i e e i e e i e e i ---------Ω-Ω++-=Ω+-Ω-+-=Ω+-Ω++-=Ω-Ω-=Ω-Ω-=Ω-Ω+Ω-Ω+-= (3.2.3)做慢变振幅近似有:t iv e 11212~-=ρρ,t iv e 21313~-=ρρ,()t v v i e 213232~--=ρρ,1111~ρρ=,2222~ρρ=,3333~ρρ=()()()()()()()()()31112*23221323223133112132131332211221**********131*********12111122213*231212*121111111~2~2~~~2~~2~~~2~~2~~~~2~~~~2~~~~2~~2~~ρρργρρρρργρρρρργρρρργρρρργρρρρρργρΩ+Ω+∆+∆--=Ω+-Ω+∆--=Ω+-Ω+∆--=Ω-Ω-=Ω-Ω-=Ω-Ω+Ω-Ω+-=i i i i i i i i i i i i i i (3.2.4)原子对光的色散和吸收是由()112ρ决定。
光场与原子相互作用的量子力学方法研究

光场与原子相互作用的量子力学方法研究在现代科学研究中,光场与原子相互作用是一个极其重要的研究领域。
通过研究光场与原子的相互作用,我们可以深入了解光的本质以及原子的行为,从而推动光学和量子力学的发展。
本文将介绍光场与原子相互作用的量子力学方法研究。
首先,我们需要了解什么是光场与原子的相互作用。
光场是由光子组成的电磁场,而原子是物质的基本单位。
当光场与原子相互作用时,光子会与原子发生相互作用,从而改变原子的能级结构和行为。
这种相互作用可以通过量子力学的方法进行研究。
量子力学是描述微观粒子行为的理论框架。
在光场与原子相互作用的研究中,我们可以使用量子力学的方法来描述光子和原子的行为。
例如,我们可以使用量子力学的波函数来描述光子和原子的状态,并使用算符来描述它们的运动和相互作用。
在研究光场与原子相互作用时,一个重要的问题是如何描述它们的相互作用过程。
量子力学提供了一个框架来描述这种相互作用。
我们可以使用量子力学的哈密顿量来描述光场与原子的相互作用能量,从而得到它们的相互作用过程。
另一个重要的问题是如何计算光场与原子的相互作用过程。
由于光场与原子的相互作用是一个复杂的问题,我们通常需要使用数值方法来进行计算。
例如,我们可以使用量子力学的数值解方法来计算光子和原子的波函数演化,从而得到它们的相互作用过程。
除了数值方法,还有一些重要的量子力学方法可以用于研究光场与原子的相互作用。
例如,量子力学中的微扰理论可以用于描述光场与原子的弱相互作用。
微扰理论可以将相互作用问题分解为一个无相互作用的问题和一个小的相互作用项,从而简化计算过程。
此外,还有一些更高级的量子力学方法可以用于研究光场与原子的相互作用。
例如,量子力学中的量子多体理论可以用于描述多个光子和多个原子的相互作用。
量子多体理论可以提供更精确的描述,并可以用于解释一些实验现象。
光场与原子相互作用的量子力学方法研究在很多领域都有重要的应用。
例如,在光学中,我们可以利用光场与原子的相互作用来实现光的调控和操控。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§9-2 光与原子相互作用
人们对于光的种种性质的了解,都是通过观察光与物质相互作用而获得的,光与物质的相互作用,可以归结为光与原子的相互作用,这种相互作用,有三种主要过程:吸收、自发辐射和受激辐射。
一、吸收
如果有一个原子,开始时处于基态1E ,若没有任何外来光子接近它,则它将保持不变
E 2E 1E 2E 1E 1
E 2
(a)(b)(c)
(图9-4)
[图9-4(a )],如果有一个能量为21hv 的光子接近这个原子,则它就有可能吸收这个光子,从而提高它的能量状态[图9-4(b )],本来处于基态1E 的原子,在吸收21hv 以后,就激发到激发态2E [图9-4(c )],整个图9-4表示原子对光的吸收过程,在吸收过程中,不是任何能量的光子都能被一个原子所吸收,只有当光子的能量正好等于原子的能级间隔2E —1E 时,这样的光子才能被吸收。
设处于基态1E 的原子密度为1n ,光的辐射能量密度为()u v ,则单位体积单位时间内吸收光子而跃迁到激发态2E 去的原子数12n 应该与1n 和()u v 成正比,因而有12n ∝1()n u v 即
12121()n B n u v = (9-6)
其中12B 为比例系数,称为受激吸收爱因斯坦系数,121()B n u v 称为吸收速率,用12ω表示,于是(9-6)式可写成
12112B n ω=
二、自发辐射
从经典力学的观点来讲,一个物体如果势能很高,它将是不稳定的,与此相类似,处于激发态的原子也是不稳定的,它们在激发态停留的时间一般都非常短,大约在8
10s -的数量级,所以我们常常说,激发态的寿命约为810s -,在不受外界的影响时,它们会自发地返回到基态去,从而放出光子,这种自发地从激发态返回较低能态而放出光子的过程,显然,如果处于激发态2E 的原子密度为2n ,则自发辐射光子数为
21221n n A = (9-7)
其中21A 为自发辐射爱因斯坦系数,
E 2E 1E 2E 1E 1E 2
(图9-5)
图9-5表示了自发辐射的全部过程。
自发辐射的特点是这种过程与外界作用无关,各个原子的辐射都是自发地、独立地进行的,因而各个原子发出来的光子在发射方向和初位相上都是不相同的,除激光器光源以外,普通光源的发光都属于自发辐射,例如霓虹灯,当灯管内的低气压氖原子,由于加上了高电压而放电时,部分氖原子被激发到各个激发态的能级,当它们从激发态跃迁回到基态时,便发出我种频率的红色光,从这里可以看到,普通光源发出来的光,其频率成分极为复杂,发射方向分散在4π球面度的立体角内,初位相也各不相同,因而不是相干光。
三、受激辐射
爱因斯坦于1905年推广了普朗克的能量子概念,提出了光量了的假设,因而成功地解释了光电效应,1917年,爱因斯坦又从纯粹的热力学出发,用具有分立能级的原子模型来推导普朗克辐射公式,在这一工作中,爱因斯坦预言了受激辐射的存在,四十年以后,由于第一台激发器开始运转,爱因斯坦的这一预言得到了有力的证实。
处于激发态的原子,如果在外来光子(即外来电磁场)的影响下,引起从高能态向低能态的跃迁,并把两个状态之间的能量差以辐射光子的形式发射出去,那么这种过程就叫做激发射,
E2E1hv 12hv 12E2
E1
hv 12
(图9-6)
图9-6表示了这一过程。
单位体积单位时间内受激发射原子数可以写为
(9-8) 其中21B 为比例系数,称为受激辐射爱因斯坦系数,21()B u v 称为受激辐射速率,用21w 表示,它表征原子体系在外来光辐射作用下产生2E 到1E 受激跃迁的本领,于是(9-8)式便可写为
'21221n n w =
这里,应特别注意自发辐射和受激辐射的区别,同时要注意,只有当外来光子的能量21hv 正好满足21hv =2E —1E 关系式时,才能引起受激辐射,而且受激辐射发出来的光子与外来光子具有相同的频率,相同的发射方向,相同的偏振态和相同的位相。
四、吸收、自发辐射和受激辐射三系数之间的关系
我们已讨论了吸收、自发辐射和受激辐射三个过程,并分别引出了表征这三种过程中跃迁本领强弱的三个系数,即122121,,B A B 。
尽管这三个系数有着不同的含义,但既然都是表征同一种原子的特性,因而它们之间必然存在着内在联系,现在,就来讲座这种联系。
当光和原子相互作用时,必然同时存在着吸收、自发辐射和受激辐射三种过程,达到平衡时,单位体积单位时间内通过吸收过程从基态跃迁到激发态去的原子数,等于从激发态通过自发辐射和受激辐射跃迁回基态的原子数,所以在平衡条件下,下列等式应该成立。
'122121n n n =+
引用(9-6)、(9-7)和(9-8)式,可得
112221221()()n B u v n A n B u v =+
或 21
112212()A u v n B B n =- (9-9)
在处于热平衡状态下,粒子数密度按能量的分布遵从玻耳兹曼定律,即12,n n 满足下列关系式 1212exp exp n E E hv n kT kT -⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦
(9-10) 式中2311.3810k J K --=⨯⋅,称为玻耳兹曼常数,T 为绝对温度,因21E E >所以
1212exp 1n E E n kT -⎡⎤=-<⎢⎥⎣⎦
即21,n n <所以在正常情况下,处于最低态的原子数总是最多的,能级越高,处于该能级的粒子数就越少。
如氖原子的某一激发态和基态能级的粒子数就越少。
1916.927.0710E eV J -∆==⨯
若该原子体系处于室温(300T K =)时,则根据玻耳兹曼分布定律,在热平衡状态下,处于该激发态能级的原子密度1n 之比为
19123265365327.0710exp exp 1.38103001/1
n E n kT e e ---⎡⎤∆⨯⎡⎤=-=-⎢⎥⎢⎥⨯⨯⎣⎦⎣⎦
==<<
把(9-10)式代入(9-9)式,可得光的辐射能量密度
()21/1221
B e B A u kT hv -=ν (9-11)
对于黑体辐射来说,在热平衡状态时,腔内的辐射场应是不随时间变化的稳定分布,这时,腔内的辐射能量密度()u v 可以认为就是腔内中心附近单位体积从周围腔壁所获得的辐射能量,根据亮度定义,并考虑到朗伯光源的亮度和面发光度之间的关系式,就可以找出()u v 和发射本领,v T ε之间的关系为
,4()v T u v c
ε= 此处,v T ε即为热平衡辐射的普朗克公式(8-13),所以
33/81()1
hv kT hv u v c e π=⋅- (9-12) 比较(9-11)和(9-12)式,可以得到吸收、自发辐射和受激辐射三个系数之间的关系为
3
32121
21128c hv B A B
B B π===。
