最优化课程设计共轭梯度法算法分析与实现样本

合集下载

最优化方法-共轭方向和共轭梯度法

由3式可以看出
2020/3/6
16
2.共轭方向-共轭方向法
• 基本定义
利用共轭方向作为搜索方向的无约束极小化算法
• 通用步骤:
(1)任取X 0 ,以及在X 0的下降方向P0 , k 0; (1)求解一维搜索问题
min f ( X k Pk ),为最优步长,是个数值．
(3) X k1 X k k Pk ;
X
T QX

bT
X

c, Q正定,
X 0是初始点,
P0

f
(X0)
X k1 X k k Pk , k 0,1...m 1, k是最优步长,且
Pk1 f ( X k1) ak Pk (这是构造的结果)
其中ak

f
( X k1)T QPk PkT QPk
,
P0
(
X
)T
k 1
Pk
)T

PkT f ( X k1)
f ( X k1) QX k1 b Q( X k k Pk ) b, ( X k 1 X k k Pk )
f ( X k1) (QX k b) kQPk f ( X k ) kQPk
当m 2时所以，P0，P1， Pm1是线性无关的。
P0T QP1

P0T Q f ( X 1 )
f ( X 1 )T QP0 P0T QP0
P0
P0T Qf ( X 1 ) f ( X 1 )T QP0 0
表明，P0与P1共轭。
2020/3/6
2020/3/6
4
1.共轭方向法的基本原理
• 已知 X1 点是在 X 0 点在直线 l0 上沿 P0 搜索方向的一个极小点。（l0 与 P0 是平行的）

共轭方向与共轭梯度法-最优化方法

f (X1)T P0 0 ，所以 f (X1)T P0 1P1TQ P0 0
P1TQ P0 0
（1）
以上就是搜索方向P1所必须满足的（必要）条件。这也是使X2是极小点的充分条件。 P1，P2称为关于Q的共轭方向。
讨论表明对于二维的具有正定矩阵Q的二次函数f(X),从任一初始点出发，依次沿关于Q共轭的两个方向进行一维搜索，必可达到 f(X)的无约束精确极小点。
Pk 1

0
且对j 0,1 , k 2, 有
PjT QPk PjT Q f ( X k ) k1Pk1

PjT Qf
(X
k
)

k
PT
1 j
QPk
1
f ( X k )T QPj
f ( X k )T f ( X j1) f ( X j ) j
f ( X k1 ) QX k1 b Q( X k k Pk ) b (2)
f ( X k1 ) f ( X k ) k QPk
所以
f ( X m ) f ( X m1) m1QPm1
f ( X m2 ) m2QPm2 m1QPm1
其中1 是最优步长，1>0 .因为 X * 是无约束极小点。
故 f ( X * ) 0 即 QX * b 0
f (X1) QX1 b
Q( X * 1P1) b (QX * b) 1QP1 1QP1
又因为 X1是f(X)沿P0方向的直线l0上的极小点，故
设 X En ,
,Q为对称正定矩阵，P0，
P1，···，Pm-1是关于Q共轭的m个共轭方向，

最优化方法课程设计参考模版讲解

《最优化方法》课程设计题目：共轭梯度法算法分析与实现院系：数学与计算科学学院专业：数学与应用数学姓名：梁婷艳学号：0800730103指导教师：李丰兵日期：2015 年12 月30 日在各种优化算法中，共轭梯度法是非常重要的一种。

本文主要介绍的共轭梯度法是介于最速下降法与牛顿法之间的一种无约束优化算法，它具有超线性收敛速度, 而且算法结构简单, 容易编程实现。

在本次实验中,我们首先分析共轭方向法、对该算法进行分析，运用基于共轭方向的一种算法—共轭梯度法进行无约束优化问题的求解。

无约束最优化方法的核心问题是选择搜索方向。

共轭梯度法的基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。

根据共轭方向的基本性质，这种方法具有二次终止性。

再结合该算法编写matlab程序，求解无约束优化问题，再结合牛顿算法的理论知识，编写matlab程序，求解相同的无约束优化问题，进行比较分析，得出共轭梯度法和牛顿法的不同之处以及共轭梯度法的优缺点。

共轭梯度法仅需利用一阶导数信息，避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。

共轭梯度法是一个典型的共轭方向法，它的每一个搜索方向是互相共轭的，而这些搜索方向仅仅是负梯度方向与上一次迭代的搜索方向的组合，因此，存储量少，计算方便。

关键词：共轭梯度法；超线性收敛；牛顿法；无约束优化In a variety of optimization algorithms, conjugate gradient method is a very important one.In this paper, the conjugate gradient method is between the steepest descent method and Newton method for unconstrained optimization between a method, it has superlinear convergence rate, and the algorithm is simple and easy programming.In this experiment, we first analyze the conjugate direction method, the algorithm analysis, the use of a conjugate direction-based algorithm - conjugate gradient method for unconstrained optimization problems. Unconstrained optimization method is to select the core issue of the search direction.Conjugate gradient method is the basic idea of the conjugate descent method with the most combined points in the gradient using the known structure of a set of conjugate directions, and search along the direction of this group, find the minimum point of objective function. According to the basic nature of the conjugate direction, this method has the quadratic termination. Combined with the preparation of this algorithm matlab program for solving unconstrained optimization problems, combined with Newton’s theory of knowledge, writing matlab program to solve the same problem of unconstrained optimization, comparison analysis, the conjugate gradient method and Newton method different Office and the advantages and disadvantages of the conjugate gradient method.Conjugate gradient method using only first derivative information, to avoid the Newton method requires storage and computing the inverse Hesse matrix and shortcomings, is not only the conjugate gradient method to solve large linear systems one of the most useful, but also large-scale solution nonlinear optimization algorithm is one of the most effective. Conjugate gradient method is a typical conjugate direction method, each of its search direction is conjugate to each other, and the search direction d is just the negative gradient direction with the last iteration of the search direction of the portfolio, therefore, storage less computational complexity.Key words: Conjugate gradient method; Superlinear convergence; Newton method Unconstrained optimization目录1、引言 (1)2、共轭梯度法的描述 (1)2.1 共轭方向法 (1)2.2 共轭梯度法 (2)2.3 Armijo准则 (6)3、数值实验 (7)3.1 代码实现 (7)3.2 算法测试 (8)3.3 结果分析 (10)4、算法比较 (10)4.1 牛顿法的构造 (10)4.2 算法实现 (11)4.3 算法测试 (12)4.4算法比较 (13)5、总结 (13)5.1 总结概括 (13)5.2 个人感言 (14)6、参考文献： (16)1、引言在各种优化算法中，共轭梯度法（Conjugate Gradient ）是非常重要的一种。

最优化共轭梯度法

x1 x2

,

A

4 0
0 2
.
f ( x) ( 4x1 , 2x2 )T .
第 1 次迭代：
令 d (1) g1 ( 8, 4 )T ,
而
1

g1T d (1) d (1)T Ad (1)

(
8
,
4
)

8 4
(

8
,

4
)
2. 共轭梯度法
Fletcher R eeves 共轭梯度法 :
min f ( x) 1 xT Ax bT x c 2
其中 x Rn , A是对称正定矩阵，b Rn，c 是常数。
基本思想：将共轭性和最速下降方向相结合，利用已知迭代点处的梯度方向构造一组共轭方向，并沿此方向进行搜索，求出函数的极小点。
取最速下降方向作为第一个搜索方向，开始下一轮搜索。
注在共轭梯度法中，也可采用其它形式的公式计算i ，如
i

giT1( gi1 giT gi
gi )
( PRP共轭梯度法）。
i

|| gi1 || d (i)T gi
(Dixon共轭梯度法）。

i

gi
T 1
(
gi1

gi
)
d (i)T ( gi1 gi )

||
gi1 ||2 d (i)T gi

|| gi1 ||2 || gi ||2
(4)
FR算法步骤：
1. 任取初始点x(1) ，精度要求，令k 1。 2. 令g1 f ( x(1) ),若 || g1 || ,停止，x(1)为所求极小点；

最优化共轭梯度法

最优化共轭梯度法最优化共轭梯度法（Conjugate Gradient Method）是一种迭代求解线性方程组或优化问题的方法。

它的特点是对于二次正定函数，可以在有限次迭代内精确地求出最优解。

在非二次函数的优化问题中，共轭梯度法表现出了较好的收敛性和全局能力。

共轭梯度法的核心思想是通过选择适当的方向，使得每一次方向的梯度互相“共轭”，从而加快收敛速度。

当目标函数为二次函数时，共轭梯度法能够在有限次迭代中得到精确解；而对于非二次函数的优化问题，共轭梯度法通过先验条件选择合适的方向，最大程度地减小目标函数值。

共轭梯度法的基本步骤如下：1.初始化参数：设置初始点的位置和方向，对于非二次函数，通常选取梯度方向作为方向。

2. 计算步长：通过线方法（如Armijo准则、Wolfe准则等）定位到目标函数上降速度最快的点，并计算目标函数在该点的梯度。

3.更新方向：利用“共轭”梯度法，根据先验条件计算新的方向。

4.判断终止条件：判断目标函数值是否满足设定的终止条件，若满足则停止迭代，否则返回步骤2对于二次函数，最优化共轭梯度法表现出了优良的性能。

当目标函数是非二次函数时，共轭梯度法的表现会有所下降，但仍然比一般的梯度下降法更具有优势。

因此，共轭梯度法常被用于求解大规模线性方程组、信号处理、数字滤波、机器学习等领域。

最优化共轭梯度法的优点在于：收敛速度较快，全局能力较强，不需要存储海量信息。

然而，该方法也存在一些缺点。

首先，共轭梯度法对目标函数的性质有一定的要求，例如目标函数必须是光滑的，并且梯度向量必须是有效的。

其次，共轭梯度法对初始点的选择较为敏感，不同的初始点可能导致不同的解。

总结来说，最优化共轭梯度法是一种高效的优化算法，可以加快目标函数收敛速度，尤其适用于解决二次函数优化问题。

在非二次函数的优化问题中，共轭梯度法以其较好的收敛性和全局能力在实际应用中发挥着重要作用。

共轭梯度法

证明：采用数学归纳法, 不过, 还是省略它
(5.8)意味着 d iT Qd j 0, j i, i 1, 2, , n - 1 即Broyden 族在用精确搜索求解凸二次函数极小化问题时, 所产生的方向关于矩阵Q相互共轭.属于共轭方向法.
前面讨论的共轭方向法需要在算法之初产生 n个共轭方向，因而需要很大的存贮量，而且不能用来求解非二次问题.
j 0 k
dT j Qp k 1 d Qp j
T j
d j,
(5.5)
步2 若k n - 2, 则停止, 否则, 令k : k 1, 转步1.
容易验证, 由算法5.1产生的向量组 d 0 , d1 , , d n-1 R n 关于矩阵Q相互共轭
下面的定理解释了第四章介绍的Broyden 族具有二次终止性的根本原因 :
其中 k 是待定参数, 适当选取 k , 使得 d kT Qd k -1 0.
一般地, 搜搜方向的计算公式为： - f ( x0 ), dk - f ( xk ) k d k -1 , k 0 k 1 (5.10)
在下面我们来推导 (5.10) 参数 k 的计算公式 :
d k -f ( xk ) k d k -1
其中 k 是由精确搜索得到的步长. 即满足
于是求得
d kT-1Qf ( xk ) k T dk -1Qd k -1
在该计算式中含矩阵Q, 为减少计算量及使共轭梯度能用于求解非二次函数的优化问题, 在计算式中消除 Q.
由上面的条件得到
T T T p0 Qp1 - p0 Qf ( x1 ) p0 Qp 0 0
等值线
f ( x1 )
由此解得所以 p Qf ( x1 ) T p0 Qp 0

共轭梯度算法分析与实现

共轭梯度算法分析与实现
梯度下降是一种常用的优化算法，用于求解优化问题。

它通过迭代的
方式不断沿着梯度的反方向更新参数，以最小化损失函数。

然而，梯度下
降算法在处理大规模数据时会变得非常慢，因为它需要计算全部训练样本
的梯度。

为了解决这个问题，共轭梯度算法被提出。

共轭梯度算法是一种适用于解决对称正定矩阵形式下的线性方程组的
优化算法。

它在每一步更新参数时，会按照预先选择好的方向进行更新。

这些方向通常是互相共轭的，这意味着每一个方向都是相对于其他方向来
说是正交的。

共轭梯度算法的原理是，通过每次迭代选择共轭方向来加速
梯度下降算法的收敛速度。

具体而言，共轭梯度算法中的每一步迭代可以分为四个部分：初始化、步长、更新参数和计算残差。

首先，在初始化阶段设定初始参数和初始残差，并选择一个适当的共轭方向。

然后，在步长阶段，通过线方法选择一
个合适的步长。

接下来，在更新参数阶段，根据步长和共轭方向更新参数。

最后，在计算残差阶段，计算新的残差，并检查是否达到停止条件。

如果
没有达到停止条件，那么就继续迭代进行和更新。

共轭梯度算法相对于梯度下降算法有几个优点。

首先，它不需要计算
全部训练样本的梯度，这样可以加速算法的收敛速度。

其次，它可以解决
对称正定矩阵形式下的线性方程组，这在很多实际问题中非常常见。

最后，共轭梯度算法在存储以及计算量上都比较少，所以可以处理大规模数据。

共轭梯度法实验报告

数值代数实验报告一、实验名称：用共轭梯度法解线性方程组。

二、实验目的：进一步熟悉理解掌握共轭梯度法解法思路，提高matlab 编程能力。

三、实验要求：已知线性方程矩阵，应用共轭梯度法在相关软件编程求解线性方程组的解。

四、实验原理：1．共轭梯度法：考虑线性方程组Ax b =的求解问题，其中A 是给定的n 阶对称正定矩阵，b 是给定的n 维向量，x 是待求解的n 维向量.为此,定义二次泛函()2T T x x Ax b x ϕ=-.定理1 设A 对称正定,求方程组Ax b =的解，等价于求二次泛函()x ϕ的极小值点. 定理1表明，求解线性方程组问题就转化为求二次泛函()x ϕ的极小值点问题.求解二次函数极小值问题，通常好像盲人下山那样，先给定一个初始向量0x ，确定一个下山方向0p ，沿着经过点0x 而方向为0p 的直线00x x p α=+找一个点1000x x p α=+，使得对所有实数α有()()00000x p x p ϕαϕα+≤+，即在这条直线上1x 使()x ϕ达到极小.然后从1x 出发，再确定一个下山的方向1p ，沿着直线11x x p α=+再跨出一步，即找到1α使得()x ϕ在2111x x p α=+达到极小：()()11111x p x p ϕαϕα+≤+.重复此步骤，得到一串012,,,ααα 和 012,,,p p p ，称k p 为搜索方向，k α为步长.一般情况下，先在k x 点找下山方向k p ，再在直线k k x x p α=+上确定步长k α使()(),k k k k k x p x p ϕαϕα+≤+最后求出1k k k k x x p α+=+.然而对不同的搜索方向和步长，得到各种不同的算法.由此，先考虑如何确定k α.设从k x 出发，已经选定下山方向k p .令 ()()k k f x p αϕα=+()()()2TT k k k k k k x p A x p b x p ααα=++-+()22TT k k k k k p Ap r p x ααϕ=-+，其中k k r b Ap =-.由一元函数极值存在的必要条件有()220TT k k k k f p Ap r p αα'=-=所确定的α即为所求步长k α，即 T k kk Tk kr p p Ap α=. 步长确定后，即可算出1k k k k x x p α+=+.此时，只要0T k k r p ≠，就有()()()()1k k k k k k x x x p x ϕϕϕαϕ+-=+-()2220T k k TT k kk k k k Tk kr p p Ap r p p Ap αα=-=-<即()()1k k x x ϕϕ+<.再考虑如何确定下山方向k p .易知负梯度方向是()x ϕ减小最快的方向，但简单分析就会发现负梯度方向只是局部最佳的下山方向，而从整体来看并非最佳.故采用新的方法寻求更好的下山方向——共轭梯度法. 下面给出共轭梯度法的具体计算过程:给定初始向量0x ，第一步仍选用负梯度方向为下山方向，即00p r =，于是有00010001000,,T T r r x x p r b Ax p Ap αα==+=-.对以后各步，例如第k+1步（k ≥1）,下山方向不再取k r ，而是在过点由向量k r 和1k p -所张成的二维平面21{|,,}k k k x x x r p R πξηξη-==++∈内找出使函数ϕ下降最快的方向作为新的下山方向k p .考虑ϕ在2π上的限制：()1,()k k k x r p ψξηϕξη-=++11()()T k k k k k k x r p A x r p ξηξη--=++++12()T k k k b x r p ξη--++. 计算ψ关于,ξη的偏导得： ()()11112,2,T T T k k k k k kT T k k k k r Ar r Ap r r r Ap p Ap ψξηξψξηη----∂=+-∂∂=+∂其中最后一式用到了10T k k r p -=，这可由k r 的定义直接验证.令 0ψψξη∂∂==∂∂，即知ϕ在2π内有唯一的极小值点001k k k x x r p ξη-=++，其中0ξ和0η满足 00101011,0.T T T k k k k k k T Tk k k k r Ar r Ap r r r Ap p Ap ξηξη----⎧+=⎨+=⎩由于0k r ≠必有00ξ≠，所以可取()01001k k k k p x x r p ηξξ-=-=+作为新的下山方向.显然，这是在平面2π内可得的最佳下山方向.令010k ηβξ-=，则可得1111.T k k k T k k r Ap p Ap β----=-注：这样确定的k p 满足10Tkk p Ap -=，即k p 与1k p -是相互共轭的. 总结上面的讨论，可得如下的计算公式：T k kk Tk kr p p Ap α= ， 1k k k k x x p α+=+， 11k k r b Ax ++=-，1T k kk Tk kr Ap p Ap β+=-， 11k k k k p r p β++=+. 在实际计算中，常将上述公式进一步简化，从而得到一个形式上更为简单而且对称的计算公式.首先来简化1k r +的计算公式：11()k k k k k k k k r b Ax b A x p r Ap αα++=-=-+=-.因为k Ap 在计算k α是已经求出，所以计算1k r +时可以不必将1k x +代入方程计算，而是从递推关系1k k k r b Ap α+=-得到.再来简化k α和k β的计算公式.此处需要用到关系式1110,T T T k k k k k k r r r p r p +-+=== 1,2,k =.从而可导出1111,T T k k k k r r r α+++=-， ()111TT T k k k k k k k k k p Ap p r r p r αα+=-=()1111T Tk k k k k k k kr r p r r βαα--=+=.由此可得,T k k k T k k r r p Ap α=， 11.T k k k T k kr r r r β++=.从而有求解对称正定方程组的共轭梯度法算法如下：0x =初值00r b Ax =-；0k =while 0k r ≠1k k =+ if 1k = 00p r =else21122T T k k k k k r r r r β-----= 1122k k k k p r p β----=+ end11111T Tk k k k k r r p Ap α-----=111k k k k x x p α---=+111k k k k r r Ap α---=-endk x x =注：该算法每迭代一次仅需要使用系数矩阵A 做一次矩阵向量积运算. 定理2 由共轭梯度法得到的向量组{}i r 和{}i p 具有如下基本性质：（1）0T i j p r =， 0;i j k ≤<≤ （2）0T i j r r =， i j ≠，0,;i j k ≤≤ （3）0T i j p Ap =， i j ≠，0,;i j k ≤≤ （4）000{,,}{,,}(,,1)k k span r r span p p A r k κ==+，其中0000(,,1){,,,}k A r k span r Ar A r κ+=，通常称之为Krylov 子空间.下面给出共轭梯度法全局最优性定理：定理3 用共轭梯度法计算得到的近似解k x 满足()(){}00min :(,,)k x x x x A r k ϕϕκ=∈+或{}**00min :(,,)k AAx x x x x x A r k κ-=-∈+，其中Ax=*x 是方程组Ax b =的解，0(,,)A r k κ是由所定义的Krylov 子空间. 定理2表明，向量组0,,k r r 和0,,k p p 分别是Krylov 子空间0(,,1)A r k κ+的正交基和共轭正交基.由此可知，共轭梯度法最多n 步便可得到方程组的解*x .因此，理论上来讲，共轭梯度法是直接法.然而实际使用时，由于误差的出现，使k r 之间的正交性很快损失，以致于其有限步终止性已不再成立.此外，在实际应用共轭梯度法时，由于一般n 很大，以至于迭代()O n 次所耗费的计算时间就已经使用户无法接受了.因此，实际上将共轭梯度法作为一种迭代法使用，而且通常是k r 是否已经很小及迭代次数是否已经达到最大允许的迭代次数max k 来终止迭代.从而得到解对称正定线性方程组的实用共轭梯度法，其算法如下：x =初值0;k =;r b Ax =-T r r ρ=while)()max2band k kε><1k k =+if 1k = p r = else;p r p βρρβ==+ end;;T Ap p x x p ωαρωα===+ ;;T r r r r αωρρρ=-== end算法中，系数矩阵A 的作用仅仅是用来由已知向量p 产生向量Ap ω=，这不仅可以充分利用A 的稀疏性，而且对某些提供矩阵A 较为困难而由已知向量p 产生向量Ap ω=又十分方便的应用问题是十分有益的。

最优化方法3-5共轭梯度法和共轭方向法

算法 3.5.1
设目标函数为 f (x) 1 xTGx bT x c，其中G 正定。 2
给定控制误差。
Step1. 给定初始点 x0及初始下降方向 p0，令k 0。
Step2. 作精确一维搜索，求步长k
f
( xk
k
pk )

min
0
f
( xk

pk
)
Step3. 令 xk1 xk k pk 。
称 Fletcher-Reeves 公式，简称 FR 公式。
k 1

gkT Gpk1 pkT1Gpk 1
Gpk 1

1
k 1
(gk

g
k 1 ) ，
gkT Gpk1

1
k 1
gkT
(gk

g
k 1)
，
pkT1Gpk 1

1
k 1
(g
k1 k2
pk2 )T
(gk

g
k 1)

1
k 1
g
g T
k 1 k
1
（2）Polak-Ribiere-Polyak 公式
故
k 1

g
T k
(
gk

g
k 1)
gkT1gk 1
此式是 Polak 和 Ribiere 以及 Polyak 分别于 1969
年提出的，故称 Polak-Ribiere-Polyak 公式，简称 PRP

0，i
1,2,L
,k
(ii) xk1是二次函数在k 维超平面Hk 上的极小点。
证明由引理 3.5.2，只需证明(i)，

No03：梯度法和共轭梯度法

梯度法和共轭梯度法1.无约束最优化问题2. 梯度法(最速下降法）3. 共轭方向法4. 共轭梯度法一. 无约束最优化问题无约束最优化问题nR x t s x f ∈..)(min有一阶连续偏导数。

其中)(x f 解析方法：利用函数的解析性质构造迭代公式使之收敛到最优解。

二. 梯度法（最速下降法）迭代公式：kk k k d x x λ+=+1如何选择下降最快的方向？)(k x f ∇)(k x f ∇−函数值下降最快的方向函数值增加最快的方向2π与负梯度的夹角小于的方向为函数值下降的方向k x 梯度法（最速下降法）：也称为最速下降方向；搜索方向：,)(.1k k x f d −∇=。

即满足取最优步长搜索步长)(min )(,:.2k k k k k k d x f d x f λλλλ+=+梯度法算法步骤：。

令允许误差给定初始点1,0,.11=>∈k R x n ε;)(.2k k x f d −∇=计算搜索方向kk k x d λε否则，求最优步长为所求极值点；则停止计算，若,||||.3≤。

使得)(min )(k k k k k d x f d x f λλλ+=+。

转令令2,1:,.41+=+=+k k d x xkk k k λ22112121.:min (),,f x x x x ⎛⎞=+=⎜⎟⎝⎠例用最速下降法求解设初始点为110ε=解：第一步迭代12()(4,2),Tf x x x ∇=∵11()(4,2).T d f x ∴=−∇=−−11(14,12).T x d ∴+=−−λλλ1122()()2(14)(12)f x d =+=−+−ϕλλλλ令，)(min λϕλ求解()16(14)4(12)0′=−−−−=ϕλλλ令1518⇒=λ21111194x x d λ−⎛⎞∴=+=⎜⎟⎝⎠1||||25d =>ε第二步迭代222484()(,),||||5999T d f x d ε=−∇=−=>221448(,).9999T x d λλλ∴+=−+−2222216()()(14)(12)8181f x d ϕλλλλ=+=−++−令，)(min λϕλ求解25()012ϕλλ′=⇒=令322212271x x d λ⎛⎞∴=+=⎜⎟⎝⎠1227x =依次迭代，得33324271(),||||d f x d −⎛⎞=−∇=>⎜⎟−⎝⎠ε421122122434279427x x −−⎛⎞⎛⎞===⎜⎟⎜⎟⎝⎠⎝⎠i 44441824321022430**(),||||.,df x d xx x ⎛⎞=−∇=<⎜⎟−⎝⎠−⎛⎞⎛⎞∴≈==⎜⎟⎜⎟⎝⎠⎝⎠ε可以验证：12112122711212794k k k kx x−−−⎛⎞⎛⎞=⎜⎟⎜⎟⎝⎠⎝⎠−⎛⎞⎛⎞=⎜⎟⎜⎟⎝⎠⎝⎠i 精确线搜索下的步长设为正定二次函数。

数值最优化(共轭梯度)ppt课件

(1)Flecher-Reeves公式
所以
29
PRP算法 FR算法中: (2)Polak-Ribiere-Polyak公式
由于gkTgk-1=0,所以有对于二次函数,这两个函数是等价的,但对于一般的函数,根据这两个公式的出的算法的计算效果有差异.
注:对于这两个算法,可以证明pkTgk= -gkTgk<0,因而都是下降算法.
min f (x0+ p0)=1600 4+42-4+1的极小点, 得0 =0.080632,(精确一维搜索方法求得,e =10-5,) 于是x1=x0+ 0 p0=(0.161264,0)T,
第五章无约束问题算法（III）
——共轭梯度法
1
共轭方向法的思路
对于简单的二次函数
1 xT x bT x c 1 ( x b)T ( x b) c bTb
2
2
任给一个初始向量x(0),沿着方向e1=(1,0,···,0)T进行搜索,即求解下面问题
由于
min 1
f1 (1 )
( x(0)
z
x(1) O
x(3) =x* x(2) y
x(0)
x
5
共轭方向法的思路
上面的方法对一般的二次函数是否适用呢?
考虑问题
其中
G
1 2
2 5
易见G是正定的,f(x)的极小点为(0,0)T.
以x(0)=(-1,-1)T为初始点,在方向e1=(1,0)T上进行一维搜索. 即求解问题
易求得1*=3,x(1)=x(0)+1*e1=(2,-1)T.
是f(x)在x1与p1,p2,···,pk所生成的k维超平面Hk上唯一极小点的充分必要条件是

共轭梯度法

《数值优化》实验报告
实验[02] [实验题目:FR共轭梯度法]
专业：信息与计算科学学号：姓名：
1 实验目的
深入学习FR共轭梯度法，并对其编译Matlab程序
2 实验内容
编译FR共轭梯度法Matlab程序，在计算机上利用Matlab程序对方程f=100*(x (1)^2-x (2))^2+(x (1)-1)^2;进行求解
3 算法设计
共轭梯度法的基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜素，求出目标函数的极小点。

根据共轭方向基本性质，这种方法具有二次终止性。

4 程序代码
val=feval (fun,x);
g=[400*x (1)*(x (1)^2-x (2))+2*(x (1)-1),-200*(x (1)^2-x (2))]';
5 运行结果
6 结果分析
利用该算法所得结果十分接近精确解，满足我们的需要。

在计算过程中一共迭代了44次，这个迭代次数是可以接受的。

最优化课程练习-共轭梯度法

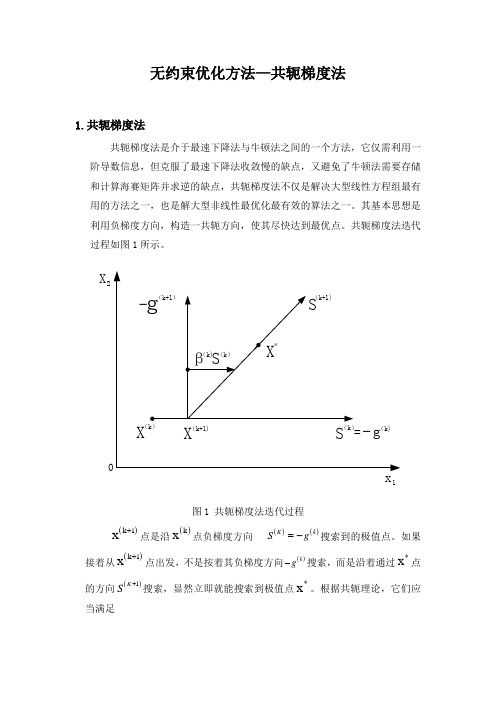
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。

其基本思想是利用负梯度方向，构造一共轭方向，使其尽快达到最优点。

共轭梯度法迭代过程如图1所示。

1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。

如果接着从()k 1x +点出发，不是按着其负梯度方向()kg -搜索，而是沿着通过*x 点的方向()1K S +搜索，显然立即就能搜索到极值点*x 。

根据共轭理论，它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向，新构造的共轭方向()1K S +，可由矢量合成，()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理，推到出：()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+，就可以构造一个与梯度矢量为共轭的矢量()1K S +，沿着该方向搜索，即可求得极值点。

共轭梯度法程序框图如图2所示。

图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解，其中：初始点()0[1,1]T X =。

收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。

共轭梯度法课程设计

最优化方法课程设计报告题目：共轭梯度软件设计院（系）：专业：学生姓名：指导教师：题目类型：实验研究工程设计软件开发2010 年1月15 日摘要共轭梯度法最早是由Hestenes 和Stiefle （1952）提出来的，用于解正定系数矩阵的线性方程组，在这个基础上，Fletcher 和Reeves （1964）首先提出了解非线性最优化问题的共轭梯度法。

共轭梯度法是解决无约束非线性最优化问题的重要的方法之一（Conjugate gradient method to solve unconstrained nonlinear optimization problem, one of the important ways.），因为共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse 矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法一。

共轭梯度对于无约束优化问题Mlnf(x)，x ∈R n 给出一初始值x1，算法选代产生x2，x3,x4,x 5，…．希望某一k X是目标函数解或点收敛于解，在我们这次的运筹学课程设计当中我们正是用这种方法要求解最小问题的最优解的。

关键字：共轭梯度法；无约束优化AbstractConjugate gradient method was first used by Hestenes and Stiefle (1952) put forward for the solution of positive definite coefficient matrix of linear equations, on this basis, Fletcher and Reeves (1964) first put forward about the problem of nonlinear optimization conjugate gradient method.The conjugate gradient method to solve unconstrained nonlinear optimization problems, one of the important ways, as the conjugate gradient method is between steepest descent method and Newton's method between a method, it requires the use of a first-order derivative information, But the steepest descent method to overcome the shortcomings of slow convergence, but also avoid the need to store and calculate Newton's method and the inverse Hesse matrix of the shortcomings of the conjugate gradient method is not only a large-scale linear equations to solve one of the ways the most useful, but also large-scale solution nonlinear optimization algorithm is the most effective one.Conjugate gradient for the unconstrained optimization problem Mlnf (x), x ∈ given an initial value of x1, the election algorithm is generated on behalf of the x2, x3, x4, x 5, .... Hope that is the objective function of a solution or point of convergence in the solution, in our curriculum design, operations research this is exactly what we were using this method requires the smallest solution of the problem the optimal solution.Keywords: conjugate gradient method；unconstrained nonlinear optimization目录一、共轭梯度法的概念....................................................... 错误！未定义书签。