新人教版七年级上册数学4.1 几何图形导学案
人教版七年级数学上册导学案 第四章几何图形初步 4.1.1立体图形与平面图形

人教版七年级数学上册导学案第四章几何图形初步 4.1.1立体图形与平面图形【学习目标】1.认识以生活中的事物为原型的几何图形;2.认识一些简单几何体的基本特性,能识别这些简单几何体.3.能由实物形状想象出几何图形,由几何图形想象出实物形状;初步理解立体图形与平面图形.【课前预习】1.下列各组图形中都是平面图形的是()A.三角形、圆、球、圆锥B.点、线段、棱锥、棱柱C.角、三角形、正方形、圆D.点、角、线段、长方体2.按组成面的平或曲划分,与圆柱为同一类的几何体是()A.长方体B.正方体C.棱柱D.圆锥3.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A.中B.考C.顺D.利4.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是()A.三棱柱B.四棱柱C.三棱锥D.四棱锥5.乐乐玩橡皮泥时,将一个底面直径为4cm,高为4cm的圆柱,捏成底面直径为3.2cm的圆柱,则圆柱的高变成了()A.7.5cm B.6.25cm C.5cm D.4.75cm6.一个无盖的正方体盒子的平面展开图可以是下列图形中的()A.图2B.图1或图2C.图2或图3D.图1或图37.如图,点D,E,F分别是等边三角形ABC的边AB,BC,CA的中点,现沿着虚线折起,使A,B,C三点重合,折起后得到的立体图形是( )A.正方体B.圆锥C.棱柱D.棱锥8.下列几何体中,属于棱柱的有()A.6个B.5个C.4个D.3个9.下列所述物体中,与球的形状最类似的是()A.电视机B.铅笔C.西瓜D.烟囱冒10.奥运会的标志是五环,这五环的每一个环的形状与下列图形中类似的是()A.三角形B.正方形C.圆D.长方体【学习探究】自主学习阅读课本,完成下列问题1、观察下列几何图形(1)图中的长方体、正方体都有六个面,它们的各部分不都在__________内。
部编RJ人教版 初一七年级数学 上册第一学期秋季(导学案)第四章 几何图形初步(全章 分课时)

第四章 几何图形初步. .根据已有的数学经验,我们能否把它们进行分类?你的标准是什么?要点归纳2. 观察小茗的房间,说说你能看到哪些立体图形.探究点3:平面图形观察与思考:说一说下面这些几何图形又有什么共同特点?画一画A. ①⑤①B. ①C. ①⑤⑥D. ⑤⑥4. 月球、西瓜、易拉罐、篮球、热水瓶胆、书本等物体中,形状类似圆柱的有6. 图中的各立体图形的表面包含哪些平面图形?试指出这些平面图形在立体图形中的 位置.第四章 几何图形初步4.1 几何图形4.1.1 立体图形与平面图形第2课时 从不同的方向看立体图形和立体图形的展开图学习目标:1. 了解立体图形与平面图形之间的联系.2. 能画出简单立体图形从不同方向看得到的平面图形.3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不 同的平面展开图.4. 通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面 展开图或根据展开图判断立体图形.重点:了解立体图形从不同方向看能够得到平面图形,了解基本几何体与其展开图的关 系,体会一个立体图形可以有多种展开图.难点:会画简单立体图形从不同方向看得到的平面图形,能够画出简单立体图形的展开 图,或根据展开图判断立体图形.二、要点探究探究点1:从不同的方向看立体图形 合作探究:画出正方体、长方体、圆柱体、圆锥、四棱锥、三棱柱从正面、左面、上面看得到的平面图形.这些展开图有没有什么规律?哪些展开图可以分为一类,为什么?2. “坚”在下,“就”在后,“胜”和“利”在哪里?3. 下面图形是一些多面体的表面展开图二、课堂小结常见几何体的展开图:1. 下图所示的从正面、上面看到的图形对应的是 ( )2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )3. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面图形,这些相同的小正方体的个数是 ( ) A .4个B .5个C .6个D .7个4. 下列的三幅平面图是三棱柱的表面展开图的有(多选) ( )5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .第四章几何图形初步..包,线和线相交的地方是.这可以说成点动成线. 类如下图,围成这些立体图形的各个面中,哪些面是平的?哪些面是曲的?请把下图中的平面图形与其绕轴旋转一周后得到的立体图形连接起来.,宽为2cm的长方形,绕其一边进行旋转得到一几何体.这个几何体是什么?4.2 直线、射线、线段第1课时 直线、射线、线段.. ..将你联想到的图形填在图形下边的横线上(填._________________ _______________ ________________ 2.自己动手,分别画一条直线、射线和线段. A ,B 可以画几条直线? .简称:两点确定一条直线.. 并使其不能转动,至少需要几个钉子?你知道这样做 .A.B相交于点O4.2 直线、射线、线段第1课时 直线、射线、线段... ....AB )等于已知线段(a )的作法: AC 上截取AB=a.,CD 的长短.AB 、CD 的长度,再进行比较:几何语言:∵ M 是线段 AB第3题图第1题图第2题图要点归纳:1.两点的所有连线中,_____最短.简称:两点之间,2.连接两点间的线段的,叫做这两点的距离.两个村庄,如图,现在要在公路l上建一个汽两村庄的距离之和最小,请在图中画出汽车站的位置第2题图4.3 角4.3.1 角.... ._______组成的图形,叫做角.这个公共端点叫做角的叫做角的两条边.四、我的疑惑______________________________________________________________________________________________________________________________________________________六、要点探究探究点1:角的概念及表示方法问题1 有哪些方式可以表示如图所示的角?问题2 下图中有哪些角?如何表示?还能用∠O 表示∠AOB 吗?要点归纳:角的表示方法:①用一个大写字母表示,该大写字母表示的点为顶点;②用三个大写字母表示;③用一个数字或一个小写希腊字母表示.注意:①当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示;②当用三个大写字母表示角时,必须把顶点字母放在中间;③用数字或希腊字母表示角时,一定要在图形中用角弧标出.思考:角也可以看做由一条射线绕着它的端点旋转所形成的图形. 如图,射线OA 绕点O 旋转,当终止位置OB 和起始位置OA 成一条直线时,形成什么角?继续旋转,OB 和OA 重合时,又形成什么角?1.用一个大写字母表示:∠_____2.用三个大写字母表示:∠_____或∠_____3.用一个小写希腊字母或数字表示:∠_____图中的角有___________________________________ ____________________________________________. ___________(填“能”或不能)用∠O 表示∠AOB.下列说法正确的是平角是一条直线填写下表,将图中的角用不同方法表示出来.°.1°=′;针对训练1.计算:(1)5°=(3)36″=当堂检测5.如图所示:-1) 条呢?4.3 角4.3.2 角的比较与运算....针对训练如图所示:(1) ∠AOC是哪两个角的和?(2) ∠AOB是哪两个角的差?(3) 如果∠AOB=∠COD,则∠AOC与∠BOD的大小关系如何?(1) 如图①,若∠AOC=35°,∠BOC=40°,则∠AOB=度.(2) 如图②,若∠AOB= 60°,∠BOC=40°,则∠AOC=度.(3) 若∠AOB=60°,∠AOC=30°,则∠BOC=度.易错提醒:在计算角的度数时,若无图,一定要注意分类讨论.试一试:如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?例2计算(1)120°-38°41′;(2)67°31′+48°49′.的角的射线,叫做这个角的平分线..4.3.3 余角和补角... . 1+∠2= °, 图① 90°(直角),就说这两个角互为______ (简称为两个角______ ). 是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.180°(平角),就说这两个角互为______ (简称为两个角______). 是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.的补角探究点3:方位角八大方位 正东: 正南: 正西: 正北: 西北方向: 西南方向: 东北方向: 东南方向:例4 如图,货轮O 在航行过程中,发现灯塔A 在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北 (即北偏西45°)方向上又分别发现了客轮B ,货轮C 和海岛D . 仿照表示灯塔方位的方法画出表示客轮B ,货轮C 和海岛D 方向的射线.针对训练1. 如图,说出下列方位(1) 射线 OA 表示的方向为 . (2) 射线 OB 表示的方向为 .(3) 射线 OC 表示的方向为 . . (4) 射线 OD 表示的方向为 .2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?的北偏东60°的方向上,那么点A在点C。
人教版七年级数学上《几何图形》导学案第1第2课时

4.1.1《几何图形》主备人:谢党育班级:姓名:【学习目标】1.能认识一些简单几何体的基本特性,并识别这些几何体。
2.探索平面图形与立体图形之间的关系.【重点难点】重点:从现实物体中抽象出几何图形,•把立体图形转化为平面图形。
难点:立体图形与平面图形之间的转化是难点。
【学前准备】回忆并写出:你所学过或熟悉的几何图形______________________【探究新知】自学教材116页-118页,完成下面学习内容:1.我们把从______________中抽象出的各种图形统称为几何图形。
2.有些图形的各部分不都在_____________,它们是立体图形。
练习:(1)写出下列物体类似的立体图形:数学课本(),金字塔(),西瓜(),日光灯()(2)请你再列举一下类似的例子如_____________ __________________(3)常见的立体图形有 _______________________________________________(4)棱柱和棱锥也是常见的__________图形,你能说出它们的特征吗?3.有些几何图形的各部分都在__________,它们是平面图形。
如____________常见的平面图形有 _______________________________。
【当堂练习】1.把下列立体图形与对应的名称用线连起来。
圆柱圆锥正方体长方体棱柱球2.下面图形中叫圆柱的是()3.长方体共有()个面.A.8 B.6 C.5 D.44.下列说法,不正确的是()A.圆锥和圆柱的底面都是圆.B.棱锥底面边数与侧棱数相等.C.棱柱的上、下底面是形状、大小相同的多边形.D.长方体是四棱柱,四棱柱是长方体.5.正方体有个面,个顶点,经过每个顶点有条棱.这些棱的长度(填相同或不同).棱长为acm的正方体的表面积为cm2.6.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.7.如图,小强拿一张正方形的纸,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线剪去一个角,再打开后的形状是()8.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?【课堂小结】1.本节课你有哪些收获?2.预习时的疑难解决了吗?你还有哪些疑惑?【拓展练习】1、完成教材123页习题4.1第1、2、3题2、写出下列几何体的名称【教学反思】4.1.2几何图形主备人:成先军班级:姓名:【学习目标】1.能画出一些基本几何体以及它们的简单组合得到的平面图形。
七年级数学上册 4.1 几何图形导学案(新版)新人教版

几何图形学习目标:1. 能画出从不同方向看一些基本几何体(直棱柱、圆柱、圆锥、球)。
2、在立体图形与平面图形相互转换的过程中,提高空间想象能力。
一、自主学习1.说一说:分别从正面、左面、上面观察乒乓球、粉笔盒、茶叶罐,各能得到什么平面图形?(出示实物)画一画:长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.(出示实物)2.动手画一画,从正面看、左面看、上面看得到的平面图形,并进行展示3、试一试 把一个长方体的包装盒沿剪开,铺平,看看它的展开图由哪些平面图形组成;再把展开的纸板复原,你有什么体会?4、比一比你们组的长方体的展开图与其他组的是否一样?二、归纳小结收获是遇到的困难是三、自我检测1.如图所示的物体,从左面看得到的图是( )2. 如图(1)放置的一个机器零件,若从正面看是如图(2),则其左面看是( )(A ) (B ) (C ) (D ) ( 2) ( 1) (第2题)3. 若左图是某几何体的三种不同方向的图,则这个几何体是( )A.圆柱B.正方体C.球D.圆锥4. 如图所示是由四个相同的小正方体组成的立体图形,从上面看到的图形( )5. 如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为6的面是底面,则朝上一面所标注的数字为( )A.5B.426. 如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是( )A .北B .京C .奥D .运7. 如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为6的面是底面,则朝上一面所标注的数字为( )A.5B.4 C.3D.28.下列图形中,不是正方形的表面展开图的是( )A . B. C .9. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )A .和B .谐 C.凉 D .山 正面 左面 上面 4题A . B . C . D . 第5题图第7题图 建 设 和 谐 凉山第9题图10. 下面形状的四张纸板,按图中线经过折叠可以围成一下直三棱柱的是( )。
七年级数学上册 第四章 几何图形初步导学案 (新版)新人教版

第四章图形认识初步第1学时 4.1.1 几何图形(1)学习目标:1.观察生活中的实物或图片,认识以生活中的事物为原型的几何图形;认识一些简单几何体的基本特性,能识别这些简单几何体.2.能由实物形状想象出几何图形,由几何图形想象出实物形状;初步理解立体图形与平面图形.学习重点:识别简单几何体.学习难点:从具体事物中抽象出几何图形.使用要求:1.阅读课本P115-P118;2.尝试完成教材P118的两组思考的问题;3.限时25分钟完成本导学案(合作或独立完成均可);4.课前在小组内交流展示.一、自主学习:1.观察P115本章的章前图:(1)知道这是什么地方吗?你对它了解多少?(可上网查找)(2)你能从中找到我们熟悉的图形吗?找找看.2.多姿多彩的图形美化了我们的生活,找一找我们生活中的你熟悉的图形.3.你能不能设计一个装墨水的墨水盒?你能不能画出一个五角星?如果能,你就试一试,如果不能,那就让我们一起走进多姿多彩的图形世界,共同学习.二、合作探究:1.观察P116的9张多姿多彩的图片,你能从中看出哪些熟悉的几何图形,与同学交流你观察到的图形.【老师提示】:对于一个物体,如果我们考虑它的颜色、材料和重量等,而只考虑它的形状(如方的、圆的)、大小(如长度、面积、体积)和位置(如平行、垂直、相交),所得到的图形就称为几何图形.如:我们学习过的长(正)方体、圆柱(锥)体、长(正)方形、圆、三角形、四边形等都是几何图形.2.立体图形:各部分不都在同一平面内的图形,叫做立体图形.①长方体、正方体、圆柱、圆锥、球等都是立体图形,棱柱、棱锥也是常见的立体图形.找一找生活中有哪些物体的形状类似于这些立体图形?(小组交流)②观察P117图4.1-3,你能由实物想到几何图形及其形状吗?③完成P118思考的问题(上),并与你的同学交流.【老师提示】:常见..的立体图形大致分为:柱体(圆柱、棱柱)、锥体(圆锥、棱锥)、球体三类.3.平面图形:各部分都在同一平面内的图形,叫做平面图形.①长方形、正方形、三角形、四边形、圆等都是平面图形.找一找生活中的平面图形,与同学交流.②完成P118思考的问题(下)4.立体图形与平面图形是两类不同的几何图形,但他们是互相联系的.任何一个立体图形图形是由一个或几个平面图形围成的.看看下面的几个立体图形是由怎样的平面图形围成的?5.下面都是生活中的物体:粉笔盒、茶杯、文具盒、砖、铅垂仪、乒乓球、黑板面.你能说出类似于这些物体的几何图形吗?三、知识应用:1.P119练习题.2.用两条线段、两个三角形、两个圆拼成图案.试着画几个,并取一个恰当的名字.机器人两盏电灯稻草人四、学习小结:五、作业:P123习题4.1第1、2、3、7、8题.(有条件的同学可准备10个正方体形状的积木,下课时备用)附:① 2008年北京奥运会即第二十九届夏季奥林匹克运动会,于2008年8月8日20时开幕,于2008年8月24日闭幕.②本届奥运会口号为“同一个世界,同一个梦想”,主办城市是中国北京.③参赛国家及地区204个,参赛运动员11438人,设302项(28种运动)比赛项目④中国51金,21银,28铜.金牌数第一,奖牌总数第二.第2学时 4.1.1 几何图形(2)学习目标:1.从不同方向观察一个物体,体会其观察结果的不一样性.2.能画出从不同方向看一些基本几何体或其简单组合得到的平面图形.3.初步建立空间观念.学习重点:识别并会画出从不同方向看简单几何体所得到的平面图形.学习难点:识别并会画出从不同方向看简单组合体所得到的平面图形.使用要求:1.阅读课本P1192.尝试完成教材P120练习第1题;3.限时15分钟完成本导学案(合作或独立完成均可);4.课前在小组内交流展示.一、自主学习:1.观察你身边的一个物体,试着从不同的角度去看它,你看到的形状是一样的吗?2.下面这几个几何体,试着从不同角度去看看,你得到了怎样的几何图形?【老师提示】:我们从不同的方向观察同一个物体时,可能看到不同的图形.为了能完整确切地表达物体的形状和大小,必须从多方面观察物体.在几何中,我们通常选择从正面、从左面、从上面三个方向来观察物体.通过这样的观察,就能把一个立体图形用几个平面图形来描述.3.分别正面、左面、上面再来观察上面的三个几何体,把观察的结果与同学交流.二、合作探究:1.分别从正面、左面、上面三个方向观察下面的几何体,把观察到的图形画出来.(1)从正面看从左面看从上面看(2)从正面看从左面看从上面看(3)从正面看从左面看从上面看2.先阅读P119的教材再完成P119的探究.(1)小组合作,可用正立体积木摆出书上的立体图形,再观察.(2)改变正立体积木的摆放位置,你摆我答,合作学习.(3)观察身边的几何体,如文具盒、同学的水杯等物品,与同学交流分别从正面、左面、上面所看到的几何图形.【老师提示】对于一些立体图形的问题,常把它们转化为平面图形来研究和处理. 3.P120练习第1题.3.苏东坡有一首诗《题西林壁》“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”为什么横看成岭侧成峰?这有怎样的数学道理?三、学习小结:四、作业:P123习题4.1第4、9、10、13题.(准备长方体形状的包装盒至少一个)第3学时 4.1.2 点、线、面、体学习目标:1.认识立体图形和它的展开图,体验平面图形和立体图形相互转换的过程.2.通过实例,认识点、线、面、体的几何特征,感受它们之间的关系.学习重点:1.了解基本几何体与其展开图之间的关系.2.认识点、线、面、体的几何特征.学习难点:正确判断一个平面图形能否可以折叠为立体图形.使用要求:1.阅读课本P120—P1222.尝试完成教材P121练习第2题,P122练习第1、2题;3.限时30分钟完成本导学案(合作或独立完成均可);4.课前在小组内交流展示.一、自主学习:1.立体图形是由平面图形围成的.观察你身边的长方体形状的包装盒,看一看它有几个面,每个面分别是怎样的平面图形,给每个面作上记号(如前、后等).右边是一个圆柱体,想一想它有几个面?2.把你刚才观察用的长方体形状的包装盒沿它的某几棱剪开铺平,观察展开后的平面图形形状,再观察你作上记号,看看它们之间有怎样的位置关系.【老师提示】①剪开之前最好先把它的包装口用胶水粘好.②不用把棱全部都剪开,只要能铺平就行了.3.再找几个长方体形状的包装盒,沿与上次不一样的方向剪开铺平,看一看你展开后的平面图形与上次展开后的平面图形是否有所不同?你能得出几种不同形状的平面展开图.4.观察一个长方体,面与面相交的地方形成了____,线与线相交的地方形成了___.5.长方体、圆柱体、球、圆锥等都是几何体.几何体也简称体.(1)包围着体的是面.面分为平面和曲面两种.如图的圆锥体有两个面,一个是平面,另一个是曲面.如图的六棱柱有_____个面,分别都是什么面?如图的圆柱有_______个面,分别都是什么面?(2)面与面相交的地方形成线.线分为直线和曲线两种.圆锥体的两个面相交形成_______线.(3)线与线相交形成点.6.(1)如果把笔尖可能看作一个点,笔尖在纸上运动会形成什么_______.如果把星星看作一个点,夜空中流星形成什么________.(2)我们可以把汽车的雨刷看成一条线,汽车的雨刷在挡风玻璃上运动形成____.生活中还有这样的例子吗?由此我们可以得出:点动成_____,线动成______.想一想,面动会成什么?生活中有没有这样的例子?【老师提示】:几何图形都是由点、线、面、体组成的,点是构成图形的最基本元素.二、合作探究1.P120的探究.(小组合作.先判断是什么样的立体图形,后动手实验验证)2.P121练习第2题.3.P122练习第1、2题.4.一个立方体的六个面上分别标有1、2、3、4、5、6中的一个数字,下面是这个立方体的三种不同放法,则三种放法中各个立方体下面的数字分别是____、___、____.左左左下下上上上下242625516三、学习小结:四、作业:P123习题4.1第5、6、11、12、14题.附:正方体展开图,共11种图形。
人教版-数学-七年级上册-4.1几何图形1 导学案

七年级(上)数学导学案班级姓名第四章几何图形初步学习目标:1、认识以生活中的事物为原型的几何图形和一些简单的几何体的基本特征。
2、能识别这些几何体,能由实物的形状想象出几何图形,由几何图形想象出几何图形。
3、通过与其他同学的交流活动,初步行成积极参与数学活动,主动与他人合作交流的意识。
学习重点:识别简单几何体。
学习难点:从具体事物中抽象出几何图形。
学法指导:学生合作交流学习,培养学生合作学习的习惯。
1、在小学你学过哪些几何图形?2、在日常生活中你能举出一些常见的图形吗?1、章前图中你能找出一些熟悉的图形吗?2、对各种各样的物体数学中是关注它们的什么?3、什么叫哦几何图形?它包括哪类图形?1、如下图的各立体图形的表面中包含哪些平面图形?试指出这些平面图形在立体图形中的位置。
2、如图,是圆柱的有_________________,是棱柱的有__________________。
(只填标号)课前预习课中探究一二三面常见平面图形平面图形立体图形常见立体图形几何图形1、 什么叫几何图形?什么叫立体图形?什么叫平面图形?2、 立体图形的表面都是由平面图形组成的吗?3、 简单的立体图形有柱、锥、球等我们可以按照这个标准来分类,还可以按照别的标准来分类吗?(一) 基础知识探究探究点:实物与几何图形的互化问题1:在P115思考题(如茶叶罐、地球仪、字典、魔方等)它与我们学过的哪些几何图形相类似? 问题2:在生活中有哪些物体的形状类似于棱柱、圆柱、棱锥、圆锥、球等? 问题3:完成在P116的思考题。
(二) 知识综合应用探究 探究点:例1:将下列立体图形分类,并说明理由。
思考1:若按立体图形柱、锥、球等分类应怎样分?思考2:若按立体图形的表面是否都是平面来分类(表面都是平面的立体图形叫多面体)应怎样分? 方法提炼:例2:将如下图所示的平面图形折成一个立方体,会得到下列选项中的( )思考:将带有“◇”的面折放在前面,想象其它面于它的位置关系怎样?方法提炼:二三 一1、下列图形是圆柱的是()2、下列图形不是棱柱的是()基础知识应用一、选择题1、如图,下列图形是柱体的是()二、填空题2、如下图所示,这些物体所对应的立体图形分别是:___________.3、如下图所示的几何体所对应的立体图形的名称分别是________,•从正面看这些立体图形可得到的平面图形分别是__________.课后训练四综合、运用、探究7、★用一个宽2 cm,长3 cm的矩形卷成一个圆柱,则此圆柱的侧面积为_______________.拓展、探究、思考8、★★下图为一个三棱柱,用一个平面去截这个三棱柱,截面形状可能为下图中的_____________(填序号)【省以致善】。
【最新】人教版七年级上册4.1.1几何图形(2) 导学案
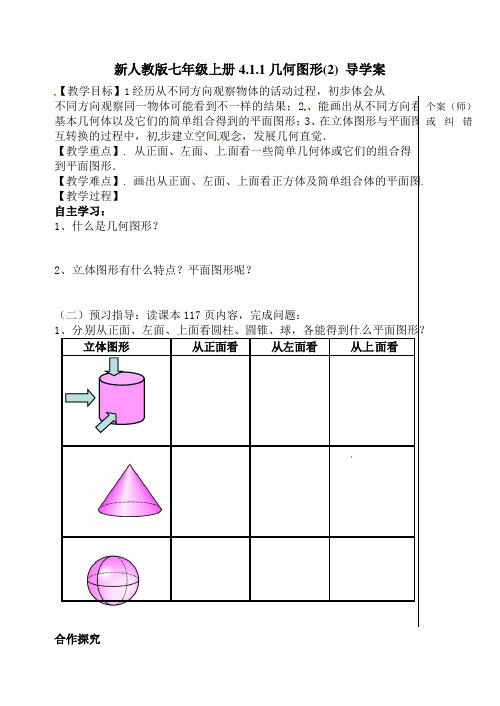
新人教版七年级上册4.1.1几何图形(2) 导学案【教学目标】1经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果;2基本几何体以及它们的简单组合得到的平面图形;3、互转换的过程中,初步建立空间观念,发展几何直觉.【教学重点】.从正面、左面、上面看一些简单几何体或它们的组合得到平面图形.【教学难点】.【教学过程】自主学习:1、什么是几何图形?2、立体图形有什么特点?平面图形呢?(二)预习指导:读课本117页内容,完成问题:、分别从正面、左面、上面看圆柱、圆锥、球,各能得到什么平面图形?从上合作探究探究点一:从不同方向看几何体说明:对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.从不同方向看立体图形,往往会得到不同形状的平面图形.在建筑、工程等设计中,也常常用从不同方向看到的平面图形来表示立体图形.1、分别从正面、左面、上面观察这个长方体,看一看各能得到什么平面图形?2、这是一个工件的立体图,请你画出从不同方向看到的几何图形:3、分别从正面、左面、上面观察三棱柱和四棱锥,看一看各能得到什么平面图形?探究点二:从不同方向看正方体的组合体1、如图是一个由 9 个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,各能得到什么平面图形?2、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
①你能说出它是由几个小立方体所搭成的?②画出这个几何体的主视图与左视图。
三、当堂检测1、下图中,不是左图所示物体视图的是( )2、如图,填出视图的名称:3、如图,填出视图的名称:4、画出下列实物的三视图:5、画出下面这些几何体的三视图:。
新人教版七年级上册数学导学案:4.1.1几何图形

新人教版七年级上册数学导学案:4.1.1几何图形课题课时使用者上课时间4.1.1几何图形第1课时学习目标1、通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形,认识一些简单几何体(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等)的基本特性,能识别这些几何体.2、能由实物形状想象出几何图形,由几何图形想象出实物形状,进一步丰富学生对几何图形的感性认识.3、从现实世界中抽象出几何图形的过程,感受图形世界的丰富多彩,激发对学习空间与图形的兴趣,通过与其他同学交流、活动,初步形成参与数学活动,主动与他人合作交流的意识。
重点识别简单几何体难点从具体事物中抽象出几何图形教学过程一、自主学习(一)、阅读教材116-118页。
(二)、导学练习1.把下列几何图形与对应的名称用线连起来.圆柱圆锥正方体长方体棱柱球2.分别画出下列平面图形:长方形正方形三角形圆3.如图,上面是一些具体的物体,下面是一些立体图形, 试找出与下面立体图形相类似的实物(用线连接).(三)自学疑难摘要:二、合作探究1.长方体有_____个顶点,经过每个顶点有______条边,共有_____条边.2.把一个八边形的一个顶点与其余各顶点连接,•可把这个八边形分割成______个三角形.3.图2中的几何体有_____个面,面与面相交成______条线.4.数一数图3中共有_____个三角形.5.如图4所示,图形绕虚线旋转一周得到的立体图形是______.(2) (3) (4)6圆柱和棱柱的相同之处在于________.7.如图,四个图形分别是四个公司的标志,请用线将它们联系起来:中国联合通信有限公司摩托罗拉(中国)电子有限公司方正数码有限公司中国电信集团公司三、展示提升1、每个同学自主完成二中的练习后先在小组内交流讨论。
2、每个组根据分配的任务把自己组的结论板书到黑板上准备展示。
3、每个组在展示的过程中其他组的同学认真听作好补充和提问。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新人教版七年级上册数学4.1 几何图形导学案
学习目标:1.观察生活中的实物或图片,认识以生活中的事物为原型的几何图形;认识一些简单几何体的基本特性,能识别这些简单几何体.
2.能由实物形状想象出几何图形,由几何图形想象出实物形状;初步理解
立体图形与平面图形.
学习重点:识别简单几何体.
学习难点:从具体事物中抽象出几何图形.
使用要求:1.阅读课本P115-P118;
2.尝试完成教材P118的两组思考的问题;
3.限时25分钟完成本导学案(合作或独立完成均可);
4.课前在小组内交流展示.
一、自主学习:
1.观察P115本章的章前图:
你能从中找到我们熟悉的图形吗?找找看.
2.多姿多彩的图形美化了我们的生活,找一找我们生活中的你熟悉的图形.
二、合作探究:
1.观察P116的9张多姿多彩的图片,你能从中看出哪些熟悉的几何图形,与同学交流你观察到的图形.
【老师提示】:对于一个物体,如果我们考虑它的颜色、材料和重量等,而只考虑它的形状(如方的、圆的)、大小(如长度、面积、体积)和位置(如平行、垂直、相交),所得到的图形就称为几何图形.如:我们学习过的长(正)方体、圆柱(锥)体、长(正)方形、圆、三角形、四边形等都是几何图形.
2.立体图形:各部分不都在同一平面内的图形,叫做立体图形.
①长方体、正方体、圆柱、圆锥、球等都是立体图形,
棱柱、棱锥也是常见的立体图形.
找一找生活中有哪些物体的形状类似于这些立体图形?(小组交流)
②观察P117图4.1-3,你能由实物想到几何图形及其形状吗?
③完成P118思考的问题(上),并与你的同学交流.
【老师提示】:常见
..的立体图形大致分为:柱体(圆柱、棱柱)、锥体(圆锥、棱锥)、球体三类.
3.平面图形:各部分都在同一平面内的图形,叫做平面图形.
①长方形、正方形、三角形、四边形、圆等都是平面图形.
找一找生活中的平面图形,与同学交流.
②完成P118思考的问题(下)
4.立体图形与平面图形是两类不同的几何图形,但他们是互相联系的.任何一个立体图形图形是由一个或几个平面图形围成的.
看看下面的几个立体图形是由怎样的平面图形围成的?
5.下面都是生活中的物体:粉笔盒、茶杯、文具盒、砖、铅垂仪、乒乓球、黑板面.你能说出类似于这些物体的几何图形吗?
三、知识应用:P119练习题.
四、学习小结:
五、作业:P123习题4.1第1、2、3、7、8题.
(有条件的同学可准备10个正方体形状的积木,下课时备用)。
