您的位置：360文档中心› 实验二源-负载耦合的交叉耦合滤波器设计与仿真

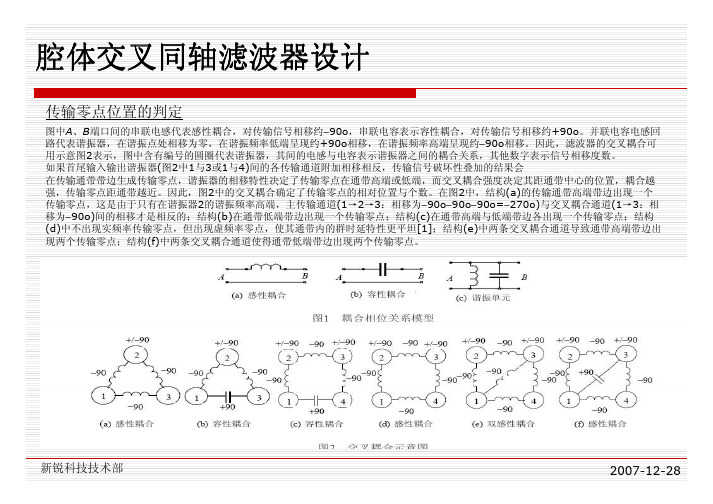
实验二源-负载耦合的交叉耦合滤波器设计与仿真

合集下载
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相关文档
最新文档