三视图练习题含答案
三视图及尺寸标注练习汇总(含答案)
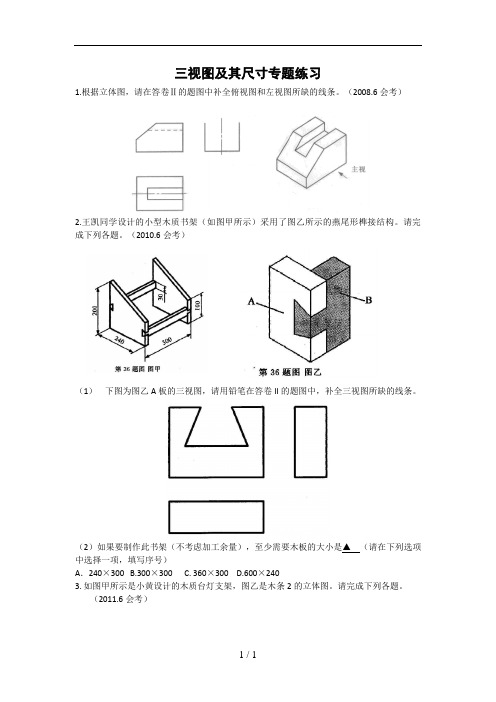
三视图及其尺寸专题练习1.根据立体图,请在答卷Ⅱ的题图中补全俯视图和左视图所缺的线条。
(2008.6会考)2.王凯同学设计的小型木质书架(如图甲所示)采用了图乙所示的燕尾形榫接结构。
请完成下列各题。
(2010.6会考)(1)下图为图乙A板的三视图,请用铅笔在答卷II的题图中,补全三视图所缺的线条。
(2)如果要制作此书架(不考虑加工余量),至少需要木板的大小是▲(请在下列选项中选择一项,填写序号)A.240×300 B.300×300 C. 360×300 D.600×2403. 如图甲所示是小黄设计的木质台灯支架,图乙是木条2的立体图。
请完成下列各题。
(2011.6会考)(1)下图为木2(图乙)的三视图,请用铅笔在题图中,补全三视图所缺的线条。
(2)制作完成后,发现该台灯支架的稳定性不够好,小黄想通过加长木条来提高稳定性,则图甲中适合加长的木条是________。
(填写木条编号)4..图甲是一款台灯。
支撑架、底座中的木条可相对转动,以调整台灯照明角度和姿势。
请完成下列各题。
(2012.6会考)(1)图乙为该台灯中一根木条的立体图及其三视图,请用铅笔在答卷n的题图中,补全三视图所缺的图线。
(2)要实现木条间可转动,连接方式应该选择▲ (选填“铰连接”或“刚连接”)。
5.如图甲所示的榫接结构,由木条①和木条②组成。
请完成下列各题。
(2013.6会考)图甲(1)图乙为木条①的立体图及其三视图,请用铅笔在题图中,补全三视图所缺的图线。
图乙(2)木条②的立体图应该是_________。
6.根据立体图,补全俯视图和左视图中所缺漏的图线。
(2008.10 高考)7.根据立体图补全三视图中所缺的图线。
(2009.3 高考)8.根据立体图补全三视图中所缺的图线。
(2009.9 高考)9.根据轴测图,补全三视图中缺少的图线。
(2010.3高考)10.根据轴测图,补全三视图中缺少的图线。
八年级上数学三视图练习4(含答案)
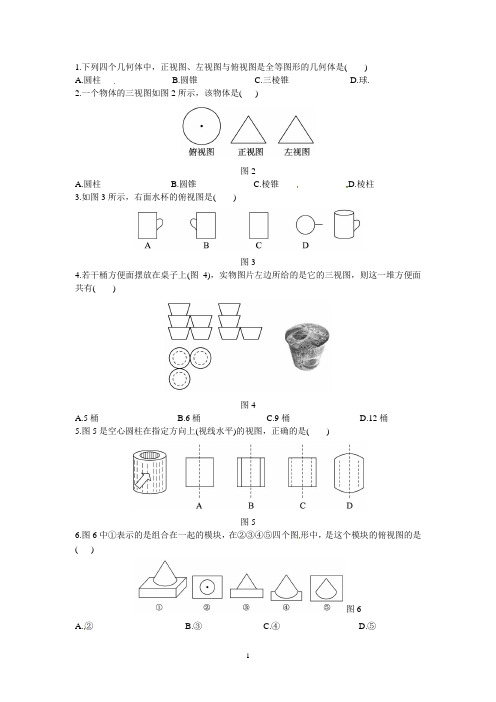
1.下列四个几何体中,正视图、左视图与俯视图是全等图形的几何体是( )
A.圆柱
B.圆锥
C.三棱锥
D.球.
2.一个物体的三视图如图2所示,该物体是( )
图2
A.圆柱
B.圆锥
C.棱锥
D.棱柱
3.如图3所示,右面水杯的俯视图是( )
图3
4.若干桶方便面摆放在桌子上(图4),实物图片左边所给的是它的三视图,则这一堆方便面共有( )
图4
A.5桶
B.6桶
C.9桶
D.12桶
5.图5是空心圆柱在指定方向上(视线水平)的视图,正确的是( )
图5
6.图6中①表示的是组合在一起的模块,在②③④⑤四个图形中,是这个模块的俯视图的是( )
图6
A.②
B.③
C.④
D.⑤
7.图7分别是什么的三视图(填教学用品或日常用品各一个).
图7
8.下列物体(如图8)是由四个小正方形搭成的,请画出它的正视图,左视图和俯视图.
图8
9.如图9为一个槽形工件,它是长方体中间切去了一个小的三角块,工人师傅要得到它的平面图形,请你画出它的三视图.
10.(2010湖北武汉模拟) 下图中几何体的主视图是( )
11.(河北模拟) 图1中几何体的主视图是( )
12.(山东泰州模拟) 如图所示的正四棱锥的俯视图是()。
三视图习题50道(含答案)

word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题(单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2(主)视图与侧(左)视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示,则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图,该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示,则其侧.面积等于(A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h=7、 一个几何体的三视图如图所示 ,则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图(也称主视图)是()8、如图,网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形,)S 2a.俯视图正(主)视图侧(左)视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示,则该几何体的体积为().A.2 2.3B. 4 2 . 3侧(左)视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c m2)为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。
三视图(含答案)

立体几何三视图1. 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是()A. 17πB. 18πC. 20πD. 28π2. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A. 20πB. 24πC. 28πD. 32π3. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A. 90πB. 63πC. 42πD. 36π4. 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为()A. 13+23πB. 13+ 23π C. 13+ 26π D. 1+ 26π5.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A. 32B. 23C. 22D. 26.某几何体的三视图如图所示,则该几何体的体积是()A. πB. 2πC. 4πD. 8π7.某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8 cm3B. 12 cm3C. 32cm33D. 40cm338.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的体积为()A. 13B. 16C. 83D. 439.如图为某几何体的三视图,根据三视图可以判断这个几何体为()A. 圆锥B. 三棱锥C. 三棱柱D. 三棱台10.堑堵,我国古代数学名词,其三视图如图所示.《九章算术》中有如下问题:“今有堑堵,下广二丈,袤一十八丈六尺,高二丈五尺,问积几何?”意思是说:“今有堑堵,底面宽为2丈,长为18丈6尺,高为2丈5尺,问它的体积是多少?”(注:一丈=十尺).答案是()A. 25500立方尺B. 34300立方尺C. 46500立方尺D. 48100立方尺11.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是()cm3A. πB. 2πC. 3πD. 4π12.某棱柱的三视图如图示,则该棱柱的体积为()A. 3B. 4C. 6D. 1213. 某几何体的三视图如图所示,则它的体积是( )A. 8−2π3B. 64−16π3C. 8−π3D. 64−12π3答案和解析1.【答案】A【解析】【分析】本题考查三视图求解几何体的体积与表面积,考查计算能力以及空间想象能力.判断三视图复原的几何体的形状,利用体积求出几何体的半径,然后求解几何体的表面积.【解答】解:由题意可知三视图复原的几何体是一个球去掉其中后的几何体,如图:可得:=,R=2.它的表面积是:×4π•22+=17π.故选A.2.【答案】C【解析】解:由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,∴在轴截面中圆锥的母线长是=4,∴圆锥的侧面积是π×2×4=8π,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π∴空间组合体的表面积是28π,故选:C.空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,在轴截面中圆锥的母线长使用勾股定理做出的,写出表面积,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,做出圆柱的表面积,注意不包括重合的平面.本题考查由三视图求表面积,本题的图形结构比较简单,易错点可能是两个几何体重叠的部分忘记去掉,求表面积就有这样的弊端.3.【答案】B【解析】【分析】由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,即可求出几何体的体积.本题考查了体积计算公式,考查了推理能力与计算能力,属于中档题.【解答】由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,V=π•32×10-•π•32×6=63π,故选:B.4.【答案】C【解析】【分析】本题考查的知识点是由三视图求体积,根据已知的三视图,判断几何体的形状是解答的关键.由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,进而可得答案.【解答】解:由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,半球的直径为棱锥的底面对角线,由棱锥的底底面棱长为1,可得.故,故半球的体积为:,棱锥的底面面积为:1,高为1,故棱锥的体积,故组合体的体积为:.故选C.5.【答案】B【解析】解:由三视图可得直观图,再四棱锥P-ABCD中,最长的棱为PA,即PA===2,故选:B.根据三视图可得物体的直观图,结合图形可得最长的棱为PA,根据勾股定理求出即可.本题考查了三视图的问题,关键画出物体的直观图,属于基础题.6.【答案】A【解析】解:由三视图可知,该几何体为一圆柱通过轴截面的一半圆柱,底面半径直径为2,高为2.体积V==π.故选:A.由三视图可知,该几何体为底面半径直径为2,高为2的圆柱的一半,求出体积即可.本题的考点是由三视图求几何体的体积,需要由三视图判断空间几何体的结构特征,并根据三视图求出每个几何体中几何元素的长度,代入对应的体积公式分别求解,考查了空间想象能力.7.【答案】C【解析】解:由已知中的三视图可得,该几何体是一个正方体与一个正四棱锥的组合体,且正方体的棱长为2,正四棱锥的高为2;所以该组合体的体积为V=V 正方体+V 正四棱锥=23+×22×2=cm 3.故选:C .根据已知中的三视图可分析出该几何体是一个正方体与一个正四棱锥的组合体,结合图中数据,即可求出体积.本题考查了由三视图求体积的应用问题,是基础题目.8.【答案】D【解析】 解:由三视图和题意知,三棱锥的底面是等腰直角三角形,底边和底边上的高分别为、,三棱锥的高是2,∴几何体的体积V==,故选:D .由三视图和题意知,三棱锥的底面边长和三棱锥的高,由锥体的体积公式求出几何体的体积.本题考查由三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.9.【答案】C【解析】解:该几何体的正视图为矩形,俯视图亦为矩形,侧视图是一个三角形,则可得出该几何体为三棱柱(横放着的)如图.故选C .如图:该几何体的正视图与俯视图均为矩形,侧视图为三角形,易得出该几何体的形状.本题考查简单几何体的三视图,考查视图能力,是基础题.10.【答案】C【解析】解:由已知,堑堵形状为棱柱,底面是直角三角形,其体积为立方尺.故选C.由三视图得到几何体为横放的三棱柱,底面为直角三角形,利用棱柱的体积公式可求.本题主要考查空间几何体的体积.关键是正确还原几何体.11.【答案】B【解析】解:由三视图可知:此几何体为圆锥的一半,圆锥的底面半径为2,高为3,圆锥的体积为V圆锥=.此几何体的体积为.故选:B.由三视图可知:此几何体为圆锥的一半,即可得出.本题考查了由三视图恢复原几何体的体积计算,属于基础题.12.【答案】C【解析】解:由已知中的三视图可得:该几何体上部是一个以俯视图为底面四棱柱,棱柱的底面面积S=×(2+4)×2=6,棱柱的高为1,故棱柱的体积V=6.故选:C.由已知中的三视图可得:该几何体上部是一个以俯视图为底面四棱柱,进而可得答案.本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.13.【答案】B【解析】解:由题意,几何体的直观图是正方体挖去一个圆锥,体积为=64-,故选B.由题意,几何体的直观图是正方体挖去一个圆锥,即可求出体积.本题考查的知识点是由三视图求体积,其中由已知中的三视图判断出几何体的形状,及棱长,高等几何量是解答的关键.。
三视图练习题

三视图练习题一、基本概念题1. 请简述三视图的概念及其作用。
2. 三视图包括哪三个视图?分别表示物体的哪些信息?3. 在三视图中,主视图、俯视图和左视图之间的位置关系是怎样的?二、识图题(1)正方体(2)长方体(3)圆柱体(1)球体(2)圆锥体(3)圆环体(1)三棱柱(2)四棱锥(3)六棱柱三、绘图题(1)一个长方体,长、宽、高分别为10cm、6cm、4cm。
(2)一个圆柱体,底面直径为8cm,高为10cm。
(3)一个圆锥体,底面直径为6cm,高为8cm。
(1)一把直尺(2)一个手机(3)一个茶壶四、分析题(1)主视图为矩形,俯视图为圆形,左视图为矩形。
(2)主视图为三角形,俯视图为矩形,左视图为三角形。
(1)主视图、俯视图和左视图均为正方形。
(2)主视图、俯视图和左视图均为圆形。
五、应用题(1)主视图为长方形,长、宽、高分别为10cm、6cm、4cm。
(2)主视图为圆形,直径为8cm,高为10cm。
(1)一个长方体木箱,长、宽、高分别为60cm、40cm、20cm。
(2)一个圆柱形水桶,底面直径为40cm,高为50cm。
六、综合题(1)一个长方体上放置一个正方体。
(2)一个圆柱体和一个圆锥体组合在一起。
(1)一个长方体挖去一个圆柱体形成的组合体,长方体的长、宽、高分别为20cm、10cm、5cm,圆柱体直径为5cm,高为10cm。
(2)一个正方体和一个四棱锥组合在一起,正方体边长为8cm,四棱锥底面边长为6cm,高为4cm。
七、判断题1. 三视图中,主视图和俯视图的长度方向一定相同。
()2. 在三视图中,左视图的宽度方向与主视图的高度方向一致。
()3. 任何物体的三视图都可以通过旋转和翻转得到。
()八、选择题A. 主视图B. 俯视图C. 正视图D. 左视图A. 主视图B. 俯视图C. 左视图D. 所有视图A. 主视图反映了物体的长度和高度B. 俯视图反映了物体的长度和宽度C. 左视图反映了物体的宽度和高度D. 三视图中的每个视图都包含了物体的所有尺寸信息九、填空题1. 三视图是用于表达物体______、______和______三个方向尺寸的图样。
三视图的应用练习题(答案)

①下图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数不可能是()。
A:3 B:4 C:5 D:6答案:D解析:3,4,5都可以参照俯视图②用若干个小立方体搭成一个几何体,使它从正面看与从左面看都是下面的同一个图,那么最多有多少个小立方体。
答案:13解析:底部最多9个,上面最多4个,所以最多13个。
参照俯视图③在墙角处堆着若干个相同的正方体箱子,问看不见的箱子共有多少个。
答案:35解析:第2层中看不见的箱子有1个。
第3层中看不见的箱子有1+2个。
第4层中看不见的箱子有1+2+3个。
第5层中看不见的箱子有1+2+3+4个。
第6层中看不见的箱子有1+2+3+4+5个。
所以看不见的箱子共有1+3+6+10+15=35个④下图是一个由8个棱长是2厘米的正方体组成的零件,求它的表面积。
答案:136(平方厘米)解析:正视图有6个正方形,左视图有4个正方形(有两个正方形看不见,需要另外加算),俯视图有6个正方形,每一个正方形的面积是4所以它的表面积是((6+4+6)×2+2)×4=136(平方厘米)⑤用若干个小立方体搭成一个几何体,使它从正面看与从左面看都是下面的同一个图,那么最少需要多少块小立方体。
答案:6解析:高的部分至少需要4块,旁边的需要2块即可,例如右图(俯视图)⑥一个由10个同样的正方体组成的零件,已知它的表面积是1000平方厘米,那么它的体积是多少答案:1250(立方厘米)解析:正视图有5个正方形,左视图有8个正方形,俯视图有7个正方形,设每一个正方形的面积是a平方厘米有方程(5+8+7)×2×a=1000解得a=25,即棱长是5,所以体积是5³×10=1250(立方厘米)。
三视图通关100题(含答案)
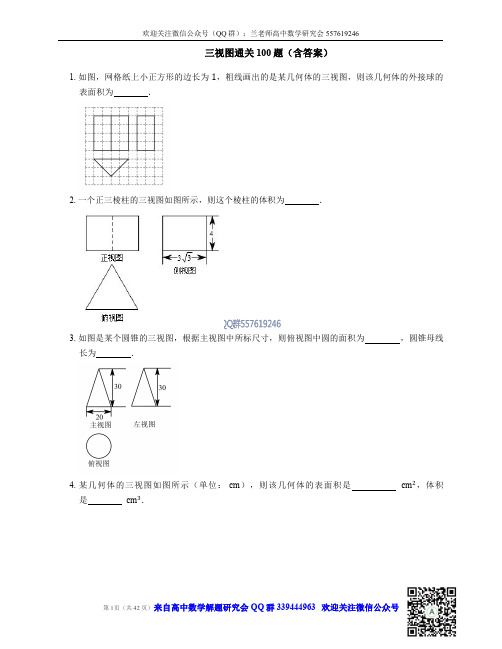
的正三角形,俯视图是等腰直角三角形,该几
51. 某几何体的三视图如图所示(单位: cm ),则该几何体的体积为 为 cm .
cm ,表面积
52. 如图是一个几何体的三视图,则这个几何体的体积为
.
53. 一空间几何体的三视图如右图所示,该几何体的体积为 为 .
π
表
,则正视图与侧视图中
的值
第 14页(共 42 页)来自高中数学解题研究会
72. 一个多面体从前面、后面、左侧、右侧、上方看到的图形分别如图所示(其中每个正方形边长 都为 ),则该多面体的表面积为 .
73. 已知正三棱锥 面积为 .
th 的正视图、俯视图如图所示,则该三棱锥的体积为
,侧视图的
74. 图中的三个直角三角形是一个体积为 㐸 cm 的几何体的三视图,该几何体的外接球表面积 为
42. 某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为
.
第 11页(共 42 页)来自高中数学解题研究会
QQ 群 339444963 欢迎关注微信公众号
欢迎关注微信公众号(QQ 群):兰老师高中数学研究会 557619246
43. 某几何体的三视图如图所示(单位:cm),则该几何体最长棱的棱长为
67. 一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形, 则该几何体的体积为 ,表面积为 .
68. 已知某三棱锥的三视图如图所示,则该三棱锥的体积为
,它的表面积为
.
69. 某几何体的三视图如图所示,则该几何体的外接球的球面面积为
第 18页(共 42 页)来自高中数学解题研究会
cm.
44. 一个四棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是 锥中侧面面积最大的是 .
三视图习题及答案

三视图练习
1.根据如图所示的组合体,在下列选项中选出正确的的左视图()
答案:B
2.如图所示为某组合体的三视图,下列主视方向(箭头方向)中与三视图对应的是
答案:A
6. [2018台州模拟]如图所示是一个模型的轴测图,其正确的三视图是()
答案:A
7.[2018浙江联考]如图所示是一个模型的轴测图,其正确的三视图是()
答案:A
8.[2018嘉兴模拟]图a是某零件的立体图,其主视图与俯视图如图b所示。
与之对应的左视图是()
答案:A
9.如图所示是某模型的三视图,下列模型中与其对应的是()
答案:D
10.[2018宁波模拟]如图所示为衣柜中支撑和固定挂衣杆的法兰座,通过自攻螺钉与木质衣柜连接,以下零件视图中,能实现法兰座功能的视图是()
答案:C
11.[2017嘉兴模拟]如图所示的结构,与构件1连接的结构正确的是()
答案:D
12.[2017.11浙江]如图所示是某形体的轴测图、主视图和俯视图,正确的左视图是()
答案:C
3. 请补全三视图中所缺的两条图线。
答案:
4. 请补全三视图中所缺的3条图线。
5. 请补全三视图中所缺的三条图线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正视图 侧视图
俯视图
第3题
三视图练习题 2013
1.某几何体的三视图如图所示,则它的体积是( ) A.283π-
B.83π-
C.π28-
D.23
π 2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )
A
.32 B.16+
16+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( )
A ..
4 C .
4.如图是某几何体的三视图,则该几何体的体积为( )
A .942π+ B.3618π+ C.9122π+ D.9182
π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( )
A. 48
B.
32+
6.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.
35233cm B.3203 3cm C.2243 3cm D.1603
3
cm
正视图
侧视图
俯视图
第4题
第5题
第1题 第2题
第6 题
7.若某空间几何体的三视图如图所示,则该几何体的体积是( )
A.2
B.1
C.
23
D.
13
8.某几何体的三视图如图所示,则该几何体的体积为( )
A.π816+
B. π88+
C. π1616+
D. π168+ 9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.3
16
D.6
10. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,
侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1 B .3 C .4
D .5
11. 一个几何体的三视图如图所示,则这个几何体的体积为( )
A
B
C
D
12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )
A .1
B .2
C .3
第7题
第8题
第9题
第11题 俯视图
正视图
第12题
13.某几何体的三视图如图所示,则其体积为______.
14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.
16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是 .
18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为
19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.
20.一个正方体的内切球与它的外接球的体积比是( ).
A .1∶33
B .1∶22
C .1∶
383 D .1∶4
2
21.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,
则球表面积是( ) A.
π964 B. π38 C. π4 D. π9
16
第17题
2
4 3
正视图 侧视图 俯视图第18题 第15题
第14题
第13题
第16题 第19题
22. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为
23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A. 4 B.3 C.2.5 D. 2
24.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 25. 当圆锥的侧面积与底面积的比值是2时,圆锥的轴截面的顶角等于 26.一平面截一球得到直径是6的圆面,球心到这个平面的距离是4,则该球的体积为 27.一个正四面体的棱长为2,四个顶点在同一个球面上,则此球的表面积为 28.已知一个三棱锥ABC P -的三条侧棱PC PB PA ,,两两垂直,且长度分别为2,3,4,则 该棱锥的外接球的表面积为
29.已知用斜二测画法得到的正方形的直观图的面积为218,则原来正方形的面积为 30.正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求该棱锥的表面积与体积,内切球的半径.
31. 在球心同侧有相距cm 9的两个平行截面,它们的面积分别为249cm π和2
400
cm π.求球的表面积.
32. 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点,其中18=AB ,
24=BC 、30=AC ,球心到这个截面的距离为球半径的一半,求球的表面积.
答案
1.A
2.B
3.C
4.D
5.C
6.B
7.B
8.A
9.B 10.A 11.A 12.A 13.3
π 14.24 15.1616-π 16.1 17.
6
7π 18.29π 19. 20+82 20.A 21.A 22.2
33
23.B 24. 2 25. ︒90
26.
3
500π 27.π6 28.π29
29.72 30. 3629+ 32 26- 31.2500π 32.π1200。
