8枚硬币问题(减治法) c语言
减治法

子问题 的规模是n/2 子问题的解
原问题的解
图5.1 减治法的典型情况(减半技术)
对于给定的整数a和非负整数n,计算an的值。
利用减治法,如果n=1,可以简单地返回a的值,如果n是偶数并且n>1,可 以把该问题的规模减半,即计算an/2的值,而且规模为n的解an和规模减半 的解an/2之间具有明显的对应关系:an=(an/2)2,如果n是奇数并且n>1,可 以先用偶指数的规则计算a(n-1),再把结果乘以a。所以,应用减治技术得到 如下计算方法:
排序问题中的减治法
堆排序
选择问题
堆排序
例
28 25 36 18 32 28 36 25 18 16 32 25 16 36 25 18 16 36 28 32
28
18 16
32
堆排序是利用堆(假设利用大根堆)的特性进 行排序的方法,其基本思想是:首先将待排序 的记录序列构造成一个堆,此时,选出了堆中 所有记录的最大者即堆顶记录,然后将它从堆 中移走(通常将堆顶记录和堆中最后一个记录 交换),并将剩余的记录再调整成堆,这样又 找出了次大的记录,以此类推,直到堆中只有 一个记录为止。
n 1 n 1
查找问题中的减治法
折半查找
二叉查找树
折半查找
在有序表{ 7, 14, 18, 21, 23, 29, 31, 35, 38, 42, 46, 49, 52 }中查找值为14的 记录的过程如图所示。
0 1
7
2
14
3
18
4
21
5
23
6
29
7
31
8
35
9
38
10
42
八枚银币游戏算法

/*八枚银币问题现有八枚银币a b c d e f g h,已知其中一枚是假币,其重量不同于真币,但不知是较轻或较重,如何使用天平以最少的比较次数,决定出哪枚是假币,并得知假币比真币较轻或较重。
*/declarea number;b number;c number;d number;e number;f number;g number;h number;x integer default 0;begina := &a;b := &b;c := &c;d := &d;e := &e;f := &f;g := &g;h := &h;if ((a + b) = (c + d)) thenx := x + 1;if (e = f) thenx := x + 1;if (g = e) thenx := x + 1;if (g < h) thenx := x + 1;dbms_output.put_line('h = ' || h || ',较重!称了' || x || '次!');elsex := x + 1;dbms_output.put_line('h = ' || h || ',较轻!称了' || x || '次!');end if;elsex := x + 1;if (g > h) thenx := x + 1;dbms_output.put_line('g = ' || g || ',较重!称了' || x || '次!');elsex := x + 1;dbms_output.put_line('g = ' || g || ',较轻!称了' || x || '次!');end if;end if;elsex := x + 1;if (e = g) thenx := x + 1;if (e < f) thendbms_output.put_line('f = ' || f || ',较重!称了' || x || '次!');elsedbms_output.put_line('f = ' || f || ',较轻!称了' || x || '次!');end if;elsex := x + 1;if (e > f) thendbms_output.put_line('e = ' || e || ',较重!称了' || x || '次!');elsedbms_output.put_line('e = ' || e || ',较轻!称了' || x || '次!');end if;end if;end if;elsex := x + 1;if (a = b) thenx := x + 1;if (c = a) thenx := x + 1;if (c < d) thendbms_output.put_line('d = ' || d || ',较重!称了' || x || '次!');elsedbms_output.put_line('d = ' || d || ',较轻!称了' || x || '次!');end if;elsex := x + 1;if (c > d) thendbms_output.put_line('c = ' || c || ',较重!称了' || x || '次!');elsedbms_output.put_line('c = ' || c || ',较轻!称了' || x || '次!');end if;end if;elsex := x + 1;if (a = c) thenx := x + 1;if (a < b) thendbms_output.put_line('b = ' || b || ',较重!称了' || x || '次!');elsedbms_output.put_line('b = ' || b || ',较轻!称了' || x || '次!');end if;elsex := x + 1;if (a > b) thendbms_output.put_line('a = ' || a || ',较重!称了' || x || '次!');elsedbms_output.put_line('a = ' || a || ',较轻!称了' || x || '次!');end if;end if;end if;end if;end;/*提示:该算法经典之处在于二叉树使用巧妙,每称一次就排除一半*/。
算法笔记_004:8枚硬币问题【减治法】

算法笔记_004:8枚硬币问题【减治法】⽬录1 问题描述(1)实验题⽬在8枚外观相同的硬币中,有⼀枚是假币,并且已知假币与真币的重量不同,但不知道假币与真币相⽐较轻还是较重。
可以通过⼀架天平来任意⽐较两组硬币,设计⼀个⾼效的算法来检测这枚假币。
(2)实验⽬的1)深刻理解并掌握减治法的设计思想并理解它与分治法的区别;2)提⾼应⽤减治法设计算法的技能。
3)理解这样⼀个观点:建⽴正确的模型对于问题的求解是⾮常重要的。
(3)实验要求1)设计减治算法实现8枚硬币问题;2)设计实验程序,考察⽤减治技术设计的算法是否⾼效;3)扩展算法,使之能处理n枚硬币中有⼀枚假币的问题。
(4)实现提⽰假设⽤⼀个数组B[n]表⽰硬币,元素B[i]中存放第i枚硬币的重量,其中n-1个元素的值都是相同的,只有⼀个元素与其他元素值不同,则当n=8时即代表8枚硬币问题。
由于8枚硬币问题限制只允许使⽤天平⽐较轻重,所以,算法中只能出现元素相加和⽐较的语句。
2 解决⽅案2.1 减治法原理叙述在说减法法原理之前,我们先来简单看看分治法原理:分治法是把⼀个⼤问题划分为若⼲⼦问题,分别求解⼦问题,然后再把⼦问题的解进⾏合并得到原问题的解。
⽽减治法同样是把⼤问题分解成为若⼲个⼦问题,但是这些⼦问题不需要分别求解,只需求解其中的⼀个⼦问题,也⽆需对⼦问题进⾏合并。
换种说法,可以说减治法是退化的分治法。
减治法原理正式描述:减治法(reduce and conquer method)将原问题的解分解为若⼲个⼦问题,并且原问题的解与⼦问题的解之间存在某种确定关系,如果原问题的规模为n,则⼦问题的规模通常是n/2 或n-1。
2.2 8枚硬币规模解法求解思路:(1)⾸先输⼊8枚硬币重量,存放在⼀个长度为8的⼀维数组中。
(2)定义a,b,c,d,e,f,g,h⼋个变量,分别对应⼀枚硬币的重量。
然后把这8枚硬币分成三组,分别为abc(abc = a+b+c)、def(def =d+e+f)、gh。
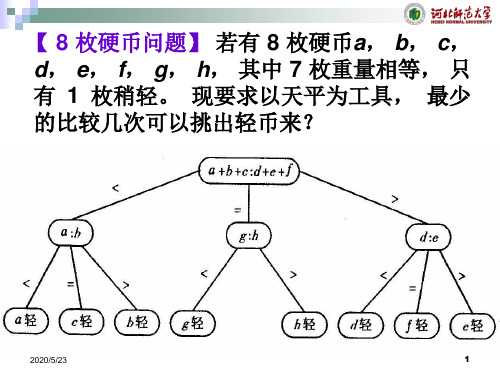
八枚硬币的判定树

树的应用举例——八枚硬币问题设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,其中有且仅有一枚硬币是假币,并且假币的重量与真币的重量不同,可能轻,也可能重。
现要求以天平为工具,用最少的比较次数挑选出假币,并同时确定这枚假币的重量比其它真币是轻还是重。
问题的解决是经过一系列的判断,这些判断构成了树结构,可以用判定树来描述这个判定过程。
解决这个问题的最自然的想法就是把硬币分成两组,也就是一分为二。
但是,如果一分为三的话,会获得更少的比较次数。
从八枚硬币中任取六枚a,b,c,d,e,f,在天平两端各放三枚进行比较。
假设a,b,c三枚放在天平的一端,d,e,f三枚放在天平的另一端,可能出现三种比较结果:⑴a+b+c > d+e+f⑵a+b+c=d+e+f⑶a+b+c < d+e+f若a+b+c >d+e+f,可以肯定这六枚硬币中必有一枚为假币,同时也说明,为真币。
这时可将天平两端各去掉一枚硬币,假设去掉和,同时将天平两端的硬币各换一枚,假设硬币,作了互换,然后进行第二次比较,比较的结果同样可能有三种:①a+e>d+b:这种情况表明天平两端去掉硬币c,f且硬币b,e互换后,天平两端的轻重关系保持不变,从而说明了假币必然是a,d中的一个,这时我们只要用一枚真币(例如h)和a进行比较,就能找出假币。
若a>h,则a是较重的假币;若a=h,则d为较轻的假币;不可能出现a②a+e=d+b:此时天平两端由不平衡变为平衡,表明假币一定在去掉的两枚硬币c,f中,同样用一枚真币(例如h)和c进行比较,若c>h,则c是较重的假币;若c=h,则f为较轻的假币;不可能出现c③a+e:此时表明由于两枚硬币b,e的对换,引起了两端轻重关系的改变,那么可以肯定b或e中有一枚是假币,同样用一枚真币(例如h)和b进行比较,若b>h,则b是较重的假币;若b=h,则e为较轻的假币;不可能出现b 对于结果⑵和⑶的情况,可按照上述方法作类似的分析。
c语言八皇后问题程序设计

2014年春季学期《C项目设计》报告题目:八皇后问题学号:092213112姓名:刘泽中组名:1指导教师:宋东兴日期:2014.05.15目录正文 (3)1.问题描述 (3)2. 总体设计与分析 (3)3. 相关代码 (5)4. 调试分析 (9)5.软件使用说明书 (11)总结 (11)附录:部分原程序代码 (12)一、问题描述1.八皇后问题:是一个古老而著名的问题。
该问题是十九世纪著名的数学家高斯1850年提出:在8×8棋盘上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?2.解决八皇后问题的关键在于:(1)找到合理的数据结构存放棋子的摆放位置。
(2)要有合理的冲突检查算法。
采用的方法是,先把8个棋子摆在棋盘上,每行摆一个,然后去检查这种摆放是否有冲突,如果没有冲突,即找到了一种解决方案。
由于皇后的摆放位置不能通过某种公式来确定,因此对于每个皇后的摆放位置都要进行试探和纠正,这就是“回溯”的思想。
在8个皇后未放置完成前,每行摆放一个皇后,摆放第i个皇后和第i+1个皇后的试探方法是相同的,因此完全可以采用递归的方法来处理。
二、总体设计与分析1.设计效果画一个8*8的国际象棋盘,在棋盘某一位置上放一棋子,并让它按从左到右的方向自动运动,用户可以使用光标键调整棋子运动的方向,找出所有可能的摆放方案,将包含指定的棋子的(如3行4列)摆放方案找出并显示出来。
2.、总体设计程序总体分为两大块:(1)八皇后摆法的寻找;(2)棋盘及棋子的设计。
3、详细模块(1)八皇后摆法的寻找:int chess[8][8]={0}; //二维数组表示8*8棋盘,全部清0,(0代表该位没有放棋子)void queen(int i,int n){ //i表示从第i行起为后续棋子选择合适位置,n代表n*n棋盘if(i==n)output(n); //输出棋盘当前布局;else{for(j=0;j<n;j++){ //每行可能有n个摆放位置chess[i][j] = 1; //在第i行,j列上放一棋子if(!canAttack(i,j)) //如果当前布局合法,不受前i-1行的攻击queen(i+1,n); //递归摆放i+1行chess[i][j] = 0; //移走第i行,j列的棋子}}}int canAttack(int i,int j){ //判断0到i-1行已摆放的棋子,对[i,j]位置是否可以攻击for(m=0;m<i;m++){for(n=0;n<8;n++){if(chess[m][n]==1){if(m==i||n==j) return 1;if(m+n==i+j || m-n==i-j) return 1;}}}return 0;}void output(){ //输出一组解,即打印出8个皇后的坐标for(int i=0;i<8;i++){for(int j=0;j<8;j++){if(chess[i][j]==1){printf("(%d,%d)",i,j);}}}printf(“\n”);}int main(){queen(0,8);return 0;}(2)棋盘及棋子的设计:void drawBlock(int i,int j){ //棋盘的设计(每一个小方块)int x0,y0,x1,y1;x0=ORGX+j*W;y0=ORGY+i*H;x1=x0+W-1;y1=y0+H-1;setcolor(WHITE);rectangle(x0,y0,x1,y1);setfillstyle(1,LIGHTGRAY);floodfill(x0+1,y0+1,WHITE);setcolor(WHITE);line(x0,y0,x1,y0);line(x0,y0,x0,y1);setcolor(BLACK);line(x1,y0,x1,y1);line(x0,y1,x1,y1);}void drawBall(Ball ball){ //棋子的设计int x0,y0;x0=ball.startX+ball.c*ball.w+ball.w/2;y0=ball.startY+ball.r*ball.h+ball.h/2;setcolor(RED);setfillstyle(1,RED);fillellipse(x0,y0,10,10);}4.程序设计思路:先设计程序,找到八皇后的摆放位置,方法是:先把8个棋子摆在棋盘上,每行摆一个,然后去检查这种摆放是否有冲突,如果没有冲突,即找到了一种解决方案。
C++程序 最少硬币问题

//
main.cpp
#include "LeastCoins.h" int main() { LeastCoins LC; LC.run(); return 0; }
{ outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<X<<endl; j-=X*T[i]; } else { outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<(X-1)<<endl; j-=(X-1)*T[i]; } } outputFile<<setw(3)<<T[i]<<setw(3)<<" "<<setw(3)<<(j/T[1])<<endl; }
要找回
钱数是 j 需要硬币数的 最少个
//
LeastCoins.cpp <iostream.h> <fstream.h> <cstdlib> <iomanip.h>
#include #include #include #include
#include "LeastCoins.h" #define N 10 // 根据实际问题规模的大小 来初始化 ifstream inputFile("input.txt",ios::out); ofstream outputFile("output.txt",ios::out);
8枚硬币问题(减治法) c语言

sum_a+=a[j];
j++;
}
if(sum_a!=sum_b)
{
sum_a=0;//a,b数组前两个数据相加比较大小
j=0;
while(j<2)
{
sum_a=a[j]+sum_a;
j++;
}
j=0;
sum_b=0;
while(j<2)
{
sum_b=b[j]+sum_b;
j++;
}
if(sum_a==sum_b)//找到数据在所输入数据的第3,或6位置
4.具体实现
(1)运行结果:
(2)具体程序实现:
#include<stdio.h>
#define N 8
int false_coin(int coin[]);
int main(void)
{
int coin[N];
int i=0;
printf("8枚硬币问题,0代表假,1代表真,请输入8个0或1数字,并且只存在一个假硬币:\n");
j=0;
while(j<2)
{
sum_a=a[j]+sum_a;
j++;
}
j=0;
sum_b=0;
while(j<2)
{
sum_b=b[j]+sum_b;
j++;
}
if(sum_a>sum_b)
flag_2=1;
else
flag_2=0;
if(flag_1==flag_2)
{
if(a[0]==a[1])
C++程序初级案例及答案参考

cout<<"请输入经纪人的底薪:";
cin>>base;
cout<<"请输入经纪人的工龄:";
cin>>seniority;
cout<<"请输入经纪人的月销售额:";
cin>>sale;
cout<<"该经纪人的月薪为:"<<fun(base,seniority,sale)<<endl;retu Nhomakorabean 0;
change=change%50; cout<<"找给顾客的壹角硬币个数为:"<<change/10<<endl;
change=change%10; cout<<"找给顾客的伍分硬币个数为:"<<change/5<<endl;
change=change%5; cout<<"找给顾客的贰分硬币个数为:"<<change/2<<endl;
//定义存放乘法结果的变量 u 并赋初值 //定义循环变量并赋初值
(四) 循环条件的嵌套
1.写出完整的程序,实现:输入密码,如果等于 1234,则显示“loading···”,并退出循 环;否则显示“input again!”。如果输入超过三次,则退出循环并结束程序。(要用到 break) 示例: 1) 密码输入 #include<iostream> using namespace std; int main() { int password; for(int i=0;i<3;i++) {
c++解决八皇后问题(绝对原创)

解决八皇后问题#include<iostream>#include<iomanip>using namespace std;int b[91][9];void jinwei(int[]);//模拟八进制数在最低位加一之后的进位机制void add(int[]);//模拟八进制数最低位加一bool judge(int[]);//根据问题的限制条件判断一组八进制数能否成为一组解void abscheckm(int[], int[][9],int);//判断两组解是否可通过镜面对称、顺时针旋转90度、180度、270度后镜面对称重合void abscheck180(int[], int[][9],int);//判断两组解是否可通过顺时针旋转180度后重合void abscheck90(int[], int[][9],int);//判断两组解是否可通过顺时针旋转90度后重合void abscheck270(int[], int[][9],int);//判断两组解是否可通过顺时针旋转270度后重合void copy(int[], int[][9], int);//复制解以待考察void display(int[][9],int);//打印所有的解void absdisplay(int[][9],int);//打印所有的“绝对解”void jinwei(int a[]){for (int i=0; i<=6; i++){if ( a[i]==8 ){a[i]=0;a[i+1]=a[i+1]+1;}}}void add(int a[]){a[0]=a[0]+1;jinwei(a);}bool judge(int a[]){for (int i=0; i<=6; i++){for (int j=i+1; j<=7; j++){if ( (a[i]==a[j])||(a[i]-i==a[j]-j)||(a[i]+i==a[j]+j) ){return false;}}}return true;}void abscheckm(int a[],int b[][9],int j){int m;b[j][8]=0;for (m=0; m<8; m++){if (a[m]!=7-b[j][m]&&b[j][7-a[m]]!=7-m&&b[j][a[m]]!=m&&a[m]!=7-b[j][7-m]){b[j][8]=1;}}}void abscheck180(int a[],int b[][9],int j){int m;b[j][8]=0;for (m=0; m<4; m++){if ( a[m]!=b[j][7-m]){b[j][8]=1;}}}void abscheck90(int a[],int b[][9],int j){int m;b[j][8]=0;for (m=0; m<8; m++){if (b[j][7-a[m]]!=m){b[j][8]=1;}}}void abscheck270(int a[],int b[][9],int j){int m;b[j][8]=0;for (m=0; m<8; m++){if (b[j][a[m]]!=7-m){b[j][8]=1;}}}void copy(int a[], int b[][9], int t){int i;for (i=0; i<8; i++)b[t][i]=a[i];}void display(int b[][9],int n){int i;for(i=0;i<n;i++)cout<<"solution "<<setw(3)<<(i+1)<<": "<<b[i][0]<<b[i][1]<<b[i][2]<<b[i][3]<<b[i][4]<<b[i][5]<<b[i][6]<<b[i][7]<<endl;}void absdisplay(int b[][9],int n){int i,j,count=1;for (i=0; i<n; i++){if(b[i][8]!=9){cout<<endl<<"abs_solution"<<count<<": ";count++;for (j=0; j<8; j++){cout<<b[i][j];}}}}int main(){int a[8]={0,0,0,0,0,0,0,0},c[9];int anscount=0,i,j,m,n;for (i=1;i<=16777216;i++){add(a);if ( judge(a) ){copy(a,b,anscount);b[anscount][8]=1;anscount++;}}display(b,anscount);for(j=0;j<anscount-1;j++) //筛选并删除非绝对解{for (i=0;i<9;i++)c[i]=b[j][i];for(i=j+1;i<anscount;i++){abscheckm(c,b,i);if(!b[i][8]){for(m=i;m<anscount-1;m++){for (n=0; n<9; n++)b[m][n]=b[m+1][n];}anscount--;if(i==anscount-1)b[i][8]=9;}}}for(j=0;j<anscount-1;j++)//筛选并删除非绝对解{for (i=0; i<9;i++)c[i]=b[j][i];for(i=j+1;i<anscount;i++){abscheck180(c,b,i);if(!b[i][8]){for(m=i;m<anscount-1;m++){for (n=0; n<9; n++)b[m][n]=b[m+1][n];}if(i==anscount-1)b[i][8]=9;anscount--;}}}for(j=0;j<anscount-1;j++)//筛选并删除非绝对解{for (i=0; i<9;i++)c[i]=b[j][i];for(i=j+1;i<anscount;i++){abscheck90(c,b,i);if(!b[i][8]){for(m=i;m<anscount-1;m++){for (n=0; n<9; n++)b[m][n]=b[m+1][n];}if(i==anscount-1)b[i][8]=9;anscount--;}}}for(j=0;j<anscount-1;j++)//筛选并删除非绝对解{for (i=0; i<9;i++)c[i]=b[j][i];for(i=j+1;i<anscount;i++){abscheck270(c,b,i);if(!b[i][8]){for(m=i;m<anscount-1;m++){for (n=0; n<9; n++)b[m][n]=b[m+1][n];}anscount--;if(i==anscount-1)b[i][8]=9;}}}cout<<"\nnow check the absolute solutions:\n";absdisplay(b,anscount);return 0;}。
实验五_8枚硬币问题

return5;
}
elsereturn2;
}
}
if(a[1]+a[2]==a[4]+a[5])
{
if(a[3]==a[2])
{
return6;
}
elsereturn3;
}
}
if(a[1]+a[2]+a[3]<a[4]+a[5]+a[6])
{
if(a[1]+a[2]<a[4]+a[5])
{
if(a[1]<a[4])
{
if(a[3]==a[2])
{
return 6;
}
else return 3;
}
}
else if(a[7]==a[3])
{
return 8;
}
else return 7;
}
五、实验结果与结论:(给出测试数据以及程序运行结果,并进行比较,得出自己的结论)
减治法算法解决8枚硬币的时间复杂度为:O(log2n)
计算机枚外观相同的硬币中有一枚是假币并且一直假币与真币的质量不同但不知道假币与真币相比较轻还是较重
实 验 报 告
实验项目:__8枚硬币问题班级:_计算机___姓 名:_______
一、实验题目:
在8枚外观相同的硬币中,有一枚是假币,并且一直假币与真币的质量不同但不知道假币与真币相比较轻还是较重。可以通过一架天平来任意比较两组硬币,设计一个搞笑的算法来检测出这枚假币。
{
if(a[1]==a[3]){Biblioteka return4;}
elsereturn1;
}
elseif(a[1]==a[4])
计算思维06-3.3 算法思想简介讲课提纲_20

第3章 算法思维3.3 算法思想简介20世纪中期以后,随着计算机的出现、发展,算法广泛地运用于种类问题的求解,成为计算机科学的灵魂,涌现出精彩纷呈的算法。
3.3.1 蛮力法蛮力法也称穷举法,其基本思想是采用一定的策略,将待解决问题的所有可能列出来,找出问题的解。
《算经》中的“百钱百鸡问题”:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,翁、母、雏各几何?该问题的解决方案是:设公鸡为x 只,母鸡为y 只,小鸡为z 只;则x 的取值范围为0到20,y 的取值范围为0到33,z 的取值范围为0到100,当然z 应该为3的倍数;这样总共有21×34×34,即24276种组合方案,其中满足条件x +y +z =100,并且5x +3y +z /3=100的组合就是问题的解。
[百钱百鸡VB 伪代码] p 1tep 3d (5x+3y+z/3=100)Then 采用的关键技术是描述,算法设计时应避免重复试探,时间复杂度较高,效率较低,分而治之N },其 中某段的和定义为1 设序列A 中有素,其最大段和为maxsum ;序列A 的开始位置为left ,结束位置为right 序列A left 和A rigth ,序列A left 的最大子段和为leftsu 相同,即用递归进一步分解子序列A left 和A left 中,其值为leftsum ;也有可能处在子序For x=0 To 20 Step 1 For y=0 To 33 Ste For z=0 To 100 S If (x+y+z=100)An Print x;y;z End If Next x Next y Next x蛮力法但现在的计算机有超强的计算能力,仍是直接解决问题的一种常用思路。
3.3.2 分治法分治法的基本思想是将一个难以直接解决的大问题划分成一些规模较小的子问题,,其求解过程通常由划分、求解子问题和合并3个阶段组成,如图3-8所示。
第九章 树
例题 判断下列哪些图是树?
v1 v2 v3 v2 v1 v3 v1 v2 v4 v3
v4
v5
v4
v5
v5
(a)
(b)
(c)
解: 图(a)是树, 因为它连通又不包含回路。图(b), (c)不 是树, 因为图(b)虽连通但有回路, 图(c)虽无回路但不连 通。 在图(a)中, v1、 v4、 v5为均为叶, v2、 v3均为分 支节点。
(1)
(2)
(3)
余树可能不连通,也可能含回路。
2018/2/4
11
定理9.3 任何连通图G至少存在一棵生成树. 推论1 设n阶无向连通图G有m条边,则 m≥n-1. 推论2 设n阶无向连通图G有m条边,T是G的生 成树,T'是T的余树,则T'中有m-n+1条边.
(1)
(2)
(3)
m=8,n=5
2018/2/4 12
T有5个树枝a, b, c, d, e, 因而有5个 基本割集:Sa={a,g,f } ; Sb={b,g,h } ; Sc={c,f,h } ; Sd={d,i,h } ; Se={e,f,i}.
基本割集系统为{Sa,Sb,Sc, Sd,Se}.
2018/2/4
a b
c d
e
g
h
i
16
定义9.5 设无向连通带权图G=<V,E,W>,T是 G的一棵生成树.T各边带权之和称为T的权,记 作W(T).G的所有生成树中带权最小的生成树 称为最小生成树. 问题的提出: 要在 n 个城市间建立通信联络 网。顶点:表示城市,权:城市间通信线路的 花费代价。希望此通信网花费代价最小。
d
20
b
C语言培训第25章八皇后问题的实现

25.2.2 问题实现
➢ 3. 主程序函数 ➢ 可实现对数据初始化,调用问题求解功能函
数,并输出最终方案个数。代码如下(代码 25-3.txt)。
25.2.2 问题实现
01 void main()
02 {
03 int pad[N][N];
04 int count=0;
05 int i ,j;
06 for(i=0;i<N;i++)
➢ 1. 输出结果 ➢ 将结果输出至屏幕,以循环打印的方式,调
用标准输入输出函数printf,将结果回显, 代码如下(代码25-1.txt)。
25.2.2 问题实现
01 #include <stdio.h>
02 #define N 8
03 void Output(int bc[][N],int *count)
04 {
05 int i;
06 int j;
07 *count=*count+1;
08 printf("第%d种:\n",*count);
09 for(i=0;i<N;i++)
10 {
11
for(j=0;j<N;j++)
12
{
13
if(bc[i][j])
14
printf("Q");
/*在皇后位置打印Q*/
25.2 问题分析及实现
➢ 25.2.1 问题分析 ➢ 25.2.2 问题实现 ➢ 25.2.3 程序运行
25.2 问题分析及实现
➢ 对于此问题,首先想到的前面提到的要 领:看清、想明、把握每一个细节。由 问题描述可知,我们要实现的是找到皇 后的行列坐标以及对应方案号即可。
最少硬币数

用改进的贪心算法解决最少硬币问题,暂称之为贪心枚举法.由贪心算法可知尽量用大面值的硬币组合来找钱,可以使使用的硬币最少。
而贪心算法对最少硬币问题的解决总是可以得到最优解很好的近似解。
本算法就是用贪心策略枚举出所有近似最优解,然后从中寻找到问题的最优解寻找近似最优xx例如:9分面值的硬币5枚,8分面值的硬币5枚,2分面值的硬币8枚,要找25分钱。
设要找的钱为m,硬币种类为n,t[i](0<i<=n)为硬币的面值,c[i]为可以使用的各种面值的硬币个数, k[i]为第i种面值的硬币可以使用的最多个数(k[i]=min{m/t[i],c[i]})(1)将硬币依面值大小排序9 8 2(2)按面值种类划分不同情况有多少种面值就划分多少种情况.每种情况的第一枚硬币面值各不一样,其后对剩余的硬币按面值从大到小排列.划分为三个情况:982,892,298。
对应k[i]为:k[0]=3, k[1]=3 ,k[2]=8得到近似最优解群为9分1枚,8分2枚;9分1枚,8分1枚,2分4枚;9分1枚,2分8枚.算法优化1,在寻找最优组合过程中,有些情况可以不予考虑。
比如上例中2 9 82,在以小面值的硬币为第一个的情况中,在寻找最优组合时,会遇到两种情况:a、使用硬币个数要比以大面值的硬币(如9和8)为第一个的情况大得多。
b、寻找到的组合与前面的情况有重复。
在程序中实现剪枝如果k[i]不比mincount大,则继续用贪心算法寻找近似最优组合。
如上例mincount初始值设为maxint。
k[0]=3 < mincount,则进行贪心选择,并将最好结果放于mincount中mincount=3;k[1]=3 <= mincount=3,进行贪心选择;k[2]=8 > mincount=3,则将其剪枝这样可以有效的减小问题的规模。
该算法的优劣1、对于硬币面值大的情况,执行效率会提高(因为k[i]变小了)。
八枚硬币问题

题目:八枚硬币问题姓名:龚晓峰学号:3110100687课程名称:应用运筹学年级与专业:2011级理科试验班类所在学院:求是学院丹青学园八枚硬币问题一.原题设有八枚硬币,其中有一枚硬币是假币,且知道假币比真币轻。
那么通过一个天平找出假币所需的最少次数是多少?答案是两次而不是三次。
下面分析:解法一:设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,先选取两组各三枚硬币,分别为a,b,c和f,g,h。
如果a+b+c=f+g+h,那么d和e中较轻的那枚时假币。
如果a+b+c>f+g+h,那么假币必在f,g,h中,比较f和g,如果f=g,那么h是假币;如果f>g,那么g是假币;如果f<g,那么f是假币。
如果a+b+c<f+g+h,则同上可得出相应结果。
a+b+c?f+g+ha+b+c>f+g+ha+b+c=f+g+ha+b+c<f+g+hf<gf=gf=gd>ed<ea>ba=ba<bg是假币h是假币f是假币e是假币d是假币b是假币c是假币a是假币f>gf<g解法二:设有八枚硬币,分别表示为a,b,c,d,e,f,g,h,先选取两组各三枚硬币,分别为a,b,c和f,g,h。
如果a+b+c=f+g+h,那么d和e中较轻的那枚时假币。
如果a+b+c<f+g+h,那么假币必在a,b,c中,再比较a+d+f和c+e+g,如果a+d+f=c+e+g,那么b是假币;如果a+d+f>c+e+g,那么c是假币;如果a+d+f<c+e+g,那么a是假币。
如果a+b+c>f+g+h,则同上可得出相应结果。
a+b+c<f+g+ha+b+c=f+g+h a+b+c>f+g+h a+d+f<c+e+g a是假币a+d+f=c+e+g b 是假币c是假币a+d+f>c+e+gd>ed<e d是假币e 是假币a+d+f<c+e+ha+d+f=c+e+ha+d+f>c+e+hf 是假币g是假币h是假币a+b+c?f+g+h解法一和解法二的区别在于解法二的第二次比较并没有用到第一次比较的结果。
C语言基础应用处理学生打分

C语⾔基础应⽤处理学⽣打分计算时间最少硬币问题详细过程第⼀题:最少硬币问题(简单版)假设有三种⾯值的硬币,分别为10、5、1。
接收⼀个整数作为⾦额数,计算要达到该⾦额数,每个⾯值的硬币最少需要多少枚。
输出结果演⽰:参考答案:#include <stdio.h>typedef struct StructrueMoneyBox {int n10;int n5;int n1;} MoneyBox;int main(void) {MoneyBox change = {0, 0, 0};int face_value[4] = {10, 5, 1};int money = 0;int i = 0;printf("请输⼊⾦额: ");scanf("%d", &money);do {if (money < face_value[i]) {i++;}switch (i) {case 0:change.n10 = money / face_value[i];break;case 1:change.n5 = money / face_value[i];break;case 2:change.n1 = money / face_value[i];break;}money = money % face_value[i];} while (money > 0);printf("10: %d\n", change.n10);printf("5: %d\n", change.n5);printf("1: %d\n", change.n1);return 0;}运⾏结果:第⼆题:计算已经过去了多久编写⼀个秒表程序来计算已经过去了多长时间。
利⽤下列结构体实现:并要求使⽤下⾯两个变量来解决问题:当程序运⾏时,取当前时间并保存到 previtimePtr 变量中。
硬币兑换问题(算法设计)

这就是贪心策略!
CS-SWPU
硬币兑换的贪心算法
//需兑换钱数=a; //可用硬币面额集合=d;
如何知道兑换未完成?
while ( 兑换未完成 ) {
选出当前可用的最大面额 x ;
用面额 x 执行兑换:使用数量=c、兑换金额=e ;
累计硬币使用总量 sum = sum + c ;
CS-SWPU
兑换硬币
贪心策略
效率高
每种面额只处理一次,无需考察不同的面额组合
动态规划:系统考察所有组合
有局限!
面额:¥0.11, 0.05, 0.01,兑换: ¥ 0.15
还能使用贪心策略吗?
CS-SWPU
贪心算法的基本思想
总是作出在当前看来最好的选择
在某种意义上的局部最优选择,不从整体最优考虑
CS-SWPU
硬币兑换的动态规划算法
假定
面额数组:d[1]>d[2]>…>d[n]=1 需兑换金额 a
最优值c (i, j)
可选面额 d[i], d[i +1], ……, d[n],需兑换金额 j 1 ≤i ≤n,0 ≤j ≤a
递归计算式
当d[i] > j 时,c (i, j) = c ( i+1, j ) 当d[i] ≤ j 时,c (i, j) = min{ c(i+1, j), j / d[i] + c(i, j mod d[i]) }
} 每种面额只考察了一次,效率高!
CS-SWPU
硬币兑换的贪心算法
//需兑换钱数=a;
面额集合如何表示?
//可用硬币面额集合=d;
while ( 剩余金额>0 ) {
减治法求八枚硬币

实验题目在八枚外观相同的硬币中,有一枚是假币,并且已知假币与真币的重量不同,但不知道假币与真币相比较轻还是较重。
可以通过一架天平来任意比较两组硬币,设计一个高效的算法来检测出这枚假币。
实验目的(1)深刻理解并掌握减治法的设计思想;(2)提高应用减治法设计算法的技能;(3)理解这样一个观点:建立正确的模型对于问题的求解是非常重要的实验内容(包括代码和对应的执行结果截图)#include<iostream>using namespace std;void bmybwt(){cout<<"请输入八枚硬币,其中有一枚是假币"<<endl;int a[8];for(int i=0;i<8;i++){cin>>a[i];}if(a[0]+a[1]+a[2]>a[3]+a[4]+a[5])if(a[0]+a[4]>a[3]+a[1])if(a[0]>a[7])cout<<"第1枚是较重的假币,重量为"<<a[0]<<endl;elsecout<<"第4枚是较轻的假币,重量为"<<a[3]<<endl;else if(a[0]+a[4]==a[3]+a[1])if(a[2]>a[7])cout<<"第3枚是较重的假币,重量为"<<a[2]<<endl;elsecout<<"第6枚是较轻的假币,重量为"<<a[5]<<endl;elseif(a[1]>a[7])cout<<"第2枚是较重的假币,重量为"<<a[1]<<endl;elsecout<<"第5枚是较轻的假币,重量为"<<a[4]<<endl;else if(a[0]+a[1]+a[2]==a[3]+a[4]+a[5])if(a[6]>a[7])if(a[6]>a[0])cout<<"第7枚是较重的假币,重量为"<<a[6]<<endl;elsecout<<"第8枚是较轻的假币,重量为"<<a[7]<<endl;elseif(a[7]>a[0])cout<<"第8枚是较重的假币,重量为"<<a[7]<<endl;elsecout<<"第7枚是较轻的假币,重量为"<<a[6]<<endl;elseif(a[0]+a[4]>a[3]+a[1])if(a[4]>a[6])cout<<"第5枚是较重的假币,重量为"<<a[4]<<endl;elsecout<<"第2枚是较轻的假币,重量为"<<a[1]<<endl;else if(a[0]+a[4]==a[3]+a[1])if(a[5]>a[6])cout<<"第6枚是较重的假币,重量为"<<a[5]<<endl;elsecout<<"第3枚是较轻的假币,重量为"<<a[2]<<endl;elseif(a[3]>a[6])cout<<"第4枚是较重的假币,重量为"<<a[3]<<endl;elsecout<<"第1枚是较轻的假币,重量为"<<a[0]<<endl; }void main(){int n;cout<<"请输入要测试的次数:";cin>>n;for(int i=0;i<n;i++){bmybwt();}}截图如下:实验结果分析在该实验中使用了减治法来解决八枚硬币的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
j=0;
while(j<=1)
{c[j]=coin[j+6];j++;}
j=0;
while(j<=2)//两边数组求和
{
sum_b+=b[j];
j++;
}
j=0;
while(j<=2)
{
sum_a+=a[j];
j++;
}
if(sum_a!=sum_b)
{
sum_a=0;//a,b数组前两个数据相加比较大小
j++;
}
j=0;
sum_b=0;
while(j<2)
{
sum_b=b[j]+sum_b;
j++;
}
if(sum_a>sum_b)
flag_2=1;
else
flag_2=0;
if(flag_1==flag_2)
{
if(a[0]==a[1])
return 4;
else
return 1;
}
else
{
temp=a[1];
3.实验要求
(1)设计减治算法实现8枚硬币问题;
(2)设计实验程序,考察用减治技术的算法是否高效;
(3)扩展算法,使之能处理n枚硬币中有1枚假币的问题。
4.具体实现
(1)运行结果:
(2)具体程序实现:
#include<stdio.h>
#define N 8
int false_coin(int coin[]);
}
int false_coin(int coin[])
{
int a[N],b[N],c[N],temp;
int j=0,sum_a=0,sum_b=0,flag_1,flag_2;
while(j<=2)//把8个硬币分配成a,b,c分别为3,3,2
{
a[j]=coin[j];
b[j]=coin[j+3];
}
else
{
if(sum_a>sum_b)//flag标志交换数后两边数组和是否相等
flag_1=1;
else
flag_1=0;
temp=a[1];
a[1]=b[1];
b[1]=temp;
sum_a=0;//a,b数组前两个数据相加比较大小
j=0;
while(j<2)
{
sum_a=a[j]+sum_a;
int main(void)
{
int coin[N];
int i=0;
printf("8枚硬币问题,0代表假,1代表真,请输入8个0或1数字,并且只存在一个假硬币:\n");
while(i<8)
{scanf("%d",&coin[i]);i++;
}
i=false_coin(coin);
printf("\n第%d个位置是假硬币",i);
a[1]=b[1];
b[1]=temp;
if(a[0]==a[1])
return 5;
else
return 2;
}
}
}
else
{
if(c[0]==a[0])
return 8;
ห้องสมุดไป่ตู้else
return 7;
}
}
5.实验心得
从开学到现在第一次完整的运行出正确结果,以前运行都是错误结果!程序中发现自己基础语法不扎实,数组作为参数传递时使用错误,数组输入出问题,还有不会使用单步运行,程序写完后,不管输入怎么样的输出结果就永远是在第3这个位置停留。最后加入自己写的相应的代码后,可以发现程序中的变量问题出现在哪里,程序里面的问题终于被找到!
实验项目——8枚硬币问题
1.实验题目
在8枚外观相同的硬币中,有一枚是假币,并且已知假币与真币的重量不同,但不知道假币与真币相比较轻还是较重。可以通过一架天平来任意比较两组硬币,设计一个高效的算法来检测出这枚假币。
2.实验目的
(1)深刻理解并掌握减治法的设计思想;
(2)提高应用减治法设计算法的技能;
(3)理解这样一个观点:建立正确的模型对于问题的求解时非常重要的。
j=0;
while(j<2)
{
sum_a=a[j]+sum_a;
j++;
}
j=0;
sum_b=0;
while(j<2)
{
sum_b=b[j]+sum_b;
j++;
}
if(sum_a==sum_b)//找到数据在所输入数据的第3,或6位置
{
if(a[0]==a[2])
return 6;
else
return 3;
