分别用蛮力法、分治法、减治法实现a的N次方
基本的算法策略

任务分配问题就是在分配成本矩阵中的每一行 选取一个元素,这些元素分别属于不同的列, 选取一个元素,这些元素分别属于不同的列,并且 元素之和最小。 元素之和最小。
可以用一个n元组 可以用一个 元组(j1, j2, …, jn)来描述任务分配问题的一个可能 元组 来描述任务分配问题的一个可能 其中第i个分量 个分量j 行中选择的列号, 解,其中第 个分量 i(1≤i≤n)表示在第 行中选择的列号, ≤ ≤ )表示在第i行中选择的列号 因此用蛮力法解决任务分配问题要求生成整数1~n的全排列, 的全排列, 因此用蛮力法解决任务分配问题要求生成整数 的全排列 然后把成本矩阵中的相应元素相加来求得每种分配方案的总 成本,最后选出具有最小和的方案。 成本,最后选出具有最小和的方案。 序号 1 2 3 4 5 6 分配方案 1, 2, 3 1, 3, 2 2, 1, 3 2, 3, 1 3, 1, 2 3, 2, 1 总成本 9+4+1=14 9+3+8=20 2+6+1=9 2+3+5=10 7+6+8=21 7+4+5=16
证明0/1背包问题满足最优性原理。 证明 背包问题满足最优性原理。 背包问题满足最优性原理 是所给0/1背包问题的一个最优解 设(x1, x2, …, xn)是所给 背包问题的一个最优解,则 是所给 背包问题的一个最优解, ( x2, …, xn)是下面一个子问题的最优解: 是下面一个子问题的最优解: 是下面一个子问题的最优解
最优分配方案是将任务2 任务1 任务3 最优分配方案是将任务2,任务1,任务3分别分配给人 员1,人员2,人员3,将使总成本达到最小值9。 人员2 人员3 将使总成本达到最小值9
算法(复习题)1

平均情况:设待查找的元素在数组中的概率为P,不在数组中的概率为1-P,若出现在数组中每个位置的概率是均等的为p/nT(n)=P1D1+P2D2+...+PiDi+(1-P)Dn+1=p/2+n(1-p/2)1.叙述分治算法和动态规划算法的基本思想,并比较两种算法的异同。
答:分治法将待求解的问题划分成K个较小规模的子问题,对这K个子问题分别求解,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解. 动态规划将待求解的问题分解成若干的子问题,自底向上地通过求解子问题的解得到原问题的解。
动态规划将每个子问题只求解一次并将其解保存在一个表格中,当需要再次求解此子问题时,只是简单的通过查表过的该子问题的解,避免了大量的重复计算.异同:分治法求解的问题分解后的子问题都是独立的,而使用动态规划求解的问题分解后得到的子问题往往不是相互独立的。
分治法是自顶向下用递归的方法解决问题,而动态规划则是自底向上非递归解决问题。
1.简述分治算法求解过程的三个阶段。
答:(1)划分:既然是分治,当然需要把规模为n的原问题划分为k个规模较小的子问题,并尽量使这k个子问题的规模大致相同。
(2)求解子问题:各子问题的解法与原问题的解法通常是相同的,可以用递归的方法求解各个子问题,有时递归处理也可以用循环来实现。
(3)合并:把各个子问题的解合并起来,合并的代价因情况不同有很大差异,分治算法的有效性很大程度上依赖于合并的实现。
2.叙述分治法的基本思想,并分析分治法与减治法二者的区别。
答:分治法将待求解的问题划分成K个较小规模的子问题,对这K个子问题分别求解,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解.区别:分治法是把一个大问题划分成若干个子问题,分别求解各个子问题,然后把子问题的解进行合并并得到原问题的解。
减治法同样是把一个大问题划分成若干个子问题,但是这些子问题不需要分别求解,只需求解其中的一个子问题,因而也无需对子问题的解进行合并。
背包问题(修改)

贪心法的一般过程
Greedy(C) //C是问题的输入集合即候选集合 {
S={ }; //初始解集合为空集 while (not solution(S)) //集合S没有构成问题的一个解 {
例:付款问题: 超市的自动柜员机(POS机)要找给顾客数量最少的现金。
假 定 POS 机 中 有 n 张 面 值 为 pi(1≤i≤n) 的 货 币 , 用 集 合 P={p1, p2, …, pn}表示,如果POS机需支付的现金为A,那么, 它必须从P中选取一个最小子集S,使得
m
pi S , pi = A (m =| S |) i =1
an=a×a×…×a n次
蛮力法所赖的基本技术——扫描技 术
关键——依次处理所有元素 基本的扫描技术——遍历
(1)集合的遍历 (2)线性表的遍历 (3)树的遍历 (4)图的遍历
虽然巧妙和高效的算法很少来自于蛮力法,基于 以下原因,蛮力法也是一种重要的算法设计技术:
(1)理论上,蛮力法可以解决可计算领域的各种问题。 (2)蛮力法经常用来解决一些较小规模的问题。 (3)对于一些重要的问题蛮力法可以产生一些合理的算 法,他们具备一些实用价值,而且不受问题规模的限制。 (4)蛮力法可以作为某类问题时间性能的底限,来衡量 同样问题的更高效算法。
减治法
普卢塔克说,萨特斯为了告诉他的士兵坚韧和 智慧比蛮力更重要的道理,把两匹马带到他们面前, 然后让两个人扒光马的尾毛.一个人是魁梧的大力 士,他抓住尾巴扒了又扒,但一点效果也没有;另 一个人是一个精明的、长相狡黠的裁缝,他微笑着, 每次扒掉一根毛,很快就把尾巴拔得光秃秃的。
蛮力法、分治法、减治法三种方法的理解和处理问题的类型的归纳

蛮力法、分治法、减治法三种方法的理解和处理问题的类型的归纳一、蛮力法蛮力法是一种基础且直接的问题解决策略,通常用于寻找问题的答案或解决方案。
其核心理念在于,通过逐一检查所有可能的解决方案,从而找到问题的答案或找到最佳的解决方案。
在蛮力法中,我们通常需要投入较多的时间和计算资源,尤其是在面对大规模或复杂的问题时。
蛮力法的应用范围广泛,包括但不限于以下几种类型的问题:1. 排序问题:例如,对一个数组进行排序,我们可以使用蛮力法,通过比较每对元素并交换它们的位置,使得整个数组有序。
2. 查找问题:例如,在排序数组中查找一个特定的元素,我们可以使用蛮力法,逐一检查数组中的每个元素直到找到目标元素。
3. 组合与排列问题:例如,计算给定集合的所有可能排列或组合,我们可以使用蛮力法,通过逐一排列或组合所有可能的元素组合得到答案。
二、分治法分治法是一种将复杂问题分解为更小、更易于处理的子问题的方法。
通过将问题分解为独立的子问题,我们可以分别解决每个子问题,然后将这些解决方案组合起来,形成原始问题的解决方案。
这种方法在处理复杂问题时非常有效,因为它可以降低问题的复杂性,使我们可以更有效地解决问题。
分治法的应用范围广泛,包括但不限于以下几种类型的问题:1. 排序问题:例如,归并排序就是一种使用分治法的排序算法,它将一个大列表分解为两个小列表,对这两个小列表分别进行排序,然后合并它们以得到有序列表。
2. 搜索问题:例如,二分搜索是一种使用分治法的搜索算法,它将搜索空间一分为二,每次迭代都排除一半的元素,直到找到目标元素或确定元素不存在。
3. 图问题:例如,Dijkstra的算法就是一种使用分治法的图搜索算法,它将图分解为最短路径树,然后通过搜索每个子图的最短路径来解决整个图的最短路径问题。
三、减治法减治法是一种通过减少问题的规模或复杂性来解决问题的方法。
其核心理念在于,通过消除或减少问题的某些部分或特性,从而降低问题的复杂性或规模,使得问题更容易解决。
算法设计与分析实验报告

算法设计与分析实验报告教师:学号:姓名:实验一:串匹配问题实验目的:(1) 深刻理解并掌握蛮力法的设计思想;(2) 提高应用蛮力法设计算法的技能;(3) 理解这样一个观点: 用蛮力法设计的算法, 一般来说, 经过适度的努力后, 都可以对算法的第一个版本进行一定程度的改良, 改进其时间性能。
三、实验要求:( 1) 实现BF 算法;(2 ) 实现BF 算法的改进算法: KMP 算法和BM 算法;(3 ) 对上述3 个算法进行时间复杂性分析, 并设计实验程序验证分析结果。
#include "stdio.h"#include "conio.h"#include <iostream>//BF算法int BF(char s[],char t[]){ int i; int a; int b; int m,n; m=strlen(s); //主串长度n=strlen(t); //子串长度printf("\n*****BF*****算法\n");for(i=0;i<m;i++){ b=0; a=i; while(s[a]==t[b]&&b!=n){a++; b++; }if(b==n){ printf("查找成功!!\n\n"); return 0;}}printf("找不到%s\n\n",t); return 0; }//前缀函数值,用于KMP算法int GETNEXT(char t[],int b){ int NEXT[10]; NEXT[0]=-1;int j,k; j=0; k=-1; while(j<strlen(t)){if ((k==-1)||(t[j]==t[k])){j++;k++;NEXT[j]=k; }else k=NEXT[k];}b=NEXT[b];return b;}//KMP算法int KMP(char s[],char t[]){int a=0; int b=0;int m,n; m=strlen(s); //主串长度n=strlen(t); //子串长度printf("\n*****KMP算法*****\n");while(a<=m-n){while(s[a]==t[b]&&b!=n){a++;b++; }if(b==n){printf("查找成功!!\n\n");return 0;}b=GETNEXT(t,b);a=a-b;if(b==-1) b++;}printf("找不到%s\n\n",t);return 0; } //滑动距离函数,用于BM算法int DIST(char t[],char c){ int i=0,x=1;int n; n=strlen(t);while(x&&i!=n-1){if(t[i]==c)x=0;else i++;}if(i!=n-1)n=n-1-i;return n; } //BM算法结果分析与体会:glibc里的strstr函数用的是brute-force(naive)算法,它与其它算法的区别是strstr不对pattern(needle)进行预处理,所以用起来很方便。
计算思维06-3.3 算法思想简介讲课提纲_20

第3章 算法思维3.3 算法思想简介20世纪中期以后,随着计算机的出现、发展,算法广泛地运用于种类问题的求解,成为计算机科学的灵魂,涌现出精彩纷呈的算法。
3.3.1 蛮力法蛮力法也称穷举法,其基本思想是采用一定的策略,将待解决问题的所有可能列出来,找出问题的解。
《算经》中的“百钱百鸡问题”:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,翁、母、雏各几何?该问题的解决方案是:设公鸡为x 只,母鸡为y 只,小鸡为z 只;则x 的取值范围为0到20,y 的取值范围为0到33,z 的取值范围为0到100,当然z 应该为3的倍数;这样总共有21×34×34,即24276种组合方案,其中满足条件x +y +z =100,并且5x +3y +z /3=100的组合就是问题的解。
[百钱百鸡VB 伪代码] p 1tep 3d (5x+3y+z/3=100)Then 采用的关键技术是描述,算法设计时应避免重复试探,时间复杂度较高,效率较低,分而治之N },其 中某段的和定义为1 设序列A 中有素,其最大段和为maxsum ;序列A 的开始位置为left ,结束位置为right 序列A left 和A rigth ,序列A left 的最大子段和为leftsu 相同,即用递归进一步分解子序列A left 和A left 中,其值为leftsum ;也有可能处在子序For x=0 To 20 Step 1 For y=0 To 33 Ste For z=0 To 100 S If (x+y+z=100)An Print x;y;z End If Next x Next y Next x蛮力法但现在的计算机有超强的计算能力,仍是直接解决问题的一种常用思路。
3.3.2 分治法分治法的基本思想是将一个难以直接解决的大问题划分成一些规模较小的子问题,,其求解过程通常由划分、求解子问题和合并3个阶段组成,如图3-8所示。
第2章 基本算法设计技术

数据结构与算法
2.3 减治法
减治法的设计思想
减治法(Reduce and Conquer Method)在将原问题分解 为若干个子问题后,利用了原问题的解与子问题的解之间 的关系,这种关系通常表现为: (1)原问题的解只存在于其中一个较小规模的子问题中; (2)原问题的解与其中一个较小规模的解之间存在某种 对应关系。 由于原问题的解与较小规模的子问题的解之间存在这种关 系,所以,只需求解其中一个较小规模的子问题就可以得 到原问题的解,无需对子问题的解进行合并,所以,严格 地说,减治法应该是一种退化了的分治法。
2.1 蛮力法
蛮力法的设计思想
蛮力法(Brute Force Method,也称穷举法)通常采用 一定的策略依次处理待求解问题的所有数据,从而找出问 题的解,是一种简单直接地解决问题的方法。例如,对于 给定的整数a和非负整数n,计算an的值,最直接的想法就 是把1和a相乘n次。 蛮力法常常直接基于问题的描述,所以是最容易应用的 方法。但是,用蛮力法设计的算法其时间性能往往也是最 低的。因此,蛮力法通常用来解决非常基本的问题。在本 书中,有关线性表的基本操作、顺序查找算法、模式匹配 BF算法、起泡排序、简单选择排序等算法都是蛮力法的应 用实例。
电子工业出版社
数据结构与算法
2.5 动态规划法
一般来说,动态规划法的求解过程由以下三个阶段组成: (1)划分子问题:将原问题分解为若干个子问题,并且子问 题之间具有重叠关系; (2)动态规划函数:根据子问题之间的重叠关系找到子问题 满足的递推关系式(称为动态规划函数); (3)填写表格:设计表格的形式及内容,根据递推式自底向 上计算,实现动态规划过程。 显然,动态规划法的关键是找到体现子问题之间重叠关系的 动态规划函数。
算法设计习题题目练习

一、选择题1.选出不是算法所必须具备的特征(C)。
A有穷性B确切性C高效性D可行性2.不属于给合问题的是(C )。
A Euler的36名军官问题B 图的Hamiliton C求二项式展开系数 D 集合的幂集3.下列(C )不是衡量算法的标准。
A 时间效率B 空间效率C 问题的难度D 适应能力4.下列函数关系随着输入量增大增加量最快的是(D )。
A logn Bn3 C2n D n!5.如果某一算法的执行时间不超过输入规模的2倍,那么算法渐近时间复杂度为(B )。
A O(2n)B O(n) CΘ (n) D Ω(n)6.下列程序段的算法时间复杂度是(D )for (i=1;i<=n;i++)for (j=1;i<=m;m++)S;A O(n2)B O(m2)C O(m+n)D O(mn)7.下列程序段S执行次数为(C )。
for (i=1;i<=n;i++)for (j=1;i<=m;m++)S;A n2B n2/2C n(n+1)D n(n+1)/28.使用F(n)=n*f(n-1)递归求F(4),递归调用子函数的次数为(D )。
A 3次B 4次C 5次D 8次9.递推关系M(n)=M(n-1)+1,M(0)=0的算法时间复杂度为(C )。
A O(n!)B O(2n)C O(n)D O(1)10.与递推关系x(n)=2x(n-1)+1,x(1)=1等价的通项公式为(B )。
A x(n)=2nB x(n)=2n-1C x(n)=2n+1D x(n)=n!11.三个盘子的汉诺塔,至少要执行移动操作次数为( D )。
A1次 B 3次 C 6次 D 7次12.Fibonacci数列第10项为(D)。
A 3B 13C 21D 3413.12个金币中有一枚是假币,至少需要称量的次数是(C )。
A 0B 1C 3D 414.二维最近邻点问题,如果使用分治法,对于一个子集上的某一点,另一个子集上需要检查的点的个数是(C )。
5算法设计技术1-蛮力法和分治法_823204234

c1 = af * bl + al * bf = (af + al) * (bf + bl) - (c2 + c0)
数据结构 (30230594)
18
吴及 电子工程系
大整数乘法
乘法的复杂度 T(n) = 3T(n/2)
的正确性和效率
数据结构 (30230594)
10
吴及 电子工程系
内容提要
算法设计技术
蛮力法 分治法 贪心算法 动态规划 搜索算法
数据结构
11
(30230594)
吴及 电子工程系
分治法
基本思想
把问题的一个实例分解成为属于同一问题的若干个较小规模的实例 重复这个过程直到规模较小的实例很容易求解, 求解这些规模较小的实例, 合并较小问题的解,以得到原始问题的解。
握某个特定算法更重要
数据结构 (30230594)
2
吴及 电子工程系
内容提要
算法设计技术 算法优化技术 计算复杂性理论简介
数据结构 (30230594)
3
吴及 电子工程系
内容提要
算法设计技术
蛮力法 分治法 贪心算法 动态规划 搜索算法
数据结构
4
(30230594)
吴及 电子工程系
全部公因子cf1, cf2, cf13…… 这个公因子序列中最大的cfk,即为m和n的最大公因子 或者从m到2,逐个判断每个整数是否可以同时整除m和n,找到的第一个
能够同时整除m和n的整数就是最大公因子
针对蛮力法的优化 其它方法
数据结构 (30230594)
算法设计(第3章蛮力法)

d = dx*dx + dy*dy;
if (d<d_best) then
d_best d;
(a,b) (i,j);
return (a,b);
时间复杂度O(n2):存在改进可能?
end
3.5.2 (0-1)背包问题
输入:n件物品的集合S (其中第i件物品的重量 和价值分别为S[i].w和S[i].v),以及背包的最大 承重量W
[最小顶点覆盖问题的蛮力算法]
Algorithm Brute_VertexCover(V: set<int>; E: set<intint>)
begin
let C = V;
foreach V’ Powerset(V) do
let cover = true;
foreach ((u,v) E) do
3.1 字符串匹配
蛮力法:从左到右扫描T,检查T中是否含有子串P
m i c r o s o f t wi n dows sof t
匹配成功,返回位置索引5
3.1 字符串匹配
[字符串匹配算法] Algorithm Brute_Match(T, P: string) begin let i = 0, n = |T|, m = |P|; while (i ≤ n−m) do
时间复杂度O(n2)
3.5 若干最优化问题最优化问 Nhomakorabea:在问题的可行域F中找到一个解x, 使得某目标函数值f(x)最小或最大。
约束条件:解x应满足某项约束c(x)=true 连续优化问题:解的数量可能有无穷多 组合优化问题:解的数量有限时,总是可以用
蛮力法求解,但算法效率可能很低。
3.5 若干最优化问题
算法设计与分析蛮力法

算法分析与设计
14
算法1如下:
input(n);//输入n
a=new int(n+1);
for (i=1; i<=n;i++)
a[i]=1;
for (i=1; i<=n;i++)
if(100==x+y+z&&100==5*x+3*y+z/3) {print("the cock number is",x); print("the hen number is", y);
print("the chick number is ",z);} }
算法分析与设计
8
算法分析与设计
9
Z能被3整除时,才会判断“5*x+3*y+z/3=100
print("the chick number is ",z);} } }
算法分析与设计
10
例2
• 求所有的三位数,它除以11所得的余数等 于它的三个数字的平方和。
解题思路:三位数只有900个,可用枚举 法解决,枚举时可先估计有关量的范围, 以缩小讨论范围,减少计算量。
算法分析与设计
11
• 解:设这个三位数的百位、十位、个位的数字分别为 x,y,z。由于任何数除以11所得余数都不大于10, 所以
蛮力法 Brute Force
• 蛮力法(枚举法、穷举法,暴力法)要求设计 者找出所有可能的方法,然后选择其中的一种 方法,若该方法不可行则试探下一种可能的方 法。
蛮力法、动归、贪心、分支限界法解01背包问题

算法综合实验报告一、实验内容:分别用蛮力、动态规划、贪心及分支限界法实现对0-1背包问题的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:1、蛮力法1.1数据结构注:结构体obj用来存放单个物品的价值和重量typedef struct obj{int w;//物品的重量int v;//物品的价值};1.2 函数组成void subset(int s[][10],int n):用来生成子集的函数void judge(int s[][10], obj obj[],int mark[],int n,int c):判断子集的可行性int getmax(int mark[],int n,int &flag):求解问题的最优解void outputObj(int flag,int s[][10],int n):输出选择物品的情况 1.3 输入/输出设计本程序通过键盘进行输入、屏幕进行输出。
1.4 符号名说明1.5 算法描述算法的伪代码描述如下:输入:背包的容量c,物品的个数n,n个物品的重量 w[n],价值v[n]输出:装入背包的物品编号以及产生的最大价值1.初始化最大价值 max=0,结果子集 s=φ;2.对集合{1,2,......n}的每一个子集T,执行下述操作:2.1初始化背包的价值 v=0,背包的重量 w=0;2.2对子集t的每一个元素j2.2.1 如果w+wj<c,则 w=w+wj,v=v+vj;2.2.2 否则,转步骤2考察下一个子集;2.3如果max<v,则 max=v;s=t;3.输出子集S中的各元素2、动态规划法2.1 数据结构该程序不涉及任何数据结构2.2 函数组成int max(int i,int j);比较并返回两个数中的较大值int KnapSack (int w[],int v[],int x[],int n,int c);求解背包取得的最大值2.3 输入/输出设计本程序通过键盘进行输入、屏幕进行输出。
蛮力法详解

算法3.1——顺序查找
int SeqSearch1(int r[ ], int n, int k) //数组r[1] ~ r[n]存放查找集合
{ i=n;
基本语句 ?
while (i>0 && r[i]!=k)
i--;
return i;
}
算法3.1的基本语句是i>0和r[i]!=k,其执行次数为:
n
2020/6/14
Chapter 3 Brute force method
教学要求 理解 掌握
√
√ √ √
√ √ √
熟练掌握 √ √
√
4
3.1 概述:蛮力法的设计思想
蛮力法中“力”是指计算机的“计算能 力”,不是人的智“力”。
蛮力法的设计思想:直接基于问题的描述, 从有限集合中,逐一列举集合的所有元素, 对每一个元素逐一判断和处理,从而找出 问题的解。
如已知:公钥为:KU={e, n},私钥为: KR={d, n},则 对明文m的加密/解密算法如下:
加密 明文: M<n 密文: C=Me (mod n)
密文: 明文:
解密 C M=Cd (mod n)
注:计算an算法的效率直接影响到RSA算法的性能
2020/6/14
Chapter 3 Brute force method
2020/6/14
Chapter 3 Brute force method
7
蛮力法的设计思想
因要穷举待处理的元素,故蛮力法的时间性能往往最低, 但基于以下原因,蛮力法也是一种重要的算法设计技术:
(1)理论上,蛮力法可以解决可计算领域的各种问题。 (2)蛮力法经常用来解决一些较小规模的问题。 (3)对于一些重要的问题(例如排序、查找等)蛮力法 可以产生一些合理的算法,他们具备一些实用价值,而且 不受问题规模的限制。 (4)蛮力法可以作为某类问题时间性能(不是复杂性, 两者恰好相反)的下界,来衡量同样问题的更高效算法。
高级算法:解决复杂计算问题的常用方法

高级算法:解决复杂计算问题的常用方法随着科技的发展,我们生活中的计算问题日益复杂,对算法的要求也越来越高。
为了解决这些复杂的计算问题,人们提出了许多高级算法。
高级算法是指在解决计算问题时使用的一些比较复杂和智能的算法。
它们通常能够有效地解决一些复杂的问题,提高计算的效率和精度。
本文将对几种常用的高级算法进行介绍,以及它们在实际问题中的应用。
一、分治算法分治算法是一种将问题分解成若干个小问题,然后分别解决的算法。
通常情况下,分治算法会将原问题划分成几个规模较小的子问题,然后递归地解决每个子问题,最后将各个子问题的解合并起来得到原问题的解。
这种算法在解决一些复杂的计算问题时表现出了很高的效率。
1.1应用案例分治算法的应用非常广泛,比如在计算机视觉中,图像分割问题可以使用分治算法进行处理。
由于图像分割需要对图像进行分区,并找出图像中各个区域的边界,因此问题的规模较大。
采用分治算法可以将图像分割问题划分成若干个小的图像区域,然后递归地对每个小区域进行处理,最后将每个小区域的处理结果合并起来,从而得到整个图像的分割结果。
1.2算法流程分治算法的流程一般包括三个步骤:分解、解决和合并。
在分解步骤中,原问题被划分成若干个规模较小的子问题;在解决步骤中,递归地解决每个子问题;在合并步骤中,将各个子问题的解合并起来,得到原问题的解。
分治算法的成功与否主要取决于解决步骤的效率和合并步骤的正确性。
二、动态规划算法动态规划算法是一种通过把原问题分解成相互重叠的子问题,然后利用子问题的解来解决原问题的算法。
它通常用于优化计算问题的解,提高算法的效率和精度。
动态规划算法的优势在于能够避免重复的计算,从而提高计算的效率。
2.1应用案例动态规划算法在资源调度领域有着广泛的应用。
比如在生产调度中,需要对生产资源进行合理的调度,以最大程度地提高生产效率。
动态规划算法可以对生产资源的使用情况进行分析,然后利用子问题的解来优化资源调度,从而达到提高生产效率的目的。
Python程序员面试分类真题18
Python程序员面试分类真题181. 给定任意一个正整数,求比这个数大且最小的“不重复数”,“不重复数”的含义是相邻两位不相同,例如1101是重复数,而1201是不重复数。
正确答案:方法一:蛮力法(江南博哥)最容易想到的方法就是对这个给定的数加1,然后判断这个数是不是“不重复数”,如果不是,那么继续加1,直到找到“不重复数”为止。
显然这种方法的效率非常低下。
方法二:从右到左的贪心法例如给定数字11099,首先对这个数字加1,变为11000,接着从右向左找出第一对重复的数字00,对这个数字加1,变为11001,继续从右向左找出下一对重复的数00,将其加1,同时把这一位往后的数字变为0101…串(当某个数字自增后,只有把后面的数字变成0101…,才是最小的不重复数字),这个数字变为11010,接着采用同样的方法,11010->12010就可以得到满足条件的数。
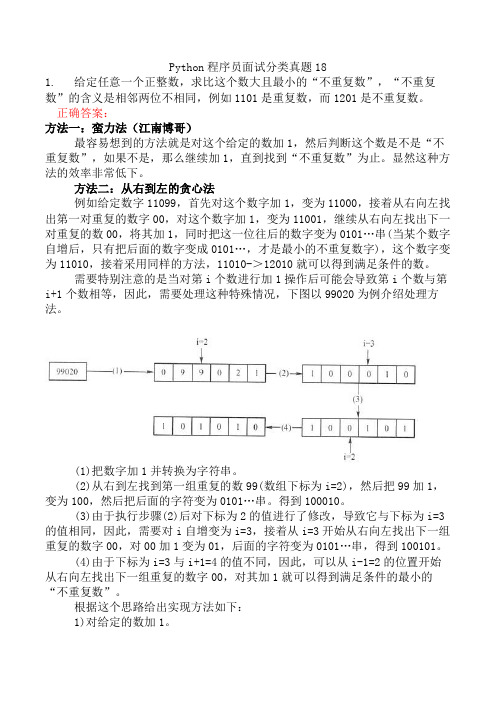
需要特别注意的是当对第i个数进行加1操作后可能会导致第i个数与第i+1个数相等,因此,需要处理这种特殊情况,下图以99020为例介绍处理方法。
(1)把数字加1并转换为字符串。
(2)从右到左找到第一组重复的数99(数组下标为i=2),然后把99加1,变为100,然后把后面的字符变为0101…串。
得到100010。
(3)由于执行步骤(2)后对下标为2的值进行了修改,导致它与下标为i=3的值相同,因此,需要对i自增变为i=3,接着从i=3开始从右向左找出下一组重复的数字00,对00加1变为01,后面的字符变为0101…串,得到100101。
(4)由于下标为i=3与i+1=4的值不同,因此,可以从i-1=2的位置开始从右向左找出下一组重复的数字00,对其加1就可以得到满足条件的最小的“不重复数”。
根据这个思路给出实现方法如下:1)对给定的数加1。
2)循环执行如下操作:对给定的数从右向左找出第一对重复的数(下标为i),对这个数字加1,然后把这个数字后面的数变为0101…得到新的数。
分别用蛮力法、分治法、减治法实现a的N次方

《算法设计与分析》实验报告一学号:姓名:日期: 2012.11.5 得分:一、实验内容:分别用蛮力法、分治法、减治法实现a^n。
二、实验要求:完成试验报告、给出对此结果。
为防止大数溢出,可以用1^n来测试在n比较大是的三种算法运行情况。
四、源程序及注释:#include <iostream>#include <windows.h>using namespace std;//蛮力法求a的n次方int Power1(int a,int n){ int as=1;for(int i=0;i<n;i++)ans*=a;return ans;//分治法求a的n次方int Power2(int a,int n){ int ans=1;if (n==0) ans=1;else if(n==1) ans=a;elseans=Power2(a,n/2)*Power2(a,(n+1)/2);return ans;}//减治法求a的n次方int Power3(int a,int n){ int ans=1;if (n==0) ans=1;else if(n==1) ans=a;else{ans=Power3(a,n/2);if(n%2==0)ans=ans*ans;//当n为偶数return ans;}int main(){int a=1;int n=10000;LARGE_INTEGER start1,end1,start2,end2,start3,end3,f;QueryPerformanceFrequency(&f);QueryPerformanceCounter(&start1) ;int p1=Power1(a,n);QueryPerformanceCounter(&end1);QueryPerformanceCounter(&start2) ;int p2=Power2(a,n);QueryPerformanceCounter(&end2);QueryPerformanceCounter(&start3) ;int p3=Power3(a,n);QueryPerformanceCounter(&end3);cout<<"a="<<a<<",n="<<n<<endl;cout<<"蛮力法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end1.QuadPart-start1.QuadPart)/f.QuadPart<<" "<<p1<<endl;cout<<"分治法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end2.QuadPart-start2.QuadPart)/f.QuadPart<<" "<<p2<<endl;cout<<"减治法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end3.QuadPart-start3.QuadPart)/f.QuadPart<<" "<<p3<<endl;return 0;}五、运行输出结果:六、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:合适的代码是实验能够成功进行的关键,当然前提是对问题的深刻理解,从实验结果我们不难看出,应用减治法处理问题的效率还是很高的。
分治法和蛮力法求解最近对问题

蛮力法与分治法求解最近对问题摘要:在计算机科学理论和程序设计实践中,往往会面对众多的问题,面对这些问题,人们想到了很多算法来解决。
最常见也最常用的是蛮力法,在解决问题和研究算法过程中,人们常在不断探索和寻求许多好的算法来求解同一个问题。
本文就最近对问题,分别对蛮力法和分治法的思想、复杂度、效率做了一定的讲述,并对两个方法在此问题中的效率进行了简单分析。
关键字:蛮力法、分治法、效率。
一.引言通常我们所说的最接近对问题是指平面上(即二维坐标平面)给定n 个点,找其中的一对点,使得在n 个点的所有点对中,,该点对的距离最小。
在求解这个问题时,我们可以采用很多算法来实现。
最朴素的解法就是蛮力法,所谓蛮力法就是将是一种简单直接地解决问题的方法,常常直接基于问题的描述和所涉及的概念定义,来求解问题。
这样一来,显得蛮力法确实比较实用而方便。
往往事物都有两面性,此算法确实简单实用,可是效率却比较低。
所以我们针对不同问题时,要采用合适的算法来求解,达到效率和求解难度综合起来达到一个比较好的极点。
本文在研究最近对问题时又采用了分治法,所谓分治法,就是分而治之即把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题直到问题解决。
本文只是针对一个比较简单的问题最近对问题采用两个不同算法求解进行分析解剖。
二.算法概述及实用范围2.1、蛮力法蛮力法是一种简单直接地解决问题的方法,常常直接基于问题的描述和所涉及的概念定义,来求解问题。
虽然巧妙和高效的算法很少来自于蛮力法,但它仍是一种重要的算法设计策略:(1)适用泛围广,是能解决几乎所有问题的一般性方法;(2)常用于一些非常基本、但又十分重要的算法(排序、查找、矩阵乘法和字符串匹配等);(3)解决一些规模小或价值低的问题;(4)可以做为同样问题的更高效算法的一个标准;(5)可以通过对蛮力法的改进来得到更好的算法。
2、分治法分治法,就是分而治之即把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题直到问题解决。
算法蛮力法

for (j=1; j<bound; j++) //一趟冒泡排序
if (A[j]>A[j+1]) {
A[j]←→A[j+1];
exchange=j;
//记录每一次发生记录交换的位置
}
}
}
12
在最好情况下,待排序记录序列为正序,算法只执行一 趟,进行了n-1次关键码的比较,不需要移动记录,时间复 杂性为O(n);
第3章 蛮 力 法(Brute Force)
选择排序和冒泡排序 顺序查找和蛮力字符串匹配 最近对和凸包问题 穷举查找
¾旅行商问题 TSP ¾背包问题 Knapsack ¾分配问题 Assignmen
蛮力法
就像宝剑不是撬棍一样,科学也很少使用蛮力。 ——Edward Lytton
认真做事常常是浪费时间。 ——Robert Byrne
在最坏情况下,待排序记录序列为反序,每趟排序在无序
序列中只有一个最大的记录被交换到最终位置,故算法执
行n-1趟,第i(1≤i<n)趟排序执行了n-i次关键码的比较
和n-i次记录的交换,这样,关键码的比较次数
为
n −1
∑( n
i =1
− i)=
n
(
n− 2
1)
,因此,时间复杂性为O(n2);
在平均情况下,其时间复杂性与最坏情况同数量级。
查找方向
i
16
算法 ——改进的顺序查找
int SeqSearch2(int A[ ], int n, int k)//数组A[1] ~ A[n]存放查找集合 { A[0]=k; i=n; while (A[i]!=k)
i --; return i; }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《算法设计与分析》实验报告一
学号:姓名:
日期: 2012.11.5 得分:
一、实验内容:
分别用蛮力法、分治法、减治法实现a^n。
二、实验要求:
完成试验报告、给出对此结果。
为防止大数溢出,可以用1^n来测试在n比较大是的三种算法运行情况。
四、源程序及注释:
#include <iostream>
#include <windows.h>
using namespace std;
//蛮力法求a的n次方
int Power1(int a,int n)
{ int as=1;
for(int i=0;i<n;i++)
ans*=a;
return ans;
//分治法求a的n次方
int Power2(int a,int n)
{ int ans=1;
if (n==0) ans=1;
else if(n==1) ans=a;
else
ans=Power2(a,n/2)*Power2(a,(n+1)/2);
return ans;
}
//减治法求a的n次方
int Power3(int a,int n)
{ int ans=1;
if (n==0) ans=1;
else if(n==1) ans=a;
else
{ans=Power3(a,n/2);
if(n%2==0)
ans=ans*ans;//当n为偶数
return ans;
}
int main()
{
int a=1;
int n=10000;
LARGE_INTEGER start1,end1,start2,end2,start3,end3,f;
QueryPerformanceFrequency(&f);
QueryPerformanceCounter(&start1) ;
int p1=Power1(a,n);
QueryPerformanceCounter(&end1);
QueryPerformanceCounter(&start2) ;
int p2=Power2(a,n);
QueryPerformanceCounter(&end2);
QueryPerformanceCounter(&start3) ;
int p3=Power3(a,n);
QueryPerformanceCounter(&end3);
cout<<"a="<<a<<",n="<<n<<endl;
cout<<"蛮力法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end1.QuadPart-start1.QuadPart)/f.QuadPart<<" "<<p1<<endl;
cout<<"分治法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end2.QuadPart-start2.QuadPart)/f.QuadPart<<" "<<p2<<endl;
cout<<"减治法求a的n次方运行时间(单位:s)及结果"<<endl<<double(end3.QuadPart-start3.QuadPart)/f.QuadPart<<" "<<p3<<endl;
return 0;}
五、运行输出结果:
六、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
合适的代码是实验能够成功进行的关键,当然前提是对问题的深刻理解,从实验结果我们不难看出,应用减治法处理问题的效率还是很高的。
