脉冲成型滤波器及matlab仿真
经典滤波器的MATLAB仿真源程序

1、%巴特沃斯低通模拟圆形滤波器clear all;n=0:0.01:2;for i=1:4switch icase 1N=2;case 2N=5;case 3N=10;case 4N=20;end[z,p,k]=buttap(N); %函数buttap--设计巴特沃斯低通滤波器[b,a]=zp2tf(z,p,k); %函数zp2tf--零极点增益模型转换为传递函数模型[H,w]=freqs(b,a,n); %函数freqs--求解模拟滤波器频率响应magH2=(abs(H)).^2; %函数abs--取模值函数hold on %函数hold--控制是否保持当前图形plot(w,magH2) %函数plot--画二维线性图axis([0 2 0 1]); %函数axis--控制坐标轴比例和外观endxlabel('w/wc');ylabel('|H(jw)|^2');title('巴特沃斯低通模拟滤波器');text(0.72,0.63,'N=2') %对不同曲线做标记text(0.98,0.85,'N=20')grid on;2、%绘制切比雪夫I型低通模拟滤波器的平方幅频响应曲线,滤波器的阶数分别为2,4,6,8.clear all;n=0:0.01:2;for i=1:4switch icase 1N=2;case 2N=4;case 3N=6;case 4N=8;endRs=10;[z,p,k]=cheb1ap(N,Rs);[b,a]=zp2tf(z,p,k);[H,w]=freqs(b,a,n);magH2=(abs(H)).^2;posplot=['22' num2str(i)];subplot(posplot)plot(w,magH2)axis([0 2 0 1]);xlabel('w/wc');ylabel('H(jw)^2');title(['N=' num2str(N)]);grid onend3、%切比雪夫II型低通模拟滤波器clear all;n=0:0.01:2;for i=1:2switch icase 1N=7;case 2N=8;endRs=10; %阻带文波系数为10dB[z,p,k]=cheb2ap(N,Rs); %函数cheb2---设计切比雪夫II型低通滤波器[b,a]=zp2tf(z,p,k);[H,w]=freqs(b,a,n);magH2=(abs(H)).^2;%输出图形posplot=['12' num2str(i)];subplot(posplot)plot(w,magH2)axis([0 2 0 1.1]);xlabel('w/wc');ylabel('|H(jw)|^2');title(['N=' num2str(N)]);end4、%运用冲击响应不变法设计一个低通Chebshev1型数字滤波器,其通带上限临界频率是3Hz,阻带临界频率是5H,采样频率是1000Hz,在通带内的最大衰减为0.3dB,阻带内的最小衰减为80dB。
脉冲成型滤波器及matlab仿真

脉冲成型滤波器matlab仿真脉冲型滤波器用成型脉冲即数字1用矩形脉冲表示用升余弦脉冲或高斯脉冲表示主要用于基带数据处理。
在数字通信系统中,基带信号进入调制器前,波形是矩形脉冲,突变的上升沿和下降沿包含高频成分较丰富,信号的频谱一般比较宽。
从本质上说,脉冲成形就是一种滤波。
数字通信系统的信号都必须在一定的频带内,但是基带脉冲信号的频谱是一个Sa函数,在频带上是无限宽的,单个符号的脉冲将会延伸到相邻符号码元内产生码间串扰,这样就会干扰到其他信号,这是不允许的。
为了消除干扰,信号在发射之前要进行脉冲成形滤波,把信号的频率约束在带内。
因此在信道带宽有限的条件下,要降低误码率,提升信道频带利用率,需要在信号传输前,对其进行脉冲成形处理,改善其频谱特,产生适合信道传输的波形。
符号/秒代表单位波特(Baud),波特率是符号信息的比特率。
一般的脉冲成型是要过采样的,不然没有意义,因为成型滤波会扩展带宽,过采样是为了减少频谱混叠。
常用的脉冲成型滤波器有RC成型(升余弦)、Gaussian成型等。
Matlab作为一个强大的仿真工具,在通信信号处理中有着广泛的应用。
新版的Matlab (2014a)中关于滤波器设计,很多API都做了更新,下面个根据文档仿真和对比几个成型滤波器。
早些版本的firrcos函数用来设计升余弦滤波器的函数,现在已经更改成了rcosdesign 函数。
例如:设计一个16阶升余弦滤波器,载波频率Fc = 1KHz,滚降系数0.25,采样率为8KHz。
N = 16;Fc = 1000;R = 0.25;Fs = 8000;h = firrcos(N, Fc, R, Fs, 'rolloff', 'normal');figure();plot(h)下图是滤波器的抽头系数,阶数为16共有17个抽头。
如果用rcosdesign函数来设计这个滤波器,那么要用下面的调用方法来实现。
基于matlab模拟滤波器的设计与仿真

本科生毕业论文(设计)题目:基于matlab模拟滤波器的设计与仿真系部电子信息工程学院学科门类工科专业电子信息工程学号xxxxxxxxxxxxxxxxxx姓名XXX指导教师XXX2012年 5 月18 日基于matlab的模拟滤波器设计与仿真摘要几乎在所有的工程技术领域中都会涉及到信号处理问题,而滤波器信号处理的重要组成部分。
本论文首先介绍了滤波器的滤波原理以及模拟滤波器的设计方法,然后系统地介绍了模拟滤波器(包括巴特沃斯滤波器和切比雪夫滤波器)的设计原理和方法,并在此基础上论述了低通、高通、带通、带阻模拟滤波器的设计。
最后,采用MATLAB对所述滤波器进行建模仿真。
仿真结果表明用matlab设计的滤波器符合技术要求,且直观简便,有利于设计的优化。
关键字:模拟滤波器频率转换MATLAB装订线ABSTRACTIn almost all areas of engineering and technology, signal processing will be involved andsignal processing is an important component of filter signal processing. This paper will firstintroduce the principle of filter and the design method of analog filters. Then the paper willpresent the design principles and methods of analog filters (including the Butterworth filter andChebyshev filter) and on this basis, the analog filters (including low-pass, high-pass, band-pass,and band-stop) design will be discussed. Last is the use of virtual realization of analog filtersMATLAB. It can be seen that based on the simulation result, the filter designed by MATLAB iscoincident in technical requirements and handy in anchauung. What’s more, it is easy to adjustthe performance of filters.Key words:Filtering Analog filters MATLAB装订线第1章绪论 (1)1.1课题研究背景及意义 (1)1.2国内外研究现状及趋势 (1)1.3本文的主要工作安排 (2)第2章基本理论知识 (3)2.1滤波器的工作原理 (3)2.1.1模拟滤波器的工作原理 (3)2.1.2数字滤波器的工作原理 (4)2.2滤波器的基本特性 (5)2.2.1模拟滤波器与数字滤波器的基本特性 (5)2.2.2无限冲激响应IIR和有限冲激响应FIR滤波器 (7)2.3滤波器的主要性能指标 (8)第3章模拟滤波器的设计 (9)3.1模拟滤波器的分类 (9)3.2 模拟滤波器的设计方法 (9)3.3模拟原型滤波器及最小阶数选择 (11)3.3.1巴特沃斯滤波器及最小阶数选择 (11)3.3.2切比雪夫滤波器及最小阶数选择 (14)3.3.3椭圆滤波器及最小阶数的选择 (20)3.3.4贝塞尔滤波器 (21)第4章 MATLAB仿真 (22)4.1MATLAB简介 (22)4.2对低通模拟滤波器的仿真 (23)4.3 模拟高通滤波器的仿真 (25)4.4 模拟带通滤波器的仿真 (26)4.5 对带阻模拟滤波器的仿真 (28)第5章频率转换 (30)5.1低通至高通的转换 (30)5.2低通至带通的变换 (31)5.3低通至带阻的变换 (34)第6章总结与展望 (36)参考文献 (37)第1章绪论1.1课题研究背景及意义凡是有能力进行信号处理的装置都可以称为滤波器。
基于MATLAB的IIR数字滤波器设计与仿真

基于MATLAB的IIR数字滤波器设计与仿真一、概述在现代数字信号处理领域中,数字滤波器扮演着至关重要的角色。
其通过对输入信号的特定频率成分进行增强或抑制,实现对信号的有效处理。
无限脉冲响应(IIR)数字滤波器因其设计灵活、实现简单且性能优良等特点,得到了广泛的应用。
本文旨在基于MATLAB平台,对IIR数字滤波器的设计与仿真进行深入研究,以期为相关领域的研究与应用提供有益的参考。
IIR数字滤波器具有无限长的单位脉冲响应,这使得其在处理信号时能够展现出优秀的性能。
与有限脉冲响应(FIR)滤波器相比,IIR滤波器在实现相同性能时所需的阶数更低,从而减少了计算复杂度和存储空间。
在需要对信号进行高效处理的场合,IIR滤波器具有显著的优势。
MATLAB作为一款功能强大的数学软件,提供了丰富的函数和工具箱,使得数字滤波器的设计与仿真变得简单而高效。
通过MATLAB,我们可以方便地实现IIR滤波器的设计、分析和优化,从而满足不同应用场景的需求。
本文将首先介绍IIR数字滤波器的基本原理和特性,然后详细阐述基于MATLAB的IIR数字滤波器的设计方法和步骤。
接着,我们将通过仿真实验验证所设计滤波器的性能,并对其结果进行分析和讨论。
本文将总结IIR数字滤波器设计与仿真的关键技术和注意事项,为相关领域的研究人员和工程师提供有益的参考和启示。
1. IIR数字滤波器概述IIR(Infinite Impulse Response)数字滤波器是数字信号处理中常用的一类滤波器,它基于差分方程实现信号的滤波处理。
与FIR (Finite Impulse Response)滤波器不同,IIR滤波器具有无限长的单位脉冲响应,这意味着其输出不仅与当前和过去的输入信号有关,还与过去的输出信号有关。
这种特性使得IIR滤波器在实现相同的滤波效果时,通常具有更低的计算复杂度,从而提高了处理效率。
IIR滤波器的设计灵活多样,可以根据不同的需求实现低通、高通、带通和带阻等多种滤波功能。
bpsk和dpskmatlab仿真
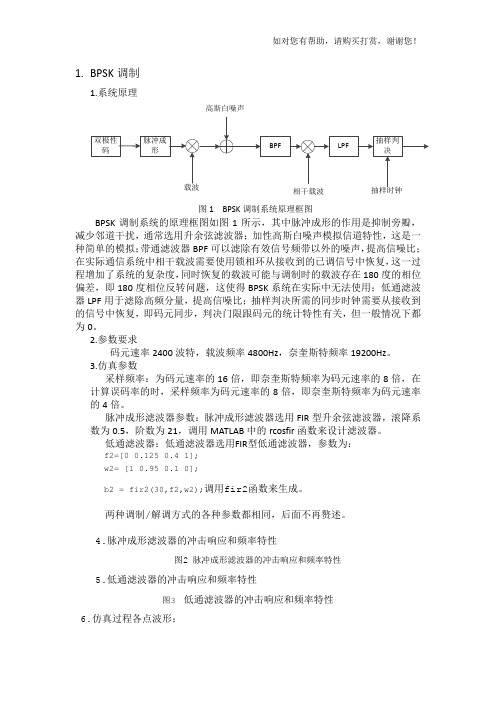
1.BPSK调制1.系统原理高斯白噪声图1 BPSK调制系统原理框图BPSK调制系统的原理框图如图1所示,其中脉冲成形的作用是抑制旁瓣,减少邻道干扰,通常选用升余弦滤波器;加性高斯白噪声模拟信道特性,这是一种简单的模拟;带通滤波器BPF可以滤除有效信号频带以外的噪声,提高信噪比;在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复,这一过程增加了系统的复杂度,同时恢复的载波可能与调制时的载波存在180度的相位偏差,即180度相位反转问题,这使得BPSK系统在实际中无法使用;低通滤波器LPF用于滤除高频分量,提高信噪比;抽样判决所需的同步时钟需要从接收到的信号中恢复,即码元同步,判决门限跟码元的统计特性有关,但一般情况下都为0。
2.参数要求码元速率2400波特,载波频率4800Hz,奈奎斯特频率19200Hz。
3.仿真参数采样频率:为码元速率的16倍,即奈奎斯特频率为码元速率的8倍,在计算误码率的时,采样频率为码元速率的8倍,即奈奎斯特频率为码元速率的4倍。
脉冲成形滤波器参数:脉冲成形滤波器选用FIR型升余弦滤波器,滚降系数为0.5,阶数为21,调用MATLAB中的rcosfir函数来设计滤波器。
低通滤波器:低通滤波器选用FIR型低通滤波器,参数为:f2=[0 0.125 0.4 1];w2= [1 0.95 0.1 0];b2 = fir2(30,f2,w2);调用fir2函数来生成。
两种调制/解调方式的各种参数都相同,后面不再赘述。
4.脉冲成形滤波器的冲击响应和频率特性图2 脉冲成形滤波器的冲击响应和频率特性5.低通滤波器的冲击响应和频率特性图3 低通滤波器的冲击响应和频率特性6.仿真过程各点波形:说明:在画图时,进行了归一化处理。
噪声的方差为1,随机序列的幅度为1,调制加噪后信噪比为-3dB,按照理想情况计算,解调后信噪比为0dB。
图2 随机序列(16个)图3 脉冲成形后的波形脉冲成形的作用是抑制旁瓣,减少邻道干扰,在实际通信过程中必不可少,但是为了与理论误码率进行对比,在后面计算误码率时,没有进行脉冲成形。
滤波器设计及调试中的MATLAB仿真技术研究

滤波器设计及调试中的MATLAB仿真技术研究引言滤波器是一种重要的电子设备,能够对信号进行降噪、频率滤波、信号分离等处理。
滤波器设计是电子工程师日常工作中常涉及的一个领域。
而MATLAB则是一种常用的数学软件,拥有强大的数值分析及仿真功能。
本文将介绍MATLAB在滤波器设计及调试中的应用技巧,以期能够帮助读者更好地完成滤波器的设计和调试工作。
滤波器基础在进入MATLAB的具体操作之前,我们需要先了解一些滤波器的基础知识。
滤波器大致可以分为两类,分别是时域滤波器和频域滤波器。
时域滤波器的输入和输出都是时域信号,常见的时域滤波器有低通滤波器、高通滤波器、带通滤波器及带阻滤波器。
频域滤波器的输入和输出都是频域信号,常见的频域滤波器有低通滤波器、高通滤波器、带通滤波器及带阻滤波器。
其中,低通滤波器的频率响应在截止频率以下为1,在截止频率以上为0。
高通滤波器的频率响应在截止频率以下为0,在截止频率以上为1。
带通滤波器的频率响应在截止频率范围内为1,其他频率为0。
带阻滤波器的频率响应在截止频率范围内为0,其他频率为1。
MATLAB在滤波器设计中的应用MATLAB可以用于滤波器设计的整个过程,包括滤波器设计、滤波器仿真和调试。
1. 滤波器设计滤波器设计是滤波器设计和调试过程中最为重要和基础的一步。
MATLAB提供了一些常用的滤波器设计函数,例如fir1、fir2、ellip等。
这些函数可以让设计师直接在MATLAB中设定滤波器的参数,例如滤波器类型、截止频率、通带波纹、阻带衰减等,并生成相应的滤波器系数。
因此,在滤波器设计时,我们可以新建一个.m文件,在文件中编写相应的代码,调用滤波器设计函数实现滤波器的设计,以此完成滤波器设计的流程。
2. 滤波器仿真滤波器仿真是滤波器设计和调试过程中非常重要的一步。
在滤波器设计后,我们需要对其进行仿真,以检验滤波器的性能和品质。
在MATLAB中,我们可以使用freqz函数来实现滤波器的仿真和频率响应分析。
深度剖析MATLAB信号处理仿真-基带脉冲成形

深度剖析MATLAB信号处理仿真-基带脉冲成形本次我们探讨另外一个在本科阶段让我们头痛的东西,通信原理之必考曲目,拼死也要背下来的内容,基带脉冲成形。
然而俺对这个东西的理解和认识却是在本科以后的事情。
早年(比如摩托罗拉手机时代)的基带成形都是用模拟电路做的,那会儿的数字电路密度极低,想想大学本科数电实验里面的各种74系列芯片,如果用这个东西拼个数字滤波器估计会疯掉。
况且,就算有数字滤波器,高速高精度的ADC、DAC也是个问题。
所以,早些年的数字电路课本的名字通常叫做“脉冲与数字电路”,言下之意,这东西用来处理脉冲信号的,而且,也就处理处理脉冲信号,千万别想着整太复杂的东西,那会还是一个模拟电路统治着通信系统的时代。
问题在于,除了打电话这种事情,人们还是有传送数据的需求的,比如说像寻呼机这种无线数字通信系统,更早的,比如郑君里老师在《教与写的记忆-信号与系统评注》提到的他年轻时候的神器“1200波特数传机”这东西用现在的话讲叫做“1200波特率调制解调器”,送你一台上网用,你肯定嫌慢,但是在当时是要国家立项的重大课题。
如果你愿意去一些通信原理或是信号与系统的课本里面考古,也许会看见有些习题专门探讨如何设计一个模拟的升余弦滚降滤波器。
在那个时代里,数字电路的任务是把要发送的比特信息变换成脉冲信号,就是一些列各种幅度(多进制调制)的方波,我们在信号与系统的课程里知道,方波信号的带宽是无穷大的,所以后级的模拟成形滤波器负责把这些方波的频谱带宽变小,同时又要满足时域采样点无失真的准则。
我们在数字信号处理课程里面学习过IIR滤波器,而且还有“双线性变换法”,“冲击响应不变法",以及各种让我们头晕的东西,我小时候第一次学这东西的时候在想,整这个玩意儿干嘛,后来才明白,这东西是为了用数字的方法来实现以前的模拟滤波器,模拟滤波器都是有极点的,映射到数字域中,就是IIR滤波器,那么为什么要替换掉模拟滤波器呢,有两个原因,一是为了提高通信产品的一致性,模拟元件比如电容、电阻的值是无法严格准确生产的,至于电感就是个更加不靠谱的东西,这就导致每个模拟电路元件被制造出来。
通信系统课程设计-基于matlab的成型与匹配滤波器设计与仿真分析

西南科技大学通信系统课程设计报告课程名称:通信系统课程设计设计名称:基于matlab的成型与匹配滤波器设计与仿真分析姓名:学号:班级:通信1204指导教师:起止日期:——西南科技大学信息工程学院制课程设计任务书学生班级:通信1204 学生姓名:梁高丽学号:20213526 设计名称:基于matlab的成型滤波器与匹配滤波器设计与仿真分析起止日期:——指导教师:候宝临课程设计学生日志基于MATLAB的成型与匹配滤波器设计与仿真分析一、摘要滤波器是一种用来消除干扰杂讯的器件,将输入或输出经过过滤而得到纯洁的直流电。
对特定频率或该频点以外的频率进行有效滤除的电路,其功能就是得到一个特定频率或消除一个特定频率。
成型滤波器是输入端常用的低通滤波器,经信道到接收滤波器的整个传输过程。
接收端的滤波是对整个传输函数的补偿,并且平滑波形,消除局部码间干扰〔ISI〕。
匹配滤波器是输出端的信号瞬时功率与噪声平均功率的比值最大的线性滤波器,匹配滤波器是一种非常重要的滤波器,广泛应用与通信、雷达等系统中。
同时在数字通信中,成型滤波器和匹配滤波器是调制的重要过程。
二、设计目的和意义2.1设计意义a.通过利用matlab simulink,熟悉matlab simulink仿真工具。
b.通过课程设计来更好的掌握课本相关知识,熟悉匹配滤波器的设计以及工作原理。
C.更好的了解通信原理的相关知识,磨练自己分析问题、查阅资料、稳固知识、创新等方面能力。
2.2 设计目的对于数字信号系统最难以做到的就是在调制过程中合理地解决码间干扰和提高输出信噪比这两点。
信号的相位跳变是瞬时变化的,瞬时变化的相位会使信号频谱发生扩散,导致需要非常大的信道带宽才能无失真地传输信号。
为了把信号频谱限制在一个比拟合理的范围内,对基带信号进行滤波是必不可少的。
但是基带滤波会使信号在时域上扩展,如果设计不好将在接收端引起严重的码间干扰〔ISI〕。
利用成型滤波消除码间干扰对信号传输的影响。
基于Matlab的滤波器仿真与演示

低通滤波器:允许低频信号通过, 抑制高频信号
带通滤波器:允许一定频段的信号 通过,抑制其他频段信号
添加标题
添加标题
添加标题
添加标题
高通滤波器:允许高频信号通过, 抑制低频信号
带阻滤波器:抑制特定频段的信号, 允许其他频段信号通过
滤波器类型:低通、高通、带通、带阻滤波器 设计步骤:确定滤波器参数、选择滤波器函数、进行滤波器设计 设计工具:Matlab自带滤波器设计工具 设计注意事项:避免过度拟合或欠拟合、考虑计算复杂度
滤波器性能指 标:如通带波 动、阻带衰减
等
仿真结果展示: 通过图表或图 像展示滤波器 频率响应、时
域响应等
案例分析:对 所选取的滤波 器类型、参数 设置等进行详
细分析
结果对比:将 仿真结果与理 论值进行对比, 分析误差及原
因
Matlab滤波器仿真 与演示总结与展望
滤波器的性能评估和优化方 法
Matlab滤波器仿真与演示的 原理和实现方法
滤波器在信号处理和通信系 统中的应用
未来发展方向和潜在应用领 域
未来滤波器技术的发展趋势 Matlab在滤波器设计中的新应用 滤波器仿真与演示的未来发展方向 基于Matlab的滤波器仿真与演示的未来研究热点
感谢您的观看
汇报人:XX
结果分析:对仿真 结果进行详细分析, 并与理论值进行对 比
结论:总结滤波 器性能评估结果, 提出改进意见
滤波器类型选择:根据信号处理需 求选择合适的滤波器类型,如低通、 高通、带通等。
滤波器阶数确定:根据信号处理精 度和实时性要求,选择合适的滤波 器阶数。
添加标题
添加标题
添加标题
添加标题
滤波器参数优化:通过调整滤波器 参数,如截止频率、阻尼因子等, 提高滤波效果。
经典滤波器的MATLAB仿真

摘要滤波器是用来选择所需的某种或某些频带的信号,而抑制不需要的其它频带信号的装置。
滤波器作为信号处理的重要组成部分,已发展的相当成熟。
滤波器可以分为两大类,即经典滤波器和现代滤波器。
本文着重讲述了经典滤波器的MATLAB仿真。
数字滤波器是数字信号处理的重要环节,数字滤波器可以分为无限脉冲响应滤波器(IIR, Infinite Impulse Response)和有限脉冲响应滤波器(FIR,Finite Impulse Response)两大类。
本文首先介绍了滤波器的滤波原理,重点介绍了IIR 滤波器和FIR滤波器的基本设计原理,以及在MATLAB环境下如何将模拟滤波器转换为数字滤波器,并给出设计实例及运行结果。
通过分析程序运行的结果得到模拟滤波器与数字滤波器的不同,以及IIR滤波器与FIR滤波器的不同之处,并与实际生产相联系得出他们各自的优缺点。
关键字:滤波模拟滤波器数字滤波器 MATLABAbstractFilter is used to select a desired one or some frequency band signal, and suppresses the unwanted other band signal device. Filter for signal processing is an important ponent, has developed quite mature. The filter can be divided into two categories, namely, classical and modern filter filter. This paper focuses on the classic MATLAB filter simulation.Digital filter digital signal processing is the important link, digital filter can be divided into infinite impulse response filters ( IIR, Infinite Impulse Response ) and the finite impulse response filter ( FIR, Finite Impulse Response ) two categories. This paper first introduces the filter principles, introduced with emphasis on the IIR filter and a FIR filter design fundamentals, as well as in the MATLAB environment how to analog filter is converted to a digital filter, and gives examples of design and operation results. Through the analysis of the program running results are analog and digital filter is different, and the IIR filter and a FIR filter difference, and with actual production is linked to that of their respective advantages and disadvantages.Key words:filter AF DF MATLAB目录1 绪论11.1 MATLAB软件简介11.2 滤波器简介21.2.1 滤波器工作原理31.2.2 数字滤波器的设计方法42 基于MATLAB的IIR数字滤波器设计52.1 模拟滤波器的设计52.1.1 巴特沃斯低通滤波器设计62.1.2 切比雪夫低通滤波器设计92.2 模拟-数字滤波器的转换162.2.1 冲击响应不变法162.2.2 双线性Z变换法212.3 频带变换及其MATLAB实现232.3.1 模拟低通滤波器转换成数字高通滤波器242.3.2 模拟低通滤波器转换成数字带通滤波器262.4 小结293 基于MATLAB的FIR数字滤波器设计303.1 常用窗函数及MATLAB实现313.1.1 常用窗函数介绍313.1.2 各种窗函数的比较与实现343.2 基于窗函数的FIR数字滤波器设计353.2.1 海明窗设计数字低通滤波器363.2.2 汉宁窗设计一线性相位FIR高通数字滤波器383.2.3 用汉宁窗设计FIR带通滤波器413.2.4 用凯塞窗函数设计一个FIR带阻滤波器463.3 小结484 滤波器的比较494.1 模拟滤波器与数字滤波器的比较494.2 IIR与FIR数字滤波器的比较505 总结51致谢52 参考文献531 绪论1.1 MATLAB软件简介MATLAB是“矩阵实验室”(Matrix Laboratoy)的缩写,是一种科学计算软件,主要适用于矩阵运算及控制和信息处理领域的分析设计。
MATLAB通信建模实验仿真实验报告

实验1:上采样与内插一、实验目的1、了解上采样与内插的基本原理和方法。
2、掌握上采样与内插的matlab程序的设计方法。
二、实验原理上采样提高采样频率。
上采样使得周期降低M倍,即新采样周期Tu和原有采样周期Ts的关系是T u=T s/M,根据对应的连续信号x(t),上采样过程从原有采样值x(kT s)生成新采样值x(kT u)=x(kT s/M)。
操作的结果是在每两个采样值之间放入M-1个零值样点。
更实用的内插器是线性内插器,线性内插器的脉冲响应定义如下:上采样值x(kT u)=x(kT s/M)通过与线性内插器的脉冲响应的卷积来完成内插。
三、实验内容仿真正弦波采样和内插,通过基本采样x(k),用M=6产生上采样x u(k),由M=6线性内插得到样点序列x i(k)。
四、实验程序% File: c3_upsampex.mM = 6; % upsample factorh = c3_lininterp(M); % imp response of linear interpolatort = 0:10; % time vectortu = 0:60; % upsampled time vectorx = sin(2*pi*t/10); % original samplesxu = c3_upsamp(x,M); % upsampled sequencesubplot(3,1,1)stem(t,x,'k.')ylabel('x')subplot(3,1,2)stem(tu,xu,'k.')ylabel('xu')xi = conv(h,xu);subplot(3,1,3)stem(xi,'k.')ylabel('xi')% End of script file.% File: c3_upsample.mfunction out=c3_upsamp(in,M)L = length(in);out = zeros(1,(L-1)*M+1); for j=1:Lout(M*(j-1)+1)=in(j); end% End of function file.% File: c3_lininterp.m function h=c3_lininterp(M) h1 = zeros(1,(M-1)); for j=1:(M-1) h1(j) = j/M; endh = [0,h1,1,fliplr(h1),0]; % End of script file.四、 实验结果012345678910x0102030405060x u01020304050607080-11x i实验二:QPSK、16QAM信号的散点图、正交、同相分量波形图一、实验目的1、了解QPSK、16QAM调制的基本原理。
Matlab滤波器设计--IIR滤波器的设计与仿真

matlab滤波器设计-IIR滤波器的设计与仿真1 引言在现代通信系统中,由于信号中经常混有各种复杂成分,所以很多信号的处理和分析都是基于滤波器而进行的。
但是,传统的数字滤波器的设计使用繁琐的公式计算,改变参数后需要重新计算,从而在设计滤波器尤其是高阶滤波器时工作量很大。
利用MATLAB信号处理箱(Signal Processing Toolbox)可以快速有效地实现数字滤波器的设计与仿真。
2 数字滤波器及传统设计方法数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化过程中,使信号按预定的形式变化。
数字滤波器有多种分类,根据数字滤波器冲激响应的时域特征,可将数字滤波器分为两种,即无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)滤波器。
IIR数字滤波器具有无限宽的冲激响应,与模拟滤波器相匹配,所以IIR滤波器的设计可以采取在模拟滤波器设计的基础上进一步变换的方法。
其设计方法主要有经典设计法、直接设计法和最大平滑滤波器设计法。
FIR数字滤波器的单位脉冲响应是有限长序列。
它的设计问题实质上是确定能满足所要求的转移序列或脉冲响应的常数问题,设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等。
在对滤波器实际设计时,整个过程的运算量是很大的。
设计阶数较高的IIR滤波器时,计算量更大,设计过程中改变参数或滤波器类型时都要重新计算。
设计完成后对已设计的滤波器的频率响应要进行校核。
要得到幅频、相频响应特性,运算量也是很大的。
平时所要设计的数字滤波器,阶数和类型并不一定是完全给定的,很多时候要根据设计要求和滤波效果不断地调整,以达到设计的最优化。
在这种情况下,滤波器设计就要进行大量复杂的运算,单纯的靠公式计算和编制简单的程序很难在短时间内完成。
利用MATLAB强大的计算功能进行计算机辅助设计,可以快速有效地设计数字滤波器,大大地简化了计算量。
如何用matlab进行滤波器设计和仿真

华中科技大学本科课程考试答题本考生姓名考生学号班级联系电话Email:考试科目考试日期一、报告摘要:本报告首先论述如何用matlab进行滤波器设计和仿真,并且将参数转换成DSP可用的滤波器参数。
然后,将这组参数在CCS上进行纯软件仿真。
随之是本次实验过程中代码拼接的问题与解决方法。
软硬件流程图及核心代码的陈述。
将实际滤波的结果进行展示。
与理想滤波器的比较之间的差异与改良。
最后是对于本课程的感想二、滤波器基础知识以及基于matlab的参数设计:设计一个能够将1000Hz一下保留,1500Hz以上的频率滤出的滤波器,利用理想的fir滤波器截止频率可以设定为(1000+1500)/2=1250Hz,利用哈明窗设计本滤波器,阶数为21阶,function[a]=ccc()clear all;clf;N=1024;%设置采样点数fs=6000;%设置采样频率dt=1/fs;for k=1:N;f1=1500;f2=1000;y(k)=sin(2*pi*f1*k*dt)+sin(2*pi*f2*k*dt)+sin(2*pi*(f1+200)*k*dt);%+sin(2*pi*12 50*k*dt);endwp=pi*1000*2/6000;%归一化的通带频率ws=pi*1500*2/6000;%归一化的阻带频率wc=(wp+ws)/2; %理想的滤波器的截止频率M=21; %设置阶数b=fir1(M-1,wc/pi,hamming(M))%;利用fir1函数得到滤波系数b[H,F]=freqz(b,1,N); %figure(1);plot(F/pi,20*log10(abs(H)));grid;xlabel('f(Hz)');ylabel('幅度');%画出幅频特性yy1=conv(b,y); %做卷积即为滤波y=fft(y,N); %做fft运算得到频域特性pyy=y.*conj(y); %乘以共轭,得到的是y的幅值的平方f=(0:(N/2-1));figure(2);plot(f*fs/N,pyy(1:N/2));y=fft(yy1,N);pyy=y.*conj(y);f=(0:(N/2-1));figure(3);plot(f*fs/N,pyy(1:N/2));执行以上函数后得到以下图像:可以看到在(2*1000)/6000=0.33处的衰减基本不变,而在(1000+1500)/6000=0.42处衰减值已经大于3dB了,而在(2*1500)/6000=0.5衰减值已经接近20dB了。
基于MATLAB环境的数字滤波器的设计与仿真

基于MATLAB环境的数字滤波器的设计与仿真摘要:数字滤波器是数字信号处理中最重要的工具之一。
在许多科学技术领域中广泛采用数字滤波器进行信号处理。
数字滤波器分为两类,即有限脉冲响应滤波器(FIR)和无限脉冲响应滤波器(IIR)。
数字滤波器是由数字乘法器、加法器和延时单元组成的一种装置。
其功能是对输入离散信号的数字代码进行运算处理,以达到改变信号频谱的目的。
由于电子计算机技术和大规模集成电路的发展,数字滤波器已可用计算机软件实现,也可用大规模集成数字硬件实时实现。
本文针对在实际设计中要大量应用数字滤波器这一现实,对数字滤波器的基本理论、性能特点、设计方法进行了全面的分析,特别是对有限冲击响应数字滤波器(FIR)的设计进行了深入的探讨。
文章运用了MA TLAB仿真手段对数字滤波器的设计理论和设计方法方法进行了研究。
论文主要包括数字滤波器以及MATLAB在信号处理方面的概述,FIR数字滤波器设计方法的介绍,MATLAB语言仿真,以及最终结论。
本论文所采用的研究方法是仿真比较,介绍了常用滤波器的设计方法,通过MATLAB软件对各种方法分别实现仿真,然后对仿真结果进行比较。
通过对数字滤波器的理论研究为今后的实践奠定理论基础。
关键词:数字滤波器;FIR滤波器;MATLAB;仿真Design and Simulation of Digital FilterBased On MATLABAbstract: Digital filter is one of the most important parts of digital signal processing. In many fields of science and technology, it is widely used for digital signal processing. Digital filter includes finite impulse response filter(FIR) and infinite impulse response filter(IIR).Digital wave filter is a kind of installation that forms by digital multiplier, adder and the unit of delay time. Its function is to carry out operational handling for inputting the digital code of dispersed signal in order to reach the purpose that changes signal frequency spectra. Because of the development of the computer technical circuit of large scale integration digital wave filter can already realize with computer software, can also realize with the digital hardware real time of large scale integration. Digital wave filter is a dispersed time system. As digital filters, in particular FIR filters, are widely used in modern designs, this dissertation comprehensively anglicized fir’s basic theory, characters and design methodologies.In this paper, MATLAB simulation is employed to study the design theory and methods of digital filter. The summary of digital filter and MATLAB language are introduced. Method of FIR filter design, results of MATLAB simulation are described in detail as well. The common design methods of digital filter are simulated with MATLAB to find the result that I need before. It is hope that it can provide a reference for future appliance.Key Words: digital filter;FIR filter;MATLAB;simulation第一章绪论1.1 数字滤波器的现状及发展数字滤波器按单位脉冲响应的性质可分为无限长单位脉冲响应滤波器IIR和有限长单位脉冲响应滤波器FIR两种。
matlab 成型滤波

matlab 成型滤波如何使用matlab进行成型滤波。
第一步:了解成型滤波的原理成型滤波是一种数字信号处理技术,主要用于非理想信号的去噪和信号重建。
它通过对信号进行频域分析和滤波处理,使信号满足特定的要求或具有特定的性质。
成型滤波广泛应用于通信系统、图像处理、声音处理等领域。
成型滤波的基本原理是根据信号的频域特征进行滤波。
具体而言,它通过设计一个成型滤波器,使滤波器在输入信号的频域上产生特定的响应,然后再将滤波器的输出进行逆变换,得到滤波后的信号。
第二步:准备成型滤波所需的工具在使用matlab进行成型滤波之前,我们需要准备一些工具,包括以下几项:1. Matlab软件:确保你已经安装了最新版本的Matlab软件,以便使用其中提供的滤波函数和工具。
2. 信号数据:为了演示成型滤波的过程,你需要准备一个用于滤波的信号数据。
可以是实际采集的信号,也可以是通过Matlab生成的虚拟信号。
第三步:加载信号数据以及滤波器设计在Matlab中,可以使用`load`函数加载信号数据,并利用`designfilt`函数设计成型滤波器。
matlab加载信号数据load('signal_data.mat');设计成型滤波器fs = 1000; 采样频率fpass = [20 100]; 通带频率范围fstop = [10 120]; 阻带频率范围d = fdesign.bandpass('Fst1, Fp1, Fp2, Fst2, Ap1, Ap2', fstop(1), fpass(1), fpass(2), fstop(2), 0.5, 0.5, fs);h = design(d, 'butter');上述代码中,`signal_data.mat`是你准备好的信号数据文件。
`fs`是信号的采样频率,`fpass`是通带的频率范围,`fstop`是阻带的频率范围。
数字滤波器的MATLAB设计与仿真及在DSP上的实现

数字滤波器的MATLAB设计与仿真及在DSP上的实现数字滤波器的MATLAB设计与仿真及在DSP上的实现概述:数字滤波器是数字信号处理(DSP)中的重要组成部分,常用于信号去噪、频率选择、滤波等应用。
本文将介绍数字滤波器的设计、仿真以及在DSP上的实现。
我们将使用MATLAB软件进行数字滤波器设计和仿真,并利用DSP芯片进行实现。
第一部分:数字滤波器的设计与仿真1. 信号基础知识在设计数字滤波器之前,我们需要了解信号的基础知识,如信号的采样率、带宽、频率等。
这些基础知识将有助于我们选择合适的滤波器类型和参数。
2. 滤波器类型数字滤波器可以分为两大类别:无限冲激响应(IIR)滤波器和有限冲激响应(FIR)滤波器。
IIR滤波器具有无限的冲激响应,因此可以实现更为复杂的频率响应特性;而FIR滤波器降低了系统的非线性,同时具有线性相位特性,适用于需要精确延迟的应用。
3. 滤波器设计方法常用的数字滤波器设计方法包括窗函数法、最小二乘法和频率抽取法等。
根据具体的应用需求,我们可以选择合适的设计方法,并通过MATLAB进行滤波器的设计和参数调整。
4. 滤波器性能评估在设计完成后,我们需要评估数字滤波器的性能。
常见的评价指标包括滤波器的频率响应、幅频特性、相频特性、群延迟等。
通过MATLAB的仿真,我们可以直观地观察并分析滤波器的性能。
第二部分:数字滤波器在DSP上的实现1. DSP概述数字信号处理器(DSP)是一种专门设计用于处理数字信号的微处理器。
与通用微处理器相比,DSP具有更高的运算速度和更低的功耗,适用于实时信号处理应用。
2. DSP开发环境搭建为了实现数字滤波器的DSP上的实现,我们首先需要搭建DSP开发环境。
选择合适的DSP芯片,安装开发工具,编写代码并进行调试。
在本文中,我们以TMS320F28335为例,使用CCS开发工具进行开发。
3. 数字滤波器的DSP实现根据数字滤波器的设计结果,我们可以将其转化为DSP上的实现代码。
基带脉冲成形数字滤波器的MATLAB设计与DSP上的实现

( c o l f 1lc mmu ia i n g n e ig Xi in Un v r i , n 71 0 Ch n ) S h o ee 0 o1 n c t0 s En i e rn , d a i e st Xi a 71 y 0 , ia
中图分类号 T 9 4 N1.2 4
M a l b- a e sg ft eBa e a d P le- a i g Di ia le ta ・ s d De i n o s b n u s ・h p n g t l t r b h s Fi a d isRe l a i n o p n t a i t n Ds z o
摘
要求。
要 介绍 了采用 M T , 设 计基带脉冲 戍形数 字滤波 器的基本原 理和设计 方法 , ALB  ̄ 以及在 定点 D P上的 实 S
现 。实现 时先在 C S 0 仿 真开发 ,然后 将程序 加载到 d p ( M 3 C 9 上 实时运行 ,其结果 实现 了 目标 C5 0 0 s T S 2V 5 a) 0 5 0 关键词 脉 冲成形 ;M t a ;数字滤 波器 a b l
x 丁
维普资讯
基 带脉冲成形 数字滤 波器 的 M T A 设 计与 D P上 的实现 A [B G
式中 1T是 符号 率 。 /
一
在无线通信Байду номын сангаас中最常 用的脉 冲成形滤波器 是升余弦
滚 降 滤波 器 ,其 传 递 函数 为 :
般 来说 ,很 多信 号 都能 设 计 为满 足此 条件 。
生既减小码 间串扰又不会 占用过多额外带宽的更 适合于信道传输的波形 。
它 的傅 里 叶变 换 x(满 足 『 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
脉冲成型滤波器matlab仿真
脉冲型滤波器用成型脉冲即数字1用矩形脉冲表示用升余弦脉冲或高斯脉冲表示主要用于基带数据处理。
在数字通信系统中,基带信号进入调制器前,波形是矩形脉冲,突变的上升沿和下降沿包含高频成分较丰富,信号的频谱一般比较宽。
从本质上说,脉冲成形就是一种滤波。
数字通信系统的信号都必须在一定的频带内,但是基带脉冲信号的频谱是一个Sa函数,在频带上是无限宽的,单个符号的脉冲将会延伸到相邻符号码元内产生码间串扰,这样就会干扰到其他信号,这是不允许的。
为了消除干扰,信号在发射之前要进行脉冲成形滤波,把信号的频率约束在带内。
因此在信道带宽有限的条件下,要降低误码率,提升信道频带利用率,需要在信号传输前,对其进行脉冲成形处理,改善其频谱特,产生适合信道传输的波形。
符号/秒代表单位波特(Baud),波特率是符号信息的比特率。
一般的脉冲成型是要过采样的,不然没有意义,因为成型滤波会扩展带宽,过采样是为了减少频谱混叠。
常用的脉冲成型滤波器有RC成型(升余弦)、Gaussian成型等。
Matlab作为一个强大的仿真工具,在通信信号处理中有着广泛的应用。
新版的Matlab (2014a)中关于滤波器设计,很多API都做了更新,下面个根据文档仿真和对比几个成型滤波器。
早些版本的firrcos函数用来设计升余弦滤波器的函数,现在已经更改成了rcosdesign 函数。
例如:设计一个16阶升余弦滤波器,载波频率Fc = 1KHz,滚降系数0.25,采样率为8KHz。
N = 16;
Fc = 1000;
R = 0.25;
Fs = 8000;
h = firrcos(N, Fc, R, Fs, 'rolloff', 'normal');
figure();plot(h)
下图是滤波器的抽头系数,阶数为16共有17个抽头。
如果用rcosdesign函数来设计这个滤波器,那么要用下面的调用方法来实现。
h1 = rcosdesign(R, N/(Fs/Fc/2), Fs/Fc/2,'normal');
h1 = h1 / max(h1) / (Fs/Fc/2);%重新量化一下系数
figure;plot(h1)
同样进行绘图,结果同上面的相同。
在Matlab工具箱中,涉及升余弦滤波器的函数有好几个:rcosflt 使用升余弦滤波器对输入信号进行滤波,rcosine设计升余弦滤波器,rcosiir 设计升余弦IIR滤波器,firrcos 升余弦滤波器设计。
他们大部分已经慢慢被Matlab抛弃(新版本的Matlab将不赞成使用,但是会因为兼容性的历史原因被保留)。
下面重点介绍一下rcosdesign函数,这个函数数Matlab推荐的用来做升余弦成型滤波的函数。
[语法]
b = rcosdesign(beta,span,sps)
b = rcosdesign(beta,span,sps,shape)
[描述]
b = rcosdesign(beta,span,sps)函数返回一个滚降系数为beta的均方根升余弦函数。
函数被截断为span个符号并且每个符号周期有sps个采样点。
滤波器的阶数为span*sps并且必须为偶数。
滤波器的能量为1。
b = rcosdesign(beta,span,sps,shape)中,最后一个参数shape,当shape设置为'sqrt'时返回均方根升余弦滤波器系数,当shape被设置为'normal'时,返回一个升余弦滤波器的系数。
[例如]
设计一个滚降系数为0.25,符号截断数为6,每符号采样点为4的滤波器。
h = rcosdesign(0.25, 6, 4);
mx = max(abs(h - rcosdesign(0.25, 6, 4)));
fvtool(h,'Analysis','impluse');
下面的程序片段做了一个成型滤波的过程。
设计一个48阶的升余弦FIR滤波器,滚降因子为0.5,发送速率为1被速率,过采样率为8倍过采样。
%% filter: order = 48, rolloff factor: alpha = 0.5, sps = 8
% b = firros(n,Fc,df,Fs) Fc:cutoff frequency,df: transmition bandwidth, Fs:oversampling frequency
h = firrcos(48, 0.5, 0.5, 8); %Fc = 1/2, h = rcosdesign(0.5, 6, 8);也可以
figure(1);
plot(h);
grid on;
xlabel('Time');
ylabel('Amplitude');
title(' raised cosine rolloff filter');
tx_bits1x = randint(100,1)*2 -1;
tx_bits8x = zeros(1,800);
tx_bits8x(1:8:end) = tx_bits1x;
tx_shaped = filter(h,1,tx_bits8x);
tx_sampled = tx_shaped(1:8:end);
figure(2);
stem(tx_bits1x(1:40));
title('orginal bitstream');
figure(3);
plot(tx_shaped(1:100));
title('output waveform');
grid on;
figure(4);
stem(tx_sampled(1:40));
grid on;
title('sampled output');
图1:成型滤波器的系数
图2:原始的数据比特流
图3:经过滤波器后的波形
图4:抽取之后的数据
rocsdesign是firrcos的替代,在新版的matlab中建议使用rcosdesign,具体请看MarthWorks的文档。
下面展示了它们之间的转换方法。
N = 48;
R = 0.5;
beta = R;
Fs = 8;
Fc = 0.5;
sps = Fs/(2*Fc);
span = N/sps;
b1 = firrcos(N,Fc,R,Fs,'rolloff','normal');
b1n = rcosdesign(beta, span, sps, 'normal');
b1n = b1n / max(b1n) /sps;
figure;
plot(b1)
hold on
plot(b1n, 'r-.')
grid on
legend('firrcos', 'rcosdesign'); max(abs(b1n-b1));。
