动能定理习题课 (20180316)
动能定理

解: 设绳的 P 端到达 B 处时,左边绳与水平地面所成夹角为θ,物体 从井底上升的高度为h,速度为v,所求的功为W,则据动能定理 可得:
因绳总长不变,所以: 根据绳联物体的速度关系得:v = v B cosθ 由几何关系得: 由以上四式求得:
如图所示,一辆汽车通过一根跨过定滑轮的绳 PQ 提升井中质量为 m的物体,绳的P端拴在车后的挂钩上,Q端拴在物体上. 设绳的总 长不变,绳的质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不 计。开始时,车在 A点,左右两侧绳都已绷紧并且是竖直的,左侧 绳长为H. 提升时,车加速向左运动,沿水平方向从A经过B驶向C, 设A到B的距离也为H,车过B点时的速度为v。求在车由A移到B的 过程中,绳Q端的拉力对物体做的功.
2 Wf μ mgLcosα 3
支持力不做功,初、末动能均为零。
由动能定理 mgLsinα-2/3 μmgLcosα=0 可解得
3 μ tgα 2
例:斜面高度为 h,A、B两点的水平距离为s,不计物体
滑过C点时的能量损失,倾角为 θ,而动摩擦因数μ未知, 且物体滑到 B点时恰好停止,则物体滑过斜面 AC与滑过 平面CB所用的时间之比为?
第五单元
动能定理习题课
A
ACD
斜面倾角为α,长为L, AB段光滑,BC段粗糙,AB =L/3, 质
ቤተ መጻሕፍቲ ባይዱ
量为 m的木块从斜面顶端无初速下滑,到达C端时速度刚
好为零.求物体和BC段间的动摩擦因数μ.
A L C B
α
分析:以木块为对象,下滑全过程用动能定理:
重力做的功为
摩擦力做功为
WG mgLsinα
动能定理习题课PPT课件 人教课标版

v
B
9.如图所示为皮带传输机简图,其 顶端为水平且高度为3m。将质量为50kg 的货物轻轻放在皮带传输机底端。运动 至顶端后抛至高度为2.2m的平板车上, 落点与抛出点间的水平距离为0.8m,求 在输送货物期间皮带对货物做的功。 (g=10m/s2)
思考 9.(3)输送货物期间带动 滚轮的电动机要消耗多少 电能? (不考虑电动机自身的能耗)
思考
10.(4)每个周期中电动 机要消耗多少电能? (不考虑电动机自身的能耗)
动能定理与牛顿运动定律的比较
用牛顿运动定律解题涉及到的有关物理量比较 多,如F、a、m、v、s、t等.对运动过程的细节 变化也要掌握得比较充分,才可列式求解。而运用 动能定理解题涉及到的物理量只有F、s、m、 v.它对运动过程的细节及其变化也不要求了解, 只需考虑始末两状态的动能和外力做的功,它还可 把不同运动过程合并成一个全过程来处理,使解题 过程简便.当然,如果题目中要求了解加速度a、 运动时间t等细节,那就需要从动力学、运动学的角 度去分析,不能直接求解了。
5.构建和谐型、节约型社会深得民心,遍 布于生活的方方面面,自动充电式电动车就是 很好的一例。电动车的前轮装有发动机,发动 机与蓄电池连接。当在骑车者用力蹬车或电动 自行车自动滑行时,电动自行车就可以连通发 动机向蓄电池充电,将其他形式的能转化成电 能储存起来。现有某人骑车以500J的初动能在 粗糙的水平路面上滑行,第一次关闭自动充电 装置,让车自由滑行,其动能随位移变化关系 如图①所示;第二次启动自动充电装置,其动 能随位移变化关系如图②所示,则第二次向蓄 电池所充的电能是 A.200J B.250J C.300J D.500J
动能定理
习题课 新海高级中学 王承金
思考
《动能定理习题课》物理 必修 第二册 人教版第一课时课件

变式训练:质量为m=4 kg的小物块静止于水平地面上的A
点,现用F=10 N的水平恒力拉动物块一段时间后撤去,
物块继续滑动一段位移停在B点,A、B两点相距x=20 m,
物块与地面间的动摩擦因数μ=0.2,g取10 m/s2,求:
(1)物块在力F作用过程发生位移x1的大小;
(2)撤去力F后物块继续滑动的时间t。
A.
mv
2 0
2
√ C.
mv
2 0
4
B.
2mv
2 0
2
D.mv
2 0
(二)动能定理在多过程问题中的应用
质量为4kg的钢球从离坑面高1.95m的高处 自由下落,钢球落入沙中,陷入0.05m后静 止,则沙坑对钢球的平均阻力是多少?
v0= 0 mg
h1= 1.95 m
f v
mg
h2= 0.05 m
vt= 0
R(FN 3mg)
A.
2
B.
R(3mg FN ) 2
R(FN mg)
C.
2 D.
R(FN 2mg) 2
解根析据:质牛点顿到第达二最定低律点有B,时,F它N 对m容g器的m正Rv压2 力为; FN,
根据动能定理,质点自A滑到B的过程中
有
Wf
mgR
mv 2 2
;
故摩擦力对其所做的功
Wf
R(FN
定理可得
v0= 0 mg
mgh1
1 2
mv 2
0
在沙中钢球受重力和沙的阻力,
f 重力做正功,阻力做负功。根据
v
动能定理可得
mg
vt= 0
m
gh2
(-fh2
高中物理动能定理典型练习题(含答案)(K12教育文档)

(完整word版)高中物理动能定理典型练习题(含答案)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)高中物理动能定理典型练习题(含答案)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)高中物理动能定理典型练习题(含答案)(word版可编辑修改)的全部内容。
动能定理典型练习题典型例题讲解1.下列说法正确的是( )A 做直线运动的物体动能不变,做曲线运动的物体动能变化B 物体的速度变化越大,物体的动能变化也越大C 物体的速度变化越快,物体的动能变化也越快D 物体的速率变化越大,物体的动能变化也越大【解析】 对于给定的物体来说,只有在速度的大小(速率)发生变化时它的动能才改变,速度的变化是矢量,它完全可以只是由于速度方向的变化而引起.例如匀速圆周运动.速度变化的快慢是指加速度,加速度大小与速度大小之间无必然的联系.【答案】D2.物体由高出地面H 高处由静止自由落下,不考虑空气阻力,落至沙坑表面进入沙坑h 停止(如图5-3-4所示).求物体在沙坑中受到的平均阻力是其重力的多少倍?【解析】 选物体为研究对象,先研究自由落体过程,只有重力做功,设物体质量为m ,落到沙坑表面时速度为v ,根据动能定理有0212-=mv mgH ① 再研究物体在沙坑中的运动过程,重力做正功,阻做负功,根据动能定理有2210mv Fh mgh -=- ② 由①②两式解得hh H mg F += 另解:研究物体运动的全过程,根据动能定理有000)(=-=-+Fh h H mg解得hh H mg F += 3。
动能定理习题课-课件PPT

v
F
v0 N f
xG
四 3、求变力做功问题
、
应v
m500t5.0105kg
用 举
vm
例0
t
t2m in1 2 0s
t
f 恒定
速度最大时:
P f F
vm
应用动能定理:
Ptfs12mvm2 0
3、求变力做功问题
例7.一颗质量m=10g的子弹,以速度v=600m/s 从枪口飞出,子弹飞出枪口时的动能为多少?若测 得枪膛长s=0.6m,则火药引爆后产生的高温高压气 体在枪膛内对子弹的平均推力多大?
大?
EK
1mv2 180J0 2
F s 1 mv2 0 2
F 30N
四 3、求变力做功问题 、 应 一辆货车的质量为5.0×105kg,在平直轨道 用 以额定功率3000kw加速行驶,当速度由 举 10m/s加速到所能达到的最大速度30m/s 例 时,共用了2min,则这段时间内货车前进的
距离是多少?
求此过程中皮球克服空气阻力做的
功?(g=9.8m/s2)
vo
h=5m
2J
4、求解曲线运动问题
例9.某人从距地面25m高处抛出一小球,小球质量100g, 出手时速度大小为10m/s,落地时速度大小为16m/s,取 g=10m/s2,试求:
(1)人抛球时对小球做多少功?
(2)小球在空中运动时克服阻力做功多少?
v=0
F
S=60m
五 、 对
3、求变力做功问题
练习6.某人从12.5m的高楼顶突然向上抛出一 个小球,不计空气阻力,小球脱手时的速度是
应 5m/s,小球的质量为0.6kg,则人对小球所做
练 功的大小是多少?
动能定理 习题课

h
(1) − w f = m( v0 ) − mv
1 2 3 4 2 1 2
2 0
wf =
7 32
mv
2 0 1 2 2 0
(2)上升: mgh − fh = 0 − mv − 下降:mgh − fh = m( v0 )
1 2 3 4 2
f =
7 25
mg
7 25
全程: −
25 v
2
mgs = 0 − mv
1 2
2 0
练习1 练习1
如图所示,质量为 的物体 的物体, 高处由静止滑下, 如图所示,质量为m的物体,从h高处由静止滑下,至水平 高处由静止滑下 面上A点静止 若使物体由A点沿原路径返回 点静止; 点沿原路径返回C点 面上 点静止;若使物体由 点沿原路径返回 点,则外力 至少做功为( 至少做功为( B ) A. mgh B. 2mgh C. 3mgh D. 不能确定
《动能定理》习题课 动能定理》
一、全过程应用动能定理
例一、 质量为m的物体以速度 竖直向上抛出, 的物体以速度v 例一、 质量为 的物体以速度 0竖直向上抛出,物体落
回地面时,速度大小为 回地面时,速度大小为3 v0/4 ,设物体在运动中所受空 气阻力大小不变,如图所示, 气阻力大小不变,如图所示,求(1)物体运动中阻力所 物体运动中阻力所 做的功; 若物体落地后与地面碰撞无机械能损失 若物体落地后与地面碰撞无机械能损失, 做的功;(2)若物体落地后与地面碰撞无机械能损失, 求物体运动的总路程。 求物体运动的总路程。
B R
4 wF = mB gR 3
A
4、 如图 所示,用细绳连接的 、B两物体质量相等,A位于倾角 、 如图4所示 用细绳连接的A、 两物体质量相等 所示, 两物体质量相等, 位于倾角 均保持静止, 为30°的斜面上,细绳跨过定滑轮后使 、B均保持静止,然后释放, °的斜面上,细绳跨过定滑轮后使A、 均保持静止 然后释放, 与斜面间的滑动摩擦力为A受重力的 设A与斜面间的滑动摩擦力为 受重力的 倍,不计滑轮质量从摩擦, 与斜面间的滑动摩擦力为 受重力的0.3倍 不计滑轮质量从摩擦, 下降1米时的速度大可 求B下降 米时的速度大可。 下降 米时的速度大可。 解法一: 解法一:对A使用动能定理 Ts-mgs·sin30o -fs = mv2/2 使用动能定理 - 对B使用动能定理 (mg -T)s = mv2/2 且f = 0.3mg 使用动能定理 ) 三式联立解得: = 米 秒 三式联立解得:v=1.4米/秒 解法二:将A、B看成一整体。(因二者速度、加 看成一整体。 因二者速度、 解法二: 、 看成一整体 因二者速度 速度大小均一样),此时拉力T为内力 为内力, 速度大小均一样 ,此时拉力 为内力,求外力做 功时不计,则动能定理写为: 功时不计,则动能定理写为: mgs-mgs·sin30o -fs = ½×2mv2 - 二式联立解得: = 米 秒 二式联立解得:v=1.4米/秒 可见,结论是一致的, 可见,结论是一致的,而方法二中受力体的选 择使解题过程简化, 择使解题过程简化,因而在使用动能定理时要适 当选取研究对象。 当选取研究对象。
《动能定理》习题课课件

1、质量一定的物体( BC ) 质量一定的物体( 速度发生变化时, A、速度发生变化时,动能一定发生变化 速度发生变化时, B、速度发生变化时,动能不一定发生变化 速度不变时, C、速度不变时,其动能一定不变 动能不变时, D、动能不变时,速度一定不变
注意点:速度是矢量,有大小、方向。 注意点:速度是矢量,有大小、方向。
总结: 总结:应用动能定理解题的一般步骤
1、确定研究对象及运动过程 2、分析物体在运动过程中的受力情 明确各个力是否做功, 况,明确各个力是否做功,是做正 功还是负功,求出总功。 功还是负功,求出总功。 明确初状态和末状态的动能, 3、明确初状态和末状态的动能,写 出始末状态动能的表达式 根据动能定理列方程求解。 4、根据动能定理列方程求解。
3、一质量为2kg的滑块,以4m/s的 一质量为2kg的滑块, 4m/s的 2kg的滑块 速度在光滑的水平面上向左滑行, 速度在光滑的水平面上向左滑行,从 某一时刻起, 某一时刻起,在滑块上作用一向右的 水平力,经过一段时间, 水平力,经过一段时间,滑块的速度 方向变为向右,大小为4 m/s, 方向变为向右,大小为4 m/s,在这 段时间里水平力做的功为( 段时间里水平力做的功为( A ) A.0 B.8J C.16J D.32J
5、一质量为1kg的物体被人用手由静止向上 一质量为1kg的物体被人用手由静止向上 1kg 提升1m,这时物体的速度2 m/s, 提升1m,这时物体的速度2 /s,则下列说法 1m 正确的是 [ ACD ]
F
V=2m/s
12J A.手对物体做功 12 12J B.合外力对物体做功 12 C.合外力对物体做功 2J
动能是标量,只有大小。 动能是标量,只有大小。
动能定理习题课ppt课件

v0=6 m/s向右运动,经过水平轨道和半圆轨道后从最高点c飞出,最后刚好落回轨道上的a点,重力加速度g取10 m/s2,求: (1)滑块从c点飞出时速度的大小; (2)水平轨道与滑块间的动摩擦因数.
【例4】 如图3所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一根光滑的细钉,已知OP=L/2,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B.求: (1)小球到达B点时的速率; (2)若不计空气阻力,则初速度v0为多少?
运动
标
Ek2-Ek1
增加
减少
3.应用动能定理解题与用牛顿定律解题的比较
牛顿定律
动能定理
相同点
确定研究对象,对物体进行受力分析和运动过程分析
适用条件
只能研究_____作用下的_____(“直线”或“曲线”)运动
物体受恒力或_____作用,物体做直线或____运动均适用
应用方法
要考虑运动过程的每一个细节,结合运动学公式解题
[目标定位] 1.进一步理解动能定理,领会应用动能定理解题的优越性. 2.会利用动能定理分析变力做功、曲线运动以及多过程问题.
2.动能定理:力在一个过程中对物体做的功,等于物体在这个过程中动能的变化,表达式为W=________. (1)当力对物体做正功时,物体的动能______. (2)当力对物体做负功时,物体的动能_____.
【例1】如图1所示,物体沿一曲面从A点无初速下滑,当滑至曲面的最低点B时,下滑的竖直高度h=5 m,此时物体的速度v=6 m/s.若物体的质量m=1 kg,g=10 m/s2,求物体在下滑过程中克服阻力所做的功. 答案 32 J
图1
二、应用动能定理分析多过程问题 1.应用动能定理解决多过程问题时,要根据问题选取合适的过程,可以分过程,也可以整过程一起研究.虽然我们列式时忽略了中间复杂过程,但不能忽略对每个过程的分析. 2.在运动过程中,物体受到的某个力可能是变化的或分阶段存在的,要注意这种力做功的表达方式.
动能定理习题课

重力势能
WG=EP1-EP2
弹力做功
弹性势能
WF=EP1-EP2
外力做功
动能
W合外力总功=EK2-EK1
1、起重机将质量为m的物体从地面静止开始匀加速 提升了h ,物体获得速度为v, 在这一过程中: (1)物体克服重力所做的功为___; (2)合力对物体做的功为____; (3)起重机对物体做的功为____;
以 为研究对象,从 到 过程,末动能为 ,初动能为 。
这个过程中有
做功。
17.2J
模型三:瞬时力(变力)做功
例3:一学生用100N的力将静置于
地面的质量为0.5kg的球以8m/s的
初速沿水平方向踢出20m远,则该
学生对球做的功是( B )
A. 2000J
B. 16J
C. 1000J
D. 无法确定
求瞬间力等变力做功时,一般用动能定理。
-5J 0.45
以 为研究对象,从 到 过程,末动能为 ,初动能为 。
这个过程中有
做功。
模型二:曲线运动+变力做功
例2:某人从距地面25m高处水平抛出一小球,小 球质量100g,人对球所做的功为5J,落地时速度大 小为16m/s,取g=10m/s2,试小球在空中运动时克 服阻力做功多少?
求瞬间力等变力做功时,一般用动能定理。
F2R 2 F1R1
2
F
例:如图所示,一质量为m的质点在半径为R的半球形容器中 (容器固定)由静止开始自边缘上的A点滑下,到达最低点B时 ,它对容器的压力为FN.重力加速度为g,则质点自A滑到B的
过程中,摩擦力对其所做的功为:( )
A. 1 R(FN-3mg) B.
1 R(3mg-FN)
2018版高中物理必修2试题:第2章 习题课三 动能定理的
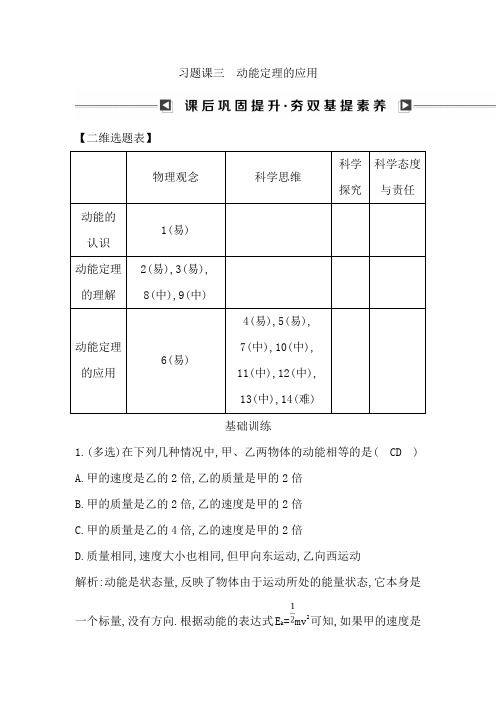
习题课三动能定理的应用【二维选题表】基础训练1.(多选)在下列几种情况中,甲、乙两物体的动能相等的是( CD )A.甲的速度是乙的2倍,乙的质量是甲的2倍B.甲的质量是乙的2倍,乙的速度是甲的2倍C.甲的质量是乙的4倍,乙的速度是甲的2倍D.质量相同,速度大小也相同,但甲向东运动,乙向西运动解析:动能是状态量,反映了物体由于运动所处的能量状态,它本身是一个标量,没有方向.根据动能的表达式E k=mv2可知,如果甲的速度是乙的两倍,质量应为乙的,故A错;同理可判断B错,C对;又因动能是标量,没有方向,所以只要两者动能大小相等即可,故D对.2. (多选)物体沿直线运动的v-t图象如图所示,已知在第1秒内合外力对物体所做的功为W,则( CD )A.从第1秒末到第3秒末合外力做功为4WB.从第3秒末到第5秒末合外力做功为-2WC.从第5秒末到第7秒末合外力做功为WD.从第3秒末到第4秒末合外力做功为-0.75W解析:设物体在第1秒末速度为v,由动能定理可得在第1秒内合外力做功W=mv2-0,从第1秒末到第3秒末物体的速度不变,所以合外力做功为W1=0,从第3秒末到第5秒末合外力做功为W2=0-mv2=-W,从第5秒末到第7秒末合外力做功为W3=m(-v)2-0=W,第4秒末的速度v4=,所以从第3秒末到第4秒末合外力做功W4=m()2-mv2=-W,故选项C,D正确.3.(多选)一质点开始时做匀速直线运动,从某时刻起受到一恒力作用.此后,该质点的动能可能( ABD )A.一直增大B.先逐渐减小至零,再逐渐增大C.先逐渐增大至某一最大值,再逐渐减小D.先逐渐减小至某一非零的最小值,再逐渐增大解析:若恒力的方向与初速度的方向相同或两者夹角为锐角,质点一直做加速运动,选项A正确;若恒力的方向与初速度的方向相反,质点先做匀减速运动,再反向做匀加速运动,选项B正确;若恒力方向与初速度方向之间的夹角为钝角(如斜上抛运动),则选项D正确.4.质量为m的金属块,当初速度为v0时,在水平面上滑行的最大距离为s.如果将金属块质量增加到2m,初速度增大到2v0,在同一水平面上该金属块最多能滑行的距离为( C )A.sB.2sC.4sD.8s解析:设金属块与水平面间的动摩擦因数为μ.则由动能定理得,-μmgs=-m,-μ·2mg·s′=-×2m×(2v0)2,解得s′=4s.C正确.5.篮球比赛中一运动员在某次投篮过程中对篮球做功为W,出手高度为h1,篮筐距地面高度为h2,球的质量为m,不计空气阻力,则篮球进筐时的动能为( A )A.W+mgh1-mgh2B.mgh2-mgh1-WC.mgh1+mgh2-WD.W+mgh2-mgh1解析:投篮过程中,篮球上升的高度h=h2-h1,根据动能定理得W-mgh =E k-0,故篮球进筐时的动能E k=W-mg(h2-h1)=W+mgh1-mgh2,A正确. 6. (多选)质量为m的小车在水平恒力F推动下,从山坡(粗糙)底部A 处由静止起运动至高为h的坡顶B,获得速度为v,AB之间的水平距离为x,重力加速度为g.下列说法正确的是( ABD )A.小车克服重力所做的功是mghB.合外力对小车做的功是mv2C.推力对小车做的功是mv2+mghD.阻力对小车做的功是mv2+mgh-Fx解析:小车克服重力做功W=Gh=mgh,选项A正确;由动能定理,小车受到的合力做的功等于小车动能的增加,W合=ΔE k=mv2,选项B正确;由动能定理,W 合=W 推+W 重+W 阻=mv 2,所以推力做的功W 推=mv 2-W 重-W 阻=mv 2+mgh-W阻,选项C 错误;阻力对小车做的功W阻=mv 2-W重-W推=mv 2+mgh-Fx,选项D 正确.7.质量为m=4 kg 的小物块静止于水平地面上的A 点,现用F=10 N 的水平恒力拉动物块一段时间后撤去,物块继续滑动一段位移停在B 点,A,B 两点相距s=20 m,物块与地面间的动摩擦因数μ=0.2,g 取 10 m/s 2,求:(1)物块在力F 作用过程发生位移s 1的大小; (2)撤去力F 后物块继续滑动的时间t.解析:(1)设物块受到的滑动摩擦力为f,则f=μmg, 根据动能定理,对物块由A 到B 整个过程,有 Fs 1-fs=0,代入数据,解得s 1=16 m.(2)设刚撤去力F 时物块的速度为v,此后物块的加速度为a,滑动的位移为s 2,则s 2=s-s 1, 由牛顿第二定律得a=,由匀变速直线运动公式得v 2=2as 2,s 2=vt, 代入数据,解得t=2 s. 答案:(1)16 m (2)2 s素养提升8.关于动能定理,下列说法中正确的是( D )A.在某过程中,外力做的总功等于各个力单独做功的绝对值之和B.只要有力对物体做功,物体的动能就一定改变C.动能定理只适用于直线运动,不适用于曲线运动D.动能定理既适用于恒力做功的情况,又适用于变力做功的情况解析:外力做的总功等于各个力单独做功的代数和,A错.根据动能定理,决定动能是否改变的是总功,而不是某一个力做的功,B错.动能定理既适用于直线运动,也适用于曲线运动;既适用于恒力做功的情况,又适用于变力做功的情况,C错,D正确.9.(多选)一物体做变速运动时,下列说法正确的有( BD )A.合外力一定对物体做功,使物体动能改变B.物体所受合外力一定不为零C.合外力一定对物体做功,但物体动能可能不变D.物体加速度一定不为零解析:物体的速度发生了变化,则合外力一定不为零,加速度也一定不为零,B,D正确;物体的速度变化,可能是大小不变,方向变化,故动能不一定变化,合外力不一定做功,A,C错误.10.一质量为m的滑块,以速度v在光滑水平面上向左滑行,从某一时刻起,在滑块上作用一向右的水平力,经过一段时间后,滑块的速度变为-2v(方向与原来相反),在这段时间内,水平力所做的功为( A ) A.mv2 B.-mv2C.mv2D.-mv2解析:由动能定理得W=m(2v)2-mv2=mv2.故A正确.11.某人把质量为0.1 kg的一块小石头,从距地面为5 m的高处以60°角斜向上抛出,抛出时的初速度大小为10 m/s,则当石头着地时,其速度大小约为(g取10 m/s2,不计空气阻力)( A )A.14 m/sB.12 m/sC.28 m/sD.20 m/s解析:由动能定理,重力对物体所做的功等于物体动能的变化,则mgh=m-m,v2==10 m/s≈14 m/s,A正确.12. 如图所示,物体与路面之间的动摩擦因数处处相同且不为零,运动中无碰撞能量损失.DO是水平面,AB是斜面,初速度为v0的物体从D 点出发沿DBA滑动到顶点A时速度刚好为零.如果斜面改为AC,让该物体从D点出发沿DCA滑动到A点时速度也刚好为零,则此时物体具有的初速度v( B )A.大于v0B.等于v0C.小于v0D.决定于斜面的倾角解析:设斜面的倾角为θ,则滑动摩擦力对物体所做的功为W f= -μmg·BD-μmgcos θ·AB=-μmg·BD-μmg·OB=-μmg·OD.可见,W f与θ无关,也就是说,物体从D点出发沿DBA或沿DCA滑动到A点,滑动摩擦力对物体所做的功相同.根据动能定理,沿DBA有W G+W f=0-m;沿DCA有W G+W f=0-mv2,解得v=v0.13.(多选)质量为m的汽车在平直公路上行驶,发动机的功率P和汽车受到的阻力f均恒定不变,在时间t内,汽车的速度由v0增加到最大速度v m,汽车前进的距离为s,则此段时间内发动机所做的功W可表示为( AC )A.W=PtB.W=fsC.W=m-m+fsD.W=m+fs解析:由题意知,发动机功率不变,故t时间内发动机做功W=Pt,所以A 正确;汽车做加速运动,故牵引力大于阻力f,故B错误;根据动能定理W-fs=m-m,所以C正确,D错误.14.近年来全国多地雾霾频发,且有愈演愈烈的趋势,空气质量问题备受关注,在雾霾天气下,能见度下降,机动车行驶速度降低,道路通行效率下降,对城市快速路、桥梁和高速公路的影响很大.如果路上能见度小于200米,应开启机动车的大灯、雾灯、应急灯,将车速控制在60 km/h以下,并与同道前车保持50米的车距;当能见度小于100米时,驾驶员将车速控制在40 km/h以下,车距控制在100米.已知汽车保持匀速正常行驶时受到地面的阻力为车重的0.1倍,刹车时受到地面的阻力为车重的0.5倍,重力加速度为g=10 m/s2(空气阻力忽略不计),则(1)若汽车在雾霾天行驶的速度为v=54 km/h,则刹车后经过多长时间才会停下来?(2)若前车因故障停在车道上,当质量为m=1 300 kg的后车距已经停止的前车为90 m时紧急刹车,刚好不与前车相撞,则后车正常行驶时的功率为多大?解析:(1)汽车的初速度v=54 km/h=15 m/s,刹车后,由牛顿第二定律得-0.5mg=ma,解得a=-0.5g=-5 m/s2,由匀变速直线运动的速度公式得v′=v+at,代入数据解得t=3 s.(2)由动能定理得-f2s=0-m,阻力f2=k2mg,代入数据解得v0=30 m/s,正常行驶时,F-f1=0,f1=k1mg=0.1mg,功率P=Fv0=0.1×1 300×10×30 W=39 000 W=39 kW.答案:(1)3 s (2)39 kW。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀变速直线运动
斜面问题
1、某物体放在倾角为θ的足够长的斜面上,斜面与物体间 滑动摩擦因素为μ .若给此物体一个沿斜面向上的初速度v0, 那么,它能沿斜面向上冲滑的最大距离为多少?
v0
θ
子弹问题 1、质量为20g的子弹,以300m/s的速度水平 射入厚度是10mm的钢板,射穿后的速度是 100m/s,子弹受到的平均阻力是多大?
功和能 动能和动能定理
习题课
动能 动能定理 1、动能——Ek = mv2/2,式中v是物体的瞬时速度 的大小,即瞬时速率(简称速率)。 2、动能定理——W 总= ΔEk 应用动能定理的一般思维程序: 1、确定研究对象,进行受力分析,认真画出受力 分析示意图; 2、若问题中涉及到F、s 、v 、m 等物理量,考虑 用动能定理! 3、确定研究的物理过程(起点和终点),分析这 过程中有哪些力对研究对象作功,作了多少功,正功还
v
0
v
f
m
l
子弹问题
3、以速度v=700m/s的速度水平飞行的子弹先后穿透两 块由同种材料制成相同厚度的木板,木板对子弹的平均 作用力相等。若子弹穿透第一块块木板后的速度为 500m/s,则穿透第二块木板速度为________?
多过程问题
直线运动
1、一物体静止在不光滑的水平面上,已知m=1kg, μ=0.1,现用水平外力F=2N拉其运动5m后立即撤去水平 外力F,求其还能滑多远?
求变力做功问题
v
(与机车相联系的问题)
m 500t 5.0 10 kg
5
vm
0
t 2 min 120s
t
t
速度最大时:
P f F vm
f 恒定
1 2 应用动能定理: Pt fs mvm 0 2
求解曲线运动问题 从高为5m处以水平速度8m/s抛出一质量为0.2kg的皮球, 皮球落地速度为12m/s,求此过程中皮球克服空气阻力 做的功?(g=9.8m/s2)
是负功,求出总功;
4、确定研究过程起点和终点的动能,列出动能定 理表达式; 5、求解,必要时讨论结果的合理性。
应用动能定理解题的一般步骤:
①确定研究对象,画出草图; ②分析物体的受力情况,分析各力做功的情况; ③确定物体的初、末状态;明确初、末状态的动能 ④列式求解; ⑤对结果进行分析讨论。 动能定理中的功是合外力做的总功, 总功的求法: (1)先求合力,再求合力功 (2)先求每个力做的功,再求代数和
vo
h=5m
2J
8、总质量为M 的列车, 沿水平直线轨道匀速 前进,其未节车厢质 量为m,中途脱节,司 机发现时,机车已行 驶了距离L,于是立即 关闭发动机,设阻力 与重量成正比,机车 牵引力恒定,当列车 的两部分都停下时, 它们之间的距离是多 少?
f1
v0 F
L
关闭发动机
s1
f2
v0 s2
分析:对车厢有: - kmgs2 = 0 – mv02/2 对机车有: FL – k(M–m)gs1 = 0 – mv02/2
求变力做功问题 1、如图所示,一质量为m的小球用长为L的轻绳悬挂于 天花板上,小球在水平力F的作用下,从平衡位置A 点缓 慢地移到B 点,此时绳子转过了θ角,求F 做的功。
θ
F
A B
求变力做功问题
(与机车相联系的问题)
3、一列货车的质量为5.0×105kg,在平直轨道以额定 功率3000kw加速行驶,当速度由10m/s加速到所能达到 的最大速度30m/s时,共用了2min,则这段时间内列车 前进的距离是多少?
v
f
0=0 Ff Nhomakorabeav =0
l
x
μ=0.1
15m
多过程问题
直线运动
2、铁球1m高处掉入沙坑,则已知铁球在下陷过程中受 到沙子的平均阻力为铁球重力的20倍,则铁球在沙中下陷 深度为多少m?
H
h
多过程问题 解法一:分段列式
(直线运动)
1 2 自由下落:mgH mv 0 2 1 沙坑减速:mgh f h 0 mv 2 2
mg H f mg
h
解法二:全程列式 mg (H h) f h 0
多过程问题
(直线运动)
3、以一恒定的初速度V0竖直向上抛出一小球,小球上 升的最大高度为h,空气阻力的大小恒定不变,则小球回 到出发点时的速度是多大?
h f
v
0
f G
v
G
瞬间力做功问题
3、质量为m的跳水运动员,从高为H的跳台上,以一 定速率起跳,落水时的速度为v,那么起跳时运动员所做 的功是多少?(不计空气阻力)
式中F = kMg
Δs = s1 – s2 = ML/(M – m)
2、质量为m的球在距地面H 高处无初速下落,运动过程 中空气阻力恒为重力的0.2倍,球与地面碰撞时无能量损 失而弹起,求:球停止运动前通过的总路程是多少? (提示:全程看,球所受的阻力为变力,但分上升和下 落各段考虑时,阻力是恒力)
