初中平面几何经典训练习题及答案
史上最全之初中平面几何经典题集锦

初中平面几何经典(史上最全)如图 ,在凸四边形 ABCD 中∠ABC =120° , ∠BCD =90°. 则 AD =______已知如图:正方形 ABCD ,BE =BD ,CE 平行于 BD ,BE 交 CD 于 F ,求证:DE =DF0ABC AB=AC,A=20,AB D AD BC BDC∠∠在等腰三角形中,在上取一点,使=,求ABCD00 ABC ABC=46D BC DC=AB DAB=21CAD ∆∠∠∠在中,,是边上一点,,,求ABC ,AB=AC,D BC ,E AD ,BDE CED BAC BD CD ∆∠∠∠在中为边上一点为上一点且满足=2=,求证:=200ABC ,BAC 60,ATB BTC CTA 120M BC TA+TB+TC=2AM∆∠=∠=∠=∠=在中点为的中点,求证:002,ABC ,D AC ,CBD ABD 60BDC 30,AB BC BD ,:DB DC ∆∠-∠=∠===如图中是边上的一个点求证ABC,O ,O AB AC X Y OX OY ≤三角形为重心过作任一条直线、于、,求证:2在直角梯形ABCD 中, ∠ABC =∠BAD =90°, AB =16.对角线AC 与BD 交于点E ,过E 作EF ⊥AB 于点F , O 为边AB 的中点, 且FE+EO =8.求AD +BC的值.已知四边形ABCD 中,AB=DC,E、F 分别为AD 与BC 的中点,连接EF 与BA 的延长线相交于N,与CD 的延长线相交于M,求证:∠BNF=∠CMF0ABC ,CB>CA,BAC 80,D AB CB-CA=BD,I ABC ,IDA _____∆∠=∆∠=在中为上一点,满足为的内心则1,G ABC ,D CB ,BD=BC 2AE DG AC E,?AC ∆=如图为的重心点在延长线上且过的直线交于点则,H O ABC BAC ABC 2,AH ?∆∠∆=如图、分别为的垂心、外心,=45若的外接圆半径为则ABC =90AD BAC BD DC=21∆∠∠∠0已知在中,C,是 的平分线交BC于D,::,则B=?,AB ,C AB D ACDE DB CA BE如图是半圆的直径点平分弧,点平分弧、交于点E,则=?0ABC ,CB>CA,ABC 35CB=CA+AI,I ABC ,BAC _____∆∠=∆∠=在中,满足为的内心则AB PC OP BP=2AP=6CP=⊥在圆内的点P在弦上,点C在圆上,若,,则?0RT ABC ABC=90D BC E CE AD AE=EF,AC=7,FC=3,cos ACB=?∆∠∠在中,,为线段的中点,在线段AB上与交于点F,则ABC BC=12AC=5AI BE D E F DE IF AB G AG=∆如图,直角中,,,角A和角B的平分线交于点I,、与边交于点、,为线段的中点,交于点,ABC A BC BC CA AB AB CC =AC BB ∆'''''’’中,G为重心,分别为、、的中点,如果A、C、G、B共圆,求证:00ABCDE AB=BC CD=DE BD=2ABC=150CDE=30ABCDE ∠∠如图,五边形满足,,,,,则五边形的面积为_00493ABC AB=AC BC=cos 25E BEC+ACB=180AED=120DE=ABC D ∆∠=∠∠∠如图,在中,,,为BC中点,点为三角形内部一点,,_ABCD O ABC AMN ABCD ∆∆如图,在平行四边形中,为对角线的交点,MN分别是BO、CD的中点,若,求证:为正方形OPQR ABC AOR BOP CRQ OPQR ∆∆∆∆如图,正方形内接于,已知、、的面积分别为1,3,1那么正方形的边长是__E F AB AD BFDE AE+EC=AF+FC AB+BC=AD+DC如图,、分别为线段、上的点,与交于点C,若,求证:已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .已知:△ABC 中,H 为垂心,O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .AFGCEBO D ·ADHEMCBO如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .PCGFBQADEE DA CBFFEP C BA设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:3 ≤L <2.PADCBFPDECBAAPC BABC AB=AC AC D BC=BD+AD A ∆∠∠如图:是一个等腰三角形,其中,若B的角平分线交于,求的度数00AB=CD=1ABC=90CBD=30AC∠∠如图:已知,,,求PA=PB APB 2ACB AC PB D P =4PD=3AD DC ∠∠如图:若,=,与交于点,且B,,则=?ABC DEC AD BE 18S =2cosC=?∆∆如图,,是锐角三角形的两条高,若S=,,则。
平面几何100题及答案(前80题)
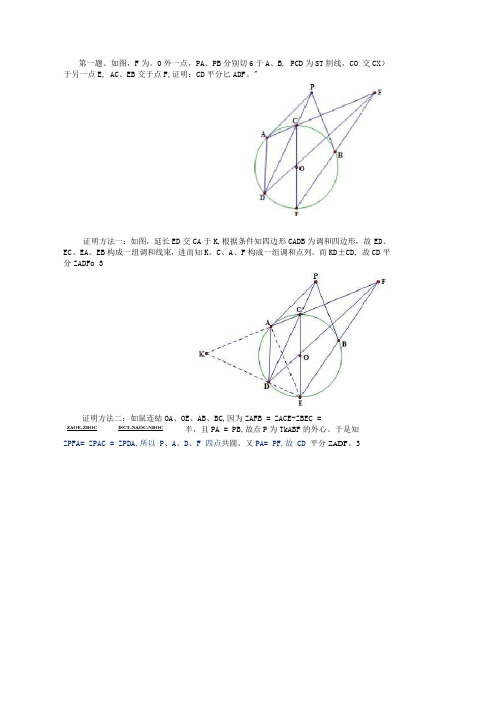
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)
![[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)](https://img.taocdn.com/s3/m/c98a8998ba4cf7ec4afe04a1b0717fd5370cb244.png)
[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)试题部分一、选择题:1. 在平行四边形ABCD中,若AB=6cm,BC=8cm,则平行四边形ABCD的周长是()cm。
A. 14cmB. 28cmC. 48cmD. 56cm2. 已知等边三角形ABC的边长为3cm,点D是边AB上的一点,且AD=1cm,则CD的长度为()cm。
A. 2cmB. 4cmC. 5cmD. 6cm3. 下列哪个图形是轴对称图形?()A. 等腰梯形B. 长方形C. 正方形D. 所有选项都是4. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)5. 若一个等腰三角形的底边长为10cm,腰长为13cm,则这个三角形的周长为()cm。
A. 26cmB. 32cmC. 42cmD. 46cm6. 下列哪个角是钝角?()A. 30°B. 45°C. 120°D. 90°7. 在三角形ABC中,若AB=AC,∠BAC=40°,则∠ABC的度数是()。
A. 40°B. 70°C.80°D. 100°8. 下列哪个图形既是中心对称图形,又是轴对称图形?()A. 正三角形B. 矩形C. 正方形D. 平行四边形9. 若一个圆的半径为5cm,则其直径的长度为()cm。
A. 5cmB. 10cmC. 15cmD. 20cm10. 在直角三角形ABC中,若∠C=90°,BC=3cm,AC=4cm,则AB 的长度为()cm。
A. 5cmB. 6cmC. 7cmD. 8cm二、判断题:1. 平行四边形的对角线互相平分。
()2. 任意两个等边三角形的面积相等。
()3. 两条平行线的距离处处相等。
()4. 在直角三角形中,斜边上的中线等于斜边的一半。
()5. 对角线互相垂直的四边形一定是矩形。
人教版初中七年级数学上册第四章《几何图形初步》经典练习题(含答案解析)
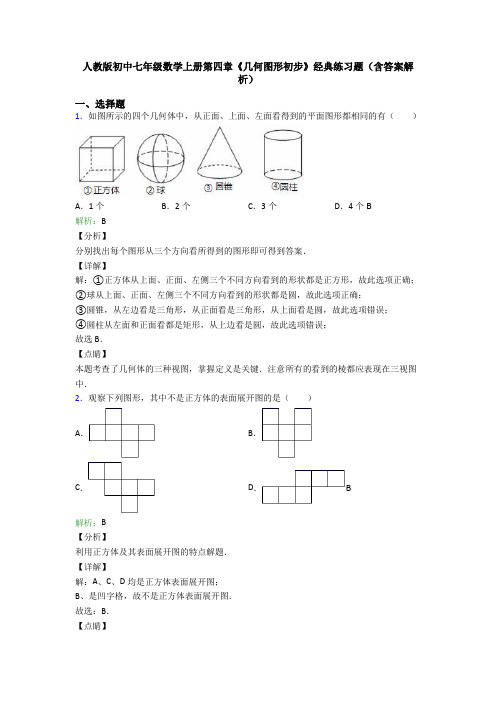
人教版初中七年级数学上册第四章《几何图形初步》经典练习题(含答案解析)一、选择题1.如图所示的四个几何体中,从正面、上面、左面看得到的平面图形都相同的有()A.1个B.2个C.3个D.4个B解析:B【分析】分别找出每个图形从三个方向看所得到的图形即可得到答案.【详解】解:①正方体从上面、正面、左侧三个不同方向看到的形状都是正方形,故此选项正确;②球从上面、正面、左侧三个不同方向看到的形状都是圆,故此选项正确;③圆锥,从左边看是三角形,从正面看是三角形,从上面看是圆,故此选项错误;④圆柱从左面和正面看都是矩形,从上边看是圆,故此选项错误;故选B.【点睛】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.2.观察下列图形,其中不是正方体的表面展开图的是()A.B.C.D. B解析:B【分析】利用正方体及其表面展开图的特点解题.【详解】解:A、C、D均是正方体表面展开图;B、是凹字格,故不是正方体表面展开图.故选:B.【点睛】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.3.一副三角板按如图方式摆放,且1∠的度数比2∠的度数小20︒,则2∠的度数为( )A .35︒B .40︒C .45︒D .55︒D解析:D【分析】 根据题意结合图形列出方程组,解方程组即可.【详解】解:由题意得,1290,2120∠+∠︒⎧⎨∠-∠︒⎩==,解得135,255.∠︒⎧⎨∠︒⎩==. 故选:D .【点睛】本题考查的是余角和补角的概念和性质,两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.4.如图,C ,D 是线段AB 上的两点,E 是AC 的中点,F 是BD 的中点,若EF m =,CD n =,则AB =( )A .m n -B .m n +C .2m n -D .2m n + C解析:C【分析】由条件可知EC+DF=m-n ,又因为E ,F 分别是AC ,BD 的中点,所以AE+BF=EC+DF=m-n ,利用线段和差AB=AE+BF+EF 求解.【详解】解:由题意得,EC+DF=EF-CD=m-n∵E 是AC 的中点,F 是BD 的中点,∴AE=EC ,DF=BF ,∴AE+BF=EC+DF=m-n ,∵AB=AE+EF+FB ,∴AB=m-n+m=2m-n故选:C【点睛】本题考查中点性质及线段和差问题,利用中点性质转化线段之间的倍分关系和灵活运用线段的和、差转化线段之间的数量关系是解答此题的关键.5.已知∠AOB=40°,∠BOC=20°,则∠AOC的度数为( )A.60°B.20°C.40°D.20°或60°D解析:D【分析】考虑两种情形①当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=40°-20°=20°,②当OC’在∠AOB外部时,∠AOC’=∠AOB+∠BOC=40°+20°=60°.【详解】解:如图当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=40°-20°=20°,当OC’在∠AOB外部时,∠AOC’=∠AOB+∠BOC=40°+20°=60°,故答案为20°或60°,故选D.【点睛】本题考查角的计算,解决本题的关键是学会正确画出图形,根据角的和差关系进行计算. 6.体育课上,小悦在点O处进行了四次铅球试投,铅球分别落在图中的M,N,P,Q四个点处,则表示他最好成绩的点是()A.M B.N C.P D.Q C解析:C【分析】根据点和圆的位置关系,知最好成绩在P点.【详解】P点与O点距离最长,且在有效范围内,所以最好成绩在P点.【点睛】考查了点和圆的位置关系.7.已知线段AB=6cm,反向延长线段AB到C,使BC=83AB,D是BC的中点,则线段AD的长为____cmA.2 B.3 C.5 D.6A 解析:A【分析】由BC =83AB 可求出BC 的长,根据中点的定义可求出BD 的长,利用线段的和差关系求出AD 的长即可.【详解】∵BC =83AB ,AB=6cm , ∴BC=6×83=16cm , ∵D 是BC 的中点,∴BD=12BC=8cm , ∵反向延长线段AB 到C ,∴AD=BD-AB=8-6=2cm ,故选A.【点睛】本题考查了比较线段的长短,理解线段中点的概念,利用中点的性质转化线段之间的倍分关系是解题关键.8.22°20′×8等于( ).A .178°20′B .178°40′C .176°16′D .178°30′B解析:B【分析】根据角的换算关系即可求解.【详解】22°×8=176°,20′×8=160′=2°40′,故22°20′×8=176°+2°40′=178°40′故选B.【点睛】本题考查了角的度量单位以及单位之间的换算,掌握'160︒=,''160'=是解题的关键. 9.如图,从A 地到C 地,可供选择的方案是走水路、走陆路、走空中,从A 地到B 地有三条水路、两条陆路,从B 地到C 地有4条陆路可供选择,走空中,从A 地不经B 地直线到C 地,则从A 地到C 地可供选择的方案有( )A .10种B .20种C .21种D .626种C解析:C【分析】本题只需分别数出A 到B 、B 到C 、A 到C 的条数,再进一步分析计算即可.【详解】观察图形,得:A到B有5条,B到C有4条,所以A到B到C有5×4=20条,A到C一条.所以从A地到C地可供选择的方案共21条.故选C.【点睛】解决本题的关键是能够有顺序地数出所有情况.10.下列说法不正确的是()A.两条直线相交,只有一个交点B.两点之间,线段最短C.两点确定一条直线D.过平面上的任意三点,一定能作三条直线D解析:D【解析】【分析】根据直线公理、线段公理进行逐一分析判断.【详解】A. 根据直线公理“两点确定一条直线”,则两条直线相交,只有一个交点,故该选项正确;B.两点之间,线段最短,是线段公理,故该选项正确;C. 两点确定一条直线,是直线公理,故该选项正确;D. 当三点共线时,则只能确定一条直线,故该选项错误.故选 D.【点睛】此题考查直线、射线、线段,直线的性质:两点确定一条直线,线段的性质:两点之间线段最短,解题关键在于掌握各性质定义.二、填空题11.如图,点C、D在线段AB上,D是线段AB的中点,AC=13AD ,CD=4cm ,则线段AB的长为_____cm【分析】根据AC=ADCD=4cm求出再根据是线段的中点即可求得答案【详解】∵AC=ADCD=4cm∴∴∵是线段的中点∴∴故答案为【点睛】本题考查了线段中点的几何意义以及求线段的长根据题目中的几何语解析:12【分析】根据AC=13AD ,CD=4cm ,求出AD,再根据D是线段AB的中点,即可求得答案.【详解】∵AC=13AD ,CD=4cm ,∴12433CD AD AC AD AD AD =-=-== ∴6AD =,∵D 是线段AB 的中点,∴212AB AD ==∴12AB cm =故答案为12【点睛】 本题考查了线段中点的几何意义以及求线段的长,根据题目中的几何语言列出等式,是解题的关键.12.线段3AB cm =,在线段AB 的延长线上截取1BC cm =,则AC =__________.4【分析】根据线段的和差关系即可求解【详解】∵线段在线段的延长线上截取则AB+BC=4cm 故填:4【点睛】此题主要考查线段的长度解题的关键是熟知线段的和差关系解析:4【分析】根据线段的和差关系即可求解.【详解】∵线段3AB cm =,在线段AB 的延长线上截取1BC cm =,则AC =AB+BC=4cm ,故填:4.【点睛】此题主要考查线段的长度,解题的关键是熟知线段的和差关系.13.如图是一个正方体的表面展开图,已知正方体的每个面上都是一个有理数,且相对面上的两个数互为倒数,那么代数式a b c-的值是_________. 【解析】【分析】将此正方体的表面展开图折叠成正方体观察abc 分别对应的值即可得出答案【详解】将图中所示图形折叠成正方体后a 与4相对应b 与2相对应c 与-1相对应∴∴【点睛】由平面图形的折叠及立体图形的解析:34- 【解析】【分析】将此正方体的表面展开图折叠成正方体,观察a ,b ,c 分别对应的值,即可得出答案.【详解】将图中所示图形折叠成正方体后,a 与4相对应,b 与2相对应,c 与-1相对应, ∴1a 4=,1b 2=,c 1=- ∴3=-4a b c - 【点睛】由平面图形的折叠及立体图形的表面展开图的特点解题.14.下午3:40时,时钟上分针与时针的夹角是_________度.130【分析】分别求出时针走过的度数和分针走过的度数用分针走过的度数减去时针走过的度数即可得出答案【详解】时针每小时走30°分针每分钟走6°∴下午3:40时时针走了3×30°+×30°=110°分针解析:130【分析】分别求出时针走过的度数和分针走过的度数,用分针走过的度数减去时针走过的度数,即可得出答案.【详解】时针每小时走30°,分针每分钟走6°∴下午3:40时,时针走了3×30°+4060×30°=110° 分针走了40×6°=240°∴夹角=240°-110°=130°【点睛】本题考查的是钟面角问题,易错点在于计算时针走过的度数时,往往大部分人只计算了前面3个小时时针走过的度数,容易忽略后面40分钟时针也在走.15.看图填空.(1)AC =AD -_______=AB +_______,(2)BC +CD =_______=_______-AB ,(3)AD =AC+___.CDBCBDADCD 【分析】根据线段之间的和差关系进行解答即可得答案【详解】(1)AC=AD-CD=AB+BC (2)BC+CD=BD=AD-AB (3)AD=AC+CD 故答案为:CD ;BC ;BD ;AD解析:CD BC BD AD CD【分析】根据线段之间的和差关系进行解答即可得答案.【详解】(1)AC=AD-CD=AB+BC ,(2)BC+CD=BD=AD-AB,(3)AD=AC+CD,故答案为:CD;BC;BD;AD;CD【点睛】本题主要考查线段之间的和差关系,灵活运用线段的和、差、倍、分转化线段之间的数量关系是解题关键.16.如图所示,∠BOD=45°,那么不大于90°的角有___个,它们的度数之和是____.450°【分析】(1)∠AOE=90°故图中所有的角都是不大于90°的角;(2)将所有的角相加发现有的角相加等于∠EOA即和为90°而有的角相加等于∠BOD即和为45°将这样的角凑在一起计算即可求出解析:450°【分析】(1)∠AOE=90°,故图中所有的角都是不大于90°的角;(2)将所有的角相加,发现有的角相加等于∠EOA,即和为90°,而有的角相加等于∠BOD,即和为45°,将这样的角凑在一起计算,即可求出所有角的度数.【详解】不大于 90°的角有∠EOD,∠EOC,∠EOB,∠EOA,∠DOC,∠DOB,∠DOA,∠COB,∠COA,∠BOA共10个;它们的度数之和是(∠EOD+∠DOA)+(∠EOC+∠COA)+(∠ EOB+∠BOA)+[(∠DOC+∠COB)+∠DOB]+∠EOA=90°+90°+90°+(45°+45°)+90°=450°.故答案为10;450°.【点睛】此题主要考查角的表示与和差关系,解题的关键是熟知角的定义运算法则.17.如图,点C是线段AB的中点,点D,E分别在线段AB上,且ADDB=23,AEEB=2,则CDCE的值为____.【分析】由线段中点的定义可得AC=BC=AB根据线段的和差关系及==2可得出CDCE与AB的关系进而可得答案【详解】∵点C是线段AB的中点∴AC=BC=AB∵==2BD=AB-ADAE=AB-BE∴解析:3 5【分析】由线段中点的定义可得AC=BC=12AB,根据线段的和差关系及ADDB=23,AEEB=2,可得出CD、CE与AB的关系,进而可得答案.【详解】∵点C是线段AB的中点,∴AC=BC=12AB,∵ADDB =23,AEEB=2,BD=AB-AD,AE=AB-BE,∴AD=25AB,BE=13AB,∵CD=AC-AD,CE=BC-BE,∴CD=12AB-25AB=110AB,CE=12AB-13AB=16AB,∴CDCE=11016ABAB=35,故答案为3 5【点睛】本题主要考查中点的定义及线段之间的和差关系,灵活运用线段的和、差、倍、分转化线段之间的数量关系是解题关键.18.(1)比较两条线段的长短,常用的方法有_________,_________.(2)比较两条线段a和b的大小,结果可能有种情况,它们是_______________.(1)度量比较法叠合比较法;(2)3a>ba=ba<b【分析】(1)比较两条线段长短的方法有两种:度量比较法叠合比较法依此即可求解;(2)两条线段a和b的大小有三种情况【详解】(1)比较两条线段的大解析:(1)度量比较法,叠合比较法;(2)3,a>b、a=b、a<b【分析】(1)比较两条线段长短的方法有两种:度量比较法、叠合比较法.依此即可求解;(2)两条线段a和b的大小有三种情况.【详解】(1)比较两条线段的大小通常有两种方法,分别是度量比较法、重合比较法.(2)比较两条线段a和b的大小,结果可能有3种情况,它们是a>b、a=b、a<b.故答案为度量比较法,重合比较法;3,a>b、a=b、a<b.【点睛】本题考查了比较线段的长短,是基础题型,是需要识记的知识.19.如图所示,能用一个字母表示的角有________个,以点A为顶点的角有________个,图中所有大于0°小于180°的角有________个.37【分析】根据角的概念和角的表示方法依题意求得答案【详解】能用一个字母表示的角有2个:∠B∠C;以A为顶点的角有3个:∠BAD∠BAC∠DAC;大于0°小于180°的角有7个:∠BAD∠BAC∠D解析:3 7【分析】根据角的概念和角的表示方法,依题意求得答案.【详解】能用一个字母表示的角有2个:∠B,∠C;以A为顶点的角有3个:∠BAD,∠BAC,∠DAC;大于0°小于180°的角有7个:∠BAD,∠BAC,∠DAC,∠B,∠C,∠ADB,∠ADC.故答案为2,3,7.【点睛】利用了角的概念求解.从一点引出两条射线组成的图形就叫做角.角的表示方法一般有以下几种:1.角+3个大写英文字母;2.角+1个大写英文字母;3.角+小写希腊字母;4.角+阿拉伯数字.20.已知∠A=67°,则∠A的余角等于______度.23【解析】∵∠A=67°∴∠A的余角=90°﹣67°=23°故答案为23解析:23【解析】∵∠A=67°,∴∠A的余角=90°﹣67°=23°,故答案为23.三、解答题21.如图所示,已知射线OC将∠AOB分成1∶3的两部分,射线OD将∠AOB分成5∶7的两部分,若∠COD=15°,求∠AOB的度数.解析:90°【分析】设∠AOB的度数为x,根据题意用含x的式子表示出∠AOC,∠AOD,根据角的关键列出方程即可求解.【详解】解:设∠AOB的度数为x.因为射线OC将∠AOB分成1∶3两部分,所以∠AOC=14 x.因为射线OD将∠AOB分成5∶7两部分,所以∠AOD=512x.又因为∠COD=∠AOD-∠AOC,∠COD=15°,所以15°=512x-14x.解得x=90°,即∠AOB的度数为90°.【点睛】本题考查了角的和差,设出未知数,表示出∠AOC,∠AOD,列出方程是解题关键.22.如图,点C是AB的中点,D,E分别是线段AC,CB上的点,且AD=23AC,DE=35AB,若AB=24 cm,求线段CE的长.解析:CE=10.4cm.【分析】根据中点的定义,可得AC、BC的长,然后根据题已知求解CD、DE的长,再代入CE=DE-CD即可.【详解】∵AC=BC=12AB=12cm,CD=13AC=4cm,DE=35AB=14.4cm,∴CE=DE﹣CD=10.4cm.23.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OE是射线OB的反向延长线.(1)求射线OC的方向角;(2)求∠COE的度数;(3)若射线OD平分∠COE,求∠AOD的度数.解析:(1)射线OC的方向是北偏东70°;(2)∠COE=70°;(3)∠AOD=90°.【分析】(1)先求出∠AOC=55°,再求得∠NOC的度数,即可确定OC的方向;(2)根据∠AOC=55°,∠AOC=∠AOB,得出∠BOC=110°,进而求出∠COE的度数;(3)根据射线OD平分∠COE,即可求出∠COD=35°再利用∠AOC=55°求出答案即可.【详解】(1)∵射线OA的方向是北偏东15°,射线OB的方向是北偏西40°即∠NOA=15°,∠NOB=40°,∴∠AOB=∠NOA+∠NOB=55°,又∵∠AOB=∠AOC,∴∠AOC=55°,=°,∴∠NOC=∠NOA+∠AOC=15°+ 55°70∴射线OC的方向是北偏东70°.(2)∵∠AOB=55°,∠AOB=∠AOC,∴∠BOC=∠AOB+∠AOC=55°+55°=110°,又∵射线OD是OB的反向延长线,∴∠BOE=180°,∴∠COE=180°-110°=70°,(3)∵∠COE=70°,OD平分∠COE,∴∠COD=35°,∴∠AOD=∠AOC+∠COD=55°+35°=90°.【点睛】此题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度.24.如图,点C为线段AD上一点,点B为CD的中点,且6cmBD=.AC=,2cm(1)图中共有多少条线段?(2)求AD的长.解析:(1)6条;(2)10cm【分析】(1)根据线段的定义,即可得到答案;(2)由点B 为CD 的中点,即可求出CD 的长度,然后求出AD 的长度.【详解】解:(1)根据题意,图中共有6条线段,分别是AC ,AB ,AD ,CB ,CD ,BD . (2)因为点B 是CD 的中点,2cm BD =,所以24cm CD BD ==,所以10cm AD AC CD =+=.【点睛】本题考查了线段中点的有关计算,以及线段的定义,解题的关键是熟练掌握线段有关的计算问题.25.如图,直线AB 与CD 相交于点O ,∠AOE=90°.(1)如图1,若OC 平分∠AOE,求∠AOD 的度数;(2)如图2,若∠BOC=4∠FOB ,且OE 平分∠FOC ,求∠EOF 的度数.解析:(1)135°;(2)54°【分析】(1)利用OC 平分∠AOE ,可得∠AOC =12∠AOE =12×90°=45°,再利用∠AOC+∠AOD=180°,即可得出.(2)由∠BOC=4∠FOB ,设∠FOB=x°,∠BOC=4x°,可得∠COF=∠COB-∠BOF=3x°,根据OE 平分∠COF ,可得∠COE=∠EOF=12∠COF=32x°,即可得出. 【详解】(1)∵∠AOE=90°,OC 平分∠AOE ,∴∠AOC =12∠AOE =12×90°=45°, ∵∠AOC+∠AOD=180°,∴∠AOD=180°-∠AOC=180°-45°=135°,即∠AOD的度数为135°.(2)∵∠BOC=4∠FOB,∴设∠FOB=x°,∠BOC=4x°∴∠COF=∠COB-∠BOF=4x°-x°=3x°∵OE平分∠COF∴∠COE=∠EOF=12∠COF=32x°∵32x+x=90°∴x=36,∴∠EOF=32x°=32×36°=54°即∠EOF的度数为54°.【点睛】本题考查了角平分线的性质、方程思想方法、数形结合方法,考查了推理能力与计算能力.26.如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数。
平面几何习题及答案

平面几何习题及答案
平面几何是数学中的重要部分,通过题的练可以加深对基本概念和定理的理解。
本文提供一些常见的平面几何题及其答案,供研究和练使用。
1. 题1
已知三角形ABC的三边长度分别为a、b和c,求三角形的面积S。
解答:
首先,可以使用海伦公式计算半周长p:
p = (a + b + c) / 2
然后,使用海伦公式计算三角形的面积S:
S = sqrt(p * (p - a) * (p - b) * (p - c))
其中,sqrt表示平方根。
2. 题2
已知三角形ABC的底边AB是一条固定的线段,顶角C的位置可以变化,求三角形的最大面积。
解答:
根据三角形面积公式S = 1/2 * base * height,当底边AB固定时,三角形的最大面积出现在高度最大的位置。
在这种情况下,高度等于底边长度的一半。
因此,三角形的最大面积为:S = 1/2 * AB * (AB/2) = AB^2 / 4
3. 题3
已知平行四边形ABCD的两条对角线交于点O,求平行四边形的面积S。
解答:
由于对角线互相平分,所以可以将平行四边形分为两个相等的三角形。
假设对角线AB和CD的交点为O,那么平行四边形的面积等于两个三角形的面积之和。
设对角线AB和CD的长度分别为d1和d2,那么平行四边形的面积为:
S = 2 * (1/2 * d1 * d2) = d1 * d2
通过以上题的练,可以提高对平面几何的理解和应用能力。
希望本文对研究者有所帮助。
参考资料
- 平面几何概念和定理的教材或课堂讲义。
平面几何练习题及解答

平面几何练习题及解答一、直线与角度1. 给定一条直线L1和两条直线L2和L3,若L1与L2垂直,L2与L3平行,则L1与L3之间的夹角为多少度?解答:由于L1与L2垂直,可得出L2的斜率为无穷大,即L2为竖直线。
而L2与L3平行,说明它们具有相同的斜率。
因此,L3的斜率也为无穷大,即L3也是竖直线。
由此可知,L1与L3之间的夹角为90度。
2. 给定一条直线L和两点A、B,若L与AB的垂线相交于点M,且角AMB为40度,则角LMA的度数是多少?解答:由垂线的性质可得出,角LMA与角AMB互补,它们的度数和为90度。
已知角AMB为40度,因此角LMA的度数为90度减去40度,即50度。
二、三角形3. 已知三角形ABC,其中∠B = 90度,AB = 3 cm,BC = 4 cm,求AC的长度。
解答:根据勾股定理可得:AC² = AB² + BC²AC² = 3² + 4²AC² = 9 + 16AC² = 25AC = √25AC = 5 cm4. 已知三角形ABC,其中AB = 6 cm,BC = 8 cm,AC = 10 cm,求∠B的度数。
解答:根据余弦定理可得:BC² = AB² + AC² - 2 * AB * AC * cosB8² = 6² + 10² - 2 * 6 * 10 * cosB64 = 36 + 100 - 120 * cosB64 = 136 - 120 * cosB120 * cosB = 136 - 64120 * cosB = 72cosB = 72 / 120cosB = 0.6根据反余弦函数可得:∠B = arccos(0.6)∠B ≈ 53.13度三、圆的性质5. 在平面直角坐标系中,给定圆心为O(2, 3),半径为5的圆C,点P(6, 7)是否在圆C上?解答:利用距离公式可计算OP的距离:OP = √((6-2)² + (7-3)²)OP = √((4)² + (4)²)OP = √(16 + 16)OP = √32OP ≈ 5.66由于OP的长度不等于圆C的半径,即5.66不等于5,因此点P不在圆C上。
2024年数学九年级上册平面几何基础练习题(含答案)

2024年数学九年级上册平面几何基础练习题(含答案)试题部分一、选择题:1. 在平面几何中,下列哪个图形既是轴对称图形又是中心对称图形?()A. 矩形B. 等腰三角形C. 梯形D. 正五边形2. 下列各角中,哪个角是补角?()A. 30°B. 45°C. 60°D. 120°3. 在直角坐标系中,点A(2, 3)关于原点对称的点是()A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)4. 下列哪个条件能判定两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一边相等C. 两边和它们的夹角相等D. 两边和其中一边的对角相等5. 若平行线l1和l2之间的距离为5cm,直线l3与l1、l2均相交,且l3与l1、l2的夹角均为45°,则l3与l1、l2之间的距离为()A. 5cmB. 5√2 cmC. 2.5cmD. 2.5√2 cm6. 下列哪个图形是正多边形?()A. 边长为1,内角为108°的多边形B. 边长为1,内角为120°的多边形C. 边长为1,内角为135°的多边形D. 边长为1,内角为140°的多边形7. 在直角三角形中,若一个锐角的度数为30°,则另一个锐角的度数为()A. 30°B. 45°C. 60°D. 90°8. 下列哪个比例式成立?()A. a² : b² = (a+b)² : (ab)²B. a² : b² = (a+b) : (ab)C. a : b = (a+b)² : (ab)²D. a : b = (a+b) : (ab)9. 若等腰三角形的底边长为8cm,腰长为5cm,则该三角形的面积为()A. 20cm²B. 40cm²C. 30cm²D. 24cm²10. 在平面几何中,下列哪个说法是正确的?()A. 对角线互相垂直的四边形一定是矩形B. 对角线互相平分的四边形一定是平行四边形C. 对角线相等的四边形一定是矩形D. 对角线互相垂直平分的四边形一定是菱形二、判断题:1. 平行线的性质是:同位角相等,内错角相等,同旁内角互补。
初二平面几何练习题及答案

在△ABC中,AB=AC,P是△ABC内部的一点,且∠APB﹥∠APC。
求证:PB<PC由于AB=AC,可将△ABP旋转至AP'C。
∵AP‘=AP,∴∠APP'=∠AP'P∵∠AP’C = ∠APB > ∠APC∴∠PP'C > ∠P'PC∴ BP=CP' < PC在△ABC中,∠C=90°,M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于点P,求证:∠BPM=45°在直角三角形ABC中,∠C=90°,M在BC上,N在AC上,且BM=AC,AN=MC,求证∠BPM=45°。
证明设AC=b,BC=a, 则CM=AM=a-b,CN=2b-a。
过N点作NH∥AM,过M点作MH∥AC,交于H.连BH.则四边形ANHM是平行四边形,所以 MH=AN=CM=a-b,AM=NH.由勾股定理得:BN^2=BC^2+CN^2=a^2+(2b-a)^2=2(a^2-2ab+2b^2);AM^2=AC^2+CM^2=b^2+(a-b)^2= a^2-2ab+2b^2;BH^2=BM^2+MH^2=b^2+(a-b)^2= a^2-2ab+2b^2.所以得 AM=BH,AM^2+BH^2=BN^2。
故三角形BHN是等腰直角三角形。
因此∠BPM=∠BNH=45°。
这里的O 点相当于你们作业上的G 点 将边长为1+n/2(n=1,2,3,……)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A1A2A3,……2011-2-19 10:16提问者: 兔兔漂亮吗 | 浏览次数:1369次(1)若摆放前6个正方形纸片,则被遮盖的线段长度和为( ),(2)若摆放前n (n 为大于1的正整数)个正方形纸片,则被遮盖的线段长度之和为( )答案为:10 1/4*(n+2)(n-1)①过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,根据正方形的性质推出∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,求出∠AA 1B=∠DA A C ,证△BAA 1≌△CDA 1,得到AB=DC ,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可;②根据①的结论求出12×(2+3+4+…+n )即可.①解:过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,∵正方形EFGH ,∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,∴∠AA 1D=∠BA 1C=90°,∴∠AA 1B=∠DA A C ,∴△BAA 1≌△CDA 1,∴AB=DC ,∴BF+FC=FA+FD=1+12=1,同理第2个虚线之和是1+22=3,同理第3个虚线之和是2,同理第4个虚线之和是5同理第5个虚线之和是3,∴1+32+2+52+3=12×(2+3+4+5+6)=10,②若摆放前n个(n为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为12×(2+3+4+…+n)=n2+n-24,故答案为:10,n2+n-24.S△DEF+S△CEF= 12S△ABC 仍然成立.证明:当∠EDF绕点D旋转到DE⊥AC于E时,连接CD.∵Rt△ABC中,AC=BC,即△ABC为等腰直角三角形.又∵D为AB边的中点,∴CD=BD,∠ECD=∠FBD=45°,∠CDB=90°,又∵∠EDF=90°,∴∠EDF-∠CDF=∠CDB-∠CDF,即∠CDE=∠BDF,∴△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S△CDE+S△CDF=S△BDF+S△CDF=S△BCD= 12S△ABC,得证.当∠EDF绕点D旋转到DE和AC不垂直时:猜想 S△DEF+S△CEF= 1/2S△ABC,证明:连接CD,同理易得△CDE≌△BDF,∴S△CDE=S△BDF,∴S△DEF+S△CEF=S四边形DECF=S△CDE+S△CDF=S△DBF+S△CDF=S△BCD,又S△BCD= 12S△ABC,则S△DEF+S△CEF= 12S△ABC.故答案是:S△DEF+S△CEF= 12S△ABC,S△DEF+S△CEF=12S△ABC.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M 放在△ABC的斜边AB的中点处,设AC=BC=a.解:(1),(1+)a;(2),2a;(3)猜想:重叠部分的面积为。
平面解析几何经典题(含答案)

平面解析几何一、直线的倾斜角与斜率1、直线的倾斜角与斜率、直线的倾斜角与斜率(1)倾斜角a 的范围000180a £<(2)经过两点的直线的斜率公式是(3)每条直线都有倾斜角,但并不是每条直线都有斜率2.两条直线平行与垂直的判定(1)两条直线平行对于两条不重合的直线12,l l ,其斜率分别为12,k k ,则有1212//l l k k Û=。
特别地,当直线12,l l 的斜率都不存在时,12l l 与的关系为平行。
的关系为平行。
(2)两条直线垂直如果两条直线12,l l 斜率存在,设为12,k k ,则12121l l k k ^Û=-注:两条直线12,l l 垂直的充要条件是斜率之积为-1,这句话不正确;由两直线的斜率之积为-1,可以得出两直线垂直,反过来,两直线垂直,斜率之积不一定为-1。
如果12,l l 中有一条直线的斜率不存在,另一条直线的斜率为0时,12l l 与互相垂直。
互相垂直。
二、直线的方程1、直线方程的几种形式名称名称方程的形式方程的形式 已知条件已知条件 局限性局限性 点斜式点斜式为直线上一定点,k 为斜率为斜率 不包括垂直于x 轴的直线轴的直线 斜截式斜截式k 为斜率,b 是直线在y 轴上的截距轴上的截距 不包括垂直于x 轴的直线轴的直线 两点式两点式是直线上两定点是直线上两定点 不包括垂直于x 轴和y 轴的直线直线截距式截距式a 是直线在x 轴上的非零截距,b 是直不包括垂直于x 轴和y 轴或线在y 轴上的非零截距轴上的非零截距过原点的直线过原点的直线 一般式一般式A ,B ,C 为系数为系数 无限制,可表示任何位置的直线直线 三、直线的交点坐标与距离公式三、直线的交点坐标与距离公式1.两条直线的交点设两条直线的方程是,两条直线的交点坐标就是方程组的解,若方程组有唯一解,则这两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立。
初中平面几何之几何作图习题(含答案)

几何作图(导学案)知识过关1. 说出日常生活现象中应用的数学原理:(1)如图1,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是__________________________________________.图1 图2(2)如图2,PC ∥AB ,QC ∥AB ,则点P ,C ,Q 在一条直线上,理由是_______________________________________.2. 估计下列角的度数,然后用量角器度量并填在横线上:(结果精确到1°)∠BOC =____,∠DOE =____,∠MON =_____,∠POQ =____.1. 常见几何语言书写:①连接AB ;②延长线段AB 到点C ,使BC =AB ; ③延长线段AB 交线段CD 的延长线于点E ; ④过点A 作AB ∥CD ; ⑤过点A 作AB ⊥CD 于点E . 2. 几何作图:①理解题意,找准_____________; ②___________________;③位置不确定时,需考虑_______________.➢ 精讲精练1. 如图,已知四点A ,B ,C ,D ,按要求作图: (1)连接AB ,CD ;(2)延长CD 交AB 的延长线于点G ; (3)过点B 作直线BM ⊥CD ,垂足为点M .Q CP AB QOOOPNMEDCB2. 如图,点M ,P 分别在直线AB 上和直线AB 外,以下是在此图基础上作图的过程及作法,请根据作图的过程叙述作法.ACB D3. 作一条线段等于已知线段.已知:如图,线段a . 求作:线段AB ,使AB =a . 作法:(1)作射线AP ;(2)以_________为圆心,_______为半径作弧,交射 线AP 于点B .___________即为所求.4. 已知线段a ,b (),作一条线段,使它等于a +b .作法:(1)作射线AP ;(2)在射线AP 上依次截取__________,_________. ___________即为所求.5. 如图,已知线段AB ,请用尺规按下列要求作图: (1)延长线段AB 到点C ,使BC =AB ; (2)延长线段BA 到点D ,使AD =AC .a b ba BA6.在直线l上任取一点A,截取AB=8 cm,再截取AC=12 cm,则线段BC的长为______________.7.在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,则点B与AC的中点D之间的距离为__________.8.已知A,B,C三点在同一条直线上,AB=60,BC=40,M,N分别为线段AB,BC的中点,则MN的长为__________.9.已知线段AB=16 cm,点C在直线AB上,AC=3BC,则BC的长为______________.10.从O点出发的三条射线OA,OB,OC,若∠AOB是直角,∠AOC为30°,则∠BOC的度数为_____________.11.已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,则∠MON的度数为_____________.12.已知∠AOB=40°,∠AOD=3∠AOB,OC平分∠AOB,OM平分∠AOD,则∠MOC的度数为_____________.13.已知∠AOB=48°,∠BOC=3∠AOC,OM平分∠AOC,ON平分∠AOB,则∠MON的度数为__________.【参考答案】➢知识过关1.(1)垂线段最短;(2)过直线外一点,有且只有一条直线与已知直线平行.2.30°,60°,110°,140°2.①关键词;②设计作图方案,作出草图;③分类讨论.➢精讲精练1.略2.(1)连接(2)PH⊥AB于点H(3)PQ∥AB3.作图略(2)点A,线段a长(3)线段AB4.作图略(2)AB=a,BC=b,线段AC5.略6.4cm或20cm7.4cm或36cm8.50或109.4cm或8cm10.60°或120°11.30°或60°12.40°或80°13.18°或36°几何作图(当堂过关)1.如图,已知点P在∠AOB的内部,过点P作PC∥OB,交OA于点C,过点P作PD⊥OA于点D.2.已知线段a,b,画一条线段,使它等于2a-b.(保留作图痕迹)ab3.已知∠AOB=80°,∠BOC=60°,OM平分∠AOB,ON平分∠BOC,则∠MON的度数为_____________,并作图说明.①作草图:②设计方案:【参考答案】1. 略2. 略3. 70°或10°,作图说明略几何作图(习题)➢ 例题示范例1:在直线l 上任取一点A ,截取AB =20cm ,再截取BC=50cm ,则AB 的中点D 与AC 的中点E 之间的距离为__________,并作图说明. 思路分析首先,理解题意,找关键词,其中l 为直线,AB ,BC 为l 上的两条线段. 其次,设计作图方案,作图.作直线l ,任取一点作为A ,取适当长作为AB ;此时点B 位置固定,但点C 可在点B 左侧或右侧,位置不定,故分两种情况. ①点C 在点B 左侧,如图,接着取AB 的中点D ,AC 的中点E .设计算法: ②点C 在点B 右侧,如图,接着取AB 的中点D ,AC 的中点E .设计算法:2050l2050l 11221225AB AC DE AD AE BC =+==+=2050l2050l综上,DE 的长度为25cm .➢ 巩固练习1. 如图1,点C ,D 是直线AB 外两点,按下列要求作图: (1)____________________________________________; (2)____________________________________________. 得到的图形如图2,请在横线填上作法.2. 如图,已知线段AB ,按要求作图:①分别以点A 和点B 为圆心、以AB 的长为半径作弧,两弧相交于点C 和点D ;②作直线CD ,交线段AB 于点E ;③请通过测量猜想线段AB 和直线CD 的位置关系,线段AE 与线段BE 的数量关系.3. 作图:已知线段a ,b (),作一条线段,使它等于.(保留作图痕迹,不必写作法)4. 已知线段AB =15cm ,点C 在直线AB 上,且BC =2AB ,则线段AC 的长为________________,并作图说明.11221225AC AB DE AE AD BC =-==-=ABCD 图1图2A Ba b >a b -ba5. 已知点C 在直线AB 上,若AC =4cm ,BC =6cm ,E ,F 分别为线段AC ,BC 的中点,则EF 的长为_____________,并作图说明.6. 已知线段AB=24,点C 在直线AB 上,BC=3AC ,M ,N 分别为线段AB ,AC 的中点,则MN 的长为_____________,并作图说明.7. 已知从点O 出发的三条射线OA ,OB ,OC ,若∠AOB =60°,,则∠BOC 的度数为________________,并作图说明.8. 已知∠AOB 为直角,∠BOC =40°,OM 平分∠AOB ,ON 平分∠BOC ,则∠MON 的度数为_______________,并作图说明.9. 已知∠AOB =120°,∠AOC =4∠BOC ,OD 平分∠AOB ,OE 平分∠AOC ,则∠EOD 的度数为____________,并作图说明.【参考答案】 ➢ 巩固练习1. (1)作射线DC 交AB 于点E(2)过点C 作CF ⊥DE 于点C ,交AB 于点F 2. 作图略,AB ⊥CD ,AE =BE 3. 作图略13AOC AOB ∠∠O BA4.15cm或45cm,作图说明略5.1cm或5cm,作图说明略6.9或18,作图说明略7.40°或80°,作图说明略8.25°或65°,作图说明略9.12°或20°,作图说明略。
(精心整理)平面几何经典难题及解答

平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.APCBACBPDA CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
(完整版)八年级数学几何经典题【含答案】
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
中学数学 平面几何最短路径 练习题(含答案)

平面图形上的最短路径问题知识点:1.两点之间,线段最短2.垂线段最短3.线段垂直平分线是的点到线段两端点的距离相等4.三角形任意两边之差小于第三边总思路:找点关于线的对称点实现“折”转“直”常考题型题:将军饮马、造桥选址、费马点(一)根据两点之间,线段最短题型一两点在直线同侧(将军饮马)题型二相交直线之间一点或两点题型四费马点(二)根据垂线段最短题型五和最小(三)根据线段垂直平分线上点到线段两端点距离相等题型六差最小(四)根据三角形任意两边之差小于第三边题型七差最大题型一两点在直线同侧例题1:如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是()A.3B.6解:在AC上取一点E,使得AE=AB,过E作EN⊥AB于N′,交AD于M,连接BM,BE,BE交AD于O,则BM+MN’最小(根据两点之间线段最短;点到直线垂直距离最短),∵AD平分∠CAB,AE=AB,∴EO=OB,AD⊥BE,∴AD是BE的垂直平分线(三线合一),∴E和B关于直线AD对称,∴EM=BM,即BM+MN′=EM+MN′=EN′,∵EN’⊥AB,∴∠EN’A=90°,∵∠CAB=60°,∴∠AEN′=30°,∵AE=AB=6,∴AN’=3,在△AEN’中,由勾股定理得:EN’即BM+MN B.巩固练习:如图,在平面直角坐标系中,R t△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则P A+PC的最小值为____ _____.解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时P A+PC的值最小.∵DP=P A,∴P A+PC=PD+PC=CD.∵B(3,∴AB OA=3,∠B=60°.由勾股定理得:OB OA×AB OB×AM,∴AM AD.∵∠AMB=90°,∠B=60°,∴∠BAM=30°.∵∠BAO=90°,∴∠OAM=60°.∵DN⊥OA,∴∠NDA=30°.∴AN由勾股定理得:DN C(1,0),∴CN=3-1在R t△DNC中,由勾股定理得:DC∴P A+PC题型二相交直线之间一或两点例题2:如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R .若△PQR 周长最小,则最小周长是( )A .10B .15C .20D .30 解:设∠POA =θ,则∠POB =30°﹣θ,作PM ⊥OA 与OA 相交于M ,并将PM 延长一倍到E ,即ME =PM . 作PN ⊥OB 与OB 相交于N ,并将PN 延长一倍到F ,即NF =PN . 连接EF 与OA 相交于Q ,与OB 相交于R ,再连接PQ ,PR , 则△PQR 即为周长最短的三角形.∵OA 是PE 的垂直平分线, ∴EQ =QP ;同理,OB 是PF 的垂直平分线, ∴FR =RP , ∴△PQR 的周长=EF . ∵OE =OF =OP =10,且∠EOF =∠EOP +∠POF =2θ+2(30°﹣θ)=60°, ∴△EOF 是正三角形,∴EF =10,即在保持OP =10的条件下△PQR 的最小周长为10,故选A .巩固练习:如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =5,ON =12,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是 .解:作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M’N’,即为MP +PQ +QN 的最小值.根据轴对称的定义可知:∠N ′OQ =∠M ′OB =30°,∠ONN ′=60°,OM’=OM =5,ON’=ON =12, ∴△ONN ′为等边三角形,△OMM ′为等边三角形, ∴∠N′OM′=90°,∴在Rt M ON ''中,''13M N = 故答案为:13.题型三 造桥选址例题3:荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A 到B点路径最短?解:作AF⊥CD,且AF=河宽,作B G⊥CE,且BG=河宽,连接GF,与河岸相交于E’、D’,作DD’、EE’即为桥证明:由做法可知,AF∥DD’,AF=DD’,则四边形AFDD’为平行四边形于是AD=FD’同理,BE=G E’由两点之间线段最短可知,GF最小即当桥建于如图所示位置时,ADD’E’EB最短巩固练习:如图,工厂A和工厂B被一条河隔开,它们到河的距离都是2km,两个工厂水平距离是3km,河宽1km,现在要架一座垂直于河岸的桥,使工厂A到工厂B的距离最短(河岸是平行的)①请画出架桥的位置(不写画法)②求从工厂A经过桥到工厂B的最短路程.解:①如图所示,AA’=1km,则MN为架桥位置A B===②过点B作BE⊥AA’,交其延长线于点E。
平面几何练习一及答案

平面几何练习题(一)1、在△ABC的边AC上取点D,E,使得AD=AB,BE=EC,(E在A与D之间),点F是△ABC外接圆上(不含A点的)BC弧的中点,求证:B、E、D、F四点共圆.FA2、在△ABC中,BC>AB,BD平分∠ABC 交AC于D,如图,CP垂直于BD,垂足为P,AQ垂直于BP,垂足为Q,M是AC的中点,E是BC的中点.若△PQM的外接圆O与AC的另一个交点为H.求证:O,H,E,M四点共圆.C3、AB是圆O的直径,C为AB延长线上一点,过点C作圆O的割线,与圆O交于D,E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交圆O1 于点G .求证:O、A、E、G四点共圆.A4、如图,在锐角△ABC中,AB<AC,AD是边BC上的高,P是线段AD内一点。
过P作PE⊥AC,垂足为E,做PF⊥AB,垂足为F。
O1、O2分别是△BDF、△CDE的外心。
求证:O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
B平面几何练习一参考答案1、证明:设∠ABC=α.因AB=AD ,故∠ABD=α,∠BAD=180°-2α.∠CBF 的度数等于21CF 弧的度数,而∠CAB 的度数等于21BC 弧的度数,所以∠CBF=21∠CAB =90°-α,点E ,F 分别与点B ,C 等距,所以EF 垂直平分BC.因此∠BFE=90°-∠CBF=90°-(90°-α)=α.于是∠BDE=∠BFE=α,所以B 、F 、D 、E 四点共圆.2、证明:如图联结PH ,作AQ 延长线交BC 于N ,则Q 为AN 的中点. M 为AC中点,∴QM ∥BC.故∠PQM=∠PBC=1/2∠ABC,同理,延长CP 交BA 延长线于N '可得P M ∥B N ',因此∠MPQ =∠ABP=1/2∠ABC ,∴QM=PM.又 Q,H,P,M 四点共圆, ∴∠PHC =∠PHM=∠PQM ,得∠PHC =∠PBC ,∴P,H,B,C 四点共圆,得∠BHC =∠BPC =90°,故HE=1/2BC=EP.结合OH=OP ,知OE 为HP 的中垂线,由∠MPQ =1/2∠ABC=∠PBC 及E 为BC 的中点可得P,M,E 共线,故∠EHO =∠EPO=∠OPM=∠OMP ,所以 O,H,E,M 四点共圆.3、证明:联结AD,DG,GA,GO,EA,EO.因为OFOF 平分∠DOB ,又因为∠DAB=1/2∠DOB ,所以∠DAB=∠DOF ,又∠DGF=∠DOF ,所以∠DAB=∠DGF ,所以G ,A,C,D 四点共圆,所以∠AGC=∠AD C ①,而∠AGC= ∠AGO +∠OGF=∠AGO+π/2,② ∠ADC=∠ADB +∠BDC=∠BDC+π/2,③结合①②③得∠AGO=∠BD C .因为B,D,E,A 四点共圆,所以∠BDC=∠EAO ,又OA=OE ,有∠AEO=∠EAO ,所以∠AGO=∠AEO ,故O,A,E,G 四点共圆.AC。
(完整版)初中数学经典几何题及答案
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初二平面几何习题及答案

精心整理习题1如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP、BP、CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数.BC 的边长是多少?把△APC绕点A顺时针旋转60°到△AMB,则AM=AP=2,BM=PC=4,∠PAM=60°连结PM,则△PAM是等边三角形,∴PM=2∴△ACD≌△BDE∴AC=BE=BC+CD习题5 如图,己知在△ABC中,AB=AC,∠BAC=90°,点D是BC上的任意一点,探究BD2+CD2与AD2的关系习题6 D,E是等腰直角三角形斜边BC所在直线上的两点,满足∠DAE=135°,求证CD2+BE2=DE2∵∠BAC=90°,AC=AB,∴将△ABE绕点A逆时针转90°,得△ACF,所以MB=MC=ME=MD角EMD=角MCD*2; 角EMB=角BCE*2所以角DMB=角EMD+角EMB=2*(角MCD+角MCB)=2*角C=90°所以BM=DM且BM垂直DM(2)证明:取AE的中点G,AC的中点F,连接DG,MG,BF,MF.又M为CE中点,则:MF=AE/2=DG;GM=AC/2=BF;GM∥AC;MF∥AE.(中位线的性质)得:∠MFC=∠EAC=∠EGM;又∠BFC=∠EGD=90度.则∠MFB=∠DGM. ∴?⊿BFM≌⊿MGD(SAS),BM=DM;∠FBM=∠GMD.又GM平行AC,BF垂直AC,则GM垂直BF.故∠FBM+∠BMG=90度=∠GMD+∠BMG,即∠BMD=90度,得:BM⊥DM.明显的对称。
如果P点距离AB与距离CD距离不一样大会是最小吗?显然不会,因为如果不一样明显可以在中线另一侧找到一个对应点拥有同样的距离。
因此P点一定在BC中垂线上,而Q的横坐标一定与P一致,原因不解释,很明显。
以A为原点,AD为x轴,BA为y轴建立坐标系,则P横坐标为500。
初二平面几何习题和答案

习题1如图.P为等边△ABC内一点.∠APB=113°.∠APC=123°.试说明:以AP、BP、CP为边长可以构成一个三角形.并确定所构成三角形的各内角的度数.解:将△APC绕点A顺时针旋转60°得△AQB.则△AQB≌△APC∴BQ=CP.AQ=AP.∵∠1+∠3=60°.∴△APQ是等边三角形.∴QP=AP.∴△QBP就是以AP.BP.CP三边为边的三角形.∵∠APB=113°.∴∠6=∠APB-∠5=53°.∵∠AQB=∠APC=123°.∴∠7=∠AQB-∠4=63°.∴∠QBP=180°-∠6-∠7=64°.∴以AP.BP.CP为边的三角形的三内角的度数分别为64°.63°.53°.习题3P是等边△ABC中的一点.PA=2,PB=2倍根号3.PC=4.则BC 的边长是多少?把△APC绕点A顺时针旋转60°到△AMB.则AM=AP=2.BM=PC=4,∠PAM=60°连结PM.则△PAM是等边三角形.∴PM=2在△PBM中.PM²+PB²=2²+(2√3)²=16BM²=4²=16∴PM²+PB²=BM²∴△PBM是直角三角形.∠BPM=90°∴∠APB=90°+60°=150°过A作AD⊥BP交BP的延长线于D.则∠APD=30°∴AD=1,PD=√3∴AB²=1²+(3√3)²=28∴BC=AB=2√7习题4已知四边形abcd中,ab=ad,∠bad=60°,∠bcd=120°,证明bc+dc=ac 证明:连接BD.延长BC到点E.使CE=CD.连接DE∵AB=AD.∠BAD=60°.AB=AD∴△ABD是等边三角形∴∠ADB=60°.AD=BD∵∠BCD=120°∴∠DCE=60°∴△DCE是等边三角形∴∠CDE=60°.DC=DE∴∠ADC=∠BDE∴△ACD≌△BDE∴AC=BE=BC+CD习题5 如图,己知在△ABC中,AB=AC,∠BAC=90°,点D是BC上的任意一点,探究BD²+CD²与AD²的关系证明:作AE⊥BC于E.如图所示:由题意得:ED=BD-BE=CE-CD.∵在△ABC中.∠BAC=90°.AB=AC.∴BE=CE= 1/2BC.由勾股定理可得:AB²+AC²=BC².AE²=AB²-BE²=AC²-CE².AD²=AE²+ED².∴2AD²=2AE²+2ED²=AB²-BE²+(BD-BE)²+AC²-CE²+(CE-CD)²=AB²+AC²+BD²+CD²-2BD×BE-2CD×CE=AB²+AC²+BD²+CD²-2× 1/2BC×BC=BD²+CD².即:BD²+CD²=2AD².习题6 D,E是等腰直角三角形斜边BC所在直线上的两点.满足∠DAE=135°.求证CD²+BE²=DE²∵∠BAC=90°.AC=AB.∴将△ABE绕点A逆时针转90°.得△ACF.则△ABE≌△ACF.∠EA F=90°.∴BE=CF.∠ACF=∠ABE=45°.AE=AF,∵∠DAE=90°.∠EAF=135°,∴∠DAF=135°,∴△ADF≌△ADE.∴DE=DF.∵∠DCF=∠DCA+∠ACF=90°.∴DC²+CF²=DF²,∴DC²+BE²=DE²习题七GF平行于AB平行于CD,P又是中点.∠ HDP=∠ GFP,∠ HPD=∠GPE,P为中点.所以△ HDP全等于△ GFP,这样DH=GF,所以CH=CG.则有等腰△ CHG.有P为HG中点,所以PC⊥PG,因为菱形ABCD ∠ ABC=60°所以∠ DCB=120° CP为角平分线.∠ PCG=60°PG:PC=√3证明:如图3.延长GP到H.使PH=PG.连接CH.CG.DH.∵P是线段DF的中点.∴FP=DP.∵∠GPF=∠HPD.∴△GFP≌△HDP.∴GF=HD.∠GFP=∠HDP.∵∠GFP+∠PFE=120°.∠PFE=∠PDC.∴∠CDH=∠HDP+∠PDC=120°.∵四边形ABCD是菱形.∴CD=CB.∠ADC=∠ABC=60°.点A、B、G又在一条直线上.∴∠GBC=120°.∵四边形BEFG是菱形.∴GF=GB.∴HD=GB.∴△HDC≌△GBC.∴CH=CG.∠DCH=∠BCG.∴∠DCH+∠HCB=∠BCG+∠HCB=120°.即∠HCG=120°∵CH=CG.PH=PG.∴PG⊥PC.∠GCP=∠HCP=60°.∴PGPC.习题8已知在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE连接EC,取EC中点M,连接DM和BM.(1)证:Rt△ABC中.因为AB=CB;所以角A=角C=45°Rt△ADE中.AD=DE.所以角AED=角ADE=45°因为M是EC中点所以MB=MC=ME=MD角EMD=角MCD*2; 角EMB=角BCE*2所以角DMB=角EMD+角EMB=2*(角MCD+角MCB)=2*角C=90°所以BM=DM且BM垂直DM(2)证明:取AE的中点G,AC的中点F,连接DG,MG,BF,MF.又M为CE中点,则:MF=AE/2=DG;GM=AC/2=BF;GM∥AC;MF∥AE.(中位线的性质)得:∠MFC=∠EAC=∠EGM;又∠BFC=∠EGD=90度.则∠MFB=∠DGM.∴⊿BFM≌⊿MGD(SAS),BM=DM;∠FBM=∠GMD.又GM平行AC,BF垂直AC,则GM垂直BF.故∠FBM+∠BMG=90度=∠GMD+∠BMG,即∠BMD=90度,得:BM⊥DM.习题九如图所示.在△ABC中.∠BAC=120°.P是△ABC内部一点.试比较PA+PB+PC与AB+AC的大小关系解:把△PAB绕A点顺时针旋转60度得△QAD.则D.A.C在同一直线上。
八年级平面几何的综合提升专项习题(含答案解析)
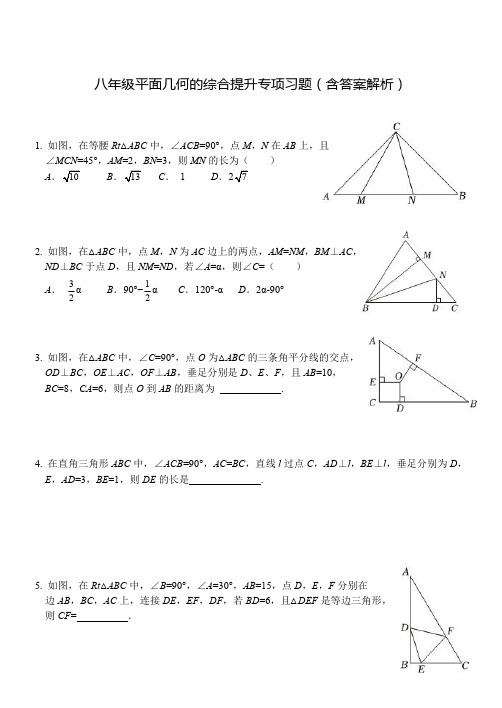
八年级平面几何的综合提升专项习题(含答案解析)1.如图,在等腰Rt△ABC中,∠ACB=90°,点M,N在AB上,且∠MCN=45°,AM=2,BN=3,则MN的长为()A10B13C.1D.72.如图,在△ABC中,点M,N为AC边上的两点,AM=NM,BM⊥AC,ND⊥BC于点D,且NM=ND,若∠A=α,则∠C=()A.32αB.90°−12αC.120°-αD.2α-90°3.如图,在△ABC中,∠C=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,垂足分别是D、E、F,且AB=10,BC=8,CA=6,则点O到AB的距离为.4.在直角三角形ABC中,∠ACB=90°,AC=BC,直线l过点C,AD⊥l,BE⊥l,垂足分别为D,E,AD=3,BE=1,则DE的长是.5.如图,在Rt△ABC中,∠B=90°,∠A=30°,AB=15,点D,E,F分别在边AB,BC,AC上,连接DE,EF,DF,若BD=6,且△DEF是等边三角形,则CF=.6.如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一点,连接BD,EC⊥AC,且AE=BD,AE与BC交于点F.⑴求证:CE=AD;⑵当AD=CF时,求证:BD平分∠ABC.答案解析1.解:把△ACM沿CM翻折至△DCM,连接DN,∴△DCM≌△ACM,∴CD=CA,∴DM=AM=2,∠DCM=∠ACM,∠CDM=∠A.又∵CA=CB,∴CD=CB.∵∠DCN=∠MCN-∠DCM=45°-∠DCM,∠BCN=∠ACB-∠MCN-∠ACM=90°-45°-∠ACM=45°-∠ACM,∴∠DCN=∠BCN.又∵CN=CN,∴△CDN≌△CBN(SAS),∴DN=BN=3,∠CDN=∠B,∴∠MDN=∠CDM+∠CDN=∠A+∠B=90°.在Rt△MDN中,MN2=DM2+DN2,即MN2=AM2+BN2.故选:B.2.解:∵AM=NM,BM⊥AC,∠A=α,∴∠ABM=∠NBM=90°-α,∵NM=ND,BM⊥AC,ND⊥BC,∴BN平分∠NDM,∴∠ABM=∠DBN=∠NBM=90°-α,∴∠ABC=∠ABM+∠DBN+∠NBM=270°-3α,∴∠C=2α-90°,故选:D.3.解:如图,连接OB,AO,∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,∴OE=OD=OF,在Rt△ODB和Rt△OFB中,∴Rt△ODB≌Rt△OFB(AAS),∴DB=FB,同理可证,AE=AF,∵∠C=∠OEC=∠ODC=90°,OD=OE,∴四边形OECD是正方形,∴CE=CD=OD=OE,设OE=OD=OF=x,CE=CD=x,BD=BF=8-x,AF=AE=6-x,∴BF+FA=AB=10,即6-x+8-x=10,解得x=2,∴OF=2,故答案为:2.4.解:如图,当A,B在直线l的异侧时,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∵BE⊥CE,AD⊥CE,∴∠BEC=∠CDA=90°,∴∠CBE+BCE=180°-90°=90°,∴∠CBE=∠ACD,在△BEC与△CDA中,∴△BEC≌△CDA(AAS),∴EC=AD=3,CD=BE=1,∴DE=EC-CD=3-1=2.当A,B在直线l的同侧时,如图,同理可得:△BEC≌△CDA(AAS),∴EC=AD=3,CD=BE=1,∴DE=EC+CD=3+1=4.故答案为:2或4.5.解:作EH⊥AC于H,∵△DEF是等边三角形,∴∠DEF=60°,DE=EF,∵∠A=30°,∠B=90°,∴∠C=90°-∠A=60°,∵∠BED+∠DEF=∠C+∠EFH,∴∠BED=∠EFH,∵∠B=∠EHF=90°,DE=EF,∴△EFH≌△DEB(AAS),∴FH=BE,EH=BD=6,6.证明:⑴∵EC⊥AC,∠BAC=90°,∴∠ACE=∠BAC=90°,在Rt△CAE与Rt△ABD中∴Rt△CAE≌Rt△ABD(HL),∴CE=AD.⑵由⑴得Rt△CAE≌Rt△ABD,∴∠EAC=∠ABD,∠E=∠ADB.由(1)得CE=AD,∵AD=CF,∴CE=CF.∴∠CFE=∠E,∵∠CFE=∠AFB,∴∠AFB=∠E.∵∠E=∠ADB,∴∠AFB=∠ADB,∵∠AGB=∠EAC+∠ADB,∠AGB=∠DBC+∠AFB,∴∠EAC=∠DBC.∵∠EAC=∠DBA,∴∠DBA=∠DBC,∴BD平分∠ABC.。
