平面几何经典难题及解答
平面几何经典难题及解答
经典难题(一)1、已知:如图,O就是半圆的圆心,C、E就是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.求证:△PBC就是正三角形.3、如图,已知四边形ABCD、A1CC1、DD1的中点.求证:四边形A2B2C2D24、已知:如图,在四边形ABCD中线交MN于E、F.求证:∠DEN=∠F.1、已知:△ABC中,H为垂心((1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=2、设MN就是圆O外一直线,过D、E,直线EB及CD分别交求证:AP=AQ.(初二)3、如果上题把直线MN设MN就是圆O的弦,过P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC与点P就是EF的中点.求证:点P到边AB1、如图,四边形ABCD为正方形求证:CE=CF.(初二)2、如图,四边形ABCD为正方形求证:AE=AF.(初二)3、设P就是正方形ABCD一边求证:PA=PF.(初二)4、如图,PC切圆O于C,AC求证:AB=DC,BC=AD.(初三1、已知:△ABC就是正三角形,P求:∠APB的度数.(初二)2、设P就是平行四边形ABCD求证:∠PAB=∠PCB.(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别就是BC 、AB 上的一点,AE AE =CF.求证:∠DPA =∠DPC.(初二)经典难题(五)1、设P 就是边长为1的正△ABC 内任一点证:≤L <2.2、已知:P 就是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a,4、如图,△ABC中,∠ABC =∠ACB =800,D 、E分别就是AB 、AC =200,求∠BED 的度数.经典难题解答:经典难题(一)1、如下图做GH ⊥AB,连接EO 。
平面几何经典难题与解答
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB C B DAF PD E C B A1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB A A CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDA A CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形. 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)APCDBAFGCEB OD D 2 C 2 B 2 A 2D 1C 1B 1D A A 1F2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自B 、C及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN的中点A 任作两弦MN于P 、Q .求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB经典难1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .2、如图,四边形ABCD F . 求证:AE =AF .(初二)3、设P 是正方形ABCDN求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,ACB 、D .求证:AB =DC,BC =AD .经典1、已知:△ABC 是正三角形,P 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD·4、平行四边形ABCD 中,设E 、F 分别是BC 、ABAE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)D1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是300,∠EBA=200,求∠BED的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

平面几何之阿布丰王创作经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .2、已知:如图,P 是正方形ABCD求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 24、已知:如图,在四边形ABCD 中,AD 的中点,AD 、BC 的延长线交MN 求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 直线,交圆于B 、C 及D 、E ,直线EB 及CD 求证:AP =AQ .(初二)3、如果上题把直线MN题:设MN 是圆O 的弦,过MN CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 方形ACDE 和正方形CBFG ,点P 是EF求证:点P 到边AB 的距离等于AB 经典难1、如图,四边形ABCD 为正方形,DE ∥交于F .求证:CE =CF 2、如图,四边形ABCD 交DA 延长线于F .求证:AE =AF 3、设P 是正方形ABCD DCE .求证:PA =PF 4、如图,PC 切圆O 于AF 与直线PO 相交于B 1、已知:△ABC 4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB+PC 的最小值.3、P 为正方形ABCD 内的一点,而且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E的点,∠DCA =300,∠EBA =200,求∠BED APC B P ADCBCBD A F PDE CBAAPC B经典难题解答:经典难题(一)⊥AB,连接EO。
平面几何经典难的题目及解答
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A PC D B AFG C EBOD D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答分解
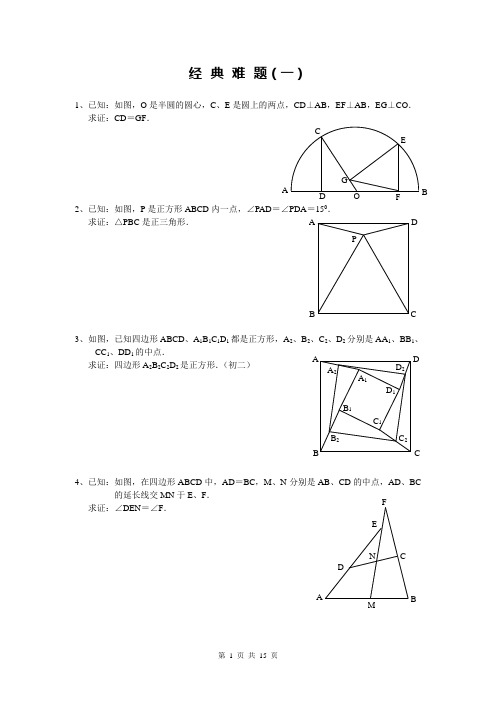
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

平面几何经典难题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.求证:△PBC是正三角形.3、如图,已知四边形ABCD、ACC1、DD1的中点.求证:四边形A2B2C2D24、已知:如图,在四边形的延长线交MN于E求证:∠DEN=∠F.1、已知:△ABC中,H(1)求证:AH=2OM;(2)若∠BAC=600,求证:2、设MN是圆O外一直线,过及D、E,直线EB及CD求证:AP=AQ.(初二)3、如果上题把直线MN设MN是圆O的弦,过于P、Q.求证:AP=AQ.4、如图,分别以△ABC的ACCBFG,点P是EF的中点.求证:点P到边AB1、如图,四边形ABCD求证:CE=CF.(初二)2、如图,四边形ABCD求证:AE=AF.(初二)3、设P是正方形ABCD一边求证:PA=PF.(初二)4、如图,PC切圆O于C,ACB、D.求证:AB=DC,BC1、已知:△ABC是正三角形,P求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC ∠EBA=200,求∠BED的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以2. 如下图做△DGC使与△ADP全等,可得△PDG△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点,连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2,EB2=12AB=12BC=F C1 ,又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2,可得△B2FC2≌△A2EB2,所以A2B2=B2C2,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A 2B 2C 2D 2是正方形。
平面几何经典难题及解答
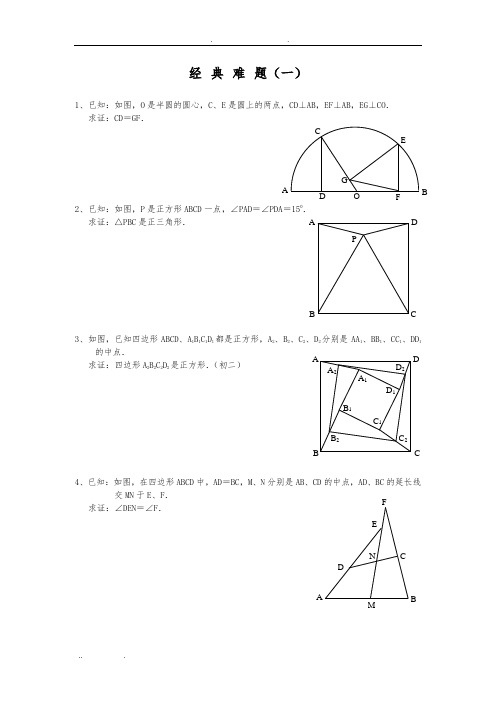
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC DCA =300,∠EBA=200,求∠BED 的度数.经典难题解答:APCBACBPDEDCB A A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答
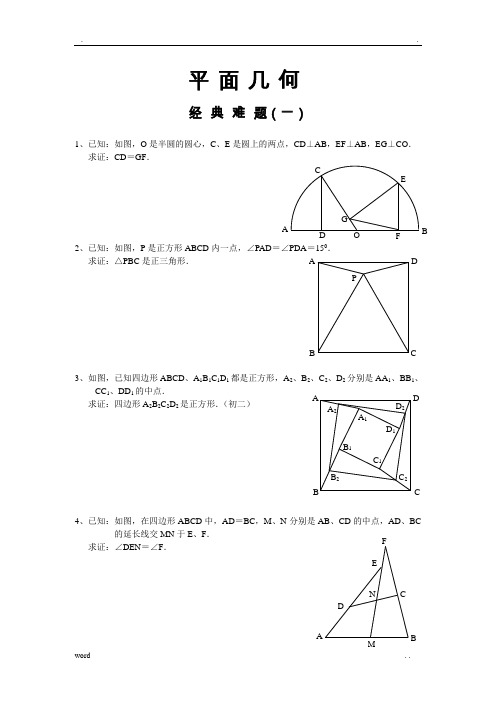
平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 0,∠EBA =200,求∠BED 的度数.APCBACBPDA CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

平面几何经典难题及解答经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.A PCDAF G C E BOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D2是正方形.(初二)4、已知:如图,在四边形ABCD ,M 、N 分别是AB 、、BC 的延长线交MN 于求证:∠DEN =∠F .D 2 C 2B 2 A 2 D 1C 1B 1CD A A1B经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(2)若∠BAC=600,求证:二)2、设MN是圆O外一直线,过O于A,自AD、E,直线EB及CD分别交求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过任作两弦BC、DE,设CD、于P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的CBFG,点P是EF求证:点P到边AB的距离等于AB的一半.(初二)经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)Array2、如图,四边形ABCD为正方形,DE∥AC,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C 为圆的割线,AE 、AFD.求证:AB=DC,BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P 为正方形ABCDPB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB E 分别是AB 、AC 上的点,∠DCA =30=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH ⊥AB,连接EO 。
平面几何经典难题及解答

平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、APCDB AFGCEBODDCC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、NBC的延长线交MN于E、F.求证:∠DEN=∠F.经典难题(二)B1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.FP DE CBAAPCB2、已知:P 是边长为1的正方形ABCD内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 0,∠EBA =200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A PC D B A F G C EBO D D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD 中,设E 、F分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC=200,求∠BED 的度数.经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何经典难题及解答

平面几何之袁州冬雪创作经典困难(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1C 2、D 2分别是AA 1、BB 1、CC 1、DD 1求证:四边形A 2B 2C 2D 24、已知:如图,在四边形ABCD 中,AD AB 、CD 的中点,AD 、BC求证:∠DEN =∠F .经典困难(二)1、已知:△ABC 中,H 心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 的两条直线,交圆于B 、C 及D 、E ,直线MN 于P 、Q .AGCEB求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 侧作正方形ACDE 和正方形CBFG求证:点P 到边AB 的间隔等于经典困难1、如图,四边形ABCD 为正方形,CD 相交于F .求证:CE =CF 2、如图,四边形线EC 交DA 延长线于求证:AE =AF 3、设P 是正方形分∠DCE .求证:PA =PF 4、如图,PC 切圆O 线,AE 、AF 与直线AD .(初三)经典困难(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 外部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典困难(五)1、设P 是边长为1的正△ABC 内任一点,=PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA+PB +PC 的最小值.APC BP AD CBCBD A F PDE CBAAPC BA CBPD3、P为正方形ABCD内的一点,而且PA=a,3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,AB、AC上的点,∠DCA=300,∠EBA=200数.经典困难解答:经典困难(一)⊥AB,毗连EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.△DGC使与△ADP全等,可得△PDG为等边△,从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图毗连BC1和AB12F与A2E并延长相交于Q点,毗连EB2并延长交C2Q于H点,毗连FB2并延长交A2Q于G 点,由A2E=12A1B1=12B1C1=FB2 ,EB2=12AB=12BC=FC1 ,又∠GFQ+∠Q=900和∠GEB2+∠Q=900,所以∠GEB2=∠GFQ又∠B2FC2=∠A2EB2,可得△B2FC2≌△A2EB2,所以A2B2=B2C2,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图毗连AC并取其中点Q,毗连QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F.经典困难(二)1.(1)延长AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)毗连OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.⊥CD,OG⊥BE,毗连OP,OA,OF,AF,OG,AG,OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG,从而可得∠AFC=∠AGE.又因为PFOA与QGOA四点共圆,可得∠AFC=∠AOP和∠AGE=∠AOQ,∠AOP=∠AOQ,从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH.可得PQ=2EGFH .由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI.从而可得PQ=2AIBI =2AB ,从而得证.经典困难(三)△ADE ,到△ABG ,毗连CG. 由于∠ABG=∠ADE=900+450=1350从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB. 推出AE=AG=AC=GC ,可得△AGC 为等边三角形. ∠AGB=300,既得∠EAC=300,从而可得∠A EC=750. 又∠EFC=∠DFA=450+300=750. 可证:CE=CF.⊥DE ,可得四边形CGDH 是正方形.由AC=CE=2GC=2CH ,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150,从而得出AE=AF. ⊥CD ,FE ⊥BE ,可以得出GFEC 为正方形. 令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X .tan ∠BAP=tan ∠EPF=XY=Z YXZ,可得YZ=XY-X 2+XZ ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP ≌△PEF , 得到PA =PF ,得证 .经典困难(四)1. 顺时针旋转△ABP 60,毗连PQ ,则△PBQ 是正三角形.可得△PQC 是直角三角形. 所以∠APB=1500.2.作过P 点平行于AD 的直线,并选一点E ,使AE ∥DC ,BE ∥PC.可以得出∠ABP=∠ADP=∠AEP ,可得: AEBP 共圆(一边所对两角相等). 可得∠BAP=∠BEP=∠BCP ,得证.3.在BD 取一点E ,使∠BCE=∠ACD ,既得△BEC ∽△ADC ,可得:BE BC=AD AC,即AD •BC=BE •AC , ①又∠ACB=∠DCE ,可得△ABC ∽△DEC ,既得AB AC=DE DC,即AB •CD=DE •AC , ②由①+②可得:AB •CD+AD •BC=AC(BE+DE)=AC ·BD ,得证.⊥AE ,AG ⊥CF ,由ADES=2ABCDS=DFC S ,可得:2AE PQ =2AE PQ ,由AE=FC.可得DQ=DG ,可得∠DPA =∠DPC (角平分线逆定理).经典困难(五)1.(1)顺时针旋转△BPC 600,可得△PBE为等边三角形.既得PA+PB+PC=AP++PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小L=(2)过P点作BC的平行线交AB,AC与点D,F.由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;由(1)和(2)既得:≤L<2 .△BPC 600,可得△PBE为等边三角形.既得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小PA+PB+PC=AF.既得213(1)42 = 23=42322(31)2 =2(31)622 .△ABP 900,可得如下图:既得正方形边长2222(2)()22a522a.4.在AB上找一点F,使∠BCF=600,毗连EF,DG,既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF ,得到BE=CF , FG=GE .推出:△FGE为等边三角形,可得∠AFE=800,既得:∠DFG=400①又BD=BC=BG ,既得∠BGD=800,既得∠DGF=400②推得:DF=DG ,得到:△DFE≌△DGE ,从而推得:∠FED=∠BED=300 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典难题(一)1、已知:如图, 0是半圆的圆心, C E 是圆上的两点, CD 丄AB, EF 丄AB, EGL CO 求证:CD= GF.4、已知:如图,在四边形 ABCD 中, AD= BC, M N 分别是AB CD 的中点,AD BC 的延长线交MN 于E 、F .求证:/ DEN=Z F .2、已知:如图,P 是正方形 ABCD 内一点, 求证:△ PBC 是正三角形. PAD=Z PDA= 150. 3、如图,已知四边形 ABCD AiBCD 都是正方形, 的中点.求证:四边形A e B 2C 2C 2是正方形.(初二) A 、E 2、C 2、D 2 分别是 AA 、BB 、CG 、DD DCDCM经典难题(二)1、已知:△ ABC 中,H 为垂心(各边高线的交点),0为外心,且 OM L BC 于M.(1) 求证:AH= 20M(2) 若/ BAC= 600,求证: 2、设MN 是圆O 外一直线,过0作OAL MN 于A 自A 引圆的两条直线, 交圆于B 、C 及D E , 直线EB 及CD 分别交MN 于P 、Q. 求证:AP = AQ (初二) 3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC DE 设CD EB 分别交MN 于P 、Q.求证:AP = AQ (初二) 4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形CBFGAH= AO (初二)H EB CM D G ECAM NPO点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)F1、如图,四边形 ABCD 为正方形,求证:CE = CF.(初二)DE// AC, AE = AC, AE 与 CD 相交于 F .2、如图,四边形 ABCD 为正方形,DE// AC,且CE= CA 直线EC 交DA 延长线于F . 求证:AE = AF.(初二) 3、设P 是正方形 ABCD-边BC 上的任一点,PF 丄AP, CF 平分/ DCE求证:PA = PF.(初二)4、如图,PC 切圆0于C, AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线P0相交于 B D.求 证:AB= DC BC = AD (初三)EA DC1、已知:△ ABC 是正三角形,P 是三角形内一点, PA = 3, PB= 4, PC = 5. 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/ PBA=Z PDA 求证:/ PAB=Z PCB (初二)4、平行四边形 ABCD 中,设E 、F 分别是BC AB 上的一点,AE 与CF 相交于P ,且 AE = CF.求证:/ DPA=Z DPC (初二)3、设ABCD 为圆内接凸四边形,求证: AB- CD^AD- BC = AC- BD.(初三)B ---------------------------- C经典难题(五)1、设P是边长为1的正△ ABC内任一点,L = PA + PB + PC ,求证:B C2、已知:P是边长为1的正方形ABCD内的一点,求PA+ PB+ PC的最小值.3、P为正方形ABCD内的一点,并且PA= a, PB= 2a, PC= 3a,求正方形的边长.A D4、如图,△ ABC中,/ ABC=Z ACB= 80°, D E分别是AB AC上的点,/ DCA= 30°, =20°,求/ BED的度数.经典难题解答经典难题(一)1.如下图做GHL AB,连接EO由于GOFE四点共圆,所以/ GFH kZ OEG, 即厶OGE可得■EO=GO=C°,又CO=EO所以CD=G碍证。
GF GH CD2.如下图做厶DGC使与厶ADP全等,可得△ PDG为等边△,从而可得△ DG QA APD^A CGP,得出PC=AD=DC和/ DCG N PCG= 15°所以/ DCP=30,从而得出△ PBC是正三角形3.如下图连接BC和AB分别找其中点F,E.连接C2F与AE并延长相交于Q点, 连接EB 并延长交C2Q于H点,连接FE2并延长交AQ于G点,由AE=*AB=*BG= FB2 , EB=》AB=2B C=F C,又/GFQ亡Q=90 和/ GE B^+Z Q=9C°,所以/ GE32=Z GFQ又/ BFC2=/A2EB ,可得△ B2FC BA AEB2,所以A zR uBC b ,又/ GFQ# HB2F=900和/ GFQ2 EBA , 从而可得/ A2B2 C2=900,同理可得其他边垂直且相等,从而得出四边形AB2GD2是正方形。
4.如下图连接AC并取其中点Q连接QN和QM所以可得/ QMF=/ F,/ QNM N DEN 和/QMN/QNM 从而得出/ DEN=/ F。
经典难题(二)1.(1)延长AD到F 连BF,做0G_ AF,又/ F=/ ACB=/ BHD,可得BH=BF从而可得HD=DF又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=20M (2)连接OB 0C既得/ BOC=120, 从而可得/ B0M=600 所以可得OB=2OM=AH=AO, 得证。
3.作0巳CD OGL BE 连接OP OA OF, AF, OG AG OQ由于AD= AC=CD=2FD = FD-2BG = BG,由此可得厶ADF^A ABQ从而可得/ AFC=Z AGE又因为PFOA与QGOA9点共圆,可得/ AFC=Z AOP和/ AGE2 AOQ / AOP=/ AOQ 从而可得AP=AQ4.过E,C,F点分别作AB所在直线的高EG CI , FHo可得PQ=EG+ FH2 由厶EGA2^AIC,可得EG=A,由厶BFrt^A CBI ,可得FH=BI。
AI + BI AB从而可得PQ= = ,从而得证。
经典难题(三)1•顺时针旋转△ ADE到厶ABG连接CG.由于/ ABG=Z ADE=90+45°=135°从而可得B, G, D在一条直线上,可得△ AGB^A CGB 推出AE=AG=AC=GC可得厶AGC为等边三角形。
/ AGB=3°,既得/ EAC=3°,从而可得/ A EC=75°。
又/ EFC玄DFA=45+30°=75°.可证:CE=CF。
2.连接BD作CH L DE可得四边形CGD是正方形。
由AC=CE=2GC=2CH可得/ CEH=3°,所以/ CAE=/ CEA玄AED=l5,又/ FAE=90+45°+15°=15O°,从而可知道/ F=15°,从而得出AE=AF3.作FGL CD FE丄BE可以得出GFEC为正方形。
令AB=Y , BP=X ,CE=Z ,可得PC=Y-X。
X Z 2tan / BAP=tan/ EPF== ,可得YZ=XY-X+XZ,Y Y- X + Z即Z(Y-X)=X(Y-X),既得X=Z,得出△ ABP^A PEF , 得到PA= PF,得证。
经典难题(四)1.顺时针旋转△ ABP 60 0,连接PQ,则△ PBQ是正三角形。
可得△ PQC是直角三角形。
所以/ APB=1500。
2•作过P点平行于AD的直线,并选一点E,使AE// DC BE// PC. 可以得出/ ABP=/ ADP=/ AEP可得:AEBP共圆(一边所对两角相等)。
可得/ BAP=/ BEP=/ BCP 得证。
3.在BD取一点E ,使/ BCE/ ACD既得△ BE3A ADC可得:BE=J AD ,即AD?BC=BEAC, ①BC AC又/ ACB/ DCE 可得△ AB3A DEC 既得些=匹,即AB?CD=DEAC ②AC DC由① + ②可得:AB ?CD+ADBC=AC(BE+DE)= AC BD ,得证。
4.过D作AQL AE , Ad CF,由S VADE= -S Y ABCD = S VDFC,可得:2AEgPQ=AEgPQ,由AE=FC2 2可得DQ=DG可得/ DPA=Z DPC(角平分线逆定理)。
经典难题(五)1. ( 1)顺时针旋转△ BPC 600,可得△ PBE为等边三角形。
既得PA+PB+PC=AP++PE+要使最小只要AP, PE EF在一条直线上,即如下图:可得最小L=(2)过P点作BC的平行线交AB,AC与点D, F。
由于/ APDN ATP=Z ADP推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;由(1)和(2)既得:2.顺时针旋转△ BPC 600,可得△ PBE为等边三角形。
既得PA+PB+PC=AP+PE+E要使最小只要AP, PE EF在一条直线上, 即如下图:可得最小PA+PB+PC=A F既得AF= 1+ (弓 + 1)2=)2+ 73= j 4 + =;于=亦3+1) _ 恵+花3.顺时针旋转△ ABP 90 °,可得如下图:4.在AB上找一点F,使/ BCF=60 , 连接EF, DG既得△ BGC为等边三角形,可得/ DCF=10 , / FCE=20 ,推出△ ABE^A ACF ,得到BE=CF , FG=GE 。
推出:△ FGE为等边三角形,可得/ AFE=8d ,既得:/ DFG=40 又BD=BC=BG 既得/ BGD=80,既得/ DGF=40 推得:DF=DG,得到:△ DFE^A DGE , 从而推得:/ FED=/ BED=30 。
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
