基础最终沉降量计算
向分层总和法计算基础中点最终沉降量案例

单向分层总和法计算基础中点最终沉降量已知柱下单独方形基础,基础底面尺寸为2.5×2.5m,埋深2m,作用于基础上(设计地面标高处)的轴向荷载N=1250kN,有关地基勘察资料与基础剖面详见下图。
试用单向分层总和法计算基础中点最终沉降量。
解:按单向分层总和法计算(1)计算地基土的自重应力。
z自基底标高起算。
当z=0m,σsD=19.5×2=39(kPa)z=1m,σsz1=39+19.5×1=58.5(kPa)z=2m,σ=58.5+20×1=78.5(kPa)sz1z=3m,σ=78.5+20×1=98.5(kPa)sz1z=4m,σ=98.5+(20-10)×1=108.5(kPa)sz1z=5m,σ=108.5+(20-10)×1=118.5(kPa)sz1z=6m,σ=118.5+18.5×1=137(kPa)sz1z=7m,σ=137+18.5×1=155.5(kPa)sz1=20kN/m3。
(2)基底压力计算。
基础底面以上,基础与填土的混合容重取γ(3)基底附加压力计算。
(4)基础中点下地基中竖向附加应力计算。
用角点法计算,L/B=1,σzi=4K si·p0,查附加应力系数表得K si。
(5)确定沉降计算深度z n考虑第③层土压缩性比第②层土大,经计算后确定z n=7m,见下表。
例题4-1计算表格1z (m)zB/2Ksσz(kPa)σsz(kPa)σz/σsz(%)zn(m)0 1 2 3 4 5 6 70.81.62.43.24.04.85.60.250 00.199 90.112 30.064 20.040 10.027 00.019 30.014 8201160.790.2951.6232.2421.7115.5211.903958.578.598.8108.5118.5137155.529.7118.3211.337.6按7m计(6)计算基础中点最终沉降量。
用分层总和法计算基础的最终沉降量

用分层总和法计算基础的最终沉降量分层总和法是一种常用于计算地基沉降量的方法,它将地基分为若干个层次,并对每个层次进行沉降计算,最终得到地基的总沉降量。
下面将详细介绍使用分层总和法计算基础的最终沉降量的步骤。
第一步:确定地基的分层结构首先需要了解地基的层次结构,通常采用土质分层的方式,将地基按照土层的差异进行划分。
根据地质勘探或者其他资料,可以得到地下丰富的土层信息。
地基的分层结构可以按照以下几种方式进行表示:1.无线性模型法:将地基分为若干个水平无限系统,每个系统具有不同的土层厚度和性质。
2.离散点法:将地基分为几个离散点,每个离散点的土层厚度和性质不同。
3.边界均匀法:将整个地基看作一个均质地层,即每个离散点的土层厚度和性质相同。
第二步:确定各层的沉降计算方法对于不同的土层,可以采用不同的沉降计算方法。
常用的沉降计算方法有:1.弹性计算法:适用于较短时间内的瞬时或短期荷载作用下的沉降计算。
该方法基于弹性力学理论,通过土层的应变-应力关系计算沉降量。
2.塑性计算法:适用于较长时间内的永久荷载作用下的沉降计算。
该方法基于土层的塑性变形特性,通过荷载作用下土体的塑性变形计算沉降量。
3.综合计算法:综合考虑了弹性和塑性因素,适用于荷载作用时间较长且变化较大的情况。
该方法常用的有双曲线法、双曲线加和法等。
第三步:计算各层的沉降量根据所选择的沉降计算方法,分别对每一层进行沉降计算。
具体步骤如下:1.弹性计算法:对于需要考虑土层弹性变形的情况,可以使用弹性模量、剪切模量等弹性参数计算每层的沉降量。
2.塑性计算法:对于需要考虑土层塑性变形的情况,可以使用塑性模量、剪切模量等塑性参数计算每层的沉降量。
3.综合计算法:根据采用的综合计算法的具体形式,可以使用不同的公式计算每层的沉降量。
将每层的沉降量进行累加,得到基础的最终沉降量。
具体步骤如下:1.按照地基的分层结构,将每层的沉降量累加得到地基的总沉降量。
2.由于地基沉降过程中存在时间效应,可以通过时间因子对每层的沉降量进行修正,得到考虑时间效应的沉降量。
常用的地基沉降计算方法汇总

6.3 常用的地基沉降计算方法这里所讲的地基沉降量是指地基最终沉降量,目前常用的计算方法有:弹性力学法、分层总和法、应力面积法和考虑应力历史影响的沉降计算法。
所谓最终沉降量是地基在荷载作用下沉降完全稳定后的沉降量,要达到这一沉降量的时间取决于地基排水条件。
对于砂土,施工结束后就可以完成;对于粘性土,少则几年,多则十几年、几十年乃至更长时间。
6.3.1 计算地基最终沉降量的弹性力学方法地基最终沉降量的弹性力学计算方法是以Boussinesq 课题的位移解为依据的。
在弹性半空间表面作用着一个竖向集中力P 时,见图6-5,表面位移w (x, y,o )就是地基表面的沉降量s :E r P s 21μπ-⋅= (6-8)式中 μ—地基土的泊松比;E —地基土的弹性模量(或变形模量E 0);r —为地基表面任意点到集中力P 作用点的距离,22y x r +=。
对于局部荷载下的地基沉降,则可利用上式,根据叠加原理求得。
如图6-6所示,设荷载面积A 内N (ξ,η)点处的分布荷载为p 0(ξ,η),则该点微面积上的分布荷载可为集中力P= p 0(ξ,η)d ξd η代替。
于是,地面上与N 点距离r =22)()(ηξ-+-y x 的M (x, y )点的沉降s (x, y ),可由式(6-8)积分求得:⎰⎰-+--=Ay x d d p E y x s 22002)()(),(1),(ηξηξηξμ (6-9)图6-5 集中力作用下地基表面的沉降曲线 图6-6 局部荷载下的地面沉降(a )任意荷载面;(b )矩形荷载面从式(6-9)可以看出,如果知道了应力分布就可以求得沉降;反过来,若沉降已知又可以反算出应力分布。
对均布矩形荷载p 0(ξ,η)= p 0=常数,其角点C 的沉降按上式积分的结果为:021bp E s c ωμ-= (6-10)式中 c ω—角点沉降影响系数,由下式确定:⎪⎪⎭⎫ ⎝⎛+++++=)1ln()11ln(122m m mm m c πω (6-11)式中 m=l/b 。
沉降量计算方法

例题4-2 计算表格z (m) L/B z/BEsi(kPa)(cm)(cm)0 0 0.2500 01.0 0.8 0.2346 0.2346 0.2346 4418 4.27 4.272.0 1.6 0.1939 0.3878 0.1532 6861 1.80 6.073.0 2.4 0.1578 0.4734 0.0856 7749 0.89 6.964.0 3.2 0.1310 0.5240 0.0506 6848 0.59 7.555.0 4.0 0.1114 0.5570 0.033 4393 0.60 8.156.0 4.8 0.0967 0.5802 0.0232 3147 0.59 8.747.0 5.6 0.0852 0.5964 0.0162 2304 0.57 9.317.6 6.08 0.0804 0.6110 0.0146 350000.03 9.34按规范确定受压层下限,z n=2.5(2.5-0.4ln2.5)=5.3m;由于下面土层仍软弱,在③层粘土底面以下取Δz厚度计算,根据表4-3的要求,取Δz=0.6m,则z n=7.6m,计算得厚度Δz的沉降量为0.03cm,满足要求。
查表4-2得沉降计算经验系数ψs=1.17。
那么,最终沉降量为:三、按粘性土的沉降机理计算沉降根据对粘性土地基在局部(基础)荷载作用下的实际变形特征的观察和分析,粘性土地基的沉降S可以认为是由机理不同的三部分沉降组成(图4-8),亦即:上式中的低值适用于较软的、高塑性有机土,高值适用于一般较硬的粘性土。
表4-4 沉降系数ω值受荷面形状L/B 中点矩形角点,圆形周边平均值刚性基础圆形— 1.00 0.64 0.85 0.79 正方形 1.00 1.12 0.56 0.95 0.88矩形1.52.03.04.06.08.010.030.050.0100.01.361.521.781.962.232.422.533.233.544.000.680.760.890.981.121.211.271.621.772.001.151.301.521.701.962.122.252.883.223.701.081.221.441.61——2.12———*平均值指柔性基础面积范围内各点瞬时沉降系数的平均值(二)固结沉降计算固结沉降是粘性土地基沉降的最主要的组成部分,可用分层总和法计算。
(整理)常用的地基沉降计算方法

6.3 常用的地基沉降计算方法这里所讲的地基沉降量是指地基最终沉降量,目前常用的计算方法有:弹性力学法、分层总和法、应力面积法和考虑应力历史影响的沉降计算法。
所谓最终沉降量是地基在荷载作用下沉降完全稳定后的沉降量,要达到这一沉降量的时间取决于地基排水条件。
对于砂土,施工结束后就可以完成;对于粘性土,少则几年,多则十几年、几十年乃至更长时间。
6.3.1 计算地基最终沉降量的弹性力学方法地基最终沉降量的弹性力学计算方法是以Boussinesq 课题的位移解为依据的。
在弹性半空间表面作用着一个竖向集中力P 时,见图6-5,表面位移w (x, y, o )就是地基表面的沉降量s :E r P s 21μπ-⋅=(6-8)式中 μ—地基土的泊松比;E —地基土的弹性模量(或变形模量E 0);r —为地基表面任意点到集中力P 作用点的距离,22y x r +=。
对于局部荷载下的地基沉降,则可利用上式,根据叠加原理求得。
如图6-6所示,设荷载面积A 内N (ξ,η)点处的分布荷载为p 0(ξ,η),则该点微面积上的分布荷载可为集中力P= p 0(ξ,η)d ξd η代替。
于是,地面上与N 点距离r =22)()(ηξ-+-y x 的M (x, y )点的沉降s (x, y ),可由式(6-8)积分求得:⎰⎰-+--=Ay x d d p E y x s 22002)()(),(1),(ηξηξηξμ (6-9)从式(6-9)可以看出,如果知道了应力分布就可以求得沉降;反过来,若沉降已知又图6-5 集中力作用下地基表面的沉降曲线图6-6 局部荷载下的地面沉降(a )任意荷载面;(b )矩形荷载面可以反算出应力分布。
对均布矩形荷载p 0(ξ,η)= p 0=常数,其角点C 的沉降按上式积分的结果为:021bp E s c ωμ-= (6-10)式中 c ω—角点沉降影响系数,由下式确定:⎪⎪⎭⎫ ⎝⎛+++++=)1ln()11ln(122m m mm m c πω (6-11)式中 m=l/b 。
地基最终沉降量的计算方法

地基最终沉降量的计算方法一、限制应力法限制应力法是一种常用的地基最终沉降量计算方法。
计算公式如下:S=Σ(dΔσ)其中,S为最终沉降量,dΔσ为不同深度处的限制应力差。
限制应力法的具体步骤如下:1.通过试验或现场勘测得到土壤层的力学参数,如土壤的自重γ、均匀固结压缩系数Cc、再固结压缩系数Cr等。
2.根据建筑物的设计荷载,计算出不同深度处的垂直应力Δσ。
3.根据试验或现场勘测得到的土壤层力学参数,计算出不同深度处的限制应力差dΔσ。
4.将不同深度处的限制应力差累加,得到最终沉降量S。
二、一维固结计算法一维固结计算法是一种根据土壤的固结性质计算地基最终沉降量的方法。
1.应力应变模型一维固结计算法通常采用本构模型,如Terzaghi's经典本构模型:Δe=ε'·HΔσ=γΔz其中,Δe为固结应变,ε'为固结应变系数,H为固结层的厚度,Δσ为固结层的应力差,γ为土壤的单位重量,Δz为固结层的厚度。
2.固结应变系数固结应变系数可以通过室内试验或现场试验得到,也可以通过经验公式估算。
根据不同的土壤类型和固结期限,选择相应的固结应变系数。
3.在垂直方向上,将所有固结层的固结应变累加,得到最终沉降量。
三、数值模拟法数值模拟法是一种利用计算机模拟土壤力学行为的方法,可以精确计算地基最终沉降量。
这种方法适用于复杂的地质条件和结构工程。
数值模拟法的具体步骤如下:1.建立土壤力学模型,包括土壤的性质、层次和边界条件等。
2.根据实测数据或试验数据,确定土壤力学参数,如剪切模量、压缩模量等。
3.根据建筑物的设计荷载、地质条件等,进行有限元分析或其他数值模拟,得到地基的最终沉降量。
数值模拟法的计算精度较高,但需要具备一定的专业知识和使用专业软件。
在实际工程中,一般会综合使用以上的方法进行地基最终沉降量的计算,以获得更准确的结果。
同时,也需要考虑到地质条件的不确定性和结构工程的变化,进行适当的修正和调整。
基础最终沉降量计算

基础最终沉降量计算基础最终沉降量是指由于地下开挖、施工等原因导致建筑物或地面沉降的总量。
计算基础最终沉降量是建筑设计中重要的一部分,旨在保证建筑物在施工后的使用过程中可以稳定地运行。
下面将介绍基础最终沉降量的计算方法。
解析法是通过一系列公式和假设来计算基础的沉降量。
采用解析法时,需要对土壤的物理力学性质和工程建筑的特点进行充分了解,以确定使用合适的公式和参数。
在计算过程中,需要考虑土壤的强度、压缩性和渗透性等因素,并进行合理的假设。
常见的解析方法有弹性半空间法、限制性应变法和弹塑性法等。
解析法的优点是计算结果准确,但需要大量的土壤力学参数和实际的工程经验。
数值法是通过数值模拟的方法来计算基础的沉降量。
采用数值法时,需要将土壤体系抽象为一个数学模型,并利用计算机程序进行模拟计算。
数值法的基本原理是以应力平衡和应变兼容条件为基础,通过有限元或有限差分等数值方法来求解土体的变形和沉降情况。
数值法的优点是可以更加全面地考虑土体的非线性、非均质性和不可排水性等复杂特性,但需要进行大量的计算和验证。
无论采用解析法还是数值法,基础最终沉降量的计算都需要一系列的步骤和工作。
首先,需要对施工过程中可能引起沉降的因素进行全面的分析,如地下开挖、地下水位变化等。
其次,需要对基础的形状和材料进行合理的假设和选择。
然后,根据所采用的计算方法,确定合适的公式和参数。
最后,将以上数据输入计算机程序或应用适当的公式进行计算,得出基础最终沉降量。
在进行基础最终沉降量的计算过程中,需要注意以下几个关键点。
首先,需要保证计算的准确性,尽可能地获得真实且可靠的土壤力学参数和工程数据。
其次,需要对计算结果进行合理的验证和校对,以确保计算的正确性。
最后,需要采用合适的沉降控制措施,如改变基础形式、加固土体等,以减小基础的最终沉降量。
总而言之,基础最终沉降量的计算是建筑设计中重要的一环。
通过合理的计算方法和步骤,可以得出基础最终沉降量的准确结果,为建筑物的设计和施工提供可靠的参考依据。
附录R:桩基础最终沉降量计算
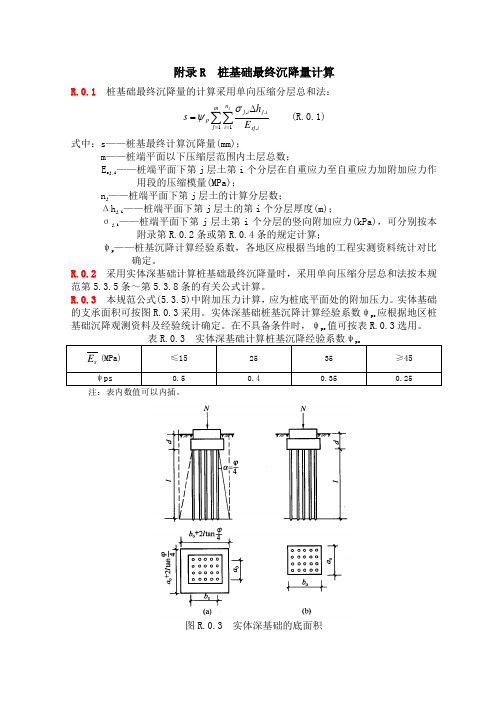
附录R 桩基础最终沉降量计算R.0.1 桩基础最终沉降量的计算采用单向压缩分层总和法:∑∑==∆=mj n i isj ij i j p jE h s 11,,,σψ (R.0.1)式中:s ——桩基最终计算沉降量(mm);m ——桩端平面以下压缩层范围内土层总数;E sj,i ——桩端平面下第j 层土第i 个分层在自重应力至自重应力加附加应力作用段的压缩模量(MPa);n j ——桩端平面下第j 层土的计算分层数;Δh j,i ——桩端平面下第j 层土的第i 个分层厚度(m);σj,i ——桩端平面下第j 层土第i 个分层的竖向附加应力(kPa),可分别按本附录第R.0.2条或第R.0.4条的规定计算;ψp ——桩基沉降计算经验系数,各地区应根据当地的工程实测资料统计对比确定。
R.0.2 采用实体深基础计算桩基础最终沉降量时,采用单向压缩分层总和法按本规范第5.3.5条~第5.3.8条的有关公式计算。
R.0.3 本规范公式(5.3.5)中附加压力计算,应为桩底平面处的附加压力。
实体基础的支承面积可按图R.0.3采用。
实体深基础桩基沉降计算经验系数ψps 应根据地区桩基础沉降观测资料及经验统计确定。
在不具备条件时,ψps 值可按表R.0.3选用。
注:表内数值可以内插。
图R.0.3 实体深基础的底面积R.0.4 采用明德林应力公式方法进行桩基础沉降计算时,应符合下列规定:1,采用明德林应力公式计算地基中的某点的竖向附加应力值时,可将各根桩在该点所产生的附加应力,逐根叠加按下式计算:()∑=+=nk k zs k zp i j 1,,,σσσ (R.0.4-1)式中:σzp,k ——第k 根桩的端阻力在深度z 处产生的应力(kPa):σzs,k ——第k 根桩的侧摩阻力在深度z 处产生的应力(kPa)。
2,第k 根桩的端阻力在深度z 处产生的应力可按下式计算;k p k zp I l Q,2,ασ=(R.0.4-2)式中:Q ——相应于作用的准永久组合时,轴心竖向力作用下单桩的附加荷载(kN);由桩端阻力Q p 和桩侧摩阻力Q s 共同承担,且Q p =αQ ,α是桩端阻力比;桩的端阻力假定为集中力,桩侧摩阻力可假定为沿桩身均匀分布和沿桩身线性增长分布两种形式组成,其值分别为βQ 和(1-α-β)Q ,如图R.0.4所示; l ——桩长(m);I p,k ——应力影响系数,可用对明德林应力公式进行积分的方式推导得出。
