初中几何经典培优题型(三角形)

合集下载

初中几何经典培优题型(三角形)

全等三角形辅助线找全等三角形的方法：（1）可以从结论出发，看要证明相等的两条线段（或角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形相等；（3）从条件和结论综合考虑，看它们能一同确定哪两个三角形全等；（4）若上述方法均不行，可考虑添加辅助线，构造全等三角形。

三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

常见辅助线的作法有以下几种：1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”．3)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．4)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”5)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答．常见辅助线写法：⑴过点A作BC的平行线AF交DE于F⑵过点A作BC的垂线，垂足为D⑶延长AB至C，使BC＝AC⑷在AB上截取AC，使AC＝DE⑸作∠ABC的平分线，交AC于D⑹取AB中点C，连接CD交EF于G点例1如图，AB ＝CD ＝1，∠AOC ＝60°，证明：AC ＋BD ≥1。

OC DAB例2(2007年北京中考）如图，已知△ABC⑴请你在BC 边上分别取两点D 、E （BC 的中点除外），连接AD 、AE ，写出使此图中只存在两对面积相等的三角形的相应条件，并表示出面积相等的三角形； ⑵请你根据使⑴成立的相应条件，证明AB ＋AC ＞AD ＋AE 。

新人教版八上第十一章《三角形》培优练习

第十一章三角形习题集第1课时三角形的边——三边关系姓名：___________☆知识导学1．若三角形的两边长分别为a，b(a＞b)，则第三边长x的取值范围是_______________________．2．三角形具有___________，四边形具有_____________．☆习题演练1．已知三角形ABC三边a、b、c满足（a-b）2+|b-c|=0，则△ABC的形状是（）A．钝角三角形B．直角三角形C．等边三角形D．以上都不对2．不能组成一个三角形的三条线段的长度是（）A．3，3，3 B．3，6，2 C．3，4，3 D．3，5，73．（2012•海南）一个三角形的两边长分别为3cm和7cm，则此三角形的第三边的长可能是（）A．3cm B．4cm C．7cm D．11cm4．（2013•南通）有3cm，6cm，8cm，9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为（）A．1 B．2 C．3 D．45．（2012•肇庆）等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（）A．16 B．18 C．20 D．16或206．下列说法中正确的是（）A．三角形的内角中至少有两个锐角B．三角形的内角中至少有两个钝角C．三角形的内角中至少有一个直角D．三角形的内角中至少有一个钝角7．图中有______个三角形，用符号表示这些三角形：__________________________．第7题图第13题图8．在△ABC中，已知两条边a=6，b=7，则第三条边c的取值范围是_________________．9．若三角形的两边长分别为3和5，且周长为奇数，则第三边可以是________（只填符合条件的一个即可）．10．（2012•哈尔滨）一个等腰三角形的两边分别为5和6，则这个等腰三角形的周长是________________．11．若三角形的两边长分别为3和5，则它的周长l的取值范围是________________．12．（提高题）△ABC的边长均为整数，且最大边的边长为7，那么这样的三角形共有________个．13．如图，木工师傅在做完门框后，为防止变形常常像图中所示那样钉上两条斜拉的木条（图中的AB，CD两根木条），这样做的数学道理是_____________________________．14．用一条长为20cm的铁丝围成一个等腰三角形能围成有一边长为6cm的等腰三角形吗？为什么？第2课时三角形的高、中线与角平分线姓名：___________ ☆知识导学如图，完成下面几何语言的表达：（1）∵AD是△ABC的高（已知）∴AD⊥BC，∠______=∠______=90º．（2）∵AE是△ABC的中线（已知）∴______=______=21______，______=2______=2______．（3）∵AF是△ABC的角平分线（已知）∴∠______=∠______=21∠______，∠______=2∠______=2∠______．☆习题演练1．如图所示的△ABC中，线段BE是三角形AC边上的高的是（）A．B．C．D．2．下列说法正确的是（）①三角形的三条中线都在三角形内部；②三角形的三条角平分线都在三角形内部；③三角形三条高都在三角形的内部．A．①②③B．①②C．②③D．①③3．如图，已知BD是△ABC的中线，AB=5，BC=3，△ABD和△BCD的周长的差是（）A．2 B．3 C．6 D．不能确定4．如图，△ABC的角平分线AD、中线BE相交于点O，则①AO是△ABE的角平分线；②BO是△ABD 的中线；③DE是△ADC的中线；④S△ADE= S△CDE，其中结论正确的有（）A．1个B．2个C．3个D．4个5．三角形中的角平分线、中线、高都是三条特殊的__________（填直线、射线、线段）．6．如图，在边长为1的正方形网格中，△ABC的顶点B的坐标是（1，-4），过点B作AC边上的高线，则垂足D点的坐标是________．AB CD EF第3题图第4题图第6题图8．如图，在△ABC中，已知CD是角平分线，∠A=70°，∠B=50°，求∠BCD的度数．9．如图，AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．10．如图，△ABC的边BC上的高为AD，且BC=9cm，AD=2cm，AB=6cm．（1）画出AB边上的高CE；（2）求CE的长．11．如图，D，E分别是△ABC的边BC和AB上的点，△ABD与△ACD的周长相等，△CAE与△CBE 的周长相等．设BC=a，AC=b，AB=c．求AE，BD的长（用含a，b，c的代数式表示）．AB CD第3课时三角形的内角姓名：___________☆知识导学如图，延长BC 至D ，过点C 作CE//AB ∵CE//AB∴∠ECD=∠______（_________________________________________） ∠ECA=∠______（_________________________________________）∵∠ECD+∠ECA+∠ACB=180°（___________________） ∴∠A+∠B+∠ACB=180°（等量代换）归纳：三角形的内角和等于____________． ☆习题演练 1．在△ABC 中，（1）若∠A=40°，∠C=35°，则∠B=_______，△ABC 是__________三角形．（2）若∠A=70°，∠B=∠C ，则∠B=_______°．（3）若∠A ∶∠B ∶∠C=1∶1∶2，则△ABC 是__________三角形．2．如图，AD 是△ABC 的角平分线，点O 在AD 上，且OE ⊥BC 于点E ，∠BAC=60°，∠C=80°，则∠EOD 的度数为（）A ．20°B ．30°C ．10°D ．15°第2题图第4题图第5题图 3．在△ABC 中，∠B 与∠C 的角平分线交于O 点，若∠A=50°，则∠BOC=（） A ．130° B ．50° C ．25° D ．115°4．将一副直角三角板如图所示放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（）A ．45°B ．60°C ．75°D ．85°5．（2012•梅州）如图，在折纸活动中，小明制作了一张△ABC 纸片，点D 、E 分别是边AB 、AC 上，将△ABC 沿着DE 折叠压平，A 与A′重合，若∠A=75°，则∠1+∠2=（） A ．150° B ．210° C ．105° D ．75°6．（2005•长沙）在△ABC 中，若∠A=38°36′，∠B=57°36′，则∠C=_________度． 7．已知△ABC 中，∠A=2（∠B+∠C ），则∠A 的度数为________度．8．（2013•上海）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内ABC DE9．如图，在△ABC 中，∠ABC=∠C ，BD 平分∠ABC ，∠A=36º，求∠BDC 的度数．10．如图，在△ABC 中，∠ABC=66°，∠ACB=54°，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，求∠ABE 、∠ACF 和∠BHC 的度数．11．如图，在△ABC 中，∠ACB=90°，CD 为AB 边上的高，BE 平分∠ABC ，分别交CD 、AC 于点F 、E ．求证：∠CFE=∠CEF ．12．如图，有一块直角三角板XYZ 放置在△ABC 上，恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B 、C ．△ABC 中，∠A=40°，求∠XBA+∠XCA 的度数． EFABCD13．如图，B岛在A岛的南偏西45°方向，C岛在A岛的南偏东15°方向，C岛在B岛的北偏东80°方向．从C岛看A，B两岛的视角∠ACB是多少度？14．如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，（1）若∠B=47°，∠C=73°，求∠DAE的度数．（2）若∠B=α，∠C=β，（α＜β），求∠DAE的度数（用含α、β的代数式表示）15．已知，如图，在△ABC中，AD平分∠BAC，DE，DF分别是△ADC的高和角平分线（∠C＞∠DAC），若∠B=80°，∠C=40°．（1）求∠DAE的度数；（2）试猜想∠EDF、∠C与∠DAC有何关系？并说明理由．第4课时三角形的外角姓名：___________☆知识导学1．如图，延长QR 至T ，∵∠PRQ+∠P+∠Q=180º（__________________________）又∵∠PRQ+∠PRT=180º（__________________________） ∴∠PRT =∠P+∠Q可得：三角形的一个外角等于__________________的两个内角的和．∵∠PRT =∠P+∠Q∴∠PRT ＞∠P ，∠PRT ＞∠Q可得：三角形的一个外角大于_______________________________．2．如图，∵∠1=∠XYZ+∠YZX ，∠2=_______+_______，∠3=_______+_______．∴∠1+∠2+∠3=（∠XYZ+∠YZX ）+（______+______）+（______+______） =2（_____+______+______）=2×_____°=_____°．归纳：三角形的外角和等于____________． ☆习题演练1．如图，（1）若∠A=50º，∠B=70º，则∠ACD=_________．（2）若∠A=40º，∠ACD =130º，则∠B =_________．（3）若∠B=80º，∠ACD =135º，则∠A =_________． 2．将一副三角板按如图所示摆放，图中∠α的度数是（） A ．75° B ．90° C ．105° D ．120°第2题图第3题图第4题图第5题图 3．一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（） A ．165° B ．120° C ．150° D ．135°4．如图，∠BDC=98°，∠C=38°，∠B=23°，∠A 的度数是（） A ．61° B ．60° C ．37° D ．39° 5．如图，∠1、∠2、∠3的大小关系为（）A ．∠2＞∠1＞∠3B ．∠1＞∠3＞∠2C ．∠3＞∠2＞∠1D ．∠1＞∠2＞∠3 6．如图，直线MA ∥NB ，∠A=70°，∠B=40°，则∠P=_______度．第6题图第7题图第8题图第9题图PQRTαABC DN A BM PEAB DCABCDXYZ 12 38．三角形三个内角之比为3∶4∶5，则它的三个外角之比为____________．9．如图，在△ABC 中，∠ACB=90°，∠A=50°，将其折叠，使点A 落在边BC 上E 处，折痕为CD ，则∠EDB=_________°．10．如图，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012=____________．11．如图，已知D 为△ABC 边BC 延长线一点，DF ⊥AB 于F ，且交AC 于E ，∠A=34°，∠D=42°．求∠ACD 的度数．12．一个零件的形状如图中阴影部分．按规定∠A 等于90°，∠B 、∠C 应分别等于29°和21°．（1）检验人员度量得∠BDC=141°，就断定这个零件不合格．你能说明理由吗？（2）你知道∠B 、∠C 、∠BDC 三个角之间有何关系吗？请写出你的结论．（不需说明理由）13．如图，在△ABC 中，∠1=100°，∠C=80°，∠2=21∠3，BE 平分∠ABC ．求∠4的度数．14．如图，已知∠BAD=∠CBE=∠ACF ，∠FDE=48°，∠DEF=64°，求△ABC 各内角的度数．15．如图，∠ACD 是△ABC 的外角，BE 平分∠ABC ，CE 平分∠ACD ，且BE 、CE 交于E 点．求证：∠E=21∠A ．16．如图①，A 、B 两点同时从原点O 出发，点A 以每秒m 个单位长度沿x 轴的正方向运动，点B 以每秒n 个单位长度沿y 轴正方向移动．（1）若|m+2n-5|+|2m-n|=0，试分别求出1秒后，A 、B 两点的坐标；（2）如图②，设∠4的邻补角和∠3的邻补角的平分线相交于点P ．试问：在点A 、B 运动的过程中，∠P 的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．17．已知：在△ABC 和△XYZ 中，∠A=40°，∠Y+∠Z=95°，将△XYZ 如图摆放，使得∠X 的两条边分别经过点B 和点C ．（1）当将△XYZ 如图1摆放时，则∠ABX+∠ACX=_______度；（2）当将△XYZ 如图2摆放时，请求出∠ABX+∠ACX 的度数，并说明理由；（3）能否将△XYZ 摆放到某个位置时，使得BX 、CX 同时平分∠ABC 和∠ACB ？为什么？ ABXA ZCX ZYB图1图24 A3OAx1 2 BB Px y y O 图2第5课时多边形的内角和、外角和姓名：___________☆知识导学1．过点A 作出下列多边形的对角线，各将多边形分成几个三角形？完成表格：归纳：（1）从n 边形的一个顶点出发可以引_______条对角线，把n 边形分成________个三角形．（2）n 边形的内角和等于___________．（其中n ≥3）2．从与每个内角相邻的两个外角中分别取1个相加，得到的和称为多边形的外角和．∠1＋∠2＋∠3=________°， ∠1＋∠2＋∠3＋∠=________°归纳：n 边形的外角和等于__________． ☆习题演练1．八边形的内角和是（）A ．540°B ．720°C ．900°D ．1080° 2．一个多边形的内角和等于720°，这个多边形的边数是（） A ．9 B ．8 C ．7 D ．6 3．下列各角不是多边形的内角和的是（）A ．1800°B ．540°C ．1900°D ．1440° 4．正六边形的每个内角都是（）A ．60°B ．80°C ．100°D ．120° 5．一个多边形的每个外角都等于72°，则这个多边形的边数为（） A ．5 B ．6 C ．7 D ．86．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（）A ．六边形B ．五边形C ．四边形D ．三角形 7．一个多边形的各个内角都等于108°，它是_______边形．8．一个多边形的内角和是1440°，则这个多边形是______边形，过其中一个顶点可以作_______条对角线，AAAA123 12349．如果一个多边形的边数增加一条，那么这个多边形的内角和增加_______，外角和__________．10．（2013•乐山）如图，在四边形ABCD中，∠A=45°．直线l与边AB，AD分别相交于点M，N，则∠1+∠2=_________．第9题图第10题图11．如图所示，将多边形分割成三角形、图（1）中可分割出2个三角形；图（2）中可分割出3个三角形；图（3）中可分割出4个三角形；由此你能猜测出，n边形可以分割出______个三角形．12．已知一个多边形的内角和是1440°，求这个多边形的边数．13．若两个多边形的边数之比为1∶2，内角和的度数之比为1∶3，求这两个多边形的边数．14．已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．15．如图，四边形ABCD中，如果∠A与∠C互为补角，求证：∠B与∠D也互为补角．16．如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值．17．如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数和．18．已知一个多边形的最小的一个内角是120°，比它稍大的一个内角是125°以后依次每一个内角比前一个内角多5°，且所有内角的和与最大的内角的度数之比是63∶8，试求这个多边形的边数．19．如图所示，小明从A点出发，沿直线前进8米后左转40°，再沿直线前进8米，又左转40°，照这样走下去，他第一次回到出发点A时，（1）整个行走路线是什么图形？（2）一共走了多少米？20．如图，BC⊥CD，∠1=∠2=∠3，∠4=70°，∠5=∠6．（1）求证：AC⊥BD；（2）求四边形ABCD各内角的度数；（3）若AC=8，BD=6，求四边形ABCD的面积．。

专题27.35 相似三角形几何模型-一线三等角(培优篇)(专项练习)-2022-2023学年九年级数

专题27.35 相似三角形几何模型-一线三等角（培优篇）（专项练习）一、单选题1．如图，∠A=∠B=90°，AB=7，AD=2，BC=3，在边AB 上取点P ，使得△PAD 与△PBC 相似，则这样的P 点共有（）A ．1个B ．2个C ．3个D ．4个2．如图，已知正方形ABCD 的边长为4，P 是BC 边上一动点（与B ，C 不重合）连接AP ，作PE ∠AP 交∠BCD 的外角平分线于E ，设BP =x ，∠PCE 的面积为y ，则y 与x 的函数关系式是（）A ．24y x x =-+B ．2122y x x =- C ．2122y x x =-+D ．24y x x =-3．如图，在平面直角坐标系中，直线12y x m =+不经过第四象限，且与x 轴，y 轴分别交于,A B 两点，点P 为OA 的中点，点C 在线段OB 上，其坐标为(0,2)，连结BP ，CP ，若BPC BAO =∠∠，那么m 的值为（）A ．B ．4C ．5D ．64．将矩形OABC 如图放置，O 为坐标原点，若点A （﹣1，2），点B 的纵坐标是72，则点C 的坐标是（）A．（4，2）B．（3，32）C．（3，94）D．（2，32）二、填空题5．如图，将等边三角形ABC折叠，使得点C落在边AB上的点D处，折痕为EF，点E，F分别在AC和BC上．若AC＝8，AD＝2，则CECF＝_______________．6．如图，矩形ABCD中，AD＝5，AB＝8，点E为DC上一个动点，把∠ADE沿AE折叠，若点D的对应点D′，连接D′B，以下结论中：∠D′B的最小值为3；∠当DE＝52时，∠ABD′是等腰三角形；∠当DE＝2是，∠ABD′是直角三角形；∠∠ABD′不可能是等腰直角三角形；其中正确的有_____．（填上你认为正确结论的序号）7．如图，在四边形ABCD中，∠A=∠B，点E为AB边的中点，∠DEC=∠A．有下列结论：∠DE平分∠AEC；∠CE平分∠DEB；∠DE平分∠ADC；∠EC平分∠BCD．其中正确的是_______________.（把所以正确结论的序号都填上）三、解答题8．如图，四边形ABCD 是正方形，点E 是BC 边上动点(不与,B C 重合)．连接,AE 过点E 作,EF AE ⊥交DC 于点F ．()1求证：ABE ECF ；()2连接AF ，试探究当点E 在BC 什么位置时，BAE EAF ∠=∠，请证明你的结论．9．如图，在ABC 中，点D E 、分别在边BC AC 、上，连接AD DE 、，且B ADEC ∠=∠=∠．（1）证明：BDA CED △∽△；（2）若45,2B BC ∠=︒=，当点D 在BC 上运动时（点D 不与B C 、重合），且ADE 是等腰三角形，求此时BD 的长．10．如图，已知∠ABC 是边长为12的正三角形，AD 是边BC 上的高线，CF 是外角ACE的平分线，点P是边BC上的一个动点（与点B，C不重合），∠APQ＝60°，射线PQ分别与边AC，射线CF交于点N，Q．（1）求证：∠ABP∠∠PCN；（2）不管点P运动到何处，在不添辅助线的情况下，除第（1）小题中的一对相似三角形外，请写出图中其它的所有相似三角形；（3）当点P从BD的中点运动到DC的中点时，点N都随着点P的运动而运动．在此过程中，试探究：能否求出点N运动的路径长？若能，请求出这个长度；若不能，请说明理由．11．如图，已知直线y=-34x+b与y轴相交于点B（0，3），与x轴交于点A，将△AOB沿y轴折叠，使点A落在x轴上的点C．（1）求点C的坐标；（2）设点P为线段CA上的一个动点，点P与点A、C不重合．联结PB．以点P为端点作射线PM交AB于点M，使∠BPM=∠BAC．∠求证：△PBC∽△MPA．∠是否存在点P，使△PBM为直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．12．如图∠,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.【试题再现】如图∠,在∠ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD∠DE于点D,BE∠DE于点E.求证:∠ADC∠∠CEB．【问题探究】在图∠中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB 上的相似点,并说明理由.【深入探究】如图∠,AD∠BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB∠AD于点A,交BC于点B．(1)请证明点P是四边形ABCD的边AB上的一个强相似点.(2)若AD=3,BC=5,试求AB的长.13．如图，四边形ABCD是矩形，点P是对角线AC上一动点(不与A、C重合)，连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，已知3AD =，4AB =.(1)求PEPB的值； (2)当PCE ∆是以PC 为底的等腰三角形时.请求出AP 的值;14．（1）【问题情境】八上《伴你学》第138页有这样一个问题：如图1，把一块三角板（,90AB BC ABC =∠=︒）放入一个“U ”形槽中，使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动，已知90D E ∠=∠=︒，在滑动过程中，你发现线段AD 与BE 有什么关系？试说明你的结论；（2）【变式探究】小明在解决完这个问题后，将其命名为“一线三等角”模型；如图2，在ABC ∆中，点D 、E 、F 分别在边BC 、AC 、AB 上，若B FDE C ∠=∠=∠，则这三个相等的角之间的联系又会使图形中出现其他的一些等角．请你写出其中的一组，并加以说理；（3）【拓展应用】如图3，在ABC ∆中，BA BC =，45B ∠=︒，点D 、F 分别是边BC 、AB 上的动点，且2AF BD =．以DF 为腰向右作等腰DEF ∆，使得DE DF =，45EDF ∠=︒，连接CE ．∠试判断线段DC 、BD 、BF 之间的数量关系，并说明理由；∠如图4，已知2AC =，点G 是AC 的中点，连接EA 、EG ，直接写出EA EG +的最小值．15．感知∠（1）数学课上，老师给出了一个模型∠如图1，∠BAD =∠ACB =∠AED =90°，由∠1+∠+2+∠BAD =180°，∠2+∠D +∠AED =180°，可得∠1=∠D ；又因为∠ACB =∠AED =90°，可得∠ABC ∠∠DAE ，进而得到BCAC= ．我们把这个数学模型称为“一线三等角”模型．应用∠（2）实战组受此模型的启发，将三等角变为非直角，如图2，在∠ABC 中，点D 在边BC 上，并且DA=DE ，∠B =∠ADE =∠C ．若BC =a ，AB=b ，求CE 的长度（用含a ，b 的代数式表示）．拓展∠（3）创新组突发奇想，将此模型迁移到平行四边形中，如图3，在平行四边形ABCD 中，E 为边BC 上的一点，F 为边AB 上的一点．若∠DEF =∠B ．求证∠AB ·FE =BE ·DE ．16．[模型建立](一线三等角)（1）如图1，等腰Rt ABC 中，90,,ACB CB CA ∠=︒=直线ED 经过点C ，过点A 作AD ED ⊥于点,D 过点B 作BE ED ⊥于点,E 求证：BEC CDA ≌；[模型应用]（2）如图2，直线14:43l y x =+与坐标轴交于点,A B 、直线2l 经过点A 与直线1l 垂直，求直线2l 的函数表达式．（3）如图3，平面直角坐标系内有一点()6,8,B -过点B 作BA x ⊥轴于点A BC y ⊥、轴于点,C 点P 是线段AB 上的动点，点D 是直线22y x =-+上的动点且在第四象限内．若CPD △成为等腰直角三角形，请直接写出点D 的坐标．参考答案1．C解：设AP=x ，则BP=7-x ，然后根据对应关系，分情况为：∠当∠ADP∠∠BCP 时，可得AD APBC BP =，即237x x =-，解得x=145，这时有一个P点；∠当∠ADP∠∠BPC 时，可得AD APBP BC =，即273x x =-，解得x=1或x=6，因此这样的点有两个；因此符合条件的P 点共有3个. 故选C【点拨】此题主要考查了相似三角形的性质，解题时，先根据相似三角形的性质，和相似三角形的对应关系，列出相应的比例式，求解即可.2．C解：过点E 作EH ∠BC 的延长线于点H ,因为∠APB+∠EPC=90°, ∠BAP+∠APB=90°,所以∠BAP=∠EPH ,因为∠B=∠H,所以∠ABP ∠∠PHE ,设EH =a ,因为∠ECH=45°,∠H=90°,所以CH =EH =a ,因为BP =x ,所以CP =4-x ,根据相似三角形的性质,可知AB PHBP EH=,即 44x ax a-+=,整理得:()()40x a x --=,解得()124,x x a ==不符合题意,所以y 与x 的函数关系式为:()211142222y PC EH x x x x =⨯⨯=⨯-⨯=-+,故选C.3．D 【分析】典型的“一线三等角”，构造相似三角形△AOB∠∠DPC,即可证明△PCD∠∠BPA ，由相似比求得边的相应关系，从而求解．解：在x 轴上找点D （4,0），连接CD.由12y x m =+可得A(-2m ，0 )，B(0，m )，直线12y x m =+不经过第四象限，所以m>0,所以OA=2m ，OB=m ；因为C 坐标为()0,2，点D （4,0）所以OC=2，OD=4, 因为12OB OC OA OD ==,∠AOB=∠DOC=90° ,所以△AOB∠∠DPC,所以∠CDO=∠BAO. 又因为BPC BAO ∠=∠，所以根据三角形内角和和平角定义可得：∠APB+∠1=∠APB+∠CPD所以∠1=∠CPD ，又因为∠CDO=∠BAO ，所以△PCD∠∠BPA ，所以AB APDP DC= , 因为点P 为OA 的中点，所以AP=OP=m ，PD=m+4，Rt △AOB 中，由勾股定理得m ，同理得AB APDP DC ==，解得m=6. 故选D.【点拨】本题考查一次函数综合题．需要掌握待定系数法求一次函数解析式，相似三角形的判定与性质，三角形面积的求法等知识点，4．B 【分析】首先构造直角三角形，利用相似三角形的判定与性质以及结合全等三角形的判定与性质得出CM ＝32=，MO ＝3，进而得出答案．解：如图，过点A 作AE ∠x 轴于点E ，过点B 作BF ∠x 轴于点F ，过点A 作AN ∠BF 于点N ，过点C 作CM ∠x 轴于点M ．∠∠EAO +∠AOE =90°，∠AOE +∠MOC =90°， ∠∠EAO =∠COM ，又∠∠AEO =∠CMO =90°，∠∠AEO ∠∠OMC ， ∠OE AE CM OM=， ∠∠BAN +∠OAN =90°，∠EAO +∠OAN =90°，∠∠BAN =∠EAO =∠COM ，在△ABN 和△OCM 中，BNA CMO BAN COM AB OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∠∠ABN ∠∠OCM （AAS ），∠BN =CM ．∠点A （﹣1，2），点B 的纵坐标是72， ∠BN 32=， ∠CM 32=， ∠1232OM =，∠MO =3，∠点C 的坐标是：（3，32）．故选：B ．【点拨】本题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识.构造直角三角形，正确得出CM 的长是解题的关键.5．75解：∠∠ABC 是等边三角形，∠∠A =∠B =∠C =60°，AB =AC =BC =8，∠AD =2，∠DB =6，由折叠的性质可知，∠EDF =∠C =60°，EC =ED ，FC =FD ，∠∠AED +∠EDA =120°，∠EDA +∠BDF =120°，∠∠AED =∠BDF ，∠∠AED ∠∠BDF ，∠DF DE =BD DF BF AE AD DE ++++=BD BC AD AC ++=1410=75，∠CF CE =DF DE =75，故答案为75．点睛：本题考查的是翻转变换的性质、相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理、翻转变换的性质是解题的关键．6．∠∠∠【分析】当D′落在线段AB 上时，D′B 的值最小，此时D′B ＝AB ﹣AD ＝3，得出∠正确；过D′作MN∠AB 交AB 于点N ，交CD 于点M ，设AN ＝x ，则EM ＝x ﹣2.5，证出∠ED′M ＝∠D′AN ，因此△EMD′∠∠D′NA ，得出对应边成比例ED EM AD D N ='''，求出x ＝4，得出AN ＝BN ，因此AD′＝D′B ，得出∠正确；当DE ＝2时，假设△ABD′是直角三角形，则E 、D′、B 在一条直线上，作EF∠AB 于点F ，由勾股定理求出D′B 、EB ，得出∠不正确；当AD′＝D′B 时，由勾股定理的逆定理得出△ABD′不是直角三角形，当△ABD′是直角三角形时，由勾股定理求出D′B ，得出AD′≠D′B ，因此△ABD′不可能是等腰直角三角形，得出∠正确．解：当D′落在线段AB 上时，D′B 的值最小，如图1所示：此时D′B ＝AB ﹣AD ＝8﹣5＝3，∠∠正确；过D′作MN∠AB 交AB 于点N ，交CD 于点M ，如图2所示：设AN ＝x ，则EM ＝x ﹣2.5，∠∠AD′N ＝∠DAD′，∠ED′M ＝180°﹣∠AD′E ﹣∠AD′N ＝180°﹣90°﹣∠AD′N ＝90°﹣∠AD′N ，∠∠ED′M ＝90°﹣∠DAD′，∠∠D′AN ＝90°﹣∠DAD′，∠∠ED′M ＝∠D′AN ，∠MN∠AB ，∠∠EMD′＝∠AND′，∠∠EMD′∠∠D′NA ， ∠ED EM AD D N='''，即，2.55=解得：x ＝4，∠AN ＝BN ，∠AD′＝D′B ，即△ABD′是等腰三角形，∠∠正确；当DE＝2时，假设△ABD′是直角三角形，则E、D′、B在一条直线上，作EF∠AB于点F，如图3所示：D′B==∠2∠∠不正确；当AD′＝D′B时，52+52≠82，∠∠ABD′不是直角三角形，当△ABD′是直角三角形时，D′B=∠AD′≠D′B，∠∠ABD′不可能是等腰直角三角形，∠∠正确；故答案为∠∠∠．【点拨】本题考查了矩形的性质、翻折变换的性质、勾股定理、等腰三角形的判定、勾股定理的逆定理、等腰直角三角形的判定等知识；本题综合性强，有一定难度，熟练掌握矩形的性质和翻折变换的性质是解决问题的关键．7．∠∠解：试题分析：在∠ADE中，∠ADE+∠AED+∠A=180°，又∠AED+∠DEC+∠BEC=180°，可得∠ADE+∠AED+∠A =∠AED+∠DEC+∠BEC，由∠A=∠DEC，可得∠ADE=∠BEC，又∠A=∠B，根据两角对应相等的两三角形相似，可得∠ADE∠∠BEC，可得DE AEEC BC=，又AE=BE，得到DE BEEC BC=，又∠DEC=∠B，根据两边对应成比例且夹角相等的两三角形相似，可知∠CDE∠∠CEB，然后根据相似三角形的对应角相等，可得∠DCE=∠BCE，因此EC平分∠BCD，即∠成立；同理∠ADE∠∠EDC，因此DE平分∠ADC；即∠成立；而∠DE平分∠AEC 不一定成立；∠CE平分∠DEB不一定成立．故答案为：∠∠.8．（1）证明见分析；（2）点E在BC中点位置时，BAE EAF∠=∠，证明见分析．【分析】（1）先根据正方形的性质可得90B C∠=∠=︒，再根据直角三角形的性质、角的和差可得BAE CEF∠=∠，然后根据相似三角形的判定即可得证；（2）如图（见分析），先根据正方形的性质、平行线的性质可得,B ECH BAE H∠=∠∠=∠，再根据三角形全等的判定定理与性质可得AE HE=，然后根据等腰三角形的判定与性质可得EAF H∠=∠，最后根据等量代换即可得．解：（1）四边形ABCD是正方形，90B C∴∠=∠=︒，90BAE BEA∴∠+∠=︒，EF AE⊥，90AEF∴∠=︒，90BEA CEF ∴∠+∠=︒，BAE CEF ∴∠=∠，在ABE △和ECF △中，B C BAE CEF ∠=∠⎧⎨∠=∠⎩， ABE ECF ∴；（2）点E 在BC 中点位置时，BAE EAF ∠=∠，证明如下：如图，连接AF ，延长AE 于DC 的延长线相交于点H ， E 为BC 中点，BE CE ∴=，四边形ABCD 是正方形，//AB DH ∴，,B ECH BAE H ∴∠=∠∠=∠，在ABE △和HCE 中，BAE H B ECH BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE HCE AAS ∴≅，AE HE ∴=，EF AH ⊥，AFH ∴是等腰三角形，EAF H ∴∠=∠，BAE EAF ∴∠=∠，故当点E 在BC 中点位置时，BAE EAF ∠=∠．【点拨】本题考查了相似三角形的判定、正方形的性质、三角形全等的判定定理与性质、等腰三角形的判定与性质等知识点，较难的是题（2），通过作辅助线，构造全等三角形和等腰三角形是解题关键．9．(1)理由见详解；（2）2BD =1，理由见详解．【分析】（1）根据题目已知条件易得：180ADE ADB EDC ∠+∠+∠=︒，180B ADB DAB ∠+∠+∠=︒，所以得到DAB EDC ∠=∠，问题得证．（2）由题意易得ABC 是等腰直角三角形，所以90BAC ∠=︒，当ADE 是等腰三角形时，根据分类讨论有三种情况：∠AD=AE ，∠AD=DE ，∠AE=DE ；因为点D 不与B C 、重合，所以第一种情况不符合，其他两种情况根据等腰三角形的性质“等边对等角”及45B ADE ∠=∠=︒，求出问题即可．解：（1）如图可知：180ADE ADB EDC ∠+∠+∠=︒在ABD △中，∴ 180B ADB DAB ∠+∠+∠=︒ 又B ADE C ∠=∠=∠∴EDC DAB ∠=∠∴BDA CED △∽△．（2）B ADE C ∠=∠=∠，45B ∠=︒∴ABC 是等腰直角三角形∴90BAC ∠=︒BC=2，∴AB=AC=2∠当AD=AE 时，∴ADE AED ∠=∠45B ∠=︒，∴=45B ADE AED ∠=∠∠=︒∴90DAE ∠=︒∴90DAE BAC ∠=∠=︒点D 在BC 上运动时（点D 不与B C 、重合）,点E 在AC 上∴此情况不符合题意．∠当AD=DE 时，∴DAE DEA ∠=∠∴由（1）结论可知：BDA CED ≌∴∴2BD =∠当AE=DE 时，45ADE DAE ∠=∠=︒∴AED 是等腰直角三角形45B ∠=︒，∴==45B C DAE ∠∠∠=︒∴90ADC ∠=︒，即AD BC ⊥ ∴1=12BD BC =．综上所诉：2BD =1．【点拨】本题主要考查相似三角形的判定及等腰三角形的存在性问题，关键是利用“K”型相似模型及根据“等边对等角”、等腰直角三角形的性质得到线段的等量关系，进而求解问题．10．（1）详见分析；（2）△ABD ∠∠ACD ；△APN ∠∠ACP ；△APN ∠∠QCN ；△ACP ∠∠QCN ；（3）1.5．【分析】（1）根据等边三角形性质得到∠ABP ＝∠PCN ＝60°，利用角的和差证明∠BAP ＝∠CPN ，根据相似三角形的判定定理证明结论；（2）因为△ABC 是正三角形，AD 是边BC 上的高线，由三线合一可证△ABD ∠∠ACD ；因为∠APN=∠ACP=60°，∠PAN=∠CAP,所以△APN ∠∠ACP ；因为∠APN=∠NCQ=60°，∠PNA=∠CNQ,所以△APN∠∠QCN ；因为△APN ∠∠ACP ，△APN∠∠QCN ，所以△ACP ∠∠QCN ；（3）当点P 在BD 的中点运动到DC 的中点时，利用相似三角形性质，设PB ＝x ，CN ＝y ，则3≤x ≤9，由第（1）题利用相似三角形性质可得：1212y x x -=，解得2112y x x =-+，又利用函数图象可知：当x ＝3或9时，y ＝94，当x ＝6时，y 最大＝3，所以点N 运动的路径长为：（3－94）×2＝1.5．解：（1）在正三角形ABC 中，∠ABP ＝∠PCN ＝60°，∠∠BAP +∠BP A ＝120°，又∠∠APQ ＝60°，∠∠CPN +∠BP A ＝120°， ∠∠BAP ＝∠CPN ，∠∠ABP ∠∠PCN ；（2）△ABD ∠∠ACD ；△APN ∠∠ACP ；△APN ∠∠QCN ；△ACP ∠∠QCN ；理由：∠△ABC 是正三角形，AD ∠BC ，由三线合一可证△ABD ∠∠ACD ；∠∠APN=∠ACP=60°，∠PAN=∠CAP ，∠△APN ∠∠ACP ；∠∠APN=∠NCQ=60°，∠PNA=∠CNQ,∠△APN∠∠QCN ；∠△APN ∠∠ACP ，△APN∠∠QCN ，∠△ACP ∠∠QCN ；（3）能，设PB ＝x ，CN ＝y ，由第（1）题可得：1212y x x -=， ∠2112y x x =-+，又3≤x ≤9，利用函数图象可知：当x ＝3或9时，y ＝94，当x ＝6时，y 最大＝3； ∠点N 运动的路径长为：（3－94）×2＝1.5．【点拨】本题考查的是相似三角形的判定和性质、正三角形的性质，掌握相关的性质定理、灵活运用所学知识是解题的关键．11．（1）C （-4，0）；（2）∠证明见分析，∠存在．使△PBM 为直角三角形的点P 有两个P1（-94，0），P2（0，0）．【分析】（1）根据B 点坐标求得直线解析式，再求得A 点坐标，然后根据A 与C 关于y 轴对称，据此即可确定C 的坐标；（2）∠根据点C 与点A 关于y 轴对称，即可得到BC=BA ，则∠BCP=∠MAP ，再根据三角形的外角的性质即可证得∠PMA=∠BPC ，从而证得两个三角形相似；∠首先求得B 的坐标，当∠PBM=90°时，则有∠BPO∠∠ABO ，根据相似三角形的对应边的比相等，即可求得PO 的长，求得P 的坐标；当∠PMB=90°时，则∠PMA═90°时，BP∠AC ，则此时点P 与点O 重合．则P 的坐标可以求得．（1）解：∠直线y=-34x+b与y轴相交于点B（0，3），∠b=3，∠直线的解析式为y=-34x+3，令y=0，得到x=4，∠A（4，0），∠点C与点A关于y轴对称，∠C（-4，0）；（2）∠证明：∠∠BPM=∠BAC，且∠PMA=∠BPM+∠PBM，∠BPC=∠BAC+∠PBM，∠∠PMA=∠BPC，又∠点C与点A关于y轴对称，且∠BPM=∠BAC，∠∠BCP=∠MAP，∠∠PBC∠∠MPA；∠解：存在．由题意：A（4，0），B（0，3），C（-4，0）当∠PBM=90°时，则有∠BPO∠∠ABO，∠POBO=BOAO，即PO3=34，∠PO=94，即：P1（-94，0）．当∠PMB=90°时，则∠PMA═90°，∠∠PAM+∠MPA=90°，∠∠BPM=∠BAC，∠∠BPM+∠APM=90°，∠BP∠AC．∠过点B只有一条直线与AC垂直，∠此时点P与点O重合，即：符合条件的点P2的坐标为：P2（0，0）．∠使∠PBM为直角三角形的点P有两个P1（-94，0），P2（0，0）．【点拨】本题是属于一次函数综合题，考查了相似三角形的判定和性质、待定系数法、一次函数的应用等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．12．【试题再现】见分析；【问题探究】点E是四边形ABCD的边AB上的相似点. 理由见分析；【深入探究】(1) 点P是四边形ABCD的边AB上的一个强相似点，见分析；(2)解：试题分析：【试题再现】易证∠BCE=∠CAD，又∠ADC=∠CEB=90°，故得∠ADC∠∠CEB.【问题探究】要证明点E是四边形ABCD的AB边上的相似点，只要证明有一组三角形相似就行，很容易证明∠ADE∠∠BEC，所以问题得解．【深入探究】（1）分别证明∠ADP∠∠PDC,∠BPC∠∠PDC,从而∠ADP∠∠PDC∠∠BPC,故点P是四边形ABCD的边AB上的一个强相似点.（2）过点P作PE∠DC于点E,过点D作DF∠BC于点F,则四边形ABFD是矩形,通过证明∠ADP∠∠EDP和∠CBP∠∠CEP得DC =8，再求出CF=2，在Rt∠CDF中,由勾股定理,得解：【试题再现】∠∠ACB=90°,∠∠ACD+∠BCE=90°,∠AD∠DE,∠∠ACD+∠CAD=90°,∠∠BCE=∠CAD,∠∠ADC=∠CEB=90°,∠∠ADC∠∠CEB.【问题探究】点E是四边形ABCD的边AB上的相似点.理由如下:∠∠DEC=40°,∠∠DEA+∠CEB=140°.∠∠A=40°,∠∠ADE+∠AED=140°,∠∠ADE=∠CEB,又∠∠A=∠B,∠∠ADE∠∠BEC,∠点E 是四边形ABCD 的边AB 上的相似点.【深入探究】(1)∠AD∠BC,∠∠ADC+∠BCD=180°,∠DP 平分∠ADC,CP 平分∠BCD, ∠∠CDP+∠DCP=12(∠ADC+∠BCD)=90°, ∠DA∠AB,DA∠BC,∠CB∠AB,∠∠DPC=∠A=∠B=90°,∠∠ADP=∠CDP,∠∠ADP∠∠PDC,同理∠BPC∠∠PDC,∠∠ADP∠∠PDC∠∠BPC,即点P 是四边形ABCD 的边AB 上的一个强相似点.(2)过点P 作PE∠DC 于点E,过点D 作DF∠BC 于点F,则四边形ABFD 是矩形,∠DF=AB,在∠ADP 与∠EDP 中,ADP EDP,DAP DEP 90,DP DP,∠∠∠∠=⎧⎪==︒⎨⎪=⎩∠∠ADP∠∠EDP,∠AD=DE,同理∠CBP∠∠CEP,∠BC=EC,∠DC=AD+BC=8.在Rt∠CDF 中,CF=BC -BF=BC -AD=5-3=2,由勾股定理,得13．(1)34;(2)75. 分析：（1）如图，过点P 作CD 的垂线，分别交AB 、CD 于M 、N ，易证△PNE∠∠BMP,从而证得PE 3tan PB 4PN PN ACD BM CN ===∠= （2）首先证明BP=BC,再过点B 作BF 垂直AC 得PF=CF,由cos ,BC FC FCB AC BC ∠==得9,5FC PF == 根据AP=AC -PC 即可求解.解：（1）P CD AB CD M N 过点作的垂线，分别交、于点、，90PNE ∴∠︒＝．ABCD 四边形是矩形，//90,AB CD ABC BCD ，∴∠=∠=︒BCMN 四边形是矩形，∴90,BMP BM CN ∴∠=︒=90,90,PNE BPE ∠=︒∠=︒90,90,NPE PCN MPB MPE ∴∠+∠=︒∠+∠=︒,90PEN MPB PNE BMP ∴∠=∠∠=∠=︒又~,PNE BMP ∴∆∆PE 3tan .PB 4PN PN ACD BM CN ∴===∠= 34PE PB ∴的值为（2）.PE CE EPC ECP =∠=∠当，则 ABCD 四边形是矩形，90,BCD ∴∠=︒,PE PB ⊥90.BPE ∴∠=︒BPC BCP ∴∠=∠.BP BC ∴=B BF AC F PF CF.⊥=过点作于点，则cos ,BC FC FCB AC BC∠== 3,53FC ∴= 9,5FC ∴= 9.5PF ∴= 187555AP AC PC ∴=-=-= 【点拨】本题考查的是矩形的性质、相似三角形的判定和性质以及解直角三角形，正确作出辅助线、灵活运用相关的定理是解题的关键．14．【小问1】AD BE =，说明见分析【小问2】BED FDC ∠=∠，EDB DFC ∠=∠；说理见分析【小问3】∠BD BF CD +=，理由见分析；∠AE EG +【分析】（1）【问题情境】证明()ABD BCE AAS ∆≅∆，即可求解．（2）【变式探究】利用等量代换即可求解．（3）【拓展应用】∠等量代换即可求解；∠在CD 上截取DM BF =，连接EM ，作点G 关于CE 的对称点N ，连接CN ，AN ，先证明()BDF MED SAS ∆≅∆，得到EM ＝CM ，在求出22.5ECM MEC ∠=∠=︒，即可确定E 点在射线CE 上运动，当A 、E 、N 三点共线时，EA ＋EG 的值最小，最小值为AN ，在Rt ANC 中求出AN 即可．解：（1）【问题情境】AD BE =，理由如下：90ABC ∠=︒，90ABD CBE ∴∠+∠=︒，90BAD ABD ∠+∠=︒，BAD CBE ∴∠=∠，AB BC =，()ABD BCE AAS ∴∆≅∆，AD BE ∴=；（2）【变式探究】BED FDC ∠=∠，EDB DFC ∠=∠；理由如下：B FDEC ∠=∠=∠，180EDB BED EDB FDC FDC DFC EDF ∴∠+∠=∠+∠=∠+∠=︒-∠，BED FDC ∴∠=∠，EDB DFC ∠=∠；（3）【拓展应用】∠AB BC =，AF BF BD CD ∴+=+，2AF BD =，2BD BF BD CD ∴+=+，BD BF CD ∴+=；∠在CD 上截取DM BF =，连接EM ，作点G 关于CE 的对称点N ，连接CN ，AN ， 45B ∠=︒，45EDF ∠=︒，BFD EDM ∴∠=∠，DF DE =，()BDF MED SAS ∴∆≅∆，BD EM ∴=，EM BD =，45B DME ∠=∠=︒，CD BD BF =+，CM BD ∴=，EM CM ∴=，MCE MEC ∴∠=∠，45EMD ∠=︒，22.5ECM MEC ∴∠=∠=︒，E ∴点在射线CE 上运动， G 点与N 的关于CE 对称，EG EN∴=，EA EG EA EN AN∴+=+，∴当A、E、N三点共线时，EA EG+的值最小，最小值为AN，45B∠=︒，AB BC=，67.5ACB∴∠=︒，45ACE∴∠=︒，由对称性可知，ACE ECN∠=∠，90ACN∴∠=︒，点G是AC的中点，2AC=，1CG∴=，1CN∴=，在Rt ANC中，ANAE EG∴+【点拨】本题是三角形的综合题，熟练掌握三角形全等的判定及性质，轴对称求最短距离的方法是解题的关键．15．（1）AEDE；（2）CE=a-b；（3）见分析【分析】（1）根据相似三角形的性质即可求得结果；（2）由已知易证∠ADB∠∠DEC，从而由全等三角形的性质即可求得CE的长度；（3）作CG//FE交DE于点G，易证得∠FBE∠∠EGC，从而可得BEFE=CGEC；可证得∠DGC∠∠DCE，可得DCDE=CGEC，即有BEFE=DCDE，再由AB=CD即可得要证的结论．解：（1）∠∠ABC∠∠DAE∠BC AE AC DE故答案为：AE DE；（2）∠∠B=∠ADE=∠C，∠ADC=∠B+∠BAD，∠ADC=∠ADE+∠EDC，∠∠EDC=∠BAD又∠DA=DE∠∠ADB∠∠DEC∠EC=BD，AB=DC=b∠BD=BC-DC=a-b．即：CE=a-b．（3）∠∠DEF=∠B∠∠BFE+∠BEF=∠BEF+∠DEC∠∠BFE=∠DEC．作CG//FE交DE于点G，如图3．∠∠DEF=∠EGC∠∠B=∠EGC∠∠FBE∠∠EGC∠BEFE=CGEC∠四边形ABCD是平行四边形∠∠B+∠BCD=180°∠∠EGC+∠DGC=180°，且∠B=∠EGC ∠∠DGC=∠BCD又∠∠EDC=∠CDG ∠∠DGC∠∠DCE∠DCDE=CGEC∠BEFE=DCDE∠DC·FE=BE·DE又∠四边形ABCD是平行四边形∠AB=DC∠AB·FE=BE·DE【点拨】本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，平行四边形的性质等知识，（3）问中作辅助线是难点，灵活运用这些知识是重点．16．（1）答案见分析；（2）直线l2的函数表达式为：y＝3944x--；（3）点D的坐标为2238,33⎛⎫-⎪⎝⎭或(8，﹣14)或1626,33⎛⎫-⎪⎝⎭【分析】（1）由垂直的定义得∠ADC=∠CEB=90°，平角的定义和同角的余角的相等求出∠DAC=∠ECB，最后由角角边证明：∠BEC∠∠CDA；（2）如图2，仿照（1）作辅助线，构建三角形全等，同理证明∠BOA∠∠AED，求出点D的坐标为（-7，3），最后利用待定系数法可得直线l2的函数表达式；（3）分三种情况：∠如图3，∠CPD=90°时，∠如图4，∠PCD=90°，此时P与A重合，∠如图5，∠CDP=90°，分别作辅助线，构建三角形全等，根据全等三角形的性质可得点D 的坐标．解：（1）如图1所示：∠AD∠ED，BE∠ED，∠∠ADC=∠CEB=90°，又∠∠ACD+∠ACB+∠BEC=180°，∠ACB=90°，∠∠ACD+∠BEC=90°，又∠∠ACD+∠DAC=90°，∠∠DAC=∠ECB ，在∠CDA 和∠BEC 中，ADC CEB DAC ECB AC BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∠∠CDA∠∠BEC （AAS ）；（2）如图2，在l 2上取D 点，使AD=AB ，过D 点作DE∠OA ，垂足为E ，∠直线y=43x+4与坐标轴交于点A 、B ， ∠A （-3，0），B （0，4），∠OA=3，OB=4，由（1）得∠BOA∠∠AED ，∠DE=OA=3，AE=OB=4，∠OE=7，∠D （-7，3）设l 2的解析式为y=kx+b ，∠3703k b k b-+⎧⎨-+⎩＝＝解得3494k b ⎧-⎪⎪⎨⎪-⎪⎩＝＝ ∠直线l 2的函数表达式为：y ＝3944x --；（3）点D 的坐标为223833⎛⎫- ⎪⎝⎭，或（8，﹣14）或162633⎛⎫- ⎪⎝⎭，分三种情况：∠如图3，∠CPD=90°时，过P作MH∠x轴，过D作DH∠y轴，MH和DH交于H，∠∠CPD是等腰直角三角形，∠CPD=90°，∠CP=PD，同理得∠CMP∠∠PHD（AAS），∠DH=PM=6，PH=CM，设PH=a，则D（6+a，a-8-6），∠点D是直线y=-2x+2上的动点且在第四象限内．∠a-8-6=-2（6+a）+2，解得：a=43，∠D（2238,33）；∠如图4，∠PCD=90°，此时P与A重合，过D作DE∠y轴于E，∠∠CPD是等腰直角三角形，同理得∠AOC∠∠CED，∠OA=CE=6，OC=DE=8，∠D（8，-14）；∠如图5，∠CDP=90°，过点D作MQ∠x轴，延长AB交MQ于Q，则∠Q=∠DMC=90°，∠∠CDP是等腰直角三角形，同理得∠PQD∠∠DMC，∠PQ=DM，DQ=CM，设CM=b，则DM=6-b，AQ=8+b，∠D（6-b，-8-b），∠点D是直线y=-2x+2上的动点且在第四象限内，∠-8-b=-2（6-b）+2，解得：b=23，∠D（1626,33-）；综上，点D的坐标为223833⎛⎫-⎪⎝⎭，或（8，﹣14）或162633⎛⎫-⎪⎝⎭，【点拨】本题是一次函数和四边形的综合题，综合考查了矩形的性质，全等三角形的性质和判定，一次函数上点的坐标的特点等知识点，重点是运用类比的方法，作辅助线，构建全等三角形依次解决问题．。

初三数学-相似三角形培优练习题(含答案)

(3题图）EDC B ADBCA NM O相似三角形练习题1、如图1，当四边形PABN 的周长最小时，a = ．2、如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（）A ．只有1个B ．可以有2个C ．有2个以上但有限D ．有无数个3、如图3，等腰ABC ∆中，底边BC=a ,A ∠=036,ABC ∠的平分线交AC 于D ，BCD ∠的平分线交BD 于E ，设512k =，则DE=( ) A 、2K a B 、3K a C 、2akD 、3a k4、如图4，菱形ABCD 中，对角线AC 、BD 相交于点O ，M 、N 分别是边AB 、AD 的中点，连接OM 、ON 、MN ，则下列叙述正确的是（）A ．△AOM 和△AON 都是等边三角形B ．四边形MBON 和四边形MODN 都是菱形C ．四边形AMON 与四边形ABCD 是位似图形 D ．四边形MBCO 和四边形NDCO 都是等腰梯形5、如图5将放置于平面直角坐标系中的三角板AOB 绕O 点顺时针旋转90°得△A′OB′．已知∠AOB =30°，∠B =90°，AB =1，则B′点的坐标为( ) A ．33()22 B ．33(22, C ．13(22, D ．31()226、如图小正方形的边长均为1，则下列图中的三角形（阴影部分）与ABC △相似的是（）y xP (a ，0) N (a +2，0)A (1，-3)（1题图） B (4，-1)O图 4 图 5FED CBA E FADCB7、如图7，梯形ABCD 中，AD BC ∥，点E 在BC 上，AE BE =，点F 是CD 的中点，且AF AB ⊥，若2.746AD AF AB ===，，，则CE 的长为 A ．2231 C. 2.5 D. 2.3(7题图)8、如图8，在ABC △中，AB AC =，点E F 、分别在AB 和AC 上，CE 与BF 相交于点D ，若AE CF D =，为BF 的中点，AE AF :的值为___________.9、如图9，已知ABC ∆，延长BC 到D ，使CD=BC 取AB 的中点F,连接FD 交AC 于点E 。

初一下学期三角形培优专题训练

初一下学期三角形培优专题训练专题一：8字形图型1. 如图所示•求 / A+Z B+Z C+Z D+Z E的大小。

3 .如图：Z A+Z B+Z C+Z D+Z E+Z F 等于（）A、180° B 、360 ° C 、270 ° D 、540°A+Z B+Z C+Z D+Z E+Z F 的大小.4.已知，如图, A B C D E F的度数为B C D E F G n度DE是Z CDB的平分线，ZA1 + Z2 +Z3 +Z 4+Z 5+Z 6+Z 7=6. 如图，7. 如图Z&如图AE是Z CAB的平分线,90 ，则n=C=40°,Z E=35° .求Z B的度数.ECEB2•如图是一个六角星，其中AOE60 , A5.如图所示.求Z专题二：燕尾形图型1. （2010?帛州）如图，/ BDC=98,A. 61°B. 60°2. 如图所示，已知/ 1=20°,/ 2=25°A. 60°B. 70 °3. 如图，已知DABC边BC延长线上一点，DF丄AB于F交AC于E, / A=35° ,? / D=42°求/ ACD的度数.4. 如图，直线DE交厶ABC的边AB、AC于D E,/ACB= 74°,/ AED= 48°，则/ BDF的度数是—5.知：如图，点E在AC上，点F在AB上, BE CF交于点O且/ C—/B= 20°,/ EO F/ A= 70°，求/ C的度数.6.下图，BE是/ ABD的角平分线，CF是/ ACD的角平分线，BE与CF交于点G,点/BDC=140 , / BGC=110，则/ A的度数为（）A. 70°B. 75C.80°D.85°:C=38，/ /B=23°,/ A的度数是（）C.37°D. 39°,/ A=35，则/ BDC的度数为（）C.80°D. 85°专题三：双垂直型1 如图所示，在△ ABC 中，/ ACB=90，/ ABC=25 , CDLAB 于 D,则/ AC ________________ 度2.图，在△ ABC 中，/ ACB=90 , CDLAB,垂足为 D.下列说法不正确的是（）A.与/ 1互余的角只有/ 2 B .Z A 与/ B 互余C.Z 仁/ B D.若/ A=2/ 1，则/ B=30°3 .如图，AC 丄BD, DE I AB,下列叙述正确的是（）4 如图，△ ABC 中，Z BAC=90 , AD 丄BC 于 D, E 是 AD 上一点, 求证：Z BED>Z C5. 如图，在 VABC C 中， ACB 90 , CD 1 2A.Z A=Z BB.Z B=Z DC.Z A=ZDD.AB , AF 是角平分线，交 CD 于点E ，求证专题四：三角形三条角平分线型1如图①，BD CD 是/ ABC 和/ACB 的角平分线且相交于点 D,请猜想/ A 与/ BDC 之间的数量关系，并说明理由。

初中几何的培优题型与解题方法

初中几何的培优题型与解题方法
初中几何的培优题型和解题方法如下：
1. 直角三角形的性质：
- 题型：给定直角三角形的两个边长或斜边长度，求第
三边长或斜边长度、面积、周长等。

- 解题方法：利用勾股定理、正弦定理、余弦定理等求解。

2. 三角形的性质：
- 题型：给定三角形的边长或角度，求面积、周长、角
度等。

- 解题方法：利用海伦公式、正弦定理、余弦定理、三
角形内角和等于180度等求解。

3. 平行线与比例：
- 题型：给定平行线与交线段的长度比例，求其他线段
的长度比例。

- 解题方法：利用平行线的性质，如对应角相等、内错
角相等等，以及相似三角形的性质求解。

4. 相似三角形：
- 题型：给定两个相似三角形的一些边长或角度，求其
他边长或角度。

- 解题方法：利用相似三角形的性质，如对应边成比例、对应角相等等求解。

5. 圆的性质：
- 题型：给定圆的半径或直径，求圆的周长、面积、弧长等。

- 解题方法：利用圆的性质，如周长公式、面积公式、弧长公式等求解。

6. 平行四边形与梯形：
- 题型：给定平行四边形或梯形的一些边长或角度，求其他边长或角度、面积等。

- 解题方法：利用平行四边形的性质，如对角线互相平分、对边平行等，以及梯形的性质，如高等求解。

7. 圆锥与圆柱：
- 题型：给定圆锥或圆柱的一些参数，求体积、表面积等。

- 解题方法：利用圆锥和圆柱的性质，如体积公式、表面积公式等求解。

以上是初中几何的一些常见培优题型和解题方法，希望对你有帮助！。

(word版)全等三角形精选证明及辅助线作法(培优)

（初中几何）全等三角形精选题目1.已知：如图，AE =AC ， AD =AB ，∠EAC =∠DAB ，求证：△EAD ≌△CAB ．2.如图，△ABC 与△DCB 中，AC 与BD 交于点E ，且∠A =∠D ，AB =DC ．（1）求证：△ABE ≌DCE ；（2）当∠AEB =50°，求∠EBC 的度数？3.如图，已知BE 、CF 是的高，且BP =AC ，CQ =AB ，求证：AP ⊥AQ ，AP =AQ4.如图，在等边△ABC 中， BD =CE ， AD 与BE 相交于点P ，求∠APE 的度数．EDCBAE OP F QCBA DP ECBAACBE D5.如图，已知等腰Rt △OAB 中，∠AOB =90°，等腰Rt △EOF 中，∠EOF =90°，连结AE 、BF ．请猜想线段AE 和线段BF 的关系，并证明你给出的结论.6.如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线，交AB 于点E ，交AD 于点F ，求证：∠ADC ＝∠BDE ．7.如图，四边形ABCD 是正方形，G 是BC 上任意一点（点G 与B 、C 不重合），AE ⊥DG 于E ，CF ∥AE 交DG 于F .求证：AE =DE +EF .OFEBAFD C BAGFE DCBA8. 正方形四条边都相等，四个角都是90°，如图，已知正方形ABCD 在直线MN 的正上方，BC 在直线MN 上，点E 是直线MN 上一点，以AE 为边在直线MN 的上方作正方形AEFG.（1）如图1，当点E 在线段BC 上（不与点B 、C 重合）时： ① 判断△ADG 和△ABE 是否全等，并说明理由：② 过点F 作FH ⊥MN ，垂足为点H ，观察并猜想线段BE 和线段CH 的数量关系，并说明理由：（2）如图2，当点E 在射线CN 上（不与点C 重合）时： ①判断△ADG 和△ABE 是否全等，并说明理由：②过点F 作FH ⊥MN ，垂足为点H ，已知GD =4，求△CFH 的面积.图1 图29.如图，在四边形ABCD 中，BC > BA ，AD=CD ，BD 平分∠ABC ，求证：∠A +∠C =180°.E H FGDCBAN MEN MHFGD CBA DCBA10.如图，已知AD ∥BC ，点E 是CD 上一点，连接AE 、BE ，且AE 、BE 恰好是∠DAB 和∠ABC 的角平分线.求证：AB =AD ＋BC .11.如图，在△ABC 中，D 是BC 边的中点，E 是AD 上一点，BE =AC ，BE 的延长线交AC 于点F ，求证：∠AEF =∠EAF ．12.如图，在△ABC 中，D 是BC 的中点，过点D 作射线交AB 于点E ，交CA 的延长线与点F ，若∠AEF =∠F ，求证：BE=CF .EDCBAF ED CB A F E DCBA13.在四边形ABCD 中，AB ∥DC ，点E 为BC 边上的中点，∠BAE =∠EAF ，AF 与DC 的延长线相交于于点F ，试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.14.如图，△ABC 中，BD =DC =AC ，E 是DC 的中点，求证，AD 平分∠BAE.15.如图：在四边形ABCD 中，AD ∥BC ，AB=AD+BC ，E 是CD 的中点，求证：AE ⊥BE .AFEDCBEDCB AEDCB A16.如图，在线段AE 同侧作两个等边三角形△ABC 和△CDE （∠ACE ＜120°），点P 与点M 分别是线段BE 和AD 的中点，请探索△CPM 是什么三角形，并进行证明.17.已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于点D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G .（1）求证：BF =AC ；（2）CE 和BF 有怎样的数量关系，写出判断并给出证明；（3）CE 与BG 的大小关系如何？试证明你的结论.MP DC BEACEFHGD BA。

全等三角形经典培优题型(含答案)

全等三角形的提高拓展训练全等三角形的性质：对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． "全等三角形的判定方法：(1) 边角边定理(SAS )：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA )：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS )：三边对应相等的两个三角形全等．(4) 角角边定理(AAS )：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL )：斜边和一条直角边对应相等的两个直角三角形全等．全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．拓展关键点：能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系．而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础．全等三角形证明经典题1已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD ?2已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2BADBC3已知：∠1=∠2，CD=DE ，EF︒=∠90ACB BC AC =MN C MN AD ⊥D MN BE ⊥E 1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=； (2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗若成立，请给出证明；若不成立，说明理由.《&C#BABCDPDA CA PEDCBADCBAMF ECB AA CB $D E F ￥A CD F21 E15如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

初中几何经典培优题型(三角形)

全等三角形辅助线找全等三角形的方法：〔1〕可以从结论出发,看要证明相等的两条线段〔或角〕分别在哪两个可能全等的三角形中；〔2〕可以从已知条件出发,看已知条件可以确定哪两个三角形相等；〔3〕从条件和结论综合考虑,看它们能一同确定哪两个三角形全等；〔4〕若上述方法均不行,可考虑添加辅助线,构造全等三角形.三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折,构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形.常见辅助线的作法有以下几种：1)遇到等腰三角形,可作底边上的高,利用"三线合一"的性质解题,思维模式是全等变换中的"对折"．2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的"旋转"．3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的"对折",所考知识点常常是角平分线的性质定理或逆定理．4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的"平移"或"翻转折叠"5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明．这种作法,适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答．常见辅助线写法：⑴过点A作BC的平行线AF交DE于F⑵过点A作BC的垂线,垂足为D⑶延长AB至C,使BC＝AC⑷在AB上截取AC,使AC＝DE⑸作∠ABC的平分线,交AC于D⑹取AB中点C,连接CD交EF于G点例1如图,AB＝CD＝1,∠AOC＝60°,证明：AC＋BD≥1.例2<2007年中考〕如图,已知△ABC⑴请你在BC边上分别取两点D、E〔BC的中点除外〕,连接AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形；⑵请你根据使⑴成立的相应条件,证明AB＋AC＞AD＋AE.例3已知线段OA、OB、OC、OD、OE、OF.∠AOB＝∠BOC＝∠COD＝∠DOE＝∠EOF＝60°.且AD＝BE＝CF＝2.求证：S△OAB＋S△OCD＋S△OEF3.例4如图1,在四边形ABCD中,连接对角线AC、BD,如果∠1＝∠2,那么∠3＝∠4.仔细阅读以上材料,完成下面的问题.如图2,设P为□ABCD内一点,∠P AB＝∠PCB,求证：∠PBA＝∠PDA.图1图2⑴集散思想：有些几何题,条件与结论比较分散,通过添加适当的辅助线,将图形中分散,远离了的元素聚集到有关的图形上,使它们相对集中,便于比较,建立关系,从而找出问题的解决途径.⑵平移只能用来作为作辅助线的思路,具体做辅助线的时候不能直接说将△ABC 平移至△DEF .1．在正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的点,且EG ⊥FH ,求证：EG ＝FH .2．如图所示,P 为平行四边形ABCD 内一点,求证：以AP 、BP 、CP 、DP 为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB 和BC .3．如图,已知△ABC 的面积为16,BC ＝8,现将△ABC 沿直线BC 向右平移a 个单位到△DEF 的位置.⑴当a ＝4时,求△ABC 所扫过的面积；⑵连接AE 、AD ,设AB ＝5,当△ADE 是以DE 为一腰的等腰三角形时,求a 的值.4．如图,AA ′=BB ′=CC ′=1,∠AOB ′=∠BOC ′=∠COA ′=60°,求证：34AOB BOC COA SS S '''++<.例1 如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且∠EAF ＝45°,AH ⊥EF ,H 为垂足,求证：AH ＝AB .例2△ABC 中,∠ACB ＝90°,AC ＝BC ,P 是△ABC 内的一点,且AP ＝3,CP ＝2,BP ＝1,求∠BPC 的度数.例3已知在△ABC 中,AB ＝AC ,P 为三角形内一点,且∠APB ＞∠APC ,求证：PB ＜PC .有边相等或者有角度拼起来为特殊角的时候可以用旋转⑴边相等时常见图形为正方形,等腰三角形和等边三角形等等 ⑵角度能拼成的特殊角指的是180°,90°等等例4已知△ABC ,∠1＝∠2,AB ＝2AC ,AD ＝BD .求证：DC ⊥AC .例5△ABC 为等腰直角三角形,∠ABC ＝90°,AB ＝AE ,∠BAE ＝30°,求证：BE ＝CE .例6在△ABC 中,E 、F 为BC 边上的点,已知∠CAE ＝∠BAF ,CE ＝BF ,求证：AC ＝AB .出现轴对称的时候可以考虑翻折,尤其注意有角平分线,有角相等或者出现特殊角的一半的时候,翻折是常用添加辅助线的思想.强调：旋转和翻折只能是一种作辅助线的思路,具体做辅助线的时候不能直接说将△ABC旋转或翻折至△DEF.1．如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心角为直角的扇形纸板的圆心方在O点处,并将纸板绕O点旋转,其半径分别交AB、AD于点M、N,求证：正方形ABCD的边被纸板覆盖部分的总长度为定值a.2．〔2008##〕在梯形ABCD中,AB∥CD,∠A＝90°,AB＝2,BC＝3,CD＝1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程.3．如图,P是等边△ABC内一点,若AP＝3,PB＝4,PC＝5,求∠APB的度数.4．已知：在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,∠DAE=45°.⑴猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明；⑵当动点E在线段BC上,动点D运动在线段CB延长线上时,其它条件不变,⑴中探究的结论是否发生改变？请说明你的猜想并给予证明.5．如图,已知等腰直角三角线ABC,BD平分∠ABC,CE⊥BD,垂足为E,求证：BD＝2CE.6．如图,折叠长方形的一边AD,使点D落在BC边的点F处,如果AB＝8,BC＝10,求EC的长.中点的妙用一、倍长中线法例1<文汇中学2009-2010期中测试题>,AD是△ABC中BC边上的中线,若AB=2,AC=4,则AD的取值范围是___________.例2已知在△ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,AF=EF,求证：AC=BE.例3⑴如图1,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,点D在AB边上.连接EC,取EC中点F,连接AF,DF,猜测AF,DF的数量关系和位置关系,并加以证明.图1⑵如图2,将△BDE旋转至如图位置,使E在AB延长线上,D在CB延长线上,其他条件不变,则⑴中AF,DF的数量关系和位置关系是否发生变化,并加以证明.图2例4已知四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,求证EFGH为平行四边形.例5如图,已知四边形ABCD中,AB=CD,M、N分别为BC、AD中点,延长MN与AB、CD延长线交于E、F,求证∠BEM=∠CFM例6已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°,连接DE,设M为DE的中点.⑴求证：MB =MC ；⑵设∠BAD =∠CAE ,固定Rt △ABD ,让Rt △ACE 移至图示位置,此时MB =MC 是否成立？请证明你的结论.出现中点的时候一般有以下作辅助线的方法⑴倍长中线法⑵构造中位线⑶如果是直角三角形,经常还会构造斜边上的中线例7如图,已知△ABC 和△ADE 都是等腰直角三角形,点M 为EC 中点,求证△BMD 为等腰直角三角形.1．在△ABC 中,AB =12,AC =30,求BC 边上的中线AD 的范围.2．在△ABC 中,D 为BC 边上的点,已知∠BAD =∠CAD ,BD =CD ,求证：AB =AC .3．如图,在△ABC 中,AD ⊥BC ,M 是BC 中点,∠B =2∠C ,如图,求证：DM =12AB 4．已知△ABC 中,AC =7,BC =4,D 为AB 中点,E 为边AC 上一点,且102AED C ∠=︒+∠9,求CE 的长.5．在任意五边形ABCDE 中,M,N,P,Q 分别为AB 、CD 、BC 、DE 的中点,K 、L 、分别为MN 、PQ 的中点,求证：KL 平行且等于14AE . 6．如图,已知△ABC 中,AB =AC ,CE 是AB 边上的中线,延长AB 到D ,使BD =AB ,那么CE 是CD 的几分之几？7．四边形ABCD 四边中点分别为E 、F 、G 、H ,当四边形ABCD 满足时,EFGH 为菱形；当四边形ABCD 满足时,EFGH 为矩形；当四边形ABCD 满足时,EFGH 为正方形.例1在△ABC 中,∠B =2∠C ,∠BAC 的平分线AD 交BC 与D .求证：AB +BD =AC .例2 ABCD 是正方形,P 为BC 上任意一点,∠P AD 的平分线交CD 于Q ,求证：DQ =AP -BP . 例3已知△ABC ,∠ABC =90°,以AB 、AC 为边向外做正方形ABDE 和ACFG ,延长BA 交EG 于H ,则BC =2AH .例4 AD 是△ABC 的角平分线,BE ⊥AD 交AD 的延长线于E ,EF //AC 交AB 于F .求证：AF =FB .截长补短法补形法例5如图,六边形ABCDEF的六个内角都相等,已知BC+CD=11,DE-AB=3,求DC+EF的值. 例6如图所示：BC>AB,AD=AC,BD平分∠ABC,求证：∠A+∠C=180°.1．如图,在△ABC中,AB+BD=AC,∠BAC的平分线AD交BC与D,求证：∠B=2∠CAB CD已知△ABC,以AB、AC为边向外作正方形ABGF、ACDE,M是BC中点,连接AM求证：EF＝2AM且AM⊥EF.3．在△ABC中,AB=AC,∠A=100°,BE评分∠B交AC与E,如图,求证：AE+BE=BC 4．在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交与F,如图所示.求证：AF⊥BF5．在△ABC中,MB、NC分别是三角形的外角∠ABE、∠ACF的角平分线,AM⊥BM,AN⊥CN,垂足分别是M,N.求证：MN∥BC,MN=12<AB+AC+BC>6．在△ABC中,MB、NC分别是三角形的内角∠ABC、∠ACB的角平分线,AM⊥BM,AN⊥CN,垂足分别是M,N.求证：MN∥BC,MN=12<AB+AC-BC>例1在四边形ABCD中,已知AB=BC=CD,∠ABC=70°,∠BCD=170°,求∠BAD的度数.例2如图,△ABC中,AB=AC,AD=BC,∠A=20°,求∠DCA的度数.例3任意△ABC,试在△ABC内找一点P,使得P A+PB+PC的值最小例4<2000 初二数学竞赛〕,在等腰△ABC中,延长边AB到点D,延长边CA到点E,连接DE, 恰有AD=BC=CE=DE.求证：∠BAC=100°.例5如图所示,在△ABC中,∠B=60°∠A=100°,E为AC的中点,∠DEC=80°,D是BC边上的点,BC=1,求△ABC的面积与△CDE的面积的两倍的和.例6如图所示,在△ABC中,∠ACB=2∠ABC,P为三角形内一点,AP=AC,PB=PC,求证：∠BAC=3∠BAP.1．如图所示,在四边形ABCD中,BC CD=,60BCA ACD∠-∠=︒,求证：AD CD AB+≥.2．在ABC∆中,AB AC=,60120A︒<∠<︒,P为ABC∆内部一点,PC AC=,120PCA A∠=︒-∠,求CBP∠的度数.巧构等边3．在等边△ABC内有一点P,它到三个顶点A、B、C的距离分别为1求∠APB的度数.4．在凸四边形ABCD中,∠DAC=30°,∠CAB=20°,∠ADB=50°,∠BDC=30°,四边形的对角线交于点P,求证：PB=PC5．在等腰△ABC中,∠B=∠C=40°,延长AB至点D,使AD=BC,求∠BCD的度数. 6．如图,D是△ABC外一点,AB=AC=BD+CD,∠ABD=60°.求∠ACD的度数.。

三角形培优训练100题集锦(一)2024

三角形培优训练100题集锦（一）【引言概述】三角形是数学中的一个重要几何概念，对于学生的数学培优训练具有重要意义。

本文整理了一份包含一百道三角形相关题目的训练集锦，旨在帮助学生系统地掌握三角形的性质、定理和计算方法，提高解题能力。

以下将从五个大点来阐述这份题集的内容。

【大点1：三角形基础知识】1. 三角形的定义及分类2. 三角形内角和的性质3. 三角形边长关系：三角不等式定理4. 三角形的周长和面积计算公式5. 三角形的特殊点：重心、垂心、外心、内心、费马点等【大点2：三角形的相似与全等】1. 相似三角形的性质2. 判定三角形相似的方法3. 三角形的全等的条件4. 利用相似三角形或全等三角形解题的方法5. 实际问题中的应用：测量、定位、相似比例等【大点3：三角形的角与线段关系】1. 角的平分线与垂直平分线的特点2. 三角形的角平分线定理3. 三垂线定理与垂心定理4. 外角与内角的关系5. 角与弧的关系及其应用：圆周角、弦切角、弧度制等【大点4：三角形的特殊性质与定理】1. 等腰三角形的性质与判定2. 直角三角形的性质与判定3. 正三角形的性质及计算4. 等边三角形的性质及计算5. 锐角三角形和钝角三角形的性质及判定【大点5：三角形的应用问题】1. 三角形的角度测量与边长测量2. 三角形在建筑工程中的应用：测量高度、角度与距离3. 三角形在地理学中的应用：测量地底深度、地图测量等4. 三角形在航空航天领域的应用：导航、角度计算等5. 三角形在日常生活中的应用：地理问题、旅行导航、地震角度计算等【总结】通过对本文中所整理的三角形培优训练100题集锦的学习，同学们将能够掌握三角形的基础知识，灵活运用三角形的相似与全等等性质和定理，熟练解决三角形的角与线段关系问题，理解各种特殊三角形的性质，并能够应用三角形的知识解决实际问题。

这将为学生的数学学习和思维能力的提高提供坚实的基础。

解三角形题型培优(学生版)

5.解三角形1.解三角形6大常考题型【知识必备】1、正弦定理、余弦定理在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则定理正弦定理余弦定理内容asin A=bsin B=csin C=2Ra2=b2+c2-2bc cos A；b2=c2+a2-2ca cos B；c2=a2+b2-2ab cos C变形(1)a=2R sin A，b=2R sin B，c=2R sin C；(2)sin A=a2R，sin B=b2R，sin C=c2R；(3)a∶b∶c=sin A∶sin B∶sin C；(4)a sin B=b sin A，b sin C=c sin B，a sin C=c sin Acos A=b2+c2-a22bc；cos B=c2+a2-b22ac；cos C=a2+b2-c22ab2、三角形面积公式：S△ABC=12ah(h表示边a上的高)；S△ABC=12ab sin C=12bc sin A=12ac sin B；3、解三角形多解情况在△ABC中，已知a，b和A时，解的情况如下：A为锐角A为钝角或直角图形a =b sin A b sin A <a <b a ≥关系式b a >b a ≤b解的个数一解两解一解一解无解4、实际应用(1)仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图①)．(2)方位角从指北方向顺时针转到目标方向线的水平角，如B 点的方位角为α(如图②)．(3)方向角：相对于某一正方向的水平角．(1)北偏东α，即由指北方向顺时针旋转α到达目标方向(如图③)．(2)北偏西α，即由指北方向逆时针旋转α到达目标方向．(3)南偏西等其他方向角类似．(4)坡角与坡度(1)坡角：坡面与水平面所成的二面角的度数(如图④，角θ为坡角)．(2)坡度：坡面的铅直高度与水平长度之比(如图④，5、相关应用(1)正弦定理的应用①边化角，角化边⇔a :b :c =sin A :sin B :sin C②大边对大角大角对大边a >b ⇔A >B ⇔sin A >sin B ⇔cos A <cos i 为坡度)．坡度又称为坡比．Ba +b +c③合分比：sin A +sin B +sin Ca +b =sin A +sin B b +c =sin B +sin C a +c =sin A +sin C a =sin A b =sin B c =sin C=2R (2)△ABC 内角和定理：A +B +C =π①sin C =sin (A +B )=sin A cos B +cos A sin B ⇔c =a cos B +b cos A 同理有：a =b cos C +c cos B ，b =c cos A +a cos C .②-cos C =cos (A +B )=cos A cos B -sin A sin B ；A +tan ③斜三角形中，-tan C =tan (A +B )=1Btan -tan ⋅A tan B⇔tan A +tan B +tan C =tan A ⋅tan B ⋅tan C④sin A +2B =cos C 2；cos A +2B=sin C 2⑤在ΔABC 中，内角A ，B ，C 成等差数列⇔B =π3,A +C =2π3.Z 【题型精讲】题型一:【已知边角元素解三角形】必备技巧已知边角元素解三角形技巧正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素，基本思想是方程思想，即根据正弦定理、余弦定理列出关于未知元素的方程，通过解方程求得未知元素．1.1(多选)(山东济南一模)在ΔABC中，角A，B，C所对的边分别为a，b，c，下列结论正确的是（）A.a2=b2+c2-2bc cos AB.a sin B=b sin AC.a=b cos C+c cos BD.a cos B+b cos A=sin C1.2(多选)(重庆市高三二模)已知在△ABC中，角A，B，C所对的边分别为a，b，c，且A=60°，b=2，c=3+1，则下列说法正确的是A.C=75°或C=105°B.B=45°C.a=6D.该三角形的面积为3+1 21.3在△ABC中，角A，B，C所对的边分别为a，b，c若sin A=35,A=2B，角C为钝角，b=5.(1)求sin(A-B)的值；(2)求边c的长.Z【跟踪精练】1.3.1在△ABC中，角A,B,C所对的边分别为a,b,c，若(a+b)2-c2=ab，则C=（）A.π6 B.π3或2π3 C.2π3 D.π6或5π61.3.2在△ABC中，内角A，B，C所对的边分别是a，b，c.若A=π3，a=23，b=22，则B=（）A.π4 B.π3 C.π4或3π4 D.π3或2π31.3.3△ABC的内角A､B､C的对边分别为a､b､c，若a=4，b=3，c=2，则中线AD的长为（）A.5B.10C.52 D.102题型二:【已知边角关系解三角形】必备技巧已知边角关系解三角形正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化，解题时可以把已知条件化为角的三角函数关系，也可以把已知条件化为三角形边的关系．1.1在△ABC中，内角A,B,C的对边分别为a，b，c，已知2cos C a cos B+b cos A=c．(1)若cos A=64，求sin2A+C的值；(2)若c=7，△ABC的面积为332，求边a，b的值．21a △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 1.2的面积为2-b 2sin C .(1)证明：sin A =2sin B ；(2)若a cos C =32b ，求cos A .Z 【跟踪精练】ΔABC 的内角A ，B ，C 的对边分别为a ，b ，c ．设(sin B -sin C )2=sin 2A 1.2.1-sin B sin C ．(1)求A ；(2)若2a +b =2c ，求sin C ．在△ABC 中，内角A ,B ,C 的对边分别为a ,b ,c ，b tan A +b tan B 1.2.2=3ccos A．(1)求角B ；(2)D 是AC 边上的点，若CD =1，AD =BD =3，求sin A 的值．题型三:【判断三角形形状】必备技巧判断三角形形状的方法(1)化边：通过因式分解、配方等得出边的相应关系．(2)化角：通过三角恒等变换，得出内角的关系，此时要注意应用A +B +C =π这个结论．在△ABC 中，已知a 2+b 2-c 2=ab ，且2cos A sin B =sin C 1.1，则该三角形的形状是（）A.直角三角形B.等腰三角形C.等边三角形D.钝角三角形在△ABC 中，已知(b +c -a )(b +c +a )=3bc ，且2cos B sin C =sin A ，则△ABC 1.2的形状为（）A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形Z 【跟踪精练】对于△ABC ，有如下四个命题1.2.1:①若sin2A =sin2B ，则△ABC 为等腰三角形，②若sin B =cos A ，则△ABC 是直角三角形③若sin 2A +sin 2B <sin 2C ，则△ABC 是钝角三角形④若acos 2A =b cos 2B =cC cos 2，则△ABC 是等边三角形.其中正确的命题序号是1.2.2a在△ABC 中，已知a +b =tan Ab +tan B ，则△ABC 的形状一定是（）A.等腰三角形B.直角三角形C.等边三角形D.等腰或直角三角形题型四:【三角形解的个数问题】1.1已知在△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，则根据条件解三角形时恰有一解的一组条件是（）A.a =3，b =4，A =π6 B.a =4，b =3，A =π3C.a =1，b =2，A =π4D.a =2，b =3，A =2π31.2△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，A =30°，a =3，若这个三角形有两解，则b 的取值范围是（）A.3<b ≤6B.3<b <6C.b <6D.b ≤6Z 【跟踪精练】1.2.1在△ABC 中，根据下列条件解三角形，则其中有两个解的是（）A.b =10,A =45°,C =70°B.a =60,c =48,B =60°C.a =5,b =7,c =8D.a =14,b =16,A =45°1.2.2在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若，满足条件a =3，A =60°的三角形有两个，则b 的取值范围是（）A.2,3B.3,33C.3,23D.22,23题型五:【解三角形中的最值范围问题】方法技巧解三角形中最值范围问题基本处理方法1、用余弦定理结合基本不等式求解，2、要求的量转化为某角的三角函数，求函数的最值或值域。

全等三角形经典培优题型(含答案)

全等三角形经典培优题型(含答案)1.已知三角形ABC中，AB=4，AC=2，D是BC的中点，AD是整数，求AD的长度。

解：由题意可得AD=AB-DB，又BD=DC=AC/2=1，故AB=AD+DB=AD+1，代入AB=4得AD=3.2.已知四边形BCDE中，BC=DE，∠B=∠E，∠C=∠D，F是CD的中点，证明∠1=∠2.解：由于BC=DE，且∠B=∠E，所以△BCE≌△EDC，从而∠1=∠BCE=∠EDC=∠2.3.已知四边形ABCD中，∠1=∠2，CD=DE，EF//AB，证明EF=AC。

解：由于EF//AB，所以△EFC∼△ABC，从而EF/AC=FC/BC，而CD=DE，所以FC=CD，代入得EF/AC=CD/BC，又由于∠1=∠2，所以△BCD∼△ECD，从而CD/BC=ED/AC，代入得EF/AC=ED/AC，即EF=AC。

4.已知三角形ABC中，AD平分∠BAC，AC=AB+BD，证明∠B=2∠C。

解：由于AD平分∠BAC，所以∠BAD=∠CAD，从而∠B=∠BAD+∠ABD=∠CAD+∠ACD，又由于AC=AB+BD，所以BD=AC-AB，代入得∠B=∠CAD+∠ACD=∠CAD+∠ABC，又由于∠CAD=∠CAB，所以∠B=∠CAB+∠ABC=2∠C。

5.已知三角形ABC中，AC平分∠BAD，CE⊥AB，∠B+∠D=180°，证明AE=AD+BE。

解：由于AC平分∠BAD，所以∠CAD=∠CAB，从而△ABE∼△DCE，所以AE/AD=BE/CD，又由于∠B+∠D=180°，所以CD=AB，代入得AE/AD=BE/AB，即AE=AD·(BE/AB)，又由于CE⊥AB，所以△CEB为直角三角形，从而BE/AB=CE/AC，代入得AE=AD·(CE/AC)，又由于AC平分∠BAD，所以△ACD∼△ABC，从而CE/AC=CD/AB，代入得AE=AD·(CD/AB)，又由于CD=AB-BD，所以AE=AD·((AB-BD)/AB)，即AE=AD+BE·(AB/AD-1)，又由于AB>AD，所以AB/AD-1<AB/AD，从而AE<AD+BE·(AB/AD)，即AE<AD+BE。

初一下学期三角形培优专题

A．10度
B．15度
C．20度
D．不能确定
5．如图，三角形ABC中，AD平分∠BAC，EG⊥AD，且分别交AB、AD、AC及BC的延长线于点E、H、F、G，下列四个式子中正确的是（）
A．∠1=1∕2（∠2-∠3）
B．∠1=2（∠2-∠3）
C．∠G=1∕2（∠3-∠2）
D．∠G=1∕2∠1
专题八：平行线型
A．∠A=∠B
B．∠B=∠D
C．∠A=∠D
D．∠A+∠D=90°
4如图，△ABC中，∠BAC=90°，AD⊥BC于D，E是AD上一点，求证：∠BED＞∠C
5．如图，在中，是角平分线，交于点，求证
专题四：三角形三条角平分线型
1．如图①，BD、CD是∠ABC和∠ACB的角平分线且相交于点D，请猜想∠A与∠BDC之间的数量关系，并说明理由。
（1）试找出∠1、∠2、∠3之间的关系并说出理由；
(2)如果点P在A、B两点之间运动时，问∠1、∠2、∠3之间的关系是否发生变化？
(3)如果点P在A、B两点外侧运动时，试探究∠1、∠2、∠3之间的关系（点P和A、B不重合）
5．如下图，AB∥CD，直线a交AB、CD分别于点E、F，点M在EF上，p是直线CD上的一个动点，（点P不与F重合）
（3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高为多少？
专题十三：三角形三边关系与周长
1．若一个等腰三角形的三边长均为整数，且周长为10，则底边长为
2．周长为16的三角形的三边长都是整数，这样的三角形有个
3．三角形三条边长是三个连续的自然数，周长小于19，则满足条件的三角形有个
4．三角形三条边长均为整数，其中两边长之差为7，三角形的周长是奇数，则第三边长可能为

三角形培优训练100题集锦学生用

三角形培优训练100题集锦(学生用)三角形培优训练专题【三角形辅助线做法】图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

线段垂直平分线，常向两端把线连。

要证线段倍与半，延长缩短可试验。

三角形中两中点，连接则成中位线。

三角形中有中线，延长中线等中线。

【常见辅助线的作法有以下几种】1、遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”。

2、遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”。

3、遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理。

4、过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”。

5、截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明。

这种作法，适合于证明线段的和、差、倍、分等类的题目。

6、已知某线段的垂直平分线，那么可以在垂直平分线上的某点向该线段的两个端点作连线，出一对全等三角形。

7、特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答。

1、已知，如图ABC ∆中，5=AB ，3=AC ，求中线AD 的取值范围。

分析：本题的关键是如何把AB ，AC ，AD 三条线段转化到同一个三角形当中。

解:延长AD 到E ，使DA DE =，连接BE 又∵CD BD =，CDA BDE ∠=∠ ∴()SAS CDA BDE ∆≅∆，3==AC BE∵BE AB AE BE AB +- (三角形三边关系定理) 即822 ADEC AB D∴41 AD2、如图，ABC ∆中，E 、F 分别在AB 、AC 上，DF DE ⊥，D 是中点，试比较CF BE +与EF 的大小。

初中三角形经典题型

1、在三角形ABC中，若∠A = 60°，∠B = 40°，则∠C的度数为：A. 70°B. 80°C. 90°D. 100°（答案）B2、已知三角形三边长度分别为3、4、5，则该三角形为：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定（答案）B3、三角形的高线、中线、角平分线：A. 都是线段B. 都是射线C. 都是直线D. 高线是射线，中线、角平分线是线段（答案）A4、在三角形ABC中，D、E分别是AB、AC的中点，则DE是三角形ABC的：A. 高B. 中线C. 角平分线D. 中位线（答案）D5、若三角形的一个外角等于与它不相邻的两个内角之和，则这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形（答案）B6、已知三角形ABC的三边a、b、c满足a²+ b²= c²+ 2ab，则三角形ABC是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰直角三角形（答案）C（注：原式可改写为a²+ b²- 2ab = c²，即(a - b)²= c²，但此题考察的是三角形的性质，实际上当a²+ b²= c²+ 2ab时，说明∠C为钝角）7、在三角形ABC中，若AB = AC，且∠B = 70°，则∠A的度数为：A. 40°B. 55°C. 70°D. 110°（答案）A8、下列说法中，正确的是：A. 三角形的角平分线、中线和高都在三角形内部B. 直角三角形只有一条高线C. 三角形的三条高线至少有一条在三角形内部D. 三角形的三条角平分线都在三角形外部（答案）C。

培优专题01 与三角形模型有关的角度计算-解析版

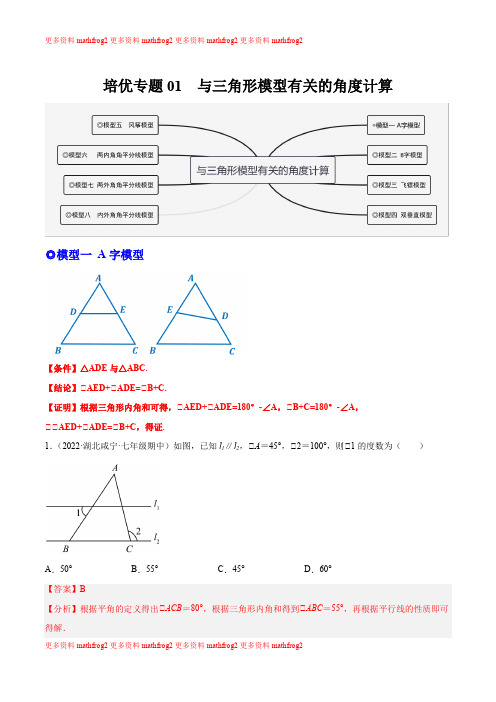
培优专题01 与三角形模型有关的角度计算◎模型一A字模型【条件】△ADE与△ABC.【结论】∠AED+∠ADE=∠B+C.【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，∠∠AED+∠ADE=∠B+C，得证.1．（2022·湖北咸宁·七年级期中）如图，已知l1∥l2，∠A＝45°，∠2＝100°，则∠1的度数为（）A．50°B．55°C．45°D．60°【答案】B【分析】根据平角的定义得出∠ACB＝80°，根据三角形内角和得到∠ABC＝55°，再根据平行线的性质即可得解．【详解】解：∠∠2＝100°，∠∠ACB ＝180°−100°＝80°， ∠∠A ＝45°，∠∠ABC ＝180°−45°−80°＝55°， ∠l 1∥l 2，∠∠1＝∠ABC ＝55°，故选：B ．【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”是解题的关键．2．（2022·全国·八年级课时练习）如图，ABC 中，65A ∠=︒，直线DE 交AB 于点D ，交AC 于点E ，则BDE CED ∠+∠=（）．A ．180︒B ．215︒C ．235︒D ．245︒【答案】D【分析】根据三角形内角和定理求出ADE AED ∠+∠，根据平角的概念计算即可．【详解】解：65A ∠=︒，18065115ADE AED ∴∠+∠=︒-︒=︒， 360115245BDE CED ∴∠+∠=︒-︒=︒，故选：D ．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180︒是解题的关键． 3．（2022·全国·八年级课时练习）如图是某建筑工地上的人字架，若1120∠=︒，那么32∠-∠的度数为_________．【答案】60︒【分析】根据平角的定义求出4，再利用三角形的外角的性质即可解决问题．【详解】解：如图14180∠+∠=︒，1120∠=︒， 460∴∠=︒，324，32460∴∠-∠=∠=︒，故答案为：60︒．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．4．（2020·湖南·常德市第二中学九年级期中）如图，在ABC ∆中，90C ∠=︒，6BC =，D ，E 分别在AB 、AC 上，将ADE ∆沿DE 折叠，使点A 落在点A '处，若A '为CE 的中点，则折痕DE 的长为__．DE BC ，故∆BC ．【详解】解：ABC ∆沿90DEA =∠'=︒，AED ∆∽，的中点，AE =∴=．ED2故答案为：2．【点睛】本题考查相似三角形的判定和性质，掌握“A ”字形三角形相似的判定和性质为解题关键． 5．（2022·全国·八年级课时练习）如图所示，DAE ∠的两边上各有一点,B C ，连接BC ，求证180DBC ECB A +∠=︒∠+∠．【答案】见解析【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可．【详解】解：DBC ∠和ECB ∠是ABC 的外角， ,DBC A ACB ECB A ABC ∴∠=∠+∠∠=∠+∠．又180A ABC ACB ∠+∠+∠=︒，180DBC ECB A ACB ABC A A ∴∠+∠=∠+∠+∠+∠︒=+∠．【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．◎模型二 8字模型【条件】AD 、BC 相交于点O.【结论】∠A +∠B =∠C +∠D.(上面两角之和等于下面两角之和)【证明】在∠ABO 中，由内角和定理：∠A +∠B +∠BOA =180°，在∠CDO 中，∠C +∠D +∠COD =180°， ∠∠A +∠B +∠BOA =180°=∠C +∠D +∠COD ，由对顶角相等：∠BOA =∠COD ∠∠A +∠B =∠C +∠D ，得证.6．（2022·全国·八年级课时练习）如图，AB 和CD 相交于点O ，∠A ＝∠C，则下列结论中不能完全确定正确的是（）A．∠B＝∠D B．∠1＝∠A＋∠D C．∠2＞∠D D．∠C＝∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∠∠A＋∠AOD＋∠D＝180°，∠C＋∠COB＋∠B＝180°，∠A＝∠C，∠AOD＝∠BOC，∠∠B＝∠D，∠∠1＝∠2＝∠A＋∠D，∠∠2＞∠D，故选项A，B，C正确，故选D．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键．7．（2022·全国·八年级课时练习）如图，∠1=60°，则∠A+∠B+∠C+∠D+∠E+∠F=（）A．240°B．280°C．360°D．540°【答案】A【分析】根据三角形内角和定理得到∠B与∠C的和，然后在五星中求得∠1与另外四个角的和，加在一起即可．【详解】解：由三角形外角的性质得：∠3=∠A+∠E，∠2=∠F+∠D，∠∠1+∠2+∠3=180°，∠1=60°，∠∠2+∠3=120°，即：∠A+∠E+∠F+∠D=120°，∠∠B+∠C=120°，∠∠A+∠B+∠C+∠D+∠E+∠F=240°．故选A．【点睛】本题考查了三角形的外角和三角形的内角和的相关知识，解决本题的关键是将题目中的六个角分成两部分来分别求出来，然后再加在一起．8．（2022·全国·八年级课时练习）如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I＝__．【答案】900°【分析】根据多边形的内角和，可得答案．【详解】解：连EF，GI，如图，∠6边形ABCDEFK的内角和＝（6－2）×180°＝720°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝720°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋（∠1＋∠2）＝720°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F∠H＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F（∠3＋∠4）＋∠5＋∠6＋∠H＝720°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＝900°，故答案为：900°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．9．（2022·全国·八年级课时练习）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为__．【答案】1080°【分析】连KF，GI，根据n边形的内角和定理得到7边形ABCDEFK的内角和＝（7－2）×180°＝900°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，由三角形内角和定理可得到∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，即可得到∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数．【详解】解：连KF，GI，如图，∠7边形ABCDEFK的内角和＝（7－2）×180°＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＝900°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K＝1080°．故∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数为1080°．故答案为：1080°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．10．（2022·全国·八年级课时练习）如图，OAB和OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M（1）如图1，当α＝90°时，∠AMD 的度数为 °；（2）如图2，当α＝60°时，求∠AMD 的度数；（3）如图3，当OCD 绕O 点任意旋转时，∠AMD 与α是否存在着确定的数量关系？如果存在，请你用α表示∠AMD ，并用图3进行证明；若不确定，说明理由．【答案】（1）90；（2）120︒；（3）180α︒-【分析】（1）如图1，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得90AMK BOK ∠=∠=︒；（2）如图2，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得60AMK BOK ∠=∠=︒；（3）如图3，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKM AKO ∠=∠，可得BMK AOK α∠=∠=，可得180AMD α∠=︒-；【详解】解：（1）如图1中，设OA 交BD 于K∠OA OB OC OD ==，，90AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠90AMK BOK ∠=∠=︒ ∠90AMD ∠=︒ 故答案为90︒（2）如图2，设OA 交BD 于K ，∠OA OB OC OD ==，，60AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠60AMK BOK ∠=∠=︒ ∠180120AMD AMK ∠=︒-∠=︒ 故答案为120︒（3）如图3，设OA 交BD 于K ，∠OA OB OC OD ==，，AOB COD α∠=∠= ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠AKO BKM ∠=∠ ∠BMK AOK α∠=∠=∠180180AMD BMK α∠=︒-∠=︒- 故答案为180α︒-【点睛】本题考查了几何变换综合题，全等三角形的判定，三角形内角和性质，解题的关键是灵活运用所学知识解决问题，学会利用“8字型”证明角相等．◎模型三飞镖模型【条件】四边形ABDC 如上左图所示.【结论】∠D =∠A +∠B +∠C.(凹四边形凹外角等于三个内角和) 【证明】如上右图，连接AD 并延长到E ，则：∠BDC =∠BDE +∠CDE =(∠B +∠1)+(∠2+∠C )=∠B +∠BAC +∠C.本质为两个三角形外角和定理证明. 11．（2022·全国·八年级课时练习）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果52,25A B ︒︒∠=∠=，30,35,72C D E ︒︒︒∠=∠=∠=，那么F ∠的度数是（）．A ．72︒B ．70︒C ．65︒D ．60︒【答案】A【分析】延长BE 交CF 的延长线于O ，连接AO ，根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠，再根据四边形的内角和求出DFO ∠，根据邻补角的性质即可求出DFC ∠的度数．【详解】延长BE 交CF 的延长线于O ，连接AO ，如图，∠180,OAB B AOB ∠+∠+∠=︒∠180,AOB B OAB ∠=︒-∠-∠ 同理得180,AOC OAC C ∠=︒-∠-∠ ∠360,AOB AOC BOC ∠+∠+∠=︒ ∠360BOC AOB AOC ∠=︒-∠-∠360(180)(180)B OAB OAC C =︒-︒-∠-∠-︒-∠-∠ 107,B C BAC =∠+∠+∠=︒ ∠72,BED ∠=︒∠180108,DEO BED ∠=︒-∠=︒ ∠360DFO D DEO EOF ∠=︒-∠-∠-∠36035108107110,=︒-︒-︒-︒=︒∠180********DFC DFO ∠=︒-∠=︒-︒=︒, 故选：A ．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：180(2)n ︒-．12．（2022·全国·八年级课时练习）如图，已知BE ，CF 分别为△ABC 的两条高，BE 和CF 相交于点H ，若△BAC=50°，则△BHC 为（）A ．115°B ．120°C ．125°D ．130°【答案】D【详解】∠BE 为∠ABC 的高，∠BAC=50°， ∠∠ABE=90°-50°=40°， ∠CF 为∠ABC 的高， ∠∠BFC=90°，∠∠BHC=∠ABE+∠BFC=40°+90°=130°．故选D．13．（2022·全国·八年级课时练习）如图，若115∠+∠+∠+∠+∠+∠=EOC∠=︒，则A B C D E F____________．【答案】230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．【详解】解：如图∠∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠∠E+∠D+∠C=115°，∠∠EOC=∠1+∠F=115°，∠1=∠A+∠B，∠∠A+∠B+∠F=115°，∠∠A+∠B+∠C+∠D+∠E+∠F=230°，故答案为：230°．【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．14．（2022·山东德州·七年级期末）如图，则∠A+∠B+∠C+∠D+∠E的度数是__．【答案】180°【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠4＝∠A＋∠2，∠2＝∠D＋∠C，进而利用三角形的内角和定理求解．【详解】解：如图可知：∠∠4是三角形的外角，∠∠4＝∠A＋∠2，同理∠2也是三角形的外角，∠∠2＝∠D＋∠C，在∠BEG中，∠∠B＋∠E＋∠4＝180°，∠∠B＋∠E＋∠A＋∠D＋∠C＝180°．故答案为：180°．【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．15．（2022·全国·八年级课时练习）模型规律：如图1，延长CO交AB于点D，则∠=∠+∠=∠+∠+∠．因为凹四边形ABOC形似箭头，其四角具有“BOC A B C 1BOC B A C B∠=∠+∠+∠”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：∠如图2，60,20,30A B C∠=︒∠=︒∠=︒，则BOC∠=__________︒；∠如图3，A B C D E F∠+∠+∠+∠+∠+∠=__________︒；（2）拓展应用：∠如图4，ABO∠、ACO∠的2等分线（即角平分线）1BO、1CO交于点1O，已知120BOC∠=︒，50BAC∠=︒，则1BO C∠=__________︒；∠如图5，BO、CO分别为ABO∠、ACO∠的10等分线1,2,3,,(,)89i=⋯．它们的交点从上到下依次为1O、2O、3O、…、9O．已知120BOC∠=︒，50BAC∠=︒，则7BO C∠=__________︒；∠如图6，ABO∠、BAC∠的角平分线BD、AD交于点D，已知120,44BOC C∠=︒∠=︒，则ADB=∠__________︒；∠如图7，BAC∠、BOC∠的角平分线AD、OD交于点D，则B、C∠、D∠之同的数量关系为__________．【详解】解：（1）∠∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；◎模型四双垂直模型【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE，∠ACB=∠CED.【证明】∠∠B=∠D=∠ACE=90°；∠∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∠∠BAC=∠DCE同理,∠ACB+∠DCE=90°，且∠CED+∠DCE=90°；∠∠ACB=∠CED，得证.16．（2021·青海海东·八年级期中）如图，已知∠ABC∠∠CDE，∠B＝90°，点C为线段BD上一点，则∠ACE的度数为（）A．94°B．92°C．90°D．88°【答案】C【分析】由全等三角形的性质得出∠ACB＝∠CED，则可得出答案．【详解】解：∠∠ABC∠∠CDE，∠∠ACB＝∠CED，∠B＝∠D＝90°，∠∠CED+∠ECD＝90°，∠∠ACB+∠ECD＝90°，∠∠ACB+∠ECD+∠ACE＝180°，∠∠ACE＝90°．故选：C．【点睛】本题考查了全等三角形的性质；熟练掌握三角形全等的性质定理是解题的关键．17．（2020·河南·郑州市第八中学模拟预测）如图所示，一副三角尺摆放置在矩形纸片的内部，三角形的三个顶点恰好在矩形的边上，若16FGC ∠=︒，则AEF ∠等于（）A ．106︒B ．114︒C ．126︒D ．134︒【答案】D【分析】根据矩形的性质可得∠C=90°，AD∠BC ，利用直角三角形的两个锐角互余求出∠GFC ，从而求出∠EFB ，然后根据平行线的性质可得∠AEF ＋∠EFB=180°，从而求出结论．【详解】解：∠四边形ABCD 为矩形 ∠∠C=90°，AD∠BC ∠16FGC ∠=︒∠∠GFC=90°－∠FGC=74° 由三角尺可知：∠EFG=60° ∠∠EFB=180°－∠GFC －∠EFG=46° ∠AD∠BC∠∠AEF ＋∠EFB=180° ∠∠AEF=180°－∠EFB=134° 故选D ．【点睛】此题考查的是矩形的性质、直角三角形的性质和平行线的性质，掌握矩形的性质、直角三角形的两个锐角互余和平行线的性质是解决此题的关键．18．（2022·山东青岛·七年级期末）如图，小虎用10块高度都是4cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离为______．【答案】40 cm【分析】根据题意可得AC＝BC，∠ACB＝90°，AD∠DE，BE∠DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE ＝∠DAC ，再证明∠ADC ∠∠CEB 即可，利用全等三角形的性质进行解答．【详解】解：由题意得：AC ＝BC ，∠ACB ＝90°，AD ∠DE ，BE ∠DE ， ∠∠ADC ＝∠CEB ＝90°，∠∠ACD ＋∠BCE ＝90°，∠ACD ＋∠DAC ＝90°， ∠∠BCE ＝∠DAC ，在∠ADC 和∠CEB 中，ADC CEB DAC BCE AC BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∠∠ADC ∠∠CEB （AAS ）；由题意得：AD ＝EC ＝12cm ，DC ＝BE ＝28cm ， ∠DE ＝DC ＋CE ＝40（cm ），答：两堵木墙之间的距离为40cm ，故答案为：40 cm ．【点睛】此题主要考查了全等三角形的应用，涉及到垂直的定义、直角三角形的性质和连个三角形全等的判定与性质等知识点，解题的关键是正确找出证明三角形全等的条件．19．（2021·江苏盐城·七年级期中）将含有30角的直角三角板（30A ∠=︒）和直尺按如图方式摆放，已知136∠=︒，则2∠=______︒．【答案】24【分析】过点B 作BC //MN ，由平行线传递性，可得BC //KL ，再由平行线的性质可得1=LBC ∠∠ ，2=ABC ∠∠ ，最后由在直角三角形中两锐角互余的关系，求出2=24∠︒ ．【详解】解：过点B 作BC //MN ，如图所示：MN //KH∴ BC //KL1LBC ∴∠=∠又1=36∠︒=36LBC ∴∠︒又 BC //MN2=ABC ∴∠∠又=30A ∠︒=60ABL ∴∠︒又=ABL LBC ABC ∠∠+∠603624ABC ∴∠=︒-︒=︒224∴∠=︒故答案为：24【点睛】本题考查了平行线的判定与性质(两直线平行，内错角相等)，平行线传递性(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)，直角三角形中两锐角互余，角的和差计算等综合知识点．难点是作已知直线的平行线．20．（2022·全国·八年级专题练习）如图1，已知ABC ∆中，90ACB ∠=︒，AC BC =，BE 、AD 分别与过点C 的直线垂直，且垂足分别为E ，D ．(1)猜想线段AD 、DE 、BE 三者之间的数量关系，并给予证明．(2)如图2，当过点C 的直线绕点C 旋转到ABC ∆的内部，其他条件不变，如图2所示，∠线段AD 、DE 、BE 三者之间的数量关系是否发生改变？若改变，请直接写出三者之间的数量关系，若不改变，请说明理由；∠若 2.8AD =， 1.5DE =时，求BE 的长．【答案】(1)DE AD BE =+，证明见解析 (2)∠发生改变，DE AD BE =-；∠1.3【分析】（1）证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ，即可求解；（2）∠证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ，即可求解；∠由∠可得DE AD BE =-，从而得到BE AD DE =-，即可求解．（1）解：DE AD BE =+，理由如下： ∠BE 、AD 分别与过点C 的直线垂直， ∠90BEC ADC ∠∠=︒＝， ∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BECCAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝EC ＋CD ，DE AD BE ∴=+；（2）解：∠发生改变．∠BE 、AD 分别与过点C 的直线垂直，∠90BEC ADC ∠∠=︒＝，∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BEC CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝CE -CD ， ∠DE AD BE=-； ∠由∠知：DE AD BE =-， ∠ 2.8 1.5 1.3BE AD DE =-=-=， ∠BE 的长为1.3.【点睛】本题主要考查了全等三角形的判定和性质、等角的余角相等，熟练掌握全等三角形的判定和性质是解题的关键．◎模型五风筝模型【条件】四边形ABPC ，分别延长AB 、AC 于点D 、E ，如上左图所示. 【结论】∠PBD+∠PCE =∠A +∠P .【证明】如上右图，连接AP ，则：∠PBD =∠PAB +∠APB ，∠PCE =∠PAC +∠APC ，∴∠PBD+∠PCE=∠PAB +∠APB+∠PAC +∠APC=∠BAC +∠BPC ，得证.21．（2022·内蒙古赤峰·八年级期末）如图，将ABC 的一角折叠，若12130∠+∠=︒，则B C ∠+∠=（）A．50°B．65°C．115°D．130°【答案】C【分析】根据折叠性质证得∠3=∠4，∠5=∠6，再根据平角定义求得∠4+∠5=115°，然后根据三角形的内角和定理求解即可．【详解】解：如图，由折叠性质得：∠3=∠4，∠5=∠6，∠∠1+∠3+∠4=180°，∠5+∠6+∠2=180°，∠∠1+∠2+2∠4+2∠5=360°，∠∠1+∠2=130°，∠2∠4+2∠5=360°－130°=230°，∠∠4+∠5=115°，∠∠4+∠5+∠A=180°，∠A+∠B+∠C=180°，∠∠B+∠C=∠4+∠5=115°，故选：C．【点睛】本题考查三角形折叠中的角度问题，熟练掌握折叠性质是解答的关键.22．（2022·海南海口·七年级期末）如图，把∠ABC纸片沿MN折叠，使点C落在∠ABC内部点C′处，若∠C=36°，则∠1+∠2等于（）A ．54°B ．62°C ．72°D ．76°【答案】C【分析】根据折叠可知∠C =∠'C ，四边形内角和为360°，即可求出'CMC ∠+'CNC ∠，用平角的定义即可求出∠1+∠2【详解】∠∠CMN 折叠得到'C MN ∠∠C =∠'C∠∠1=180°-'CMC ∠，∠2=180°-'CNC ∠∠∠1+∠2=180°-'CMC ∠+180°-'CNC ∠=360°-（'CMC ∠+'CNC ∠） ∠'CMC ∠+'CNC ∠=360°-∠C -'C ∠=360°-36°-36°=288° ∠∠1+∠2=360°-288°=72° 故选：C【点睛】本题主要考查了折叠问题，掌握三角形的内角和定理，四边形的内角和以及平角的定义是解题的关键．23．（2022·山东烟台·七年级期中）如图，在三角形纸片ABC 中65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在∠ABC 内，若150∠=︒，则∠2的度数为_________.【答案】30°##30度【分析】根据题意，已知∠A =65°，∠B =75°，可结合三角形内角和定理和四边形内角和求解．【详解】解：如图，设折痕为DE ；∠65A ∠=︒，75B ∠=︒，∠180180657540C A B ∠=︒-∠+∠=︒-︒+︒=︒（）（）， ∠180140CDE CED C ∠+∠=︒-∠=︒，又∠150∠=︒，∠2360(1)36030030A B CED CDE ∠=︒-∠+∠+∠+∠+∠=︒-︒=︒，故答案为：30°．【点睛】本题主要是考查了三角形、四边形内角和，即三角形的内角和为180°，四边形的内角和为360°；熟练掌握三角形的内角和定理是解题的关键．24．（2022·湖北恩施·一模）图，把等边ABC 沿直线DE 折叠，点A 落在'A 处，若150∠=︒，则2∠=______．【答案】40︒【分析】先求出AED ∠的度数，再根据折叠得到AED A ED '∠=∠，即可求出2∠的度数．【详解】∠等边ABC 沿直线DE 折叠 ∠60A ∠=︒，AED A ED '∠=∠ ∠150∠=︒∠180170AED A ∠=︒-∠-∠=︒ ∠70AED A ED '∠=∠=︒∠420180AED A ED ∠=︒-'∠-∠=︒ 故答案为：40︒【点睛】此题考查翻折问题，折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．25．（2022·江苏·扬州市竹西中学七年级期末）如图∠，把∠ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A＝∠1+∠2．请你继续探索：(1)如果把∠ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图∠，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．(2)如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图∠，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）（1）解：如图所示，连接AA'，◎模型六两内角角平分线模型【条件】△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I. 【结论】A I ∠+︒=∠2190 【证明】∵BI 是∠ABC 平分线，∴ABC ∠=∠212∵CI 是∠ACB 平分线，∴ACB ∠=∠213 由A →B →I →C →A 的飞镖模型可知： ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 26．（2022·山东东营·七年级期末）如图，在△ABC 中，BF 平分△ABC ，CF 平分△ACB ，△BFC =125°，则△A 的度数为（）A ．60°B ．80°C ．70°D ．45°【答案】C【分析】先根据三角形内角和定理得出CBF BCF ∠+∠的度数，再由角平分线的性质得出ABC ACB ∠+∠的度数，根据三角形内角和定理即可得出结论．【详解】解：∠125BFC ∠=︒， ∠18012555BCF CBF ∠+∠=︒︒=︒﹣． ∠BF 平分ABC ∠，CF 平分ACB ∠，∠()2110ABC ACB BCF CBF ∠+∠=∠+∠=︒， ∠180A ABC ACB ∠+∠+∠=︒，∠18011070﹣．A∠=︒︒=︒故选：C ．【点睛】本题考查的是三角形内角和定理，以及三角形角平分线的定义，熟知三角形内角和是180°是解答此题的关键．27．（2022·福建·泉州五中七年级期末）如图，在四边形ABCD 中，∠A +∠D ＝α，∠ABC 的平分线与∠BCD 的平分线交于点P ，则∠P ＝（）A ．90°﹣12α B ．12αC ．90°+12α D ．360°﹣α28．（2022·河南鹤壁·七年级期末）已知ABC 中，A α∠=．在图1中B 、C ∠的平分线交于点1O ，则可计算得11902BO C α∠=︒+；在图2中，设B 、C ∠的两条三等分角线分别对应交于2O 、3O ，则3BO C ∠=_______________．【详解】解：Aα∠=，180ACB=︒-B∠、C∠的两条三等分角线分别对应交于332 ( 3CBO BCO ABC ∴∠+=∠3(BO C CBO∴∠=-∠+故答案为：【点睛】本题考查三角形内角和定理，解题的关键是熟练运用三等分角线求解．29．（2022·江苏常州·七年级期中）如图，在∠MBC中，∠ABC、∠ACB的角平分线OB、OC交于点O，若∠O=m°，则∠A的度数是______________________________°（用含m的代数式表示）．【答案】（2m-180）【分析】先由角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，再利用三角形内角和定理求解即可．【详解】解：∠OB，OC分别是∠ABC和∠ACB的角平分线，∠∠ABC=2∠OBC，∠ACB=2∠OCB，∠∠O+∠OBC+∠OCB=180°，∠∠OBC+∠OCB=180°-∠O=180°-m°，∠∠ABC+∠ACB=2∠OBC+2∠OCB=360°-2m°，∠∠A=180°-∠ABC-∠ACB=2m°-180°，故答案为：（2m-180）．【点睛】本题主要考查了三角形内角和定理，角平分线的定义，熟知相关知识是解题的关键．30．（2021·重庆·垫江第八中学校七年级阶段练习）在∠ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN∠BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．(1)如图1，若∠A=110°，∠BEC=130°，则∠2= °，∠3－∠1= °；(2)如图2，猜想∠3－∠1与∠A的数量关系，并证明你的结论；(3)若∠BEC=α，∠BDC=β，用含α和β的代数式表示∠3－∠1的度数．（直接写出结果即可）∠BD平分∠ABD，【点睛】本题主要考查了三角形内角和定理，三角形外角的像这种，角平分线的定义，垂直的定义，熟知三角形内角和为180度是解题的关键．◎模型七两外角角平分线模型【条件】△ABC 中，BI 、CI 分别是△ABC 的外角的角平分线，且相交于点O. 【结论】A O ∠-︒=∠2190. 【证明】∵BO 是∠EBC 平分线，∴EBC ∠=∠212，∵CO 是∠FCB 平分线，∴FCB ∠=∠215 由△BCO 中内角和定理可知：∠O =180°-∠2 -∠5 =180°-EBC ∠21 -FCB ∠21 =180°-)180(21ABC ∠-︒ -)180(21ACB ∠-︒=)(21ACB ABC ∠+∠=)180(21A ∠-︒=A O ∠-︒=∠2190. 31．（2022·江苏·江阴市祝塘第二中学七年级阶段练习）如图，在△ABC 中，设∠A ＝x °，∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2；…；∠A 2021BC 与∠A 2021CD 的平分线相交于点A 2022，得∠A 2022，则∠A 2022是（）度．A ．202012x B ．202112x C ．202212x D ．202312x∠∠A＝∠ACD−∠ABC，∠A1＝∠A1CD−∠A1BC，∠BA1和CA1分别是∠ABC和∠ACD的角平分线，32．（2022·浙江·八年级专题练习）如图，ABC 中，56A ∠=︒，BD 平分ABC ∠，CD 平分ABC 的外角ACE ∠，BD 、CD 交于点D ，则D ∠的度数（）A ．28︒B ．56︒C ．30D ．26︒BD 平分平分ABC 的外角DBC ∴∠=12DCE ACE =∠根据外角性质：DBC D +∠28D DCE α∴∠=∠-=︒．故选：A ．33．（2022·陕西·西安博爱国际学校八年级期末）如图，在∠ABC中，∠ABC=75°，∠A=40°，∠ACD是∠ABC的外角，若∠ABC与∠ACD的平分线交于点P，则∠BPC的大小为_____．∠34．（2022·陕西·西安市曲江第一中学八年级期末）如图，在ABC中，ABC的内角CAB∠和外角CBD 的角平分线交于点P，已知42∠=︒，则CAPB∠的度数为____________．【答案】84︒##84度为ABC外角CBD=∠C+∠以求出答案．【详解】解：如下图，。

《全等三角形》培优题型全集

《全等三角形》培优题型全集题型一：倍长中线（线段）造全等1、已知：如图，AD 是△ABC 的中线，BE 交AC 于E ，交AD 于F ，且 AE=EF ，求证：AC=BFC2、如图，△ABC 中，AB=5，AC=3，则中线AD 的取值范围是______.DCBA3、在△ABC 中,AC=5,中线AD=7，则AB 边的取值范围是( ) A 、1<AB<29 B 、4<AB<24C 、5<AB<19D 、9<AB<194、已知：AD 、AE 分别是△ABC 和△ABD 的中线，且BA=BD ，求证：AE=21AC CE5、已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ABFDEC题型二：截长补短1、已知，四边形ABCD 中，AB ∥CD ，∠1＝∠2，∠3＝∠4。

求证：BC ＝AB ＋CD 。

2、已知：如图，在△ABC 中，∠C ＝2∠B ，∠1＝∠2，求证：AB=AC+CD.3、如图，在△ABC 中，∠BAC=60°， AD 是∠BAC 的平分线，且AC=AB+BD ，求∠ABC 的度数DCBA4、已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．DOECB ADCB A 12题型三：角平分线上的点向角两边引垂线段1、如图，在四边形ABCD中，BC＞BA,AD＝CD，求证：∠BAD+∠C=180°DCBA2、如图，四边形ABCD中，AC平分∠BAD，CE⊥AB于E ，AD+AB=2AE，则∠B与∠ADC互补，为什么？3、如图，△ABD和△ACD，BD=CD，∠ABD=∠ACD,求证AD平分∠BAC.4、已知，AB＞AD，∠1＝∠2，CD＝BC。