北京市三种专利申请数量数据分析2018版

合集下载

中国专利发展成就、问题及建议

53New Economy Leader |2021年第01期 |摘要：中国近年来在知识产权保护上取得了巨大进步，迅速崛起成为年申请量和授权量居世界第一的专利大国，但在这亮丽增长的背后还存在哪些短板和不足？本文在梳理文献既有研究成果的基础上，结合对中外专利数据的比较和解读，归纳和总结中国专利量迅猛增长下出现的一些主要问题及其成因。

根据对这些成因的分析，我们推导出若干政策建议，希望有助于优化国家科技创新战略，使知识产权制度更有效地促进科技创新，提高我国专利产出的整体质量水平。

关键词：专利；中国；创新；知识产权中国专利发展：成就、问题及建议*□ 郦光伟陆丁一、中国专利发展取得历史性成就中国在知识产权的保护力度上取得巨大进步，显著体现在专利数量的迅速增长。

从1985年开始实施专利法后，中国的专利制度从无到有，专利数量由少到多。

自2011年起，中国在受理发明专利申请数量上超过了美国；自2015年起，又在发明专利授权量上超越美国，成为全球发明专利申请量和授权量的第一大国。

中国仅用30年时间就从零开始崛起为世界第一专利大国，堪称专利事业发展的奇迹。

近年来，中国通过世界知识产权组织《专利合作条约》（PCT）申请的专利在申请数量和授权率上都显著增长。

十年左右的时间里，中国从世界五大知识产权局中PCT 申请量最少的位置起步，由申请量只有美国的1/9，迅速迎头赶上，到2018年已经与多年来保持第一位申请量的美国持平。

PCT 申请的专利代表了申请人赋予其国际化的期待，与仅在国内申请的专利相比，其质量往往更高、创新性更强。

所以，中国PCT 专利量的增长，体现了中国专利总体质量的提升。

中国崛起为知识产权大国的原因是多方面的。

首先，近40年来中国经济实力的快速增长为科技研发投入提供了日益雄厚的物质基础。

中国研发强度（即研发经费在GDP 中所占比重）自2014年起一直在2%以上，与OECD 国家的平均水平逐年接近，研发年投入总额已经接近世界第一的美国。

资料分析——综合分析问题

真题五：2005年国考卷一第135题
2003年部分城市日照指数
135.针对上图日照数据，下面说法不正确的是（）。
A．拉萨日照最高月份的日照时数少于哈尔滨最高月份的日照时数
日照时数差别最小的是拉萨
D．10月份，各个城市的日照时数差别最小
我国的实用新型专利、外观设计专利和商标的年申请量已跃居世界第一，其中90％以上为国内申请。
135.下列说法正确的是（）。
A.我国的专利审批总体能力已居于世界前列
B.目前我国的各项专利年申请量均居于世界第一
C. “十五”末期，我国的专利在提交申请后的两年内都可完成审查
D.若同比增长不变，2005年全年我国的专利申请量将超过40万件
真题六：2004年国考第107题
1998～2002年广东省各类投资增长变化情况表（％）
年份
全社会固定资
产投资增速
基本建设
投资增速
更新改造
投资增速
房地产开发
投资增速
其他类
投资增速
1998
16.1
18.7
19.5
14.1
12.3
1999
13.5
15.9
12.6
17.8
6.1
2000
6.8
-6.3
11.8
真题四：2006年国考第121题
2004年广播、电视宣传基本情况表
130.根据上表所列数据，下列说法错误的是（）。
A.中央电视台只播自办节目
B.地方电视台播自办节目的时间占总播出时间的70％以上
C.地方电视台2004年全年平均每套节目播出自办教育节目0.213小时
D.地方无线广播电台2004年平均每天每套节目播出自办教育节目0.446小时

20-16 中国统计年鉴数据处理：分地区国内三种专利申请受理数和授权数(便于2005-2018多年数据分析对比)

7468
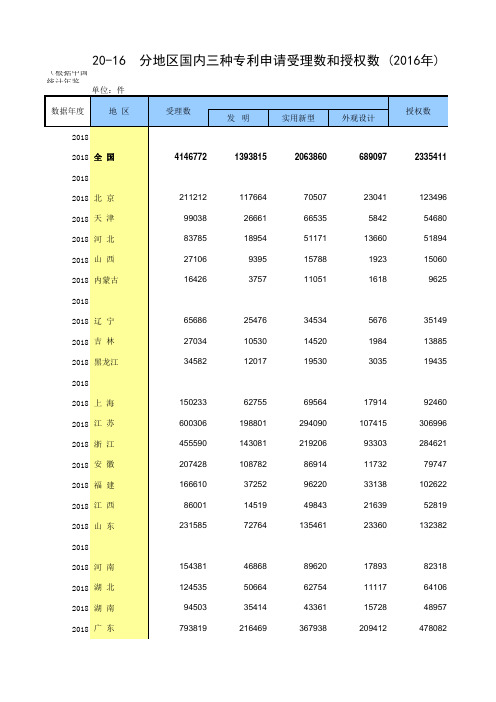
18361 4669
11172 1599 1388
106948 41675 35348 11311 6271
49871 20450
20500 7780
25456 10964
3915 1706
26495 11090
4330 489
6570 11697
2081 2297
73
8884 1280
298 744 923
21331 42019 32550 14846
9858 2524 20338
55581 200333 172451
55445 67822 34796 94249
15548 64644 79620
9456 24942 15499 17795
8339 11393
8261 53259
59417 44350 29132 268508
135461
23360
132382
2018
2018 河南
154381
46868
89620
17893
82318
2018 湖北
124535
50664
62754
11117
64106
2018 湖南
94503
35414
43361
15728
48957
2018 广东
793819
216469
367938
209412
455590
143081
219206
93303
284621
2018 安徽
207428
108782
86914
11732
79747

2022年人教版中考第二次模拟检测《数学卷》含答案解析

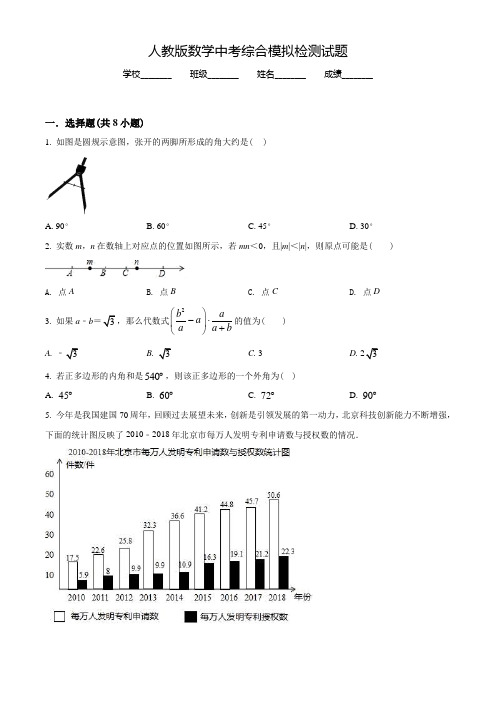
人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一．选择题(共8小题)1. 如图是圆规示意图，张开的两脚所形成的角大约是()A. 90°B. 60°C. 45°D. 30°2. 实数m，n在数轴上对应点的位置如图所示，若mn＜0，且|m|＜|n|，则原点可能是( )A. 点AB. 点BC. 点CD. 点D3. 如果a﹣b＝3，那么代数式2b aaa a b⎛⎫-⋅⎪+⎝⎭的值为( )A. ﹣3B. 3C. 3D. 234. 若正多边形的内角和是540︒，则该正多边形的一个外角为( )A. 45︒B. 60︒C. 72︒D. 90︒5. 今年是我国建国70周年，回顾过去展望未来，创新是引领发展的第一动力，北京科技创新能力不断增强，下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况．根据统计图提供的信息，下列推断合理的是( ) A. 2010﹣2018年，北京市毎万人发明专利授权数逐年增长B. 2010﹣2018年，北京市毎万人发明专利授权数的平均数超过10件C. 2010年申请后得到授权的比例最低D. 2018年申请后得到授权的比例最高6. 弹簧原长(不挂重物)15cm ，弹簧总长L (cm )与重物质量x (kg )的关系如下表所示：弹簧总长L (cm ) 16 17 18 19 20 重物重量x (kg )0.51.01.52.02.5当重物质量为5kg (在弹性限度内)时，弹簧总长L (cm )是( ) A. 22.5B. 25C. 27.5D. 307. 如图，抛物线2815y x x =-+与轴交于、两点，对称轴与轴交于点，点(0,2)D -，点(0,6)E -，点是平面内一动点，且满足90DPE ∠=︒，M 是线段PB 的中点，连结CM ．则线段CM 的最大值是( )．A. 3B.412C.72D. 58. 如图，点A ，B ，C 是⊙O 上的三个点，点D 在BC 的延长线上.有如下四个结论：①在∠ABC 所对的弧上存在一点E ，使得∠BCE =∠DCE ;②在∠ABC 所对的弧上存在一点E ，使得∠BAE =∠AEC ;③在∠ABC 所对的弧上存在一点E ，使得EO 平分∠AEC ;④在∠ABC 所对的弧上任意取一点E (不与点A ，C 重合) ，∠DCE=∠ABO +∠AEO 均成立.上述结论中，所有．．正确结论的序号是( )A. ①②③B. ①③④C. ②④D. ①②③④二．填空题(共8小题)9. 质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，投掷这个骰子一次，则向上一面的数字是偶数的概率为10. 用一组，，的值说明命题”若ac bc =，则a b =“是错误的，这组值可以是a =__________，b =__________，c =__________．11. 如图，某人从点A 出发，前进5m 后向右转60°，再前进5m 后又向右转60°，这样一直走下去，当他第一次回到出发点A 时，共走了_____m ．12. 如图所示的网格是正方形网格，△ABC 是_____三角形．(填”锐角”“直角”或”钝角”)13. 如图，过⊙O 外一点P 作⊙O 的两条切线P A ，PB ，切点分别为A ，B ，作直线BC ，连接AB ，AC ，若∠P ＝80°，则∠C ＝_____°．14. 如图，在矩形ABCD 中，过点B 作对角线AC 的垂线，交AD 于点E ，若AB ＝2，BC ＝4，则AE ＝_____．15. 2019年2月，全球首个5G 火车站在上海虹桥火车站启动.虹桥火车站中5G 网络峰值速率为4G 网络峰值速率的10倍.在峰值速率下传输8千兆数据，5G 网络比4G 网络快720秒，求这两种网络的峰值速率.设4G 网络的峰值速率为每秒传输x 千兆数据，依题意，可列方程为___.16. ▱ABCD 中，对角线AC 、BD 相交于点O ，E 是边AB 上的一个动点(不与A 、B 重合)，连接EO 并延长，交CD 于点F ，连接AF ，CE ，下列四个结论中： ①对于动点E ，四边形AECF 始终是平行四边形;②若∠ABC ＜90°，则至少存在一个点E ，使得四边形AECF 是矩形; ③若AB ＞AD ，则至少存在一个点E ，使得四边形AECF 菱形; ④若∠BAC ＝45°，则至少存在一个点E ，使得四边形AECF 是正方形．以上所有正确说法的序号是_____．三．解答题(共12小题)17.计算：052sin 60(2019)π-︒--18. 解不等式组: 4(21)31385x x x x -<+⎧⎪-⎨<⎪⎩19. 已知：如图1，直线，所成的角跑到画板外面去了，你有什么办法作出这两条直线所成角的角平分线? 小明的做法是： (1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，; (3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图： ∵PC a ∥∴1PDA ∠=∠( )∵以圆心，任意长为半径画圆弧，分别交直线，PC 于点， ∴PA PD =∴PAB ∠=∠ ∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形( ) 根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：．20. 已知关于的方程mx2+(2m-1)x+m-1=0(m≠0) .(1)求证：方程总有两个不相等的实数根;(2)若方程的两个实数根都是整数，求整数的值.21. 如图，在△ABC中，AB＝AC，D为BC中点，AE∥BD，且AE＝BD．(1)求证：四边形AEBD是矩形;(2)连接CE交AB于点F，若∠ABE＝30°，AE＝2，求EF的长．22. 在平面直角坐标系xOy中，直线l：y＝x+b与x轴交于点A(﹣2，0)，与y轴交于点B．双曲线ykx =与直线l交于P，Q两点，其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;(2)当点P的横坐标为2时，求k的值;(3)连接PO，记△POB的面积为S．若112S＜＜，结合函数图象，直接写出k的取值范围．23. 如图，AB是O的直径，CB与O相切于点B．点D在O上，且BC BD=，连接CD交O于点E．过点E作EF⊥AB于点H，交BD于点M，交O于点F．(1)求证：∠MED=∠MDE．(2)连接BE，若3ME=，MB=2．求BE的长．24. 为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理，描述和分析，下面给出了部分信息．a．甲部门成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x ＜90，90≤x≤100)b．乙部门成绩如下：40 52 70 70 71 73 77 78 80 8182 82 82 82 83 83 83 86 91 94c．甲、乙两部门成绩的平均数、方差、中位数如下：平均数方差中位数甲79.6 36.84 78.5乙77 147.2 md．近五年该单位参赛员工进入复赛的出线成绩如下：2014年2015年2016年2017年2018年出线成绩(百79 81 80 81 82分制)根据以上信息，回答下列问题：(1)写出表中m值;(2)可以推断出选择部门参赛更好，理由为;(3)预估(2)中部门今年参赛进入复赛的人数为．25. 如图，P是直径AB上的一点，AB=6，CP⊥AB交半圆AB于点C，以BC为直角边构造等腰Rt△BCD，∠BCD=90°，连接OD．小明根据学习函数的经验，对线段AP，BC，OD的长度之间的关系进行了探究．下面是小明的探究过程，请补充完整：(1)对于点P在AB上的不同位置，画图、测量，得到了线段AP，BC，OD的长度的几组值，如下表：位置1 位置2 位置3 位置4 位置5 位置6 位置…AP 0.00 1.00 2.00 3.00 4.00 5.00 …BC 6.00 5.48 4.90 4.24 3.46 2.45 …OD 6.71 7.24 7.07 6.71 6.16 5.33 …在AP，BC，OD的长度这三个量中，确定________的长度是自变量，________的长度和________的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中，画出(1)中所确定的函数的图象;(3)结合函数图象，解决问题：当OD=2BC时，线段AP的长度约为________．26. 在平面直角坐标系xOy中，抛物线y＝mx2﹣6mx+9m+1(m≠0)．(1)求抛物线的顶点坐标;(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧)，且AB＝4，求m的值．(3)已知四个点C(2，2)、D(2，0)、E(5，﹣2)、F(5，6)，若抛物线与线段CD和线段EF都没有公共点，请直接写出m的取值范围．27. 已知C为线段AB中点，∠ACM＝α．Q为线段BC上一动点(不与点B重合)，点P在射线CM上，连接P A，PQ，记BQ＝kCP．(1)若α＝60°，k＝1，①如图1，当Q为BC中点时，求∠P AC的度数;②直接写出P A、PQ的数量关系;(2)如图2，当α＝45°时．探究是否存在常数k，使得②中的结论仍成立?若存在，写出k的值并证明;若不存在，请说明理由．28. 对于平面直角坐标系xOy中的点P，Q，给出如下定义：若P，Q为某个三角形的顶点，且边PQ上的高h，满足h＝PQ，则称该三角形为点P，Q的”生成三角形”．(1)已知点A(4，0);①若以线段OA为底的某等腰三角形恰好是点O，A的”生成三角形”，求该三角形的腰长;②若Rt△ABC是点A，B“生成三角形”，且点B在x轴上，点C在直线y＝2x﹣5上，则点B的坐标为;(2)⊙T的圆心为点T(2，0)，半径为2，点M的坐标为(2，6)，N为直线y＝x+4上一点，若存在Rt△MND，x的取值范围．是点M，N的”生成三角形”，且边ND与⊙T有公共点，直接写出点N的横坐标N答案与解析一．选择题(共8小题)1. 如图是圆规示意图，张开的两脚所形成的角大约是()A. 90°B. 60°C. 45°D. 30°【答案】B【解析】【分析】观察图形，直接判断结果．【详解】解：观察图形，张开的两脚所形成的角大约是60，故选B．【点睛】本题考查了角的概念，正确的识别图形是解题的关键．2. 实数m，n在数轴上对应的点的位置如图所示，若mn＜0，且|m|＜|n|，则原点可能是( )A. 点AB. 点BC. 点CD. 点D【答案】B【解析】【分析】由若mn＜0可知，m、n异号，所以原点可能是点B或点C，而又由|m|＜|n|即可根据距离正确判断．【详解】解：∵mn＜0∴m、n异号∴原点可能是点B或点C又由|m|＜|n|，观察数轴可知，原点应该是点B．故选B．【点睛】本题考查的是绝对值的意义，利用数形结合的思想研究绝对值会让问题更加明确清晰，是一种常用的方法．3. 如果a ﹣b 2b a a a a b ⎛⎫-⋅ ⎪+⎝⎭的值为( )A. C. 3 D. 【答案】A【解析】【分析】先化简分式，然后将a ﹣b ＝代入计算即可．【详解】解：原式＝22b a a a a b⋅-+ ＝()()a b a b a a a b-+-⋅+ ＝﹣(a ﹣b )，∵a ﹣b，故选A ．【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算法则是解题的关键．4. 若正多边形的内角和是540︒，则该正多边形的一个外角为( )A. 45︒B. 60︒C. 72︒D. 90︒【答案】C【解析】【分析】根据多边形的内角和公式()2180n -•︒求出多边形的边数，再根据多边形的外角和是固定的360︒，依此可以求出多边形的一个外角．【详解】正多边形的内角和是540︒，多边形的边数为54018025︒÷︒+＝，多边形的外角和都是360︒，多边形的每个外角360572÷︒＝＝．故选．【点睛】本题主要考查了多边形的内角和与外角和之间的关系，关键是记住内角和的公式与外角和的特征，难度适中．5. 今年是我国建国70周年，回顾过去展望未来，创新是引领发展第一动力，北京科技创新能力不断增强，下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况．根据统计图提供的信息，下列推断合理的是( )A. 2010﹣2018年，北京市毎万人发明专利授权数逐年增长B. 2010﹣2018年，北京市毎万人发明专利授权数的平均数超过10件C. 2010年申请后得到授权的比例最低D. 2018年申请后得到授权的比例最高【答案】B【解析】【分析】根据统计图得出各年的具体数据，依据增长情况和百分比概念逐一判断即可得．【详解】解：A ．2010﹣2018年，北京市毎万人发明专利授权数在2012﹣2013年不变，此选项错误; B ．2010﹣2018年，北京市毎万人发明专利授权数的平均数为5.989.99.910.916.319.121.222.39++++++++≈13.7，超过10件，此选项正确; C ．2014年申请后得到授权的比例最低，此选项错误;D ．2017年申请后得到授权的比例最高，此选项错误;故选B ．【点睛】本题考查条形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．6. 弹簧原长(不挂重物)15cm ，弹簧总长L (cm )与重物质量x (kg )的关系如下表所示：弹簧总长L (cm )16 17 18 19 20 重物重量x (kg ) 0.5 1.0 1.5 2.0 2.5当重物质量为5kg (在弹性限度内)时，弹簧总长L (cm )是( )A. 22.5B. 25C. 27.5D. 30【答案】B【解析】【分析】根据表格数据，建立数学模型，进而利用待定系数法可得函数关系式，当x ＝5时，代入函数解析式求值即可．【详解】设弹簧总长L (cm )与重物质量x (kg )的关系式为L ＝kx +b ，将(0.5，16)、(1.0，17)代入，得：0.51617k b k b +=⎧⎨+=⎩，解得：k 2b 15=⎧⎨=⎩， ∴L 与x 之间的函数关系式为：L ＝2x +15;当x ＝5时，L ＝2×5+15＝25(cm ) 故重物为5kg 时弹簧总长L 是25cm ，故选B ．【点睛】此题主要考查根据实际问题列一次函数关系式，解决本题的关键是得到弹簧长度的关系式，难点是得到x 千克重物在原来基础上增加的长度．7. 如图，抛物线2815y x x =-+与轴交于、两点，对称轴与轴交于点，点(0,2)D -，点(0,6)E -，点是平面内一动点，且满足90DPE ∠=︒，M 是线段PB 的中点，连结CM ．则线段CM 的最大值是( )．A. 3B. 412C.72D. 5【答案】C【解析】【分析】解方程x2−8x＋15＝0得A(3，0)，利用抛物线的性质得到C点为AB的中点，再根据圆周角定理得到点P 在以DE为直径的圆上，圆心Q点的坐标为(−4，0)，接着计算出AQ＝5，⊙Q的半径为2，延长AQ交⊙Q于F，此时AF的最大值为7，连接AP，利用三角形的中位线性质得到CM＝12AP，从而得到CM的最大值．【详解】解方程x2−8x＋15＝0得x1＝3，x2＝5，则A(3，0)，∵抛物线的对称轴与x轴交于点C，∴C点为AB的中点，∵∠DPE＝90°，∴点P在以DE为直径的圆上，圆心Q点的坐标为(−4，0)，AQ＝2234＝5，⊙Q的半径为2，延长AQ交⊙Q于F，此时AF最大，最大值为2＋5＝7，连接AP，∵M是线段PB的中点，∴CM为△ABP为中位线，∴CM＝12 AP，∴CM的最大值为72．故选：C．【点睛】本题考查了抛物线与x轴的交点：把求二次函数y＝ax2＋bx＋c(a，b，c是常数，a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质和圆周角定理．8. 如图，点A，B，C是⊙O上的三个点，点D在BC的延长线上.有如下四个结论：①在∠ABC所对的弧上存在一点E，使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E，使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E，使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A，C重合)，∠DCE=∠ABO +∠AEO均成立.上述结论中，所有．．正确结论的序号是( )A. ①②③B. ①③④C. ②④D. ①②③④【答案】D【解析】【分析】①当BE是⊙O的直径时，根据圆周角定理和邻补角的定义得到结论;②当AE∥BC时，得到弧AB=弧CE，根据圆周角定理得到结论;③当点E是弧AC的中点时，根据角平分线的定义得到结论;④根据圆内接四边形的性质和四边形的内角和得到结论．【详解】解：①当BE是⊙O的直径时，∠BCE=∠DCE=90°，故①正确;②当AE∥BC时，弧AB=弧CE，∴弧BCE=弧ABC，∴∠BAE=∠AEC;故②正确;③当点E是弧AC的中点时，EO平分∠AEC;故正确;④如图2，∵∠A=∠ECD，∠A+12∠BOE=180°，∴∠ABO+∠AEO=360°-∠A-∠BOE=360°-∠DCE-2(180°-∠COE)，∴∠DCE=∠ABO+∠AEO，故正确;故选D ．【点睛】本题考查圆周角定理，解题关键是正确的理解题意．二．填空题(共8小题)9. 质地均匀的正方体骰子，其六个面上分别刻有1，2，3，4，5，6六个数字，投掷这个骰子一次，则向上一面的数字是偶数的概率为【答案】12 【解析】【分析】向上一面的数字是偶数的情况数除以总情况数6即为所求的概率．【详解】解：正方体骰子，六个面上分别刻有的1，2，3，4，5，6六个数字中，偶数为2，4，6，则向上一面的数字是偶数的概率为3162=．【点睛】明确概率的意义是解答的关键，用到的知识点为：概率等于所求情况数与总情况数之比． 10. 用一组，，的值说明命题”若ac bc =，则a b =“是错误的，这组值可以是a =__________，b =__________，c =__________．【答案】 (1). -1 (2). -2 (3). 0【解析】【分析】根据题意选择a 、b 、c 的值即可．【详解】当c ＝0，a ＝−1，b ＝−2，所以ac ＝bc ，但a ≠b ，当c ＝0，a ＝3，b ＝−2，所以ac ＝bc ，但a ≠b ，故答案不唯一;故答案为：-1;-2，0．【点睛】本题考查了命题与定理，要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．11. 如图，某人从点A出发，前进5m后向右转60°，再前进5m后又向右转60°，这样一直走下去，当他第一次回到出发点A时，共走了_____m．【答案】30【解析】【分析】从A点出发，前进5m后向右转60°，再前进5m后又向右转60°，…，这样一直走下去，他第一次回到出发点A时，所走路径为正多边形，根据正多边形的外角和为360°，判断多边形的边数，再求路程．【详解】解：依题意可知，某人所走路径为正多边形，设这个正多边形的边数为n，则60n＝360，解得n＝6，∴他第一次回到出发点A时一共走了：5×6＝30(m)，故答案为30．【点睛】本题考查了多边形的外角和，正多边形的判定与性质．关键是根据每一个外角判断多边形的边数．12. 如图所示的网格是正方形网格，△ABC是_____三角形．(填”锐角”“直角”或”钝角”)【答案】锐角【解析】【分析】根据三边的长可作判断．【详解】解：∵AB2＝32+12＝10，AC2＝12+42＝17，BC2＝32+42＝25，∴AB2+AC2＞BC2，∴△ABC为锐角三角形，故答案为锐角．【点睛】本题考查了三边的关系，会利用三边关系确定三角形的形状：若三角形的三边分别为a、b、c，①当a2+b2＞c2时，△ABC为锐角三角形;②当a2+b2＜c2时，△ABC为钝角三角形;③当a2+b2＝c2时，△ABC为直角三角形．13. 如图，过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，作直线BC，连接AB，AC，若∠P＝80°，则∠C＝_____°．【答案】50【解析】【分析】根据切线的性质得出∠P AO＝∠PBO＝90°，求出∠AOB的度数，根据圆周角定理求出∠C即可．【详解】解：连接OA，∵过⊙O外一点P作⊙O的两条切线P A，PB，切点分别为A，B，∴∠P AO＝∠PBO＝90°，∵∠P＝80°，∴∠AOB＝360°﹣90°﹣90°﹣80°＝100°，∴∠C＝12AOB＝50°，故答案为50．【点睛】本题考查了切线的性质，圆周角定理等知识点，能求出∠AOB的度数和根据圆周角定理得出∠C＝12AOB是解此题的关键．14. 如图，在矩形ABCD中，过点B作对角线AC的垂线，交AD于点E，若AB＝2，BC＝4，则AE＝_____．【答案】1【解析】【分析】根据矩形的性质得到∠DAB＝∠ABC＝90°，AD＝BC＝4，根据勾股定理得到AC＝22AB BC+＝25，设AC与BE交于F，根据相似三角形的性质即可得到结论．【详解】解：∵四边形ABCD是矩形，∴∠DAB＝∠ABC＝90°，AD＝BC＝4，∴AC＝22AB BC+＝25，设AC与BE交于F，∵BE⊥AC，∴AB2＝AF•AC，∴AF＝2225525=，∴CF＝AC﹣AF＝855，∵AE∥BC，∴△AEF∽△CBF，∴AE AF BC CF=，∴255 4855AE=，∴AE＝1，故答案为1．【点睛】本题考查了矩形的性质，相似三角形的判定和性质，勾股定理，熟练掌握正方形的性质是解题的关键．15. 2019年2月，全球首个5G火车站在上海虹桥火车站启动.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输8千兆数据，5G网络比4G网络快720秒，求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x千兆数据，依题意，可列方程为___.【答案】8872010x x-=【解析】【分析】设4G网络的峰值速率为每秒传输x千兆，则5G网络的峰值速率为每秒传输10x千兆，根据在峰值速率下传输8千兆数据，5G网络快720秒列出方程即可．【详解】解：设4G网络的峰值速率为每秒传输x千兆，则5G网络的峰值速率为每秒传输10x千兆，根据题意，得8872010x x-=．故答案为8872010x x-=．【点睛】本题考查了由实际问题抽象出分式方程，理解题意，找到等量关系列出方程是解题的关键．16. ▱ABCD中，对角线AC、BD相交于点O，E是边AB上的一个动点(不与A、B重合)，连接EO并延长，交CD于点F，连接AF，CE，下列四个结论中：①对于动点E，四边形AECF始终是平行四边形;②若∠ABC＜90°，则至少存在一个点E，使得四边形AECF是矩形;③若AB＞AD，则至少存在一个点E，使得四边形AECF是菱形;④若∠BAC＝45°，则至少存在一个点E，使得四边形AECF是正方形．以上所有正确说法的序号是_____．【答案】①③④【解析】分析】①根据平行四边形的性质得AB∥DC，OA＝OC，再由平行线的性质和对顶角相等可得∠OAE＝∠OCF，∠AOE＝∠COF，根据ASA来判定△AOE≌△COF，推出AE=CF,由此可判断四边形为平行四边形;②根据矩形的判定定理可知，当CE⊥AB时，四边形AECF为矩形，而图2-2中，AB<AD时，点E不在线段AB上;③根据菱形的判定定理可知：当EF⊥AC时，四边形AECF为菱形;④当CE⊥AB且∠BAC＝45°时，四边形AECF为正方形，在AB上一定存在一点E【详解】解：(1)如图1，∵四边形ABCD为平行四边形，对角线AC与BD交于点O，∴AB∥DC，AB＝DC，OA＝OC，OB＝OD，∴∠OAE＝∠OCF，∵∠AOE＝∠COF，∴△AOE≌△COF(ASA)，∴AE＝CF，又∵AE∥CF，∴四边形AECF为平行四边形，即E在AB上任意位置(不与A、B重合)时，四边形AECF恒为平行四边形，故选项①正确;(2)如图2，当∠ABC＜90°,当CE⊥AB时，四边形AECF为矩形，在图2中，AB>AD时，存在一点E, 使得四边形AECF是矩形;而图2-2中，AB<AD时，点E不在线段AB上;故选项②不正确．(3)如图3，当EF⊥AC时，四边形AECF为菱形，∵AB＞AD，∴在AB 上一定存在一点E, 使得四边形AECF 是矩形;故选项③正确．(4)如图4，当CE ⊥AB 且∠BAC ＝45°时，四边形AECF 为正方形，故选项④正确．故答案为：①③④．【点睛】本题主要考查平行四边形以及几种特殊平行四边形的判定．熟悉平行四边形、矩形、菱形、正方形的判定方法是解答此题的关键．三．解答题(共12小题)17. 计算：05122sin 60(2019)π-︒-- 【答案】4 3.+【解析】【分析】原式第一项利用绝对值的代数意义化简，第二项化为最简二次根式，第三项利用利用特殊角的三角函数值计算，第四项利用零指数幂法则计算，最后进行加减运算即可. 【详解】()05122sin602019π-︒--， =35321+-， =4 3.【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 18. 解不等式组: 4(21)31385x x x x -<+⎧⎪-⎨<⎪⎩ 【答案】4x 1-<<.【解析】【分析】分别解出两不等式的解集，再求其公共解．【详解】()42131385x x x x ⎧-+⎪⎨-⎪⎩＜①＜② 解不等式①得：x ＜1，解不等式②得：x ＞-4，所以不等式组的解集为：-4＜x ＜1．【点睛】此题考查解一元一次不等式组，求不等式组的解集应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．19. 已知：如图1，直线，所成的角跑到画板外面去了，你有什么办法作出这两条直线所成角的角平分线? 小明的做法是：(1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，;(3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图：∵PC a ∥∴1PDA ∠=∠( )∵以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，∴PA PD =∴PAB ∠=∠∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形( )根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：．【答案】两直线平行，同位角相等;PDA ;等角对等边;等腰三角形三线合一【解析】【分析】根据平行线的性质及圆的特点得到1PAB ∠=∠，故可得以直线，的交点和点、为顶点所构成的三角形为等腰三角形，然后根据等腰三角形三线合一即可作图．【详解】(1)如图2，画PC a ∥;(2)以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，;(3)连结AD 并延长交直线于点;请你先完成下面的证明，然后完成第(4)步作图：∵PC a ∥∴1PDA ∠=∠(两直线平行，同位角相等)∵以为圆心，任意长为半径画圆弧，分别交直线，PC 于点，∴PA PD =∴PAB ∠=∠PDA∴1PAB ∠=∠∴以直线，的交点和点、为顶点所构成的三角形为等腰三角形(等角对等边)根据上面的推理证明完成第(4)步作图(4)请在图2画板内作出”直线，所成的跑到画板外面去的角”的平分线(画板内的部分)，尺规作出图形，并保留作图痕迹．第(4)步这么作图的理论依据是：等腰三角形三线合一故答案为：两直线平行，同位角相等;PDA ;等角对等边;等腰三角形三线合一．【点睛】此题主要考查复杂尺规作图，解题的关键是熟知平行线的性质、圆的基本性质及等腰三角形的判定与性质．20. 已知关于的方程mx 2+(2m-1)x+m-1=0(m≠0) .(1)求证：方程总有两个不相等的实数根;(2)若方程的两个实数根都是整数，求整数的值.【答案】(1)证明见解析(2)m=1或m=-1【解析】试题分析：(1)由于m≠0，则计算判别式的值得到1=，从而可判断方程总有两个不相等的实数根;(2)先利用求根公式得到1211,1x xm=-=-，然后利用有理数的整除性确定整数的值．试题解析：(1)证明：∵m≠0，∴方程为一元二次方程，2(21)4(1)10m m m=---=>，∴此方程总有两个不相等的实数根;(2)∵(21)12mxm--±=，1211,1x xm∴=-=-，∵方程的两个实数根都是整数，且m是整数，∴m=1或m=−1.21. 如图，在△ABC中，AB＝AC，D为BC中点，AE∥BD，且AE＝BD．(1)求证：四边形AEBD是矩形;(2)连接CE交AB于点F，若∠ABE＝30°，AE＝2，求EF的长．【答案】(1)证明见解析27．【解析】【分析】(1)由AE∥BD，且AE＝BD可得四边形AEBD是平行四边形,再根据AB＝AC，D为BC中点,可知AD⊥BC 即可得出四边形AEBD是矩形.(2)根据30°所对的直角边是斜边的一半即可求出EB,再根据矩形的性质求出BC即可利用勾股定理求出EC,由题意可证△AEF∽△BCF,再根据对应边成比例即可求出结果.【详解】(1)证明：∵AE∥BD，AE＝BD，∴四边形AEBD是平行四边形，∵AB＝AC，D为BC的中点，∴AD⊥BC，∴∠ADB＝90°，∴四边形AEBD是矩形．(2)解：∵四边形AEBD是矩形，∴∠AEB＝90°，∵∠ABE＝30°，AE＝2，∴BE＝23，BC＝4，∴EC＝27，∵AE∥BC，∴△AEF∽△BCF，∴12 EF AECF BC，∴EF13=EC=273．【点睛】本题为矩形与等腰三角形的结合题型,关键在于熟练掌握矩形与等腰三角形的性质.22. 在平面直角坐标系xOy中，直线l：y＝x+b与x轴交于点A(﹣2，0)，与y轴交于点B．双曲线ykx =与直线l交于P，Q两点，其中点P的纵坐标大于点Q的纵坐标(1)求点B的坐标;(2)当点P的横坐标为2时，求k的值;(3)连接PO，记△POB的面积为S．若112S＜＜，结合函数图象，直接写出k的取值范围．【答案】(1)点B的坐标为(0，2);(2)k的值为8;(3)54＜k＜3.【解析】【分析】(1)有点A的坐标，可求出直线的解析式，再由解析式求出B点坐标．(2)把点P的横坐标代入直线解析式即可求得点P的纵坐标，然后把点P代入反比例函数解析式即可得k值．(3)根据△POB的面积为S的取值范围求点P的横坐标取值，然后把横坐标代入直线解析式，即可求得点P 纵坐标的取值范围，进而求得k的取值范围．【详解】解：(1)∵直线l：y＝x+b与x轴交于点A(﹣2，0)∴﹣2+b＝0∴b＝2∴一次函数解析式为：y＝x+2∴直线l与y轴交于点B为(0，2)∴点B的坐标为(0，2);(2)∵双曲线ykx=与直线l交于P，Q两点∴点P在直线l上∴当点P的横坐标为2时，y＝2+2＝4 ∴点P的坐标为(2，4)∴k＝2×4＝8∴k的值为8(3)如图：S△BOP12=⨯2×x p＝x p，∵11 2S＜＜，∴12＜x p＜1，∴52＜y p＜3，∴54＜k＜3【点睛】本题主要涉及一次函数与反比例函数相交的知识点．根据交点既在一次函数上又在反比例函数上，即可解决问题．23. 如图，AB 是O 的直径，CB 与O 相切于点B ．点D 在O 上，且BC BD =，连接CD 交O 于点E ．过点E 作EF ⊥AB 于点H ，交BD 于点M ，交O 于点F ． (1)求证：∠MED=∠MDE ．(2)连接BE ，若3ME =，MB=2．求BE 的长．【答案】(1)证明见解析;(2)10【解析】【分析】(1)由题意得//EF BC ，则C DEM ∠=∠，又C MDE ∠=∠，则结论得证;(2)连BE ，BE BF =，可得BEF D ∠=∠，可证BEM BDE ∆∆∽，则2BE BM BD =，可求BE 的长．【详解】(1)证明：CB 与O 相切于点，OB BC ∴⊥，EF AB ⊥，//EF BC ∴，DEM C ∴∠=∠，BC BD =，C MDE ∴∠=∠，MED MDE ∴∠=∠;(2)EF AB ⊥，AB 是O 的直径，BE BF =，D BEF ∴∠=∠，EBM DBE ∠=∠，BEM BDE ∆∆∽，BE BD BM BE=，即2BE BM BD =， MED MDE ∠=∠3∴==ME MDBM=,2BD MB MD∴=+=5BE=．10【点睛】本题主要考查了等腰三角形和平行线之间的角度转化以及圆周角定理和相似综合，熟练的在圆中找出对应的相似三角形是求解本题的关键.24. 为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理，描述和分析，下面给出了部分信息．a．甲部门成绩的频数分布直方图如下(数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x ＜90，90≤x≤100)b．乙部门成绩如下：40 52 70 70 71 73 77 78 80 8182 82 82 82 83 83 83 86 91 94c．甲、乙两部门成绩的平均数、方差、中位数如下：平均数方差中位数甲79.6 36.84 78.5乙77 147.2 md．近五年该单位参赛员工进入复赛的出线成绩如下：2014年2015年2016年2017年2018年出线成绩(百79 81 80 81 82分制)。

中国(北京)知识产权保护中心专利快速预审备案管理办法

中国（北京）知识产权保护中心专利快速预审备案管理办法（试行）第一条按照《关于严格专利保护的若干意见》(国知发管字〔2016〕93号）、《关于开展知识产权快速协同保护工作的通知》（国知发管字〔2016〕92号）等相关工作要求，为发挥中国（北京）知识产权保护中心专利快速预审服务支撑产业创新发展的积极作用，规范专利快速预审服务申请主体备案工作，特制定本办法。

第二条中国（北京）知识产权保护中心（以下简称“北京保护中心”）负责北京市相关产业专利快速预审备案管理工作。

第三条本办法所称备案主体，是指在北京保护中心所服务区域内进行登记注册，拟申请北京保护中心专利快速审查与确权预审服务并进行备案登记的企事业单位。

本办法所称申请主体，是指在北京保护中心完成备案，通过北京保护中心快速预审通道提交专利预审申请的单位。

第四条对申请主体的备案工作遵循科学、公平、公开、规范的原则。

第五条备案主体备案应当满足如下条件：（一）登记注册地在北京市行政区域，且具有独立法人资格的企业、事业单位。

（二）属于新一代信息技术产业或高端装备制造产业领域。

（三）具有良好的知识产权工作基础，有稳定的知识产权管理团队，建立规范的知识产权管理制度。

第六条备案主体应提供下列备案材料：（一）中国（北京）知识产权保护中心专利快速审查确权业务备案申请表（试行）（附件1）。

（二）企业营业执照复印件或事业法人证书复印件（加盖公章）。

（三）北京保护中心要求提供的其他证明材料。

第七条备案主体申请备案时，应当递交备案材料；北京保护中心对备案材料进行初步审核，形成拟备案申请主体名录，经复核、确认后，备案完成。

第八条定期分析申请主体在快速预审工作中存在的问题，在听取申请主体的意见陈述后进行评价。

对于评价不合格的申请主体，根据评价结果酌情取消其备案，并通知申请主体。

第九条对完成备案的申请主体，有下列情形之一的，一经发现，立即取消其备案：（一）提交虚假材料的；（二）违反国家知识产权局《关于规范专利申请行为的若干规定(2017)(局令第75号)第三条的规定，并被国家知识产权局标记有非正常申请案件的；（三）专利申请经预审合格、进入快速审查通道后，违反《中国（北京）知识产权保护中心专利申请须知》（附件2）及《承诺书》（附件3）要求，导致专利快速审查无法顺利进行的；（四）对提交专利预审材料质量不高、经过反复多次修改仍达不到预期要求，且数量占其提交的专利预审申请的50%以上的；（五）专利申请获得授权后，一年内专利权转让超过5件且未报备或者报备理由明显不充分的；（六）有不良信用记录的。

基于专利的北京市知识创新能力现状分析

年专利申请量／上一年专利申请量。（５）区域即时影响因素，即区域近五年专利当年被引次数／所有近五年专利当年被引次数。（６）区域技术强度，即区域专利数量区域专利即时影响指数④ 。通过对这些指标的测量则可以得出
年以来，北京市专利产出中外观设计型数量远远小于实用新型和发明专利，发明专利数量在整体上始终高于实用新
型和外观设计专利。近五年来，外观设计的绝对数量并非始终呈增长态势，其中，２ＯＯ８年至２ＯＯ９年和２０１０年至２０１１年均出现递减现象，虽然２Ｏ０９年至２０１０年外观设计的数
量增长迅速，翻了一番，但总量始终不足实用新型和发明
产业经济
基于专利的北京市知识
创新能力现状分析木
●晋佳雯洪倩蒋贵凰
［内容提要］本文基于专利产出与知识创新能力间的关系，依据近十年来北京市的专利产出情况，分析了
北京市４￣ｉｅ，＇ｔ，Ｊ新能力现状，从行业角度看，北京市的创新能力主要集中在生活需要，作业、运输，化学冶金方面；
照创新知识的构成以及创新方式可以分为原始创新能力、集成创新能力和引进知识再创新能力。本文综合各类创新能力的分类方式，按照投入创新元素的多少及投入新科技、新思想的复杂程度，将知识创新分为知识创造能力和
指一个国家或组织创造、整合、运用知识，实现管理或技术
上的突破的能力②，它受到知识创新的导向能力、知识创新
键组成部分。现有知识能力可以通过现有专利申请情况反映，主要可以通过对以下指标的测量分析得出：（１）近几

大数据时代的专利运用策略-题库

继续教育-大数据时代的专利运用策略题库1.国家知识产权局（专利审查）能力成为世界五大强局之一。

2.构建中国专利运营体系的目的是（支撑创新驱动发展）3.国家专利导航试点工程首批试点园区包括：长春生物医药专利导航示范区、上海张江生物医药专利导航示范区、杭州物联网专利导航示范区4.国家知识产权局下属（专利局）成为世界五大强局之一。

5.根据本讲，2018年我国进行了第（5）批专利导航试点工程。

6.（专利运营）是高价值的专利应用，是知识产权的价值最大化的实现。

7.下列选项中属于区域创新质量评价专利导航应用城市是（武汉）8.下列选项中属于超硬材料产业发展方向的是（产业链和专利布局的关联、产业竞争中的专利控制力、专利布局揭示出的产业发展方向）9.本课中，（美国）超硬材料产业布局的优化路径为产业价值链环节的结构优化和产业链不断升级奠定了基础。

10.郑州超硬材料产业链与专利布局的关系是（如影随形）。

11.超硬材料产业共有（三次）转移，每次转移和专利布局时间、区域演进完全吻合，完全匹配。

12.（科学技术）是引领发展的第一动力。

13.《国家知识产权战略纲要》颁布后，连续（7年）按照制度运行三大板块实施专利战略年度推进计划。

主要任务是（制度运行保障体系、支撑经济社会发展、制度创新）。

14.区域类专利导航强调（匹配度）15.通过实践、探索和总结，专利导航项目包括（区域布局、人才管理、科技研发）。

16.下列选项中属于区域创新质量评价类专利导航应用城市是（武汉）。

17.专利导航源于（专利信息）的公开。

18.区域类专利导航项目包括（创新要素投入、专利匹配度、区域创新发展竞争力）19.通过实践、探索和总结，专利导航项目包括：产业规划、区域布局、研发立项20.（）HSV-1技术发展方向重组治疗性基因或调节性基因的优化溶瘤病毒系统改进和优化溶瘤病毒启动子改进和优化溶瘤病毒联用21.在信息公开属性中体现，如果要开展创新活动，充分利用发明创造信息可以为新活动节约40%的（时间成本）和60%的（经费成本）22.大数据发展的重大意义为（大数据成为推动经济发展的新动力、大数据成为社会监督的新方式、大数据成为重塑国家竞争优势的新机遇、大数据成为新时达经济效益提升的新能源）。

河南省专利发展现状分析与展望

河南科技Henan Science and Technology知识产权与专利导航总第818期第24期2023年12月收稿日期：2023-10-30作者简介：林璐（1968—），女，本科，副研究馆员，研究方向：图书资料。

河南省专利发展现状分析与展望林璐（河南工业大学，河南郑州450000）摘要：【目的】以国家知识产权局和河南省统计局发布的河南统计年鉴为参考，从多个维度分析河南省专利发展现状。

【方法】统计分析河南省2010—2022年三种专利申请受理量、授权量及2022年河南省的详细数据，如申请专利类型、专利增长、专利占比、专利申请团体、专利运营情况等，来深入发掘河南省专利发展中存在的问题，并提出相应的解决问题的对策。

【结果】河南省专利发展存在高校专利转化率低、企业对专利申请后运营不当、专利层次不够丰富、核心专利占比不够理想等问题。

【结论】可以通过构建知识产权协同治理体系、加强知识产权人才建设、夯实专利保护体制机制建设、发展专利密集型产业等措施促进河南省专利高质量发展。

关键词：河南；专利；发展现状；展望中图分类号：G306文献标志码：A文章编号：1003-5168（2023）24-0131-04DOI ：10.19968/ki.hnkj.1003-5168.2023.24.027Analysis and Prospect of Patent Development in Henan ProvinceLIN Lu(Henan University of Technology,Zhengzhou 450000,China)Abstract:[Purposes ]Taking China National Intellectua Property Administration and the Henan Statisti⁃cal Yearbook issued by the Henan Provincial Bureau of Statistics as a reference,this paper analyzes the current situation of patent development in Henan Province from multiple dimensions.[Methods ]Statisti⁃cal analysis of the acceptance and authorization of three kinds of patent applications in Henan Provincefrom 2010to 2022and detailed data of Henan Province in 2022.Such as the type of patent application,patent growth,patent proportion,patent application group,patent operation,etc.,to explore the problemsexisting in the development of patents in Henan Province,and put forward corresponding countermea⁃sures to solve the problems.[Findings ]There are some problems in patent development in Henan Prov⁃ince,such as low patent conversion rate in universities,improper operation of enterprises after patent ap⁃plication,insufficient patent level,and unsatisfactory proportion of core patents.[Conclusions ]By con⁃structing a collaborative governance system of intellectual property rights,strengthening the construction of intellectual property talents,consolidating the construction of patent protection system and mecha⁃nism,and developing patent-intensive industries,we will promote the high-quality development of pat⁃ents in Henan Province..Keywords:Henan province;patents;current situation;prospect引言2004年，我国政府工作报告中首次提出“中部崛起”战略，并于2006年被正式确定为国家战略［1］。

内蒙古国内三种专利申请数量数据分析报告2019版

内蒙古国内三种专利申请数量数据分析报告2019版引言本报告借助数据对内蒙古国内三种专利申请数量进行深度剖析，从专利申请总数量，发明专利申请数量，实用新型专利申请数量，外观设计专利申请数量等方面进行阐述，以全面、客观的角度展示内蒙古国内三种专利申请数量真实现状及发展脉络，为组织及个人制定战略、为投资者投资提供参考和借鉴。

内蒙古国内三种专利申请数量数据分析报告相关知识产权为发布方即我公司天津旷维所有，任何机构及个人引用我方报告，均需注明出处。

内蒙古国内三种专利申请数量分析报告的数据来源于权威政府部门如中国国家统计局、重点科研机构及行业协会等，数据以事实为基准，公正，客观、严谨。

内蒙古国内三种专利申请数量数据分析报告旨在全面梳理内蒙古国内三种专利申请数量的真实现状、发展脉络及趋势，相信能够为从业者、投资者和研究者提供有意义的启发和借鉴。

目录第一节内蒙古国内三种专利申请数量和授权数量现状概况 (1)第二节内蒙古专利申请总数量指标分析（均指国内三种专利） (3)一、内蒙古专利申请总数量现状统计 (3)二、全国专利申请总数量现状统计 (3)三、内蒙古专利申请总数量占全国专利申请总数量比重统计 (3)四、内蒙古专利申请总数量（2016-2018）统计分析 (4)五、内蒙古专利申请总数量（2017-2018）变动分析 (4)六、全国专利申请总数量（2016-2018）统计分析 (5)七、全国专利申请总数量（2017-2018）变动分析 (5)八、内蒙古专利申请总数量同全国专利申请总数量（2017-2018）变动对比分析 (6)第三节内蒙古发明专利申请数量指标分析(均指国内三种专利) (7)一、内蒙古发明专利申请数量现状统计 (7)二、全国发明专利申请数量现状统计分析 (7)三、内蒙古发明专利申请数量占全国发明专利申请数量比重统计分析 (7)四、内蒙古发明专利申请数量（2016-2018）统计分析 (8)五、内蒙古发明专利申请数量（2017-2018）变动分析 (8)六、全国发明专利申请数量（2016-2018）统计分析 (9)七、全国发明专利申请数量（2017-2018）变动分析 (9)八、内蒙古发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比分析 (10)第四节内蒙古实用新型专利申请数量指标分析（均指国内三种专利） (11)一、内蒙古实用新型专利申请数量现状统计 (11)二、全国实用新型专利申请数量现状统计分析 (11)三、内蒙古实用新型专利申请数量占全国实用新型专利申请数量比重统计分析 (11)四、内蒙古实用新型专利申请数量（2016-2018）统计分析 (12)五、内蒙古实用新型专利申请数量（2017-2018）变动分析 (12)六、全国实用新型专利申请数量（2016-2018）统计分析 (13)七、全国实用新型专利申请数量（2017-2018）变动分析 (13)八、内蒙古实用新型专利申请数量同全国实用新型专利申请数量（2017-2018）变动对比分析 (14)第五节内蒙古外观设计专利申请数量指标分析（均指国内三种专利） (15)一、内蒙古外观设计专利申请数量现状统计 (15)二、全国外观设计专利申请数量现状统计 (15)三、内蒙古外观设计专利申请数量占全国外观设计专利申请数量比重统计 (15)四、内蒙古外观设计专利申请数量（2016-2018）统计分析 (16)五、内蒙古外观设计专利申请数量（2017-2018）变动分析 (16)六、全国外观设计专利申请数量（2016-2018）统计分析 (17)七、全国外观设计专利申请数量（2017-2018）变动分析 (17)八、内蒙古外观设计专利申请数量同全国外观设计专利申请数量（2017-2018）变动对比分析 (18)图表目录表1：内蒙古国内三种专利申请数量和授权数量现状统计表 (1)表2：内蒙古专利申请总数量现状统计表 (3)表3：全国专利申请总数量现状统计表 (3)表4：内蒙古专利申请总数量占全国专利申请总数量比重统计表 (3)表5：内蒙古专利申请总数量（2016-2018）统计表 (4)表6：内蒙古专利申请总数量（2017-2018）变动统计表（比上年增长%） (4)表7：全国专利申请总数量（2016-2018）统计表 (5)表8：全国专利申请总数量（2017-2018）变动统计表（比上年增长%） (5)表9：内蒙古专利申请总数量同全国专利申请总数量（2017-2018）变动对比统计表 (6)表10：内蒙古发明专利申请数量现状统计表 (7)表11：全国发明专利申请数量现状统计表 (7)表12：内蒙古发明专利申请数量占全国发明专利申请数量比重统计表 (7)表13：内蒙古发明专利申请数量（2016-2018）统计表 (8)表14：内蒙古发明专利申请数量（2017-2018）变动统计表（比上年增长%） (8)表15：全国发明专利申请数量（2016-2018）统计表 (9)表16：全国发明专利申请数量（2017-2018）变动统计表（比上年增长%） (9)表17：内蒙古发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比统计表（比上年增长%）10表17：内蒙古发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比统计表（比上年增长%） (10)表18：内蒙古实用新型专利申请数量现状统计表 (11)表19：全国实用新型专利申请数量现状统计分析表 (11)表20：内蒙古实用新型专利申请数量占全国实用新型专利申请数量比重统计表 (11)表21：内蒙古实用新型专利申请数量（2016-2018）统计表 (12)表22：内蒙古实用新型专利申请数量（2017-2018）变动分析表（比上年增长%） (12)表23：全国实用新型专利申请数量（2016-2018）统计表 (13)表24：全国实用新型专利申请数量（2017-2018）变动分析表（比上年增长%） (13)表25：内蒙古实用新型专利申请数量同全国实用新型专利申请数量（2017-2018）变动对比统计表（比上年增长%） (14)表26：内蒙古外观设计专利申请数量现状统计表 (15)表27：全国外观设计专利申请数量现状统计表 (15)表28：内蒙古外观设计专利申请数量占全国外观设计专利申请数量比重统计表 (15)表29：内蒙古外观设计专利申请数量（2016-2018）统计表 (16)表30：内蒙古外观设计专利申请数量（2017-2018）变动统计表（比上年增长%） (16)表31：全国外观设计专利申请数量（2016-2018）统计表 (17)表32：全国外观设计专利申请数量（2017-2018）变动统计表（比上年增长%） (17)表33：内蒙古外观设计专利申请数量同全国外观设计专利申请数量（2017-2018）变动对比统计表（比上年增长%） (18)。

北京市技术发展预测

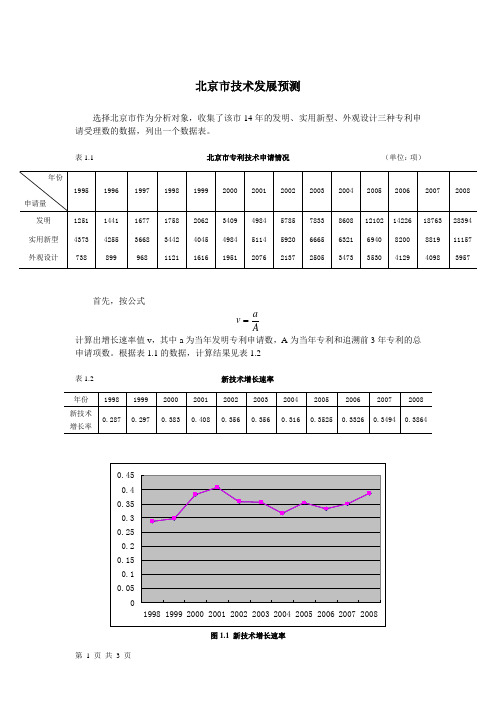
北京市技术发展预测
选择北京市作为分析对象，收集了该市14年的发明、实用新型、外观设计三种专利申请受理数的数据，列出一个数据表。

表1.1 北京市专利技术申请情况（单位：项）
首先，按公式
A
a v
计算出增长速率值v ，其中a 为当年发明专利申请数，A 为当年专利和追溯前3年专利的总申请项数。

根据表1.1的数据，计算结果见表1.2
表1.2 新技术增长速率
图1.1 新技术增长速率
从图1.1看出，虽然增长速率v 的值上下波动，但从整体上看还是呈现出增长的趋势，说明北京市的发明专利技术处于增长发展阶段，其新产品（技术）的竞争力强。

其次，我们还可以计算出成熟系数α和衰老系数β的历年数值，计算公式分别为
b a a +=
α c
b a b a +++=β
其中： a ——当年的发明专利申请数
b ——当年实用新型专利申请数
c ——当年外观设计专利申请数利用公式计算出结果如下
表1.3 技术成熟系数
图1.2 技术成熟系数
表1.4 技术衰老系数
图1.3 技术成熟系数
从图1.2可见，成熟系数α的值呈逐年递增趋势，衰老系数β虽然也有波动，但近几年都呈现出上升的趋势，而且β值均在0.78以上，这些说明北京市的专利技术处于蓬勃发展
的成长期，既未进入成熟阶段，更远远不到衰老期。

北京应该在此基础上继续加大科研方面的投入，利用其人才优势，健全法制，保护知识产权，努力创造有利于技术发明和创造的软硬环境。

同时要注意把发明和创造转化为生产力，实现良性循环，促进企业的发明创造等。

国家知识产权局办公室关于请提供向国外申请专利数据的函

国家知识产权局办公室关于请提供向国外申请专利数据的函文章属性•【制定机关】国家知识产权局•【公布日期】2009.02.25•【文号】•【施行日期】2009.02.25•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】专利申请正文国家知识产权局办公室关于请提供向国外申请专利数据的函各涉外专利代理机构：为做好2008年《专利统计年报》编辑出版工作，现请提供2008年由你单位代理的国内（含港、澳、台地区）向国外申请专利的有关数据。

请于2009年3月6日前将有关数据报我局规划发展司，有关数据表格可到我局主页（）下载，电子邮件发送至*****************.cn。

如无涉外代理案件，也请来函或发电子邮件予以说明。

为确保工作的连续性和数据的准确性，请指定专人负责专利代理统计工作，并将人员姓名和联系方式一并报我局。

特此致函。

附件：1.2008年向国外申请专利及被授权状况（按国别或组织计）2.2008年向欧洲专利组织成员国申请专利及被授权状况（按国别计）3.2008年向国外申请专利-按IPC分类统计（按申请件数计）4.2008年向国外申请专利-按申请人所在地（省、自治区、直辖市）统计（按申请件数计）联系人：于大伟刘晓斌电话：62083890 62083776传真：62010931地址：北京市海淀区蓟门桥西土城路6号国家知识产权局规划发展司邮政编码：100088E-mail：*****************.cn国家知识产权局办公室二○○九年二月二十五日附件1：2008年向国外申请专利及被授权状况注：“授权量”包括PCT申请进入国家阶段后被授权的数量。

说明：1.“巴黎公约”和“PCT进入国家阶段”是以国家为统计对象，不是按申请件数。

例如，一份申请向十个不同国家提出，则按国家计的专利申请数为十件；授权亦然。

“PCT申请”是通过PCT途径向国外的国际申请。

2.对于向欧洲专利局提出的申请，不论其指定所有成员国，或指定部分成员国，均视为一件申请；授权亦然。

澳门国内三种专利申请数量和授权数量数据分析报告2019版

澳门国内三种专利申请数量和授权数量数据分析报告2019版序言本报告以数据为基点对澳门国内三种专利申请数量和授权数量的现状及发展脉络进行了全面立体的阐述和剖析，相信对商家、机构及个人具有重要参考借鉴价值。

澳门国内三种专利申请数量和授权数量数据分析报告相关知识产权为发布方即我公司天津旷维所有，任何机构及个人引用我方报告，均需要注明出处。

澳门国内三种专利申请数量和授权数量数据分析报告主要收集国家政府部门如中国国家统计局及其它权威机构数据，并经过专业统计分析处理及清洗。

数据严谨公正，通过整理及清洗，进行澳门国内三种专利申请数量和授权数量的分析研究，整个报告覆盖专利申请总数量，发明专利申请数量，实用新型专利申请数量，外观设计专利申请数量，专利授权总数量，发明专利授权数量，实用新型专利授权数量等重要维度。

目录第一节澳门国内三种专利申请数量和授权数量现状概况 (1)第二节澳门专利申请总数量指标分析（均指国内三种专利） (3)一、澳门专利申请总数量现状统计 (3)二、全国专利申请总数量现状统计 (3)三、澳门专利申请总数量占全国专利申请总数量比重统计 (3)四、澳门专利申请总数量（2016-2018）统计分析 (4)五、澳门专利申请总数量（2017-2018）变动分析 (4)六、全国专利申请总数量（2016-2018）统计分析 (5)七、全国专利申请总数量（2017-2018）变动分析 (5)八、澳门专利申请总数量同全国专利申请总数量（2017-2018）变动对比分析 (6)第三节澳门发明专利申请数量指标分析(均指国内三种专利) (7)一、澳门发明专利申请数量现状统计 (7)二、全国发明专利申请数量现状统计分析 (7)三、澳门发明专利申请数量占全国发明专利申请数量比重统计分析 (7)四、澳门发明专利申请数量（2016-2018）统计分析 (8)五、澳门发明专利申请数量（2017-2018）变动分析 (8)六、全国发明专利申请数量（2016-2018）统计分析 (9)七、全国发明专利申请数量（2017-2018）变动分析 (9)八、澳门发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比分析 (10)第四节澳门实用新型专利申请数量指标分析（均指国内三种专利） (11)一、澳门实用新型专利申请数量现状统计 (11)二、全国实用新型专利申请数量现状统计分析 (11)三、澳门实用新型专利申请数量占全国实用新型专利申请数量比重统计分析 (11)四、澳门实用新型专利申请数量（2016-2018）统计分析 (12)五、澳门实用新型专利申请数量（2017-2018）变动分析 (12)六、全国实用新型专利申请数量（2016-2018）统计分析 (13)七、全国实用新型专利申请数量（2017-2018）变动分析 (13)八、澳门实用新型专利申请数量同全国实用新型专利申请数量（2017-2018）变动对比分析 (14)第五节澳门外观设计专利申请数量指标分析（均指国内三种专利） (15)一、澳门外观设计专利申请数量现状统计 (15)二、全国外观设计专利申请数量现状统计 (15)三、澳门外观设计专利申请数量占全国外观设计专利申请数量比重统计 (15)四、澳门外观设计专利申请数量（2016-2018）统计分析 (16)五、澳门外观设计专利申请数量（2017-2018）变动分析 (16)六、全国外观设计专利申请数量（2016-2018）统计分析 (17)七、全国外观设计专利申请数量（2017-2018）变动分析 (17)八、澳门外观设计专利申请数量同全国外观设计专利申请数量（2017-2018）变动对比分析 (18)第六节澳门专利授权总数量指标分析（均指国内三种专利） (19)一、澳门专利授权总数量现状统计 (19)二、全国专利授权总数量现状统计 (19)三、澳门专利授权总数量占全国专利授权总数量比重统计 (19)四、澳门专利授权总数量（2016-2018）统计分析 (20)五、澳门专利授权总数量（2017-2018）变动分析 (20)六、全国专利授权总数量（2016-2018）统计分析 (21)七、全国专利授权总数量（2017-2018）变动分析 (21)八、澳门专利授权总数量同全国专利授权总数量（2017-2018）变动对比分析 (22)第七节澳门发明专利授权数量指标分析（均指国内三种专利） (23)一、澳门发明专利授权数量现状统计 (23)二、全国发明专利授权数量现状统计分析 (23)三、澳门发明专利授权数量占全国发明专利授权数量比重统计分析 (23)四、澳门发明专利授权数量（2016-2018）统计分析 (24)五、澳门发明专利授权数量（2017-2018）变动分析 (24)六、全国发明专利授权数量（2016-2018）统计分析 (25)七、全国发明专利授权数量（2017-2018）变动分析 (25)八、澳门发明专利授权数量同全国发明专利授权数量（2017-2018）变动对比分析 (26)第八节澳门实用新型专利授权数量指标分析（均指国内三种专利） (27)一、澳门实用新型专利授权数量现状统计 (27)二、全国实用新型专利授权数量现状统计分析 (27)三、澳门实用新型专利授权数量占全国实用新型专利授权数量比重统计分析 (27)四、澳门实用新型专利授权数量（2016-2018）统计分析 (28)五、澳门实用新型专利授权数量（2017-2018）变动分析 (28)六、全国实用新型专利授权数量（2016-2018）统计分析 (29)七、全国实用新型专利授权数量（2017-2018）变动分析 (29)八、澳门实用新型专利授权数量同全国实用新型专利授权数量（2017-2018）变动对比分析 (30)第九节澳门外观设计专利授权数量指标分析（均指国内三种专利） (31)一、澳门外观设计专利授权数量现状统计 (31)二、全国外观设计专利授权数量现状统计 (31)三、澳门外观设计专利授权数量占全国外观设计专利授权数量比重统计 (31)四、澳门外观设计专利授权数量（2016-2018）统计分析 (32)五、澳门外观设计专利授权数量（2017-2018）变动分析 (32)六、全国外观设计专利授权数量（2016-2018）统计分析 (33)七、全国外观设计专利授权数量（2017-2018）变动分析 (33)八、澳门外观设计专利授权数量同全国外观设计专利授权数量（2017-2018）变动对比分析 (34)图表目录表1：澳门国内三种专利申请数量和授权数量现状统计表 (1)表2：澳门专利申请总数量现状统计表 (3)表3：全国专利申请总数量现状统计表 (3)表4：澳门专利申请总数量占全国专利申请总数量比重统计表 (3)表5：澳门专利申请总数量（2016-2018）统计表 (4)表6：澳门专利申请总数量（2017-2018）变动统计表（比上年增长%） (4)表7：全国专利申请总数量（2016-2018）统计表 (5)表8：全国专利申请总数量（2017-2018）变动统计表（比上年增长%） (5)表9：澳门专利申请总数量同全国专利申请总数量（2017-2018）变动对比统计表 (6)表10：澳门发明专利申请数量现状统计表 (7)表11：全国发明专利申请数量现状统计表 (7)表12：澳门发明专利申请数量占全国发明专利申请数量比重统计表 (7)表13：澳门发明专利申请数量（2016-2018）统计表 (8)表14：澳门发明专利申请数量（2017-2018）变动统计表（比上年增长%） (8)表15：全国发明专利申请数量（2016-2018）统计表 (9)表16：全国发明专利申请数量（2017-2018）变动统计表（比上年增长%） (9)表17：澳门发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比统计表（比上年增长%）10表17：澳门发明专利申请数量同全国发明专利申请数量（2017-2018）变动对比统计表（比上年增长%） (10)表18：澳门实用新型专利申请数量现状统计表 (11)表19：全国实用新型专利申请数量现状统计分析表 (11)表20：澳门实用新型专利申请数量占全国实用新型专利申请数量比重统计表 (11)表21：澳门实用新型专利申请数量（2016-2018）统计表 (12)表22：澳门实用新型专利申请数量（2017-2018）变动分析表（比上年增长%） (12)表23：全国实用新型专利申请数量（2016-2018）统计表 (13)表24：全国实用新型专利申请数量（2017-2018）变动分析表（比上年增长%） (13)表25：澳门实用新型专利申请数量同全国实用新型专利申请数量（2017-2018）变动对比统计表（比上年增长%） (14)表26：澳门外观设计专利申请数量现状统计表 (15)表27：全国外观设计专利申请数量现状统计表 (15)表28：澳门外观设计专利申请数量占全国外观设计专利申请数量比重统计表 (15)表29：澳门外观设计专利申请数量（2016-2018）统计表 (16)表30：澳门外观设计专利申请数量（2017-2018）变动统计表（比上年增长%） (16)表31：全国外观设计专利申请数量（2016-2018）统计表 (17)表32：全国外观设计专利申请数量（2017-2018）变动统计表（比上年增长%） (17)表33：澳门外观设计专利申请数量同全国外观设计专利申请数量（2017-2018）变动对比统计表（比上年增长%） (18)表34：澳门专利授权总数量现状统计表 (19)表35：全国专利授权总数量现状统计表 (19)表36：澳门专利授权总数量占全国专利授权总数量比重统计表 (19)表37：澳门专利授权总数量（2016-2018）统计表 (20)表38：澳门专利授权总数量（2017-2018）变动统计表（比上年增长%） (20)表39：全国专利授权总数量（2016-2018）统计表 (21)表40：全国专利授权总数量（2017-2018）变动统计表（比上年增长%） (21)表41：澳门专利授权总数量同全国专利授权总数量（2017-2018）变动对比统计表 (22)表42：澳门发明专利授权数量现状统计表 (23)表43：全国发明专利授权数量现状统计表 (23)表44：澳门发明专利授权数量占全国发明专利授权数量比重统计表 (23)表45：澳门发明专利授权数量（2016-2018）统计表 (24)表46：澳门发明专利授权数量（2017-2018）变动统计表（比上年增长%） (24)表47：全国发明专利授权数量（2016-2018）统计表 (25)表48：全国发明专利授权数量（2017-2018）变动统计表（比上年增长%） (25)表49：澳门发明专利授权数量同全国发明专利授权数量（2017-2018）变动对比统计表（比上年增长%） (26)表50：澳门实用新型专利授权数量现状统计表 (27)表51：全国实用新型专利授权数量现状统计分析表 (27)表52：澳门实用新型专利授权数量占全国实用新型专利授权数量比重统计表 (27)表53：澳门实用新型专利授权数量（2016-2018）统计表 (28)表54：澳门实用新型专利授权数量（2017-2018）变动分析表（比上年增长%） (28)表55：全国实用新型专利授权数量（2016-2018）统计表 (29)表56：全国实用新型专利授权数量（2017-2018）变动分析表（比上年增长%） (29)表57：澳门实用新型专利授权数量同全国实用新型专利授权数量（2017-2018）变动对比统计表（比上年增长%） (30)表58：澳门外观设计专利授权数量现状统计表 (31)表59：全国外观设计专利授权数量现状统计表 (31)表60：澳门外观设计专利授权数量占全国外观设计专利授权数量比重统计表 (31)表61：澳门外观设计专利授权数量（2016-2018）统计表 (32)表62：澳门外观设计专利授权数量（2017-2018）变动统计表（比上年增长%） (32)表63：全国外观设计专利授权数量（2016-2018）统计表 (33)表64：全国外观设计专利授权数量（2017-2018）变动统计表（比上年增长%） (33)表65：澳门外观设计专利授权数量同全国外观设计专利授权数量（2017-2018）变动对比统计表（比上年增长%） (34)。

浙江省嘉兴市区专利申请受理量和授权量3年数据专题报告2020版

浙江省嘉兴市区专利申请受理量和授权量3年数据专题报告2020版引言本报告借助数据对嘉兴市区专利申请受理量和授权量进行深度剖析，从专利申请受理总量，专利申请授权总量等方面进行阐述，以全面、客观的角度展示嘉兴市区专利申请受理量和授权量真实现状及发展脉络，为需求者制定战略、为投资者投资提供参考和借鉴。

嘉兴市区专利申请受理量和授权量专题报告的数据来源于权威部门如中国国家统计局等，数据以事实为基准，公正，客观、严谨。

嘉兴市区专利申请受理量和授权量数据专题报告知识产权为发布方即我公司天津旷维所有，其他方引用我方报告均需注明出处。

嘉兴市区专利申请受理量和授权量数据专题报告旨在全面梳理嘉兴市区专利申请受理量和授权量的真实现状、发展脉络及趋势，相信能够为从业者、投资者和研究者提供有意义的启发和借鉴。

目录第一节嘉兴市区专利申请受理量和授权量现状 (1)第二节嘉兴市区专利申请受理总量指标分析 (3)一、嘉兴市区专利申请受理总量现状统计 (3)二、全省专利申请受理总量现状统计 (3)三、嘉兴市区专利申请受理总量占全省专利申请受理总量比重统计 (3)四、嘉兴市区专利申请受理总量（2017-2019）统计分析 (4)五、嘉兴市区专利申请受理总量（2018-2019）变动分析 (4)六、全省专利申请受理总量（2017-2019）统计分析 (5)七、全省专利申请受理总量（2018-2019）变动分析 (5)八、嘉兴市区专利申请受理总量同全省专利申请受理总量（2018-2019）变动对比分析..6 第三节嘉兴市区专利申请授权总量指标分析 (7)一、嘉兴市区专利申请授权总量现状统计 (7)二、全省专利申请授权总量现状统计分析 (7)三、嘉兴市区专利申请授权总量占全省专利申请授权总量比重统计分析 (7)四、嘉兴市区专利申请授权总量（2017-2019）统计分析 (8)五、嘉兴市区专利申请授权总量（2018-2019）变动分析 (8)六、全省专利申请授权总量（2017-2019）统计分析 (9)七、全省专利申请授权总量（2018-2019）变动分析 (9)八、嘉兴市区专利申请授权总量同全省专利申请授权总量（2018-2019）变动对比分析.10图表目录表1：嘉兴市区专利申请受理量和授权量现状统计表 (1)表2：嘉兴市区专利申请受理总量现状统计表 (3)表3：全省专利申请受理总量现状统计表 (3)表4：嘉兴市区专利申请受理总量占全省专利申请受理总量比重统计表 (3)表5：嘉兴市区专利申请受理总量（2017-2019）统计表 (4)表6：嘉兴市区专利申请受理总量（2018-2019）变动统计表（比上年增长%） (4)表7：全省专利申请受理总量（2017-2019）统计表 (5)表8：全省专利申请受理总量（2018-2019）变动统计表（比上年增长%） (5)表9：嘉兴市区专利申请受理总量同全省专利申请受理总量（2018-2019）变动对比统计表.6 表10：嘉兴市区专利申请授权总量现状统计表 (7)表11：全省专利申请授权总量现状统计表 (7)表12：嘉兴市区专利申请授权总量占全省专利申请授权总量比重统计表 (7)表13：嘉兴市区专利申请授权总量（2017-2019）统计表 (8)表14：嘉兴市区专利申请授权总量（2018-2019）变动统计表（比上年增长%） (8)表15：全省专利申请授权总量（2017-2019）统计表 (9)表16：全省专利申请授权总量（2018-2019）变动统计表（比上年增长%） (9)表17：嘉兴市区专利申请授权总量同全省专利申请授权总量（2018-2019）变动对比统计表（比上年增长%）10表17：嘉兴市区专利申请授权总量同全省专利申请授权总量（2018-2019）变动对比统计表（比上年增长%） (10)第一节嘉兴市区专利申请受理量和授权量现状嘉兴市区专利申请受理量和授权量现状详细情况见下表（2019年）：表1：嘉兴市区专利申请受理量和授权量现状统计表注：本报告以国家各级统计部门数据为基准，并借助专业统计分析方法得出。

北京绿色发展指标体系

北京绿色发展指标体系北京绿色发展指标体系是评价北京市绿色发展程度和效果的重要标准。

它是根据北京市的实际情况和绿色发展的要求，建立起来的一套评价指标，可以科学、全面地评估北京市的绿色经济、环境保护和社会发展等方面的表现和成效。

以下是北京绿色发展指标体系的一些主要内容。

首先，经济指标是北京绿色发展指标体系的重要组成部分。

其中包括GDP增长率、能源消费强度、资源利用率等方面的指标。

GDP增长率可以反映北京市经济的增长速度和质量，能源消费强度指标可以评估能源的使用效率，资源利用率指标可以衡量资源的合理利用程度。

这些经济指标的合理性和高效性，是评价北京市绿色发展水平的重要标志。

其次，环境指标也是北京绿色发展指标体系的关键内容。

其中包括大气污染物排放量、水质状况、土壤环境质量等方面的指标。

大气污染物排放量指标可以反映北京市大气环境污染的程度，水质状况指标可以评估水资源的质量，土壤环境质量指标可以衡量土壤的健康状况。

这些环境指标的优良程度，是评判北京市绿色发展水平的重要参考。

再次，社会指标也是北京绿色发展指标体系的重要组成部分。

这些社会指标包括居民生活水平、就业机会、教育资源、医疗服务等方面的指标。

居民生活水平可以反映人民群众的幸福感和满意度，就业机会指标可以衡量就业市场的活力，教育资源指标可以评估教育发展水平，医疗服务指标可以反映医疗卫生系统的发展状况。

这些社会指标的改善程度，是评价北京市绿色发展水平的重要依据。

最后，科技创新指标也是北京绿色发展指标体系的重要内容。

这些科技创新指标包括科研经费投入、专利申请数量、高新技术产业的发展等方面的指标。

科研经费投入指标可以反映创新领域的投入力度，专利申请数量指标可以评估科技成果的产出情况，高新技术产业的发展指标可以衡量科技创新对经济增长的贡献程度。

这些科技创新指标的优秀程度，是评价北京市绿色发展水平的重要标准。

总之，北京绿色发展指标体系科学合理，全面多元，能够客观地评价北京市的绿色发展情况和成效。

北京市全社会固定资产投资总额及金融业固定资产投资额数据分析报告2018版

北京市全社会固定资产投资总额及金融业固定资产投资额数据分析报告2018版前言北京市全社会固定资产投资总额及金融业固定资产投资额数据分析报告围绕核心要素全社会固定资产投资总数量，金融业固定资产投资数量等展开深入分析，深度剖析了北京市全社会固定资产投资总额及金融业固定资产投资额的现状及发展脉络。

北京市全社会固定资产投资总额及金融业固定资产投资额分析报告中的数据来源于政府部门如中国国家统计局、相关科研机构及行业协会等，通过整理和清洗等方法分析得出，具备权威性、严谨性、科学性。

本报告从多维角度借助数据全面解读北京市全社会固定资产投资总额及金融业固定资产投资额现状及发展态势，客观反映当前北京市全社会固定资产投资总额及金融业固定资产投资额真实状况，趋势、规律以及发展脉络，北京市全社会固定资产投资总额及金融业固定资产投资额数据分析报告必能为大众提供有价值的指引及参考，提供更快速的效能转化。

目录第一节北京市全社会固定资产投资总额和金融业固定资产投资额现状概况 (1)第二节北京市全社会固定资产投资总数量指标分析 (3)一、北京市全社会固定资产投资总数量现状统计 (3)二、全国全社会固定资产投资总数量现状统计 (3)三、北京市全社会固定资产投资总数量占全国全社会固定资产投资总数量比重统计 (3)四、北京市全社会固定资产投资总数量（2015-2017）统计分析 (4)五、北京市全社会固定资产投资总数量（2016-2017）变动分析 (4)六、全国全社会固定资产投资总数量（2015-2017）统计分析 (5)七、全国全社会固定资产投资总数量（2016-2017）变动分析 (5)八、北京市全社会固定资产投资总数量同全国全社会固定资产投资总数量（2016-2017）变动对比分析 (6)第三节北京市金融业固定资产投资数量指标分析 (7)一、北京市金融业固定资产投资数量现状统计 (7)二、全国金融业固定资产投资数量现状统计分析 (7)三、北京市金融业固定资产投资数量占全国金融业固定资产投资数量比重统计分析 (7)四、北京市金融业固定资产投资数量（2015-2017）统计分析 (8)五、北京市金融业固定资产投资数量（2016-2017）变动分析 (8)六、全国金融业固定资产投资数量（2015-2017）统计分析 (9)七、全国金融业固定资产投资数量（2016-2017）变动分析 (9)八、北京市金融业固定资产投资数量同全国金融业固定资产投资数量（2016-2017）变动对比分析 (10)图表目录表1：北京市全社会固定资产投资总额和金融业固定资产投资额现状统计表 (1)表2：北京市全社会固定资产投资总数量现状统计表 (3)表3：全国全社会固定资产投资总数量现状统计表 (3)表4：北京市全社会固定资产投资总数量占全国全社会固定资产投资总数量比重统计表 (3)表5：北京市全社会固定资产投资总数量（2015-2017）统计表 (4)表6：北京市全社会固定资产投资总数量（2016-2017）变动统计表（比上年增长%） (4)表7：全国全社会固定资产投资总数量（2015-2017）统计表 (5)表8：全国全社会固定资产投资总数量（2016-2017）变动统计表（比上年增长%） (5)表9：北京市全社会固定资产投资总数量同全国全社会固定资产投资总数量（2016-2017）变动对比统计表 (6)表10：北京市金融业固定资产投资数量现状统计表 (7)表11：全国金融业固定资产投资数量现状统计表 (7)表12：北京市金融业固定资产投资数量占全国金融业固定资产投资数量比重统计表 (7)表13：北京市金融业固定资产投资数量（2015-2017）统计表 (8)表14：北京市金融业固定资产投资数量（2016-2017）变动统计表（比上年增长%） (8)表15：全国金融业固定资产投资数量（2015-2017）统计表 (9)表16：全国金融业固定资产投资数量（2016-2017）变动统计表（比上年增长%） (9)表17：北京市金融业固定资产投资数量同全国金融业固定资产投资数量（2016-2017）变动对比统计表（比上年增长%） (10)第一节北京市全社会固定资产投资总额和金融业固定资产投资额现状概况北京市全社会固定资产投资总额和金融业固定资产投资额现状详细情况见下表（2017年）：表1：北京市全社会固定资产投资总额和金融业固定资产投资额现状统计表第二节北京市全社会固定资产投资总数量指标分析一、北京市全社会固定资产投资总数量现状统计表2：北京市全社会固定资产投资总数量现状统计表二、全国全社会固定资产投资总数量现状统计表3：全国全社会固定资产投资总数量现状统计表三、北京市全社会固定资产投资总数量占全国全社会固定资产投资总数量比重统计分析表4：北京市全社会固定资产投资总数量占全国全社会固定资产投资总数量比重统计表指标数量（亿元）占总值比重四、北京市全社会固定资产投资总数量（2015-2017）统计分析表5：北京市全社会固定资产投资总数量（2015-2017）统计表五、北京市全社会固定资产投资总数量（2016-2017）变动分析表6：北京市全社会固定资产投资总数量（2016-2017）变动统计表（比上年增长%）六、全国全社会固定资产投资总数量（2015-2017）统计分析表7：全国全社会固定资产投资总数量（2015-2017）统计表七、全国全社会固定资产投资总数量（2016-2017）变动分析表8：全国全社会固定资产投资总数量（2016-2017）变动统计表（比上年增长%）八、北京市全社会固定资产投资总数量同全国全社会固定资产投资总数量（2016-2017）变动对比分析表9：北京市全社会固定资产投资总数量同全国全社会固定资产投资总数量（2016-2017）变动对比表（比上年增长%）第三节北京市金融业固定资产投资数量指标分析一、北京市金融业固定资产投资数量现状统计表10：北京市金融业固定资产投资数量现状统计表二、全国金融业固定资产投资数量现状统计分析表11：全国金融业固定资产投资数量现状统计表三、北京市金融业固定资产投资数量占全国金融业固定资产投资数量比重统计分析表12：北京市金融业固定资产投资数量占全国金融业固定资产投资数量比重统计表指标数量（亿元）占总值比重四、北京市金融业固定资产投资数量（2015-2017）统计分析表13：北京市金融业固定资产投资数量（2015-2017）统计表五、北京市金融业固定资产投资数量（2016-2017）变动分析表14：北京市金融业固定资产投资数量（2016-2017）变动统计表（比上年增长%）六、全国金融业固定资产投资数量（2015-2017）统计分析表15：全国金融业固定资产投资数量（2015-2017）统计表七、全国金融业固定资产投资数量（2016-2017）变动分析表16：全国金融业固定资产投资数量（2016-2017）变动统计表（比上年增长%）八、北京市金融业固定资产投资数量同全国金融业固定资产投资数量（2016-2017）变动对比分析表17：北京市金融业固定资产投资数量同全国金融业固定资产投资数量（2016-2017）变动对比表（比上年增长%）。

测量方法[发明专利]

(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 201880024727.X(22)申请日 2018.03.15(30)优先权数据17166691.0 2017.04.14 EP18156860.1 2018.02.15 EP(85)PCT国际申请进入国家阶段日2019.10.11(86)PCT国际申请的申请数据PCT/EP2018/056554 2018.03.15(87)PCT国际申请的公布数据WO2018/188891 EN 2018.10.18(71)申请人 ASML荷兰有限公司地址荷兰维德霍温(72)发明人 N ·潘迪　廉晋　S ·U ·雷曼　M ·J ·J ·贾克　(74)专利代理机构北京市金杜律师事务所 11256代理人吕世磊(51)Int.Cl.G03F 7/20(2006.01) (54)发明名称测量方法(57)摘要公开了用于测量在衬底上形成的多个结构的方法和设备。

在一种布置中，方法包括从第一测量过程获取数据。

第一测量过程包括单独地测量多个结构中的每个结构以测量结构的第一特性。

第二测量过程被用于测量多个结构中的每个结构的第二特性。

第二测量过程包括利用具有辐射特性的辐射照射每个结构，辐射特性是使用针对该结构所测量的第一特性针对该结构单独地被选择的。

权利要求书1页说明书20页附图8页CN 110622068 A 2019.12.27C N 110622068A1.一种测量在衬底上形成的多个结构的方法，所述方法包括：从第一测量过程获取数据，所述第一测量过程包括单独地测量所述多个结构中的每个结构以测量所述结构的第一特性；以及使用第二测量过程来测量所述多个结构中的每个结构的第二特性，所述第二测量过程包括利用具有辐射特性的辐射照射每个结构，所述辐射特性是使用针对所述结构所测量的第一特性针对所述结构单独地被选择的。

我国与日韩pct专利申请情况比较分析及政策建议

第16卷　第12期2019年 12月中国发明与专利China Invention & PatentV ol.16 No.12Dec. 2019我国与日韩ＰＣＴ专利申请情况比较分析及政策建议张杰罗啸谢楠梁岩张鸣刘的帝（北京三聚阳光知识产权代理有限公司，北京100080）摘　要：自我国加入《专利合作条约》以来，PCT已成为我国用户向国外申请专利的重要途径，PCT专利申请量逐年增长。

2018年中国PCT专利申请的数量共53345件，在全球排名第二，同比增长9.1%。

与此相对应的，依PCT规则进入其他国家阶段的专利申请数量却不多。

本文通过对中、日、韩三国以及华为公司PCT国际专利申请数量及进入国家阶段申请情况的分析，就这一现象产生的原因进行了剖析，进而提出相应建议。

关键词：知识产权PCT专利专利申请资助政策专利质量中图分类号： G306 文献标识码：A0引言世界知识产权组织（WIPO）每年定期发布国际专利申请年报，通过对全球数据的统计调查，为各国/地区政府全局把握知识产权发展趋势，优化知识产权发展路径、监测知识产权发展进程提供了充分的数据支撑。

2019年3月19日，WIPO发布了2018年国际专利申请年报，对2018年全球知识产权活动最新发展态势作出分析。

报告显示，2018年通过PCT途径提交的全部国际专利申请中，半数以上来自亚洲，中国、印度和韩国皆有强劲表现。

中国知识产权申请量的快速增长已成为全球知识产权数量增长的巨大驱动力，并呈现出持续而明显趋势。

与此同时，我国申请人在海外进行全球专利布局及寻求专利保护方面仍处于弱势地位。

在专利先行已成为越来越多中国企业共识的当下，与中国走向海外市场企业的数量以及欧、美、日、韩等发达国家全球专利布局情况相比，我国的海外专利申请量仍然较少，获得授权的专利更少，专利布局仍显薄弱，亟待改善。

1我国2018年PCT申请概况2019年3月19日，世界知识产权组织（WIPO）发布了2018年国际专利申请年报。