数字电路与系统设计课后习题答案

数字电路与系统设计课后习题答案之欧阳科创编

1.1将下列各式写成按权展开式：（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-2 1.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4 将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6 将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7 将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8 转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9 用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10 已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

2021年数字电路与系统设计课后习题答案之欧阳学文创编

1.1将下列各式写成按权展开式：欧阳光明（2021.03.07）（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4 将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6 将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7 将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8 转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9 用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD （2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD 1.10 已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字逻辑电路与系统设计习题答案

图 P3.5
题 3.5 解：由逻辑图可写出 Y 的逻辑表达式为：
Y S3 AB S 2 AB S1 B S0 B A
图中的 S3 、S2 、S1 、S0 作为控制信号，用以选通待传送数据 A、B，两类信号作用不同，分析中应区别开来，否则得不出正确结果。由于 S3 、S2 、S1 、S0 共有 16 种取值组合，因此输出 Y 和 A、B 之间应有 16 种函数关系。列表如下：

（4） F ( A, B, C, D) 题 1.15 解：（1） F ABC BC
m0,2,3,8,9,10,11,13
F B C AC B C
或
F B C B C A B
（2） F A C A B C A B C

（1） F A B C D ABC ACD （2） F AC AB （3） F A, B, C
且 AB CD 0
且 A, B, C 不能同时为 0 或同时为 1
m3,5,6,7 d 2,4 m0,4,6,8,13 d 1,2,3,9,10,11 m0,1,8,10 d 2,3,4,5,11 m3,5,8,9,10,12 d 0,1,2,13
2.7 在图 P2.7 各电路中，每个输入端应怎样连接，才能得到所示的输出逻辑表达式。
&
F1 A B
≥1
F2 AB
VCC
&
≥1
&
F4 A B
F3 AB CD
&
图 P2.7

数字电路习题及答案

·数字电路与系统-习题答案1第1 章数字逻辑基础1.1 什么是数字电路？与模拟电路相比，数字电路具有哪些特点？答：处理数字信号并能完成数字运算的电路系统称为数字电路。

特点：采用二进制，结构简单易于集成；可用于数值计算和逻辑运算；抗干扰，精度高；便于长期存储和远程传输，保密性好，通用性强。

1.3 把下列二进制数转换成十进制数。

（1）(11000101)2 = (197)10（2）(0.01001)2 = (0.28125)10（3）(1010.001)2 = (10.125)101.4 把下列十进制数转换成二进制数。

（1）(12.0625)10 = (1100.0001)2（2）(127.25)10 = (1111111.01)2（3）(101)10 = (1100101)21.5 把二进制数(110101111.110)2分别转换成十进制数、八进制数和十六进制数。

答：(110101111.110)2 =(431.75)10 =(657.6)8 =(1AF.C)161.6 把八进制数(623.77)8分别转换成十进制数、十六进制数和二进制数。

答：(623.77)8 =(403.98)10 =(193.FC)16 =(110010011.111111)21.7 把十六进制数(2AC5.D)16分别转换成十进制数、八进制数和二进制数。

答：(2AC5.D)16 =(10949.81)10 =(25305.64)8 =(10101011000101.1101)21.8 把十进制数(432.13)10转换成五进制数。

答：(432.13)10 =(3212.0316)51.9 用8421BCD 码表示下列十进制数。

（1）(42.78)10 =(0100 0010.0111 1000)8421BCD（2）(103.65)10 =(0001 0000 0011.0110 0101)8421BCD（3）(9.04)10 =(1001.0000 0100)8421BCD数字电路与系统-习题答案21.10 把下列8421BCD 码表示成十进制数。

数字电路与系统设计课后习题答案之欧阳引擎创编

1.1将下列各式写成按权展开式：欧阳引擎（2021.01.01）（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4 将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6 将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7 将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8 转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9 用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10 已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字电路与系统设计：第2章习题答案

习题目录2.1 (2)2.2 (2)2.3 (2)2.4 (3)2.5 (3)2.6 (4)2.7 (4)2.8 (4)2.9 (4)2.10 (4)2.11 (5)2.12 (5)2.13 (7)2.14 (8)2.1 有A 、B 、C 三个输入信号，试列出下列问题的真值表，并写出最小项表达式∑m （）。

（1）如果A 、B 、C 均为0或其中一个信号为1时。

输出F=1，其余情况下F=0。

（2）若A 、B 、C 出现奇数个0时输出为1，其余情况输出为0。

（3）若A 、B 、C 有两个或两个以上为1时，输出为1，其余情况下，输出为0。

F 1m 4）F 2m ）3m 7）2.2 试用真值表证明下列等式：（1）A ⎺B+B ⎺C+A ⎺C=ABC+⎺A ⎺B ⎺C （2）⎺A ⎺B+⎺B ⎺C+⎺A ⎺C=AB BC AC 证明：（1）真值表相同，所以等式成立。

（真值表相同，所以等式成立。

2.3 对下列函数，说明对输入变量的哪些取值组合其输出为1？（1）F （A,B,C ）=AB+BC+AC（2）F （A,B,C ）=(A+B+C)(⎺A+⎺B+⎺C) （3）F （A,B,C ）=(⎺AB+⎺BC+A ⎺C)AC解：本题可用真值表、化成最小项表达式、卡诺图等多种方法求解。

（1）F 输出1的取值组合为：011、101、110、111。

（2）F 输出1的取值组合为：001、010、011、100、101、110。

（3）F输出1的取值组合为：101。

2.4试直接写出下列各式的反演式和对偶式。

(1)F(A,B,C,D,E)=[(A⎺B+C)·D+E]·B(2) F(A,B,C,D,E)=AB+⎺C⎺D+BC+⎺D+⎺CE+B+E(3) F(A,B,C)=⎺A⎺B+C ⎺AB C解：(1) ⎺F=[(⎺A+B)·⎺C+⎺D]·⎺E+⎺BF'=[(A+⎺B)·C+D]·E+B(2) ⎺F=(⎺A+⎺B)(C+D)·(⎺B+⎺C)·D·(C+⎺E)·⎺B·⎺EF'=(A+B)(⎺C+⎺D)·(B+C)·⎺D·(⎺C+E)·B·E(3)⎺F=(A+B)·⎺C+ A+⎺B+CF'=(⎺A+⎺B)·C+⎺A+B+⎺C2.5用公式证明下列等式：(1)⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D=⎺A+BC(2)AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=⎺A + B +⎺C+⎺D证明：(1) ⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D ——⎺A⎺C⎺D被⎺A⎺C削去=⎺A(⎺B+⎺C)+BC=⎺A BC+BC ——削去互补因子=⎺A+BC(2) AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+BC D+BC ——增加冗余因子BC，为了削去BCD中的BC =AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C⎺D ——B⎺CD与BCD合并成BD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C ——BD与B⎺C⎺D削去互补因子=⎺BC⎺D+BD+ACD+⎺BCD+B⎺C ——⎺AB⎺C⎺D被B⎺C削去=⎺BC+BD+ACD+B⎺C ——⎺BC⎺D与⎺BCD合并=⎺BC+BD+CD+ACD+B⎺C ——增加CD，可削去ACD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=A⎺B⎺C (BC+BC⎺D)+⎺A+B+⎺D ——BC+BC⎺D削去互补因子=A⎺B⎺C (⎺B+⎺C+⎺D)+⎺A+B+⎺D=A⎺B⎺C +A⎺B⎺C⎺D+⎺A+B+⎺D=A⎺B⎺C+⎺A+B+⎺D=⎺A+ B +⎺C+⎺D2.6已知⎺ab+a⎺b=a⊕b,⎺a⎺b+ab=a b,证明：（1）a⊕b⊕c=a b c（2）a⊕b⊕c=⎺a ⎺b ⎺c证明：(1)a⊕b⊕c=(a⊕b)⊕c=a⊕b · c+(a⊕b)·⎺c=(a b)·c+ a b⎺c=a b c(2)(a⊕b)⊕c = (a⊕b) c=a b c=a b ⎺c=⎺a ⎺b ⎺c2.7试证明：（1）若⎺a⎺b+ a b=0则a x+b y=a⎺x + b⎺y证明：⎺a⎺b+ a b=0 即a b=0 ∴a =⎺bax + by =⎺bx + by = ⎺bx · by=(b+⎺x)(⎺b+⎺y)=b⎺y+⎺b⎺x+⎺x⎺y=a⎺x+b⎺y（2）若⎺a b+a⎺b=c，则⎺a c + a⎺c=b证明：a⊕b=c => a⊕b⊕c=c⊕c => a⊕b⊕c=0 => a⊕b⊕c⊕b=0⊕b => a⊕c=b2.8将下列函数展开成最小项之和：（1）F（ABC）=A+BC（2）F（ABCD）=（B+⎺C）D+(⎺A+B) C（3）F(ABC)=A+B+C+⎺A+B+C解：（1）F（ABC）=A+BC=A（B+⎺B）(C+⎺C)+(A+⎺A)BC=⎺ABC+A⎺B⎺C+A⎺BC+AB⎺C=∑m(3,4,5,6)(2) F（ABCD）=（B+⎺C）D+(⎺A+B) C=BD+⎺CD+⎺AC+BC=∑m(1,3,5,6,7,9,13,14,15)(3) F(ABC)=A+B+C+⎺A+B+C=∑m(0,2,6)2.9将题2.8中各题写成最大项表达式，并将结果与2.8题结果进行比较。

数字电路与系统设计课后习题答案之欧阳计创编

1.1将下列各式写成按权展开式：（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136），（88）1610解：结果都为：（10001000）21.6将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字电路与系统设计课后习题答案之欧阳计创编

1.1将下列各式写成按权展开式：（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4 将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6 将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7 将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8 转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9 用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10 已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字逻辑电路与系统设计习题答案

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

《数字电路与系统设计》第6章习题答案

6.1试分析下图所示电路。
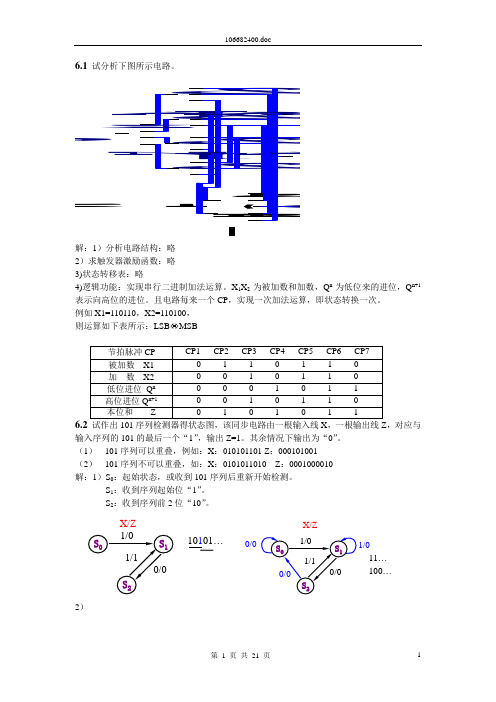
解：1）分析电路结构：略
2）求触发器激励函数：略
3)状态转移表：略
4)逻辑功能：实现串行二进制加法运算。X1X2为被加数和加数，Qn为低位来的进位，Qn+1表示向高位的进位。且电路每来一个CP，实现一次加法运算，即状态转换一次。
例如X1=110110，X2=110100，
则运算如下表所示：LSBMSB
RD
6.24试写出图6.24中各电路的状态编码表及模长。
解：（1）异步清0，8421BCD码（2）异步置9 5421BCD码
Q3Q2Q1Q0
Q0Q3Q2Q1
0000
0001
0010
0011
0100
M=5
0000
0001
0010
0011
0100
1000
1001
1100
M=8
6.25试用7490设计用8421BCD编码的模7计数器。（1）用R01、R02作反馈端；（2）用S91、S92作反馈端。
10000
11000
11100
11110
11111
01111
00111
00011
00001
0
0
0
0
0
1
。
6.39试写出图6.39的74194输出端的编码表及数据选择器输出端F处的序列信号。
解：F处的序列为：0100001011。
6.40写出图6.40中74161输出端的状态编码表及74151输出端产生的序列信号。
解：题6.7的状态转移表
X
Q4n
Q3n
Q2n
Q1n
Q4n+1
Q3n+1

数字逻辑电路与系统设计习题答案

第1章习题及解答将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（）2（3）（1101101）2 （4）（）2（5）（）2（6）（）2（7）（）2（8）（）2题解：（1）（11011）2 =（27）10 （2）（）2 =（151）10（3）（1101101）2 =（109）10 （4）（）2 =（255）10（5）（）2 =（）10（6）（）2 =（）10（7）（）2=（）10（8）（）2 =（）10将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（1）2（3）（）2 （4）（）2题解：（1）（1010111）2 =（57）16 =（127）8（2）（0）2 =（19A）16 =（632）8（3）（）2 =（）16 =（）8（4）（）2 =（2C.61）16 =（）8将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（）10（3）（）10 （4）（）10题解：（1）（43）10 =（01000011）8421BCD（2）（）10 =（.00010010）8421BCD（3）（）10 =（）8421BCD（4）（）10 =（.0001）8421BCD将下列有符号的十进制数表示成补码形式的有符号二进制数。

（1） +13 （2）−9 （3）+3 （4）−8题解：（1） +13 =（01101）2（2）−9 =（10111）2（3） +3 =（00011）2（4）−8 =（11000）2用真值表证明下列各式相等。

（1）BA+=+B+BBAA（2）()()()=⊕A⊕CACABB（3）()C BA+=+BCA（4）CAB++A=AABC题解：（1）证明BA+=++BABBA（2）证明()()()ACABCBA⊕=⊕（3）证明()C BACBA+=+（4）证明CAB++=AACBA用逻辑代数公式将下列逻辑函数化成最简与或表达式。

（1）D++A=F+BCBCACA（2）()()D++=F+AACCDA（3）()()B++F+=B+DCDBDDA（4）()D++F+=ADCBCBA（5）()C A B C B AC F ⊕++= （6）()()C B B A F ⊕⊕= 题解：（1）BC A D C A BC C A B A F +=+++= （2）()()CD A D CD A C A A F +=+++=（3）()()C B B A D B D A C B D D D B F ++=++++= （4）()D C B A D C B AD C B A F +=+++= （5）()C B AC C A B C B AC F +=⊕++=（6）()()C A BC B A C B B A F ++=⊕⊕=或C A C B AB ++= 用卡诺图将下列逻辑函数化成最简与或表达式。

数字电路与系统设计课后习题答案之欧阳科创编

1.1将下列各式写成按权展开式：（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字逻辑电路及系统设计习题答案

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

数字电路与系统设计课后习题答案之欧阳体创编

1.1将下列各式写成按权展开式：（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6将下列个数分别转换成八进制数：（111111）2，（63）10，（3F）16解：结果都为（77）81.7将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD （2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD 1.10已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。

数字逻辑电路与系统设计[蒋立平主编][习题解答]

第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2 （2）（10010111）2（3）（1101101）2 （4）（11111111）2（5）（0.1001）2（6）（0.0111）2（7）（11.001）2（8）（101011.11001）2题1.1 解：（1）（11011）2 =（27）10 （2）（10010111）2 =（151）10（3）（1101101）2 =（109）10 （4）（11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10（6）（0.0111）2 =（0.4375）10（7）（11.001）2=（3.125）10（8）（101011.11001）2 =（43.78125）10 1.3 将下列二进制数转换为等值的十六进制数和八进制数。

（1）（1010111）2 （2）（110111011）2（3）（10110.011010）2 （4）（101100.110011）2题1.3 解：（1）（1010111）2 =（57）16 =（127）8（2）（110011010）2 =（19A）16 =（632）8（3）（10110.111010）2 =（16.E8）16 =（26.72）8（4）（101100.01100001）2 =（2C.61）16 =（54.302）81.5 将下列十进制数表示为8421BCD码。

（1）（43）10 （2）（95.12）10（3）（67.58）10 （4）（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BCD（2）（95.12）10 =（10010101.00010010）8421BCD（3）（67.58）10 =（01100111.01011000）8421BCD（4）（932.1）10 =（100100110010.0001）8421BCD1.7 将下列有符号的十进制数表示成补码形式的有符号二进制数。

数字电路与系统设计课后习题答案

A-B=（90）10-（47）10=（43）10
C×D=（84）10×（6）10=（504）10
C÷D=（84）10÷（6）10=（14）10
两种算法结果相同。
1.11试用8421BCD码完成下列十进制数的运算。
解：（1）5+8=（0101）8421BCD+（1000）8421BCD=1101 +0110=（1 0110）8421BCD=13
（1）F输出1的取值组合为：011、101、110、111。
（2）F输出1的取值组合为：001、010、011、100、101、110。
（3）F输出1的取值组合为：101。
2.4试直接写出下列各式的反演式和对偶式。
(1)F(A,B,C,D,E)=[(AB+C)·D+E]·B
(2) F(A,B,C,D,E)=AB+CD+BC+D+CE+B+E
(2)F=∑m(0,1,2,3,12,13)
F'=∑m(2,3,12,13,14,15)
2.11试用公式法把下列各表达式化简为最简与或式
（1）F=A+ABC+ABC+BC+B
解：F =A+B
(2) F=(A+B)(A+B+C)(A+C)(B+C+D)
解：F'=AB+AC
(3) F=AB+ABBC+BC
（1）如果A、B、C均为0或其中一个信号为1时。输出F=1，其余情况下F=0。
（2）若A、B、C出现奇数个0时输出为1，其余情况输出为0。
（3）若A、B、C有两个或两个以上为1时，输出为1，其余情况下，输出为0。

《数字电路与系统设计》课后答案

F2：ABCD比2大。
F3：ABCD在8～11之间。
F4：ABCD不等于0。
解：由题意，各函数是4变量函数，故须将
74138扩展为4-16线译码器，让A、B、C、D分别接4-16线译码器的地址端A3、A2、A1、A0，可写出各函数的表达式如下：
F1(A,B,C,D)
m(0,4,8,12)
= m0m4m8m12
自低位的借位、本位差、本位向高位的借位。
A
－B
F2C
F1
被减数减数
借位
差
4.4设ABCD是一个8421BCD码，试用最少与非
门设计一个能判断该8421BCD码是否大于等于5的电路，该数大于等于5，F=1；否则为0。
解：(1)列真值表
(2)写最简表达式
CD
AB00
00
01
11
10
011110
F = A + BD +BC
B
CF1
A
F2
图P4.2
解：(1)从输入端开始，逐级推导出函数表达式
F1=A⊕B⊕C
F2= A(B⊕C) +BC
= A BC + ABC + ABC + ABC
(2)列真值表
(3) 确定逻辑功能
假设变量A、B、C和函数F1、F2均表示一位二进制数，那么，由真值表可知，该电路实现了全减器的功能。
A、B、C、F1、F2分别表示被减数、减数、来
BC
A00011110
0
1
F1=A+B
00011110
0
1
F2=AB
4.11试将2/4译码器扩展成4/16译码器
A3A2
A1A0

数字逻辑电路与系统设计第6章习题及解答

第6章题解：6.1 试用4个带异步清零和置数输入端的负边沿触发型JK 触发器和门电路设计一个异步余3BCD 码计数器。

题6.1 解：余3BCD 码计数器计数规则为：0011→0100→…→1100→0011→…，由于采用异步清零和置数，故计数器应在1101时产生清零和置数信号，所设计的电路如图题解6.1所示。

CLK13图题解6.1题6.2 试用中规模集成异步十进制计数器74290实现模48计数器。

题6.2 解：6.3 试用D 触发器和门电路设计一个同步4位格雷码计数器。

题6.3 解：根据格雷码计数规则，Q 3 Q 2Q 1 Q 0计数器的状态方程和驱动方程为:1333031210122202131011110320320100321321321321n n n n n n n nn n n n n n n n n n n n n n n n n n n n n n n n n n n n n n Q D Q Q Q Q Q Q Q Q D Q Q Q Q Q Q Q QD Q Q Q Q Q Q Q QQ D Q Q Q Q Q Q Q Q Q Q Q Q ++++==++==++==++==+++按方程画出电路图即可，图略。

题 6.4 解：反馈值为1010。

十一进制计数器6.5 试用4位同步二进制计数器74163实现十二进制计数器。

74163功能表如表6.4所示。

题 6.5 解：可采取同步清零法实现。

电路如图题解6.5所示。

题 6.6 解：当M=1时：六进制计数器当M=0时：八进制计数器图题解6.5图题解6.56.7 试用4位同步二进制计数器74163和门电路设计一个编码可控计数器，当输入控制变量M=0时，电路为8421BCD 码十进制计数器，M=1时电路为5421BCD 码十进制计数器，5421BCD 码计数器状态图如下图P6.7所示。

74163功能表如表6.4所示。

图 P 6.7Q 3Q 2Q 1Q 01010题6.7 解：实现8421BCD 码计数器，可采取同步清零法；5421BCD 码计数器可采取置数法实现，分析5421BCD 码计数规则可知，当21Q =时需置数，应置入的数为：32103000D D D D Q =。

蒋立平版数字逻辑电路与系统设计习题答案

蒋立平版数字逻辑电路与系统设计第1章习题及解答1.1 将下列二进制数转换为等值的十进制数。

（1）（11011）2（2（10010111）2 （3）（1101101）2（4 （11111111）2 （5）（0.1001）2 （6 （0.0111）2 （7）（11.001）2 （8 （101011.11001）2题1.1 解：（1）（11011）2 =（27）10（10010111）2 =（151）10（3）（1101101）2 =（109）10 （11111111）2 =（255）10（5）（0.1001）2 =（0.5625）10 （0.0111）2 =（0.4375）10（7）（11.001）2 =（3.125）10 （101011.11001）2 =（43.78125）101.3 数。

（1）（1010111）2（110111011）2 （3）（10110.011010）2（4）（101100.110011）2 题1.3 解：（1）（1010111）2=（57）16 =（127）8（2）（110011010）2 =（19A ）16 =（632）8 （3）（10110.111010）2 =（16.E8）16 =（（4）（101100.01100001）2 =（2C.61）16 =1.5 将下列十进制数表示为8421BCD 码。

（1）（43）10 （95.12）10 （3）（67.58）10 （（932.1）10题1.5 解：（1）（43）10 =（01000011）8421BC D（2）（95.12）10 =（10010101.00010010）8421BC D （3）（67.58）10 =（01100111.01011000）8421BC D （4）（932.1）10 =（1.7 将下列有符号的十进制数表示成补二进制数。

（1） +13 （2）−9 （3）+3 （4）−题1.7解：（1） +13 =（01101）2 （（10111）2（3） +3 =（00011）2 （（11000）21.9 用真值表证明下列各式相等。

数字电路与系统设计课后习题答案之欧阳学文创编之欧阳索引创编

1.1将下列各式写成按权展开式：欧阳家百（2021.03.07）（352.6）10=3×102+5×101+2×100+6×10-1（101.101）2=1×22+1×20+1×2-1+1×2-3（54.6）8=5×81+54×80+6×8-1（13A.4F）16=1×162+3×161+10×160+4×16-1+15×16-21.2按十进制0~17的次序，列表填写出相应的二进制、八进制、十六进制数。

解：略1.3二进制数00000000~11111111和0000000000~1111111111分别可以代表多少个数？解：分别代表28=256和210=1024个数。

1.4 将下列个数分别转换成十进制数：（1111101000）2，（1750）8，（3E8）16解：（1111101000）2=（1000）10（1750）8=（1000）10（3E8）16=（1000）101.5将下列各数分别转换为二进制数：（210）8，（136）10，（88）16解：结果都为：（10001000）21.6 将下列个数分别转换成八进制数：（111111）2，（63）10，解：结果都为（77）81.7 将下列个数分别转换成十六进制数：（11111111）2，（377）8，（255）10解：结果都为（FF）161.8 转换下列各数，要求转换后保持原精度：解：（1.125）10=（1.0010000000）10——小数点后至少取10位（0010 1011 0010）2421BCD=（11111100）2（0110.1010）余3循环BCD码=（1.1110）21.9 用下列代码表示（123）10，（1011.01）2：解：（1）8421BCD码：（123）10=（0001 0010 0011）8421BCD（1011.01）2=（11.25）10=（0001 0001.0010 0101）8421BCD（2）余3 BCD码（123）10=（0100 0101 0110）余3BCD（1011.01）2=（11.25）10=（0100 0100.0101 1000）余3BCD1.10 已知A=（1011010）2，B=（101111）2，C=（1010100）2，D=（110）2（1）按二进制运算规律求A+B，A-B，C×D，C÷D，（2）将A、B、C、D转换成十进制数后，求A+B，A-B，C×D，C÷D，并将结果与（1）进行比较。