八级上册数学全等三角形知识点与练习

合集下载

初二年级数学八上第十二章全等三角形知识点总结复习及常考题型练习

第十二章全等三角形一、知识框架：二、知识概念：1.基本定义：⑴全等形：能够完全重合的两个图形叫做全等形.⑵全等三角形：能够完全重合的两个三角形叫做全等三角形.理解：①全等三角形形状与大小完全相等，与位置无关；②一个三角形经过平移、翻折、旋转可以得到它的全等形；③三角形全等不因位置发生变化而改变。

⑶对应顶点：全等三角形中互相重合的顶点叫做对应顶点.⑷对应边：全等三角形中互相重合的边叫做对应边.⑸对应角：全等三角形中互相重合的角叫做对应角.2.基本性质：⑴三角形的稳定性：三角形三边的长度确定了，这个三角形的形状、大小就全确定，这个性质叫做三角形的稳定性.⑵全等三角形的性质：全等三角形的对应边相等，对应角相等.理解：①长边对长边，短边对短边；最大角对最大角，最小角对最小角；②对应角的对边为对应边，对应边对的角为对应角。

(3)全等三角形的周长相等、面积相等。

(4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。

3.全等三角形的判定定理：⑴边边边（SSS）：三边对应相等的两个三角形全等.⑵边角边（SAS）：两边和它们的夹角对应相等的两个三角形全等.⑶角边角（ASA）：两角和它们的夹边对应相等的两个三角形全等.⑷角角边（AAS）：两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边（HL）：斜边和一条直角边对应相等的两个直角三角形全等.4.证明两个三角形全等的基本思路：5.角平分线：⑴画法：⑵性质定理：角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.(4)三角形的三条角平分线交于三角形内部一点，并且这点到三边的距离相等6.证明的基本方法：⑴明确命题中的已知和求证.（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系）⑵根据题意，画出图形，并用数字符号表示已知和求证.⑶经过分析，找出由已知推出求证的途径，写出证明过程.7.学习全等三角形应注意以下几个问题：(1)要正确区分“对应边”与“对边”，“对应角”与“对角”的不同含义；(2)表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；(4)中线倍长法、截长补短法证三角形全等。

八上数学全等三角形章节复习及经典例题

八上数学全等三角形章节复习及经典例题【知识梳理】一、全等三角形1.概念能够完全重合的两个三角形叫做全等三角形。

一个三角形经过平移、翻折、旋转可以得到它的全等形。

2.全等三角形的性质①全等三角形的对应边相等、对应角相等。

②全等三角形的周长相等、面积相等。

③全等三角形的对应边上的对应中线、角平分线、高线分别相等。

3.全等三角形的判定边边边：三边对应相等的两个三角形全等（可简写成“SSS”)边角边:两边和它们的夹角对应相等两个三角形全等（可简写成“SAS”)角边角:两角和它们的夹边对应相等的两个三角形全等（可简写成“ASA”)角角边:两角和其中一角的对边对应相等的两个三角形全等（可简写成“AAS”)斜边、直角边：斜边和一条直角边对应相等的两个直角三角形全等（可简写成“HL”)4.证明两个三角形全等的基本思路：⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩SAS SSS HL AAS SAS ASA AAS ASA AAS找夹角已知两边找第三边找直角边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一对边二、角的平分线：1.（性质）角的平分线上的点到角的两边的距离相等.2.（判定）角的内部到角的两边的距离相等的点在角的平分线上。

三、学习全等三角形应注意以下几个问题（1）要正确区分“对应边”与“对边”，“对应角”与 “对角”的不同含义；（2）表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；（3）要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；（4）时刻注意图形中的隐含条件，如 “公共角” 、“公共边”、“对顶角”【例题精讲】例1．如图，在ABC ∆中, 90=∠C ，D 、E 分别为AC 、AB 上的点，且AD=BD,AE=BC,DE=DC.求证：DE ⊥AB 。

人教版八年级上册数学第12章全等三角形讲义知识点+典型例题

BPAa【变式1】如图，在t R ABC △中，AB AC =，90BAC ∠=︒，过点A 的任一直线AN ，BD AN ⊥于D ，BD AN ⊥于E求证：DE BD CE =-NEDCBA【变式2】如图，在ABC △中，90ACB ∠=︒，AC BC =，直线MN 经过点C ，且AD MN ⊥于D ，BE MN ⊥于E ，求证：DE AD BE =+.EDCBA专题三角形的尺规作图知识点解析作三角形的三种类型：① 已知两边及夹角作三角形：作图依据------SAS ② 已知两角及夹边作三角形：作图依据------ASA ③ 已知三边作三角形：作图依据------SSS典型例题【例1】作一条线段等于已知线段。

已知：如图，线段a . 求作：线段AB ，使AB = a .【例2】作一个角等于已知角。

已知：如图，∠AOB 。

求作：∠A’O’B’，使A’O’B’=∠AOB【例3】已知三边作三角形已知：如图，线段a，b，c.求作：△ABC，使AB = c，AC = b，BC = a.作法：【例4】已知两边及夹角作三角形已知：如图，线段m，n, ∠α.求作：△ABC，使∠A=∠α，AB=m，AC=n.【例5】已知两角及夹边作三角形已知：如图，∠α，∠β，线段c .求作：△ABC，使∠A=∠α，∠B=∠β,AB=c.随堂练习1．根据已知条件作符合条件的三角形，在作图过程中主要依据是（）A．用尺规作一条线段等于已知线段；B．用尺规作一个角等于已知角C．用尺规作一条线段等于已知线段和作一个角等于已知角；D．不能确定2．已知三角形的两边及其夹角，求作这个三角形时，第一步骤应为（）A．作一条线段等于已知线段B．作一个角等于已知角C．作两条线段等于已知三角形的边，并使其夹角等于已知角D．先作一条线段等于已知线段或先作一个角等于已知角3．用尺规作一个直角三角形，使其两条直角边分别等于已知线段时，实际上就是已知的条件是（）A．三角形的两条边和它们的夹角B．三角形的三条边C．三角形的两个角和它们的夹边；D．三角形的三个角4.已知三边作三角形时，用到所学知识是（）A．作一个角等于已知角B．作一个角使它等于已知角的一半C．在射线上取一线段等于已知线段D．作一条直线的平行线或垂线专题利用三角形全等测距离知识点解析一、利用三角形全等测距离目的：变不可测距离为可测距离。

人教版八年级数学上册第12章全等三角形知识点复习总结及常考题型练习.doc

第十二章一、：：二、：：1.：：⑴全等形：能够完全重合的两个图形叫做全等形.⑵全等三角形：能够完全重合的两个三角形叫做全等三角形.理解：：①全等三角形形状与大小完全相等，与位置无关；②一个三角形经过平移、翻折、旋转可以得到它的全等形；③三角形全等不因位置发生变化而改变。

⑶对应顶点：全等三角形中互相重合的顶点叫做对应顶点.⑷对应边：全等三角形中互相重合的边叫做对应边.⑸对应角：全等三角形中互相重合的角叫做对应角.2.：：⑴三角形的稳定性：三角形三边的长度确定了，这个三角形的形状、大小就全确定，这个性质叫做三角形的稳定性.⑵全等三角形的性质：全等三角形的对应边相等，对应角相等.理解：：①长边对长边，短边对短边；最大角对最大角，最小角对最小角；②对应角的对边为对应边，对应边对的角为对应角。

(3)全等三角形的周长相等、面积相等。

(4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。

3.全等三角形的判定定理：：⑴边边边（ SSS）：三边对应相等的两个三角形全等.⑵边角边（ SAS ）：两边和它们的夹角对应相等的两个三角形全等.⑶角边角（ASA ）：两角和它们的夹边对应相等的两个三角形全等.⑷角角边（AAS ）：两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边（HL ）：斜边和一条直角边对应相等的两个直角三角形全等..4.：：5.：：⑴画法：⑵性质定理：角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.(4)三角形的三条角平分线交于三角形内部一点，并且这点到三边的距离相等6.：：⑴明确命题中的已知和求证. （包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系）⑵根据题意，画出图形，并用数字符号表示已知和求证.⑶经过分析，找出由已知推出求证的途径，写出证明过程.7.：：(1) 要正确区分“对应边”与“对边”，“对应角”与“对角”的不同含义；(2)表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；(4)中线倍长法、截长补短法证三角形全等。

(完整)人教版八年级数学上册知识整理与经典例题

八年级数学上册知识总结与相关练习第十一章全等三角形一、全等形能够完全重合的两个图形叫做全等形。

二、全等三角形１、概念：能够完全重合的两个三角形叫做全等三角形。

注意：（１）两个三角形全等，互相重合的顶点叫做对应点，互相重合的边叫做对应边，互相重合的角叫做对应角。

（２）“能够完全重合”是指在一定的叠放下，能够完全重合。

２、全等三角形的符号表示、读法△ＡＢＣ与△Ａ′Ｂ′Ｃ′全等记作△ＡＢＣ≌△Ａ′Ｂ′Ｃ′，“≌”读作“全等于” 。

注意：（１）两个三角形全等时，通常把对应顶点的字母写在对应的位置上，这样对应的两个字母为端点的线段是对应边；对应的三个字母表示的角是对应角（若用一个字母表示一个角亦是如此）。

（２）对应角夹的边是对应边，对应边的夹角是对应角。

（３）对应边、对应角是对两个三角形而言的，指两条边、两个角的关系，而对边、对角是指同一个三角形的边和角的位置关系，对边是与角相对的边，对角是与边相对的角。

３、全等三角形的性质全等三角形的对应边相等，对应角相等。

４、三角形全等的识别方法（１）三边对应相等的两个三角形全等，简写成“边边边”和“ＳＳＳ” 。

（２）两边和他们的夹角对应相等的两个三角形全等，简写成“边角边”和“ＳＡＳ”。

（３）两角和他们的夹边对应相等的两个三角形全等，简写成“角边角”和“ＡＳＡ”。

（４）两个角和其中一个角的对边对应相等的两个三角形全等，简写成“角角边”和“ＡＡＳ”。

（５）斜边和一条直角边对应相等的两个直角三角形全等，简写成“斜边、直角边”和“ＨＬ”。

注意：ＳＳＡ、ＡＡＡ不能识别两个三角形全等，识别两个三角形全等时，必须有边的参与，如果有两边和一角对应相等时，角必须是两边的夹角。

５、三角形全等的证明思路找夹角——ＳＡＳ（１）已知两边都是直角三角形——ＨＬ找另一边——ＳＳＳ找边的对角——ＡＡＳ（２）已知一边一角找夹角的另一边——ＳＡＳ找夹边的另一角——ＡＳＡ（３）已知两角找夹边——ＡＳＡ找其他任意一边——ＡＡＳ６、全等变换一个图形与另一个图形的形状一样，大小相等，只是位置不同，我们称这个图形是另一个图形的全等变换，三种基本全等变换：（１）旋转；（２）翻折；（３）平移。

八年级上册数学三角形全等整章知识点和对应练习

T——全等三角形课堂导入形状与大小都完全相同的两个图形就是全等形一、知识梳理：1、能够完全重合的两个三角形,叫全等三角形（1）“全等”用符号________来表示，读作“全等于”。

（2）记作:△ABC≌△DEF，读作 : _________________互相重合的顶点叫做___________互相重合的边叫做_________互相重合的角叫做_____________2、全等三角形的性质:（1）.全等三角形的对应边_______；（2）.全等三角形的对应角_________。

二、考点分类考点一：判断全等【例】1.下列图形中，和所给图形全等的图形是（）A．B．C．D．2．下列说法正确的有（）①两个图形全等，它们的形状相同；②两个图形全等，它们的大小相同；③面积相等的两个图形全等；④周长相等的两个图形全等．A．1个B．2个 C．3个D．4个考点二：对应关系【例2】如图（1），△AOB ≌△COD ，∠AOB =∠COD ，∠A =∠C ，则∠D 的对应角是__________，图中相等的线段有__________图（1）图（2）【变式训练】如图（2），△ABC ≌△AED ，∠C =40°，∠EAC =30°，∠B =30°，则∠EAD =___________.考点三：全等三角形性质【例5】如图(3)，小强利用全等三角形的知识测量池塘两端M 、N 的距离，如果△PQO ≌△NMO ，则只需测出其长度的线段是_____________.图（3）图（6）图（7）【变式训练】如图（6），△ABE ≌△ACD ，AE =5 cm ，∠A =60°，∠B =30°，则∠ADC =__________°，AD =__________cm ．3、如图（7），已知，△ABC ≌△BAE ，∠ABE =60°，∠E =92°，则∠ABC 的度数为__________度．如图，ΔABC ≌ΔDEF ，∠A =25°，∠B =65°，BF =3 cm ，求∠DFE 的度数和EC 的长．强化练习C——边边边、边角边一、知识梳理：全等三角形的条件（1）、三角形全等的判定------三边对应相等的两个三角形全等（“边边边”或“”）（2）、三角形全等的判定-----两边和它们的夹角对应相等的两个三角形全等(“边角边”或“”)。

初中数学--八年级上册全等三角形知识点归纳及经典练习题

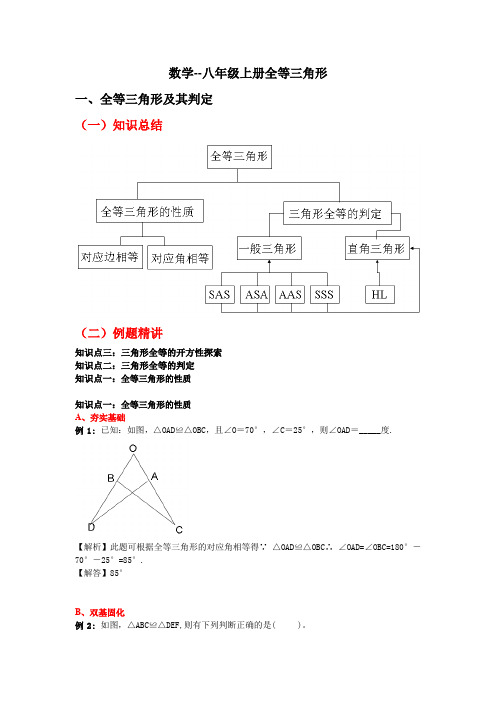
数学--八年级上册全等三角形一、全等三角形及其判定（一）知识总结（二）例题精讲知识点三：三角形全等的开方性探索知识点二：三角形全等的判定知识点一：全等三角形的性质知识点一：全等三角形的性质A、夯实基础例1:已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠OAD＝_____度.【解析】此题可根据全等三角形的对应角相等得∵△OAD≌△OBC∴∠OAD=∠OBC=180°－70°－25°=85°.【解答】85°B、双基固化例2:如图，△ABC≌△DEF,则有下列判断正确的是( )。

A.AB=DFB.AC=DFC.∠A=∠FD.∠B=∠D【解析】本题根据全等三角形的对应边相等,对应角相等判断即可.【解答】B.C、能力提升例3:如图,△ABC≌△AED,B和E是对应顶点,写出图中相等的线段和相等的角.【解析】根据全等三角形的对应边相等,对应角相等判断即可.关键要做到不重不漏. 【解答】相等的线段有:AB=AE,AC=AD,BC=DE，BD=EC相等的角有:∠B=∠E,∠BAC=∠EAD,∠ACB=∠ADE。

知识点二：三角形全等的判定A、夯实基础例4:如图，AE=CF，∠AFD=∠CEB，DF=BE，△AFD与△ CEB全等吗？为什么？【解答】△AFD≌△ CEB理由：∵AE=CF∴AE－FE=CF－EF，即AF=CE在△AFD和△ CEB中AF=CE∠AFD=∠CEB，DF=BE∴△AFD≌△CEB（SAS）B、双基固化例5:（2010年福州）如图，点B、E、C、F在一条直线上，BC=EF，AB∥DE，∠A=∠D。

求证：△ABC≌△DEF。

【解答】证明：∵ AB∥DE，∴∠B=∠DEF在△ABC和△DEF中，B=∠DEF∠A=∠DBC=EF∴△ABC≌△DEF（AAS）C、能力提升例6:（2010年宁德市）如图，已知AD是△ABC的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是：____________，并给予证明.【解答】解法一：添加条件：AE＝AF证明：在△AED与△AFD中，∵AE＝AF，∠EAD＝∠FAD，AD＝AD，∴△AED≌△AFD（SAS）.解法二：添加条件：∠EDA＝∠FDA证明：在△AED与△AFD中，∵∠EAD＝∠FAD，AD＝AD，∠EDA＝∠FDA，∴△AED≌△AFD（ASA）.知识点三：三角形全等的开方性探索A、夯实基础例7:如图，已知△ABC和△DCB中，AB=DC，请补充一个条件_____，使△ABC≌△DCB。

人教版初二八年级数学上第十二单元全等三角形知识点及单元测试

第十二章全等三角形一．知识框架二．知识概念1.全等三角形：两个三角形的形状、大小、都一样时，其中一个可以经过平移、旋转、对称等运动（或称变换）使之与另一个重合，这两个三角形称为全等三角形。

2．全等三角形的性质：全等三角形的对应角相等、对应边相等。

3.三角形全等的判定公理及推论有：（1）“边角边”简称“SAS”（2）“角边角”简称“ASA”（3）“边边边”简称“SSS”（4）“角角边”简称“AAS”（5）斜边和直角边相等的两直角三角形（HL）。

除了边边角和角角角。

4.角平分线推论：角的内部到角的两边的距离相等的点在角的平分线上。

5.证明两三角形全等或利用它证明线段或角的相等的基本方法步骤：①、确定已知条件（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系），②、回顾三角形判定，搞清我们还需要什么，③、正确地书写证明格式(顺序和对应关系从已知推导出要证明的问题).在学习三角形的全等时，教师应该从实际生活中的图形出发，引出全等图形进而引出全等三角形。

通过直观的理解和比较发现全等三角形的奥妙之处。

在经历三角形的角平分线、中线等探索中激发学生的集合思维，启发他们的灵感，使学生体会到集合的真正魅力。

【同步练习（§12.1～12.2）】一、填空题（每题3分，共30分）32681．如图，△ABC≌△DEF，A与D，B与E分别是对应顶点，∠B=，∠A=，AB=13cm，则∠F=______度，ADE =______cm ．2．由同一张底片冲洗出来的两张五寸照片的图案全等图形，而由同一张底片冲洗出来的五寸照片和七寸照片全等图形（填“是”或“不是”）.3．如图，△ABC 与△DBC 能够完全重合，则△ABC 与△DBC 是____________，表示为△ABC ____△DBC ．4．如图，已知△ABC ≌△BAD ，BC =AD ，写出其他的对应边和对应角．5．如图所示，，的延长线交于，交于，，，，则的度数为．6．如图，已知，垂足为，，垂足为，，，则＝___________．7．如图，已知，，，经分析．此时有． 8．如图所示，AB ，CD 相交于O ，且AO ＝OB ，观察图形，图中已具备的另一相等的条件是________，联想到SAS ，只需补充条件________，则有△AOC ≌△________．9．如图所示，有一块三角形的镜子，小明不小心弄破裂成1、2两块，现需配成同样大小的一块．为了方便起见，需带上________块，其理由是__________． 10．如图，把两根钢条，的中点连在一起，可以做成一个测的长量工件内槽宽的工具（工人把这种工具叫卡钳）只要量出度，就可以知道工件的内径是否符合标准，你能简要说出工人这ABC ADE △≌△BC DA F DE G 105ACB AED ∠=∠=15CAD ∠=30B D ∠=∠=1∠AB BD ⊥B ED BD ⊥D AB CD =BC DE =ACE ∠AF BE =A B ∠=∠AC BD =≌F ∠=AA 'BB 'O A B ''AB A BC OD （第4题）A F CB DG E 1 （第5题）AEC （第6题）CEF（第7题）ACODBB A1 2（第8题）（第9题）样测量的道理吗？．二、选择题（每题3分，共24分）11．下列说法：①全等图形的形状相同、大小相等；②全等三角形的对应边相等；③全等三角形的对应角相等；④全等三角形的周长、面积分别相等，其中正确的说法为（）Ａ．①②③④Ｂ．①③④Ｃ．①②④Ｄ．②③④12．如果是中边上一点，并且，则是（）Ａ．锐角三角形Ｂ．钝角三角形Ｃ．直角三角形Ｄ．等腰三角形13．一个正方形的侧面展开图有（）个全等的正方形.A．2个 B．3个 C．4个 D．6个14．对于两个图形，给出下列结论：①两个图形的周长相等；②两个图形的面积相等；③两个图形的周长和面积都相等；④两个图形的形状相同，大小也相等．其中能获得这两个图形全等的结论共有（）A．1个 B．2个C．3个 D．4个15．如图，在和中，已知，，根据（SAS）判定，还需的条件是（）Ａ．Ｂ．Ｃ．Ｄ．以上三个均可以16．下面各条件中，能使△ABC≌△DEF的条件的是（）Ａ．AB＝DE，∠A＝∠D，BC＝EFＢ．AB＝BC，∠B＝∠E，DE＝EFC．AB＝EF，∠A＝∠D，AC＝DFＤ．BC＝EF，∠C＝∠F，AC＝DF17．如图，相交于点，，．下列结论正确的是（）A．． B． C． D．18．如图，已知，，．下列结论不正确的有（）．A． B． C．AB=BC D．三、解答题（共46分）19．（7分）找出下列图形中的全等图形．D ABC△BC ADB ADC△≌△ABC△ABC△DEF△AB DE=BC EF=ABC DEF△≌△A D∠=∠B E∠=∠C F∠=∠AD BC，O OA OD=OB OC=AOB DOC△≌△ABO DOC△≌△A C∠=∠B D∠=∠AB AC=AD AE=BAC DAE∠=∠BAD CAE∠=∠ABD ACE△≌△BD CE=（第15题）（第17题）（第18题）（1）（2）（3）（4）（5）（6）（7）（8）（9）（10）（11）（12）20．（7分）如图，AB=DC，AC=DB，求证AB∥CD．21．（8分）如图，已知AB∥DC，AD∥BC.证明：（1）AB=CD；（2）AD=BC．D CBA22．（8分）如图，点在一条直线上，△△你能得出哪些结论?（请写出三个以上的结论）23．（8分）如图，点分别在上，且，．求证：．24．（8分）如右图，已知DE⊥AC，BF⊥AC，垂足分别是E、F，AE=CF，DC∥AB，（1）试证明：DE=B F；（2）连接DF、BE，猜想DF与BE的关系？并证明你的猜想的正确性．【同步练习§12.1】一、填空题（每题3分，共30分）1．到一个角的两边距离相等的点都在_________.2．∠AOB的平分线上一点M，M到OA的距离为1.5 cm，则M到OB的距离为_________.A B C D，，，ABF≌DCE，D E，AB AC，AD AE=BDC CEB∠=∠BD CE=DFCBAE④①② ③ （第14题）3．如图，∠AOB =60°，CD ⊥OA 于D ，CE ⊥OB 于E ，且CD =CE ，则∠DOC =_________.4．如图，在△ABC 中，∠C =90°，AD 是角平分线，DE ⊥AB 于E ，且DE =3 cm ，BD =5 cm ，则BC =_________ cm ． 5．如图，已知AB 、CD 相交于点E ，过E 作∠AEC 及∠AED 的平分线PQ 与MN ，则直线MN 与PQ 的关系是_________． 6．三角形内一点到三角形的三边的距离相等，则这个点是三角形_________的交点． 7．△ABC 中，∠C =90°，AD 平分∠BAC 交BC 于D ，且BD ：CD =3：2，BC =15cm ，则点D 到AB 的距离是__________． 8．角平分线的性质定理：角平分线上的点_____________________________． 9．（1）如图，已知∠1 =∠2，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，则DE ____DF ．（2）已知DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，且DE = DF ，则∠1_____∠2．10．直角三角形两锐角的平分线所夹的钝角为_______度．二、选择题（每题3分，共24分）11．如图，OP 平分∠AOB ，PC ⊥OA ，PD ⊥OB ，垂足分别是C 、D ．下列结论中错误的是（）A ．PC = PDB ．OC = OD C ．∠CPO = ∠DPO D ．OC = PC12．如图，△ABC 中，∠C = 90°，AC = BC ，AD 是∠BAC 的平分线，DE ⊥AB 于E ，若AC = 10cm ，则△DBE 的周长等于( )A ．10cmB ．8cmC ．6cmD ．9cm13．到三角形三条边的距离都相等的点是这个三角形的（）A ．三条中线的交点B ．三条高的交点C ．三条边的垂直平分线的交点D ．三条角平分线的交点 14．如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）Ａ．1处Ｂ．2处Ｃ．3处Ｄ．4处 15．给出下列结论，正确的有（）①到角两边距离相等的点，在这个角的平分线上；②角的平分线与三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的（第3题）（第4题）（第5题） 21A BCDEF（第9题）A BC DO P（第11题）ED CB A （第12题）逆命题一定是假命题A．1个B．2个C．3个D．4个16．已知，Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=32，且BD∶CD=9∶7，则D到AB的距离为（）A．18 B．16 C．14 D．1217．两个三角形有两个角对应相等，正确说法是（）A．两个三角形全等B．两个三角形一定不全等C．如果还有一角相等，两三角形就全等D．如果一对等角的角平分线相等，两三角形全等18．如图，OB、OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式为（）A．2α－βB．α－βC．α+βD．2α三、解答题（共46分）19．（7分）如图，已知OE、OD分别平分∠AOB和∠BOC，若∠AOB=90°，∠EOD=70°，求∠BOC的度数．20．（7分）已知：有一块三角形空地，若想在空地中找到一个点，使这个点到三边的距离相等，试找出该点．（保留画图痕迹）（第18题）21．（8分）如图，点D 、B 分别在∠A 的两边上，C 是∠A 内一点，AB = AD ，BC = CD ，CE ⊥AD 于E ，CF ⊥AF 于F ．求证：CE = CF22．（8分）已知：如图，在△ABC 中，∠A =90°，AB = AC ，BD 平分∠ABC ．求证：BC = AB + AD23．（8分）如图，PB 和PC 是△ABC 的两条外角平分线． ①求证：∠BPC =90°-∠BAC ． ②根据第①问的结论猜想：三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形？12F A B EC D D AC PC B AD E24．（8分）如图，BP是△ABC的外角平分线，点P在∠BAC的角平分线上．求证：CP是△ABC的外角平分线．。

八年级数学上册第十二章全等三角形知识点汇总(带答案)

八年级数学上册第十二章全等三角形知识点汇总单选题1、如图，已知点A、D、C、F在同一条直线上，∠B=∠E =90°，AB=DE，若添加一个条件后，能用“HL”的方法判定Rt△ABC≌Rt△DEF，添加的条件可以是（）A．BC=EF B．∠BCA=∠F C．AB∥DE D．AD=CF答案：D分析：根据题目给的条件可知道直角边和直角，因为需用“HL”的方法判定Rt△ABC≌Rt△DEF，故只能添上斜边这一条件，即可解答．解：∵∠B=∠E=90°，AB=DE，∴添加条件AC=DF，根据“HL”即可判定Rt△ABC≌Rt△DEF；或添加条件AD=CF，也可得出AC=DF，根据“HL”即可判定Rt△ABC≌Rt△DEF，故D正确．故选：D．小提示：本题主要考查了利用“HL”判定三角形全等，掌握三角形全等的判定是解题的关键．2、如图，锐角△ABC的两条高BD、CE相交于点O，且CE＝BD，若∠CBD＝20°，则∠A的度数为（）A．20°B．40°C．60°D．70°答案：B分析：由BD、CE是高，可得∠BDC=∠CEB=90°，可求∠BCD＝70°，可证Rt△BEC≌Rt△CDB（HL），得出∠BCD ＝∠CBE＝70°即可．解：∵BD、CE是高，∠CBD＝20°，∴∠BDC=∠CEB=90°，∴∠BCD＝180°﹣90°﹣20°＝70°，在Rt△BEC和Rt△CDB中，{CE=BDBC=CB，∴Rt△BEC≌Rt△CDB（HL），∴∠BCD＝∠CBE＝70°，∴∠A＝180°﹣70°﹣70°＝40°．故选：B．小提示：本题考查三角形高的定义，三角形全等判定与性质，三角形内角和公式，掌握三角形高的定义，三角形全等判定与性质，三角形内角和公式是解题关键．3、如图，为测量桃李湖两端AB的距离，南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C，测得∠ACB的度数，在AC的另一侧测得∠ACD=∠ACB，CD=CB，再测得AD的长，就是AB的长．那么判定△ABC≌△ADC的理由是（）A．SASB．SSSC．ASAD．AAS答案：A分析：已知条件是∠ACD=∠ACB，CD=CB，AC=AC，据此作出选择．解：在△ADC与△ABC中，{CD=CB∠ACD=∠ACBAC=AC．∴△ADC≌△ABC（SAS）．故选：A．小提示：此题考查了全等三角形的应用，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，做题时注意选择．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．4、为了测量工件的内径，设计了如图所示的工具，点O为卡钳两柄的交点，且有OA＝OB＝OC＝OD，只要量得CD之间的距离，就可知工件的内径AB．其数学原理是利用△AOB≌△COD，判断的依据是（）A．SSSB．SASC．ASAD．AAS答案：B分析：利用“边角边”证明△ABO和△CDO全等，根据全等三角形对应边相等解答．解：在△ABO和△CDO中{OA=OC ∠AOB=COD OB=OD∴△ABO≌△CDO（SAS）故选B小提示：本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．5、观察下列作图痕迹，所作线段CD为△ABC的角平分线的是（）A．B．C ．D ．答案：C 分析：根据角平分线画法逐一进行判断即可．A ：所作线段为AB 边上的高，选项错误；B ：做图痕迹为AB 边上的中垂线，CD 为AB 边上的中线，选项错误；C ：CD 为∠ACB 的角平分线，满足题意。

八年级数学全等三角形知识点归纳及分类练习

八年级数学全等三角形知识点归纳及分类练习、.知识框架:二、知识概念：1 .根本定义：⑴全等形：能够完全重合的两个图形叫做全等形^⑵全等三角形：能够完全重合的两个三角形叫做全等三角形^⑶对应顶点：全等.三角形中互相重合的顶点叫做对应顶点⑷对应边：全等三角形中互相重合的边叫做对应边.⑸对应角：全等三角形中互相重合的角叫做对应角^2 .根本性质：⑴三角形的稳定性：三角形三边的长度确定了,这个三角形的形状、大,小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质：全等三角形的对应边相等,对应角相等^3 .全等三角形的判定定理：⑴边边边〔S SS〕：三边对应相等的两个三角形全等.⑵边角边〔SAS〕：两边和它们的夹角对应相等的两个三角形全等^⑶角边角〔ASA〕：两角和它们的夹边对应相等的两个三角形全等^⑷角角边〔AAS〕：两角和其中一个角的对边对应相等的两个三角形全等^⑸斜边、直角边〔HL〕：斜边和一条直角边对应相等的两个直角三角形全等.1性质定理：角平分线上.的点到角的两边的距离相等.2性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.5.证实的根本方法：⑴明确命题中的和求证.〔包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系〕⑵根据题意,画出图形,并用数字符号表示和求证^⑶经过分析,找出由推出求证的途径,写出证实过程 ^练习一12.1全等三角形、根底达标1 .如图12-1-4 所示,AACB^A ACB ； / BCB'= 30°,那么/ACA 的度数为〔〕图12-1-4A. 20° B, 30°C. 35° D, 40°2.如图12-1-5所示,AABC^ACDA ,那么以下结论错误的选项是〔〕图12-1-5A. / 1= / 2B. AC=CAC. / D= / BD. AC=BC3.如图12-1-6, Z^ABC^A DEF, BE= 4, -AE= 1 ,那么DE 的长是〔〕A. 5B. 4C. 3 D . 2图12-1-64 . [2021 成都]如图12-1-7, Z^ABC^A A BC；其中/A=36°, / C'= 24°,那么 / B =C C图 12-1-75 .如图 12-1-8, Z^AOC^A BOD ,试证实 AC // BD.二、水平提升6 .如图 12-1-9, AABC^A DCB.⑴分别写出它们的对应角和对应边;(2)请说明/ 1= /2的理由.7.如图 12-1-10, AACEZ^DBF,CE=BF, AE=DF, AD = 8, BC=2.1V图 12-1-8⑴求AC的长度；(2)求证:CE//BF.三、创新题型8.如图12-1-11,△ABC^A DEB ,点E在AB上,DE与AC相交于点F.(1)当DE=8, BC = 5时,线段AE的长为 .(2)/D=35°, /C=60°.①求/DBC的度数；②求/AFD的度数.图12-1-11参考答案【知识治理】1.完全重合2.完全重合顶点边角全等于对应顶点3.相等相等【归类探究】4 1 AC的对应边是DE , AB的对应边是DF , CB的对应边是EF; Z A与/ D, Z C与/DEF, / ABC与/ F是对应角.5 2 A【当堂测评】1. B 2,C 3.61 ° 15【分层作业】1. B2.D3.A4.120 °5.略6. (1)对应角是/A和/D, /1和/2, /ABC和/DCB,对应边是AB和DC, AC和DB , BC和CB ;(2)理由：全等三角形的对应角相等.7. (1)AC= 5 (2)略8. (1)3 (2)/DBC=25°; /AFD=130°.练习二12.2三角形全等的判定三角形全等的判定(SSS)、根底达标1.如图12-2-6所示,在那BC中,AB=AC, BE = CE ,那么由“SSStf以判定()图12-2-6A. AABD0^ACDB. ABDE^A CDEC, 9BEACE -D,以上都不正确2 .如图12-2-7,点D, E 在线段BC 上,AB =AC, AD = AE , BE = CD,要判定ZxABD^AACE ,较为快捷的判定依据是.图12-2-73 . 一个平分角的仪器如图12-2-8所示,其中AB = AD , BC = DC.求证：/ BAC = / DAC.图12-2-84 .如图12-2-9,四边形ABCD 中,AB = CD, CB = AD.求证：Z^ABC CDA.图 12-2-9二、水平提升5 .如图 12-2-10, AB=AC, AE=AD, BD = CE,求证：AAEB ADC.6 .如图 12-2-11,点 B, E, C, F 在同一直线上, AB = DE , AC = DF, BE=CF,求证：AC三、创新题型7 .如图 12-2-12 所示,AB=AE, BC=ED, CF=DF, AC =AD.图 12-2-10 DF. 图 12-2-11fiI)图12-2-12求证：/BAF=/EAF.【知识治理】2.相等【归类探究】例1 略例2 (1)略(2)AB //DE , AC// DF.理由略.【当堂测评】1. D2.SSS3.36 °4.AB = DC三角形全等的判定(SAS)、根底达标1.如图12-2-18所示,/1=/2,假设用“SAS证实△ACB^A BDA ,还需要-加上条件()图12-2-18A. AD = BCB. AC = BDC. / C= / DD. OA = OB2 .如图12-2-19 所示,BE=CD, AE=AD , / 1 = /2, Z 2= 100°, / BAE =60°,贝U / CAE 的度数为〔〕B D E C图12-2-19A. 20° B, 30° C. 40° D, 50°3 .如图12-2-20,点B, E, C, F在同一直线上, AB = DE , BE = CF.请你添加一个条件：〔只需添加一个即可〕,使那BC叁' DEF.8 E C F图12-2-204 .如图12-2-21, C 是线段AB 的中点,CD = BE, CD // BE.求证：/ D = / E.图1 2-2-21二、水平提升5 .如图12-2-22,点A, F, C, D在同一直线上,点B和点E分别在直线AD的两侧,且AB = DE, Z A =ZD, AF= DC.求证：BC // EF.图12-2-226 .如图12-2-23,在AABC中, AB = AC , AD平分/ BAC ,点M , N分别在AB , AC边上,AM = 2MB , AN=2NC.求证：DM = DN.图1 2-2-23三、创新题型7 .如图12-2-24,点A, B, C, D 在同一直线上, CE//DF, EC=BD, AC = FD.求证：AE = FB.图12-2-24参考答案【知识治理】1 .唯一确定2 .夹角对应关系【归类探究】例1 略例2 △OAB^^ODC,那BC^A DCB.理由略.【当堂测评】1. A2.D3.〔1〕〔3〕4.不是AC=DF【分层作业】1. B2.C3.AC= DF 或/B=/DEF 或AB // DE三角形全等的判定〔ASA, AAS〕一■、根底达标1 .如图12-2-30,/ABC=/BAD,添加以下条件还不能判定AABC BAD的是〔〕D图12-2-30A . AC = BDB . / CAB = / DBAC. ZC=ZDD. BC = AD2.如图12-2-31 ,点D, E分别在线段AB , AC上,AE = AD ,不添加新的线段和字母,要使AABE^AACD ,需添加的一个条件是_ _〔只写一个条件即可〕.图12-2-313 . [2021 福州]如图12-2-32, 3 1=/2, /3=/4,求证：AC = AD.图12-2-32三、水平提升4 .如图12-2-33,/AOD=/COB, / A= / C, O 是AC 的中点.图12-2-33求证：△AOB^^COD.5 .如图12-2-34, BD^AC 于点D, CEL AB 于点E, AD=AE.求证：BE = CD.图12-2-34四、创新题型6 .两块完全相同的三角形纸板ABC和DEF,按如图12-2-35所示的方式叠放,阴影局部为重叠局部,点O为边AC和DF的交点.不重叠的两局部AAOF与4DOC是否全等？为什,么？图12-2-35参考答案【知识治理】2 .夹边3 .对边【归类探究】例1 略例2 〔1〕略〔2〕/D=75°【当堂测评】1. D 2,B 3.D 4.B【分层作业】1. A2./ADC = / AEB 或 / CEB= / BDC 或 / C= / B 或AB =AC 或BD = CE3.略4.略5.略6. AAOF与4DOC全等.理由略.直角三角形全等的判定〔HL〕一根底过关1 .在9BC和4DEF中,/A=/D=90°,那么以下条件中不能判定AABC和4DEF全等白^是〔〕A . AB = DE , AC = DF B. AC = EF, BC = DFC. AB = DE , BC= EFD. /C=/F, BC = EF2.如图12-2-40, AB LAC于A, BD^CD于D,假设AC = DB ,那么以下结论中不正确的选项是〔〕I〕c图12-2-40A. /A=/DB. / ABC = / DCBC. OB = ODD. OA = OD3.如图12-2-41,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角/ AB C和/ DFE之间的关系是〔〕图12-2-41A. /ABC = ZDFEB . / ABC> / DFEC. /ABC</DFED. /ABC +/DFE = 90 °4 .如图12-2-42, AABC 中,AD^BC 于D,要使^ABD ACD ,假设根据“HL判定,假设加条件/B=/C,那么可用判定.5 .如图12-2-43, AB = CD , DE ±AC , BFXAC , E, F 是垂足,DE = BF.求证:图12-2-43 (1)AF = CE;(2)AB // CD.、水平提升6 .如图12-2-44,/A=/D=90°, E, F 在线段BC 上,DE 与AF 交于点O,且AB = DC , BE = CF.还需要加条件IIIK 图12-2-42图122-44求证：RtAABF 色 RtADCE.三、创新题型7 .如图12245,在4ABC中,AB =AC, DE是过点A的直线,BD,DE于点D, CEL DE于点E.(1)假设B, C 在DE 的同侧(如图12-2-45(1)所示),AD = CE.求证：AB XAC.(2)假设B, C在DE的两侧(如图12-2-45(2)所示),AD=CE, AB与AC仍垂直吗？假设是,请给出证实；假设不是,请说明理由.(2)参考答案【知识治理】2. 一条直角边【归斜边、直角边(或HL)类探究】例1 AD是4ABC的中线,理由略.例2 (1)3 对,分别是：AABD0^ACD, AADE0^ADF, ABDE^A CDF.(2)答案不唯一,略.【当堂测评】1. B2.A3.A4.HL【分层作业】1. B2.C3.D4.AB = AC AAS5. (1)略(2)略6.略7. (1)略(2)AB ±A C.证实略.角的平分线的性质一、根底过关1 .如图12-3-6,在RtAABC中,ZC=90°,以顶点A为圆心,适当长为半径画弧,分别交AC, AB于1 .......................................... ......................点M , N,再分别以点M, N为圆心,大于2MN的长为半径回弧,两弧交于点P,作射线AP交边BC于点D,假设CD =4, AB = 15,那么4ABD的面积是()图12-3-6A. 15B. 30C. 45D. 602 .如图12-3-7,在GABC 中,ZC=90°, AC = BC , AD 平分 / BAC 交BC 于D , DELAB 于E,假设^BDE 的周长是5 cm,那么AB的长为图12-3-73 .证实命题角的平分线上的点到角的两边的距离相等〞,要根据题意,画出图形,并用符号表示和求证,写出证实过程.下面是小明同学根据题意画出的图形,并写出了不完整的和求证.：如图12-3-8, /AOC=/BOC,点P 在OC 上.求证:请你补全和求证,并写出证实过程.⑴求DE的长；(2)求那DB的面积.中,ZC=90°, AD 平分 / CAB , DEXAB 于E,假设AB = 10, CD 3.图12-3-8二、水平提升5 .如图12-3-10, PB, PC分别是那BC的两个外角的平分线且相交于点P.求证：点P在/ A的平分线上.图12-3-106 .如图12-3-11,BD为/ABC的平分线,AB = BC ,点P在BD上,PMLAD于M, PNLCD于N, 求证：PM =PN.If图12-3-11三、创新题型7.如图12-3-12,在那BC中,D是BC的中点,DE^AB, DFXAC,垂足分别是E, F, BE=CF.H图12-3-12求证：AD是4ABC的角平分线.【知识治理】1 .距离相等2 .角的平分线上3 .相等【归类探究】例1 略例2 略【当堂测评】1. B 2,B 3.A 4.3【分层作业】1. B2.5 cm3. PDXOA , PEXOB,垂足分别为D, E. PD = PE.证实略.4. (1)DE = 3 (2)SAADB =155.略6.略7.略。

初二全等三角形所有知识点总结和常考题提高难题压轴题练习含答案解析

初二全等三角形所有知识点总结和常考题知识点：1. 基本定义：⑴全等形：能够完全重合的两个图形叫做全等形.⑵全等三角形：能够完全重合的两个三角形叫做全等三角形•⑶对应顶点：全等三角形中互相重合的顶点叫做对应顶点.⑷对应边：全等三角形中互相重合的边叫做对应边.⑸对应角：全等三角形中互相重合的角叫做对应角.2. 基本性质：⑴三角形的稳定性：三角形三边的长度确定了，这个三角形的形状、大小就全确定，这个性质叫做三角形的稳定性.⑵全等三角形的性质：全等三角形的对应边相等，对应角相等.3. 全等三角形的判定定理：⑴边边边（SSS）:三边对应相等的两个三角形全等.⑵边角边（SAS）：两边和它们的夹角对应相等的两个三角形全等. ⑶角边角（ASA）：两角和它们的夹边对应相等的两个三角形全等.⑷角角边（AAS）：两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边（HL）：斜边和一条直角边对应相等的两个直角三角形全等.4. 角平分线：⑴画法：⑵性质定理：角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上5. 证明的基本方法：⑴明确命题中的已知和求证.（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系）⑵根据题意，画出图形，并用数字符号表示已知和求证.⑶经过分析，找出由已知推出求证的途径，写出证明过程.常考题:.选择题（共14小题）1 •使两个直角三角形全等的条件是（）A. —个锐角对应相等B.两个锐角对应相等C•一条边对应相等D.两条边对应相等2 .如图，已知AE=CF / AFD=Z CEB那么添加下列一个条件后，仍无法判定△D. AD//BC3•如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A. SSSB. SASC. AASD. ASA4•到三角形三条边的距离都相等的点是这个三角形的（）A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点5. 如图，△ ACB^A A CBV BCB =30°则/ACA的度数为（）A. 20°B. 30°C. 35°D. 40°6 .如图，直线11、12、13表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）A. 1处B. 2处C. 3处D. 4处7 .如图，AD是厶ABC中/BAC的角平分线，DE± AB于点E, S SBC=7, DE=2AB=4,贝U AC 长是（）8 .如图，在△ ABC和厶DEC中，已知AB=DE还需添加两个条件才能使△ ABC ◎△ DEC不能添加的一组条件是（）A. BC=EC Z B=Z EB. BC=EC AC=DCC. BC=DC / A=Z DD.Z B=Z E，10. 要测量河两岸相对的两点 A ，B 的距离，先在AB 的垂线BF 上取两点C ，D ，使CD=BC 再定出BF 的垂线DE,使A ，C, E 在一条直线上（如图所示），可以说明△ EDC^A ABC,得ED=AB 因此测得 ED 的长就是 AB的长，判定△ EDC^ △ ABC 最恰当的理由是（）A .边角边B .角边角 C.边边边 D .边边角11. 如图，△ ABC 的三边AB, BC, CA 长分别是20, 30, 40,其三条角平分线将12. 尺规作图作/ AOB 的平分线方法如下：以 O 为圆心，任意长为半径画弧交OA , OB 于C, D ,再分别以点C, D 为圆心，以大于丄CD 长为半径画弧，两弧交于点P ,作射线OP 由作法得厶OCF ^A ODP 的根据是（）9. 如图，已知在△ ABC 中，CD 是AB 边上的高线, BE 平分/ ABC,交CD 于点E ,4 D. 3: 4: 55D . 4S A BCO ： S A CAO 等于△ ABC 分为三个三角形，则S AA . 1: 1: 1 B. 1: 2: 3 C. 2: 3: A .有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等，且有一角为 30°勺两个等腰三角形全等C •有一角和一边对应相等的两个直角三角形全等D .有两角和一边对应相等的两个三角形全等14.如图，已知/ 仁/2, AC=AD,增加下列条件：① AB=AE ②BC=ED ③/ C= /D ;④/ B=ZE .其中能使厶ABC ^A AED 的条件有（）二.填空题（共11小题）15.如图，在△ ABC 中，/ C=90°, AD 平分/ CAB BC=8cm, BD=5cm,那么点 D 到线段AB 的距离是 _________ cm .AD 平分/ BAQ AB=5, CD=2,则厶ABD 的面积17. 如图为6个边长等的正方形的组合图形，则/ 1+Z 2+Z 3= _____18. 如图，△ ABC ^A DEF 请根据图中提供的信息，写出19. _________________________________________ 如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事2个D. 1个的办法是带______________________________________ 去玻璃店.20. ____________________________________________________________ 如图，已知 AB// CF, E 为 DF 的中点，若 AB=9cm, CF=5cm J 则 BD= _______ cm .21 •在数学活动课上，小明提出这样一个问题：/ B=Z C=90°, E 是BC 的中点,DE 平分/ ADC, / CED=35,如图，则/ EAB 是多少度？大家一起热烈地讨论交流，小英第一个得出正确答案，是 _______ 度.23.如图所示，将两根钢条 AA ，BB'的中点O 连在一起，使A A', BB 可以绕着点O 自由转动，就做成了一个测量工具，则 A 的长等于内槽宽AB,那么判定 △OAB^A OA 的理由是 ___________ .24.如图，在四边形 ABCD 中, / A=90°, AD=4,连接 BD, BD 丄 CD, / ADB=Z C.若 P 是BC 边上一动点，则DP 长的最小值为 ____./ B=100o ，/ BAC=30，那么/ AED= 度.三•解答题（共15小题）26.已知：如图，C 为BE 上一点，点A , D 分别在BE 两侧，AB// ED, AB=CE29. 如图，C 是 AB 的中点，AD=BE CD=CE 求证：/ A=Z B.C=90°, CA=CB 点 M 在线段 AB 上，/ GMB 二 / A ,BG cm .若 MH=8cm ，贝UBG=30. 已知：如图，在梯形ABCD中，AD// BC, BC=DC CF平分/ BCD DF// AB, BF 的延长线交DC于点E.求证：(BFC^A DFQ(2) AD=DE31. 如图，已知，EC=AC Z BCE W DCA / A=Z E 求证：BC=DC32. 如图，把一个直角三角形ACB(/ACB=90)绕着顶点B顺时针旋转60°使得点C 旋转到AB边上的一点D,点A旋转到点E的位置.F，G分别是BD，BE 上的点，BF=BG延长CF与DG交于点H.(1)求证：CF=DG(2)求出/ FHG的度数.33. 已知，如图，△ ABC和厶ECD都是等腰直角三角形，/ ACB=Z DCE=90，D 为AB边上一点.求证：BD=AE36. 如图，△ ABC 和厶ADE 都是等腰三角形，且/ BAC=90, / DAE=90, B , C,D 在同一条直线上.求证：BD=CE37. 我们把两组邻边相等的四边形叫做筝形”如图，四边形ABCD 是一个筝形, 其中AB=CB AD=CD 对角线AC, BD 相交于点O , 0E 丄AB, 0F 丄CB,垂足分别是E ,F.求证OE=OFABCDE 的边BC CD 上的点，且 BM=CN,(1) 求证：△ ABM ^ABCN ；(2) 求/ APN 的度数.ABCD 中，E 点在 AD 上，其中/ BAE=/ BCE W ACD=90,且AM 交BN 于点P.BC=CE 求证：△ ABC 与厶DEC 全等.D38. 如图，在△ ABC 中，/ ACB=90, CE L AB于点E, AD=AG AF 平分/ CAB 交CE于点F, DF的延长线交AC于点G.求证：(1) DF// BC; (2) FG=FE39. 如图：在厶ABC中，BE CF分别是AC AB两边上的高，在BE上截取BD=AC 在CF的延长线上截取CG=AB连接AD、AG.(1)求证：AD=AG(2)AD与AG的位置关系如何，请说明理由.40. 如图，已知△ ABC中，AB=AC=10cm BC=8cm 点D为AB的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等，经过1s后，△ BPD与厶CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△ BPD与厶CQP全等？(2)若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ ABC三边运动，求经过多长时间点P与点Q第一次在厶ABC 的哪条边上相遇？初二全等三角形所有知识点总结和常考题提高难题压轴题练习（含答案解析）参考答案与试题解析一•选择题（共14小题）1. （2013?西宁）使两个直角三角形全等的条件是（）A、—个锐角对应相等B.两个锐角对应相等C•一条边对应相等D.两条边对应相等【分析】利用全等三角形的判定来确定. 做题时，要结合已知条件与三角形全等的判定方法逐个验证.【解答】解：A、一个锐角对应相等，利用已知的直角相等，可得出另一组锐角相等，但不能证明两三角形全等，故A选项错误；B、两个锐角相等，那么也就是三个对应角相等，但不能证明两三角形全等，故B 选项错误；C、一条边对应相等，再加一组直角相等，不能得出两三角形全等，故C选项错误；D、两条边对应相等，若是两条直角边相等，可利用SAS证全等；若一直角边对应相等，一斜边对应相等，也可证全等，故D选项正确.故选：D.【点评】本题考查了直角三角形全等的判定方法；三角形全等的判定有ASA SAS AAS SSS HL,可以发现至少得有一组对应边相等，才有可能全等.2. （2013?安顺）如图，已知AE=CF / AFD=Z CEB那么添加下列一个条件后，仍无法判定△ ADF^A CBE的是（）A __________ ?A. Z A=Z CB. AD=CBC. BE=DFD. AD// BC【分析】求出AF=CE再根据全等三角形的判定定理判断即可.【解答】解：：AE=CF••• AE+EF=C+EF,••• AF=CEA、t在厶ADF和厶CBE中|fZA=ZCIZAFD=ZCEB•••△ADF^A CBE（ASA，正确，故本选项错误；B、根据AD=CB AF=CE / AFD=Z CEB不能推出厶ADF^A CBE错误，故本选项正确；C 、・.•在△ ADF 和厶CBE 中AF=CE DF=BE•••△ ADF^A CBE （ SAS ,正确，故本选项错误；D 、t AD// BC,•••/ A=Z C,•••在△ ADF 和厶CBE 中|fZA=ZC{ACEHZAFD=ZCEB•••△ ADF^A CBE （ASA ,正确，故本选项错误；故选B .【点评】本题考查了平行线性质，全等三角形的判定的应用，注意：全等三角形的判定定理有SAS ASA AAS SSS3. （2014秋？江津区期末）如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A . SSS B. SAS C. AAS D . ASA【分析】根据图象，三角形有两角和它们的夹边是完整的，所以可以根据角边角”画出.【解答】解:根据题意，三角形的两角和它们的夹边是完整的，所以可以利用角边角”定理作出完全一样的三角形.故选D .【点评】本题考查了三角形全等的判定的实际运用，熟练掌握判定定理并灵活运用是解题的关键.4. （2007?中山）至9三角形三条边的距离都相等的点是这个三角形的（）A .三条中线的交点B.三条高的交点 C.三条边的垂直平分线的交点 D.三条角平分线的交点【分析】因为角的平分线上的点到角的两边的距离相等，所以到三角形的三边的距离相等的点是三条角平分线的交点.【解答】解：•••角的平分线上的点到角的两边的距离相等，•••到三角形的三边的距离相等的点是三条角平分线的交点.故选：D .【点评】该题考查的是角平分线的性质，因为角的平分线上的点到角的两边的距离[相等，所以到三角形的三边的距离相等的点是三条角平分线的交点，易错选项为c .5.（2011?呼伦贝尔）如图，△ACB^A A C , BCB =30则/ACA 的度数为（）【分析】本题根据全等三角形的性质并找清全等三角形的对应角即可.【解答】解：•••△ ACB^A A CB•••/ ACB=/ A CB即/ ACA+Z A CB=B' CHB/ A CB•••/ ACA = B ' C,B又Z B' CB=30 •••Z ACA =30°故选：B.【点评】本题考查了全等三角形的判定及全等三角形性质的应用，利用全等三角形的性质求解.6. （2000?安徽）如图，直线11、12、13表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）A . 1处B. 2处C. 3处D. 4处【分析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点. 把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求.【解答】解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角两两平分线的交点，共三处. 故选：D.D . 40【点评】本题考查了角平分线的性质；这是一道生活联系实际的问题，解答此类题目时最直接的判断就是三角形的角平分线，很容易漏掉外角平分线，解答时一定要注意，不要漏解.7. （2014?遂宁）如图，AD是厶ABC中/ BAC的角平分线，DE± AB于点E,S A ABC=7,DE=2 AB=4,贝U AC长是（）A. 3B. 4C. 6D. 5【分析】过点D作DF丄AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF再根据S A ABC=S ABC+&ACD列出方程求解即可.【解答】解：如图，过点D作DF丄AC于F，••• AD是厶ABC中/ BAC的角平分线，DE丄AB，••• DE=DF由图可知，S ABC=S ABD+S ACD,.•.J-X 4X 2「X ACX 2=7，解得AC=3.故选：A.【点评】本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键.8. （2013?铁岭）如图，在△ ABC和厶DEC中，已知AB=DE还需添加两个条件才能使△ ABC^A DEC不能添加的一组条件是（）A、BC=EC Z B=Z EB. BC=EC AC=DC C. BC=DC / A=Z D D.Z B=Z E, / A=Z D 【分析】根据全等三角形的判定方法分别进行判定即可.【解答】解：A、已知AB=DE再加上条件BC=EC / B=Z E可利用SAS证明△ABC^A DEC故此选项不合题意；B、已知AB=DE再加上条件BC=EC AC=DC可利用SSS证明厶ABC^A DEC 故此选项不合题意；C、已知AB=DE再加上条件BC=DC / A=Z D不能证明厶ABC^A DEC故此选项符合题意；D、已知AB=DE再加上条件/ B=Z E , / A=Z D可利用ASA证明△ ABC^A DEC 故此选项不合题意；故选：C.【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS SAS ASA AAS HL注意：AAA SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角.9. （2015?湖州）如图，已知在厶ABC中，CD是AB边上的高线，BE平分/ ABC 交CD于点E, BC=5 DE=2则厶BCE的面积等于（）B CA. 10B. 7C. 5D. 4【分析】作EF丄BC于F，根据角平分线的性质求得EF=DE=2然后根据三角形面积公式求得即可.【解答】解：作EF丄BC于F，••• BE平分/ ABC ED丄AB，EF丄BC••• EF=DE=2S^BCE^^BC?EF= X 5 X 2=5，故选C.【点评】本题考查了角的平分线的性质以及三角形的面积，作出辅助线求得三角形的高是解题的关键.10. （1998?南京）要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C, D,使CD=BC再定出BF的垂线DE,使A，C，E在一条直线上（如图所示），可以说明△ EDC^A ABC,得ED=AB因此测得ED的长就是AB的长，判定△ EDC^A ABC最恰当的理由是（A .边角边B .角边角 C.边边边 D .边边角【分析】由已知可以得到/ ABCN BDE 又CD=BC / ACB W DCE 由此根据角边角即可判定△ EDC^A ABC.【解答】解：：BF 丄AB , DE± BD•••/ ABC2 BDE又••• CD=BC Z ACBN DCE•••△ EDC^A ABC （ASA ）故选B .【点评】本题考查了全等三角形的判定方法；需注意根据垂直定义得到的条件，以及隐含的对顶角相等，观察图形，找着隐含条件是十分重要的.11. （2017?石家庄模拟）如图，△ ABC 的三边AB, BC, CA 长分别是20, 30, 40,其三条角平分线将△ ABC 分为三个三角形，则 & ABO ： S BCO ： S CAO 等于【分析】利用角平分线上的一点到角两边的距离相等的性质，可知三个三角形高相等，底分别是20, 30, 40,所以面积之比就是2: 3: 4.【解答】解：禾I 」用同高不同底的三角形的面积之比就是底之比可知选 C .故选C .【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式.做题时应用了三个三角形的高时相等的，这点式非常重要的.12. （2009?鸡西）尺规作图作/ AOB 的平分线方法如下：以 O 为圆心，任意长为半径画弧交OA, OB 于C, D ,再分别以点C , D 为圆心，以大于二CD 长为半径画弧，两弧交于点P ,作射线OP 由作法得厶OCF ^A ODP 的根据是（）3 C. 2: 3:4 D. 3: 4: 5【分析】认真阅读作法，从角平分线的作法得出厶0。

直角三角形全等的判定(1个知识点+5大题型+18道强化训练)(学生版) 24-25学年八年级数学上册

第09讲直角三角形全等的判定（1个知识点+5大题型+18道强化训练）知识点01：HL 证明三角形全等定理：在两个直角三角形中，有斜边和一条直角边对应相等的两个直角三角形全等（可以简写成“HL”）.要点诠释：（1）“HL”从顺序上讲是“边边角”对应相等，由于其中含有直角这个特殊条件，所以三角形的形状和大小就确定了.（2）判定两个直角三角形全等首先考虑用斜边、直角边定理，再考虑用一般三角形全等的证明方法.（3）应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件，书写时必须在两个三角形前加上“Rt”.【即学即练1】1．如图，在ABC V 中，90C Ð=°，D 是AC 上一点，DE AB ^于点E ，BE BC =，连接BD ，若8cm AC =，则AD DE +等于（）A ．6cmB ．7cmC ．8cmD ．10cm【即学即练2】2．如图所示，已知在△ABC 中，∠C =90°，AD =AC ，DE ⊥AB 交BC 于点E ，若∠B =28°，则∠AEC =（）A ．28°B ．59°C ．60°D ．62°题型01 用HL 证明三角形全等1．如图，O 是BAC Ð内一点，且点O 到AB ，AC 的距离OE OF =，则AEO AFO ≌△△的依据是（）A ．HLB ．AASC ．SSSD ．ASA2．如图，AB BC ^，AD DC ^，要根据“HL ”证明Rt Rt ABC ADC ≌△△，还应添加一个条件是（）A ．12Ð=ÐB ．24ÐÐ=C ．AB AD =D ．AB AC=3．如图，点B 、F 、C 、E 在一条直线上，90A D Ð=Ð=°，AB DE =，若用“HL ”判定ABC DEF ≌△△，则添加的一个条件是．4．如图，AC AB ^，AC CD ^，要使得ABC CDA △△≌，若以“HL ”为依据，需添加条件．5．已知：如图，45ABC Ð=°，AD 为ABC V 的高，E 为AC 上一点，BE 交AD 于F 且有BF AC =．求证：Rt Rt BFD ACD △≌△．题型02 利用直角三角形全等的判定求角度1．如图，已知DB AN ^于点B ，交AE 于点O ，OC AM ^于点C ，且OB OC =．若54ADB Ð=°，则OAB Ð的大小为（）A ．15°B ．18°C ．22°D ．30°2．如图，ABC V 中，ABC Ð的平分线与AC 边的垂直平分线交于点D ，过D 作DE BC ^于点E ，连接CD ，若35BAC Ð=°，30ACD Ð=°，则DCE Ð的度数为（）A ．45°B ．60°C ．65°D ．70°3．如图，已知PA ON ^于点A ，PB OM ^于点B ，且PA PB =，50MON Ð=°，20OPC Ð=°，则PCA Ð= ．4．如图，ABC V 中，AC BC =，且点D 在ABC V 外，D 在AC 的垂直平分线上，连接BD ，若30DBC Ð=°，12ACD Ð=°，则A Ð= °．5．如图，AC 平分BAD Ð，CE AB ^，CF AD ^交AD 的延长线于点F ，在AB 上有一点M ，且CM CD =，(1)若12AF =，4DF =，求AM 的长．(2)试说明CDA Ð与CMA Ð的关系．题型03 利用直角三角形全等的判定求长度1．如图，在Rt ABC △中，90,C BAC Ð=°Ð的平分线AE 交BC 于点,E ED AB ^于点D ，若ABC V 的周长为12,BDE V 的周长为6，则AC =（）A ．4B ．3C ．6D ．82．如图，在Rt ABC △中，90C Ð=°，6AC =，8BC =，以点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，射线AP 与BC 交于点D ，DE AB ^，垂足为E ，则BE 为（）A ．3B ．4C ．4.5D ．53．如图，ABC V 的外角DAC Ð的平分线交BC 边的垂直平分线于P 点，PD AB ^于D ，PE AC ^于E ．若6cm AB =，10cm AC =，则AD 的长是．4．如图，在ABC V 中，DE AC ^于点D ，且AD CD =，180ABE CBE Ð+Ð=°，EF BC ^于点F ，若7AB =，1BF =，则BC = ．5．已知：如图，BAC Ð角平分线与BC 的垂直平分线DG 交于点D ，DE AB ^，DF AC ^，垂足分别为E 、F ．(1)求证：BE CF =；(2)若8AB =，6AC =，求BE 的长．题型04 直角三角形全等证明的常见辅助线添加1．如图，AD 是ABC V 的角平分线，DF AB ^于点F ，且DE DG =，26ADG S =△，18AED S =△，则DEF V 的面积为（）A ．2B ．3C ．4D ．62．如图，在四边形ABCD 中，DE BC ^，BD 平分ABC Ð，AD CD =，4BE =，3DE =，1CE =，则ABD △的面积是（）A ．4.5B ．6C ．9D ．123．如图，AE 是CAM Ð的角平分线，点B 在射线AM 上，DE 是线段BC 的中垂线交AE 于E ，EF AM ^．若23,21ACB CBE Ð=°Ð=°，则BEF Ð= ．4．如图，四边形ABCD 中，AC 平分BAD Ð，BC DC CE AD =^，于点E ，127AD AB ==，，则DE 的长为．5．如图，CB CD =，180D ABC Ð+Ð=°，CE AD ^于E ．(1)求证：AC 平分DAB Ð；(2)若10AE =，4DE =，求AB 的长．题型05 全等的性质和HL 综合1．如图，在ABC V 中，P 为BC 上一点，PR AB ^，垂足为R PS AC ^，，垂足为S AQ PQ PR PS ==，，，下面结论：①AS AR =；②QP AR ∥；③△≌△ARP ASP ，其中正确的是（）A ．①②B ．②③C ．①③D ．①②③2．如图，在等边ABC V 中，AD BC ^于D ，延长BC 到E ，使12CE BC =，F 是AC 的中点，连接EF 并延长EF 交AB 于G ，BG 的垂直平分线分别交BG AD ，于点M ，点N ，连接GN CN ，，下列结论：①ACN BCN Ð=Ð；②12GF EF =；③120GNC Ð=°；④GM CN =；⑤EG AB ^，其中正确的个数是（）A ．2个B ．3个C ．4个D ．5个3．如图所示，在ABC V 中，P Q ，分别是BC AC ，上的点，作PR AB ^，PS AC ^，垂足分别为点R S ，，若AQ PQ =，PR PS =，QD AP ^．现有下列结论：①AS AR =；②AP 平分BAC Ð；③BRP CSP △≌△；④PQ AR ∥．其中正确的是（把所有正确结论的序号都选上）4．如图，ABC V 的两条外角平分线AP CP ，相交于点P ，PH AC ^于点H ．若60ABC Ð=°，则下面的结论：①30ABP Ð=°；②60APC Ð=°；③2PB PH =；④APH BPC Ð=Ð．其中正确的结论是．（填序号）5．如图，已知在Rt ABC △中，90ACB Ð=°，4AC =，8BC =，D 是AC 上的一点，32CD =．点P 从B 点出发沿射线BC 方向以每秒1个单位的速度向右运动．设点P 的运动时间为t ，连接AP ．(1)当3t =秒时，求AP 的长度；(2)当点P 在线段AB 的垂直平分线上时，求t 的值；(3)过点D 作DE AP ^于点E ．在点P 的运动过程中，当t 为何值时，能使DE CD =？请直接写出t 的值．1．如图，在ABC V 中，AC BC =，90C Ð=°，AD 是ABC V 的角平分线，DE AB ^于点E ．若1CD =，则AB 的长为（）A B ．1C ．2D ．22．如图，在ABC V 中，90C Ð=°，AC BC =，AD 平分CAB Ð，交BC 于点D ，DE AB ^于点E ，且6cm AB =，则DEB V 的周长为（）A ．4cmB ．6cmC ．8cmD ．10cm 3．如图，在Rt ABC V 中，90C Ð=°，BAC Ð的平分线AE 交BC 于点E ，ED AB ^于点 D ，若 ABC V 的周长为12，则 BDE V 的周长为 4 ，则AC 为（）A ．3B ．4C ．6D ．84．如图，ABC V 中，ABC Ð的平分线与AC 边的垂直平分线交于点D ，过D 作DE BC ^于点E ，连接CD ，若35BAC Ð=°，30ACD Ð=°，则DCE Ð的度数为（）A ．45°B ．60°C ．65°D ．70°5．如图，在ABC V 中，延长BA 到点E ，延长BC 到点F ．,ABC EAC ÐÐ的角平分线,BP AP 交于点P ，过点P 分别作,PM BE PN BF ^^，垂足为,M N ，则下列结论正确的有（）①CP 平分ACF Ð；②2180ABC APC Ð+Ð=°；③2ACB APB =∠∠；④PAC MAP NCP S S S +=△△△．A ．1个B ．2个C ．3个D ．4个6．如图，CA AB ^，垂足为点A ，8AB =，4AC =，射线BM AB ^，垂足为点B ，一动点E 从A 点出发以2/秒的速度沿射线AN 运动，点D 为射线BM 上一动点，随着E 点运动而运动，且始终保持ED CB =，当点E 运动t 秒时，DEB V 与BCA V 全等．则符合条件的t 值有（）个A ．2B ．3C ．4D ．57．如图，在ABC V 中，90ACB Ð=°，1,AC BC AD ==是BAC Ð的平分线且交BC 于点D ，DE AB ^于点E ，则BDE V 的周长为．8．如图，在四边形ABCD 中，BD 平分ABC Ð，AD CD =，DE BC ^，垂足为点E ，ABD △的面积为38，BCD △的面积为50，则CDE V 的面积为．9．如图，ABC V 中，90ACB Ð=°，222AC BC AB +=，点D ，E 分别在边BC ，AC 上，DE DB =，DEC B Ð=Ð，若3CE =，15AB =，则四边形ABDE 的面积是．10．如图，在ABC V 中，D 为AB 中点，DE AB ^，180ACE BCE Ð+Ð=°，EF BC ^交BC 于F ，8AC =，12BC =，那么BF = ．11．如图，在ABC V 中，AB AC =，过点A 作AD BC ∥，连接DC ，点E 是AB 边上一点，DE DC =，过点D 作DF AC ^于F ，若6BE =，则AF = ．12．如图，ABC V 中，AC BC =，且点D 在ABC V 外，D 在AC 的垂直平分线上，连接BD ，若30DBC Ð=°，12ACD Ð=°，则A Ð= °．13．如图，CB CD =，180D ABC Ð+Ð=°，CE AD ^于E ．(1)求证：AC 平分DAB Ð；(2)若10AE =，4DE =，求AB 的长．14．如图，180CB CD D ABC CE AD =Ð+Ð=°^，，于E ，CF AB ^交AB 的延长线于点F ．(1)求证：AC 平分DAB Ð；(2)若82AE DE ==，，求AB 的长．15．如图，四边形ABDC 中，90D ABD Ð=Ð=°，点O 为BD 的中点，且OA 平分BAC Ð．(1)求证：OC 平分ACD Ð；(2)求证：OA OC ^；(3)猜想AB 、CD 与AC 的关系，并说明理由．16．如图，四边形ABCD 中，90B Ð=°，连接对角线AC ，且AC AD =，点E 在边BC 上，连接DE ，过点A作AF D E ^，垂足为F ，若AB AF =．(1)求证：①DAC FAB ÐÐ=；②DF CE EF =+；(2)若AB BC =，20CDE Ð=°，求CAF Ð的度数．17．图，已知CD BE =，DG BC ^于点G ，EF BC ^于点F ，且DG EF =．(1)求证：DGC EFB ≌△△；(2)OB OC =吗？请说明理由；(3)若30B Ð=°，ADO △是什么三角形？18．已知：点P 为EAF Ð平分线上一点，PB AE ^于B ，PC AF ^于C ，点M 、N 分别是射线AE 、AF 上的点，且PM PN =．(1)当点M 在线段AB 上，点N 在线段AC 的延长线上时（如图1）．求证：BM CN =；(2)在（1）的条件下，求证：2AM AN AC +=；(3)当点M 在线段AB 的延长线上时（如图2），若:2:1AC PC =，4PC =，则四边形ANPM 的面积为_______．。