2019-2020学年浙江省嘉兴市高一下学期期末考试数学试题
2019-2020学年高一下学期课后复习卷数学试题(平面向量)含答案

六安一中高一线上学习课后复习卷平面向量自学巩固练习(时间:90分钟)一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1.设21,e e 是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是( ) A .21e e +和21e e - B .212e e +和122e e + C .2123e e -和1264e e - D .2e 和21e e +2.已知向量(4,1),(2,)m =-=a b ,且()+a a b P ,则m =( ) A .12B .2C .12-D .2- 3.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则=EB ( )A .AC AB 4143- B .AC AB 4341- C .AC AB 4143+ D .AC AB 4341+4.对任意向量,a b ,下列关系式中不恒成立的是( )A .||||||⋅≤a b a bB .||||||||--≤a b a bC .22()||+=+a b a b D .22()()+-=-a b a b a b 5.设02θπ≤<,已知两个向量,,则向量21P P 长度的最大值是( )2 3 C.32 D.36.设向量,a b 满足||1,||2==a b ,且()⊥+a a b ,则向量a 在向量b 方向上的投影为( )A .1B 13C .1-D .12-7.已知向量(,6)x =a ,(3,4)=b ,且a 与b 的夹角为锐角,则实数x 的取值范围为( ) A .),8(+∞-B .),29()29,8(+∞-YC .),8[+∞-D .),29()29,8[+∞-Y8.点O 是△ABC 所在平面内的一点,满足OA OC OC OB OB OA ⋅=⋅=⋅,则点O 是△ABC的( )A .三条高的交点B .三条边的垂直平分线的交点C .三条中线的交点D .三个内角的角平分线的交点9.已知向量2,3==OB OA ,OB n OA m OC +=,若OA u u u r 与OB uuu r的夹角为60°,且AB OC ⊥,则实数mn 的值为( )A .21 B .31 C .41 D .61 10.已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则)(PC PB PA +⋅的最小值是( )A .2-B .32-C .43- D .1-二、填空题11.已知向量a 与b 的夹角为120o ,3=a ,13+=a b ,则=b .12.如图所示,一力作用在小车上,其中力F 的大小为10N ,方向与水平面成60︒角.当小车向前运动10m 时,则力F 做的功为 .13.已知12,e e 是夹角为60°的两个单位向量,则a =2e 1+e 2和b =2e 2-3e 1的夹角为_______. 14.设ABC ∆是边长为2的正三角形,E 是BC 的中点,F 是AE 的中点,则)(+⋅的值为 .15.在平行四边形ABCD 中,1=AD ,60BAD ︒∠=,E 为CD 的中点.若1=⋅, 则AB 的长为 .三、解答题(解答应写出文字说明、证明过程或演算步骤)16.已知平面向量)0,5(),3,4(=-=b a . (1)求a 与b的夹角的余弦值;(2)若向量b k a +与b k a -互相垂直,求实数k 的值.17.设a 、b 是两个不共线的向量,(1)记OA =a ,OB =tb ,OC =13(a +b ),当实数t 为何值时,A 、B 、C 三点共线?(2)若|a |=|b |=1且a 与b 的夹角为120°,那么实数x 为何值时,|a -x b |的值最小?18.如图,在平面直角坐标系中,点1(,0)2A -,3(,0)2B ,锐角α的终边与单位圆O 交于点P .(1)当41-=⋅时,求α的值; (2)在x 轴上是否存在定点M MP AP 21=恒成立?若存在,求出点M 坐标;若不存在,说明理由.六安一中高一线上学习课后复习卷平面向量自学巩固练习(时间:90分钟)一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1.设21,e e 是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是(C ) A .21e e +和21e e - B .212e e +和122e e + C .2123e e -和1264e e - D .2e 和21e e +2.已知向量(4,1),(2,)m =-=a b ,且()+a a b P ,则m =( C ) A .12B .2C .12-D .2- 3.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则=EB ( A )A .AC AB 4143- B .AC AB 4341- C .AC AB 4143+ D .AC AB 4341+4.对任意向量,a b ,下列关系式中不恒成立的是( B ) A .||||||⋅≤a b a b B .||||||||--≤a b a b C .22()||+=+a b a b D .22()()+-=-a b a b a b 5.设02θπ≤<,已知两个向量,,则向量21P P 长度的最大值是( B)2 3 C.32 D.36.设向量,a b 满足||1,||2==a b ,且()⊥+a a b ,则向量a 在向量b 方向上的投影为( D ) A .1B 13C .1-D .12-7.已知向量(,6)x =a ,(3,4)=b ,且a 与b 的夹角为锐角,则实数x 的取值范围为( C B )A .),8(+∞-B .),29()29,8(+∞-YC .),8[+∞-D .),29()29,8[+∞-Y8.点O 是△ABC 所在平面内的一点,满足OA OC OC OB OB OA ⋅=⋅=⋅,则点O 是△ABC的( B A )A .三条高的交点B .三条边的垂直平分线的交点C .三条中线的交点D .三个内角的角平分线的交点9.已知向量2,3==OB OA ,OB n OA m OC +=,若OA u u u r 与OB uuu r的夹角为60°,且AB OC ⊥,则实数mn 的值为( C D )A .21 B .31 C .41 D .6110.已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则)(PC PB PA +⋅的最小值是( A B )A .2-B .32-C .43- D .1-二、填空题11.已知向量a 与b 的夹角为120o ,3=a ,13+=a b ,则=b 4 . 12.如图所示,一力作用在小车上,其中力F 的大小为10N ,方向与水平面成60︒角.当小车向前运动10m 时,则力F 做的功为 50 .13.已知12,e e 是夹角为60°的两个单位向量,则a =2e 1+e 2和b =2e 2-3e 1的夹角为____120⁰____.14.设ABC ∆是边长为2的正三角形,E 是BC 的中点,F 是AE 的中点,则)(+⋅的值为 2 3 .15.在平行四边形ABCD 中,1=AD ,60BAD ︒∠=,E 为CD 的中点.若1=⋅, 则AB 的长为 1/3 1/2 .三、解答题(解答应写出文字说明、证明过程或演算步骤)16.已知平面向量)0,5(),3,4(=-=.(1)求与的夹角的余弦值;(2)若向量k+与k-互相垂直,求实数k的值.⑴解:由题意:a(4,-3),b(5,0)∴cosa,b=a·b/|a||b|=20/5×5=4/5∴a与b夹角的余弦值为4/5⑵解:由题意知:(a+kb)·(a-kb)=a²-k²b²=0∵a²=25=b²∴25-25k²=0∴k=1或-117.设a、b是两个不共线的向量,(1)记=a,=tb,=13(a+b),当实数t为何值时,A、B、C三点共线?(2)若|a|=|b|=1且a与b的夹角为120°,那么实数x为何值时,|a-x b|的值最小?⑴解:由题意知:AB=λAC,即-a+tb=λ(b-a)解得:t=1∴当t=1时,A,B,C三点共线⑵解:由题意知:|a-xb|=√(a-xb)²解得x=-1/2∴当x=-1/2时,其最小值为√3/218.如图,在平面直角坐标系中,点1(,0)2A -,3(,0)2B ,锐角α的终边与单位圆O 交于点P .(1)当41-=⋅时,求α的值; (2)在x 轴上是否存在定点M MP AP 21=恒成立?若存在,求出点M 坐标;若不存在,说明理由.⑴解:设点p (cosα,sinα),AP=(cosα+1/2,sinα),BP=(cosα-3/2,sinα) ∵AP·BP=-1/4,解得cosα=1/3∵α是锐角∴α=π/3 ⑵解:设M 点坐标为(t,0),则MP=(cosα-t,sinα) 由题意知(4+2t )cosα-t²+4=0恒成立,解得t=-2 ∴M (-2,0)。
【期末冲刺】2019—2020学年高一年级下学期期末冲刺满分训练卷——第十一章 立体几何初步(解析版)

2019—2020学年高一年级下学期期末冲刺满分训练卷第十章 立体几何初步 期末单元测试卷(范围:新教材人教B 版 必修四 考试时间:90分钟 满分:150分)一、选择题(本题共12道小题,每小题5分,共60分)1.以下命题(其中a 、b 表示直线,α表示平面)中,正确的命题是( )A. 若//a b ,b α⊂,则//a αB. 若//a α,//b α,则//a bC. 若//a b ,b α⊥,则a α⊥D. 若//a α,b α⊂,则//a b答案及解析:1.C【分析】根据线线、线面有关定理对选项逐一分析,由此确定正确选项.【详解】对于A 选项,直线a 可能含于平面α,所以A 选项错误.对于B 选项,,a b 可能异面,所以B 选项错误.对于C 选项,由于//a b ,b α⊥,所以a α⊥,所以C 选项正确.对于D 选项,,a b 可能异面,所以D 选项错误.故选:C【点睛】本小题主要考查空间线线、线面位置关系的判断,属于基础题.2.下列命题正确的是( )A. 有两个面平行,其余各面都是四边形的几何体叫棱柱。
B. 有两个面平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行的几何体叫棱柱。
C. 绕直角三角形的一边旋转所形成的几何体叫圆锥。
D. 用一个面去截棱锥,底面与截面之间的部分组成的几何体叫棱台。
答案及解析:2.B【分析】根据课本中的相关概念依次判断选项即可.【详解】对于A 选项,几何体可以是棱台,满足有两个面平行,其余各面都是四边形,故选项不正确;对于B ,根据课本中棱柱的概念得到是正确的;对于C ,当绕直角三角形的斜边旋转时构成的几何体不是圆锥,故不正确;对于D ,用平行于底面的平面截圆锥得到的剩余的几何体是棱台,故不正确.故答案为:B.【点睛】这个题目考查了几何体的基本概念,属于基础题.3.在正方体ABCD - A 1B 1C 1D 1中,动点E 在棱BB 1上,动点F 在线段A 1C 1上,O 为底面ABCD 的中心,若1,BE x A F y ==,则四面体O-AEF 的体积( )A. 与x ,y 都有关B. 与x ,y 都无关C. 与x 有关,与y 无关D. 与y 有关,与x 无关答案及解析:3.B【分析】 根据等体积法以及锥体体积公式判断选择.【详解】因为V O -AEF =V E -OAF ,所以,考察△AOF 的面积和点E 到平面AOF 的距离的值,因为BB 1∥平面ACC 1A 1,所以,点E 到平面AOE 的距离为定值,又AO ∥A 1C 1,所以,OA 为定值,点F 到直线AO 的距离也为定值,即△AOF 的面积是定值,所以,四面体O-AEF 的体积与x ,y 都无关,选B 。
数学卷·2015届浙江省嘉兴市高一下学期期末考试

三、解答题19.已知α为锐角,且53cos =α,求)3sin(πα+和α2tan 的值.20.如图,在ABC ∆中,︒=45B ,D 是BC 边上的一点,5=AD ,7=AC ,3=DC .(1)求ADC ∠的大小; (2)求A B 的长.21.已知函数x x x a x f 2cos 2cos sin 2)(+=,且2)3(=πf(1)求a 的值,并写出函数)(x f 的最小正周期; (2)求函数)(x f 在]2,0[π内的最值和取到最值时的x 值.22.已知递增的等差数列}{n a 满足:4532=a a ,1441=+a a(1)求数列}{n a 的通项公式及前n 项和n S ;(2)设n n n S a b 1+=,求数列}{1+n n b b 的前n 项和n T .23.在ABC ∆中,三个内角C B A ,,所对的边分别为c b a ,,,若C a A c a cos sin 3-=.(1)求角C 的大小;(2)若2=c ,求ABC ∆周长的取值范围.24.已知数列}{n a 的前n 项和为n S ,且87=+n n S a .(1)求数列}{n a 的通项公式;(2)设)12(1+⋅=+n a b n n ,是否存在常数*N m ∈,使mn b b ≤恒成立,若不存在说明理由,若存在求m 的值.嘉兴市2012—2013学年第二学期期末检测 高一数学(B ) 参考答案 (2013.6)一、选择题(每小题3分,共36分) 1.C ; 2.C ; 3.B ; 4.A ; 5.A ; 6.D ; 7.A ;8.D ;9.C ;10.C ;11.A ;12.C .二、填空题(每小题3分,共18分)13.23;14.︒45;15.3或-4; 16.)6,7(--;17.0;18.}1,21{三、解答题(有6小题,共46分) 19.解:∵α为锐角,且53cos =α,∴54sin =α,34tan =α 则10334cos 23sin 21)3sin(+=+=+ααπα; ……3分724916138tan 1tan 22tan 2-=-=-=ααα. ……6分 20.解:(1)∵2135249925cos -=⨯⨯-+=∠A DC∴︒=∠120ADC……3分(2)在A B D ∆中,︒=∠60ADB ,5=AD ,︒=45B 由正弦定理:︒=︒45sin 60sin A DA B ,得26523225=⨯=AB . ……6分21.解:(1)∵2)3(=πf ,代入得3=a ……2分则1)62sin(212cos 2sin 3)(++=++=πx x x x f得ππ==22T . ……4分 (2)1)62sin(2)(++=πx x f∵20π≤≤x ,∴πππ67626≤+≤x当262ππ=+x 时,即6π=x 时,3)(max =x f ……6分 当6762ππ=+x 时,即2π=x 时,0)(min =x f ……8分 22.解:(1)⎩⎨⎧=+=14453232a a a a即32,a a 是方程045142=+-x x 的两根,且32a a <解得9,532==a a ,34-=n a n……2分n n n a a S nn -=⨯+=2122 ……4分 (2)n nn n b n 22242=--=)1(41+=+n n b b n n )111(4+-=n n14)111(413221+=+-=+++=+n nn b b b b b b T n n n . ……8分23.解:(1)C A A C A cos sin sin sin 3sin -= 消去A sin 得C C cos sin 31-= 则21)6sin(=-πC ,解得3π=C ; ……3分(2)周长2)sin (sin 2++=++=B A R c b a C2)sin 23cos 23(342)]32sin([sin 232++=+-+=A A A A π2)21cos 23(sin 4++=A A2)6sin(4++=πA ……6分∵)32,0(π∈A ,∴)65,6(6πππ∈+A 得周长的取值范围为]6,4(. ……8分 24.(本题10分)解:(1)∵87=+n n S a ① 则8711=+--n n S a ②①-②得0771=+--n n n a a a ,即871=-n n a a )2(≥n ……2分令1=n ,得11=a ……3分 ∴1)87(-=n n a ……4分 (2)记)12()87(+⋅=n b n n )12()87()32()87(11+-+=-++n n b b n n n n)8132()87()881682114()87(+-=+-+=n n n n n ……8分显然6≤n 时,n n b b >+1,6>n 时,n n b b <+1,故7max )(b b n =,即7=m . …10分。
2020-202年近三年浙江省嘉兴市高一化学下学期期末考试题汇编4-非选择题含详解

浙江省嘉兴市2020-2022三年高一化学下学期期末试题汇编4-非选择题1.(2020春·浙江嘉兴·高一统考期末)(1)①写出钡餐的化学式:__________;②写出溴乙烷的结构简式:__________。
(2)写出钢铁发生吸氧腐蚀时,负极的电极反应式:___________。
2.(2021春·浙江嘉兴·高一统考期末)按要求完成下列填空:(1)①写出乙醛的结构简式_______;②写出过氧化钠的化学式_______;(2)写出铝与氢氧化钠溶液反应的化学方程式_______;(3)胆矾晶体遇浓硫酸变白,体现了浓硫酸的_______性。
3.(2022春·浙江嘉兴·高一统考期末)回答下列问题:(1)①胆矾的化学式是_______;②乙醛的结构简式是_______。
(2)过氧化钠与水反应的化学方程式是_______。
Cu(OH)悬浊液中加入葡萄糖溶液,加热,观察到的现象是_______。
(3)向新制的24.(2022春·浙江嘉兴·高一统考期末)浓硫酸与木炭在加热条件下可发生化学反应,为检验反应的部分产物,某同学设计了如下图所示的实验。
请据此回答下列问题:(1)设备I的仪器名称是_______。
(2)设备II中盛放的试剂是_______,该试剂的作用是_______。
(3)浓硫酸与木炭反应的化学方程式是_______。
(4)证明产物中含有CO2的实验现象是_______。
5.(2020春·浙江嘉兴·高一统考期末)称取有机物A6.0 g,在足量氧气中充分燃烧,并使产物依次缓慢通过浓硫酸、碱石灰,两者分别增重7.2 g和13.2 g。
已知有机物A气态时的密度是相同条件下氢气密度的30倍。
请计算:(1)有机物A的分子式______。
(2)另取A 6.0 g,跟足量的金属钠反应生成1.12 L氢气(标准状况),A可能的结构简式为________。
(立体几何基础题)(原卷版)-2020-2021学年高一数学下学期期末考试考前必刷题

2020-2021高一下学期期末考试考前必刷题(苏教版 2019)(立体几何基础题)一、单选题1.(2021·江苏高一课时练习)已知直线a∥平面α,直线a∥平面β,α∩β=b,直线a与直线b()A.相交B.平行C.异面D.不确定2.(2021·江苏高一课时练习)已知平面与平面平行,且直线,则下列说法正确的是()A.与内所有直线平行B.与内的无数条直线平行C.与内的任何一条直线都不平行D.与内的任何一条直线平行3.(2021·江苏高一课时练习)棱台的上、下底面面积分别是2,4,高为3,则该棱台的体积是()A.18+6B.6+C.24D.184.(2021·江苏高一课时练习)在正方体ABCD-A1B1C1D1中,截面A1BD与底面ABCD所成的二面角A1-BD-A的正切值等于()A.B.C.D.5.(2021·江苏高一课时练习)已知一个二面角的两个半平面分别平行于另一个二面角的两个半平面,若这两个二面角的平面角均为锐角,则这两个二面角的关系是()A.相等B.互补C.相等或互补D.既不相等也不互补6.(2021·江苏高一课时练习)侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是()A.a2B.a2C.a2D.a27.(2021·江苏高一课时练习)已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是()A.cm B.4 cm C.cm D.cm8.(2021·江苏高一课时练习)已知平面α与平面β、γ都相交,则这三个平面可能的交线有()A.1条或2条B.2条或3条C .1条或3条D .1条或2条或3条9.(2021·江苏高一课时练习)如图所示,定点A 和B 都在平面α内,定点P∥α,PB∥α,C 是平面α内异于A 和B 的动点,且PC∥AC ,则∥ABC 为 ( )A .锐角三角形B .直角三角形C .钝角三角形D .无法确定10.(2021·江苏高一课时练习)过球面上任意两点A ,B 作大圆,可能的个数是 ( )A .有且只有一个B .一个或无穷多个C .无数个D .以上均不正确11.(2021·江苏高一课时练习)如图所示,∥A′B′C′是水平放置的∥ABC 的直观图,则在∥ABC 的三边及中线AD 中,最长的线段是 ( )A .AB B .ADC .BCD .AC12.(2021·江苏高一课时练习)将半径为1,圆心角为的扇形围成一个圆锥,则该圆锥的体积为( ) A . B . C . D .13.(2021·江苏高一课时练习)如图的正方体ABCD - A ’B ’C ’D ’中,二面角D ’-AB -D 的大小是A .300B .450C .600D .90014.(2021·江苏高一课时练习)已知S 为四边形外一点,分别为上的点,若平面,则A .//GH SAB .//GH SDC .//GH SCD .以上均有可能15.(2021·江苏高一课时练习)在三棱柱111ABC A B C 中,各棱长均相等,侧棱垂直于底面,点是侧面的中心,则与平面所成角的大小是A .B .C .D .16.(2021·江苏高一课时练习)下列命题正确的是( )A .如果一条直线不在平面内,则这条直线就与这个平面平行B .过直线外一点,可以作无数个平面与这条直线平行C.如果一条直线与平面平行,则它与平面内的任何直线平行D.如果一条直线平行于平面内的无数条直线,则该直线与平面平行二、填空题17.(2021·江苏高一课时练习)已知三个球的表面积之比是,则这三个球的体积之比为________. 18.(2021·江苏高一课时练习)已知和是异面直线,且平面,平面,,,则平面与的位置关系是________.19.(2021·江苏高一课时练习)已知一个正四棱柱的对角线的长是9 cm,表面积等于144 cm2,则这个棱柱的侧面积为________ cm2.20.(2021·江苏高一课时练习)有一塔形空间图形由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形空间图形的表面积(含最底层正方体的底面面积)为________.21.(2021·江苏高一课时练习)如图,在正方体ABCD —A1B1C1D1中,三棱锥D1—AB1C的表面积与正方体的表面积的比为________.22.(2021·江苏高一课时练习)一个正四棱台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13 cm,则其表面积为____ cm2.23.(2021·江苏高一课时练习)下列说法正确的是________(填序号).①底面是正多边形的棱锥为正棱锥;②各侧棱都相等的棱锥为正棱锥;③各侧面都是等腰三角形的棱锥为正棱锥;④各侧面都是全等的等腰三角形的棱锥是正棱锥;⑤底面是正多边形且各侧面全等的棱锥为正棱锥.24.(2021·江苏高一课时练习)从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.其中正确结论的个数为________.25.(2021·江苏高一课时练习)水平放置的斜二测直观图如图所示,已知,,则边上的中线的长度为______.26.(2021·江苏高一课时练习)如图,在五面体FE-ABCD中,四边形CDEF为矩形,M、N分别是BF、BC的中点,则MN与平面ADE的位置关系是_______.27.(2021·江苏高一课时练习)已知正三棱锥的棱长都为2,则侧面和底面所成二面角的余弦值为________.28.(2021·江苏高一课时练习)若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的母线长为________.29.(2021·江苏高一课时练习)在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别为棱CC1、C1D1、D1D、DC的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足条件________时,有MN∥平面B1BDD1.30.(2021·江苏高一课时练习)已知A、B、C、D四点不共面,且AB∥平面α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG是_______四边形.31.(2021·江苏高一课时练习)如图.M是棱长为2cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是______cm.32.(2021·江苏高一课时练习)三棱锥S-ABC中,G为∥ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的关系为________.。
浙江省嘉兴市第一中学高一下学期3月月考数学试题(含答案)

精品基础教育教学资料,仅供参考,需要可下载使用!嘉兴一中高一第二学期阶段性测试数学一、选择题(本大题共l2小题,每小题3分,共36分)1.下列转化结果错误的是 ( ) A . 0367'化成弧度是π83rad B. π310-化成度是-600度 C . 150-化成弧度是π67rad D. 12π化成度是15度 2.已知α是第二象限角,那么2α是 ( ) A .第一象限角 B. 第二象限角 C. 第二或第四象限角 D .第一或第三象限角 3.已知0tan ,0sin ><θθ,则θ2sin 1-化简的结果为 ( ) A .θcos B. θcos - C .θcos ± D. 以上都不对 4.已知角α的终边过点P (-8m ,-6sin 30°),且cos α=45-,则m 的值为( ) A .12B.12±C. 12- D.以上都不对 5.已知函数f (x )=A cos(ωx +θ)的图像如图所示,f ⎝⎛⎭⎫π2=-23,则f ⎝⎛⎭⎫-π6=( ) A .-23 B .-12 C.23 D .126.函数xx xx x f sin cos sin cos )(-+=的最小正周期为 ( )A .1 B.2πC. π2D. π 7.若函数f (x )=A sin ⎝⎛⎭⎫π2x +φ(A >0)满足f (1)=0,则( )A .f (x -2)一定是奇函数B .f (x +1)一定是偶函数C .f (x +3)一定是偶函数D .f (x -3)一定是奇函数 8.对任意(0,)2a π∈,都有 ( )A.sin(sin )cos cos(cos )a a a <<B.sin(sin )cos cos(cos )a a a >>C.sin(cos )cos cos(sin )a a a >>D.sin(cos )cos cos(sin )a a a <<9.将函数)0,0)(sin()(>>+=ωϕωA x A x f 图象向左平移2π个单位,所得函数的图象与函数)(x f y =的图象关于x 轴对称,则ω的值不可能是 ( )A. 2B. 4C. 6D. 1010.函数)0)(3sin()(>+=ωπωx x f 与x 轴正方向的第一个交点为)0,(0x ,若230ππ<<x ,则ω的取值范围为 ( ) A. 21<<ω B.234<<ω C. 341<<ω D. 231<<ω 11.若S n =sin π7+sin 2π7+…+sin n π7(n ∈N *),则在S 1,S 2,…,S 100中,正数的个数是( ).A .16B .72C .86D .10012.若]2,2[,ππβα-∈,且0sin sin >-ββαα,则下列结论正确的是 ( ) A. βα> B. 0>+βα C. βα< D. 22βα> 二、填空题(本大题共7小题,每小题3分,共21分)13.把函数)32sin(π+=x y 先向右平移2π个单位,然后向下平移2个单位后所得的函数解析式为________________________________14.已知cos sin 2cos sin αααα+=+,则ααα2cos 2cos sin 31-⋅+=_______________15.函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如右图所示,则.________)3(=πf16.若动直线a x =与函数x x f sin )(=和1cos 2)(2-=x x g 的图象分别交于N M ,两点,则||MN 的最大值为________. 17.设)2(61)(,21sin )(-==x x g x x f π,则方程)()(x g x f =的所有解的和为_________.18.若函数sin()3y A x πω=-(A>0,0ω>)在区间[]0,1上恰好出现50次最大值和50次最小值,则ω的取值范围是_______________ 19.给出下列命题:①存在实数α,使1cos sin =⋅αα ②存在实数α,使23cos sin =+αα ③函数)23sin(x y +=π是偶函数 ④8π=x 是函数)452sin(π+=x y 的一条对称轴方程 ⑤若βα、都是第一象限的角,且βα>,则βαsin sin > 其中正确命题的序号是________________________________ 三、解答题(本大题共5小题,共43分)20.(本小题8分)(1)已知角α终边上一点P (-4,3),求)29sin()211cos()sin()2cos(απαπαπαπ+---+的值(2) 已知c os(π+α)=-12,且α是第四象限角,计算:sin[α+(2n +1)π]+sin[α-(2n +1)π]sin (α+2n π)·cos (α-2n π)(n ∈Z ).21. (本小题8分)已知sin θ-cos θ=12,求下列各式的值:(1)sin θcos θ; (2)sin 3θ-cos 3θ; (3)sin 4θ+cos 4θ.22. (本小题8分)如图,点)2,0(AP 是函数)92sin(ϕπ+=x A y (其中))2,0[,0(πϕ∈>A 的图象与y 轴的交点,点Q是它与x 轴的一个交点,点R 是它的一个最低点.O-226π1211πyx yP(1)求ϕ的值;(2)若PR PQ ⊥,求A 的值.23. (本小题9分)已知定义在区间]23,[ππ-上的函数)(x f y =的图象关于直线4π=x 对称,当4π≥x 时,x x f sin )(-=(1)作出)(x f y =的图象; (2)求)(x f y =的解析式;(3)若关于x 的方程a x f =)(有解,将方程中的a 取一确定的值所得的所有的解的和记为a M ,求a M 的所有可能的值及相应的a 的取值范围.24. (本小题10分)已知函数2()231f x x x =-+,()sin()6g x k x π=-,(0k ≠) (1)问a 取何值时,方程(sin )sin f x a x =-在[)0,2π上有两解;(2)若对任意的[]10,3x ∈,总存在[]20,3x ∈,使12()()f x g x =成立,求实数k 的取值范围.x嘉兴一中高一第二学期阶段性测试数学一、选择题(本大题共l2小题,每小题3分,共36分)1.下列转化结果错误的是 ( C ) A . 0367'化成弧度是π83rad B. π310-化成度是-600度 C . 150-化成弧度是π67rad D. 12π化成度是15度 2.已知α是第二象限角,那么2α是 ( D ) A .第一象限角 B. 第二象限角 C. 第二或第四象限角 D .第一或第三象限角 3.已知0tan ,0sin ><θθ,则θ2sin 1-化简的结果为 ( B ) A .θcos B. θcos - C .θcos ± D. 以上都不对 4.已知角α的终边过点P (-8m ,-6sin 30°),且cos α=45-,则m 的值为( A ) A .12B.12±C. 12- D.以上都不对 5.已知函数f (x )=A cos(ωx +θ)的图像如图所示,f ⎝⎛⎭⎫π2=-23,则f ⎝⎛⎭⎫-π6=( A ) A .-23 B .-12 C.23 D .126.函数xx xx x f sin cos sin cos )(-+=的最小正周期为 ( D )A .1 B.2πC. π2D. π 7.若函数f (x )=A sin ⎝⎛⎭⎫π2x +φ(A >0)满足f (1)=0,则( D ) A .f (x -2)一定是奇函数 B .f (x +1)一定是偶函数 C .f (x +3)一定是偶函数 D .f (x -3)一定是奇函数 8.对任意(0,)2a π∈,都有 ( D )A.sin(sin )cos cos(cos )a a a <<B.sin(sin )cos cos(cos )a a a >>C.sin(cos )cos cos(sin )a a a >>D.sin(cos )cos cos(sin )a a a <<9.将函数)0,0)(sin()(>>+=ωϕωA x A x f 图象向左平移2π个单位,所得函数的图象与函数)(x f y =的图象关于x 轴对称,则ω的值不可能是 ( B )A. 2B. 4C. 6D. 1010.函数)0)(3sin()(>+=ωπωx x f 与x 轴正方向的第一个交点为)0,(0x ,若230ππ<<x ,则ω的取值范围为 ( B ) A. 21<<ω B.234<<ω C. 341<<ω D. 231<<ω 11.若S n =sin π7+sin 2π7+…+sin n π7(n ∈N *),则在S 1,S 2,…,S 100中,正数的个数是( C ).A .16B .72C .86D .100 12.若]2,2[,ππβα-∈,且0sin sin >-ββαα,则下列结论正确的是 ( D )A. βα>B. 0>+βαC. βα<D. 22βα>二、填空题(本大题共7小题,每小题3分,共21分)13.把函数)32sin(π+=x y 先向右平移2π个单位,然后向下平移2个单位后所得的函数解析式为________________________________()2sin(2)23f x x π=--14.已知cos sin 2cos sin αααα+=+,则ααα2cos 2cos sin 31-⋅+=_______________11015.函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如右图所示,则.________)3(=πf 116.若动直线a x =与函数x x f sin )(=和1cos 2)(2-=x x g 的图象分别交于N M ,两点,则||MN 的最大值为________.2 17.设)2(61)(,21sin )(-==x x g x x f π,则方程)()(x g x f =的所有解的和为_________.1018.若函数sin()3y A x πω=-(A>0,0ω>)在区间[]0,1上恰好出现50次最大值和50次最小值,则ω的取值范围是_______________599605,66ππ⎡⎫⎪⎢⎣⎭ 19.给出下列命题:①存在实数α,使1cos sin =⋅αα ②存在实数α,使23cos sin =+αα ③函数)23sin(x y +=π是偶函数 ④8π=x 是函数)452sin(π+=x y 的一条对称轴方程 ⑤若βα、都是第一象限的角,且βα>,则βαsin sin >其中正确命题的序号是________________________________③④ 三、解答题(本大题共5小题,共43分)20.(本小题8分)(1)已知角α终边上一点P (-4,3),求)29sin()211cos()sin()2cos(απαπαπαπ+---+的值 (2) 已知cos(π+α)=-12,且α是第四象限角,计算:sin[α+(2n +1)π]+sin[α-(2n +1)π]sin (α+2n π)·cos (α-2n π)(n ∈Z ).解:(1)34-(2)-4 21. (本小题8分)已知sin θ-cos θ=12,求下列各式的值:(1)sin θcos θ; (2)sin 3θ-cos 3θ; (3)sin 4θ+cos 4θ.解:(1)38 (2)1116 (3)233222. (本小题8分)如图,点)2,0(AP 是函数O-226π1211πyx yP)92sin(ϕπ+=x A y (其中))2,0[,0(πϕ∈>A 的图象与y 轴的交点,点Q 是它与x 轴的一个交点,点R 是它的一个最低点.(1)求ϕ的值;(2)若PR PQ ⊥,求A 的值.解:(1)56πϕ= (2)15A =23. (本小题9分)已知定义在区间]23,[ππ-上的函数)(x f y =的图象关于直线4π=x 对称,当4π≥x 时,x x f sin )(-=(1)作出)(x f y =的图象; (2)求)(x f y =的解析式;(3)若关于x 的方程a x f =)(有解,将方程中的a 取一确定的值所得的所有的解的和记为a M ,求a M 的所有可能的值及相应的a 的取值范围.解:(2)3sin ,42()cos ,4x x f x x x ππππ⎧-≤<⎪⎪=⎨⎪--≤<⎪⎩(3)当21-12a a =-≤或<时,2a M π= 当2a =34a M π= 当22a <--1<时,a M π=(1)O 1-12π23π2π-ππ-yx24. (本小题10分)已知函数2()231f x x x =-+,()sin()6g x k x π=-,(0k ≠) (1)问a 取何值时,方程(sin )sin f x a x =-在[)0,2π上有两解;(2)若对任意的[]10,3x ∈,总存在[]20,3x ∈,使12()()f x g x =成立,求实数k 的取值范围. 解:(1)22sin 3sin 1sin x x a x -+=-化为22sin 2sin 1x x a -+=在[0,2]π上有两解 换sin t x = 则2221t t a -+=在[1,1]-上解的情况如下:①当在(1,1)-上只有一个解或相等解,x 有两解(5)(1)0a a --<或0∆= ∴(1,5)a ∈或12a =②当1t =-时,x 有惟一解32x π= ③当1t =时,x 有惟一解2x π=故 (1,5)a ∈或12a =(2)当1[0,3]x ∈ ∴1()f x 值域为1[,10]8- 当2[0,3]x ∈时,则23666x πππ-≤-≤-有21sin()126x π-≤-≤ ①当0k >时,2()g x 值域为1[,]2k k -②当0k <时,2()g x 值域为1[,]2k k -而依据题意有1()f x 的值域是2()g x 值域的子集则0101182k k k⎧⎪>⎪≤⎨⎪⎪-≥-⎩ 或 0110218k k k ⎧⎪<⎪⎪≤-⎨⎪⎪-≥⎪⎩∴10k ≥或20k ≤-。
湖南省怀化市2019-2020学年高一下学期期末考试数学试题含答案

湖南省怀化市2019-2020学年高一下学期期末考试数学试题含答案注意事项:1。
答题前,考生务必将自己的姓名、准考证号写在答题卡上。
2。
考生作答时,选择题和综合题均须做在答题卡上,在本试卷上答题无效。
考生在答题卡上按答题卡中注意事项的要求答题。
3。
考试结束后,将答题卡收回.4.本试题卷共4页,如有缺页,考生须声明,否则后果自负.怀化市中小学课程改革教育质量监测试卷2020年上期期末考试高一数学一、单项选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.为了了解某地参加计算机水平测试的5000名学生的成绩,从中抽取了200名学生的成绩进行统计分析.在这个问题中,5000 名学生成绩的全体是A.总体B。
个体 C.从总体中抽取的一个样本D.样本的容量2.设α是第三象限角,且tan1α=,则cosα=A。
-12B. 22C. 22- D. 12-3。
同时掷3枚硬币,那么互为对立事件的是A.至少有1枚正面和最多有1枚正面B.最多1枚正面和恰有2枚正面C 。
至多1枚正面和至少有2枚正面 D.至少有2枚正面和恰有1枚正面4。
某中学高三从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100 分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+ y 的值为A.7 B 。
8 C.9 D 。
10 5.若4sin cos 3θθ-=则sin()cos()πθπθ--=A 。
16B 。
16- C 。
718-D. 7186.如图所示,用两种方案将块顶角为120°, 腰长为2的等腰三角形钢板OAB 裁剪成扇形,设方案一、二的扇形的面积分别为S 1,S 2,周长分别为l 1,l 2,则A.S 1=S 2,l 1>l 2B.S 1=S 2, l 1<l 2 C 。
S 1〉S 2,l 1=l 2 D.S 1〈S 2, l 1=l 2 7。
2019-2020年高二下学期期末数学试卷(文科)含解析

2019-2020年高二下学期期末数学试卷(文科)含解析一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,A={x|x(x﹣2)<0},B={x|x﹣1>0},则A∩B=()A.(﹣2,1)B.[1,2)C.(﹣2,1] D.(1,2)2.已知数列…,则2是这个数列的()A.第6项B.第7项C.第11项D.第19项3.下列四个命题中的真命题为()A.∃x0∈Z,1<4x0<3 B.∃x0∈Z,5x0+1=0C.∀x∈R,x2﹣1=0 D.∀x∈R,x2+x+2>04.函数y=在x=1处的导数等于()A.1 B.2 C.3 D.45.“a=﹣2”是“复数z=(a2﹣4)+(a+1)i(a,b∈R)为纯虚数”的()A.充分非必要条件B.必要非充分条件C.充要条件 D.既非充分又非必要条件6.已知a=30.2,b=log64,c=log32,则a,b,c的大小关系为()A.c<a<b B.c<b<a C.b<a<c D.b<c<a7.设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(5)=()A.0 B.1 C.D.58.高二第二学期期中考试,按照甲、乙两个班级学生数学考试成绩优秀和不优秀统计后,得到如表:A.0.600 B.0.828 C.2.712 D.6.0049.已知函数f(x)=x|x|﹣2x,则下列结论正确的是()A.f(x)是偶函数,递增区间是(0,+∞)B.f(x)是偶函数,递减区间是(﹣∞,1)C.f(x)是奇函数,递减区间是(﹣1,1)D.f(x)是奇函数,递增区间是(﹣∞,0)10.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为a0a1a2,a i∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1,其中h0=a0⊕a1,h1=h0⊕a2,⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是()A.11010 B.01100 C.10111 D.00011二、填空题(本大题共6小题,每小题3分,共18分)11.设复数z满足(1﹣i)z=2i,则z=_______.12.函数y=的值域为_______.13.若P=﹣1,Q=﹣,则P与Q的大小关系是_______.14.已知变量x,y具有线性相关关系,测得(x,y)的一组数据如下:(0,1),(1,2),(2,4),(3,5),其回归方程为=1.4x+a,则a的值等于_______.15.已知函数则的值为_______.16.按程序框图运算:若x=5,则运算进行_______次才停止;若运算进行3次才停止,则x的取值范围是_______.三、解答题(本大题共5小题,共52分.解答应写出文字说明,证明过程或演算步骤)17.已知函数f(x)=log a(x+1)﹣log a(1﹣x),a>0且a≠1.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明.18.命题p方程:x2+mx+1=0有两个不等的实根,命题q:方程4x2+4(m+2)x+1=0无实根.若“p或q”为真命题,“p且q”为假命题,求m的取值范围.19.在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?20.已知函数f(x)=ax+lnx(a∈R).(Ⅰ)若a=2,求曲线y=f(x)在x=1处的切线方程;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.21.在无穷数列{a n}中,a1=1,对于任意n∈N*,都有a n∈N*,且a n<a n+1.设集合A m={n|a n ≤m,m∈N*},将集合A m中的元素的最大值记为b m,即b m是数列{a n}中满足不等式a n≤m的所有项的项数的最大值,我们称数列{b n}为数列{a n}的伴随数列.例如:数列{a n}是1,3,4,…,它的伴随数列{b n}是1,1,2,3,….(I)设数列{a n}是1,4,5,…,请写出{a n}的伴随数列{b n}的前5项;(II)设a n=3n﹣1(n∈N*),求数列{a n}的伴随数列{b n}的前20项和.2015-2016学年北京市东城区高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,A={x|x(x﹣2)<0},B={x|x﹣1>0},则A∩B=()A.(﹣2,1)B.[1,2)C.(﹣2,1] D.(1,2)【考点】交集及其运算.【分析】先求出不等式x(x﹣2)<0的解集,即求出A,再由交集的运算求出A∩B.【解答】解:由x(x﹣2)<0得,0<x<2,则A={x|0<x<2},B={x|x﹣1>0}={x|x>1},∴A∩B═{x|1<x<2}=(1,2),故选D.2.已知数列…,则2是这个数列的()A.第6项B.第7项C.第11项D.第19项【考点】数列的概念及简单表示法.【分析】本题通过观察可知:原数列每一项的平方组成等差数列,且公差为3,即a n2﹣a n﹣12=3从而利用等差数列通项公式an2=2+(n﹣1)×3=3n﹣1=20,得解,n=7【解答】解:数列…,各项的平方为:2,5,8,11,…则a n2﹣a n﹣12=3,又∵a12=2,∴a n2=2+(n﹣1)×3=3n﹣1,令3n﹣1=20,则n=7.故选B.3.下列四个命题中的真命题为()A.∃x0∈Z,1<4x0<3 B.∃x0∈Z,5x0+1=0 C.∀x∈R,x2﹣1=0 D.∀x∈R,x2+x+2>0【考点】四种命题的真假关系.【分析】注意判断区分∃和∀.【解答】解:A错误,因为,不存在x0∉ZB错误,因为C错误,x=3时不满足;D中,△<0,正确,故选D答案:D4.函数y=在x=1处的导数等于()A.1 B.2 C.3 D.4【考点】导数的运算.【分析】先求原函数的导函数,再把x=1的值代入即可.【解答】解:∵y′=,∴y′|x=1==1.故选:A.5.“a=﹣2”是“复数z=(a2﹣4)+(a+1)i(a,b∈R)为纯虚数”的()A.充分非必要条件B.必要非充分条件C.充要条件 D.既非充分又非必要条件【考点】必要条件、充分条件与充要条件的判断;复数的基本概念.【分析】把a=﹣2代入复数,可以得到复数是纯虚数,当复数是纯虚数时,得到的不仅是a=﹣2这个条件,所以得到结论,前者是后者的充分不必要条件.【解答】解:a=﹣2时,Z=(22﹣4)+(﹣2+1)i=﹣i是纯虚数;Z为纯虚数时a2﹣4=0,且a+1≠0∴a=±2.∴“a=2”可以推出“Z为纯虚数”,反之不成立,故选A.6.已知a=30.2,b=log64,c=log32,则a,b,c的大小关系为()A.c<a<b B.c<b<a C.b<a<c D.b<c<a【考点】对数值大小的比较.【分析】a=30.2>1,利用换底公式可得:b=log64=,c=log32=,由于1<log26<log29,即可得出大小关系.【解答】解:∵a=30.2>1,b=log64=,c=log32==,∵1<log26<log29,∴1>b>c,则a>b>c,故选:B.7.设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(5)=()A.0 B.1 C.D.5【考点】函数奇偶性的性质;函数的值.【分析】利用奇函数的定义、函数满足的性质转化求解函数在特定自变量处的函数值是解决本题的关键.利用函数的性质寻找并建立所求的函数值与已知函数值之间的关系,用到赋值法.【解答】解:由f(1)=,对f(x+2)=f(x)+f(2),令x=﹣1,得f(1)=f(﹣1)+f(2).又∵f(x)为奇函数,∴f(﹣1)=﹣f(1).于是f(2)=2f(1)=1;令x=1,得f(3)=f(1)+f(2)=,于是f(5)=f(3)+f(2)=.故选:C.8.高二第二学期期中考试,按照甲、乙两个班级学生数学考试成绩优秀和不优秀统计后,得到如表:A.0.600 B.0.828 C.2.712 D.6.004【考点】独立性检验的应用.【分析】本题考查的知识点是独立性检验公式,我们由列联表易得:a=11,b=34,c=8,d=37,代入K2的计算公式:K2=即可得到结果.【解答】解:由列联表我们易得:a=11,b=34,c=8,d=37则K2===0.6004≈0.60故选A9.已知函数f(x)=x|x|﹣2x,则下列结论正确的是()A.f(x)是偶函数,递增区间是(0,+∞)B.f(x)是偶函数,递减区间是(﹣∞,1)C.f(x)是奇函数,递减区间是(﹣1,1)D.f(x)是奇函数,递增区间是(﹣∞,0)【考点】函数奇偶性的判断.【分析】根据奇函数的定义判断函数的奇偶性,化简函数解析式,画出函数的图象,结合图象求出函数的递减区间.【解答】解:由函数f(x)=x|x|﹣2x 可得,函数的定义域为R,且f(﹣x)=﹣x|﹣x|﹣2(﹣x )=﹣x|x|+2x=﹣f(x),故函数为奇函数.函数f(x)=x|x|﹣2x=,如图所示:故函数的递减区间为(﹣1,1),故选C.10.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为a0a1a2,a i∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1,其中h0=a0⊕a1,h1=h0⊕a2,⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是()A.11010 B.01100 C.10111 D.00011【考点】抽象函数及其应用.【分析】首先理解⊕的运算规则,然后各选项依次分析即可.【解答】解:A选项原信息为101,则h0=a0⊕a1=1⊕0=1,h1=h0⊕a2=1⊕1=0,所以传输信息为11010,A选项正确;B选项原信息为110,则h0=a0⊕a1=1⊕1=0,h1=h0⊕a2=0⊕0=0,所以传输信息为01100,B 选项正确;C选项原信息为011,则h0=a0⊕a1=0⊕1=1,h1=h0⊕a2=1⊕1=0,所以传输信息为10110,C 选项错误;D选项原信息为001,则h0=a0⊕a1=0⊕0=0,h1=h0⊕a2=0⊕1=1,所以传输信息为00011,D 选项正确;故选C.二、填空题(本大题共6小题,每小题3分,共18分)11.设复数z满足(1﹣i)z=2i,则z=﹣1+i.【考点】复数相等的充要条件;复数代数形式的乘除运算.【分析】由条件利用两个复数相除,分子和分母同时乘以分母的共轭复数,计算求得结果.【解答】解:∵复数z满足(1﹣i)z=2i,则z====﹣1+i,故答案为:﹣1+i.12.函数y=的值域为{y|y≠2} .【考点】函数的值域.【分析】函数y===2+,利用反比例函数的单调性即可得出.【解答】解:函数y===2+,当x>1时,>0,∴y>2.当x<1时,<0,∴y<2.综上可得:函数y=的值域为{y|y≠2}.故答案为:{y|y≠2}.13.若P=﹣1,Q=﹣,则P与Q的大小关系是P>Q.【考点】不等式比较大小.【分析】利用作差法,和平方法即可比较大小.【解答】解:∵P=﹣1,Q=﹣,∴P﹣Q=﹣1﹣+=(+)﹣(+1)∵(+)2=12+2,( +1)2=12+2∴+>+1,∴P﹣Q>0,故答案为:P>Q14.已知变量x,y具有线性相关关系,测得(x,y)的一组数据如下:(0,1),(1,2),(2,4),(3,5),其回归方程为=1.4x+a,则a的值等于0.9.【考点】线性回归方程.【分析】求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程即可.【解答】解:∵==1.5,==3,∴这组数据的样本中心点是(1.5,3)把样本中心点代入回归直线方程,∴3=1.4×1.5+a,∴a=0.9.故答案为:0.9.15.已知函数则的值为﹣.【考点】函数的值;函数迭代.【分析】由题意可得=f(﹣)=3×(﹣),运算求得结果.【解答】解:∵函数,则=f(﹣)=3×(﹣)=﹣,故答案为﹣.16.按程序框图运算:若x=5,则运算进行4次才停止;若运算进行3次才停止,则x 的取值范围是(10,28] .【考点】循环结构.【分析】本题的考查点是计算循环的次数,及变量初值的设定,在算法中属于难度较高的题型,处理的办法为:模拟程序的运行过程,用表格将程序运行过程中各变量的值进行管理,并分析变量的变化情况,最终得到答案.【解答】解:(1)程序在运行过程中各变量的值如下表示:x x 是否继续循环循环前5∥第一圈15 13 是第二圈39 37 是第三圈111 109 是第四圈327 325 否故循环共进行了4次;(2)由(1)中数据不难发现第n圈循环结束时,经x=(x0﹣1)×3n+1:x 是否继续循环循环前x0/第一圈(x0﹣1)×3+1 是第二圈(x0﹣1)×32+1 是第三圈(x0﹣1)×33+1 否则可得(x0﹣1)×32+1≤244且(x0﹣1)×33+1>244解得:10<x0≤28故答案为:4,(10,28]三、解答题(本大题共5小题,共52分.解答应写出文字说明,证明过程或演算步骤)17.已知函数f(x)=log a(x+1)﹣log a(1﹣x),a>0且a≠1.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并予以证明.【考点】函数奇偶性的判断;函数的定义域及其求法.【分析】(1)使函数各部分都有意义的自变量的范围,即列出不等式组,解此不等式组求出x范围就是函数的定义域;(2)根据函数奇偶性的定义进行证明即可.【解答】解:(1)由题得,使解析式有意义的x范围是使不等式组成立的x范围,解得﹣1<x<1,所以函数f(x)的定义域为{x|﹣1<x<1}.(2)函数f(x)为奇函数,证明:由(1)知函数f(x)的定义域关于原点对称,且f(﹣x)=log a(﹣x+1)﹣log a(1+x)=﹣log a(1+x)+log a(1﹣x)=﹣[log a(1+x)﹣log a (1﹣x)]=﹣f(x)所以函数f(x)为奇函数.18.命题p方程:x2+mx+1=0有两个不等的实根,命题q:方程4x2+4(m+2)x+1=0无实根.若“p或q”为真命题,“p且q”为假命题,求m的取值范围.【考点】复合命题的真假.【分析】先将命题p,q分别化简,然后根据若“p或q”为真命题,“p且q”为假命题,判断出p,q一真一假,分类讨论即可.【解答】解:由题意命题P:x2+mx+1=0有两个不等的实根,则△=m2﹣4>0,解得m>2或m<﹣2,命题Q:方程4x2+4(m+2)x+1=0无实根,则△<0,解得﹣3<m<﹣1,若“p或q”为真命题,“p且q”为假命题,则p,q一真一假,(1)当P真q假时:,解得m≤﹣3,或m>2,(2)当P假q真时:,解得﹣2≤m<﹣1,综上所述:m的取值范围为m≤﹣3,或m>2,或﹣2≤m<﹣1.19.在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?【考点】函数模型的选择与应用;基本不等式在最值问题中的应用.【分析】先设箱底边长为xcm,则箱高cm,得箱子容积,再利用导数的方法解决,应注意函数的定义域.【解答】解:设箱底边长为xcm,则箱高cm,得箱子容积(0<x<60).(0<x<60)令=0,解得x=0(舍去),x=40,并求得V(40)=16 000由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值答:当x=40cm时,箱子容积最大,最大容积是16 000cm320.已知函数f(x)=ax+lnx(a∈R).(Ⅰ)若a=2,求曲线y=f(x)在x=1处的切线方程;(Ⅱ)求f(x)的单调区间;(Ⅲ)设g(x)=x2﹣2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【分析】(Ⅰ)把a的值代入f(x)中,求出f(x)的导函数,把x=1代入导函数中求出的导函数值即为切线的斜率,可得曲线y=f(x)在x=1处的切线方程;(Ⅱ)求出f(x)的导函数,分a大于等于0和a小于0两种情况讨论导函数的正负,进而得到函数的单调区间;(Ⅲ)对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),等价于f(x)max<g(x)max,分别求出相应的最大值,即可求得实数a的取值范围.【解答】解:(Ⅰ)由已知,f'(1)=2+1=3,所以斜率k=3,又切点(1,2),所以切线方程为y﹣2=3(x﹣1)),即3x﹣y﹣1=0故曲线y=f(x)在x=1处切线的切线方程为3x﹣y﹣1=0.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(Ⅱ)①当a≥0时,由于x>0,故ax+1>0,f'(x)>0,所以f(x)的单调递增区间为(0,+∞).﹣﹣﹣﹣﹣﹣②当a<0时,由f'(x)=0,得.在区间上,f'(x)>0,在区间上,f'(x)<0,所以,函数f(x)的单调递增区间为,单调递减区间为.﹣﹣﹣﹣﹣﹣﹣﹣(Ⅲ)由已知,转化为f(x)max<g(x)max.g(x)=(x﹣1)2+1,x∈[0,1],所以g (x)max=2由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.(或者举出反例:存在f(e3)=ae3+3>2,故不符合题意.)当a<0时,f(x)在上单调递增,在上单调递减,故f(x)的极大值即为最大值,,所以2>﹣1﹣ln(﹣a),解得.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣21.在无穷数列{a n}中,a1=1,对于任意n∈N*,都有a n∈N*,且a n<a n+1.设集合A m={n|a n ≤m,m∈N*},将集合A m中的元素的最大值记为b m,即b m是数列{a n}中满足不等式a n≤m的所有项的项数的最大值,我们称数列{b n}为数列{a n}的伴随数列.例如:数列{a n}是1,3,4,…,它的伴随数列{b n}是1,1,2,3,….(I)设数列{a n}是1,4,5,…,请写出{a n}的伴随数列{b n}的前5项;(II)设a n=3n﹣1(n∈N*),求数列{a n}的伴随数列{b n}的前20项和.【考点】数列的求和;数列的应用.【分析】(I)由{a n}伴随数列{b n}的定义可得前5项为1,1,1,2,3.(II)由a n=3n﹣1≤m,可得n≤1+log3m,m∈N*,分类讨论:当1≤m≤2时,m∈N*,b1=b2=1;当3≤m≤8时,m∈N*,b3=b4=…=b8=2;当9≤m≤20时,m∈N*,b9=b10=…=3;即可得出数列{a n}的伴随数列{b n}的前20项和.【解答】解:(Ⅰ)数列1,4,5,…的伴随数列{b n}的前5项1,1,1,2,3;(Ⅱ)由,得n≤1+log3m(m∈N*).∴当1≤m≤2,m∈N*时,b1=b2=1;当3≤m≤8,m∈N*时,b3=b4=…=b8=2;当9≤m≤20,m∈N*时,b9=b10=…=b20=3.∴b1+b2+…+b20=1×2+2×6+3×12=50.2016年9月9日。
2020-202年近三年浙江省嘉兴市高一化学下学期期末考试题汇编1-选择题含详解

浙江省嘉兴市2020-2022三年高一化学下学期期末试题汇编1-选择题1.(2020春·浙江嘉兴·高一统考期末)氧气的分子式是A.H2B.N2C.O2D.Cl22.(2020春·浙江嘉兴·高一统考期末)治疗新冠肺炎中使用的药物利托那韦(分子式C37H48N6O5S2),按物质的组成和性质进行分类,属于A.单质B.氧化物C.有机物D.无机物3.(2020春·浙江嘉兴·高一统考期末)下列仪器名称为“容量瓶”的是A.B.C.D.4.(2020春·浙江嘉兴·高一统考期末)下列物质中,属于高分子化合物的是A.乙酸乙酯B.淀粉C.葡萄糖D.油脂5.(2020春·浙江嘉兴·高一统考期末)下列物质的水溶液能使蓝色石蕊试纸变红的是A.NH3B.Na2CO3C.NaHSO4D.NaOH 6.(2020春·浙江嘉兴·高一统考期末)在化学反应3CO+Fe2O3∆=2Fe+3CO2中,还原剂是A.CO B.Fe C.Fe2O3D.CO27.(2020春·浙江嘉兴·高一统考期末)下列属于非电解质的是A.盐酸B.酒精C.CaCO3D.铜8.(2020春·浙江嘉兴·高一统考期末)下列表示正确的是A.硝基苯的结构简式:B.Cl-的结构示意图:C.NH3的电子式:D.乙炔分子的球棍模型:9.(2020春·浙江嘉兴·高一统考期末)下列说法不正确...的是A.C60和金刚石互为同素异形体B.1H和2H互为同位素C.和互为同分异构体D.CH4和C3H8互为同系物10.(2020春·浙江嘉兴·高一统考期末)下列说法不正确...的是A.钠和钾的合金可用于快中子反应堆作热交换剂B.石灰石可用于燃煤烟气的脱硫C.用酒精可以萃取碘水中的I2D.CO2可用于生产可降解高聚物11.(2020春·浙江嘉兴·高一统考期末)W、X、Y、Z、M、N六种主族元素,它们在周期表中位置如图所示,下列说法不正确...的是A.X的原子半径比Y的大B.元素的非金属性:W>ZC.氧化物对应水化物的酸性M>ZD.元素N位于金属与非金属的分界线附近,可以推断N元素的单质可作半导体材料12.(2020春·浙江嘉兴·高一统考期末)下列有关实验的说法正确的是A.用无水硫酸铜检验乙醇中是否有水B.配制一定物质的量浓度的溶液时,容量瓶必须干燥C.除去乙烷中含有的少量乙烯可用酸性高锰酸钾溶液洗气D.往2%的稀氨水中加入2%的硝酸银溶液,至沉淀恰好溶解,制得澄清的银氨溶液13.(2020春·浙江嘉兴·高一统考期末)下列说法不正确...的是A.可燃冰的主要成分是CH4·nH2OB.一定条件下,煤和氢气作用,可以得到液体燃料C.往油脂皂化反应后的溶液中加入热的饱和食盐水,搅拌后在烧杯底部析出固体D.石油催化裂化、裂解都是炼制石油加工的重要手段,均属于化学变化14.(2020春·浙江嘉兴·高一统考期末)下列说法不正确...的是A.利用植物的秸秆生产乙醇,是对生物质能的有效利用B.蛋白质中除含有碳、氢、氧外,一定含有氮元素C.75%的医用酒精和84消毒液可以使蛋白质变性,均可用于新冠病毒的消毒D.淀粉与稀硫酸充分反应后的溶液中,加入NaOH溶液中和,再加入碘水,此时溶液不变蓝色,说明淀粉已完全水解15.(2020春·浙江嘉兴·高一统考期末)过碳酸钠2Na2CO3·3H2O2,外观为白色结晶,主要用作漂白剂和氧化剂。
浙江省嘉兴市2023-2024学年高二下学期6月期末检测数学试题2

8.已知函数 ,若 ,则 的最小值为()
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数 (其中 是虚数单位),则下列说法正确的是()
A. 的虚部为
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
19.已知函数 .
(1)当 时,求 的单调区间;
(2)当 时,求证: 在区间 有唯一的极值点;
(3)若对于任意的 恒成立,求实数 的取值范围.
(1)求角 的大小;
(2)若 ,求 的面积.
17.如图, 和 都垂直于平面 ,且 .
(1)证明:平面 平面 ;
(2)当平面 与平面 的夹角为 时,求几何体 的体积.
18.为了了解某市市民平均每天体育锻炼 时间,在该市随机调查了 位市民,将这 位市民每天体育锻炼的时间(单位:分钟)分为 五组,得到如图所示的频率分布直方图:
嘉兴市2023~2024学年第二学期期末检测
高二数学试题卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合 ,则 ()
A. B. C. D.
2. 的展开式中 的系数为()
A. B. C. D.
3.已知 , 是两个不同 平面,直线m满足 ,则“ ”是“ ”的()
14.已知 为球 的球面上四个点,且满足 , 平面 ,则球 的表面积的最小值为__________.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
浙江省嘉兴市平湖市当湖高级中学2023-2024学年高一下学期5月月考数学试题

浙江省嘉兴市平湖市当湖高级中学2023-2024学年高一下学期5月月考数学试题一、单选题1.某射击运动员7次的训练成绩分别为:86,88,90,89,88,87,85,则这7次成绩的第80百分位数为( ) A .88.5B .89C .91D .89.52.一个圆柱的侧面展开图是长为4,宽为2的矩形,则该圆柱的轴截面的面积为( ) A .32B .32πC .16π D .8π3.某校高一共有10个班,编号1至10,某项调查要从中抽取三个班作为样本,现用抽签法抽取样本,每次抽取一个号码,共抽3次,设五班第一次抽到的可能性为a ,第二次被抽到的可能性为b ,则( ) A .310=a ,29b = B .110a =,19b =C .310=a ,310b =D .110a =,110b = 4.已知直线m 和两个不同的平面,αβ,则下列四个命题中正确的是( ) A .若,m αββ⊥⊂,则m α⊥ B .若//,//m αβα,则//m β C .若//,//m m αβ,则//αβD .若//,m αβα⊥,则m β⊥5.下图是一组数据的频率分布直方图,设这组数据的平均数为M ,中位数为N ,则关于M 与N 的大小关系,下面说法正确的是( )A .M N >B .M N <C .M N =D .不确定6.已知某人收集一个样本容量为50的一组数据,并求得其平均数为70,方差为75,现发现在收集这些数据时,其中两个数据记录有误,一个错将80记录为60,另一个错将70记录为90,在对错误数据进行更正后,重新求得样本的平均数为X ,方差为2S ,则( )A .270,75X S <<B .270,75X S >>C .270,75X S =<D .270,75X S =>7.在边长为2的正方形ABCD 中,E 是AB 的中点,点F 是BC 的中点,将AED △,BEF △,DCF V 分别沿DE ,EF ,DF 折起,使A ,B ,C 三点重合于点A ',则A '到平面EFD 的距离为( )A .1B .23C .43D .28.如图是某零件结构模型,中间大球为正四面体的内切球,小球与大球和正四面体三个面均相切,若12AB =,则该模型中一个小球的体积为( )A .3πB .3π2C D二、多选题9.学校“未来杯”足球比赛中,甲班每场比赛平均失球数是1.9,失球个数的标准差为0.3;乙班每场比赛平均失球数是1.3,失球个数的标准差为1.2,你认为下列说法中正确的是( ) A .平均来说乙班比甲班防守技术好 B .乙班比甲班防守技术更稳定C .乙班在防守中有时表现非常好,有时表现比较差D .甲班很少不失球10.已知圆台的轴截面如图所示,其上、下底面半径分别为1r =上,2r =下,母线AB 长为2,点E 为AB 的中点,则( )A B .圆台的侧面积为12πC .圆台母线AB 与底面所成角为60oD .在圆台的侧面上,从点C 到点E 的最短路径长为411.如图,在四边形ABCD 中,AD //,2,45,90BC AD AB BCD BAD ︒︒==∠=∠=,将ABD △沿BD 进行翻折,在这一翻折过程中,下列说法正确的是( )A .始终有AC BD ⊥B .当平面ABD ⊥平面BCD 时,AB ⊥平面ACDC .当平面ABD ⊥平面BCD 时,直线BC 与平面ABD 成45︒角 D .当平面ABD ⊥平面BCD 时,三棱锥A BCD -外接球表面积为16π三、填空题12.常言道:国以民为本,民以食为天.食品安全问题是人类生存的第一需要.学校为了解学生对食堂满意情况组织了一次座谈会,并利用分层抽样的方法从高中3个年级中随机抽取了150人参加,其中高一、高二年级各抽取了40人,50人,若高三年级有学生1200人,则该高中共有学生人.13.四面体ABCD 中,BD =AC =2,M 、N 分别为BC 、AD 的中点,MN =1,则异面直线AC 与BD 所成的角是.14.在棱长为1的正方体1111ABCD A B C D -中,E ,F 分别为BC 和1CC 的中点,M 是侧面11BCC B 内一点,若1//D M 平面DEF ,则线段1D M 长度的取值范围是.四、解答题15.如图所示,以线段AB 为直径的半圆上有一点C ,满足:1BC =,AC 阴影部分绕直线AB 旋转180°得到一个几何体.(1)求阴影部分形成的几何体的体积; (2)求阴影部分形成的几何体的表面积.16.已知在正方体1111ABCD A B C D -中,M 、E 、F 、N 分别是11A B 、11B C 、11C D 、11D A 的中点.求证:(1)E 、F 、D 、B 四点共面 (2)平面//AMN 平面EFDB .17.我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x (吨),用水量不超过x 的部分按平价收费,超过x 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),...,[4,4.5]分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a 的值;(2)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由; (3)若该市政府希望使85%的居民每月的用水量不超过标准x (吨),估计x 的值,并说明理由.18.如图,在斜三棱柱111ABC A B C -中,,AB BC M ⊥为AC 的中点,1MB AB ⊥.(1)证明:1MC AB ⊥.(2)若112,4,AB BC BB MB ====1B C 与平面11MB C 所成角的正弦值. 19.如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,122AB BC AD ===,90BAD ABC ∠=∠=︒,O 是AD 的中点.(1)求证:平面PAC ⊥平面POB ;(2)点M 在棱PC 上,满足(01)PM PC λλ=<>,且三棱锥P ABM -,求λ的值及二面角M AB D --的正切值.。
人教版数学高三期末测试精选(含答案)4

人教版数学高三期末测试精选(含答案)学校:___________姓名:___________班级:___________考号:___________一、单选题1.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:2222(1)(21)1236n n n n ++++++=L )A .1624B .1024C .1198D .1560【来源】2020届湖南省高三上学期期末统测数学(文)试题 【答案】B2.在ABC ∆中,若222sin sin sin A B C +<,则ABC ∆的形状是( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .不能确定【来源】海南省文昌中学2018-2019学年高一下学期段考数学试题 【答案】A3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a ﹣b =c cos B ﹣c cos A ,则△ABC 的形状为( ) A .等腰三角形 B .等边三角形C .直角三角形D .等腰三角形或直角三角形【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】D4.已知圆C 1:(x +a )2+(y ﹣2)2=1与圆C 2:(x ﹣b )2+(y ﹣2)2=4相外切,a ,b 为正实数,则ab 的最大值为( )A .B .94C .32D .2【来源】安徽省安庆市五校联盟2018-2019学年高二(上)期中数学(理科)试题 【答案】B5.已知等比数列{}n a 满足122336a a a a +=+=,,则7a =( )【来源】甘肃省兰州市第一中学2016-2017学年高二下学期期末考试数学(文)试题 【答案】A6.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把100个面包分给五个人,使每个人所得成等差数列,最大的三份之和的17是最小的两份之和,则最小的一份的量是 ( ) A .116B .103C .56D .53【来源】湖南省湘南三校联盟2018-2019学年高二10月联考文科数学试卷 【答案】D7.若ABC ∆的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC ∆( ) A .一定是锐角三角形 B .一定是直角三角形C .一定是钝角三角形D .可能是锐角三角形,也可能是钝角三角形【来源】广东省中山市第一中学2019-2020学年高二上学期10月月考数学试题 【答案】C8.若不等式22log (5)0x ax -+>在[4,6]x ∈上恒成立,则a 的取值范围是( )A .(,4)-∞)B .20(,)3-∞ C .(,5)-∞D .29(,)5-∞【来源】重庆市七校(渝北中学、求精中学)2019-2020学年高一上学期期末联考数学试题 【答案】C9.港珠澳大桥通车后,经常往来于珠港澳三地的刘先生采用自驾出行.由于燃油的价格有升也有降,现刘先生有两种加油方案,第一种方案:每次均加30升的燃油;第二种方案,每次加200元的燃油,则下列说法正确的是( ) A .采用第一种方案划算 B .采用第二种方案划算 C .两种方案一样D .无法确定【来源】2020届广东省珠海市高三上学期期末数学(文)试题 【答案】B10.已知正项等比数列{}n a 的前n 项和为n S ,12a =,23434a a a +=,则5S =( )【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题 【答案】A11.在ABC ∆中3AB =,5BC =,7AC =,则边AB 上的高为( )A B C D 【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B12.不等式220ax bx ++>的解集是()1,2-,则a b -=( ) A .3-B .2-C .2D .3【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B13.各项均为正数的数列{}n a ,其前n 项和为n S ,若224n n n a S a -=,则2019S 为( )A .BC .2019D .4038【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】A14.设m ,n 为正数,且2m n +=,则2312m n m n +++++的最小值为( ) A .176B .145 C .114D .83【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】B15.已知数列{}n a 的前n 项和为n S ,且314n n S a +=,则使不等式1000成立的n 的最大值为( )A .7B .8C .9D .10【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】C16.ABC ∆中角A ,B ,C 的对边分别是a ,b ,c ,若1a =,b =4B π=,则A =( )A .6π B .56π C .6π或56πD .23π【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题 【答案】A17.等差数列{}n a 前n 项和为n S ,已知46a =,36S =,则( ) A .410n a n =-B .36n a n =-C .2n S n n =-D .224n S n n =-【来源】2020届安徽省芜湖市高三上学期期末数学(理)试题 【答案】C18.在等差数列{}n a 中,652a a =,则17a a +=( ) A .0B .1C .2-D .3【来源】2020届福建省三明市高三上学期期末质量检测文科数学试题 【答案】A19.若0,0,a b c d >><<则一定有( ) A .a b c d> B .a b c d< C .a b d c> D .a b d c< 【来源】2014年全国普通高等学校招生统一考试理科数学(四川卷带解析) 【答案】D20.已知平面上有四点O ,A ,B ,C ,向量,,OA OB OC u u u r u u u r u u u r 满足:0OA OB OC ++=u u u r u u u r u u u r r1OA OB OB OC OC OA ⋅=⋅=⋅=-u u u v u u u v u u u v u u u v u u u v u u u v,则△ABC 的周长是( )A .B .C .3D .6【来源】福建省晋江市季延中学2017-2018学年高一下学期期末考试数学试题 【答案】A21.在ABC ∆中,60A =︒,1b =,则sin sin sin a b c A B C ++++的值为( )A .1B .2C D .【来源】辽宁省实验中学分校2016-2017学年高一下学期期末数学(文)试题 【答案】B二、填空题22.在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为________. 【来源】2018年全国普通高等学校招生统一考试数学(江苏卷) 【答案】923.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知5a =8b ,A =2B ,则sin B =_____.【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】3524.如图,为测得河对岸塔AB 的高,先在河岸上选一点C,使C 在塔底B 的正东方向上,测得点A 的仰角为60°,再由点C 沿北偏东15°方向走10 m 到位置D,测得∠BDC =45°,则塔AB 的高是_____.【来源】2014届江西省南昌大学附属中学高三第三次月考理科数学试卷(带解析) 【答案】1025.设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为 . 【来源】智能测评与辅导[文]-等比数列 【答案】6426.设x ,y 满足约束条件20260,0x y x y x y +-≥⎧⎪+≤⎨⎪≥≥⎩,则23z x y =-+的最小值是______.【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题 【答案】9-27.已知数列{}n a 是等差数列,且公差0d <,()11a f x =+,20a =,()31a f x =-,其中()242f x x x =-+,则{}n a 的前10项和10S =________.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题 【答案】70-28.若x ,y 满足约束条件22020x x y x y ≤⎧⎪-+≥⎨⎪+-≥⎩,则3z x y =-的最小值为________.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题 【答案】2-29.已知数列{}n a 满足11a =,()13N n n n a a n *+⋅=∈,那么数列{}n a 的前9项和9S =______.【来源】2020届安徽省芜湖市高三上学期期末数学(理)试题 【答案】24130.设a ,b ,c 分别为ABC ∆内角A ,B ,C 的对边.已知2cos cos a B C=,则222a cb ac+-的取值范围为______.【来源】2020届吉林省通化市梅河口市第五中学高三上学期期末数学(理)试题【答案】()()0,2U三、解答题31.如图,在平面四边形ABCD 中,BC =3,CD =5,DA 2=,A 4π=,∠DBA 6π=.(1)求BD 的长: (2)求△BCD 的面积.【来源】江苏省常州市2018-2019学年高一下学期期末数学试题 【答案】(1)7;(2 32.近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G ,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产x (千部)手机,需另投入成本()R x 万元,且 210100,040()100007019450,40x x x R x x x x ⎧+<<⎪=⎨+-≥⎪⎩,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.(I )求出2020年的利润()W x (万元)关于年产量x (千部)的函数关系式,(利润=销售额—成本);(II)2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?【来源】湖北省四校(襄州一中、枣阳一中、宜城一中、曾都一中)2018-2019学年高一下学期期中联考数学试题【答案】(Ⅰ)210600250,040()10000()9200,40x x x W x x x x ⎧-+-<<⎪=⎨-++≥⎪⎩(Ⅱ)2020年产量为100(千部)时,企业所获利润最大,最大利润是9000万元. 33.设集合A={x|x 2<9},B={x|(x-2)(x+4)<0}. (1)求集合A∩B ;(2)若不等式2x 2+ax+b <0的解集为A ∪B ,求a ,b 的值.【来源】2013-2014学年广东阳东广雅、阳春实验中学高二上期末文数学卷(带解析) 【答案】(1){x |3x 2}-<<(2)2,24a b ==- 34.已知数列{}n a 满足11a =,()111n n n a na n ++-=+. (1)求数列{}n a 的通项公式; (2)n S 为数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和,求证:223n S ≤<. 【来源】2020届山西省吕梁市高三上学期第一次模拟考试数学(文)试题【答案】(1)12n n a +=(2)证明见解析 35.在ABC V 中,a ,b ,c 分别为内角A ,B ,C的对边,且满()(sin sin )sin )b a B A c B C -+=-.(1)求A 的大小;(2)再在①2a =,②4B π=,③=c 这三个条件中,选出两个使ABC V 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求ABC V 的面积. 【来源】2020届山东省滨州市高三上学期期末考试数学试题 【答案】(1)6A π=;(2)见解析36.设函数()22sin cos 3x x f x π⎛⎫=+⎪⎝⎭. (1)若0,2x π⎡⎤∈⎢⎥⎣⎦,求()f x 的单调递增区间;(2)在ABC ∆中,1AB =,2AC =,()2f A =-,且A 为钝角,求sin C 的值. 【来源】2020届浙江省嘉兴市高三上学期期末考试数学试题【答案】(1)5,122ππ⎡⎤⎢⎥⎣⎦(2)1437.在四边形ABCD 中,120BAD ︒∠=,60BCD ︒∠=,1cos 7D =-,2AD DC ==.(1) 求cos DAC ∠及AC 的长; (2) 求BC 的长.【来源】2020届宁夏石嘴山市第三中学高三上学期期末考试数学(文)试题【答案】(1) cos 7DAC ∠=,7AC =;(2) 3 38.在ABC V 中,内角A B C ,,所对的边分别为a b c ,,,已知sin cos 2sin cos A B c bB A b-=.(1)求A ;(2)设5b =,ABC S =V 若D 在边AB 上,且3AD DB =,求CD 的长. 【来源】2020届福建省莆田市(第一联盟体)学年上学期高三联考文科数学试题【答案】(1)3π;(239.在ABC ∆中,45,B AC ︒∠==cos C =. (1)求BC 边长;(2)求AB 边上中线CD 的长.【来源】北京101中学2018-2019学年下学期高一年级期中考试数学试卷【答案】(1)(240.已知函数2()2()f x x mx m R =-++∈,()2x g x =. (1)当2m =时,求2()(log )f x g x >的解集;(2)若对任意的1[1,1]x ∈-,存在2[1,1]x ∈-,使不等式12()()f x g x ≥成立,求实数m 的取值范围.【来源】重庆市七校(渝北中学、求精中学)2019-2020学年高一上学期期末联考数学试题【答案】(1)(0,2)(2)11[,]22-41.已知1x =是函数2()21g x ax ax =-+的零点,()()g x f x x=. (Ⅰ)求实数a 的值;(Ⅱ)若不等式(ln )ln 0f x k x -≥在2,x e e ⎡⎤∈⎣⎦上恒成立,求实数k 的取值范围;(Ⅲ)若方程()3213021xxf k k ⎛⎫⎪-+-= ⎪-⎝⎭有三个不同的实数解,求实数k 的取值范围.【来源】天津市滨海新区2018-2019学年高一上学期期末检测数学试题【答案】(Ⅰ)1;(Ⅱ)(],0-∞;(Ⅲ)103k -<<.42.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,cos sin C c B =. (1)求角C 的大小(2)若c =ABC ∆的面积为,求ABC ∆的周长.【来源】天津市蓟州等部分区2019届高三上学期期末联考数学(文)试题【答案】(Ⅰ)3C π=.(Ⅱ)10+43.已知等差数列{}n a 中,首项11a =,523a a =.(1)求{}n a 的通项公式;(2)若等比数列{}n b 满足13b =,2123b a a a =++,求{}n b 的前n 项和n S . 【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1) 21n a n =-;(2) 1332n n S +-= 44.对于正项数列{}n a ,定义12323nn a a a na G n+++⋅⋅⋅+=为数列{}n a 的“匀称”值.(1)若当数列{}n a 的“匀称”值n G n =,求数列{}n a 的通项公式; (2)若当数列{}n a 的“匀称”值2n G =,设()()128141n n nb n a +=--,求数列{}n b 的前2n 项和2n S 及2n S 的最小值.【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1) 21n n a n -=;(2)21141n S n =-+,4545.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且2sin tan c B b C =.(1)求角C 的值;(2)若c =3a b =,求ABC ∆的面积.【来源】重庆市松树桥中学2018-2019学年高一下学期期末数学试题【答案】(1)3C π=,(2)ABC S ∆=46.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足1cos cos a cB C b b-=-. (1)求角C 的大小;(2)若2c =,a b +=ABC V 的面积.【来源】2020届安徽省芜湖市高三上学期期末数学(文)试题【答案】(1)3C π=;(2)447.已知ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,且sin cos a B A =. (1)求A ;(2)若a =,ABC V 的面积为ABC V 的周长.【来源】2020届福建省三明市高三上学期期末质量检测文科数学试题试卷第11页,总11页 【答案】(1)3A π=(2)7+48.在正项数列{}n a中,11a =,()()2211121n n n n a a a a ++-=-,1n n nb a a =-. (1)求数列{}n a 与{}n b 的通项公式;(2)求数列(){}22n n n a b -的前n 项和nT . 【来源】2020届吉林省通化市梅河口市第五中学高三上学期期末数学(理)试题【答案】(1)22n n a +=,2n n b =,(2)()()13144219n n n T n n +-+=++49.在ABC ∆中,10a b +=,cos C 是方程22320x x --=的一个根,求ABC ∆周长的最小值。
高考数学二轮复习考点知识与题型专题讲解与训练35 一元二次不等式及其解法
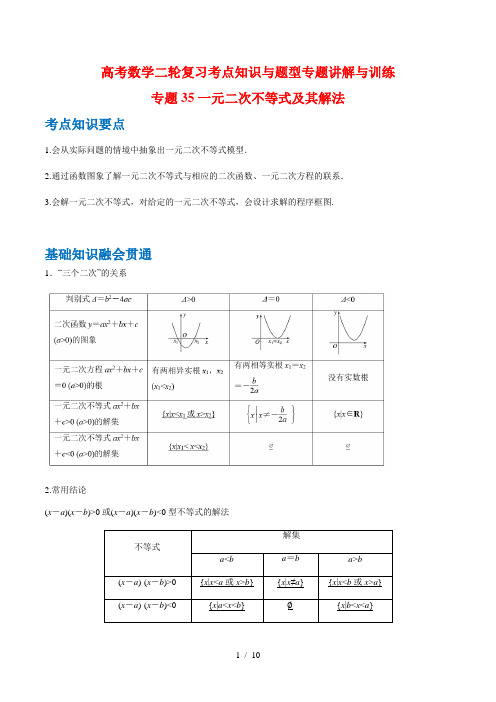
高考数学二轮复习考点知识与题型专题讲解与训练专题35一元二次不等式及其解法考点知识要点1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.基础知识融会贯通1.“三个二次”的关系2.常用结论(x-a)(x-b)>0或(x-a)(x-b)<0型不等式的解法解集不等式a<b a=b a>b(x-a)·(x-b)>0{x|x<a或x>b} {x|x≠a}{x|x<b或x>a}(x-a)·(x-b)<0{x|a<x<b}∅{x|b<x<a}口诀:大于取两边,小于取中间.【知识拓展】(1)f xg x>0(<0)⇔f(x)·g(x)>0(<0).(2)f xg x≥0(≤0)⇔f(x)·g(x)≥0(≤0)且g(x)≠0.以上两式的核心要义是将分式不等式转化为整式不等式.重点难点突破【题型一】一元二次不等式的求解命题点1不含参的不等式【典型例题】不等式x2+5x﹣6>0的解集是()A.{x|x<﹣2或x>3}B.{x|﹣2<x<3}C.{x|x<﹣6或x>l}D.{x|﹣6<x<l}【再练一题】不等式6x2+17x+12<0的解集是.命题点2含参不等式【典型例题】设a>1,则关于x的不等式的解集是()A.B.(a,+∞)C.D.【再练一题】已知不等式ax2+bx+c>0的解集是{x|α<x<β}(α>0),则不等式cx2+bx+a>0的解集是()A.(,)B.(﹣∞,)∪(,+∞)C.{x|α<x<β}D.(﹣∞,α)∪(β,+∞)思维升华含有参数的不等式的求解,往往需要对参数进行分类讨论.(1)若二次项系数为常数,首先确定二次项系数是否为正数,再考虑分解因式,对参数进行分类讨论,若不易分解因式,则可依据判别式符号进行分类讨论.(2)若二次项系数为参数,则应先考虑二次项系数是否为零,确定不等式是不是二次不等式,然后再讨论二次项系数不为零的情形,以便确定解集的形式;(3)对方程的根进行讨论,比较大小,以便写出解集.【题型二】一元二次不等式恒成立问题命题点1在R上的恒成立问题【典型例题】若不等式ax2﹣x+a>0对一切实数x都成立,则实数a的取值范围为()A.a或a B.a或a<0C.a D.【再练一题】已知关于x的不等式x2﹣x+a﹣1≥0在R上恒成立,则实数a的取值范围是.命题点2在给定区间上的恒成立问题【典型例题】已知[(m﹣1)x+1](x﹣1)>0,其中0<m<2,(1)解不等式.(2)若x>1时,不等式恒成立,求实数m的范围.【再练一题】已知关于x的不等式:x2﹣mx+m>0,其中m为参数.(1)若该不等式的解集为R,求m的取值范围;(2)当x>1时,该不等式恒成立,求m的取值范围.命题点3给定参数范围的恒成立问题【典型例题】已知不等式2x﹣1>m(x2﹣1).(1)若对于所有实数x,不等式恒成立,求m的取值范围;(2)若对于m∈[﹣2,2]不等式恒成立,求x的取值范围.【再练一题】已知不等式mx2﹣2x﹣m+1<0.(1)若对任意实数x上述不等式恒成立,求m的取值范围;(2)若对一切m∈[﹣2,2]上述不等式恒成立,求x的取值范围.思维升华(1)对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.(2)解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.跟踪训练【题型三】一元二次不等式的应用如果关于x的一元二次不等式ax2+bx+c>0的解集为{x|x<﹣2或x>4},那么对于函数应有()A.f(5)<f(2)<f(﹣1)B.f(2)<f(5)<f(﹣1)C.f(﹣1)<f(2)<f(5)D.f(2)<f(﹣1)<f(5)【再练一题】已知关于x 的不等式x 2﹣4ax +3a 2<0(a <0)的解集为(x 1,x 2),则的最大值是( )A .B .C .D .思维升华 求解不等式应用题的四个步骤(1)阅读理解,认真审题,把握问题中的关键量,找准不等关系.(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型. (3)解不等式,得出数学结论,要注意数学模型中自变量的实际意义. (4)回归实际问题,将数学结论还原为实际问题的结果.基础知识训练1.【贵州省铜仁市思南中学2018-2019学年高一下学期期中考试】不等式210x mx ++<的解集为空集,则m 的取值范围是( )A .(-2,2)B .[-2,2]C .(,2)(2,)-∞-⋃+∞D .(,2][2,)-∞-+∞2.【北省宜昌市部分示范高中教学协作体2018-2019学年高一下学期期中考试】不等式240ax ax +-<的解集为R ,则a 的取值范围是( ) A .160a ≤<B .16a >-C .160a -<≤D .0a <3.【安徽省安庆市第一中学2018-2019学年高一下学期期中考试】若不等式20ax x a -+>对一切实数x 都成立,则实数a 的取值范围为( ) A .12a <-或12a >B .12a >或0a < C .12a >D .1122a -<<4.【黑龙江省牡丹江市第一高级中学2018-2019学年高二下学期期中考试】不等式20ax bx c ++>的解集为(-4,1),则不等式2(1)(3)0b x a x c +-++>的解集为( )A .4(1,)3-B .4(,1)(,)3-∞-⋃+∞C .4(,1)3-D .4(,)(1,)3-∞-⋃+∞ 5.【广东省佛山市南海区桂城中学2018-2019学年第二学期高一数学第二次阶段考试】已知关于x 的不等式20x ax b --<的解集是()2,3-,则+a b 的值是( )A .11-B .11C .7D .76.【广东省深圳市四校发展联盟体2018-2019学年高二第二学期期中考试】在R 上定义运算():x y=x 1y ⊗⊗-,若对任意x 2>,不等式()x a x a 2-⊗≤+都成立,则实数a 的取值范围是( )A .(7,⎤-∞⎦B .17,⎡⎤-⎣⎦C .(3,⎤-∞⎦D .()17,,⎤⎡-∞-+∞⎦⎣7.【黑龙江省鹤岗市第一中学2018-2019学年高一下学期期中考试】在上定义运算,若存在使不等式成立,则实数的取值范围为A .B .C .D .8.【山东省济宁市2019届高三二模】已知函数,若不等式恒成立,则实数的取值范围为( ) A . B . C .D .9.【江西师范大学附属中学2018-2019学年高一下期期中考试】已知正实数,x y 满足3x y xy ++=,若对任意满足条件的,x y ,都有2()()60x y a x y +-++≥恒成立,则实数a 的最大值为( ) A .26B .7C .46D .810.【湖北省荆州市沙市中学2018-2019学年高一5月月考】若正实数x ,y 满足141x y +=,且234y x a a +>-恒成立,则实数a 的取值范围为( ) A .[]1,4-B .()1,4-C .[]4,1-D .()4,1-11.【福建省上杭县第一中学2018-2019学年高一5月月考】若两个正实数x ,y 满足211x y+=,且不等式2220x y m m +--<有解,则实数m 的取值范围为( )A .(,2)(4,)-∞-⋃+∞B .(,4)(2,)-∞-+∞C .(2,4)-D .(4,2)-12.【河北廊坊2018-2019学年高一年级第二学期期中联合调研考试高一】已知函数,如果不等式的解集为,那么不等式的解集为( )A .B .C .D .13.【内蒙古包头市第九中学2018-2019学年高一下学期期中考试】二次不等式210ax bx ++>的解集为113x x ⎧⎫-<<⎨⎬⎩⎭,则ab 的值为_______.14.【贵州省凯里市第一中学2018-2019学年高一下学期期中考试】已知不等式20ax bx c ++<的解集为{x | 2<x<3},则252b c a +++的最小值为__________. 15.【内蒙古赤峰二中2018-2019学年高一下学期第二次月考】不等式()2230x a a x a -++>的解集为{|x 2x a < 或x a >},则实数a 的取值范围______.16.【江西省南昌市第十中学2018-2019学年高一下学期第二次月考】已知关于x 的不等式20ax bx c ++<的解集是1{|2,}2x x x <->-或,则20ax bx c -+>的解集为_____.17.【四川省大竹中学2018-2019学年高一第二学期5月月考考前模拟】已知函数2()45()f x x x x R =-+∈. (1)求关于x 的不等式()2f x <的解集;(2)若不等式()|3|f x m >-对任意x R ∈恒成立,求实数m 的取值范围.18.【福建省三明市三地三校2018-2019学年高一下学期期中联考】已知函数2()28f x x x =-- (1)解不等式()0f x ≥;(2)若对一切0x >,不等式()9f x mx ≥-恒成立,求实数m 的取值范围.19.【内蒙古赤峰市2018-2019学年高一下学期期中考试】已知函数2()3f x x x m =++. (1)当m=-4时,解不等式()0f x ≤; (2)若m>0,()0f x <的解集为(b ,a),求14a b+的最大値. 20.【黑龙江省哈尔滨市呼兰一中、阿城二中、宾县三中、尚志五中四校2018-2019学年高一下学期期中考试】已知函数()22f x x x a =++.(1)当2a =时,求不等式()1f x >的解集(2)若对于任意[)1,x ∈+∞,()0f x >恒成立,求实数a 的取值范围.21.【安徽省固镇县第一中学2018-2019学年高二5月月考】设命题p :实数x 满足22430x mx m -+<;命题q :实数x 满足31x -<(1)若1m =,且p q ∧为真,求实数x 的取值范围;(2)若0m >,且p ⌝是q ⌝的充分不必要条件,求实数m 的取值范围.22.【湖北省荆州市沙市中学2018-2019学年高一5月月考】设函数()24f x ax x b =++(I )若1b =,且对于[]0,1x ∈,有()0f x ≥恒成立,求a 的取值范围; (II )若4a b +=,解关于x 的不等式()0f x ≥能力提升训练1.【2019年河北省藁城市第一中学高一下学期7月月考】设1a >,则关于x 的不等式1(1)()0a x a x a ⎛⎫---< ⎪⎝⎭的解集是( )A .1(,),a a ⎛⎫-∞+∞ ⎪⎝⎭B .(),a +∞C .1,a a ⎛⎫ ⎪⎝⎭D .()1,,a a ⎛⎫-∞+∞ ⎪⎝⎭2.【河南省濮阳市2018-2019学年高二下学期升级考试】设,a b 是关于x 的一元二次方程2260x mx m -++=的两个实根,则22(1)(1)a b -+-的最小值是( )A .494-B .18C .8D .-63.【江苏省无锡市锡山区天一中学2019年高一期末】已知关于x 的不等式2680kx kx k -++≥对任意x ∈R 恒成立,则k 的取值范围是( )A .01k ≤≤B .01k <≤C .k 0<或1k >D .0k ≤或1k4.【江西省南昌市东湖区第二中学2018-2019学年高二下学期期末】已知0,0x y >>,且211x y+=,若对任意的正数,x y ,不等式222x y m m +>+恒成立,则实数m 的取值范围是( ) A .4m ≥或2m ≤- B .2m ≥或4m ≤- C .24m -<<D .42m -<<5.【宁夏回族自治区银川一中2018-2019高二下学期期中考试】若存在1[,3]2x ∈,使不等式210x ax -+≥成立,则实数a 取值范围是( ) A .2a ≤B .522a ≤≤C .103a ≤D .1023a ≤≤6.【浙江省绍兴市第一中学2018-2019学年高二下学期期中考试】已知01b a <<+,若关于x 的不等式2()x b ->2()ax 的解集中的整数恰有3个,则a 的取值范围为( )A .11a -<<B .02a <<C .13a <<D .25a <<7.【安徽省淮南市第一中学2018-2019年高一年级第二学期第二次段考】已知关于x 的不等式2420ax x -+>的解集为{|}x x b ≠.(1)求实数,a b 的值; (2)解关于x 的不等式0x cax b-≥-.(c 为常数)8.【浙江省嘉兴市2018-2019学年高一下学期期末考试】已知函数2()2f x x ax =++. (Ⅰ)当3a =时,解不等式()0f x <;(Ⅱ)当[1,2]x ∈时,()0f x ≥恒成立,求a 的取值范围.9.【浙江“七彩阳光”新高考研究联盟2018-2019学年高一下学期期中考试】设函数()42,x a x f x a a R +=--∈.(Ⅰ)当2a =时,解不等式:()30f x >;(Ⅱ)当()1,1x ∈-时,()f x 存在最小值2-,求a 的值.10.【安徽省淮南市第一中学2018-2019年高一年级第二学期第二次段考】设函数2()2f x x ax a =++,2()2()g x x bx c b c =++≠.已知关于x 的不等式()55b c g x -≤≤的解集恰好为,55b c ⎡⎤-⎢⎥⎣⎦.(1)求()g x ;(2)对于0(2,)x ∈-+∞使得()()00f x g x <恒成立,求实数a 的取值范围.。
2019-2020学年人教A版浙江省宁波市九校高一第一学期期末数学试卷 含解析

2019-2020学年高一第一学期期末数学试卷一、选择题1.已知集合A={x|x>0},集合B={x|﹣1<x≤6},则A∩B=()A.(﹣1,0)B.(0,6] C.(0,6)D.(﹣1,6] 2.函数的值域是()A.(﹣1,1)B.C.D.3.已知x,y∈R,且x>y>0,则()A.B.cos x﹣cos y>0C.D.lnx+lny>04.已知向量,,且.则与的夹角为()A.B.C.D.5.已知半径为2的扇形AOB中,的长为3π,扇形的面积为ω,圆心角AOB的大小为φ弧度,函数h(x)=sin(x+φ),则下列结论正确的是()A.函数h(x)是奇函数B.函数h(x)在区间[﹣2π,0]上是增函数C.函数h(x)图象关于(3π,0)对称D.函数h(x)图象关于直线x=﹣3π对称6.已知a=log72,b=log0.70.2,c=0.70.2,则a,b,c的大小关系为()A.b<c<a B.a<b<c C.c<a<b D.a<c<b7.已知4个函数:①y=x|sin x|;②y=x cos|x|;③;④y=4cos x﹣e|x|的图象如图所示,但是图象顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的为()A.①④②③B.③②④①C.①④③②D.③①④②8.在△ABC中,,则△ABC为()A.直角三角形B.三边均不相等的三角形C.等边三角形D.等腰非等边三角形9.若(log22019)x+(log20202)﹣y<(log22019)﹣y+(log20202)x,则()A.x+y<0 B.x+y>0 C.x﹣y<0 D.x﹣y>010.设函数,则方程16f(x)+(x2+x﹣1)=0根的个数为()A.2 B.3 C.4 D.5二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.已知函数,则f(0)=,函数定义域是.12.已知是单位向量,,,,,若,则实数λ=;若A,B,D三点共线,则实数λ=.13.己知函数的最小正周期是3.则a=,f(x)的对称中心为.14.已知a,b∈R,定义运算“⊗”:,设函数f(x)=(2x⊗2)﹣(1⊗log2x),x∈(0,2),则f(1)=,f(x)的值域为.15.已知函数f(x)=(2m﹣9)x a为幂函数,且其图象过点,则函数的单调递增区间为.16.已知,是平面向量,且,若,则的取值范围是.17.函数f(x)=﹣2﹣5x,g(x)=sin x,若,使得f(x1)+f(x2)+…+f(x n﹣1)+g(x n)=g(x1)+g(x2)+…+g(x n﹣1)+f(x n),则正整数n的最大值为.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.已知向量,其中.(1)若的,求tan x的值;(2)若与垂直,求实数m的取值范围.19.已知集合.C={x|(x﹣m﹣1)(x+m+1)≤0,m∈R}(1)若(∁R A)∩B=∅,求a的取值范围;(2)若A∩C=C,求m的取值范围.20.已知f(x)为偶函数,当x≥0时,f(x)=2lg(x+1).(1)求f(x)的解析式;(2)若对于任意的x∈(﹣∞,0),关于x的不等式lg(kx)<f(x)恒成立,求k 的取值范围.21.已知函数f(x)=sin(2x+),g(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(1)求g(x)的解析式,并说明f(x)的图象怎样经过2次变换得到g(x)的图象;(2)若对于任意的,不等式|f(x)﹣m|<2恒成立,求实数m的取值范围.22.在函数定义域内,若存在区间[m,n],使得函数值域为[m+k,n+k],则称此函数为“k 档类正方形函数”,已知函数f(x)=log3[2k•9x﹣(k﹣1)3x+k+2].(1)当k=0时,求函数y=f(x)的值域;(2)若函数y=f(x)的最大值是1,求实数k的值;(3)当x>0时,是否存在k∈(0,1),使得函数f(x)为“1档类正方形函数”?若存在,求出实数k的取值范围,若不存在,请说明理由.参考答案一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x>0},集合B={x|﹣1<x≤6},则A∩B=()A.(﹣1,0)B.(0,6] C.(0,6)D.(﹣1,6] 【分析】进行交集的运算即可.解:∵A={x|x>0},B={x|﹣1<x≤6},∴A∩B=(0,6].故选:B.2.函数的值域是()A.(﹣1,1)B.C.D.【分析】先判断出函数y=tan x在(﹣,)单调递增,分别求出特殊值,再写出函数的值域即可.解:因为函数y=tan x在(﹣,)单调递增,且tan=;tan(﹣)=﹣1,则所求的函数的值域是(﹣1,),故选:C.3.已知x,y∈R,且x>y>0,则()A.B.cos x﹣cos y>0C.D.lnx+lny>0【分析】利用不等式的基本性质、函数的单调性即可判断出结论.解:x>y>0,则﹣>0,cos x﹣cos y>0,lnx+lny>0不一定成立,而﹣<0一定成立.故选:C.4.已知向量,,且.则与的夹角为()A.B.C.D.【分析】分别求出向量的模长,代入向量的数量积即可求解,注意夹角的范围.解:设与的夹角为θ;因为,所以||=1;∴=||×||cosθ=⇒cosθ=;∵θ∈[0,π];∴θ=;故选:A.5.已知半径为2的扇形AOB中,的长为3π,扇形的面积为ω,圆心角AOB的大小为φ弧度,函数h(x)=sin(x+φ),则下列结论正确的是()A.函数h(x)是奇函数B.函数h(x)在区间[﹣2π,0]上是增函数C.函数h(x)图象关于(3π,0)对称D.函数h(x)图象关于直线x=﹣3π对称【分析】先通过扇形的弧长和面积公式表示出ω和φ,并代入函数h(x)的解析式,整理得,再结合余弦函数的图象与性质逐一判断每个选项的正误即可.解:∵扇形弧长=2φ=3π,∴φ=,又∵扇形面积ω=∴h(x)=sin(x+φ)=,对于A选项,函数h(x)为偶函数,即A错误;对于B选项,令,则x∈[6kπ,3π+6kπ],k∈Z,而[﹣2π,0]⊈[6kπ,3π+6kπ],k∈Z,即B错误;对于C选项,令,则,∴函数的对称中心为,即C错误;对于D选项,令,则x=3kπ,k∈Z,∴函数的对称轴为x=3kπ,k∈Z,当k=﹣1时,有x=﹣3π,即D正确.故选:D.6.已知a=log72,b=log0.70.2,c=0.70.2,则a,b,c的大小关系为()A.b<c<a B.a<b<c C.c<a<b D.a<c<b【分析】本题根据对数函数及指数函数来比较大小,解题关键是找到中间值,将a、b、c与中间值进行比较即可得到结果.解:由题意,∵2=<,∴a=log72<log7=;b=log0.70.2>log0.70.7=1,<0.7<c=0.70.2<1,∴a<c<b,故选:D.7.已知4个函数:①y=x|sin x|;②y=x cos|x|;③;④y=4cos x﹣e|x|的图象如图所示,但是图象顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的为()A.①④②③B.③②④①C.①④③②D.③①④②【分析】分别判断函数的奇偶性,对称性,利用函数值的特点进行判断即可.解:①y=x|sin x|是奇函数,图象关于原点对称;当x>0时,y≥0恒成立,②y=x cos|x|=x cos x是奇函数,图象关于原点对称;③为非奇非偶函数,图象关于原点和y轴不对称,且y≥0恒成立,④y=4cos x﹣e|x|是偶函数,图象关于y轴对称,则第一个图象为③,第三个图象为④,第四个图象为①,第二个图象为②即对应函数序号为③②④①,故选:B.8.在△ABC中,,则△ABC为()A.直角三角形B.三边均不相等的三角形C.等边三角形D.等腰非等边三角形【分析】直接代入数量积的计算公式第一个条件求出A=C;第二个条件得到B即可求出结论解:因为在△ABC中,A,B,C∈(0,π),∴+=0⇒||cos A﹣||coC=0⇒cos A=cos C⇒A=C;∵•=||×||×cos B=||×||⇒cos B=⇒B=;∴△ABC为等边三角形;故选:C.9.若(log22019)x+(log20202)﹣y<(log22019)﹣y+(log20202)x,则()A.x+y<0 B.x+y>0 C.x﹣y<0 D.x﹣y>0【分析】令f(x)=﹣(log22020)﹣x,然后结合函数的单调性即可判断.解:令f(x)=﹣(log22020)﹣x,则易得f(x)在(﹣∞,+∞)上单调递增,结合已知不等式的特点,考虑构造函数∵(log22019)x+(log20202)﹣y<(log22019)﹣y+(log20202)x,∴(log22019)x﹣(log22020)﹣x<(log22019)﹣y﹣(log22020)y,即f(x)<f(﹣y),所以x<﹣y,故x+y<0.故选:A.10.设函数,则方程16f(x)+(x2+x﹣1)=0根的个数为()A.2 B.3 C.4 D.5【分析】方程16f(x)+(x2+x﹣1)=0根的个数等价于函数f(x)与函数g(x)=﹣的交点个数,画出两个函数的大致图象,观察交点个数即可.解:方程16f(x)+(x2+x﹣1)=0根的个数等价于函数f(x)与函数g(x)=﹣的交点个数,画出两个函数的大致图象,如图所示:,∵,∴在(0,+∞)内有1个交点,∵,∴两个函数在(﹣∞,0]内有3个交点,综上所述,函数f(x)与函数g(x)共有4个交点,所以方程16f(x)+(x2+x﹣1)=0根的个数是4个,故选:C.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.已知函数,则f(0)= 2 ,函数定义域是.【分析】直接在函数解析式中取x=0求得f(0);由对数式的真数大于0,分母中根式内部的代数式大于0联立不等式组求解函数定义域.解:由,得f(0)=;由,解得﹣.∴函数定义域是(﹣,1).故答案为:2,(﹣,1).12.已知是单位向量,,,,,若,则实数λ=;若A,B,D三点共线,则实数λ=﹣.【分析】利用向量垂直和向量平行的性质直接求解.解:∵是单位向量,,,,,,∴=()•()=2λ﹣1=0,解得实数λ=.∵A,B,D三点共线,=,,解得实数λ=﹣.故答案为:.13.己知函数的最小正周期是3.则a=,f(x)的对称中心为(,0),k∈Z .【分析】根据正切的周期求出a,利用整体法求出对称中心即可.解:函数的最小正周期是3,则3=,得a=,所以函数f(x)=2tan(),由,k∈Z,得x=,故对称中心为(,0),k∈Z14.已知a,b∈R,定义运算“⊗”:,设函数f(x)=(2x⊗2)﹣(1⊗log2x),x∈(0,2),则f(1)= 1 ,f(x)的值域为[1,3).【分析】由所给的函数定义求出分段函数f(x)的解析式,进而求出结果.解:由题意f(x)=,,所以f(1)=1,x∈(0,2),f(x)∈[1,3),故答案分别为:1,[1,3)15.已知函数f(x)=(2m﹣9)x a为幂函数,且其图象过点,则函数的单调递增区间为(﹣∞,2).【分析】根据函数f(x)是幂函数求出m的值,再根据f(x)的图象过点,求出a的值;由此得出函数g(x)的解析式,根据复合函数的单调性:同增异减,求出g(x)的单调递增区间.解:函数函数f(x)=(2m﹣9)x a为幂函数,2m﹣9=1,解得m=5,且其图象过点,所以3a=,解得a=,所以函数即函数g(x)=,令x2﹣5x+6>0,解得x<2或x>3;所以函数g(x)的单调递增区间为(﹣∞,2).故答案为:(﹣∞,2).16.已知,是平面向量,且,若,则的取值范围是[3,+∞).【分析】先根据()•=+•=6得到×cosθ=3;进而表示出即可求解解:设()与的夹角为θ;∵()•=+•=6=×||×cosθ;∴×cosθ=3;∴0<cosθ≤1=≥3;故答案为:[3,+∞)17.函数f(x)=﹣2﹣5x,g(x)=sin x,若,使得f(x1)+f(x2)+…+f(x n﹣1)+g(x n)=g(x1)+g(x2)+…+g(x n﹣1)+f(x n),则正整数n的最大值为 6 .【分析】由题意可得g(x)﹣f(x)=sin x+5x+2,由正弦函数和一次函数的单调性可得g(x)﹣f(x)﹣2=sin x+5x的范围是[0,1+],将已知等式整理变形,结合不等式的性质,可得所求最大值n.解:函数f(x)=﹣2﹣5x,g(x)=sin x,可得g(x)﹣f(x)=sin x+5x+2,由x∈[0,],可得y=sin x,y=5x递增,则g(x)﹣f(x)﹣2=sin x+5x的范围是[0,1+],f(x1)+f(x2)+…+f(x n﹣1)+g(x n)=g(x1)+g(x2)+…+g(x n﹣1)+f(x n),即为[g(x1)﹣f(x1)]+[g(x2)﹣f(x2)]+…+[g(x n﹣1)﹣f(x n﹣1)]=g(x n)﹣f (x n),即为(sin x1+5x1)+(sin x2+5x2)+…+(sin x n﹣1+5x n﹣1)+2(n﹣1)=sin x n+5x n+2,即(sin x1+5x1)+(sin x2+5x2)+…+(sin x n﹣1+5x n﹣1)+2(n﹣2)=sin x n+5x n,由sin x n+5x n∈[0,1+],可得2(n﹣2)≤1+,即n≤+,而+∈(6,7),可得n的最大值为6,故答案为:6.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.已知向量,其中.(1)若的,求tan x的值;(2)若与垂直,求实数m的取值范围.【分析】(1)根据平面向量的数量积列方程求出tan x的值,再根据x的范围确定tan x 的值;(2)根据平面向量的数量积和模长公式求出m的解析式,再求m的取值范围.解:(1)因为,即,所以,所以2tan2x﹣5tan x+2=0,解得tan x=2或.因为,所以tan x∈[0,1],即.(2)因为与垂直,所以,所以m2=1+sin2x,因为,所以,解得m的取值范围是.19.已知集合.C={x|(x﹣m﹣1)(x+m+1)≤0,m∈R}(1)若(∁R A)∩B=∅,求a的取值范围;(2)若A∩C=C,求m的取值范围.【分析】(1)可以求出A={x|﹣3≤x≤1},从而得出∁R A=(﹣∞,﹣3)∪(1,+∞),根据(∁R A)∩B=∅可讨论B是否为空集:B=∅时,a﹣1≥2a+1;B≠∅时,,解出a的范围即可;(2)根据A∩C=C即可得出C⊆A,然后可讨论m+1与﹣(m+1)的大小关系,从而得出集合C,根据C⊆A即可得出m的范围.解:(1)A={x|(x+3)(1﹣x)≥0}={x|﹣3≤x≤1},B=(a﹣1,2a+1),∴∁R A=(﹣∞,﹣3)∪(1,+∞),且(∁R A)∩B=∅,∴①B=∅时,a﹣1≥2a+1,解得a≤﹣2;②B≠∅时,,解得﹣2<a≤0,∴a的取值范围为(﹣∞,0];(2)∵A∩C=C,∴C⊆A,∴①m+1>﹣(m+1),即m>﹣1时,C=(﹣(m+1),m+1),∴,解得﹣1<m≤0;②m+1<﹣(m+1),即m<﹣1时,C=(m+1,﹣(m+1)),∴,解得﹣2≤m<﹣1;③m+1=﹣(m+1),即m=﹣1时,C={0},满足C⊆A,∴综上得,m的取值范围为[﹣2,0].20.已知f(x)为偶函数,当x≥0时,f(x)=2lg(x+1).(1)求f(x)的解析式;(2)若对于任意的x∈(﹣∞,0),关于x的不等式lg(kx)<f(x)恒成立,求k 的取值范围.【分析】(1)设x<0,则﹣x>0,f(x)=f(﹣x)=2lg(﹣x+1),再求出f(x)的解析式;(2)当x<0时,因为kx>0,所以k<0,结合分离参数法求出k的范围.解:(1)设x<0,则﹣x>0,f(x)=f(﹣x)=2lg(﹣x+1),所以,(2)当x<0时,因为kx>0,所以k<0,所以lg(kx)<2lg(﹣x+1),即lg(kx)<lg(﹣x+1)2,即kx<(﹣x+1)2.因为x<0,所以恒成立,因为x<0时,最大值为﹣4,所以﹣4<k,所以﹣4<k<0.21.已知函数f(x)=sin(2x+),g(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(1)求g(x)的解析式,并说明f(x)的图象怎样经过2次变换得到g(x)的图象;(2)若对于任意的,不等式|f(x)﹣m|<2恒成立,求实数m的取值范围.【分析】(1)现根据图象求出g(x)的解析式;再结合图象变化规律说明f(x)的图象怎样经过2次变换得到g(x)的图象;(2)先结合正弦函数的性质求出f(x)的范围;再结合恒成立问题即可求解.解:(1)由图得,因为为函数递增区间上的零点,所以,即.因为,所以,即,图象变换:将函数f(x)=sin(2x+)的图象上所有点的横坐标伸长到原来的4倍(纵坐标不变)得到y=sin(x+),再将所得图象向左平移个单位长度得到的图象;(2)因为,所以,所以当时,f(x)取最小值,当时,f(x)取最大值1,因为|f(x)﹣m|<2恒成立,即﹣2+m<f(x)<2+m恒成立,所以,即.22.在函数定义域内,若存在区间[m,n],使得函数值域为[m+k,n+k],则称此函数为“k 档类正方形函数”,已知函数f(x)=log3[2k•9x﹣(k﹣1)3x+k+2].(1)当k=0时,求函数y=f(x)的值域;(2)若函数y=f(x)的最大值是1,求实数k的值;(3)当x>0时,是否存在k∈(0,1),使得函数f(x)为“1档类正方形函数”?若存在,求出实数k的取值范围,若不存在,请说明理由.【分析】本题第(1)题根据指数函数的性质和对数函数想性质可得到函数y=f(x)的值域;第(2)题利用换元法设t=3x,t>0,然后对参数k进行分类讨论,分k≥0和k <0两种情况进行讨论函数g(t)的最大值,根据最大值取得的情况计算出k的取值;第(3)题继续利用换元法设t=3x,t>0,设真数为g(t)=2k•t2﹣(k﹣1)t+k+2.根据二次函数的性质可得f(x)在(1,+∞)上为增函数,则f(x)min=f(m)=m+1,f (x)max=f(n)=n+1,将问题转化为方程在(0,+∞)上有两个不同实根进行思考,再次利用换元法转化为一元二次方程,根据△>0,及韦达定理可计算出实数k的取值范围.解:(1)由题意,当k=0时,,∵3x+2>2.∴,∴函数y=f(x)的值域为(log32,+∞).(2)由题意,设t=3x,t>0,则,①若k≥0,则函数g(t)=2k•t2﹣(t﹣1)t+k+2无最大值,即f(t)无最大值,不合题意;②若k<0,则g(t)=2k•t2﹣(k﹣1)t+k+2最大值在时取到,且,∴,解得k=1,或.由k<0,可得.(3)由题意,因为0<k<1时,设t=3x(t>1).设真数为g(t)=2k•t2﹣(k﹣1)t+k+2.此时对称轴,∴当t>1时,g(t)为增函数,且g(t)>g(1)=2k+3>0,即f(x)在(1,+∞)上为增函数.∴f(x)min=f(m)=m+1,f(x)max=f(n)=n+1,即方程在(0,+∞)上有两个不同实根,即2k•9x﹣(k﹣1)3x+k+2=3x﹣1,设t=3x(t>1).∴2k•t2﹣(k﹣1)t+k+2=3t.即方程2k•t2﹣(k+2)t+k+2=0有两个大于l的不等实根,∵0<k<1,∴,解得,由0<k<1,得,即存在m,n,使得函数f(x)为“1档类正方形函数”,且.。
浙江省嘉兴市洪合中学高一数学文下学期期末试卷含解析

浙江省嘉兴市洪合中学高一数学文下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 与函数相等的函数是( )A. B. C. D.参考答案:C略2. 若展开式中存在常数项,则的最小值为()A.5 B.6 C.7 D.8参考答案:A3. 下列四个函数中,在区间上是减函数的是()A. B. C.D.参考答案:A4. 已知数列{a n}满足a1=3,a n+1=,则a2012=A. 2B. -3C.D.参考答案:C5. 利用计算机产生0~1之间的均匀随机数a,则使关于x的一元二次方程x2-x+a=0无实根的概率为()A. B. C.D.参考答案:C6. (3分)下列说法正确的是()A.三点确定一个平面B.四边形一定是平面图形C.梯形一定是平面图形D.平面α和平面β有不同在一条直线上的三个公共点参考答案:C考点:命题的真假判断与应用.专题:阅读型;空间位置关系与距离.分析:由公理3知:不共线的三个点确定一个平面,即可判断A;四边形有平面四边形和空间四边形两种,由不共面的四个点构成的四边形为空间四边形,即可判断B;在同一平面内,只有一组对边平行的四边形为梯形,即可判断C;由公理3得不同在一条直线上的三个公共点确定一个平面,即可判断D.解答:A.由公理3知:不共线的三个点确定一个平面,故A错;B.四边形有平面四边形和空间四边形两种,由不共面的四个点构成的四边形为空间四边形,故B错;C.在同一平面内,只有一组对边平行的四边形为梯形,故C对;D.由公理3得不同在一条直线上的三个公共点确定一个平面,故D错.故选C.点评:本题考查空间确定平面的条件,掌握三个公理和三个推论,是迅速解题的关键,本题属于基础题.7. 函数的最小正周期为 ( )A B C D参考答案:B8. (5分)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f (x)=x,则函数y=f(x)=log3|x|的零点个数是()A.多于4个B.4个C.3个D.2个参考答案:B考点:对数函数的图像与性质;函数的周期性.专题:压轴题;数形结合.分析:根据定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f (x)=x,我们易画出函数f(x)的图象,然后根据函数y=f(x)﹣log3|x|的零点个数,即为对应方程的根的个数,即为函数y=f(x)与函数y=log3|x|的图象交点的个数,利用图象法得到答案.解答:若函数f(x)满足f(x+2)=f(x),则函数是以2为周期的周期函数,又由函数是定义在R上的偶函数,结合当x∈[0,1]时,f(x)=x,我们可以在同一坐标系中画出函数y=f(x)与函数y=log3|x|的图象如下图所示:由图可知函数y=f(x)与函数y=log3|x|的图象共有4个交点,即函数y=f(x)﹣log3|x|的零点个数是4个,故选B点评:本题考查的知识点是对数函数的图象与性质,利用转化思想,将函数的零点个数问题,转化为函数图象交点个数问题,是解答本题的关键.9. 在等差数列{a n}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于()A.45 B.75 C.180 D.300参考答案:C10. 函数f(x) = ,则不等式x+(x+2)·f(x+2)≤5的解集是A.(-∞,] B.[2,]C.(-∞, -2)D.(-∞, +∞)参考答案:A∵不等式x+(x+2)f(x+2)≤5,∴x+2+(x+2)f(x+2)≤7,当x+2≥0时,f(x+2)=1,代入原不等式得:x+2+x+2≤7?-2≤x≤;当x+2<0时,f(x+2)=-1,代入原不等式得:x+2-x-2≤7?0≤7,即x<-2;综上,原不等式的解集为(-∞,].故选A .二、填空题:本大题共7小题,每小题4分,共28分11. 用100米扎篱笆墙的材料扎一个矩形羊圈,欲使羊的活动范围最大,则应取矩形长米,宽米.参考答案:25,25.12. 若等比数列{a n }满足,则q= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
嘉兴市2019~2020学年第二学期期末检测高一数学 试题卷(2020.7)姓名 准考证号本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页;非选择题部分3至6页。
满分150分,考试时间120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.直线12-=x y 在y 轴上的截距为 A . 1- B .21C . 1D . 2 2.在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,若1,2,60===c b A ,则ABC ∆的面积为A .21B .23C .1D .33.计算30tan 130tan 22-的值是A .33B .13-C .3D .13+4.已知等差数列}{n a 中,32=a ,79=a ,则}{n a 的前10项和=10S A .7330 B .7530C .100D .50 5.若实数y x ,满足条件⎪⎩⎪⎨⎧≤≥-+≥+-10101x y x y x ,则y x +2的最小值是A .0B .1C .2D . 4 6.已知数列}{n a 的前n 项和为n S ,且满足32-=n n a S ,)N (*∈n ,则=6S A. 192B. 189C. 96D. 937.在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,若满足A b B a c cos cos -=,则ABC ∆一定是A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形8.若对任意0≠x ,不等式|12|1|1|x a x --≥-恒成立,则实数a 的取值范围是 A .1≥aB .3≤aC .1≤a 或3≥aD .31≤≤a9.在平面直角坐标系中,记d 为点)sin ,(cos ααP 到直线02=-+y mx 的距离,当α,m变化时,d 的最大值为 A .1B .2C .3D .410.对于数列}{n a ,若存在常数M ,使对任意*N ∈n ,都有M a n ≤||成立,则称数列}{n a 是有界的.若有数列}{n a 满足11=a ,则下列条件中,能使}{n a 有界的是 A .n a a n n +=++11 B .na a n n 111-=-+ C .n n n a a 211+=+D .2111na a n n +=+非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.已知等差数列}{n a 的前3项依次是1,1,1--a ,则=a ▲ ;通项公式=n a ▲ .12.直线0:1=--m y x l 与直线03:2=+-y mx l 平行,则=m ▲ ;1l 与2l 之间的距离为 ▲ .13.已知)2,(ππα∈,若43tan =α,则=+)4tan(πα ▲ ;=2cos 2α ▲ .14. 已知0,1>>b a ,且42=+b a ,则ab 的最大值为 ▲ ;b a 211+-的最小值为 ▲ .15.在ABC ∆中,10,4==BC AB ,点D 是BC 中点,且21=AD ,=CBsin sin ▲ .16.数列}{n a 满足11=a ,22=a ,且2cos 2)2sin 1(222ππn a n a n n +⋅+=+)N (*∈n , 则=2020a ▲ .17.如图,已知矩形ABCD 的对角线长为1,其中AD AB >,将ABC ∆沿着AC 折叠,点B 落在点B '处,且边B A '与边CD 相交,则B AD '∆面积的最大值为 ▲ .三、解答题:本大题共5小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
BACDB '第17题图18.(本题满分14分)已知点)2,1(A 和直线02:1=+-a y x l . (Ⅰ)若点A 在直线1l 上,求a 的值;(Ⅱ)若直线2l 过点A 且与直线1l 垂直,求直线2l 的方程.19.(本题满分15分)已知βα,都是锐角,且135)cos(,54sin =+=βαα. (Ⅰ)求αα2cos ,2sin 的值; (Ⅱ)求βsin 的值.20.(本题满分15分)设等差数列}{n a 的公差为d ,前n 项和为n S ,且满足2-=d ,764=S .等比数列}{n b满足1031=+b b ,2042=+b b .(Ⅰ)求数列}{n a 和}{n b 的通项公式;(Ⅱ)设n n n b a c )23(-=,求数列}{n c 的前n 项和n T .21.(本题满分15分)在ABC ∆中,已知2π≠B ,且B B C B A C 2sin cos sin sin cos sin =+-,设角C B A ,,所对的边分别是c b a ,,.(Ⅰ)求证:c b a ,,成等差数列; (Ⅱ)若3sin sin sin sin =+ACC A ,求C A sin sin +的值.22.(本题满分15分)已知数列}{n a 满足11=a ,且nn n a a a +=+11(*N ∈n ).(Ⅰ)求}{n a 的通项公式;(Ⅱ)设n n n a a b -+=31,数列}{n b 的前n 项和为n S ,求证:210<-≤n S n .嘉兴市2019—2020学年第二学期期末检测高一数学 参考答案 (2020.7)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A 2.B 3.C 4.D 5.B 6.B 7.B 8.C 9.C 10.D 第10题解析:对于A 选项,假设{}n a 有界,即存在常数M ,对任意*n N ∈,都有1,n n a M a M +≤≤, 则M M M a a n n n 211=+≤+=++.由于左边n +1递增到无穷大,而右边为常数,从而A 项错误;同理,C 项2112n n n a a M +=+≤,错误; 对于B 项,2n ≥时,11112n n a a n +-=-≥,累加可得,21(2)2n a a n -≥-,21,2n na a =≥,显然不是有界的;对于D 选项,22a =,2221222111==(1)(1)111n n a n n n n na n n n n n n n ++=+<=⋅+-+-- , 累乘可得13122122122()()13231n n n n a a a n n n n a a a n n n n -------⨯⨯⨯=⨯⨯⨯⋅⨯⨯⨯--- , 22(1)2n a n a n=⋅-<,从而4n a <,D 正确. 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.1;2-n . 12.1; 13.7;101. 14.2;3 15.219. 16.2020. 17.18. 第17题解析:设()4CAB πθθ∠=<,则折叠后,θπθθ22,sin ,cos -='∠=='AD B AD B A ,故814sin 81)22sin(cos sin 21sin 21≤=-⋅⋅='∠⋅⋅'='A θθπθθB DA AD B A S B AD , 取最大值时=8πθ.三、解答题:本大题共5小题,共74分。
解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)已知点)2,1(A 和直线02:1=+-a y x l . (Ⅰ)若点A 在直线1l 上,求a 的值;(Ⅱ)若直线2l 过点A 且与直线1l 垂直,求直线2l 的方程. 解:(Ⅰ)点)2,1(A 代入直线1l 的方程,得022=+-a ,解得0=a .(Ⅱ)直线1l 的斜率为2,所以2l 的斜率为21-, 从而2l 的方程为)1(212:--=-x y ,即052=-+y x .19.(本题满分15分)已知βα,都是锐角,且135)cos(,54sin =+=βαα. (Ⅰ)求αα2cos ,2sin 的值; (Ⅱ)求βsin 的值. 解:(Ⅰ)由α是锐角,且54sin =α,则53cos =α. 所以252454532cos sin 22sin =⨯⨯==ααα,257251621sin 212cos 2-=⨯-=-=αα.(Ⅱ)由,135)cos(,0=+<+<βαπβα则1312)sin(=+βα,故αβααβααβαβsin )cos(cos )sin(])sin[(sin +-+=-+=651654135531312=⋅-⋅=.20.(本题满分15分)设等差数列}{n a 的公差为d ,前n 项和为n S ,且满足2-=d ,764=S .等比数列}{n b 满足1031=+b b ,2042=+b b .(Ⅰ)求数列}{n a 和}{n b 的通项公式;(Ⅱ)设n n n b a c )23(-=,求数列}{n c 的前n 项和n T . 解:(Ⅰ)41434762S a d ⨯=+=,解得122a =,从而242n a n =-. 2113111020b b q b q b q ⎧+=⎪⎨+=⎪⎩,两式相除得2q =,21=b ,所以2n n b =. (Ⅱ)n n n n n b ac 2)12()23(⋅-=-=.n n n T 2)12(252321321-++⋅+⋅+⋅= , 1322)12(2)32(23212+-+-++⋅+⋅=n n n n n T ,相减得:1212)12()22(22+--+++=-n n n n T62)23(2)12(212422111--=----+=+++n n n n n ,从而62)32(1+-=+n n n T . 21.(本题满分15分)在ABC ∆中,已知2π≠B ,且B B C B A C 2sin cos sin sin cos sin =+-,设角C B A ,,所对的边分别是c b a ,,.(Ⅰ)求证:c b a ,,成等差数列; (Ⅱ)若3sin sin sin sin =+ACC A ,求C A sin sin +的值. 解:(Ⅰ)sin()cos sin sin cos 2sin cos A B A B C B B B +-+=.sin cos sin cos 2sin cos A B C B B B +=,2B π≠,从而sin sin 2sin A C B +=,2a c b += ,即c b a ,,成等差数列.(Ⅱ)223,3a c a c ac c a +=+=,又2a c b +=,22215(2)44b ac ac ac =++=. 2225374cos 228ac aca cb B ac ac -+-===,sin B = .即sin sin 2sin A C B +==.22.(本题满分15分)已知数列}{n a 满足11=a ,且nn n a a a +=+11(*N ∈n ).(Ⅰ)求}{n a 的通项公式;(Ⅱ)设n n n a a b -+=31,数列}{n b 的前n 项和为n S ,求证:210<-≤n S n . 解:(Ⅰ)由题设得11111+=+=+nnnn a a a a ,从而}1{na 是首项为1,公差为1的等差数列,所以n a n=1,即21n a n =. (Ⅱ)222222123111)31(113131n n n n n n a a b n n n -++≤-+⋅=-+=-+= )111(2112112n n n --+<+=(2≥n ). 故)1()1()1(21-++-+-=-n n b b b n S)111(21)3121(21)2111(210n n --++-+-+≤ 21)11(21<-=n .另一方面:24242221)11(12113131n n n n n n n a a b n n n --+++=-+=-+=11)11(22=-+≥n n . 从而n S n ≥,即0≥-n S n . 综上得:210<-≤n S n .。
