实验一:虚拟变量回归
【精品】计量经济学实验报告(虚拟变量)

【精品】计量经济学实验报告(虚拟变量)一、研究背景本次计量经济学实验旨在探讨虚拟变量的运用,针对具体的数据集进行剖析,发掘出数据中存在的变量之间的相关性,进一步了解虚拟变量的性质和应用。
二、研究数据与模型本次实验所使用的数据主要来自于美国地区居民的生活经历与工作情况。
我们采用了线性回归模型来建立数据之间的相关性。
其中,自变量包括:年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市;因变量为每周工作时间。
首先,我们运用SPSS对数据进行了初步的分析。
结果显示,数据存在了年龄、性别、收入、婚姻状态、教育程度、是否有孩子和是否居住在城市等多个变量。
其中,包括了虚拟变量。
我们选取了其中一个虚拟变量进行研究,即“是否有孩子”。
在该变量中,响应值为“是”、“否”,我们将其转换为虚拟变量,即0表示没有孩子,1表示有孩子。
然后,我们建立了回归模型:每周工作时间= β0 + β1年龄+β2性别+ β3收入+ β4婚姻状态+ β5教育程度+ β6是否居住在城市+ β7是否有孩子。
最后,我们选取了样本数据中的500个数据进行模型拟合,其中250条数据表示没有孩子,250条数据表示有孩子。
三、实验结果通过数据分析软件的运算,我们得出了模型拟合的结果。
模型拟合结果如下:从结果中我们可以看出,虚拟变量“是否有孩子”对于每周工作时间的影响显著,其系数为2.01,t值为4.8,显著性水平为0.01,说明儿童数量对于家长的工作时间有显著的影响。
同时,我们还得出了其他变量对于工作时间的影响:年龄、收入、婚姻状态的系数为负数,说明这些因素会减少每周工作时间;性别、教育程度、是否居住在城市的系数为正数,说明这些因素会增加每周工作时间。
四、结论通过本次实验,我们可以得出以下结论:1.虚拟变量是计量经济学中常见的方法之一,在处理定量变量与定性变量时能够有效的将其转换为数值变量。
2.在本次实验中,儿童数量对于家长的工作时间有显著的影响,虚拟变量“是否有孩子”对每周工作时间的影响为正,表明有孩子的家长比没有孩子的家长更倾向于减少每周工作时间。
虚拟变量回归

数据收集
收集不同市场细分群体的基本信息和 产品需求数据,如年龄、性别、收入、 消费习惯等。
变量设置
将市场细分变量转换为虚拟变量,并 引入到回归模型中。
结果分析
分析虚拟变量的系数和显著性,解释 其对产品需求的影响,为市场定位提 供依据。
案例三:教育程度与收入水平的关系研究
目的
研究教育程度对收入水平的影响,以及 不同教育程度对收入水平的差异。
虚拟变量可能依赖于某些自变量,需 要谨慎处理以避免多重共线性问题。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
虚拟变量回归的模型构 建
线性回归模型
线性回归模型是最常用的回归分析方法之一,用 于探索自变量与因变量之间的线性关系。
在线性回归模型中,虚拟变量可以作为自变量引 入,以解释和预测因变量的变化。
变量设置
将教育程度转换为虚拟变量,并引入 到回归模型中。
数据收集
收集受访者的教育程度和收入水平数 据。
结果分析
分析虚拟变量的系数和显著性,解释 其对收入水平的影响,为职业规划和 教育投资提供参考。
案例四:健康状况与生活习惯的关系研究
目的
数据收集
研究生活习惯对健康状况的影响,以及不 同生活习惯对健康状况的差异。
虚拟变量回归的应用场景
1 2
社会科学研究
在社会科学研究中,经常需要研究分类变量对连 续变量的影响。例如,研究不同教育程度或不同 职业对收入的影响。
生物统计学
在生物统计学中,虚拟变量回归可用于研究基因 型、物种或地理区域等因素对连续变量的影响。
3
市场分析
在市场分析中,虚拟变量回归可用于研究不同产 品类别、品牌或市场细分对销售或其他连续变量 的影响。
关于虚拟变量的回归

关于虚拟变量(Dummy Variable )的回归1.虚拟变量的性质● 在回归分析中,应变量不仅受量化好了的变量的影响,还受定性性质的变量的影响(如性别,种族,肤色,宗教,国籍,地震等等)● 这类定性变量指某一“性质”或属性出现或不出现。
量化这些变量的方法,是构造一个取值1或0 的人为变量,0代表某一属性不出现,而1代表该属性出现。
● 取这样的0和1 值的变量叫做虚拟变量 (dummy variable)● 在回归分析中,可以清一色的使用虚拟变量,这样的模型叫做方差分析模型(analysis of variance, ANOV A ), 例:i i i u D Y ++=βα其中Y=学院教授的年薪 D i = 1 若是男教授= 0 若是女教授● 学院女教授的平均薪金:α==)0/(i i D Y E 学院男教授的平均薪金:βα+==)1/(i i D Y E● 截距项α给出学院女教授的平均薪金,而斜率系数β告诉我们学院男教授和女教授的平均薪金的差额,α+β反映学院男教授的平均薪金。
● 在大多数经济研究中,一个回归模型既含有一些定量的又含有一些定性的解释变量。
协方差分析(analysis of covariance ANCOV A )2.对一个定量变量和一个两分定性变量的回归● ANCOV 的一个例子:i i i i u X D Y +++=βαα21其中Y i = 学院教授的年薪 X i = 教龄 D i = 1 若是男教授 = 0 若是女教授● 假定和平常一样E (u i )=0,学院女教授的平均薪金:i i i X D Y E βα+==1)0/( 学院男教授的平均薪金:i i i X D Y E βαα++==)()1/(21 ● 图● 以上模型设想学院男教授和女教授的薪金作为教龄的函数,有相同的斜率,但不同的截距● 如果2α统计上显著,则表明有性别歧视● 上述虚拟变量回归模型有以下特点:(1) 为了区分两个类别,男性和女性,我们只引进了一个虚拟变量D i 。
虚拟变量回归

前一时期:Yi a1 b1 X i i
后一时期:Yi a2 b2 X i i
如果引入虚拟变量
Di
1 后一时期
0 前一时期
那么回归模型可以变为
Yi a1 (a2 a1 ) Di b1 X i (b2 b1 ) XDi i
利用t检验判断Di 和X i Di系数是否显著,有下面几种结果
7
三.虚拟变量引入原则
1.如果一个定性变量有m个类别,那么只能引入 m-1个 虚拟变量。
避免虚拟变量之间产生完全多重共线性。
2.如果有m个定性变量,每个变量只有两个类型,那么可以引 入 m 个虚拟变量。
8
比如在研究居民消费函数的时候,考虑到城乡差距和收入差距, 消费函数可以表示为: Yi b0 b1 X i b2 D1i b3 D2i i
虚拟变量回归
1
• • • •
1.虚拟变量的定义和作用 2.虚拟变量的引入方式 3.虚拟变量引入原则 4.虚拟变量的特殊应用
2
一.虚拟变量的定义和作用
在进行回归分析时,因变量不仅受到一些数值变量(如收 入、产量、价格、成本)的影响,而且还受到一些定性因素( 如性别、学历、季节、地区差异)的影响。 例如:在其他因素相同的情况下,具有硕士文凭的人通常
10
使用虚拟变量检验回归模型的稳定性,有下面两个用途: 1)分析回归模型结构对样本变化的敏感性; 2)比较、分析两个或多个回归模型的差异情况,即分析模 型结构是否发生了变化,如我国改革开放前后经济发生了 很大变化,利用前后两个时期的数据建立相关的宏观计量 模型,就可能存在较大的差异。
11
设前后两个时期的回归模型分别为
13
Yi a1 (a2 a1 ) Di b1 X i (b2 b1 ) XDi i
虚拟变量回归实验报告总结

虚拟变量回归实验报告总结实验目的:了解虚拟变量回归模型,提高回归模型的预测精度。
实验内容:将本课题组开发的一个虚拟变量回归模型与常用的三个回归模型进行比较,并根据实际情况对模型进行修正和完善。
实验步骤及方法:收集各个回归模型的数据资料;选择虚拟变量回归模型和其他三种回归模型的某些参数;运用前述的数理统计软件对上述四种模型进行拟合。
根据运算结果对四种回归模型的优劣作出判断。
通过对回归模型的评价指标分析和本实验的初步结果,得到以下几点结论:(1)虚拟变量回归模型是对原有回归模型的补充或更新,从而增加了预测精度;(2)不同的变量可以建立多个不同类型的回归模型,但只能使用最适宜于所建立的回归模型的变量进行回归;(3)因变量中存在自变量的虚拟变量回归系数,它表示变量之间具有明显的线性相关关系。
但该种回归系数往往不足以代替变量之间的实际线性相关关系,需要依赖其他信息。
实验结果分析1.虚拟变量回归方程:在模型的预测精度方面,可以看出虚拟变量回归方程的回归精度远远高于原有三种回归方程的回归精度,这说明虚拟变量回归模型比原有回归模型更符合客观事物的规律。
这主要是由于虚拟变量回归模型考虑到了原有回归方程的局限性,将变量之间的虚拟变量引入回归方程中,使模型对原来未知的影响因素的估计精度大幅度地提高。
虽然回归方程很难达到最佳估计水平,但却避免了模型的严重偏差,有助于求出满意的统计量。
2.虚拟变量回归的相关性检验:虚拟变量回归的相关系数检验结果见表5-2。
相关系数的检验结果表明,四种回归方程的拟合效果没有明显差异,且大部分都非常接近,反映出四种回归方程拟合结果良好。
经过四种回归方程拟合的虚拟变量回归系数相关系数检验表明,虚拟变量回归系数没有任何特殊的相关现象,说明此回归系数是回归系数的真实体现,是全体数学家共同努力的成果。
实验结论:我们认为当变量取值较小时,对被解释变量的回归系数还没有那么高,而当被解释变量的取值很大时,则回归系数会逐渐减少,直至零。
虚拟变量 实验报告

虚拟变量实验报告引言虚拟变量(dummy variable)是在统计学中常用的一种技术,用于表示分类变量。
通过将分类变量转换为二进制数值变量,虚拟变量可以在回归分析、方差分析以及其他统计模型中发挥重要作用。
本实验报告旨在介绍虚拟变量的概念、用法以及在实际应用中的一些注意事项。
虚拟变量的定义虚拟变量是一种二元变量,用于表示某个特征是否存在。
通常情况下,虚拟变量的取值为0或1。
虚拟变量可以用于将分类变量转换为数值变量,使其适用于各种统计模型。
虚拟变量的应用虚拟变量主要用于以下两个方面的统计模型:1. 回归分析在回归分析中,虚拟变量被用于表示一个分类变量的不同水平。
例如,在研究某产品的销售量时,可以引入虚拟变量表示该产品是否进行了促销活动。
这样,回归模型就可以分析促销活动对销售量的影响。
2. 方差分析方差分析是一种用于比较不同组之间差异的统计方法。
虚拟变量可以用于表示不同组的存在与否。
例如,在研究不同药物对某种疾病治疗效果时,可以引入虚拟变量表示不同药物的使用与否,进而进行方差分析。
如何创建虚拟变量创建虚拟变量的方法通常有两种:1. 单变量编码单变量编码是最常见的创建虚拟变量的方法。
对于具有k个水平的分类变量,单变量编码将该变量转换为k-1个虚拟变量。
其中,k-1个虚拟变量分别表示k个水平的存在与否。
例如,在研究不同颜色对产品销售量的影响时,可以使用单变量编码将颜色变量转换为两个虚拟变量,分别表示是否为蓝色和是否为红色。
2. 二进制编码二进制编码是一种使用更少虚拟变量的方法。
对于具有k个水平的分类变量,二进制编码将该变量转换为log2(k)个虚拟变量。
其中,每个虚拟变量都表示一个水平的存在与否。
例如,在研究不同国家对某项政策的支持时,可以使用二进制编码将国家变量转换为几个虚拟变量,每个虚拟变量表示一个国家的存在与否。
虚拟变量的注意事项在使用虚拟变量时需要注意以下几点:1.避免虚拟变量陷阱:虚拟变量陷阱是指多个虚拟变量之间存在完全共线性的情况,这会导致回归模型的多重共线性。
计量经济学第八章关于虚拟变量的回归.

类的截距。
2
2:级差截距系数
教龄X
1
0
薪金与性别:估计结果
1,若是男性 Di 0,若是女性
ˆ 17.969 1.371X 3.334D Y i i i se : (0.192) (0.036) (0.155) t : (93.61) (38.45) (21.455) r 2 0.993
一、虚拟变量的性质
例:教授薪金与性别、教龄的关系
男教授平均薪金和女 教授平均薪金水平相 差2,但平均年薪对 教龄的变化率是一样 的
Yi=1+2Di+Xi+I (1) 1,若是男性 D 其中:Yi=教授的薪金, Xi=教龄, Di=性别 0,若是女性 i 女教授平均薪金:E(Yi | X i , Di 0) 1 X i 被赋予0值的 男教授平均薪金:E(Yi | X i , Di 1) (1 2) X i 类别是基底(基 准),1是基底 男教授
比较英国在第二次大战后重建时期和重建后时期的总 储蓄-收入关系是否发生变化。数据如表。 Yt 1 2 Dt 1 X t 2 ( Dt X t ) t
D=1,重建时期
级差截距:区分两 个时期的截距 级差斜率系数:区分 两个时期的斜率 =0,重建后时期
D=1 D=0
E(Yt | Dt 0, X t ) 1 1 X t E(Yt | Dt 1, X t ) (1 2 ) ( 1 2 ) X t
男教授平均薪金水平比 女教授显著高$3.334K (男:21.3,女:17.969)
1,若是女性 Di 0,若是男性
ˆ 21.303 1.371X 3.334D Y i i i se : (0.182) (0.036) (0.155) t : (117.2) (38.45) (21.455)
第八章 虚拟变量实验报告
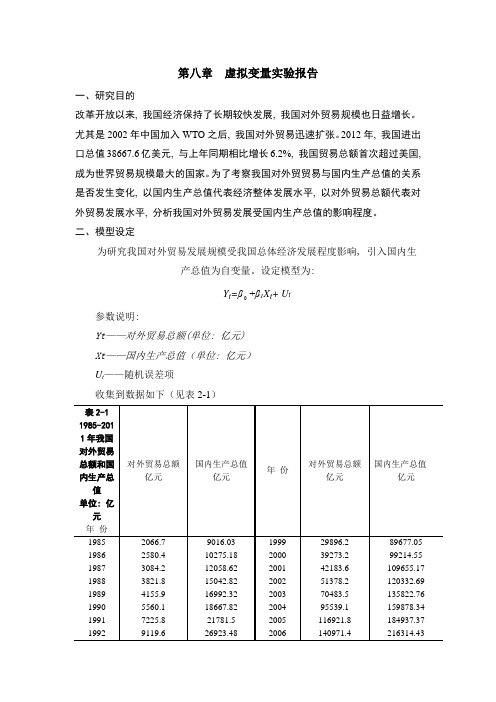
第八章虚拟变量实验报告一、研究目的改革开放以来, 我国经济保持了长期较快发展, 我国对外贸易规模也日益增长。
尤其是2002年中国加入WTO之后, 我国对外贸易迅速扩张。
2012年, 我国进出口总值38667.6亿美元, 与上年同期相比增长6.2%, 我国贸易总额首次超过美国, 成为世界贸易规模最大的国家。
为了考察我国对外贸贸易与国内生产总值的关系是否发生变化, 以国内生产总值代表经济整体发展水平, 以对外贸易总额代表对外贸易发展水平, 分析我国对外贸易发展受国内生产总值的影响程度。
二、模型设定为研究我国对外贸易发展规模受我国总体经济发展程度影响, 引入国内生产总值为自变量。
设定模型为:+β1X t+ U tY t=β参数说明:Yt——对外贸易总额(单位: 亿元)Xt——国内生产总值(单位: 亿元)U t——随机误差项收集到数据如下(见表2-1)1993 11271 35333.92 2007 166740.2 265810.31 1994 20381.9 48197.86 2008 179921.5 314045.43 1995 23499.9 60793.73 2009 150648.1 340902.81 1996 24133.8 71176.59 2010 201722.1 401512.8 1997 26967.2 78973.03 2011 236402 472881.56 1998 26693.823 73617.66322注: 资料来源于《中国统计年鉴》1986-2012。
为了研究1985-2011年期间我国对外贸易总额随国内生产总值的变化规律是否有显著不同, 考证对外贸易与国内生产总值随时间变化情况, 如下图所示。
图2-1 对外贸易总额(Y)与国内生产总值(X)随时间变化趋势图从图2-1中, 可以看出对外贸易总额明显表现出了阶段特征: 在2002年、2007年和2009年有明显的转折点。
虚拟变量的回归分析

的截据为1.41,年龄每上升1岁,参照类妇 女的平均曾生子女数上升0.068个。 城市妇女比农村妇女的平均曾生子女数少 0.49个。 小学、初中、高中和大学文化程度妇女的 平均曾生子女数分别比文盲妇女少1.13、 1.31、1.58、1.57个(在年龄和居住地相同 时)。
表明所有参照类妇女年龄每上升1岁,其曾 生子女数的平均变化量为0.068个。
回归方程的解释
当文化程度为小学,居住地为农村时:
表明,对于相同年龄和居住地而言,小学 文化程度妇女比文盲妇女曾生子女数多出 b2个部分,即少生1.13个子女。
回归方程的解释
当教育程度为文盲、居住地为城市时,
表明,对于相同年龄和文化程度而言,城市妇女
回归方程的解释
文化程度在实际中是一个序次变量。可以
用
表示序次变量个相邻分类的
实际效应,如初中的边际效应为:
类似,可以计算下面的边际效应: 小学= -1.13 初中= -0.18
高中= -0.27 大学= 0.01
回归分析
利用同样的方法我们可以对例7.2进行回归 分析。
例7.2的数据中,还有一个自变量是定性变量 “收入”,以虚拟变量或哑元(dummy variable)的方式出现。
SPSS输出结果
SPSS输出结果
回归分析
回归方程为:
总统任期对工业指数变化的影响案例
现有道琼斯工业平均指数(DJIA)在8任总 统的每一个四年任期之内的变化,利用回 归分析来确定政党和总统任期对道琼斯工 业平均指数变化的影响。
所有的数据在数据文件:回归分析-总统对 指数的影响案例.SAV。
3-2虚拟变量的回归

大学及其以上: E(Yi | X i , D1 0, D2 1) ( 0 3 ) 1 X i假定3>2>0
保健
其几何意义:
支出
3 2
0
大学教育 高中教育 低于高中教育
收入
3.模型中包含二个定性变量
• 例如,在上述职工薪金模型中,再引入代表学历的虚拟变量D2。
1 本科及以上学历
D2
0
本科以下学历
• 男职工的平均薪金为: E(Yi | Xi , Di 1) (0 2 ) 1Xi
• 假定2>0,则两个函数有相同的斜率,但有不同的截距。意即, 男女职工平均薪金对教龄的变化率是一样的,但两者的平均薪金 水平相差2。
• 可以通过传统的回归检验,对2的统计显著性进行检验,以判断 企业男女职工的平均薪金水平是否有显著差异。
• 斜率的变化可通过以乘法的方式引入虚拟变量来测度。
例:根据消费理论,消费水平(C)主要取决于收入水平(Y),但在一个较长的时
期,人们的边际消费倾向会发生变化,尤其是在自然灾害、战争等反常年份, 边际消费倾向往往出现变化。
这种边际消费倾向的变化可通过在收入的系数中引入虚拟变量来考察。
1 正常年份
设
重合回归
平行回归
同截距回归
不同的回归
思考:当我们运用样本数据对金融危机前后两个消费模型进行回归后,如何界定所得结果在
统计意义上属于哪一种类型呢? • 这时可采用以乘法形式引入虚拟变量。例如,对于金融危机前后消费—收入模型,可设
定为:
• 假设: E(t)= 0,上述模型所表示的函数可化为:
2.交互效应分析
Yi 0 1 X i 2 D1 3 D2 i
在 E(i)=0 的初始假定下,高中以下、高中、大学及其以上教育水平
虚拟变量回归

这里的 D1i 和 D2i代表的是两个不同的定性变量,各分为两种类
型基础类型: E(Yi Xi , D1 0, D2 0) 0 1Xi
对比类型: E(Yi Xi , D1 1, D2 0) (0 1) 1Xi
E(Yi Xi , D1 0, D2 1) (0 2 ) 1Xi
E(Yi Xi , D1 1, D2 1) (0 1 2 ) 1 Xi
差异
●一个定性变量有多种类型时,虚拟变量可同时取值为0,
但不能同时取值为1,因同一定性变量的各类型间“非此
即彼”
17
4、解释变量包含一个定量变量和两个定性变量
例如模型: Yi 0 1D1i 2D2i X i ui
Y为文化支出,X为收入
D1i 0 农村居民 D1i 1 城镇居民
D2i 0 高中以下文化程度 D2i 1 高中及以上文化程度
如 伊拉克战争、“911事件”、四川汶川大地震
● 时间序列分析中——作为季节(月份)的代表
● 分段回归——研究斜率、截距的变动
● 比较两个回归模型的差异
● 虚拟被解释变量模型:被解释变量本身是定性变量
● 面板数据回归中的应用
6
二、虚拟变量模型
虚拟变量模型:包含有虚拟变量的模型称虚拟变量模型 三种类型: 1. 解释变量中只包含虚拟变量
D1 1, D2 0, D3 0时
Yi 1 X i ui
D2 1, D1 0, D3 0时
Yi 2 X i ui
D3 1, D1 0, D2 0时
Yi 3 X i ui
11
第二节 虚拟解释变量回归
定性变量作为解释变量,既可以影响模型的截距,也可以 影响模型的斜率,还可以同时影响截距和斜率
计量经济学专题1虚拟变量的回归

其中:
为某人的工资水平, 为工作年限,为一个普通变量。
为虚拟变量:
则:
中学及以下教育水平的员工平均工资水平:
大学教育水平的员工平均工资水平:
研究生及以上教育水平的员工平均工资水平:
模型含义:通过 的显著性检验判断教育水平是否对工资差异有显著的影响。
散点图略。
(3)对一个普通变量与两个两分虚拟变量的回归
则 为截距差异, 为斜率差异。
Estimation Equation:
S = C(1) + C(2)*D1 + C(3)*Y + C(4)*(D1*Y)
结果:
为截距差异, 为斜率差异,在统计上都通过了1%的显著性检验,表明两个时期的回归结构是相异的。
相对于chow检验的优越性:(1)可以清楚的知道两个时期的差异究竟是截距差异、斜率差异,还是截距差异与斜率差异共存。(2)由于合并而增加了自由度,提高了参数估计的精度。
例:种族及性别差异对薪金的影响。
假定薪金除了受工作年限、性别的影响之外,还受种族的影响。
为某人的工资水平, 为工作年限,为一个普通变量。
为虚拟变量:
则:
白人男性的工资水平:
白人女性的工资水平:
其他人种男性的平均工资:
其他人种女性的平均工资:
3、虚拟变量的应用:检验回归模型的稳定性
数字实例:英国1946-1963年的个人储蓄与个人收入的数据。
注意:如果虚拟变量回归涉及到异方差问题,可以用前面提过的方法进行异方差调整。
虚拟变量的应用实例:
论文:外商直接投资、产业结构与中国的出口竞争力
其中: 为某人的工资水平, 为虚拟变量:
如果影响工Leabharlann 的其他因素保持不变,由上述模型很容易得到:
含虚拟变量问题的回归分析

实验五实验项目:运用EVIEWS 软件进行含虚拟变量问题的回归分析实验目的:掌握运用EVIEWS 软件对解释变量中含有虚拟变量的情况进行回归分析的基本操作方法和步骤,并能够对软件运行结果进行解释。
实验内容提要:1.根据具体的经济现象,选择合适的虚拟变量。
2.建立关于虚拟变量的回归模型,并进行估计和检验。
3.对软件运行的结果给出合理的经济学解释。
实验内容及步骤: 1.模型假设将某大学学生的绩分点设为因变量Y ,统计成绩设为自变量1X ,是否使用计算机设为自变量2X ,建立虚拟变量回归模型,得: 01122++i i i i Y X X βββε=+其中,1,20={i X 有使用计算机,没有使用计算机其原始数据如下表1:统计成绩绩分点是否使用计算机100 4 是 95 3.4 是 56 1.2 是 是否75 2.1 是86 3.1 是63 1.7 是96 4 是80 3.4 否90 2.9 否84 3.1 否62 1.9 否68 2.2 否92 3.7 是66 1.9 是60 1.7 否92 4 否63 1.1 是否2.模型估计将数据录入EVIEWS软件中,采用这些数据对模型进行OLS回归,结果如表2:表2Dependent Variable: YMethod: Least SquaresDate: 06/02/12 Time: 20:09Sample: 1 20Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. X1 0.063385 0.004848 13.07383 0.0000 X2 -0.372084 0.137953 -2.697176 0.0153 C-2.0356990.376632-5.4050100.0000R-squared 0.909538 Mean dependent var 2.710000 Adjusted R-squared 0.898896 S.D. dependent var 0.944736 S.E. of regression 0.300396 Akaike info criterion 0.570054 Sum squared resid 1.534047 Schwarz criterion 0.719414 Log likelihood -2.700541 Hannan-Quinn criter. 0.599211 F-statistic 85.46258 Durbin-Watson stat 2.403154 Prob(F-statistic)0.00000012ˆ 2.0360.0630.372i i iY X X =-+- (0.377)(0.005) (0.138) t=(-5.405)(13.074) (-2.697)20.909r = 85.463F = 由模型的2r 可知,该模型的回归拟合效果比较好。
虚拟变量(哑变量)回归

汇报时间
汇报人姓名
虚拟变量回归系数的意义
1. 只考虑年级对月支出的影响 等价于 单因素方差分析(1-way ANOVA)
2. 同时考虑年级、性别对月支出的影响 等价于 双因素方差分析(2-way ANOVA)
只考虑主效应的双因素方差分析
3. 同时考虑年级、性别、家庭月收入的影响 等价于 协方差分析(ANCOVA)
——虚拟变量的应用
单击添加副标题
多元线性回归
虚拟变量的建立
虚拟变量回归系数的意义
虚拟变量回归分析的检验
SPSS实例操作
Contents
1
第一部分
2
第二部分
一、虚拟变量的建立
虚拟变量(Dummy Variable):取值为0和1的变量,当案例属于一个虚拟 变量所代表的类别时,这个虚拟变量就赋值为1,否则变赋值为0
Di = 1 ,是女性 = 0 ,不是女性
例1:
例2:大学生年级变量具有四个类别,如何构造?
其中, D1=1,是大一,否则为0; D2=1,是大二,否则为0; D3=1,是大三,否则为0; D4=1,是大三,否则为0。
“虚拟2+D3+D4=1,说明D1,D2,D3,D4存在线性相关,造成多重共线性
解决办法:
原则:当一个分类量具有k个类别时,则仅引入k-1个虚拟变量。 当所有k-1个自变量都取0的时候,那这个案例就属于第k类,我们称这类为参照类,参照类不仅解决了共线性的问题,而且在分析回归结果时也有非常重要的意义
参照类:大一男生(所有虚拟变量均取0)
变式1:大二男生(DG2=1,虚拟变量均取0)
变式2:大一女生(DS=1,虚拟变量均取0)
参照类中,b0为直线的截距,b1为直线斜率,即 INCOME 的回归系数 由式(1)到式(2),截距项增加了b2,因此b2就是大二男生比大一男生月支出高的部分;由式(1)到式(3),截距项增加了b4,因此b4就是大一女生比大一男生月支出高的部分。 差别截距:所有表示各类别虚拟变量的回归系数(bj)表示的是该类与参照类的均值之差。(对于序次变量还可计算相邻分类的边际效应,任意两类的边际效应)
虚拟变量回归课件

例1
(1)
D
=
1 0
男 女
( 2)D=1 0
改 革 开 放 以 后 改 革 开 放 以 前
(3)D1 =0 1
天气阴 其 他(4)D2
=1 0
天气雨 其他
问题:
为何只选0、1,选2、3、4行吗?为什么?
虚拟变量回归
14
属性的状态(水平)数与虚拟变量 数量的关系
定性因素的属性既可能为两种状态,也可能为多种 状态。例如,性别(男、女两种)、季节(4种状 态),地理位置(东、中、西部),行业归属,所 有制,收入的分组等。
虚拟变量回归
11
二、虚拟变量设置规则
虚拟变量的设置规则涉及三个方面: 1.“0”和“1”选取原则 2.属性(状态、水平)因素与设置虚拟变量
数量的关系 3.虚拟变量在回归分析中的角色以及作用等
方面的问题
虚拟变量回归
12
“0”和“1”选取原则
虚拟变量取“1”或“0”的原则,应从分析问题的 目的出发予以界定。
虚拟变量回归
16
一个例子(虚拟变量陷阱)
研究居民住房消费支出 Yi 和居民可支配收入 Xi 之间的
数量关系。回归模型的设定为:Y i= 0 + 1 X i+ u i( 1 )
现在要考虑城镇居民和农村居民之间的差异,如何办?
为了对 “城镇居民”、“农村居民”进行区分,分析
各自在住房消费支出 Yi上的差异,设 D1i = 1 为城镇;
非数值性的因素。 基本思想: 直接在回归模型中加入定性因素存在诸多的困难 (那些困难?),是否可将这些定性因素进行量 化,以达到定性因素能与定量因素有着相同作用 之目的。
虚拟变量回归
10
计量经济学-虚拟变量回归

虚拟变量模型有三种类型
1. 解释变量中只包含虚拟变量 2. 解释变量中既包含定量变量也包含虚拟
变量。 3. 被解释变量本身为虚拟变量。
20
第二节 虚拟解释变量的回归
本节基本内容:
●加法类型 ●乘法类型 ●虚拟解释变量综合应用
21
在计量经济学中,通常引入虚拟变量的方式分为 加法方式和乘法方式两种:即
分为四种情形讨论: (1)解释变量只有一个定性变量而无定量变量,而且定性
变量为两种相互排斥的属性; (2)解释变量分别为一个定性变量(两种属性)和一个定
量解释变量;
23
(3)解释变量分别为一个定性变量(两种以上属 性)和一个定量解释变量;
(4)解释变量分别为两个定性变量(各自分别是 两种属性)和一个定量解释变量;
计量经济学
第八章 虚拟变量回归
1
引子:男女大学生消费真有差异吗?
由共青团中央,全国学联共同发布的 《 2004中国大学生消费与生活型态研究报 告》显示,当代大学生的消费行为呈现多元 化的结构。除日常生活开支外还有人际交往 消费、手机类消费、衣着类消费、化妆品类 消费、电脑类消费、旅游类消费等等。
2
4
第一节 虚拟变量
本节基本内容:
●基本概念 ●虚拟变量设置规则
5
一、基本概念
定量因素:可直接测度的数值型因素。 如收入、产出、价格、人数等。
定性因素:属性因素,不能直接测度、 表征某种属性或状态存在与否的非数值型 因素。如性别、婚否、政府经济政策不变 与改革、城市居民或非城市居民等。
6
在以前的学习中,解释变量主要是定 量变量,但现实经济生活中影响被解释 变量的还包括定性变量,比如:研究某 个企业的销售水平,所有制(私营、非 私营)、地理位置(东、中、西部)等 是必须考虑的因素。
虚拟变量回归实训报告心得

一、实训背景随着我国经济的快速发展,社会科学研究在各个领域都得到了广泛应用。
在社会科学研究中,计量经济学作为一种重要的研究方法,被广泛应用于实证分析中。
虚拟变量回归作为一种常见的计量经济学方法,在处理分类变量对因变量的影响方面具有独特的优势。
为了提高自身对虚拟变量回归方法的理解和应用能力,我参加了虚拟变量回归实训,以下是我对实训的心得体会。
二、实训内容1. 虚拟变量回归的基本概念虚拟变量回归,又称哑元变量回归,是一种将分类变量转换为数值变量的方法。
在虚拟变量回归中,每个类别都被分配一个虚拟变量,通常采用二元变量(0或1)表示。
其中一个类别作为参考类别,其虚拟变量为0,而其他类别的虚拟变量为1。
虚拟变量回归可以控制分类变量对因变量的影响,同时考虑其他连续变量的影响。
2. 虚拟变量回归的应用(1)处理分类变量对因变量的影响在社会科学研究中,很多研究涉及到分类变量对因变量的影响。
例如,研究性别对收入的影响、地区对消费水平的影响等。
虚拟变量回归可以将分类变量转换为数值变量,从而在回归模型中处理这些影响。
(2)分析两个或多个组之间的差异虚拟变量回归可以分析两个或多个组之间的差异。
例如,分析性别对某种健康指标的影响、地区对某种商品销售额的影响等。
通过虚拟变量回归,可以探究不同组别在因变量上的差异。
3. 虚拟变量回归的注意事项(1)选择合适的参考类别在虚拟变量回归中,选择合适的参考类别非常重要。
通常,选择具有最大样本量的类别作为参考类别。
如果参考类别不合适,可能会影响回归结果的准确性。
(2)避免多重共线性虚拟变量回归中,多个虚拟变量可能会存在多重共线性问题。
在模型中,应尽量避免这种情况,以免影响回归结果的准确性。
(3)处理异常值在虚拟变量回归中,异常值可能会对回归结果产生较大影响。
在分析数据时,应关注异常值,并采取相应的处理措施。
三、实训心得1. 提高了理论水平通过虚拟变量回归实训,我对虚拟变量回归的基本概念、应用和注意事项有了更加深入的理解。
虚拟解释变量回归
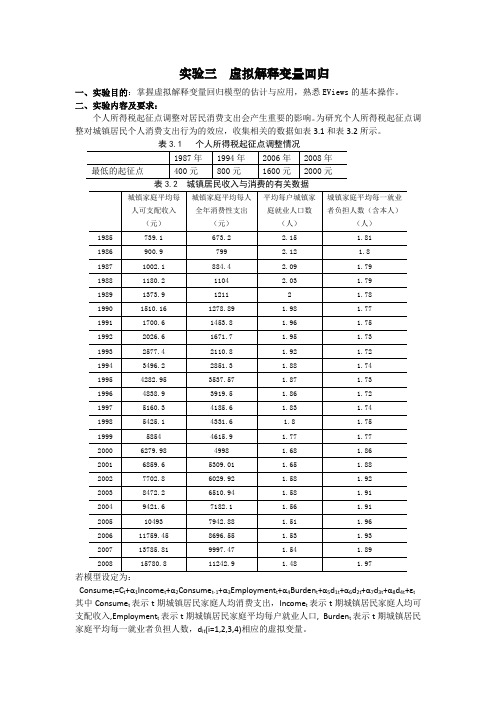
实验三虚拟解释变量回归一、实验目的:掌握虚拟解释变量回归模型的估计与应用,熟悉EViews的基本操作。
二、实验内容及要求:个人所得税起征点调整对居民消费支出会产生重要的影响。
为研究个人所得税起征点调整对城镇居民个人消费支出行为的效应,收集相关的数据如表3.1和表3.2所示。
Consume t=C t+α1Income t+α2Consume t-1+α3Employment t+α4Burden t+α5d1t+α6d2t+α7d3t+α8d4t+εt 其中Consume t表示t期城镇居民家庭人均消费支出,Income t表示t期城镇居民家庭人均可支配收入,Employment t表示t期城镇居民家庭平均每户就业人口, Burden t表示t期城镇居民家庭平均每一就业者负担人数,d it(i=1,2,3,4)相应的虚拟变量。
1)构造用于描述个人所得税调整的虚拟变量,并简要说明其理由;2)用散点图描述两两变量之间的关系,并给出你对模型设定的结论;3)依据测算,选择你认为更能描述客观实际的模型,并简要说明其理由;4)根据分析结果,你对提高个人所得税起征点影响居民消费的有效性能得出什么结论?解答如下:1,根据题意要求,需要构造4个虚拟变量:D1、D2、D3、D4。
D1=1,t为1987年及以后D2=1,t为1994年及以后0,t为1987年以前0,t为1994年以前D3= 1,t为2006年及以后D4=1,t为2008年及以后0,t为2006年以前0,t为2008年以前其中(D1=0 、D2=0、D3=0、D4=0)表示:1987年与之前的情况;(D1=1 、D2=0、D3=0、D4=0)表示:1988年到1994年的情况;(D1=1 、D2=1、D3=0、D4=0)表示:1995年到2005年的情况;(D1=1 、D2=1、D3=1、D4=0)表示:2006年到2007年的情况;(D1=1 、D2=1、D3=1、D4=1)表示:2008年的情况。
计量经济学作用-虚拟变量回归

计量经济学作用-虚拟变量回归虚拟变量回归实验目的:分析1965~1970年美国制造业利润和销售额,季度的关系。
实验要求:假定利润不仅与销售额有关,而且和季度因素有关(1)如果认为季度影响使利润平均值发生变异,应如何引入虚拟变量?(2)如果认为季度影响使利润对销售额的变化率发生变异,应如何引入虚拟变量?(3)如果认为上诉两种情况都存在,又当如何引入虚拟变量?(4)对上述三种情况分别估计利润模型,进行对比分析。
实验原理:最小二乘法原理实验步骤:由于有四个季度,因此引入三个季度虚拟变量:其它一季度=012D 其它二季度=013D 其它三季度?=014D 一、如果认为季度影响使利润平均值发生变异,应以加法类型引入三个虚拟变量,设其模型为:u X D D D Y tt t +++++=βαααα4433221 对模型进行回归,得到以下回归结果:Dependent Variable: YMethod: Least SquaresDate: 11/26/10 Time: 15:02Sample: 1965Q1 1970Q4Included observations: 24 Variable Coefficient Std. Error t-Statistic Prob. C 6910.449 1922.350 3.594792 0.0019X 0.038008 0.011670 3.256914 0.0041D2 -187.7317 660.1218 -0.284390 0.7792D3 1169.320 637.0766 1.835446 0.0821D4 -417.1182 640.8333 -0.650900 0.5229 R-squared 0.517642 Mean dependent var 12838.54Adjusted R-squared 0.416093 S.D. dependent var 1433.284 S.E. of regression 1095.227 Akaike info criterion 17.01836Sum squared resid 22790932 Schwarz criterion 17.26379Log likelihood -199.2204 F-statistic 5.097454Durbin-Watson stat 0.396350 Prob(F-statistic) 0.005810 Y t ^=6910.449-187.7317D 2+1169.320D 3-417.1182D 4+0.038008X tSe=(1922.350)(660.1218)(637.0766)(640.8333)(0.011670)t=(3.594792)(-0.284390)(1.835446)(-0.650900)(3.256914) R 2=0.517642 R -2=0.416093 F=5.097454 DW=0.396350二、如果认为季度影响使利润对销售额的变化率发生变化,应以乘法类型引入三个虚拟变量,设其模型为:Y t =u D X D X D X X t t t t t +++++43322110αααββ 对上述模型进行回归,得到以下结果:Dependent Variable: YMethod: Least SquaresDate: 11/26/10 Time: 17:53Sample: 1965Q1 1970Q4Included observations: 24Variable Coefficient Std. Error t-StatisticProb. C 7014.757 1782.932 3.9343940.0009 X 0.037068 0.011322 3.2738960.0040 X*D2 -0.000933 0.004302 -0.2167760.8307 X*D3 0.007910 0.004018 1.9685410.0638 X*D4 -0.002385 0.004074 -0.5852900.5652 R-squared 0.519733 Mean dependent var12838.54 Adjusted R-squared 0.418624 S.D. dependent var 1433.284 S.E. of regression 1092.851 Akaike info criterion17.01402 Sum squared resid 22692129 Schwarz criterion17.25945 Log likelihood -199.1682 F-statistic5.140331 Durbin-Watson stat 0.429628 Prob(F-statistic)0.005594=Y t ^7014.757+0.037068X t -0.000933D X t 2+0.007910D X t 3-0.002385D X t 4 se=(1782.932)(0.011322)(0.004302)(0.004018)(0.004074)t=(3.934394)(3.273896)(-0.216776)(1.968541)(-0.585290)R 2=0.519733 R -2=0.418624 F=5.140331 DW=0.429628三、若上述两种情况都存在,应以加法和乘法相结合的方式引入三个虚拟变量,设模型为:u D X D X D X X D D D Y t t t t t t ++++++++=44332214433221ββββαααα对上述回归模型进行回归得到以下回归结果:Dependent Variable: YMethod: Least SquaresDate: 11/26/10 Time: 17:54Sample: 1965Q1 1970Q4Included observations: 24 Variable Coefficient Std. Error t-Statistic Prob. C 10457.39 4075.199 2.566105 0.0207X 0.015868 0.025265 0.628075 0.5388D2 -4752.257 5441.682 -0.873307 0.3954D3 -3764.208 5484.872 -0.686289 0.5024D4 -4635.464 5570.057 -0.832211 0.4175X*D2 0.029207 0.035426 0.824467 0.4218X*D3 0.031169 0.034647 0.899626 0.3817X*D4 0.026577 0.035475 0.749176 0.4646 R-squared 0.546701 Mean dependent var 12838.54Adjusted R-squared 0.348383 S.D. dependent var 1433.284 S.E. of regression 1156.987 Akaike info criterion 17.20623Sum squared resid 21417911 Schwarz criterion 17.59891Log likelihood -198.4747 F-statistic 2.756686Durbin-Watson stat 0.464982 Prob(F-statistic) 0.044081 Y t ^=10457.39-4752.257D 2-3764.208D 3-4635.464D 4+0.015868X t Se=(4075.199)(5441.682)(5484.872)(5570.057)(0.025265)t=(2.566105)(-0.873307)(-0.686289)(-0.832211)(0.628075)+0.029207D X t 2+0.031169D X t 3+0.026577D X t 4se=(0.035426)(0.034647)(0.035475) t=(0.824467)(0.899626)(0.749176) R2=0.546701 R 2=0.348383F=2.756686 DW=0.464982 四、通过对三个模型进行对比分析可看出,第三个模型的参数估计值均不显著,模型一和二的销售额的参数估计显著,其余参数估计也不显著。
虚拟变量回归模型

实验报告课程名称:计量经济学实验项目名称:单方程线性回归模型的扩展——虚拟变量回归模型院(系):专业班级:姓名:学号:实验地点:实验日期:年月日实验目的:掌握虚拟变量回归模型的建立、参数估计和统计检验。
实验内容:1)生成趋势变量2)生成季节虚拟变量3)生成分段虚拟变量4)建立虚拟变量回归模型5)虚拟变量回归模型的参数估计和统计检验实验方法、步骤和结果:⑴生成趋势变量打开EViews,新建工作文件并输入数据重新命名ser01为gdp打开gdap,选择view-Graph-Line,即可显示趋势图⑵点击quick-generate series,输入公式如此即可生成季节性虚拟变量⑶点击quick-generate series,输入公式d5=0,并将sample中2002Q4改为1997Q4再次点击quick-generate series,输入公式d5=1,并将sample中1990Q1改为1998Q1如此即可生成分段虚拟变量D5⑷引入季节性虚拟变量应该用加法,又从趋势图中可以看出,两端曲线的截距和斜率均有所变化,所以应该用乘法加法方式引入分段虚拟变量,虚拟变量回归模型为Gdp=ß1+ ß2*D2+ ß3*D3+ ß4*D4+ ß5*D5+ ß5D5*T+ų⑸选择Quick-estimate equation,输入公式点击确定,即可出现OLS结果从上述结果中可以看出R^2=0.993780很大,P值极小,模型具有总体显著性成绩评定__________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Hale Waihona Puke 2、练习23、P227 案例分析
实验一:虚拟变量回归
实验目的: 掌握虚拟变量的设置方法 实验内容: 一、构造虚拟变量 二、估计虚拟变量模型
1
构造虚拟变量; 方式1:使用DATA命令直接输入; 方式2:使用SMPL和GENR命令直接定义
估计虚拟变量模型: 例如: LS Y C X D XD
1、练习
试根据表1的1998年我国城镇居民人均收入与彩电每百户 拥有量的统计资料建立我国城镇居民彩电需求函数。 表1 我国城镇居民家庭抽样调查资料
中等偏上户
高收入户 最高收入户
109.64
115.13 122.54
6370.59
7877.69 10962.16
1
1 1
6370.59
7877.69 10962.16
3
由此可见我国城镇居民家庭现阶段彩电消费需求的特点: 对于人均年收入在3300元以下的低收入家庭,需求量随着 收入水平的提高而快速上升,人均年收入每增加1000元, 百户拥有量将平均增加12台;对于人均年收入在4100元 以上的中高收入家庭,虽然需求量随着收入水平的提高也 在增加,但增速趋缓,人均年收入每增加1000元,百户拥 有量只增加3台。事实上,现阶段我国城镇居民中国收入 家庭的彩电普及率已达到百分之百,所以对彩电的消费需 求处于更新换代阶段。
收入等级 困难户 最低收入户 低收入户 中等偏下户 中等收入户
彩电拥有量Y (台/百户)
83.64 87.01 96.75 100.9 105.89
人均收入X (元/年)
2198.88 2476.75 3303.17 4107.26 5118.99
D1
0 0 0 1 1
XD1
0 0 0 4107.26 5118.99
