第八章 虚拟变量回归
第八章 包含虚拟变量的回归模型

第八章 包含虚拟变量的回归模型一、虚拟变量的基本含义通常在回归分析中,因变量不仅受一些定量变量的影响,而且还受一些定性变量的影响,比如性别、种族、婚姻状况等等。
为了在模型中反映这些因素的影响,需要把定性因素进行“量化”。
通常是引进人工变量完成。
通过定性因素的属性类别,构造取值为0或者1的变量,如、 1代表男性, 0代表女性; 1代表某人是大学毕业, 0代表某人不是大学毕业,这类取值为0,1的变量称为虚拟变量(dummy variable )。
虚拟变量与定量变量一样可用于回归分析。
事实上,一个回归模型的解释变量可以仅仅是虚拟变量。
解释变量仅是虚拟变量的模型称为方差分析模型( analysis-of-variance models ) (ANOVA)。
例1:1i i Y D i βα=++ε,其中Y 表示职工工资,。
10i D ⎧=⎨⎩,本科学历,非本科学历这个模型与我们前面讨论过的双变量模型类似,但这里的解释变量是虚拟变量。
1(0)i E Y D β==,1(1)i E Y D βα==+显然,1β表示非大学毕业生的平均初职年薪,1βα+表示具有大学学历职工的平均工资,α代表二者之差。
回归模型中可以有同时有虚拟变量以及定量变量。
例2:考虑是否上过大学和工龄作为职工工资的模型:12i i i Y X D i ββαε=+++Y ,表示职工工资,X表示工龄,D同上。
含虚拟变量的模型只要扰动项符合古典假定,仍用OLS方法估计模型。
注意:虚拟变量系数显著性检验的意义::0H 0α=;:1H 0α≠。
同学们思考:这个检验在上面两个例子中分别具有何实际意义?二、虚拟变量的引入模型的方式 1、加法方式上面考察的例子都是加法方式。
注意虚拟变量模型的几何意义:以上述例2考察。
例3:如果上述职工工资方程(例2)中,学历考虑三个层次:高中以下、高中、大学及以上。
该如何建模?引进两个虚拟变量:,1 1 0 D ⎧=⎨⎩高中其他2 1 0 D ⎧=⎨⎩大学及以上其他121222Y X D D ββαα=++++ε请同学们分析模型的含义。
第八章 带虚拟变量的回归预测技术

以Y为储蓄,X为收入,可令:
1990年前:Yi=1+2Xi+1i i=1,2…,n1
1990年后:Yi=1+2Xi+2i
i=1,2…,n2
则有可能出现下述四种情况中的一种:
• (1) 1=1 ,且2=2 ,即两个回归相同,称为重 合回归(Coincident Regressions);
• 分离异常因素的影响, 例如分析我国GDP的时间序列,必须 考虑“文革”因素对国民经济的破坏性影响, 剔除不可比 的“文革”因素。 • 检验不同属性类型对因变量的作用, 例如工资模型中的文 化程度、季节对销售额的影响。 • 提高模型的精度, 相当于将不同属性的样本合并, 扩大了样
本容量(增加了误差自由度, 从而降低了误差方差)。
• 前面没有考虑协变量——税后收入,重新 建立模型: • Yi = 1+2Di+3Xi+ui • 利用前例的数据, 分析得到如下结果:
ˆ 1506.244 228.9868D 0.0589 X Y i i i
se (188.0096) (107.0582) (0.0061) t (8.0115) ( 2.1388) (9.6417) p (.000) (.0611) (.000)
• 若在某研究中,需要考虑k个非定 量因素,每个因素有mi种互斥属性, 则在模型中应引入虚拟变量个数为:
(m
i 1
k
i
1)
• 虚拟变量回归模型及参数估计
例1男女个体消费者每年的食品支出(美元)
年龄 女性食品支出 女性税后收入 男性食品出 男性税后收入
<25 25-34
35-44 45-54 55-64 >65
第八章-虚拟变量回归

1 高中 D2 0 其它
1 博士 D5 0 其它
1 大 学 D3 0 其 它
1 小 学 D6 0 其 它
则总体回归模型:
w 0 1 X 2 D1 3 D2 4 D3 5 D4 6 D5 7 D6+u
17
二、用虚拟变量测量斜率变动
基本思想
引入虚拟变量测量斜率变动,是在所设立的模型中,将虚 拟解释变量与其它解释变量的乘积,作为新的解释变量出 现在模型中,以达到其调整设定模型斜率系数的目的。
可能的情形:
(1)截距不变;
(2)截距和斜率均发生变化;
分析手段:仍然是条件期望。
18
(1)截距不变
模型形式:
意义:若α1显著,表明城市居民的平均人均可支配收入比农村 高α1元。但这种差异可能是由其它因素引起的,并不一定是由 户籍差异引起。
12
(2) 一个两属性定性解释变量和一个定量 解释变量
模型形式 Yi = f(Di,X i )+ μi 例如:Yi = 0 1 Di + X i + μi 1 城市 其中: Y-人均可支配收入;X-工作时间; Di 0 农村
会受到一些定性因素的影响,如性别、国籍、民族、自 然灾害和政治体制等。
问题:我们如何把这些定性想:将这些定性因素进行量化
由于定性变量通常表示某种属性是否存在,如是否男性、 是否经济特区、是否有色人和等。因此若该属性存在, 我们就将变量赋值为1,否则赋值为0,从而将定性因素 定量化。 计量经济学中,将取值为0和1的人工变量称为虚拟变量 (DUMMY)或哑元变量。通常用字母D或DUM表示。
7
一个例子(虚拟变量陷阱)
研究工资收入与学历之间的关系:
计量经济学第八章 虚拟变量回归

第八章
虚拟变量回归
1
第八章 虚拟变量回归
本章主要讨论:
●虚拟变量
●虚拟解释变量的回归
2
本章的教学目标
(1)深刻理解定性因素在计量经济分析中的 背景和含义; (2)明确虚拟变量在建立和估计计量经济模 型中的意义和作用; (3)熟练掌握引入和应用虚拟变量的基本思 想和方法; (4)能够运用虚拟变量模型作相应的经济实 证分析方面的应用; (5)掌握Eviews软件中相关内容的操作方法。
这表明三个时期居民储蓄增加额的回归方程在统计 意义上确实是不相同的。1996年以前收入每增加1 亿元,居民储蓄存款的平均增加0.1445亿元;在 2000年以后,则为0.4133亿元,已发生了很大变化。
20
上述模型与城乡居民储蓄存款与国民总收入之间 的散布图是吻合的,与当时中国的实际经济运行 状况也是相符的。 需要指出的是,在上述建模过程中,主要是从教 学的目的出发运用虚拟变量法则,没有考虑通货 膨胀因素。而在实证分析中,储蓄函数还应当考
单位:亿元
城乡居民 人民币储 蓄存款增 额 (YY) 2121.8 2517.8 3444.1 6315.3 8143.5 8858.5
年 份
城乡居民 国民总收 人民币储 蓄存款年 入 (GNI) 底余额 (Y) 3624.1 4038.2 4517.8 4860.3 5301.8 5957.4 210.6 281 399.5 532.7 675.4 892.5
(1,0) 天气阴 如:(D1 ,D2)= (0,1) 天气雨 (0,0) 其 他
29
虚拟变量数量的设置规则
1.若定性因素具有 m 个 (m 2) 相互排斥属性(或 几个水平),当回归模型有截距项时,只能引入
(完整版)第八章 虚拟变量回归 答案

第八章 虚拟变量回归一、判断题1。
虚拟变量只能作为解释变量.(F)2。
引入虚拟变量后,用普通最小二乘法得到的估计量仍是无偏的。
( T )3.引入虚拟变量的个数与模型有无截距项无关.(F )4。
虚拟变量用来表示某些具有若干属性的变量.(T)5。
引入虚拟变量的个数与样本容量大小有关。
(F )二、单项选择题1.设消费函数011t t t y a a D b x u =+++,其中虚拟变量10D ⎧=⎨⎩东中部西部,如果统计检验表明10a =成立,则东中部的消费函数与西部的消费函数是( D ).A. 相互平行的 B 。
相互垂直的 C. 相互交叉的 D 。
相互重叠的2.虚拟变量( A )A 。
主要来代表质的因素,但在有些情况下可以用来代表数量因素B 。
只能代表质的因素C 。
只能代表数量因素D.只能代表季节影响因素3。
分段线性回归模型的几何图形是( D )A 。
平行线 B. 垂直线 C 。
光滑曲线 D. 折线4.如果一个回归模型中(包含截距项),对一个具有m 个特征的质的因素要引入虚拟变量数目为( B ).A.m B 。
m-1 C 。
m —2 D.m+15.设某商品需求模型为01t t t y b b x u =++,其中Y 是商品的需求量,X 是商品的价格,为了考虑全年12个月份季节变动的影响,假设模型中引入了12个虚拟变量,则会产生的问题为( D )。
A .异方差性B .序列相关C .不完全的多重共线性D .完全的多重共线性6.设消费函数为i i i 33i 22i 11o i u bx D D D y +++++=αααα,其中y 为消费,x 为收入,虚拟变量⎩⎨⎧=⎩⎨⎧=⎩⎨⎧=其他季度第三季度,其他季度第二季度,其他季度第一季度 0 0 0 321D 1D 1D 1,该模型中包含了几个定性影响因素?( A )。
A 。
1B 。
2C 。
3D 。
47。
设消费函数为i i i o i u Dx b x b D y ++++=101αα,其中虚拟变量⎩⎨⎧=农村家庭城镇家庭 0 1D ,当统计检验表明下列哪项成立时,表示城镇家庭与农村家庭有一样的消费行为( A ).A 。
计量经济学第八章关于虚拟变量的回归.

类的截距。
2
2:级差截距系数
教龄X
1
0
薪金与性别:估计结果
1,若是男性 Di 0,若是女性
ˆ 17.969 1.371X 3.334D Y i i i se : (0.192) (0.036) (0.155) t : (93.61) (38.45) (21.455) r 2 0.993
一、虚拟变量的性质
例:教授薪金与性别、教龄的关系
男教授平均薪金和女 教授平均薪金水平相 差2,但平均年薪对 教龄的变化率是一样 的
Yi=1+2Di+Xi+I (1) 1,若是男性 D 其中:Yi=教授的薪金, Xi=教龄, Di=性别 0,若是女性 i 女教授平均薪金:E(Yi | X i , Di 0) 1 X i 被赋予0值的 男教授平均薪金:E(Yi | X i , Di 1) (1 2) X i 类别是基底(基 准),1是基底 男教授
比较英国在第二次大战后重建时期和重建后时期的总 储蓄-收入关系是否发生变化。数据如表。 Yt 1 2 Dt 1 X t 2 ( Dt X t ) t
D=1,重建时期
级差截距:区分两 个时期的截距 级差斜率系数:区分 两个时期的斜率 =0,重建后时期
D=1 D=0
E(Yt | Dt 0, X t ) 1 1 X t E(Yt | Dt 1, X t ) (1 2 ) ( 1 2 ) X t
男教授平均薪金水平比 女教授显著高$3.334K (男:21.3,女:17.969)
1,若是女性 Di 0,若是男性
ˆ 21.303 1.371X 3.334D Y i i i se : (0.182) (0.036) (0.155) t : (117.2) (38.45) (21.455)
9第八章 虚拟变量回归模型

Logit 模型的估计
区分两类数据:
(1)个体水平数据
购房概率 p 0 0 1 1
收入 X(千美元) 6 8 10 12
如果
pi
0,
Zi
ln
0 1
pi
1,
Zi
ln
1 0
可见,Z 表达式无意义,无法用OLS,需用ML(最大似然法)
冰箱销售量(千台) FRIG 1317 1615 1662 1295 1271 1555 1639 1238 1277 1258 1417 1185 1196 1410 1417 919 943 1175 1269
耐用品支出(10亿美元) DUR 252.6 272.4 270.9 273.9 268.9 262.9 270.9 263.4 260.6 231.9 242.7 248.6 258.7 248.4 255.5 240.4 247.7 249.1 251.8
4 回归分析操作命令: equation eq.ls Frig c Dur D1 D2 D3
提问 根据回归分析结果,发现存在什么问题?如何修改回归模型?
8.4 虚拟被解释变量的回归模型
【例】 研究是否购买住房与收入水平的关系。
设是否购房为被解释变量,用 Y 表示;收入为解释变量, 用 X 表示。
1 变量分析:
将DUR作为解释变量;FRIG作为被解释变量; 引入3个季度虚拟变量D1,D2,D3。 (虚拟变量数 = 属性数 – 1 )
2 季度虚拟变量的赋值规则:
D1=
1 (第1季度) 0 (其他季度)
D3=
1 (第3季度) 0 (其他季度)
D2=
第八章 虚拟变量实验报告
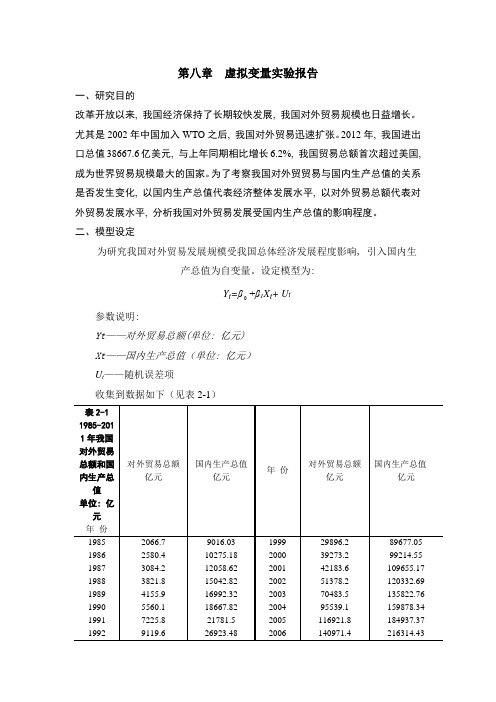
第八章虚拟变量实验报告一、研究目的改革开放以来, 我国经济保持了长期较快发展, 我国对外贸易规模也日益增长。
尤其是2002年中国加入WTO之后, 我国对外贸易迅速扩张。
2012年, 我国进出口总值38667.6亿美元, 与上年同期相比增长6.2%, 我国贸易总额首次超过美国, 成为世界贸易规模最大的国家。
为了考察我国对外贸贸易与国内生产总值的关系是否发生变化, 以国内生产总值代表经济整体发展水平, 以对外贸易总额代表对外贸易发展水平, 分析我国对外贸易发展受国内生产总值的影响程度。
二、模型设定为研究我国对外贸易发展规模受我国总体经济发展程度影响, 引入国内生产总值为自变量。
设定模型为:+β1X t+ U tY t=β参数说明:Yt——对外贸易总额(单位: 亿元)Xt——国内生产总值(单位: 亿元)U t——随机误差项收集到数据如下(见表2-1)1993 11271 35333.92 2007 166740.2 265810.31 1994 20381.9 48197.86 2008 179921.5 314045.43 1995 23499.9 60793.73 2009 150648.1 340902.81 1996 24133.8 71176.59 2010 201722.1 401512.8 1997 26967.2 78973.03 2011 236402 472881.56 1998 26693.823 73617.66322注: 资料来源于《中国统计年鉴》1986-2012。
为了研究1985-2011年期间我国对外贸易总额随国内生产总值的变化规律是否有显著不同, 考证对外贸易与国内生产总值随时间变化情况, 如下图所示。
图2-1 对外贸易总额(Y)与国内生产总值(X)随时间变化趋势图从图2-1中, 可以看出对外贸易总额明显表现出了阶段特征: 在2002年、2007年和2009年有明显的转折点。
庞浩计量经济学课件第八章虚拟变量回归资料重点

初中、小学及以下)作为解释变量引入下面的
模型中。
Yi 1 1 X i ui
0, 其他
0, 其他
0, 其他
D2i 1, 初中 D3i 1, 高中 D4i 1, 大专及以上
Yi 1 1 X i 2 D2i 3 D3i 4 D4i ui
7
三、虚拟变量的作用
虚拟变量可以作为下列因素的代表: 属性因素 非精确计量的数量因素 偶然因素或政策因素 时间序列分析中的季节(或月份)因素 用于分段回归
Di 1, 表示男性
3
二、虚拟变量的设置规则
1.虚拟变量个数的设置规则 若定性因素有m个相互排斥的类型(或属性、水
平),则: 在有截距项的模型中,只能引入m-1个虚拟变
量,否则会陷入“虚拟变量陷阱”(即:出 现完全的多重共线性); 在无截距项的模型中,可以引入m个虚拟变量, 不会导致完全的多重共线性。
第八章 虚拟变量回归
第一节 第二节 第三节 第四节
虚拟变量 虚拟解释变量的回归 虚拟被解释变量 案例分析
1
第一节 虚拟变量
一、虚拟变量的基本概念 二、虚拟变量的设置规则 三、虚拟变量的作用
2
一、虚拟变量的基本概念
定量因素:指那些可直接测度的数值型因素。
定性因素:也称为属性因素,指不能直接测度的,说 明某种属性或状态存在与否的非数值型因素。
解释变量包含一个定量变量和一个分为两种类型 定性变量的回归
解释变量包含一个定量变量和一个两种以上类型 的定性变量的回归
解释变量包含一个定量变量和两个定性变量的回 归
10
解释变量只有一个分为两种相互排斥类型 的定性变量,而无定量变量的回归
假定文化程度、职业、性别等不变,研究农村居 民与城镇居民的年平均可支配收入是否有差异。
计量经济学第八章虚拟变量回归

Y D D D X i 0 1 1 2 2 3 3 4 i i
D1
D2
1 一季度
1 二季度
D3
1 三季度
2 0 其他
2 0 其他
2 0 其他
15
例:美国制造业利润-销售额模型分析
Y X D D D 0 1 i 2 2 i 3 3 i 3 4 i i
比如在研究居民消费函数的时候,考虑到城乡差距和收入差距, 消费函数可以表示为: Y b b X b D b D
i 0 1i 2 1 i 32 i
i
D1i
1 城镇居民 2 0 农村 居民 农村低收入家庭 农村高收入家庭 城市低收入家庭 城市高收入家庭
D2i
1 高收入家庭
2 0 低收入家庭
计参数是否能通过显著性检验,最终确定虚拟变量的具体引入 方式。
9
课本P125页例7中数据建立的我国城镇居民彩电消费模型
ˆ Y 57 . 6113 0 . 0118 X 31 . 8731 D 0 . 0088 D X i i i i i
t
Di
(9.03)
(8.32)
(-6.59)
从这一章开始引入定性变量作为自变量,从而使线性 回归模型作为一种及其灵活的工具,可以处理经验研究中
许多实际的问题
2
• 由于这些定性变量通常指某一性质或属性的出现或不出现,
比如男性或女性、大学学历或专科学历等,因此量化这些 变量的方法就是构造一个取值为0或1的人为变量,可以用 0表示某种属性不出现,1表示某种属性出现。 • 这种人为设定的变量就称作虚拟变量(Dummy Variable) 1 大学毕业
第八章 虚拟变量回归 答案

第八章 虚拟变量回归一、判断题1.虚拟变量只能作为解释变量。
(F )2. 引入虚拟变量后,用普通最小二乘法得到的估计量仍是无偏的。
( T )3.引入虚拟变量的个数与模型有无截距项无关。
(F )4.虚拟变量用来表示某些具有若干属性的变量。
(T )5.引入虚拟变量的个数与样本容量大小有关。
(F )二、单项选择题1.设消费函数011t t t y a a D b x u =+++,其中虚拟变量10D ⎧=⎨ ⎩东中部西部,如果统计检验表明10a =成立,则东中部的消费函数与西部的消费函数是( D )。
A. 相互平行的B. 相互垂直的C. 相互交叉的D. 相互重叠的2.虚拟变量( A )A.主要来代表质的因素,但在有些情况下可以用来代表数量因素B.只能代表质的因素C.只能代表数量因素D.只能代表季节影响因素3.分段线性回归模型的几何图形是( D )A. 平行线B. 垂直线C. 光滑曲线D. 折线4.如果一个回归模型中(包含截距项),对一个具有m 个特征的质的因素要引入虚拟变量数目为( B )。
A.mB.m-1C.m-2D.m+15.设某商品需求模型为01t t t y b b x u =++,其中Y 是商品的需求量,X 是商品的价格,为了考虑全年12个月份季节变动的影响,假设模型中引入了12个虚拟变量,则会产生的问题为( D )。
A .异方差性B .序列相关C .不完全的多重共线性D .完全的多重共线性6.设消费函数为i i i 33i 22i 11o i u bx D D D y +++++=αααα,其中y 为消费,x 为收入,虚拟变量⎩⎨⎧=⎩⎨⎧=⎩⎨⎧=其他季度第三季度,其他季度第二季度,其他季度第一季度 0 0 0 321D 1D 1D 1,该模型中包含了几个定性影响因素?( A )。
A.1B. 2C. 3D. 47. 设消费函数为i i i o i u Dx b x b D y ++++=101αα,其中虚拟变量⎩⎨⎧=农村家庭城镇家庭 0 1D ,当统计检验表明下列哪项成立时,表示城镇家庭与农村家庭有一样的消费行为( A )。
第8章 虚拟变量回归

(2)比较两个回归结构稳定性:虚拟变量法 上节中探讨的邹检验程序,可以通过虚拟变量的使用而大为简化。 仍然使用储蓄-回归的例子,将n1和n2次观测值合并,用下列回归方 程:
其中Yi和Xi仍然代表储蓄和收入。而Di=1,如果观测值属于重建时期
(时期I);Di=0,如果观测值属于重建后时期(时期II)。 为了看清楚,实际上方程等效于:
它们分别是第二(重建后)和第一(重建)两个时期的平均储蓄函
数。相当于取γ1=α1,γ2=β1,λ1=α1+α2,和λ2=β1+β2。这样上述回归方 程等效于估计两个个别的储蓄函数。 α2和先前一样是级差截距;β2是级差斜率系数,表明在第一时期储蓄 函数的斜率和第二时期储蓄函数的斜率系数相差多少。
现在我们要问,在时期I(1946-1954)和时期II(1955-1963)中,储 蓄与收入之间的关系,是否是一回事呢?或者说,两个时期的储蓄 函数是否存在有结构性的变换呢?
这里,结构性变化是指两个截距或两个斜率不同,或者指截距和斜
率均不同,以致任何其他适当的参数组合有所不同。 为了判明这个变化是否真实,假定两个时期的储蓄函数分别是:
工资的重要决定性因素。
上述讨论的结论:模型可推广到含有多个定量变量和多个定性变量
的情形。唯一要提醒注意的是:每一个定性变量所需的虚拟变量的 个数要比该变量的类别数少一。
一个例子:“兼职”经济学
所谓“兼职”是指一个人执有两分或两分以上的工作,其中一份是
主业,其他称为副业。希斯克和罗斯特克研究了影响兼职者工薪的 因素,他们利用一个有318兼职者调查数据的样本,做了如下回归:
图中数据编排为女教
授和男教授两类。图 形可见导出的回归函 数是一个阶梯函数。 女教授的平均工资为 18000美元,而男教 授的工资则跃升了 3280美元,达到了 21280美元。
第八章(虚拟变量回归)_图文

5.社会因素:包括社会治安、城市化水平、消费心理等;
6.行政(政策)因素:包括土地与住房制度、房地产价格政策等;
7.区域因素:包括所处地段的市政基础设施、交通状况等;
8.个别因素:包括朝向、结构、材料、功能设计、施工质量等;
9.房地产投机因素:投机者在房地产市场中的投机活动;
10.自然因素:包括自然环境、地质、地形、地势及气候等。
使用虚拟变量需注意的问题
v 虚拟变量陷阱:若定性变量有m个类别,则引入 m个虚拟变量将会产生完全多重共线性问题,避 免方法:
Ø 只引入(m-1)个虚拟变量 Ø 引入m个虚拟变量但去掉截距项
v 哪种方法更好:包含截距项更方便,可以很容易 地检验某个组与基准组之间是否存在显著差异以 及差异程度。
2、避免落入“ 虚拟变量陷阱”
•男职工本科以上学历的平均薪金:
1.解释变量只有一个分为两种类型的定性变量无 定量变量的回归
这种模型又称方差分析模型
其中:Y为公立学校教师工资,
D=0为农村学校;D=1为城镇学校
分析条件期望:
基础类型:
比较类型:
为差异截距系数,通过对系数 可检验
的 t 检验:
在其他因素不变的条件下,城乡教师的工资是否有显2著323
D=0 表示某种属性或状态不出现或不存在 5
虚拟变量的作用
● 作为属性因素的代表,如性别 ● 作为某些非精确计量的数量因素的代表,
如受教育程度(高中及以下、专科、本科及以上) ● 作为某些偶然因素或政策因素的代表,
如 伊拉克战争、“911事件”、四川汶川大地震 ● 时间序列分析中作为季节(月份)的代表 ● 分段回归——研究斜率、截距的变动 ● 比较两个回归模型的差异 ● 虚拟被解释变量模型:
第八章虚拟变量回归

能否把定性的因素也引入计量经济模型中呢? 怎样才能在模型中有
效地表示这些定性因素的作用呢?
第一节 虚拟变量
一、什么是虚拟变量
变量可分为:
数量变量
属性变量
只表明属性的不连续变量
可用数量表现的连续变量
属性变量:不能精确计量的说明某种属性或状态的定 性变量,如性别、民族、战争、政治事件 ◆本身是定性的二分类变量(非此即彼) ◆本来是连续变量也可转换为二分类变量(上线/不上线) 虚拟变量:人工构造的取值为0和1的作为属性变量代 表的变量称虚拟变量,一般常用D表示 D=0 表示某种属性或状态不出现或不存在 D=1 表示某种属性或状态出现或存在 2
i
大学毕业及以上
1
0
15
E(Yi X i , D 1) ( 0 1 ) X i
Xi
3、解释变量包含一个定量变量和一个两种以上类 型的定性变量的回归
类型:高中以下、中毕业、大学毕业及以上——三种类型
模型
Yi 0 1D1i 2 D2i X i ui
这里的 D1i 和 D2i 代表的是两个不同的定性变量
例如:Y为文化支出,X为收入
D1i 为城镇或农村,D2i是否高中以上
基础类型:
对比类型:
E(Yi X i , D1 0, D2 0) 0 1 X i E(Yi X i , D1 1, D2 0) ( 0 1 ) 1 X i E(Yi X i , D1 0, D2 1) ( 0 2 ) 1 X i
注意:
● u i 应服从基本假定 ●一个定性变量有三种类型,使用了两个虚拟变量, 和 D 代表的是同一个定性变量的两种不同类型 D2 1 ●两个差异截距系数 类型的差异
计量经济学-虚拟变量回归

虚拟变量模型有三种类型
1. 解释变量中只包含虚拟变量 2. 解释变量中既包含定量变量也包含虚拟
变量。 3. 被解释变量本身为虚拟变量。
20
第二节 虚拟解释变量的回归
本节基本内容:
●加法类型 ●乘法类型 ●虚拟解释变量综合应用
21
在计量经济学中,通常引入虚拟变量的方式分为 加法方式和乘法方式两种:即
分为四种情形讨论: (1)解释变量只有一个定性变量而无定量变量,而且定性
变量为两种相互排斥的属性; (2)解释变量分别为一个定性变量(两种属性)和一个定
量解释变量;
23
(3)解释变量分别为一个定性变量(两种以上属 性)和一个定量解释变量;
(4)解释变量分别为两个定性变量(各自分别是 两种属性)和一个定量解释变量;
计量经济学
第八章 虚拟变量回归
1
引子:男女大学生消费真有差异吗?
由共青团中央,全国学联共同发布的 《 2004中国大学生消费与生活型态研究报 告》显示,当代大学生的消费行为呈现多元 化的结构。除日常生活开支外还有人际交往 消费、手机类消费、衣着类消费、化妆品类 消费、电脑类消费、旅游类消费等等。
2
4
第一节 虚拟变量
本节基本内容:
●基本概念 ●虚拟变量设置规则
5
一、基本概念
定量因素:可直接测度的数值型因素。 如收入、产出、价格、人数等。
定性因素:属性因素,不能直接测度、 表征某种属性或状态存在与否的非数值型 因素。如性别、婚否、政府经济政策不变 与改革、城市居民或非城市居民等。
6
在以前的学习中,解释变量主要是定 量变量,但现实经济生活中影响被解释 变量的还包括定性变量,比如:研究某 个企业的销售水平,所有制(私营、非 私营)、地理位置(东、中、西部)等 是必须考虑的因素。
计量经济学:第八章虚拟变量回归

计量经济学:第⼋章虚拟变量回归第⼋章虚拟变量回归第⼀节虚拟变量的概念⼀、问题的提出计量经济学模型对变量的要求——可观测、可计量。
但在现实经济问题中,存在定性影响因素,⽐如1、属性(品质)因素的表达。
在经济活动中,有的经济变量的变动要受到属性因素(或品质因素)的影响。
如收⼊在形成过程中,不同的性别所得到的收⼊是不⼀样的;在城乡、不同地区等收⼊存在差距;再⽐如,在我国,经济的发展⽔平对于不同的区域有不同的表现。
2、异常值现象。
当经济运⾏过程中,可能会受到突发事件的影响,那么,其值有可能出现异常,偏离正常轨迹很远,对这类现象需要加以修正。
3、季节因素的影响。
有的经济现象存在明显的季节特征,如啤酒的消费。
那么,在建模过程中,季节变动这⼀因素怎样考虑?4、离散选择现象的描述。
如公共交通与私⼈交通的选择、商品购买与否的决策、求职者对职业的选择等。
第1、2、3种情况属于解释变量为定性变量,第4情况为被解释变量属于定性变量。
称前⼀种情况为虚拟解释变量,后⼀种为虚拟被解释变量。
本章主要介绍虚拟解释变量的内容。
⼆、虚拟变量的定义1、定义。
设变量D 表⽰某种属性,该属性有两种类型,即当属性存在时D 取值为1;当属性不存在时D 取值为0。
记为=不具有该属性具有某种属性01D2、虚拟变量引⼊的规则。
(1)在模型⾥存在截距项的条件下,如果⼀个属性存在m 个相互排斥类型(⾮此即彼),则在模型⾥引⼊m-1个虚拟变量。
否则,会出现完全的多重共线性。
但要注意,在模型⽆截距项的情况下,如果⼀个属性存在m 个类型,即便引⼊m 个变量,不会出现多重共线性问题。
(请思考为什么?)(2)虚拟变量取值为0,意味着所对应的类型是基础类型。
⽽虚拟变量取值为1,代表与基础类型相⽐较的类型,称为⽐较类型。
例如“有学历”D 为1,“⽆学历”D 为0,则“⽆学历”就是基础类型,“有学历”为⽐较类型。
(3)当属性有m 个类型时,不能把虚拟变量的取值设成如下情况D=0,第⼀个类型;D=1,第⼆个类型;……D=m-1,第m 个类型。
第八章__虚拟解释变量回归

第八章虚拟变量回归第一节虚拟变量一、虚拟变量的基本概念在前面的分析中,被解释变量主要受到一些可以直接度量的变量影响,如收入、产出、商品需求量、价格、成本、资金、人数等。
但现实经济生活中,影响被解释变量变动的因素,除了这些可以直接获得实际观测数据的定量变量外,还包括一些本质上为定性因素(或称属性因素)的影响,例如性别、种族、肤色、职业、季节、文化程度、战争、自然灾害、政府经济政策的变动等因素。
在实际经济分析中,这些定性变量有时具有不可忽视的重要影响。
例如,研究某个企业的销售水平,产业部门(制造业、零售业)、所有制(私营、非私营)、地理位置(东、中、西部)、管理者素质的高低等是值得经常考虑的影响因素,这些因素有共同的特征,即都是表示某种属性的,不能直接用数据精确描述的因素。
因此,被解释变量的变动经常是定量因素和属性因素共同作用的结果。
在计量经济模型中,应当同时包含定量和属性两种因素对被解释变量的影响作用。
定量因素是指那些可直接测度的数值型因素,如GDP、M2等。
定性因素,或称为属性因素,是不能直接测度的、说明某种属性或状态存在与否的非数值型因素,如男性或女性、城市居民或非城市居民、气候条件正常或异常、政府经济政策不变与改革等。
在计量经济学的建模中应当将定量因素和定性因素同时纳入模型之内。
为了在模型中反映定性因素,可以将定性因素转化为虚拟变量去表现。
虚拟变量(或称为属性变量、双值变量、类型变量、定性变量、二元型变量等),是人工构造的取值为0和1的作为属性变量代表的变量,一般用字母D(或DUM,英文dummy的缩写)表示。
属性因素通常具有若干类型或水平,通常虚拟变量的取值为0和1,当虚拟变量取值为0,即D=0时,表示某种属性或状态不出现或不存在,即不是某种类型;当虚拟变量取值为1,即D=1时,表示某种属性或状态出现或存在,即是某种类型。
例如,构造政府经济政策人工变量,当经济政策不变时,虚拟变量取值为0,当经济政策改变时,虚拟变量取值为1。
第八章带虚变量的回归预测

• (一)虚拟变量(虚变量): 1.虚拟变量: 2. 水平: 如:性别有男和女;季节分春、夏、秋 、冬 • 虚变量常用字母D来描述 3.虚变量主要应用于以下两方面: • (1)消除数据序列的异常值; • (2)消除季节性因素。
(二)带虚变量的回归分析
• 1、临时虚拟:也称为突发虚拟;为了更好地对 模型进行估算,有时需要在模型中消除一些由 突发事件产生的异常值对模型的影响。 • 如:
Y b0 b1 x b2 D
• 就是一个引入临时虚变量的多元线性回归模型 • 其中 D=1:表示异常时期; D=0:平时 • 一般而言,如果只有一个异常值(样本数据 中),就引入一个虚变量:有两个异常值就引 入两个临时虚变量。 • (1) 、目的:消除样本数据中的异常值。
临时虚拟 例数据
年份
产量y
耕种面积x
D
85 86 87 88 89 90 91 92 93 94
116 116 106 99 103 105 96 105 78 120
232 228 212 209 208 206 203 209 213 220
0 0 0 0 0 0 0 0 1 0
临时虚拟例散点图
ú ¿ ² Á 150 100 50 0 200 210 220 230 240 ú ¿ ² Á
• 把上式计算的D-w值,与德宾—沃森 给出的不同显著性水平α的D-W值之 上限dU和下限dL(它们与样本容量n和 自变量个数p有关)进行比较,D-W的 取值域在0-4之间。
自相关检验步骤
• Step1:提出假设:H0: 0 • Steo2:构造D-W统计量; • Step3:确定dL(下限)和dU(上限); • Step4:判断:
第八章 虚拟变量回归

其中:
1 t = 1996年以后 D1t = 0 t = 1996年及以前
1 t = 2000年以后 D2 t = 0 t = 2000年及以前
1
基本思路:采用乘法方式引入虚拟变量的手 段。显然,1979年是一个转折点,可考虑在 这个转折点作为虚拟变量设定的依据。若设 X*=1979,当 t < X* 时可引入虚拟变量。 (为什么选择1979作为转折点?)
2
依据上述思路,有如下描述我国居民在不同时段消费 行为模型:
Yt = β 0 + β1t + β 2 (t X * ) D + ut
5
表8.1
年 份 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 国民总收入 (GNI) 3624.1 4038.2 4517.8 4860.3 5301.8 5957.4 7206.7 8989.1 10201.4 11954.5 14922.3 16917.8 18598.4
9
为了分析居民储蓄行为在1996年前后和2000年前 后三个阶段的数量关系,引入虚拟变量D1和D2。 D1和D2的选择,是以1996、2000年两个转折点 作为依据,1996年的GNI为66850.50亿元,2000年 的GNI为国为民8254.00亿元,并设定了如下以加法 和乘法两种方式同时引入虚拟变量的的模型:
城乡居民人民 币储蓄存款年 底余额(Y) 210.6 281 399.5 532.7 675.4 892.5 1214.7 1622.6 2237.6 3073.3 3801.5 5146.9 7119.8
第八章 虚拟变量回归

其中括号内这T-统计量,所有参数 均为显著的,拟合集优度R2=0.999 ,但DW值存在自相关,进行AR(1)
修正,重新估计得:
以上回归的模拟效果:
2500 2000 1500 40 20 0 -20 -40 1975 1980 1985 1990 Actual 1995 2000 Fitted 1000 500 0
有时我们所研究的变量之间 的变化趋势在某一时点上发生 了转折,如图8-3中所呈现的样 本散布点图,它表明变量Y与变 量X之间的变化关系在点X*处发 生了转折,一般来说,这样的 转折点是由于突发
Y
X X
*
0
图8.3
从图中可以算出,消费随时间 有规律地变化,为了模拟消费的 变化趋势,从而对其进行预测, 我们选择时间变量(T)为解释 变量,考虑到季节变动,引入虚 拟 变 量 , D1,D2,D3( 定 义 同 上)等。 由图可知,PCE随时间的变化 是二次曲线,设定模型为下式:
PCEt 0 4Tt 5 D1 t * T 6 D2 t * T 2 7 D3 t * T 8T ut
假设模型中仅有一个解释 变量X,线性概率模型可以表 示为:
Yi 0 1 Xi u i
由于Yi 只取两个值0与1, 设Yi 取1的概率为Pi ,则Yi 取0 的概率为(1-Pi ),于是,
E(Yi ) 1* Pi 0 * (1 Pi ) Pi
而
E(Yi ) 0 1Xi
Pi
1
0 1X i) (
作出该项选择与不作出该项选 择的概率之比的对数值增加一 个 1 。
三、概率单位模型(Probit)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
城市 农村
21
Y
X
共同的特征:截距发生改变(?)
22
(3)一个定性解释变量(两种以上 属性)和一个定量解释变量的情形
模型形式 Yi = f ( X i, D1, D2, ...) + μi (如:民族有56种特性;季度有4种特性) 例如: 啤酒售量Y、人均收入X 、季度D; Yi 0 1D1 2 D2 3 D3 X i i 1 一季度 1 其中: D1 D2 0 其 它 0 1 三季度 D3 0 其 它 二季度 其 它
8
“0”和“1”选取原则
虚拟变量取“1”或“0”的原则,应从分析问 题的目的出发予以界定。
从理论上讲,虚拟变量取“0”值通常代表比较 的基础类型;而虚拟变量取“1”值通常代表被 比较的类型。
“0”代表基期(比较的基础,参照物);
“1”代表报告期(被比较的效应)。
9
例如,比较收入时考察性别的作用。当研究男性收入是否 高于女性时,是将女性作为比较的基础(参照物),故有 男性为“1”,女性为“0”。
加法方式引入 = 0 + 1D 乘法方式引入 = 1 + 2 D
实质:加法方式引入虚拟变量改变的是截距;
乘法方式引入虚拟变量改变的是斜率。
17
一、加法类型
以加法方式引入虚拟变量时,主要考虑的问 题是定性因素的属性和引入虚拟变量的个数。
分为四种情形讨论:
(1)解释变量只有一个定性变量而无定量变量, 而且定性变量为两种相互排斥的属性; ( 2 )解释变量分别为一个定性变量(两种属性)
1 反常年份 其中: Y 消费支出;X 收入; Dt 0 正常年份 反常年份 E Yt | X t , Dt 1 0 1 ( 1 2 ) X t 正常年份 E Yt | X t , Dt 0 1 X t 在正常年份基础上比较,截距和斜率系数都改变,为什么?
28
加法方式引入虚拟变量的主要作用为: 1.在有定量解释变量的情形下,主要改变方程
截距;
2.在没有定量解释变量的情形下,主要用于方
差分析。
29
二、乘法类型
基本思想
以乘法方式引入虚拟变量时,是在所设立的模型中,将虚拟 Xi 解释变量与其它解释变量的乘积,作为新的解释变量出现在
模型中,以达到其调整设定模型斜率系数的目的。或者将模 型斜率系数表示为虚拟变量的函数,以达到相同的目的。
6
虚拟变量的定义
计量经济学中,将取值为0和1的人工变量称为虚 拟变量。虚拟变量也称:哑元变量、定性变量等 等。通常用字母D或DUM加以表示(英文中虚拟 或者哑元Dummy的缩写)。 对定性变量的量化可采用虚拟变量的方式实现。
7
二、虚拟变量设置规则
虚拟变量的设置规则涉及三个方面: 1.“0”和“1”选取原则 2.属性(状态、水平)因素与设置虚拟变量 数量的关系 3.虚拟变量在回归分析中的角色以及作用等 方面的问题
例1
(1)
1 男 D= 0 女
1 改革开放以后 (2) D = 0 改革开放以前
1 天气阴 1 天气雨 ( 3) D1 = ( 4) D2 = 0 其 他 0 其 他
问题: 为何只选0、1,选2、3、4行吗?为什么?
பைடு நூலகம்10
属性的状态(水平)数与虚拟变量 数量的关系
定性因素的属性既可能为两种状态,也可能为多种 状态。例如,性别(男、女两种)、季节(4种状 态),地理位置(东、中、西部),行业归属,所 有制,收入的分组等。
3
第八章 虚拟变量回归
本章主要讨论:
●虚拟变量
●虚拟解释变量的回归
●虚拟被解释变量的回归(选讲,不包括)
4
第一节 虚拟变量
本节基本内容:
●基本概念 ●虚拟变量设置规则
5
一、基本概念
定量因素:可直接测度、数值性的因素。 定性因素:属性因素,表征某种属性存在与否的 非数值性的因素。
基本思想:
直接在回归模型中加入定性因素存在诸多的困难 (那些困难?),是否可将这些定性因素进行量 化,以达到定性因素能与定量因素有着相同作用 之目的。
冬季、城市居民 E Yi | X i , D1 0, D2 1 ( 0 2 )+ X i
冬季、农村居民
E Yi | X i , D1 0, D2 0 0 X i
26
D1 1, D2 1
Y
D1 1, D2 0
D1 0, D2 1
13
Yi = 0 + 1 X i + 1D1 + ui
(2)
若对两个相互排斥的属性 “居民属性” ,仍然 引入 m 2 个虚拟变量,则有
1 城镇居民 D1i = 0 农村居民
1 农村居民 D2i = 0 城镇居民
则模型(1)为 Yi 0 1 X i 1D1 2 D2 ui (3) 则对任一家庭都有: D1 + D2 = 1 D1 + D2 - 1 = 0 , 即产生完全共线,陷入了“虚拟变量陷阱”。 “虚拟变量陷阱”的实质是:完全多重共线性。
1 其中:Di= 0 城市 农村 (比较的基础:农村)
那么: E Yi | Di = 1 = ( 0 + 1)
Yi ( 0 1) i Yi 0 i
E Yi | Di = 0 = 0
城市
农村
20
(2) 一个定性解释变量(两种属性) 和一个定量解释变量的情形
模型形式 Yi = f(Di,X i )+ μi 0 1Di 例如:Yi = 0 1Di + X i + μi 1 城市 其中: Y-支出;X -收入; Di 0 农村
E Yi | X i , Di 1 ( 0 1) Xi E Yi | X i , Di 0 ( 0) Xi
乘法引入方式:
(1)截距不变;
(2)截距和斜率均发生变化;
分析手段:仍然是条件期望。
30
(1)截距不变的情形
模型形式: Yt = f X t , Dt X t ut , 1 2 D 例:研究消费支出 Y 受收入 X 、年份状况 D 的影响 Yt 1 X t 2 ( Dt X t ) t
14
虚拟变量在回归模型中的角色
虚拟变量既可作为被解释变量,也可作为解释 虚拟被解释变量的研究是当前计量经济学研究的
变量,分别称其为虚拟被解释变量和虚拟解释变量。 前沿领域,如MacFadden、Heckmen等人的微观计
本课程只是讨论虚拟解释变量的问题
量经济学研究,大量涉及到虚拟被解释变量的分析。
1 反常年份 其中: Y 消费支出;X 收入; Dt 0 正常年份 反常年份 E Yt | X t , Dt 1 ( 1 2 ) X t 正常年份 E Yt | X t , Dt 0 1 X t 在正常年份的基础上进行比较,(只有斜率系数发生改变)。
和一个定量解释变量;
18
(3)解释变量分别为一个定性变量(两种以上属 性)和一个定量解释变量; (4)解释变量分别为两个定性变量(各自分别是 两种属性)和一个定量解释变量;
思考:
四种加法方式引入虚拟变量会产生什么效应?
19
(1)一个两种属性定性解释变量而 无定量变量的情形
模型形式:Yi f ( Di ) i 0 1Di 例如:Yi 0 1Di i
生的消费支出结构差异,应当如何建立模型?
面临的问题:如何把男女生这样的非数量变量引
入方程?
2
问题的一般性描述
在实际建模中,一些定性变量具有不可忽视的重要
影响。例如,研究某个企业的销售水平,产业属性
(制造业、零售业)、所有制(私营、非私营)、
地理位置(东、中、西部)、管理者的素质、不同
的收入水平等是值得考虑的重要影响因素,但这些 因素共同的特征是定性描述的。 如何对非定量因素进行回归分析? 采用“虚拟变量”对定性变量进行量化一种思路。
(1,0) 天气阴 如:(D1 ,D2)= (0,1) 天气雨 (0,0) 其 他
11
虚拟变量数量的设置规则
1.若定性因素具有 m 个 (m 2) 相互排斥属性(或 几个水平),当回归模型有截距项时,只能引入
m -1个虚拟变量;
2.当回归模型无截距项时,则可引入 m 个虚拟变 量;否则,就会陷入“虚拟变量陷阱”。(为什 么?)
31
(2)截距和斜率均发生变化
模型形式:
Yi f X t , Dt , Dt X t 0 1D, 1 2 D
例,同样研究消费支出 Y 、收入 X 、年份状况 D 间的影 响关系。 Yt 0 1 X t 1Dt 2 ( Dt X t ) t
基准:四季度
24
(4)两个定性解释变量(均为两种 属性)和一个定量解释变量的情形
25
夏季、城市居民
夏季、农村居民
E Yi | X i , D1 1, D2 1 ( 0 1 2) Xi
E Yi | X i ,D1 = 1, D2 = 0 = ( 0 + 1) + Xi
23
一季度:E Yi | X1, D1 1, D2 D3 0 ( 0 1) X i 二季度:E Yi | X1, D2 1, D1 D3 0 ( 0 2 ) X i 三季度:E Yi | X1, D3 1, D1 D2 0 ( 0 3 ) X i 四季度:E Yi | X1, D1 D2 D3 0 0 X i
