受弯构件
《受弯构件》课件

THANKS
直于截面。
扭矩
在扭矩作用下,受弯构件的截面上产 生扭矩,其大小与扭矩成正比,方向
垂直于截面。
剪应力
在剪力作用下,受弯构件的截面上产 生剪应力,其大小与剪力成正比,方 向与剪力方向相同。
挠度与转角
在弯矩作用下,受弯构件的截面会产 生挠度和转角,其大小与弯矩和跨度 有关。
02 受弯构件的受力分析
弯矩与剪力
构造要求与细节设计
配筋设计
根据弯矩分布情况合理布置钢筋,以提高构 件的承载力和延性。
预应力设计
通过施加预应力,改善构件的受力性能,提 高抗弯承载力和刚度。
连接与锚固设计
确保构件之间的连接可靠,防止因连接问题 导致的整体失稳或破坏。
细部构造处理
如钢筋的弯钩、搭接和锚固等,需满足相关 规范和构造要求。
稳定性
受弯构件在受到外部作用力时,可能会发生失稳现象,即构件失去承载能力而发 生弯曲或扭曲变形。稳定性分析是受弯构件设计的重要内容之一,需要采取相应 的措施来提高构件的稳定性。
03 受弯构件的截面设计
截面尺寸的选择
截面高度
01
根据跨度、荷载和材料特性选择合适的截面高度,以满足抗弯
承载力和刚度要求。
受弯构件
目录
Contents
• 受弯构件简介 • 受弯构件的受力分析 • 受弯构件的截面设计 • 受弯构件的施工与质量控制 • 受弯构件的加固与修复 • 受弯构件的发展趋势与展望
01 受弯构件简介
定义与分类
定义
受弯构件是指主要承受弯曲应力的构 件,通常为梁和板。
分类
根据材料可分为混凝土受弯构件、钢 受弯构件等;根据截面形式可分为矩 形、T形、I形等。
受弯构件

W pnx
py
受弯构件抗弯强度
工程上以梁内塑性发展到一定深度作为设计极限状态,
即采用有限塑性准则。
单向弯曲:
Mx f xWn
Mx、My ——梁截面内绕x、y轴的
最大计算弯矩 Wnx、Wny ——截面对x、y轴的净截面 抵抗矩 x、y ——截面对x、y轴的有限塑性
受弯构件抗弯强度
塑性发展系数:
p
Mp Me
Wnpx Wnx
W pn f y Wn f y
W pn Wn
对矩形截面:
px
bh 2 4 2 1.5 bh 6
受弯构件抗弯强度
【例一】弹性截面模量与塑性截面模量计算。
T形截面: 250 200 10 10 求:强轴方向和弱轴方向的塑性截面模量, 并与弹性截面模量比较。
【例二】受弯构件正应力强度验算。 一焊接工字钢梁截面, 用 Q235 制成,正应力强度 设计值 f 215 N mm 2 , 集中力作用处设有加劲肋,
计算步骤:
a、找出达到极限弯矩时截面中和轴,
即:与弯曲主轴平行面积平分线,
该中和轴两边面积相等。
在双轴对称截面中,该轴就是主轴。
b、分别求两侧面积对中和轴的面积矩, 面积矩之和即为塑性截面模量。
h h bh 2 对矩形截面: W pnx b 2 2 4 4
bh 2 6
而:Wenx
解:
1、截面面积
A 200 10 240 10 4400mm2
受弯构件抗弯强度
2、求强轴方向塑性截面模量
(250 - y p ) 10 4400 2
受弯构件_精品文档

受弯构件受弯构件是工程结构中常见的一种结构元素,主要用于承受弯曲荷载。
它是由一根或多根材料组成的构件,常见的形状有梁、柱和弯曲杆。
受弯构件的设计和分析是工程领域中的重要课题,因为它的性能直接影响到结构的稳定性和安全性。
在设计受弯构件时,需要考虑多种因素,包括材料的强度、几何形状、加载方式以及构件的支撑情况等。
首先,材料的强度对受弯构件的设计至关重要。
常用的材料有钢、混凝土和木材等。
钢材具有高强度和良好的延展性,适用于承受大荷载的情况。
混凝土材料具有良好的抗压性能,适用于承受压力的构件。
木材则具有较好的抗拉性能,适用于某些特殊构件的设计。
在设计受弯构件时,需要根据材料的特性选择合适的截面形状和尺寸。
其次,几何形状对受弯构件的性能有直接影响。
常见的受弯构件包括矩形梁、I型梁和圆形柱等。
矩形梁是一种简单的几何形状,容易计算和分析,适用于小跨度和中等荷载的情况。
I型梁由上下两个平行的平板和一个连接两个平板的腹板组成,它的截面形状使得承载能力更大,适用于大跨度和大荷载的情况。
圆形柱具有良好的稳定性,适用于承受压力的情况。
受弯构件在实际使用中通常会承受不同的加载方式,包括集中力、均布力和扭矩等。
集中力是指作用在受弯构件上的单个力,常见的例子有梁的支座反力和集中载荷等。
均布力是指作用在一段长度上的力,常见的例子有均布载荷和自重等。
扭矩是指作用在受弯构件上的旋转力,常见的例子有在梁两端施加的扭矩等。
在设计受弯构件时,需要根据加载方式确定合适的设计参数,以确保结构的稳定性和安全性。
最后,支撑情况对受弯构件的性能也有重要影响。
支撑是指构件的两端或多个点的固定或支持。
常见的支撑方式有固定支持、铰支持和滑动支持等。
固定支持是指构件两端受到约束,不允许产生位移和转动。
铰支持是指构件的某一端可以自由转动,但不允许产生位移。
滑动支持是指构件的某一端可以发生位移,但不允许产生转动。
根据支撑方式的不同,受弯构件的受力特点也会有所差异,因此在设计中需要合理选择支撑方式。
5章受弯构件概述

构件可能突然产生在弯矩作用平面外的侧移和扭转,构 件由平面内弯曲状态变为弯扭状态,这就是整体失稳。
2.梁丧失整体稳定的现象:
产生侧向弯曲并伴随着扭转——出平面弯扭屈 曲; 有两个位移u,v和一个转角。
3.梁丧失整体稳定的原因:
不同形式的截面形状系数见P117表5.1。
(3)按有限塑性发展强度准则,限制截面塑性区在截 面高度两侧一定范围(<0.15h)内发展,采用有限截 面塑性发展系数x或y(P118表5.2)。
设计计算公式为:
MxxMex
2. 双向弯曲时的抗弯强度:
(1)按边缘屈服准则,要求截面边缘一点的最大弯曲应力 满足:
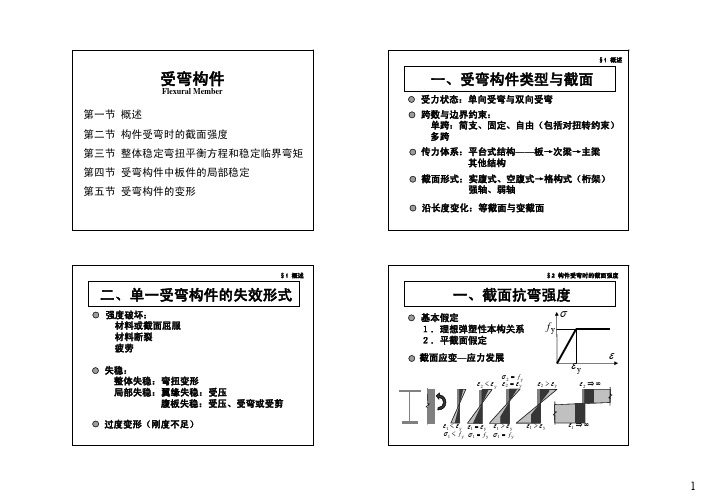
一、截面强度破坏
梁在纯弯矩作用下
截面的正应力: 1)弹性阶段 2)弹塑性阶段 3)塑性阶段(塑性铰形成并转动) 4)强化阶段
二、整体失稳
绕强轴单向受弯的构件,当弯矩增大到某一数值时,构 件可能突然产生在弯矩作用平面外的侧移和扭转,构件由 平面内弯曲状态变为弯扭状态,称整体失稳。
x a)
M
z
M
d)
令 h/2l2(EIy/GIt)
1 2
——整体稳定屈曲系数
M crx l EI yGIt
荷载形式不同、作用的位置不同,整体稳定 屈曲系数也不同。如P 124 表5.5
四、影响临界弯矩的主要因素:
1.截面的侧向抗弯刚度EIy、抗扭刚度GIt、翘曲刚度EI; 2.构件的侧向支承点间距; 3.截面的不对称程度,受压翼缘加强,By大, Mcrx大。 4.荷载种类,纯弯曲时, Mcrx最小。 5.支承对位移的约束程度大, Mcrx也大。 6.荷载作用的位置,在下翼缘时有利,a值大。
受弯构件

型钢梁
实腹式截面梁
按截面构成方式分
焊接组合截面梁
空腹式截面梁 组合梁
由若干钢板或钢板与型钢连接而成。它 截面布置灵活,可根据工程的各种需要 布置成工字形和箱形截面,多用于荷载 较大、跨度较大的场合。
3
钢结构原理与设计
图4.1 工作平台梁格
1-主梁 2-次梁 3-面板 4-柱 5-支撑
4
钢结构原理与设计
M x Wnx
a
M x f yWnx
a
σ
fy
fy
fy
M xp f yW pnx
M xp f y S1nx S2nx f yWpnx
式中: S1nx、S2nx 分别为中和轴以上、以下截面对中 和轴的面积矩; Wpnx 截面对中和轴的塑性抵抗矩。
(4-2) 5 2) (
16
钢结构原理与设计
2) 梁的抗剪强度 剪应力的计算公式:
VS fv It w
(4.6)
式中:V ——计算截面的剪力; S ——计算剪应力处以上毛截面对中和轴的面积矩; I ——毛截面惯性矩;
17
钢结构原理与设计
3) 梁的局部承压强度
图4.6 梁局部承压应力
18
钢结构原理与设计
式中:F ——集中荷载,动力荷载需考虑动力系数; ψ ——集中荷载增大系数,重级工作制吊车梁ψ=1.35; Lz ——集中荷载在腹板计算高度上边缘的假定腹板长度,按下式计算: Lz=a+2hy a ——集中荷载沿梁跨度方向的支承长度,吊车梁可取a为50mm; hy ——自吊车梁轨顶或其它梁顶面至腹板计算高度上边缘的距离
t1
ho
t1
b
20
钢结构原理与设计
受弯构件——精选推荐
闭口截面: It
=
4 A02
/
∫
ds t
§3 整体稳定弯扭平衡方程和稳定临界弯矩
四、其他条件下的临界弯矩(续)
截面形式与横向荷载作用位置变化
M crx
=
β1
π
2 EI A2
y
[β2a
+
β3By
+
(β2a
+
β3By )2
+
Iω Iy
(1 +
GI tA 2 π 2 EI ω
= θl''
=
0
函数(a)代入方程(6-47)得
(
EI
ωn 4π A4
4
+
GI t n 2π A2
2
−
M
2 x
EI y
)⋅C
⋅ sin
nπz A
=
0
(b)
欲满足式(b)且函数(a)有非零解,则括弧内值应为零。得
Mx
⇒
M crx
= π 2 EI y A2
Iω Iy
(1
+
GI t A 2 π 2 EI ω
2 max
+
3τ
2 max
哪些点有复杂应力状态?
受弯构件中的折算应力 σ zs =
σ
2
+
σ
2 c
−
σ
⋅σ
c
+
3τ
2
——应力分量的符号:拉正压负
工程计算公式 σ zs ≤ β1 ⋅ fd
β1 = 1 弹性准则 β1 > 1 允许局部塑性发展
钢结构第五章受弯构件

适用于可拆卸的结构和临时性连接,具有施工方便、质量易于保证等优 点;但用钢量较大,且需要定期紧固。
03
铆钉连接
适用于承受动力荷载的结构,具有传力可靠、韧性和塑性好等优点;但
铆接工艺复杂、劳动强度高、用钢量也较大。
节点类型及其适用范围
刚接节点
能传递弯矩和剪力,适用 于固定支座和连续梁等需 要传递弯矩的结构。
03
受弯构件截面设计与优化
截面形状选择原则
01
02
03
符合受力要求
根据受弯构件所受荷载类 型、大小及分布情况,选 择能够有效承受弯矩和剪 力的截面形状。
便于加工制作
考虑现有加工设备和技术 水平,选择易于加工成型 的截面形状。
经济性
在满足受力要求和加工制 作的前提下,尽量选择材 料用量少、成本低的截面 形状。
连接固定
采用合适的连接方式将构件与基础或相邻构 件连接固定,确保稳定性和安全性。
验收标准和方法
验收标准
构件的尺寸偏差、形位公差、表面质量等应符合相关标准和 设计要求。
验收方法
采用测量工具对构件的尺寸、形位等进行测量,目视检查表 面质量,查阅相关质量证明文件等。对于不合格的构件,应 及时进行整改或返工处理,直至符合要求为止。
节点法
对于超静定结构,通过选取节点建立平衡方程,进 而求解内力的方法。
力矩分配法
适用于连续梁和无侧移刚架等结构,通过力矩分配 系数求解内力的方法。
剪力、弯矩图绘制
80%
剪力图的绘制
根据截面法或节点法求得的剪力 值,在构件上按比例绘制剪力图 。
100%
弯矩图的绘制
根据截面法或节点法求得的弯矩 值,在构件上按比例绘制弯矩图 。
《受弯构件计算》课件

总结词
基于弹性理论的计算方法,适用于小变形和线弹性材料。
详细描述
该方法假设材料在小变形时满足胡克定律,即应力与应变 成正比。通过弹性理论公式,可以计算出受弯构件的弯矩 、剪力和挠度等参数。
适用范围
适用于梁、板等简单受弯构件的静力分析。
塑性理论计算方法
总结词
基于塑性理论的计算方法,适用于大变形和塑性材料。
详细描述
该方法考虑了材料进入塑性阶段的特性,通过塑性理论公式,可以 计算出受弯构件在达到极限承载力时的变形和应力分布。
适用范围
适用于梁、板等简单受弯构件的极限承载力分析。
极限承载力计算方法
总结词
基于极限承载力的计算方法,适用于各种材料和变形情况 。
详细描述
该方法通过分析受弯构件的极限承载力,确定构件在达到极限状 态时的变形和应力分布。极限承载力计算方法通常采用试验数据
受弯构件的优化实例
01
截面优化
通过改变受弯构件的截面形状、尺寸或者材料,可以减小弯矩和剪切应
力,提高构件的承载能力和稳定性。
02
支撑结构优化
通过改变支撑结构的布局和连接方式,可以减小受弯构件的弯矩和剪切
应力,提高构件的承载能力和稳定性。
03
预应力技术
预应力技术可以改变受弯构件的受力状态,减小弯矩和剪切应力,提高
件。
建筑工程
02
建筑物中的楼板、屋顶、墙体等也常常是受弯构件。
其他领域
03
如机械工程中的传动轴、压力容器等也涉及到受弯构件的设计
与计算。
02
受弯构件的力学性能
弯曲变形
弯曲变形
受弯构件在弯矩作用下发生的弯曲变形,导致构件轴线由直线变 为曲线。
钢结构5-受弯构件

施工图绘制
完成图纸绘制,准备施工。
优化方法与实例
尺寸优化
调整梁、柱等构件的截面尺寸,以实 现最优承载能力。
形状优化
改变构件的形状,如采用H形、箱形 等,提高稳定性。
优化方法与实例
• 拓扑优化:确定结构中最佳的材料分布,以满足性能要求。
优化方法与实例
大跨度桥梁
05
受弯构件的设计与优化
设计原则与流程
确保结构安全
满足承载力、稳定性和疲劳强度要求。
经济性
优化材料用量,降低成本。
设计原则与流程
• 可持续性:考虑环境影响,选择环保材料和工艺。
设计原则与流程
需求分析
明确结构用途、载荷和约束条件。
初步设计
确定梁、柱等主要构件的尺寸和布局。
设计原则与流程
详细设计
未来发展方向与挑战
高性能材料研发
满足更高强度、韧性和耐久性要求。
跨学科合作
加强结构工程、材料科学、计算机科学等多学科交叉融合。
THANKS
感谢观看
有限元法
利用计算机模拟技术,对钢结构进 行详细的数值分析,可以更准确地 预测其稳定性。
提高稳定性的措施
1 2
加强支撑
增加侧向支撑和加强筋,提高钢梁的侧向刚度和 稳定性。
选择合适的截面形状和尺寸
根据受力要求和稳定性要求,选择合适的截面形 状和尺寸。
3
预应力处理
通过施加预应力来提高钢结构的稳定性,防止失 稳的发生。
钢结构5-受弯构件
目录
• 受弯构件概述 • 受弯构件的受力分析 • 受弯构件的承载能力 • 受弯构件的稳定性分析 • 受弯构件的设计与优化
钢结构-受弯构件

受弯构件要点:♦受弯构件概述;强度准则在受弯构件中的体现;边缘屈服弯矩与极限弯矩;截面塑性模量;单轴与双轴抗弯强度♦截面抗剪强度;局部承压强度;折算应力♦整体稳定♦局部稳定受弯构件概述的主要破坏形式受弯构件类型与受力特点1.基本概念♦受弯构件:弯矩作用或受弯矩和剪力共同作用的构件。
♦强轴:形心主轴中惯性矩、截面模量最大的主轴。
♦弱轴:与强轴垂直的主轴。
2.构件类型♦单向弯曲构件:构件在一个主平面受弯。
♦双向弯曲(斜弯曲)构件:构件在两个主平面受弯。
3.受力特点♦屈服点♦ 弹性核 ♦ 塑性区♦ 极限抗弯承载力主要破坏形式1. 截面强度破坏截面的平均应力达到屈服点f y ,截面应变迅速增加最后导致结构破坏。
通常以截面的平均应力达到屈服点f y 为轴心受压构件强度破坏准则。
2. 整体失稳破坏由于侧向干扰力或构件初始偏心等原因,受弯构件离开原来的平面,发生侧向挠曲和扭转称为受弯构件的整体失稳。
当轴力达到某一值时结构不能保持稳定的平衡状态,结构变形迅速增大开始丧失稳定性,最后导致结构破坏。
这时的轴心压力称为临界压力。
3. 局部失稳破坏构成受弯构件的板件在压应力和剪应力作用下局部出现波浪状的鼓曲变形,但轴线变形仍在弯曲平面内的的现象。
一般不一定作为构件整体破坏的判别准则。
受弯构件的截面强度强度准则1. 边缘纤维屈服准则截面上边缘处的最大应力达到屈服时即认为受弯构件的截面达到了强度极限,截面上的弯矩称为屈服弯矩。
此时构件在弹性阶段工作。
2. 全截面屈服准则一整个截面的应力达到截面承载极限强度的状态作为强度破坏的界限,此时截面上的弯矩称为塑性弯矩或极限弯矩。
3. 部分发展塑性准则将截面塑性区限制在某一范围,一旦塑性区达到规定的范围即视为强度破坏。
抗弯强度1. 缘纤维屈服准则 单向弯曲构件 双向弯曲构件 截面应力:d xn x f W M ≤=σ;d yny xn x f W M W M≤+=σ(或()()d xyn yn xn xyn x xn y xyn y yn x f I I I y I M I M x I M I M ≤--+-=2σ) 相关准则:1≤exdxM M ; 1≤+eydy exd xM M M M屈服弯矩:d xn exd f W M =;d yn eyd f W M =2. 全截面屈服准则 中性轴:⎰=dA f N y;⎰=ydA f My x;⎰=xdA f M y y相关准则:1≤pxdxM M ; 1≤+pydy pxd xM M M M极限弯矩:d pxn pxd f W M =;d pyn pyd f W M =3. 部分发展塑性准则截面应力:d exn x x f W M ≤γ; d eyny y exn x xf W M W M ≤+γγ截面塑性发展系数:ep x M M =γ相关准则:直线关系式:1≤exdx xM M γ; 1≤+eydy y exd x xM M M M γγ屈服弯矩:d xn exd f W M =;d yn eyd f W M =抗剪强度1. 单方向横向力作用 截面应力:vyd x x y f tI S V ≤=τ(vyd wy f A V ≤=τ)2. 双方向横向力作用vyd y y x x x y f tI S V tI S V ≤+=τ(或()()()vyd xyyx xxy x x y y xy y yx f tI II V I S I S V I S IS ≤--+-=2τ)局部承压强度y zw c f l t F≤=σ; 其中,分布长度y z h a l 2+= 否则,需要设置支承加劲肋。
钢桥受弯构件验算内容-公式

一、受弯构件(一)在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求:双向受弯的实腹式构件:f d ≥γ0(M y W y,eff +M z W z,eff )式中:γ0——结构重要性系数;M y 、M z ——计算截面的弯矩设计值;W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量,其中受拉翼缘应考虑剪力滞影响,受压翼缘应同时考虑剪力滞和局部稳定影响。
2、腹板剪应力应满足下列要求。
闭口截面腹板剪应力应按剪力流理论计算。
γ0τ≤f vd式中:γ0——结构重要性系数;τ——剪应力;f vd ——钢材的抗剪强度设计值。
3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时,应满足下列要求。
γ0√(σx f d )2+(τf vd)2≤1 式中:σx ——x 方向正应力;f d ——钢材的抗拉、抗压和抗弯强度设计值。
(二)受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件,应按下列规定验算整体稳定。
γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ,λLT,z =√W z,eff f y M cr,z式中: M y 、M z ——构件最大弯矩;βm,y、βm,z——等效弯矩系数;χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下,构件弯扭失稳模态的整体稳定折减系数;λ̅̅̅LT,y、λLT,z——弯扭相对长细比;W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量,其中受拉翼缘应考虑剪力滞影响,受压翼缘应同时考虑剪力滞和局部稳定影响。
M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下,考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩,可采用有限元方法计算。
第5章 受弯构件

5.1 概述
5.1.1 受弯构件的概念及分类
➢ 受弯构件:只受弯矩作用或受剪力与弯矩作用的构件。实际 工程中,以受弯受剪为主但作用着很小的轴力的构件,也常称 为受弯构件。 工程中的受弯构件是指承受横向荷载的构件,通常称为梁。 铁路桥梁中的钢板梁、箱型梁;工业与民用建筑中的吊车梁、 屋盖梁、工作平台梁以及檩条等。
工作平台梁结构布置
➢ 受弯构件的分类
受弯构件包括实腹式受弯构件(梁)和格构式受弯构件(桁架) 两个系列。
按照受力主要有单向受弯构件和双向受弯构件
按照截面形式可分为型钢梁和组合梁
按照支撑条件可分为简支梁、连续梁和悬臂梁
根据主梁与次梁的排列情况,梁格可分为单向 梁格、双向梁格、复式梁格
跨中无侧向支承点
跨中有侧向支承点
5.3 梁的整体稳定
5.3.1 梁整体稳定的设计原理 当梁上荷载不大时,仅在垂直方向有位移,当荷载加到
一定值时,梁有侧向位移产生并伴随扭转,梁从平面弯曲状态转 变为弯曲扭转屈曲状态的现象称为整体失稳,也称弯扭失稳。
梁丧失整体 稳定现象
临界弯矩Mcr 梁维持稳定状态所能承受的最大弯矩。 若保证梁不丧失整体稳定性,
EIy---梁的侧向刚度;
GIt---自由扭转刚度;
l---受压翼缘的计算长度。
(5-12)
k= 1+( 2 h )2 EIy
2l GIt
2.横向荷载作用下双轴对称工字型截面梁的临界弯矩,见课 本表5-3。 (1)在横向荷载作用于形心时,其临界弯矩都比纯弯曲时高 。 (2)横向荷载作用于上翼缘比作用于下翼缘的临界弯矩低。
3.根据弹性稳定理论,在最大刚度平面内受弯的单轴对称截 面简支梁的Mcr普通式为:
M cr
受弯构件

加劲肋间距公式说明
τ 式中: =
V h0t w
— 腹板平均剪应力;
1 = 1 σ h 0 1− 715 100t w
2
η=
σ 1− σ cr
2
2
— 考虑σ的影响增大系数;
M h0 σ = ⋅ — 腹板计算高度边缘的弯曲压应力; W h
塑性发展系数
γ — 塑性发展系数或形状系数,它只取决于截面几
何形状,与材料强度无关。
γ=
如:矩形截面
W pn Wn
γ =1.5
工字形截面(对强轴) γ =1.7~1.1。
塑性发展系数取值
《规范》在对梁抗弯强度计算时,考虑部分 截面发展塑性,用γ 来控制: 对于承受静力或间接动力荷载: 单向弯曲梁:
梁局部失稳图
工形梁受压边宽厚比限值
二、满足梁局部稳定的措施 1. 焊接工字形截面梁受压翼缘的宽厚比限值 规范规定: b1 ≤ 15 235
t fy
(按弹性设计)
b1 t
b1 235 ≤ 13 t fy
(允许截面部 分发展塑性)
式中:b1 — 受压翼缘的外伸宽度。
腹板加劲肋
2. 腹板加劲肋设计(侧向支承) A、 加劲肋的分类 横向加劲肋 纵向加劲肋 加劲肋 短加劲肋 支承加劲肋
加劲肋配置规定2
235 h0 235 当 80 < ≤ 170 时,按计算配置横向加 劲肋。 fy tw fy 235 h0 当 时,宜同时按计算配置纵、横向加劲肋。 > 170 tw fy
• 梁的支座处和上翼缘受有较大固定集中荷载处,宜 设置支承加劲肋,对简支吊车梁在吊车轮压很大时, 尚应在受压区配置短加劲肋。
钢结构基本原理课件第六章受弯构件

腹板错位焊接 按锯齿形切开
(a)
蜂窝梁(a)切割线; (b)蜂窝梁
(b)
6.1.3 空腹式受弯构件
另一类型的空腹式受弯构件,工程上称之为桁架,与梁相 比,其特点是以弦杆代替翼缘、以腹杆代替腹板,而在各 节点将腹杆与弦杆连接。这样,桁架整体受弯时,弯矩表 现为上、下弦杆的轴心压力和拉力,剪力则表现为各腹杆
的轴心压力或拉力。
(a)
梁式桁架形式
(d)
(b)
(e)
6.1.3 空腹式受弯构件
(a)
(d)
(b)
梁式桁架形式
(e)
(c)
(f)
钢桁架可以根据不同使用要求制成所需的外形,对跨度和 高度较大的构件,其钢材用量比实腹梁有所减少,而刚度
却有所增加。只是桁架的杆件和节点较多,构造较复杂,
制造较为费工。
6.2 受弯构件的设计
本节目录
6.2.1 概述 6.2.2 梁的强度 6.2.3 梁的刚度 6.2.4 梁的整体稳定性 6.2.5 梁的局部稳定性 6.2.6 型钢梁的截面设计
6.2.1 概述
梁设计中应满足的两种极限状态
内容 极限状态 需要满足 需要满足 抗弯强度 强度承载力 抗剪强度 局部承压强度 复杂应力状态下强度 稳定承载力 正常使用极限状态 梁的变形极限状态 整体稳定
3m 3 m
3m 3m
3m 3 m
3m 3m
q
6m
解:①荷载及内力计算
梁上的荷载标准值为: qk 3 4.5 7.5kN / m 2 荷载设计值为: qd 1.2 3 1.3 4.5 9.45kN / m 2
受弯构件

2.1 抗弯强度
正应力发展过程
弹性 阶段
2011《钢结构基本原理》 2011《钢结构基本原理》
弹塑性 阶段
塑性 阶段
第06章 受弯构件 06章
2.1 抗弯强度
截面的弯矩-转角曲线 截面的弯矩-转角曲线 弯矩
硬化
塑性
【思考04】材料 思考04】 04 塑性与截面塑性 塑性与 之间有何联系与 区别? 区别?
——2个及以上应力分量存在的状态 个及以上应力分量存在的状态 ——同一点上同时出现的应力状态 同一点上同时出现的应力状态
受弯构件中的折算应力
2 σ zs = σ 2 + σ c − σ ⋅ σ c + 3τ 2
——应力分量的符号:拉正压负 应力分量的符号: 应力分量的符号
工程计算公式
σ zs ≤ β1 ⋅ f d
2011《钢结构基本原理》 2011《钢结构基本原理》
第06章 受弯构件 06章
1.3 破坏形式
受弯构件的主要破坏形式 受弯构件的主要破坏形式
强度破坏: 强度破坏:材料或截面屈服 整体失稳: 整体失稳:弯扭失稳 局部失稳:翼缘, 局部失稳:翼缘,腹板 疲劳,断裂:反复荷载, 疲劳,断裂:反复荷载,受拉区 变形过大: 变形过大:刚度不足
弹塑性 弹性
2011《钢结构基本原理》 2011《钢结构基本原理》
第06章 受弯构件 06章
2.1 抗弯强度
强度计算公式
1. 边缘屈服准则
M x ≤ M ex
工程计算 公式
σ =
M x ≤ fd W xn
【思考05】假如工字形受弯构件的翼缘采用Q345钢,腹板采用 思考05】假如工字形受弯构件的翼缘采用Q345钢 05 Q345 Q235钢 如何确定其边缘屈服弯矩?两种材料互换又如何? Q235钢,如何确定其边缘屈服弯矩?两种材料互换又如何?
第3章 受弯构件

85(kN m) 80(kN m) 故安全
第三节 正截面承载力计算
例3-6: 某简支梁,受力情况如下图所示。试对该梁进 行截面设计。
gk=12.3kN/m qk=7.8kN/m
第3章 受弯构件
第二节 受弯构件的一般构造要求
例3-2:某雨篷板,悬挑长度 l = 1200mm,求板厚h = ?
根部: h l0 1200 100mm 12 12
自由端:60 mm
第3章 受弯构件
第二节 受弯构件的一般构造要求
3.板的支承长度
支承长度a h(板厚)及 120 mm
第3章 受弯构件
4.钢筋
第二节 受弯构件的一般构造要求
第3章 受弯构件
第二节 受弯构件的一般构造要求
板中纵向受力钢筋:
直径d: d=6~12mm
间距S: 当板厚h≤150mm时,70mm≤S≤200mm 当板厚h>150mm时,S≤1.5h,且S≤250mm
板中分布钢筋:
面积:分布筋截面面积/m 受力筋截面面积的15%/m 间距S: S≤250mm
(2)截面尺寸
第二节 受弯构件的一般构造要求
必须满足承载力,刚度,抗裂度三方面要求
1)梁的截面高度h —— 一般根据刚度条件确定
不需作挠度计算的截面最小高度
项次 结构种类
简支 两端连续 悬臂
整 体 次梁 l0/20
l0/25
l0/8
1 肋形梁 主梁
l0/12
l0/15
l0/6
2
独立梁
l0/12
l0/15
—纵向受拉钢筋的截面面积
—截面的宽度
梁
—截面的高度
板
as
as as
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等效原则:
合力不变 合力作用点不变
b
x0
h0
Mu
As
(a)横截面
α1 f c x
fy As Ⅲa
(b)实际应力图形 b
Mu
fy As
(c)等效应力图形
h0
As
(d)计算截面
受弯构件正截面应力图形
2.基本公式及其适用条件
a. 基本公式
1 fcc f
C 1fcfbx C= c bx
M Mu
II
IIa III IIIa
钢筋:屈服阶段;混凝土:塑性、压区应力图形更加 M-f呈曲线,裂缝 饱满 宽度发展较快 中心轴一直上升
混凝土压碎,破 坏 承载力计算依据
二、单筋矩形截面受弯构件正截面承载力计算 (一)基本假定
a.平截面假定 b.不考虑混凝土抗拉
fc
n c 1 1 c fc 0
4.5钢筋混凝土受弯构件 受弯构件:弯矩和剪力共同作用,轴力忽略不计的构件 板和梁是最常见的受弯构件.
受弯构件常见截面形式:
主要破坏形态: 正截面破坏
斜截面破坏
斜截面破坏
正截面破坏
受弯构件破坏截面
一、板的构造
1. 板的厚度
单跨板,≥l0 /35;
Ac
分布钢筋
受力钢筋 分布钢筋
@
多跨连续板,≥ l0 /40。且≥ 60mm
1 f c bx
fy
1.0 9.6 250 88 704mm2 300
将x代入下式,受拉钢筋的截面面积为:
3.验算条件
最小配筋率经过计算比较取ρ min =0.2% 由以上验算,截面符合适要求。 4.选配钢筋 选用2 Φ18+1 Φ 16(As=710mm2) 一排钢筋时钢筋净间距:
当b> 350mm或一层纵筋多于5根,或受压钢筋多于三根,用四肢。
三、混凝土保护层和截面有效高度
>C
1. 混凝土保护层厚(C)
>C h0 h
钢筋外缘砼厚度。
2. 截面的有效高度(h0) 受压砼边缘至受拉钢筋合 力点的距离.
单排受拉钢筋,
>C >30 >1.5d
as >C
>C
h0 h a s
f y As 300 804 x 125.6mm b h0 0.55 460 253mm 1 f cb 1.0 9.6 200
2.验算适用条件 经计算比较取ρ min =0.2%
As 804 0.80% min bh 200 500
3.计算截面受弯承载力Mu(极限弯矩)
min bh 0.002 250 500 250mm2 AS =704mm2
S净=(250-2×30-2×18-1×16)/2=69mm >25mm
例3 某跨度为5.2米的钢筋混凝土矩形截面梁,截面最大弯矩设计 值为64.0KN.m,环境类别为一类结构安全等级为二级。设计此梁的 截面并配置纵向受拉钢筋;若最大弯矩改为100KN.m,截面尺寸不 变,试计算所需的受拉钢筋。
这种破坏称为界限破坏。
超筋破坏 适筋破坏
xb b h0
x b h0 b
b可用来判断构件破坏类型,衡量破坏时钢筋强度是否充分利用。
b.最大配筋率
b xb b h0 max
经济配筋率:梁: =(0.5~1.6)%;板: =(0.4~0.8)%
2. 板的配筋
a. 受力钢筋 计算确定
As
承受拉力
h 150mm , @ 200mm h 150mm , @ 1.5h& 250mm & @ 70mm
受力钢筋
b. 分布钢筋
As分布 15% As且 0.15% Ac , & 6 @ 250
固定受力筋位置;阻止砼开裂
(1)设计参数 环境类别为一类,选C25混凝土,HRB335钢筋,则: f c 11.9 N / mm 2 , f t 1.27 N / mm 2 , f y 300 N / mm 2 , 1.0, b 0.55 取c 25mm, 按一排布置a 35mm l 5000 设h 433mm, 取b h 200mm 450mm, 12 12 h0 450 35 415mm
As 1 fc b bh0 fy
4、设计计算方法 截面复核 已知材料、截面尺寸和配筋等,求承载力设计值
第一步:计算x :1 fcbx f y As
第二步:计算弯矩设计值
x b h0
:
Mu max 1 fcbh02b: 0.5b ) (1
x b h0
N 0, M 0
1 f c bx f y As
x M M u 1 f c bx( h0 ) 2 x M M u f y As ( h0 ) 2
M
x=b x n x
h0 x 2
fys Ts=sAAs
b. 适用条件 a) 防止超筋破坏
x b h0
c. 混凝土的应力应变关系
d. 钢筋的应力应变关系
0
0 A
B
fy
Es
Es fy
y y
y
(二)单筋矩形截面承载力计算 1、计算简图
B
fc C
o Z fyAs xn Mu
1 fc
x
A
Mu
Z
fyAs
钢筋已经屈服,混凝土刚刚压碎。 将钢筋的应力取为 f y;混凝土的极 限应变取为 cu ,此时混凝土的边 缘压应力为 fc
IIIa
f y As
阶 段 I Ia
现象
特点 弯矩小,应变小, 钢筋:弹性阶段 ;混凝土:弹性阶段,受拉区略显塑 性。拉力由钢筋和混凝土共同承担
M-f图呈直线
混凝土即将开裂, 混凝土达到受拉应变,是严格不允许出现裂缝构件的 转折点1 设计依据。 钢筋:弹性阶段;混凝土:压区出现塑性,拉区逐渐 M-f呈曲线,裂缝 退出工作 出现并开展 拉力主要由钢筋承担 钢筋即将屈服, 转折点2 是使用阶段的裂缝开展与宽度计算的依据。
Mu = α1 f cb x(h0-0.5x) = 1.0×9.6×200×125.6×(460-62.8)
=95785574.4(N.mm)=95.8(KN.m) 4.比较 M=90kN.m < Mu =95.8(KN.m) 所以:此梁安全
补充例题2
例题:已知某矩形截面梁b×h=250 mm×500mm,由荷载产生 的弯矩设计值M=88.13kN· m,混凝土强度等级为C20,钢筋采 用HRB335级, 试求所需纵向受拉钢筋截面面积As。 解 : 查 表 得 : fc=9.6N/mm2 , ft=1.1N/mm2, ; fy=300N/mm2 ; ξb=0.55;截面有效高度h。=500-40=460mm
2 0
没有唯一解
设计人员应根据受力性能、材料供应、施工条件、使用 要求等因素综合分析,确定较为经济合理的设计。
查表法:
令:s (1 0.5 ) M 则:M 1 f cbh a as 1 1 2 as 2 1 f cbh0
2 0 s
令: s 1 0.5 M 则:M AS f y h0 s As f y h0 s 设计过程:as s As
截面校核不建议用查表法
补充例题1: 已知钢筋混凝土矩形截面梁b×h=200 mm×500mm, 混 凝 土 强 度 等 级 C20 , 采 用 HRB335 级 钢 筋 , 受 拉 钢 筋 4 Φ 16 (As=804mm2),承受的弯矩设计值是90kN.m,试验算此梁是否安 全。
解:查表得:fc=9.6N/mm2,; fy=300N/mm2; ξb=0.55;截面有效高 度h。=500-40=460mm ;纵向受拉钢筋按一排放置,则梁的有效高 度h0=500-40=460mm。 1.计算受压区高度x
As minbh
M u 1 fcbx(h0 x / 2)
:
M u M cr
截面设计
已知荷载效应,求材料、截面尺寸和配筋等
第一步:选择混凝土等级和钢筋品种 第二步:确定截面尺寸:按照配筋率确定; 按照跨度(刚度)确定 第三步:求受压区高度x:
2M M 1 f c bx(h0 x / 2) x h0 h a1 f c b x b h0 第四步:验算: 第五步:计算As: 1 fcbx f y As
特征是屈服弯矩和开裂弯矩相等,是区分适筋破坏和少筋 破坏的定量指标
(二)、适筋受弯构件 受力的三个阶段
Mu
1. 第Ⅰ阶段:弹性工作阶段
III
My
带裂缝工作阶段 2. 第Ⅱ阶段:
3. 第Ⅲ 阶段:破坏阶段
ቤተ መጻሕፍቲ ባይዱ
II
Mcr
I
M
Mcr
M
My
Mu
s As
I Ia
s As
II
s As
IIa
f y As
1.直接公式求解X 根据基本公式可推导出求解X的公式如下:
2M x h0 h 1 f c b
2 0
2 88130000 460 460 1.0 9.6 250 88mm b h0 0.55 460 253mm
2
2.计算受拉钢筋面积
As
破坏形态: 超筋梁
(c)
少筋梁
二受弯构件的试验研究
2. 试验结果
P
当配筋适中时----适筋梁的破坏 过程
L/3 L
L/3
c
