快速指数取模运算与用扩展欧几里得算法求解最大公约数和求乘法逆元
欧几里德算法

欧几里得算法的概述欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数。
其计算原理依赖于下面的定理:定理:gcd(a,b) = gcd(b,a mod b)证明:a可以表示成a = kb + r,则r = a mod b假设d是a,b的一个公约数,则有d|a, d|b,而r = a - kb,因此d|r因此d是(b,a mod b)的公约数假设d 是(b,a mod b)的公约数,则d | b , d |r ,但是a = kb +r因此d也是(a,b)的公约数因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等,得证欧几里得算法原理Lemma 1.3.1 若a, b 且 a = bh + r, 其中h, r , 则gcd(a, b) = gcd(b, r).证明. 假设d1 = gcd(a, b) 且d2 = gcd(b, r). 我们证明d1| d2 且d2| d1, 因而可利用Proposition 1.1.3(2) 以及d1, d2 皆為正数得证d1 = d2.因d1| a 且d1| b 利用Corollary 1.1.2 我们知d1| a - bh = r. 因為d1| b, d1| r 且d2 = gcd(b, r) 故由Proposition 1.2.5 知d1| d2. 另一方面, 因為d2| b 且d2| r 故d2| bh + r = a. 因此可得d2| d1.Lemma 1.3.1 告诉我们当 a > b > 0 时, 要求a, b 的最大公因数我们可以先将 a 除以 b 所得餘数若為r, 则a, b 的最大公因数等於 b 和r 的最大公因数. 因為0r < b < a, 所以当然把计算简化了. 接著我们就来看看辗转相除法. 由於gcd(a, b) = gcd(- a, b) 所以我们只要考虑a, b 都是正整数的情况.Theorem 1.3.2 (The Euclidean Algorithm) 假设a, b 且 a > b. 由除法原理我们知存在h0, r0 使得a = bh0 + r0, 其中0r0 < b.若r0 > 0, 则存在h1, r1 使得b = r0h1 + r1, 其中0r1 < r0.若r1 > 0, 则存在h2, r2 使得r0 = r1h2 + r2, 其中0r2 < r1.如此继续下去直到rn = 0 為止. 若n = 0 (即r0 = 0), 则gcd(a, b) = b. 若n1, 则gcd(a, b) = rn - 1.証明. 首先注意若r0 0, 由於r0 > r1 > r2 > ... 是严格递减的, 因為r0 和0 之间最多仅能插入r0 - 1 个正整数, 所以我们知道一定会有nr0 使得rn = 0.若r0 = 0, 即 a = bh0, 故知 b 為 a 之因数, 得证 b 為a, b 的最大公因数. 若r0 > 0, 则由Lemma 1.3.1 知gcd(a, b) = gcd(b, r0) = gcd(r0, r1) = ... = gcd(rn - 1, rn) = gcd(rn - 1, 0) = rn - 1.现在我们来看用辗转相除法求最大公因数的例子Example 1.3.3 我们求 a = 481 和 b = 221 的最大公因数. 首先由除法原理得481 = 2 . 221 + 39, 知r0 = 39. 因此再考虑 b = 221 除以r0 = 39 得221 = 5 . 39 + 26, 知r1 = 26. 再以r0 = 39 除以r1 = 26 得39 = 1 . 26 + 13, 知r2 = 13. 最后因為r2 = 13 整除r1 = 26 知r3 = 0, 故由Theorem 1.3.2 知gcd(481, 221) = r2 = 13.在利用辗转相除法求最大公因数时, 大家不必真的求到rn = 0. 例如在上例中可看出r0 = 39 和r1 = 26 的最大公因数是13, 利用Lemma 1.3.1 马上得知gcd(a, b) = 13.在上一节Corollary 1.2.5 告诉我们若gcd(a, b) = d, 则存在m, n 使得 d = ma + nb. 当时我们没有提到如何找到此m, n. 现在我们利用辗转相除法来介绍一个找到m, n 的方法. 我们沿用Theorem 1.3.2 的符号. 首先看r0 = 0 的情形, 此时 d = gcd(a, b) = b 所以若令m = 0, n = 1, 则我们有 d = b = ma + nb. 当r0 0 但r1 = 0 时, 我们知d = gcd(a, b) = r0. 故利用a = bh0 + r0 知, 若令m = 1, n = - h0, 则d = r0 = ma + nb. 同理若r0 0, r1 0 但r2 = 0, 则知d = gcd(a, b) = r1. 故利用a = bh0 + r0 以及b = r0h1 + r1 知r1 = b - r0h1 = b - (a - bh0)h1 = - h1a + (1 + h0h1)b.因此若令m = - h1 且n = 1 + h0h1, 则 d = r1 = ma + nb. 依照此法, 当r0, r1 和r2 皆不為0 时, 由於d = gcd(a, b) = rn - 1 故由rn - 3 = rn - 2hn - 1 + rn - 1 知d = rn - 3 - hn - 1rn - 2. 利用前面推导方式我们知存在m1, m2, n1, n2 使得rn - 3 = m1a + n1b 且rn - 2 = m2a + n2b 故代入得d = (m1a + n1b) - hn - 1(m2a + n2b) = (m1 - hn - 1m2)a + (n1 - hn - 1n2)b.因此若令m = m1 - hn - 1m2 且n = n1 - hn - 1n2, 则 d = ma + nb.上面的说明看似好像当r0 0 时对每一个i {0, 1,..., n - 2} 要先将ri 写成ri = mia + nib, 最后才可将d = rn - 1 写成ma + nb 的形式. 其实这只是论证时的方便, 在实际操作时我们其实是将每个ri 写成mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回d = ma + nb. 请看以下的例子.Example 1.3.4 我们试著利用Example 1.3.3 所得结果找到m, n 使得13 = gcd(481, 221) = 481m + 221n. 首先我们有13 = r2 = 39 - 26 = r0 - r1. 而r1 = 221 - 5 . 39 = b - 5r0, 故得13 = r0 - (b - 5r0) = 6r0 - b. 再由r0 = 481 - 2 . 221 = a - 2b, 得知13 = 6(a - 2b) - b = 6a - 13b. 故得m = 6 且n = - 13 会满足13 = 481m + 221n.要注意这裡找到的m, n 并不会是唯一满足 d = ma + nb 的一组解. 虽然上面的推演过程好像会只有一组解, 不过只能说是用上面的方法会得到一组解, 并不能担保可找到所有的解. 比方说若令m' = m + b, n' = n - a, 则m'a + n'b = (m + b)a + (n - a)b = ma + nb = d. 所以m', n' 也会是另一组解. 所以以后当要探讨唯一性时, 若没有充分的理由千万不能说由前面的推导过程看出是唯一的就断言是唯一. 一般的作法是假设你有两组解, 再利用这两组解所共同满足的式子找到两者之间的关系. 我们看看以下的作法.Proposition 1.3.5 假设a, b 且 d = gcd(a, b). 若x = m0, y = n0 是 d = ax + by 的一组整数解, 则对任意t , x = m0 + bt/d, y = n0 - at/d 皆為d = ax + by 的一组整数解, 而且 d = ax + by 的所有整数解必為x = m0 + bt/d, y = n0 - at/d 其中t 这样的形式.証明. 假设x = m, y = n 是 d = ax + by 的一组解. 由於已假设x = m0, y = n0 也是一组解, 故得am + bn = am0 + bn0. 也就是说a(m - m0) = b(n0 - n). 由於d = gcd(a, b), 我们可以假设 a = a'd, b = b'd 其中a', b' 且gcd(a', b') = 1 (参见Corollary 1.2.3). 因此得a'(m - m0) = b'(n0 - n). 利用b'| a'(m - m0), gcd(a', b') = 1 以及Proposition 1.2.7(1) 得b'| m - m0. 也就是说存在t 使得m - m0 = b't. 故知m = m0 + b't = m0 + bt/d. 将m = m0 + bt/d 代回am + bn = am0 + bn0 可得n = n0 - at/d, 因此得证 d = ax + by 的整数解都是x = m0 + bt/d, y = n0 -at/d 其中t 这样的形式. 最后我们仅要确认对任意t , x = m0 + bt/d, y = n0 - at/d 皆為d = ax + by 的一组整数解. 然而将x = m0 + bt/d, y = n0 - at/d 代入ax + by 得a(m0 + bt/d )+ b(n0 - at/d )= am0 + bn0 = d, 故得证本定理.利用Proposition 1.3.5 我们就可利用Example 1.3.4 找到13 = 481x + 221y 的一组整数解x = 6, y = - 13 得到x = 6 + 17t, y = - 13 - 37t 其中t 是13 = 481x + 221y 所有的整数解.欧几里得算法设计辗转相除法是利用以下性质来确定两个正整数 a 和 b 的最大公因子的:1. 若r 是 a ÷ b 的余数, 则gcd(a,b) = gcd(b,r)2. a 和其倍数之最大公因子为a。
解 二 元 一 次 方 程 — — — 拓 展 欧 几 里 得 算 法

欧几里得算法与扩展欧几里得算法(求二元一次不定方程、乘法逆元)1.欧几里得算法,即辗转相除法。
用于求两个整数的最大公约数比较方便,时间复杂度为O(logN)N为两个整数的规模。
最大公约数,是能够同时被两个整数整除的最大整数。
比如说,求56和21的最大公约数:(每行数分别代表a=56,b=21,a%b)此时得到最大公约数为7。
递归代码如下:int gcd(int a, int b)return b ? gcd(b, a%b) : a;2.扩展欧几里得算法顾名思义,扩展欧几里得算法就是对欧几里得算法的扩展,可以应用于求二元一次方程的通解、乘法逆元等。
对于上面的欧几里得算法,当递归到出口时,a=7,b=0。
很容易就可以得到一组ax+by=7的解:x=1,y=0。
那么如何通过7x+y=7的解逆推出56x+21y=7的解呢?对于欧几里得算法的每一个状态,都存在ax+by=gcd(a,b)的解,我们假设有这样两组解(且他们为相邻状态):ax1+by1=gcd(a,b)a'x2+b'y2=gcd(a',b')那么可以知道:a'=b b'=a%b 且gcd(a',b')=gcd(b,a%b)=gcd(a,b),所以有ax1+by1=bx2+(a%b)y2 另a%b可写为 a-a-b所以有 ax1+by1=bx2+(a-(a-b)b)y2故ax1+by1=ay2+bx2+(a-b)by2故ax1=ay2 by1 = b(x2+ (a-b)by2)故 x1=y2 y1 = x2 +(a-b)y2故可以得到x1,y1与x2,y2的关系 : x1=y2 y1 = x2 +(a-b)y2我们已知的是最后一组解,那么就要根据最后一组解逆推上去,就可以得到ax+by=gcd(a,b)的一组解了。
代码如下:int exgcd(int a, int b, intx, int y)return a;int r = exgcd(b, a%b, x, y); --递归到求出公约数,开始倒着求每一组的x,y。
扩展欧几里得算法以及求逆元的几种方法

扩展欧⼏⾥得算法以及求逆元的⼏种⽅法扩展欧⼏⾥得算法:ax+by=gcd(a,b)a x+by=gcd(a,b)a x+by=gcd(a,b)求出满⾜条件唯⼀的x,y的值设:设:设:r0=q1∗r1+r2r_{0}=q_{1}*r_{1}+r_{2}r0=q1∗r1+r2r1=q2∗r2+r3r_{1}=q_{2}*r_{2}+r_{3}r1=q2∗r2+r3r2=q3∗r3+r4r_{2}=q_{3}*r_{3}+r_{4}r2=q3∗r3+r4..............................rk−1=qk∗rk r_{k-1}=q_{k}*r_{k}r k−1=qk∗rk其中rk r_{k}r k就是最⼤公约数,因为rk r_{k}r k可由rk−1r_{k-1}r k−1和rk−2r_{k-2}r k−2,且rn=rn−2−qn−1∗rn−1r_{n}=r_{n-2}-q_{n-1}*r_{n-1}r n=rn−2−qn−1∗rn−1故rk−1r_{k-1}r k−1可表⽰为rk−2r_{k-2}r k−2和rk−3r_{k-3}r k−3的线性组合同理rk−2r_{k-2}rk−2也可向上表⽰。
这样得到最⼤公约数之后,⼀直向上回溯即可找到满⾜条件的x,y#include<cstdio>#include<algorithm>using namespace std;typedef long long ll;ll ExGcd(ll a,ll b,ll &x,ll &y)//求 a b 最⼤公约数,且得到gcd(a,b)=x*a+y*b;{if(!b){x=1;y=0;return a;}ll gcd=ExGcd(b,a%b,x,y);ll temp,k;k=a/b;temp=x;x=y;y=temp-k*y;return gcd;}利⽤扩展欧⼏⾥得求⼀次同余⽅程形如式⼦a∗x=c (mod m)a*x=c\ \ \ (mod \ \ m)a∗x=c (mod m),求满⾜条件的x。
扩展的欧几里得算法

扩展的欧几里得算法扩展的欧几里得算法是一种求解最大公约数的算法,也被称为扩展欧几里得算法或扩展辗转相除法。
它不仅可以求出最大公约数,还可以求出一组使得两个数的线性组合等于最大公约数的系数。
本文将介绍扩展的欧几里得算法的原理、应用及其优化。
一、原理扩展的欧几里得算法是基于欧几里得算法(辗转相除法)的扩展。
欧几里得算法是一种求解最大公约数的方法,其基本思想是:用较小的数除较大的数,再用余数去除除数,如此反复,直到余数为零为止。
最后的除数就是最大公约数。
例如,求出48和18的最大公约数,过程如下:48 ÷ 18 = 2 (12)18 ÷ 12 = 1 (6)12 ÷ 6 = 2 0因此,最大公约数是6。
扩展的欧几里得算法的主要思想是在欧几里得算法的基础上,求出一组使得两个数的线性组合等于最大公约数的系数。
设a、b为两个正整数,d为它们的最大公约数,那么必定存在整数x和y,使得ax + by = d。
扩展的欧几里得算法就是通过辗转相除的过程,递归求解x和y的值。
具体来说,假设a、b为两个正整数,d为它们的最大公约数,且a > b。
则有:1. 如果b = 0,那么d = a,此时x = 1,y = 0。
2. 如果b ≠ 0,那么可以将a除以b,得到a = bq + r(其中q为a÷b的商,r为余数)。
因为d是a和b的公约数,所以d也是b和r的公约数。
因此,可以递归地求解b和r的系数x1和y1,即有:bx1 + ry1 = d由于a = bq + r,可以将其代入上式,得到:bx1 + (a - bq)y1 = d展开后得到:ay1 + b(x1 - qy1) = d因此,x = y1,y = x1 - qy1。
通过递归求解,最终可以得到x和y的值,从而求出a和b的最大公约数d以及一组使得两个数的线性组合等于最大公约数的系数。
二、应用扩展的欧几里得算法在密码学、数论、计算机图形学等领域都有广泛的应用。
用欧几里得扩展算法求67模119的逆元

用欧几里得扩展算法求67模119的逆元欧几里得扩展算法是一种求整数逆元的常用方法,逆元的概念在数论和密码学中经常被提及。
在本篇文章中,我将以从简到繁的方式来解释欧几里得扩展算法的原理和应用,帮助你更深入地理解这一概念。
一、欧几里得算法欧几里得算法,又称辗转相除法,是求两个正整数最大公约数的一种方法。
其基本原理是利用辗转相除的过程,即不断用较小的数去除较大的数,直到余数为0为止。
这时较大的数即为最大公约数。
以求119和67的最大公约数为例,进行辗转相除的过程如下:119 ÷ 67 = 1 (52)67 ÷ 52 = 1 (15)52 ÷ 15 = 3 (7)15 ÷ 7 = 2 (1)7 ÷ 1 = 7 0根据算法得到最大公约数为1。
二、扩展欧几里得算法扩展欧几里得算法不仅可以求出最大公约数,还可以找到一组整数x 和y,使得ax + by = gcd(a, b)。
在密码学中,扩展欧几里得算法常用于求解模的逆元。
以求67模119的逆元为例,我们需要找到一个整数x,满足67x ≡ 1 (mod 119)。
使用扩展欧几里得算法,我们可以求得x的值。
我们使用欧几里得算法求得最大公约数和辅助参数:119 ÷ 67 = 1 (52)67 ÷ 52 = 1 (15)52 ÷ 15 = 3 (7)15 ÷ 7 = 2 (1)7 ÷ 1 = 7 0根据算法,得到最大公约数为1,并且可以得到一组x和y的系数:7和(-1)。
我们可以得到67模119的逆元为7。
即67*7 ≡ 1 (mod 119)。
三、个人观点和理解欧几里得扩展算法是一种非常重要的算法,它不仅能够求出最大公约数,还可以在模运算中求出逆元。
在实际应用中,逆元的概念很常见,例如在密码学的RSA加密算法中就需要用到逆元来计算私钥。
通过学习欧几里得扩展算法,我们可以更好地理解模运算和逆元的概念,提高我们的数论和密码学知识水平。
快速指数取模运算与用扩展欧几里得算法求解最大公约数和求乘法逆元

y2 = t2;
y3 = t3;
}
}
int main()
{
int x, y, z ;
int a, b;
int *p, *q;
p = &x; q = &y;
z = 0;
printf("请输入两个数: ");
scanf("%d%d", &a, &b);
if (extended_Gcd(a,b, *p, *q) == 1)
{
x = 1;
y = 0;
retቤተ መጻሕፍቲ ባይዱrn a;
}
else
{
int gcd = extended_Gcd(b, a%b, x, y);
int t = x;
x = y;
y = t - (a / b) * y;
return gcd;
}
}
int extended_Ivn(int f, int d, int *result) //求乘法逆元
cout<<"........................................................."<<endl;
cout<<"请输入指数a:"<<endl;
cin>>a;
cout<<"请输入该基数b:"<<endl;
cin>>b;
cout<<"请输入被除数n:"<<endl;
{
int c=1;
do{
用扩展欧几里得算法求乘法逆元例题

用扩展欧几里得算法求乘法逆元例题扩展欧几里得算法是计算两个整数的最大公约数的算法,并且可以根据最大公约数得到一组解,用于求解线性同余方程的解,也可以用来求乘法逆元。
下面以求解$a$的乘法逆元为例,即寻找一个整数$x$,使得$a times x equiv 1 (text{mod} p)$,其中$p$是一个质数。
使用扩展欧几里得算法,先计算$a$和$p$的最大公约数$gcd(a,p)$,假设为$d$,则有:$gcd(a,p) = d = ax + py$,其中$x$和$y$是扩展欧几里得算法得到的一组解。
由于$d$是$a$和$p$的最大公约数,所以$d$必定是$a$的约数,即$d|a$。
同时,由于$p$是质数,所以$d$不可能是$p$的约数,即$d$与$p$互质。
因此,我们可以将等式两边同时除以$d$,得到:$dfrac{a}{d}x + dfrac{p}{d}y = 1$由于$d$与$p$互质,所以$dfrac{p}{d}$的乘法逆元存在,假设为$k$,即$dfrac{p}{d} times k equiv 1 (text{mod} d)$。
将$k$乘到等式两边,得到:$dfrac{a}{d} times k times x + dfrac{p}{d} times k times y = k$由于$dfrac{p}{d} times k equiv 1 (text{mod} d)$,所以可以将$dfrac{p}{d} times k$替换为$z$,得到:$dfrac{a}{d} times k times x + z times y = k$这个等式可以看成是一个线性同余方程$dfrac{a}{d} times k times x + z times y equiv k (text{mod} d)$,使用扩展欧几里得算法求解即可得到$x$的值。
总结一下求乘法逆元的步骤:1. 使用扩展欧几里得算法计算$a$和$p$的最大公约数$gcd(a,p)$,得到一组解$x$和$y$,使得$gcd(a,p) = ax + py$。
欧几里得算法

Euclid算法定义gcd(a,b)=gcd(b, a+kb) a,b,k为任意整数即gcd(a,b)=gcd(b, a mod b) a≥0,b>0• Example:gcd(55,22)=gcd(22, 55mod22)=gcd(22,11)=11证明:假定d=gcd(a,b),那么有d|a和d|b.对任何正整数b,a可表示为如下形式:a=kb+r ≡r mod b, a mod b =r , 因此,有(a mod b )= a-kb,k为某个整数。
但由于d|b,b也能整除kb, 而d|a,故有d|(a mod b), 这表明d 也是b 和(amod b) 的公因子。
由于这是可逆的,如果d 是b 和(a modb) 的公因子,那么d|kb,且d|[kb+(a mod b)],这等同于d|a。
这样a和b的公因子集合等同于b 和(a mod b) 的公因子集合。
编辑本段C语言的Euclid算法描述int gcd(int a,int b)//注释:两个数辗转相除。
a>b,如果a<b,需要将他们交换,这里不想写交换部分代码{if(a==0)return b;if(b==0)return a;return gcd(b,a%b);}编辑本段Euclid算法的应用求两个数的最大公约数gcd(55,22)=gcd(22, 55mod22)=gcd(22,11)=11最常用的就是在RSA里边求密钥RSA算法,是非对称加密的标准算法,其实算法很简单:找到两个素数p,q,再找一个数r,使gcd(r,(p-1)(q-1))=1,也就是说互素,然后再找一个数m,使rm=1(mod (p-1)(q-1)),然后再作乘法n=pq,然后把pq 丢掉,最好是让任何人都不知道,包括自己(免得说梦话的时候被人听到),然后手里拿到r,m,n,r就是Private Key,只有你知道,而m,n就是Public Key。
扩展欧几里得

扩展欧几里得
扩展欧几里得算法是欧几里得算法(又叫辗转相除法)的扩展。
除了计算a、b两个整数的最大公约数,此算法还能找到整数x、y(其中一个很可能是负数)。
通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。
有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数——这是众所周知的。
然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
扩展欧几里得算法(英语:Extended Euclidean algorithm)是欧几里得算法(又叫辗转相除法)的扩展。
已知整数a、b,扩展欧几里得算法可以在求得a、b的最大公约数的同时,能找到整数x、y(其中一个很可能是负数),使它们满足贝祖等式
如果a是负数,可以把问题转化成
,然后令x'=(-x)。
通常谈到最大公约数时,我们都会提到一个非常基本的事实:给予二个整数a、b,必存在整数x、y使得ax + by = gcd(a,b)。
有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数——这是众所周知的。
然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
扩展欧几里得算法可以用来计算模反元素(也叫模逆元),而模反元素在RSA加密算法中有举足轻重的地位。
拓展的欧几里得算法求乘法逆元

拓展的欧几里得算法求乘法逆元拓展的欧几里得算法又叫扩展欧几里得算法,是一种求解一元线性同余方程的方法,可以用来求解乘法逆元。
假设要求a在模n下的乘法逆元,即找到x满足ax ≡ 1 (mod n)。
算法步骤如下:1. 用欧几里得算法求出a和n的最大公约数gcd(a,n)以及对应的系数s和t。
2. 如果gcd(a,n)不等于1,则a在模n下没有乘法逆元。
3. 如果gcd(a,n)等于1,则ax ≡ 1 (mod n)可以转化为ax + ny = 1的形式,其中y为x的系数。
4. 用扩展的欧几里得算法求出gcd(a,n)的系数s和t,使得sa + tn = gcd(a,n)。
5. 把等式ax + ny = 1中的a用sa + tn替换,得到(sx +n'y)a + (ty) n = 1,其中n'为n的系数。
6. 取模得到(sx + n'y)a ≡ 1 (mod n),即ax在模n下的乘法逆元为sx + n'y。
举例说明:计算16在模21下的乘法逆元。
1. 计算gcd(16,21):21 = 1 × 16 + 5,16 = 3 × 5 + 1,gcd(16,21) = 1。
2. gcd(16,21) = 1,继续下一步。
3. 转化为16x + 21y = 1的形式,求出y的系数。
4. 用扩展的欧几里得算法求出gcd(16,21)的系数s和t,使得16s + 21t = gcd(16,21),得到s = 11,t = -8。
5. 代入得到(11x - 8y)16 + 21y = 1,即(11x - 8y)16 ≡ 1 (mod 21)。
6. 求解得到x = 11,即16在模21下的乘法逆元为11。
注意事项:1. 模数n必须是正整数,且与a互质,否则a在模n下没有乘法逆元。
2. 扩展的欧几里得算法有多组解,根据具体问题设置取值范围。
模p意义下的乘法逆元

模p意义下的乘法逆元在模运算中,乘法逆元是指对于给定的整数 a 和模数 p 的情况下,可以找到另一个整数 b,使得(a * b) mod p = 1、简而言之,乘法逆元就是 a 关于模 p 的乘法逆元。
在本文中,我们将详细讨论如何找到模p 意义下的乘法逆元,并探讨一些相关的重要概念和性质。
首先,我们需要明确一个基本的观点:乘法逆元并不是对于所有的 a 来说都一定存在。
对于 a 和 p 来说,它们在模运算的范围内必须满足一些条件,才能找到乘法逆元。
具体来讲,一个整数 a 的乘法逆元存在的条件是 a 和 p 互质。
也就是说,a 和 p 不能有任何一个公因数,除了1、如果 a 和 p 不互质,那么相当于存在一个公因数,我们无法找到另一个数 b 使得(a * b) mod p = 1、因此,我们只对 a 和 p 互质的情况进行讨论。
接下来,让我们考虑如何找到模 p 意义下的乘法逆元。
一种常用的方法是使用扩展欧几里得算法。
该算法可以在给定 a 和 p 的情况下,求出 a 的乘法逆元。
更具体地说,扩展欧几里得算法通过递归地调用自身,找到满足恒等式 gcd(a, p) = a * s + p * t 的 s 和 t。
其中,gcd(a, p) 表示 a 和 p 的最大公约数。
如果 a 和 p 互质,那么最大公约数就是 1,此时,恒等式可以简化为 1 = a * s + p * t。
根据模运算的性质,我们可以将恒等式两边同时取模 p,得到1 ≡ a * s (mod p)。
因此,s 就是 a 在模 p 意义下的乘法逆元。
这样,我们就可以使用扩展欧几里得算法来找到模 p 意义下的乘法逆元。
除了扩展欧几里得算法,还有一种更快速的方法来求解模 p 意义下的乘法逆元,即费马小定理。
费马小定理指出,如果 p 是一个质数,且a 是一个与之互质的整数,那么有 a^(p-1) ≡ 1 (mod p)。
根据这个定理,我们可以得出 a 在模 p 意义下的乘法逆元为 a^(p-2) (mod p)。
欧几里德算法及其扩展

欧几里德与扩展欧几里德算法欧几里德算法欧几里德算法乂称辗转相除法,用丁计算两个整数a,b的最大公约数。
基本算法:设a=qb+r,其中a, b, q, r都是整数,贝U gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd(b,a%b)。
第一种证明:a 可以表示成a = kb + r ,贝U r = a mod b假设d是a,b的一个公约数,则有d|a, d|b ,而r = a - kb ,因此d|r因此d是(b,a mod b)的公约数假设d是(b,a mod b)的公约数,贝Ud | b , d |r ,但是a = kb +r因此d也是(a,b)的公约数因此(a,b)和(b,a modb)的公约数是一样的,其最大公约数也必然相等,得证第二种证明:要证欧几里德算法成立,即证:gcd(a,b)=gcd(b,r), 其中gcd是取最大公约数的意思,r=a mod b下面证gcd (a, b) =gcd (b, r)设 c 是a, b的最大公约数,即c=gcd (a, b),贝U有a=mc, b=nc,其中m, n为正整数,且m n五为质数由r= a mod b 可知,r= a- qb 其中,q是正整数,贝U r=a-qb=mc-qnc= (m-qn) cb=nc,r=(m-qn)c ,且n, (m-qn)互质(假设n, m-qn不互质,贝U n=xd, m-qn=yd 其中x,y,d都是正整数,且d>1则a=mc=(qx+y)dc, b=xdc,这时a,b的最大公约数变成dc,与前提矛盾,所以n , m-qn一定互质)贝U gcd (b,r ) =c=gcd (a,b)得证。
算法的实现:最简单的方法就是应用递归算法,代码如下: 日巳1 int gcd( int a, int b)2 (3 if (b==0)4 return a;5 return6 gcd(b,a%b);7}代码可优化如下:1 int gcd( int a, int b)2 (3 return b ? gcd(b,a%b) : a;4 }当然你也可以用迭代形式:日电1 int Gcd( int a, int b)扩展欧几里德算法基本算法:对丁不完全为0的非负整数a , b, gcd (a, b)表示a , b 的最大公约数,必然存在整数对x , y ,使得gcd (a, b) =ax+by 。
快速指数取模运算与用扩展欧几里得算法求解最大公约数和求乘法逆元

快速指数取模运算与用扩展欧几里得算法求解最大公约数和求乘法逆元1.将指数N转换为二进制表示,例如N=13,二进制表示为11012.从左往右遍历二进制表示,如果当前位的值为1,则将底数X乘以自身的幂次。
3.在每次乘法操作后,将结果取模M,即取结果与M的余数。
4.继续遍历下一位,重复2-3步骤。
5. 最后的结果即为X^N mod M。
例如,计算13的12次方对11取模的结果,可以按照上述步骤进行计算:1.将指数12转换为二进制表示为1100。
2.从左往右遍历二进制表示,初始底数为13,结果为1- 第1位为1,计算结果为1^2 mod 11 = 1- 第2位为1,计算结果为1^2 mod 11 = 1- 第3位为0,计算结果为1^2 mod 11 = 1- 第4位为0,计算结果为1^2 mod 11 = 13.最后的结果为1使用快速指数取模运算可以大幅提高指数幂的计算效率,尤其在需要进行大数运算或者需要频繁计算指数模的场景下更加明显。
扩展欧几里得算法也是一种常用的数学算法,用于求解两个整数的最大公约数以及求解两个整数的乘法逆元。
该算法的基本原理是基于贝祖等式和欧几里得算法的扩展版本。
扩展欧几里得算法的具体步骤如下:1.初始化参数,设a为被除数,b为除数,x=0,y=1,u=1,v=0。
2.通过欧几里得算法求解a除b的余数,并更新a和b的值。
3.计算商q和a除b的余数r,并更新x、y、u和v的值。
- x <- u - qx- y <- v - qy-u<-x-v<-y4.重复步骤2-3,直到余数r等于0。
5.最大公约数为b,乘法逆元为v。
使用扩展欧几里得算法可以快速求解两个数的最大公约数和乘法逆元。
最大公约数在数论和密码学中有广泛的应用,而乘法逆元则常用于求解同余方程和模运算相关的问题。
综上所述,快速指数取模运算和扩展欧几里得算法是两个重要的数学算法,在很多应用领域中具有广泛的应用。
用欧几里得扩展算法求67模119的逆元

让我们来掏空欧几里得扩展算法。
欧几里得算法,也称为辗转相除法,是一种用来计算两个数的最大公约数的有效算法。
而欧几里得扩展算法,则可以进一步应用到求解模运算的逆元问题上。
现在,让我们来解决一个具体的问题:用欧几里得扩展算法求67模119的逆元。
我们需要明确逆元的概念。
在模运算中,如果存在一个数x,使得a*x ≡ 1 (mod m),那么x就是a在模m意义下的逆元。
逆元就是在模m 意义下,对于给定的数,能够使得它与另一个数的乘积模m后得到1的数。
接下来,我们可以使用欧几里得扩展算法来求解逆元。
该算法的一般步骤如下:步骤1:我们需要使用欧几里得算法来计算出67和119的最大公约数。
这可以通过不断地进行辗转相除来逐步缩小问题规模,直到找到最大公约数为止。
假设最终的最大公约数为d。
步骤2:利用欧几里得算法中的倒推过程,我们可以得到一个关于67和119的线性组合,使得这个组合等于d。
也就是说,存在整数x和y,使得67*x + 119*y = d。
步骤3:如果d=1,说明67和119互质,我们可以继续进行下一步。
如果d不等于1,那么67和119不互质,说明67在模119意义下没有逆元。
步骤4:我们可以根据步骤2中得到的线性组合,通过适当的变换,找到一个关于67和119的线性组合,使得这个组合等于1。
这个线性组合中的系数就是67在模119意义下的逆元。
通过上述步骤,我们可以求解出67在模119意义下的逆元。
将这个逆元记为x,即67 * x ≡ 1 (mod 119)。
这样,我们就成功地用欧几里得扩展算法求解了67模119的逆元。
值得注意的是,欧几里得扩展算法不仅可以用来求解模运算的逆元问题,还可以在密码学、数论和离散数学等领域中发挥重要作用。
对于这一算法的掌握和理解具有重要的实际意义。
总结回顾一下,通过本文的讨论,我们对欧几里得扩展算法的应用有了更深入的了解。
从最大公约数的计算到线性组合的推导,再到逆元的求解,我们逐步揭开了算法的神秘面纱。
扩展的欧几里得算法求乘法逆元举例

扩展的欧几里得算法求乘法逆元举例扩展的欧几里得算法是求解线性同余方程的一种重要方法,而乘法逆元就是线性同余方程的一种特殊情况。
本文将以扩展的欧几里得算法求乘法逆元举例,为读者介绍这一算法的基本原理和应用。
一、乘法逆元的定义在模运算中,如果存在一个数a和模数m,使得a与m互质,那么我们称a在模m下有乘法逆元。
具体来说,如果存在一个数b,满足以下条件:a*b ≡ 1 (mod m)则我们称b是a在模m下的乘法逆元。
需要注意的是,不是所有数都有乘法逆元。
例如,在模10下,数2没有乘法逆元,因为它与10不互质。
二、扩展的欧几里得算法扩展的欧几里得算法是求解线性同余方程ax ≡ b (mod m)的一种方法,其中a和m是已知正整数,b是未知数。
该算法的基本思想是利用欧几里得算法求解a和m的最大公约数,并同时求得一个关于a和m的线性组合,使得它们的最大公约数等于1。
具体来说,我们可以用以下递归式表示扩展的欧几里得算法:gcd(a, m) = gcd(m, a % m)其中,%表示模运算。
当a % m = 0时,gcd(a, m) = m。
否则,我们可以继续递归,直到a % m = 0为止。
最终得到的gcd(a, m)就是a和m的最大公约数。
在递归的过程中,我们可以维护一个关于a和m的线性组合x和y,满足以下式子:gcd(a, m) = ax + my当a % m = 0时,我们有m = gcd(a, m),此时x = 0,y = 1。
否则,我们可以通过递归求得m和a % m的线性组合y1和x1,然后可以根据以下公式求得x和y:x = y1 - (a / m) * x1y = x1当我们求得了x和y之后,我们可以利用它们来求解线性同余方程ax ≡ b (mod m)的解。
具体来说,我们可以先检查gcd(a, m)是否为b的因子,如果不是,则方程无解。
否则,我们可以将方程两边同时乘以x和b / gcd(a, m),得到以下等价方程:ax * x' ≡ b / gcd(a, m) (mod m)其中,x' = x * (b / gcd(a, m))。
欧几里得最大公约数算法

欧几里得最大公约数算法算法介绍欧几里得最大公约数算法,也称作辗转相除法,是一种用于求解两个数的最大公约数的算法。
这个算法是根据古希腊数学家欧几里得提出的,可以追溯到公元前300年左右。
这个算法基于一个简单的观察:两个数的最大公约数等于其中较小数和两数相除的余数的最大公约数。
这个算法非常简单而有效,被广泛应用于数学和计算机科学领域。
算法实现下面是使用欧几里得算法计算最大公约数的伪代码:function gcd(a, b)if b is 0return aelsereturn gcd(b, a % b)在这段伪代码中,a 和 b 是两个输入的数。
算法会递归地调用自身,每次将 b 和a % b 作为新的输入,直到 b 变为0。
此时,a 就是最大公约数。
算法分析欧几里得算法的时间复杂度取决于两个输入数的大小。
在最坏情况下,如果两个数相差很大,算法的时间复杂度是O(log n),其中n是较大的输入数。
这是因为每次迭代,a 的值都会缩小至约为原来的一半。
总体来说,欧几里得算法具有很好的时间复杂度,并且可以在较短的时间内找到最大公约数。
算法应用欧几里得算法有许多实际应用,其中一些常见的应用包括:1. 分数的约简在分数运算中,我们经常需要将分数约简到最简形式。
最简分数的特点是分子和分母没有共同的因子,也就是它们的最大公约数为1。
欧几里得算法可以用来求解分数的最大公约数,并将分子和分母都除以最大公约数,从而得到最简分数。
2. 数学证明在数学证明中,我们经常需要证明两个整数具有某种性质。
而要证明两个整数具有某种性质,可以通过证明它们的最大公约数具有该性质。
欧几里得算法可以帮助我们高效地计算最大公约数,从而简化证明过程。
3. 加解密算法在加解密算法中,我们经常需要使用模运算。
而欧几里得算法可以帮助我们高效地计算出模运算的结果。
例如,在RSA加密算法中,欧几里得算法被用于计算公钥和私钥。
4. 图论和网络分析在图论和网络分析中,我们经常需要计算某两个节点之间的最短路径。
拓展的欧几里得算法求逆元c++

拓展的欧几里得算法求逆元欧几里得算法(Euclidean algorithm)是一种用于求两个正整数最大公约数的算法。
在数论和密码学中,拓展的欧几里得算法经常被用来求解模线性方程 a * x ≡ 1 (mod m)中的模反元素x。
算法步骤1.若m 为0,则返回a,此时a 的模反元素不存在。
2.使用递归调用函数自身,传入参数(m, a % m),并将结果保存为 d = gcd(m,a % m),其中gcd 表示最大公约数。
3.若d 不为1,则a 的模反元素不存在。
4.若d 为1,则根据拓展的欧几里得定理计算模反元素x = y - (a / m) *z,其中y 和z 是递归调用函数的返回值。
5.返回x 作为a 的模反元素。
C++ 代码示例#include <iostream>using namespace std;int extendedGCD(int a, int b, int &x, int &y) { if (b == 0) { x = 1; y = 0; return a; } int x1, y1; int gcd = extendedGCD(b, a % b, x1, y1); x = y1; y = x1 - (a / b) * y1; return gcd;}int modInverse(int a, int m) { int x, y; int gcd = extendedGCD(a, m, x, y); if (gcd != 1) return -1; return (x % m + m) % m;}int main() { int a, m; cout << Enter a: ; cin >> a; cout << Enter m: ; cin >> m; int inverse = modInverse(a, m); if (inverse == -1) cout << Modular inverse doesn't exist. << endl; else cout << Modular inverse of << a << mod << m << is << inverse << endl; return 0;}。
乘法逆元计算详解

乘法逆元计算详解乘法逆元是指在模n的情况下,对于整数a,如果存在一个整数b,使得ab ≡ 1 (mod n),则b被称为a的乘法逆元。
乘法逆元在数论和密码学中都有广泛的应用。
在计算乘法逆元之前,我们需要了解一些数论的基本概念。
首先,我们知道,对于给定的正整数n,如果a和b满足ab ≡ 1 (mod n),则称a是b的模n乘法逆元,b是a的乘法逆元,记为b ≡a⁻¹ (mod n)。
其次,在模n下,a的乘法逆元存在的充分必要条件是a与n互质,即gcd(a, n) = 1、如果a与n不互质,则不存在a的乘法逆元。
因此,在计算乘法逆元时,我们需要先判断a与n是否互质。
有了上述基础知识,我们可以通过扩展欧几里得算法来计算乘法逆元。
扩展欧几里得算法是一种计算两个整数a和b的最大公约数gcd(a, b)以及满足ax + by = gcd(a, b)的整数解x和y的算法。
在计算乘法逆元时,我们可以将乘法逆元问题转化为求解一个线性方程的问题。
具体步骤如下:1.判断a与n是否互质。
如果不互质,则a的乘法逆元不存在。
2. 使用扩展欧几里得算法计算a和n的最大公约数gcd(a, n)以及满足ax + ny = gcd(a, n)的整数解x和y。
3. 如果gcd(a, n) = 1,则a的乘法逆元存在。
乘法逆元b = x (mod n)。
下面我们通过一个具体的例子来说明乘法逆元的计算过程。
假设我们要计算a=7在模n=26下的乘法逆元。
首先,判断7和26是否互质。
由于它们的最大公约数为1,因此它们互质。
接下来,使用扩展欧几里得算法计算7和26的最大公约数以及整数解。
由于7较小,我们可以使用欧几里得算法来计算最大公约数。
计算过程如下:26=7*3+57=5*1+25=2*2+12=1*2+0我们可以倒推得到两个整数解x和y:x=-1y=3由于7与26互质,因此7的乘法逆元存在。
根据乘法逆元的定义,b ≡ x (mod n)。
逆元讲解(三种方法)
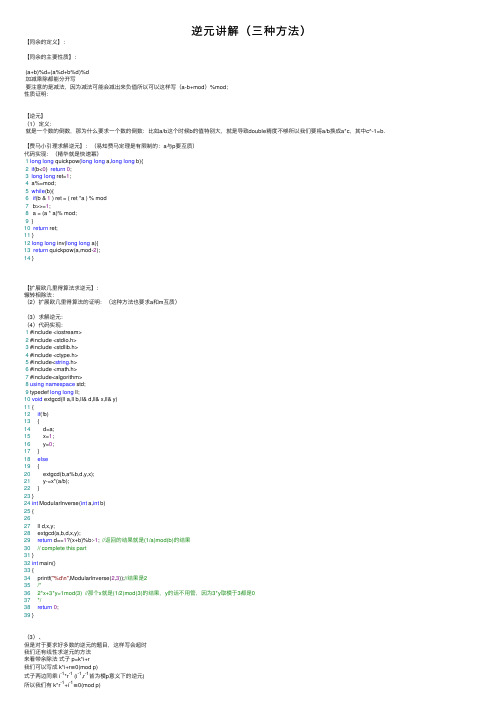
逆元讲解(三种⽅法)【同余的定义】:【同余的主要性质】:(a+b)%d=(a%d+b%d)%d加减乘除都能分开写要注意的是减法,因为减法可能会减出来负值所以可以这样写(a-b+mod)%mod;性质证明:【逆元】(1)定义:就是⼀个数的倒数,那为什么要求⼀个数的倒数:⽐如a/b这个时候b的值特别⼤,就是导致double精度不够所以我们要将a/b换成a*c,其中c^-1=b.【费马⼩引理求解逆元】:(易知费马定理是有限制的:a与p要互质)代码实现:(精华就是快速幂)1long long quickpow(long long a,long long b){2if(b<0) return0;3long long ret=1;4 a%=mod;5while(b){6if(b & 1 ) ret = ( ret *a ) % mod7 b>>=1;8 a = (a * a)% mod;9 }10return ret;11 }12long long inv(long long a){13return quickpow(a,mod-2);14 }【扩展欧⼏⾥得算法求逆元】:辗转相除法:(2)扩展欧⼏⾥得算法的证明:(这种⽅法也要求a和m互质)(3)求解逆元:(4)代码实现:1 #include <iostream>2 #include <stdio.h>3 #include <stdlib.h>4 #include <ctype.h>5 #include<string.h>6 #include <math.h>7 #include<algorithm>8using namespace std;9 typedef long long ll;10void extgcd(ll a,ll b,ll& d,ll& x,ll& y)11 {12if(!b)13 {14 d=a;15 x=1;16 y=0;17 }18else19 {20 extgcd(b,a%b,d,y,x);21 y-=x*(a/b);22 }23 }24int ModularInverse(int a,int b)25 {2627 ll d,x,y;28 extgcd(a,b,d,x,y);29return d==1?(x+b)%b:-1; //返回的结果就是(1/a)mod(b)的结果30// complete this part31 }32int main()33 {34 printf("%d\n",ModularInverse(2,3));//结果是235/*36 2*x+3*y=1mod(3) //那个x就是(1/2)mod(3)的结果,y的话不⽤管,因为3*y取模于3都是037*/38return0;39 }(3)、但是对于要求好多数的逆元的题⽬,这样写会超时我们还有线性求逆元的⽅法来看带余除法式⼦ p=k*i+r我们可以写成 k*i+r≡0(mod p)式⼦两边同乘 i-1*r-1 (i-1,r-1皆为模p意义下的逆元)所以我们有 k*r-1+i-1≡0(mod p)i-1≡-k*r-1(mod p)i-1≡-(p/i)*(p%i)-1(mod p)所以i-1可以⽤(p%i)-1推出,所以就可以⽤递推式求出来1到i之间所有数的逆元代码:1//1、线性求逆元2int inv[MAXN];3void INV(int a,int p)//线性求到a的逆元4 {5 inv[1] = 1;6for (int i=2; i<=a; ++i)7 inv[i] = (-(p/i))*inv[p%i]%p;8 }910//2、单独求某个值的逆元11int INV(int a)//线性求a的逆元12 {13if (a==1) return1;14return ((-(p/a)*INV(p%a))%p);15 }。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验1.1源代码:#include来自"stdio.h"
#include "stdlib.h"
#include "iostream"
using namespace std;
void Mode(int a, int b, int n)
{
int c=1;
do{
if(a%2==0)
return 1;
}
q = x3 / y3;
t1 = x1 - q*y1;
t2 = x2 - q*y2;
t3 = x3 - q*y3;
x1 = y1;
x2 = y2;
x3 = y3;
y1 = t1;
y2 = t2;
y3 = t3;
}
}
int main()
{
int x, y, z ;
int a, b;
int extended_Gcd(int a,int b, int &x, int &y) //求最大公约数
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
else
{
int gcd = extended_Gcd(b, a%b, x, y);
int t = x;
x = y;
y = t - (a / b) * y;
cout<<"请输入指数a:"<<endl;
cin>>a;
cout<<"请输入该基数b:"<<endl;
cin>>b;
cout<<"请输入被除数n:"<<endl;
cin>>n;
Mode(a,b,n);
}
二、实验效果图:
实验1.2用扩展欧几里得算法求解最大公约数和求乘法逆元
一、实验1.2源代码:
#include <stdio.h>
y3 = (f >= d) ? d : f;
while (1)
{
if (y3 == 0)
{
*result = x3; //两个数不互素则result为两个数的最大公约数,此时返回值为零
return 0;
}
if (y3 == 1)
{
*result = y2; //两个数互素则resutl为其乘法逆元,此时返回值为1
return gcd;
}
}
int extended_Ivn(int f, int d, int *result) //求乘法逆元
{
int x1, x2, x3, y1, y2, y3, t1, t2, t3, q;
x1 = y2 = 1;
x2 = y1 = 0;
x3 = (f >= d) ? f : d;
int *p, *q;
p = &x; q = &y;
z = 0;
printf("请输入两个数: ");
scanf("%d%d", &a, &b);
if (extended_Gcd(a,b, *p, *q) == 1)
{
extended_Ivn(a, b, &z);
printf("%d和%d互素,乘法的逆元是:%d\n", a, b, z);
}
else
{
z=extended_Gcd(a,b, *p, *q);
printf("%d和%d不互素,最大公约数为:%d\n", a, b, z);
}
return 0;
}
二、实验效果图:
{
a=a/2;
b=(b*b)%n;
}
else
{
a=a-1;
c=(b*c)%n;
}
}while(a!=0);
cout<<"取余结果为:"<<c<<endl;
}
void main ()
{
int a, b, n;
cout<<"输入格式范例b^a mod n"<<endl;
cout<<"........................................................."<<endl;
