点群、空间群和晶体结构介绍PPT课件
合集下载
《化学中的群论》课件

02
子群
一个群G的子集H也是群(称为“子 群”),如果H关于H上的群运算也 是群。
03
同态
如果存在一个映射f,使得对于G中的 任意两个元素a和b,都有 f(a*b)=f(a)*f(b),则称f为同态映射, G和它的同态像之间存在一一对应关 系。
02
分子对称性与群论
对称操作与对称元素
对称操作
旋转、反演、镜面反射等。
可以使得电子云更好地重叠,反键轨道则会使得电子云分离,而非键轨
道则对分子稳定性没有明显影响。
03
分子轨道的填充规则
根据泡利不相容原理和洪特规则,电子优先填充能量较低的轨道,并且
优先占据空轨道。
群论在分子轨道理论中的应用
群论的基本概念
群论是研究对称性问题的数学工具,它可以用来描述分子中的电子云分布和分子整体的对 称性。
群论在分子轨道理论中的应用
群论可以用来描述分子轨道的对称性和分类,以及分析分子中的电子云分布和分子整体的 对称性。这有助于理解分子的性质和反应机理。
群论在化学反应中的应用
群论还可以用来描述化学反应中的对称性变化,以及预测反应产物的结构和性质。这有助 于设计新的化学反应和合成路线。
化学键的稳定性与群论
化学反应的预测与群论
01Biblioteka 0203化学反应的预测是计算 化学中的重要任务之一 ,通过理论计算可以预 测可能的反应途径和产
物。
群论在化学反应预测中 的应用主要体现在对反 应中间体的对称性和反
应路径的分析上。
通过群论的方法,可以 更好地理解反应机理, 预测可能的反应产物, 并为实验研究提供理论
支持。
晶体结构可以通过X射线晶体 学、中子散射和电子显微镜等 技术进行测定。
2.2.3点群和空间群

该图形显然具有一个对称中心
因此 3 次倒转轴相当于 1 条 3 次旋转轴加上一个对称中心
3 3i
4 次倒转轴
相当于旋转90后再对中 心反演而图形不变。
这是一个独立的对称操 作。它既没有 4 次旋转 轴也没有对称中心,不 能分解成其他基本对称 要素的组合。
注意这里的 2、6、4、 8 这四个点是不存在的, 也是过渡点。
对称面
对称面是一个假想的平面,相应 的对称操作为对此平面的反映。对 称面就像一面镜子,把物体的两个 相同的部分以互成镜像反映的关系 联系起来。 垂直于对称面作任意直线,位于 直线两侧等距离的两点是性质完全 相同的对应点 晶体中如果存在有对称面,则必 定通过晶体的几何中心并将晶体分 为互成镜像反映的两个相同部分 在结晶学中,对称面一般用符号 “m” 表示。
倒转轴
倒转轴是一种复合对称 要素,由一根假想的直线 和在此直线上的一个定点 组成。相应的对称操作是 绕此直线旋转一定角度以 及对此定点的倒反。 根据晶体对称轴定律,倒 转轴也只有 1 次、2 次、 3 次、4 次和 6 次 5 种
倒反类倒转轴 中,只有 4 次倒转轴是一个独立的基本对称操
点群:在宏观晶体中存在的所有对称要素都必定 通过晶体的中心,因此不论如何进行对称操作,晶
体中至少有一个点是不变的,因此对称型也称为点
群。32点群
特征对称元素与7 大晶系
在32晶体学点群中,某些点群均含有一种相同的对称元素, 这样的对称元素叫做特征对称元素。
根据相应的对称性特征,晶体结构可以分为 7 类, 称为 7 大晶系。这 7 大晶系按对称程度增加的次序
在旋转操作中,使物体复原所需的最小旋转角 称为基转角。轴次 n 可以写成
刘胜新-第三章点群、空间群和晶体结构PPT课件

上述的推导过程完全可以推广到其它晶系的空间群。把上述办
法依次用于7种晶系,共导出66种空间群。如果再考虑点群元素与
布喇菲点阵之间的取向关系,又能得到另一些空间群,结果总共得
出7320种20/1点0/9式空间群。
1
附表3 73种点式空间群
1 2020/10/9
3.4.2 非点式空间群
非点式空间群必包含1个非初基平移T的非点式操作,引入了 这种非点式操作,又可以导出157种非点式空间群。
石英的基本结构可以看成是硅氧四面体在三和六次螺旋轴 附近的螺旋链。左边为其中一个三次螺旋,右方显示的是螺旋连 接构成晶体框架。
1 2020/10/9
滑移面
由镜面和平移组合产生的对称元素称为滑移反映面,简称滑移
1 2020/10/9
子群、母群及生殖元素
子群:若群GA的全部元素是群G中的元素,并且两者的结合律 相同,称GA是群G的子群,而G是群GA的母群。如果对称元素GA和 GB能够得到G的全部对称元素,则称这两个对称元素为群G中的两 个生殖元素(Generating Element).
3.2点群的描述及图示
的全2对020/称10/点9 群。
1
从上述两种点群的极射投影再一次说明在投影图上一般位置的 正规点系的数目和点群具有对称操作的数目相同,即与点群的阶数 相同。
1 2020/10/9
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等效 点系共有48个点。
230种
对称操作全部作用于同一个公共点上的,至少包
含一个比初基平移还要小的平移τ。 157种
1
材料科学基础第三章典型晶体结构(共71张PPT)

Zn离子的位置交叉错开。
表示方法:球体堆积法;坐标法;投影图;配位多面体连 接方式
与金刚石晶胞的比照 ,有什么不同?
同型结构的晶体β-SiC,GaAs,AlP 等
5、 -ZnS〔纤锌矿〕型结构 〔AB type〕
六方晶系,简单六方格子
配位数:
晶胞中正负离子个数
堆积及空隙情况
同型结构的晶体:BeO, ZnO, AlN等
笼外俘获其它原子或基团,形成类C60的衍生物,例如
C60F60。再如,把K、Cs、Ti等金属原子掺进C60分子 的笼内,就能使其具有超导性能。再有C60H60这些相 对分子质量很大地碳氢化合物热值极高,可做火箭的 燃料等等。
2〕碳纳米管
碳纳米管又称纳米碳管〔 Carbon nanotube,CNT〕,是 单质碳的一维结构形式。碳纳米 管按照石墨烯片的层数分类可分 为:单壁碳纳米管〔Singlewalled nanotubes, SWNTs〕和多 壁碳纳米管〔Multi-walled nanotubes, MWNTs〕。
4. -ZnS〔闪锌矿〕型结构 〔AB type〕 点群:
空间群:
配位数:
晶胞中正负离子个数Z:
堆积及间隙情况:
• 以体积较大的S2-作立方紧密堆积 • Zn2+如何填充? • 空隙如何分布?
等同点分布:
共有2套等同点。这种结构 可以看作是Zn离子处在由S离 子组成的面心立方点阵的4个
四面体间隙中,即有一半四面 体间隙被占据,上层和下层的
晶体结构的描述通常有三种方法:
1〕坐标法:给出单位晶胞中各质点的空间坐标,这种采用
数值化方式描述晶体结构是最标准化的。为了方便表示晶胞, 化学式可写为MO,其中M2+是二价金属离子,结构中M2+和O2-分别占据了NaCl中钠离子和氯离子的位置。 以由体正积 负还较离大子可的半径S以2比-作rN采立a方+/r用紧cl-密≈堆投0.积 影图,即所有的质点在某个晶面〔001〕上的投
表示方法:球体堆积法;坐标法;投影图;配位多面体连 接方式
与金刚石晶胞的比照 ,有什么不同?
同型结构的晶体β-SiC,GaAs,AlP 等
5、 -ZnS〔纤锌矿〕型结构 〔AB type〕
六方晶系,简单六方格子
配位数:
晶胞中正负离子个数
堆积及空隙情况
同型结构的晶体:BeO, ZnO, AlN等
笼外俘获其它原子或基团,形成类C60的衍生物,例如
C60F60。再如,把K、Cs、Ti等金属原子掺进C60分子 的笼内,就能使其具有超导性能。再有C60H60这些相 对分子质量很大地碳氢化合物热值极高,可做火箭的 燃料等等。
2〕碳纳米管
碳纳米管又称纳米碳管〔 Carbon nanotube,CNT〕,是 单质碳的一维结构形式。碳纳米 管按照石墨烯片的层数分类可分 为:单壁碳纳米管〔Singlewalled nanotubes, SWNTs〕和多 壁碳纳米管〔Multi-walled nanotubes, MWNTs〕。
4. -ZnS〔闪锌矿〕型结构 〔AB type〕 点群:
空间群:
配位数:
晶胞中正负离子个数Z:
堆积及间隙情况:
• 以体积较大的S2-作立方紧密堆积 • Zn2+如何填充? • 空隙如何分布?
等同点分布:
共有2套等同点。这种结构 可以看作是Zn离子处在由S离 子组成的面心立方点阵的4个
四面体间隙中,即有一半四面 体间隙被占据,上层和下层的
晶体结构的描述通常有三种方法:
1〕坐标法:给出单位晶胞中各质点的空间坐标,这种采用
数值化方式描述晶体结构是最标准化的。为了方便表示晶胞, 化学式可写为MO,其中M2+是二价金属离子,结构中M2+和O2-分别占据了NaCl中钠离子和氯离子的位置。 以由体正积 负还较离大子可的半径S以2比-作rN采立a方+/r用紧cl-密≈堆投0.积 影图,即所有的质点在某个晶面〔001〕上的投
晶体结构基本知识共36页PPT资料

1
c轴方向
-1
晶胞形状:轴长不相等,轴角不相等
单斜晶系-Monoclinic
点群符号
各符号的方位
2
b轴方向
m
2/m
晶胞形状:
a<>b<>c α==90,<>90
斜方晶系-Orthohombic
点群符号
各符号的方位
222
abc
mm
mmm
晶胞形状:
a<>b<>c α= ==90
四方晶系-Tetrogobal
10 P2/m 11 P21/m 12 C 2/m 15 C 2/c
13 P 2/c 14 P 21/c
16 P222 17 P2221 18 P21212 19 P212121 20 C2221 21
C222 22 F222 23 I222
24 I212121
25 Pmm2 26 Pmc21 27 Pcc2 28 Pma2 29 Pca21 30 Pnc2 31Pmn21 32 Pba2 33 Pna21 34 Pnn2 35 Cmm2 36 Cmc21 37 Ccc2 38 Amm2 39Abm2 40 Ama2 41 Aba2 42 Fmm2 43 Fdd2 44Imm2
晶体结构基本知识
——晶体的对称及空间群——
1. 单位晶胞 (unit cell)
晶体三维周期重复的最小单位,并且可 以在晶胞范围包含所有的晶体对称要素—— 对称面(滑移面)、对称中心、对称轴 (螺旋轴)。
2. 32点群 (point symmetry)
三斜晶系-Triclinic
点群符号
各符号的方位
c
四方
点群和空间群ppt课件

❖ 宏观对称要素和微观对称要素在三维空间的组合,称为空 间群。
❖ 经过严格证明可以得出,晶体中可能存在230种空间群,任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群,而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之,空间群
59
60
61
62
63
64
重要对称元素的书写与图形记号
65
5
3
3
5
1
1
4
6
2
4
6 2
19
20
(3) 6 象转轴——实际上就是3度转轴+对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
21
22
(3) 4 象转轴
3
1 2
2
3
1 4
4
23
24
结论: 晶体的宏观对称性中有以下八种基本的对称
操作:1,2,3,4,6,1, m, 4 。 这些基本的操
作组合起来,就可以得到32种不包括平移的宏观 操作类型。
12
二、中心反演(中心反映)
1.中心反演
如图所示,有对称心i,晶体中
iA
任一点A过中心 i 连线Ai并延长到A',
使Ai = A' i, A与A'是等同点, i点称
A
为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
❖ 经过严格证明可以得出,晶体中可能存在230种空间群,任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群,而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之,空间群
59
60
61
62
63
64
重要对称元素的书写与图形记号
65
5
3
3
5
1
1
4
6
2
4
6 2
19
20
(3) 6 象转轴——实际上就是3度转轴+对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
21
22
(3) 4 象转轴
3
1 2
2
3
1 4
4
23
24
结论: 晶体的宏观对称性中有以下八种基本的对称
操作:1,2,3,4,6,1, m, 4 。 这些基本的操
作组合起来,就可以得到32种不包括平移的宏观 操作类型。
12
二、中心反演(中心反映)
1.中心反演
如图所示,有对称心i,晶体中
iA
任一点A过中心 i 连线Ai并延长到A',
使Ai = A' i, A与A'是等同点, i点称
A
为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
晶体学基础PPT课件
14
2.1.2 晶向指数和晶面指数
晶向:空间点阵中节点列的方向。空间中任两节点的 连线的方向,代表了晶体中原子列的方向。
晶面:空间中不在一直线任三个阵点的构成的平面, 代表了晶体中原子列的方向。 c
阵点坐标 op ua vb wc
b
a
15
1. 晶向指数
c
求法:
1)确定坐标系
[101]
3! 4 4组,如{111} 3!
d)h k l 有一个为0,应除以2,则有
3! 4 12组,如{1 2 0} 2
有二个为0,应除以22,则有
3! 2!22
4
3组,如{1
0
0}
24
3.六方晶系指数
三坐标系 a1,a2,c
120°
四轴坐标系 a1,a2,a3,c
120°
120°
(h k i l ) [u v t w]
晶胞 原胞
差别:晶胞能完整反映晶体内部原 子或离子在三维空间分布;原胞一 般不能保持晶体结构的对称性
8
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
• 简单晶胞(初级晶胞):只有在平行六面体每个顶角上有一阵点 • 复杂晶胞: 除在顶角外,在体心、面心或底心上有阵点
9
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
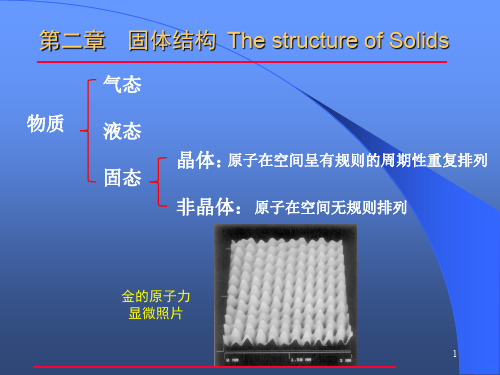
第二章 固体结构 The structure of Solids
气态
物质
液态 固态
晶体:原子在空间呈有规则的周期性重复排列 非晶体: 原子在空间无规则排列
金的原子力 显微照片
1
高分辨率电镜直接观察晶体中原子的排列
2
※ 2.1 晶体学基础
晶体结构的基本特征:原子(或分子、离子)在三维空 间呈周期性重复排列,即存在长程有序
点群与晶系分析课件

空间群确定
根据晶体结构分析结果, 确定空间群,以便进一步 研究晶体结构和性质。
点群与空间群关系
理解点群与空间群之间的 关系,有助于理解晶体结 构和物理性质。
晶系分析方法
晶系分类
01
根据晶体对称性对晶系进行分类,包括立方、四方、六方等晶
系。
晶格常数
02
测量和计算晶体的晶格常数,有助于确定晶系和进一步研究晶
晶系的特点
每个晶系都有其独特的几何特征和对 称元素,这些特征决定了晶体在三维 空间中的结构和性质。
晶系的对称性
对称操作
晶体的对称性是指晶体在三维空 间中能够通过某些操作保持不变 的性质。这些操作包括旋转、平
移和反演等。
对称元素
晶体中存在的对称元素,如对称面 、旋转轴和反演中心等,决定了晶 体的对称性。通过对称元素可以将 晶体分类到不同的晶系。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
点群与晶系的实际应用
材料科学中的点群与晶系应用
晶体结构预测
利用点群和晶系分析,可以预测材料的晶体结构,从而影响其物理 和化学性质。
相变研究
通过分析点群和晶系,有助于研究材料在不同温度和压力下的相变 行为,为材料制备和应用提供指导。
生物学
在生物学中,点群和晶系分析可用于研究蛋白质的结构和功能,对 于药物设计和疾病治疗具有重要意义。
点群与晶系的发展趋势
高压和高温下的点群和晶系研究
随着实验技术的不断发展,人们开始探索高压和高温条件下晶体结构的对称性和稳定性。
点群和晶系的计算模拟
利用计算机模拟技术,可以更准确地预测和理解晶体结构和性质,有助于发现新的材料和 化合物。
第二章 晶体结构ppt课件

1-1 晶向指数 [u v w]
建立步骤: ①建立坐标系。以某一阵点为坐标原点,三个棱边为 坐 标轴,并以点阵常数(a、b、c)作为各个坐标轴的单位长度; ②作 OP // AB ; ③确定P点的三个坐标值(找垂直投影); ④将坐标值化为互质的最小整数,并放入到[ ] 中,则 [uvw]即为所求;
1.晶体结构与空间点阵(续)
1-4 晶胞 ①定义:在空间点阵中,能够代表晶格中原子排列特征的最小单元体。 晶胞通常是平行六面体,将晶胞作三维的重复堆砌就构成了空间点 阵。 ②晶胞的选取原则:
几何形状与晶体具有同样的对称性; 平行六面体内相等的棱与角的数目最多; 当平行六面体棱间有直角时,直角数目最多; 在满足上述条件下,晶胞的体积应最小。
o o a a a c , 9 0 , 1 2 0 1 2 3
菱方:简单菱方 o a b c , 9 0
单斜:简单单斜 底心单斜
a b c ,
9 0
o
三斜:简单三斜
a b c ,
9 0
第二章 晶体结构
第一节 晶体的特征
各项异性 晶体由于具有按照一定几何规律排列的内 部结构,空间不同方向上原子排列的特征不同, 如原子间距及周围环境,因而在一般情况下, 单晶体的许多宏观物理量(如弹性模量、电阻 率、热膨胀悉数、折射率、强度及外表面化学 性质等)的大小是随测试方向的不同而改变的, 这个性质称为各项异性。晶体断裂的解理性就 是晶体具有各项异性的最明显例子。
晶体具有确定的熔点
熔点是晶体物质的结晶状态与非结晶状态互相转 变的临界温度,晶体熔化时发生体积变化。 晶体有一些其他共同特征:晶体中存在不完整性, 晶体内原子排列并不是理想的有序排列,而是有 缺陷的;晶体的原子周期排列促成晶体有一些共 同的性质,如均匀性、自限性和对称性等。
晶体结构与空间点阵PPT课件

第17页/共53页
晶向指数的确定
1. 建立坐标系,结点为原点,三 棱为方向,点阵常数为单位 ;
2. 在晶向上任两点的坐标 (x1,y1,z1) (x2,y2,z2)。(若 平移晶向或坐标,让在第一点 在原点则下一步更简单);
3. 计算x2-x1 : y2-y1 : z2z1 ;
4. 化成最小、整数比u:v:w ; 5. 放在方括号[uvw]中,不加逗
七个晶系及有关特征
特征对称元素
晶胞特点
4个按立方体对 角线取向的3重
旋转轴
6重对称轴
4重对称轴
a=b=c α=β=γ=90°
a=b≠c α=β=90°,γ=12
0°
a=b≠c α=β=γ=90°
3重对称轴
a=b=c α=β=γ≠90°
2个互相垂直的 对称面或3个互 相垂直的2重对
称轴
a≠b≠c α=β=γ=90°
a/h、b/k、c/l。
即与原点位置无关;每一指数对应一组平行的晶面。
第23页/共53页
立方晶系几组晶面及其晶面指标。
(100)晶面表示晶面与a轴相截与b轴、c轴平行; (110)晶面表示与a和b轴相截,与c轴平行; (111)晶面则与a、b、c轴相截,截距之比为1:1:1
(100) (110) (111) 在点阵中的取向
表示方法:用{hkl}表示。
例如:立方晶系中{100}晶面族包括六个晶面
(100)、(010)、(001)、(-100)、(0-10)、(00-1)
注意,在其他晶系中,通过数字位置互换而得到的晶面不一定属于同 一晶面族,例如,正方晶系中a=bc,因此,{100}晶面族分为两组, 一个包含(100)(010)(-100)(0-10)晶面;另一个包含(001) (00-1)两个晶面。
晶向指数的确定
1. 建立坐标系,结点为原点,三 棱为方向,点阵常数为单位 ;
2. 在晶向上任两点的坐标 (x1,y1,z1) (x2,y2,z2)。(若 平移晶向或坐标,让在第一点 在原点则下一步更简单);
3. 计算x2-x1 : y2-y1 : z2z1 ;
4. 化成最小、整数比u:v:w ; 5. 放在方括号[uvw]中,不加逗
七个晶系及有关特征
特征对称元素
晶胞特点
4个按立方体对 角线取向的3重
旋转轴
6重对称轴
4重对称轴
a=b=c α=β=γ=90°
a=b≠c α=β=90°,γ=12
0°
a=b≠c α=β=γ=90°
3重对称轴
a=b=c α=β=γ≠90°
2个互相垂直的 对称面或3个互 相垂直的2重对
称轴
a≠b≠c α=β=γ=90°
a/h、b/k、c/l。
即与原点位置无关;每一指数对应一组平行的晶面。
第23页/共53页
立方晶系几组晶面及其晶面指标。
(100)晶面表示晶面与a轴相截与b轴、c轴平行; (110)晶面表示与a和b轴相截,与c轴平行; (111)晶面则与a、b、c轴相截,截距之比为1:1:1
(100) (110) (111) 在点阵中的取向
表示方法:用{hkl}表示。
例如:立方晶系中{100}晶面族包括六个晶面
(100)、(010)、(001)、(-100)、(0-10)、(00-1)
注意,在其他晶系中,通过数字位置互换而得到的晶面不一定属于同 一晶面族,例如,正方晶系中a=bc,因此,{100}晶面族分为两组, 一个包含(100)(010)(-100)(0-10)晶面;另一个包含(001) (00-1)两个晶面。
点群空间群和晶体结构

点群空间群和晶体结构
一、点群
点群是模拟物体在实际应用中的一种常用方法,它可以使用离散的点
来模拟物体的形状,形成空间网格。
它比传统三维建模技术更易于实现,
更少的信息就可以获得一个物体的完整几何描述。
点群可以被用来快速创建几何模型,而且可以利用点的位置和位置关
系来描述一个物体的形状特征,例如法向量和曲率,这对于计算机视觉、
求解机器人运动规划任务等都是非常有用的信息。
点群技术也被用来提取
复杂物体的特征,比如可以通过计算点群中局部点的法向量和曲率等特征
来识别物体的形状。
点群技术的另一个重要应用是三维重构,也就是把两个点群之间的关
系映射为3D模型,这样可以根据点群之间的变换关系或者任意点群之间
的距离来精确恢复模型的几何形状和位置变换。
点群技术的另一个作用就是可以将点群视为物体制作模型的基础构件,如通过点群文件可以构建3D打印、CAD和CAM模型。
二、空间群
空间群是由含有三维空间元素的群体组成的,是用来描述三维物体的
空间结构的一种技术。
空间群可以帮助科学家和工程师深入理解物体的表
面结构,从而更好地控制物体的生长和变化。
晶体对称.空间点群PPT共62页

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
晶体对称.空间点群
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
44、卓越的人一大优点是:在不利与艰 难的遭遇里折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
晶体对称.空间点群62页PPT

础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
晶体对称.空间点群
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
晶体对称.空间点群
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
子群:若群GA的全部元素是群G中的元素,并且两者的结合律 相同,称GA是群G的子群,而G是群GA的母群。如果对称元素GA和 GB能够得到G的全部对称元素,则称这两个对称元素为群G中的两 个生殖元素(Generating Element).
3.2点群的描述及图示
一组变换矩阵表示
点群 极射投影
该点群所有元素的极射投影以及一般位置点的正规点系 (Regular Point System,RPS)的极射投影。
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。
5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴,例如点群(a) 和(b) 就没有4次轴。另 外,立方晶系并不一定总是具有最高的对称性,例如四方晶系的 点群D4h-4/mmm(16阶)和六方晶系的点群D6h-6/mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
素的变换矩阵就是点群的生成矩阵。
三斜晶系
三斜晶系单胞的棱长及其夹角不受任何限制。它可能的对称
操作是1(C1)或1 (i)。这晶系可以有2个点群。
1) 如果物体只有一个1(C1)恒等操作,它所属的点群是1阶 的{C1)或{1}。其熊夫利斯符号是C1,国际简略符号是l,即点 群符号是C1-1。
这种点群符号和其对称操作符号相同。因为C1-1 点群只有 一种单一对称操作,所以,尽管点群符号和对称操作符号相同 也不会引起混乱。这种点群的生殖对称元素就是C1(E),生殖 矩阵就是恒等操作的变换矩阵。这种点群的极射投影图如附图 1(a)所示。
材料结构与性能
授课教师:刘胜新 (18课时)
第三章点群、空间群和晶体结构
引言
群(Group)是某些具有相互联系规律的元素的组合.晶体对称 操作符合一定规律的组合,这种群即是对称群(Symmetry Group )。晶体外形是一个有限对称图象,对其进行对称操作时,至少 保持一点不动,即这些操作是点对称操作,它们组成点对称群, 称为点群(Point Group)。 讨论点对称操作有哪些可能的组合方式,并对晶体做进一步划分。
A)从五种循环群1(C1)、2(C2)、3(C3)、4(C4)、6(C6)开始,再在 每种循环群上加进各种新的对称操作,最终导出32种点群。 例如:
在垂直于循环群对称轴的方向加上2次对称轴;在垂直于循环 轴的方向或包含循环轴加上镜面;用非真旋转轴代替真旋转轴等。 用这些操作或者这些操作的某一种组合可能会得出一些新的点群。
B) 首先找出仅由真旋转构成的所有群,这种纯旋转结晶学点群 共有11种。然后在这11种点群的基础上,把每一种都加上反演对 称操作,又获得11种点群。由这11种中心对称点群,又可以找出 与11种纯旋转点群不同的10种非中心对称子群,最后导出了32种 点群,是一种最快和最好的方法。
ቤተ መጻሕፍቲ ባይዱ
上述的两种导出方法有一个共同的缺点,就是导出点群后, 还要再确定每一种点群分属于哪一种晶系。
一般位置点指不处在对称元素上的点;正规点系是指某一点 经过点群所有对称操作导出的全部点的集合。
一般位置点的正规点系的总点数(又称等效位置点数)和点 群的阶数相等。
在极射投影时,点群中所有对称操作都经过投影基圆中心。
3.3点群的推导方法
通过对晶体外形的研究,人们发现共有32种晶态,每一种晶态 对应着一种点群。可以用不同方法导出32种点群。
C)用推导7种晶系的方法也可以推导出32种点群。对每一种晶 系在保证晶系的对称性不变的前提下,加入可能的对称操 作,这种导出方法的优点在于使点群与晶系的关系十分明 确。
下面将用这种方法导出32种点群。
在导出点群时应该注意到在每一个点群中都有主导生
殖对称元素,群内其它对称元素可以由主导生殖对称元素
组合增殖生成。如果由一组矩阵表示点群,则生殖对称元
附图1
除了上述两种点群,我们不可能再 增加任何对称操作而使物体仍属于三斜 晶系,所以,属于三斜晶系的晶类只有 两种。 Ci-1点群的对称操作最多(不严 格地说它具有最高的对称性),称这种 点群为该晶系的全对称点群。
从上述两种点群的极射投影再一次说明在投影图上一般位置 的正规点系的数目和点群具有对称操作的数目相同,即与点群 的阶数相同。
有唯一的单位元素(E)。它和群中任何一个元素的组合是元素 本身。
群中每一个元素,必有一个相应的逆元素(Inverse Element)使 得两者相乘为其本身。
以一个4次对称轴C4的全部操作所构成的群G来说明4个基本性 质。
两个独立群的直接积
设有两个独立群GA和GB,其中GA是n阶群,GB是m阶群。两个 群中除了恒等元素外,没有其它共有元素,两个群的元素间相乘有
3.1 群的概念和基本性质
群是某些具有相互联系规律的一些元素的组合,群的元素可 以是字母、数字、对称操作、点阵等。
任何一个群都应具有以下4个基本性质:
封闭性(Closure)
群G的n个不等效元素中,任两个元素组合或一个同类元素自 身组合都是群中的一个元素。
群中所有元素都遵循组合律,但组合次序不能变。
交换律,即
ai ·bj=bj ·ai
两个群的直接积G以 GGAGB 表示:
G G A G B { a 1 b 1 , a 1 b 2 ,a . 1 b m , .a . 2 b m . ,a . n b m . } .
G是n×m阶群。群的直接积是扩大群的一种最简单的方法。
子群、母群及生殖元素
附图1
在图中没有标出对称元素的投影,因为 任何方向都可以是1次轴,故不能标出它的位 置。投影图中的一般位置点的等效点只有一 个点,因为经对称操作后这个点仍在原来位 置。
2)如果物体有1(E)和1(i)对称操作,这个点 群是2阶的:{E,i}或{1,1}。点群的熊夫利斯 符号是Ci,国际简略符号是1,即点群的符号 是Ci-1。这个点群的生殖对称元素是1,生殖 矩阵就是反演操作的变换矩阵。这种点群的极 射投影图如附图l(b)所示:在图中心标出对称 中心。一般位置点的等效点系是一个在上半球 (用●表示),另一个在下半球(用○表示)的2个等 效点。
3.2点群的描述及图示
一组变换矩阵表示
点群 极射投影
该点群所有元素的极射投影以及一般位置点的正规点系 (Regular Point System,RPS)的极射投影。
立方系各晶类的投影图
在(e)所示:在投影面上{111)位置4个3轴,单胞3个轴为4次轴, 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。
5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴,例如点群(a) 和(b) 就没有4次轴。另 外,立方晶系并不一定总是具有最高的对称性,例如四方晶系的 点群D4h-4/mmm(16阶)和六方晶系的点群D6h-6/mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
素的变换矩阵就是点群的生成矩阵。
三斜晶系
三斜晶系单胞的棱长及其夹角不受任何限制。它可能的对称
操作是1(C1)或1 (i)。这晶系可以有2个点群。
1) 如果物体只有一个1(C1)恒等操作,它所属的点群是1阶 的{C1)或{1}。其熊夫利斯符号是C1,国际简略符号是l,即点 群符号是C1-1。
这种点群符号和其对称操作符号相同。因为C1-1 点群只有 一种单一对称操作,所以,尽管点群符号和对称操作符号相同 也不会引起混乱。这种点群的生殖对称元素就是C1(E),生殖 矩阵就是恒等操作的变换矩阵。这种点群的极射投影图如附图 1(a)所示。
材料结构与性能
授课教师:刘胜新 (18课时)
第三章点群、空间群和晶体结构
引言
群(Group)是某些具有相互联系规律的元素的组合.晶体对称 操作符合一定规律的组合,这种群即是对称群(Symmetry Group )。晶体外形是一个有限对称图象,对其进行对称操作时,至少 保持一点不动,即这些操作是点对称操作,它们组成点对称群, 称为点群(Point Group)。 讨论点对称操作有哪些可能的组合方式,并对晶体做进一步划分。
A)从五种循环群1(C1)、2(C2)、3(C3)、4(C4)、6(C6)开始,再在 每种循环群上加进各种新的对称操作,最终导出32种点群。 例如:
在垂直于循环群对称轴的方向加上2次对称轴;在垂直于循环 轴的方向或包含循环轴加上镜面;用非真旋转轴代替真旋转轴等。 用这些操作或者这些操作的某一种组合可能会得出一些新的点群。
B) 首先找出仅由真旋转构成的所有群,这种纯旋转结晶学点群 共有11种。然后在这11种点群的基础上,把每一种都加上反演对 称操作,又获得11种点群。由这11种中心对称点群,又可以找出 与11种纯旋转点群不同的10种非中心对称子群,最后导出了32种 点群,是一种最快和最好的方法。
ቤተ መጻሕፍቲ ባይዱ
上述的两种导出方法有一个共同的缺点,就是导出点群后, 还要再确定每一种点群分属于哪一种晶系。
一般位置点指不处在对称元素上的点;正规点系是指某一点 经过点群所有对称操作导出的全部点的集合。
一般位置点的正规点系的总点数(又称等效位置点数)和点 群的阶数相等。
在极射投影时,点群中所有对称操作都经过投影基圆中心。
3.3点群的推导方法
通过对晶体外形的研究,人们发现共有32种晶态,每一种晶态 对应着一种点群。可以用不同方法导出32种点群。
C)用推导7种晶系的方法也可以推导出32种点群。对每一种晶 系在保证晶系的对称性不变的前提下,加入可能的对称操 作,这种导出方法的优点在于使点群与晶系的关系十分明 确。
下面将用这种方法导出32种点群。
在导出点群时应该注意到在每一个点群中都有主导生
殖对称元素,群内其它对称元素可以由主导生殖对称元素
组合增殖生成。如果由一组矩阵表示点群,则生殖对称元
附图1
除了上述两种点群,我们不可能再 增加任何对称操作而使物体仍属于三斜 晶系,所以,属于三斜晶系的晶类只有 两种。 Ci-1点群的对称操作最多(不严 格地说它具有最高的对称性),称这种 点群为该晶系的全对称点群。
从上述两种点群的极射投影再一次说明在投影图上一般位置 的正规点系的数目和点群具有对称操作的数目相同,即与点群 的阶数相同。
有唯一的单位元素(E)。它和群中任何一个元素的组合是元素 本身。
群中每一个元素,必有一个相应的逆元素(Inverse Element)使 得两者相乘为其本身。
以一个4次对称轴C4的全部操作所构成的群G来说明4个基本性 质。
两个独立群的直接积
设有两个独立群GA和GB,其中GA是n阶群,GB是m阶群。两个 群中除了恒等元素外,没有其它共有元素,两个群的元素间相乘有
3.1 群的概念和基本性质
群是某些具有相互联系规律的一些元素的组合,群的元素可 以是字母、数字、对称操作、点阵等。
任何一个群都应具有以下4个基本性质:
封闭性(Closure)
群G的n个不等效元素中,任两个元素组合或一个同类元素自 身组合都是群中的一个元素。
群中所有元素都遵循组合律,但组合次序不能变。
交换律,即
ai ·bj=bj ·ai
两个群的直接积G以 GGAGB 表示:
G G A G B { a 1 b 1 , a 1 b 2 ,a . 1 b m , .a . 2 b m . ,a . n b m . } .
G是n×m阶群。群的直接积是扩大群的一种最简单的方法。
子群、母群及生殖元素
附图1
在图中没有标出对称元素的投影,因为 任何方向都可以是1次轴,故不能标出它的位 置。投影图中的一般位置点的等效点只有一 个点,因为经对称操作后这个点仍在原来位 置。
2)如果物体有1(E)和1(i)对称操作,这个点 群是2阶的:{E,i}或{1,1}。点群的熊夫利斯 符号是Ci,国际简略符号是1,即点群的符号 是Ci-1。这个点群的生殖对称元素是1,生殖 矩阵就是反演操作的变换矩阵。这种点群的极 射投影图如附图l(b)所示:在图中心标出对称 中心。一般位置点的等效点系是一个在上半球 (用●表示),另一个在下半球(用○表示)的2个等 效点。
