图论方法.ppt
合集下载
简要版PPT4图论方法4-5(完全图有向图之发掘性质)
温馨提示为了设计教学场景互动效果的需要，课件中采用了大量“播放后隐藏”的文本，从而导致预览模式下出现诸多文本重叠，影响阅读。
但在放映模式下，这些现象都不会出现。
另外，课件中的图像均不是一次性形成，而是展现了“尝试-修改-成形”等发生过程，这可能导致预览模式下出现诸多乱码，但在放映模式下，图形则非常生动、美观。
图论方法4-5（完全图有向图之发掘性质）●冯跃峰本讲内容本节为第4板块（图论方法）第4专题（完全图有向图）的第5小节（发掘性质），包含如下3个部分内容：第一部分，概述问题涉及的知识方法体系；第二部分，思维过程剖析。
这是课件的核心部分，重在发掘问题特征，分析如何找到解题方法。
按照教师场景授课互动效果设计，立足于启发思维；第三部分，详细解答展示。
提供笔者重新书写的解答（简称“新写”），力求严谨、流畅、简练。
所谓“完全图”，就是任何点都连边的图；所谓“有向图”，就是给每条边标注了一个方向。
特别地，一个图是完全图又是有向图，则称为“竞赛图”。
它们包括三种常见的思路：三种思路局部扩展从一点或边出发，逐步扩充为完全图反面剔除去掉若干引出虚边的点，使不再有虚边，得到完全图考察极端跃峰奥数本节介绍“局部扩展”的相关例子■。
在特定范围内取某种容量最大的图或考察元素的极端分布。
【图论方法（完全图、有向图）】【图论4-5】给定正整数n≥3，试证：n阶竞赛图Gn 存在一个三角形回路的充分必要条件是，Gn存在两个出度相等的点。
【题感】从目标看【1】，属于“存在性”问题【1】。
就充分性而言，是要找到“一个三角形回路【1】”；就必要性而言，是要找到“两个出度相等的点【1】”。
前者可采用构造的方法，后者有明显的“抽屉”影子，但无法用抽屉原理求解：题中唯一的条件“三角形回路”难以找到“空抽屉”，只能从反面来验证，导出矛盾（假定结论不成立，导出与“存在三角形回路”矛盾）。
先考虑充分性。
假定d+（Ai ）= d+（Aj），我们要找到一个长为3的有向圈，这可从Ai 、Aj出发，利用“局部扩展”策略，由边AiA j扩充为长为3的有向圈即可■。
图论-总结PPT课件
degu + degv≥p-1，
则G是连通的。[这个定理是一个充分条件]
定理3 设G=(V,E)是至少有一个顶点不是弧立顶 点的图。若对任意v∈V，degv为偶数，则G中 有回路。
定理4 若图G中的两个不同顶点u与v间有两条不 同的路联结，则G中有回路。
.
6
例1 若G是一个恰有两个奇度顶点u和v的无向图，则 G连通G+uv连通。
(1) 若Δ(G)=δ(G)=3，则称3-度正则图,也叫做三次 图。
(2) 若Δ(G)=δ(G)=0，则称为零图，即0-度正则图。 (3) 若Δ(G)=δ(G)=p-1，则称为p-1度正则图，即
degv=p-1。 (4) p-1度正则图也称为p个顶点的完全图，记为Kp。
在Kp中，每个顶点与其余各顶点均邻接。 显然，Kp有p(p-1)/2条边。
则G是一个哈密顿图。 定理3 设G是一个有P个顶点的图，若对G的每 一对不邻接的顶点u和v，均有degu+degv≥p1，则G有哈密顿路。 (书上习题)
.
11
习题
例1(1) 证明具有奇数顶点的偶图不是哈密顿图；用
此结论证明如图所示的图不是哈密顿图。 (2) 完全偶图Km,n为哈密顿图的充要条件是什么？
例2 设G是一个(p,q)无向图,若q>(p-1)(p-2)/2，则G 是连通的。
例3 设G是一个(p,q)无向图,若δ(G)≥[p]/2,则G是连 通的。
例4 证明：若G不连通，则GC是连通图。 例5 设G是有个p顶点，q条边的无向图，各顶点的度数 均为3。则
(1)若q=3p-6,证明:G在同构意义下唯一，并求p,q。 (2)若p=6，证明:G在同构的意义下不唯一。
例2 试求Kp中不同的哈密顿圈的个数。 例3 给出一个10个顶点的非哈密顿图的例子，使得每 一对不邻接的顶点u和v，均有degu+degv≥9。 例4证明：彼德森图不是哈密顿图。 例5图G是哈密顿图。试证明：若图中的哈密顿回路中 含边e1，则它一定同时也含e2。 例9菱形12面体的表面上有无哈密顿回路？ 例10设G=(V,E)是连通图且顶点数为p,最小度数为δ， 若p>2δ,则G中有一长至少为2δ的路。
则G是连通的。[这个定理是一个充分条件]
定理3 设G=(V,E)是至少有一个顶点不是弧立顶 点的图。若对任意v∈V，degv为偶数，则G中 有回路。
定理4 若图G中的两个不同顶点u与v间有两条不 同的路联结，则G中有回路。
.
6
例1 若G是一个恰有两个奇度顶点u和v的无向图，则 G连通G+uv连通。
(1) 若Δ(G)=δ(G)=3，则称3-度正则图,也叫做三次 图。
(2) 若Δ(G)=δ(G)=0，则称为零图，即0-度正则图。 (3) 若Δ(G)=δ(G)=p-1，则称为p-1度正则图，即
degv=p-1。 (4) p-1度正则图也称为p个顶点的完全图，记为Kp。
在Kp中，每个顶点与其余各顶点均邻接。 显然，Kp有p(p-1)/2条边。
则G是一个哈密顿图。 定理3 设G是一个有P个顶点的图，若对G的每 一对不邻接的顶点u和v，均有degu+degv≥p1，则G有哈密顿路。 (书上习题)
.
11
习题
例1(1) 证明具有奇数顶点的偶图不是哈密顿图；用
此结论证明如图所示的图不是哈密顿图。 (2) 完全偶图Km,n为哈密顿图的充要条件是什么？
例2 设G是一个(p,q)无向图,若q>(p-1)(p-2)/2，则G 是连通的。
例3 设G是一个(p,q)无向图,若δ(G)≥[p]/2,则G是连 通的。
例4 证明：若G不连通，则GC是连通图。 例5 设G是有个p顶点，q条边的无向图，各顶点的度数 均为3。则
(1)若q=3p-6,证明:G在同构意义下唯一，并求p,q。 (2)若p=6，证明:G在同构的意义下不唯一。
例2 试求Kp中不同的哈密顿圈的个数。 例3 给出一个10个顶点的非哈密顿图的例子，使得每 一对不邻接的顶点u和v，均有degu+degv≥9。 例4证明：彼德森图不是哈密顿图。 例5图G是哈密顿图。试证明：若图中的哈密顿回路中 含边e1，则它一定同时也含e2。 例9菱形12面体的表面上有无哈密顿回路？ 例10设G=(V,E)是连通图且顶点数为p,最小度数为δ， 若p>2δ,则G中有一长至少为2δ的路。
图论4-6-平面图ppt课件
•图论4-6-平面图
证明 假设K3,3图是平面图。
在K3,3中任取三个结点，其中必有两个结点不 邻接，故每个面的次数都不小于4， 由4r≤2e，r≤e/2，即 v-e+e/2≥v-e+r=2， v-e/2≥2， 2v- e ≥ 4， 2v4≥e。
在K3,3中有6个结点9条边， 2v-4=2×6-4=8<9,与 2v-4≥e 矛盾， 故 K3,3不是平面图。
整理后得: e≤3v – 6
本定理的用途:判定某图是非平面图。
说明：这是简单 图是平面图的必 要条件。 •图论4-6-平面图
例如：K5中e=10，v=5，3v-6=9，从而e>3v-6， 所以K5不是平面图。
定理4.6.3的条件不是充分的。如K3,3图满 足定理4-6.3的条件（v=6，e=9，3v-6=12， e≤3v-6成立），但K3,3不是平面图。 证明K3,3图不是平面图。
例如图
deg(r1)=3 deg(r2)=3 deg(r3)=5 deg(r4)=4 deg(r5)=3
deg(r1)+deg(r2)+deg(r3)+deg(r4)+deg(r5)
=18
•图论4-6-平面图
3.定理4-6.1 设G为一有限平面图，面的次数之 和等于其边数的两倍。 证明思路：任一条边或者是两个面的共同边界 （贡献2次），或者是一个面的重复边（贡献2次）
•图论4-6-平面图
一、平面图 1、定义4-6.1 如果无向图G=<V,E>的所有结点和边 可以在一个平面上图示出来，而使各边仅在顶点处 相交。无向图G称为平面图，否则称G为非平面图。
有些图形从表面看有几条边是相交的，但是不 能就此肯定它不是平面图，例如，下面左图表面看 有几条边相交，但如把它画成右图，则可看出它是 一个平面图。
证明 假设K3,3图是平面图。
在K3,3中任取三个结点，其中必有两个结点不 邻接，故每个面的次数都不小于4， 由4r≤2e，r≤e/2，即 v-e+e/2≥v-e+r=2， v-e/2≥2， 2v- e ≥ 4， 2v4≥e。
在K3,3中有6个结点9条边， 2v-4=2×6-4=8<9,与 2v-4≥e 矛盾， 故 K3,3不是平面图。
整理后得: e≤3v – 6
本定理的用途:判定某图是非平面图。
说明：这是简单 图是平面图的必 要条件。 •图论4-6-平面图
例如：K5中e=10，v=5，3v-6=9，从而e>3v-6， 所以K5不是平面图。
定理4.6.3的条件不是充分的。如K3,3图满 足定理4-6.3的条件（v=6，e=9，3v-6=12， e≤3v-6成立），但K3,3不是平面图。 证明K3,3图不是平面图。
例如图
deg(r1)=3 deg(r2)=3 deg(r3)=5 deg(r4)=4 deg(r5)=3
deg(r1)+deg(r2)+deg(r3)+deg(r4)+deg(r5)
=18
•图论4-6-平面图
3.定理4-6.1 设G为一有限平面图，面的次数之 和等于其边数的两倍。 证明思路：任一条边或者是两个面的共同边界 （贡献2次），或者是一个面的重复边（贡献2次）
•图论4-6-平面图
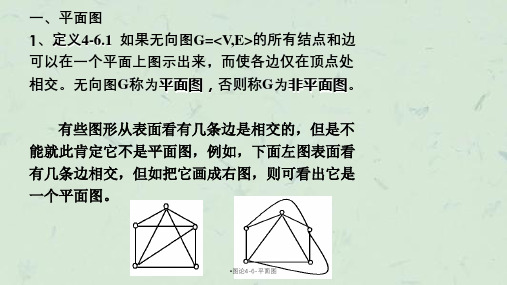
一、平面图 1、定义4-6.1 如果无向图G=<V,E>的所有结点和边 可以在一个平面上图示出来，而使各边仅在顶点处 相交。无向图G称为平面图，否则称G为非平面图。
有些图形从表面看有几条边是相交的，但是不 能就此肯定它不是平面图，例如，下面左图表面看 有几条边相交，但如把它画成右图，则可看出它是 一个平面图。
图论课件-PPT课件
学习方法
目的明确
态度端正 理论和实践相结合
充分利用资源
逐步实现从知识到能力到素质的深化和
升华
课程考核
平时成绩 （30%-40%）
闭卷考试 （60%-70%）
图论模型
为了抽象和简化现实世界，常建立数学模型。图是关 系的数学表示，为了深刻理解事物之间的联系，图 是常用的数学模型。 (1) 化学中的图论模型 19世纪，化学家凯莱用图论研究简单烃——即碳氢 化合物 用点抽象分子式中的碳原子和氢原子，用边抽象原子间 的化学键。
E={w1r1, w1r2, w2r2, w2r3, w2r4, w3r3, w3r5}代表每个仓库和每个 零售店间的关联。则图模型图形为： w1 w2 w3
r1
r2
r3
r4
r5
29
(3) 最短航线问题 用点表示城市，两点连线当且仅当两城市有航线。为了 求出两城市间最短航线，需要在线的旁边注明距离值。 例如：令V={a, b, c, d, e}代表5个城市} E={a b, ad, b c , be, de}代表城市间的直达航线 则航线图的图形为： a 320 500 d 370 b 140 430 e c
图论学科简介 （2）
19世纪末期，图论应用于电网络方程组
和有机化学中的分子结构 20世纪中叶，由于计算机的发展，图论 用来求解生产管理、军事、交通运输、 计算机和网络通信等领域中的离散性问 题 物理学、化学、运筹学、计算机科学、 电子学、信息论、控制论、网络理论、 社会科学、管理科学等领域应用
七桥问题
近代图论的历史可追溯到18世纪的七桥问题:
穿过Kö nigsberg城的七座桥，要求每座桥通过 一次且仅通过一次。
图论课件-图的因子分解
对于同一个图，可能存在多种不同的因子分解，如何找到最优的因 子分解是一个挑战。
因子分解的应用场景
虽然图的因子分解在理论计算机科学中有广泛的应用，但在实际应 用中，如何将理论应用于实际问题仍需进一步探索。
未来可能的研究方向和挑战
寻找高效算法
01
未来研究的一个重要方向是寻找更高效的算法来解决图的因子
分解问题。
04
图的因子分解的应用
在计算机科学中的应用
计算机网络
图的因子分解可以用于优化路由算法，通过将网络分解为 若干个连通子图，可以更有效地进行路由选择和流量控制 。
并行计算
在并行计算中，图的因子分解可以用于任务分配，将一个 大任务分解为若干个小任务，并分配给不同的处理器执行 ，从而提高计算效率。
数据挖掘和机器学习
一个图，其中任意两个不 同的顶点之间都恰有一条 边相连。
空图
一个图，其中任意两个不 同的顶点之间都无边相连 。
图的因子分解的重要性
理论意义
图的因子分解是图论中的重要概 念，它有助于深入理解图的性质 和结构。
应用价值
图的因子分解在计算机科学、运 筹学、电子工程等领域有广泛的 应用，如网络设计、电路优化等 。
资源配置和调度。
金融风险管理
在金融风险管理中，图的因子分 解可以用于识别和评估风险因素 之间的关联关系，从而更好地进
行风险管理和控制。
在网络设计中的应用
01
社交网络分析
在构和群体关系，
从而更好地理解社交行为的模式和规律。
02 03
推荐系统
在推荐系统中，图的因子分解可以用于用户兴趣分析和物品关联推荐， 通过将用户和物品之间的关系进行分解和分析，可以更有效地进行个性 化推荐。
因子分解的应用场景
虽然图的因子分解在理论计算机科学中有广泛的应用，但在实际应 用中，如何将理论应用于实际问题仍需进一步探索。
未来可能的研究方向和挑战
寻找高效算法
01
未来研究的一个重要方向是寻找更高效的算法来解决图的因子
分解问题。
04
图的因子分解的应用
在计算机科学中的应用
计算机网络
图的因子分解可以用于优化路由算法，通过将网络分解为 若干个连通子图，可以更有效地进行路由选择和流量控制 。
并行计算
在并行计算中，图的因子分解可以用于任务分配，将一个 大任务分解为若干个小任务，并分配给不同的处理器执行 ，从而提高计算效率。
数据挖掘和机器学习
一个图，其中任意两个不 同的顶点之间都恰有一条 边相连。
空图
一个图，其中任意两个不 同的顶点之间都无边相连 。
图的因子分解的重要性
理论意义
图的因子分解是图论中的重要概 念，它有助于深入理解图的性质 和结构。
应用价值
图的因子分解在计算机科学、运 筹学、电子工程等领域有广泛的 应用，如网络设计、电路优化等 。
资源配置和调度。
金融风险管理
在金融风险管理中，图的因子分 解可以用于识别和评估风险因素 之间的关联关系，从而更好地进
行风险管理和控制。
在网络设计中的应用
01
社交网络分析
在构和群体关系，
从而更好地理解社交行为的模式和规律。
02 03
推荐系统
在推荐系统中，图的因子分解可以用于用户兴趣分析和物品关联推荐， 通过将用户和物品之间的关系进行分解和分析，可以更有效地进行个性 化推荐。
离散数学——图论 ppt课件
ppt课件
11
哥尼斯堡七桥问题
把四块陆地用点来表示，桥用点与点连线表 示。
ppt课件
12
欧拉将问题转化为：任何一点出发，是否存在通过 每条边一次且仅一次又回到出发点的路？欧拉的结 论是不存在这样的路。显然，问题的结果并不重要， 最为重要的是欧拉解决这个问题的中间步骤，即抽 象为图的形式来分析这个问题 。
因此，尽管本教材介绍的是较为基础的图论内容， 但阅读理解与完成习题是学习图论必不可少的步骤。
ppt课件
8
图是人们日常生活中常见的一种信息载体， 其突出的特点是直观、形象。图论，顾名思 义是运用数学手段研究图的性质的理论，但 这里的图不是平面坐标系中的函数，而是由 一些点和连接这些点的线组成的结构 。
P（G）表示连通分支的个数。连通图的连通 分支只有一个。
ppt课件
40
练习题---图的连通性问题
1.若图G是不连通的，则补图是连通的。 提示：直接证法。
根据图的不连通，假设至少有两个连通分 支；任取G中两点，证明这两点是可达的。
ppt课件
41
2.设G是有n个结点的简单图，且 |E|>(n-1)(n-2)/2，则G是连通图。
33
§8.2通路、回路与连通性
定义：通路与回路 设有向图G=<V,E>，考虑G中一条边的序列
（vi1,vi2,…, vik）,称这种边的序列为图的通路。 Vi1、vik分别为起点、终点。通路中边的条数称
为通路的长度。 若通路的起点和终点相同，则称为回路。
ppt课件
34
简单通路、基本通路
简单通路：通路中没有重复的边。 基本通路：通路中没有重复的点。 简单回路和基本回路。 基本通路一定是简单通路，但反之简单通路
第七章图论PPT课件
v V
ห้องสมุดไป่ตู้
deg(v)为偶数，2|E|亦为偶数
vV2
deg(v)为偶数 vV1
|V1|为偶数
定理： 有向图中所有结点的入度之和等于所有结点的出度之和
-
12
7-1 图的基本概念
（5）多重图：含有平行边的图
简单图：不含有平行边和环的图
完全图：每一对结点之间都有边关联的简单图
有向完全图：完全图中每条边任意确定一个方向所得的图
a
e
b
d
f
h
c
g
定理： n个结点的无向（有向）完全图Kn的边数为n(n-1)/2
证明： 在完全图中，每个结点的度数应为n－1，则n个结点的
度数之和为n(n-1)，因此|E|＝n(- n-1)/2
13
7-1 图的基本概念
（6）子图：
G V , E ， 有 G ' V ', E ' ， 且 E ' E ， V ' V ，
a到b的有向边
孤立结点：无邻接点的结点
a
e hi
k
b
df
c
j
l
g
无向边：(a,b), (b,c), (b,d), (c,d), (i,l), (k,l)
有向边：<e,f>, <f,g>, <g,e>, <e,h>, <k,j>, <j,l>
-
5
7-1 图的基本概念
（2）无向图：图中每一边都为无向边
e f
g
deg+(e)=2, deg-(e)=1, deg(e)=3
h deg+(f)=1, deg-(f)=2, deg(f)=3
图论讲义ppt教学课件
旅行商问题（TSP）
• 给出城市之间的距离，要求一位推销员从某一城 市出发，周游每个城市一次，然后回到出发的城 市，并且选的路径最短。(Traveling Salesman Problem)
• 这是一个图论优化问题，最早由美国数学家威特 涅于1934年在普林斯顿一次讨论班上提出。 1954年几位美国数学家写了第一篇论文，用线性 方程的方法解决了49个城市的旅行售货员问题。 后来也有不少论文讨论这个问题，在理论和应用 上都很有价值。
• 有向图: 一个有向图是指一个有序三元组 (V(G),A(D), ),其中V(G)是一个非空有限集，A(D) 是与Ｖ(G)不相交的有限集合,是关联函数，它使 A(D)中每一元素对应于V(G)中的有序元素对（可 以相同）
• 图/Graph：可直观地表示离散对象之 间的相互关系，研究它们的共性和特 性，以便解决具体问题。
• 无向图（简称图）: 一个图是指一个有序三元组 (V(G),E(G), ),其中V(G)是一个非空有限集，Ｅ(G) 是与Ｖ(G)不相交的有限集合,是关联函数，它使 E(G)中每一元素对应于V(G)中的无序元素对（可 以相同）
关键路径问题
一项工程任务,大到建造一座大坝,一座体育中心,小
至组装一台机床,一架电视机, 都要包括许多工序.这些工 序相互约束,只有在某些工序完成之后, 一个工序才能开 始. 即它们之间存在完成的先后次序关系,一般认为这些 关系是预知的, 而且也能够预计完成每个工序所需要的 时间.
这时工程领导人员迫切希望了解最少需要多少时间才 能够完成整个工程项目, 影响工程进度的要害工序是哪 几个？
第一部分
引言
两个有趣的问题
• 1.任意一群人中（人数不小于2），总有两人在该 人群中认识相同的朋友数
《图论课件第五章匹配与因子分解》课件
二、因子分解
2.1 定义
因子分解是将图进行拆分，使得每个因子都是图的 一个子图。
2.2 贪心算法
贪心算法用于在因子分解时选择边或顶点。
2.3 DAG上的匈牙利算法
用于在有向无环图上寻找因子分解的算法。
2.4 Tutte定理
用于判断一个图是否存在完美匹配。
三、应用实例
1
3.1 二分图最大匹配的应用
《图论课件第五章匹配与 因子分解》PPT课件
图论课件第五章匹配与因子分解
一、匹配
1.1 定义
匹配指的是图中的一组边，这些边不相交并且 没有公共顶点。
1.3 最大匹配
最大匹配是图中包含边数最多的匹配。
1.2 匹配的分类
分类包括完美匹配、最大匹配和最小匹配。
1.4 匈牙利算法
匈牙利算法用于寻找二分图的最大匹配。
应用于任务分配、婚姻匹配等场景。
3.2 带权二分图匹配的应用
2
应用于资源分配、工作调度等场景。
3
3.3 双倍经验的关卡通关问题
使用匹配算法解决游戏中的关卡设计问
3.4 理发店问题
4
题。
利用匹配算法解决顾客理发需要和理发 师时间安排的问题。
四、参考资料
4.1 书籍
《图论导论》、《算法导论》等
4.3 网站
Grap h Alg orithm s, Grap h Theo ry Online等
4.2 论文
Graph Matching Alg orithm s: A C om prehensive C om parison
4.4 其他资源
相关研究报告、课程讲义等
《图论及其应用》课件
图像处理
探索图论在图像处理领域的应用，如图像分割 和模式识别。
七、总结
图论的重要性
强调图论在计算机科学和现实 世界中的重要性和广泛应用。
现实中的应用价值
讨论图论在实际问题中解决方 案的应用价值和优势。
对于未来的展望
探索图论在未来可能的发展方 向和应用领域，如人工智能和 物联网。
2
Floyd算法
介绍Floyd算法的原理和使用方法，用于计算图中所有节点之间的最短路径。
四、最小生成树算法
Prim算法
解释Prim算法的工作原理和应用，用于寻找图中的 最小生成树。
Kruskal算法
讨论Kruskal算法的概念和实现，用于生成图的最小 生成树。
五、网络流算法
1
最大流
介绍网络流问题和最大流算法，用于解
《图论及其应用》PPT课 件
本PPT课件将带您深入了解图论及其应用。图论是一门关于图的性质及其应用 的学科，将为您揭开图论的奥秘。
一、图论基础
图的定义及术语
介绍图的基本定义以及相关的术语，为后续内 容打下基础。
无向图与有向图
解释无向图和有向图的区别，并介绍它们之间 的关系和应用。
图的表示方法
讲解图的常用表示方法，如邻接矩阵和邻接表， 并比较它们的优缺点。
连通性和路径
讨论图的连通性概念以及如何找到两个节点之 间的最短路径。
二、图的遍历算法
1
广度优先搜索（BFS）
2
介绍广度优先搜索算法的工作原理和常 见应用。
深度优先搜索（DFS）
深入探讨深度优先搜索算法的原理和应 用场景。
三、最短路径算法
1
Dijkstra算法
详细讲解Dijkstra算法的步骤和应用，用于寻找图中两个节点间的最短路径。
图论课件
例v1v2图中v3d (v1) = 5 d (v2) = 4
d (v3) = 3 d (v4) = 0
v4
d (v5) = 2
v5
注：该图中各点的度数 之和等于14，恰好
是边数7的两倍
(3) 易证，图的同构关系是一个等价关系。该关系将所有 的图的集合，划分为一些等价类，即相互同构的图作成 同一个等价类。
显然，V1 ∪V2= V,V1∩V2=Φ 。由握手定理
2m = d(v) = d (v) + d (v) （1）
vV
vV1
vV2
（1）式中2m为偶， d (v)也为偶（因其中每个d(v)为偶），
vV2
从而推知 d (v) 也为偶。而和式中每个d(v)均为奇，故和
vV1
式中的被加项的项数应为偶，这表明G 中度为奇数的点有
例2 设V = {v1,v2,v3,v4}，E = {e1,e2,e3,e4,e5}，其中 e1= v1v2， e2 = v2v3， e3 = v2v3， e4 = v3v4， e5 = v4v4
则 G = (V, E) 是一个图。
v1
v4
e5
e1
e2
e4
v2
v3
e3
相关概念: (1) 若边e = uv , 此时称 u 和v 是 e 的端点;
由图的同构定义知，图(a)与(b)是同构的。
例 判断下面两图是否同构。
u1
v1
解 两图不同构。
这是因若同构，则两图中唯一的与环关联的两个点u1 与v1 一定相对应，而u1的两个邻接点与v1的两个邻接点状况不 同（ u1邻接有4度点，而v1 没有）。
所以，两图不同构。
例4 指出4个顶点的非同构的所有简单图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
各边 (vi , v j ) 有权 lij ( lij 表示 vi ，v j 之间没有边）,
vs , vt 为图中任意两点，求一条道路 ，使它是从 vs 到
vt 的所有路中总权最小的路。即：
最小。
L() lij (vi ,v j )
最短路算法中1959年由 Dijkstra （狄克斯特洛）提出的 算法被公认为是目前最好的方法，我们称之为 Dijkstra算
25
16 3
v5
17
v4
v1 23 v6
v2
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
3
v5
17
v4
v1
v2
23
1
4
v7
v6
标号（0）。画第一个弧。（表明已 v1标号，或已走出v1 ） 2）从 v1 出发，只有两条路可走 (v1, v2 ), (v1, v3) ，其距离为
l12 4, l13 6.
v2 (4)
5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v3
7
v5
6
1
v7
可能最短路为
min{ k12 , k13} min{l12 , l13} min{ 4,6} 4
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
一般研究无向图
树图：倒置的树，根(root)在上，树叶(leaf)在下
多级辐射制的电信网络、管理的指标体系、家谱、分 类学、组织结构等都是典型的树图
C1 根
C2
C3
C4
叶
一 树的定义及其性质
无圈连通图称为树(tree)，记为T
树的性质： 任何树必存在次数为 1 的点
具有 n 个节点的树 T 的边恰好为 n1 条，反之，任何有n 个 节点， n1 条边的连通图必是一棵树
v2 (4)
5
v4
9
引言 图论(Graph Theory)是专门研究图的理论 的一门数学分支，属于离散数学范畴，与运筹 学有交叉，它有200多年历史，大体可划分为三 个阶段： 第一阶段是从十八世纪中叶到十九世纪中叶， 处于萌芽阶段，多数问题围游戏而产生，最有 代表性的工作是所谓的Euler七桥问题，即一笔 画问题。
第二阶段是从十九世纪中叶到二十世纪中叶， 这时，图论问题大量出现，如Hamilton问题， 地图染色的四色问题以及可平面性问题等， 这时，也出现用图解决实际问题，如Cayley 把树应用于化学领域，Kirchhoff用树去研究 电网络等.
① 给 (v1, v2 ) 划成粗线。 ② 给 v2 标号（4）。 ③ 划第二个弧。
v2 (4)
5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v3
7
v5
6
1
v7
表明走出 v1 后走向 v8 的最短路目前看是 (v1, v2 ) ，最优距离 是4 。
现已考察完毕第二个圈内的路，或者说，已完成 v1, v2 的标号。
第三阶段是二十世纪中叶以后，由生产管理、 军事、交通、运输、计算机网络等方面提出 实际问题，以及大型计算机使大规模问题的 求解成为可能，特别是以Ford和Fulkerson 建立的网络流理论，与线性规划、动态规划 等优化理论和方法相互渗透，促进了图论对 实际问题的应用。
1 图与网络的基本概念
例6.1：哥尼斯堡七桥问题
例10-7 v1
20
v2
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
破圈法
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2 20
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2 20
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
总造价=1+4+9+3+17+23=57
4： 最短路问题
最短路问题是网络理论中应用最广泛的问题之一。许多优 化问题都可以使用这个模型，如设备更新、管道的铺设、 线路的安排、厂区的布局等。
最短路问题的一般提法是：设 G (V , E) 为连通图，图中
9
v3
28 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
3
v5
17
v4
总造价=1+4+9+3+17+23=57
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
避圈法
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
法。下面通过例子来说明此法的基本思想。
条件：所有的权数 lij 0
思路：逐步探寻。
v2 5
v4
9
v6
4
4
1 75
v1
6
4
5
v8
1
v3
7
v5
6
v7
v2 5
v4
9
v6
4
4
v1 (0)
1
75
5
v8
①
64
1
v3
7
v5
6
v7
下求 v1 到 v8 的最短路： 1）从 v1 出发，向 v8 走。首先，从 v1 到 v1 的距离为0，给 v1
图的生成树:若图G的一个支撑图T是一棵树,则称T是G的一棵生成树
(spanning tree).
A
CA
CA
CA
C
B
DB
DB
DB
D
在赋权图G中，一棵生成树所有边上权的和，称为生成树的权。 具有最小权的生成树，称为最小树（或最优树）,求最小树有破圈法 和避圈法.
3 最小枝杈树问题
定理 图 G有生成树的充分必要条件为图 是连通图。 定义（最优树）在赋权图G中，一棵生成树 所有树柱上权的和，称为生成树的权。具有 最小权的生成树，称为最优树（或最小树）。 求最小树的方法有破圈法和避圈法。
哥尼斯堡七桥问题 (Königsberg Bridge Problem) Leonhard Euler (1707-1783) 在1736年发表第一篇图论方面
的论文，奠基了图论中的一些基本定理. 很多问题都可以用点和线来表示，一般点表示实体，线表示
实体间的关联
A
A D
C
C
D
B
B
2 最小支撑树(生成树)
vs , vt 为图中任意两点，求一条道路 ，使它是从 vs 到
vt 的所有路中总权最小的路。即：
最小。
L() lij (vi ,v j )
最短路算法中1959年由 Dijkstra （狄克斯特洛）提出的 算法被公认为是目前最好的方法，我们称之为 Dijkstra算
25
16 3
v5
17
v4
v1 23 v6
v2
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28
25
3
v5
17
v4
v1
v2
23
1
4
v7
v6
标号（0）。画第一个弧。（表明已 v1标号，或已走出v1 ） 2）从 v1 出发，只有两条路可走 (v1, v2 ), (v1, v3) ，其距离为
l12 4, l13 6.
v2 (4)
5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v3
7
v5
6
1
v7
可能最短路为
min{ k12 , k13} min{l12 , l13} min{ 4,6} 4
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
一般研究无向图
树图：倒置的树，根(root)在上，树叶(leaf)在下
多级辐射制的电信网络、管理的指标体系、家谱、分 类学、组织结构等都是典型的树图
C1 根
C2
C3
C4
叶
一 树的定义及其性质
无圈连通图称为树(tree)，记为T
树的性质： 任何树必存在次数为 1 的点
具有 n 个节点的树 T 的边恰好为 n1 条，反之，任何有n 个 节点， n1 条边的连通图必是一棵树
v2 (4)
5
v4
9
引言 图论(Graph Theory)是专门研究图的理论 的一门数学分支，属于离散数学范畴，与运筹 学有交叉，它有200多年历史，大体可划分为三 个阶段： 第一阶段是从十八世纪中叶到十九世纪中叶， 处于萌芽阶段，多数问题围游戏而产生，最有 代表性的工作是所谓的Euler七桥问题，即一笔 画问题。
第二阶段是从十九世纪中叶到二十世纪中叶， 这时，图论问题大量出现，如Hamilton问题， 地图染色的四色问题以及可平面性问题等， 这时，也出现用图解决实际问题，如Cayley 把树应用于化学领域，Kirchhoff用树去研究 电网络等.
① 给 (v1, v2 ) 划成粗线。 ② 给 v2 标号（4）。 ③ 划第二个弧。
v2 (4)
5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v3
7
v5
6
1
v7
表明走出 v1 后走向 v8 的最短路目前看是 (v1, v2 ) ，最优距离 是4 。
现已考察完毕第二个圈内的路，或者说，已完成 v1, v2 的标号。
第三阶段是二十世纪中叶以后，由生产管理、 军事、交通、运输、计算机网络等方面提出 实际问题，以及大型计算机使大规模问题的 求解成为可能，特别是以Ford和Fulkerson 建立的网络流理论，与线性规划、动态规划 等优化理论和方法相互渗透，促进了图论对 实际问题的应用。
1 图与网络的基本概念
例6.1：哥尼斯堡七桥问题
例10-7 v1
20
v2
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
破圈法
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2 20
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1 23 v6
v2 20
1
4
v7 9
15 v3
28
25
16 3
v5
17
v4
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
总造价=1+4+9+3+17+23=57
4： 最短路问题
最短路问题是网络理论中应用最广泛的问题之一。许多优 化问题都可以使用这个模型，如设备更新、管道的铺设、 线路的安排、厂区的布局等。
最短路问题的一般提法是：设 G (V , E) 为连通图，图中
9
v3
28 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
28 3
v5
17
v4
v1
v2
23
1
4
v7
v6
9
v3
3
v5
17
v4
总造价=1+4+9+3+17+23=57
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
16 3
v5
17
v4
避圈法
v1
v2 20
23
1
4
v7
v6
36
9
15 v3
28
25
法。下面通过例子来说明此法的基本思想。
条件：所有的权数 lij 0
思路：逐步探寻。
v2 5
v4
9
v6
4
4
1 75
v1
6
4
5
v8
1
v3
7
v5
6
v7
v2 5
v4
9
v6
4
4
v1 (0)
1
75
5
v8
①
64
1
v3
7
v5
6
v7
下求 v1 到 v8 的最短路： 1）从 v1 出发，向 v8 走。首先，从 v1 到 v1 的距离为0，给 v1
图的生成树:若图G的一个支撑图T是一棵树,则称T是G的一棵生成树
(spanning tree).
A
CA
CA
CA
C
B
DB
DB
DB
D
在赋权图G中，一棵生成树所有边上权的和，称为生成树的权。 具有最小权的生成树，称为最小树（或最优树）,求最小树有破圈法 和避圈法.
3 最小枝杈树问题
定理 图 G有生成树的充分必要条件为图 是连通图。 定义（最优树）在赋权图G中，一棵生成树 所有树柱上权的和，称为生成树的权。具有 最小权的生成树，称为最优树（或最小树）。 求最小树的方法有破圈法和避圈法。
哥尼斯堡七桥问题 (Königsberg Bridge Problem) Leonhard Euler (1707-1783) 在1736年发表第一篇图论方面
的论文，奠基了图论中的一些基本定理. 很多问题都可以用点和线来表示，一般点表示实体，线表示
实体间的关联
A
A D
C
C
D
B
B
2 最小支撑树(生成树)