迈克尔逊干涉仪测定空气折射率

合集下载

用迈克尔逊干涉原理测量空气折射率

用迈克尔逊干涉原理测量空气折射率摘要：空气的折射率与真空的折射率（等于1）非常接近。

用一般的方法很难测出其差值一确定空气的折射率。

但用光的干涉法即可以精确地测出来。

比如用迈克尔逊干涉仪对折射率的变化的敏感性，可以准确地测出空气的折射率。

关键词：研究型物理实验;迈克耳逊干涉仪;空气折射率；一、原理迈克尔逊干涉仪的原理见上图。

光源S 发出的光束射到分光板1G 上，1G 的后面镀有半透膜，光束在半透膜上反射和透射，被分成光强接近相等、并相互垂直的两束光。

这两束光分别射向两平面镜1M 和2M ，经它们反射后又汇聚于分光板1G ，再射到光屏E 处，从而得到清晰的干涉条纹。

平面镜1M 可在光线1的方向上平行移动。

补偿板2G 的材料和厚度与1G 相同，也平行于1G ，起着补偿光线2的光程的作用。

如果没有2G ，则光线1会三次经过玻璃板，而光线2只能一次经过玻璃板。

2G 的存在使得光线1、2由于经过玻璃板而导致的光程相等，从而使光线1、2的光程差只由其它几何路程决定。

由于本实验采用相干性很好的激光，故补偿板2G 并不重要。

但如果使用的是单色性不好、相干性较差的光，如纳光灯或汞灯，甚至白炽灯，2G 就成为必需了。

这是因为波长不同的光折射率不同，由分光板1G 的厚度所导致的光程就会各不一样。

补偿板2G 能同时满足这些不同波长的光所需的不同光程补偿于是反射光束1与透射光束2在空间相遇，发生干涉。

当光束垂直入射至M1，M2镜时，两光束的光程差δ=2（n 1L 1-n 2L 2）（1）式中n 1和n 2分别是路程L 1，L 2上介质的折射率。

设单色光在真空中的波长为λ，当δ=k λ,k=0,1,2,3,…时干涉加强相应的接收屏中心的光强为极大。

由式（1-1）知，两束相干光的光程差不但与几何路程有关，还与路程上介质的折射率有关。

计算公式 n=1+(N λ/2L)*（P amb /ΔP ）其中已知条件L=80mm ，P amb =101325Pa , λ=632.8nm 由公式可知只要N ，ΔP 知道就能求出折射率n .当ΔP 改变时，光程相应的改变，并引起干涉圆环“涌出”或“缩进”N 条.二、测量P与N1．在光学平台上按设计实验装置示意图摆好光路。

用迈克尔逊干涉仪测量气体折射率

实验用迈克耳孙干涉仪测量气体折射率[引言]大气中随着海拔高度的上升，空气变得稀薄，大气折射率n 随气体压强的降低而减小，使得光线在大气中传播发生弯曲，对航海中天顶角的测定有一定影响。

而天顶角的测定对船舶的定位起着重要作用，因此，了解气体折射率与大气压强之间的关系具有重要的实际意义。

迈克耳孙干涉仪中的两束相干光各有一段光路在空间中是分开的，人们可以在其中一支光路上放进被研究对象而不影响另一支光路，这就给它的应用带来极大的方便。

实际上常用它来测物质的折射率、厚度和气压等一切可以转化为光程变化的物理量。

[实验目的]1．了解迈克耳孙干涉仪的结构、工作原理和使用方法。

2．学习一种测量气体折射率的方法。

[实验器材]氦氖激光器，扩束镜，迈克尔孙干涉仪，气室（带充气装置），数字气压计。

[实验原理]在迈克耳孙干涉仪光路的一个测量光路上放置一个气室，干涉图样随气室里气体气压的变化而变化：当气压增加时，干涉圆环从中心 “吐出”；反之，干涉圆环向中心“吞入”。

通过研究气体压强变化与条纹移动的关系可以得到气体折射率。

当气室内气体压强改变p ∆时，使气体折射率改变n ∆，光程差改变n L ∆2，从而引起干涉条纹移动N 个，则有λN n L =∆2，于是有：LN n 2λ=∆ （1）其中，L 为气室长度，λ是光的真空波长。

通常，在温度处于15～30C范围时，空气折射率可用下式计算：9,10003671.018793.2)1(-⨯+=-tpn p t （2）式中温度t 的单位为C ，气压p 的单位为Pa 。

在温度一定下，气体折射率p n )1(-与气压p成正比。

因此有：=∆∆=-pnp n 1常数整理得： p p nn ∆∆+=1将式（1）代入上式得： ppL N n ∆+=21λ （3）式（3）给出了在气压p 时的空气折射率。

[实验内容]1．调节迈克耳孙干涉仪，使其在接收屏上观察到干涉条纹。

2．向气室中充气加压，记录气压值1p 。

利用迈克耳逊干涉仪测气体折射率实验报告

利用迈克耳逊干涉仪测气体折射率实验报告实验目的，利用迈克耳逊干涉仪测量气体的折射率，了解气体在不同压力下的折射率变化规律。

实验仪器，迈克耳逊干涉仪、气体压力计、气体容器、激光器等。

实验原理，迈克耳逊干涉仪是一种利用干涉现象来测量光程差的仪器。

当光线通过不同介质时，由于介质折射率的不同，会产生光程差，从而产生干涉条纹。

通过测量干涉条纹的移动情况，可以计算出介质的折射率。

实验步骤：1. 将气体压力计连接到气体容器上，调节气体压力，使其在不同压力下保持稳定。

2. 将激光器的光线引入迈克耳逊干涉仪中，观察干涉条纹的情况。

3. 调节气体压力，记录不同压力下的干涉条纹移动情况。

4. 根据干涉条纹的移动情况，计算出气体在不同压力下的折射率。

实验结果，通过实验测得不同压力下气体的折射率随压力的变化情况。

实验结果表明，随着气体压力的增加，气体的折射率也随之增加，呈现出一定的规律性。

实验结论，通过迈克耳逊干涉仪测量气体折射率的实验，我们得出了气体折射率随压力变化的规律性。

这对于进一步研究气体光学性质具有一定的参考意义。

实验中可能存在的误差，在实验过程中，由于气体压力的微小变化可能会对实验结果产生一定的影响。

同时，光线的稳定性、干涉条纹的观察等因素也可能会对实验结果产生一定的误差。

改进方案，为了减小实验中的误差，可以采取一些措施，比如提高气体压力计的精度、稳定光源的输出、增加干涉条纹的观察次数等。

总结，通过本次实验，我们对迈克耳逊干涉仪测量气体折射率的方法有了更深入的了解，同时也对气体折射率随压力变化的规律性有了一定的认识。

希望通过进一步的实验和研究，可以更深入地探究气体光学性质的规律。

利用迈克耳逊干涉仪测气体折射率实验报告

利用迈克耳逊干涉仪测气体折射率实验报
告
实验目的：
通过利用迈克耳逊干涉仪测量气体折射率，了解气体对光的折射现象，并掌握实验方法和数据处理技巧。

实验原理：
迈克耳逊干涉仪是一种利用干涉现象来测量光波长和折射率的仪器。

当光波通过气体时，会发生折射现象，导致光程差的变化，从而影响干涉条纹的位置，通过测量干涉条纹的位移，可以计算出气体的折射率。

实验步骤：
1. 将迈克耳逊干涉仪放置在稳定的平台上，调整好光源和反射镜的位置。

2. 将待测气体装入干涉仪的测量室内，确保气体均匀分布。

3. 调整干涉仪，使得观察到清晰的干涉条纹。

4. 记录气体的压强和温度，并测量干涉条纹的位移。

5. 根据实验数据计算气体的折射率。

实验数据处理：
根据实验测得的干涉条纹位移和气体的压强、温度，利用适当
的公式计算出气体的折射率。

同时，需考虑气体的折射率随压强和
温度的变化而变化的影响。

实验结果：
根据实验测得的数据和数据处理，得出了气体的折射率，并与
已知数据进行对比和分析。

实验结论：
通过本次实验，成功利用迈克耳逊干涉仪测量了气体的折射率，并得出了相应的结论。

同时，也发现了一些实验中可能存在的误差
和改进的地方。

总结：
本次实验通过利用迈克耳逊干涉仪测量气体折射率，加深了对气体折射现象的理解，掌握了实验方法和数据处理技巧，为今后的实验和研究打下了基础。

迈克耳逊干涉仪的调整和使用及测空气折射率

第16页/共22页
第17页/共22页
结果分析
查的文献值n空气=1.00102。相对误差>0.02% 原因如下：
第18页/共22页
1.在实验时氦氖激光只能做到与镜大体平行、与镜大体垂直，所以说会与理论上推导出来的公式有一定的误差
第19页/共22页
2.大小鼓轮反转而引进的空转误差，在每次测量必须沿同一方向旋转转盘，不得中途倒退
目录
一. 背景知识介绍二. 实验目的三. 实验原理四. 实验内容五. 注意事项六. 实验数据及处理
第1页/共22页
迈克耳孙（A.A.Michelson）美籍德国人
50.60455
固定“冒出”（或“消失”）的干涉条纹数N=50
测He-Ne激光的波长数据表格
第15页/共22页
数据处理
Δd1=d4-d0=50.55215-50.48225=0.06990mmΔd2=d5-d1=50.56975-50.50045=0.06930mmΔd3=d6-d2=50.58642-50.51740=0.06902mmΔd4=d7-d3=50.60455-50.53518=0.06937mmΔd= (Δd1+Δd2+Δd3+Δd4) =0.06940mm
背景知识介绍
第2页/共22页
实验目的
了解迈克尔孙干涉仪的结构和工作原理，掌握其调节和使用方法。学习一种测量气体折射率的方法学习迈克尔孙干涉仪测定波长的方法。
第3页/共22页
实验原理
迈克尔孙干涉仪的结构与光路迈克尔孙干涉仪的调节与读数方法
第4页/共22页
பைடு நூலகம்
半透半反膜
M1和M2是精密磨光的平面反射镜，分别装在相互垂直的两臂上，M2固定， M1而可通过精密丝杆沿臂长的方向移动。

迈克尔逊干涉仪测量空气折射率实验报告

迈克尔逊干涉仪测量空气折射率实验报告一、实验目的1、了解迈克尔逊干涉仪的结构和工作原理。

2、掌握用迈克尔逊干涉仪测量空气折射率的方法。

3、加深对光的干涉现象的理解。

二、实验原理迈克尔逊干涉仪是一种利用分振幅法产生双光束干涉的精密光学仪器。

其光路图如下图所示：此处可插入迈克尔逊干涉仪光路图由光源 S 发出的光射在分光板 G1 上，被分成两束光，反射光（1）射向平面镜 M1，透射光（2）射向平面镜 M2。

两束光分别被 M1、M2 反射后，又回到分光板 G1，在观察屏 E 处相遇产生干涉条纹。

当 M1 和 M2 严格垂直时，得到的是等倾干涉条纹；当 M1 和 M2 有微小夹角时，得到的是等厚干涉条纹。

本实验中，我们通过测量等倾干涉条纹的变化来测量空气折射率。

假设初始时，干涉仪两臂长度相等，即 L1 ＝ L2，对应的光程差为Δ ＝ 2(L2 L1) ＝ 0，此时观察屏上出现中心为亮点的等倾干涉条纹。

当向迈克尔逊干涉仪的一臂中缓慢充入空气时，光在空气中的传播速度变慢，导致光程增加。

设充入空气后光程变化量为ΔL，空气折射率为 n，则有：ΔL ＝（n 1)L （其中 L 为充入空气的光路长度）通过测量充入空气前后干涉条纹的变化数Δk，以及已知的波长λ和干涉仪的臂长 L，可以计算出空气折射率 n：n ＝ 1 ＋ΔL ／ L ＝ 1 ＋Δkλ ／ 2L三、实验仪器迈克尔逊干涉仪、HeNe 激光器、气室、气压表、真空泵等。

四、实验步骤1、仪器调节调节迈克尔逊干涉仪的底座螺钉，使仪器大致水平。

打开激光器，使激光束大致垂直入射到分光板 G1 上，并通过调节M1 和 M2 背后的螺钉，使反射回来的两束光在屏上重合，出现干涉条纹。

仔细调节 M1 和 M2 背后的螺钉，使干涉条纹为圆心在视场中心的同心圆环。

2、测量干涉条纹的变化记录初始时干涉条纹的位置和个数。

打开气室阀门，用真空泵缓慢抽出气室内的空气，观察干涉条纹的变化，记录条纹消失的个数。

迈克尔干涉仪测量空气折射率

实验四用迈克尔逊干涉仪空气的折射率一、实验目的用分离的光学元件构建一个迈克尔逊干涉仪。

通过降低空气的压强测量其折射率。

二、仪器和光学元件光学平台；HeNe 激光；调整架，35x35mm ；平面镜，30x30mm ；磁性基座；分束器50:50；透镜，f=+20mm ；白屏；玻璃容器，手持气压泵，组合夹具，T 形连接，适配器，软管，硅管三、实验原理借助迈克尔逊干涉仪装置中的两个镜，光线被引进干涉仪。

通过改变光路中容器内气体的压强，推算出空气的折射率。

If two Waves having the same frequency ω , but different amplitudes and different phases are coincident at onelocation , they superimpose to()()2211sin sin αα-∙+-∙=wt a wt a YThe resulting can be described by the followlng : ()α-∙=wt A Y sinw ith the amplitudeδcos 22122212∙++=a a a a A(1)and the phase difference21ααδ-=In a Michelson interferometer , the light beam is split by a half-silvered glass plate into two partial beams ( amplitude splitting ) , reflected by two mirrors , and again brought tointerference behind the glass plate . Since only large luminous spots can exhibit circular interference fringes , the Iight beam is expanded between the laser and the glass plate by a lens L . If one replaces the real mirror M3 with its virtual image M3 /, , Which is formed by reflection by the glass plate , a point P of the real light source appears as the points P / , and P " of the virtual light sources L l and L 2 · Due to the different lightpaths , using the designations in Fig . 2 , 图 2the phase difference is given by :θλπδcos 22∙∙∙=d （2）λis the wavelength of the laser ljght used .According to ( 1 ) , the intensity distribution fora a a ==21 is2cos 4~222δ∙∙=a A I (3)Maxima thus occur whenδis equal to a multiple ofπ2,hence with ( 2 )λθ∙=∙∙m d cos 2；m=1，2，….. ( 4 )i. e . there are circular fringes for selected , fixed values of m , and d , sinceθ remains constant ( see Fig . 3 ) . If onealters the position of the movable mirror M 3 ( cf.Fig.1 ) such that d,e.g.,decreases , according to ( 4 ) , the ciroular fringe diameter would also diminish since m is indeed defined for this ring . Thus , a ring disappears each time d is reduced by 2λ. For d = 0 the ciroular fringe pattern disappears . If the surfaces of mirrors M 4 and M 3 are not parallelin the sense of Fig . 2, one obtains curved fringes , which gradually change into straight fringes at d = 0 . 空气衍射系数的确定To measure the diffraction n of air , an air-filled cell with plane- parallel boundaries is used . The diffraction index n of a gas is a linear function of the pressure P . For pressure P = 0 an absolute vacuum exists so that n=1.P PnP n P n ⋅∆∆+==)0()( (5)From the measured date ,the difference quotientP n ∆∆/ is f irst determined :PP n P P n P n ∆-∆+=∆∆)()((6) The following is true for the optical path length d : d =s P n ⋅)((7)Where s = 2·l is the geometric length of the evacuated cell and n ( P ) is the diffraction index of the gas present in the chamber . l is the lenght of the gas column in the glass cell . The fact that the path is traversed twice due to the reflect- ion on the mirror M4 is to be taken into consideration. Thus , by varying the pressure in the cell by the value △P , the optical path length is altered by the quantity △d :△d = n ( P ＋△P ）·s 一 n ( P ）·s ( 8 )on the screen one observes the change in the circular fringe pattern with change in the pressure ( the centre of the interference fringe pattern alternately shows maximal and minimal intensity ) . Proceeding from the ambient pressure Po,one observes the N-fold resetting of the initial position of the interference pattern (i.e. , establishment of an intensity minimum in the ring ’s centre ) until a specific pressure value P has been reached . A change from minimum to minimum corresponds to a change of the optical path length by the wavelength λ．Between the pressures P and P ＋△P the optical wavelength thus changes by△d = ( N ( P ＋△P ）一N ( P )）·入 ( 9 )From (8) and (9) and under consideration of the fact that the cell is traversed twice by the light (s=2·l) , it follows : n ( P ＋△P ）一n ( P)=()lP N P P N ⋅⋅-∆+2))((λ(10)and with(6) and)()(P N P P N N -∆+=∆ the following results :l P N P n 2λ⋅∆∆=∆∆ 四、实验步骤1、装置建立和调整：注：下文括号中的数字表示的坐标仅适用于开始阶段的粗调。

空气折射率的测定实验报告

一、实验目的1. 了解空气折射率的基本概念及其与温度、压强的关系。

2. 熟悉迈克尔逊干涉仪和夫琅禾费双缝干涉装置的原理及操作方法。

3. 利用迈克尔逊干涉仪和夫琅禾费双缝干涉装置测定空气的折射率。

二、实验原理1. 迈克尔逊干涉仪原理：迈克尔逊干涉仪是一种利用分振幅法进行干涉的仪器。

其原理是利用分束镜将一束光分为两束，分别照射到两个互相垂直的平面反射镜上，然后反射回来在分束镜处发生干涉。

当两束光的光程差为整数倍波长时，发生相长干涉，形成明条纹；当光程差为半整数倍波长时，发生相消干涉，形成暗条纹。

2. 夫琅禾费双缝干涉原理：夫琅禾费双缝干涉是一种利用分波前法进行干涉的仪器。

其原理是利用双缝将一束光分为两束，分别通过双缝后在观察屏上发生干涉。

当两束光的光程差为整数倍波长时，发生相长干涉，形成明条纹；当光程差为半整数倍波长时，发生相消干涉，形成暗条纹。

三、实验仪器1. 迈克尔逊干涉仪2. 夫琅禾费双缝干涉装置3. 激光器4. 光阑5. 空气室6. 压力测定仪7. 橡胶管四、实验步骤1. 迈克尔逊干涉仪实验：（1）搭建迈克尔逊干涉仪，调节仪器使光路畅通。

（2）将激光器发出的光束通过分束镜分成两束，分别照射到M1和M2反射镜上。

（3）调节M1和M2反射镜的位置，使两束光的光程差最小。

（4）观察干涉条纹，记录明条纹和暗条纹的位置。

（5）根据干涉条纹的位置，计算空气的折射率。

2. 夫琅禾费双缝干涉实验：（1）搭建夫琅禾费双缝干涉装置，调节仪器使光路畅通。

（2）将激光器发出的光束通过双缝，分别照射到观察屏上。

（3）调节双缝间距和观察屏距离，使干涉条纹清晰可见。

（4）观察干涉条纹，记录明条纹和暗条纹的位置。

（5）根据干涉条纹的位置，计算空气的折射率。

五、实验数据及结果分析1. 迈克尔逊干涉仪实验数据：- 室温：20℃- 大气压：1.01325×10^5 Pa- 激光波长：633.0 nm- 观察到的明条纹位置：L1- 观察到的暗条纹位置：L2根据干涉条纹的位置，计算空气的折射率：n = (L2 - L1) / (2Lλ)2. 夫琅禾费双缝干涉实验数据：- 室温：20℃- 大气压：1.01325×10^5 Pa- 激光波长：633.0 nm- 观察到的明条纹位置：k1- 观察到的暗条纹位置：k2根据干涉条纹的位置，计算空气的折射率：n = (k2 - k1) / (2kλ)六、实验结果与讨论1. 通过迈克尔逊干涉仪和夫琅禾费双缝干涉实验，测得空气的折射率分别为1.000296和1.000300，与参考值1.000296基本一致。

自组迈克耳孙干涉仪测量空气的折射率

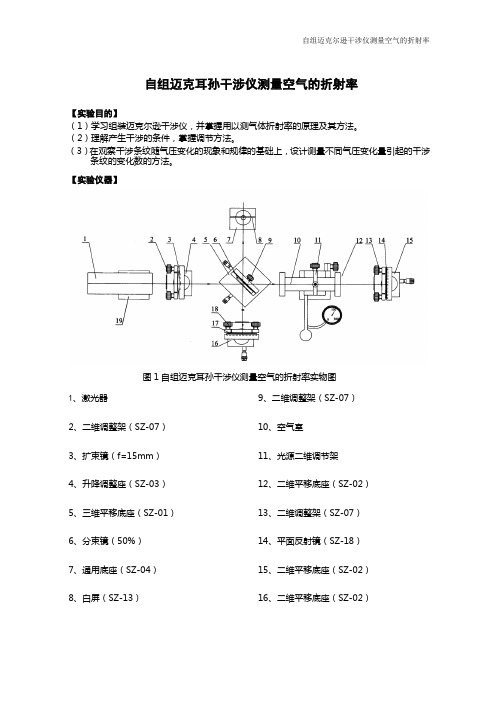
自组迈克尔逊干涉仪测量空气的折射率自组迈克耳孙干涉仪测量空气的折射率【实验目的】（1）学习组装迈克尔逊干涉仪，并掌握用以测气体折射率的原理及其方法。

（2）理解产生干涉的条件，掌握调节方法。

（3）在观察干涉条纹随气压变化的现象和规律的基础上，设计测量不同气压变化量引起的干涉条纹的变化数的方法。

【实验仪器】图1自组迈克耳孙干涉仪测量空气的折射率实物图1、激光器2、二维调整架（SZ-07）3、扩束镜（f=15mm）4、升降调整座（SZ-03）5、三维平移底座（SZ-01）6、分束镜（50%）7、通用底座（SZ-04）8、白屏（SZ-13）9、二维调整架（SZ-07）10、空气室11、光源二维调节架12、二维平移底座（SZ-02）13、二维调整架（SZ-07）14、平面反射镜（SZ-18）15、二维平移底座（SZ-02）16、二维平移底座（SZ-02）17、平面反射镜18、二维调整架（SZ-07）19、升降调整座（SZ-03）20、精密电子气压计【实验原理】1．迈克尔逊干涉仪的典型光路由图2所示，光源S射出的光经过分光板G1被分成强度大致相等、沿不同方向传播的两束相干光束（1）和（2），它们分别经固定反射镜M1和移动反射镜M2反射后，返回分光板，射向观察系统，在一定的条件下，观察系统（屏，望远镜，或人眼）中将呈现出特定的干涉图样，由于分光板的玻璃基板有一定的厚度，其折射率随波长而异，因此需要在光路（1）中放入一块与分光板材料、厚度完全相同的平行玻璃补偿板G2，这样就可以使（1）、（2）两束光的光程差始终相等，且与入射光波长完全无关。

当入射光为单色光而不需要确定零光程位置时，补偿板可以省略（本实验就是这种情况），如图3，但对于需要确定两路光程相等时的位置（又称零光程差位置）的某些实验，如观测白光干涉实验时，补偿板是必不可少的。

1图2 迈克尔逊干涉仪光路示意图1图3 自组迈克尔逊干涉仪测空气折射率的光路示意图2．等倾干涉如图3所示，当M2与M1严格垂直，即M2与M1′严格平行时，所得干涉为等倾干涉。

迈克尔孙干涉仪测空气折射率实验报告

系别___________ 班号____________ 姓名______________ 同组姓名 __________实验日期_________________________ 教师评定______________【实验名称】迈克耳孙干涉仪【目的要求】1.掌握M-干涉仪的调节方法;2.调出非定域干涉和定域干涉条纹;3.了解各类型干涉条纹的形成条件, 花纹特点, 变化规律及相互间的区别;用M-干涉仪测量气体折射率.【仪器用具】M-干涉仪(旧仪器第3组).He-Ne激光器及其电源.扩束透镜.小孔光阑.白炽灯.毛玻璃.小气室.打气皮囊.气压表.凸透镜. 【实验原理】系别 ___________ 班号 ____________ 姓名 ______________ 同组姓名 __________实验日期 _________________________ 教师评定 ______________1.M-干涉仪光路M-干涉仪是一种分振幅双光束的干涉仪.其光路如图.期中M1可以移动.G1为分束板.2.干涉花纹的图样(1) 点光源照明——非定域干涉条纹考虑虚光源S1和S2’.若毛玻璃垂直于两者连线.则得到圆条纹.若毛玻璃垂直于两者的垂直平分线.则得到线条纹.若其它情况.则得到椭圆或双曲线条纹.非定域圆条纹特性:∆L = 2d(1 − r 22z2) ........................................................................ .(i)亮纹条件:k λ = 2d(1 − r 22z2) ........................................................................ .(ii)条纹间距:2系别 ___________ 班号 ____________ 姓名 ______________ 同组姓名 __________实验日期 _________________________ 教师评定 ______________∆r = r k-1 − r k ≈ λz 22r k d.................................................................... .(iii)条纹的”吞吐”:缓慢移动M 1镜, 改变d, 可以看到条纹条纹吞或吐的数目N 有:2∆d = N λ .................................................................................. .(iv)(2) d 增大.rk 增大.即条纹”吐”.d 减小.rk 减小.即条纹”吞”. (3) 扩展光源照明－－定域干涉条纹(a) 等倾干涉条纹－－定域于无穷远相邻两条纹角间距:∆θk = θk − θk+1 ≈ λ2d θk.............................................................. .(v)(b) 等厚干涉条纹－－定域于镜面附近∆ = 2d cos θ ≈ 2d(1 − d θ2 / 2) ............................................... .(vi)2. 在交棱附近, 可忽略.因此在交棱附近看到的是直条纹.离棱远就慢慢变成弧形.且弯曲方向是凸向交棱方向的. 3. 测量空气折射率n = 1 + N λ2D ∙ p||∆p .................................................................. .(vii)系别___________ 班号____________ 姓名______________ 同组姓名 __________实验日期_________________________ 教师评定______________公式给出了气压为p时的空气折射率n.其中N为条纹吞吐量.△p为气室气压变化.【实验步骤和过程记录】1.了解M-干涉仪的构造(略)调节干涉条纹.错误！未定义书签。

迈克耳逊干涉仪的调整和使用及测空气折射率

提供稳定的相干光源，通常采用单色光源或激光光源。光源的稳定性对干涉条纹的清晰度和测量精度有很大影响。
用于调整反射镜的位置和角度，以改变光程差和干涉条纹的分布。调整机构需要具备高精度和稳定性，以保证测量结果的准确性。
02 调整迈克耳逊干涉仪的步骤与方法
准备工作与注意事项
确保实验室环境稳定，避免振动和温度变化对干涉仪的影响。
光纤传感
迈克耳逊干涉仪可用于光纤传感中，通过测量光纤中传输光的干涉条纹变化来检测外界物理量的变化，如温度、压力、应变等。
光学精密测量
迈克耳逊干涉仪可用于光学精密测量中，如测量光学元件的面形、光学表面的反射系数和透射系数、光学系统的像差等。
未来发展趋势预测
微型化、集成化
自动化、智能化
随着微纳加工技术的发展，迈克耳逊干涉仪将进一步实现微型化和集成化，使得其更加便携、易于使用和维护。
• 干涉现象：当两束或多束相干光波在空间某一点叠加时，它们的振幅相加，而光强则与振幅的平方成正比。如果两束光波的相位差是固定的，那么它们的光强就会呈现周期性的强弱变化，形成干涉现象。
干涉现象及条件
干涉条件：要产生干涉现象，需要满足以下条件
2. 两束光波的振动方向相同。
1. 两束光波的频率相同。 3. 两束光波的相位差恒定。
迈克耳逊干涉仪光路图
基本光路
迈克耳逊干涉仪的光路主要由分束器、反射镜和观测屏组成。入射光经过分束器分为两束，分别经过两个反射镜反射后再次经过分束器，最终在观测屏上形成干涉条纹。
光程差
由于两束光波经过的路径不同，它们之间存在光程差。通过调整反射镜的位置，可以改变光程差，从而改变干涉条纹的分布。
操作流程规范指导

迈克尔逊干涉仪空气折射率实验

迈克尔逊干涉仪测空气折射率实验摘要空气折射率是空气光学性质的一个基本参量。

本文介绍采用迈克尔逊干涉仪来测量空气折射率的方法，该方法简单易行。

引言利用迈克尔逊干涉仪的两束相干光在空间各有一段光路分开，通过在其中一支光路放进被研究对象而不影响另一支光路，让学生进一步了解光的干涉现象及其形成条件，以及学习调节光路的方法，同时也为测量空气折射率提供了一种思路和方法。

实验仪器：GSZF-4型迈克尔逊干涉仪选压器游标卡尺实验原理：1、等倾（薄膜）干涉在熟悉迈克尔逊干涉仪调节和使用的前提下，如图 1 所示，两束光到达 O 点形成的光程差δ为：δ=2L2-2L1=2（L2-L1）（1）若在 L2臂上加一个为 L的气室，如图 2 所示，则光程差为：δ=2（L2-L）+2nL-2L1整理得：δ=2（L2-L1）+2(n-1)L （2）保持空间距离L2、L1、L不变，折射率n变化时，则δ随之变化，即条纹级别也随之变化。

（根据光的干涉明暗条纹形成条件，当光程差δ=kλ时为明纹）以明纹为例有：δ1=2（L2-L1）+2(n1-1)L=k1λδ2=2（L2-L1）+2(n2-1)L=k2λ实验内容：1、安装固件熟读光学实验常用仪器部分迈克尔逊干涉仪的调节使用说明,并按此调节好；将气管 1 一端与空气室相连，另一端与气囊进气孔相连；将气管 2 一端与空气室相连，另一端与选压器相连；2、将空气室放在导轨上，观察干涉条纹（观察到条纹即可进行下面测量）3、关闭气囊阀门，向气室充气；使气压值大于 0.090MPa，，读出选压仪表数值，记为p2；打开气囊阀门，慢慢放气，使条纹慢慢变化，当改变m条时（实验要求m≧20），读出选压器数值，记为p1 ；4、重复第 3步，共取 10组数据；5、用游标卡尺测量空气室的长度，重复测量10次，得出10个数据。

实验注意事项1、激光属强光，注意不要让激光直接照射眼睛；2、充气阀门不要用力旋转，以免损坏；3、不得用手直接接触光学元件;4、向选压器里充气时，注意不可超过其量程实验数据记录大气压强 Pb＝5Pa；λ＝ 632.8 nm；温度t=12.0 ℃1.0132510结果讨论及误差分析：59662.8793 2.8793 1.01325101011 1.00027610.00367110.00367116.0P t δ---⨯⨯⨯=⨯+=+=+⨯+⨯⨯⨯标准值n 空气折射率的准确值为1.000276，与本实验的测量结果相差1.000276-1.000281=510。

实验十一迈克尔逊干涉法测量空气折射率

实验十一用迈克尔逊干涉光路测空气折射率光的干涉是重要的光学现象之一，是光的波动性的重要实验依据。

两列频率相同、振动方向相同和位相差恒定的相干光在空间相交区域将会发生相互加强或减弱现象，即光的干涉现象。

光的波长虽然很短(4×10－７～8×10－７m 之间)，但干涉条纹的间距和条纹数却很容易用光学仪器测得。

根据干涉条纹数目和间距的变化与光程差、波长等的关系式，可以推出微小长度变化(光波波长数量级)和微小角度变化等，因此干涉现象在照相技术、测量技术、平面角检测技术、材料应力及形变研究等领域有着广泛地应用。

相干光源的获取除用激光外，在实验室中一般是将同一光源采用分波阵面或分振幅2种方法获得，并使其在空间经不同路径会合后产生干涉。

迈克尔逊干涉仪是1883年美国物理学家迈克尔逊和莫雷合作，为研究“以太”漂移而设计制造出来的精密光学仪器。

它是利用分振幅法产生双光束以实现干涉。

在近代物理和近代计量技术中，如在光谱线精细结构的研究和用光波标定标准米尺等实验中都有着重要的应用。

利用该仪器的原理，研制出多种专用干涉仪。

一、实验目的1、掌握迈克尔逊干涉光路的原理和调节方法。

2、学会调出非定域干涉条纹、等倾干涉条纹、等厚干涉条纹。

3、学习利用迈克尔逊干涉光路测量常温下空气的折射率。

二、实验仪器He-Ne 激光器及电源，扩束镜（短焦距凸透镜），全反镜，温度计，小孔光阑，密封玻璃管，气压计等。

三、实验原理1、迈克尔逊干涉光路图11.1是迈克尔逊干涉光路原理图，从光源S 发出的一束光射到分束板1G 上，1G 的后表面镀有半反射膜（一般镀金属银），光在半反射膜上反射和透射，被分成光强接近相等的两束光，一束为反射光1，一束为透射光2。

当激光束以45°角射向分束板1G 时，被分成相互垂直的两束光。

这两束光分别垂直射向两平面反射镜1M 和2M ，经它们反射后再回到分束板1G 的半反射膜上，又汇聚成一束光，射到光屏E 处。

迈克尔逊干涉仪测空气折射率的原理

迈克尔逊干涉仪测空气折射率的原理嘿，朋友们！今天咱来唠唠迈克尔逊干涉仪测空气折射率这档子事儿。

你说这迈克尔逊干涉仪啊，就像是一个神奇的魔法盒子。

咱平常看空气，啥也看不出来对吧，就觉得那就是透明的啥也没有。

可这干涉仪就能让空气的秘密给现形喽！想象一下哈，干涉仪就像一双超级厉害的眼睛，能捕捉到空气里那些我们平常根本注意不到的细微变化。

它通过巧妙的设计和神奇的光的路径，让我们能看到空气折射率的变化呢。

这干涉仪里面的光线啊，就跟那调皮的小孩子似的，跑来跑去，一会儿这样一会儿那样。

然后呢，我们就能根据它们跑的情况来了解空气啦。

咱就说，这空气折射率可不是个随便的东西。

它就好像空气的一个隐藏属性，平常我们不知道，但是在一些特殊的情况下，比如说科学研究啦，或者一些对精度要求很高的实验里，它可就重要得很呐！你看哈，如果我们不知道空气折射率，那很多实验结果可能就不准确啦，就好像你走路没看清楚路，那不得摔跟头嘛！用迈克尔逊干涉仪来测空气折射率，就像是一场有趣的探索之旅。

我们调整这里，摆弄那里，看着那些奇妙的干涉条纹出现、变化，心里那个兴奋呐！这过程中啊，可得有耐心，要像个细心的侦探一样，一点点去观察、去分析。

稍微马虎一点，可能就错过了重要的线索哦。

而且啊，这可不仅仅是在实验室里玩玩的哦，它的用处可大着呢！比如说在一些光学仪器的设计里，了解空气折射率那是必须的，不然仪器可能就不好使啦。

咱再回过头来想想，这迈克尔逊干涉仪真的是个了不起的发明。

它让我们能看到那些原本隐藏起来的东西，就像给我们打开了一扇通往微观世界的门。

总之啊，迈克尔逊干涉仪测空气折射率这事儿，真的是既有趣又重要。

它让我们对空气有了更深的了解，也让我们的科学研究能更上一层楼。

咱可得好好珍惜这个神奇的工具，让它为我们带来更多的惊喜和发现呀！原创不易，请尊重原创，谢谢!。

用迈克尔逊干涉仪测空气的折射率实验报告

用迈克尔逊干涉仪测空气的折射率迈克尔逊干涉仪是一种典型的分振幅干涉仪，本实验要求自己组装迈氏干涉仪，M 1和M 2之间的距离每改变半个波长，其中心就“生出”或“消失”一个圆环。

两平面反射镜之间的距离增大时，中心就“吐出”一个个圆环。

反之，距离减小时中心就“吞进”一个个圆环，同时条纹之间的间隔（即条纹的稀疏）也发生变化。

由公式λn h 21=∆可知，只要读出干涉仪中M 1移动的距离∆h 和数出相应吞进（或吐出）的环数就可求得波长。

本实验中是通过改变气压从而改变光程差，通过数中心吐出圆环的数目来测量光程差。

光程差△d = n ( P ＋△P ）·s 一 n ( P ）·s =( N ( P ＋△P ）一N ( P )）·入，而折射率随压强的变化率P P n P P n P n ∆-∆+=∆∆)()(，由上面可以推得l P N P n 2λ⋅∆∆=∆∆，记录数据算出⎪⎭⎫ ⎝⎛∆∆P N ，就可以算出n p ∆∆，由()()p p n p n p n •∆∆+==0就可以推算P 下的空气折射率。

实验仪器光学平台；HeNe激光；调整架，35x35mm；平面镜，30x30mm；磁性基座；分束器50:50；透镜，f=+20mm；白屏；玻璃容器，手持气压泵，组合夹具，T形连接，适配器，软管，硅管。

实验内容1.装置建立和调整：注：下文括号中的数字表示的坐标仅适用于开始阶段的粗调。

a)参照图1摆放元件，推荐的光束高度130mm。

b)使用调整镜M1(1,8)和镜M2(1,4)调整光路时，光线要沿着平台上y=4的直线延伸。

c) 最初不需要放置分束器BS,光线直射M3（9,4）, 被M3反射后的光线能够和M2上初始光点重合。

然后放置分束器在(6,4)，BS的镀膜面朝向镜M2，这样一部分的光仍然可无阻碍的到达M3，另外的光射到M4(6,1)。

d)现在屏SC(6,6)上出现两个光点，调整M4使它们重合，此时观测到的应是一个轻微抖动的亮点。

用迈克尔逊干涉仪测不同压强下空气的折射率

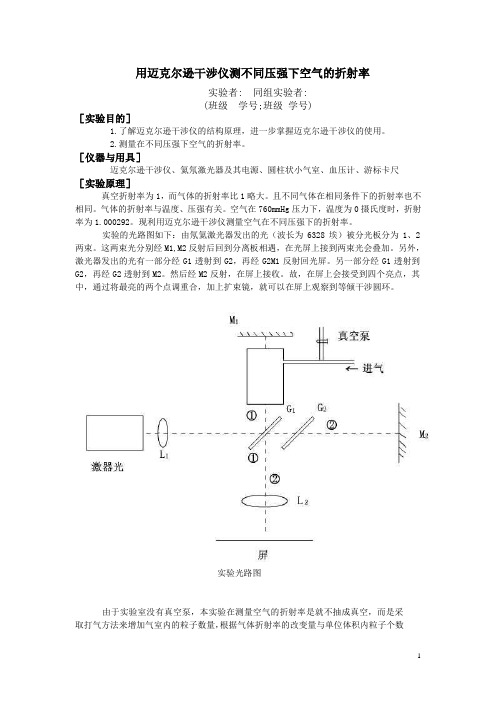
用迈克尔逊干涉仪测不同压强下空气的折射率实验者: 同组实验者:(班级学号;班级学号)［实验目的］1.了解迈克尔逊干涉仪的结构原理，进一步掌握迈克尔逊干涉仪的使用。

2.测量在不同压强下空气的折射率。

［仪器与用具］迈克尔逊干涉仪、氦氖激光器及其电源、圆柱状小气室、血压计、游标卡尺［实验原理］真空折射率为1，而气体的折射率比1略大。

且不同气体在相同条件下的折射率也不相同。

气体的折射率与温度、压强有关。

空气在760mmHg压力下，温度为0摄氏度时，折射率为1.000292。

现利用迈克尔逊干涉仪测量空气在不同压强下的折射率。

实验的光路图如下：由氖氦激光器发出的光（波长为6328埃）被分光板分为1、2两束。

这两束光分别经M1,M2反射后回到分离板相遇，在光屏上接到两束光会叠加。

另外，激光器发出的光有一部分经G1透射到G2，再经G2M1反射回光屏。

另一部分经G1透射到G2，再经G2透射到M2。

然后经M2反射，在屏上接收。

故，在屏上会接受到四个亮点，其中，通过将最亮的两个点调重合，加上扩束镜，就可以在屏上观察到等倾干涉圆环。

实验光路图由于实验室没有真空泵，本实验在测量空气的折射率是就不抽成真空，而是采取打气方法来增加气室内的粒子数量，根据气体折射率的改变量与单位体积内粒子个数的改变量成正比的规律求出相当于标准状况下的空气折射率n 0。

根据单位体积内的粒子数量与密度ρ成正比，Δn=k Δρ(其中k 为比例系数)。

设ρ0为空气在标况下的密度，n 0是在相应状态下的空气折射率；n 和p 是对应任意温度和压强下的折射率和密度。

又因为真空时的折射率为1，压强为0，所以标准状况下，以及任意温度压强下的折射率和密度相对真空的方程如下：)0(100-=-ρk n …………………………①)0(1-=-ρk n …………………………②由②/①有：0011ρρ=--n n根据PV=nRT(其中n 气体摩尔数，Mm n =)可得RT M m PV =故有：ρ==RTPM Vm所以：11000--=n n RT MP RT PM即：11000--=n n TP PT若实验温度不变有，p TT p n n ∆⋅⋅-=∆0001…………………………③ 考虑到T=T 0(1+at) (a 为空气膨胀系数，等于1/273=0.00367。

空气折射率的测量

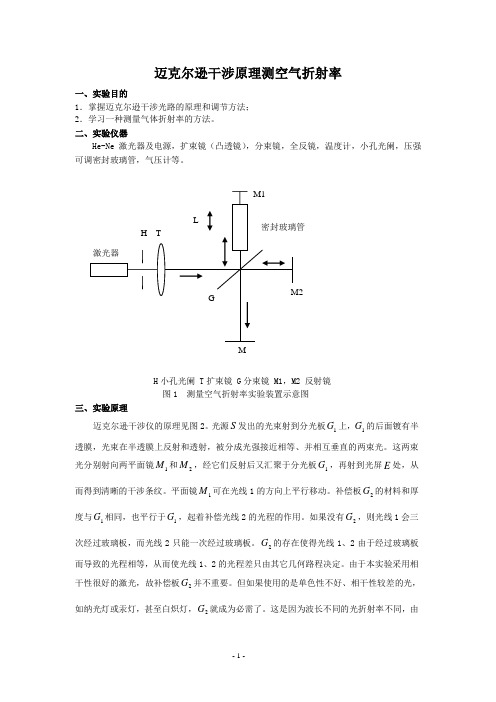
迈克尔逊干涉原理测空气折射率一、实验目的1．掌握迈克尔逊干涉光路的原理和调节方法； 2．学习一种测量气体折射率的方法。

二、实验仪器He-Ne 激光器及电源，扩束镜（凸透镜），分束镜，全反镜，温度计，小孔光阑，压强可调密封玻璃管，气压计等。

H 小孔光阑 T 扩束镜 G 分束镜 M1，M2 反射镜图1 测量空气折射率实验装置示意图三、实验原理迈克尔逊干涉仪的原理见图2。

光源S 发出的光束射到分光板1G 上，1G 的后面镀有半透膜，光束在半透膜上反射和透射，被分成光强接近相等、并相互垂直的两束光。

这两束光分别射向两平面镜1M 和2M ，经它们反射后又汇聚于分光板1G ，再射到光屏E 处，从而得到清晰的干涉条纹。

平面镜1M 可在光线1的方向上平行移动。

补偿板2G 的材料和厚度与1G 相同，也平行于1G ，起着补偿光线2的光程的作用。

如果没有2G ，则光线1会三次经过玻璃板，而光线2只能一次经过玻璃板。

2G 的存在使得光线1、2由于经过玻璃板而导致的光程相等，从而使光线1、2的光程差只由其它几何路程决定。

由于本实验采用相干性很好的激光，故补偿板2G 并不重要。

但如果使用的是单色性不好、相干性较差的光，如纳光灯或汞灯，甚至白炽灯，2G 就成为必需了。

这是因为波长不同的光折射率不同，由M分光板1G 的厚度所导致的光程就会各不一样。

补偿板2G 能同时满足这些不同波长的光所需的不同光程补偿。

图2 干涉原理图于是反射光束1与透射光束2在空间相遇，发生干涉，形成干涉条纹。

如果1M 、2M 镜严格垂直，则相应的干涉为等倾干涉，形成同心圆环状干涉条纹；如果1M 、2M 镜不是严格垂直，则相应的干涉为等厚干涉，形成平行直线状干涉条纹。

当光束垂直入射至1M 、2M 镜时，两光束的光程差)(22111L n L n -=δ （1-1）式中1n 和2n 分别是光路1L 和2L 上介质的折射率。

设单色光在真空中的波长为λ，当λδk =， ,3,2,1,0=k 时干涉加强，相应的接收屏中心的光强为极大。

迈克尔逊干涉仪测定空气折射率

用迈克尔逊干涉原理测量空气折射率

用迈克尔逊干涉仪测量气体折射率

利用迈克耳逊干涉仪测气体折射率实验报告

利用迈克耳逊干涉仪测气体折射率实验报告

迈克耳逊干涉仪的调整和使用及测空气折射率

迈克尔逊干涉仪测量空气折射率实验报告

迈克尔干涉仪测量空气折射率

空气折射率的测定实验报告

自组迈克耳孙干涉仪测量空气的折射率

迈克尔孙干涉仪测空气折射率实验报告

迈克耳逊干涉仪的调整和使用及测空气折射率

迈克尔逊干涉仪空气折射率实验

实验十一 迈克尔逊干涉法测量空气折射率

迈克尔逊干涉仪测空气折射率的原理

用迈克尔逊干涉仪测空气的折射率实验报告

用迈克尔逊干涉仪测不同压强下空气的折射率

空气折射率的测量

实验十一迈克尔逊干涉法测量空气折射率