用MATLAB实现共轭梯度法求解实例
运筹学实验报告(F-R共轭梯度法、Wolfe简约梯度法)

一、实验目的:1、掌握求解无约束最优化问题的 F-R 共轭梯度法,以及约束最优化问题 Wolfe 简约梯度法。
2、学会用MATLAB 编程求解问题,并对以上方法的计算过程和结果进行分析。
二、实验原理与步骤: 1、F-R 共轭梯度法基本步骤是在点)(k X 处选取搜索方向)(k d , 使其与前一次的搜索方向)1(-k d关于A 共轭,即(1)()(1),0k k k d d Ad --<>=然后从点)(k X 出发,沿方向)(k d 求得)(X f 的极小值点)1(+k X ,即)(m in )()()(0)1(k d X f X f k k λλ+=>+如此下去, 得到序列{)(k X }。
不难求得0,)1()(>=<-k k Ad d的解为)()1()1()()()()1(,,k k k k k k k d Ad d d AX b XX><>-<+=--+注意到)(k d 的选取不唯一,我们可取)1(1)()()(--+-∇=k k k k d X f d β由共轭的定义0,)1()(>=<-k k Add 可得: ><><-=----)1()1()1()(1,,k k k k k Ad d Ad r β共轭梯度法的计算过程如下:第一步:取初始向量)0(X , 计算⎪⎪⎩⎪⎪⎨⎧+=><><-=-=-∇==(0)0(0)(1))0()0()0()0(0(0)(0)(0)(0)d X X ,,X )X (r d λλAd d Ad r A b f第1+k 步:计算⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=><><-=+=><><-=-=-∇=+------(k)0(k)1)(k )()()()()1(1(k))()1()1()1()(1(k)(k)(k)d X X ,,r ,,X )X (r λλββk k k k k k k k k k k k k Ad d Ad r d d Ad d Adr A b f2、Wolfe 简约梯度法Wolfe 基本计算步骤:第一步:取初始可行点 x 0∈X l ,给定终止误差ε>0 ,令k:=0;第二步:设 I B k是x k 的 m 个最大分量的下标集,对矩阵A 进行相应分解 A =(B k ,N k );第三步:计算 ∇f(x k)=(∇B f(x k )∇Nf(x k )) ,然后计算简约梯度r N k=−(B k −1N k )T ∇B f(x k )+∇N f(x k );第四步:构造可行下降方向 p k . 若||p k ||≤ε ,停止迭代,输出x k 。
求解无约束优化问题的共轭梯度法

求解无约束优化问题的共轭梯度法李芳梅,姚瑞哲指导教师:李良摘要:本文主要针对无约束优化问题,利用共轭梯度法(CG方法)求解此类问题,并得出其迭代次数及问题的解。
论文对此种方法给出了具体事例,并对例子进行了matlab软件实现。
1.引言共轭梯度法时介于最速下降法与牛顿法之间的一个方法。
它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点。
共轭梯度法最早是由Hestenes和Stiefel(1952)提出来的,用于解正定系数矩阵的线性方程组。
由于共轭梯度法不需要矩阵存储,且有较快的收敛速度和二次终止性等优点,现已广泛应用与实际问题中。
2.共轭梯度法共轭梯度法是共轭方向法的一种。
所谓共轭方向法就是其所有的搜索方向都是相互共轭的方法。
定义设G是n×n对称正定矩阵,d1,d2是n维非零向量。
如果d1T G d2=0,则称向量d1和d2是G-共轭的,简称共轭的。
设d1,d2,…,d m是R n中任一组非零向量,如果d i T G d j=0 (i≠j),则称d1,d2,…,d m是G-共轭的,简称共轭的。
显然,如果d1,d2,…,d m是共轭的,则它们是线性无关的。
算法(共轭梯度法)步1.初始步:给出x0,ε>0,计算r0=G x0-b,令d0=-r0,k:=0. 步2.如果‖r k‖≤ε,停止.步3.计算αk=r k T r k/d k T Gd k,x k+1=x k+αk d k,r k+1=r k+αk Gd k,βk=r k+1T r k+1/r k T r k,d k+1=-r k+1+βk d k.步4.令k:=k+1,转步2.1.共轭梯度法的matlab实现(数值例子)首先建立如下的m.文件function[x,iter]=cgopt(G,b,x0,max_iter,tol)x=x0;fprintf('\n x0=');fprintf('%10.6f',x0);r=G*x-b;%残差d=-r;for k=1:max_iterif norm(r)<=toliter=k-1;fprintf('\n Algorithm finds a solution!');return endalpha=(r'*r)/(d'*G*d);%收敛速度 xx=x+alpha*d; rr=r+alpha*G*d; beta=(rr'*rr)/(r'*r); d=-rr+beta*d; x=xx; r=rr;fprintf('\n x%d=',k); fprintf('%10.6f',x); enditer=max_iter; return然后建立CG_main 的m.文件,带入数值例子function CG_main()12345123451234512345123451023412923277351432312174351512x x x x x x x x x x x x x x x x x x x x x x x x x ++++=⎧⎪+-+-=-⎪⎪-++-=⎨⎪+++-=-⎪---+=⎪⎩ G=[10 1 2 3 4;1 9 -1 2 -3;2 -1 7 3 -5;3 2 3 12 -1;4 -3 -5 -1 15]; b=[12 -27 14 -17 12]'; x0=[0 0 0 0 0]'; max_iter=1000; tol=1e-6;fprintf('\n');fprintf('Conjugate Gradiant Method:\n'); fprintf('=================\n');[x,iter]=cgopt(G,b,x0,max_iter,tol);fprintf('Iterative number:\n %d\n',iter); fprintf('Solution:\n'); fprintf('%10.6f',x);fprintf('\n================\n');4.结论实际上,共轭梯度法是最速下降法的一种改进。
matlab梯度算法

matlab梯度算法Matlab梯度算法在数学和计算机科学中,梯度是指一个多元函数在某一点上的变化率或斜率。
梯度算法是一种优化算法,用于找到函数的最小值或最大值。
在Matlab中,有多种方法可以使用梯度算法来优化函数,包括梯度下降和共轭梯度法。
本文将详细介绍Matlab中的梯度算法,并逐步讲解其原理和应用。
I. 梯度下降法梯度下降法是一种基于迭代的优化算法,通过计算函数的梯度来更新参数的值,以逐步接近函数的最小值。
在Matlab中,可以使用"gradientDescent"函数来实现梯度下降法。
1. 实现梯度下降法首先,我们需要定义一个优化目标函数,例如:f(x) = x^2 + 2x + 1。
然后,定义其梯度函数为g(x) = 2x + 2。
接下来,我们可以使用以下代码来计算梯度下降:matlab定义优化目标函数f = (x) x^2 + 2*x + 1;定义梯度函数g = (x) 2*x + 2;初始化参数x0 = 0;设置学习率和迭代次数alpha = 0.01;iterations = 100;梯度下降法for i = 1:iterationsx0 = x0 - alpha * g(x0);end打印最优解disp(['Optimal solution: ', num2str(x0)]);在这个例子中,我们使用了学习率(alpha)为0.01,迭代次数(iterations)为100。
通过不断更新参数x0的值,最终得到了最优解。
2. 梯度下降法的原理梯度下降法的核心思想是利用函数在当前点的梯度信息来更新参数的值,以便能够向着函数的最小值前进。
具体来说,算法的步骤如下:a. 初始化参数的值:选择一个初始参数的值作为起始点。
b. 计算梯度:计算函数在当前点的梯度,即求解函数关于参数的偏导数。
c. 更新参数:根据当前点的梯度和学习率,通过减去梯度的乘积来更新参数的值。
最优化方法实验报告(2)

最优化方法实验报告Numerical Linear Algebra And ItsApplications学生所在学院:理学院学生所在班级:计算数学10-1学生姓名:甘纯指导教师:单锐教务处2013年5月实验三实验名称:无约束最优化方法的MATLAB实现实验时间: 2013年05月10日星期三实验成绩:一、实验目的:通过本次实验的学习,进一步熟悉掌握使用MATLAB软件,并能利用该软件进行无约束最优化方法的计算。
二、实验背景:(一)最速下降法1、算法原理最速下降法的搜索方向是目标函数的负梯度方向,最速下降法从目标函数的负梯度方向一直前进,直到到达目标函数的最低点。
2、算法步骤用最速下降法求无约束问题n R()min的算法步骤如下:xxf,a )给定初始点)0(x ,精度0>ε,并令k=0;b )计算搜索方向)()()(k k x f v -∇=,其中)()(k x f ∇表示函数)(x f 在点)(k x 处的梯度;c )若ε≤)(k v ,则停止计算;否则,从)(k x 出发,沿)(k v 进行一维搜索,即求k λ,使得)(min )()()(0)()(k k k k v x f v x f λλλ+=+≥; d )令1,)()()1(+=+=+k k v x x k k k k λ,转b )。
(二)牛顿法1、算法原理牛顿法是基于多元函数的泰勒展开而来的,它将)()]([-)(1)(2k k x f x f ∇∇-作为搜索方向,因此它的迭代公式可直接写出来:)()]([)(1)(2)()(k k k k x f x f x x ∇∇-=-2、算法步骤用牛顿法求无约束问题n R x x f ∈),(min 的算法步骤如下:a )给定初始点)0(x ,精度0>ε,并令k=0;b )若ε≤∇)()(k x f ,停止,极小点为)(k x ,否则转c );c )计算)()]([,)]([)(1)(2)(1)(2k k k k x f x f p x f ∇∇-=∇--令;d )令1,)()()1(+=+=+k k p x x k k k ,转b )。
用共轭梯度法解最小二乘问题

用共轭梯度法求解最小二乘问题摘要 本文先讨论了求解对称正定线性方程组的共轭梯度法.然后对系数矩阵列满秩的线性方程组运用正则化方法将其转化为对称正定线性方程组后再运用实用共轭梯度法进行求解,最后举例并通过Matlab 程序实现其结果.关键词 共轭梯度法;正则化方法;最小二乘问题;Krylov 子空间1 引言在实际的科学与工程问题中,常常将问题归结为一个线性方程组的求解问题,而求解线性方程组的数值解法大体上可分为直接法和迭代法两大类.直接法是指在没有舍入误差的情况下经过有限次运算可求得方程组的精确解的方法.因此,直接法又称为精确法.迭代法则是采取逐次逼近的方法,亦即从一个初始向量出发,按照一定的计算格式,构造一个向量的无穷序列,其极限才是方程组的精确解,只经过有限次运算得不到精确解.当线性方程组的系数矩阵为对称正定矩阵时,我们常用共轭梯度法(或简称CG 法)求解,目前有关的方法与理论已经相当成熟,并且已成为求解大型稀疏线性方程组最受欢迎的一类方法.2 最小二乘问题定义1[1] 给定矩阵m n A R ⨯∈,A 列满秩及向量m b R ∈,确定nx R ∈使得()()2222min min n ny Ry Rb Ax r x r y Ay b ∈∈-===-. 该为问题称为最小二乘问题,简记为LS (Least Squares )问题,其中()r x 称为残向量.最小二乘问题的解x 又可称为线性方程组Ax b =,m n A R ⨯∈的最小二乘解,即x 在残向量()r x b Ax =-的2范数最小的意义下满足线性方程组 Ax b =,m n A R ⨯∈.3 共轭梯度法考虑线性方程组Ax b =的求解问题,其中A 是给定的n 阶对称正定矩阵,b 是给定的n 维向量,x 是待求解的n 维向量.为此,定义二次泛函()2T T x x Ax b x ϕ=-.定理1[1]设A 对称正定,求方程组Ax b =的解,等价于求二次泛函()x ϕ的极小点. 定理1表明,求解线性方程组问题就转化为求二次泛函()x ϕ的极小点问题.求解二次函数极小值问题,通常好像盲人下山那样,先给定一个初始向量0x ,确定一个下山方向0p ,沿着经过点0x 而方向为0p 的直线00x x p α=+找一个点1000x x p α=+,使得对所有实数α有()()00000x p x p ϕαϕα+≤+,即在这条直线上1x 使()x ϕ达到极小.然后从1x 出发,再确定一个下山的方向1p ,沿着直 线11x x p α=+再跨出一步,即找到1α使得()x ϕ在2111x x p α=+达到极小:()()11111x p x p ϕαϕα+≤+.重复此步骤,得到一串012,,,ααα 和 012,,,p p p ,称k p 为搜索方向,k α为步长.一般情况下,先在k x 点找下山方向k p ,再在直线k k x x p α=+上确定步长k α使()(),k k k k k x p x p ϕαϕα+≤+最后求出1k k k k x x p α+=+.然而对不同的搜索方向和步长,得到各种不同的算法.由此,先考虑如何确定k α.设从k x 出发,已经选定下山方向k p .令()()k k f x p αϕα=+()()()2TT k k k k k k x p A x p b x p ααα=++-+()22TT k k k k k p Ap r p x ααϕ=-+,其中k k r b Ap =-.由一元函数极值存在的必要条件有()220TT k k k k f p Ap r p αα'=-=所确定的α即为所求步长k α,即T k kk Tk kr p p Ap α=. 步长确定后,即可算出1k k k k x x p α+=+.此时,只要0Tk k r p ≠,就有()()()()1k k k k k k x x x p x ϕϕϕαϕ+-=+-()2220T kk TTk k k k k kT k kr p p Ap r p p Ap αα=-=-<即()()1k k x x ϕϕ+<.再考虑如何确定下山方向k p .易知负梯度方向是()x ϕ减小最快的方向,但简单分析就会发现负梯度方向只是局部最佳的下山方向,而从整体来看并非最佳.故采用新的方法寻求更好的下山方向——共轭梯度法.定义2[2]若n 维非零向量,x y 满足0T x Ay =其中A 为n 阶对称正定矩阵,则称x 与y 是相互共轭(A -共轭)的. 下面给出共轭梯度法的具体计算过程:给定初始向量0x ,第一步仍选用负梯度方向为下山方向,即00p r =,于是有00010001000,,T T r r x x p r b Ax p Ap αα==+=-.对以后各步,例如第k+1步(k ≥1),下山方向不再取k r ,而是在过点由向量k r 和1k p -所张成的二维平面21{|,,}k k k x x x r p R πξηξη-==++∈内找出使函数ϕ下降最快的方向作为新的下山方向k p .考虑ϕ在2π上的限制:()1,()k k k x r p ψξηϕξη-=++11()()Tk k k k k k x r p A x r p ξηξη--=++++12()Tk k k b x r p ξη--++.计算ψ关于,ξη的偏导得:()()11112,2,T T T k k k k k k T Tk k k k r Ar r Ap r r r Ap p Ap ψξηξψξηη----∂=+-∂∂=+∂其中最后一式用到了10Tk k r p -=,这可由k r 的定义直接验证.令0ψψξη∂∂==∂∂, 即知ϕ在2π内有唯一的极小值点001k k k x x r p ξη-=++,其中0ξ和0η满足00101011,0.T T T k k k k k k T Tkk k k r Ar r Ap r r r Ap p Ap ξηξη----⎧+=⎨+=⎩ 由于0k r ≠必有00ξ≠,所以可取()0101k k k k p x x r p ηξξ-=-=+作为新的下山方向.显然,这是在平面2π内可得的最佳下山方向.令010k ηβξ-=,则可得 1111.T k k k T k k r Ap p Ap β----=-注:这样确定的k p 满足10Tk k p Ap -=,即k p 与1k p -是相互共轭的.总结上面的讨论,可得如下的计算公式:T k kk Tk kr p p Ap α= , 1k k k k x x p α+=+, 11k k r b Ax ++=-, 1T k kk Tk kr Ap p Ap β+=-, 11k k k k p r p β++=+. 在实际计算中,常将上述公式进一步简化,从而得到一个形式上更为简单而且对称的计算公式.首先来简化1k r +的计算公式:11()k k k k k k k k r b Ax b A x p r Ap αα++=-=-+=-.因为k Ap 在计算k α是已经求出,所以计算1k r +时可以不必将1k x +代入方程计算,而是从递推关系1k k k r b Ap α+=-得到.再来简化k α和k β的计算公式.此处需要用到关系式1110,T T T k k k k k k r r r p r p +-+=== 1,2,k =.从而可导出1111,T T k k k kr r r α+++=-,()111T TTk k k k k k k kkp Ap p r r p r αα+=-=()1111T T k k k k k k kkr r p r r βαα--=+=.由此可得,T k k k T k k r r p Ap α=, 11.T k k k T k kr r r r β++=.从而有求解对称正定方程组的共轭梯度法算法如下:0x =初值00r b Ax =-;0k =while 0k r ≠1k k =+if 1k = 00p r =else21122T Tk k k k k r r r r β-----= 1122k k k k p r p β----=+ end11111T Tk k k k k r r p Ap α-----= 111k k k k x x p α---=+ 111k k k k r r Ap α---=-endk x x =注:该算法每迭代一次仅需要使用系数矩阵A 做一次矩阵向量积运算. 定理2 [1]由共轭梯度法得到的向量组{}i r 和{}i p 具有如下基本性质:(1)0Ti j p r =, 0;i j k ≤<≤ (2)0Ti j r r =, i j ≠,0,;i j k ≤≤ (3)0Ti j p Ap =, i j ≠,0,;i j k ≤≤ (4)000{,,}{,,}(,,1)k k span r r span p p A r k κ==+,其中0000(,,1){,,,}k A r k span r Ar A r κ+=,通常称之为Krylov 子空间.下面给出共轭梯度法全局最优性定理:定理3[1]用共轭梯度法计算得到的近似解k x 满足()(){}00min :(,,)k x x x x A r k ϕϕκ=∈+或{}**00min :(,,)k AAx x x x x x A r k κ-=-∈+,其中Ax=,*x 是方程组Ax b =的解,0(,,)A r k κ是由所定义的Krylov 子空间.定理2表明,向量组0,,k r r 和0,,k p p 分别是Krylov 子空间0(,,1)A r k κ+的正交基和共轭正交基.由此可知,共轭梯度法最多n 步便可得到方程组的解*x .因此,理论上来讲,共轭梯度法是直接法.然而实际使用时,由于误差的出现,使k r 之间的正交性很快损失,以致于其有限步终止性已不再成立.此外,在实际应用共轭梯度法时,由于一般n 很大,以至于迭代()O n 次所耗费的计算时间就已经使用户无法接受了.因此,实际上将共轭梯度法作为一种迭代法使用,而且通常是k r 是否已经很小及迭代次数是否已经达到最大允许的迭代次数max k 来终止迭代.从而得到解对称正定线性方程组的实用共轭梯度法,其算法如下:x =初值0;k =;r b Ax =-T r r ρ=while)()max2band k kε><1k k =+if 1k =p r = else;p r p βρρβ==+ end;;TAp p x x p ωαρωα===+ ;;Tr r r r αωρρρ=-== end算法中,系数矩阵A 的作用仅仅是用来由已知向量p 产生向量Ap ω=,这不仅可以充分利用A 的稀疏性,而且对某些提供矩阵A 较为困难而由已知向量p 产生向量Ap ω=又十分方便的应用问题有益.4 共轭梯度法求解最小二乘问题的正则化方程组(法方程组)定理4[1] 当A 列满秩时,求最小二乘问题的解等价于解T TA Ax A b =.应用共轭梯度法于对称正定方程组T T A Ax A b =来求方程组Ax b =,m nA R ⨯∈()m n ≥且A 列满秩的最小二乘解,即为Krylov 子空间法中的正则化方法.由A 列满秩有T A A 对称正定,则方程组T T A Ax A b =,m nA R ⨯∈()m n ≥存在唯一解.下面给出其实用共轭梯度法的详细算法且算法中不出现计算TA A 情形:x =初值0;;;;T T k b A b m Ax r b A m ====-while)()max2band k kε><1k k =+if 1k =p r = else;p r p βρρβ==+end;;;T Tn Ap A n p x x p ωαρωα====+ ;;Tr r r r αωρρρ=-==end注:算法中采用了两次矩阵向量积来避免出现计算T A A 情形.算例编写实用共轭梯度法的Matlab 程序求解方程组TTA Ax A b =,其中11112231A -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦, 1234b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦. 解 先建立conjgrad.m 文件,内容如下:function [x]=conjgrad(A,b,x) A=[1 -1;-1 1;2 -2;-3 1]; b=[1;2;3;4]; x=rand(2,1); k=0;b=A'*b;m=A*x; r=b-A'*m; T=r'*r;While norm(r)>1e-10*norm(b) k=k+1; if k==1 p=r;else B=T/t; p=r+B*p;endn=A*p;w=A'*n; a=T/(p'*w); x=x+a*p; r=r-a*w; t=T; T=r'*r; end然后运行后得 ans =-2.4167 -3.2500即有方程组的数值解 2.41673.2500x -⎡⎤=⎢⎥-⎣⎦.而其精确解可由如下方法求得: 111123111591121229731T A A -⎡⎤⎢⎥----⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎢⎥-⎣⎦,11123271121314T A b ⎡⎤⎢⎥---⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎢⎥⎣⎦, 则有121597971x x --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦, 解得122912134x x ⎡⎤-⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦,即方程精确解为*2912134x ⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦,故可验证通过Matlab 程序求得的数值解2.41673.2500x -⎡⎤=⎢⎥-⎣⎦满足精度要求.5 总结本文首先给出最小二乘问题的定义,随后从盲人下山法开始讨论了共轭梯度法的具体推导过程及其相关性质与算法.继而重点给出正则化方法的实用共轭梯度算法并举例进行检验.最后,需要说明虽然正则化方法是求一般线性方程组Ax b =,m nA R⨯∈()m n ≥且A 列满秩的最小二乘解的一种方法且简单易行,但是也有许多不足之处,如m n >时一般无解;TA A 形成时运算量大,A 中某些信息会丢失;当A 病态时其收敛性速度由于222()()T A A A κκ=很大变得非常之慢等,故为了避免正则化方法的缺点,还可运用残量极小化方法或残量正交化方法等更好的方法来解决此类问题.参考文献[1] 徐树方,高立,张平文.数值线性代数[M].北京:北京大学出版社,2000.139--151. [2] 施光燕,董加礼.最优化方法[M].北京:高等教育出版社,1999.47--52.。
共轭梯度法求解线性方程组
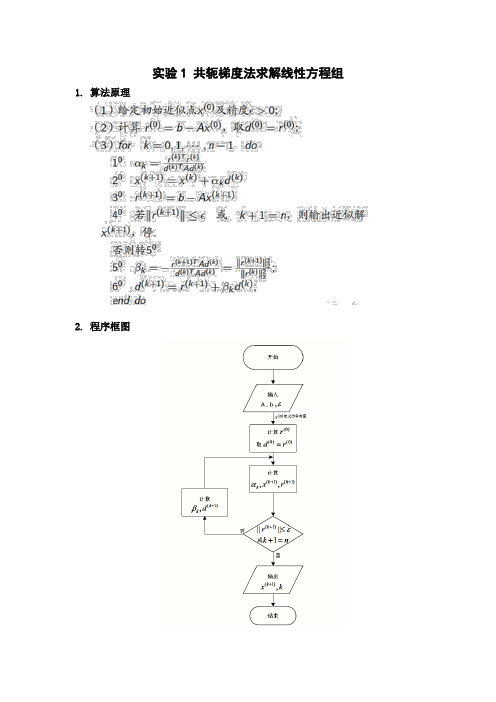
实验1 共轭梯度法求解线性方程组1.算法原理2.程序框图3.程序使用说明。
本程序使用MATLAB来求解线性方程组Ax b源程序文件“gongetidu1.m”为共轭梯度法源程序,x为方程组的解,k为迭代次数,A为方程组的系数矩阵,b为方程组的右端项,ep为精度。
定义A, b,ep后,在命令窗口输入[x,k] = gongetidu1(A,b,ep),回车后即可算出方程组的解和迭代次数。
源程序文件“gongetidu2.m”为共轭梯度算例3.2中构造A,b矩阵的程序。
定义阶数n的数值后,在命令窗口输入[A,b] = gongetidu2(n)即可算出A, b矩阵。
4.算例计算结果此算例为课本113页计算实习3.2.首先,设定MATLAB的数值格式为“long”。
当n=100时,在命令窗口中输入“[A,b]=gongetidu2(100)”,回车后可得到A 和b的矩阵;假设精度ep = 10-3,然后在命令窗口输入“[x,k] = gongetidu1(A,b,10^-3)”即可算出方程组的解x和迭代次数k。
x=( 0.999999999999988,0.999999999999995,1.000000000000009,···0.9999 99999999997,0.999999999999998 )T(x向量一共有100个元素)k=49.同理,可以算出n=200,400的结果。
n=200时,同样假设精度ep = 10-3,结果为:x=( 0.999999999999974,1.000000000000023,0.999999999999935,···1.000000 000000029, 0.999999999999987)T (x向量一共有200个元素)k=99.n=400时,同样假设精度ep = 10-3,结果为:x=( 1.000000000000017,0.999999999999846,1.000000000000039,···0.99999999 9999881,1.000000000000062)T (x向量一共有400个元素)k=199。
共轭梯度法matlab程序

共轭梯度法matlab程序共轭梯度法是一种用于求解无约束优化问题的迭代算法。
以下是一个简单的MATLAB 程序示例,用于实现共轭梯度法:matlab复制代码function[x, fval, iter] = conjugate_gradient(A, b, x0, tol,max_iter)% A: 矩阵% b: 向量% x0: 初始解% tol: 容忍度% max_iter: 最大迭代次数r = b - A*x0;p = r;x = x0;fval = A*x - b;iter = 0;while (norm(r) > tol) && (iter < max_iter)Ap = A*p;alpha = dot(p, r) / dot(p, Ap);x = x + alpha*p;r = r - alpha*Ap;if iter == 0fval_new = dot(r, r);elsebeta = dot(r, r) / dot(p, Ap);p = r + beta*p;fval_new = dot(r, r);endif fval_new < fvalfval = fval_new;enditer = iter + 1;endend该程序接受一个矩阵A、一个向量b、一个初始解x0、一个容忍度tol和一个最大迭代次数max_iter作为输入,并返回最终解x、目标函数值fval和迭代次数iter。
使用该函数时,您需要将要优化的目标函数转换为矩阵形式,并调用该函数来找到最优解。
例如,假设您要最小化一个函数f(x),可以将该函数转换为矩阵形式A*x - b,其中A是目标函数的雅可比矩阵,b是目标函数的常数项向量。
然后,您可以调用该函数来找到最优解,例如:matlab复制代码A = jacobian(f); % 计算目标函数的雅可比矩阵b = [1, 2, 3]; % 目标函数的常数项向量x0 = [0, 0, 0]; % 初始解向量tol = 1e-6; % 容忍度max_iter = 1000; % 最大迭代次数[x, fval, iter] = conjugate_gradient(A, b, x0, tol, max_iter); % 调用共轭梯度法函数求解最优解。
共轭梯度法

3. 算法的 MATLAB 实现
在 MATLAB 中编程实现的共轭梯度法函数为: min GETD 功能:用共轭梯度法求解多维函数的极值。
调用格式: [ x, min f ] min GETD( f , x0, var, eps) 其中, f :目标函数;
x0 :初始点; :自变量向量; var x :目标函数取最小值时的自变量值;
(6) 若 k 1 n ,令 x(0) x( n ) ,转步骤(3) ,否则转步骤(7) ;
(7) 令 p
( k 1)
f ( x
( k 1)
) k p
(k )
, k
f ( x ( k 1) ) f ( x )
(k )
2 2
, 置 k k 1, 转步骤 (4) 。
t 0
(k ) ( k ) (4) 用 一 维 搜 索 法 求 t k , 使 得 f ( x kt p ) m i n f
( ) 5; x( k 1 ) x k( ) kt p k,转步骤
k( ) x
) 令, tk p( ,
(5) 若 f ( x
( k 1)
) ,停止,极小值点为 x ( k 1) ,否则转步骤(6) ;
1 f ( X ) d1 + x1 -x1* 2 1 =d1 + x1 -x1* 2
2
*
2
1 d1 a x1 -x1* 2
2b x1 -x1*
x -x c x -x
2
2b x1 -x1*
数值计算实例MATLAB实现(附带详细源码)

数值计算实例MATLAB实现附带详细源码1.在化学反应中,A 的一个分子和 B 的一个分子结合形成物质 C 的分子。
若在时刻t 时,物质 C 的浓度为() y t ,则其是下述初值问题的解()()() ,00y k a y b y y '=--=其中k 为正常数,a 和 b 分别表示 A 和 B 的初始浓度。
假设k = 0.01, a =70毫摩/升, b = 50 毫摩/升. 该方程的真解为0.20.2350(1)()75t te y t e---=- (1)自己编写程序,使用四阶经典Runge-Kutta (龙格-库塔法),以步长为0.5h =,在区间[0, 20]上给出() y t 的近似解; (2)列表给出真解和近似解的比较;(3)讨论当t →∞时,近似解的变化趋势,并分析该数值结果。
解:数学原理:四阶经典Runge-Kutta (龙格-库塔法)112341213243(22)6(,)(,)22(,)22(,)m m m m m m m m m m hu u k k k k k f t u h hk f t u k h hk f t u k k f t h u hk +=++++==++=++=++程序设计见附录 结果如下表:(3)近似解变化趋势当t→∞时,由以下极限方程可知:0.20.2350(1)()75lim()tttey tey t--→∞⎧-=-⎪⎨⎪⎩随着t→∞,近似值越来越接近真实值,极限的真实值为50,lim()50ty t→∞=,变化趋势也可由一下曲线图表示:感想:四阶Runge-Kutta法计算的结果精度非常好,其结果与真实解误差不大。
2.考虑定义在闭区间[−5, 5]上的函数()2112()5f x x -=+ ;(1)利用等距节点构造次数分别为 n = 4,8,16, 32 的插值多项式()n p x ,并分别画()()()()481632,,,p x p x p x p x ;(2)利用chebyshev 零点构造次数分别为 n = 4,8,16, 32 的插值多项式()n pp x()()()()481632,,,pp x pp x pp x pp x ;(3)画出当 n = 32 时,两种插值多项式的比较图,误差图,并给出相应的误差估计;(4)在这个问题中能观察到龙格现象吗? 解:数学原理:拉格朗日插值多项式:001122()()()()()n n n L x l x y l x y l x y l x y =+++011011()()()()(),0,1,2,()()()()k k n k k k k k k k n x x x x x x x x l x k n x x x x x x x x -+-+----==----0()()()nn n in k k k k k j k jj kx x L x l x y y x x ===≠-==-∑∑∏程序设计见附录(1) 利用等距节点构造次数分别为 n = 4,8,16, 32 的插值多项式如下: ()43240.00160.00.0640.60061400p x x x x x ++=++()876542830.00280.00640.02500.02500.00640.00260.000168.001p x x x x x x x x x ++++++=++()1615141312161110987654320.00210.00280.00410.0064 60.01120.02500.09290.09290.02050 0.01120.00640.00410.002.00160180.021.000p x x x x x x x x x x x x x x x x x ++++++++++++++=++()3231302928272632252423222120191817160001600018000210002400028000340004100050006400083001120016100250004350092902906029p x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .x x .=+++++++++++++++++151413121110987654320600929004350025000161001120008300064000500041000340002800024000210001800016x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .+++++++++++++++(2)利用chebyshev 零点构造次数分别为 n = 4,8,16, 32 的插值多项式如下:()43240.00160.00320.00320.0016x x p x x p x =++++()87654328+0.00190.00320.01080.01080.00320.00196=0.0.0106001pp x x x x x x x x x +++++++()161514131211109168765432=0.0016 0.0017 0.0019 0.00230.00320.00520.01080.0403 1.00000.04030.01080.00520.00320.00230.0019 0.0017 0.0016 pp x x x x x x x x x x x x x x x x x ++++++++++++++++()323130292827263225242322212019181700016000160001700017000190002100023000270003200040000520007100108001860040301428pp x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .x x =+++++++++++++++++16151413121110987654320142800403001860010800071000520004000320002700023000210001900017000170001600016.x .x .x .x .x .x .x .x .x .x .x .x .x .x .x .+++++++++++++++++(3)两种插值多项式的比较误差图如下(a)等距插值误差 (b) chebyshev零点插值误差(4) 等距插值在高次插值中能观察到龙格现象,而chebyshev零点插值观察不到龙格现象。
双共轭梯度法matlab_概述及解释说明

双共轭梯度法matlab 概述及解释说明1. 引言1.1 概述引言部分将介绍“双共轭梯度法(Matlab)”,该方法是一种用于解决优化问题的迭代算法,常用于求解大规模线性方程组、最小二乘问题和非线性最优化等。
本文将全面讲解双共轭梯度法的基础知识、算法流程及其在MATLAB中的应用与实现。
1.2 文章结构本文按照以下方式组织:- 第二节将介绍双共轭梯度法的基础知识,包括梯度下降法、共轭梯度法和双共轭梯度法的简介。
- 第三节将详细阐述双共轭梯度法的算法流程及具体步骤解释,包括初始化步骤、迭代更新步骤以及收敛准则和结束条件设定。
- 第四节将以MATLAB为工具,展示双共轭梯度法在实践中的应用与实现举例。
这一部分将给出MATLAB代码编写指导原则,描述一个示例问题,并说明求解过程和结果分析。
- 最后一节是结论与展望,总结了双共轭梯度法的优点和局限性,并提供对未来可能的研究方向的展望和建议。
1.3 目的本文旨在介绍双共轭梯度法的原理、算法流程及其在MATLAB中的实际应用。
读者将通过本文了解如何使用该方法解决优化问题,并深入理解算法背后的理论基础。
同时,本文还将探讨双共轭梯度法存在的局限性,并展望未来可能的研究方向,为相关领域的研究提供参考。
2. 双共轭梯度法基础知识2.1 梯度下降法简介梯度下降法是一种优化算法,用于求解无约束问题的最小值。
其基本思想是通过沿着目标函数的负梯度方向进行迭代更新,以逐步减小目标函数值。
具体而言,对于一个可微分的目标函数f(x),初始值$x_0$被选为起点,然后通过以下公式进行迭代更新:$$x_{k+1} = x_k - \alpha_k \nabla f(x_k)$$其中$\alpha_k$是步长或学习率,$\nabla f(x_k)$表示在点$x_k$处的梯度(即函数$f(x)$在$x_k$处的导数)。
该过程将重复执行直到满足预设的终止条件。
2.2 共轭梯度法简介共轭梯度法是一种高效的迭代方法,用于解决对称正定线性系统的问题。
计算方法——共轭梯度法求解线性方程组

n-1 do
k
r r ; k T k d Ad
x
k 1
x k d ;
k k
1
1 共轭梯度法求解线性方程组
③
r
k 1
b Ax
k 1
k 1
;
④ 若 || r k 1 || 或 k 1 n ,则输出近似解 x(k+1),停止;否则,转⑤; ⑤ ⑥
18 9 27 9 1 18 45 0 45 2 ,b A 9 16 0 126 9 27 45 9 135 8
由于该方程组的系数矩阵以及右端项都比较简单,因此采用从 matlab 命令窗口手 动输入的方式来输入数据,取计算精度为 10-6,运行过程及结果如图 2 和图 3(由于迭 代的初始值为随机产生,因此每次得到的残量图会有所不同,但最终都趋于 0) :
|| r ||2 k k 22 ; || r ||2
d
k 1
r
k 1
k d ;
k
end do
图 1 共轭梯度法求解线性方程组程序框图
1.2 程序使用说明 共轭梯度法求解线性方程组的 matlab 程序见附录 1,该程序可以求解系数矩阵为 对称正定矩阵的线性方程组。在使用该程序时,可将程序复制到 matlab 命令窗口中直 接运行或者复制到编辑窗口中保存运行,运行时刻根据提示输入,直至得到结果。 开始运行程序时,会出现提示“请选择系数矩阵、右端项以及系数矩阵阶数的输
图 4 命令窗口显示的运行结果
1.6 1.4 1.2 1
残量
0.8 0.6 0.4 0.2 0 0 20 40 60 80 100
最新a03共轭梯度法编程汇总

a03共轭梯度法编程MK7FCCK282Z3SVMK6CZBW26Q6LZ9 MKHMNXTJJQ4S83MKMDE2RESG33HSP90 第二章 11(2)用大M法求解min w=2x1+x2-x3-x4s.t x1-x2+2x3-x4=22x1+x2-3x3+x4=6x1+x2+x3+x4=7xi≥0, i = 1, 2, 3, 4用matlab求解如下:f=[2,1,-1,-1,200,200,200];a=[1 -1 2 -1 1 0 0;2 1 -3 1 0 1 0;1 1 1 1 0 0 1];b=[2 6 7];lb=zeros(7,1);[x,fval,exitflag,output,lambda]=linprog(f,[],[],a,b,lb) Optimization terminated.运行结果如下:x =3.00000.00001.00003.00000.00000.00000.0000fval =2.0000exitflag =1output =iterations: 7algorithm: 'large-scale: interior point'cgiterations: 0message: 'Optimization terminated.'lambda =ineqlin: [0x1 double]eqlin: [3x1 double]upper: [7x1 double]lower: [7x1 double]从上述运行结果可以得出:最优解为x= ,最小值约为f*=2。
P151 第三章 26用共轭梯度算法求f(x) = (x1-1)^2+5*(x2-x1^2)^2的极小点,取初始点x0= 。
用matlab求解如下:function mg=MG()%%共轭梯度法求解习题三第26题%clc;clear;n=2;x=[2 0]';max_k=100;count_k=1;trace(1,1)=x(1);trace(2,1)=x(2);trace(3,1)=f_fun(x);k=0;g1=f_dfun(x);s=-g1;while count_k<=max_kif k==ng0=f_dfun(x);s=-g0;k=0;elser_min=fminbnd(@(t) f_fun(x+t*s),-100,100);x=x+r_min*s;g0=g1;g1=f_dfun(x);if norm(g1)<10^(-6)break;endm=(norm(g1)^2)/(norm(g0)^2);s=-g1+m*s;count_k=count_k+1;trace(1,count_k)=x(1);trace(2,count_k)=x(2);trace(3,count_k)=f_fun(x);k=k+1;endendcount_kxf=f_fun(x)function g=f_dfun(x)g(1,1)=20*x(1)^3-20*x(1)*x(2)+2*x(1)-2;g(2,1)=10*x(2)-10*x(1)^2;function f=f_fun(x)f=5*x(1)^4-10*x(1)^2*x(2)+x(1)^2-2*x(1)+1+5*x(2)^2;运行结果如下:k =59x0 =1.00001.0000f0 =从上述运行结果可以得出:最优解为x= ,最小值约为f*=0。
共轭梯度法的matlab源程序

共轭梯度法的matlab源程序functiong=conjugate_grad_2d(x0,t)%please input thisconjugate_grad_2d([2,2],0.05)x=x0;syms xi yiaf=xi^2-xiyi+3yi^2;fx=diff(f,xi);fy=diff(f,yi);fx=subs(fx,{xi,yi },x0);fy=subs(fy,{xi,yi},x0);fi=[fx,fy];count=0;whiledouble(sqrt(fx^2+fy^2))ts=-fi;ifcount=0s=-fi;elses=s1;endx=x+as;f=subs(f,{xi,yi},x);f1=diff(f);f1=solve(f1);iff1~=0ai=double(f1);elsebreakx,f=subs(f,{xi,yi},x),countend x=subs(x,a,ai);f=xi^2-xiyi+3yi^2;fxi=diff(f,xi);fyi=diff(f,yi);f xi=subs(fxi,{xi,yi},x);fyi=subs(fyi,{xi,yi},x);fii=[fxi,fyi];d=(fxi^ 2+fyi^2)(fx^2+fy^2);s1=-fii+ds;count=count+1;fx=fxi;fy =fyi;endx,f=subs(f,{xi,yi},x),count史锋的共轭梯度法matlab程序以函数f=1-(1/(sqrt(2*pi)))*(exp((-(xi-3)^2+yi^2)/2)+0.6*exp((-(xi+3)^2+yi^2)/2));为例求解最小值function f=conjugate_gradient(x0,eps)x=x0;syms xi yi af=1-(1/(sqrt(2*pi)))*(exp((-(xi-3)^2+yi^2)/2)+0.6*exp((-(xi+3)^2+yi^2)/2));fx=diff(f,xi);fy=diff(f,yi);fx=subs(fx,{xi,yi},x0);fy=subs(fy,{xi,yi},x0);fi=[fx,fy];n=0;while double(sqrt(fx^2+fy^2))>epss=-fi;if n<=0s=-fi;elses=s1;endx=x+a*s;f=subs(f,{xi,yi},x);f1=diff(f);f1=solve(f1);if f1~=0ai=double(f1);elsebreakx,nendx=subs(x,a,ai);f=1-(1/(sqrt(2*pi)))*(exp((-(xi-3)^2+yi^2)/2)+0.6*exp((-(xi+3)^2+yi^2)/2));fxi=diff(f,xi);fyi=diff(f,yi);fxi=subs(fxi,{xi,yi},x);fyi=subs(fyi,{xi,yi},x);fii=[fxi,fyi];d=(fxi^2+fyi^2)/(fx^2+fy^2);s1=-fii+d*s; %搜索方向n=n+1; %搜索次数fx=fxi;fy=fyi;endx,n%请输入:conjugate_gradient([0,0],10^(-6))后运行中国振动联盟标题: 共轭梯度法的matlab源程序[打印本页]作者: suffer 时间: 2006-10-11 09:15 标题: 共轭梯度法的matlab源程序1.function g=conjugate_grad_2d(x0,t)2.%please input this:conjugate_grad_2d([2,2],0.05)3.x=x0;4.syms xi yi a5.f=xi^2-xi*yi+3*yi^2;6.fx=diff(f,xi);7.fy=diff(f,yi);8.fx=subs(fx,{xi,yi},x0);9.fy=subs(fy,{xi,yi},x0);10.fi=[fx,fy];11.count=0;12.while double(sqrt(fx^2+fy^2))>t13.s=-fi;14.if count<=015.s=-fi;16.else17.s=s1;18.end19.x=x+a*s;20.f=subs(f,{xi,yi},x);21.f1=diff(f);22.f1=solve(f1);23.if f1~=024.ai=double(f1);25.else26.break27.x,f=subs(f,{xi,yi},x),count28.end29.x=subs(x,a,ai);30.f=xi^2-xi*yi+3*yi^2;31.fxi=diff(f,xi);32.fyi=diff(f,yi);33.fxi=subs(fxi,{xi,yi},x);34.fyi=subs(fyi,{xi,yi},x);35.fii=[fxi,fyi];36.d=(fxi^2+fyi^2)/(fx^2+fy^2);37.s1=-fii+d*s;38.count=count+1;39.fx=fxi;40.fy=fyi;41.end42.x,f=subs(f,{xi,yi},x),count复制代码本程序由tammy友情提供作者: bainhome 时间: 2006-10-15 23:40这段代码是我编的吧,函数名称命名风格一看就是自己...^_^当时刚学没几天,代码里大段大段的都是符号工具箱里的函数,运行慢得要死要活。
用MATLAB实现共轭梯度法求解实例

用MATLAB实现共轭梯度法求解实例介绍共轭梯度法是一种迭代优化算法,用于求解线性方程组或最小化二次函数的问题。
在本文档中,我们将使用MATLAB来实现共轭梯度法,并通过一个实例来演示它的应用。
共轭梯度法共轭梯度法是一种迭代优化算法,用于求解形如Ax=b的线性方程组。
它的主要思想是利用迭代过程中的残差和共轭梯度的特性,逐步逼近方程的解。
共轭梯度法的优点是收敛速度快,尤其适用于大规模稀疏线性方程组的求解。
共轭梯度法的具体步骤共轭梯度法的具体步骤如下: 1. 初始化解向量x和残差r,令初始残差r0等于b减去Ax的乘积,初始搜索方向p等于r0。
2. 迭代更新解向量: - 计算搜索步长α:α等于r的转置乘以r除以p的转置乘以Ap的乘积。
- 更新解向量和残差:x等于x加上α乘以p,r等于r减去α乘以Ap。
- 计算残差的L2范数:如果残差的L2范数小于预设阈值,停止迭代;否则,继续迭代。
- 计算搜索方向的系数β:β等于r的转置乘以r除以上一次迭代的残差r的转置乘以上一次迭代的残差r的乘积。
- 更新搜索方向:p等于r加上β乘以上一次迭代搜索方向p。
3. 输出解向量x,即为线性方程组的解。
实例在这个实例中,我们将使用共轭梯度法来求解以下线性方程组:A = [4, -1, 0; -1, 4, -1; 0, -1, 4]b = [5; 5; 10]首先,我们将初始化解向量x、残差r和搜索方向p:A = [4, -1, 0; -1, 4, -1; 0, -1, 4];b = [5; 5; 10];x = zeros(size(b)); % 初始化解向量xr = b - A*x; % 初始化残差rp = r; % 初始化搜索方向p然后,我们将进行迭代更新解向量:while norm(r) > 1e-6% 设置迭代终止条件为残差的L2范数小于1e-6Ap = A*p; % 计算Apalpha = (r'*r) / (p'*Ap); % 计算搜索步长alphax = x + alpha*p; % 更新解向量xr_new = r - alpha*Ap; % 计算新的残差rbeta = (r_new'*r_new) / (r'*r); % 计算搜索方向系数betap = r_new + beta*p; % 更新搜索方向pr = r_new; % 更新残差rend最后,输出解向量x的值:x共轭梯度法是一种有效的迭代优化算法,用于求解线性方程组。
matlab共轭梯度法求解方程组

主题:matlab共轭梯度法求解方程组近年来,随着科学技术的不断发展,数学建模和计算机仿真成为科学研究和工程技术领域的重要手段。
在实际应用中,我们常常需要解决线性方程组的求解问题,而共轭梯度法作为一种高效的迭代求解方法,广泛应用于信号处理、图像处理、地球物理勘探和优化问题等领域。
本文将介绍如何利用matlab中的共轭梯度法求解线性方程组的基本原理和实际操作方法。
1. 共轭梯度法的基本原理共轭梯度法是一种迭代法,用于求解对称正定线性方程组Ax=b。
该方法的核心思想是通过一系列的迭代操作,逐步逼近方程组的解,直到满足一定的精度要求。
在每一步迭代中,共轭梯度法利用残差和方向向量的共轭性质,不断寻找最优的步长,从而实现方程组的求解。
2. matlab中共轭梯度法的基本调用方法在matlab中,调用共轭梯度法求解线性方程组非常简单。
需要将方程组的系数矩阵A和右端向量b输入到matlab中,然后利用内置函数conjugateGradient进行求解。
具体的调用方法如下:x = conjugateGradient(A, b, x0, maxIter, tol)其中,A为系数矩阵,b为右端向量,x0为初始解向量,maxIter为最大迭代次数,tol为精度要求。
调用完毕后,matlab将返回方程组的近似解x。
3. 共轭梯度法在实际工程中的应用共轭梯度法作为一种高效的求解方法,在工程技术领域得到了广泛的应用。
以图像处理为例,图像处理中经常需要解决大规模的线性方程组,而共轭梯度法能够高效地求解这类问题,提高了图像处理算法的效率和稳定性。
另外,在地球物理勘探中,共轭梯度法也被广泛应用于三维数据的快速处理和解释。
可以说,共轭梯度法在实际工程中发挥着重要的作用。
4. 共轭梯度法的优缺点分析尽管共轭梯度法具有非常高的效率和稳定性,但是该方法也存在一些缺点。
该方法只适用于对称正定的线性方程组,对于一般的线性方程组并不适用。
共轭梯度法的收敛速度受到方程条件数的影响,对于病态问题,可能收敛速度较慢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用MATLAB 实现共轭梯度法求解实例康福 201103710031一.无约束优化方法1.1 无约束优化方法的必要性一般机械优化设计问题,都是在一定的限制条件下追求某一指标为最小,它们都属于约束优化问题。
但是为什么要研究无约束优化问题?(1)有些实际问题,其数学模型本身就是一个无约束优化问题。
(2)通过熟悉它的解法可以为研究约束优化问题打下良好的基础。
(3)约束优化问题的求解可以通过一系列无约束优化方法来达到。
所以无约束优化问题的解法是优化设计方法的基本组成部分,也是优化方法的基础。
(4)对于多维无约束问题来说,古典极值理论中令一阶导数为零,但要求二阶可微,且要判断海赛矩阵为正定才能求得极小点,这种方法有理论意义,但无实用价值。
和一维问题一样,若多元函数F(X)不可微,亦无法求解。
但古典极值理论是无约束优化方法发展的基础。
1.2共轭梯度法目前已研究出很多种无约束优化方法,它们的主要不同点在于构造搜索方向上的差别。
(1)间接法——要使用导数,如梯度法、(阻尼)牛顿法、变尺度法、共轭梯度法等。
(2)直接法——不使用导数信息,如坐标轮换法、鲍威尔法单纯形法等。
用直接法寻找极小点时,不必求函数的导数,只要计算目标函数值。
这类方法较适用于解决变量个数较少的(n ≤20)问题,一般情况下比间接法效率低。
间接法除要计算目标函数值外,还要计算目标函数的梯度,有的还要计算其海赛矩阵。
搜索方向的构成问题乃是无约束优化方法的关键。
共轭梯度法是沿着共轭方向进行搜索,属于共轭方向法中的一种,该方法中每一个共轭向量都是依赖于迭代点处的负梯度而构造出来。
共轭梯度法作为一种实用的迭代法,它主要有下面的优点:(1)算法中,系数矩阵A的作用仅仅是用来由已知向量P 产生向量W=AP ,这不仅可充分利用A的稀疏性,而且对某些提供矩阵A较为困难而由已知向量P 产生向量W=AP 又十分方便的应用问题是很有益的。
(2)不需要预先估计任何参数就可以计算,这一点不像SOR 等;(3)每次迭代所需的计算,主要是向量之间的运算,便于并行化。
共轭梯度法原理的知识较多,请详见《机械优化设计》第四章的第四、五节。
图1为共轭梯度法的程度框图 1(0,1,2,)k k k k s k α+=+=x x图1为共轭梯度法的程度框图二.设计题目及要求2.1设计题目用共轭梯度法求二次函数221212112(,)242f x x x x x x x =+--的极小点及极小值。
2.2设计要求(1)使用matlab 编写程序,熟练撑握matlab 编程方法。
(2)学习并撑握共轭梯度法的原理、方法及应用,并了解不同无约束优化方法的区别、优缺点及特殊要求。
(3)编写程序,计算出二次函数的极小点及极小值,并适当选取不同的初始点及迭代精度精度,分析比较结果。
三.计算步骤3.1计算求解解:已知初始点[1,1]T 迭代精度 0.001ε=1)第一次沿负梯度方向搜寻计算初始点处的梯度:为一维搜索最佳步长,应满足得:2)第二次迭代代入目标函数由 得从而有: 因收敛。
0120212244()422x x f x x ---⎡⎤⎡⎤∇==⎢⎥⎢⎥-⎣⎦⎣⎦x x 010000014141212αααα+⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦x x d 1002()min ()min(40203)f f ααααα=+=--x x d 00.25α=120.5⎡⎤=⎢⎥⎣⎦x 11()2f -⎡⎤∇=⎢⎥-⎣⎦x 21200()50.2520()f f β∇===∇x x 11002() 1.5f β⎡⎤=-∇+=⎢⎥⎣⎦d x d 21122220.5 1.50.5 1.5αααα+⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦x x d 22()(22)2(0.5 1.5)2(22)(0.5 1.5)4(22)()f x αααααφα=+++-++-+=()0φα'=1α=22240,()8,()20f f ⎡⎤⎡⎤==-∇=⎢⎥⎢⎥⎣⎦⎣⎦x x x 2()0f ε∇=<x3.2运行与程序运行:打开matlab,确定conjugate_grad_2d.m文件夹为当前目录。
在命令窗中输入:f=conjugate_grad_2d([1,1],0.001)选择不同的初始点坐标[0,0],[0,1],[1,0],和迭代精度0.01,0.0001,进行运行时,需要多次调用conjugate_grad_2d函数。
程序及说明:function f=conjugate_grad_2d(x0,t)%用共轭梯度法求已知函数f(x1,x2)=x1^2+2*x2^2-4*x1-2*x1*x2的极值点%已知初始点坐标:x0%已知收敛精度:t%求得已知函数的极值:fx=x0;syms xi yi a; %定义自变量,步长为符号变量f=xi^2+2*yi^2-4*xi-2*xi*yi; %创建符号表达式ffx=diff(f,xi); %求表达式f对xi的一阶求导fy=diff(f,yi); %求表达式f对yi的一阶求导fx=subs(fx,{xi,yi},x0); %代入初始点坐标计算对xi的一阶求导实值fy=subs(fy,{xi,yi},x0); %代入初始点坐标计算对yi的一阶求导实值fi=[fx,fy]; %初始点梯度向量count=0; %搜索次数初始为0while double(sqrt(fx^2+fy^2))>t %搜索精度不满足已知条件s=-fi; %第一次搜索的方向为负梯度方向if count<=0s=-fi;elses=s1;endx=x+a*s; %进行一次搜索后的点坐标f=subs(f,{xi,yi},x); %构造一元搜索的一元函数φ(a)f1=diff(f); %对函数φ(a)进行求导f1=solve(f1); %得到最佳步长aif f1~=0ai=double(f1); %强制转换数据类型为双精度数值elsebreak %若a=0,则直接跳出循环,此点即为极值点endx=subs(x,a,ai); %得到一次搜索后的点坐标值f=xi^2+2*yi^2-4*xi-2*xi*yi;fxi=diff(f,xi);fyi=diff(f,yi);fxi=subs(fxi,{xi,yi},x);fyi=subs(fyi,{xi,yi},x);fii=[fxi,fyi]; %下一点梯度向量d=(fxi^2+fyi^2)/(fx^2+fy^2);s1=-fii+d*s; %下一点搜索的方向向量count=count+1; %搜索次数加1fx=fxi;fy=fyi; %搜索后终点坐标变为下一次搜索的始点坐标endx,f=subs(f,{xi,yi},x),count %输出极值点,极小值以及搜索次数四.运行结果及分析此程序运行2秒后终止,结果如下:x = 4 2 极小点坐标f = -8 极小值数值count = 2 迭代次数ans = -8分析可得:(1)由结果看出,程序经过2次迭代,得到二次函数的极小值坐标[4,2],极小值-8;表明共轭梯度法收敛速度较快,计算量较小,稳定性高。
(2)选择不同的初始点坐标[0,0],[0,1],[1,0],[1,1],都是经过2次迭代得到一致的结果;表明共轭梯度法初始点的选择不影响收敛结果。
(3)选择迭代精度0.0001,程序将近运行15秒才结束;可知迭代精度越高时,程序运行的时候越长,所以在实际应用中选择适当的迭代精度,有利于提高计算的效率。
(4)从共轭梯度法的计算过程可以看出,第一个搜索方向取作负梯度方向,这就是最速下降法。
其余各步的搜索方向是将负梯度偏转一个角度,也就是对负梯度进行修正。
所以共轭梯度法实质上是对最速下降法进行的一种改进,故它又被称作旋转梯度法。
五.结束语优化设计是是机械行业发展起来的一门新学科,将最优化原理和计算机应用于设计领域,为工程设计提供一种重要的科学设计方法。
利用它,人们可以从众多的设计方案中寻找最佳设计方案,从而大大提高设计效率和质量,广泛应用于各个工业部门。
在自然科学和工程技术中很多问题的解决常常归结为约束优化或无约束优化的问题。
首先根据实际的机械问题建立相应的数学模型,即应用数学形式描述实际设计问题。
同时需要用专业的知识确定设计的限制条件和所追求的目标,确立各设计变量之间的相互关系等。
一旦建立数学模型,应用数学规划理论的方法,根据数学模型的特点可以选择适当的优化方法,进而可以选择适当的计算机程序,以计算作为工具求得最佳优化设计参数。
通过学习发现,共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
如何把实际的工程技术问题转化为理论的数学模型,进行分析运算求解,是检验我们是否学好这一课的关键。
这可以让我们在以后的研究生生涯中有更加透彻的理解能力,扎实地撑握机械知识,培养创造性思维,专业技能有新的提高。
通过这次作业的完成,越来越觉得数学方法在机械优化设计中的重要性。
无论是优化设计,CAD,CAE,其理论支撑都是来自高等数学、数值分析、矩阵分析这几门课程,这让我对原本枯燥无味的数学课程,又有了新的态度,新的激情。
认真学习好数学,理论联系实践,同时借助于强大的计算机工具,解决实际问题。
Matlab是一种强大的科学计算工具,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种有力的工具。
在使用Matlab编写程序时,对于编程的基本规则及函数的调用缺乏清晰的认识,程序运行中经常出现错误,一点一滴地调试再纠正。
比如:程序运行过程中经常出现错误:Error using ==>Too many input arguments。
查阅了些书籍,上网求助,最后查明原因是自定义的M 文件名称与Matlab内部函数名相似,导致无法运行。
浪费了大量的时间与精力,庆幸的是,经过自己的努力,纠正错误,按时完成了作业。
研究生培养过程中,必须系统地学习编程软件,达到精通熟练的程度,并能够自主开发一些小程序,我相信在以后学习工作中它会提供更大的帮助。
参考文献:[1] 孙靖民,哈尔滨工业大学.机械优化设计.北京:机械工业出版社,2006.。
