离散数学尹宝林版第6章作业答案

合集下载

离散数学习题答案.docx

精品文档离散数学习题答案习题一及答案：（ P14-15 ）14、将下列命题符号化：（ 5）李辛与李末是兄弟解：设 p：李辛与李末是兄弟，则命题符号化的结果是p（ 6）王强与刘威都学过法语解：设 p：王强学过法语； q：刘威学过法语；则命题符号化的结果是p q （ 9）只有天下大雨，他才乘班车上班解：设 p：天下大雨； q：他乘班车上班；则命题符号化的结果是q p（ 11）下雪路滑，他迟到了解：设 p：下雪； q：路滑； r ：他迟到了；则命题符号化的结果是( p q)r15、设 p： 2+3=5.q：大熊猫产在中国 .r：太阳从西方升起 .求下列复合命题的真值：（ 4）(p q r )(( p q)r )解： p=1， q=1，r=0 ，(p q r )(110)1，((p q)r )((11)0)(00)1(p q r )(( p q)r ) 1 1119、用真值表判断下列公式的类型：（ 2）( p p)q解：列出公式的真值表，如下所示：p q p qp) ( p p)q( p001111011010100101110001由真值表可以看出公式有 3 个成真赋值，故公式是非重言式的可满足式。

20、求下列公式的成真赋值：精品文档（ 4）( p q)q解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：( p q)1p0q0q0所以公式的成真赋值有： 01，10， 11。

习题二及答案：（ P38）5、求下列公式的主析取范式，并求成真赋值：（ 2）(p q) (q r )解：原式( p q) q r q r( p p) q r( p q r ) ( p q r )m3m7，此即公式的主析取范式，所以成真赋值为011， 111。

6、求下列公式的主合取范式，并求成假赋值：（ 2）( p q) ( p r )解：原式( pp r ) ( p q r )( p q r )M 4，此即公式的主合取范式，所以成假赋值为 100。

国防科大版离散数学习题答案

第一章集合习题1.11.a){0, 1, 2, 3, 4}b){11, 13, 17, 19}c){12, 24, 36, 48, 64}2.a){x | x ∈ N 且x ≤ 100}b)E v = {x | x ∈ N 且2整除x }O d = {x | x ∈ N 且2不能整除x }c){y | 存在x ∈ I 使得y = 10 • x } 或{x | x/10 ∈ I }3. 极小化步骤省略a)①{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ⊆ A ；②若α, β∈ A，则α•β∈ A 。

或①{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ⊆ A ；②若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则a•α∈ A 。

或①{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ⊆ A ；②若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则α•a ∈ A 。

b)①{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ⊆ A ；②若α, β∈ A 且α≠ 0，则α•β∈ A 。

c)①若a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则a. ∈ A ；②若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则α•a ∈ A ；若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则a•α∈ A 。

或①{0., 1., 2., 3., 4., 5., 6., 7., 8., 9.} ⊆ A ；②若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则α•a ∈ A ；若α∈ A 且a ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，则a•α∈ A 。

d)①{0, 10} ⊆ A ；②若α∈ A，则1•α∈ A ；若α, β∈ A 且α≠ 0，则α•β∈ A 。

离散数学习题答案解析

离散数学习题答案解析(总16页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案：（P14-15）14、将下列命题符号化：（5）李辛与李末是兄弟解：设p：李辛与李末是兄弟，则命题符号化的结果是p（6）王强与刘威都学过法语∧解：设p：王强学过法语；q：刘威学过法语；则命题符号化的结果是p q（9）只有天下大雨，他才乘班车上班→解：设p：天下大雨；q：他乘班车上班；则命题符号化的结果是q p （11）下雪路滑，他迟到了解：设p：下雪；q：路滑；r：他迟到了；则命题符号化的结果是()∧→p q r 15、设p：2+3=5.q：大熊猫产在中国.r：太阳从西方升起.求下列复合命题的真值：（4）()(())∧∧⌝↔⌝∨⌝→p q r p q r解：p=1，q=1，r=0，∧∧⌝⇔∧∧⌝⇔，p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型：（2）()→⌝→⌝p p q解：列出公式的真值表，如下所示：由真值表可以看出公式有3个成真赋值，故公式是非重言式的可满足式。

20、求下列公式的成真赋值：（4）()p q q ⌝∨→解：因为该公式是一个蕴含式，所以首先分析它的成假赋值，成假赋值的条件是：()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有：01，10，11。

习题二及答案：（P38）5、求下列公式的主析取范式，并求成真赋值：（2）()()p q q r ⌝→∧∧解：原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨，此即公式的主析取范式，所以成真赋值为011，111。

*6、求下列公式的主合取范式，并求成假赋值：（2）()()p q p r ∧∨⌝∨解：原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔，此即公式的主合取范式，所以成假赋值为100。

离散部分作业答案

P125 21.a)N={1,3} Φ(4)=2b)N={1,3,7,9}Φ(10)=4c)N={1,2,3,…,12}Φ(13)=12P149 25b) 5^2003 mod 1001=983P183 4“the sailing race will be held and the lifesaving demonstration will go on”: this sentence should be split into two propositions ,one is the “sailing race will be held “, the other is “the lifesaving demonstration will go on.”P202 64N is odd and not divisible by 3 , so we can express n=6k+1 or 6k+5(k>=1) Basis step: It is easy to prove the correction of the proposition when n=7 and n=11.Inductive step: assume that if n=6k+1, the proposition is true,and if n=6(k+1)+1=(6k+1)+6, as shown in the figure below :the square is split into 4 parts asa)(6k+1)*(6k+1), b) 7*7-1 ( pleaseallow me to write this way), c)6k*6 andd)6*6k . it is clear that a) is fit to theproposition , b) can be filled withL-shaped pieces and c),d) can be filled with a rectangle consist of 2 L-shaped pieces.If n=6(k+1)+5 , the proposition can be also proved as above.So , we can believe that the proposition is true.P259 49a)We need to find something to count so that the left-hand side of theequation counts it in one way and the right-hand side counts it in different way. After much thought , we might try the following. We will count the number of bit strings of length n+r+1containing exactly r 0’s and n+1 1’s . There are C(n+r+1,r) such strings , sincea string is completely specified by deciding which r of the bits areto be the 0’s . To see that the left-hand side of the identity counts the same thing,let l+1 be the position of the last 1 in the string . Since there are n+1 1’s , we know that l cannot be less than n . thus there are disjoint cases for each l from n to n+r . For each such l, we completely determine the string by deciding which of the l positionsI the string before the last 1 are to be 0’s . Since there are n 1’s inthis range, there are l-n 0’s. Thus there are C(l,l-n) .ways to choose the positions of the 0’s . Now by the sum rule , the total number of bit strings will be ∑(l=n to n+r)C(l,l-n) . By making the change of variable k=l-n,this transforms into the left-hand side, and we arefinished.P243 33a)there can clearly be no one-to-one function from {1,2,…n} to {0,1}if n>2. if n=1 ,then there are 2 such functions , the one that sends 1 to 0, and the one that sends 1 to 1. if n=2 , then there are again 2 such functions since once it is determined where 1 is sent , the function must send 2 to the other value in the codomain.b)If the function assigns 0 to both 1 and n , then there are n-2 functionvalues free to be chosen. Each can be chosen in 2 ways. Therefore by product rule, there are 2^n-2 such functions ,as long as n>1. if n=1 ,then clearly there is just one such function.c)If n=1, then there are no such functions.If n>1, we will decide which of the numbers from 1 to n-1 , inclusive,will get sent to 1. there are n-1 ways to make this choice.finally , we are free to specify the value if the function at n,and this may be done in 2ways ,hence by the product rule ,the answer is 2(n-1).P383 25b)for each unordered pair {a.b} of distinct elements of A, we have a3-way choice----either include (a,b) only, include (b,a) only , orinclude neither .For each element of A we have a 2-way choice .Therefore the answer is (3^C(n,2))*(2^n) .c)as in part (b) we have a 3-way choice for a!=b . there is no choiceabout including (a,a) in the relation——the definition prohibits it.Therefore the answer is 3^C(n,2)。

《离散数学》题库及答案解析

《离散数学》题库与答案一、选择或填空（数理逻辑部分）1、下列哪些公式为永真蕴含式？( A )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答：在第三章里面有公式（1）是附加律，（4）可以由第二章的蕴含等值式求出（注意与吸收律区别）2、下列公式中哪些是永真式？( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答：（2），（3），（4）可用蕴含等值式证明3、设有下列公式，请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答：（2）是第三章的化简律，（3）类似附加律，（4）是假言推理，（3），（5），（6）都可以用蕴含等值式来证明出是永真蕴含式4、公式∀x((A(x)→B(y，x))∧∃z C(y，z))→D(x)中，自由变元是( )，约束变元是( )。

答：x,y, x,z（考察定义在公式∀x A和∃x A中，称x为指导变元，A为量词的辖域。

在∀x A和∃x A的辖域中，x的所有出现都称为约束出现，即称x为约束变元，A中不是约束出现的其他变项则称为自由变元。

于是A(x)、B(y，x)和∃z C(y，z)中y为自由变元，x和z为约束变元，在D(x)中x为自由变元）5、判断下列语句是不是命题。

若是，给出命题的真值。

( )(1)北京是中华人民共和国的首都。

(2) 陕西师大是一座工厂。

(3) 你喜欢唱歌吗？ (4) 若7+8＞18，则三角形有4条边。

(5) 前进！ (6) 给我一杯水吧！答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是（命题必须满足是陈述句，不能是疑问句或者祈使句。

）6、命题“存在一些人是大学生”的否定是( )，而命题“所有的人都是要死的”的否定是( )。

习题参考解答

离散数学部分课后习题答案习题1.11、（3）P ：银行利率降低Q ：股价没有上升P ∧Q（5） P ：他今天乘火车去了北京Q ：他随旅行团去了九寨沟Q P ∇（7） P ：不识庐山真面目Q ：身在此山中Q →P ，或～P →～Q（9） P ：一个整数能被6整除Q ：一个整数能被3整除R ：一个整数能被2整除T ：一个整数的各位数字之和能被3整除P →Q ∧R ，Q →T2、（1）T （2）F （3）F （4）T （5）F（6）T （7）T （F ）（8）悖论习题 1.31、（3）)()()()()()(R P Q P R P Q P R Q P R Q P →∨→⇔∨⌝∨∨⌝⇔∨∨⌝⇔∨→（4） ()()()(())()(()())(())()()()()P Q Q R R P P R Q R P P R R P Q R P P R P R Q R Q P ∧∨∧∨∧=∨∧∨∧=∨∨∧∧∨∧=∨∧∨∧∨∧∨=右2、不，不，能习题 1.42、①③3、，4、习题 1.51(3) (())~((~))(~)()~(~(~))(~~)(~)P R Q P P R Q P P R T P R P R Q Q P R Q P R Q →∧→=∨∧∨=∨∧=∨=∨∨∧=∨∨∧∨∨、主合取范式)()()()()()()()()()()()()()())(())(()()(())()())(()((Q P R P Q R P Q R R Q P R Q P R Q P Q P R Q P R P Q R P Q R R Q P R Q P R Q P R Q P Q Q P R P P Q R R R Q Q P P R Q R P P Q R P P Q R P ∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∧∧∨⌝∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∨⌝∧∧∨∨⌝∧⌝∧∨∨⌝∧∨⌝∧⌝=∧∨⌝∧∨⌝=∨⌝∧∨⌝=→∧→ ————主析取范式(2) ()()(~)(~)(~(~))(~(~))(~~)(~)(~~)P Q P R P Q P R P Q R R P R Q Q P Q R P Q R P R Q →∧→=∨∧∨=∨∨∧∧∨∨∧=∨∨∧∨∨∧∨∨ 2、()~()(~)(~)(~~)(~)(~~)P Q R P Q R P Q P R P Q R P Q R P R Q →∧=∨∧=∨∧∧=∨∨∧∨∨∧∨∨∴等价3、解：根据给定的条件有下述命题公式：（A →（C ∇D ））∧～（B ∧C ）∧～（C ∧D ）⇔（～A ∨（C ∧～D ）∨（～C ∧D ））∧（～B ∨～C ）∧（～C ∨～D ） ⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（C ∧～D ∧～C ）∨（～C ∧D ∧～C ））∧（～C ∨～D ） ⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ∧～C ）） ∧（～C ∨～D ）⇔（～A ∧～B ∧～C ）∨（C ∧～D ∧～B ∧～C ）∨（～C ∧D ∧～B ∧～C ）∨ （～A ∧～C ∧～C ）∨（～C ∧D ∧～C ∧～C ）∨（～A ∧～B ∧～D ）∨ （C ∧～D ∧～B ∧～D ）∨（～C ∧D ∧～B ∧～D ）∨（～A ∧～C ∧～D ）∨ （～C ∧D ∧～C ∧～D ）（由题意和矛盾律可得下式）（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ）∨（C ∧～D ∧～B ） ⇔（～C ∧D ∧～B ∧A ）∨ （～C ∧D ∧～B ∧～A ）∨ （～A ∧～C ∧B ）∨ （～A ∧～C ∧～B ）∨ （～C ∧D ∧A ）∨ （～C ∧D ∧～A ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～A ∧～C ∧B ∧～D ）∨ （～A ∧～C ∧～B ∧D ）∨ （～A ∧～C ∧～B ∧～D ）∨（～C ∧D ∧A ∧B ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ）∨ （～C ∧D ∧～A ∧～B ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ）（由题意可得下式）（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ） ∨（C ∧～D ∧～B ∧A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨（C ∧～D ∧～B ∧A ）三种方案：A 和D 、 B 和D 、 A 和C习题 1.61、（1）需证()(())P Q P P Q →→→∧为永真式()(())~(~)(~())~~(~)(()(~))~(~)(~)()P Q P P Q P Q P P Q P P P Q P Q TP Q P Q T P Q P P Q →→→∧=∨∨∨∧∨=∨∨∧∨=∨∨∨=∴→⇒→∧ （3）需证S R P P →∧⌝∧为永真式SR P P T S F S R F S R P P ⇒∧⌝∧∴⇔→⇔→∧⇔→∧⌝∧3A B A B ⇒∴→ 、为永真式。

离散数学答案版(全)

1.2.4
0 0 1 11
Q
0 1 1 1
P Q
0 0 1 1 1.2.5 双条件联结词
P
0 1 0 1
Q
1 1 0 1
P Q
1.2.6
0 0 1 1 与非联结词↑
P
0 1 0 1
Q
1 0 0 1
PQ
1 1 1 0
0 0 1 1
0 1 0 1
性质：（1） P↑P ﹁（P∧P）﹁P；（2）（P↑Q）↑（P↑Q）﹁（P↑Q） P∧Q；（3）（P↑P）↑（Q↑Q）﹁P↑﹁Q P∨Q。 1.2.7 或非联结词↓
定义设pq是两个命题公式复合命题pq称为命题pq的条件否定当且仅当p的真值为1q的真值为0时pq的真值为1否则pq的真值为0172最小联结词组定义设s是一些联结词组成的非空集合如果任何的命题公式都可以用仅包含s中的联结词的公式表示则称s是联结词的全功能集
第一章
命题逻辑
内容：命题及命题联结词、命题公式的基本概念，真值表、基本等价式及永真蕴涵式，命题演算的推理理论中常用的直接证明、条件证明、反证法等证明方法。教学目的： 1．熟练掌握命题、联结词、复合命题、命题公式及其解释的概念。 2．熟练掌握常用的基本等价式及其应用。 3．熟练掌握（主）析/合取范式的求法及其应用。 4．熟练掌握常用的永真蕴涵式及其在逻辑推理中的应用。 5．熟练掌握形式演绎的方法。
式中每一个析取项都是 P1，P2，…，Pn 的一个极大项，则称该合取范式为 G 的主合取范式。通常，主合取范式用↕表示。重言式的主合取范式中不含任何极大项，用 1 表示。定理任意的命题公式都存在一个唯一的与之等价的主合取范式。
1.6
公式的蕴涵

离散数学习题解答第6部分(图论)

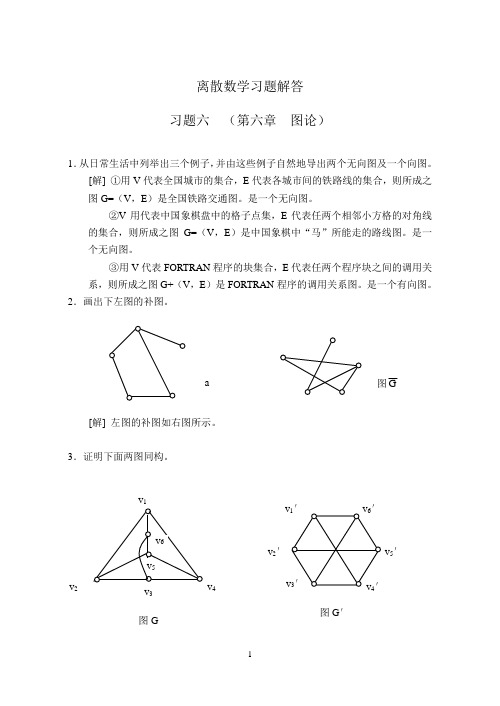
离散数学习题解答习题六（第六章图论）1．从日常生活中列举出三个例子，并由这些例子自然地导出两个无向图及一个向图。

[解] ①用V 代表全国城市的集合，E 代表各城市间的铁路线的集合，则所成之图G=（V ，E ）是全国铁路交通图。

是一个无向图。

②V 用代表中国象棋盘中的格子点集，E 代表任两个相邻小方格的对角线的集合，则所成之图G=（V ，E ）是中国象棋中“马”所能走的路线图。

是一个无向图。

③用V 代表FORTRAN 程序的块集合，E 代表任两个程序块之间的调用关系，则所成之图G+（V ，E ）是FORTRAN 程序的调用关系图。

是一个有向图。

2．画出下左图的补图。

[解] 左图的补图如右图所示。

3．证明下面两图同构。

a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1，v 2)=(v 1′，v 2′) ϕ (v 2)=v 2′ ϕ (v 2，v 3)=(v 2′，v 3′) ϕ (v 3)=v 3′ ϕ (v 3，v 4)=(v 3′，v 4′) ϕ (v 4)=v 4′ ϕ (v 4，v 5)=(v 4′，v 5) ϕ (v 5)=v 5′ ϕ (v 5，v 6)=(v 5′，v 6′) ϕ (v 6)=v 6′ϕ (v 6，v 1)=(v 6′，v 1′) ϕ (v 1，v 4)=(v 1′，v 4′) ϕ (v 2，v 5)=(v 2′，v 5′) ϕ (v 3，v 6)=(v 3′，v 6′)显然使下式成立：ψ (v i ，v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。

4．证明（a ），（b ）中的两个图都是不同构的。

图G 中有一个长度为4的圈v 1v 2v 6v 5v 1，其各顶点的度均为3点，而在图G ′中却没有这样的圈，因为它中的四个度为3的顶点v 1'，v 5'，v 7'，v 3'不成长度的4的圈。

离散数学(第五版)清华大学出版社第6章习题解答

离散数学（第五版）清华大学出版社第6章习题解答6.1 A:⑨; B:⑨; C:④; D:⑥; E:③分析对于给定的集合和运算判别它们是否构成代数系统的关键是检查集合对给定运算的封闭性,具体方法已在5.3节做过说明. 下面分别讨论对各种不同代数系纺的判别方法.1°给定集合S和二元运算°,判定<S, °>是否构成关群、独导点和群.根据定义，判别时要涉及到以下条件的验证：条件1 S关于°运算封闭：条件2 °运算满足结合集条件3 °运算有幺元，条件4 °∀x∈S,x−1∈S.其中关群判定只涉及条件1和2；独导点判定涉及条件1、2、和3；而群的判定则涉及到所有的四个条件。

2 ° 给定集合S和二元运算°和*，判定<S, °, *>是否构成环,交换环,含幺环,整环,域.根据有关定义需要检验的条件有:条件1 <S, °>S构成交换群,条件2 <S, *> 构成关群,条件3 * 对°运算的分配律,条件4 * 对运算满足交换律,条件5 * 运算有幺元,条件6 * 运算不含零因子——消去律，条件7 |S|≥2,∀x∈S,x≠0,有x−1∈S（对*运算）.其中环的判定涉及条件1,2和3;交换环的判定涉及条件1,2,3和4;含幺环的判定涉及条件1,2,3和5;整环的判定涉及条件1-6;而域的判定则涉及全部7个条件. 3° 判定偏序集<S,≤>或代数系统<S,o,*>是否构成格、分本配格、有补格和布尔格. 73若<S,≤>为偏序集,首先验证∀x,y∧y和x∨y是否属于S.若满足条件则S为格,且<S,∨,∧>构成代数系统.若<S,o,*>是代数系统且°和*运算满足交换律、结合律和吸收律，则<S,o,*>构成格。

离散数学习题及解答

离散数学习题及解答作业题与解答第⼀章19 (2)、(4) 、(6)21 (1)、(2) 、(3)19、(2)解答: (p→┐p)→┐q 真值表如下:所以公式(p→┐q)→┐q 为可满⾜式19、(4)解答: (p→q)→(┐q→┐p) 真值表如下:所以公式(p→q)→(┐q→┐p)为永真式19、(6)解答: ((p→q)∧(q→r))→(p→r) 真值表如下:所以公式((p→q)∧(q→r))→(p→r)为永真式21、(1)解答: ┐(┐p∧q)∨┐r 真值表如下:所以成假赋值为:01121、(2)解答: (┐q∨r)∧(p→q)真值表如下:所以成假赋值为:010,100,101,11021、(3)解答: (p→q)∧(┐(p∧r)∨p)真值表如下:所以成假赋值为:100,101第⼆章5、(1) (2) (3) 6、(1) (2) (3) 7、(1) (2) 8、(1) (2) (3) 5、求下列公式的主析取范式,并求成真赋值(1) (┐p→q)→(┐q∨p)┐(┐p→q) ∨(┐q∨p)┐(┐(┐p) ∨q) ∨(┐q∨p)(┐p ∧┐q) ∨(┐q∨p)(┐p ∧┐q) ∨(p ∧┐q)∨(p ∧q)所以00，10，11 为成真赋值。

(2) (┐p→q)∧(q∧r)(┐┐p∨q)∧(q∧r)(p∨q)∧(q∧r)(p∧q∧r)∨(q∧r)(p∧q∧r)∨(p∧q∧r)∨(┐p∧q∧r)(p∧q∧r)∨(┐p∧q∧r)m3∨m 7，所以011，111 为成真赋值。

(3) (p∨(q∧r))→(p∨q∨r)┐(p∨(q∧r))∨(p∨q∨r)(┐p∧(┐q∨┐r))∨(p∨q∨r)(┐p∧┐q)∨(┐p∧┐r)∨(p∨q∨r)(┐p∧┐q)∨((┐p∧┐r)∨(p∨q∨r))(┐p∧┐q)∨((┐p∨p∨q∨r)∧(┐r∨p∨q∨r) )(┐p∧┐q)∨(1∧1)(┐p∧┐q)∨11m0∨m1∨m 2∨m3∨m4∨m5∨m 6 ∨m 7，所以000, 001, 010, 011, 100, 101, 110, 111 为成真赋值。

离散数学第6章习题解答

第6章习题解答6.1 A: ⑨；B:⑨;C:④；D:⑥;E:③分析对于给定的集合和运算判别它们是否构成代数系统的关键是检查集合对给定运算的封闭性，具体方法已在5.3节做过说明.下面分别讨论对各种不同代数系纺的判别方法.1 °给定集合S和二元运算°,判定<S, ° >是否构成关群、独导点和群.根据定义，判别时要涉及到以下条件的验证：条件1 S关于。

运算封闭：条件2。

运算满足结合集条件3 °运算有幺元，条件 4 ° - x S, x J S.其中关群判定只涉及条件1和2;独导点判定涉及条件1、2、和3;而群的判定则涉及到所有的四个条件。

2 °给定集合S和二元运算°和*，判定<S, ° , *>是否构成环，交换环，含幺环,整环,域.根据有关定义需要检验的条件有：条件1 <S, ° >S构成交换群,条件2 <S, *> 构成关群,条件3 * 对°运算的分配律，条件4 *对运算满足交换律，条件5 *运算有幺元，条件6 *运算不含零因子一一消去律，条件7 |S|_2,-x・ S,x = O,有x J S （对* 运算）.其中环的判定涉及条件1,2和3;交换环的判定涉及条件1,2,3和4;含幺环的判定涉及条件1,2,3和5;整环的判定涉及条件1-6;而域的判定则涉及全部7 个条件.3°判定偏序集：::S,「或代数系统：::S, ,* •是否构成格、分本配格、有补格和布尔格.若:::S, 一为偏序集,首先验证-x, y y和x y是否属于S.若满足条件则S为格,且:::S,,.构成代数系统•若:::S, ,*是代数系统且。

和*运算满足交换律、结合律和吸收律，则:::S, ,* •构成格。

在此基础上作为分配格的充分必要条件是不含有与图格。

而有补格和布尔格的判定只要根据定义进行即可。

离散数学第二版答案(6-7章)

离散数学第二版答案(6-7章)第六章代数系统6.1第129页1．证明：任取,x y I ∈，(,)*(,)g y x y x y x yx x y xy g x y ==+-=+-=，因此，二元运算*是可交换的；任取,,x y z I ∈，(,(,))*(*)*()()g x g y z x y z x y z yz x y z yz x y z yz x y z xy xz yz xyz==+-=++--+-=++---+((,),)(*)*()*()(,(,))g g x y z x y z x y xy zx y xy z x y xy z x y z xy xz yz xyz g x g y z ==+-=+-+-+-=++---+=因此，运算*是可结合的。

该运算的么元是0，0的逆元是0，2的逆元是2，其余元素没有逆元。

2．(*,x,)*的最小公倍数=*=y)y（zz的最小公倍数x和yxz因此对于任意的z，x，都有)*，yzy）（=，即二x（x*y**z元运算*是可结合的。

③设幺元为e==的最小公倍数和**，则1=e，即幺元为1.x=exxxee④对于所有的元素I*，所以所有元x∈，都有xx=x素都是等幂的。

4．解：设nX=①设f是X上的二元运算，则f是一个从X2的X→映射。

求X上有多少个二元运算即相当于求这样的映射的个数。

由于22nX=，映射f的个数为2n n，即X上有2n n个二元运算。

②可交换即>yxff,,<>=y<x设集合}4,3,2,1{=X，要求X上可交换的二元运算的个数，即相当于求映射f的个数，X:，其中：f→A><><>><><><<=A><<><><4,41,1,2,23,3}4,34,2,2,1{>3,14,13,2具体如下图所示：A><><><><><><><><><><><><><><><><4,43,32,21,13,4,4,32,4,4,22,3,3,21,4,4,12,3,3,11,2,2,1 X4321此时映射f 的个数44642444++==C N推广到X 有n 个元素时，映射f 的个数nC n n n N +=2③ 单位元素即幺元，若存在必唯一。

离散数学习题解答

第1章习题解答1．1 除（3），（4），（5），（11）外全是命题，其中，（1），（2），（8），（9），（10），（14），（15）是简单命题，（6），（7），（12），（13）是复合命题。

分析首先应注意到，命题是陈述句，因而不是陈述句的句子都不是命题。

本题中，（3）为疑问句，（5）为感叹句，（11）为祈使句，它们都不是陈述句，所以它们都不是命题。

其次，（4）这个句子是陈述句，但它表示的判断结果是不确定。

又因为（1），（2），（8），（9），（10），（14），（15）都是简单的陈述句，因而作为命题，它们都是简单命题。

（6）和（7）各为由联结词“当且仅当”联结起来的复合命题，（12）是由联结词“或”联结的复合命题，而（13）是由联结词“且”联结起来的复合命题。

这里的“且”为“合取”联结词。

在日常生活中，合取联结词有许多表述法，例如，“虽然……，但是……”、“不仅……，而且……”、“一面……，一面……”、“……和……”、“……与……”等。

但要注意，有时“和”或“与”联结的是主语，构成简单命题。

例如，（14）、（15）中的“与”与“和”是联结的主语，这两个命题均为简单命题，而不是复合命题，希望读者在遇到“和”或“与”出现的命题时，要根据命题所陈述的含义加以区分。

:p是无理数，p为真命题。

1．2 （1）2（2）5:p能被2整除，p为假命题。

（6）qp→。

其中，2:p是素数，q：三角形有三条边。

由于p与q都是真命题，因而qp→为假命题。

p→，其中，p：雪是黑色的，q：太阳从东方升起。

由于p为假命（7）qp→为假命题。

题，q为真命题，因而q（8）2000:p年10月1日天气晴好，今日（1999年2月 13日）我们还不知道p的真假，但p的真值是确定的（客观存在的），只是现在不知道而已。

（9）p：太阳系外的星球上的生物。

它的真值情况而定，是确定的。

（10）p ：小李在宿舍里. p 的真值则具体情况而定，是确定的。

(完整版)《离散数学》试题及答案解析,推荐文档

则在解释 I 下取真值为 1 的公式是( ).
(A)xyP(x,y) (B)xyP(x,y) (C)xP(x,x) (D)xyP(x,y). 6. 若供选择答案中的数值表示一个简单图中各个顶点的度，能画出图的是( ).
(A)(1,2,2,3,4,5) (B)(1,2,3,4,5,5) (C)(1,1,1,2,3) (D)(2,3,3,4,5,6). 7. 设 G、H 是一阶逻辑公式，P 是一个谓词，G＝xP(x), H＝xP(x),则一阶逻辑公式
(A)下界 (B)上界 (C)最小上界
(D)以上答案都不对
6
4 下列语句中，( )是命题。
5
(A)请把门关上 (B)地球外的星球上也有人 (C)x + 5 > 6 (D)下午有会吗？
3
4
2
5 设 I 是如下一个解释：D＝{a,b}, P(a, a) P(a, b) P(b, a) P(b, b)
1
1010
AB＝_________________________;A－B＝ _____________________ . 7. 设 R 是集合 A 上的等价关系，则 R 所具有的关系的三个特性是______________________,
________________________, _______________________________. 8. 设命题公式 G＝(P(QR))，则使公式 G 为真的解释有
(1)
1
4
2
3
1 0 0 0
(2)
MR
1 1
1 1
0 1
0 0
1 1 1 1
3. (1)•＝((x))＝(x)+3＝2x+3＝2x+3.

离散数学答案(尹宝林版)第四章习题解答

q p →q p ∨⌝⇔，r p →r p ∨⌝⇔，)(r q p ∧→⌝)())((r q p r q p ⌝∨⌝∧⇔∧∨⌝⌝⇔给出子句集},,,{r q p r p q p ⌝∨⌝∨⌝∨⌝的反驳如下。

① q p ∨⌝ ② r p ∨⌝ ③ p④ r q ⌝∨⌝ ⑤ q 由①和③ ⑥ r 由②和③ ⑦ r ⌝ 由④和⑤⑧ □由⑥和⑦因此，q p →,r p →=|r q p ∧→(2) 将p → r ，q → r ，⌝( p ∨ q → r ) 化为合取范式。

p → r ⇔ ⌝p ∨ r ，q → r ⇔ ⌝q ∨ r ，⌝( p ∨ q → r ) ⇔ ( p ∨ q ) ∧ ⌝r给出子句集 { ⌝p ∨ r , ⌝q ∨ r , p ∨ q , ⌝r } 的反驳如下： ① ⌝p ∨ r ② ⌝q ∨ r ③ p ∨ q ④ ⌝r ⑤ q ∨ r 由①和③ ⑥ r 由②和⑤ ⑦ □ 由④和⑥ 因此，p → r ，q → r |= p ∨ q → r 。

(3) 首先将r q p ∨→,))()((r p q p →∨→⌝化为合取范式。

r q p ∨→r q p ∨∨⌝⇔，))()((r p q p →∨→⌝r q p r p q p ⌝∧⌝∧⇔∨⌝∨∨⌝⌝⇔))()((给出子句集{r q p ∨∨⌝,p , q ⌝,r ⌝}的反驳如下。

① r q p ∨∨⌝ ② p③ q ⌝④ r ⌝⑤ r q ∨由①和② ⑥ r 由③和⑤⑦□由④和⑥因此，r q p ∨→=|)()(r p q p →∨→(4) 首先将r q p →∧,))()((r q r p →∨→⌝化为合取范式。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章习题答案2. 设P = {< 1, 2 >, < 2, 4 >, < 3, 3 >}，Q = {< 1, 3 >, < 2, 4 >, < 4, 2 >}找出P⋃Q, P⋂Q, dom(P), dom(Q), ran(P)及ran(Q)，并证明：dom(P ⋃ Q) = dom(P) ⋃ dom(Q)ran(P⋂ Q) ⊆ ran(P) ⋂ ran(Q)解P ⋃ Q ={< 1, 2 >, < 2, 4 >, < 3, 3 >, < 1, 3 >, < 4, 2 >}，P ⋂ Q ={< 2, 4 >}dom(P)={1, 2, 3}，dom(Q)= {1, 2, 4}，ran(P) = {2, 3, 4}，ran(Q) = {2, 3, 4}。

x∈ dom(P⋃Q)⇔∃y (< x, y > ∈ P ⋃ Q)⇔∃y (< x, y > ∈ P∨ < x, y > ∈ Q)⇔∃y (< x, y > ∈ P) ∨∃y (< x, y > ∈ Q)⇔ x∈ dom(P) ∨ x∈ dom(Q)⇔ x∈ dom(P) ⋃ dom(Q)y∈ ran(P⋂ Q)⇔∃x (< x, y > ∈ P⋂Q)⇔∃x (< x, y > ∈ P ∧ < x, y > ∈ Q)⇒∃x (< x, y > ∈ P) ∧∃x (< x, y > ∈ Q)⇔y∈ ran(P) ∧ y∈ ran(Q)⇔y∈ ran(P) ⋂ ran(Q)如上例，ran(P⋂ Q) = {4}⊂ {2, 3, 4} = ran(P) ⋂ ran(Q)3. 若关系R和S自反的，对称的和传递的，证明：R⋂S也是自反的，对称的和传递的。

证明设R和S是集合A上的关系。

因为R和S是自反的，所以，对于A中的任意元素x，有< x, x >∈R和< x, x >∈S。

因此< x, x >∈R⋂S，即R⋂S是自反的。

因为R和S是对称的，所以对于任意< x, y >，< x, y >∈R⋂S⇔ < x, y >∈R∧ < x, y >∈S⇔ < y, x >∈R∧ < y, x >∈S⇔ < y, x >∈R⋂S因此，R⋂S是对称的。

因为R和S是传递的，所以对于任意< x, y >和< y, z >，< x, y >∈R⋂S∧ < y, z >∈R⋂S⇔ < x, y >∈R∧ < x, y >∈S∧ < y, z >∈R∧ < y, z >∈S⇔ (< x, y >∈R∧ < y, z >∈R)∧ ( < x, y >∈S∧< y, z >∈S)⇒ < x, z >∈R∧ < x, z >∈S⇔ < x, z >∈R⋂S因此，R⋂S是传递的。

5．设A = {1, 2, 3}，A上的关系R1, R2, R3, R4, R5分别由图6.17给出，试问：R1, R2, R3, R4, R5各有哪些性质？解R 1：自反、对称、反对称、传递。

R 2：对称。

R 3：反自反、反对称。

R 4：反自反、对称、反对称、传递。

R 5：自反、传递。

8. 设R 1和R 2是集合X = {0, 1, 2, 3}上的关系，而R 1 = {< i , j > | j = i + 1或j = i /2}，R 2 = {< i , j > | i = j + 2}求复合关系：(1) R 1 ︒ R 2(2) R 2 ︒ R 1(3) R 1 ︒ R 2 ︒ R 1(4)21R并给出各复合关系的关系矩阵。

解 R 1 = {< 0, 1>, < 1, 2 >, < 2, 3 >, < 0, 0 >, < 2, 1 >} R 2 = { < 2, 0 >, < 3, 1 >} R 1 ︒ R 2 = {< 1, 0 >, < 2, 1 >} R 2 ︒ R 1 = {< 2, 0 >, < 2, 1 >, < 3, 2 >} R 1 ︒ R 2 ︒ R 1 ={< 1, 1 >, < 1, 0 >, < 2, 2 >}21R ={ < 1, 1 >, < 0, 0 >, < 0, 2 >, < 2, 2 >, < 0, 1 >, < 1, 3 >}⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=0010000100000000000010100100001121R R M M⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=010000110000000000000010000100001221R R R R M M⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000010010100111000001000011000021121R R R R M M 13. 求R 2的自反、对称、传递闭包的关系图。

R 2及其自反、对称、传递闭包的关系图从左至右排列如下。

14. 令R1, R2是集合A上的二元关系，并设R1 ⊆ R2，试证明下列关系式。

(3) t (R1) ⊆ t (R2)证明R1⊆R2⊆t (R2)，t(R2)是包含R1的传递关系，由传递闭包定义知道，t(R1)是包含R1的最小传递关系，所以，t(R1)⊆ t(R2)。

15. 设R1, R2是A上的二元关系，试证明(3) t (R1 ⋃ R2) ⊇t (R1) ⋃t (R2)并用反例说明t (R1⋃R2) = t (R1) ⋃t (R2)不一定成立。

证明因为R1⊆ R1 ⋃R2，所以t(R1)⊆ t(R1⋃R2)。

因为R2⊆ R1⋃R2，所以t(R2)⊆ t(R1⋃R2)。

因此，t (R1) ⋃t (R2) ⊆ t (R1⋃R2)。

令A ={1, 2}，R1 ={< 1, 2 >}，R2 ={< 2, 1 >}。

因为R1是传递的，故t (R1) = R1。

因为R2是传递的，故t(R2)= R2。

因此，t (R1) ⋃t (R2) = R1 ⋃R2 ={< 1, 2 >, < 2, 1 >}，而t (R1⋃R2) = {< 1, 2 >, < 2, 1 >, < 1, 1 >, < 2, 2 >}。

18. 对于下列集合上的整除关系，画出哈斯图。

(1) A = {1, 2, 3, 4, 6, 8, 12, 24}(2) B = {1, 2, 3,…, 12}(1) {2, 3, 4}没有最大元、最小元，极大元为3和4，极小元为2和3，上界为12和24，上确界为12，下界为1，下确界为1。

(2) {2, 3, 4}没有最大元、最小元，极大元为3和4，极小元为2和3，上界为12，上确界为12，下界为1，下确界为1。

20. 图6.21上给出了集合A = {1, 2, 3, 4}上的四个偏序关系，试画出它们的哈斯图。

并判别哪一个是全序或良序关系。

1348 12637125911(a) 去掉关系图中的自环，没有进入顶点4的有向边，将4画在最下面，去掉从4发出的有向边，没有进入顶点1的有向边，将1画在第二层，去掉从1发出的有向边，剩下两个孤立点2和3，将2和3画在最上面。

连接4和1，1和2，1和3，得到哈斯图。

23. 令T 是笛卡尔平面 R ⨯R 上的关系，T 的定义如下：< x 1, y 1 > T < x 2, y 2 > 当且仅当 x 1 ≤ x 2 ∧ y 1 ≤ y 2请据此判断下面哪个断言是真哪个是假，如果断言是假，说明理由。

(1) T 是偏序的。

(2) T 是线序的。

(3) T 是良序的。

答 T 是偏序，不是线序，更不是良序。

< 0, 1 > 和 < 1, 0 > 不可比。

25. 正整数集合上的关系R 被定义为n i Rn j ⇔ n i / n j 能够被表达成2m 的指数形式，其中m 是任意整数。

(1) 证明关系R 是等价关系。

(2) 等价类是什么？解 (1) 任取正整数x ，x / x = 1 = 20，所以xRx ，R 是自反的。

若xRy ，则有整数m 使得x / y = 2m ，y / x = 2-m ，- m 也是整数，所以yRx ，R 是对称的。

44 41111223333422若xRy且yRz，则有整数m, n使得x / y = 2m，y / z = 2n，x / z = (x / y)*( y / z) = 2m* 2n = 2m+nm + n也是整数，所以xRz，R是传递的。

R是等价关系。

(2) 对于每个正奇数k，{ x | ∃m (m∈N ∧x = k ⨯ 2m)}是等价类。

[1]R = {1, 2, 4, 8, 16,…}[3]R = {3, 6, 12, 24, 48,…}…26. 设R表示正整数的有序偶集合上的关系，并且< x, y >R< u, v >当且仅当xv = yu，证明R是等价关系。

证明任取正整数的有序偶< x, y >，因为xy = yx，所以< x, y > R < x, y >，R是自反的。

若< x, y > R < u, v >，则xv = yu，故uy = vx，所以< u, v > R < x, y >，R是对称的。

若< x, y > R < u, v > 且< u, v > R < w, t >，则xv = yu且ut = vw，因而xvut = yuvw，故xt = yw，< x, y > R < w, t >，R是传递的。