人教版高一数学必修二导学案
新人教版高一数学导学案必修2 第2章 点线面的位置关系

§2.1.1 平面1. 了解平面的描述性概念;2. 掌握平面的表示方法和基本画法;3. 掌握平面的基本性质;4. 能正确地用数学语言表示点、直线、平面以及它们之间的关系.4043引入:平面是构成空间几何体的基本要素.那么什么是平面呢?平面如何表示呢?平面又有哪些性质呢?二、新课导学 ※ 探索新知探究1:平面的概念与表示问题:生活中哪些物体给人以平面形象?你觉得平面可以拉伸吗?平面有厚薄之分吗?新知1:平面(plane)是平的;平面是可以无限延展的;平面没有厚薄之分.问题:通常我们用一条线段表示直线,那你认为用什么图形表示平面比较合适呢?新知2:如上图,通常用平行四边形来表示平面.平面可以用希腊字母,,αβγ来表示,也可以用平行四边形的四个顶点来表示,还可以简单的用对角线的端点字母表示.如平面α,平面ABCD ,平面AC 等.规定:①画平行四边形,锐角画成45°,横边长等于其邻边长的2倍;②两个平面相交时,画出交线,被遮挡部分用虚线画出来;③用希腊字母表示平面时,字母标注在锐角内.问题:点动成线、线动成面.联系集合的观点,点和直线、平面的位置关系怎么表示?直线和平面呢?新知3:⑴点A 在平面α内,记作A α∈;点A 在平面α外,记作A α∉.⑵点P 在直线l 上,记作P l ∈,点P 在直线外,记作P l ∉.⑶直线l 上所有点都在平面α内,则直线l 在平面α内(平面α经过直线l ),记作l α⊂;否则直线就在平面外,记作l α⊄.探究2:平面的性质问题:直线l 与平面α有一个公共点P ,直线l 是否在平面α内?有两个公共点呢?新知4:公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.用集合符号表示为:,,A l B l ∈∈且,A B l ααα∈∈⇒⊂问题:两点确定一直线,两点能确定一个平面吗?任意三点能确定一个平面吗?新知5:公理2 过不在一条直线上的三点,有且只有一个平面. 如上图,三点确定平面ABC .问题:把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于点B ?为什么?新知6:公理3如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.如下图所示:平面α与平面β相交于直线l ,记作l αβ=.公理3用集合符号表示为,P a ∈且P β∈⇒l αβ=,且P l ∈※ 典型例题例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.例2 如图在正方体ABCD A B C D ''''-中,判断下⑴直线AC 在平面⑵设上下底面中心为,O 则平面AA C C ''与平面DD'的交线为OO '; ⑶点,,AO C '⑷平面AB C ''与平面AC 重合.※ 动手试试练 用符号表示下列语句,并画出相应的图形: ⑴点A 在平面α内,但点B 在平面α外; ⑵直线a 经过平面α外的一点M ;⑶直线a 既在平面α内,又在平面β内.三、总结提升 ※ 学习小结1. 平面的特征、画法、表示;2. 平面的基本性质(三个公理);3. 用符号表示点、线、面的关系.※ 知识拓展平面的三个性质是公理(不需要证明,直接可以用),是用公理化方法证明命题的基础.其中公理1可以用来判断直线或者点是否在平面内;公理2用来确定一个平面,判断两平面重合,或者证明点、线共面;公理3用来判断两个平面相交,证明点共线或者线共点的问题. ※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差 ※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 下面说法正确的是( ).①平面ABCD 的面积为210cm ②100个平面重合比50个平面重合厚③空间图形中虚线都是辅助线④平面不一定用平行四边形表示. A.① B.② C.③ D.④ 2. 下列结论正确的是( ).①经过一条直线和这条直线外一点可以确定一个平面②经过两条相交直线,可以确定一个平面③经过两条平行直线,可以确定一个平面④经过空间任意三点可以确定一个平面A.1个B.2个C.3个D.4个3. 如图在四面体中,若直线EF 和GH 相交,则它们的交点一定( A.在直线DB 上B.在直线AB 上C.在直线CB 上D.都不对4. 直线12,l l 相交于点P ,并且分别与平面γ相交于点,A B 两点,用符号表示为____________________.5. 两个平面不重合,在一个面内取4点,另一个面内取3点,这些点最多能够确定平面_______个. 1. 画出满足下列条件的图形:⑴三个平面:一个水平,一个竖直,一个倾斜; ⑵ ,,,l AB CD αβαβ=⊂⊂AB ∥l ,CD ∥l .2.如图在正方体中,A 是顶点,,B C 都是棱的中点,请作出经过,,A B C 三点的平面与正方体的截面.§2.1.2空间直线与直线之间的位置关系学习目标1. 正确理解异面直线的定义;2. 会判断空间两条直线的位置关系;3. 掌握平行公理及空间等角定理的内容和应用;4. 会求异面直线所成角的大小. 学习过程一、课前准备4447复习1:平面的特点是______、 _______ 、_______.复习2:平面性质(三公理)公理1___________________________________; 公理2___________________________________; 公理3___________________________________.二、新课导学 ※ 探索新知探究1:异面直线及直线间的位置关系问题:平面内两条直线要么平行要么相交(重合不考虑),空间两条直线呢?观察:如图在长方体中,直线A B '与CC '的位置关系如何?结论:直线A B '与CC '既不相交,也不平行.新知1:像直线A B '与CC '这样不同在任何一个平面内的两条直线叫做异面直线(skew lines).试试:请在上图的长方体中,再找出3对异面直线.问题:作图时,怎样才能表示两条直线是异面的?新知2:异面直线的画法有如下几种(,a b 异面):试试:请你归纳出空间直线的位置关系.探究2:平行公理及空间等角定理问题:平面内若两条直线都和第三条直线平行,则这两条直线互相平行,空间是否有类似规律?观察:如图2-1,在长方体中,直线C D ''∥A B '',AB ∥A B '',那么直线AB 与C D ''平行吗?图2-1新知3: 公理4 (平行公理)平行于同一条直线的两条直线互相平行.问题:平面上,如果一个角的两边与另一个角的两边分别平行,则这两个角相等或者互补,空间是否有类似结论?观察:在图2-1中,ADC ∠与A D C '''∠,ADC ∠与A B C '''∠的两边分别对应平行,这两组角的大小关系如何?新知4: 定理 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.探究3:异面直线所成的角问题:平面内两条直线的夹角是如何定义的?想一想异面直线所成的角该怎么定义?b a α b a α βαa b图2-2新知5: 如图2-2,已知两条异面直线,a b ,经过空间任一点O 作直线 a '∥a ,b '∥b ,把a '与b '所成的锐角(或直角)叫做异面直线,a b 所成的角(夹角).如果两条异面直线所成的角是直角,就说这两条直线互相垂直,记作a b ⊥. 反思:思考下列问题. ⑴ 作异面直线夹角时,夹角的大小与点O 的位置有关吗?点O 的位置怎样取才比较简便? ⑵ 异面直线所成的角的范围是多少? ⑶ 两条互相垂直的直线一定在同一平面上吗? ⑷ 异面直线的夹角是通过什么样的方法作出来的?它体现了什么样的数学思想? ※ 典型例题 例 1 如图2-3,,,,E F G H 分别为空间四边形ABCD 各边,,,AB BC CD DA 的中点,若对角线2,BD = 4AC =,则22EG HF +的值为多少?(性质:平行四边形的对角线的平方和等于四条边的平方和).图2-3 例2 如图2-4,在正方体中,求下列异面直线所成的角.⑴BA '和CC ' ⑵B D ''和C A '图2-4 ※ 动手试试 练 正方体ABCD A B C D ''''-的棱长为a ,求异面直线AC 与A D ''所成的角. 三、总结提升 ※ 学习小结 1. 异面直线的定义、夹角的定义及求法; 2. 空间直线的位置关系; 3. 平行公理及空间等角定理. ※ 知识拓展 异面直线的判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.如图,,,,a A B B a ααα⊂∉∈∉,则直线AB 与直※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. ,,a b c 为三条直线,如果,a c b c ⊥⊥,则,a b 的位置关系必定是( ). A.相交 B.平行 C.异面 D.以上答案都不对 2. 已知,a b 是异面直线,直线c 平行于直线a ,那么c 与b ( ).A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线 3. 已知l αβ=,,a b αβ⊂⊂,且,a b 是异面直线,那么直线l ( ).A.至多与,a b 中的一条相交B.至少与,a b 中的一条相交C.与,a b 都相交D.至少与,a b 中的一条平行 4. 正方体ABCD A B C D ''''-的十二条棱中,与直线AC '是异面直线关系的有___________条. 5. 长方体1111ABCD A B C D -中,3AB =,2,BC =1AA=1,异面直线AC 与11A D 所成角的余弦值是______.1. 已知,E E 是正方体AC '棱AD ,A D ''的中点,求证:CEB C E B '''∠=∠.2. 如图2-5,在三棱锥P ABC -中,PA BC ⊥,E 、F 分别是PC 和AB 上的点,且32PE AF EC FB ==,设EF 与PA 、BC 所成的角分别为,αβ, 求证:90αβ+=°.图2-5§2.1.3空间直线与平面之间的位置关系§2.1.4平面与平面之间的位置关系1. 掌握直线与平面之间的位置关系,理解直线在平面外的概念,会判断直线与平面的位置关系;2. 掌握两平面之间的位置关系,会画相交平面的图形.4850复习1:空间任意两条直线的位置关系有_______、_______、_______三种.复习2:异面直线是指________________________的两条直线,它们的夹角可以通过______________ 的方式作出,其范围是___________.复习3:平行公理:__________________________ ________________;空间等角定理:_______________________________________________________.二、新课导学 ※ 探索新知探究1:空间直线与平面的位置关系问题:用铅笔表示一条直线,作业本表示一个平面,你试着比画,它们之间有几种位置关系?观察:如图3-1,直线A B '与长方体的六个面有几种位置关系?图3-1新知1:直线与平面位置关系只有三种: ⑴直线在平面内—— ⑵直线与平面相交—— ⑶直线与平面平行——其中,⑵、⑶两种情况统称为直线在平面外.反思:⑴从交点个数方面来分析,上述三种关系对应的交点有多少个?请把结果写在新知1的——符号后面⑵请你试着把上述三种关系用图形表示出来,并想想用符号语言该怎么描述.探究2:平面与平面的位置关系问题:平面与平面的位置关系有几种?你试着拿两个作业本比画比画.观察:还是在长方体中,如图3-2,你看看它的六个面两两之间的位置关系有几种?图3-2新知2:两个平面的位置关系只有两种:⑴两个平面平行——没有公共点⑵两个平面相交——有一条公共直线试试:请你试着把平面的两种关系用图形以及符号语言表示出来.※典型例题例1 下列命题中正确的个数是()①若直线l上有无数个点不在平面α内,则l∥α.②若直线l与平面α平行,则l与平面α内的任意一条直线都平行.③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.A.0B.1C.2D.3例 2 已知平面,αβ,直线,a b,且α∥β,aα⊂,bβ⊂,则直线a与直线b具有怎样的位置关系? ※动手试试练1. 若直线a不平行于平面α,且aα⊄,则下列结论成立的是()A.α内的所有直线与a异面B.α内不存在与a平行的直线C.α内存在唯一的直线与a平行D.α内的直线与a都相交.练2. 已知,,a b c为三条不重合的直线,,,αβγ为三个不重合的平面:①a∥c,b∥c⇒a∥b;②a∥γ,b∥γ⇒a∥b;③a∥c,c∥α⇒a∥α;④a∥γ,a∥αα⇒∥γ;⑤aα⊄,bα⊂,a∥b⇒a∥α.其中正确的命题是()A.①⑤B.①②C.②④D.③⑤三、总结提升※学习小结1. 直线与平面、平面与平面的位置关系;2. 位置关系用图形语言、符号语言如何表示;3. 长方体作为模型研究空间问题的重要性.※知识拓展求类似确定空间的部分、平面的个数、交线的条数、交点的个数问题,都应对相应的点、线、面的位置关系进行分类讨论,做到不重不漏.分类讨论是数学中常用的重要数学思想方法,可以.※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 直线l在平面α外,则().A.l∥αB.l与α至少有一个公共点C.l Aα= D.l与α至多有一个公共点2. 已知a∥α,bα⊂,则().A.a∥bB.a和b相交C.a和b异面D.a与b平行或异面3. 四棱柱的的六个面中,平行平面有().A.1对B.1对或2对C.1对或2对或3对D.0对或1对或2对或3对4. 过直线外一点与这条直线平行的直线有____条;过直线外一点与这条直线平行的平面有____个.5. 若在两个平面内各有一条直线,且这两条直线互相平行,那么这两个平面的位置关系一定是______.1. 已知直线,a b及平面α满足: a∥α,b∥α,则直线,a b的位置关系如何?画图表示.2. 两个不重合的平面,可以将空间划为几个部分?三个呢?试画图加以说明.§2.1 空间点、直线、平面之间1. 理解和掌握平面的性质定理,能合理运用;2. 掌握直线与直线、直线与平面、平面与平面的位置关系;3. 会判断异面直线,掌握异面直线的求法;4. 会用图形语言、符号语言表示点、线、面的位置关系.4050复习1:概念与性质⑴平面的特征和平面的性质(三个公理);⑵平行公理、等角定理;⑶直线与直线的位置关系⎧⎪⎨⎪⎩平行相交异面⑷直线与平面的位置关系⎧⎪⎨⎪⎩在平面内相交平行⑸平面与平面的位置关系⎧⎨⎩平行相交复习2:异面直线夹角的求法:平移线段作角,解三角形求角.复习3:图形语言、符号语言表示点、线、面的位置关系⑴点与线、点与面的关系;⑵线与线、线与面的关系;⑶面与面的关系.二、新课导学※典型例题例1 如图4-1,ABC∆在平面α外,AB Pα=,BCQα=,AC Rα=,求证:P,Q,R三点共线.图4-1小结:证明点共线的基本方法有两种⑴找出两个面的交线,证明若干点都是这两个平面的公共点,由公理3可推知这些点都在交线上,即证若干点共线.⑵选择其中两点确定一条直线,证明另外一些点也都在这条直线上.例2 如图4-2,空间四边形ABCD 中,E ,F 分别是AB 和CB 上的点,G ,H 分别是CD 和AD 上的点,且E H F G 与相交于点K .求证:EH ,BD ,FG 三条直线相交于同一点.图4-2小结:证明三线共点的基本方法为:先确定待证的三线中的两条相交于一点,再证明此点是二直线所在平面的公共点,第三条直线是两个平面的交线,由公理3得证这三线共点.例3 如图4-3,如果两条异面直线称作“一对”,那么在正方体的12条棱中,共有异面直线多少对?图4-3反思:分析清楚几何特点是避免重复计数的关键,计数问题必须避免盲目乱数,分类时要不重不漏.※ 动手试试练1. 如图4-4,是正方体的平面展开图,图4-4则在这个正方体中:①BM 与ED 平行 ②CN 与BE 是异面直线③CN 与BM 成60°角 ④DM 与BN 是异面直线其中正确命题的序号是( )A.①②③B.②④C.③④D.②③④练2. 如图4-5,在正方体中,E ,F 分别为AB 、AA '的中点,求证:CE ,DF',DA 三线交于一点.图4-5练 3. 由一条直线和这条直线外不共线的三点,能确定平面的个数为多少?小结:分类讨论的数学思想三、总结提升 ※ 学习小结1. 平面及平面基本性质的应用;2. 点、线、面的位置关系;3. 异面直线的判定及夹角问题.※ 知识拓展异面直线的判定方法:①定义法:利用异面直线的定义,说明两直线不平行,也不相交,即不可能在同一个平面内. ②定理法:利用异面直线的判定定理说明. ③反证法(常用):假设两条直线不异面,则它们一定共面,即这两条直线可能相交,也可能平行,.※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差 ※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 直线1l ∥2l ,在1l 上取3个点,在2l 上取2个点,由这5个点确定的平面个数为( ). A.1个 B.3个 C.6个 D.9个 2. 下列推理错误的是( ).A.A l ∈,A α∈,B l ∈,B α∈l α⇒⊂B.A α∈,A β∈,B α∈,B β∈AB αβ⇒=C.l α⊄,A l A α∈⇒∉D.A ,B ,C α∈, A ,B ,C β∈,且A ,B ,C 不共线αβ⇒与重合3. a ,b 是异面直线,b ,c 是异面直线,则a ,c 的位置关系是( ).A.相交、平行或异面B.相交或平行C.异面D.平行或异面4. 若一条直线与两个平行平面中的一个平面平行,则它与另一平面____________.5. 垂直于同一条直线的两条直线位置关系是__________________;两条平行直线中的一条与某一条直线垂直,则另一条和这条直线______.1. 如图4-6,在正方体中M ,N 分别是AB 和DD '的中点,求异面直线B M '与CN 所成的角.图4-62. 如图4-7,已知不共面的直线a ,b ,c 相交于O 点,M ,P 点是直线α上两点,N ,Q 分别是直线b ,c 上一点.求证:图4-7§2.2.1 直线与平面平行的判定1. 通过生活中的实际情况,建立几何模型,了解直线与平面平行的背景;2. 理解和掌握直线与平面平行的判定定理,并会用其证明线面平行. 5455复习:直线与平面的位置关系有______________,_______________,_________________.讨论:直线和平面的位置关系中,平行是最重要的关系之一,那么如何判定直线和平面是平行的呢?根据定义好判断吗?二、新课导学 ※ 探索新知探究1:直线与平面平行的背景分析实例1:如图5-1,一面墙上有一扇门,门扇的两边是平行的.当门扇绕着墙上的一边转动时,观察门扇转动的一边l与墙所在的平面位置关系如何?图5-1实例2:如图5-2,将一本书平放在桌面上,翻动书的封面,观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系?图5-2结论:上述两个问题中的直线l与对应平面都是平行的.探究2:直线与平面平行的判定定理问题:探究1两个实例中的直线l为什么会和对应的平面平行呢?你能猜想出什么结论吗?能作图把这一结论表示出来吗?新知:直线与平面平行的判定定理定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 如图5-3所示,a∥α.图5-3反思:思考下列问题⑴用符号语言如何表示上述定理;⑵上述定理的实质是什么?它体现了什么数学思想?⑶如果要证明这个定理,该如何证明呢?※典型例题例1 有一块木料如图5-4所示,P为平面BCEF 内一点,要求过点P在平面BCEF内作一条直线与平面ABCD平行,应该如何画线?图5-4例2 如图5-5,空间四边形ABCD中,,E F分别是,AB AD的中点,求证:EF∥平面BCD.图5-5※动手试试练 1. 正方形ABCD与正方形ABEF交于AB,M和N分别为AC和BF上的点,且AM FN=,如图5-6所示.求证:MN∥平面BEC.图5-6练2. 已知ABC∆,,D E分别为,AC AB的中点,沿DE将ADE∆折起,使A到A'的位置,设M是A B'的中点,求证:ME∥平面A CD'.三、总结提升※学习小结1. 直线与平面平行判定定理及其应用,其核心是线线平行⇒线面平行;2. 转化思想的运用:空间问题转化为平面问题. ※知识拓展判定直线与平面平行通常有三种方法:⑴利用定义:证明直线与平面没有公共点.但直接证明是困难的,往往借助于反正法来证明.⑵利用判定定理,其关键是证明线线平行.证明线线平行可利用平行公理、中位线、比例线段等等.⑶利用平面与平面平行的性质.(后面将会学习到)※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 若直线与平面平行,则这条直线与这个平面内的().A.一条直线不相交B.两条直线不相交C.任意一条直线都不相交D.无数条直线不相交2. 下列结论正确的是().A.平行于同一平面的两直线平行B.直线l与平面α不相交,则l∥平面αC.,A B是平面α外两点,,C D是平面α内两点,若AC BD=,则AB∥平面αD.同时与两条异面直线平行的平面有无数个3. 如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是().A.平行B.相交C.AC在此平面内D.平行或相交4. 在正方体1111ABCD A B C D-的六个面和六个对角面中,与棱AB平行的面有________个. 5. 若直线,a b相交,且a∥α,则b与平面α的位置关系是_____________.1. 如图5-7,在正方体中,E为1DD的中点,判断1BD与平面AEC的位置关系,并说明理由.图5-72. 如图5-8,在空间四边形ABCD中,P、Q分别是ABC∆和BCD∆的重心.求证:PQ∥平面ACD.图5-8§2.2. 2 平面与平面平行的判定1. 能借助于长方体模型讨论直线与平面、平面与平面的平行问题;2. 理解和掌握两个平面平行的判定定理及其运用;3. 进一步体会转化的数学思想.学习过程一、课前准备5657复习1:直线与平面平行的判定定理是______________________________________________________.复习2:两个平面的位置关系有___种,分别为_______和_______.讨论:两个平面平行的定义是两个平面没有公共点,怎样证明两个平面没有公共点呢?你觉得好证吗?二、新课导学※探索新知探究:两个平面平行的判定定理问题1:平面可以看作是由直线构成的.若一平面内的所有直线都与另一个平面平行,则这两个平面平行吗?由此你可以得到什么结论?结论:两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.问题2:一个平面内所有直线都平行于另外一个平面好证明吗?能否只证明一个平面内若干条直线和另外一个平面平行,那么这两个平面就平行呢?试试:在长方体中,回答下列问题⑴如图6-1,AA AA B B'''⊂面,AA'∥面BB C C'',则面AA B B''∥面BB C C''吗?图6-1⑵如图6-2,AA'∥EF,AA'∥DCC D''面,EF∥DCC D''面,则A ADD''面∥DCC D''面吗?图6-2⑶如图6-3,直线A C''和B D''相交,且A C''、B D''都和平面ABCD平行(为什么),则平面A B C D''''∥平面ABCD吗?图6-3反思:由以上3个问题,你得到了什么结论?新知:两个平面平行的判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.如图6-4所示,α∥β.图6-4反思:⑴定理的实质是什么?⑵用符号语言把定理表示出来.⑶如果要证明定理,该怎么证明呢?※典型例题例1 已知正方体1111ABCD A B C D-,如图6-5,求证:平面11AB D∥1CB D.图6-5例2 如图6-6,已知,a b 是两条异面直线,平面α过a ,与b 平行,平面β过b ,与a 平行, 求证:平面α∥平面β图6-6小结:证明面面平行,只需证明线线平行,而且这两条直线必须是相交直线.※ 动手试试练. 如图6-7,正方体中,,,,M N E F 分别是棱A B '',A D '',BC '',CD ''AMN 平面EFDB .图6-7三、总结提升 ※ 学习小结1. 平面与平面平行的判定定理及应用;2. 转化思想的运用.※ 知识拓展判定平面与平面平行通常有5种方法 ⑴根据两平面平行的定义(常用反证法); ⑵根据两平面平行的判定定理;⑶垂直于同一条直线的两个平面平行(以后学习);⑷两个平面同时平行于第三个平面,则这两个平面平行(平行的传递性);⑸一个平面内的两条相交直线分别平行于另外一个平面内的两条直线,则这两个平面平行(判※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差 ※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 平面α与平面β平行的条件可以是( ). A.α内有无穷多条直线都与β平行B.直线a 与,αβ都平行,且不在α和β内C.直线a α⊂,直线b β⊂,且a ∥β,b ∥αD.α内的任何直线都与β平行2. 经过平面α外的一条直线a 且与平面α平行的平面( ).A.有且只有一个B.不存在C.至多有一个D.至少有一个3. 设有不同的直线,a b ,及不同的平面α、β,给出的三个命题中正确命题的个数是( ). ①若a ∥α,b ∥α,则a ∥b ②若a ∥α,α∥β,则a ∥β③若,a αα⊂∥β,则a ∥β. A.0个 B.1个 C.2个 D.3个4. 如果两个平面分别经过两条平行线中的一条,则这两个平面的位置关系是________________.5. 若两个平面都平行于两条异面直线中的每一条,则这两平面的位置关系是_______________. 1. 如图6-8,在几何体ABC A B C '''-中,1∠+ 2180∠=°,34180∠+∠=°,求证:平面ABC ∥平面A B C '''.图6-82. 如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:面A B C '''∥ABC 面.图6-9§2.2.3 直线与平面平行的性质1. 掌握直线和平面平行的性质定理;2. 能灵活运用线面平行的判定定理和性质定理,掌握“线线”“线面”平行的转化.5860复习1:两个平面平行的判定定理是_________________________________________________;它的实质是由__________平行推出__________平行.复习2:直线与平面平行的判定定理是________________________________________________.讨论:如果直线a与平面α平行,那么a和平面α内的直线具有什么样的关系呢?二、新课导学※探索新知探究:直线与平面平行的性质定理问题1:如图7-1,直线a与平面α平行.请在图中的平面α内画出一条和直线a平行的直线b.图7-1问题2:我们知道两条平行线可以确定一个平面(为什么?),请在图7-1中把直线,a b确定的平面画出来,并且表示为β. 问题3:在你画出的图中,平面β是经过直线,a b 的平面,显然它和平面α是相交的,并且直线b是这两个平面的交线,而直线a和b又是平行的.因此,你能得到什么结论?请把它用符号语言写在下面.问题4:在图7-2中过直线a再画另外一个平面γ与平面α相交,交线为c.直线a,c平行吗?和你上面得出的结论相符吗?你能不能从理论上加以证明呢?图7-2新知:直线与平面平行的性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线都与该直线平行.反思:定理的实质是什么?※典型例题例1 如图7-3所示的一块木料中,棱BC平行于A C''面.⑴要经过A C''面内的一点P和棱BC将木料锯开,应怎样画线?⑵所画的线与平面AC是什么位置关系?图7-3。
人教版高中数学必修二精讲练导学案7.3.2 复数乘、除运算的三角表示及其几何意义(解析版)

7.3.2复数乘、除运算的三角表示及其几何意义导学案编写:XXX 初审:XXX 终审:XXX 廖云波【学习目标】1.利用复数三角形式熟练进行复数乘除运算,并能根据乘除运算的几何意义解决相关问题2.注意多种解题方法的灵活运用,体会数形结合、分类讨论等数学思想方法【自主学习】知识点1 复数的三角形式的运算设z 1=r 1( cos θ1+isin θ1),z 2=r 2( cos θ2+isin θ2),则( 1)乘法:z 1·z 2=r 1r 2[cos( θ1+θ2)+isin( θ1+θ2)],这就是说,两个复数相乘,积的模等于各复数的模的积,积的辐角等于各复数的辐角的和.( 2)除法:z 1÷z 2=z 1z 2=r 1r 2[cos( θ1-θ2)+isin( θ1-θ2)]( 其中z 2≠0),这就是说,两个复数相除,商的模等于被除数的模除以除数的模所得的商,商的辐角等于被除数的辐角减去除数的辐角所得的差. ( 3)乘方:z n =r n ( cos nθ+isin nθ).( 4)开方:n z =nr ( cos θ+2k πn +isin θ+2k πn )( k =0,1,2,…,n -1).知识点2 复数三角形式乘、除运算的几何意义两个复数z 1,z 2相乘时,可以像图中所示那样,先分别画出与z 1,z 2对应的向量OZ1→,OZ2→,然后把向量OZ1→绕点O 按逆时针方向旋转一个角θ2( 如果θ2<0,就要把OZ1→按顺时针方向旋转一个角|θ2|),再把它的模变为原来的r 2倍,得到向量OZ →,OZ →表示的复数就是积z 1z 2.这就是复数乘法的几何意义.z 2≠0,z 1z 2的几何意义是把z 的对应向量OZ1→按顺时针方向旋转一个角θ2( 如果θ2<0,就要把OZ1→按逆时针方向旋转一个角|θ2|),再把它的模变为原来的1r 2倍,所得的向量即表示商z 1z 2.【合作探究】探究一 复数的三角形式的乘、除运算 【例1】2( cos π12+isin π12)·3( cos π6+isin π6).[解]2( cos π12+isin π12)·3( cos π6+isin π6)=2·3[cos(π12+π6)+isin( π12+π6)] =6( cos π4+isin π4)=6( 22+22i)=3+3i.归纳总结:r 1( cos θ1+isin θ1( ·r 2( cos θ2+isin θ2( =r 1r 2[cos ( θ1+θ2( +isin ( θ1+θ2( ]计算,简便得多.这就是复数的三角形式乘法运算公式.【练习1】设复数z =cos θ+isin θ,θ∈( π,2π),求复数z 2+z 的模和辐角. 解:z 2+z =( cos θ+isin θ)2+cos θ+isin θ =cos2θ+isin2θ+cos θ+isin θ =( cos2θ+cos θ)+i( sin2θ+sin θ) =2cos 3θ2cos θ2+i( 2sin 3θ2cos θ2)=2cos θ2( cos 32θ+isin 32θ)=-2cos θ2⨯⎣⎡⎦⎤cos (-π+32θ)+isin (-π+32θ).∵θ∈( π,2π),∴θ2∈( π2,π),∴-2cos θ2>0,所以复数z 2+z 的模为-2cos θ2,辐角为( 2k -1)π+3θ2( k ∈Z ).探究二 复数的乘、除运算的几何意义【例2】向量OZ →与-1+i 对应,把OZ →按逆时针方向旋转120°,得到OZ ′→,求与向量OZ ′→对应的复数[解] 将向量OZ →逆时针方向旋转120°,得到OZ ′→,由于模未发生变化,应当是OZ →对应复数乘以1·( cos120°+isin120°),即z ′=( -1+i)( cos120°+isin120°)=2( cos135°+isin135°)( cos120°+isin120°)=2( cos255°+isin255°)=1-32-1+32i.归纳总结:利用复数乘、除法的几何意义来解决三角形中角的大小问题,十分方便【练习2】如图,已知平面内并列的三个相等的正方形,利用复数证明∠1+∠2+∠3=π2.证明:∈1,∈2,∈3分别等于复数1+i,2+i,3+i 的辐角主值,这样∈1+∈2+∈3就是( 1+i)( 2+i)( 3+i)=10i 的辐角,∈1,∈2,∈3都是锐角,所以∈1+∈2+∈3=π2.课后作业A 组 基础题一、选择题1.复数( sin10°+icos10°)3的三角形式为( )A .sin30°+icos30°B .cos240°+isin240°C .cos30°+isin30°D .sin240°+icos240°【正确答案】B2.若z =cos θ-isin θ,则使z 2=-1的θ值可能是( )A .0 B.π2 C .π D .2π【正确答案】B详细解析:∈z =cos θ-isin θ=cos( -θ)+isin( -θ), ∈z 2=z ·z =cos( -2θ)+isin( -2θ)=cos2θ-isin2θ=-1,∈⎩⎪⎨⎪⎧cos2θ=-1,-sin2θ=0∈θ=π2.3.4( cos60°+isin60°)×3( cos150°+isin150°)=( )A .63+6iB .63-6iC .-63+6iD .-63-6i【正确答案】D详细解析:4( cos60°+isin60°)×3( cos150°+isin150°)=12[cos( 60°+150°)+isin( 60°+150°)]=12( cos210°+isin210°)=12⎝⎛⎭⎫-32-12i =-63-6i.故选D. 4.复数z 1=1,z 2是由z 1绕原点O 逆时针方向旋转π6而得到,则arg( z 2-z 12)的值为( )A.π12 B.π3 C.5π12D.7π12【正确答案】D5.( 多选)设z 1、z 2是复数,arg z 1=α,arg z 2=β,则arg( z 1·z 2)有可能是下列情况中的( )A .α+βB .α+β-2πC .2π-( α+β)D .π+α+β【正确答案】ABC详细解析:因为arg z 1=α,arg z 2=β,所以α∈[0,2π),β∈[0,2π),而arg( z 1·z 2)∈[0,2π),则当α+β∈[0,2π)时,arg( z 1·z 2)=α+β;当α+β∈[2π,4π)时,α+β-2π∈[0,2π),则arg( z 1·z 2)=α+β-2π;当α+β=π时,2π-( α+β)=π=α+β,此时arg( z 1·z 2)=α+β=2π-( α+β),故选ABC. 二、填空题6.复数-i 的一个立方根是i,它的另外两个立方根是 . 【正确答案】-32-12i,32-12i 详细解析:∵-i =cos 3π2+isin 3π2,其立方根是cos 2k π+3π23+isin 2k π+3π23,k ∈0,1,2,即i,-32-12i,32-12i. 三、参考解答题7.计算:4( cos 4π3+isin 4π3)÷2( cos 5π6+isin 5π6).解:原式=2[cos(4π3-5π6)+isin( 4π3-5π6)] =2( cos π2+isin π2)=2i.8.把复数z 1与z 2对应的向量OA →,OB →分别按逆时针方向旋转π4和5π3后,重合于向量OM →且模相等,已知z 2=-1-3i,求复数z 1的代数形式和它的辐角主值. 解:由复数乘法的几何意义得 z 1( cos π4+isin π4)=z 2( cos 5π3+isin 5π3),又z 2=-1-3i =2( cos 4π3+isin 4π3),∴z 1=2(cos 4π3+isin 4π3)·(cos 5π3+isin 5π3)cos π4+isin π4=2[cos( 3π-π4)+isin( 3π-π4)]=-2+2i,z 1的辐角主值为3π4.9.计算:3( cos π6+isin π6)·4( cos π12+isin π12).解:原式=43[cos( π6+π12)+isin( π6+π12)]=43( cos π4+isin π4)=26+26i.10.若z =3( cos π6+isin π6),求z 2与z 3的值.解:z 2=z ·z =( 3)2[cos( π6+π6)+isin( π6+π6)]=3( cos π3+isin π3)=32+332i.z 3=z ·z ·z =( 3)3[cos( π6×3)+isin( π6×3)]=33( cos π2+isin π2)=33i.11.在复平面上A ,B 表示复数为α,β( α≠0),且β=( 1+i)α,判断△AOB 形状, 并证明S △AOB =12|α|2.解:∈AOB 为等腰直角三角形. 证明:∵α≠0,∴β=( 1+i)α,∴βα=1+i =2( cos π4+isin π4),∴∠AOB =π4; ∵OA →,AB →分别表示复数α,β-α,由β-α=αi,得β-αα=i =cos π2+isin π2,∴∠OAB =90°,∴△AOB 为等腰直角三角形. ∴S △AOB =12|OA |2=12|α|2.12.设复数z 1=3+i,复数z 2满足|z 2|=2,已知z 1·z 22的对应点在虚轴的负半轴上,且arg z 2∈( 0,π),求z 2的代数形式.解:因为z 1=2( cos π6+isin π6),设z 2=2( cos α+isin α),α∈( 0,π),所以z 1z 22=8[cos( 2α+π6)+isin( 2α+π6)].由题设知2α+π6=2k π+3π2( k ∈Z ),所以α=k π+2π3( k ∈Z ),又α∈( 0,π),所以α=2π3,所以z 2=2( cos 2π3+isin 2π3)=-1+3i.B 组 能力提升一、选择题1.复数z =sin π6-icos π6,若z n =Z ( n ∈N ),则n 的最小值是( )A .1B .3C .5D .7【正确答案】C详细解析:因为z =sin π6-icos π6=cos 5π3+isin 5π3,所以z n =cos 5n 3π+isin 5n 3π,Z =cos 5π3-isin 5π3=cos π3+isin π3.因为z n =Z ,所以5n 3π=π3+2k π,n =6k +15,因为n ∈N ,k ∈Z ,所以当k =4时,n =5. 2.设复数z 1=2sin θ+icos θ( π4<θ<π2)在复平面上对应向量OZ 1→,将OZ 1→按顺时针方向旋转3π4后得到向量OZ 2→,OZ 2→对应复数z 2=r ( cos φ+isin φ),则tan φ=( )A.2tan θ+12tan θ-1B.2tan θ-12tan θ+1C.12tan θ+1D.12tan θ-1 【正确答案】A 二、填空题3.( 1-3i)7详细解析:( 1-3i)7=⎣⎡⎦⎤2⎝⎛⎭⎫cos 5π3+isin 5π37 =27⎝⎛⎭⎫cos 35π3+isin 35π3 =128⎝⎛⎭⎫12-32i =64-643i.三、参考解答题4.若z ∈C ,|z -2|≤1,求|z |的最大值,最小值和arg z 范围.解:如图,由|z -2|≤1,知z 的轨迹为复平面上以( 2,0)为圆心,1为半径的圆面( 包括圆周),|z |表示圆面上任一点到原点的距离.显然1≤|z |≤3,∈|z |max =3,|z |min =1,另设圆的两条切线为OA ,OB ,A ,B 为切点,由|CA |=1,|OC |=2知∈AOC =∈BOC =π6,∈arg z ∈[0,π6]∈[116π,2π).5.已知复数z 1=-2+i 对应的点为P 1,z 2=-3+4i 对应的点为P 2,把向量P 1P 2→绕P 1点按顺时针方向旋转π2后,得到向量P 1P →,求向量P 1P →和点P 对应的复数分别是什么? 解:由题意知向量P 1P 2→对应的复数是z 2-z 1=( -3+4i)-( -2+i)=-1+3i.再由复数乘法的几何意义得,向量P 1P →对应的复数是( -1+3i)·⎣⎡⎦⎤cos ⎝⎛⎭⎫-π2+isin ⎝⎛⎭⎫-π2=3+i,最后由复数加法的几何意义得,向量OP →=OP 1→+P 1P →,其对应的复数是( -2+i)+( 3+i)=1+2i,故点P 对应的复数为1+2i.6.已知z =-1+i i -2i,z 1-z ·z 2=0,arg z 2=7π12,若z 1,z 2在复平面上分别对应点A ,B ,且|AB |=2,求z 1的立方根.解:由题设知z =1-i,因为|AB |=2,即|z 1-z 2|=2,所以|z 1-z 2|=|z z 2-z 2|=|( 1+i)z 2-z 2|=|i z 2|=|z 2|=2,又arg z 2=7π12, 所以z 2=2( cos 7π12+isin 7π12),z 1=z z 2=( 1+i)z 2 =2( cos π4+isin π4)·2( cos 7π12+isin 7π12) =2( cos 5π6+isin 5π6),所以z 1的立方根为32[cos 5π6+2k π3+isin 5π6+2k π3],k =0,1,2, 即32( cos 5π18+isin 5π18),32( cos 17π18+isin 17π18), 32( cos 29π18+isin 29π18).。
圆柱、圆锥、圆台的表面积和体积 导学案-高一下学期数学人教A版(2019)必修第二册
8.3.2圆柱、圆锥、圆台的表面积和体积一、预习导入阅读课本116页,填写。
圆柱(底面半径为r,母线长为l)圆锥(底面半径为r,母线长为l)圆台(上、下底面半径分别为r′,r,母线长为l)侧面展开图底面积S底=2πr2S底=____S底=________侧面积S侧=____S侧=____S侧=________表面积S表=________S表=________S表=_________体积V圆柱=(r是底面半径,h是高)V圆锥=(r是底面半径,h是高)V圆台=(r′、r分别是上、下底面半径,h是高).思考:观察圆柱、圆锥、圆台的展开图,怎么求出各自的表面积?【牛刀小试】1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是;其表面积等于2.若圆锥的母线长为5,底面半径为3,则其侧面积等于;其表面积等于3.已知圆台的上、下底面半径分别为3和4,母线长为6,则其侧面积是;其表面积等于三、巩固练习1.若一个高为2的圆柱,底面周长为2π,则该圆柱的体积为2.已知圆柱的上、下底面的中心分别为O1,O2过直线O1O2的平面,截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A12√2πB12πC8√2πD10π3.若圆锥的底面半径为3,母线长为5,则圆锥的体积为4.圆锥的轴截面是等腰直角三角形,侧面积是16√2π,则圆锥的体积是5.已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则该圆台较小底面的半径为( )A.7 B.6 C.5 D.3四、课堂小结了解并会运用圆柱、圆锥、圆台的表面积和体积的公式。
五、课后作业必做题:书本第120页的第四题金版第102页的例1、跟踪训练1、例2、跟踪训练2。
选做题:阅读书本第121页的“探究与发现”——祖暅原理与柱体、锥体的体积。
人教版高中数学必修二精讲练导学案9.2.2 总体百分位数的估计(解析版)

9.2.2总体百分位数的估计导学案编写:XXX 初审:XXX 终审:XXX 廖云波【学习目标】1.理解百分位数的概念2.掌握计算百分位数的方法【自主学习】知识点1 百分位数( 1)如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数.一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有( 100-p)%的数据大于或等于这个值.( 2)第25百分位数又称第一四分位数或下四分位数;第75百分位数又称第三四分位数或上四分位数.知识点2 如何计算百分位数下面的步骤来说明如何计算第p百分位数.第1步:以递增顺序排列原始数据( 即从小到大排列).第2步:计算i=np%.第3步:①若i不是整数,将i向上取整.大于i的比邻整数即为第p百分位数的位置;①若i是整数,则第p百分位数是第i项与第( i+1)项数据的平均值.【合作探究】探究一 百分位数的计算【例1】从某珍珠公司生产的产品中,任意抽取12颗珍珠,得到它们的质量( 单位:g) 如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0. ( 1)分别求出这组数据的第25,75,95百分位数. ( 2)请你找出珍珠质量较小的前15%的珍珠质量.( 3)若用第25,50,95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品,依照这个样本的数据,给出该公司珍珠等级的划分标准.[解] ( 1)将所有数据从小到大排列,得 7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9,因为共有12个数据,所以12×25%=3,12×75%=9,12×95%=11.4, 则第25百分位数是8.0+8.32=8.15,第75百分位数是8.6+8.92=8.75,第95百分位数是第12个数据( 2)因为共有12个数据,所以12×15%=1.8,则第15百分位数是第2个数据为7.9.即产品质量较小的前15%的产品有2个,它们的质量分别为7.8,7.9.( 3)由( 1)可知样本数据的第25百分位数是8.15 g,第50百分位数为8.5 g, 第95百分位数是9.9 g,所以质量小于或等于8.15 g 的珍珠为次品,质量大于8.15 g 且小于或等于8.5 g 的珍珠为合格品,质量大于8.5 g 且小于等于9.9 g 的珍珠为优等品,质量大于9.9 g 的珍珠为特优品.归纳总结:【练习1】以下数据为参加数学竞赛决赛的15人的成绩:78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是( ) A.90 B.90.5C.91D.91.5正确答案B[把成绩按从小到大的顺序排列为: 56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,因为15×80%=12,所以这15人成绩的第80百分位数是90+912=90.5.]探究二百分位数的综合应用【例2】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200千瓦时的部分按0.5元/千瓦时收费,超过200千瓦时但不超过400千瓦时的部分按0.8元/千瓦时收费,超过400千瓦时的部分按1.0元/千瓦时收费.( 1)求某户居民用电费用y( 单位:元)关于月用电量x( 单位:千瓦时)的函数详细解析式.( 2)为了了解居民的用电情况,通过抽样获得了今年1月份100户居民每户的用电量,统计详细分析后得到如图所示的频率分布直方图.若这100户居民中,今年1月份用电费用不超过260元的占80%,求a,b的值.( 3)根据( 2)中求得的数据计算用电量的75%分位数.[解]( 1)当0≤x≤200时,y=0.5x;当200<x≤400时,y=0.5×200+0.8×( x-200)=0.8x-60;当x >400时,y =0.5×200+0.8×200+1.0×( x -400)=x -140. 所以y 与x 之间的函数详细解析式为 y =⎩⎪⎨⎪⎧0.5x ,0≤x ≤200,0.8x -60,200<x ≤400,x -140,x >400.( 2)由( 1)可知,当y =260时,x =400,即用电量不超过400千瓦时的占80%, 结合频率分布直方图可知⎩⎪⎨⎪⎧0.001×100+2×100b +0.003×100=0.8,100a +0.000 5×100=0.2, 解得a =0.001 5,b =0.002 0. ( 3)设75%分位数为m ,因为用电量低于300千瓦时的所占比例为( 0.001+0.002+0.003)×100=60%, 用电量不超过400千瓦时的占80%,所以75%分位数为m 在[300,400)内,所以0.6+( m -300)×0.002=0.75, 解得m =375千瓦时,即用电量的75%分位数为375千瓦时.归纳总结:【练习2】某市对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分( 90分及以上为认知程度高),现从参赛者中抽取了x 人,按年龄分成5组( 第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45]),得到如图所示的频率分布直方图,已知第一组有5人.( 1)求x ;( 2)求抽取的x 人的年龄的50%分位数( 结果保留整数); ( 3)以下是参赛的10人的成绩:90,96,97,95,92,92,98,88,96,99,求这10人成绩的20%分位数和平均数,以这两个数据为依据,评价参赛人员对一带一路的认知程度,并谈谈你的感想.【正确答案】( 1)第一组频率为0.01×5=0.05,所以x =50.05=100. ( 2)由题图可知年龄低于30岁的所占比例为40%,年龄低于35岁的所占比例为70%,所以抽取的x 人的年龄的50%分位数在[30,35)内,由30+5×0.50-0.400.70-0.40=953≈32,所以抽取的x 人的年龄的50%分位数为32.( 3)把参赛的10人的成绩按从小到大的顺序排列: 88,90,92,92,95,96,96,97,98,99,计算10×20%=2,所以这10人成绩的20%分位数为90+922=91,这10人成绩的平均数为110( 88+90+92+92+95+96+96+97+98+99)=94.3.评价:从百分位数和平均数来看,参赛人员的认知程度很高. 感想:结合本题和实际,符合社会主义核心价值观即可.课后作业A 组 基础题一、选择题1.数据12,14,15,17,19,23,27,30的第70百分位数是( )A . 14B .17C . 19D .23【正确答案】D [因为8×70%=5.6,故70%分位数是第6项数据23.]2.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度( 棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.估计棉花纤维的长度的样本数据的90%分位数是( )A .32.5 mmB .33 mmC .33.5 mmD .34 mm【正确答案】A [棉花纤维的长度在30 mm 以下的比例为 ( 0.01+0.01+0.04+0.06+0.05)×5=0.85=85%, 在35 mm 以下的比例为85%+10%=95%,因此,90%分位数一定位于[30,35]内,由30+5×0.90-0.850.95-0.85=32.5,可以估计棉花纤维的长度的样本数据的90%分位数是32.5 mm.]3.如图所示是根据某市3月1日至3月10日的最低气温( 单位:℃)的情况绘制的折线统计图,由图可知这10天最低气温的第80百分位数是( )A .-2B .0C .1D .2【正确答案】D [由折线图可知,这10天的最低气温按照从小到大的顺序排列为:-3,-2,-1,-1,0,0,1, 2, 2, 2,因为共有10个数据,所以10×80%=8,是整数,则这10天最低气温的第80百分位数是2+22=2.]4.某厂10名工人在一小时内生产零件的个数分别是15,17,14,10,15,17,17,16,14,12,设该组数据的平均数为a ,第50百分位数为b ,则有( )A .a =13.7, b =15.5B .a =14, b =15C .a =12, b =15.5D .a =14.7, b =15【正确答案】D [把该组数据按从小到大的顺序排列为10,12,14,14,15,15,16,17,17,17,其平均数a =110×( 10+12+14+14+15+15+16+17+17+17)=14.7,第50百分位数为b =15+152=15.] 5.已知甲、乙两组数据:甲组:27,28,39,40,m,50; 乙组:24,n,34,43,48,52.若这两组数据的第30百分位数、第80百分位数分别相等,则mn等于( )A .127B .107C .43D .74【正确答案】A [因为30%×6=1.8,80%×6=4.8,所以第30百分位数为n =28,第80百分位数为m =48,所以m n =4828=127.]二、填空题6.某学校组织学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],则60分为成绩的第________百分位数.【正确答案】30 [因为[20,40),[40,60)的频率为( 0.005+0.01)×20=0.3,所以60分为成绩的第30百分位数.]7.某年级120名学生在一次百米测试中,成绩全部介于13秒与18秒之间.将测试结果分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积之比为1∶3∶7∶6∶3,那么成绩的70%分位数约为________秒.【正确答案】16.5 [设成绩的70%分位数为x ,因为1+3+71+3+7+6+3=0.55,1+3+7+61+3+7+6+3=0.85,所以x ① [16,17),所以0.55+( x -16)×61+3+7+6+3=0.70,解得x =16.5秒.]8.已知30个数据的第60百分位数是8.2,这30个数据从小到大排列后第18个数据是7.8,则第19个数据是________.【正确答案】8.6 [由于30×60%=18,设第19个数据为x ,则7.8+x2=8.2,解得x =8.6,即第19个数据是8.6.] 三、参考解答题9.某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:( 1)试确定x ,y ,p ,q 的值,并补全频率分布直方图( 如图).( 2)估计网购金额的25%分位数( 结果保留3位有效数字). 【正确答案】( 1)根据题意有:⎩⎪⎨⎪⎧16+24+x +y +16+14=200,16+24+x y +16+14=32,解得⎩⎪⎨⎪⎧x =80,y =50,所以p =0.4,q =0.25.补全频率分布直方图如图所示:( 2) 由( 1)可知,网购金额不高于2千元的频率为0.08+0.12=0.2, 网购金额不高于3千元的频率为0.2+0.4=0.6, 所以网购金额的25%分位数在[2,3)内,则网购金额的25%分位数为2+0.25-0.20.6-0.2×1≈2.13千元.B 组 能力提升一、选择题1.数据3.2,3.4,3.8,4.2,4.3,4.5,x,6.6的第65百分位数是4.5,则实数x 的取值范围是( )A .[4.5,+∞)B .[4.5,6.6)C .( 4.5,+∞)D .[4.5,6.6]【正确答案】A [因为8×65%=5.2,所以这组数据的第65百分位数是第6项数据4.5,则x ≥4.5,故选A .]2.( 多选题)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则下列说法正确的是( )甲 乙A .甲的成绩的平均数等于乙的成绩的平均数B .甲的成绩的中位数等于乙的成绩的中位数C .甲的成绩的第80百分位数等于乙的成绩的第80百分位数D .甲的成绩的极差大于乙的成绩的极差【正确答案】AC [由题图可得,x -甲=4+5+6+7+85=6,x -乙=3×5+6+95=6,A 项正确;甲的成绩的中位数为6,乙的成绩的中位数为5,B 项错误;甲的成绩的第80百分位数7+82=7.5,乙的成绩的第80百分位数6+92=7.5,所以二者相等,C 项正确;甲的成绩的极差为4,乙的成绩的极差也为4,D 项不正确.]二、填空题3.( 一题两空)如图是某市2019年4月1日至4月7日每天最高、最低气温的折线统计图,这7天的日最高气温的第10百分位数为________,日最低气温的第80百分位数为________.【正确答案】24 ①16 ①[由折线图可知,把日最高气温按照从小到大排序,得24, 24.5, 24.5, 25, 26,26, 27.因为共有7个数据,所以7×10%=0.7,不是整数,所以这7天日最高气温的第10百分位数是第1个数据,为24 ①.把日最低气温按照从小到大排序,得12, 12, 13, 14, 15, 16, 17.因为共有7个数据,所以7×80%=5.6,不是整数,所以这7天日最低气温的第80百分位数是第6个数据,为16 ①.]三、参考解答题4.下表记录了一个家庭6月份每天在食品上面的消费金额:( 单位:元)【正确答案】该样本共有30个数据,所以30×5%=1.5,30×25%=7.5,30×50%=15,30×75%=22.5,30×95%=28.5.将所有数据由小到大排列得:26,26,26,27,28,28,28,28,28,29,29,30,30,31,31,31,32,32,32,34,34,34,34,34,34,34,35,35,35,35.从而得5个百分位数如下表:5.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:( 1)估计总体400名学生中分数小于70的人数;( 2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;( 3)根据该大学规定,把15%的学生划定为不及格,利用( 2)中的数据,确定本次测试的及格分数线,低于及格分数线的学生需要补考.【正确答案】( 1)根据频率分布直方图可知,样本中分数不小于70的频率为( 0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.所以总体400名学生中分数小于70的人数为400×0.4=160.( 2)根据题意,样本中分数不小于50的频率为( 0.01+0.02+0.04+0.02)×10=0.9, 分数在区间[40,50)内的人数为100-100×0.9-5=5. 所以总体中分数在区间[40,50)内的人数估计为400×5100=20.( 3) 设分数的第15百分位数为x ,由( 2)可知,分数小于50的频率为5+5100=0.1,分数小于60的频率为0.1+0.1=0.2,所以x ①[50,60),则0.1+( x -50)×0.01=0.15,解得x =55,则本次考试的及格分数线为55分.。
人教课标版(B版)高中数学必修2导学案-棱柱、棱锥和棱台的结构特征

1.1.2棱柱、棱锥和棱台的结构特征一.学习要点:棱柱、棱锥和棱台的几何结构特征 二.学习过程: 1.多面体观察·探索·研究:多面体的哪些性质可以作为它的特征性质?多面体的每个面都是多边形.(圆柱、圆锥、球等其他几何体就不具有这种性质.多面体的有关概念:(a ) 多面体:由若干个平面多边形所围成的几何体. (b ) (c ) (d ) (e ) (f)凸多面体:把一个多面体的任意一个面延展为平面,如果 其余的各面都在这个平面的同一侧,则这样的多面体就叫做凸多面体.特别说明:我们所说的多面体,如果没有特别说明,指的都是凸多面体. (g)多面体的分类:按照围成它的面的个数分为四面体、五面体、六面体…… (h)几何体的截面:一个几何体和一个平面相交所得到的平面图形,叫做这个几何体的截面. 2.棱柱观察·探索·研究:棱柱有哪些性质?哪些性质可以作为棱柱的特征性质? (1) 棱柱的特征性质:棱柱有两个面互相平行,而其余每相邻两个面的交线都互相平行. (2)棱柱的有关概念:(a)棱柱:将一个多边形上各点沿着同一方向移动相同的距离所形成的几何体. (b)棱柱的底面:棱柱的两个互相平行的面叫做棱柱的底面. (c)棱柱的侧面:除底面外的各面叫做棱柱的侧面. (d)棱柱的侧棱:两侧面的公共边叫做棱柱的侧棱. (e)棱柱的高:棱柱两底面之间的距离叫做棱柱的高. (3)棱柱的表示法:棱柱ABCDE 11111A B C D E ,或棱柱1AC . (4)棱柱的分类:按底面多边形的边数分类: 三棱柱、四棱柱、五棱柱……按侧棱与底面的位置关系及底面的形状分类: ✦ 斜棱柱:侧棱与底面不垂直的棱柱叫做斜棱柱. ✦ 直棱柱:侧棱与底面垂直的棱柱叫做直棱柱. ✦ 正棱柱:底面是正多边形的直棱柱叫做正棱柱. (5) 特殊的四棱柱:平行六面体:底面是平行四边形的棱柱叫做平行六面体.直平行六面体:侧棱与底面垂直的平行六面体叫做直平行六面体.长方体:底面是矩形的直平行六面体叫做长方体. 正方体:棱长都相等的长方体叫做正方体.3.棱锥(1)棱锥的特征性质:棱锥有一个面是多边形,而其余各面都是有一个公共顶点的三角形. (2) 棱锥的有关概念:(a)棱锥的侧面:棱锥中有公共顶点的各三角形叫做棱锥的侧面. (b)棱锥的顶点:棱锥的各侧面的公共顶点叫做棱锥的顶点. (c)棱锥的侧棱:棱锥的相邻两侧面的公共边叫做棱锥的侧棱. (d)棱锥的底面:多边形叫做棱锥的底面. (e)棱锥的高:顶点到底面的距离叫做棱锥的高. (3)棱锥的表示法:棱锥S ABCDE ,或棱锥S AC . (4)棱锥的分类:(5)按底面多边形的边数分类: 三棱锥、四棱锥、五棱锥……四棱柱 平行六面体直平行六面体长方体正四棱柱正方体(6)正棱锥与非正棱锥:正棱锥:如果棱锥的底面是正多边形,它的顶点又在过底面中心且与底面垂直的直线上,则这个棱锥叫做正棱锥.棱锥的斜高:正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.4. 棱台(1)棱台的有关概念:(a) 棱台:棱锥被平行于底面的平面所截,截面和底面间的部分叫做棱台. (b)棱台的底面:原棱锥的底面和截面分别叫做棱台的下底面和上底面. (c)棱台的侧面:棱台中除上、下底面的其他各面叫做棱台的侧面. (d)棱台的侧棱:棱台的相邻两侧面的公共边叫做棱台的侧棱. (e)棱台的高:棱台两底面间的距离叫做棱台的高. (f) (g)(2) 例1 四棱台的高和斜高.课堂练习:1.教材第8、10页练习题2.下列说法正确的是()A.棱柱的侧面都是矩形B.棱柱的侧棱不全相等C.棱柱是有两个面互相平行,其余各面都是四边形的几何体D.棱柱至少有两个面平行3.用一个过正四棱柱底面一边的平面去截正四棱柱,截面的形状是()A.正方形B.矩形C.菱形D.一般平行四边形4.长方体的全面积等于11,所有的棱长之和是24,则这个长方体的对角线长为()A.BC.5D.65.具备下列哪个条件的多面体是棱台()A.两底面是相似多边形的多面体B.侧面是梯形的多面体C.两底面平行的多面体D.两底面平行,侧棱延长后交于一点的多面体6.两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,使它们重叠起来组成一个新的长方体,在这些长方体中,最长的对角线的长度是()AB.C.D.7.已知正三棱锥P111A B C的底面边长为2,侧棱长为3.正三棱台ABC111A B C的下底边长为7,把正三棱锥的底面与正三棱台的上底面重叠,恰好能够拼成一个正三棱锥,求棱台和新的三棱锥的侧棱长.PCBAA1B1C1。
高中数学 第一章 空间几何体 第三节 球的表面积与体积导学案(无答案)新人教版必修2 学案

C B
A
O O'
第一章第三节球的表面积与体积
三维目标
1.了解球的表面积和体积公式;
2. 能运用球的表面积和体积公式解决简单实际问题.
________________________________________________________________________________ 目标三导 学做思1
问题1. 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,冰淇淋会从杯子溢出吗?请说明理由.
【学做思2】
1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm 2
)
2.已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半,且
2AB BC CA ===,求球的表面积.
3.有三个球123O O O 、、,球1O 切于正方体的各面,球2O 切于正方体的各侧棱,球3O 过正方体的各顶点,
求这三个球的表面积以及体积之比.
*4.已知球的半径为R ,在球内作一个内接圆柱,当这个圆柱底面半径为何值时,它的侧面积最大,并求出最大值。
达标检测
1.如图,求图中阴影部分绕AB 旋转一周所形成的几何体的表面积和体积.
A
B
C
D
O R
r
O 1
2.表面积为324π的球,其内接正四棱柱的高是14,求这个正四棱柱的表面积.
===,求这个球的体积.
3. 在球面上有四个点P、A、B、C,如果PA、PB、PC两两垂直且PA PB PC a。
人教版高一数学必修2全册导学案及答案

人教版高一数学必修2全册导学案及答案第一章:集合及其运算1. 集合的概念及表示方法a) 集合的定义:集合是由一些确定的、互不相同的对象构成的整体。
b) 集合的表示方法:i) 列举法:把集合中的元素逐个列举出来,用大括号括起来表示,如A={1, 2, 3}。
ii) 描述法:用条件描述集合中的元素,如A={x|x是自然数,且x<4}。
2. 集合的运算a) 交集:设A和B为两个集合,A∩B表示同时属于A和B的元素组成的集合。
b) 并集:设A和B为两个集合,A∪B表示属于A或者属于B的元素组成的集合。
c) 差集:设A和B为两个集合,A-B表示属于A但不属于B的元素组成的集合。
d) 互斥与互补:若A∩B=∅,则A和B互斥;若A∪B=U(全集),则称A和B互为互补集。
练习题:1. 设A={1, 2, 3, 4},B={3, 4, 5},求A∩B和A∪B。
2. 若A={1, 2, 3, 4},B={2, 3, 4, 5},求A-B和B-A。
3. 设全集U={1, 2, 3, 4, 5},A={1, 2, 3},B={3, 4},求A的补集和B的补集。
答案:1. A∩B={3, 4},A∪B={1, 2, 3, 4, 5}。
2. A-B={1},B-A={5}。
3. A的补集U-A={4, 5},B的补集U-B={1, 2, 5}。
第二章:不等式与不等式组1. 不等式的概念a) 不等式的定义:设a和b是两个实数,用符号"<"表示a小于b,用符号">"表示a大于b,用符号"≤"表示a小于等于b,用符号"≥"表示a大于等于b。
b) 不等式的解集:使不等式不等号成立的实数的集合,称为不等式的解集。
2. 一元一次不等式a) 不等式的性质:两边加上(或减去)同一个实数,不等式的大小方向不变;两边乘以正实数(或除以正实数),不等式的大小方向不变;两边乘以负实数(或除以负实数),不等式的大小方向相反。
高中数学:面面垂直的判定定理教案新人教版必修2

高中数学:面面垂直的判定定理教案新人教版必修2高一数学导学案课题:平面与平面垂直的判定定理 时间:2009.12.3 班级:___________________________ 姓名:___________________________ 【学习目标】1.了解空间角中二面角的定义2.掌握并运用平面与平面垂直的判定定理 【重点难点】平面与平面垂直的判定定理的运用【学习过程】一、二面角的平面角:1、半平面:一个平面内的一条直线把这个平面分成__________________,其中的__________________都叫作半平面.2、二面角:从一条直线出发的__________________所组成的图形叫作二面角,______________叫作二面角的棱,这_________________叫作二面角的面.3、二面角的记法: __________________.4、二面角的平面角:以二面角的棱上___________为端点,在两个半平面内分别作__________________的两条射线,这两条射线所成的角叫作二面角的平面角.其中_________________________________的二面角叫作直二面角注释:① 通过学习二面角及二面角的平面角的概念,试探究在作二面角的平面角时,它的大小随着角的顶点的选取而改变吗?② 我们常说:“把门开大一些”是指哪个角大一些?③ 能否把“二面角的平面角”理解为“在二面角的棱上任取一点,在两个面内分别过该点画一条射线,两射线所成的角为二面角的平面角”?5、平面与平面垂直的判定定理的内容:6、判定定理用符号及图形表示:环节设计二、定理运用例1、课本37页例1.例2、AB 是圆O 的直径,PA 垂直于圆O 所在平面,C 是圆上任意一点,求证:面PAC 面PBC .例3、课本38页练习2的3、4题,课本41页习题1-6A 组第2题和第6题.环节设计。
新人教版新高考高中数学必修第二册全套导学案课后练习题

平面向量的概念【学习过程】一、问题导学预习教材P2-P4的内容,思考以下问题: 1.向量是如何定义的?向量与数量有什么区别? 2.怎样表示向量?向量的相关概念有哪些?3.两个向量(向量的模)能否比较大小?4.如何判断相等向量或共线向量?向量AB →与向量BA →是相等向量吗?二、合作探究探究点1: 向量的相关概念例1:给出下列命题:①若AB→=DC →,则A ,B ,C ,D 四点是平行四边形的四个顶点; ②在▱ABCD 中,一定有AB →=DC →;③若a =b ,b =c ,则a =c .其中所有正确命题的序号为________.解析:AB→=DC →,A ,B ,C ,D 四点可能在同一条直线上,故①不正确;在▱ABCD 中,|AB →|=|DC→|,AB →与DC →平行且方向相同,故AB →=DC →,故②正确;a =b ,则|a |=|b |,且a 与b 的方向相同;b =c ,则|b |=|c |,且b 与c 的方向相同,则a 与c 长度相等且方向相同,故a =c ,故③正确.答案:②③ 探究点2: 向量的表示例2:在如图所示的坐标纸上(每个小方格的边长为1),用直尺和圆规画出下列向量:(1)OA→,使|OA →|=42,点A 在点O 北偏东45°方向上; (2)AB→,使|AB →|=4,点B 在点A 正东方向上; (3)BC→,使|BC →|=6,点C 在点B 北偏东30°方向上. 解:(1)由于点A 在点O 北偏东45°方向上,所以在坐标纸上点A 距点O 的横向小方格数与纵向小方格数相等.又|OA→|=42,小方格的边长为1,所以点A 距点O 的横向小方格数与纵向小方格数都为4,于是点A 的位置可以确定,画出向量OA→,如图所示.(2)由于点B 在点A 正东方向上,且|AB →|=4,所以在坐标纸上点B 距点A 的横向小方格数为4,纵向小方格数为0,于是点B 的位置可以确定,画出向量AB→,如图所示.(3)由于点C 在点B 北偏东30°方向上,且|BC →|=6,依据勾股定理可得,在坐标纸上点C 距点B 的横向小方格数为3,纵向小方格数为33≈5.2,于是点C 的位置可以确定,画出向量BC→,如图所示.探究点3:共线向量与相等向量例3:如图所示,O 是正六边形ABCDEF 的中心,且OA →=a ,OB →=b ,在每两点所确定的向量中.(1)与a 的长度相等、方向相反的向量有哪些? (2)与a 共线的向量有哪些?解:(1)与a 的长度相等、方向相反的向量有OD→,BC →,AO →,FE →.(2)与a 共线的向量有EF →,BC →,OD →,FE →,CB →,DO →,AO →,DA →,AD →. 互动探究1.变条件、变问法:本例中若OC →=c ,其他条件不变,试分别写出与a ,b ,c 相等的向量.解:与a 相等的向量有EF →,DO →,CB →;与b 相等的向量有DC →,EO →,F A →;与c 相等的向量有FO→,ED →,AB →. 2.变问法:本例条件不变,与AD→共线的向量有哪些?解:与AD →共线的向量有EF →,BC →,OD →,FE →,CB →,DO →,AO →,DA →,OA →.三、学习小结1.向量的概念及表示(1)概念:既有大小又有方向的量. (2)有向线段①定义:具有方向的线段. ②三个要素:起点、方向、长度.③表示:在有向线段的终点处画上箭头表示它的方向.以A 为起点、B 为终点的有向线段记作AB→. ④长度:线段AB 的长度也叫做有向线段AB →的长度,记作|AB →|.(3)向量的表示■名师点拨(1)判断一个量是否为向量,就要看它是否具备大小和方向两个因素.(2)用有向线段表示向量时,要注意AB →的方向是由点A 指向点B ,点A 是向量的起点,点B 是向量的终点.2.向量的有关概念(1)向量的模(长度):向量AB →的大小,称为向量AB →的长度(或称模),记作|AB →|.(2)零向量:长度为0的向量,记作0. (3)单位向量:长度等于1个单位长度的向量. 3.两个向量间的关系(1)平行向量:方向相同或相反的非零向量,也叫做共线向量.若a ,b 是平行向量,记作a ∥b .规定:零向量与任意向量平行,即对任意向量a ,都有0∥a .(2)相等向量:长度相等且方向相同的向量,若a ,b 是相等向量,记作a =b . ■名师点拨(1)平行向量也称为共线向量,两个概念没有区别. (2)共线向量所在直线可以平行,与平面几何中的共线不同. (3)平行向量可以共线,与平面几何中的直线平行不同. 四、精炼反馈1.如图,在▱ABCD 中,点E ,F 分别是AB ,CD 的中点,图中与AE →平行的向量的个数为( )A .1B .2C .3D .4解析:选C.图中与AE→平行的向量为BE →,FD →,FC →共3个.2.下列结论中正确的是( ) ①若a ∥b 且|a |=|b |,则a =b ; ②若a =b ,则a ∥b 且|a |=|b |;③若a 与b 方向相同且|a |=|b |,则a =b ; ④若a ≠b ,则a 与b 方向相反且|a |≠|b |. A .①③ B .②③ C .③④D .②④解析:选B .两个向量相等需同向等长,反之也成立,故①错误,a ,b 可能反向;②③正确;④两向量不相等,可能是不同向或者长度不相等或者不同向且长度不相等.3.已知O 是正方形ABCD 对角线的交点,在以O ,A ,B ,C ,D 这5点中任意一点为起点,另一点为终点的所有向量中,写出:(1)与BC→相等的向量;(2)与OB→长度相等的向量;(3)与DA→共线的向量.解:画出图形,如图所示.(1)易知BC ∥AD ,BC =AD ,所以与BC→相等的向量为AD →.(2)由O 是正方形ABCD 对角线的交点知OB =OD =OA =OC ,所以与OB→长度相等的向量为BO →,OC →,CO →,OA →,AO →,OD →,DO →.(3)与DA→共线的向量为AD →,BC →,CB →.平面向量的应用【第一学时】学习重难点学习目标核心素养向量在平面几何中的应用会用向量方法解决平面几何中的平行、垂直、长度、夹角等问题数学建模、逻辑推理向量在物理中的应用会用向量方法解决物理中的速度、力学问题数学建模、数学运算【学习过程】一、问题导学预习教材内容,思考以下问题:1.利用向量可以解决哪些常见的几何问题?2.如何用向量方法解决物理问题? 二、合作探究探究点1:向量在几何中的应用角度一:平面几何中的垂直问题如图所示,在正方形ABCD 中,E ,F 分别是AB ,BC 的中点,求证:AF ⊥DE .证明:法一:设AD→=a ,AB →=b ,则|a |=|b |,a·b =0, 又DE→=DA →+AE →=-a +12b ,AF →=AB →+BF →=b +12a , 所以AF →·DE →=⎝ ⎛⎭⎪⎫b +12a ·⎝ ⎛⎭⎪⎫-a +12b =-12a 2-34a ·b +12b 2=-12|a |2+12|b |2=0.故AF→⊥DE →,即AF ⊥DE . 法二:如图,建立平面直角坐标系,设正方形的边长为2,则A (0,0),D (0,2),E (1,0),F (2,1),AF →=(2,1),DE →=(1,-2).因为AF→·DE →=(2,1)·(1,-2)=2-2=0, 所以AF→⊥DE →,即AF ⊥DE . 角度二:平面几何中的平行(或共线)问题如图,点O 是平行四边形ABCD 的中心,E ,F 分别在边CD ,AB 上,且CE ED =AFFB=12.求证:点E ,O ,F 在同一直线上.证明:设AB→=m ,AD →=n ,由CE ED =AF FB =12,知E ,F 分别是CD ,AB 的三等分点, 所以FO →=F A →+AO→=13BA →+12AC → =-13m +12(m +n )=16m +12n , OE→=OC →+CE →=12AC →+13CD → =12(m +n )-13m =16m +12n .所以FO→=OE →. 又O 为FO→和OE →的公共点,故点E ,O ,F 在同一直线上.角度三:平面几何中的长度问题如图,平行四边形ABCD 中,已知AD =1,AB =2,对角线BD =2,求对角线AC的长.解:设AD→=a ,AB →=b ,则BD →=a -b ,AC →=a +b ,而|BD→|=|a -b |=a 2-2a ·b +b 2=1+4-2a ·b =5-2a ·b =2, 所以5-2a ·b =4,所以a ·b =12,又|AC →|2=|a +b |2=a 2+2a ·b +b 2=1+4+2a ·b =6,所以|AC →|=6,即AC =6.探究点2:向量在物理中的应用(1)在长江南岸某渡口处,江水以12.5 km/h 的速度向东流,渡船的速度为25km/h .渡船要垂直地渡过长江,其航向应如何确定?(2)已知两恒力F 1=(3,4),F 2=(6,-5)作用于同一质点,使之由点A (20,15)移动到点B (7,0),求F 1,F 2分别对质点所做的功.解:(1)如图,设AB →表示水流的速度,AD →表示渡船的速度,AC →表示渡船实际垂直过江的速度.因为AB→+AD →=AC →,所以四边形ABCD 为平行四边形. 在Rt △ACD 中,∠ACD =90°,|DC→|=|AB →|=12.5.|AD→|=25,所以∠CAD =30°,即渡船要垂直地渡过长江,其航向应为北偏西30°. (2)设物体在力F 作用下的位移为s ,则所做的功为W =F ·s .因为AB →=(7,0)-(20,15)=(-13,-15). 所以W 1=F 1·AB→=(3,4)·(-13,-15) =3×(-13)+4×(-15)=-99(焦),W 2=F 2·AB→=(6,-5)·(-13,-15)=6×(-13)+(-5)×(-15)=-3(焦). 三、学习小结1.用向量方法解决平面几何问题的“三个步骤”2.向量在物理学中的应用(1)由于物理学中的力、速度、位移都是矢量,它们的分解与合成与向量的减法和加法相似,可以用向量的知识来解决.(2)物理学中的功是一个标量,即为力F 与位移s 的数量积,即W =F·s =|F ||s |cos θ(θ为F 与s 的夹角). 四、精炼反馈1.河水的流速为2 m/s ,一艘小船以垂直于河岸方向10 m/s 的速度驶向对岸,则小船在静水中的速度大小为( )A .10 m/sB .226 m/sC .4 6 m/sD .12 m/s解析:选B .由题意知|v 水|=2 m/s ,|v 船|=10 m/s ,作出示意图如图. 所以小船在静水中的速度大小 |v |=102+22=226(m/s ).2.已知三个力f 1=(-2,-1),f 2=(-3,2),f 3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,再加上一个力f 4,则f 4=( )A .(-1,-2)B .(1,-2)C .(-1,2)D .(1,2)解析:选D .由物理知识知f 1+f 2+f 3+f 4=0,故f 4=-(f 1+f 2+f 3)=(1,2). 3.设P ,Q 分别是梯形ABCD 的对角线AC 与BD 的中点,AB ∥DC ,试用向量证明:PQ ∥AB .证明:设DC →=λAB →(λ>0且λ≠1),因为PQ →=AQ →-AP →=AB →+BQ →-AP →=AB →+12(BD→-AC →) =AB→+12[(AD →-AB →)-(AD →+DC →)] =AB→+12(CD →-AB →) =12(CD →+AB →)=12(-λ+1)AB→, 所以PQ →∥AB →,又P ,Q ,A ,B 四点不共线,所以PQ ∥AB .【学习过程】一、问题导学预习教材内容,思考以下问题: 1.余弦定理的内容是什么?2.余弦定理有哪些推论?二、合作探究探究点1:已知两边及一角解三角形(1)(2018·高考全国卷Ⅱ)在△ABC 中,cos C 2=55,BC =1,AC =5,则AB =( ) A .42 B .30 C .29D .25(2)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a =5,c =2,cos A =23,则b =( )A .2B .3C .2D .3 解析:(1)因为cos C =2cos 2 C 2-1=2×15-1=-35,所以由余弦定理,得AB 2=AC 2+BC 2-2AC ·BC cos C =25+1-2×5×1×⎝ ⎛⎭⎪⎫-35=32,所以AB =42,故选A .(2)由余弦定理得5=22+b 2-2×2b cos A ,因为cos A =23,所以3b 2-8b -3=0,所以b =3⎝ ⎛⎭⎪⎫b =-13舍去.故选D .答案:(1)A (2)D 互动探究:变条件:将本例(2)中的条件“a =5,c =2,cos A =23”改为“a =2,c =23,cos A =32”,求b 为何值?解:由余弦定理得: a 2=b 2+c 2-2bc cos A ,所以22=b 2+(23)2-2×b ×23×32, 即b 2-6b +8=0,解得b =2或b =4. 探究点2:已知三边(三边关系)解三角形(1)在△ABC 中,已知a =3,b =5,c =19,则最大角与最小角的和为( ) A .90°B .120°C .135°D .150°(2)在△ABC 中,若(a +c )(a -c )=b (b -c ),则A 等于( ) A .90° B .60° C .120°D .150°解析:(1)在△ABC 中,因为a =3,b =5,c =19,所以最大角为B ,最小角为A ,所以cos C =a 2+b 2-c 22ab =9+25-192×3×5=12,所以C =60°,所以A +B =120°,所以△ABC 中的最大角与最小角的和为120°.故选B .(2)因为(a +c )(a -c )=b (b -c ),所以b 2+c 2-a 2=bc ,所以cos A =b 2+c 2-a 22bc =12.因为A ∈(0°,180°),所以A =60°.答案:(1)B (2)B 探究点3: 判断三角形的形状在△ABC 中,若b 2sin 2C +c 2sin 2B =2bc cos B cos C ,试判断△ABC 的形状.解:将已知等式变形为b 2(1-cos 2C )+c 2(1-cos 2B )=2bc cos B cos C . 由余弦定理并整理,得b 2+c 2-b 2⎝⎛⎭⎪⎫a 2+b 2-c 22ab 2-c 2⎝ ⎛⎭⎪⎫a 2+c 2-b 22ac 2 =2bc ×a 2+c 2-b 22ac ×a 2+b 2-c22ab ,所以b 2+c 2=[(a 2+b 2-c 2)+(a 2+c 2-b 2)]24a 2=4a 44a 2=a 2.所以A =90°.所以△ABC 是直角三角形. 三、学习小结2.余弦定理的推论cos A=b2+c2-a22bc;cos B=a2+c2-b22ac;cos C=a2+b2-c22ab.3.三角形的元素与解三角形(1)三角形的元素三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.(2)解三角形已知三角形的几个元素求其他元素的过程叫做解三角形.四、精炼反馈1.在△ABC中,已知a=5,b=7,c=8,则A+C=()A.90°B.120°C.135°D.150°解析:选B.cos B=a2+c2-b22ac=25+64-492×5×8=12.所以B=60°,所以A+C=120°.2.在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A等于()A.30°B.60°C.120°D.150°解析:选B.因为(b+c)2-a2=b2+c2+2bc-a2=3bc,所以b2+c2-a2=bc,所以cos A=b2+c2-a22bc=12,所以A=60°.3.若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2-c2=4,且C=60°,则ab =________.解析:因为C=60°,所以c2=a2+b2-2ab cos 60°,即c2=a2+b2-ab.①又因为(a +b )2-c 2=4, 所以c 2=a 2+b 2+2ab -4.②由①②知-ab =2ab -4,所以ab =43. 答案:434.在△ABC 中,a cos A +b cos B =c cos C ,试判断△ABC 的形状.解:由余弦定理知cos A =b 2+c 2-a 22bc ,cos B =c 2+a 2-b 22ca,cos C =a 2+b 2-c 22ab ,代入已知条件得a ·b 2+c 2-a 22bc +b ·c 2+a 2-b 22ca+c ·c 2-a 2-b 22ab =0,通分得a 2(b 2+c 2-a 2)+b 2(a 2+c 2-b 2)+c 2(c 2-a 2-b 2)=0, 展开整理得(a 2-b 2)2=c 4.所以a 2-b 2=±c 2,即a 2=b 2+c 2或b 2=a 2+c 2. 根据勾股定理知△ABC 是直角三角形.【学习过程】一、问题导学预习教材内容,思考以下问题:1.在直角三角形中,边与角之间的关系是什么?2.正弦定理的内容是什么?二、合作探究探究点1:已知两角及一边解三角形在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.解:因为A=45°,C=30°,所以B=180°-(A+C)=105°.由asin A=csin C得a=c sin Asin C=10×sin 45°sin 30°=102.因为sin 75°=sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=2+64,所以b=c sin Bsin C=10×sin(A+C)sin 30°=20×2+64=52+56.探究点2:已知两边及其中一边的对角解三角形已知△ABC中的下列条件,解三角形:(1)a=10,b=20,A=60°;(2)a=2,c=6,C=π3.解:(1)因为bsin B=asin A,所以sin B=b sin Aa=20sin 60°10=3>1,所以三角形无解.(2)因为asin A=csin C,所以sin A=a sin Cc=22.因为c>a,所以C>A.所以A=π4.所以B=5π12,b=c sin Bsin C=6·sin5π12sinπ3=3+1.互动探究:变条件:若本例(2)中C=π3改为A=π4,其他条件不变,求C,B,b.解:因为asin A=csin C,所以sin C=c sin Aa=32.所以C=π3或2π3.当C=π3时,B=5π12,b=a sin Bsin A=3+1.当C=2π3时,B=π12,b=a sin Bsin A=3-1.探究点3:判断三角形的形状已知在△ABC中,角A,B所对的边分别是a和b,若a cos B=b cos A,则△ABC一定是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形解析:由正弦定理得:a cos B=b cos A⇒sin A cos B=sin B cos A⇒sin(A-B)=0,由于-π<A-B<π,故必有A-B=0,A=B,即△ABC为等腰三角形.答案:A变条件:若把本例条件变为“b sin B=c sin C”,试判断△ABC的形状.解:由b sin B=c sin C可得sin2B=sin2C,因为三角形内角和为180°,所以sin B=sin C.所以B=C.故△ABC为等腰三角形.三、学习小结1.正弦定理2.正弦定理的变形若R为△ABC外接圆的半径,则(1)a=2R sin A,b=2R sin B,c=2R sin C;(2)sin A=a2R,sin B=b2R,sin C=c2R;(3)sin A∶sin B∶sin C=a∶b∶c;(4)a+b+csin A+sin B+sin C=2R.四、精炼反馈1.(2019·辽宁沈阳铁路实验中学期中考试)在△ABC中,AB=2,AC=3,B=60°,则cos C=()A.33B.63C.32D.62解析:选B.由正弦定理,得ABsin C=ACsin B,即2sin C=3sin 60°,解得sin C=33.因为AB<AC,所以C<B,所以cos C=1-sin2C=6 3.2.在△ABC中,角A,B,C的对边分别为a,b,c,且A∶B∶C=1∶2∶3,则a∶b∶c =()A.1∶2∶3B.3∶2∶1C.2∶3∶1D.1∶3∶2解析:选D.在△ABC中,因为A∶B∶C=1∶2∶3,所以B=2A,C=3A,又A+B+C =180°,所以A=30°,B=60°,C=90°,所以a∶b∶c=sin A∶sin B∶sin C=sin 30°∶sin 60°∶sin 90°=1∶3∶2.3.在△ABC中,角A,B,C的对边分别是a,b,c,若c-a cos B=(2a-b)cos A,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形解析:选D.已知c-a cos B=(2a-b)cos A,由正弦定理得sin C-sin A cos B=2sin A cos A-sin B cos A,所以sin(A+B)-sin A cos B=2sin A cos A-sin B cos A,化简得cos A(sin B-sin A)=0,所以cos A=0或sin B-sin A=0,则A=90°或A=B,故△ABC为等腰三角形或直角三角形.【学习过程】一、问题导学预习教材内容,思考以下问题:1.什么是基线?2.基线的长度与测量的精确度有什么关系?3.利用正、余弦定理可解决哪些实际问题?二、合作探究探究点1:测量距离问题海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B岛与C岛间的距离是________.解析:如图,在△ABC中,∠C=180°-(∠B+∠A)=45°,由正弦定理,可得BCsin 60°=ABsin 45°,所以BC=32×10=56(海里).答案:56海里互动探究:变条件:在本例中,若“从B岛望C岛和A岛成75°的视角”改为“A,C两岛相距20海里”,其他条件不变,又如何求B岛与C岛间的距离呢?解:由已知在△ABC中,AB=10,AC=20,∠BAC=60°,即已知两边和两边的夹角,利用余弦定理求解即可.BC2=AB2+AC2-2AB·AC·cos 60°=102+202-2×10×20×12=300.故BC=103.即B,C间的距离为103海里.探究点2测量高度问题如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D 在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.解析:由题意,在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,故∠ACB=45°.又AB=600 m,故由正弦定理得600sin 45°=BCsin 30°,解得BC=300 2 m.在Rt△BCD中,CD=BC·tan 30°=3002×33=1006(m).答案:1006互动探究:变问法:在本例条件下,汽车在沿直线AB方向行驶的过程中,若测得观察山顶D点的最大仰角为α,求tan α的值.解:如图,过点C,作CE⊥AB,垂足为E,则∠DEC=α,由例题可知,∠CBE=75°,BC=3002,所以CE=BC·sin∠CBE=3002sin 75°=3002×2+6 4=150+1503.所以tan α=DCCE=1006150+1503=32-63.探究点3:测量角度问题岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行(如图所示),观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时103海里的速度前往拦截.(1)问:海监船接到通知时,在距离岛A多少海里处?(2)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.解:(1)根据题意得∠BAC=45°,∠ABC=75°,BC=10,所以∠ACB=180°-75°-45°=60°,在△ABC中,由ABsin∠ACB=BCsin∠BAC,得AB=BC sin∠ACBsin∠BAC=10sin 60°sin 45°=10×3222=56.所以海监船接到通知时,在距离岛A 5 6 海里处.(2)设海监船航行时间为t小时,则BD=103t,CD=10t,又因为∠BCD=180°-∠ACB=180°-60°=120°,所以BD2=BC2+CD2-2BC·CD cos 120°,所以300t 2=100+100t 2-2×10×10t ·⎝ ⎛⎭⎪⎫-12,所以2t 2-t -1=0,解得t =1或t =-12(舍去). 所以CD =10,所以BC =CD ,所以∠CBD =12(180°-120°)=30°, 所以∠ABD =75°+30°=105°.所以海监船沿方位角105°航行,航行时间为1个小时. (或海监船沿南偏东75°方向航行,航行时间为1个小时) 三、学习小结1.基线在测量过程中,我们把根据测量的需要而确定的线段叫做基线. 2.基线与测量精确度的关系一般来说,基线越长,测量的精确度越高. 图示南偏西60°(指以正南方向为始边,转向目标方向线形成的角)四、精炼反馈1.若P 在Q 的北偏东44°50′方向上,则Q 在P 的( ) A .东偏北45°10′方向上 B .东偏北45°50′方向上 C .南偏西44°50′方向上D .西偏南45°50′方向上解析:选C.如图所示.2.如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于()A.1002米B.50(3+1)米C.100(3+1)米D.200米解析:选C.设AB=x米,在Rt△ACB中,∠ACB=45°,所以BC=AB=x.在Rt△ABD中,∠D=30°,则BD=3AB=3x.因为BD-BC=CD,所以3x-x=200,解得x=100(3+1).故选C.3.已知台风中心位于城市A东偏北α(α为锐角)度的150公里处,以v公里/小时沿正西方向快速移动,2.5小时后到达距城市A西偏北β(β为锐角)度的200公里处,若cos α=34cos β,则v=()A.60B.80C.100D.125解析:选C.画出图象如图所示,由余弦定理得(2.5v)2=2002+1502+2×200×150cos(α+β)①,由正弦定理得150sin β=200sin α,所以sin α=43sin β.又cos α=34cos β,sin2α+cos2α=1,解得sin β=35,故cos β=45,sin α=45,cos α=35,故cos(α+β)=1225-1225=0,代入①解得v=100.4.某巡逻艇在A处发现在北偏东45°距A处8海里处有一走私船,正沿南偏东75°的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以123海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇的航行方向.解:设经过t 小时在点C 处刚好追上走私船,依题意:AC =123t ,BC =12t ,∠ABC =120°,在△ABC 中,由正弦定理得123tsin 120°=12tsin ∠BAC,所以sin ∠BAC =12,所以∠BAC =30°,所以AB =BC =8=12t ,解得t =23,航行的方向为北偏东75°.即巡逻艇最少经过23小时可追到走私船,沿北偏东75°的方向航行.平面向量的运算【第一课时】向量的加法运算【学习重难点】【学习目标】【核心素养】平面向量加法的几何意义理解向量加法的概念以及向量加法的几何意义数学抽象、直观想象平行四边形法则 和三角形法则掌握向量加法的平行四边形法则和三角形法则, 会用它们解决实际问题 数学抽象、直观想象平面向量加法的运算律 掌握向量加法的交换律和结合律,会用它们进行计算数学抽象、数学运算【学习过程】一、问题导学预习教材内容,思考以下问题:1.在求两向量和的运算时,通常使用哪两个法则?2.向量加法的运算律有哪两个?二、新知探究探究点1:平面向量的加法及其几何意义例1:如图,已知向量a ,b ,c ,求作和向量a +b +c .解:法一:可先作a +c ,再作(a +c )+b ,即a +b +c .如图,首先在平面内任取一点O ,作向量OA→=a ,接着作向量AB →=c ,则得向量OB→=a +c ,然后作向量BC →=b ,则向量OC→=a +b +c 为所求.法二:三个向量不共线,用平行四边形法则来作.如图,(1)在平面内任取一点O ,作OA →=a ,OB →=b ;(2)作平行四边形AOBC ,则OC→=a +b ;(3)再作向量OD→=c ;(4)作平行四边形CODE , 则OE→=OC →+c =a +b +c .OE →即为所求.探究点2:平面向量的加法运算 例2:化简:(1)BC→+AB →; (2)DB→+CD →+BC →; (3)AB →+DF →+CD →+BC →+F A →.解:(1)BC→+AB →=AB →+BC →=AC →.(2)DB→+CD →+BC → =BC→+CD →+DB → =(BC→+CD →)+DB → =BD→+DB →=0. (3)AB →+DF →+CD →+BC →+F A → =AB →+BC →+CD →+DF →+F A → =AC →+CD →+DF →+F A → =AD →+DF →+F A →=AF →+F A →=0. 探究点3:向量加法的实际应用例3:某人在静水中游泳,速度为43千米/小时,他在水流速度为4千米/小时的河中游泳.若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度大小为多少?解:如图,设此人游泳的速度为OB→,水流的速度为OA →,以OA →,OB →为邻边作▱OACB ,则此人的实际速度为OA→+OB →=OC →.由勾股定理知|OC→|=8,且在Rt △ACO 中,∠COA =60°,故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8千米/小时. 三、学习小结即a +b =AB+BC =AC对角线OC就是a 与b 的和2.|a +b |,|a |,|b |之间的关系一般地,|a +b |≤|a |+|b |,当且仅当a ,b 方向相同时等号成立. 四、精炼反馈1.化简OP→+PQ →+PS →+SP →的结果等于( )A .QP →B .OQ →C .SP →D .SQ→ 解析:选B .OP→+PQ →+PS →+SP →=OQ →+0=OQ →.2.在四边形ABCD 中,AC →=AB →+AD →,则一定有( )A .四边形ABCD 是矩形B .四边形ABCD 是菱形C .四边形ABCD 是正方形D .四边形ABCD 是平行四边形解析:选D .由AC→=AB →+AD →得AD →=BC →,即AD =BC ,且AD ∥BC ,所以四边形ABCD的一组对边平行且相等,故为平行四边形.3.已知非零向量a ,b ,|a |=8,|b |=5,则|a +b |的最大值为______. 解析:|a +b |≤|a |+|b |,所以|a +b |的最大值为13. 答案:134.已知▱ABCD ,O 是两条对角线的交点,E 是CD 的一个三等分点(靠近D 点),求作:(1)AO→+AC →; (2)DE→+BA →.解:(1)延长AC ,在延长线上截取CF =AO ,则向量AF→为所求.(2)在AB 上取点G ,使AG =13AB , 则向量BG→为所求.【第二课时】【学习过程】一、问题导入预习教材内容,思考以下问题: 1.a 的相反向量是什么?2.向量减法的几何意义是什么? 二、新知探究探究点1: 向量的减法运算例1:化简下列各式:(1)(AB →+MB →)+(-OB →-MO →); (2)AB →-AD →-DC →.解:(1)法一:原式=AB →+MB →+BO →+OM →=(AB →+BO →)+(OM →+MB →)=AO →+OB →=AB→. 法二:原式=AB →+MB →+BO →+OM →=AB →+(MB →+BO →)+OM →=AB →+MO →+OM →=AB →+0 =AB→. (2)法一:原式=DB→-DC →=CB →.法二:原式=AB →-(AD →+DC →)=AB →-AC →=CB →. 探究点2:向量的减法及其几何意义例2:如图,已知向量a ,b ,c 不共线,求作向量a +b -c .解:法一:如图①,在平面内任取一点O ,作OA →=a ,OB →=b ,OC →=c ,连接BC ,则CB→=b -c . 过点A 作AD 綊BC ,连接OD , 则AD→=b -c , 所以OD→=OA →+AD →=a +b -c . 法二:如图②,在平面内任取一点O ,作OA→=a ,AB →=b ,连接OB ,则OB →=a +b ,再作OC →=c ,连接CB ,则CB →=a +b -c .法三:如图③,在平面内任取一点O , 作OA→=a ,AB →=b ,连接OB , 则OB→=a +b ,再作CB →=c ,连接OC , 则OC→=a +b -c .探究点3:用已知向量表示其他向量例3:如图所示,四边形ACDE 是平行四边形,点B 是该平行四边形外一点,且AB →=a ,AC→=b ,AE →=c ,试用向量a ,b ,c 表示向量CD →,BC →,BD →.解:因为四边形ACDE 是平行四边形,所以CD→=AE →=c ,BC →=AC →-AB →=b -a , 故BD →=BC →+CD →=b -a +c . 三、学习小结1.相反向量(1)定义:与a 长度相等,方向相反的向量,叫做a 的相反向差,记作-a ,并且规定,零向量的相反向量仍是零向量.(2)结论①-(-a )=a ,a +(-a )=(-a )+a =0;②如果a 与b 互为相反向量,那么a =-b ,b =-a ,a +b =0. 2.向量的减法(1)向量a 加上b 的相反向量,叫做a 与b 的差,即a -b =a +(-b ).求两个向量差的运算叫做向量的减法.(2)作法:在平面内任取一点O ,作OA→=a ,OB →=b ,则向量BA →=a -b ,如图所示.(3)几何意义:a -b 可以表示为从向量b 的终点指向向量a 的终点的向量. 四、精炼反馈1.在△ABC 中,D 是BC 边上的一点,则AD→-AC →等于( )A .CB → B .BC → C .CD→ D .DC→ 解析:选C .在△ABC 中,D 是BC 边上一点,则由两个向量的减法的几何意义可得AD →-AC→=CD →. 2.化简:AB→-AC →+BD →-CD →+AD →=________.解析:原式=CB →+BD →+DC →+AD →=CD →+DC →+AD →=0+AD →=AD →.答案:AD→3.已知错误!=10,|错误!|=7,则|错误!|的取值范围为______.解析:因为CB →=AB →-AC →,所以|CB→|=|AB →-AC →|. 又错误!≤|错误!-错误!|≤|错误!|+|错误!|, 3≤|AB→-AC →|≤17, 所以3≤|CB →|≤17.答案:[3,17]4.若O 是△ABC 所在平面内一点,且满足|OB→-OC →|=|OB →-OA →+OC →-OA →|,试判断△ABC 的形状.解:因为OB→-OA →+OC →-OA →=AB →+AC →,OB →-OC →=CB →=AB →-AC →.又|OB→-OC →|=|OB →-OA →+OC →-OA →|, 所以|AB→+AC →|=|AB →-AC →|,所以以AB ,AC 为邻边的平行四边形的两条对角线的长度相等,所以该平行四边形为矩形,所以AB ⊥AC ,所以△ABC 是直角三角形.【第三课时】【学习过程】一、问题导学预习教材内容,思考以下问题:1.向量数乘的定义及其几何意义是什么?2.向量数乘运算满足哪三条运算律?3.向量共线定理是怎样表述的?4.向量的线性运算是指的哪三种运算? 二、新知探究探究1: 向量的线性运算 例1:(1)计算:①4(a +b )-3(a -b )-8a ;②(5a -4b +c )-2(3a -2b +c );③23⎣⎢⎡⎦⎥⎤(4a -3b )+13b -14(6a -7b ). (2)设向量a =3i +2j ,b =2i -j ,求⎝ ⎛⎭⎪⎫13a -b -⎝ ⎛⎭⎪⎫a -23b +(2b -a ).解:(1)①原式=4a +4b -3a +3b -8a =-7a +7b .②原式=5a -4b +c -6a +4b -2c =-a -c .③原式=23⎝ ⎛⎭⎪⎫4a -3b +13b -32a +74b=23⎝ ⎛⎭⎪⎫52a -1112b =53a -1118b .(2)原式=13a -b -a +23b +2b -a =⎝ ⎛⎭⎪⎫13-1-1a +⎝ ⎛⎭⎪⎫-1+23+2b =-53a +53b =-53(3i +2j )+53(2i -j )=⎝ ⎛⎭⎪⎫-5+103i +⎝ ⎛⎭⎪⎫-103-53j =-53i -5j . 探究点2:向量共线定理及其应用例2:已知非零向量e 1,e 2不共线.(1)如果AB →=e 1+e 2,BC →=2e 1+8e 2,CD →=3(e 1-e 2),求证:A 、B 、D 三点共线; (2)欲使k e 1+e 2和e 1+k e 2共线,试确定实数k 的值.解:(1)证明:因为AB →=e 1+e 2,BD →=BC →+CD →=2e 1+8e 2+3e 1-3e 2=5(e 1+e 2)=5AB→. 所以AB→,BD →共线,且有公共点B , 所以A 、B 、D 三点共线. (2)因为k e 1+e 2与e 1+k e 2共线, 所以存在实数λ,使k e 1+e 2=λ(e 1+k e 2), 则(k -λ)e 1=(λk -1)e 2,由于e 1与e 2不共线,只能有⎩⎨⎧k -λ=0,λk -1=0,所以k =±1. 探究点3:用已知向量表示其他向量例3:如图,ABCD 是一个梯形,AB →∥CD →且|AB →|=2|CD →|,M ,N 分别是DC ,AB 的中点,已知AB→=e 1,AD →=e 2,试用e 1,e 2表示下列向量.(1)AC→=________; (2)MN→=________.解析:因为AB→∥CD →,|AB →|=2|CD →|,所以AB→=2DC →,DC →=12AB →. (1)AC →=AD →+DC →=e 2+12e 1. (2)MN→=MD →+DA →+AN → =-12DC →-AD →+12AB →=-14e 1-e 2+12e 1=14e 1-e 2.答案:(1)e 2+12e 1(2)14e 1-e 2 互动探究变条件:在本例中,若条件改为BC →=e 1,AD →=e 2,试用e 1,e 2表示向量MN →.解:因为MN→=MD →+DA →+AN →,MN→=MC →+CB →+BN →, 所以2MN →=(MD →+MC →)+DA →+CB →+(AN →+BN →). 又因为M ,N 分别是DC ,AB 的中点,所以MD→+MC →=0,AN →+BN →=0. 所以2MN→=DA →+CB →, 所以MN →=12(-AD →-BC →)=-12e 2-12e 1. 三、学习小结1.向量的数乘的定义一般地,规定实数λ与向量a 的积是一个向量,这种运算叫做向量的数乘,记作λa ,它的长度与方向规定如下:(1)|λa |=|λ||a |.(2)当λ>0时,λa 的方向与a 的方向相同;当λ<0时,λa 的方向与a 的方向相反;当λ=0时,λa =0.2.向量数乘的运算律 设λ,μ为实数,那么: (1)λ(μa )=(λμ)a .(2)(λ+μ)a =λa +μa . (3)λ(a +b )=λa +λb . 3.向量的线性运算及向量共线定理(1)向量的加、减、数乘运算统称为向量的线性运算.对于任意向量a ,b ,以及任意实数λ,μ1,μ2,恒有λ(μ1a ±μ2b )=λμ1a ±λμ2b .(2)向量a (a ≠0)与b 共线的充要条件是:存在唯一一个实数λ,使b =λa . 四、精炼反馈 1.13⎣⎢⎡⎦⎥⎤12(2a +8b )-(4a -2b )等于( )A .2a -bB .2b -aC .b -aD .a -b解析:选B .原式=16(2a +8b )-13(4a -2b )=13a +43b -43a +23b =-a +2b . 2.若点O 为平行四边形ABCD 的中心,AB →=2e 1,BC →=3e 2,则32e 2-e 1=( ) A .BO→ B .AO→ C .CO→ D .DO→ 解析:选A .BD →=AD →-AB →=BC →-AB →=3e 2-2e 1,BO →=12BD →=32e 2-e 1.3.已知e 1,e 2是两个不共线的向量,若AB →=2e 1-8e 2,CB →=e 1+3e 2,CD →=2e 1-e 2,求证A ,B ,D 三点共线.证明:因为CB →=e 1+3e 2,CD →=2e 1-e 2,所以BD→=CD →-CB →=e 1-4e 2. 又AB →=2e 1-8e 2=2(e 1-4e 2),所以AB →=2BD →,所以AB →与BD →共线. 因为AB 与BD 有交点B ,所以A ,B ,D 三点共线.【第四课时】【学习过程】一、问题导学预习教材内容,思考以下问题: 1.什么是向量的夹角? 2.数量积的定义是什么? 3.投影向量的定义是什么? 4.向量数量积有哪些性质? 5.向量数量积的运算有哪些运算律? 二、新知探究探究点1:平面向量的数量积运算例1:(1)已知|a |=6,|b |=4,a 与b 的夹角为60°,求(a +2b )·(a +3b ).(2)如图,在▱ABCD 中,|AB →|=4,|AD →|=3,∠DAB =60°,求:①AD →·BC →;②AB →·DA →.解:(1)(a +2b )·(a +3b ) =a·a +5a·b +6b·b =|a |2+5a·b +6|b |2 =|a |2+5|a ||b |cos 60°+6|b |2=62+5×6×4×cos 60°+6×42=192.(2)①因为AD→∥BC →,且方向相同,所以AD→与BC →的夹角是0°, 所以AD→·BC →=|AD →||BC →|·cos 0°=3×3×1=9. ②因为AB→与AD →的夹角为60°,所以AB→与DA →的夹角为120°, 所以AB→·DA →=|AB →||DA →|·cos 120°=4×3×⎝ ⎛⎭⎪⎫-12=-6.互动探究:变问法:若本例(2)的条件不变,求AC→·BD →.解:因为AC→=AB →+AD →,BD →=AD →-AB →,所以AC →·BD →=(AB →+AD →)·(AD →-AB →) =AD →2-AB →2=9-16=-7. 探究点2: 向量模的有关计算例2:(1)已知平面向量a 与b 的夹角为60°,|a |=2,|b |=1,则|a +2b |=( ) A .3 B .23C .4D .12(2)向量a ,b 满足|a |=1,|a -b |=32,a 与b 的夹角为60°,则|b |=( )A .13B .12C .15D .14 解析:(1)|a +2b |=(a +2b )2=a 2+4a·b +4b 2 =|a |2+4|a ||b |cos 60°+4|b |2= 4+4×2×1×12+4=23.(2)由题意得|a -b |2=|a |2+|b |2-2|a ||b |·cos 60°=34,即1+|b |2-|b |=34,解得|b |=12. 答案:(1)B (2)B 探究点3: 向量的夹角与垂直命题角度一:求两向量的夹角例3:(1)已知|a |=6,|b |=4,(a +2b )·(a -3b )=-72,则a 与b 的夹角为________;(2)(2019·高考全国卷Ⅰ改编)已知非零向量a ,b 满足|a |=2|b |,且(a -b )⊥b ,则a 与b 的夹角为______.解析:(1)设a 与b 的夹角为θ,(a +2b )·(a -3b )=a ·a -3a ·b +2b ·a -6b ·b =|a |2-a ·b -6|b |2=|a |2-|a ||b |cos θ-6|b |2=62-6×4×cos θ-6×42=-72, 所以24cos θ=36+72-96=12,所以cos θ=12.又因为θ∈[]0,π,所以θ=π3.(2)设a 与b 的夹角为θ,由(a -b )⊥b ,得(a -b )·b =0,所以a ·b =b 2,所以cos θ=b 2|a ||b |.又因为|a |=2|b |,所以cos θ=|b |22|b |2=12.又因为θ∈[0,π],所以θ=π3.答案:(1)π3(2)π3命题角度二:证明两向量垂直例4:已知a ,b 是非零向量,当a +t b (t ∈R )的模取最小值时,求证:b ⊥(a +t b ).证明:因为|a +t b |=(a +t b )2=a 2+t 2b 2+2t a ·b =|b |2t 2+2a ·b t +|a |2,所以当t =-2a ·b 2|b |2=-a·b|b |2时,|a +t b |有最小值.此时b ·(a +t b )=b·a +t b 2=a·b +⎝ ⎛⎭⎪⎫-a·b |b |2·|b |2=a·b -a·b =0.所以b ⊥(a +t b ). 命题角度三:利用夹角和垂直求参数例5:(1)已知a ⊥b ,|a |=2,|b |=3且向量3a +2b 与k a -b 互相垂直,则k 的值为( )A .-32 B .32 C .±32D .1(2)已知a ,b ,c 为单位向量,且满足3a +λb +7c =0,a 与b 的夹角为π3,则实数λ=________.解析:(1)因为3a +2b 与k a -b 互相垂直, 所以(3a +2b )·(k a -b )=0, 所以3k a 2+(2k -3)a·b -2b 2=0. 因为a ⊥b ,所以a ·b =0, 又|a |=2,|b |=3, 所以12k -18=0,k =32.(2)由3a +λb +7c =0,可得7c =-(3a +λb ), 即49c 2=9a 2+λ2b 2+6λa ·b , 而a ,b ,c 为单位向量, 则a 2=b 2=c 2=1, 则49=9+λ2+6λcos π3,即λ2+3λ-40=0,解得λ=-8或λ=5. 答案:(1)B (2)-8或5 三、学习小结1.两向量的夹角(1)定义:已知两个非零向量a ,b ,O 是平面上的任意一点,作OA →=a ,OB →=b ,则∠AOB =θ(0≤θ≤π)叫做向量a 与b 的夹角.(2)特例:①当θ=0时,向量a 与b 同向;②当θ=π2时,向量a 与b 垂直,记作a ⊥b ; ③当θ=π时,向量a 与b 反向. 2.向量的数量积已知两个非零向量a 与b ,它们的夹角为θ,把数量|a ||b |cos__θ叫做向量a 与b 的数量积(或内积),记作a ·b ,即a ·b =|a ||b |cos__θ.规定零向量与任一向量的数量积为0. 3.投影向量如图(1),设a ,b 是两个非零向量,AB→=a ,CD →=b ,我们考虑如下变换:过AB →的起点A 和终点B ,分别作CD →所在直线的垂线,垂足分别为A 1,B 1,得到A 1B 1→,我们称上述变换为。
高一数学必修二2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质导学案(解析版)
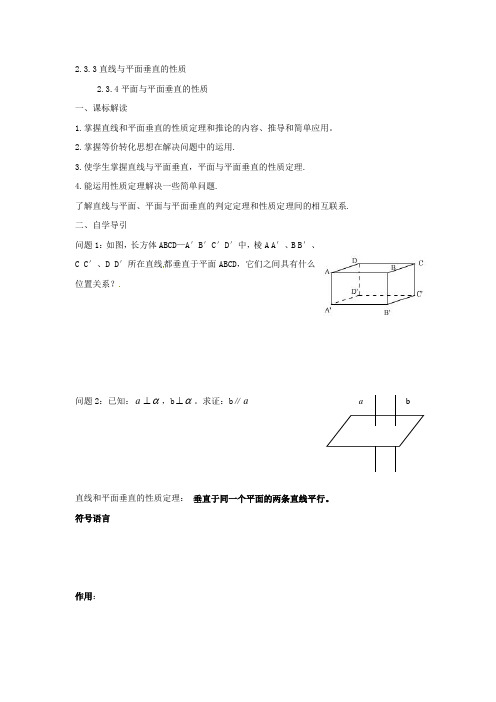
2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质一、课标解读1.掌握直线和平面垂直的性质定理和推论的内容、推导和简单应用。
2.掌握等价转化思想在解决问题中的运用.3.使学生掌握直线与平面垂直,平面与平面垂直的性质定理.4.能运用性质定理解决一些简单问题.了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系.二、自学导引问题1:如图,长方体ABCD —A ′B ′C ′D ′中,棱A A ′、B B ′、C C ′、D D ′所在直线都垂直于平面ABCD ,它们之间具有什么位置关系?问题2:已知:a α⊥,b α⊥。
求证:b ∥a直线和平面垂直的性质定理: 垂直于同一个平面的两条直线平行。
符号语言作用:a b问题3:黑板所在平面与地面所在平面垂直,你们能否在黑板上画一条直线与地面垂直呢?问题4:如图,长方体ABCD-A'B'C'D中,平面A'ADD’与平面ABCD垂直,直线A'A垂直于其交线AD,平面A'ADD’内的直线A'A与平面ABCD垂直吗?问题5:设α⊥β,α∩β=CD,A B α,AB⊥CD,AB∩CD=B,研究直线AB与平面β的位置关系。
归纳得到平面与平面垂直的性质定理:定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
想一想:用符号语言如何表述这个定理?三、典例精析例1 如图所示,正方体1111ABCD A B C D -中,D A AC EF 1及与异面直线都垂直相交. 求证:EF ∥1BD变式训练1 如图所示,已知SA 垂直于ABCD 所在平面,过A 且垂直于SC 的平面分别交 .,,,,G F E SD SC SB 于求证:SB AE ⊥例2 如图所示,平面⊥⊥PAC ABC PAB 平面平面,平面ABC ,⊥AE 平面PBC ,E 为垂足.(1) 求证:ABC PA 平面⊥(2) 当E 为PBC ∆的垂心时,求证:ABC ∆是直角三角形变式训练2 如图所示,是所在平面外一点,是四边形ABCD ABCD P60=∠DAB 且 边长ABCD PAD a 面垂直于底面为正三角形,其所在平的菱形,侧面. (1) 若PAD BG AD G 平面边的中点,求证:为⊥ (2) 求证:PB AD ⊥四、自主反馈 1.两异面直线在平面α内的射影( )A .相交直线B .平行直线C .一条直线—个点D .以上三种情况均有可能2.若两直线a 与b 异面,则过a 且与b 垂直的平面( )A .有且只有—个B .可能存在也可能不存在C .有无数多个D .—定不存在3.在空间,下列哪些命题是正确的( )①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行;④垂直于同—个平面的两条直线互相平行.A .仅②不正确B .仅①、④正确C .仅①正确D .四个命题都正确4.若平面α的斜线l 在α上的射影为l ′,直线b ∥α,且b ⊥l ′,则b 与l ( )A .必相交B .必为异面直线C .垂直D .无法确定5.下列命题①平面的每条斜线都垂直于这个平面内的无数条直线;②若一条直线垂直于平面的斜线,则此直线必垂直于斜线在此平面内的射影; ③若平面的两条斜线段相等,则它们在同一平面内的射影也相等;④若一条线段在平面外并且不垂直于这个平面,则它的射影长一定小于线段的长. 其中,正确的命题有( )A .1个B .2个C .3个 n 4个6.在下列四个命题中,假命题为( )A .如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直B .垂直于三角形两边的直线必垂直于第三边C .过点A 垂直于直线a 的所有直线都在过点A 垂直于a 的平面内D .如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面7.已知P 是四边形ABCD 所在平面外一点且P 在平面ABCD 内的射影在四边形ABCD 内,若P 到这四边形各边的距离相等,那么这个四边形是( )A .圆内接四边形B .矩形C .圆外切四边形D .平行四边形8.在△ABC 中,AB =AC =5,BC =6,P A ⊥平面ABC ,P A =8,则P 到BC 的距离等于( )A .5B .52C .35D .45答案2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质例1 证明:连接BD C B AB ,,11ABCD AC ABCD DD 平面平面⊂⊥,1D DD BD BD AC AC DD =⊥⊥∴11,, 又111,BD AC B BDD AC ⊥∴⊥∴平面C AB BD C B BD 1111,平面同理可证⊥∴⊥C BD A AD EF AC EF 11//,,又⊥⊥C AB EF C B EF 11,平面⊥∴⊥∴1//BD EF ∴例2 证明(1)在平面F AC DF D ABC 于作内取一点⊥,AC ABC PAC 且交线为平面平面,⊥AP DF PAC PA PAC DF ⊥∴⊂⊥∴,,平面平面AP DG G AB DG ⊥⊥同理可证于作,D DF DG ABC DF DG = 内,且都在平面,ABC PA 平面⊥∴(2)连接H PC BE 于并延长交BE PC PBC E ⊥∴∆的垂心,是又已知AE PC PBC AE ⊥∴的垂线,是平面AB PC ABE PC ⊥∴⊥∴,平面PAC AB AB PA ABC PA 平面平面又⊥∴⊥∴⊥,, 是直角三角形即ABC AC AB ∆⊥∴,变式训练1.SA BC ABCD BC ABCD SA ⊥∴⊂⊥,平面,平面证明:SAB SA SAB AB A SA AB AB BC 平面平面⊂⊂=⊥,,, BC AE SAB AE SAB BC ⊥∴⊂⊥∴,,平面平面 SC AE AEFG AE AEFG SC ⊥∴⊂⊥,,平面平面 SBC BC SBC SC C BC SC 平面平面又⊂⊂=,, SB AE SBC SB SBC AE ⊥∴⊂⊥∴,,平面平面2.略自主反馈1.D 2.B 3.B 4.C 5.A 6.A 7.C 8.D。
高一数学必修二2.3.1直线与平面垂直的判定2.3.2平面与平面垂直的判定导学案(解析版)

2.3.1直线与平面垂直的判定 2.3.2平面与平面垂直的判定一、课标解读(1)使学生掌握直线和平面垂直的定义及判定定理; (2)使学生掌握直线和平面所成角的概念(3)使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念;(4)使学生掌握两个平面垂直的判定定理及其简单的应用;(5)培养学生的几何直观能力,使他们在直观感知,操作确认的基础上学会归纳、概括结论。
二、自学导引问题1:(1)请同学们观察图片,说出旗杆与地面、树干与地面的位置有什么关系?(2)请把自己的数学书打开直立在桌面上,观察书脊与桌面的位置有什么关系? (3)思考:一条直线与平面垂直时,这条直线与平面内的直线有什么样的位置关系?有什么生活实例能验证这一关系呢?直线与平面垂直的定义:用符号语言表示为:问题2:如图,请同学们拿出准备好的一块(任意)三角形的纸片,我们一起来做一个实验:过△ABC 的顶点A 翻折纸片,得到折痕AD ,将翻折后的纸片竖起放置在桌面上,(BD 、DC 与桌面接触).观察并思考:①折痕AD 与桌面垂直吗?DCBA②如何翻折才能使折痕AD 与桌面所在的平面垂直? 直线与平面垂直的判定定理:用符号语言表示为:问题3:直线与平面所成角的概念?问题4:怎样作出二面角的平面角?问题5:平面与平面垂直的定义?问题6:两个平面互相垂直的判定方法有哪些? 三、典例精析例1 已知两两垂直所在平面外一点,是PC PB PA ABC P ,,∆,H 是ABC ∆ 的垂心.求证:⊥PH 平面ABC变式训练1 如图所示,ABC PA O C O AB 平面上的一点,为圆的直径,为圆⊥, F CP AF E BP AE 于于⊥⊥,.求证:AEF BP 平面⊥例2 如图所示,已知 60,90=∠=∠=∠CSA BSA BSC ,又SC SB SA ==. 求证:平面SBC ABC 平面⊥变式训练2 如图所示,在四面体ABCD 中,AC CD CB AD AB a BD =====,2 =a ,求证:平面BCD ABD 平面⊥._ C例3 如图所示,已知的斜线,是平面内,在平面ααOA BOC ∠且AOCAOB ∠=∠=60,a OC OB OA ===,a BC 2=,求所成的角与平面αOA .变式训练3 如图所示,在矩形ABCD 中,3,33==BC AD ,沿着对角线BD 将BCD ∆折起,使点C 移到'C 点,且'C 点在平面ABD 上的射影O 恰在AB 上.(1)求证:D AC BC ''平面⊥(2)求直线AB 与平面D BC '所成角的正弦值四、自主反馈1. 如图BC 是Rt ⊿ABC 的斜边,过A 作⊿ABC 所在平面α 垂线AP ,连PB 、PC ,过A 作AD ⊥BC 于D ,连PD ,那么图中直角三角形的个数是 ( )A .4个B .6个C .7个D .8个2.下列说法正确的是 ( ) A .直线a 平行于平面M ,则a 平行于M 内的任意一条直线 B .直线a 与平面M 相交,则a 不平行于M 内的任意一条直线C .直线a 不垂直于平面M ,则a 不垂直于M 内的任意一条直线D .直线a 不垂直于平面M ,则过a 的平面不垂直于M3.直三棱柱ABC —A 1B 1C 1中,∠ACB =90°,AC =AA 1=a ,则点A 到平面A 1BC 的距离是 ( )A.aB. 2aC.22a D. 3a 4.已知PA 、PB 、PC 是从点P 发出的三条射线,每两条射线的夹角都是60︒,则直线PC 与平面PAB 所成的角的余弦值为 。
高一数学必修二2.1平面性质导学案(解析版)

2.1.1平面一、目标解读1.利用生活中的实物对平面进行描述;2.掌握平面的表示法及水平放置的直观图的画法;3.掌握平面的基本性质及性质的作用;4.培养空间想象能力。
二、自学导引问题1:生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象,你们能举出更多例子吗?问题2:你能描述一下平面的含义吗?问题3:平面的画法问题4:平面的表示问题5:如果直线l与平面α有一个公共点,直线l是否在平面α内?如果直线l与平面α有两个公共点呢?公理1:符号表示为:图形表示为:公理1的作用是什么?问题6:在平面中,两点确定一条直线.请大家想一想,在空间中,过三个点可以有几个平面?公理2:公理2的作用是什么?问题7:两条直线相交,有一个公共点,那么两个平面相交呢?公理3:符号表示:图形表示:公理3的作用是什么?三、合作探究经过两条平行直线,能否确定唯一一个平面?如果能,如何证明?经过一条直线和这条直线外的一点呢?经过两条相交直线呢?四、典例精析例1 判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.(1)平面α与平面β相交,它们只有有限个公共点. ( )(2)如果两个平面有三个不共线的公共点,那么这两个平面重合.( )(3)四边形是平面图形. ( )变式训练1:下列说法中正确的是________.(1)平行四边形是一个平面;(2) 任何一个平面图形都是一个平面; (3) 平静的太平洋面就是一个平面; (4) 圆和平行四边形都可以表示平面. 变式训练2:西瓜人人都喜欢吃,给你一个西瓜,只许切三刀,最多能切几块?请说出你的切法.例2 已知ABC ∆在平面α外,P AB =α ,R AC =α ,Q BC =α ,如图2.1-1所示.求证:P 、Q 、R 三点共线.例3 如图2.1-2所示,在四面体在的中点,、分别为中,F AB BCG E ABCD ,H 在32:::上,且==HA DH FC DF AD求证:交于一点、、BD GH EF变式训练3三个平面c =βαγβα 即两两相交于三条直线,,,,b a ==αγγβ ,,若直线.不平行和b a 求证:.,,三条直线必过同一点c b a 自主反馈1. 判断下列说法是否正确,说明理由:(1) 若一个平面长3m ,宽4m ,则面积等于122m ;(2) 若ABC ∆的两边,AB AC 在平面α内,则第三边BC 也在平面α内; (3) 对边相等的四边形是平行四边形;(4) 梯形ABCD 中的两条边在平面α内,那么它的另外两条边也在平面α内. 2. 若,l P αββ=∈且α∈P ,则_______P l .3.(1)3条直线两两相交可以确定_______ 个平面; (2)3条直线两两平行可以确定_______ 个平面.4.A B C ,,表示不同的点,, a l 表示不同的直线,, αβ表示不同的平面,下列推理中,不正确的是( ).A. ,,,A l A B l B l ααα∈∈∈∈⇒⊆B. ,,,A A B B AB αβαβαβ∈∈∈∈⇒=C. ,l A l A αα⊄∈⇒∉D. ,,,,,,,A B C A B C A B C αβαβ∈∈⇒且不共线与重合 5. 对于空间3条直线,有下列4个条件:① 3条直线两两相交且不共点;② 3条直线两两平行;③ 3条直线共点;④ 有两条直线平行,第3条直线和这两条直线都相交. 其中,使3条直线共面的条件有( ).A.1个B.2个C.3个D.4个6. 正方体1111ABCD A BC D -中,,,P Q R 分别是11,,AB AD B C 的中点.那么,正方体的过,,P Q R 的截面图形是( ).A. 三角形B. 四边形C. 五边形D. 六边形答案: 2.1 平面 例1 (4)正确 例2证明: ∵AB ∩平面α=P ∴P ∈AB P ∈平面α ∵AB ⊂平面ABC ∴P ∈平面ABC∴P ∈平面α∩平面ABC [意思是P 在平面α于平面ABC 的交线上] 同理R ∈平面α∩平面ABC ,Q ∈平面α∩平面ABC ∵两个相交平面只有一条交线 ∴P ,Q,R 三点共例3 证明:AC GE AB BC G E //,,∴的中点,分别为AC FH HA DH FC DF //32::∴==,:又四点共面故从而G H F E CE FH ,,,,//HD AH GB AG HD AH GB AG ::23:11:≠∴==∴,:,:BD EF BD GH 不平行,同理,不平行∴是一个梯形四边形不平行EFHG EF GH GE FH ∴∴≠,, 内内,又在平面点在平面交于一点和BCD ABD O O EF GH ∴,上在,即点在两个平面的交线上BD O O ∴交于一点直线BD GH EF ,,∴变式训练 1.最多能切八块2.证明:过ββββ⊂⊂⊂BC AC AB C B A ,,,,,则作一平面,,,,l G F E =∈∈∈∴βαβββ 设 ,,,,,G F E CA BC AB 相交于分别与α的交线上与必在βααααG F E G F E ,,,,,∴∈∈∈∴ 三点共线G F E ,,∴3.证明:γγγββα⊂⊂∴==b a a b ,,, 由于直线b a 与不平行,必相交b a ,∴ 设b P a P P b a ∈∈=,,则βααβ∈∈∴⊂⊂P P b a ,,,P c c P c 经过点即直线又,,∈∴=βα 相交于一点直线c b a ,,∴自主反馈答案1.(1)错误 (2)正确 (3)错误 (4)正确2.∈3.(1)1个或3个 (2)1个或3个4.C5.B 6,.D。
高一数学必修二2.1.2空间中直线与直线的位置关系导学案(解析版)

2.1.2空间中直线与直线的位置关系一、课标解读(1)了解空间中两条直线的位置关系;(2)理解异面直线的概念、画法,培养学生的空间想象能力;(3)理解并掌握公理4;(4)理解并掌握等角定理;(5)异面直线所成角的定义、范围及应用。
二、自学导引问题1、观察长方体模型,归纳空间中两条直线的关系:异面直线:1、定义2、异面直线的画法问题2:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。
在空间中,是否有类似的规律?公理4:问题3:思考教材P47的思考题,∠ADC与A'D'C'、∠ADC与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?等角定理:异面直线所成的角:三、合作探究1、如何理解异面直线的定义?2、求异面直线所成的角的步骤?四、典例精析例1 如图所示,已知E,F,G,H 分别为空间四边形ABCD 的边AB,BC,CD,DA 的中点,求证: (1)E,F,G,H 四点共面(2)若四边形EFGH 是矩形;求证:AC ⊥BD变式训练1.已知11111,D C B A ABCD E E -分别是正方体的棱11,D A AD 的中点,求证: E E 1‖B B 1例2 如图所示,在正方体1111D C B A ABCD -中,的中点分别是1111,,C B B A N M .问:(1)理由是否是异面直线?说明和CN AM (2)理由是否是异面直线?说明和11CC B D变式训练 2 如图所示,分别是是异面直线,F E b D C a B A b a ,,,,,,∈∈线段,的中点,和BD AC 的结论的位置关系,并证明你和、和判断b EF a EF .例3 如图所示,正方体1AC 中,的中点,、分别是1111,C B B A F E 求异面直线1DB 与EF 所成角的大小.变式训练3 正方体1111D C B A ABCD -,求所成的角与111D B B AABCDD 1C 1B 1 A 1MN五、自主反馈1、正方体的一条对角线与正方体的棱可以组成异面直线的对数是( ) A 、2对 B 、3对 C 、6对D 、12对2、过平面内一点与平面外一点的直线,和平面内不过该点的直线是( ) A 、平行线 B 、相交直线 C 、异面直线D 、互相垂直的相交直线 3、平面与平面相交,直线a,直线b,则这三个命题中,不正确的命题个数是( )①a 、b 必为异面直线 ②a 、b 必为平行直线③a 、b 必为相交直线 A 、0B 、1C 、2D 、34、在正方体ABCD —A 1B 1C 1D 1的面对角线中,与AD 1成60°角的有( ) A 、4条 B 、6条 C 、8条D 、10条5、异面直线a 、b 成60°角,直线c ⊥a ,则直线b 与c 所成的角的范围是( ) A 、[30°,90°]B 、[60°,90°]C 、[60°,120°]D 、[30°,120°]6、在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 和N 分别为A 1B 1和B1C1的中点,那么直线AM 与CN 所成角的余弦值是: A 、23 B 、1010C 、53 D 、54答案2.1.2 空间中直线与直线的位置关系 例1 证明:(1)在中ABD ∆,//,,BD EH AD AB H E ∴的中点,分别是 四点共面同理H G F E FG EH BD FG ,,,,//,//∴∴(2)由(1)知GH AC BD EH //,//同理,GH EH EFGH ⊥∴是矩形,四边形又BD AC ⊥∴例2 (1)不是异面直线,理由:111111//,,C A MN C B B A N M ∴的中点,分别是 C C A A C C D D D D A A 111111//,//,//=∴==而又 AC C A ACC A //1111∴∴是平行四边形四边形 在同一个平面内得到C N M A AC MN ,,,,//∴不是异面直线和CN AM ∴(2)是异面直线,证明略例3 解:连接1111,D B C A ,点,设它们相交于O 1111//,//,,C A EF D B OG OG G DD 则连接的中点取 所成的角或补角与为异面直线EF DB GOA 11∠∴ 111111,C A GO C A O GC GA ⊥∴=的中点,为 901所成的角为与异面直线EF DB ∴变式训练 1. 略2.证明:假设α共面,设为和a EFααα∈∴⊂⊂F E B A a EF ,,,,,则,,αα⊂⊂∴AE BF ,,BF D AE C ∈∈ 又共面,从而b a b D C ,,,αα∈∴∈∴假设不成立这与题设矛盾,∴∴EF与a是异面直线603.自主反馈答案1. C;2、C;3、D;4、C;5、A ;6、D。
湖北省荆州市沙市第五中学高中数学 2.1.1平面导学案 新人教版必修2

高中数学高一年级必修二第二章 第2.1.1节 :平面导学案A.学习目标1、知识与技能(1)利用生活中的实物对平面进行描述;(2)掌握平面的表示法及水平放置的直观图;(3)掌握平面的基本性质及作用;(4)培养学生的空间想象能力。
2、过程与方法(1)通过师生的共同讨论,使学生对平面有了感性认识;(2)让学生归纳整理本节所学知识。
3、情感与价值 使用学生认识到我们所处的世界是一个三维空间,进而增强了学习的兴趣。
B.学习重点、难点重点:1、平面的概念及表示;2、平面的基本性质,注意他们的条件、结论、作用、图形语言及符号语言。
难点:平面基本性质的掌握与运用。
C.学法指导 学生通过阅读教材,联系身边的实物思考、交流,师生共同讨论等,从而较好地完成本节课的教学目标。
D .知识链接实物引入、揭示课题E .自主学习 生活中常见的如黑板、平整的操场、桌面、平静的湖面等等,都给我们以平面的印象,你们能举出更多例子吗?引导学生观察、思考、举例和互相交流。
与此同时,教师对学生的活动给予评价。
F.合作探究1、平面含义 师:以上实物都给我们以平面的印象,几何里所说的平面,就是从这样的一些物体中抽象出来的,但是,几何里的平面是无限延展的。
2、平面的画法及表示师:在平面几何中,怎样画直线?(一学生上黑板画)之后教师加以肯定,解说、类比,将知识迁移,得出平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
如果几个平面画在一起,当一个平面的一部分被另一个平面遮住时,应画成虚线或不画(打出投影片)D C BA α课本P41 图 2.1-4 说明平面内有无数个点,平面可以看成点的集合。
点A 在平面α内,记作:A ∈α点B 在平面α外,记作:B α 2.1-43、平面的基本性质教师引导学生思考教材P41的思考题,让学生充分发表自己的见解。
人教版高中数学必修2第三章《直线的方程》导学案(无答案)

必修2人教版数学 高一第三章 直线的方程课程目标: 一、考点突破1. 理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式。
2. 能根据斜率判定两条直线平行或垂直。
3. 通过学习直线的倾斜角、斜率等概念,探索并掌握直线方程的几种形式:点斜式,斜截式,两点式,截距式等;通过理解、欣赏、运用直线方程各具特征的丰富多彩的不同形式,感觉数学世界的奇异美、简洁美、和谐美,增强美学意识。
通过对直线方程四种特殊形式和一般形式的分析和运用,体会形式和内容、对立和统一的辩证唯物主义思想。
4. 通过直线的方程,研究直线间的位置关系:平行和垂直,以及两条直线的交点坐标,点到直线的距离公式等。
理解事物之间相互联系、互相转化的辩证唯物主义思想。
二、重难点提示重点:直线的倾斜角和斜率概念,直线方程,两直线的位置关系及其应用。
难点:直线方程的应用。
精讲精练:微课程1:基本公式及直线的倾角和斜率【考点精讲】1. 数轴上两点间距离公式:()11x P ,()22x P 为数轴上两点,则2121x x P P-= 2. 平面上两点间距离:()111,y x P ,()222,y x P 为平面上两点,则12PP =3. 线段中点坐标公式:若点P 1、P 2的坐标分别为(x 1,y 1)、(x 2,y 2),且线段P 1P 2的中点M 的坐标为(x ,y ),则x=x 1+x 22,y=y 1+y 22,此公式为线段P 1P 2的中点坐标公式。
4. 直线的倾斜角与斜率 (1)直线的倾斜角①定义:当直线l 与x 轴相交时,我们取x 轴作为基准,x 轴正向与直线l 向上方向之间所成的角α叫做直线l 的倾斜角。
当直线l 与x 轴平行或重合时,规定它的倾斜角为0°。
①倾斜角的范围为[0°,180°)。
(2)直线的斜率①定义:一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k 表示,即k =tan α,倾斜角是90°的直线斜率不存在。
高一数学必修2第4章圆与方程的导学案

高一数学必修2导学案 主备人: 备课时间: 备课组长:圆的标准方程一、学习目标学问与技能:1、驾驭圆的标准方程,能依据圆心、半径写出圆的标准方程。
2、会用待定系数法求圆的标准方程。
过程与方法:进一步培育学生能用解析法探讨几何问题的实力,渗透数形结合思想,通过圆的标准方程解决实际问题的学习,留意培育学生视察问题、发觉问题和解决问题的实力。
情感看法与价值观:通过运用圆的学问解决实际问题的学习,从而激发学生学习数学的热忱和爱好。
二、学习重点、难点: 学习重点: 圆的标准方程学习难点: 会依据不同的已知条件,利用待定系数法求圆的标准方程。
三、运用说明及学法指导:1、先阅读教材118—120页,然后细致审题,细致思索、独立规范作答。
2、不会的,模棱两可的问题标记好。
3、对小班学生要求完成全部问题,试验班完成90℅以上,平行班完成80℅以上 四、学问链接: 1.两点间的距离公式?2.具有什么性质的点的轨迹称为圆?圆的定义?平面内与肯定点的距离等于定长的点的轨迹称为圆,定点是圆心,定长是半径. 五、学习过程:(自主探究)A 问题1阅读教材118页内容,回答问题已知在平面直角坐标系中,圆心A 的坐标用(a ,b )来表示,半径用r 来表示,则我们如何写出圆的方程?问题2圆的方程形式有什么特点?当圆心在原点时,圆的方程是什么?例1:1写出下列各圆的方程:(1)圆心在原点,半径是3; (2) 圆心在C(3,4),半径是5 (3)经过点P(5,1),圆心在点C(8,-3); 2、写出下列各圆的圆心坐标和半径:(1) (x -1)2 + y 2 = 6 (2) (x +1)2+(y -2)2= 9(3) 222()()x a y a ++=例2:写出圆心为(2,3)A -半径长等于5的圆的方程,推断12(5,7),(1)M M --是否在这个圆上。
问题3点M 0(x 0,y 0)在圆(x-a)2+(y-b)2=r 2上、内、外的条件是什么?例3△ABC 的三个顶点的坐标是(5,1),(7,3),(2,8),A B C --求它的外接圆的方程例4已知圆心为C 的圆经过点(1,1)A 和(2,2)B -,且圆心在:10l x y -+=上,求圆心为C 的圆的标准方程.注:比较例3、例4可得出△ABC 外接圆的标准方程的两种求法:1.依据题设条件,列出关于a b r 、、的方程组,解方程组得到a b r 、、得值,写出圆的标准方程.2.依据确定圆的要素,以及题设条件,分别求出圆心坐标和半径大小,然后再写出圆的标准方程. 六、达标检测1、已知两点P 1(4,9)和P 2(6,3),求以P 1P 2为直径的圆的方程,试推断点M(6,9)、N(3,3)、 Q(5,3)是在圆上,在圆内,还是在圆外?2、求圆心C 在直线 x+2y+4=0 上,且过两定点A(-1 , 1)、B(1,-1)的圆的方程。
高中数学(必修二)导学案

高中数学(必修二)导学案第一章:平面直角坐标系1.1 坐标系的引入- 了解平面直角坐标系的基本概念- 掌握点在平面直角坐标系中的坐标表示方法1.2 平面直角坐标系上的距离公式- 了解平面直角坐标系上两点之间距离的公式- 掌握如何使用距离公式计算两个点之间的距离1.3 直线的斜率- 了解直线斜率的概念及其计算方法- 掌握如何根据两点坐标计算直线的斜率第二章:二次函数2.1 二次函数的图像和性质- 了解二次函数的基本概念和特点- 掌握根据二次函数的参数确定二次函数图像的方法2.2 二次函数的最值和零点- 了解二次函数最值和零点的基本概念及其计算方法- 掌握如何根据二次函数求解实际问题2.3 二次函数与一次函数的比较- 了解二次函数和一次函数的基本概念及其图像特点- 掌握如何比较二次函数和一次函数的大小关系第三章:三角函数3.1 任意角及其测量- 了解任意角的基本概念及其测量方法- 掌握如何将任意角的三角函数转化为其它角度的三角函数3.2 常用角的三角函数值- 掌握常用角的三角函数值及其推导方法- 掌握如何根据三角函数值求解实际问题3.3 三角函数的图像和性质- 了解三角函数的图像及其性质- 掌握如何根据三角函数图像解决实际问题第四章:概率统计4.1 随机事件与概率- 掌握随机事件和概率的基本概念和运算法则- 掌握如何计算简单事件的概率4.2 条件概率和独立性- 了解条件概率和独立性的基本概念及其计算方法- 掌握如何根据条件概率和独立性计算事件的概率4.3 离散型随机变量及其分布律- 了解离散型随机变量及其分布律的概念- 掌握如何根据分布律计算离散型随机变量的期望值和方差以上是本章节的导学内容,希望同学们认真学习,做好课后习题。
祝学习愉快!。
人教版高一数学必修2全册导学案及答案

1.1.1棱柱、棱锥、棱台的结构特征
一、学习目标:
1、知识与技能:(1)能根据几何结构特征对空间物体进行分类。(2)会用语言概述棱柱、棱锥、棱台的结构特征。(3)会表示有关几何体以及柱、锥、台的分类。
2、过程与方法:(1)通过直观感受空间物体,概括出柱、锥、台的几何结构特征。(2)观察、讨论、归纳、概括所学的知识。
B例2.用斜二测画法画长、宽、高分别是4cm、3cm、2cm的长方体 的直观图。
B例3.课本P18图1.2-13,请说出三视图表示的几何体?并用斜二测画法画出它的直观图。
六、达标测试
A1、利用斜二测画法得到的下列结论正确的是 ( )
①三角形的直观图是三角形 ②平行四边形的直观图是平行四边形
③正方形的直观图是正方形 ④菱形的直观图是菱形
B问题3:什么是棱柱、锥、台?有何特征?如何表示?如何分类?
C问题4;探究一下各种四棱柱之间有何关系?
C问题5:质疑答辩,排难解惑
1.有两个面互相平行,其余各面都是平行四边形的几何体是不是棱柱?(举反例说明)
2.棱柱的任何两个平面都可以作为棱柱的底面吗?
A例1:如图,截面BCEF把长方体分割成两部分,这两部分是否是棱柱?
①点H与点C重合; ②点D与点M与点R重合;
③点B与点Q重合; ④点A与点S重合.
其中正确命题的序号是____.(注:把你认为正确的命题的序号都填上)
12、在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,如图,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为_____.
13、高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图象如图所示,那么水瓶的形状是______.
人教版高中数学必修二精讲练导学案7.3.1 复数的三角表示式(原卷版)

7.3.1复数的三角表示式导学案编写:XXX 初审:XXX 终审:XXX 廖云波【学习目标】1.知道复数的模和辐角的定义2.会求复数的模和辐角主值3.能求出复数的三角形式【自主学习】知识点1 复数的三角形式1.定义:r ( cos θ+isin θ)叫做复数z =a +b i 的三角表示式,简称三角形式.其中,r 是复数z 的模;θ是以x 轴的非负半轴为始边,向量OZ →所在射线( 射线OZ )为终边的角,叫做复数z =a +b i 的辐角.为了与三角形式区分开来,a +b i 叫做复数的代数表示式,简称代数形式.2.非零复数z 辐角θ的多值性以x 轴正半轴为始边,向量OZ →所在的射线为终边的角θ叫复数z =a +b i 的辐角,因此复数z 的辐角是θ+2k π( k ∈Z ) ( k ∈Z ).3.辐角主值( 1)表示法:用arg z 表示复数z 的辐角主值.( 2)定义:适合[0,2π)的角θ叫辐角主值.( 3)唯一性:复数z 的辐角主值是 的、 的.知识点2 复数的代数形式与三角形式的互化复数z =a +b i =r ( cos θ+isin θ)的两种表示式之间的关系为⎩⎨⎧ a= ,b = ,r =a 2+b 2.【合作探究】探究一代数形式与三角形式的转换【例1】下列各式是否是三角形式,若不是,化为三角形式:( 1)z1=-2( cosθ+isinθ); ( 2)z2=cosθ-isinθ.归纳总结:【练习1】下列各式是否是三角形式,若不是,化为三角形式:( 1)z3=-sinθ+icosθ; ( 2)z4=-sinθ-icosθ; ( 3)z5=cos60°+isin30°.探究二将复数的三角形式化为代数形式【例2】将复数⎪⎭⎫⎝⎛+32sin32cos23ππi化为代数形式为________.归纳总结:【练习2】复数⎪⎭⎫⎝⎛34sin-34cos6ππi的代数形式是.探究三复数的模与辐角主值【例3】求复数z=1+cosθ+isinθ( π<θ<2π)的模与辐角主值.归纳总结:【练习3】将z =1+itan θ1-itan θ( 114π<θ<3π)化为三角形式,并求其辐角主值.探究四 复数辐角的应用【例4】复数z 满足arg( z +3)=56π,求|z +6|+|z -3i|最小值.归纳总结:【练习4】已知|z -2i|≤1,求arg( z -4i)最大值.课后作业A 组 基础题一、选择题1.若复数z =( a +i)2的辐角主值是3π2,则实数a 的值是( )A .1B .-1C .-2D .-32.设π<θ<5π4,则复数cos2θ+isin2θcos θ-isin θ的辐角主值为( )A .2π-3θB .3θ-2πC .3θD .3θ-π3.设复数2-i 和3-i 的辐角主值分别为α,β,则α+β等于() A .135° B .315°C .675°D .585°4.复数z 满足1|1|=-Z Z ,复数z 的辐角为30°,复数z 的模为()A .1B .-1C .-2D .-35.复数sin 50°-isin 140°的辐角的主值是( )A .150°B .40°C .-40°D .320°6.若复数cos θ+isin θ和sin θ+icos θ相等,则θ的值为( )A .π4B .π4或5π4C .2k π+π4( k ∈Z ) D .k π+π4( k ∈Z )7.( 多选)复数z =3+3i 化为三角形式正确的是( )A .z =23( cos π6+isin π6) B .z =23( cos π6-isin π6) C .z =23( cos 76π+isin 7π6) D .z =23( cos 136π+isin 13π6)二、填空题8.复数1cos π3+isin π3的代数形式是 .9.已知复数z 满足z z -2i z =3-2a i( a ∈R ),且π2<arg z <π,则a 的取值范围为 .10.已知z =cos 2π3+isin 2π3,则arg z 2=________.三、参考解答题11.下列复数是不是三角形式?如果不是,把它们表示成三角形式. ( 1)⎪⎭⎫ ⎝⎛+54sin 54cos 2-ππi ; ( 2)sin 3π5+icos 3π5.12.已知复数z 满足等式|1|ZZ -=12,且arg z =π6,求z .B 组 能力提升一、选择题1.若复数z =( a +i)2的辐角的主值是3π2,则实数a 的值是( ) A .1 B .-1C .-2D .-32.设π<θ<5π4,则复数cos 2θ+isin 2θcos θ-isin θ的辐角的主值为( ) A .2π-3θB .3θ-2πC .3θD .3θ-π二、填空题3.已知复数z 的模为2,实部为3,则复数z 的代数形式和三角形式为 .三、参考解答题4.把下列复数转化为三角形式.( 1)-1;( 2)2i.5.设O为复平面的原点,A、B为单位圆上两点,A、B所对应的复数分别为z1、z2,z1、z2的辐角的主值分别为α、β.若△AOB的重心G对应的复数为13+115i,求tan( α+β).6.已知复数z1=3cosθ-isinθ,z2=sinθ-3icosθ,当θ∈[0,2π),求arg( z1-z2)的值.。
人教A版高中数学必修2第三章 直线与方程3.2 直线的方程导学案(4)

讲义:直线与方程内容讲解:1、直线的倾斜角和斜率:(1)设直线的倾斜角为α()0180α≤<,斜率为k ,则tan 2k παα⎛⎫=≠ ⎪⎝⎭.当2πα=时,斜率不存在.(2)当090α≤<时,0k ≥;当90180α<<时,0k <. (3)过111(,)P x y ,222(,)P x y 的直线斜率212121()y y k x x x x -=≠-.2、两直线的位置关系:两条直线111:l y k x b =+,222:l y k x b =+斜率都存在,则:(1)1l ∥2l ⇔12k k =且12b b ≠; (2)12121l l k k ⊥⇔⋅=-; (3)1l 与2l 重合⇔12k k =且12b b =3、直线方程的形式:(1)点斜式:()00y y k x x -=-(定点,斜率存在) (2)斜截式:y kx b =+(斜率存在,在y 轴上的截距)(3)两点式:1121212121(,)y y x x y y x x y y x x --=≠≠--(两点)(4)一般式:()2200x y C A B A +B += +≠(5)截距式:1x ya b+=(在x 轴上的截距,在y 轴上的截距)4、直线的交点坐标:设11112222:0,:0l A x B y c l A x B y c ++=++=,则: (1)1l 与2l 相交1122A B A B ⇔≠;(2)1l ∥2l 111222A B C A B C ⇔=≠;(3)1l 与2l 重合111222A B C A B C ⇔==. 5、两点111(,)P x y ,222(,)P x y间的距离公式12PP =原点()0,0O 与任一点(),x y P的距离OP =6、点000(,)P x y 到直线:0l x y C A +B +=的距离d =(1)点000(,)P x y 到直线:0l x C A +=的距离0Ax Cd A +=(2)点000(,)P x y 到直线:0l y C B +=的距离0By Cd B+=(3)点()0,0P 到直线:0l x y C A +B +=的距离d =7、两条平行直线10x y C A +B +=与20x y C A +B +=间的距离d =8、过直线1111:0l A x B y c ++=与2222:0l A x B y c ++=交点的直线方程为()111222()()0A x B y C A x B y c R λλ+++++=∈9、与直线:0l x y C A +B +=平行的直线方程为()0x y D C D A +B +=≠ 与直线:0l x y C A +B +=垂直的直线方程为0x y D B -A += 10、中心对称与轴对称:(1)中心对称:设点1122(,),(,)P x y E x y 关于点00(,)M x y 对称,则12012022x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩(2)轴对称:设1122(,),(,)P x y E x y 关于直线:0l x y C A +B +=对称,则: a 、0B =时,有122x x C A +=-且12y y =; b 、0A =时,有122y y CB+=-且12x x =c 、0A B ⋅≠时,有12121212022y y Bx x Ax x y y A B C -⎧=⎪-⎪⎨++⎪⋅+⋅+=⎪⎩典型例题例1. 已知直线(2m 2+m -3)x +(m 2-m)y =4m -1. ① 当m = 时,直线的倾斜角为45°.②当m = 时,直线在x 轴上的截距为1.③ 当m = 时,直线在y 轴上的截距为-23.④ 当m = 时,直线与x 轴平行.⑤当m = 时,直线过原点.变式训练1.(1)直线3y + 3 x +2=0的倾斜角是 ( )A .30° B .60° C .120° D .150°(2)设直线的斜率k=2,P 1(3,5),P 2(x 2,7),P (-1,y 3)是直线上的三点,则x 2,y 3依次是 ( )A .-3,4B .2,-3C .4,-3D .4,3(3)直线l 1与l 2关于x 轴对称,l 1的斜率是-7 ,则l 2的斜率是 ( )A .7 B.-7 C.7D .-7 (4)直线l 经过两点(1,-2),(-3,4),则该直线的方程是 .例2. 已知三点A (1,-1),B (3,3),C (4,5).求证:A 、B 、C 三点在同一条直线上.变式训练2. 设a ,b ,c 是互不相等的三个实数,如果A (a ,a 3)、B (b ,b 3)、C (c ,c 3)在同一直线上,求证:a+b+c=0.例3.直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为( ) (A)1133y x =-+ (B)113y x =-+ (C)33y x =- (D)113y x =+例4.(全国Ⅰ文)若直线m 被两平行线12:10:30l x y l x y -+=-+=与所截得的线段的长为22,则m 的倾斜角可以是①15 ②30 ③45 ④60 ⑤75其中正确答案的序号是 .(写出所有正确答案的序号)例5.已知三角形的顶点是A(-5,0)、B(3,-3)、C(0,2) ,求这个三角形三边所在的直线方程.例6.一条直线从点A(3,2)出发,经过x轴反射,通过点B(-1,6),求入射光线与反射光线所在的直线方程例7、已知点A(-3,5) 和B(2,15) , 在直线l:3x-4y+4=0上找一点P, 使|PA|+|PB|最小, 并求这个最小值.例8、在等腰直角三角形中,已知一条直角边所在直线的方程为2x-y=0,斜边的中点为A(4,2),求其它两边所在直线的方程.例9、求过点P(-5,-4)且与坐标轴围成的三角形面积为5的直线方程.例10、已知点A(2,5)与点B(4,-7),试在y轴上求一点P,使及PBPA+的值为最小.例11、过点A(0,1)做一直线l,使它夹在直线1l:x-3y+10=0和2l:2x+y-8=0间的线段被A点平分,试求直线l的方程.巩固训练1、直线(2m2-5m-3)x-(m2-9)y+4=0的倾斜角为π4,则m的值是()A、3B、2C、-2D、2与32、点(a,b)关于直线x+y=0对称的点是 ( )A、 (-a,-b) B 、 (a,-b) C、 (b,a) D、 (-b,-a)3、已知l 平行于直线3x+4y-5=0, 且l和两坐标轴在第一象限内所围成三角形面积是24,则直线l的方程是 ( )A、3x+4y-122=0B、 3x+4y+122=0C、 3x+4y-24=0D、3x+4y+24=04、若直线l经过点(1,1),且与两坐标轴所围成的三角形的面积为2,则直线l的条数为( )A、1B、2C、3D、45、已知菱形的三个顶点为(a,b )、(-b,a )、(0,0),那么这个菱形的第四个顶点为 ( )A 、(a -b,a +b)B 、(a +b, a -b)C 、(2a,0)D 、(0,2a)6、若点(4,a)到直线4x-3y=1的距离不大于3,则a 的取值范围是( )A 、[]010, B 、(0,10)C 、13313,⎡⎣⎢⎤⎦⎥ D 、(-∞,0] [10,+∞)7、过定点P(2,1)作直线l ,交x 轴和y 轴的正方向于A 、B ,使△ABC 的面积最小,那么l的方程为 ( )A 、x-2y-4=0B 、x-2y+4=0C 、2x-y+4=0D 、x+2y-4=08、若直线Ax +By +C=0与两坐标轴都相交,则有( )A 、A·B ≠0 B 、A ≠0或B ≠0C 、C ≠0D 、A 2+B 2=09、已知直线l 1:3x +4y=6和l 2:3x-4y=-6,则直线l 1和l 2的倾斜角是( )A 、互补B 、互余C 、相等D 、互为相反数10、直线(2m 2-5m-3)x-(m 2-9)y +4=0的倾斜角为π4,则m 的值是( )A 、3B 、2C 、-2D 、2与311、△ABC 的一个顶点是A(3,-1),∠B、∠C 的平分线分别是x=0,y=x ,则直线BC 的方程是 ( ) A 、y=2x+5 B 、y=2x+3 C 、y=3x+5 D 、y=-252x + 12、直线kx -y=k -1与ky -x=2k 的交点位于第二象限,那么k 的取值范围是( )A 、k >1B 、0<k <21C 、k <21D 、21<k <113、直线(m+2)x+m y m m 2)32(2=--在x 轴上的截距是3,则实数m 的值是( )A 、52B 、6C 、- 52D 、-614、若平行四边形三个顶点的坐标为(1,0),(5,8),(7,-4),则第四个顶点坐标为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【12份】人教版高一数学必修二导学案目录1.1空间几何体的结构 (2)1.2空间几何体的三视图和直观图 (17)1.3空间几何体的表面积与体积 (31)2.1空间点、直线、平面之间的位置关系 (49)2.2直线、平面平行的判定及其性质 (69)2.3 直线、平面垂直的判定及其性质 (85)§3.1.1直线的倾斜角与斜率 (99)3. 2. 1直线的点斜式方程 (109)3.3.1两条直线的交点坐标 (123)4.1.1圆的标准方程 (136)4.2.1直线与圆的位置关系 (146)4.3.1空间直角坐标系&4.3.2空间两点间的距离公式 (156)第一章、空间几何体本章概述几何学是研究现实世界中物体的形状、大小与位置关系的数学学科.空间几何体是几何学的重要组成部分,它在土木建筑、机械设计、航海测绘等大量实际问题中都有着广泛的应用,是下一章研究空间点、线、面的位置关系的载体,是初中学过的平面几何的继续和发展.另外,三维空间是人类生存的现实空间,认识空间图形,培养和发展空间想象力、推理理论证能力、运用图形语言进行交流的能力,是高中阶段必修系列课程的基本要求.本章从我们周围存在的各种物体的“形”的角度把握和认识了柱、锥、台、球的结构特征,它们是我们认识空间几何体的基础.在此基础上,我们认识了简单组合体,并从不同的方面对空间几何体进行了分类.学习在平面上画出空间几何体的三视图和直观图,并掌握两者的联系.最后学习如何计算空间几何体的表面积和体积,从中了解解决空间几何问题的基本方法.本章重点是空间几何体的结构特征,三视图和直观图的画法,几何体的表面积和体积的计算.本章难点是对柱、锥、台、球的结构特征的概括,识别三视图所表示的空间几何体,对一些几何体的表面积和体积公式的推导.1.1空间几何体的结构1.1.1柱、锥、台、球的结构特征(一)【考纲要求】[学习目标]1.知道空间几何体的概念及其含义,了解空间几何体的分类及相关概念.2.了解棱柱、棱锥、棱台的定义,知道这三种几何体的结构特征,给出几何体能够识别和区分.[目标解读]1.理解棱柱、棱锥、棱台的定义及结构特征是重点;2.通过实例,培养学生的观察能力和空间想象能力是难点.【自主学习】1.空间几何体(1)空间几何体的定义空间中的物体都占据着空间的一部分,若只考虑这些物体的和,2.多面体多面体定义图形及表示相关概念棱柱有两个面互相,其余各面都是,并且每相邻两个四边形的公共边都互相,由这些面所围成的多面体叫做棱柱.如图可记作:棱柱底面(底):两个互相平行的面.侧面:.侧棱:相邻侧面的.顶点:侧面与底面的.棱锥有一个面是,其余各面都是有一个公共顶点的,由这些面所围成的多面体叫做棱锥如图可记作:棱锥底面(底):面.侧面:有公共顶点的各个.侧棱:相邻侧面的.顶点:各侧面的.棱台用一个的平面去截棱锥,底面与截面之间的部分叫做棱台.如图可记作:棱台上底面:原棱锥的.下底面:原棱锥的.侧面:其余各面.侧棱:相邻侧面的公共边.顶点:侧面与上(下)底面的公共顶点.特别提醒:面数最少的棱锥是三棱锥,棱台的各侧面是梯形.【考点突破】要点一棱柱、棱锥、棱台的概念1.棱柱的结构特征侧棱都相等,侧面都是平行四边形,两个底面相互平行;2.棱锥的结构特征有一个面是多边形,其余各面是有一个公共顶点的三角形;3.棱台的结构特征上下底面相互平行,各侧棱的延长线交于同一点.典型例题1、有下列说法:①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;②各个面都是三角形的几何体是三棱锥;③用一个平行于棱锥底面的平面去截棱锥,得到的几何体叫做棱台;④棱柱的各相邻侧面的公共边互相平行.以上说法中,正确说法的序号是________(写出所有正确说法的序号).【思路启迪】根据棱柱、棱锥、棱台的概念解答.由图甲知,说法①错误;如图乙,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,说法②错误;由棱台的定义知,说法③错误;由棱柱的特点知,说法④正确.【答案】④方法指导:解决该类题目需准确理解多面体的定义,要真正把握多面体的结构特征.要学会通过反例对概念进行辨析,即要说明一个说法是错误的,设法举出一个反例即可.反馈训练1、有下列说法:①一个棱锥至少有四个面;②如果四棱锥的底面是正方形,那么这个四棱锥的四条侧棱都相等;③五棱锥只有五条棱;④用与底面平行的平面去截三棱锥,得到的截面三角形和底面三角形相似.以上说法中,正确说法的序号是________(写出所有正确说法的序号).典型例题2、如图所示为长方体ABCD-A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.【思路启迪】可先确定两个互相平行的面,再根据棱柱的定义作出判断.【解】截面BCFE右侧部分是棱柱,因为它满足棱柱的定义.它是三棱柱BEB′-CFC′,其中△BEB′和△CFC′是底面,EF,B′C′,BC是侧棱,截面BCFE左侧部分也是棱柱.它是四棱柱ABEA′-DCFD′.其中四边形ABEA′和四边形DCFD′是底面,A′D′,EF,BC,AD为侧棱.方法指导:根据形成几何体的结构特征的描述,结合棱柱、棱锥、棱台的定义进行判断,注意判断时要充分发挥空间想象能力,必要时做几何模型,通过演示进行准确判断.反馈训练2、下列说法:①有两个面互相平行,其余的面都是平行四边形的几何体的侧棱一定不相交于一点,故一定不是棱台;②两个互相平行的面是平行四边形,其余各面是四边形的几何体不一定是棱台;③两个互相平行的面是正方形,其余各面是四边形的几何体一定是棱台.其中正确的个数为()A.3 B.2 C.1 D.0要点三多面体的表面展开图1.绘制多面体的表面展开图要结合多面体的几何特征,发挥空间想象能力或者是亲手制作多面体模型,在解题过程中,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面,便可得到其表面展开图.2.若是给出多面体的表面展开图,来判断是由哪一个多面体展开的,则可把上述过程逆推.典型例题3、请画出如图所示的几何体的表面展开图.【思路启迪】假定一个面不动,进行空间想象,展开几何体.【解】展开图如图所示.方法指导:解答此类问题要结合多面体的结构特征,发挥空间想象能力和亲自动手制作模型的能力。
反馈训练3、根据下图所给的几何体的表面展开图,画出立体图形.考点巩固一、选择题1.下列说法中正确的是( )A.棱柱中两个互相平行的平面一定是棱柱的底面B.棱柱的面中,至少有两个面互相平行C.棱柱中一条侧棱的长叫棱柱的高D.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形2.如图,D,E,F分别是等边△ABC各边的中点,把该图按虚线折起,可以得到一个( )A.棱柱B.棱锥C.棱台D.旋转体3.下列三个说法,其中正确的是( )①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.A.0个B.1个C.2个D.3个4.在长方体ABCD-A1B1C1D1中,AB=3,AD=2,CC1=1,一条绳子从点A沿表面拉到点C1,则绳子的最短的长是( )A.3 2 B.2 5C.26 D.65.如图,下列几何体中,________是棱柱,________是棱锥,________是棱台.6.在正方体上任意选择4个顶点,它们可能是如下各种几何图形的4个顶点,这些几何体是________(写出所有正确结论的序号).①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.7.在如图所示的三棱柱ABC -A 1B 1C 1中,请连接三条线,把它分成三部分,使每一部分都是一个三棱锥.8.如图所示,在正三棱柱ABC -A 1B 1C 1中,AB =2,AA 1=2,由顶点B 沿棱柱侧面(经过棱AA 1)到达顶点C 1,与AA 1的交点记为M .求:(1)三棱柱侧面展开图的对角线长; (2)从B 经M 到C 1的最短路线长及此时A 1MAM的值.考点巩固-答案1、详细分析:把该图按虚线部分折起后,点A、B、C重合,得到一个三棱锥.答案:B2、详细分析:棱柱中也存在互相平行的侧面,故A错;棱柱上、下底面的距离叫棱柱的高,若侧棱与底面垂直,则侧棱长即为高;若侧棱与底面不垂直,则侧棱长就不是棱柱的高,故C错;长方体是棱柱,其底面为平行四边形,故D错.综上,选B.答案:B3、详细分析:对①,如图(1),当截面不平行于底面时棱锥底面和截面之间的部分不是棱台.对于②③,如图(2)中AA1,DD1交于一点,而BB1,CC1交于另一点,此几何体不能还原成四棱锥,故不是棱台.答案:A4、详细分析:①沿平面AA1B1B、平面A1B1C1D1铺展成平面,此时AC1=3 2.②沿平面AA1D1D、平面A1D1C1B1铺展成平面,此时AC1=2 5.③沿平面AA1B1B、平面BB1C1C铺展成平面,此时AC1=26.故绳子的最短的长为3 2.答案:A5、详细分析:由多面体的定义及其结构特征可得.答案:(1)(2) (3)(4) (5)6、详细分析:如图,在正方体ABCD—A1B1C1D1中,四边形ABCD和四边形ABC1D1为矩形,故①正确;在三棱锥D-ACD1中,有三个面为等腰直角三角形,一个面为等边三角形,故③正确;在三棱锥B1-ACD1中,每个面都是等边三角形,故④正确;在三棱锥A-CDC1中,每个面都是直角三角形,故⑤正确.故满足条件的序号为①③④⑤.答案:①③④⑤7、解:如图,连接A1B,BC1,A1C,则三棱锥ABC-A1B1C1被分成三部分,形成三个三棱锥,分别是A1-ABC,A1-BB1C1,A1-BCC1.8、解:沿侧棱BB1将正三棱柱的侧面展开,得到一个矩形BB1B′1B′(如图).(1)矩形BB1B′1B′的长BB′=6,宽BB1=2.所以三棱柱侧面展开图的对角线长为62+22=210.(2)由侧面展开图可知:当B,M,C1三点共线时,由B经M到C1点的路线最短.所以最短路线长为BC1=42+22=2 5.显然Rt △ABM ≌Rt △A 1C 1M , 所以A 1M =AM ,即A 1M AM=1.1.1.1柱、锥、台、球的结构特征(二)1.1.2简单组合体的结构特征【考纲要求】[学习目标]1.掌握圆柱、圆锥、圆台、球的结构特征.2.会用柱、锥、台、球的结构特征描述简单组合体的结构特征. 3.理解柱、锥、台体的关系. 4.培养观察能力和空间想象能力. [目标解读]1.理解并掌握圆柱、圆锥、圆台、球的结构特征是重点;2.用柱、锥、台、球的结构特征描述简单组合体的结构特征是难点. 【自主学习】旋转体 结构特征 图形 表示圆柱以矩形的一边所在直线为旋转轴,其余三边旋转形成的 所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴; 于轴的边旋转而成的圆面叫做圆柱的底面; 于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置, 于轴的边都叫做圆柱侧面的母线我们用表示圆柱轴的字母表示圆柱,左图可表示为圆锥以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的所围成的旋转体叫做圆锥我们用表示圆锥轴的字母表示圆锥,左图可表示为圆台用平行于的平面去截圆锥,底面与截面之间的部分叫做圆台我们用表示圆台轴的字母表示圆台,左图可表示为球以半圆的直径所在直线为旋转轴,旋转一周所形成的旋转体叫做球体,简称球.半圆的圆心叫做球的,半圆的半径叫做球的半径,半圆的直径叫做球的直径球常用球心字母进行表示,左图可表示为2.简单组合体的结构特征(1)定义:由组合而成的几何体叫做简单组合体.(2)简单组合体的两种基本形式:由简单几何体而成;由简单几何体一部分而成.特别提醒:圆是一条封闭的曲线,圆面是一个圆围成的圆内平面.球是几何体,球面是指半圆沿直径旋转形成的曲面,球是旋转体.【考点突破】要点一、旋转体的结构特征圆柱、圆锥、圆台、球从生成过程来看,它们分别是由矩形、直角三角形、直角梯形、半圆绕着某一条直线旋转而成的几何体,因此它们统称为旋转体.但应注意的是:所谓旋转体就是一个平面图形绕着这个平面图形所在的平面内一条直线旋转一周所得到的几何体,因此它还含有除圆柱、圆锥、圆台、球之外的几何体.典型例题1、下列说法:①在圆柱的上、下两底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下两底面的圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线相互平行.其中正确的是( )A.①②B.②③C.①③D.②④【思路启迪】紧扣母线的定义及相关性质即可解题.方法指导:圆柱、圆锥、圆台和球都是由平面图形绕着某条轴旋转而成的,平面图形不同,得到的旋转体也不同,即使是同一平面图形,所选轴不同,得到的旋转体也不一样.判断旋转体,要抓住定义,分清哪条线是轴,什么图形,怎样旋转,旋转后生成什么样的几何体.反馈训练1、下列说法中正确的是( )A.圆台是直角梯形绕其一边旋转而成的B.圆锥是直角三角形绕其一边旋转而成的C.圆柱不是旋转体D.圆台可以看作是平行于底面的平面截一个圆锥而得到的要点二圆柱、圆锥、圆台的侧面展开图把柱、锥、台体沿一条侧棱或母线展开成平面图,这样便把空间问题转化成了平面问题,对解决简单空间几何体的面积问题或侧面上(球除外)两点间的距离问题,是很有效的方法.典型例题2、如图,底面半径为1,高为2的圆柱,在A点有一只蚂蚁,现在这只蚂蚁要围绕圆柱由A点爬到B点,问蚂蚁爬行的最短距离是多少?【思路启迪】把圆柱侧面展开,由图分析求解.【解】把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连接AB′,则AB′即为蚂蚁爬行的最短距离.∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,∴AB′=A′B′2+AA′2=4+2π2=21+π2,所以蚂蚁爬行的最短距离为21+π2.方法指导:解此类题的关键要清楚几何体的侧面展开图是什么样的平面图形,并进行合理的空间想象,且记住以下常见几何体的侧面展开图:反馈训练2、若本例中蚂蚁围绕圆柱转两圈,如图所示,则它爬行的最短距离是多少?要点三简单组合体的结构特征判断实物图是由哪些简单几何体所组成的图形问题,首先要熟练掌握简单几何体的结构特征,其次要善于将复杂的组合体“分割”成几个简单的几何体.简单组合体有以下三种形式:1.多面体与多面体的组合体:即由两个或两个以上的多面体组合而成的几何体.2.多面体与旋转体的组合体:即由一个多面体与一个旋转体组合而成的几何体.3.旋转体与旋转体的组合体:即由两个或两个以上的旋转体组合而成的几何体.典型例题3、请描述如图所示的组合体的结构特征.【思路启迪】本题主要考查简单组合体的结构特征和空间想象能力.依据柱、锥、台、球的结构特征依次作出判断.【解】(1)是由一个圆锥和一个圆台拼接而成的组合体;(2)是由一个圆台挖去一个圆锥后剩下的部分得到的组合体;(3)是由一个四棱锥和一个四棱柱拼接而成的组合体.方法指导(1)明确组合体的结构特征,主要弄清它是由哪些简单几何体组成的.(2)会识别较复杂的图形是学好立体几何的第一步,因此我们应注意观察周围的物体,然后将它们“分拆”成几个简单的几何体,进而培养我们的空间想象能力和识图能力.反馈训练3、说出下列几何体的结构特征.考点巩固1.下列说法正确的是( )A.圆锥的母线长等于底面圆直径B.圆柱的母线与轴垂直C.圆台的母线与轴平行D.球的直径必过球心2.底面半径为2且底面水平放置的圆锥被过高的中点且平行于底面的平面所截,则截得的截面圆的面积为( )A.πB.2πC.3πD.4π3.下列说法正确的有( )①球的半径是球面上任意一点与球心的连线段②球的直径是球面上任意两点间的连线段③用一个平面截一个球,得到的是一个圆④不过球心的截面截得的圆的半径小于球半径A.①②B.①④C.①②④D.③④4.如图所示的几何体,关于其结构特征,下列说法不正确的是( )A.该几何体是由两个同底的四棱锥组成的几何体B.该几何体有12条棱、6个顶点C.该几何体有8个面,并且各面均为三角形D.该几何体有9个面,其中一个面是四边形,其余均为三角形5.给出下列说法:(1)直角三角形绕一边旋转得到的旋转体是圆锥(2)夹在圆柱的两个平行截面间的几何体还是一个旋转体(3)圆锥截去一个小圆锥后剩余部分是圆台(4)通过圆台侧面上一点,有无数条母线其中正确的说法是________(写出所有正确说法的序号).6.把一个圆锥截成圆台,已知圆台的上下底面半径之比是14,母线长为10,则圆锥的母线长是________.7.如图(1)所示,正三棱柱的底面边长是4cm、过BC的一个平面交侧棱AA′于D,若AD的长为2cm,求截面△BCD的面积.图(1) 图(2)8.从一个底面半径和高都是R的圆柱中,挖去一个以圆柱上底面为底,下底面中心为顶点的圆锥,得到如下图所示的几何体.如果用一个与圆柱下底面距离等于l并且平行于底面的平面去截它,求所得截面的面积.考点巩固-答案1、详细分析:对于A ,圆锥的母线长不一定等于底面圆直径;对于B ,圆柱的母线与轴平行;对于C ,圆台的母线与轴延长后相交于一点;D 正确.答案:D2、详细分析:作出截面图,如图,由△A 1B 1C 1∽△ABC ,得B 1C 1=1,∴截面圆面积为π. 答案:A3、详细分析:根据题意知①④正确.球面上任意两点的连线段不一定是直径,故②错.用一个平面截一个球,得到的是一个圆面,故③错.答案:B4、详细分析:该几何体用平面ABCD 可分割成两个四棱锥,因此它是这两个四棱锥的组合体,因而四边形ABCD 是它的一个截面而不是一个面,故选D.答案:D5、详细分析:对于(1),直角三角形绕斜边旋转形成两个同底的圆锥;对于(2),若两平行截面平行于圆柱的轴,截面间的几何体不是一个旋转体;对于(4),过圆台侧面上一点,只有一条母线.答案:(3)6、详细分析:把圆台还原为圆锥,利用三角形相似得,x -10x =14(其中x 为圆锥母线长),∴x =403.答案:4037、解:如图(2),取BC 的中点E ,连接AE 、DE ,则AE ⊥BC ,DE ⊥BC ,∵AE =32×4=23,∴DE =232+22=4.∴S =12BC ·ED =12×4×4=8cm 2.∴截面△BCD 的面积为8cm 2.8、解:过轴作截面,如下图所示:被平行于下底面的平面所截得的圆柱的截面圆的半径O 1C =R ,设圆锥的截面圆的R 半径O 1D 为x .∵OA=OB=R,∴△OAB是等腰直角三角形.又∵CD∥OA,则CD=BC.故x=l.∴截面面积S=πR2-πx2=πR2-πl2=π(R2-l2).1.2空间几何体的三视图和直观图1.2.1中心投影与平行投影1.2.2空间几何体的三视图【考纲要求】[学习目标]1.了解中心投影和平行投影.2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.3.能识别三视图所表示的立体模型.[目标解读]1.会画简单空间图形的三视图是重点;2.识别三视图所表示的立体模型是难点.【自主学习】1.投影(1)投影的定义由于光的照射,在物体后面的屏幕上可以留下这个物体的,这种现象叫做投影.其中,我们把叫做投影线,把的屏幕叫做投影面.(2)投影的分类①中心投影:光由散射形成的投影.②平行投影:在一束照射下形成的投影.当投影线时,叫做正投影,否则叫做.(3)投影的性质①中心投影的性质:中心投影的交于一点;当光源距离物体越近,投影形成的影子.②平行投影的性质:平行投影的投影线.2.三视图(1)分类①正视图:光线从几何体的向正投影,得到的投影图;②侧视图:光线从几何体的向正投影,得到的投影图;③俯视图:光线从几何体的向正投影,得到的投影图.(2)三视图的画法规则①视图都反映物体的长度——“长对正”;②视图都反映物体的高度——“高平齐”;③视图都反映物体的宽度——“宽相等”.特别提醒:画几何体的三视图时,能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示.【考点突破】要点一平行投影与中心投影中心投影与平行投影都是空间图形的基本画法,是投影的两种形式.通过中心投影与平行投影将三维物体转换成二维平面物体,可以通过投影想象实际物体的形状,但还不能完全反映真实情况,只能反映部分形状,只有在特殊情况下反映真实尺寸.画立体几何图形时一般采用平行投影法,画实际效果图时采用中心投影法,中心投影的投影线交于一点,点光源离物体越近,投影形成的影子越大;平行投影的投影线是平行的.典型例题1、在正方体ABCD-A′B′C′D′中,E、F分别是A′A、C′C的中点,则下列判断正确的是________.①四边形BFD′E在底面ABCD内的投影是正方形②四边形BFD′E在面A′D′DA内的投影是菱形③四边形BFD′E在面A′D′DA内的投影与在面ABB′A′内的投影是全等的平行四边形【思路启迪】先根据平行投影的定义知投影线垂直于投影面,从而确定四边形BFD′E四点在各投影面的位置.再把各投影点连线成图.①四边形BFD′E的四个顶点在底面ABCD内的投影分别是点B、C、D、A,故投影是正方形,正确;②设正方体的边长为2,则AE=1,取D′D的中点G,则四边形BFD′E在面A′D′DA 内的投影是四边形AGD′E,由AE∥D′G,且AE=D′G,∴四边形AGD′E是平行四边形.但AE=1,D′E=5,故四边形AGD′E不是菱形.对于③,由②知是两个边长分别相等的平行四边形,从而③正确.方法指导:画出一个图形在一个投影面上的投影的关键是确定该图形的关键点(如顶点,端点等),先画出这些关键点的投影,再依次连接即可得此图形在投影面上的投影.反馈训练1、如图甲所示,在正方体ABCD-A1B1C1D1中,E、F分别是AA1、C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的________.要点二画空间几何体的三视图1.三视图是用两两相互垂直的三个平面(正面、侧面、水平面)作为投影面,把物体放在这个空间内,分别向三个平面进行正投影,然后将水平投影绕水平面和正面的交线向下转90°,将侧面投影绕侧面和正面的交线向右转90°,就得到了三视图,即画出的三视图需要符合长对正、高平齐、宽相等的基本特征.2.画简单组合体的三视图时,先要分析该组合体的结构特征,再想象模型,从正前方、左方、正上方三个不同角度各能看到什么形状,再借助简单几何体的三视图,画出简单组合体的三视图.典型例题2、画出下列几何体的三视图.【思路启迪】先弄清几何体的结构特征,再确定三视图的形状,并注意轮廓线的虚实.【解】(1)三视图如图所示.方法指导:(1)在画三视图时,务必做到正(视图)侧(视图)高平齐,正(视图)俯(视图)长对正,俯(视图)侧(视图)宽相等.(2)三视图的排列方法是正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.反馈训练2、画出如下图所示的四棱锥的三视图.。
