n阶Hermite多项式的matlab 代码
matlab设计多阶MTI滤波器
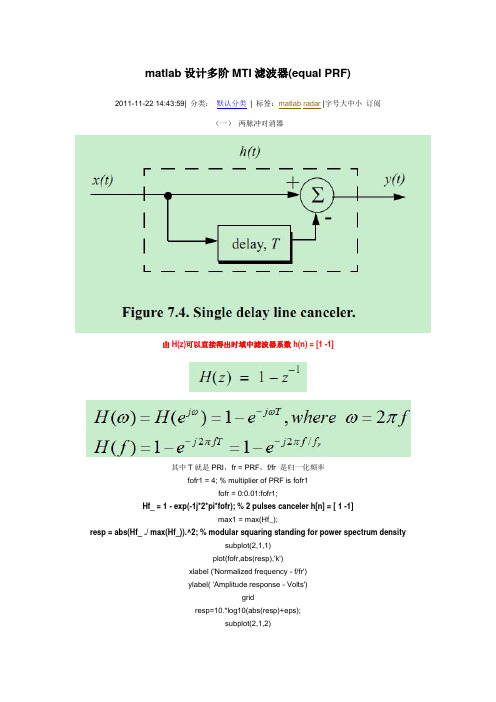
matlab设计多阶MTI滤波器(equal PRF) 2011-11-22 14:43:59| 分类:默认分类| 标签:matlab radar |字号大中小订阅(一)两脉冲对消器由H(z)可以直接得出时域中滤波器系数h(n) = [1 -1]其中T就是PRI,fr = PRF,f/fr 是归一化频率fofr1 = 4; % multiplier of PRF is fofr1fofr = 0:0.01:fofr1;Hf_ = 1 - exp(-1j*2*pi*fofr); % 2 pulses canceler h[n] = [ 1 -1]max1 = max(Hf_);resp = abs(Hf_ ./ max(Hf_)).^2; % modular squaring standing for power spectrum densitysubplot(2,1,1)plot(fofr,abs(resp),'k')xlabel ('Normalized frequency - f/fr')ylabel( 'Amplitude response - Volts')gridresp=10.*log10(abs(resp)+eps);subplot(2,1,2)plot(fofr,resp,'k');axis tight;grid;xlabel ('Normalized frequency - f/fr');ylabel( 'Amplitude response - dB');(二)三脉冲对消器fofr1 = 4; % multiplier of PRF is fofr1fofr = 0:0.01:fofr1;Hf_ = 1 - 2*exp(-1j*2*pi*fofr) + exp(-2*1j*2*pi*fofr); % 3 pulses canceler h[n] = [1 -2 1]resp = abs(Hf_ ./ max(Hf_)).^2; %modular squaring standing for power spectrum densitysubplot(2,1,1)plot(fofr,abs(resp),'k')xlabel ('Normalized frequency - f/fr')ylabel( 'Amplitude response - Volts')gridresp=10.*log10(abs(resp)+eps);subplot(2,1,2)plot(fofr,resp,'k');axis tight;grid;xlabel ('Normalized frequency - f/fr');ylabel( 'Amplitude response - dB');以上代码与MATLAB Simulations for Radar Systems Design - Bassem R. Mahafza提供的一下代码执行结果完全相同,但是该书中没有指出以上等PRF下的MTI滤波器设计的实质。
matlab中多项式的表示

matlab中多项式的表示多项式是数学中常见且重要的一种数学表达式, matlab中也提供了多项式的表示方法。
本文将围绕matlab中多项式的表示进行介绍,主要包括以下部分:一、多项式的创建在matlab中,创建多项式主要有两种方法:手动输入系数和使用符号变量。
下面分别进行介绍。
1.手动输入系数在matlab中,我们可以手动输入多项式的系数创建多项式。
比如,我们创建一个3次曲线函数y=ax^3+bx^2+cx+d,可以通过输入命令:> a=2; b=3; c=1; d=4;> poly=polyfit(x,y,3);在输入命令后,polyfit函数可以给出调整后最佳拟合曲线的系数,从而得到多项式。
2.使用符号变量在matlab中,我们还可以使用符号变量来创建一个多项式,比如我们想创建一个2次多项式函数y=ax^2+bx+c,可以通过输入命令:syms x a b cf=a*x^2+b*x+c;在输入命令后,输入符号变量和多项式表达式即可创建多项式。
二、多项式的基本运算在matlab中,多项式也可以进行基本的数学运算,比如加减乘除和求导等等。
1.加法和减法在matlab中,多项式的加法和减法可以用函数polyadd和polysub来表示,比如我们想计算多项式P(x)=2x^2+3x+1和Q(x)=-4x^2+2x-5的和与差,可以输入命令:p=[2,3,1];q=[-4,2,-5];sum=polyadd(p,q)diff=polysub(p,q)在输入命令后,polyadd和polysub函数可以给出两个多项式的和与差。
2.乘法和除法在matlab中,多项式的乘法和除法可以用函数polyval和deconv来表示,比如我们想计算多项式P(x)=x^3+3x^2+2x+1和Q(x)=x+2的积和商,可以输入命令:p=[1,3,2,1];q=[1,2];prod=conv(p,q)div=deconv(p,q)在输入命令后,conv和deconv函数可以给出两个多项式的积和商。
matlab窗函数代码

matlab窗函数代码在信号处理和数字滤波器设计中,窗函数是一种常用的工具,用于限制信号的时间或频率特性。
MATLAB提供了多种窗函数的函数,为用户提供了便捷的窗函数生成方法。
本文将介绍使用MATLAB实现窗函数的代码,并展示窗函数在信号处理中的一些应用。
一、窗函数的概念和作用窗函数,顾名思义,是将信号与一个窗口函数进行相乘的操作。
窗口函数通常是一个在有限时间或有限频率范围内非零的函数,其作用是在截断信号的同时减小频谱泄露或干扰的效果。
窗函数主要用于以下几个方面:1. 信号截断:在信号处理中,常常需要将信号截断到特定的时间或频率范围内,窗函数可以实现这一功能。
2. 频谱分析:窗函数可以减少频谱泄露的问题,提高频谱分析的准确性。
3. 滤波器设计:窗函数可以用于设计数字滤波器,限制滤波器的频率响应,降低滤波器的波纹和旁瓣响应。
4. 信号调制:窗函数可以对信号进行调制,从而改变信号的频谱特性。
二、常见的窗函数在MATLAB中,常见的窗函数有以下几种:1. 矩形窗函数(rectwin):矩形窗函数是最简单的窗口函数,其在指定范围内等于1,在其他范围内等于0。
矩形窗函数常常用于频谱分析和滤波器设计中。
MATLAB代码实现:```matlabN = 256; % 窗口长度w = rectwin(N); % 生成矩形窗函数```2. 汉宁窗函数(hann):汉宁窗函数是一种改进的窗口函数,其在给定范围内平滑过渡,减少频谱泄露和旁瓣响应。
MATLAB代码实现:```matlabN = 256; % 窗口长度w = hann(N); % 生成汉宁窗函数```3. 汉明窗函数(hamming):汉明窗函数也是一种改进的窗口函数,类似于汉宁窗函数,但其衰减更快。
MATLAB代码实现:```matlabN = 256; % 窗口长度w = hamming(N); % 生成汉明窗函数```4. 埃尔米特窗函数(hermite):埃尔米特窗函数在MATLAB中用chebwin函数实现,其在给定范围内呈现类似埃尔米特多项式的特性。
matlab对hermite矩阵分解-概述说明以及解释

matlab对hermite矩阵分解-概述说明以及解释1.引言1.1 概述概述部分的内容可以包括对Hermit矩阵分解的定义和背景的介绍。
下面是一个可能的概述内容的例子:在数学和计算科学的领域中,矩阵分解是一种重要的技术,用于将复杂的大矩阵表示转化为更简洁、可处理的形式。
其中一种矩阵分解方法是Hermit矩阵分解,它是对Hermit矩阵进行分解的一种特殊方法。
Hermit矩阵是一种具有特殊属性的正方矩阵,其元素复共轭对称。
在Hermit矩阵分解的过程中,通过将一个Hermit矩阵表示为两个特定形式的矩阵的乘积,可以使得矩阵运算更加有效,并且可以提取出矩阵的结构信息。
本文旨在介绍MATLAB在Hermit矩阵分解中的应用,并讨论Hermit 矩阵分解的算法和实现。
首先,我们将详细介绍Hermit矩阵分解的概念和相关背景知识。
接着,我们将探讨MATLAB在Hermit矩阵分解中的具体应用,包括如何使用MATLAB进行矩阵分解和分析。
最后,我们将总结Hermit矩阵分解的优势和局限性,并展望未来相关研究的发展方向。
通过本文的阐述,读者将能够了解Hermit矩阵分解及其在科学和工程问题中的应用价值,同时也能够熟悉MATLAB在这一方面的操作和实现。
无论是对于研究人员还是对于对矩阵分解感兴趣的读者来说,本文都将为他们提供有用的信息和参考。
1.2文章结构1.2 文章结构本文共分为以下几个部分进行讨论和叙述。
第一部分为引言部分,对整篇文章进行概述,并介绍文章的结构和目的。
在这一部分中,我们将简要介绍Hermit矩阵分解的概念以及MATLAB 在该领域的应用。
第二部分为正文部分,主要讨论Hermit矩阵分解的概念、MATLAB 在该领域的具体应用以及Hermit矩阵分解的算法与实现。
我们将详细介绍Hermit矩阵分解的相关概念,包括其定义、特性等,并探讨MATLAB 在该领域中的重要作用和应用。
此外,我们还将介绍一些常用的Hermit 矩阵分解算法,包括其原理、步骤和实现方式。
基于降阶法的hermite插值多项式求解方法

基于降阶法的hermite插值多项式求解方法基于降阶法的Hermite插值多项式求解方法是一种数值分析方法,用于求解函数在给定点的值。
该方法的基本思想是将高阶多项式转化为低阶多项式,从而简化计算过程。
具体步骤如下:1. 定义插值点:选择一组已知的插值点 $(x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)$,其中 $x_0 < x_1 < \ldots < x_n$。
2. 构造降阶多项式:对于 $i = 0, 1, \ldots, n$,定义 $p_i(x) = (x - x_i)\cdot q_i(x)$,其中 $q_i(x)$ 是 $(n-1)$ 阶多项式。
3. 求解 $q_i(x)$:对于 $i = 0, 1, \ldots, n$,求解 $(n-1)$ 阶方程$q_i(x_j) = \delta_{ij}$,其中 $\delta_{ij}$ 是 Kronecker delta 函数。
4. 求解 $p_i(x)$:对于 $i = 0, 1, \ldots, n$,求解 $(n+1)$ 阶方程$p_i(x_j) = y_j$。
5. 计算插值多项式:最终的插值多项式为 $H(x) = \sum_{i=0}^{n} p_i(x)\cdot \varphi_i(x)$,其中 $\varphi_i(x) = \frac{(x - x_0)(x - x_1) \cdots (x - x_{i-1})(x - x_{i+1}) \cdots (x - x_n)}{(x_i - x_0)(x_i - x_1) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_n)}$。
通过以上步骤,可以求解出满足给定插值条件的 Hermite 插值多项式。
在实际应用中,可以根据具体问题选择合适的插值点,并利用该方法进行数值计算。
第5讲MATLAB多项式及插值

第5讲MATLAB多项式及插值
5.1.2 求和与求积
数据序列求和与求积的函数是sum和prod,其使用方 法类似。设X是一个向量,A是一个矩阵,函数的调用格 式为:
sum(X):返回向量X各元素的和。 prod(X):返回向量X各元素的乘积。 sum(A):返回一个行向量,其第i个元素是A的第i列的元素和。 prod(A):返回一个行向量,其第i个元素是A的第i列的元素乘积。 sum(A,dim):当dim为1时,该函数等同于sum(A);当dim为2时, 返回一个列向量,其第i个元素是A的第i行的各元素之和。 prod(A,dim):当dim为1时,该函数等同于prod(A);当dim为2时, 返回一个列向量,其第i个元素是A的第i行的各元素乘积。
为解决Rung问题,引入分段插值。 第5讲MATLAB多项式及插值
算法分析:所谓分段插值就是通过插值点用折线或低次曲线 连接起来逼近原曲线。
MATLAB实现 可调用内部函数。 ➢ 命令 interp1
功能 : 一维数据插值(表格查找)。该命令对数据点之 间计算内插值。它找出一元函数f(x)在中间点的数值。其 中函数f(x)由所给数据决定。
t = 1900:10:1990; p = [75.995 91.972 105.711 123.203 131.669...
150.697 179.323 203.212 226.505 249.633]; 对应于美国从1900年到1990年的每10年的人口数,求 1975年的人口。由此推断美国1900年到2000年每一年的 人口数,并画出图形。
k1
j1
xxj ) xk xj
jk
MATLAB中没有直接实现拉格朗日算法的函数,我们已经介 绍过该函数的书写:
MATLAB应用多项式插值

多项式为 y 0.2015x3 1.4385x2 2.7477x 5.4370 Polyfit的第三个参数是多项式的阶数。
要求导数值也相等,甚至要求高阶导数值也相等,满足 这一要求的插值多项式就是Hermite插值多项式。下面 只讨论函数值与一阶导数值个数相等且已知的情况。
已知n个插值点 x1, x2, , xn 及对应的函数值 y1, y2, , yn 和一阶导数值 y1', y2', , y'n 。则对插值区间 内任意x的函数值y的Hermite插值公式:
n
y(x) hi[(xi x)(2ai yi yi' ) yi ] i 1
其中
hi
n ( x xj )2; j1 xi x j
ji
ai
n j 1
xi
1 xj
ji
• MATLAB实现
% hermite.m
function y=hermite(x0,y0,y1,x)
n
y(x) hi[(xi x)(2ai yi yi' ) yi ]
• polyval: 可用命令polyval计算多项式的值。 例: y 3x4 7x3 2x2 x 1 计算y(2.5)
>> c=[3,-7,2,1,1]; xi=2.5; yi=polyval(c,xi) yi =
23.8125 如果xi是含有多个横坐标值的数组,则yi也
为与xi长度相同的向量。 >> c=[3,-7,2,1,1]; xi=[2.5,3]; >> yi=polyval(c,xi) yi =
Matlab多项式及其函数

Matlab多项式及其函数多项式及其函数多项式及其函数Matlab⽤⼀维向量表⽰多项式例:创建⼀个通⽤的⼀维向量转化为字符串格式的表达式function s = pprintf(p)%pprintf 该函数可将⼀维向量转变为字符串格式的数学表达式 % p:输⼊参数,格式为⼀维向量 % s:输出参数,格式为字符串if nargin>1 %输⼊参数过多时的判断error("Too much input arguements");endwhile(p(1)==0) %输⼊向量的元素全为0p(1)=[];endL=length(p); %计算向量长度s='';for v=1:Lif p(v)==0 %当常数项为0continue;elseif L==1 %当向量长度为1s=strcat(num2str(p(v)));elseif v==L %当v为向量最后⼀个值s=strcat(s,'+',num2str(p(v)));elseif v==1 %当v为向量第⼀个值s=strcat(num2str(p(v)),'x^{',num2str(L-v),'}');elseif p(v)==1当向量元素的值为1s=strcat(s,'+','x^{',num2str(L-v),'}');elses=strcat(s,'+',num2str(p(v)),'x^{',num2str(L-v),'}');endendend执⾏以下脚本(创建⼀个图形窗⼝把该函数表达式字符串设置为标题):p=[5 4 6 1 0 8 7 6];figure;title(pprintf(p));运⾏结果:求解多项式的根,对⽅程求解p=[3 -2 -4];r=roots(p)解得:r =1.5352-0.8685r = roots()以列向量的形式返回p表⽰的多项式的根。
hermite插值以及两种MATLAB程序

给定矢量P 0, P 1, R 0, R 1,称满足下列条件的参数三次多项式曲线P (t ),t ∈[0,1]为Hermite 曲线:H (x 0)=y 0,H (x 1)=y 1,H ′(x 0)=m 0,H ′(x 1)=m 1,即Hermite 曲线两个端点为P 0, P 1,在两端点的切矢量分别R 0, R 1。
记几何矩阵和基矩阵分别为G H , M H , G H , M H 是未知的.取G H =[P 0,P 1,R 0,R 1],则只要M H 就可以了。
一般的曲线经过多项式分解, 得到参数多项式曲线的矩阵表示:P (t )=G ∙M ∙T将(1)式代入(2)得到:G H ∙M H ∙T H |t=0=G H ∙M H ∙(1,0,0,0)T =P 0, G H ∙M H ∙T H |t=1=G H ∙M H ∙(1,1,1,1)T =P 1, G H ∙M H ∙T H |t=0=G H ∙M H ∙(0,1,0,0)T =R 0, G H ∙M H ∙T H |t=0=G H ∙M H ∙(0,1,2,3)T =R 1, 将上面四个式子合并如下形式:G H ∙M H ∙[101001111020103]=[P 0,P 1,R 0,R 1]=G H 上面方程的解不唯一,不妨取M H =[101001111020103]−1=[1000−320−3−21−2100−11] 从而得到三次Hermite 曲线的方程:P(t)=G H∙M H∙T其中M H∙T确定了一组Hermite基函数G0(t),G1(t),H0(t),H1(t),即M H∙T=[10−320−3−21−2100−11][1tt2t3]=[1−3t2+2t33t2−2t3t−2t2+t3−t2+t3]附:MATLAB程序function yy=hermite(x,y,dy,xx)% 输入X——左右两个端点的X轴坐标Y——左右两个端点的Y轴坐标dy——左右两个端点的切矢xx——中间插值的点X轴坐标%输出yy——中间插值的点Y轴坐标function yy=hermite(x,y,dy,xx)k=length(xx);z=zeros(1,k);for i=1:k;s=0;xaix=xx(i);a=1-3.*(xaix)^2+2.*(xaix)^3;b=2.*(xaix)^2-2.*(xaix)^3;c=xaix-2.*(xaix)^2+(xaix)^3;d=-2.*(xaix)^2+(xaix)^3;s=y(1)*a+y(2)*b+dy(1)*c+dy(2)*d;z(i)=s;endyy=z;function yy=hermite(x,y,dy,xx) % 输入X——左右两个端点的X轴坐标Y——左右两个端点的Y轴坐标dy——左右两个端点的切矢xx——中间插值的点X轴坐标%输出yy——中间插值的点Y轴坐标m=length(x);n=length(y);l=length(dy);k=length(xx);if m~=n,error('向量长度不一样'); end;if n~=l,error('向量长度不一样'); end;z=zeros(1,k);for i=1:k;s=0;a=xx(i)-x(1);b=x(1)-x(2);c=xx(i)-x(2);a1=(1-2*a/b)*(c/b)^2;aa=xx(i)-x(2);a2=(1+2*aa/b)*(a/b)^2;b1=a*(c/b)^2;b2=c*(a/b)^2;s=y(1)*a1+y(2)*a2+dy(1)*b1+dy(2)*b2; z(i)=s;endyy=z;。
数值分析实验报告Hermite插值法、Runge现象,比较Language插值、分段线性插值、分段三次Hermie插值

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度,并画出插值多项式的图像。
1)运用Hermite插值法画出图像,如图4-1,并求质点在时刻1.8时的速度。
>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计(一)Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X,X中第一行每个元素都是插值节点,X中第二行每个元素都是插值节点对应的函数值;%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例:给定函数55,11)(2≤≤-+=x xx f ; (1) 验证表2-10的误差结果(高次插值的Runge 现象);(2) 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值,画出三种插值函数以及f(x)的图像,比较三种插值结果。
hermite polynomial多项式

Hermite多项式在数学中有着重要的应用,它们是一类特殊的多项式,具有许多重要的性质。
以下是关于Hermite多项式使用方法和注意事项的详细介绍:1.定义和性质:Hermite多项式是一类定义在实数域上的多项式,其定义如下:$H_n(x) = \sum_{k=0}^{[n/2]} (-1)^k (x-k)^n C_{n-k,k}$其中,$C_{n-k,k}$ 是二项式系数,即$C_{n-k,k} = \frac{(n-k)!k!}{n!}$。
Hermite多项式具有一些重要的性质,比如它们是递推的,即$H_{n+1}(x) = xH_n(x) - nH_{n-1}(x)$。
此外,它们还具有一些微分性质,如$H_n'(x) = nH_{n-1}(x)$ 和$(x^2-1)H_n'(x) = n(2x-1)H_{n-1}(x)$。
2.使用方法:使用Hermite多项式时,需要注意以下几点:●初始化:要计算Hermite多项式的值,需要先定义一个变量$x$ 和一个整数$n$。
●计算:根据定义,计算出$H_n(x)$ 的值。
●应用:将计算出的$H_n(x)$ 值应用于实际问题的求解中。
以下是一个使用Python实现计算Hermite多项式的示例代码:3.注意事项:在使用Hermite多项式时,需要注意以下几点:●递归性质:由于Hermite多项式是递推的,因此计算时需要注意递归调用,避免出现栈溢出等问题。
●数值稳定性:由于Hermite多项式的计算涉及到高次幂运算和整数除法运算,因此可能会出现数值不稳定的问题。
为了提高数值稳定性,可以使用一些数值稳定的算法,如快速幂算法和模运算等。
●应用场景:虽然Hermite多项式在数学中有着广泛的应用,但是在实际应用中需要注意它们的应用场景和适用范围。
同时,还需要考虑它们与其他数学工具和算法的结合使用。
4.应用案例:以下是几个使用Hermite多项式的应用案例:例1:求解常微分方程Hermite多项式可以用于求解常微分方程。
matlab常用函数与常用指令大全[整理版]
![matlab常用函数与常用指令大全[整理版]](https://img.taocdn.com/s3/m/ff905ddadb38376baf1ffc4ffe4733687f21fc56.png)
matlab常用函数与常用指令大全matlab, 函数, 指令, 大全matlab常用函数与常用指令大全matlab常用函数- -1、特殊变量与常数ans 计算结果的变量名computer 确定运行的计算机eps 浮点相对精度Inf 无穷大I 虚数单位inputname 输入参数名NaN 非数nargin 输入参数个数nargout 输出参数的数目pi 圆周率nargoutchk 有效的输出参数数目realmax 最大正浮点数realmin 最小正浮点数varargin 实际输入的参量varargout 实际返回的参量操作符与特殊字符+ 加- 减* 矩阵乘法.* 数组乘(对应元素相乘)^ 矩阵幂 .^ 数组幂(各个元素求幂)\ 左除或反斜杠/ 右除或斜面杠./ 数组除(对应元素除)kron Kronecker张量积: 冒号() 圆括[] 方括 . 小数点.. 父目录 ... 继续, 逗号(分割多条命令); 分号(禁止结果显示)% 注释! 感叹号' 转置或引用= 赋值== 相等<> 不等于& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或2、基本数学函数abs 绝对值和复数模长acos,acodh 反余弦,反双曲余弦acot,acoth 反余切,反双曲余切acsc,acsch 反余割,反双曲余割angle 相角asec,asech 反正割,反双曲正割secant 正切asin,asinh 反正弦,反双曲正弦atan,atanh 反正切,双曲正切tangent 正切atan2 四象限反正切ceil 向着无穷大舍入complex 建立一个复数conj 复数配对cos,cosh 余弦,双曲余弦csc,csch 余切,双曲余切cot,coth 余切,双曲余切exp 指数fix 朝0方向取整floor 朝负无穷取整*** 最大公因数imag 复数值的虚部lcm 最小公倍数log 自然对数log2 以2为底的对数log10 常用对数mod 有符号的求余nchoosek 二项式系数和全部组合数real 复数的实部rem 相除后求余round 取整为最近的整数sec,sech 正割,双曲正割sign 符号数sin,sinh 正弦,双曲正弦sqrt 平方根tan,tanh 正切,双曲正切3、基本矩阵和矩阵操作blkding 从输入参量建立块对角矩阵eye 单位矩阵linespace 产生线性间隔的向量logspace 产生对数间隔的向量numel 元素个数ones 产生全为1的数组rand 均匀颁随机数和数组randn 正态分布随机数和数组zeros 建立一个全0矩阵colon) 等间隔向量cat 连接数组diag 对角矩阵和矩阵对角线fliplr 从左自右翻转矩阵flipud 从上到下翻转矩阵repmat 复制一个数组reshape 改造矩阵roy90 矩阵翻转90度tril 矩阵的下三角triu 矩阵的上三角dot 向量点集cross 向量叉集ismember 检测一个集合的元素intersect 向量的交集setxor 向量异或集setdiff 向是的差集union 向量的并集数值分析和傅立叶变换cumprod 累积cumsum 累加cumtrapz 累计梯形法计算数值微分factor 质因子inpolygon 删除多边形区域内的点max 最大值mean 数组的均值mediam 中值min 最小值perms 所有可能的转换polyarea 多边形区域primes 生成质数列表prod 数组元素的乘积rectint 矩形交集区域sort 按升序排列矩阵元素sortrows 按升序排列行std 标准偏差sum 求和trapz 梯形数值积分var 方差del2 离散拉普拉斯diff 差值和微分估计gradient 数值梯度cov 协方差矩阵corrcoef 相关系数conv2 二维卷积conv 卷积和多项式乘法filter IIR或FIR滤波器deconv 反卷积和多项式除法filter2 二维数字滤波器cplxpair 将复数值分类为共轭对fft 一维的快速傅立叶变换fft2 二维快速傅立叶变换fftshift 将FFT的DC分量移到频谱中心ifft 一维快速反傅立叶变换ifft2 二维傅立叶反变换ifftn 多维快速傅立叶变换ifftshift 反FFT偏移nextpow2 最靠近的2的幂次unwrap 校正相位角多项式与插值conv 卷积和多项式乘法roots 多项式的根poly 具有设定根的多项式polyder 多项式微分polyeig 多项式的特征根polyfit 多项式拟合polyint 解析多项式积分polyval 多项式求值polyvalm 矩阵变量多项式求值residue 部分分式展开interp1 一维插值interp2 二维插值interp3 三维插值interpft 使用FFT的一维插值interpn 多维插值meshgrid 为3维点生成x和y的网格ndgrid 生成多维函数和插值的数组pchip 分段3次Hermite插值多项式ppval 分段多项式的值spline 3次样条数据插值绘图函数bar 竖直条图barh 水平条图hist 直方图histc 直方图计数hold 保持当前图形loglog x,y对数坐标图pie 饼状图plot 绘二维图polar 极坐标图semilogy y轴对数坐标图semilogx x轴对数坐标subplot 绘制子图bar3 数值3D竖条图bar3h 水平3D条形图comet3 3D慧星图cylinder 圆柱体fill3 填充的3D多边形plot3 3维空间绘图quiver3 3D震动(速度)图slice 体积薄片图sphere 球stem3 绘制离散表面数据wate***ll 绘制瀑布trisurf 三角表面clabel 增加轮廓标签到等高线图中datetick 数据格式标记grid 加网格线gtext 用鼠标将文本放在2D图中legend 图注plotyy 左右边都绘Y轴title 标题xlabel X轴标签ylabel Y轴标签zlabel Z轴标签contour 等高线图contourc 等高线计算contourf 填充的等高线图hidden 网格线消影meshc 连接网格/等高线mesh 具有参考轴的3D网格peaks 具有两个变量的采样函数surf 3D阴影表面图su***ce 建立表面低层对象surfc 海浪和等高线的结合surfl 具有光照的3D阴影表面trimesh 三角网格图1 常用指令(General Purpose Commands) 1.1 通用信息查询(General information) demo 演示程序help 在线帮助指令helpbrowser 超文本文档帮助信息helpdesk 超文本文档帮助信息helpwin 打开在线帮助窗info MA TLAB 和MathWorks 公司的信息subscribe MA TLAB 用户注册ver MA TLAB 和TOOLBOX 的版本信息version MA TLAB 版本whatsnew 显示版本新特征1.2 工作空间管理(Managing the workspace)clear 从内存中清除变量和函数exit 关闭MA TLABload 从磁盘中调入数据变量pack 合并工作内存中的碎块quit 退出MA TLABsave 把内存变量存入磁盘who 列出工作内存中的变量名whos 列出工作内存中的变量细节workspace 工作内存浏览器1.3 管理指令和函数(Managing commands and functions) edit 矩阵编辑器edit 打开M 文件inmem 查看内存中的P 码文件mex 创建MEX 文件open 打开文件pcode 生成P 码文件type 显示文件内容what 列出当前目录上的M、MA T、MEX 文件which 确定指定函数和文件的位置1.4 搜索路径的管理(Managing the seach patli) addpath 添加搜索路径rmpath 从搜索路径中删除目录path 控制MA TLAB 的搜索路径pathtool 修改搜索路径1.5 指令窗控制(Controlling the command window) beep 产生beep 声echo 显示命令文件指令的切换开关diary 储存MA TLAB 指令窗操作内容format 设置数据输出格式more 命令窗口分页输出的控制开关1.6 操作系统指令(Operating system commands) cd 改变当前工作目录computer 计算机类型copyfile 文件拷贝delete 删除文件dir 列出的文件dos 执行dos 指令并返还结果getenv 给出环境值ispc MA TLAB 为PC(Windows)版本则为真isunix MA TLAB 为Unix 版本则为真mkdir 创建目录pwd 改变当前工作目录unix 执行unix 指令并返还结果vms 执行vms dcl 指令并返还结果web 打开web 浏览器! 执行外部应用程序2 运算符和特殊算符(Operators and special characters)2.1 算术运算符(Arithmetic operators)+ 加- 减* 矩阵乘.* 数组乘^ 矩阵乘方.^ 数组乘方\ 反斜杠或左除/ 斜杠或右除./或.\ 数组除张量积[注]本表第三栏括号中的字符供在线救助时help 指令引述用2.2 关系运算符(Relational operators)= = 等号~= 不等号< 小于> 大于<= 小于或等于>= 大于或等于2.3 逻辑操作(Logical operators) & 逻辑与| 逻辑或~ 逻辑非xor 异或any 有非零元则为真all 所有元素均非零则为真2.4 特殊算符(Special characters) :冒号( ) 圆括号[ ] 方括号{ } 花括号@ 创建函数句柄. 小数点. 构架域的关节点.. 父目录续行号, 逗号; 分号% 注释号! 调用操作系统命令= 赋值符号ˊ引号ˊ复数转置号.ˊ转置号[,] 水平串接[;] 垂直串接( ),{ },. 下标赋值( ),{ },. 下标标识subsindex 下标标识3 编程语言结构(Programming language constructs) 3.1 控制语句(Control flow)break 终止最内循环case 同switch 一起使用catch 同try 一起使用continue 将控制转交给外层的for 或while 循环else 同if 一起使用elseif 同if 一起使用end 结束for,while,if 语句for 按规定次数重复执行语句if 条件执行语句otherwise 可同switch 一起使用return 返回switch 多个条件分支try try-cathch 结构while 不确定次数重复执行语句3.2 计算运行(Evaluation and execution)assignin 跨空间赋值builtin 执行内建的函数eval 字符串宏指令evalc 执行MA TLAB 字符串evalin 跨空间计算串表达式的值feval 函数宏指令run 执行脚本文件3.3 脚本文件、函数及变量(Scripts,function,and variables) exist 检查变量或函数是否被定义function 函数文件头global 定义全局变量isglobal 若是全局变量则为真iskeyword 若是关键字则为真mfilename 正在执行的M 文件的名字persistent 定义永久变量script MA TLAB 命令文件3.4 宗量处理(Augument handling) inputname 实际调用变量名nargchk 输入变量个数检查nargin 函数输入宗量的个数nargout 函数输出宗量的个数nargoutchk 输出变量个数检查varagin 输入宗量varagout 输出宗量3.5 信息显示(Message display)disp 显示矩阵和文字内容display 显示矩阵和文字内容的重载函数error 显示错误信息fprintf 把格式化数据写到文件或屏幕lasterr 最后一个错误信息lastwarn 最后一个警告信息sprintf 按格式把数字转换为串warning 显示警告信息3.6 交互式输入(Interactive input)input 提示键盘输入keyboard 激活键盘做为命令文件pause 暂停uicontrol 创建用户界面控制uimenu 创建用户界面菜单4 基本矩阵函数和操作(Elementary matrices and matrix manipulation)4.1 基本矩阵(Elementary matrices)eye 单位阵linspace 线性等分向量logspace 对数等分向量meshgrid 用于三维曲面的分格线坐标ones 全1 矩阵rand 均匀分布随机阵randn 正态分布随机阵repmat 铺放模块数组zeros 全零矩阵: 矩阵的援引和重排4.2 矩阵基本信息(Basic array information)disp 显示矩阵和文字内容isempty 若是空矩阵则为真isequal 若对应元素相等则为1islogical 尤其是逻辑数则为真isnumeric 若是数值则为真length 确定向量的长度logical 将数值转化为逻辑值ndims 数组A 的维数size 确定矩阵的维数4.3 矩阵操作(Matrix manipulateion)blkdiag 块对角阵串接diag 创建对角阵,抽取对角向量end 数组的长度,即最大下标find 找出非零元素1 的下标fliplr 矩阵的左右翻转flipud 矩阵的上下翻转flipdim 交换对称位置上的元素ind2sub 据单下标换算出全下标reshape 矩阵变维rot90 矩阵逆时针90°旋转sub2idn 据全下标换算出单下标tril 抽取下三角阵triu 抽取上三角阵4.4 特殊变量和常数(Special variables and constants) ans 最新表达式的运算结果eps 浮点相对误差i,j 虚数单位inf 或Inf 无穷大isfinite 若是有限数则为真isinf 若是无穷大则为真isnan 若为非数则为真NaN 或nan 非数pi 3.1415926535897?.realmax 最大浮点数realmin 最小正浮点数why 一般问题的简明答案4.5 特殊矩阵(Specialized matrices) compan 伴随矩阵gallery 一些小测试矩阵hadamard Hadamard 矩阵hankel Hankel 矩阵hilb Hilbert 矩阵invhilb 逆Hilbert 矩阵magic 魔方阵pascal Pascal 矩阵rosser 典型对称特征值实验问题toeplitz T oeplitz 矩阵vander V andermonde 矩阵wilkinson Wilkinson’s 对称特征值实验矩阵5 基本数学函数(Elementary math functions)5.1 三角函数(T rigonometric) acos 反余弦acosh 反双曲余弦acot 反余切acoth 反双曲余切acsc 反余割acsch 反双曲余割asec 反正割asech 反双曲正割asin 反正弦asinh 反双曲正弦atan 反正切atanh 反双曲正切atan2 四象限反正切cos 余弦cosh 双曲余弦cot 余切coth 双曲余切csc 余割csch 双曲余割sec 正割sech 双曲正割sin 正弦sinh 双曲正弦tan 正切tanh 双曲正切5.2 指数函数(Exponential)exp 指数log 自然对数log10 常用对数log2 以2 为底的对数nestpow2 最近邻的2 的幂pow2 2 的幂sqrt 平方根5.3 复数函数(Complex)abs 绝对值angle 相角complex 将实部和虚部构成复数conj 复数共轭cplxpair 复数阵成共轭对形式排列imag 复数虚部isreal 若是实数矩阵则为真real 复数实部unwrap 相位角360°线调整5.4 圆整和求余函数(Rounding and remainder)ceil 朝正无穷大方向取整fix 朝零方向取整floor 朝负无穷大方向取整mod 模数求余rem 求余数round 四舍五入取整sign 符号函数6 特殊函数(Specialized math functions)cart2pol 直角坐标变为柱(或极)坐标cart2sph 直角坐标变为球坐标cross 向量叉积dot 向量内积isprime 若是质数则为真pol2cart 柱(或极)坐标变为直角坐标sph2cart 球坐标变为直角坐标7 矩阵函数和数值线性代数(Matrix functions-numerical linear algebra) 7.1 矩阵分析(Matrix analysis)det 行列式的值norm 矩阵或向量范数normest 估计2 范数null 零空间orth 值空间rank 秩rref 转换为行阶梯形trace 迹subspace 子空间的角度7.2 线性方程(Linear equations)chol Cholesky 分解cholinc 不完全Cholesky 分解cond 矩阵条件数condest 估计1-范数条件数inv 矩阵的逆lu LU 分解luinc 不完全LU 分解lscov 已知协方差的最小二乘积nnls 非负二乘解pinv 伪逆qr QR 分解rcond LINPACK 逆条件数\、/ 解线性方程7.3 特性值与奇异值(Eigenvalues and singular values) condeig 矩阵各特征值的条件数eig 矩阵特征值和特征向量eigs 多个特征值gsvd 归一化奇异值分解hess Hessenberg 矩阵poly 特征多项式polyeig 多项式特征值问题qz 广义特征值schur Schur 分解svd 奇异值分解svds 多个奇异值7.4 矩阵函数(Matrix functions)expm 矩阵指数expm1 矩阵指数的Pade 逼近expm2 用泰勒级数求矩阵指数expm3 通过特征值和特征向量求矩阵指数funm 计算一般矩阵函数logm 矩阵对数sqrtm 矩阵平方根7.5 因式分解(Factorization utility)cdf2rdf 复数对角型转换到实块对角型balance 改善特征值精度的平衡刻度rsf2csf 实块对角型转换到复数对角型8 数据分析和傅里叶变换(Date analysis and Fourier transforms)8.1 基本运算(Basic operations) cumprod 元素累计积cumsum 元素累计和cumtrapz 累计积分hist 统计频数直方图histc 直方图统计max 最大值mean 平均值median 中值min 最小值prod 元素积sort 由小到大排序sortrows 由小到大按行排序std 标准差sum 元素和trapz 梯形数值积分var 求方差8.2 有限差分(Finite differentces) del2 五点离散Laplaciandiff 差分和近似微分gradient 梯度8.3 相关(Correlation)corrcoef 相关系数cov 协方差矩阵subspace 子空间之间的角度8.4 滤波和卷积(Filtering and convoluteion) conv 卷积和多项式相乘conv2 二维卷积convn N 维卷积detrend 去除线性分量deconv 解卷和多项式相除filter 一维数字滤波器fliter2 二维数字滤波器8.5 傅里叶变换(Fourier transforms)fft 快速离散傅里叶变换fft2 二维离散傅里叶变换fftn N 维离散傅里叶变换fftshift 重排fft 和fft2 的输出ifft 离散傅里叶反变换ifft2 二维离散傅城叶反变换ifftn N 维离散傅里叶反变换ifftshift 反fftshift9 音频支持(Audio support)9.1 音频硬件驱动(Audio hardware drivers)sound 播放向量soundsc 自动标刻并播放waveplay 利用系统音频输出设配播放waverecor 利用系统音频输入设配录音9.2 音频文件输入输出(Audio file import and export) auread 读取音频文件(.au)auwrite 创建音频文件(.au)wavread 读取音频文件(.wav)wavwrite 创建音频文件(.wav)9.3 工具(Utilities)lin2mu 将线性信号转换为μ 一律编码的信号mu2lin 将μ 一律编码信号转换为线性信号10 插补多项式函数(Interpolation and polynomials) 10.1 数据插补(Data Interpolation)griddata 分格点数据griddata3 三维分格点数据griddatan 多维分格点数据interpft 利用FFT 方法一维插补interp1 一维插补interp1q 快速一维插补interp2 二维插补interp3 三维插补intern N 维插补pchip hermite 插补10.2 样条插补(Spline Interpolation)ppval 计算分段多项式spline 三次样条插补10.3 多项式(Polynomials)conv 多项式相乘deconv 多项式相除poly 由根创建多项式polyder 多项式微分polyfit 多项式拟合polyint 积分多项式分析polyval 求多项式的值polyvalm 求矩阵多项式的值residue 求部分分式表达roots 求多项式的根1#caidaoyiba11 数值泛函函数和ODE 解算器(Function functions and ODE solvers) 11.1 优化和寻根(Optimization and root finding)fminbnd 非线性函数在某区间中极小值fminsearch 单纯形法求多元函数极值点指令fzero 单变量函数的零点11.2 优化选项处理(Optimization Option handling)optimget 从OPTIONS 构架中取得优化参数optimset 创建或修改OPTIONS 构架11.3 数值积分(Numerical intergration)dblquad 二重(闭型)数值积分指令quad 低阶法数值积分quadl 高阶法数值积分11.4 绘图(Plotting)ezcontour 画等位线ezcontourf 画填色等位线ezmesh 绘制网格图ezmeshc 绘制含等高线的网格图ezplot 绘制曲线ezplot3 绘制3 维曲线ezpolar 采用极坐标绘图ezsurf 画曲面图ezsurfc 画带等位线的曲面图fplot 画函数曲线图11.5 内联函数对象(Inline function object) argnames 给出函数的输入宗量char 创建字符传输组或者将其他类型变量转化为字符串数组formula 函数公式inline 创建内联函数11.6 差微分函数解算器(Differential equation solvers) ode113 变阶法解方程ode15s 变阶法解刚性方程ode23 低阶法解微分方程ode23s 低阶法解刚性微分方程ode23t 解适度刚性微分方程odet23tb 低阶法解刚性微分方程ode45 高阶法解微分方程12 二维图形函数(Two dimensional graphs)12.1 基本平面图形(Elementary X-Y graphs) loglog 双对数刻度曲线plot 直角坐标下线性刻度曲线plotyy 双纵坐标图polar 极坐标曲线图semilogx X 轴半对数刻度曲线semilogy Y 轴半对数刻度曲线12.2 轴控制(Axis control)axes 创建轴axis 轴的刻度和表现box 坐标形式在封闭式和开启词式之间切换grid 画坐标网格线hold 图形的保持subplot 创建子图zoom 二维图形的变焦放大12.3 图形注释(Graph annotation)gtext 用鼠标在图上标注文字legend 图例说明plotedit 图形编辑工具text 在图上标注文字texlabel 将字符串转换为T ex 格式title 图形标题xlabel X 轴名标注ylabel Y 轴名标注12.4 硬拷贝(Hardcopy and printing)orient 设置走纸方向print 打印图形或把图存入文件printopt 打印机设置13 三维图形函数(Three dimensional graphs) 13.1 基本三维图形(Elementary 3-D plots) fill3 三维曲面多边形填色mesh 三维网线图plot3 三维直角坐标曲线图surf 三维表面图13.2 色彩控制(Color control)alpha 透明色控制brighten 控制色彩的明暗caxis (伪)颜色轴刻度colordef 用色风格colormap 设置色图graymon 设置缺省图形窗口为单色显示屏hidden 消隐shading 图形渲染模式whitebg 设置图形窗口为白底13.3 光照模式(Lighting)diffuse 漫反射表面系数light 灯光控制lighting 设置照明模式material 使用预定义反射模式specular 漫反射surfnorm 表面图的法线surfl 带光照的三维表面图13.4 色图(Color maps)autumn 红、黄浓淡色bone 蓝色调灰度图colorcube 三浓淡多彩交错色cool 青和品红浓淡色图copper 线性变化纯铜色调图flag 红-白-蓝黑交错色图gray 线性灰度hot 黑-红-黄-白交错色图hsv 饱和色彩图jet 变异HSV 色图lines 采用plot 绘线色pink 淡粉红色图prism 光谱色图spring 青、黄浓淡色summer 绿、黄浓淡色vga 16 色white 全白色winter 蓝、绿浓淡色13.5 轴的控制(Axis control)axes 创建轴axis 轴的刻度和表现box 坐标形式在封闭式和开启式之间切换daspect 轴的DataAspectRatio 属性grid 画坐标网格线hold 图形的保持pbaspect 画坐标框的PlotBoxAspectRatio 属性subplot 创建子图xlim X 轴范围ylim Y 轴范围zlim Z 轴范围zoom 二维图形的变焦放大13.6 视角控制(V iewpoint control)rotate3d 旋动三维图形view 设定3-D 图形观测点viewmtx 观测点转换矩阵13.7 图形注释(Graph annotation)colorbar 显示色条gtext 用鼠标在图上标注文字plotedit 图形编辑工具text 在图上标注文字title 图形标题xlabel X 轴名标注ylabel Y 轴名标注zlabel Z 轴名标注13.8 硬拷贝(Hardcopy and printing)orient 设置走纸方向print 打印图形或把图存入文件printopt 打印机设置verml 将图形保存为VRML2.0 文件14 特殊图形(Specialized graphs)14.1 特殊平面图形(Specialized 2-D graphs) area 面域图bar 直方图barh 水平直方图comet 彗星状轨迹图compass 从原点出发的复数向量图errorbar 误差棒棒图ezplot 画二维曲线ezpolar 画极坐标曲线feather 从X 轴出发的复数向量图fill 多边填色图fplot 函数曲线图hist 统计频数直方图pareto Pareto 图pie 饼形统计图plotmatrix 散点图阵列scatter 散点图stairs 阶梯形曲线图stem 火柴杆图14.2 等高线及二维半图形(Contour and 2-1/2D graphs) clabel 给等高线加标注contour 等高线图contourf 等高线图contour3 三维等高线ezcontour 画等位线ezcontourf 画填色等位线pcolor 用颜色反映数据的伪色图voronoi V oronoi 图14.3 特殊三维图形(Specialized 3-D graphs)bar3 三维直方图bar3h 三维水平直方图comet3 三维彗星动态轨迹线图ezgraph3 通用指令ezmesh 画网线图ezmeshc 画等位线的网线图ezplot3 画三维曲线ezsurf 画曲面图ezsurfc 画带等位线的曲面图meshc 带等高线的三维网线图meshz 带零基准面的三维网线图pie3 三维饼图ribbon 以三维形式绘制二维曲线scatter3 三维散点图stem3 三维离散杆图surfc 带等高线的三维表面图trimesh 三角剖分网线图trisurf 三角剖分曲面图waterfall 瀑布水线图14.4 内剖及向量视图(V olume and vector visualization) coneplot 锥体图contourslice 切片等位线图quiver 矢量场图quiver3 三维方向箭头图slice 切片图14.5 图像显示及文件处理(Image display and file I/O) brighten 控制色彩的明暗colorbar 色彩条状图colormap 设置色图contrast 提高图像对比度的灰色图gray 线性灰度image 显示图像imagesc 显示亮度图像imfinfo 获取图像文件的特征数据imread 从文件读取图像的数据阵(和伴随色图))imwrite 把强度图像或真彩图像写入文件14.6 影片和动画(Movies and animation)capture 当前图的屏捕捉frame2im 将影片动画转换为编址图像getframe 获得影片动画图像的帧im2frame 将编址图像转换为影片动画movie 播放影片动画moviein 影片动画内存初始化rotate 旋转指令14.7 颜色相关函数(Color related function)spinmap 颜色周期性变化操纵14.8 三维模型函数(Solid modeling)cylinder 圆柱面patch 创建块sphere 球面Surf2patch 将曲面数据转换为块数据15 句柄图形(Handle Graphics)15.1 图形窗的产生和控制(Figure window creation and control) clf 清除当前图close 关闭图形figure 打开或创建图形窗口gcf 获得当前图的柄openfig 打开图形refresh 刷新图形shg 显示图形窗15.2 轴的产生和控制(Axis creation and control) axes 在任意位置创建轴axis 轴的控制box 坐标形式在封闭式和开启式之间切换caxis 控制色轴的刻度cla 清除当前轴gca 获得当前轴的柄hold 图形的保持ishold 若图形处保持状态则为真subplot 创建子图15.3 句柄图形对象(Handle Graphics objects) axex 在任意位置创建轴figure 创建图形窗口image 创建图像light 创建光line 创建线patch 创建块rectangle 创建方surface 创建面text 创建图形中文本uicontextmenu 创建现场菜单对象uicontrol 用户使用界面控制uimenu 用户使用菜单控制15.4 句柄图形处理(Handle Graphics operations) copyobj 拷贝图形对象及其子对象delete 删除对象及文件drawnow 屏幕刷新findobj 用规定的特性找寻对象gcbf “正执行回调操作”的图形的柄gcbo “正执行回调操作”的控件图柄指令gco 获得当前对象的柄get 获得对象特性getappdat 获得应用程序定义数据isappdata 检验是否应用程序定义数据reset 重设对象特性rmappdata 删除应用程序定义数据set 建立对象特性setappdata 建立应用程序定义数据15.5 工具函数(Utilities)closereq 关闭图形窗请求函数ishandle 若是图柄代号侧为真newplot 下一个新图16 图形用户界面工具(Graphical user interface tools) align 对齐用户控件和轴cbedit 编辑回调函数ginput 从鼠标得到图形点坐标guide 设计GUImenu 创建菜单menuedit 菜单编辑propedit 属性编辑uicontrol 创建用户界面控制uimenu 创建用户界面菜单2#caidaoyiba17 字符串(Character string)17.1 通用字符串函数(General)blanks 空格符号cellstr 通过字符串数组构建字符串的元胞数组char 创建字符传输组或者将其他类型变量转化为字符串数组deblank 删除最后的空格double 把字符串变成ASCII 码值eval 执行串形式的MATLAB 表达式17.2 字符串查询(String tests)iscellstr 若是字符串组成的元胞数组则为真ischar 若是字符串则为真isletter 串中是字母则为真isspace 串中是空格则为真isstr 若是字符串则为真17.3 字符串操作(String operations)base2dec X-进制串转换为十进制整数bin2dec 二进制串转换为十进制整数dec2base 十进制整数转换为X 进制串dec2bin 十进制整数转换为二进制串dec2hex 十进制整数转换为16 进制串findstr 在一个串中寻找一个子串hex2dec 16-进制串转换为十进制整数hex2num 16-进制串转换为浮点数int2str 将整数转换为字符串lower 把字符串变成小写mat2str 将数组转换为字符串num2str 把数值转换为字符串strcat 把多个串连接成长串strcmp 比较字符串strcmpi 比较字符串(忽略大小写)strings MA TLAB 中的字符串strjust 字符串的对齐方式strmatch 逐行搜索串strnomp 比较字符串的前N 个字符strncmpi 比较字符串的前N 个字符(忽略大小写)strrep 用另一个串代替一个串中的子串strtok 删除串中的指定子串strvcat 创建字符串数组str2mat 将字符串转换为含有空格的数组str2num 将字符串转换为数值upper 把字符串变成大写18 文件输入/输出(File input/output)clc 清除指令窗口disp 显示矩阵和文字内容fprintf 把格式化数据写到文件或屏幕home 光标返回行首input 提示键盘输入load 从磁盘中调入数据变量pause 暂停sprintf 写格式数据到串sscanf 在格式控制下读串19 时间和日期(T ime and dates)clock 时钟cputme MA TLAB 战用CPU 时间date 日期etime 用CLOCK 计算的时间now 当前时钟和日期pause 暂停tic 秒表启动toc 秒表终止和显示20 数据类型(Data types and structures)20.1 数据类型(Data types)cell 创建元胞变量char 创建字符传输组或者将其他类型变量转化为字符串数组double 转化为16 位相对精度的浮点数值对象function handle 函数句柄inline 创建内联函数JavaArray 构建Java 数组JavaMethod 调用某个Java 方法JavaObject 调用Java 对象的构造函数single 转变为单精度数值sparse 创建稀疏矩阵struct 创建构架变量uint8(unit16、unit32) 转换为8(16、32)位无符号整型数int8(nit16、nit32) 转换为8(16、32)位符号整型数20.2 多维数组函数(Multi-dimensional array functions) cat 把若干数组串接成高维数组ndims 数组A 的维数ndgrid 为N-D 函数和插补创建数组ipermute 广义反转置permute 广义非共轭转置shiftdim 维数转换squeeze 使数组降维20.3 元胞数组函数(Cell array functions)cell 创建元胞变量celldisp 显示元胞数组内容cellfun 元胞数组函数cellplot 图示元胞数组的内容cell2struct 把元胞数组转换为构架数组deal 把输入分配给输出is cell 若是元胞则为真num2 cell 把数值数组转换为元胞数组struct2 cell 把构架数组转换为元胞数组20.4 构架函数(Structure functions)fieldnames 获取构架的域名getfield 获取域的内容isfield 若为给定构架的域名则为真isstruct 若是构架则为真rmfield 删除构架的域setfield 指定构架域的内容struct 创建构架变量20.5 函数句柄函数(Function handle functions)@ 创建函数句柄functions 列举函数句柄对应的函数func2str 将函数句柄数组转换为字符串str2func 将字符串转换为函数句柄20.6 面向对象编程(Object oriented programming functions) dlass 查明变量的类型isa 若是指定的数据类型则为真inferiorto 级别较低isjava 若是java 对象则为真isobject 若是对象则为真methods 显示类的方法名substruct 创建构架总量superiorto 级别较高21 示例(E xamples and demonstrations)demo 演示程序flow 无限大水体中水下射流速度数据intro 幻灯演示指令peaks 产生peaks 图形数据22 符号工具包(Symbolic Math T oolbox) 22.1 微积分(Calculus)diff 求导数limit 求极限int 计算积分jacobian Jacobian 矩阵symsum 符号序列的求和trylor T rylor 级数22.2 线性代数(Linear Algebra)det 行列式的值diag 创建对角阵,抽取对角向量eig 矩阵特征值和特征向量expm 矩阵指数inv 矩阵的逆jordan Jordan 分解null 零空间poly 特征多项式rank 秩rref 转换为行阶梯形svd 奇异值分解。
matlab多项式函数

matlab多项式函数多项式函数在数学中是一个重要的概念,它在各个领域都有广泛的应用。
通过使用MATLAB这一强大的工具,我们可以对多项式函数进行各种操作和分析。
我们可以使用MATLAB创建多项式函数。
通过指定多项式的系数,我们可以定义一个多项式函数。
例如,我们可以使用以下代码定义一个二次多项式函数:p = [1, -2, 1];这里,p是一个包含三个元素的数组,分别表示二次多项式的系数。
第一个元素1表示二次项的系数,第二个元素-2表示一次项的系数,第三个元素1表示常数项的系数。
接下来,我们可以使用polyval函数来计算多项式函数在给定点的值。
例如,我们可以使用以下代码计算上述二次多项式在x=2的值:x = 2;y = polyval(p, x);这里,y将会得到4的值,表示在x=2处的函数值。
除了计算多项式函数在给定点的值,我们还可以对多项式函数进行求导、积分等操作。
MATLAB提供了丰富的函数来实现这些操作。
例如,我们可以使用polyder函数来计算多项式函数的导函数:dp = polyder(p);这里,dp将会得到一个包含两个元素的数组,分别表示导函数的系数。
对于上述二次多项式来说,dp将会是[-2, 2],表示导函数为-2x+2。
我们还可以使用polyint函数来计算多项式函数的不定积分。
例如,我们可以使用以下代码计算上述二次多项式的不定积分:ip = polyint(p);这里,ip将会得到一个包含四个元素的数组,分别表示不定积分的系数。
对于上述二次多项式来说,ip将会是[1/3, -1, 1, 0],表示不定积分为(1/3)x^3-x^2+x+C,其中C为常数。
MATLAB提供了丰富的函数和工具来操作和分析多项式函数。
通过使用这些函数,我们可以方便地计算多项式函数在给定点的值、求导、积分等操作,从而深入理解和应用多项式函数。
无论是在科学研究、工程应用还是数学教学中,多项式函数都具有重要的作用。
实习:Matlab作业hermite插值

题目:利用Matlab实现数据的Hermite插值和分段三次Hermite插值小组成员:王晓波(38)蔡明宇(20)一、程序实现意义:一般的,从各种试验得来的数据总有一定的数量,而利用插值技术能够从有限的数据中获取整体的状态。
而Hermite插值不仅保证了插值函数与原函数在给定数据点处得拟合,同时保证了在相应点处导数的相同,从而在很大程度上保证了曲线的“光滑性”。
因此,通过Matlab实现Hermite插值具有很普遍的意义。
二、实现过程:1、Hermite插值由于并不是所有的Matlab版本都提供现有的Hermite插值函数包,故我们首先编写了实现给定五个观测点的Hermite插值的M程序,代码如下:function [f,f0] = Hermite1(x,y,y_1)syms t;f = ;!if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('y和y的导数的维数不相等');return;endelsedisp('x和y的维数不相等! ');return;end*for i=1:nh = ;a = ;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));endendf = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));<endf0 = subs(f,'t');其中x为给定点横坐标数组,y为给定点纵坐标数组,y_1为原函数在给定点处的导数数组。
测试证明该程序可以实现,例如输入如下数组:x=1::;y_1=[ ];y=[1 ];>> [f,f0] = Hermite1(x,y,y_1);运行结果如下:f =$(390625*((3972231*t)/35 - 28321/0000)*(t - 1)^2*(t - 7/5)^2*(t - 8/5)^2*(t - 9/5)^2)/36 - (390625*(t - 1)^2*(t - 6/5)^2*(t - 7/5)^2*(t - 9/5)^2*((28557*t)/28 - 23/2000))/36 + (390625*((64*t)/3 - 61/3)*(t - 6/5)^2*(t - 7/5)^2*(t - 8/5)^2*(t - 9/5)^2)/576 + (390625*((763*t)/1984 + 043/6240000)*(t - 1)^2*(t - 6/5)^2*(t - 8/5)^2*(t - 9/5)^2)/16 - (390625*((77623*t)/28 - 931/60000)*(t - 1)^2*(t - 6/5)^2*(t - 7/5)^2*(t - 8/5)^2)/576f0 =.利用matlab绘制图像:2、程序的窗口化:利用Matlab提供的GUIDE工具以及callback函数实现相应函数的窗口化,GUI代码如下:function varargout = untitled(varargin)?% UNTITLED M-file for% UNTITLED, by itself, creates a new UNTITLED or raises the existing% singleton*.%% H = UNTITLED returns the handle to a new UNTITLED or the handle to% the existing singleton*.%% UNTITLED('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in with the given input arguments.%% UNTITLED('Property','Value',...) creates a new UNTITLED or raises the,% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before untitled_OpeningFcn gets called. An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to untitled_OpeningFcn via varargin.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help untitled%% Last Modified by GUIDE 15-Sep-2011 22:24:48% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @untitled_OpeningFcn, ...'gui_OutputFcn', @untitled_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);】if nargin && ischar(varargin{1})= str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT<% --- Executes just before untitled is made visible.function untitled_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% varargin command line arguments to untitled (see VARARGIN)% Choose default command line output for untitled= hObject;>% Update handles structureguidata(hObject, handles);% UIWAIT makes untitled wait for user response (see UIRESUME)% uiwait;% --- Outputs from this function are returned to the command line.function varargout = untitled_OutputFcn(hObject, eventdata, handles)% varargout cell array for returning output args (see VARARGOUT);…% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = ;function edit1_Callback(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)…% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit1 as text% str2double(get(hObject,'String')) returns contents of edit1 as a double guidata(hObject, handles);% --- Executes during object creation, after setting all properties.function edit1_CreateFcn(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)(% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end¥function edit2_Callback(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit2 as text% str2double(get(hObject,'String')) returns contents of edit2 as a double guidata(hObject, handles);% --- Executes during object creation, after setting all properties.、function edit2_CreateFcn(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end—function edit3_Callback(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit3 as text% str2double(get(hObject,'String')) returns contents of edit3 as a double guidata(hObject, handles);·% --- Executes during object creation, after setting all properties.function edit3_CreateFcn(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');·endfunction edit4_Callback(hObject, eventdata, handles)% hObject handle to edit4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit4 as text% str2double(get(hObject,'String')) returns contents of edit4 as a double '% --- Executes during object creation, after setting all properties.function edit4_CreateFcn(hObject, eventdata, handles)% hObject handle to edit4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'));set(hObject,'BackgroundColor','white');end% --- Executes on button press in pushbutton1.function pushbutton1_Callback(hObject, eventdata, handles)% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)x=str2num(get,'string'));y=str2num(get,'string'));<y_1=str2num(get,'string'));x0=str2num(get,'string'));syms t;f = ;if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('yºÍyµÄµ¼ÊýµÄάÊý²»ÏàµÈ');return;end—elsedisp('xºÍyµÄάÊý²»ÏàµÈ£¡ ');return;endfor i=1:nh = ;a = ;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));、endendf = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));endf0 = subs(f,'t',x0);plot,x,y,'*');^function edit5_Callback(hObject, eventdata, handles)% hObject handle to edit5 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit5 as text% str2double(get(hObject,'String')) returns contents of edit5 as a doubleguidata(hObject, handles);{% --- Executes during object creation, after setting all properties.function edit5_CreateFcn(hObject, eventdata, handles)% hObject handle to edit5 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))~set(hObject,'BackgroundColor','white');end程序运行结果:其中左上方纵列的三个对话框从上到下分别输入给定点的横坐标x,纵坐标y以及导数值y_1,右侧空白框输入维数,下方坐标图显示插值函数图像,例如仍插入上面所给定的点列,得出结果:从图上看拟合程度还是比较不错的。
MATLAB多项式与符号运算

精选课件
10
1.恰定方程组的解
方程ax=b(a为非奇异) x=a-1 b 矩阵逆
两种解: x=inv(a)b — 采用求逆运算解方程 x=a\b — 采用左除运算解方程
精选课件
11
例: x1+2x2=8 2x1+3x2=13
方程ax=b
1 2
2 3
拟合函数:p=polyfit(x,y,n)
其中x、y为离散数据点的坐标向量,n为拟 合次数,即用n次多项式拟合,p为n次 多项式的系数
精选课件
17
拟合程序例1:
将下列离散点用直线拟合,并绘制:
(0,11.2)、(0.2,16.5)、(0.4,20.4)、(0.6,26.3)、(0.8,30.5)、(1,28.7)
一组根用列向量表示。
精选课件
4
多项式加减运算
计算a(x)+b(x)
如:2x3+4x2+6x+8
3x2+6x+9
则:a=[2,4,6,8];
b=[3,6,9]
→b=[0,3,6,9]
c=a+b =[2,7,12,17]
→ 2x3+7x2+612x+17
编写子程序文件自动完成两多项式加减运算
精选课件
5
精选课件
6
多项式乘运算conv()
例:a(x)=x2+2x+3; b(x)=4x2+5x+6; c = (x2+2x+3)(4x2+5x+6) a=[1 2 3];b=[4 5 6]; c=conv(a,b)=conv([1 2 3],[4 5 6]) c = 4.00 13.00 28.00 27.00 18.00 p=poly2str(c,'x') p = 4 x^4 + 13 x^3 + 28 x^2 + 27 x + 18 注:多项式乘运算不涉及补零的问题
多项式的内插法(POLYNOMIAL

第二章多項式的內插法(Polynomial Interpolation)在本章中包含 Matlab 的m-file1.coeff.m ntpoly.m2.evalnt.mgrange.m4.coeffh.m hermite.m5.nevl.m ( Neville's Algorithm)6.example42.m (example42)7.rhextrap.m (Richardson Extrapolation)8. example21.m (natural cubic spline) example22.m(quadratic spline)ncspline.m ncsplinex.m將須要的m-file之檔案夾加入搜尋路徑中path('d:\yeh\numerical', path)註: 如果你有安裝Matlab Notebook 要執行下列input cells (綠色指令敘述)之前必須先執行上面的cell –[path (…) ]藍色的內容是Matlab [output cells]1. coeff .m -- 用來計算Newton interpolating polynomial的係數顯示coeff.m的內容type coeff.mfunction c= coeff( x, y, n)%to get the coefficients of the Newton interpolating polynomial%c(:,1)=y' ;for j = 2:nfor i= j:nc(i,j) = (c(i,j-1)-c(i-1, j-1))/ (x(i)-x(i-j+1));end %loop iend %loop j1-1. ntpoly .m -- 用來計算Newton interpolating polynomial(採用符號計算) 顯示ntpoly.m的內容type ntpoly.mfunction px=ntpoly(a,b)% px :Newton interpolating polynomial%%get the divided-difference tablem=length(a);c=coeff(a,b,m);syms wx=sym(a) ;y=sym(b) ;%m=length(x) ;nx=sym(zeros(1,m)) ; %initializefor j=1:mnt=1 ;for k=1:j-1nt=nt* (w-x(k)) ;end %for knx(j)=nt ;end %for jpx=0;for k=1:mpx=px +c(k,k)*nx(k) ;end %for k% px= simplify(px) ;例題 1: To find the Newton Interpolating Polynomial for the following table: x 1 3/2 0 2f(x) 3 13/4 3 5/3準備必要的參數n = 4 ;x = [ 1 3/2 0 2] ;y = [ 3 13/4 3 5/3];C = coeff( x, y , n)C =3.0000 0 0 03.2500 0.5000 0 03.0000 0.1667 0.3333 01.6667 -0.6667 -1.6667 -2.0000取出上面C 矩陣主對角上的值, 則polynomial p(x) = 3+0.5(x-1)+0.3333(x-1) (x-1.5)- 2(x-1) (x-1.5) x .下面我們直接用符號計算(Matlab/Symbolic toolbox)得到多項式n = 4 ;x = [ 1 3/2 0 2] ;y = [ 3 13/4 3 5/3];pw = ntpoly( x, y )spw = simplify(pw)pw =5/2+1/2*w+1/3*(w-1)*(w-3/2)-2*(w-1)*(w-3/2)*wspw =3-10/3*w+16/3*w^2-2*w^32. evalnt .m -- 計算Newton interpolating polynomial在某個t點的值顯示evalnt.m的內容type evalnt.mfunction rs = evalnt( c, x, t, n)%to get the value of the Newton interpolating polynomial%with coefficients in vector c at some point t%temp = c(n) ;for j = n-1:-1:1temp = temp *(t-x(j)) + c(j);endrs = temp;接著利用evalnt( )來計算在t = 1.6的值C=coeff(x,y,n) ;t = 1.6;for j =1:nc (j)= C(j, j) ;endval = evalnt(c, x, t, n) ;fprintf('The value of p(x) at t=%f is :%f',t,val) The value of p(x) at t=1.600000 is :3.1280003. lagrange .m -- 計算Lagrange interpolating polynomial顯示lagrange.m的內容type lagrange.mfunction [px ,lx]=lagrange(a,b)% px: Lagrange Interpolating polynomial% lx: Cardinal functionsm=length(a) ;syms wx=sym(a) ;y=sym(b) ;lx=sym(zeros(1,m)) ; %initializefor j=1:mlg=1 ;for k=1:mif (k ~= j)lg=lg* ((w-x(k))/(x(j)-x(k))) ;endend %for klx(j)=lg ;end %for jpx=0;for k=1:mpx=px +y(k)*lx(k) ;end %for k%px= simplify(px) ;同樣例題 1的資料:To find Lagrange Interpolating Polynomialx 1 3/2 0 2f(x) 3 13/4 3 5/3x = [ 1 3/2 0 2] ;y = [ 3 13/4 3 5/3];pw = lagrange(x, y )spw = simplify(pw)pw =3*(-2*w+3)*w*(-w+2)+13/6*(2*w-2)*w*(-2*w+4)+3*(-w+1)*(-2/3*w+1)*(-1/2*w+1)+5/6*(w-1)*(2*w-3)*wspw =3-10/3*w+16/3*w^2-2*w^3經過化簡後其結果與Newton Form一致 .4. coeffh .m -- 用來計算Hermite interpolating polynomial的係數(divided-difference)顯示coeffh.m的內容type coeffh.mfunction c= coeffh( x, y, dy, n)%to get the the divided-difference table for the coefficients of%Hermite interpolating polynomial%for k= 1 : nz(2*k-1) = x(k) ; c(2*k-1, 1) = y(k) ;z(2*k) = x(k) ; c(2*k , 1) = y(k) ;end ;%% c(:,2) 2nd column of the divided-difference tablefor k= 1 : n-1c(2*k ,2) =dy(k) ;c(2*k+1 ,2) = (c(2*k+1,1)-c(2*k,1))/ (z(2*k+1)-z(2*k)) ;end ;c(2*n, 2) = dy(n) ;%c(:, 3:2n)for j = 3: 2*nfor i= j: 2*nc(i,j) = (c(i,j-1)-c(i-1, j-1))/ (z(i)-z(i-j+1));end %loop iend %loop j例題 2: To find the Hermite Interpolating Polynomial for the following table: x 1 2f(x) 2 6f '(x) 3 7準備必要的參數n = 2 ;x = [1 2] ;y = [2 6]; dy=[3 7] ;C = coeffh( x, y ,dy, n)C =2 0 0 02 3 0 06 4 1 06 7 3 2取出上面C 矩陣主對角上的值, 則polynomial h(x) = 2+3(x-1)+3(x-1)2 + 2(x-1)2 (x-2) .下面我們直接用符號計算(Matlab/Symbolic toolbox)得到Hermite多項式n = 2 ;x = [1 2] ;y = [2 6]; dy=[3 7] ;hw = htpoly( x, y ,dy)hw =-1+3*w+(w-1)^2+2*(w-1)^2*(w-2)5. nevl .m -- Neville's Algorithm計算Interpolating Polynomial在某個t點的值顯示nevl.m的內容type nevl.mfunction rs= nevl(x, y, n, t)%to get the results of the polynomial interpolation at t%by Neville's Algorithm%c(:,1)=y ;for j = 2:nfor i= j:nc(i,j)=((t-x(i-j+1))*c(i,j-1)+ (x(i)-t)*c(i-1, j-1))/(x(i)-x(i-j+1)); end %loop iend %loop jrs =c ;例題 2:相同例題 1的數據, 利用 Neville's Algorithm計算Interpolating Polynomial在某個t點的值x 1 3/2 0 2f(x) 3 13/4 3 5/3準備必要的參數n = 4 ; t = 1.6 ;x = [ 1 3/2 0 2]' ;y = [ 3 13/4 3 5/3]';rs = nevl(x, y, n, t)rs =3.0000 0 0 03.2500 3.3000 0 03.0000 3.2667 3.3200 01.6667 1.9333 3.0000 3.1280從上面的資料, 我們如果取前三個樣本點x0=1, x1=1.5 , x2=0 其內插多項式p012 在 t = 1.6之值為 3.3200 . 如果取後三個樣本點x1=1.5 , x2=0 , x3=2則其內插多項式p123 在 t = 1.6之值為 3.0000 .如果取全部四個樣本點, 則其內插多項式p0123 在 t = 1.6之值為3.1280 此與例題 1之結果一致.6. 內插多項式的誤差當一個函數f(x)在[a, b]區間由內插多項式p(x)逼近, 也許我們會認為內插多項式的節點(nodes)愈多則 , 函數與多項式的差 | f(x)-p(x) | 愈小,事實不然, 考慮下面函數(Range function)f(x) = 1/ (1+x^2) on [-5, 5]Let p n(x) be the polynomial that interpolates f(x) at n+1 equally spacedpoints on [-5, 5]. Then lim n->∞ max -5≦x ≦5 | f(x) – p n(x) | = ∞我們利用example42.m產生數據與繪圖供參考.type example42.m%chapter4 example2%a=-5; b = 5;n=20;h=(b-a)/n;for i =1:n+1x(i)=a+(i-1)*h ; % nodes-xend ;y=(1+x.^2).^(-1); % nodes-yc=coeff(x,y,n+1); %計算Newton divided-difference tablefor i=1:n+1cd(i)=c(i,i);end ;t=-5:h/2:5 ;yt=(1+t.^2).^(-1);for j=1:length(t)pt(j)=evalnt(cd,x,t(j),n+1);end ;fprintf(' j t f(t) p(t) \n') for j=1:length(t)fprintf('%3d %8.6f %13.6f %13.6f\n',j,t(j),yt(j),pt(j) ) end;plot(t,yt, t,pt,'g*',x,y ,'ro')title('Interpolate f(x)=1/(1+x^2) by the equally spaced nodes')執行example42.m的程式, 產生下列數據以及圖形example42j t f(t) p(t)1 -5.000000 0.038462 0.0384622 -4.750000 0.042440 -39.9524493 -4.500000 0.047059 0.0470594 -4.250000 0.052459 3.4549585 -4.000000 0.058824 0.0588246 -3.750000 0.066390 -0.4470527 -3.500000 0.075472 0.0754728 -3.250000 0.086486 0.2024239 -3.000000 0.100000 0.10000010 -2.750000 0.116788 0.08066011 -2.500000 0.137931 0.13793112 -2.250000 0.164948 0.17976313 -2.000000 0.200000 0.20000014 -1.750000 0.246154 0.23844615 -1.500000 0.307692 0.30769216 -1.250000 0.390244 0.39509317 -1.000000 0.500000 0.50000018 -0.750000 0.640000 0.63675519 -0.500000 0.800000 0.80000020 -0.250000 0.941176 0.94249021 0.000000 1.000000 1.00000022 0.250000 0.941176 0.94249023 0.500000 0.800000 0.80000024 0.750000 0.640000 0.63675525 1.000000 0.500000 0.50000026 1.250000 0.390244 0.39509327 1.500000 0.307692 0.30769228 1.750000 0.246154 0.23844629 2.000000 0.200000 0.20000030 2.250000 0.164948 0.17976331 2.500000 0.137931 0.13793132 2.750000 0.116788 0.08066033 3.000000 0.100000 0.10000034 3.250000 0.086486 0.20242335 3.500000 0.075472 0.07547236 3.750000 0.066390 -0.44705237 4.000000 0.058824 0.05882438 4.250000 0.052459 3.45495839 4.500000 0.047059 0.04705940 4.750000 0.042440 -39.95244941 5.000000 0.038462 0.038462紅色符號'o'表節點(nodes), 綠色符號'*'是估算點.從數據上顯示雖然在節點f(x)與p n(x)一致, 但其他非節點則有些相差甚遠. 為了更清楚看到它的差異, 將圖形y-axis 縮小至 [-5, 5]之範圍下面我們取Chebyshev Polynomial的根當做內插多項式的節點(nodes), 觀察此型態之內插多項式的圖形:type example43.m%chapter4 example3%Schbyshev interpolationa=-5; b = 5;n=20;h=(b-a)/n ;for i =1:n+1theta= (2*i-1)/(2*(n+1)) ;x(i)=cos(theta* pi); %zeros of Schbyshev polynomial on [-1,1]x(i)=((b-a)*x(i)+b+a)/2 ; %zeros of Schbyshev polynomial on [a,b]end ;y=(1+x.^2).^(-1);c=coeff(x,y,n+1); %計算Newton divided-difference tablefor i=1:n+1cd(i)=c(i,i);end ;t=-5:h/2:5 ;yt=(1+t.^2).^(-1);for j=1:length(t)pt(j)=evalnt(cd,x,t(j),n+1);end ;fprintf(' j t f(t) p(t) \n') for j=1:length(t)fprintf('%3d %8.6f %13.6f %13.6f\n',j,t(j),yt(j),pt(j) ) end;plot(t,yt, t,pt,'g*',x,y,'ro')title('Interpolate f(x)=1/(1+x^2) by the zeros of Chebyshev Polynomial')執行example43.m的程式, 產生下列數據以及圖形example43j t f(t) p(t)1 -5.000000 0.038462 0.0443912 -4.750000 0.042440 0.0482003 -4.500000 0.047059 0.0405364 -4.250000 0.052459 0.0566495 -4.000000 0.058824 0.0630616 -3.750000 0.066390 0.0597697 -3.500000 0.075472 0.0710398 -3.250000 0.086486 0.0929909 -3.000000 0.100000 0.10750910 -2.750000 0.116788 0.11351611 -2.500000 0.137931 0.12729812 -2.250000 0.164948 0.16073213 -2.000000 0.200000 0.20870014 -1.750000 0.246154 0.25865415 -1.500000 0.307692 0.30933016 -1.250000 0.390244 0.37777817 -1.000000 0.500000 0.48635218 -0.750000 0.640000 0.63969919 -0.500000 0.800000 0.81062520 -0.250000 0.941176 0.94747121 0.000000 1.000000 1.00000022 0.250000 0.941176 0.94747123 0.500000 0.800000 0.81062524 0.750000 0.640000 0.63969925 1.000000 0.500000 0.48635226 1.250000 0.390244 0.37777827 1.500000 0.307692 0.30933028 1.750000 0.246154 0.25865429 2.000000 0.200000 0.20870030 2.250000 0.164948 0.16073231 2.500000 0.137931 0.12729832 2.750000 0.116788 0.11351633 3.000000 0.100000 0.10750934 3.250000 0.086486 0.09299035 3.500000 0.075472 0.07103936 3.750000 0.066390 0.05976937 4.000000 0.058824 0.06306138 4.250000 0.052459 0.05664939 4.500000 0.047059 0.04053640 4.750000 0.042440 0.04820041 5.000000 0.038462 0.044391上圖顯示利用Chebyshev Polynomial的根當做內插多項式的節點, 此內插多項式與函數相當吻合, 多項式在非節點的值與函數差距不大.7. Richardson Extrapolation顯示rhextrap.m的內容type rhextrap.mfunction D=rhextrap(s, a, n, h)%Richardson Extrapolation for 1st derivative%at some point a, by f'(a)~(f(a+h)-f(a-h))/2h%syms x ;fun=sym(s);for i=1:n+1D(i,1)= (subs(fun,x,a+h)- subs(fun,x,a-h))/(2*h);for j= 1:i-1D(i,j+1)=D(i,j)+(D(i,j)-D(i-1,j))/(4^j -1) ;endh = h/2 ;end例題 : To find the approximation value f'(x0) of f(x) = sin x at x0 = 1.23096準備必要的參數s = 'sin(x)' ;h = 1.0 ;a = 1.23096 ;n = 3 ;rhs = rhextrap(s, a, n, h)從上面的數據我們得到 f'(x0)的近似值 0.3333, 採用Matlab 'format long'比較cos( x0 )之值, 我們可達到小數點後九位, O(h8)的效果format longrhscos(a)format shortrhs =0.28048986601862 0 0 00.31961649900430 0.33265870999952 0 00.32987140204065 0.33328970305277 0.33333176925632 00.33246540778694 0.33333007636904 0.333332767923460.33333278377532ans =0.333332783996898 Natural Cubic Spline–有關的m-file 請參考輔助教材chapter5.doc . ncspline.m --計算三次 natural spline interpolation at knots t0,t1,t2, …,t n with S(t i) = y i , S''(t0) = S''(t n) =0有關的係數 c i。
编程实现Hermit多项式的逼近问题(智能控制技术试验)

智能控制理论与应用实验实验三:利用MATLAB神经网络工具箱编程实现Hermit多项式逼近一、实验目的:(1)加深对神经网络控制概念的理解;(2)掌握神经网络工具箱的应用;(3)熟练编程操作。
二、实验内容:利用MATLAB神经网络工具箱编程实现Hermit多项式逼近。
三、实验步骤:F(x)=1.1*(1—x+2*x2)exp(—x2/2)训练样本按以下方式产生:样本数P=100,其中输入样本X1服从区间[-4,4]内的均匀分布,样本输出为F(xi)+ei,ei为添加的噪声,服从均值为0,标准差为0.1的正态分布。
(1)试用聚类方法求数据中心和扩展常数,输出权值和阈值用伪逆法求解。
隐节点数M=10,隐节点重叠系数λ=1,初始聚类中心取前10个训练样本。
(2)试用梯度算法训练RBF网络,设η=0.001,M=10,初始权值为[-0.1,0.1]内的随机数,初始数据中心为[-4.0,4.0]内的随机数,初始扩展常数取[0.1,0.3]内的随机数,目标误差为0.9,最大训练次数为5000。
(3)编写代码如下:function main()SamNum=100;TestSamNum=101;InDim=1;ClusterNum=10;Overdap=1.0;rand('state',sum(100*clock))NoiseVar=0.1;Noise=NoiseVar*rand(1,SamNum);Samln=8*rand(1,SamNum)-4;SamOutNoNoise=1.1*(1-SamIn+2*SamIn.^2).*exp(-SamIn.^2/2);SamOut=SamOutNoNoise+Noise;TestSamIn=-4:0.08:4;TestSamOut=1.1*(1-TestSamIn+2*TestSamIn.^2).*exp(-TestSamIn.^2/2); figurehold ongridplot(SamIn,SamOut,'k+')plot(TestSamIn,TestSamOut,'k-')xlabel('Input x');ylabel('Output y');Centers=SamIn(:,1:ClusterNum);NumberInClustem=zeros(ClusterNum,1);IndexInClusters=zeros(ClusterNum,SamNum);while 1NumberInClustem=zeros(ClusterNum,1);IndexInClusters=zeros(ClusterNum,SamNum);for i=1:SantNumAllDistance=dist(Center,SamIn(:,i);[MinDist,Pos]=min(AllDistance);NumberInClusters(pos)=NumberInClusters(pos)+1; IndexInClusters(Pos,NumberInClusters(Pos))=i;endOldCenters=Centers;for i=1:ClusterNumIndex=IndexInClusters(i,1:NumberInClusters((i)); Centers(:,i)=mean(SamIn(:,Index)')';endEqualNum=Sum(sun(Centers==OldCenters));if EqualNum==InDim*ClusterNum,break,endendAllDistances=dist(Centers',Centers);Maximum=max(max(AllDistances));for i=1:ClusterNumAllDistances(i,i)=Maximum+1;endSpreads=Overlap*min(AllDistances)';Distance=dist(Centers',SamIn);SpreadsMat=repmat(Spreads,1,SamNunl);HiddenUnitOut=radbas(Distance./SpreadsMat) HiddenUnitOutEx=[HiddenUnitOut'ones(SamNum,1)]';W2Ex=SamOut*pinv(HiddenUnitOutEx);W2=W2Ex(:,1:ClusterNum);B2=W2Ex(:,ClusterNum+1);TestDistance=dist(Centers',TestSamIn);TestSpreadsMat=repmat(Spreads,1,TeasSamNum); TestHiddenUnitOut=radbas(TestDistance./TestSpreadsMat); TestNNOut=W2*TestHiddenUnitOut+B2;plot(TestSamIn,TestNN+t,'k-')(4)编写代码说明:SamNum为训练样本数;TestSamNum为测试样本数;InDim为样本输入维数;ClusterNum为隐节点数,即聚类样本数;Overdap为隐节点重叠系数;在while语句之前将各类样本数初始化为零,语句如下:NumberInClustem=zeros(ClusterNum,1);IndexInClusters=zeros(ClusterNum,SamNum)表示各类语句的索取号;然后按照最小距离原则对所有样本进行分类,保存了旧的聚类中心后再重新计算各类的聚类中心,如果新旧聚类中心一致,则结束聚类。
埃尔米特曲线 matlab

埃尔米特曲线matlab埃尔米特曲线(Hermite Curve)是一种用于表示曲线的数学曲线。
在MATLAB 中,你可以使用hermite函数来生成埃尔米特曲线。
hermite函数的基本语法如下:H = hermite(X, Y, M, T);埃尔米特曲线(Hermite Curve)是一种用于表示曲线的数学曲线。
在MATLAB 中,你可以使用hermite函数来生成埃尔米特曲线。
hermite函数的基本语法如下:matlabCopy codeH = hermite(X, Y, M, T);其中:•X和Y是输入点的横纵坐标向量。
•M是每个点对应的切向量的斜率向量。
•T是参数向量,用于生成曲线上的点。
以下是一个简单的MATLAB 示例,演示如何使用hermite函数创建埃尔米特曲线:定义输入点X = [0, 1, 2, 3];Y = [0, 1, 0, 1];定义切向量的斜率M = [1, 2, -1, -2];定义参数向量T = linspace(0, 1, 100);生成埃尔米特曲线上的点H = hermite(X, Y, M, T);绘制埃尔米特曲线plot(H(1, :), H(2, :), 'r-', X, Y, 'bo');title('Hermite Curve');xlabel('X');ylabel('Y');legend('Hermite Curve', 'Control Points', 'Location', 'Best');grid on;在这个示例中,X和Y定义了控制点,M定义了每个点对应的切向量的斜率,T定义了参数向量。
hermite函数生成埃尔米特曲线上的点,然后使用plot函数绘制曲线和控制点。
请根据你的具体需求调整控制点、切向量等参数。
