(完整word)2012年高考试题理科数学(新课标1卷)
2012年山东省高考数学试题(附答案和解释)(理科Word版)

2012年山东省高考数学试题(附答案和解释)(理科Word版)2012年普通高等学校招生全国统一考试(山东卷)理科数学本试卷分第I卷和第II卷两部分,共4页。
满分150分。
考试用时120分钟,考试结束,务必将试卷和答题卡一并上交。
注意事项: 1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
参考公式:锥体的体积公式:V= Sh,其中S是锥体的底面积,h是锥体的高。
如果事件A,B互斥,那么P(A+B)=P(A)+P(B);如果事件A,B独立,那么P(AB)=P(A)•P(B)。
第I卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1 若复数x满足z(2-i)=11+7i(i为虚数单位),则z为 A 3+5i B 3-5i C -3+5i D -3-5i 解析: .答案选A。
另解:设,则根据复数相等可知,解得,于是。
2 已知全集 ={0,1,2,3,4},集合A={1,2,3,},B={2,4} ,则(CuA) B为 A {1,2,4} B {2,3,4} C {0,2,4} D {0,2,3,4} 解析:。
答案选C。
3 设a>0 a≠1 ,则“函数f(x)= ax在R上是减函数”,是“函数g(x)=(2-a) 在R上是增函数”的 A 充分不必要条件 B 必要不充分条件 C 充分必要条件 D 既不充分也不必要条件解析:p:“函数f(x)= ax在R上是减函数”等价于;q:“函数g(x)=(2-a) 在R 上是增函数”等价于,即且a≠1,故p是q成立的充分不必要条件. 答案选A。
2012年高考湖南理科数学试卷和答案(word完美解析版)

2012年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合}1,0,1{-=M ,}{2x x x N ≤=,则=N MA .}0{B .}1,0{C .}1,1{-D .}1,0,1{- 【答案】B【解析】{}0,1N = M={-1,0,1} ∴M ∩N={0,1}. 【点评】本题考查了集合的基本运算,较简单,易得分. 先求出{}0,1N =,再利用交集定义得出M ∩N.2.命题“若4πα=,则1tan =α”的逆否命题是A .若4πα≠,则1tan ≠α B .若4πα=,则1tan ≠αC .若1tan ≠α,则4πα≠ D .若1tan ≠α,则4πα=【答案】C【解析】因为“若p ,则q ”的逆否命题为“若p ⌝,则q ⌝”,所以 “若α=4π,则tan α=1”的逆否命题是 “若tan α≠1,则α≠4π”. 【点评】本题考查了“若p ,则q ”形式的命题的逆命题、否命题与逆否命题,考查分析问题的能力.3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能...是A B C D 【答案】D【解析】本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.【点评】本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型.4.设某大学的女生体重y (单位:kg )与身高x (单位:cm )具有线性相关关系,根据一组样本数据),(i i y x ),,2,1(n i =,用最小二乘法建立的回归方程为71.8585.0ˆ-=x y ,则下列结论中不正确...的是 A .y 与x 具有正的线性相关关系 B .回归直线过样本点的中心),(y xC .若该大学某女生身高增加1cm ,则其体重约增加85.0kgD .若该大学某女生身高为170cm ,则可断定其体重比为79.58kg 【答案】D【解析】由回归方程为 y =0.85x-85.71知y 随x 的增大而增大,所以y 与x 具有正的线性相关关系,由最小二乘法建立的回归方程得过程知ˆ()ybx a bx y bx a y bx =+=+-=-,所以回归直线过样本点的中心(x ,y ),利用回归方程可以预测估计总体,所以D 不正确. 【点评】本题组要考查两个变量间的相关性、最小二乘法及正相关、负相关的概念,并且是找不正确的答案,易错.5.已知双曲线1:2222=-by a x C 的焦距为10 ,点)1,2(P 在C 的渐近线上,则C 的方程为A .152022=-y x B .120522=-y x C .1208022=-y x D .1802022=-y x 【答案】A【解析】设双曲线C :22x a -22y b=1的半焦距为c ,则210,5c c ==.又 C 的渐近线为b y x a =±,点P (2,1)在C 的渐近线上,12ba∴= ,即2a b =.又222c a b =+,a ∴==∴C 的方程为220x -25y =1.【点评】本题考查双曲线的方程、双曲线的渐近线方程等基础知识,考查了数形结合的思想和基本运算能力,是近年来常考题型.6.函数)6cos(sin )(π+-=x x x f 的值域为A .]2,2[-B .]3,3[-C .]1,1[-D .]23,23[- 【答案】B【解析】f (x )=sinx-cos(x+6π)1sin sin )26x x x x π=+=-,[]sin()1,16x π-∈- ,()f x ∴值域为【点评】利用三角恒等变换把()f x 化成sin()A x ωϕ+的形式,利用[]sin()1,1x ωϕ+∈-,求得()f x 的值域.7.在ABC ∆中,2=AB ,3=AC ,1=⋅BC AB ,则=BCA B C . D 【答案】A【解析】由下图知AB BC = cos()2(cos )1AB BC B BC B π-=⨯⨯-=.1cos 2B BC∴=-.又由余弦定理知222cos 2AB BC AC B AB BC+-=⋅,解得BC =【点评】本题考查平面向量的数量积运算、余弦定理等知识.考查运算能力,考查数形结合思想、等价转化思想等数学思想方法.需要注意,AB BC的夹角为B ∠的外角.8.已知两条直线m y l =:1和)0(128:2>+=m m y l ,1l 与函数x y 2log =的图像从左至右相交于点B A ,,2l 与函数x y 2log =的图像从左至右相交于点D C ,.记线段AC 和BD 在x 轴上的投影长度分别为b a ,.当m 变化时,ba的最小值为 A. B. C .348 D .344 【答案】B【解析】在同一坐标系中作出y=m ,y=821m +(m >0),2log y x =图像如下图,由2log x = m ,得122,2mmx x -==,2log x = 821m +,得821821342,2m m x x +-+==.依照题意得8218218218212222,22,22m m mmmm m m b a b a++--+--+-=-=-=-821821222m m mm +++==.8141114312122222m m m m +=++-≥-=++,min ()b a ∴=【点评】在同一坐标系中作出y=m ,y=821m +(m >0),2log y x =图像,结合图像可C821m =+xm解得.二、填空题: 本大题共8小题,考生作答7小题,每小题5分 ,共35分,把答案填在答.题卡..中对应题号后的横线上. (一)选做题(请考生在第9,10,11三题中任选两题作答,如果全做,则按前两题记分)9. 在直角坐标系xOy 中,已知曲线⎩⎨⎧-=+=t y t x C 21,1:1(t 为参数)与曲线⎩⎨⎧==θθcos 3,sin :2y a x C (θ为参数,0>a )有一个公共点在x 轴上,则=a . 【答案】32【解析】曲线1C :1,12x t y t=+⎧⎨=-⎩直角坐标方程为32y x =-,与x 轴交点为3(,0)2;曲线2C :sin ,3cos x a y θθ=⎧⎨=⎩直角坐标方程为22219x y a +=,其与x 轴交点为(,0),(,0)a a -, 由0a >,曲线1C 与曲线2C 有一个公共点在X 轴上,知32a =. 【点评】本题考查直线的参数方程、椭圆的参数方程,考查等价转化的思想方法等.曲线1C 与曲线2C 的参数方程分别等价转化为直角坐标方程,找出与x 轴交点,即可求得.10.不等式01212>--+x x 的解集为 . 【答案】14x x ⎧⎫>⎨⎬⎩⎭【解析】令()2121f x x x =+--,则由()f x 13,()2141,(1)23,(1)x x x x ⎧-<-⎪⎪⎪=--≤≤⎨⎪>⎪⎪⎩得()f x 0>的解集为14x x ⎧⎫>⎨⎬⎩⎭.【点评】绝对值不等式解法的关键步骤是去绝对值,转化为代数不等式(组).11.如图2,过点P 的直线与⊙O 相交于B A ,两点.若1=PA ,2=AB ,3=PO ,则⊙O 的半径等于 .【答案】14x x ⎧⎫>⎨⎬⎩⎭【解析】令()2121f x x x =+--,则由()f x 13,()2141,(1)23,(1)x x x x ⎧-<-⎪⎪⎪=--≤≤⎨⎪>⎪⎪⎩得()f x 0>的解集为14x x ⎧⎫>⎨⎬⎩⎭.【点评】绝对值不等式解法的关键步骤是去绝对值,转化为代数不等式(组).(二)必做题(12~16题)12.已知复数2)3(i z +=(i 为虚数单位),则=z . 【答案】10【解析】2(3)z i =+=29686i i i ++=+,10z ==.【点评】本题考查复数的运算、复数的模.把复数化成标准的(,)a bi a b R +∈形式,利用z =.13.6)12(xx -的二项展开式中的常数项为 .(用数字作答)【答案】-160 【解析】()6的展开式项公式是663166C (C 2(1)r r r r rr r r T x ---+==-.由题意知30,3r r -==,所以二项展开式中的常数项为33346C 2(1)160T =-=-.【点评】本题主要考察二项式定理,写出二项展开式的通项公式是解决这类问题的常规办法.14.如果执行如图3所示的程序框图,输入3,1=-=n x ,则输出的数=S .【答案】4-【解析】输入1x =-,n =3,,执行过程如下:2:6233i S ==-++=-;1:3(1)115i S ==--++=;0:5(1)014i S ==-++=-,所以输出的是4-.【点评】本题考查算法流程图,要明白循环结构中的内容,一般解法是逐步执行,一步步将执行结果写出,特别是程序框图的执行次数不能出错.15.函数)sin()(ϕω+=x x f 的导函数)(x f y '=的部分图象如图4所示,其中,P 为图象与y 轴的交点,C A ,为图象与x 轴的两个交点,B 为图象的最低点.(1)若6πϕ=,点P 的坐标为)233,0(,则=ω ; (2)若在曲线段ABC 与x 轴所围成的区域内随机取一点,则该点在ABC ∆内的概率为 .【答案】(1)3;(2)4π【解析】(1)()y f x '=cos()x ωωϕ=+,当6πϕ=,点P 的坐标为(0)时cos362πωω=∴=; (2)由图知222T AC ππωω===,122ABC S AC πω=⋅= ,设,A B 的横坐标分别为,a b .设曲线段ABC 与x轴所围成的区域的面积为S则()()sin()sin()2bbaaS f x dx f x a b ωϕωϕ'===+-+=⎰,由几何概型知该点在△ABC内的概率为224ABC S P S ππ=== . 【点评】本题考查三角函数的图像与性质、几何概型等,(1)利用点P 在图像上求ω,(2)几何概型,求出三角形面积及曲边形面积,代入公式即得.16.设*2(,)nN n N n =∈≥2,将N 个数12,,,N x x x 依次放入编号为1,2,,N 的N 个位置,得到排列012N P x x x = .将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前2N 和后2N个位置,得到排列113124N N P x x x x x x -= ,将此操作称为C 变换.将1P 分成两段,每段2N个数,并对每段作C 变换,得到2P ;当22i n ≤≤-时,将i P 分成2i 段,每段2iN个数,并对每段作C 变换,得到1i P +.例如,当8N =时,215372648P x x x x x x x x =,此时7x 位于2P 中的第4个位置. (1)当16N =时,7x 位于2P 中的第 个位置; (2)当2()nN n =≥8时,173x 位于4P 中的第 个位置. 【答案】(1)6;(2)43211n -⨯+【解析】(1)当N=16时,012345616P x x x x x x x = ,可设为(1,2,3,4,5,6,,16) ,113571524616P x x x x x x x x x = ,即为(1,3,5,7,9,2,4,6,8,,16) ,2159133711152616P x x x x x x x x x x x = ,即(1,5,9,13,3,7,11,15,2,6,,16) , x 7位于P 2中的第6个位置,;(2)方法同(1),归纳推理知x 173位于P 4中的第43211n -⨯+个位置.【点评】本题考查在新环境下的创新意识,考查运算能力,考查创造性解决问题的能力. 需要在学习中培养自己动脑的习惯,才可顺利解决此类问题.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.已知这100位顾客中的一次购物量超过8件的顾客占55%.(Ⅰ)确定,x y 的值,并求顾客一次购物的结算时间X 的分布列与数学期望; (Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过...2.5分钟的概率.(注:将频率视为概率) 【解析】(1)由已知,得251055,35,y x y ++=+=所以15,20.x y ==该超市所有顾客一次购物的结算时间组成一个总体,所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,将频率视为概率得153303251(1),( 1.5),(2),10020100101004p X p X p X =========201101( 2.5),(3).100510010p X p X ====== X 的分布为X 的数学期望为33111()11.522.53 1.920104510E X =⨯+⨯+⨯+⨯+⨯=. (Ⅱ)记A 为事件“该顾客结算前的等候时间不超过2.5分钟”,(1,2)i X i =为该顾客前面第i 位顾客的结算时间,则121212()(11)(1 1.5)( 1.51)P A P X X P X X P X X ===+==+==且且且. 由于顾客的结算相互独立,且12,X X 的分布列都与X 的分布列相同,所以 121212()(1)1)(1)( 1.5)( 1.5)(1)P A P X P X P X P X P X P X ==⨯=+=⨯=+=⨯=( 333333920202010102080=⨯+⨯+⨯=. 故该顾客结算前的等候时间不超过2.5分钟的概率为980. 【点评】本题考查概率统计的基础知识,考查分布列及数学期望的计算,考查运算能力、分析问题能力.第一问中根据统计表和100位顾客中的一次购物量超过8件的顾客占55%知251010055%,35,y x y ++=⨯+=从而解得,x y ,计算每一个变量对应的概率,从而求得分布列和期望;第二问,通过设事件,判断事件之间互斥关系,从而求得该顾客结算前的等候时间不超过...2.5分钟的概率.18.(本小题满分12分)如图5,在四棱锥P ABCD -中,PA ⊥平面ABCD ,4AB =,3BC =,5AD =,90DAB ABC ∠=∠=︒,E 是CD 的中点.(Ⅰ)证明:CD ⊥平面PAE ;(Ⅱ)若直线PB 与平面PAE 所成的角和PB 与平面ABCD 所成的角相等,求四棱锥P ABCD -的体积.【解析】解法1(Ⅰ如图(1)),连接AC ,由AB=4,3BC =,90 5.ABC AC ∠==,得5,AD =又E是CD的中点,所以.CD AE ⊥,,PA ABCD CD ABCD ⊥⊂ 平面平面所以.PA CD ⊥而,PA AE 是平面PAE 内的两条相交直线,所以CD ⊥平面PAE. (Ⅱ)过点B作,,,,.BG CD AE AD F G PF //分别与相交于连接由(Ⅰ)CD ⊥平面PAE 知,BG⊥平面PAE.于是BPF ∠为直线PB与平面PAE 所成的角,且BG AE ⊥.由PA ABCD ⊥平面知,PBA ∠为直线PB 与平面ABCD 所成的角.4,2,,AB AG BG AF ==⊥由题意,知,PBA BPF ∠=∠ 因为sin ,sin ,PA BF PBA BPF PB PB∠=∠=所以.PA BF = 由90//,//,DAB ABC AD BC BG CD ∠=∠= 知,又所以四边形BCDG 是平行四边形,故 3.GD BC ==于是 2.AG =在Rt ΔBAG 中,4,2,,AB AG BG AF ==⊥所以2AB BG BF BG =====于是5PA BF == 又梯形ABCD 的面积为1(53)416,2S =⨯+⨯=所以四棱锥P ABCD -的体积为111633515V S PA =⨯⨯=⨯⨯=解法2:如图(2),以A 为坐标原点,,,AB AD AP 所在直线分别为x y z 轴,轴,轴建立空间直角坐标系.设,PA h =则相关的各点坐标为:(4,0,0),(4,0,0),(4,3,0),(0,5,0),(2,4,0),(0,0,).A B C D E P h(Ⅰ)易知(4,2,0),(2,4,0),(0,0,).CD AE AP h =-== 因为8800,0,CD AE CD AP ⋅=-++=⋅= 所以,.CD AE CD AP ⊥⊥而,AP AE 是平面PAE 内的两条相交直线,所以.CD PAE ⊥平面(Ⅱ)由题设和(Ⅰ)知,,CD AP 分别是PAE 平面,ABCD 平面的法向量,而PB 与PAE 平面所成的角和PB 与ABCD 平面所成的角相等,所以cos ,cos ,.CD PB PA PB CD PB PA PB CD PB PA PB⋅⋅<>=<>=⋅⋅ ,即 由(Ⅰ)知,(4,2,0),(0,0,),CD AP h =-=- 由(4,0,),PB h =- 故=解得5h =. 又梯形ABCD 的面积为1(53)4162S =⨯+⨯=,所以四棱锥P ABCD -的体积为1151633515V S PA =⨯⨯=⨯⨯=. 【点评】本题考查空间线面垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明PA CD ⊥即可,第二问算出梯形的面积和棱锥的高,由13V S PA =⨯⨯算得体积,或者建立空间直角坐标系,求得高几体积.19.(本小题满分12分)已知数列{}n a 的各项均为正数,记12()n A n a a a =+++ ,231()n B n a a a +=+++ ,342()n C n a a a +=+++ ,1,2,.n =(Ⅰ)若121,5a a ==,且对任意*n N ∈,三个数(),(),()A n B n C n 组成等差数列,求数列{}n a 的通项公式.(Ⅱ)证明:数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意*n N ∈,三个数(),(),()A n B n C n 组成公比为q 的等比数列.【解析】解(1)对任意N n *∈,三个数(),(),()A n B n C n 是等差数列,所以()()()(),B n A n C n B n -=-即112,n n a a a ++-=亦即2121 4.n n a a a a +--=-=故数列{}n a 是首项为1,公差为4的等差数列.于是1(1)44 3.n a n n =+-⨯=-(Ⅱ)(1)必要性:若数列{}n a 是公比为q的等比数列,则对任意N n *∈,有 1.n nq a a -=由0n a >知,(),(),()A n B n C n 均大于0,于是12)2311212(......(),()......n n n nq a a a a a a B n q A n a a a a a a +++++++===++++++ 231)342231231(......(),()......n n n n q a a a a a a C n q B n a a a a a a ++++++++++===++++++ 即()()B n A n =()()C n B n =q ,所以三个数(),(),()A n B n C n 组成公比为q 的等比数列. (2)充分性:若对于任意N n *∈,三个数(),(),()A n B n C n 组成公比为q 的等比数列,则()(),()B n q A n C n q B n==, 于是[]()()()(),C n B n q B n A n -=-得2211(),n n a a q a a ++-=-即212.n n a qa a a ++-=-由1n =有(1)(1),B qA =即21a qa =,从而210n n a qa ++-=.因为0n a >,所以2211n n a a q a a ++==,故数列{}n a 是首项为1a ,公比为q 的等比数列, 综上所述,数列{}n a 是公比为q 的等比数列的充分必要条件是:对任意n ∈N ﹡,三个数(),(),()A n B n C n 组成公比为q 的等比数列.【点评】本题考查等差数列、等比数列的定义、性质及充要条件的证明.第一问由等差数列定义可得;第二问要从充分性、必要性两方面来证明,利用等比数列的定义及性质易得证.20.(本小题满分13分)某企业接到生产3000台某产品的A ,B ,C 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A 部件6件,或B 部件3件,或C 部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B 部件的人数与生产A 部件的人数成正比,比例系数为k (k 为正整数).(Ⅰ)设生产A 部件的人数为x ,分别写出完成A ,B ,C 三种部件生产需要的时间; (Ⅱ)假设这三种部件的生产同时开工,试确定正整数k 的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.【解析】解:(Ⅰ)设完成A,B,C 三种部件的生产任务需要的时间(单位:天)分别为123(),(),(),T x T x T x 由题设有1232300010*******50(),(),(),6200(1)T x T x T x x x k x k x ⨯====-+ 期中,,200(1)x kx k x -+均为1到200之间的正整数.(Ⅱ)完成订单任务的时间为{}123()max (),(),(),f x T x T x T x =其定义域为2000,.1x x x N k *⎧⎫<<∈⎨⎬+⎩⎭易知,12(),()T x T x 为减函数,3()T x 为增函数.注意到212()(),T x T x k =于是(1)当2k =时,12()(),T x T x = 此时{}1310001500()max (),()max ,2003f x T x T x x x ⎧⎫==⎨⎬-⎩⎭,由函数13(),()T x T x 的单调性知,当100015002003x x =-时()f x 取得最小值,解得4009x =.由于134002503004445,(44)(44),(45)(45),(44)(45)91113f T f T f f <<====<而.故当44x =时完成订单任务的时间最短,且最短时间为250(44)11f =.(2)当2k >时,12()(),T x T x > 由于k 为正整数,故3k ≥,此时{}1375(),()max (),()50T x x T x T x x ϕ==-易知()T x 为增函数,则{}13()max (),()f x T x T x ={}1max (),()T x T x ≥1000375()max ,50x x x ϕ⎧⎫==⎨⎬-⎩⎭. 由函数1(),()T x T x 的单调性知,当100037550x x =-时()x ϕ取得最小值,解得40011x =.由于14002502503752503637,(36)(36),(37)(37),119111311T T ϕϕ<<==>==>而 此时完成订单任务的最短时间大于25011. (3)当2k <时,12()(),T x T x < 由于k 为正整数,故1k =,此时{}232000750()max (),()max ,.100f x T x T x x x ⎧⎫==⎨⎬-⎩⎭由函数23(),()T x T x 的单调性知, 当2000750100x x =-时()f x 取得最小值,解得80011x =.类似(1)的讨论.此时 完成订单任务的最短时间为2509,大于25011. 综上所述,当2k =时完成订单任务的时间最短,此时生产A,B,C三种部件的人数 分别为44,88,68.【点评】本题为函数的应用题,考查分段函数、函数单调性、最值等,考查运算能力及用数学知识分析解决实际应用问题的能力.第一问建立函数模型;第二问利用单调性与最值来解决,体现分类讨论思想.21.(本小题满分13分)在直角坐标系xOy 中,曲线1C 上的点均在圆222:(5)9C x y -+=外,且对1C 上任意一点M ,M 到直线2x =-的距离等于该点与圆2C 上点的距离的最小值.(Ⅰ)求曲线1C 的方程;(Ⅱ)设000(,)(3)P x y y ≠±为圆2C 外一点,过P 作圆2C 的两条切线,分别与曲线1C 相交于点,A B 和,C D .证明:当P 在直线4x =-上运动时,四点,A B ,,C D 的纵坐标之积为定值.【解析】(Ⅰ)解法1 :设M 的坐标为(,)x y ,由已知得23x +=,易知圆2C 上的点位于直线2x =-的右侧.于是20x +>,所以5x =+.化简得曲线1C 的方程为220y x =.解法2 :由题设知,曲线1C 上任意一点M 到圆心2C (5,0)的距离等于它到直线5x =-的距离,因此,曲线1C 是以(5,0)为焦点,直线5x =-为准线的抛物线,故其方程为220y x =.(Ⅱ)当点P 在直线4x =-上运动时,P 的坐标为0(4,)y -,又03y ≠±,则过P 且与圆 2C 相切得直线的斜率k 存在且不为0,每条切线都与抛物线有两个交点,切线方程为0(4),y y k x -=+0即kx-y+y +4k=0.于是3.=整理得2200721890.k y k y ++-= ① 设过P 所作的两条切线,PA PC 的斜率分别为12,k k ,则12,k k 是方程①的两个实根,故001218.724y y k k +=-=- ② 由101240,20,k x y y k y x -++=⎧⎨=⎩得21012020(4)0.k y y y k -++= ③ 设四点A,B,C,D 的纵坐标分别为1234,,,y y y y ,则是方程③的两个实根,所以0112120(4).y k y y k +⋅=④ 同理可得 0234220(4).y k y y k +⋅=⑤ 于是由②,④,⑤三式得 010*******400(4)(4)y k y k y y y y k k ++=2012012124004()16y k k y k k k k ⎡⎤+++⎣⎦= 22001212400166400y y k k k k ⎡⎤-+⎣⎦=.所以,当P 在直线4x =-上运动时,四点A ,B ,C ,D 的纵坐标之积为定值6400.【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问用直接法或定义法求出曲线的方程;第二问设出切线方程,把直线与曲线方程联立,由一元二次方程根与系数的关系得到,,,A B C D 四点纵坐标之积为定值,体现“设而不求”思想.22.(本小题满分13分)已知函数()ax f x e x =-,其中0a ≠.(Ⅰ)若对一切x R ∈,()1f x ≥恒成立,求a 的取值集合.(Ⅱ)在函数()f x 的图像上取定两点112212(,()),(,())()A x f x B x f x x x <,记直线AB 的斜率为k .问:是否存在012(,)x x x ∈,使()f x k '>成立?若存在,求0x 的取值范围;若不存在,请说明理由.【解析】(Ⅰ)若0a <,则对一切0x >,()f x 1ax e x =-<,这与题设矛盾,又0a ≠,故0a >.而()1,ax f x ae '=-令11()0,ln .f x x a a'==得 当11ln x a a <时,()0,()f x f x '<单调递减;当11ln x a a>时,()0,()f x f x '>单调递增,故当11ln x a a =时,()f x 取最小值11111(ln )ln .f a a a a a =- 于是对一切,()1x R f x ∈≥恒成立,当且仅当111ln 1a a a-≥. ① 令()ln ,g t t t t =-则()ln .g t t '=-当01t <<时,()0,()g t g t '>单调递增;当1t >时,()0,()g t g t '<单调递减.故当1t =时,()g t 取最大值(1)1g =.因此,当且仅当11a=即1a =时,①式成立. 综上所述,a 的取值集合为{}1. (Ⅱ)由题意知,21212121()() 1.ax ax f x f x e e k x x x x --==--- 令2121()(),ax ax axe e xf x k ae x x ϕ-'=-=--则 121()12121()()1,ax a x x e x e a x x x x ϕ-⎡⎤=----⎣⎦- 212()21221()()1.ax a x x e x e a x x x x ϕ-⎡⎤=---⎣⎦- 令()1tF t e t =--,则()1t F t e '=-.当0t <时,()0,()F t F t '<单调递减;当0t >时,()0,()F t F t '>单调递增.故当0t =,()(0)0,F t F >=即10.t e t --> 从而21()21()10a x x e a x x ---->,12()12()10,a x x e a x x ---->又1210,ax e x x >-2210,ax e x x >- 所以1()0,x ϕ<2()0.x ϕ>因为函数()y x ϕ=在区间[]12,x x 上的图像是连续不断的一条曲线,所以存在),(21x x c ∈,使0)(=c ϕ,2()0,()axx a e x ϕϕ'=>单调递增,故这样的c 是唯一的,且21211ln ()ax ax e e c a a x x -=-.故当且仅当212211(ln ,)()ax ax e e x x a a x x -∈-时, 0()f x k '>. 综上所述,存在012(,)x x x ∈使0()f x k '>成立.且0x 的取值范围为212211(ln ,)()ax ax e e x a a x x --. 【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想,转化与划归思想等数学思想方法.第一问利用导函数法求出()f x 取最小值11111(ln )ln .f a a a a a=-对一切x ∈R ,f(x) ≥1恒成立转化为min ()1f x ,从而得出a 的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.。
2012年新课标数学高考试题(理科数学理科数学高考试题,word教师版【免费下载】)

2012年普通高等学校招生全国统一考试(新课标) 理科数学第一卷一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素的个数为( )()A 3()B 6 ()C 8 ()D 10【解析】选D5,1,2,3,x y ==,4,1,2,3x y ==,3,1,2x y ==,2,1x y ==共10个 (2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )()A 12种()B 10种 ()C 9种()D 8种【解析】选A甲地由1名教师和2名学生:122412C C =种 (3)下面是关于复数21z i=-+的四个命题:其中的真命题为( )1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【解析】选C 22(1)11(1)(1)iz i ii i --===---+-+--1:p z =22:2p z i =,3:p z 的共轭复数为1i -+,4:p z 的虚部为1-(4)设12F F 是椭圆2222:1(0)x y E a b ab+=>>的左、右焦点,P 为直线32a x =上一点,∆21F P F 是底角为30 的等腰三角形,则E 的离心率为( )()A 12()B23()C 34()D 45【解析】选C ∆21F P F 是底角为30的等腰三角形221332()224c P F F F a c c e a ⇒==-=⇔==(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( )()A 7()B 5 ()C -5()D -7【解析】选D472a a +=,56474784,2a a a a a a ==-⇒==-或472,4a a =-= 471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-(6)如果执行右边的程序框图,输入正整数(2)N N ≥和实数12,,...,n a a a ,输出,A B ,则( )()A A B +为12,,...,n a a a 的和()B 2A B +为12,,...,n a a a 的算术平均数()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A和B 分别是12,,...,n a a a 中最小的数和最大的数【解析】选C(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )()A 6()B 9 ()C 12 ()D 18【解析】选B该几何体是三棱锥,底面是俯视图,高为3 此几何体的体积为11633932V =⨯⨯⨯⨯=(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =C 的实轴长为( )()A ()B ()C 4 ()D 8【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(4,A -(4,B --得:222(4)4224a a a =--=⇔=⇔=(9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
2012年数学高考试题(甘肃卷)(理工农医类)

B A ,则 m
D.1 或 3
C.1 或 3
B A B A ,因为 A {1,3, m}, B {1, m} ,
m ,所以 m 3, m 0, m 1 (舍去),
所以 m A m 3或m
所以 m 3, m 0 ,故选 B. 【点评】本题主要考查了集合的概念和集合的并集运算,集合的关系的运用,元素与集合的关系的综合运 用,同时考查了分类讨论的思想. 3.椭圆的中心在原点,焦距为 4,一条准线为 x 4 ,则该椭圆的方程为 A.
作者:曹亚云
2012 年普通高等学校招生全国统一考试 理科数学(大纲卷)
一.选择题 1.复数
1 3i 1 i A. 2 i B. 2 i
C. 1 2i
D. 1 2i
【答案】C 【解析 1】i 2 4i 1 2i ,故选 C. 1 i 2 1 i 1 i
【解析 2】Excel2013 1.A1 单元格输入公式=IMSUM(-1,"3i"); 2.B1 单元格输入公式=IMSUM(1,"i"); 3.C1 单元格输入公式=Imdiv(A1,B1),回车得复数 1+2i。
【解析 3】Mathematica9.0 In[1]:=
−1+3ⅈ 1+ⅈ
Out[1]=1 + 2ⅈ 【点评】本题主要考查了复数的四则运算,通过利用除法运算求解复数. 2.已知集合 A {1,3, m} , B {1, m} , A A.0 或 3 【答案】B 【解析】由题意得, A B.0 或 3
【解析】 由题意得, 椭圆的一条准线方程为 x 4 , 即 【点评】 本题主要考查了椭圆的方程以及椭圆的几何性质的运用, 通过椭圆的准线方程确定焦点的位置, 然 后借助于焦距和准线求解参数 a, b, c 从而得到椭圆的方程. 4.已知正四棱柱 ABCD A1B1C1D1 中, AB 2 , CC1 2 2 ,E 为 CC1 的中点,则直线 AC1 与平面 BED 的距离为
2012年高考语法题(18套完整版)

2012年高考语法题(18套完整版)安徽卷21. Carl is studying food science at college and hopes to open up meatprocessing factory of his own one day.A. / ;aB. / ;theC. the ; aD. the ; the22.——May I help you? You seem to be having some problems.——, thanks. I think I can manage.A. All rightB. No problemC. It‘all rightD. There‘s no way23. Interest is as to learning as the ability to understand ,even more so.A. vitalB. availableC. specificD. similar24. I remenbered the door before I left the office, but forgot to turn off the lights.A. lockingB. to lockC. having lockedD. to have locked25. You can chang your job, you can move house,but friengdship is meant to be life.A. ofB. onC. toD. for26. In order to find the missing child , villagers all they can over the past five hours.A. didB. doC. had doneD. have been doing27.The limits of a person‘s intelligengce,generally speaking, are fixed at birth, but he reaches these limits will depengd on his environment.A. whereB. whetherC. thatD. why28. The at hlete‘s years of hard training when she finally won the Olympic gold medal.A. went onB. got throughC. paid offD. ended up29. Alot of language learning, has been discovered, is happening in the first year of life,so parents should talk much to their children during that period.A. asB. itC. whichD. this30. When for his views about his teaching job, Philip said he found it very interesting andrewarding.A. askingB. askedC. having askedD. to be asked31. Grace doesn‘t want to move to New York because she thinks if she there, shewouldn‘t be able to see her parents very often.A. livesB. would liveC. has livedD. were to live32. —I love the Internet. I‘ve come to know many friends on the Net.—. Few of them would become your real friends.A. That‘s for sureB. It‘s not the caseC. I couldn‘t agree moreD. I‘m pleased to know that33. Walmart, which is one of the largest American supermarket chains, some of its storeopen 24 hours on Mondays through Saturdays.A. keepsB. keepC. have keptD. had kept34.Queen Elizabeth Ⅱis often to be richest woman in the world. , her personal wealth seems rather small.A. BesidesB. OtherwiseC. HoweverD. Altogether35. After school we went to the reading-room to do some reading, only to be told that it .A. was decoratedB. had decoratedC. had been decoratingD. was being decorated山东卷21. When you are done with the book, just give it to Lucy or Helen or __________.A. whoeverB. whereverC. whateverD. however22. —Sorry I‘m late. I got stuck in traffic.—_________. You‘re here now. Come in and sit down.A. You are welcomeB. That‘s rightC. I have no ideaD. Never mind23. Maria has written two novels, both of ________ have been made into television series.A. themB. thatC. whichD. what24. My first _______ of him was that he was a kind and thoughtful young man.A. expressionB. attentionC. satisfactionD. impression25. It doesn‘t matter ________ you pay by cash or credit card in this store.A. howB. whetherC. whatD. why26. George returned after the war, only _______ that his wife had left him.A. to be toldB. tellingC. being toldD. told27. He smiled politely ______ Mary apologized for her drunken friends.A. asB. ifC. unlessD. though28. After Jack had sent some e-mails, he _______ working on his project.A. had startedB. has startedC. startedD. starts29. Being able to afford _______ drink would be ______ comfort in those tough times.A. the; theB. a; aC. a; 不填D. 不填;a30. If we _______ adequate preparations, the conference wouldn‘t have been so successful.A. haven‘t madeB. wouldn‘t ma keC. didn‘t makeD. hadn‘t made31. —I don‘t know about you, but I‘m sick and tired of this weather.—_________. I can‘t stand all this rain.A. I don‘t careB. It‘s hard to sayC. So am I I hope not32. A number of high buildings have arisen _______ there was nothing a year ago but ruins.A. whenB. whereC. beforeD. until33. Be _______ —you can‘t expect me to finish all this work in so little time.A. reasonableB. confidentC. creativeD. grateful34. The manager was concerned to hear that two of his trusted workers ______.A. will leaveB. are leavingC. have leftD. were leaving35. After completing and signing it, please return the form to us in the envelope ________.A. providingB. providedC. having providedD. provide北京卷21. -- Look at those clouds!-- Don't worry. ___ it rains, we'll still have a great time.A. Even ifB. As thoughC. In caseD. If only22. By the time you have finished this book, your meal ___ cold.A. getsB. has gotC. will getD. is getting23. One learns a language by making mistakes and ___ them.A. correctsB. correctC. to correctD. correcting24. Jerry did not regret giving the comment but felt ___ he could have expressed it differently.A. whyB. howC. thatD. whether25. George said that he would come to school to see me the next day, but he ___.A. wouldn'tB. didn'tC. hasn'tD. hadn't26. When deeply absorbed in work, ___ he often was, he would forget all about eating or sleeping.A. thatB. whichC. whereD. when27. ___ with care, one tin will last for six weeks.A. UseB. UsinC. UsedD. To use28. Many people have donated that type of blood: however, the blood bank needs ___.A. someB. lessC. muchD. more29. --- Have you heard about the fire in the market?--- Yes. Fortunately no one ____.A. HurtB. was hurtC. has hurtD. had been hurt30. Our friendship quickly over the weeks that followed.A. had developedB. was developingC. would developD. developed31. ____ at the door before you enter my room, please.A. KnockB. KnockingC. Knocked C. To knock32. Bird's singing is warning to other birds ___ away.A. to stayB. stayingC. stayedD. stay33. We the difficulty together, but why didn't you tell me?A. should faceB. might faceC. could have facedD. must have faced34. Do you think this shirt is too tight the shoulders?A. atB. onC. toD. across35. Don't handle the vase as if it made of steel.A. isB. wereC. has beenD. had been天津卷01.---Can I have a day off tomorrow, Mr. Johnson?---__________. I can manage without you.A.Forget itB. I‘m afraid notC. It dependsD. Of course02.The letters for the boss___________ on his desk but he didn‘t read them until three later.A.were putB. was putC. putD. has put03.You were working too hard. You‘d better keep a ________between work and relaxation.A.promiseB. leadC. balanceD. diary04.The dog may be a good companion for the old. _______, the need to take it for walk s may be a disadvantage.A.Besides.B. HoweverC. ThereforeD. Instead.05.---You have to believe in yourself. No one else will, if you don‘t.---__________. Confidence is really important.A.It‘s not my cup of teaB. That‘s not the pointC. I don‘t think soD. I couldn‘t agre e more06.Only after Mary read her composition the second time_________ the spelling mistake.A.did she noticeB. she noticedC. does she noticeD. she has noticed07.I wish to thank Professor Smith, without_______help I would never have got this far.A.whoB. whoseC. whomD. which08.It‘s quite warm here; we __________turn the heating on yet.A.couldn‘tB. mustn‘tC. needn‘tD. wouldn‘t09.It doesn‘t matter _________you turn right or left at the crossing ---both roads lead to the park.A.whetherB. howC. ifD.when10.The secretary arranged a(n)___________time and space for the applicants to have an interview.A. importantB. spareC. publicD. convenient11. He got up late and hurried to his office, _________the breakfast untouched.A. leftB. to leaveC. leavingD. having left12. The three of us___________around Europe for about a month last summer.A. travelledB. have travelledC. had travelledD. travel13. Parents and children should communicate more to ________the gap between them so that they can understand each other better.A.openB. narrowC. widenD. leave14. Everything was placed exactly ___________he wanted it for the graduation ceremony.A. whileB. whenC. whereD. though15. We wouldn have called a taxi yesterday if Harold __________us a ride home.A. didn‘t offerB. wouldn‘t offerC. hasn‘t offeredD. hadn‘t offered上海春招:25. A huge amount of money has been spent______the new bridge.A. inB. onC. withD. for26. They don't come to the book club any more, for ______reasons or other.A. someB. allC. eitherD. both27. You _____ bring your identification when you open a bank account.A. mayB. canC. mustD. will28. After the accident, we are _____ concerned with the safety of school buses than we used to be.A. littleB. lessC. muchD. more29. Before I began this job, I _____ a baby sitter for two years.A. have beenB. wasC. would beD. had been30. The diamond mine _______ accidentally by a little boy when he was playing hide-and-seek.A. discoveredB. was discoveredC. has been discoveredD.would discover31. Tom looked upon the test as an obstacle _____ his classmates regarded it as a challenge.A. whileB. becauseC. unlessD. if32. People have learnt the importance of keeping a balanced diet _____ their nutritional needs.A. satisfyB. satisfiedC. to satisfyD. having satisfied33. Once __, Jo devoted her life to looking after children and being a full-time homemaker.A. having marriedB. being marriedC. marryingD. married34. _____ you take a photo, you should always check the position of the sun.A. BeforeB. AfterC. BecauseD. Though35. Despite the fact _____ they lacked food, the explorers continued towards the goal.A. whichB. thatC. whatD. whether36. Sailing across the ocean alone was an achievement_______took courage.A. whatB. whoC. whichD. where37. _____a wet football can hurt your foot if you are not careful.A. KickingB. KickedC. Having kickedD. Kick38. It was not until 1920 American women had the chance to vote in national elections.A. whenB. thatC. whereD. which39. Portable videophones will show us _____ is happening at the other end of the line.A. whichB. whatC. howD. why40. Big companies usually have a lot of branch offices _____ in different parts of the world.A. to have operatedB. be operatedC. operatingD. having operated上海卷:25. passion, people won't have the motivation or the joy necessary for creative thinking.A.For .B.WithoutC.BeneathD.By26. Is honesty the best policy? We _ that it is when we are little.A. will teachB. teachC. are taughtD. will be taught27. As Jack left his membership card at home, he wasn't allowed into the sports club.A. goingB. to goC. goD. gone28. The new law states that people _ drive after drinking alcohol.A. wouldn'tB. needn'tC. won'tD. mustn't29. Only with the greatest ofluck _ to escape from the rising flood waters.A. managed sheB. she managedC. did she manageD. she did manage30. - I hear that Jason is planning to buy a car.-I know. By next month, he _ enough for a used one.A. will have savedB. will be savingC. has savedD. saves31. When he took his gloves off, I noticed that one had his name written inside.A. eachB. everyC. otherD. another32. I have a tight budget for the trip, so I'm not going to fly _ the airlines lower ticket prices.A. onceB.ifC. afterD. unless33. When Peter speaks in public, he always has trouble _ the right things to say.A. thinking ofB. to think ofC. thought ofD. think of .34. There is much truth in the idea _ kindness is usually served by frankness.A. whyB. whichC. thatD. whether35. Have you sent thank-you notes to the relatives from _ _ you received gifts?A. whichB. themC.thatD. whom36. The club, _ _ 25 years ago, is holding a party for past and present members.A. foundedB. foundingC. being foundedD. to be founded37. - Was it by cutting down staff _ _she saved the firm?- No, it was by improving work efficiency.A.whenB.whatC.howD.that38. - We've only got this small bookcase. Will that do?- No, _ _ I am looking for is something much bigger and stronger.A. whoB. thatC. whatD. which39. "Genius" is a complicated concept, _ _ many different factors.A.involvedB.involving ,C.toinvolveD.beinginvolved40. The map is one of the best tools a man has _ _ he goes to a new place.A. wheneverB. whateverC. whereverD. however重庆卷:21.-John, when shall we meet again, Thursday or Friday?-_________.I‘ll be off to London then.A. EitherB. NeitherC. BothD. None22.-kevin,you look worried. Anything wrong?-Well, I____ a test and I‘m waiting for th e result.A. will takeB. tookC. had takenD. take23.______to work overtime that evening, I missed a wonderful film.A. Having been askedB. To askC. Having askedD. To be asked24.Sam has been appointed _______ manager of the engineering department to take ____ place of George.A. /,/B. the,/ C the the D./, the25.-____you interrupt now? Can‘t you see I‘m on the phone?-Sorry Sir, but it‘s urgent.A. CanB. ShouldC. MustD. Would26.-The Modern Art Exhibition in the City Museum has been cancelled.-Oh, no!______.A. It‘s a pityB. It doesn‘t matterC.I knew it alreadyD. It‘s not interesting at all27. Food supplies in the flood-stricken area ______.We must act immediately before there‘s left.A. have run outB. are running outC. have been run outD. are being run out28. We‘re having a meeting in half an hour. The decision ______ at the meeting will in the future of our company.A. to be madeB. being madeC. madeD. having been made29. Sales director is a position ______ communication ability is just as important as salesA. whichB. thatC. whenD. where30.—Coach, can I continue with the training?—Sorry, y ou can‘t ______you haven‘t recovered from the knee injury.A. untilB. beforeC. to considerD. unless31. Before you quit your job, ______how your family would feel about your decision.A. considerB. consideringC. to considerD. considered32. It was 80 years before Christopher Columbus crossed the Atlantic______ Zheng sailed to East AfricaA. whenB. thatC. afterD. since33. The headmaster will not permit the change in the course, nor______ it a thought.A. does he even givenB. he even givesC. whetherD. he will even given34. Evdence has been found through years of study______ children‘s early sleeping problem likely to continue when they grow up.A. whyB. howC. whetherD. that35.—Look, here comes your dream girl. Invite her to dance.—______W hat if she refuses me?A.I don‘t knowB. Why me?C. With pleasureD. So what?福建卷:21. —What are you going to do this weekend?一. If time permits, I may go to Shanghai with my friends.A. Don‘t mention itB. It doesn‘t matterC. Forget itD. It depends22. 一Have you figured out how much the trip will cost?—$4,000, or like that.A. anythingB. everythingC. somethingD. nothing23. The air quality in the city, ________is shown in the report, has improved over the past two months.A. thatB. itC. asD. what24. 一When did the computer crash?一This morning, while I the reading materials downloaded from some websites.A. have sortedB. was sortingC. am sortingD. had sorted25. 一Why do you choose to work in an international travel agency?一Well, you know, English is my . So it is my best choice.A. strengthB. talentC. abilityD.' skill27. Anyone, whether he is an official or a bus driver, should be respected.A. especiallyB. equallyC. naturally .D. normally28. China recently tightened its waters controls near the Huangyan Island to prevent Chinese fishing boats from in the South China Sea.A. attackingB. having attackedC. being attackedD. having been attacked29. You had better________ some time every day for sports so that you can keep yourself energetic.A. set asideB. take upC. put awayD. give out30. It is hard for the Greek government to get over the present difficulties_________ gets more financial support from the European Union.A. ifB. unlessC. becauseD. since31. We lost our way in that small village, otherwise we________ more places of interest yesterday.A. visitedB. had visitedC. would visitD. would have visited32. — Can you lend me the book Gone with the Wind? ks5u— Sorry. I returned it to the library just now. Maybe it is still ____.A. availableB. affordableC. acceptableD. valuable33. Nothing is so easy as parents raise their expectations of their children too high.A. ofB. toC. byD. for34. Pressed from his parents, and ______that he has wasted too much time , the boy is determined to stop playing video games.A. realizingB. realizedC. to realizeD. being realized35. We promise attends the party a chance to have a photo taken with the movie star.A. whoB. whomC. whoeverD. whomever江西卷:21. The Smiths don‘t usually like staying at __ hotel, but last summer they spent a few days at a very nice hotel by ___sea.A. /:aB. the;theC. /;the ^D. the;a22. We __ have bought so much food now that Suzie won't be with us for dinner.A. may notB. needn'tC. can‘tD. mustn't23. My brother would like to buy a good watch but ___was available from that shop.A. nothingB. none C no one D. neither24. I‘ve __the habit of calling in on my grandparents on my way home from school..A. come intoB. gone intoC. got intoD., run into25. It suddenly occurred to him___ he had left his keys in the office.A. whether ;B. whereC. whichD. that26.――Look! Somebody ____the sofa..――Well, it wasn‘t me. I didn‘t do it.A. is cleaningB. was cleaningC. has cleanedD. had cleaned27. ――Have you paid? What‘s my share of the bill?―― ___ . It wasn‘t very much.A. Don't worry about itB. It‘s my shareC. None of your business.D. It's up to you28.By16:30, _ was almost closing time, nearly all the paintings had been sold.A. whichB. whenC. whatD. that29. You'd better write down the phone number of the restaurant for future ____.A. purposeB. referenceC. progressD. memory30. We were all agreed that the cottage would ___ perfect holiday home for the family.A. makeB. turnC. takeD. have31. You can borrow my car ___ you promise not too fast.A. unlessB. even 'C. in caseD.a s long as32. Never before _seen anybody who can play tennis as well as Robert.A. had sheB. she hadC. has sheD. she has33. Having finished her project, she was invited by the school_____ t o the new students.A. speakingB. having spokenC. to speakD. to have spoken34. He seems to be giving the impression that he didn't enjoy himself in Paris. ___, he had a wonderful l time.A. Above allB. what‘s moreC. As a resultD. On the contrary35. John has really got the job because he showed me the official letter____ him it.A. offeredB. offeringC. to offerD. to be offered辽宁卷:21. I woke up with bad headache, yet by evening the pain had gone.A. the; theB. the; anC. a; theD. a; an22. We used to see each other , but I hav en‘t head from him since last year.A. especiallyB. regularlyC. particularlyD. approximately23. —I‘m terribly sorry to interrupt, but may I use your phone? It‘s rather urgent.— Yes, .A. with pleasureB. no burryC. it doesn‘t matterD. of course24. One of our rules is that every student wear school uniform while at school.A. mightB. couldC. shallD. will25. The old couple often take a walk after supper in the park with their pet dog them.A. to followB. followingC. followedD. follows26. Rod loves clocks. However, he never manages to put them together again.A. taking apartB. giving awayC. making upD. turning off27. The Well Hotel stands in a quiet place the main road at the far end of the lake.A. toB. forC. offD. out28. If you‘re buying today‘s paper f rom the stand, could you get for me?A. oneB. suchC. thisD. that29. This machine is very easy . Anybody can learn to use it in a few minutes.A. operatingB. to be operatingC. operatedD. to operate30. Leave your key with your neighbor you lock yourself out one day.A. as long asB. even thoughC. in caseD. as if31. I feel so excited! At this time tomorrow morning I to Shanghai.A. will be flyingB. will flyC. have been flyingD. have flown32. Not until he retired from teaching three years ago having a holiday abroad.A. he had consideredB. had he consideredC. he consideredD. did he consider33. Jack is a great talker. It‘s high time that he something instead of just talking.A. will doB. has doneC. doD. did34. The newcomer went to the library the other day and scarched for he couldfind about Mark Twain.A. whereverB. howeverC. whateverD. whichever35. Mum, I was wondering if you could lend me a few dollars until I on Friday.A. get paidB. got paidC. have paidD. had been paid湖南卷:21. We‘ve had a good start, but next, more work needs _____to achieve the final success.A. being doneB. doC. to be doneD. to do22. Don‘t worry. The hard work that you do now ______later in life.A. will be repaidB. was being repaidC. has been repaidD. was repaid23. Time, ________ correctly, is money in the bank.A. to useB. usedC. usingD. use24. Bicycling is good exercise; _______, it does not pollute the air.A. neverthelessB. besidesC. otherwiseD. therefore25. Close the door of fear behind you, and you _____ the door of faith open before you.A. sawB. have seenC. will seeD. are seeing26. Everyone in the village is very friendly. It doesn‘t matter ____you have lived there for a short ora long time.A. whyB. howC. whetherD. when27. "The moment _____soon," he thought to himself, waiting nervously.A. cameB. has tomeC. was comingD. is coming28. _____I always felt I would pass the exam, I never thought I would get an A.A. WhileB. OnceC. IfD. Until29. Sorry, I am too busy now. If I _____ time, I would certainly go for an outing with you.A. have hadB. had hadC. haveD. had30. It was not until I came here _____I realized this place was famous for not only its beauty butalso its weather.A. whoB. thatC. whereD. before31. The lecture, _____at 7:00 pm laze night, was followed by an observation of the moon withtelescopes.A. startingB. being startedC. to startD. to be started32. hard you try, it is difficult to lose weight without cutting down the amount you eat.A. HoweverB. WhateverC. WhicheverD. Whenever33. -I remember you were a talented pianist at college. Can you play the piano for me?- Sorry, I the piano for years.A. don't playB. wasn't playingC. haven't playedD. hadn't played34. Care of the soul is a gradual process _____even the small details of life should be considered.A. whatB. in whatC. whichD. in which35. All the scientific evidence that increasing use of chemicals in farming damaging ourhealth.A. show; areB. shows; areC. show; isD. shows; is四川卷:1. —Excuse me. How much is the shirt?— _______.A. Extra LargeB. 50 eachC. It sells wellD. Altogether there are 52. New technologies have made ____ possible to turn out new products faster and at a lower cost.A. thatB. thisC. oneD. it3. —Goodbye, John. Come back again sometime.—Sure. ______.A. I didB. I doC. I shallD. I will4. At school, some students are active ______ some are shy, yet they can be good friends with one another.A. whileB. althoughC. soD. as5. This is not my story, nor ______ the whole story. My story plays out differently.A. is thereB. there isC. is itD. it is6. Tom took a taxi to the airport, only _____ his plane high up in the sky.A. findingB. to findC. being foundD. to have found7. The hotel is almost finished, but it _____ needs one or two weeks to get ready for guests.A. onlyB. alsoC. evenD. still8. I looked up and noticed a snake ______ its way up the tree to catch its breakfast.A. to windB. windC. windingD. wound9. —Did you catch what I said?—Sorry. I ______ a text message just now.A. had answeringB. have answeredC. would answerD. was answering10. If you happen to get lost in the wild, you‘d better stay ______ you are and wait for help.A. whyB. whereC. whoD. what11. They are living with their parents for the moment because their own house ____.A. is being rebuiltB. has been rebuiltC. is rebuiltD. has rebuilt12. Before driving into the city, you are required to get your car ____.A. washedB. washC. washingD. to wash13. In our class there are 46 students, _____ half wear glasses.A. in whomB. in themC. of whomD. of them14. This training program can give you a lift at work, ____ increase your income by 40%.A. as well asB. so long asC. so much asD. as soon as15. He will come to understand your efforts sooner or later. It‘s just a matter of _____.A. luckB. valueC. timeD. fact16. I make $2,000 a week, 60 surely won‘t make ______ difference to me.A. that a bigB. a that bigC. big a thatD. that big a17. Scientists study ____ human brains work to make computers.A. whenB. howC. thatD. whether18. We are said to be living in ____ Information Age, ____ time of new discoveries and great changes.A. an; theB. 不填; theC. 不填; aD. the; a19. I got close enough to hear them speaking Chinese, and I said ―Ni Hao ‖ just as I ____ do in China.A. mustB. mightC. canD. should20. It‘s sur prising that your brother _____ Russian so quickly—he hasn‘t lived there very long.A. picked upB. looked upC. put upD. made up浙江卷:1. ----- Is there anything else to discuss?------ _________, I guess.A. Not at allB. No ,that‘s allC. Yes , I ‗m sureD. Yes , of course2. The development of industry has been _______ gradual process throughout ______human existence from stone tools to modern technology.A, / , the B, the , a C, a, / D, a, a3. No matter how brig ht a talker you are , there are times when it ‗s better ______ silent.A, remain B, be remaining C, having remained D, to remain。
(完整word版)2019高考新课标1卷试题

2019年全国高考新课标Ⅰ数学试卷(理科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2019新课标Ⅰ卷·理1)已知集合{|42}M x x =-<<,2{|60}N x x x =--<,则M N =I A.{|43}x x -<< B.{|42}x x -<<- C.{|22}x x -<< D.{|23}x x <<2.(2019新课标Ⅰ卷·理2)设复数z 满足||1z i -=,z 在复平面内对应的点为(,)x y ,则 A.22(1)1x y ++=B.22(1)1x y -+=C.22(1)1x y +-=D.22(1)1x y ++=3.(2019新课标Ⅰ卷·文理3)已知2log 0.2a =,0.22b =,0.30.2c =,则 A.a b c << B.a c b << C.c a b << D.b c a <<4.(2019新课标Ⅰ卷·文理4)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5151(0.61822--≈,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是512-.若某人满足上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是A.165cmB.175cmC.185cmD.190cm5.(2019新课标Ⅰ卷·文理5)函数2sin ()cos x xf x x x +=+的图象在[π-,]π的大致为A. B.C. D.6.(2019新课标Ⅰ卷·理6)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“”和阴爻“”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A.516B.1132C.2132D.1116 7.(2019新课标Ⅰ卷·文8理7)已知非零向量a r,b r 满足||2||a b =r r ,且()a b b -⊥r r r ,则a r与b r 的夹角为A.6πB.3πC.23πD.56π8.(2019新课标Ⅰ卷·文9理8)如图是求112122++的程序框图,图中空白框中应填入A.12A A =+B.12A A=+C.112A A=+ D.112A A=+9.(2019新课标Ⅰ卷·理9)记n S 为等差数列{}n a 的前n 项和.已知40S =,55a =,则A.25n a n =-B.310n a n =-C.228n S n n =-D.2122n S n n =-10.(2019新课标Ⅰ卷·文12理10)已知椭圆C 的焦点为1(1,0)F -,2(1,0)F ,过2F 的直线与C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为A.2212x y += B.22132x y += C.22143x y += D.22154x y +=11.(2019新课标Ⅰ卷·理11)关于函数()sin |||sin |f x x x =+有下述四个结论:①()f x 是偶函数 ②()f x 在区间(2π,)π单调递增③()f x 在[π-,]π有4个零点 ④()f x 的最大值为2 其中所有正确结论的编号是 A.①②④ B.②④ C.①④ D.①③12.(2019新课标Ⅰ卷·理12)已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC ∆是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,90CEF ∠=︒,则球O 的体积为 A.86π B.46π C.26π D.6π 二、填空题:本题共4小题,每小题5分,共20分.13.(2019新课标Ⅰ卷·理14)曲线23()x y x x e =+在点(0,0)处的切线方程为 .14.(2019新课标Ⅰ卷·理14)记n S 为等比数列{}n a 的前n 项和.若113a =,246a a =,则5S = . 15.(2019新课标Ⅰ卷·理15)甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是 .16.(2019新课标Ⅰ卷·理16)已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为1F ,2F ,过1F 的直线与C 的两条渐近线分别交于A ,B 两点.若1F A AB =u u u r u u u r ,120F B F B ⋅=u u u r u u u u r,则C 的离心率为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.(2019新课标Ⅰ卷·理17)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .设22(sin sin )sin sin sin B C A B -=-C . (1)求A ;(2)若22a b c +=,求sin C .18.(2019新课标Ⅰ卷·理18)如图,直四棱柱1111ABCD A B C D -的底面是菱形,14AA =,2AB =,60BAD ∠=︒,E ,M ,N 分别是BC ,1BB ,1A D 的中点. (1)证明://MN 平面1C DE ; (2)求二面角1A MA N --的正弦值.19.(2019新课标Ⅰ卷·理19)已知抛物线2:3C y x =的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若||||4AF BF +=,求l 的方程;(2)若3AP PB =u u u r u u u r,求||AB .20.(2019新课标Ⅰ卷·理20)已知函数()sin (1)f x x ln x =-+,()f x '为()f x 的导数.证明:(1)()f x '在区间(1,)2π-存在唯一极大值点;(2)()f x 有且仅有2个零点.21.(2019新课标Ⅰ卷·理21)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X . (1)求X 的分布列;(2)若甲药、乙药在试验开始时都赋予4分,(0i p i =,1,⋯,8)表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11(1i i i i p ap bp cp i -+=++=,2,⋯,7),其中(1)a P X ==-,(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=.()i 证明:1{}(0i i p p i +-=,1,2,⋯,7)为等比数列;()ii 求4p ,并根据4p 的值解释这种试验方案的合理性. (二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)22.(2019新课标Ⅰ卷·文理22)在直角坐标系xOy 中,曲线C 的参数方程为2221,1(41t x t t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2cos sin 110ρθθ++=. (1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值. [选修4-5:不等式选讲](10分)23.(2019新课标Ⅰ卷·文理23)已知a ,b ,c 为正数,且满足1abc =.证明:(1)222111a b c a b c++++„;(2)333()()()24a b b c c a +++++….。
2012年高考真题——数学理(陕西卷)试题及答案word版

2012年陕西省高考理科数学试题一、选择题:在每小题给出的四个选项中,只有一项符合题目要求的(本大题共10小题,每小题5分,共50分)、1、 集合{|lg 0}M x x =>,2{|4}N x x =≤,则MN =( C )(A ) (1,2) (B ) [1,2) (C ) (1,2] (D ) [1,2] 2、 下列函数中,既是奇函数又是增函数的为( D )(A ) 1y x =+ (B ) 3y x =- (C ) 1y x= (D ) ||y x x = 3、 设,a b R ∈,i 是虚数单位,则“0ab =”是“复数ba i+为纯虚数”的( B )(A )充分不必要条件 (B ) 必要不充分条件 (C )充分必要条件 (D ) 既不充分也不必要条件 4、 已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则( A )(A )l 与C 相交 (B ) l 与C 相切 (C )l 与C 相离 (D ) 以上三个选项均有可能5、 如图,在空间直角坐标系中有直三棱柱111ABC A B C -,12CA CC CB ==,则直线1BC 与直线1AB 夹角的余弦值为( A )(A )(B (C )(D ) 356、 从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为x 甲,x 乙,中位数分别为m 甲,m 乙,则( B )(A ) x x <甲乙,m 甲>m 乙(B ) x x <甲乙,m 甲<m 乙 (C ) x x >甲乙,m 甲>m 乙 (D ) x x >甲乙,m 甲<m 乙7、 设函数()x f x xe =,则( D )(A ) 1x =为()f x 的极大值点 (B )1x =为()f x 的极小值点 (C ) 1x =-为()f x 的极大值点 (D )1x =-为()f x 的极小值点8、 两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( C )(A ) 10种 (B )15种 (C ) 20种 (D ) 30种9、 在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( C )(A )(B ) 2(C ) 12 (D ) 12-10、 右图是用模拟方法估计圆周率π值的程序框图,P 表示估计结果,则图中空白框内应填入( D )(A ) 1000NP = (B ) 41000NP =(C ) 1000MP =(D ) 41000MP =二、填空题:把答案填在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分)11、 观察下列不等式213122+< 231151233++<,222111712344+++<……照此规律,第五个...不等式为 2222211111111++234566+++<、 12、 5()a x +展开式中2x 的系数为10, 则实数a 的值为 1 。
2012年高考真题——理综(全国卷)Word版 含答案

2012年普通高等学校招生全国统一考试理科综合能力测试本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至4页,第II卷5至11页。
考试结束后,将本试题卷和答题卡一并交回。
第I卷注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效.........。
3.第I卷共21小题,每小题6分,共126分。
一下数据可供解题时参考:相对原子质量(原子量):H 1 C 12 N 14 O 16 Na 23 Cl 35.5 K 39 Fe 56 Cu64 Br 80 Ag 108一、选择题:本题共13小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于膝跳反射的叙述,错误的是A.反射活动由一点的刺激引起B.反射活动中兴奋在突触处双向传递C.反射活动的发生需要反射弧结构完整D.发射活动中需要神经递质参与兴奋的传递2.下列关于叶绿体和线粒体的叙述,正确的是A.线粒体和叶绿体均含有少量的DNAB.叶绿体在光下和黑暗中均能合成ATPC.细胞生命活动所需的ATP均来自线粒体D.线粒体基质和叶绿体基质所含酶的种类相同。
3.一块农田中有豌豆、杂草、田鼠和土壤微生物等生物,其中属于竞争关系的是A.田鼠和杂草B.豌豆和杂草C.豌豆和其根中的根瘤菌D.细菌和其细胞内的噬菌体4.下列关于森林群落垂直结构的叙述,错误的是A.群落中的植物具有垂直分层现象B.群落中的动物具有垂直分层现象C.动物在群落中的垂直分层与植物的分层有关D.乔木层的疏密程度不会影响草木层的水平结构5、下列关于细菌的叙述,正确的是A 不同种类细菌的生长均需要相同碳源B 常用液体培养基分离获得细菌单菌落C 细菌大量培养过程中,芽孢形成于细菌生长的调整期D 培养基中含有高浓度NaCl 有利于金黄色葡萄球菌的筛选6 、下列关于化学键的叙述,正确的一项是A 粒子化合物中一定含有离子键B 单质分子中均不存在化学键C 含有极性键的分子一定是极性分子D 含有共价键的化合物一定是共价化合物7 、能正确表示下列反应的离子方程式是A 硫酸铝溶液中加入过量氨水 3Al ++3OH=Al(OH)3 ↓B 碳酸钠溶液中加入澄清石灰水 Ca(OH) 2 +23CO -=CaCO 3 ↓ + 2OH -C 冷的氢氧化钠溶液中通入氯气 Cl 2 + 2OH -=Cl O - + Cl -+ H 2OD 稀硫酸中加入铁粉 2Fe + 6 H += 23Fe + + 3H 2 ↑ 8 、合成氨所需的氢气可用煤和水作原料经多步反映值得,其中的一步反应为CO (g )+ H 2O(g) −−−→←−−−催化剂CO 2(g) + H 2(g) △H <0 反应达到平衡后,为提高CO 的转化率,下列措施中正确的是A 增加压强B 降低温度C 增大CO 的浓度D 更换催化剂9 、反应 A+B →C (△H <0)分两步进行 ① A+B →X (△H >0) ② X →C (△H <0)下列示意图中,能正确表示总反应过程中能量变化的是10 、 元素X 形成的离子与钙离子的核外电子排布相同,且X 的离子半径小于负二级硫的离子半径,X 元素为A AlB PC ArD K11、 ①②③④ 四种金属片两两相连浸入稀硫酸中都可组成原电池 ,①②相连时,外电路电流从②流向① ;①③相连时,③为正极,②④相连时,②有气泡逸出 ;③ ④ 相连时,③ 的质量减少 ,据此判断这四种金属活动性由大到小的顺序是A ①③②④B ①③④②C ③ ④ ②①D ③ ① ②④12.在常压和500℃条件下,等物质的量的A g2 ,F E (OH)3 ,NH 4HCO 3 ,N a HCO 3完全分解,所得气体体积依次是V 1\V 2\V 3\V 4.体积大小顺序正确的是A.V 3>V 2>V 4>V 1B. V 3>V 4>V 2>V 1C.V 3>V 2>V 1>V 4D.V 2>V 3>V 1>V 413.橙花醇具有玫瑰及苹果香气,可作为香料,其结构简式如下下列关于橙花醇的叙述,错误的是A . 既能发生取代反应,也能发生加成反应B.在浓硫酸催化下加热脱水,可以生成不止一种四烯烃C.1mo1橙花醇在氧气中充分燃烧,需消耗470.4氧化(标准状况D.1mo1橙花醇在室温下与溴四氯化碳溶液反应,最多消耗240g溴二,选择题:本题共8题。
年河南高考理科数学试卷真题答案解析及点评(WORD文字版)

年河南高考理科数学试卷真题答案解析及点评(WORD文字版)20XX年河南高考理科数学试卷真题答案解析及点评(WORD文字版)xx年高考数学新课标全国1卷是以《课程标准》、《考试大纲》为依据,试卷的构造保持了新课程高考数学试卷的一贯风格,试题设计表达了“大稳定、小创新”稳健、成熟的设计理念。
xx年试卷仍然注重根底,贴近中学教学实际,在坚持对高中数学五大能力(空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力)、两个意识(应用意识和创新意识)考查的同时,也注重对数学思想与方法的考查,表达了数学的根底性、应用性和工具性的学科特色。
以支撑学科知识体系的重点内容为考点来挑选合理背景,善于应用知识之间的内在联系进展融合构建试卷的主体构造,在新课程新增内容和传统内容的结合处寻找创新点,考查更加科学。
xx—xx年考点与分值统计如下表:三、试题分析:构造稳定、计算量稍有下降1、试题的数量和题型没有发生变化,仍然以12道选择题、4道填空题、5道解答题、3道选考题的形式出现,保持稳定。
从考试的内容上和一样仍然以函数、三角函数、数列、概率、几何、导数等重点知识为主,在分值上占有较大比例。
这集中表达了重要内容重点考查,主干知识反复考查的原那么,例如:17题(数列)、18题(立体几何),19题(概率)、20题(解析几何)、21题(函数)以及22—24(选考题)这些没有发生变化,只是在排列顺序上,从难易程度上作了适当的'调整,表达了考点不变、考法变化的思想,既符合考生的学情,也符合考试说明和大纲的要求。
2、相对于而言,xx年考察了逻辑用语这一知识点,立体几何知识相比略有增加而解析几何的考察要求有所降低,总体考点根本不变,计算能力的要求略微降低,表达了稳中有变的原那么。
最后,笔者衷心祝愿广阔考生在xx年高考中取得优异的成绩,走进理想的大学。
也祝愿xx届考生在未来高三复习过程中能以近年高考命题趋势为参考,在一轮复习中着重根底知识原理的复习,在xx年高考中取得优异的成绩。
(完整word版)导数单调性分类讨论

类型二:导数单调性专题类型1。
导数不含参。
类型2.导数含参。
类型3:要求二次导 求单调性一般步骤:(1) 第一步:写出定义域,一般有()0ln >⇒x x(2) 第二步:求导,(注意有常数的求导)若有分母则通分。
一般分母都比0大,故去死若无分母,因式分解(提公因式,十字相乘法)或求根(观察分子)判断导函数是否含参,再进行讨论(按恒成立与两个由为分界)(3) 第三步由()()⎩⎨⎧≤≥解出是减区间解出是增区间00x f x f(4) 下结论类型一:导函数不含参:()()()⎪⎩⎪⎨⎧-+=--++=++=21223,22,,x x e m e x f x x c bx ax x f x b kx x f 如指数型如:二次型如:一次型对于这类型的题,直接由导函数大于0,小于0即可(除非恒成立) 例题1求函数()()x e x x f 3-=的单调递增区间 解:()()()23'-=-+=x e e x e x f x x x 由()()202'>⇒>-=x x e x f x 所以函数在区间()+∞,2单调递增 由()()202'<⇒<-=x x e x f x所以函数在区间()2,∞-单调递减例题2:求函数()()2211x e x x f x --=的单调区间解:()()()()x e e x e x xe e x f x x x x x +-=-+-=-+-=11111'由()()()01011'>-<⇒>+-=x x x e x f x 或所以函数在区间(][)∞+-∞-,和01,单调递增由()()()01011'<<-⇒<+-=x x e x f x 所以函数在区间()0,1-单调递减 例题3:求函数()xxx f ln =的单调区间例题4:已知函数()()()R k kx e x x f x ∈--=21 (1)若1=k 时,求函数()x f 的单调区间例题5.(2010·新课标全国文,21)设函数f (x )=x (e x -1)-ax 2.(1)若a =错误!,求f (x )的单调区间;例题6:已知函数()()112++-=x e ax x f x (1)若0=a ,求函数()x f 的单调区间7。
2012年高考试题(全国新课标)数学(理科)试卷及答案

2012年普通高等学校招生全国统一考试(新课标全国卷)理科数学第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1、已知集合A={1,2,3,4,5},B={(x ,y )|x ∈A ,y ∈A ,x-y ∈A},则B 中所含元素的个数为(A )3 (B )6 (C )8 (D )102、将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组有1名教师和2名学生组成,不同的安排方案共有(A )12种 (B )10种 (C )9种 (D )8种 3、下面是关于复数z=21i-+的四个命题 P1:z =2 P2: 2z =2i P3:z 的共轭复数为1+i P4 :z 的虚部为-1 其中真命题为(A ). P2 ,P3 (B ) P1 ,P2 (C )P2,P4 (D )P3,P44、设F1,F2是椭圆E:22x a +22yb=1 (a >b >0)的左、右焦点 ,P 为直线32a x =上的一点,12PF F △是底角为30°的等腰三角形,则E 的离心率为 (A )12 (B )23 (C ) 34 (D )455、已知{n a }为等比数列,214=+a a ,865-=⋅a a ,则=+101a a(A )7 (B )5 (C )-5 (D )-76、如果执行右边的程序图,输入正整数)2(≥N N 和实数n a a a ⋯,,21,输入A ,B ,则(A )A+B 为的n a a a ⋯,,21和 (B )2A B+为n a a a ⋯,,21的算式平均数 (C )A 和B 分别是n a a a ⋯,,21中最大的数和最小的数 (D )A 和B 分别是n a a a ⋯,,21中最小的数和最大的数7、如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A )6(B )9 (C )12 (D )188、等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于A ,B 两点,34=AB ,则C 的实轴长为(A )2 (B ) 22 (C ) 4 (D )89、已知w >0,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是(A )]45,21[ (B )]43,21[ (C )]21,0( (D )(0,2]10、已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为O O O O 11111111xyxy xy xy)(A )(B11、已知三棱锥S-ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为O 的直径,且SC=2,则此棱锥的体积为(A )26 (B )36 (C )23 (D )2212、设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则|PQ|的最小值为 (A )2ln 1- (B ))2ln 1(2- (C )2ln 1+ (D ))2ln 1(2+第Ⅱ卷本卷包括必考题和选考题两部分。
(完整word)2017年高考理科数学全国1卷(附答案)

学校:____________________ _______年_______班 姓名:____________________ 学号:________- - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -绝密★启用前2017年普通高等学校招生全国统一考试理科数学 全国I 卷(全卷共10页)(适用地区:河南、河北、山西、江西、湖北、湖南、广东、安徽、福建)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答案卡一并交回。
一、 选择题:本题共12小题,每小题5分,共60分。
在每个小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知集合A ={x |x <1},B ={x |31x <},则 A .{|0}A B x x =<I B .A B =R U C .{|1}A B x x =>UD .A B =∅I2.如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A .14 B .π8 C .12D .π43.设有下面四个命题1p :若复数z 满足1z∈R ,则z ∈R ;2p :若复数z 满足2z ∈R ,则z ∈R ; 3p :若复数12,z z 满足12z z ∈R ,则12z z =; 4p :若复数z ∈R ,则z ∈R .其中的真命题为 A .13,p pB .14,p pC .23,p pD .24,p p4.记n S 为等差数列{}n a 的前n 项和.若4524a a +=,648S =,则{}n a 的公差为 A .1B .2C .4D .85.函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是A .[2,2]-B .[1,1]-C .[0,4]D .[1,3] 6.621(1)(1)x x++展开式中2x 的系数为 A .15B .20C .30D .357.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为 A .10 B .12C .14D .168.右面程序框图是为了求出满足3n −2n >1000的最小偶数n ,那么在和两个空白框中,可以分别填入 A .A >1 000和n =n +1 B .A >1 000和n =n +2 C .A ≤1 000和n =n +1 D .A ≤1 000和n =n +29.已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2 C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 210.已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为 A .16B .14C .12D .1011.设xyz 为正数,且235x y z ==,则A .2x <3y <5zB .5z <2x <3yC .3y <5z <2xD .3y <2x <5z12.几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N :N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A .440B .330C .220D .110二、填空题:本题共4小题,每小题5分,共20分。
2012年北京高考数学理科试题(word含答案)

2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.已知集合A={x∈R|3x+2>0﹜·B={x∈R|(x+1)(x-3)>0﹜则A∩B=( )A.(﹣∞,﹣1) B.{﹣1,-⅔} C. ﹙﹣⅔,3﹚ D.(3,+∝)2. 设不等式组表示的平面区域为D.在区域D内随机取一个点.则此点到坐标原点的距离大于2的概率是()A. B. C. D.3.设a,b∈R.“a=O”是‘复数a+bi是纯虚数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.执行如图所示的程序框图,输出的S值为()A. 2B .4C.8D. 165.如图. ∠ACB=90º。
CD⊥AB于点D,以BD为直径的圆与BC交于点E.则( )A. CE·CB=AD·DBB. CE·CB=AD·ABC. AD·AB=CD ²D.CE·EB=CD ²6.从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 67.某三梭锥的三视图如图所示,该三梭锥的表面积是()A. 28+6B. 30+6C. 56+ 12D. 60+128.某棵果树前n前的总产量S与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高。
m值为()A.5B.7C.9D.11第二部分(非选择题共110分)二.填空题共6小题。
每小题5分。
共30分.9.直线(t为参数)与曲线(“为多α数)的交点个数为10.已知﹛﹜等差数列为其前n项和.若=,=,则=11.在△ABC中,若α=2,b+c=7,=-,则b=12.在直角坐标系xOy中.直线l过抛物线=4x的焦点F.且与该撇物线相交于A、B两点.其中点A在x轴上方。
2015-2018高考全国1卷理科数学试题及答案-word版(K12教育文档)

(直打版)2015-2018高考全国1卷理科数学试题及答案-word版(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)2015-2018高考全国1卷理科数学试题及答案-word版(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)2015-2018高考全国1卷理科数学试题及答案-word版(word版可编辑修改)的全部内容。
2018年普通高等学校招生全国统一考试理科数学一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.设121iz i i-=++,则z =( ) A .0B .12C .1D .22.已知集合{}2|20A x x x =-->,则A =R ( ) A .{}|12x x -<<B .{}|12x x -≤≤C .{}{}|1|2x x x x <->D .{}{}|1|2x x x x -≤≥3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.记n S 为等差数列{}n a 的前n 项和.若3243S S S =+,12a =,则3a =( )A .12-B .10-C .10D .125.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为( ) A .2y x =-B .y x =-C .2y x =D .y x =6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =( ) A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC +7.某圆柱的高为2,底面周长为16,其三视图如右图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( ) A .217B .25C .3D .28.设抛物线24C y x =:的焦点为F ,过点()20-,且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅=( )A .5B .6C .7D .89.已知函数()0ln 0x e x f x x x ⎧=⎨>⎩,≤,,()()g x f x x a =++,若()g x 存在2个零点,则a 的取值范围是( ) A .[)10-,B .[)0+∞,C .[)1-+∞,D .[)1+∞,10.下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC ,ABC △的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为1p ,2p ,3p ,则( )A .12p p =B .13p p =C .23p p =D .123p p p =+11.已知双曲线2213x C y -=:,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M ,N .若OMN △为直角三角形,则MN =( ) A .32B .3 C. D .412.已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( ) ABCD二、填空题(本题共4小题,每小题5分,共20分)13.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为________.14.记n S 为数列{}n a 的前n 项和.若21n n S a =+,则6S =________.15.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有________种.(用数字填写答案)16.已知函数()2sin sin 2f x x x =+,则()f x 的最小值是________.三、解答题(共70分。
2012年辽宁省高考理科数学试题word版含答案

2012年普通高等学校招生全国统一考试(辽宁卷)数学(供理科考生使用)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8}, 则)()(B C A C U U 为(A){5,8} (B){7,9} (C){0,1,3} (D){2,4,6} 【答案】B【解析一】因为全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},所以{}{}9,7,3,1,0,9,7,6,4,2==B C A C U U ,所以)()(B C A C U U 为{7,9}。
故选B【解析二】 集合)()(B C A C U U 为即为在全集U 中去掉集合A 和集合B 中的元素,所剩的元素形成的集合,由此可快速得到答案,选B 【点评】本题主要考查集合的交集、补集运算,属于容易题。
采用解析二能够更快地得到答案。
(2)复数22ii -=+ (A)3455i - (B)3455i +(C) 415i-(D) 315i+【答案】A 【解析】2(2)(2)34342(2)(2)555ii i i iii i ----===-++-,故选A【点评】本题主要考查复数代数形式的运算,属于容易题。
复数的运算要做到细心准确。
(3)已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是 (A) a ∥b (B) a ⊥b (C){0,1,3} (D)a +b =a -b 【答案】B【解析一】由|a +b |=|a -b |,平方可得a ⋅b =0, 所a ⊥b ,故选B【解析二】根据向量加法、减法的几何意义可知|a +b |与|a -b |分别为以向量a ,b 为邻边的平行四边形的两条对角线的长,因为|a +b |=|a -b |,所以该平行四边形为矩形,所以a ⊥b ,故选B【点评】本题主要考查平面向量的运算、几何意义以及向量的位置关系,属于容易题。
2012年高考试题:理科数学(全国卷)——含答案及解析

2012年普通高等学校招生全国统一考试理科数学(必修+选修II )本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷第1至2页,第II 卷第3至第4页。
考试结束,务必将试卷和答题卡一并上交。
第I 卷注意事项:全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准该条形码上的准考证号、姓名和科目。
2.没小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效.........。
3.第I 卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、 选择题(1)、复数131i i-++= A. 2 B. 2 C. 12 D. 12i i i i +-+- 【考点】复数的计算【难度】容易【答案】C 【解析】13(13)(1)24121(1)(1)2i i i i i i i i -+-+-+===+++-. 【点评】本题考查复数的计算。
在高二数学(理)强化提高班下学期,第四章《复数》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(理)强化提高班中有对复数相关知识的总结讲解。
(2)、已知集合A ={1.3. },B ={1,m } ,A B =A , 则m =A. 0B. 0或3C. 1D. 1或3【考点】集合【难度】容易【答案】B【解析】(1,3,),(1,)30,1()3A B A B A A m B m m A m m m m m ⋃=∴⊆==∴∈∴=====或舍去Q .【点评】本题考查集合之间的运算关系,及集合元素的性质。
在高一数学强化提高班下学期课程讲座1,第一章《集合》中有详细讲解,其中第02讲中有完全相同类型题目的计算。
在高考精品班数学(理)强化提高班中有对集合相关知识及综合题目的总结讲解。
(完整word版)2012年全国高考新课标1卷数学文科高考试题
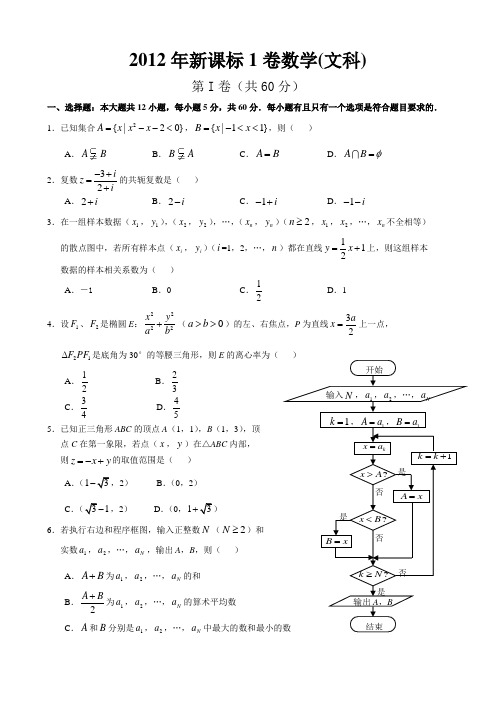
2012年新课标1卷数学(文科)第I 卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.每小题有且只有一个选项是符合题目要求的. 1.已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则( )A .AB B .B AC .A B =D .A B φ=2.复数32iz i-+=+的共轭复数是( ) A .2i + B .2i -C .1i -+D .1i --3.在一组样本数据(1x ,1y ),(2x ,2y ),…,(n x ,n y )(2n ≥,1x ,2x ,…,n x 不全相等)的散点图中,若所有样本点(i x ,i y )(i =1,2,…,n )都在直线112y x =+上,则这组样本 数据的样本相关系数为( ) A .-1B .0C .12D .14.设1F 、2F 是椭圆E :2222x y a b +(0a b >>)的左、右焦点,P 为直线32ax =上一点,21F PF ∆是底角为30°的等腰三角形,则E 的离心率为( )A .12B .23C .34D .455.已知正三角形ABC 的顶点A (1,1),B (1,3),顶 点C 在第一象限,若点(x ,y )在△ABC 内部, 则z x y =-+的取值范围是( )A .(13-,2)B .(0,2)C .(31-,2)D .(0,13+)6.若执行右边和程序框图,输入正整数N (2N ≥)和 实数1a ,2a ,…,N a ,输出A ,B ,则( )A .AB +为1a ,2a ,…,N a 的和B .2A B +为1a ,2a ,…,N a 的算术平均数C .A 和B 分别是1a ,2a ,…,N a 中最大的数和最小的数否是是1k k =+B x=A x=结束输出A ,B ?k N ≥?x B <kx a =?x A >开始输入N ,1a ,2a ,…,N a1k =,1A a =,1B a =否是 否D .A 和B 分别是1a ,2a ,…,N a 中最小的数和最大的数7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .158.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的 距离为2,则此球的体积为( ) A .6πB .43πC .46πD .63π9.已知0ω>,0ϕπ<<,直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=( ) A .4π B .3πC .2πD .34π 10.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A ,B 两点,||43AB =,则C 的实轴长为( )A .2B .22C .4D .811.当102x <≤时,4log xa x <,则a 的取值范围是( ) A .(0,22) B .(22,1) C .(1,2) D .(2,2) 12.数列{n a }满足1(1)21nn n a a n ++-=-,则{n a }的前60项和为( )A .3690B .3660C .1845D .1830第Ⅱ卷(共90分)本试卷包括必考题和选考题两部分。
近十年(2011——2020)高考全国卷

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年普通高等学校招生全国统一考试(新课标)理科数学(解析卷)注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第I 卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第II 卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合{}5,4,3,2,1=A ,(){}A y x A y A x y x B ∈-∈∈=,,|,,则B 中所含元素的个数为 A .3 B .6 C .8 D .102.将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有 A .12种 B .10种 C .9种 D .8种3.下面是关于复数=z 21i -+的四个命题1P :2=z 2P :i z 22= 3P :z 的共轭复数为i +1 4P :z 的虚部为1-其中真命题为A .2P , 3PB .1P ,2PC .2P ,4PD 3P ,4P4.设21,F F 是椭圆E :12222=+b y a x ()0>>b a 的左、右焦点 ,P 为直线32ax =上的一点,12PF F ∆是底角为ο30的等腰三角形,则E 的离心率为A .12B .23C .34D .455.已知{}n a 为等比数列,8,26574-==+a a a a 则=+101a aA .7B .5 C.5-D .7-6.如果执行右边的程序图,输入正整数()2≥N N N 和实数n a a a a Λ321,,,输出B A ,则A .B A +为n a a a a Λ321,,的和 B .2A B+为n a a a a Λ321,,的算式平均数 C .A 和B 分别是n a a a a Λ321,,中最大的数和最小的数D .A 和B 分别是n a a a a Λ321,,中最小的数和最大的数7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A .6B .9C .12D .188.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于B A ,两点,34=AB ,则C 的实轴长为A .2B .22C .4D .89)已知0>ω,函数⎪⎭⎫ ⎝⎛+=4sin )(πωx x f 在2ππ⎛⎫⎪⎝⎭,单调递减,则ω的取值范围是A .⎥⎦⎤⎢⎣⎡45,21B .⎥⎦⎤⎢⎣⎡43,21C .⎥⎦⎤ ⎝⎛21,0D .(]2,010.已知函数()xx x f -+=1ln 1)(,则)(x f y =的图像大致为11)已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为O 的直径,且2=SC ,则此棱锥的体积为A .26B .36C .23D .2212)设点P 在曲线x e y 21=上,点Q 在曲线()x y 2ln =上,则PQ 的最小值为A .2ln 1-B .()2ln 12-C .2ln 1+D .()2ln 12+第Ⅱ卷本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必须作答。
第22题~第24题为选考题,考试依据要求作答。
二。
填空题:本大题共4小题,每小题5分。
13.已知向量b a ϖϖ,夹角为ο45,且1=a ϖ,102=-b a ϖρ,则=b ρ____________.14.设yx,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+-≥-31yxyxyx则yxz2-=的取值范围为__________.15)某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作。
设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作互相独立,那么该部件的使用寿命超过1000小时的概率为_________________.16)数列{}n a满足()1211-=-++naannn,则{}n a的前60项和为________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17)(本小题满分12分)已知cba,,分别为ABC∆的三个内角CBA,,的对边,0sin3cos=--+cbCaCa。
(Ⅰ)求A;(Ⅱ)若ABCa∆=,2的面积为3,求cb,。
18)(本小题满分12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。
如果当天卖不完,剩下的玫瑰花作垃圾处理。
(Ⅰ)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:以100天记录的各需求量的频率作为各需求量发生的概率。
(ⅰ)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;(ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由。
19.(本小题满分12分)如图,直三棱柱111C B A ABC -中,121AA BC AC ==,D 是棱1AA 的中点,BD DC ⊥1。
(1)证明:BC DC ⊥1;(2)求二面角11C BD A --的大小。
20.(本小题满分12分)设抛物线C :)0(22>=p py x 的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于D B ,两点。
(1)若ο90=∠BFD ,ABD ∆的面积为2,求p 的值及圆F 的方程;(2)若F B A ,,三点在同一直线m 上,直线n 与m 平行,且n 与C 有一个公共点,求坐标原点到m ,n 距离的比值。
21.(本小题满分12分) 已知函数()x f 满足()()()212101x x f e f x f x +-'=-. (1)求()x f 的解析式及单调区间; (2)若()b ax x x f ++≥221,求()b a 1+的最大值。
请考生在第22、23、24题中任选一道作答,如果多做,则按所做的第一题计分。
作答时请写清题号。
22.(本小题满分10分)选修4—1;几何证明选讲如图,E D ,分别为ABC ∆边AC AB ,的中点,直线DE 交ABC ∆的外接圆于G F ,两点,若AB CF //,证明:(Ⅰ)BC CD =;(Ⅱ)BCD ∆~GBD ∆。
23.(本小题满分10分)选修4—4;坐标系与参数方程已知曲线1C 的参数方程式⎩⎨⎧==ϕϕsin 3cos 2y x (ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线2C 的极坐标方程式2=ρ.正方形ABCD 的顶点都在2C 上,且D C B A ,,,依逆时针次序排列,点A 的极坐标为2,2π⎛⎫⎪⎝⎭。
(Ⅰ)求点D C B A ,,,的直角坐标;(Ⅱ)设P 为1C 上任意一点,求2222PD PC PB PA +++的取值范围。
已知函数()2-++=x a x x f . (Ⅰ)当3-=a 时,求不等式()3≥x f 的解集;(2)若()4-≤x x f 的解集包含[]2,1,求a 的取值范围。
第一卷一. 选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的。
(1)【解析】选D5,1,2,3,4x y ==,4,1,2,3x y ==,3,1,2x y ==,2,1x y ==共10个(2)【解析】选A甲地由1名教师和2名学生:122412C C =种 (3)【解析】选C22(1)11(1)(1)i z i i i i --===---+-+--1:p z =22:2p z i =,3:p z 的共轭复数为1i -+,4:p z 的虚部为1- (4)【解析】选C∆21F PF 是底角为30o的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔== (5)【解析】选D 472a a +=,56474784,2a a a a a a ==-⇒==-或472,4a a =-=471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-(6)【解析】选C (7)【解析】选B该几何体是三棱锥,底面是俯视图,高为3此几何体的体积为11633932V =⨯⨯⨯⨯=(8)【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(4,A -(4,B --得:222(4)4224a a a =--=⇔=⇔=(9)【解析】选A592()[,]444x πππωω=⇒+∈ 不合题意 排除()D351()[,]444x πππωω=⇒+∈ 合题意 排除()()B C另:()22πωππω-≤⇔≤,3()[,][,]424422x ππππππωωπω+∈++⊂得:315,2424224πππππωπωω+≥+≤⇔≤≤(10) 【解析】选B()ln(1)()1()010,()00()(0)0xg x x x g x xg x x g x x g x g '=+-⇒=-+''⇒>⇔-<<<⇔>⇒<= 得:0x >或10x -<<均有()0f x < 排除,,A C D (11)【解析】选AABC ∆的外接圆的半径r =O 到面ABC的距离d ==SC 为球O 的直径⇒点S 到面ABC的距离为23d =此棱锥的体积为11233436ABC V S d ∆=⨯=⨯⨯=另:123ABC V S R ∆<⨯=排除,,B C D(12)【解析】选A 函数12x y e =与函数ln(2)y x =互为反函数,图象关于y x =对称函数12x y e =上的点1(,)2x P x e 到直线y x =的距离为d =设函数min min 11()()1()1ln 222x x g x e x g x e g x d '=-⇒=-⇒=-⇒=由图象关于y x =对称得:PQ最小值为min 2ln 2)d =-本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必须作答,第22-第24题为选考题,考生根据要求做答。
