第十章 含有耦合电感的电路
10章 含有耦合电感的电路

jω L2 (支路 支路3)L ± 同侧取 同侧取“ 支路 3=±M(同侧取“+”,异 异
R2
侧取“ 侧取“-”) (支路 1’=L1 m M,M前所取符 支路1)L 支路 , 前所取符 号与L 号与 3中的相反 (支路 2’=L2 m M,M前所取 支路2)L 支路 , 前所取 符号与L 符号与 3中的相反
反相串联无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
Z = Z1 + Z 2 = R1 + R2 + jω ( L1 + L2 − 2 M )
R1
L1 u1
2、顺向串联 、 每一耦合电感支路的阻抗为: 每一耦合电感支路的阻抗为:
Z1 = R1 + jω ( L1 + M )
两个耦合线圈的磁通链可表示为: 两个耦合线圈的磁通链可表示为:
ψ 1 = ψ 11 ± ψ 12
= L1i1±Mi2
ψ 2 = ±ψ 21 + ψ 22
= ±Mi1+L2i2 上式表明, 上式表明 , 耦合线圈中的磁通链与施感电流 线性关系 关系, 成 线性 关系 , 是各施感电流独立产生的磁通链叠 加的结果。 加的结果。
di di u2 = R2i + ( L2 −M ) dt dt di = R2i + ( L2 − M ) dt
无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
di u = u1 + u 2 = ( R1 + R2 )i + ( L1 + L2 − 2 M ) dt
L1 N1 L2 N2
电路第十章含有耦合电感的电路
.. . . .. .. . . .. 一致,故1,4是同名端,(不2是,同名端,1,4是同名端,
3也是同名i1 端) i2 (2,3也是同名端i1 ) i2
1 23 4
1 23 4
同名端只与线圈的绕向有关,与电流方向无关。 只要知道线圈的绕向,就能标出同名端。
L L1L2 M2 L1 L2 2M
M2 L1L2
M L1L2 M L1 L2
2
几何平均值(小) 算术平均值(大)
除非两电感相同,一般:几何平均值< 算术平均值
∴用几何平均值求M更严格
∴互感M必须满足 M L1L2 的要求 ∴ M的最大值 Mmax L1L2
3.耦合系数 k M M max
最大值
i(t)
••
u ( t ) L1 L2
i(t)
u(t)
L1 -
di
M
dt +
L2
+
M
di
- dt
utL1d d ti Md d ti L2d d ti Md dti
L1
L2
2Mdi
dt
L
di dt
反接时,串联电感值为
LL1L22M
电感贮能 WL 12LiL2 0
即L一定为正值
L1L22M
M L1 L2 2
实际值
M L1 L 2
0k1
k 反应了磁通相耦合的程度
k=1 k→1 k<0.5 k=0
全耦合
线圈中电流产生的磁通全部与另一个线 圈交链达到使M无法再增加
紧耦合,强耦合
松耦合,弱耦合
无耦合
4.耦合电感的T型等效
第十章含有耦合电感的电路-精选文档

d di u L dt dt
+
u _
在此电感元件中,磁链Ψ和感 应电压u均由流经本电感元件的电 流所产生,此磁链感应电压分别称 为自感磁链和自感电压。
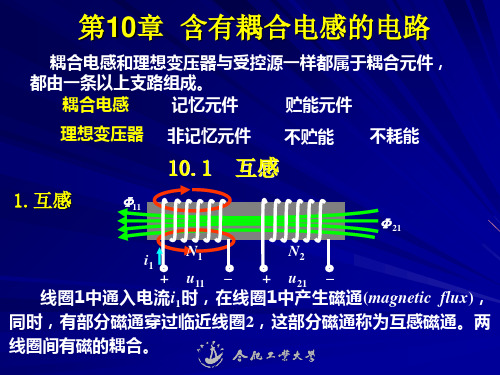
2、互感:如图所示表示两个耦合电感,电流i1在线 圈1和2中产生的磁通分别为Φ11和Φ21,则Φ21≤Φ11。 这种一个线圈的磁通交链于另一线圈的现象,称为 磁耦合。电流i1称为施感电流。Φ11称为线圈1的自感 磁通,Φ21称为耦合磁通或互感磁通。如果线圈2的 匝数为N2,并假设互感磁通Φ21与线圈2的每一匝都 交链,则互感磁链为Ψ21=N2Φ21。
§10-1 互感
耦合电感:耦合元件,储能元件,记忆元件。
一、耦合电感:为互感线圈的理想化电路模型
1 、自感:对于线性非时变电感元件,当电流的 参考方向与磁通的参考方向符合右螺旋定则时, 磁链Ψ与电流I满足Ψ=Li,L为与时间无关的正实 常数。
根据电磁感应定律和线圈的绕向,若电压的参考 正极性指向参考负极性的方向与产生它的磁通的参 考方向符合右螺旋定则时,也就是在电压和电流关 联参考方向下,则
输入阻抗Z为
Z Z Z ( 8 j 4 ) 8 . 94 26 . 57 1 2
为: 50 0 V 令U ,解得 I
50 0 I U / Z A 5 . 59 26 . 57 A 8 . 94 26 . 57
第十章 含有耦合电感的电路
内容提要
本章主要介绍耦合电感中的磁耦合 现象、互感和耦合因数、耦合电感的同 名端和耦合电感的磁通链方程、电压电 流关系;还介绍含有耦合电感电路的分 析计算及空心变压器、理想变压器的初 步概念。
§10-1 互感 §10-2 含有耦合电感电路的计算 §10-3 空心变压器
电路原理第十章含耦合电感电路

•
•
•
•
U R1 I1 +j L1 I1 -j M I 2
•
•
•
•
U R 2 I 2 +j L2 I 2 -j M I1
•
•
•
I I1 I2
根据前面的电路图,列写方程:
U (R1 jL1)I1 jMI2 Z1I1 ZM I2
U (R2 jL2 )I2 jMI1 Z2I2 ZM I1
Ψ21 Ψ22
Ψ11 Ψ12
Ψ21 Ψ22
i1 a + u1
i2
-b
c+
u2
d
i1 *a + u1 -b
i2 c + u2 -d *
(a)
(b)
说明耦合线圈的伏安关系用图
Ψ1=Ψ11 +Ψ12 Ψ2=Ψ22 +Ψ21
Ψ1=Ψ11 -Ψ12 Ψ2=Ψ22 -Ψ21
11
21
N1 i1
N2
+ u11 – + u21 –
同名端与两个线圈的绕向和相对位置有关。
11
s
0
N1 i1 * •
+ u11 –
N2
N3
*
•
+ u21 – – u31 +
i
1*
*2
1•*
2
3
1'
2'
1'
2'*
3' •
两个以上线圈彼此耦合时,同名端应一对一对加以标记。 如果每个电感都有电流时,每个电感的磁通链等于自感磁 通链和所有互感磁通链的代数和。
通链Ψ22 。22 部分或全部与线圈1相链,产生线圈2对线圈
第十章含耦合电感的电路

r R
E
(a)
r R
E
(b)
直接连接
P
I
2
R
E R
r
2
R
8
6 100
2
8
25mW
用匝比为n = 3的变压器耦合
扬声器的反射阻抗
R'
N1 N2
2
R
300 100
i1 * N1
n :1
i2
பைடு நூலகம்
+
N2
u2
*
-
实际变压器与理想变压器近似的条件
变压器原、副边线圈自电感 :L1、L2 耦合电感 : M k L1L2 近似条件: k M 1 L1、L2很大
L1L2
n n1 n2
例题
一个理想变压器的额定值是2400V/120V,9.6kVA且 在次级有50匝。计算:(a)匝数比,(b)初级的匝 数,(c)初级绕组和次级绕组的额定电流值。
原、副边匝比: 初级匝数:
n V1 2400 20 V2 120
n1 n 50 2050 1000 匝
初级绕组和次级绕组的额定电流值
I1
9600 V1
9600 2400
4A
I2
9600 V2
9600 120
80A
例题
求负载的端电压 U 2。
副边电压、电流关系。 配合电阻元件等,可模拟实际变压器
第10章电路邱关源课件PPT

电路第十章含有耦合电感的电路电路§1010--1 1 互互感1121i 111'22'L 2N 2L 1N 1i 222212ΨΨΨ+±=12111ΨΨΨ±=电路22122111i L Mi ΨMi i L Ψ+±=±=1111i L Ψ=2222i L Ψ=21212i M Ψ=12121i M Ψ=**ML 1L 2+−i 1i 2u 1u 2+−11'22'dt di Mdt di L dt d u 21111±=Ψ=dtdi L dt di M dt d u 22122+±=Ψ=ML 1L 2+−i 1i 2u 1u 2+−122122111i L Mi ΨMi i L Ψ+±=±=2111I M j I L j U &&&ωω+=2212I L j I M j U &&&ωω+=Mj Z M ω=121≤=L L Mk 22211112ΨΨΨΨ=k电路§1010--2 2 含有耦合电感电路的计算含有耦合电感电路的计算I L j R U &&)(111ω+=[]I M L L j R R U &&)22121(−+++=ω1R R 1L −+1u −+uM••i 1R R ML −21−+1u −+ui I L j R U &&)(222ω+=[]I M I M j L j R &&)(−=−+11ωω[]I M I M j L j R &&)(−=−+22ωω电路[])22121(M L L j R R U I−+++=ω&&))222111((M M L j R Z L j R Z −−+=+=ωω)22121(M L L j R R Z −+++=ω))222111((M M L j R Z L j R Z ++=++=ωω)22121(M L L j R R Z ++++=ω电路cos10002**12M1R 2+−iu s4522000°∠Z cos 22121×L L ∠2电路1R R 1L −+1u −+uM••i SS 826.05.125.782121=×===L L ML L M k ωωωΩ−∠=−=−+=o46.904.35.03)(111j M L j R Z ωΩ∠=+=−+=o4237.65.45)(222j M L j R Z ωΩ∠=+=+=o57.2694.84821j Z Z Z o &050∠=U57.2659.557.2694.8050−∠=∠∠==oo &&Z U I1212121Z I X jI R I S =+=AV 63.14025.1564237.659.52222⋅+=∠×==j Z I S oAV 12525057.2659.550*⋅+=∠×==j I U S o &&21S S S +=A V .....⋅−=−∠×=631575934690435952j o1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω2111I j I L j R U M &&&ωω++=)(1R R 2L j ω1L j ω−+U&••I&1I &I &Mj ω22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++−=−+=2221I L j R I j U M &&&)(ωω++=2112I I I I I I &&&&&&−=−=[]I j I M L j R M &&m ωω±+=111)(1R R ML −1−+U&I&1I &I &ML −21R R ML +1−+U&I&1I &I &ML +222212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=[]222I M L j R I j U M &m &&)(ωω++±=)()(1111I I j I L j R U M &&&&−±+=ωω电路410CL =ωH 05.0662410510411===−×××C L ωA87.36025.0240320010)(2111o o &&−∠=+∠=−+−+=j M L M L j R U I AB ωV13.53387.36025.0120)(12o o &&∠=−∠×=−=j I M L j U ED ωW2.0025.03202211=×==I R P电路+−U S500 V o13ΩIR 25Ω1j ωL 2I 1**j ωM+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1()22电路()+−U S500 V o13ΩIR 25Ω1j (+)ωL M 2I 1电路§1010--3 3 空心变压器空心变压器()21111I j I L j R U M &&&ωω++=11Z22Z MZ 2221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′2221)(0I jX R L j R I j L L M &&++++=ωω1222⋅−=I Z Z I M &1⋅I电路11222111112221112)(Y M jX R L j R U MY j Y Z Z U Y Z I L L M M ωωω++++−=−−=&&&−+1U &222)(Y M ω1I 12221112221111)(Y M Z U Y Z Z U I M ω+=−=&&&Z 2I −+111U MY j &ω1222⋅−=I Z Z I M &电路1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′Ω==50111j L j Z ωΩ+=++=123222j jX R L j Z L L ωΩ−=+=37.3184.7123400)(222j j Y M ωo &021001∠=U o &&2.675.337.3184.7502/100)(2221111−∠=−+=+=j j Y M Z U I ωo o &&84.12666.51232.675.3202212∠=+−∠×=−=j j Z I M j I ω)84.12610cos(266.5)2.6710cos(25.321oo +=−=t i t i电路cos3142115**+−u sa i 112L 1L 2R LM电路+−a b422Ω−Ωj189U 1I 1电路§1010--3 3 理想变压器理想变压器1N ••1−+1u ••2N ••−+u 21i n −••1−+1••11u n 2211N u N u =12211=+i N i N 122211=+i u i u 1N N电路11N ••1−+1u ••2N ••−+u 21in ••1−+1••11u n −22211nu u N N u −=−=212112ii i n N N ==电路11N ••1−+1u ••2N ••Z ••1−+1u 11I U Z in &&=1N ••1−+1u ••2N ••Z Ln in Z n I U n I U Z 221211=−==&&&&L n Z n I U n 2212=−=&&电路1−+s u ••Z −+2u −+1u 110:Ω+=+×==300300)33(1022j j Z n Z L in inZ −+sU &1I 13003001000220011j Z R U I in s ++∠=+=&&09.3644.0−∠=211I nI &&−=12I n I &&=A9.364.4−∠=电路21210I nI I &&&==1−+s u ••−+2u −+1u 1n sU U &&=1000221∠==s c U nU &&22I U Z in &&=Ω===1)1(12111R n I n U n &&9.364.433102202−∠=++∠=+=j Z Z U I L in oc &&in−+oc u 2i电路1••iI &−+1U &22••2I &−+2U &−+1u 1:2R 1I &ii I U R &&1=221212)11(1I U R R U R &&&−=++−11U U n &&=)(22112R U U I n I n I i &&&&&−−=−=121U U n &&=i I n R n nR nR U &&=−++)211(2121Ω==381ii I U R &&电路Ω−5j V 4=sU &Ω−=)5(222j n Z in Ω+−=5120141222n j j Y 05120122=+−n j j 22=n 2211Z n Z in =100=Ω=42Z 100421=n 51=n W 04.01004422m ax=×=×=ssUR U P电路)1(21==R R 21122111I L j I M j U I M j I L j U &&&&&&ωωωω+=+=21,1)2(L L M k ==1R 1L j ω••−+1U &1′••2R 2L j ωR ω••2′−+2U&2121u u L L =121212L L L L L L 221212221111I L j I L L j U I L L j I L j U &&&&&&ωωωω+=+=n=电路nL L L =∞→211211i ni −=212111I L L L j U I &&&−=ω2121I L L I &&−=n L L =21)3(221111I L L j I L j U &&&ωω+=电路M j Z L j R Z L j R Z M ωωω=+=+=222111221211I Z I Z U I Z I Z U M M &&&&&&+±=±=U Z Z Z Z Z I MM &m &22121−=U Z Z Z Z Z I MM &m &22112−=U Z Z Z Z Z Z I I I M M &m &&&2212121−+=+=22212111)()(I L j R I j U I j I L j R U M M &&&&&&ωωωω++±=±+=电路。
10第十章 含有耦合电感的电路PPT课件

图10-1(b)
对于图10-l(b)所示的情况有:
11112L1i1M12i2 22122M21i1L2i2
式中11、22表示电流在本身线圈形成的磁链,称为 自感磁链。12、21表示另一个线圈中电流产生的磁场在
本线圈中形成的磁链,称为互感磁链。也就是说每个线圈
根据以上叙述,定义一种称为耦合电感的双口电路元 件,其元件符号和电压电流关系分别如下所示:
u1
L1
d i1 dt
M
d i2 dt
u2
M
d i1 dt
L2
d i2 dt
u1
L1
d i1 dt
M
d i2 dt
u2
M
d i1 dt
L2
d
i2
d t
u1
L1
d i1 dt
M
d i2 dt
中的总磁链为自感磁链与互感磁链的代数和。
当电流i1和i2随时间变化时,线圈中磁场及其磁链也随 时间变化,将在线圈中产生感应电动势。
图(a)
对于图(a)的情况,根据电磁感应定律可以得到:
u1
d1
dt
d11
dt
d12
dt
L1
di1 dt
Mdi2 dt
u2
d2
dt
d21
dt
d22
dt
Mdi1 dt
L2
最后得到图(a)单口网络的等效电路为5电阻与10H电
感的串联。
§ 10.3 耦合电感的功率
当耦合电感中的施感电流变化时,将出现变化的 磁场,从而产生电场(互感电压),耦合电感通过 变化的电磁场进行电磁能的转换和传输,电磁能从 耦合电感一边传输到另一边。
电路PPT课件第10章含有耦合电感的电路

由同名端及u、i参考方向确定互感线圈的特性方程
有了同名端,以后表示两个线圈相互作用,就不再考虑实际绕向,而只画 出同名端及参考方向即可。
M
*
*
i1
+ u21 –
M
*
*
i1
– u21 +
u21
M
di1 dt
u21
M
di1 dt
例
i1
M
i2
+*
*+
u1 L1 _
L2 u2 _
u1
L1
di1 dt
M
di2 dt
u
L1
L2
–
i1
M
i2
+
**
+
u
L1
L2
u
–
–
•
I
jM
j(L1-M)
•
•
I1 I2
j(L2-M)
•
I1
j(L1-M)
•
I2
j(L2-M)
jM
4. 受控源等效电路
i1
M
i2
+
**
+
u
L1
L2 u
–
–
•
I1
+
j L1
•
U1
+
•
jM
–
I–2
•
I2
+
j L2
•
+
U2
•
jMI 1
–
–
•
•
•
U 1 jL1 I 1 jM I 2
US
j (L1 L3 2M31)
第十章 含有耦合电感电路

§10.3
二、分析方法
1、方程法分析
空心变压器
在正弦稳态情况下,空心变压器电路的回路方程为:
令
Z11 R1 jL1
Z 22 R2 jL2 Z
称为原边回路阻抗
称为副边回路阻抗
§10.3
则上述方程简写为:
空心变压器
从上列方程可求得原边和副边电流:
§10.3
2、等效电路法分析
,求:原、副边电流 I 1
I2
§10.3
空心变压器
例10-9 全耦合互感电路如图(a)所示,求电路初级端 ab 间的等效阻抗。
例 10 — 9 图 ( a )
例 10 — 9 图( b )
§10.3
空心变压器
例10-10、已知L1=L2=0.1mH , M =0.02mH , R1=10Ω , C1=C2=0.01μF , ω=106rad/s, U s 10 0 V 问:R2=?时能吸收最大功率,并求最大功率。
例 10-3 图(a)
例 10-3 图(b)
§10.2
例10-4
含有耦合电感电路的计算
图(a)为有耦合电感的电路,试列写电路的回路电流方程。
电路的开路电压。
§10.2
含有耦合电感电路的计算
例10-6 图(a)为有互感的电路,若要使负载阻抗 Z 中的电 流 i =0 ,问电源的角频率为多少?
第十章 含有耦合电感电路
§10.1 §10.2 §10.3 §10.4 互感 含有耦合电感电路的计算 空心变压器 理想变压器
§10.1
一、互感
互感
两个靠得很近的电感线圈之间有磁的耦合,如图所示,当 线圈1中通电流i1时,不仅在线圈1中产生磁通φ11,同时,有 部分磁通φ21穿过临近的线圈2;同理,若在线圈2中通电流i2 时,不仅在线圈2中产生磁通φ22,同时,有部分磁通φ12穿 过线圈1,φ12和φ21称为互感磁通。
电路第10章---含有耦合电感的电路讲解

§10.1 互感耦合电感元件属于多端元件,在实际电路中,如收音机、电视机中的中周线圈、振荡线圈,整流电源里使用的变压器等都是耦合电感元件,熟悉这类多端元件的特性,掌握包含这类多端元件的电路问题的分析方法是非常必要的。
1. 互感两个靠得很近的电感线圈之间有磁的耦合,如图10.1所示,当线圈1中通电流 i 1 时,不仅在线圈1中产生磁通f 11,同时,有部分磁通 f 21 穿过临近线圈2,同理,若在线圈2中通电流i 2 时,不仅在线圈2中产生磁通f 22,同时,有部分磁通 f 12 穿过线圈1,f 12和f 21称为互感磁通。
定义互磁链:图 10.1ψ12 = N 1φ12 ψ21 = N 2φ21当周围空间是各向同性的线性磁介质时,磁通链与产生它的施感电流成正比,即有自感磁通链:互感磁通链:上式中 M 12 和 M 21 称为互感系数,单位为(H )。
当两个线圈都有电流时,每一线圈的磁链为自磁链与互磁链的代数和:需要指出的是:1)M 值与线圈的形状、几何位置、空间媒质有关,与线圈中的电流无关,因此,满足M12 =M21 =M2)自感系数L 总为正值,互感系数 M 值有正有负。
正值表示自感磁链与互感磁链方向一致,互感起增助作用,负值表示自感磁链与互感磁链方向相反,互感起削弱作用。
2. 耦合因数工程上用耦合因数k 来定量的描述两个耦合线圈的耦合紧密程度,定义一般有:当k =1 称全耦合,没有漏磁,满足f11 = f21,f22 = f12。
耦合因数k 与线圈的结构、相互几何位置、空间磁介质有关。
3. 耦合电感上的电压、电流关系当电流为时变电流时,磁通也将随时间变化,从而在线圈两端产生感应电压。
根据电磁感应定律和楞次定律得每个线圈两端的电压为:即线圈两端的电压均包含自感电压和互感电压。
在正弦交流电路中,其相量形式的方程为注意:当两线圈的自感磁链和互感磁链方向一致时,称为互感的“增助”作用,互感电压取正;否则取负。
电路邱关源第五版10第十章

di1 di2 u1 L1 M dt dt 0 1 t M i1 (t ) 0 u1 ( )d i2 (t ) L1 L1
理想变压器模型
考虑理想化条件: k 1 M L1 L2
L1 , L1 L2 N1 N 2 n
M L2 1 L1 L1 n
1 i1 (t ) i2 (t ) n
大小,不改变阻抗的性质。
n2Z
注意 理想变压器的阻抗变换只改变阻抗的
返 回 上 页 下 页
已知电源内阻RS=1k,负载电阻RL=10。为 例1 使RL获得最大功率,求理想变压器的变比n。 RS RS n:1 + + * * uS RL uS n2RL _ – 解 应用变阻抗性质 当 n2RL=RS 时匹配,即
M k 1 L1L2
def
F11= F21 ,F22 =F12
M M2 ( Mi1 )( Mi2 ) 12 21 k 1 L1L2 L1i1L2i2 11 22 L1L2
注意 耦合系数k与线圈的结构、相互几何位置、
空间磁介质有关。
返 回 上 页 下 页
例
i1
M
i2
i1 + * u1 L1 _
返 回 上 页 下 页
②反接串联 R1 L1 i
+ + u1 * M – + u
L2 R2 *u – 2 –
+ i R
u
–
L
u R1i L1 di M di L2 di M di R2i dt dt dt dt ( R1 R2 )i ( L1 L2 2M ) di Ri L di dt dt
10n2=1000
第十章 含有耦合电感的电路

含有耦合电感的电路
§10-1 互感 §10-2 含有耦合电感电路的计算 §10-3 耦合电感的功率 §10-4 变压器原理 §10-5 理想变压器
制作群
主
页
总目录
章目录
上一页
下一页
退
出
理解耦合电感的定义;掌握判断同名端的方法; 掌握运用去耦法分析计算含有耦合电感的电路;了解 含有空心变压器电路的阻抗折算;掌握理想变压器的 VCR和阻抗变换关系。
R jL I U 1 1 1 jMI 2 Z1 I1 Z M I 2 jMI R jL I U 1 2 2 2 Z M I1 Z 2 I 2
I I I 3 1 2
+
I 3
jM
①
I 1
解: 1 L1i1 Mi2 2 1 1 5 cos10t
2 5 cos10t Wb
1
+
i1 L1
M L2
i2
2
+
2 Mi1 L2i2 11 3 5 cos10t
1 15 cos10t Wb
制作群
主
u1
u2
1'
jL1
I 2
jL2
U
-
R1
R2
① jM I 3
+
jMI R j L M I U 3 1 1 1
I 1
jL1 M jL2 M
I 2
jMI R j L M I U U 3 2 2 2
1'
11 ห้องสมุดไป่ตู้2 21 22
1 i1
第10章 含有耦合电感的电路

R1
L1 u1
i
R1
u1
L1
u
M
R2 u2
u
M R2 u2
L2
L2(a)顺向串联电路(来自)反向串联电路1、计算公式
对于反向串联电路,按图示参考方向,列写 KVL方程为: di di
u 1 R 1 i ( L1 M )
i
R1 u1
L1
dt
dt di dt di dt di dt )
R 1 i ( L1 M ) u 2 R2i ( L2 di dt
1 L1 i1 M i 2
2
M i1 L 2 i 2
i L 例1:下图中,i1 1 0 A ,2 5 co s(1 0 t ) A ,1 2 H , L M 求 2 3 H , 1H 。求两耦合线圈中的磁通链。
1
i1
M
i2
2
L2 u2 2’
1 1 L1 i1 2 0 W b
U j M I 3 [ R 1 j ( L1 M )] I 1 U j M I 3 [ R 2 j ( L 2 M )] I 2
根据上述方程可以给出一个无互感的等效电路, 如右下图所示:
I3
j M
I3
I2
j M
I1
解:
1 L1 i1 M i 2 [ 2 0 5 co s(1 0 t )]W b
2
M i1 L 2 i 2 [1 0 1 5 co s(1 0 t )]W b
u 1 L1 u2 M
ww含有耦合电感的电路

(
L1
L2 )
互感不不小于两个自感旳算术平均值。
二、串联顺接
i ++ u
––
R1
u1 – +
u2
* L1 M
* L2
i
+ R
u L
–
R2
u
R1 i
L1
di dt
M
di dt
L2
di dt
M
di dt
R2 i
( R1
R2 )i
(L1
L2
2M ) di dt
Ri
L di dt
R R1 R2
L L1 L2 2M
副边等效电路
一样可解得:
•
•
I
2
- jM U S/ Z11 Z22 (M )2 / Z11
•
•
U oc
jωM U S
Z11
—副边开路时,原边电 流在副边产生旳互感电压。
Z11=R1+jL1, Z22=(R2+R)+j(L2+X)
引入电抗
负号反应了副边旳感性阻抗 反应到原边为一种容性阻抗
当I2 0, 即副边开路, Zin Z11
•
I 1 R1
j M
•
R2 I 2
(ωM )2
+
•
US
–
**
j L1
j L2
Z11
•
Z=R+jX
+
•
I2
U oc
Z22
–
•
•
•
(R1 jωL1 )I 1 jM I 2 U S
•
•
jM I 1 (R2 jωL2 Z ) I 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P= I12(R1+Rl)
I12R1 消耗在一次侧; I12Rl 消耗在二次侧
证 明
+
二次侧开路时,一次电流在二 次侧产生的互感电压。
Z22
– 二次侧等效电路
一次侧对二次侧的引入阻抗。
注意 利用戴维宁定理可以求得变压器的二
次侧等效电路 。
③去耦等效法分析
对含互感的电路进行去耦等效,再进行分析。
互感现象
利用——变压器:信号、功率传递 避免——干扰
克服:合理布置线圈相互位置或增加屏蔽减少互感 作 用。
电抗器
电抗器磁场
铁磁材料屏蔽磁场
3. 耦合电感上的电压、电流关系
当 i1 为时变电流时,磁通也将随时间变化,从 而在线圈两端产生感应电压。 当 i1 、 u11 、 u21 方向与 符合右手螺旋法则时, 根据电磁感应定律和楞次定律有 自感电压 互感电压 当两个线圈同时通以电流时,每个线圈两 端的电压均包含自感电压和互感电压。
R2=0.08 , RL=42 , =314rad/s, + – + – R1 j M jL *
1
R2 RL
解法1 应用一次 等效电路
* jL2 Z11
+ –
Z11
解法2 应用二次等效电路
+
Z22
–
例4-3 全耦合电路如图,求ab端的等效阻抗。
a +
b – 解法1
* L1
M
* L2
例4-1 已知 Us=20 V , 一次侧引入阻抗 Zl=(10–j10)。
求: ZX 并求负载获得的有功功率。 (10+j10) j2 10 * j10 * j10 + ZX – Zl
+ – 解
负载获得功率: 实际是最佳匹配:
例4-2 L1=3.6H , L2=0.06H , M=0.465H , R1=20 ,
例2-2 列写电路的回路
电流方程。
R1 i1 u S * L1 C
+
+ R2 ki1 - - * L2 M
解
R1 i1 1uS
* L1 C
+
+ R2 ki12 - - * L2 M 3
例2-3 求图示电路的开路电压。 M
R1
+ 解法1 _
L2 * + M31 L3 M 23 * _
L1
L2 *
+ u2 _
解
i1 + * u1 L1 _
M
i2 L2 *
i1
M
i2 L2 * u2 +
+ u2 _
+ * u1 L1 _
写 出 图 示 电 路 电 压、 电 流 关 系 式
例1-2 已知
10 M * R2 L2 + u2 _ 10
O
。 i1/A
+ u _
解
i1 R1 * L1
1
2
t/s
10-2 含有耦合电感电路的计算
1. 耦合电感的串联
①顺接串联 i + R1 L1 + u1 * M – +* u L2 R2
u2 – –
+ i
去耦等效电路
R L
u
–
②反接串联
R1 L1 i + + u1 * M –+ u L2 R2 *u – 2 –
+ i u –
R L
注意
互感的测量方法:
顺接一次,反接一次,就可以测出互感:
空心线圈, 与i 成正比。当只有一个线圈时:
1 = 11=L1i1 L1 为自感系数,单位 H(亨)
当两个线圈都有电流时,每一线圈的磁通链 为自感磁通链与互感磁通链的代数和:
1 = 11 12= L1i1 M12 i2 2 = 22 21= L2i2 M21 i1
注意 M值与线圈的形状、几何位置、空间媒
②等效电路法分析
+
Z22
根据以上表示式得等效电路。 –
Z11 +
– 一次侧等效电路 二次侧对一次侧的引入阻抗。 引入电阻。恒为正 , 表示二次回路吸收 的功率是靠一次回路供给的。 引入电抗。负号反映了引入电抗与二次 回路电抗的性质相反。
注意
引入阻抗反映了二次回路对一次回路的影响。 一、二次回路虽然没有电的连接,但互感的作用使 二次回路产生电流,这个电流又影响一次回路的电 流、电压。
第十章 含有耦合电感的电路
本章重点
10-1 10-2
互感 含有耦合电感电路的计算
耦合电感的功率 变压器原理 理想变压器
10-3
10-4 10-5
重点
1.互感和互感电压 2.有互感电路的计算
3.变压器和理想变压器原理
10-1 互感
耦合电感元件属于多端元件,在实际电路中, 如收音机、电视机中的中周线圈、振荡线圈,整 流电源里使用的变压器等都是耦合电感元件,熟 悉这类多端元件的特性,掌握包含这类多端元件 的电路问题的分析方法是非常必要的。
12
解法2
作出去耦等效电路,(一对一对消):
M12 L1 L3 * L2 L1–M12 L2–M12 L3+M12 *
*
M23
M31
M31 *
M23
L1–M12 +M23 –M13 L2–M12–M23 +M13 L1–M12 +M23 L3+M12–M23 –M13
L2–M12 –M23 L3+M12 –M23
2. 耦合电感的并联
①同侧并联
+ u –
i i1
M
L1
* * i2 L2
i = i1 +i2
解得u, i 的关系
等效电感:
去耦等效电路
如全耦合:L1L2=M2 当 L1L2 ,Leq=0 (短路)
+ u –
i Leq
当 L1=L2 =L , Leq=L (相当于导线加粗,电感不变)
② 异侧并联 + u –
质有关,与线圈中的电流无关,满足 M12=M21。 ② L 总为正值,M 值有正有负。
2. 耦合系数
用耦合系数k 表示两个线 圈磁耦合的紧密程度。 k=1 称全耦合: 漏磁 1 = 2=0 满足:
11= 21 ,22 =12
注意 耦合系数 k 与线圈的结构、相互几何位置、
空间磁介质有关。
在正弦交流电路中,其相量形式的方程为
注意
两线圈的自感磁通链和互感磁通链方向一 致,互感电压取正,否则取负。表明互感电压 的正、负: (1)与电流的参考方向有关。 (2)与线圈的相对位置和绕向有关。
4.互感线圈的同名端
对自感电压,当 u, i 取关联参考方向, u、i 与 符合右手螺旋法则,其表达式为 i1 u11 上式说明,对于自感电压由于电压、电流为 同一线圈上的,只要参考方向确定了,其数学描 述便可容易地写出,可不用考虑线圈绕向。
i i1
M
*
*
i2 L2
L1
i = i1 +i2
解得u, i 的关系: 等效电感:
3.耦合电感的T型等效
①同名端为共端的T型去耦等效 j M 1 1 2 j(L1-M) * * jL1 jL2 3
2
j(L2-M) jM 3
②异名端为共端的T型去耦等效 1 * jL1 3 j M jL2 * 2 1 j(L1+M) 2 j(L2+M) -jM 3
变压器
电力变压器
三相电力变压器
小变压器
调压器
整流器
电流互感器
牵引电磁铁
1. 互感
11 21
i1 N1 + u11 – N2 + u21 –
线圈 1 中通入电流 i1 时,在线圈 1 中产生磁通, 同时,有部分磁通穿过临近线圈 2,这部分磁通称 为互感磁通。两线圈间有磁的耦合。 定义 :磁通链 , =N
1.变压器电路(工作在线性段)
j M + R1 * * R2
二次回路
–
一次回路
jL1
jL2
Z=R+jX
2. 分析方法
①方程法分析 回路方程:
jM jL1 Z=R+jX
+
–
R1
* *
R2 jL2
令
Z11=R1+j L1, Z22=(R2+R)+j( L2+X)
+ –
Z11
一次 侧等 效电 路 二次侧 等效电 路
+
二次回路开路,对一次回路无影响,开路电压 u2(t)中只有互感电压。先应用三要素法求电流i(t)。
10 M=0.1H 10 * 0.2H * 0.4H u2 +
-
10-3 耦合电感的功率
当耦合电感中的施感电流变化时,将出现变化 的磁场,从而产生电场(互感电压),耦合电感通 过变化的电磁场进行电磁能的转换和传输,电磁能 从耦合电感一边传输到另一边。
+ u2
–
+
j L 1 +
j L 2 + –
+
–
–
–
例2-1
a 2H 4H
M=3H
6H
a
M=4H 5H
6H
b 解 a
0.5H 2H
b
2H
3H M=1H
a 7H 9H -3H 0.5H b
1H 3H
2H
Lab=5H b
Lab=6H 3H
4H
