_奥本海姆信号与系统二版中文版答案
资料-奥本海姆信号与系统上册2版课后答案

1答案习题1.1用笛卡儿坐标形式(x+yj)表示下列复数。
解:利用欧拉公式:和复平面性质,有:,,1.2用极坐标形式(re jθ,-π<θ≤π)表示下列复数。
解:根据,有:1.3对下列每一个信号求P∞和E∞。
解:(a)(b)(c)(d)(e)(f)1.1设n<-2和n>4时x[n]=0,对以下每个信号确定其值保证为零的n值。
解:(a)x[n-3]=0,n-3<-2或n-3>4,即x[n-3]=0,n<1或n>7(b)x[n+4]=0,n+4<-2或n+4>4,即x[n+4]=0,n<-6或,n>0(c)x[-n]=0,-n<-2或-n>4,即x[-n]=0,n<-4或n>2(d)x[-n+2]=0,-n+2<-2或-n+2>4,即x[-n+2]=0,n<-2或n>4(e)x[-n-2]=0,-n-2<-2或-n-2>4,即x[-n-2]=0,,n<-6或n>01.2设t<3时x(t)=0,确定以下每个信号的值保证为零的t值。
解:(a)x(1-t)=0,1-t<3,即x(1-t)=0,t>-2(b)x(1-t)+x(2-t)=0,1-t<3且2-t<3,即x(1-t)+z(2-t)=0,t>-1(c)x(1-t)x(2-t)=0,1-t<3或2-t<3,即x(1-t)x(2-t)=0,t>-2(d)x(3t)=0,3t<3,即x(3t)=0,t<1(e)x(t/3)=0,t/3<3,即x(t/3)=0,t<91.3判断下列信号的周期性。
解:(a)由于对于-∞<t<∞,x1(t)的值不具备重复性,所以x1(t)不是周期信号。
(b)由于所以x2[n]也不具备周期性。
(c)由于所以x3[n]是基波周期为4的周期序列。
1.4对以下每个信号求信号的偶部保证为零的所有自变量值。
解:(a)只有当|n|>3时,(b)即对一切t,(c)所以当|n|<3及|n|→∞时,(d),由于所以只有当|t|→∞时,1.5将下列信号的实部表示成的形式,其中A,a,ω和都是实数,A>0且-π<≤π。
信号与系统 奥本海姆 中文答案 chapter 2

Chapter 22.1解:(a) 1[][][][0][][1][1][3][3]y n x n h n x h n x h n x h n =*=+-+-2[1]4[]2[1]2[2]2[4]n n n n n δδδδδ=+++-+---(图略)(b) 21[][2][][2]y n x n h n y n =+*=+2[3]4[2]2[1]2[]2[2]n n n n n δδδδδ=++++++--(图略)(c) 32[][][2][]y n x n h n y n =*+=(图略)2.5解:9[][][]k y n x k h n k ==-∑,由[4]5y =可知:4N ≥由[14]0y =可知:9114N ++≤,即:4N ≤ 所以:4N =2.11解:(a) 3t ≤时,()0y t =35t <≤时,3()(3)()(3)()ty t u t h t u h t d τττ=-*=--⎰3(3)3()313t tt e ed ττ-----==⎰5t >时,[]()63(5)53()31()(3)(5)()3t t e e y t t u t u h t e d ττ------=---*==⎰因此:()3(3)63(5)0,31(),3531,53t t t e y t t e e t -----⎧⎪≤⎪⎪-=<≤⎨⎪⎪-⎪>⎩(b )()(3)(5)dx t t t dtδδ=--- 3(3)3(5)()()()(3)(5)(3)(5)t t dx t g t h t h t h t e u t e u t dt----∴=*=---=---(c) ()()dy t g t dt=2.13解:(a) 将1[][]5n h n u n ⎛⎫= ⎪⎝⎭代入式子得:111[][1][]55n n u n A u n n δ-⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭即:()1[]5[1][]5nu n Au n n δ⎛⎫--= ⎪⎝⎭从而可得:51A =,即:15A = (b)由(a)可知:1[][1][]5h n h n n δ--= 则1S 的逆系统2S 的单位脉冲响应为:11[][][1]5h n n n δδ=--2.16解:(a)对。
信号与系统第二版课后习题解答(3-4)奥本海姆

Chap 33.1 A continuous-time periodic signal x(t) is real value and has a fundamental period T=8. The nonzero Fourier series coefficients for x(t) arej a a a a 4,2*3311====--.Express x(t) in the form)cos()(0k k k k t A t x φω+=∑∞=Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑A discrete-time periodic signal x[n] is real valued and has afundamental period N=5.The nonzero Fourier series coefficients for x[n] are10=a ,4/2πj e a --=,4/2πj e a =,3/*442πj e a a ==- Express x[n] in the form)sin(][10k k k k n A A n x φω++=∑∞=Solution:for, 10=a , 4/2πj ea --= , 4/2πj ea = ,3/42πj e a --=,3/42πj e a =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=n j j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++=)358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n nFor the continuous-time periodic signal)35sin(4)32cos(2)(t t t x ππ++= Determine the fundamental frequency 0ω and the Fourier seriescoefficients k a such thattjk k kea t x 0)(ω∑∞-∞==.Solution:for the period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6, i.e. 3/6/20ππ==w )35sin(4)32cos(2)(t t t x ππ++=)5sin(4)2cos(21200t t ωω++=0000225512()2()2j t j t j t j t e e j e e ωωωω--=++-- then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Let 1()x t be a continuous-time periodic signal with fundamental frequency1ω and Fourier coefficients k a . Given that211()(1)(1)x t x t x t =-+-How is the fundamental frequency2ω of 2()x t related to? Also,find a relationship between the Fourier series coefficients k b of2()x t and the coefficients k a You may use the properties listed inTable 3.1. Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x , that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw t k TT b x t e dt x t x t e dt T --==-+-⎰⎰ 111111(1)(1)jkw t jkw t TTx t e dt x t e dt T T --=-+-⎰⎰111)(jkw k k jkw k jkw k e a a e a e a -----+=+=Suppose given the following information about a signal x(t): 1. x(t) is real and odd.2. x(t) is periodic with period T=2 and has Fourier coefficients k a .3. 0=k a for 1||>k .4 1|)(|21202=⎰dt t x .Specify two different signals that satisfy these conditions. Solution:0()j kt k k x t a e ω∞=-∞=∑while: )(t x is real and odd, then k a is purely imaginary and odd , 00=a , k k a a --=,.2=T , then 02/2ωππ==and0=k a for 1>kso0()j kt k k x t a e ω∞=-∞=∑00011j t j t a a e a e ωω--=++)sin(2)(11t a e ea t j tj πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x∴ j a 2/21±=∴)sin(2)(t t x π±=3 Consider a continuous-time LTI system whose frequency response is⎰∞∞--==ωωωω)4sin()()(dt e t h j H t jIf the input to this system is a periodic signal⎩⎨⎧<≤-<≤=84,140,1)(t t t x With period T=8,determine the corresponding system output y(t). Solution:Fundamental period 8T =.02/8/4ωππ==0()j kt k k x t a e ω∞=-∞=∑∴ 00()()jk t k k y t a H jk e ωω∞=-∞=∑0004, 0sin(4)()0, 0k k H jk k k ωωω=⎧==⎨≠⎩ ∴ 000()()4jkw t k k y t a H jk e a ω∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=⎰⎰⎰另:x(t)为实奇信号,则a k 为纯虚奇函数,也可以得到a 0为0。
奥本海姆信号与系统(第二版)复习题参考答案

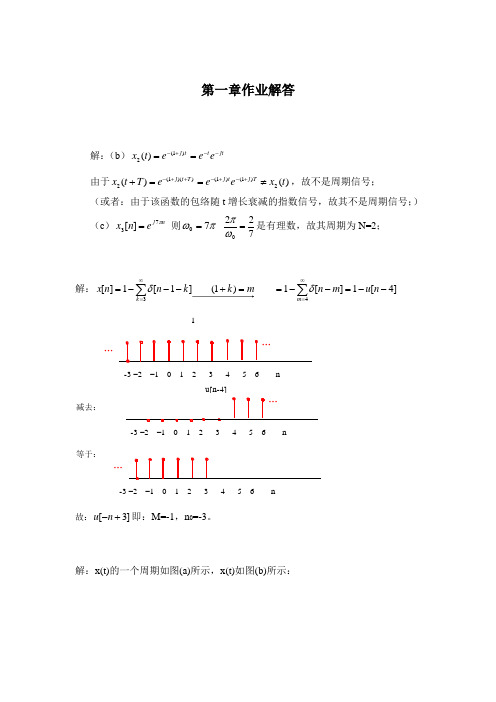
第一章作业解答1.9解:(b )jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-,故不是周期信号;(或者:由于该函数的包络随t 增长衰减的指数信号,故其不是周期信号;) (c )n j e n x π73][= 则πω70= 7220=ωπ是有理数,故其周期为N=2; 1.12解:]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去:-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于:-3 –2 –1 0 1 23 4 5 6 n…故:]3[+-n u 即:M=-1,n 0=-3。
1.14解:x(t)的一个周期如图(a)所示,x(t)如图(b)所示:而:g(t)如图(c)所示……dtt dx )(如图(d )所示:……故:)1(3)(3)(--=t g t g dtt dx 则:1t ,0t 3,32121==-==;A A 1.15解:该系统如下图所示: 2[n](1)]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即:]4[2]3[5]2[2][-+-+-=n x n x n x n y(2)若系统级联顺序改变,该系统不会改变,因为该系统是线性时不变系统。
(也可以通过改变顺序求取输入、输出关系,与前面做对比)。
1.17解:(a )因果性:)(sin )(t x t y =举一反例:当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关,不是因果的;(b )线性:按照线性的证明过程(这里略),该系统是线性的。
信号与系统第二版课后答案_西安交大_奥本海姆(汉语)

第一章1.3 解:(a). 2401lim(),04Tt T TE x t dt e dt P ∞-∞∞→∞-====⎰⎰(b) dt t x TP T TT ⎰-∞→∞=2)(21lim121lim ==⎰-∞→dt T TTT∞===⎰⎰∞∞--∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞--∞∞→∞→∞--===∞+===⎰⎰⎰⎰(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→-=∞→∞∑∑N N n x N P N Nn n N N N n N 34)21()(lim202===∑∑-∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=-=-===++∑∑ (f) ∑-=∞→∞=+=NNn N n x N P 21)(121lim 2∑-=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的; c) 00007,,22mN N ωωππ=== d). 010;N = e). 非周期的; 1.12 解:∑∞=--3)1(k k n δ对于4n ≥时,为1即4≥n 时,x(n)为0,其余n 值时,x(n)为1易有:)3()(+-=n u n x , 01,3;M n =-=- 1.15 解:(a)]3[21]2[][][222-+-==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+-, 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=-+-+-+-,1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =-+-+- 其中][n x 为系统输入。
信号与系统_第二版_奥本海默 _课后答案[1-10章]
![信号与系统_第二版_奥本海默 _课后答案[1-10章]](https://img.taocdn.com/s3/m/6ff45c8f83c4bb4cf6ecd112.png)
学霸助手[]-课后答案|期末试卷|复习提纲
学霸h助us手 Contents baz Chapter 1 ······················································· 2 xue Chapter 2 ······················································· 17
e 5 = 5 j0 ,
e -2 = 2 ,jp
e -3 j = 3
-
j
p 2
e 1
2
-
j
3 2
=
, -
j
p 2
e 1+ j =
2
, j
p 4
( ) 1- j e 2 =2
-
j
p 2
ep
j(1- j) = 4 ,
e 1+
1-
j j
=
p 4
e 2 + j 2 = -1p2
1+ j 3
ò e 1.3.
(a)
xue学ba霸zh助usS手hoiug.ncoaml(Sseco&nd EdSitioyn)stems
—Learning Instructions
xu(eEbxe学arzc霸hisue助sshA手onus.wceorms)
Department
of
Computer 2005.12
Enginexeurein学bga霸zh助us手
=¥
E¥
0
-4tdt
=
1 4
,
P ¥ =0, because
E¥ < ¥
手 om ò (b)
x e , 2(t) = j(2t+p4 )
奥本海姆《信号与系统(第二版)》习题参考答案
第一章作业解答解:(b )jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-,故不是周期信号;(或者:由于该函数的包络随t 增长衰减的指数信号,故其不是周期信号;) (c )n j e n x π73][= 则πω70= 7220=ωπ是有理数,故其周期为N=2;解:]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去:-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于:-3 –2 –1 0 1 2 34 5 6 n…故:]3[+-n u 即:M=-1,n 0=-3。
解:x(t)的一个周期如图(a)所示,x(t)如图(b)所示:而:g(t)如图(c)所示……dtt dx )(如图(d )所示:……故:)1(3)(3)(--=t g t g dtt dx 则:1t ,0t 3,32121==-==;A A 1.15解:该系统如下图所示: 2[n](1)]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即:]4[2]3[5]2[2][-+-+-=n x n x n x n y(2)若系统级联顺序改变,该系统不会改变,因为该系统是线性时不变系统。
(也可以通过改变顺序求取输入、输出关系,与前面做对比)。
解:(a )因果性:)(sin )(t x t y =举一反例:当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关,不是因果的;(b )线性:按照线性的证明过程(这里略),该系统是线性的。
本海默信号与系统第二版课后习题解信号与系统部分习题答案51页PPT

11、不为五斗米折腰。 12、芳菊开林耀,青松冠岩列。怀此 贞秀姿 ,卓为 霜下杰 。
13、归去来兮,田蜀将芜胡不归。 14、酒能祛百虑,菊为制颓龄。 15、春蚕收长丝的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
奥本海姆信号与系统中文版课后习题答案

1.对一个LTI 系统,我们已知如下信息:输入信号2()4()tx t e u t =-;输出响应22()()()t t y t e u t e u t -=-+(a) 确定系统的系统函数H(s)及收敛域。
(b) 求系统的单位冲激响应h(t)(c) 如果输入信号x(t)为(),tx t e t -=-∞<<+∞ 求输出y(t)。
解:(a)4114(),Re{}2,(),2Re{}2222(2)(2)X s s Y s s s s s s s ---=<=+=<-<--+-+1(),Re{}22H s s s =>-+(b)2()()t h t e u t -= (c)()2()()t ty t e e u d e τ+∞---τ--∞=ττ=⎰; ()(1)t ty t H e e --=-=.2. 已知因果全通系统的系统函数1()1s H s s -=+,输出信号2()()ty t e u t -=(a) 求产生此输出的输入信号x(t). (b) 若已知dt ∞∞<∞⎰+-|x(t)|,求输出信号x(t).(c) 已知一稳定系统当输入为2()te u t -时,输出为上述x(t)中的一个,确定是哪个?求出系统的单位冲激响应h(t).解:(a)1()2Y s s =+。
Re{}2s >-,()1()()(1)(2)Y s s X s H s s s +==-+ 由于()H s 的ROC 为Re{}1s >-,()X s ∴的ROC 为2Re{}1s -<<或Re{}1s >若 1ROC 为-2<Re{s}<1,则2112()()()33t tx t e u t e u t -=--若2ROC 为Re{s}>1,221()(2)()3t t x t e e u t -=+(b) 若 dt ∞∞<∞⎰+-|x(t)|,则只能是1()()x t x t =即:212()()()33t t x t e u t e u t -=--(c)212()()()()33t ty t x t e u t e u t-==--;1(),2Re{}1(1)(2)sY s ss s+=-<<-+()1()()1Y s sH sX s s+∴==-, 这就是(a)中系统的逆系统。
信号与系统 奥本海姆 第二版 习题详解

对方程两边同时做反变换得:
y[n] −
1 处有一个二阶极点,因为系统是因果的,所以 H ( z ) 的收敛域是 z > , (b)H ( z) 在 z = 1 3 3 包括单位圆,所以系统是稳定的。
解: (a) x[n] = δ [n + 5] ← → X ( z ) = z , ROC : 全部z 因为收敛域包括单位圆,所以傅立叶变换存在。
( )
χ (s ) = uL{e −2t u (t )} =
H (s ) =
H (s )如图所示。
Y (s ) 1 = 2 . X (s ) s − s − 2
1 1 1 3 3 ( ) , ⇒ H s = − s2 − s − 2 s − 2 s +1 (i )如果系统是稳定的,H (s )的ROC为 − 1〈ℜe {s}〈2.
∞ ∞
n =−∞
∑
∞
x[n]z − n =
− n−2
1 −n ∞ 1 n z = ∑− z ∑ −3 3 n =−∞ n =2
−2 n −n
z n + 2 = 9 z 2 /(1 + 3z ) = 3z /(1 + (1/ 3) z −1 ), z < 1 3 1 = ∑ n =2 3
1 1 (b) H (s) = 1 − 3 s − 2 s +1
(1)系统是稳定的,说明 H (s) 的收敛域应该包括虚轴在内,即: − 1 < Re{s} < 2 , 所以 h(t ) = 1 (− e u (−t ) − e u (t )) 3 (2)系统是因果的,则 H (s) 的收敛域应为 Re{s} > 2 ,所以 h(t ) = 1 (e u (t ) − e u (t )) 3 ( 3 ) 系 统 既 不 因 果 又 不 稳 定 , 则 H (s) 的 收 敛 域 应 为 Re{s} < −1 , 所 以
信号与系统奥本海姆第二版课后答案

信号与系统 奥本海姆第二版 习题解答Department of Computer Engineering2005.12ContentsChapter 1 (2)Chapter 2 (17)Chapter 3 (35)Chapter 4 (62)Chapter 5 (83)Chapter 6 (109)Chapter 7 (119)Chapter 8 (132)Chapter 9 (140)Chapter 10 (160)Chapter 1 Answers1.1 Converting from polar to Cartesian coordinates:111cos 222j eππ==- 111c o s ()222j e ππ-=-=- 2cos()sin()22jj j eπππ=+=2c o s ()s i n ()22jjj eπππ-=-=- 522j jj eeππ==4c o s ()s i n ())144jjj πππ+=+9441j jj ππ=-9441j j j ππ--==-41jj π-=-1.2 055j=, 22j e π-=,233jj e π--=212je π--=, 41j j π+=, ()2221jj eπ-=-4(1)j je π-=, 411j je π+=-12e π-1.3. (a) E ∞=4014tdt e∞-=⎰, P ∞=0, because E ∞<∞ (b) (2)42()j t t x eπ+=, 2()1t x =.Therefore, E ∞=22()dt t x +∞-∞⎰=dt +∞-∞⎰=∞,P ∞=211limlim222()TTTTT T dt dt TTt x --→∞→∞==⎰⎰lim11T →∞=(c) 2()t x =cos(t). Therefore, E ∞=23()dt t x +∞-∞⎰=2cos()dt t +∞-∞⎰=∞, P ∞=2111(2)1lim lim 2222cos()TTTTT T COS t dt dt T Tt --→∞→∞+==⎰⎰(d)1[][]12nn u n x =⎛⎫ ⎪⎝⎭,2[]11[]4nu n n x =⎛⎫ ⎪⎝⎭. Therefore, E ∞=24131[]4nn n x +∞∞-∞===⎛⎫∑∑ ⎪⎝⎭P ∞=0,because E ∞<∞.(e) 2[]n x =()28n j e ππ-+,22[]n x =1. therefore, E ∞=22[]n x +∞-∞∑=∞,P ∞=211limlim1122121[]NNN N n Nn NN N n x →∞→∞=-=-==++∑∑.(f) 3[]n x =cos 4nπ⎛⎫ ⎪⎝⎭. Therefore, E ∞=23[]n x +∞-∞∑=2cos()4n π+∞-∞∑=2cos()4n π+∞-∞∑,P ∞=1limcos 214nNN n NN π→∞=-=+⎛⎫∑ ⎪⎝⎭1cos()112lim ()2122NN n Nn N π→∞=-+=+∑ 1.4. (a) The signal x[n] is shifted by 3 to the right. The shifted signal will be zero for n<1, And n>7. (b) The signal x[n] is shifted by 4 to the left. The shifted signal will be zero for n<-6. And n>0. (c) The signal x[n] is flipped signal will be zero for n<-1 and n>2.(d) The signal x[n] is flipped and the flipped signal is shifted by 2 to the right. The new Signal will be zero for n<-2 and n>4.(e) The signal x[n] is flipped and the flipped and the flipped signal is shifted by 2 to the left. This new signal will be zero for n<-6 and n>0.1.5. (a) x(1-t) is obtained by flipping x(t) and shifting the flipped signal by 1 to the right. Therefore, x (1-t) will be zero for t>-2. (b) From (a), we know that x(1-t) is zero for t>-2. Similarly, x(2-t) is zero for t>-1, Therefore, x (1-t) +x(2-t) will be zero for t>-2. (c) x(3t) is obtained by linearly compression x(t) by a factor of3. Therefore, x(3t) will be zero for t<1.(d) x(t/3) is obtained by linearly compression x(t) by a factor of 3. Therefore, x(3t) will bezero for t<9.1.6(a) x1(t) is not periodic because it is zero for t<0.(b) x2[n]=1 for all n. Therefore, it is periodic with a fundamental period of 1.(c) x3[n1.7. (a)()1[]vnxε={}1111[][]([][4][][4])22n n u n u n u n u nx x+-=--+----Therefore, ()1[]vnxεis zero for1[]nx>3.(b) Since x1(t) is an odd signal, ()2[]vnxεis zero for all values of t.(c)(){}11311[][][][3][3]221122vn nn n n u n u nx x xε-⎡⎤⎢⎥=+-=----⎢⎥⎢⎥⎣⎦⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭Therefore, ()3[]vnxεis zero when n<3 and when n→∞.(d) ()1554411()(()())(2)(2)22vt tt t t u t u tx x x e eε-⎡⎤=+-=---+⎣⎦Therefore, ()4()vtxεis zero only when t→∞.1.8. (a) ()01{()}22cos(0)tt tx eπℜ=-=+(b) ()02{()}cos()cos(32)cos(3)cos(30)4tt t t tx eππℜ=+==+(c) ()3{()}sin(3)sin(3)2t tt t tx e eππ--ℜ=+=+(d) ()224{()}sin(100)sin(100)cos(100)2t t tt t t tx e e eππ---ℜ=-=+=+1.9. (a)1()tx is a periodic complex exponential.101021()j t j tt jx e eπ⎛⎫+⎪⎝⎭==(b)2()tx is a complex exponential multiplied by a decaying exponential. Therefore,2()tx is not periodic.(c)3[]nx is a periodic signal. 3[]n x=7j neπ=j neπ.3[]nx is a complex exponential with a fundamental period of 22ππ=.(d)4[]nx is a periodic signal. The fundamental period is given by N=m(23/5ππ)=10().3mBy choosing m=3. We obtain the fundamental period to be 10.(e)5[]nx is not periodic. 5[]nx is a complex exponential with 0w=3/5. We cannot find any integer m such that m(2wπ) is also an integer. Therefore,5[]nxis not periodic.1.10. x(t)=2cos(10t+1)-sin(4t-1)Period of first term in the RHS =2105ππ=.Period of first term in the RHS =242ππ=.Therefore, the overall signal is periodic with a period which the least commonmultiple of the periods of the first and second terms. This is equal toπ.1.11. x[n] = 1+74j n e π−25j n e πPeriod of first term in the RHS =1. Period of second term in the RHS =⎪⎭⎫ ⎝⎛7/42π=7 (when m=2)Period of second term in the RHS =⎪⎭⎫ ⎝⎛5/22ππ=5 (when m=1)Therefore, the overall signal x[n] is periodic with a period which is the least common Multiple of the periods of the three terms inn x[n].This is equal to 35.1.12. The signal x[n] is as shown in figure S1.12. x[n] can be obtained by flipping u[n] and thenShifting the flipped signal by 3 to the right. Therefore, x[n]=u[-n+3]. This implies that M=-1 and no=-3.1.13y (t)=⎰∞-tdt x )(τ =dt t))2()2((--+⎰∞-τδτδ=⎪⎩⎪⎨⎧>≤≤--<2,022,12,0,t t tTherefore ⎰-==∞224d t E∑∑∞-∞=∞-∞=----=k k k t k t t g 12(3)2(3)(δδ)This implies that A 1=3, t 1=0, A 2=-3, and t 2=1.1.15 (a) The signal x 2[n], which is the input to S 2, is the same as y 1[n].Therefore ,y 2[n]= x 2[n-2]+21x 2[n-3] = y 1[n-2]+ 21y 1[n-3]=2x 1[n-2] +4x 1[n-3] +21( 2x 1[n-3]+ 4x 1[n-4]) =2x 1[n-2]+ 5x 1[n-3] + 2x 1[n-4] The input-output relationship for S isy[n]=2x[n-2]+ 5x [n-3] + 2x [n-4](b) The input-output relationship does not change if the order in which S 1and S 2 are connected series reversed. . We can easily prove this assuming that S 1 follows S 2. In this case , the signal x 1[n], which is the input to S 1 is the same as y 2[n].Therefore y 1[n] =2x 1[n]+ 4x 1[n-1]= 2y 2[n]+4 y 2[n-1]=2( x 2[n-2]+21 x 2[n-3] )+4(x 2[n-3]+21x 2[n-4]) =2 x 2[n-2]+5x 2[n-3]+ 2 x 2[n-4]The input-output relationship for S is once againy[n]=2x[n-2]+ 5x [n-3] + 2x [n-4]1.16 (a)The system is not memory less because y[n] depends on past values of x[n].(b)The output of the system will be y[n]= ]2[][-n n δδ=0(c)From the result of part (b), we may conclude that the system output is always zero for inputs of the form ][k n -δ, k ∈ ґ. Therefore , the system is not invertible .1.17 (a) The system is not causal because the output y(t) at some time may depend on future values of x(t). For instance , y(-π)=x(0).(b) Consider two arbitrary inputs x 1(t)and x 2(t).x 1(t) →y 1(t)= x 1(sin(t)) x 2(t) → y 2(t)= x 2(sin(t))Let x 3(t) be a linear combination of x 1(t) and x 2(t).That is , x 3(t)=a x 1(t)+b x 2(t)Where a and b are arbitrary scalars .If x 3(t) is the input to the given system ,then the corresponding output y 3(t) is y 3(t)= x 3( sin(t))=a x 1(sin(t))+ x 2(sin(t)) =a y 1(t)+ by 2(t)Therefore , the system is linear.1.18.(a) Consider two arbitrary inputs x 1[n]and x 2[n].x 1[n] → y 1[n] =][01k x n n n n k ∑+-=x 2[n ] → y 2[n] =][02k x n n n n k ∑+-=Let x 3[n] be a linear combination of x 1[n] and x 2[n]. That is :x 3[n]= ax 1[n]+b x 2[n]where a and b are arbitrary scalars. If x 3[n] is the input to the given system, then the corresponding outputy 3[n] is y 3[n]=][03k x n n n n k ∑+-==])[][(2100k bx k ax n n n n k +∑+-==a ][001k x n n n n k ∑+-=+b ][02k x n n n n k ∑+-== ay 1[n]+b y 2[n]Therefore the system is linear.(b) Consider an arbitrary input x 1[n].Lety 1[n] =][01k x n n n n k ∑+-=be the corresponding output .Consider a second input x 2[n] obtained by shifting x 1[n] in time:x 2[n]= x 1[n-n 1]The output corresponding to this input isy 2[n]=][02k x n n n n k ∑+-== ]n [1100-∑+-=k x n n n n k = ][01011k x n n n n n n k ∑+---=Also note that y 1[n- n 1]=][01011k x n n n n n n k ∑+---=.Therefore , y 2[n]= y 1[n- n 1] This implies that the system is time-invariant.(c) If ][n x <B, then y[n]≤(2 n 0+1)B. Therefore ,C ≤(2 n 0+1)B.1.19 (a) (i) Consider two arbitrary inputs x 1(t) and x 2(t). x 1(t) → y 1(t)= t 2x 1(t-1)x 2(t) → y 2(t)= t 2x 2(t-1)Let x 3(t) be a linear combination of x 1(t) and x 2(t).That is x 3(t)=a x 1(t)+b x 2(t)where a and b are arbitrary scalars. If x 3(t) is the input to the given system, then the corresponding output y 3(t) is y 3(t)= t 2x 3 (t-1)= t 2(ax 1(t-1)+b x 2(t-1))= ay 1(t)+b y 2(t)Therefore , the system is linear.(ii) Consider an arbitrary inputs x 1(t).Let y 1(t)= t 2x 1(t-1)be the corresponding output .Consider a second input x 2(t) obtained by shifting x 1(t) in time:x 2(t)= x 1(t-t 0)The output corresponding to this input is y 2(t)= t 2x 2(t-1)= t 2x 1(t- 1- t 0)Also note that y 1(t-t 0)= (t-t 0)2x 1(t- 1- t 0)≠ y 2(t) Therefore the system is not time-invariant.(b) (i) Consider two arbitrary inputs x 1[n]and x 2[n]. x 1[n] → y 1[n] = x 12[n-2]x 2[n ] → y 2[n] = x 22[n-2].Let x 3(t) be a linear combination of x 1[n]and x 2[n].That is x 3[n]= ax 1[n]+b x 2[n]where a and b are arbitrary scalars. If x 3[n] is the input to the given system, then the corresponding output y 3[n] is y 3[n] = x 32[n-2]=(a x 1[n-2] +b x 2[n-2])2=a 2x 12[n-2]+b 2x 22[n-2]+2ab x 1[n-2] x 2[n-2]≠ ay 1[n]+b y 2[n]Therefore the system is not linear.(ii) Consider an arbitrary input x 1[n]. Let y 1[n] = x 12[n-2]be the corresponding output .Consider a second input x 2[n] obtained by shifting x 1[n] in time:x 2[n]= x 1[n- n 0]The output corresponding to this input isy 2[n] = x 22[n-2].= x 12[n-2- n 0]Also note that y 1[n- n 0]= x 12[n-2- n 0] Therefore , y 2[n]= y 1[n- n 0] This implies that the system is time-invariant.(c) (i) Consider two arbitrary inputs x 1[n]and x 2[n].x 1[n] →y 1[n] = x 1[n+1]- x 1[n-1] x 2[n ]→y 2[n] = x 2[n+1 ]- x 2[n -1]Let x 3[n] be a linear combination of x 1[n] and x 2[n]. That is :x 3[n]= ax 1[n]+b x 2[n]where a and b are arbitrary scalars. If x 3[n] is the input to the given system, then the corresponding output y 3[n] is y 3[n]= x 3[n+1]- x 3[n-1]=a x 1[n+1]+b x 2[n +1]-a x 1[n-1]-b x 2[n -1]=a(x 1[n+1]- x 1[n-1])+b(x 2[n +1]- x 2[n -1])= ay 1[n]+b y 2[n]Therefore the system is linear.(ii) Consider an arbitrary input x 1[n].Let y 1[n]= x 1[n+1]- x 1[n-1]be the corresponding output .Consider a second input x 2[n] obtained by shifting x 1[n] in time: x 2[n]= x 1[n-n 0]The output corresponding to this input isy 2[n]= x 2[n +1]- x 2[n -1]= x 1[n+1- n 0]- x 1[n-1- n 0] Also note that y 1[n-n 0]= x 1[n+1- n 0]- x 1[n-1- n 0] Therefore , y 2[n]= y 1[n-n 0] This implies that the system is time-invariant.(d) (i) Consider two arbitrary inputs x 1(t) and x 2(t).x 1(t) → y 1(t)= d O {}(t) x 1 x 2(t) → y 2(t)= {}(t) x 2d OLet x 3(t) be a linear combination of x 1(t) and x 2(t).That is x 3(t)=a x 1(t)+b x 2(t)where a and b are arbitrary scalars. If x 3(t) is the input to the given system, then the corresponding output y 3(t) is y 3(t)= d O {}(t) x 3={}(t) x b +(t) ax 21d O=a d O {}(t) x 1+b {}(t) x 2d O = ay 1(t)+b y 2(t)Therefore the system is linear.(ii) Consider an arbitrary inputs x 1(t).Lety 1(t)= d O {}(t) x 1=2)(x -(t) x 11t -be the corresponding output .Consider a second input x 2(t) obtained by shifting x 1(t) in time:x 2(t)= x 1(t-t 0)The output corresponding to this input isy 2(t)= {}(t) x 2d O =2)(x -(t) x 22t -=2)(x -)t -(t x 0101t t --Also note that y 1(t-t 0)= 2)(x -)t -(t x 0101t t --≠ y 2(t)Therefore the system is not time-invariant.1.20 (a) Givenx )(t =jt e 2 y(t)=t j e 3x )(t =jt e 2- y(t)=t j e 3- Since the system liner+=tj e t x 21(2/1)(jt e 2-))(1t y =1/2(tj e 3+tj e 3-)Thereforex 1(t)=cos(2t))(1t y =cos(3t)(b) we know thatx 2(t)=cos(2(t-1/2))= (j e -jte 2+je jt e 2-)/2Using the linearity property, we may once again writex 1(t)=21( j e -jt e 2+j e jte 2-))(1t y =(j e -jt e 3+je jte 3-)= cos(3t-1)Therefore,x 1(t)=cos(2(t-1/2)))(1t y =cos(3t-1)1.21.The signals are sketched in figure S1.21.1.24 The even and odd parts are sketched in Figure S1.24 1.25 (a) periodic period=2π/(4)= π/2 (b) periodic period=2π/(4)= 2(c) x(t)=[1+cos(4t-2π/3)]/2. periodic period=2π/(4)= π/2 (d) x(t)=cos(4πt)/2. periodic period=2π/(4)= 1/2 (e) x(t)=[sin(4πt)u(t)-sin(4πt)u(-t)]/2. Not period. (f) Not period.1.26 (a) periodic, period=7.(b) Not period.(c) periodic, period=8.(d) x[n]=(1/2)[cos(3πn/4+cos(πn/4)). periodic, period=8. (e) periodic, period=16. 1.27 (a) Linear, stable(b) Not period. (c) Linear(d) Linear, causal, stable(e) Time invariant, linear, causal, stable (f) Linear, stable(g) Time invariant, linear, causal 1.28 (a) Linear, stable(b) Time invariant, linear, causal, stable (c)Memoryless, linear, causal (d) Linear, stable (e) Linear, stable(f) Memoryless, linear, causal, stable (g) Linear, stable1.29 (a) Consider two inputs to the system such that[][][]{}111.S e x n y n x n −−→=ℜand [][][]{}221.Se x n y n x n −−→=ℜNow consider a third inputx3[n]=x2[n]+x 1[n]. The corresponding system outputWill be [][]{}[][]{}[]{}[]{}[][]33121212e e e e y n x n x n x n x n x n y n y n ==+=+=+ℜℜℜℜtherefore, we may conclude that the system is additive Let us now assume that inputs to the system such that [][][]{}/4111.Sj e x n y n e x n π−−→=ℜand[][][]{}/4222.Sj e x n y n e x n π−−→=ℜNow consider a third input x 3 [n]= x 2 [n]+ x 1 [n]. The corresponding system outputWill be[][]{}()[]{}()[]{}()[]{}()[]{}()[]{}()[]{}[]{}[]{}[][]/433331122/4/41212cos /4sin /4cos /4sin /4cos /4sin /4j e m e m e m e j j e e y n e x n n x n n x n n x n n x n n x n n x n e x n e x n y n y n πππππππππ==-+-+-=+=+ℜℜI ℜI ℜI ℜℜ therefore, we may conclude that the system is additive (b) (i) Consider two inputs to the system such that()()()()211111Sdx t x t y t x t dt ⎡⎤−−→=⎢⎥⎣⎦and ()()()()222211S dx t x t y t x t dt ⎡⎤−−→=⎢⎥⎣⎦ Now consider a third input x3[t]=x2[t]+x 1[t]. The corresponding system outputWill be()()()()()()()()()2333211111211dx t y t x t dt d x t x t x t x t dt y t y t ⎡⎤=⎢⎥⎣⎦⎡⎤+⎡⎤⎣⎦=⎢⎥+⎢⎥⎣⎦≠+ therefore, we may conclude that the system is not additiveNow consider a third input x 4 [t]= a x 1 [t]. The corresponding system output Will be()()()()()()()()2444211211111dx t y t x t dt d ax t ax t dt dx t a x t dt ay t ⎡⎤=⎢⎥⎣⎦⎡⎤⎡⎤⎣⎦=⎢⎥⎢⎥⎣⎦⎡⎤=⎢⎥⎣⎦=Therefore, the system is homogeneous.(ii) This system is not additive. Consider the fowling example .Let δ[n]=2δ[n+2]+2δ[n+1]+2δ[n] andx2[n]=δ[n+1]+ 2δ[n+1]+ 3δ[n]. The corresponding outputs evaluated at n=0 are [][]120203/2y andy ==Now consider a third input x 3 [n]= x 2 [n]+ x 1 [n].= 3δ[n+2]+4δ[n+1]+5δ[n]The corresponding outputs evaluated at n=0 is y 3[0]=15/4. Gnarly, y 3[0]≠ ]0[][21y y n +.This[][][][][]444442,1010,x n x n x n y n x n otherwise ⎧--≠⎪=-⎨⎪⎩[][][][][][]4445442,1010,x n x n ax n y n ay n x n otherwise ⎧--≠⎪==-⎨⎪⎩Therefore, the system is homogenous.1.30 (a) Invertible. Inverse system y(t)=x(t+4)(b)Non invertible. The signals x(t) and x 1(t)=x(t)+2πgive the same output (c) δ[n] and 2δ[n] give the same output d) Invertible. Inverse system; y(t)=dx(t)/dt(e) Invertible. Inverse system y(n)=x(n+1) for n ≥0 and y[n]=x[n] for n<0 (f) Non invertible. x (n) and –x(n) give the same result (g)Invertible. Inverse system y(n)=x(1-n) (h) Invertible. Inverse system y(t)=dx(t)/dt(i) Invertible. Inverse system y(n) = x(n)-(1/2)x[n-1] (j) Non invertible. If x(t) is any constant, then y(t)=0 (k) δ[n] and 2δ[n] result in y[n]=0 (l) Invertible. Inverse system: y(t)=x(t/2)(m) Non invertible x 1 [n]= δ[n]+ δ[n-1]and x 2 [n]= δ[n] give y[n]= δ[n] (n) Invertible. Inverse system: y[n]=x[2n]1.31 (a) Note that x 2[t]= x 1 [t]- x 1 [t-2]. Therefore, using linearity we get y 2 (t)= y 1 (t)- y 1 (t-2).this is shown in Figure S1.31(b)Note that x3 (t)= x1 [t]+ x1 [t+1]. .Therefore, using linearity we get Y3 (t)= y1 (t)+ y1 (t+2). this is2(4) y 2(t) periodic, period T; x(t) periodic, period T/2;1.33(1) True x[n]=x[n+N ]; y 1 (n)= y 1 (n+ N 0)i.e. periodic with N 0=n/2if N is even and with period N 0=n if N is odd.(2)False. y 1 [n] periodic does no imply x[n] is periodic i.e. Let x[n] = g[n]+h[n] where0,1,[][]0,(1/2),nn even n even g n and h n n odd n odd⎧⎧==⎨⎨⎩⎩ Then y 1 [n] = x [2n] is periodic but x[n] is clearly not periodic. (3)True. x [n+N] =x[n]; y 2 [n+N 0] =y 2 [n] where N 0=2N (4) True. y 2 [n+N] =y 2 [n]; y 2 [n+N 0 ]=y 2 [n] where N 0=N/2 1.34. (a) ConsiderIf x[n] is odd, x[n] +x [-n] =0. Therefore, the given summation evaluates to zero. (b) Let y[n] =x 1[n]x 2[n] .Theny [-n] =x 1[-n] x 2[-n] =-x 1[n]x 2[n] =-y[n]. This implies that y[n] is odd.(c)ConsiderUsing the result of part (b), we know that x e [n]x o [n] is an odd signal .Therefore, using the result of part (a) we may conclude thatTherefore,(d)ConsiderAgain, since x e (t) x o (t) is odd,Therefore,1.35. We want to find the smallest N 0 such that m(2π /N) N 0 =2πk or N 0 =kN/m,{}1[][0][][]n n x n x x n x n ∞∞=-∞==++-∑∑22[][]e o n n n n x x ∞∞=-∞=-∞=+∑∑222[][][]e on n n n n n x x x∞∞∞=-∞=-∞=-∞==+∑∑∑2[][]0eon n n x x ∞=-∞=∑222[][][].e on n n n n n xx x ∞∞∞=-∞=-∞=-∞==+∑∑∑2220()()()2()().eoet dt t dt t dt t t dt x x x x x ∞∞∞∞-∞-∞-∞-∞=++⎰⎰⎰⎰0()()0.et t dt x x ∞-∞=⎰222()()().e ot dt t dt t dt xx x ∞∞∞-∞-∞-∞=+⎰⎰⎰()()()()()().xy yx t x t y d y t x d t φττττττφ∞-∞∞-∞=+=-+=-⎰⎰where k is an integer, then N must be a multiple of m/k and m/k must be an integer .this implies that m/k is a divisor of both m and N .Also, if we want the smallest possible N 0, then m/k should be the GCD of m and N. Therefore, N 0=N/gcd(m,N). 1.36.(a)If x[n] is periodic0(),0..2/j n N T o e where T ωωπ+= This implies that022o T kNT k T T Nππ=⇒==a rational number . (b)T/T 0 =p/q then x[n] =2(/)j n p q e π,The fundamental period is q/gcd(p,q) and the fundmental frequencyis(c) p/gcd(p,q) periods of x(t) are needed .1.37.(a) From the definition of ().xy t φWe havepart(a) that()().xx xx t t φφ=-This implies that()xy t φis(b) Note from even .Therefore,the odd part of().xx t φis zero.(c) Here, ()().xy xx t t T φφ=-and ()().yy xx t t φφ= 1.38.(a) We know that /22(2)().t t δδ=ThereforeThis implies that1(2)().2t t δδ=(b)The plot are as shown in Figure s3.18. 1.39 We havelim ()()lim (0)()0.u t t u t δδ→→==Also,0022gcd(,)gcd(,)gcd(,)gcd(,).T pp q p q p q p q q p q p pωωππ===/21lim (2)lim ().2t t δδ→∞→∞=01lim ()()().2u t t t δδ→=u Δ'(t ) 1 1/2Δ/2-Δ/2t 0tu Δ'(t )12Δ t 0tu Δ'(t ) 1 1/2Δ-Δttu Δ'(t )1 1/2Δ-Δt 0t⎰⎰∞∞∞--=-=0)()()()()(ττδτττδτd t u d t u t gTherefore,0,0()1,00t g t t undefined for t >⎧⎪=<⎨⎪=⎩()0()()()t u t t δττδτδτ-=-=-1.40.(a) If a system is additive ,then also, if a system is homogeneous,then(b) y(t)=x 2(t) is such a systerm . (c) No.For example,consider y(t) ()()ty t x d ττ-∞=⎰with ()()(1).x t u t u t =--Then x(t)=0for t>1,but y(t)=1 for t>1.1.41. (a) y[n]=2x[n].Therefore, the system is time invariant.(b) y[n]=(2n-1)x[n].This is not time-invariant because y[n- N 0]≠(2n-1)2x [n- N 0]. (c) y[n]=x[n]{1+(-1)n +1+(-1)n-1}=2x[n].Therefore, the system is time invariant .1.42.(a) Consider two system S 1 and S 2 connected in series .Assume that if x 1(t) and x 2(t) arethe inputs to S 1..then y 1(t) and y 2(t) are the outputs.respectively .Also,assume thatif y 1(t) and y 2(t) are the input to S 2 ,then z 1(t) and z 2(t) are the outputs, respectively . Since S 1 is linear ,we may write()()()()11212,s ax t bx t ay t by t +→+where a and b are constants. Since S 2 is also linear ,we may write()()()()21212,s ay t by t az t bz t +→+We may therefore conclude that)()()()(212121t b t a t b t a z z x x s s +−→−+Therefore ,the series combination of S 1 and S 2 is linear. Since S 1 is time invariant, we may write()()11010s x t T y t T -→-and()()21010s y t T z t T -→-Therefore,()()121010s s x t T z t T -→-Therefore, the series combination of S 1 and S 2 is time invariant.(b) False, Let y(t)=x(t)+1 and z(t)=y(t)-1.These corresponds to two nonlinear systems. If these systems are connected in series ,then z(t)=x(t) which is a linear system.00.()().00x t y t =→=0()()()()0x t x t y t y t =-→-=(c) Let us name the output of system 1 as w[n] and the output of system 2 as z[n] .Then11[][2][2][21][22]24y n z n w n w n w n ==+-+-[][][]241121-+-+=n x n x n xThe overall system is linear and time-invariant.1.43. (a) We have())(t y t x s−→−Since S is time-invariant.())(T t y T t x s-−→−-Now if x (t) is periodic with period T. x{t}=x(t-T). Therefore, we may conclude that y(t)=y(t-T).This impliesthat y(t) is also periodic with T .A similar argument may be made in discrete time . (b)1.44 (a) Assumption : If x(t)=0 for t<t 0 ,then y(t)=0 for t< t 0.To prove That : The system is causal.Let us consider an arbitrary signal x 1(t) .Let us consider another signal x 2(t) which is the same as x 1(t)fort< t 0. But for t> t 0 , x 2(t) ≠x 1(t),Since the system is linear,()()()()1212,x t x t y t y t -→-Since ()()120x t x t -=for t< t 0 ,by our assumption =()()120y t y t -=for t< t 0 .This implies that()()12y t y t =for t< t 0 . In other words, t he output is not affected by input values for 0t t ≥. Therefore, thesystem is causal .Assumption: the system is causal . To prove that :If x(t)=0 for t< t 0 .then y(t)=0 for t< t 0 .Let us assume that the signal x(t)=0 for t< t 0 .Then we may express x(t) as ()()12()x t x t x t =-, Where()()12x t x t = for t< t 0 . the system is linear .the output to x(t) will be()()12()y t y t y t =-.Now ,since the system is causal . ()()12y t y t = for t< t 0 .implies that()()12y t y t = for t< t 0 .Therefore y(t)=0 for t< t 0 .(b) Consider y(t)=x(t)x(t+1) .Now , x(t)=0 for t< t 0 implies that y(t)=0 for t< t 0 .Note that the system is nonlinear and non-causal .(c) Consider y(t)=x(t)+1. the system is nonlinear and causal .This does not satisfy the condition of part(a). (d) Assumption: the system is invertible. To prove that :y[n]=0 for all n only if x[n]=0 for all n . Consider[]0[]x n y n =→. Since the system is linear :2[]02[]x n y n =→.Since the input has not changed in the two above equations ,we require that y[n]= 2y[n].This implies that y[n]=0. Since we have assumed that the system is invertible , only one input could have led to this particular output .That input must be x[n]=0 .Assumption: y[n]=0 for all n if x[n]=0 for all n . To prove that : The system is invertible . Suppose that11[][]x n y n → and21[][]x n y n →Since the system is linear ,1212[][][][]0x n x n y n y n -=→-=By the original assumption ,we must conclude that 12[][]x n x n =.That is ,any particular y 1[n] can be produced that by only one distinct input x 1[n] .Therefore , the system is invertible. (e) y[n]=x 2[n]. 1.45. (a) Consider ,()111()()shx x t y t t φ→= and()222()()shx x t y t t φ→=.Now, consider ()()()312x t ax t bx t =+. The corresponding system output will be()()12331212()()()()()()()()()hx hx y t x h t d a x h t d b x t h t d a t b t ay t by t ττττττττφφ∞-∞∞∞-∞-∞=+=+++=+=+⎰⎰⎰Therefore, S is linear .Now ,consider x 4(t)=x 1(t-T).The corresponding system output will be()14411()()()()()()()hx y t x h t d x T h t d x h t T d t T τττττττττφ∞-∞∞-∞∞-∞=+=-+=++=+⎰⎰⎰Clearly, y 4(t)≠ y 1(t-T).Therefore ,the system is not time-invariant.The system is definitely not causal because the output at any time depends on future values of the input signal x(t).(b) The system will then be linear ,time invariant and non-causal. 1.46. The plots are in Figure S1.46.1.47.(a) The overall response of the system of Figure P1.47.(a)=(the response of the system to x[n]+x 1[n])-the response of the system to x 1[n]=(Response of a linear system L to x[n]+x 1[n]+zero input response of S)- (Response of a linear system L to x 1[n]+zero input response of S)=( (Response of a linear system L to x[n]).Chapter 2 answers2.1 (a) We have know that 1[]*[][][]k y x n h n h k x n k ∞=-∞==-∑1[][1][1][1][1]y n h x n h x n =-++-2[1]2[1]x n x n =++-This gives1[]2[1]4[]2[1]2[2]2[4]y n n n n n n δδδδδ=+++-+--- (b)We know that2[][2]*[][][2]k y n x n h n h k x n k ∞=-∞=+=+-∑Comparing with eq.(S2.1-1),we see that21[][2]y n y n =+(c) We may rewrite eq.(S2.1-1) as1[][]*[][][]k y n x n h n x k h n k ∞=-∞==-∑Similarly, we may write3[][]*[2][][2]k y n x n h n x k h n k ∞=-∞=+=+-∑Comparing this with eq.(S2.1),we see that31[][2]y n y n =+2.2 Using given definition for the signal h[n], we may write{}11[][3][10]2k h k u k u k -⎛⎫=+-- ⎪⎝⎭The signal h[k] is non zero only in the rang 1[][2]h n h n =+. From this we know that the signal h[-k] is non zero only in the rage 93k -≤≤.If we now shift the signal h[-k] by n to the right, then the resultant signal h[n-k] will be zero in the range (9)(3)n k n -≤≤+. Therefore ,9,A n =- 3B n =+ 2.3 Let us define the signals11[][]2nx n u n ⎛⎫= ⎪⎝⎭and1[][]h n u n =. We note that1[][2]x n x n =- and 1[][2]h n h n =+ Now,。
本海默信号与系统第二版课后习题解信号与系统部分习题答案51页文档

60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
本海默信号与系统第二版课后习题解 信号与系统部分习题答案
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若ห้องสมุดไป่ตู้
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
信号与系统奥本海姆第二版答案

第1章信号与系统1.1复习笔记1,连续时间和离散时间信号1个连续时间信号和离散时间信号(1)连续时间信号(图1-1(a))①定义连续时间信号是指自变量是连续变量的信号,并且该信号是在自变量的连续值上定义的。
②代表自变量由T表示,表示连续时间。
连续时间信号表示为X(T)。
(2)离散时间信号(图1-1(b))①定义离散时间信号的自变量仅在一组离散值中选择,并且仅在离散时间点定义信号。
②代表自变量由N表示,N表示离散时间。
离散时间信号表示为x [n]。
说明:hwocrtemp_ ROC60图1-1信号的图形表示(a)连续的时间表示;(b)离散时间信号2.信号能量和功率(1)有限间隔内信号的总能量和功率①描述中的连续时间信号x(T):hwocrtemp_ roc120中的总能量说明:hwocrtemp_ ROC130哪里x |是X的模块(可能是复数)。
通过将上述公式除以长度t2-t1,可以获得平均功率。
②描述中的离散时间信号x [n]:hwocrtemp_ roc140中的总能量说明:hwocrtemp_ ROC150将其除以interval_中的点数即可。
Roc160获得该范围内的平均功率。
(2)无限间隔内信号的总能量和功率①无限时间连续时间信号的总能量x(T)说明:hwocrtemp_ ROC180无限时间连续时间信号x(T)的平均功率说明:hwocrtemp_ ROC220②无限时间中离散时间信号x [n]的总能量说明:hwocrtemp_ ROC190无限时间间隔内离散时间信号x [n]的平均功率说明:hwocrtemp_ ROC230(3)根据信号能量和功率的限制进行分类①该信号的总能量有限,即:hwocrtemp_ Roc240,该信号的平均功率为零。
②如果平均功率P∞是有限的,则其能量是无限的。
③具有无限大的P∞和E∞的信号。
2,自变量的变换基本转型(1)时移①X(t-t0)表示具有延迟|的X(T)。
信号与系统奥本海姆第二版答案

Systems(Second Edition) —Learning Instructions (Exercises Answers) Department ComputerEngineering 2005.12 ContentsChapter 17Chapter 35Chapter 62Chapter 83Chapter 109Chapter 119Chapter 132Chapter 140Chapter 10 160 Answers1.1 Converting from polar Cartesiancoordinates: 1.2converting from Cartesian polarcoordinates: limlim dtdt =cos(t).Therefore, limlim dtdt limlim limcos shiftedsignal shiftedsignal flippedsignal flippedsignal newSignal flippedsignal newsignal flippedsignal right.Therefore, weknow t>-2.Similarly, x(2-t) t>-1,Therefore, (1-t)+x(2-t) linearlycompression Therefore,x(3t) linearlycompression Therefore,x(3t) periodicbecause fundamentalperiod FigureS1.6. Therefore, fundamentalperiod oddsignal, allvalues zerowhen zeroonly when periodiccomplex exponential. 10 10 complexexponential multiplied decayingexponential. Therefore, periodicsignal. complexexponential fundamentalperiod periodicsignal. fundamentalperiod Weobtain fundamentalperiod complexexponential =3/5.We cannot find any integer integer.Therefore, periodic.1.10. x(t)=2cos(10t+1)-sin(4t-1) Period firstterm firstterm overallsignal periodwhich leastcommon multiple secondterms. -3-1 -1-2 -3 -3-3 firstterm secondterm secondtermoverallsignal periodwhich leastcommon Multiple threeterms inn 35.1.12. figureS1.12. flippedsignal right.Therefore, no=-3.1.13 itsderivative FigureS1.14. Therefore [n-3]=2x [n-2]+4x [n-3]+4x [n-4])=2x [n-2]+5x input-outputrelationship y[n]=2x[n-2]+5x [n-3] 2x[n-4] input-outputrelationship does connectedseries reversed. Wecan easily prove [n-3])+4(x input-outputrelationship onceagain y[n]=2x[n-2]+ 5x [n-3] 2x[n-4] 1.16 memoryless because pastvalues wemay conclude systemoutput alwayszero causalbecause sometime may depend futurevalues Considertwo arbitrary inputs (sin(t))Let linearcombination arbitraryscalars givensystem correspondingoutput linear.1.18.(a) Consider two arbitrary inputs linearcombination arbitraryscalars. givensystem, correspondingoutput arbitraryinput correspondingoutput .Consider secondinput outputcorresponding Alsonote +1)B.Therefore +1)B.1.19 Considertwo arbitrary inputs (t-1)Let linearcombination arbitraryscalars. givensystem, correspondingoutput linear.(ii) Consider arbitraryinputs correspondingoutput .Consider secondinput outputcorresponding Alsonote Considertwo arbitrary inputs [n-2].Let linearcombination arbitraryscalars. givensystem, correspondingoutput linear.(ii) Considerarbitraryinput correspondingoutput .Consider secondinput outputcorresponding Alsonote Considertwo arbitrary inputs -1]Let linearcombination arbitraryscalars. givensystem, correspondingoutput linear.(ii) Consider arbitraryinput correspondingoutput .Consider secondinput outputcorresponding Alsonote Considertwo arbitrary inputs linearcombination arbitraryscalars. givensystem, correspondingoutput linear.(ii) Consider arbitraryinputs correspondingoutput .Consider secondinput outputcorresponding Alsonote systemliner Thereforex1 weknow x2(t)=cos(2(t-1/2))= linearityproperty, we may once again write x1 cos(3t-1)Therefore, x1 (t)=cos(2(t-1/2)) =cos(3t-1)1.21.The signals figureS1.21. Figure S1.21 1.22 figureS1.22 1.23 oddparts FigureS1.23 1/2-1/2 -1 0.50.5 3/2-3/2 x(2t+1)x(4-t/2) 1012 1/2-1/2 -1 1/2-1/2 1/2-1 -2 1/2-1 -2 1/2-1 -2 FigureS1.22 -4-1 -2 -7xo[n] 3t/2-3t/2 -1/2-7 FigureS1.24 -2 FigureS1.23 1/2 1/2-7 1/2-1 3/2-3/2 -1/2 101.24 oddparts FigureS1.24。
信号与系统第二版课后习题解答(6-7-9)奥本海姆

Chap 66.1 Consider a continuous-time LTI system with frequency response()()|()|H j H j H j e ωωω=and real impulse response h(t). Suppose that we apply an input 00()cos()x t t ωφ=+ to this system .The resulting output can be shown to be of the form0()()y t Ax t t =-Where A is a nonnegative real number representing anamplitude-scaling factor and 0t is a time delay.(a)Express A in terms of |()|H j ω.(b)Express 0t in terms of0()H j ω Solution:(a) For 0()()y t Ax t t =-So 0()()jt Y j AX j eωωω-= 0()()()j t Y j H j Ae X j ωωωω-== So |()|A H j ω=(b) for 0()H j t ωω=- So 0()H j t ωω=-6.3 Consider the following frequency response for a causal and stable LTI system:1()1j H j j ωωω-=+ (a) Show that |()|H j A ω=,and determine the values of A. (b)Determine which of the following statements is true about ()τω,the group delay of the system.(Note()(())/d H j d τωωω=-,where ()H j ωis expressed in aform that does not contain any discontinuities.)1.()0 0for τωω=>2.()0 0for τωω>>3 ()0 0for τωω<>Solution:(a) for |()|1H j ω== So A=1(b) for )(2)()()1()1()(ωωωωωωarctg arctg arctg j j j H -=--=+∠--∠=∠ 212)()(ωωωωτ+=∠-=d j H d So ()0 0for τωω>>6.5 Consider a continuous-time ideal bandpass filter whose frequency response is⎩⎨⎧≤≤=elsewherej H c c,03||,1)(ωωωω (a) If h(t) is the impulse response of this filter, determine a functiong(t) such that)(sin )(t g t t t h c πω=(b) As c ω is increased, dose the impulse response of the filter get more concentrated or less concentrated about the origin?Solution(a) Method 1. Let1()()()()()()2h t x t g t H j X j G j ωωωπ=↔=* They are shown in the figures,where1,sin ()(){0,c c ctx t X j t ωωωωωωπ<=↔=> So we can get()2cos(2)()2[(2)(2)]c c c g t t G j ωωπδωωδωω=↔=-++Method 2. Using the inverse FT definition,it is obtained331(){}2c c c cj t j t h t e d e d ωωωωωωωωπ--=+⎰⎰ 11{sin 3sin }{sin }{2cos 2}c c c c t t t t t tωωωωππ=-= (b) more concentrated.Chap 77.1 A real-valued signal x(t) is know to be uniquely determined by its samples when the sampling frequency is10,000s ωπ=.For what values ofω is ()X j ω guaranteed to be zero? Solution:According to the sampling theorem 2s M w w > That is 110000500022M s w w ππ<== So if 5000M w w π>=,0)(=jw X7.2 A continuous-time signal x(t) is obtained at the output of an ideal lowpass filter with cutoff frequency 1,000c ωπ=.If impulse-train sampling is performed on x(t), which of the following sampling periods would guarantee that x(t) can be recovered from its sampled version using an appropriate lowpass filter?(a) 30.510T -=⨯(b) 3210T -=⨯(c) 410T -= Solution: π1000==c M w wFrom the sampling theorem,∴π20002=>M s w w ,that is 3102000222-==<πππM s w T ∴the conditions (a) and (c) are satisfied with the sampling theorem,(b) is not satisfied.7.3 The frequency which, under the sampling theorem, must be exceeded by the sampling frequency is called the Nyquist rate. Determine the Nyquist rate corresponding to each of the following signals:(a)()1cos(2,000)sin(4,000)x t t t ππ=++ (b)sin(4,000)()t x t tππ=(c) 2sin(4,000)()()t x t t ππ= Solution: (a) )4000sin()2000cos(1)(t t t x ππ++=max(0,2000,4000)4000M w πππ==∴ the Nyquist rate is 28000s M w w π>= (b) sin(4000)()t x t tππ= 4000M w π=∴ the Nyquist rate is 28000s M w w π>= (c) 2sin(4000)()t x t t ππ⎛⎫= ⎪⎝⎭ 2sin(4000)()t x tt ππ⎛⎫= ⎪⎝⎭221(1cos(8000))2t t ππ=- ∴8000M w π=∴the Nyquist rate is 216000s M w w π>=7.4 Let x(t) be a signal with Nyquist rate 0ω. Determine the Nyquist rate for each of the following signals:(a)()(1)x t x t +- (b)()dx t dt(c)2()x t(d)0()cos x t t ωSolution:(a) we let 1()()(1)y t x t x t =+-So 1()()()(1)()j j Y j X j e X j e X j ωωωωωω--=+=+ So the Nyquist rate of signal (a) is 0ω.(b) we let 2()()dx t y t dt= So 2()()Y j j X j ωωω=So the Nyquist rate of signal (b) is0ω. (c) we let 23()()y t x t = So 31()()*()2Y j X j X j ωωωπ= So the Nyquist rate of signal (c) is 20ω.(d) we let 40()()cos y t x t t ω=For 000cos [()()]FT t ωπδωωδωω→-++ So 4001()((()(())2Y j X j X j ωωωωω=-++ So the Nyquist rate of signal (d) is 03ω7.9 Consider the signal 2sin 50()()t x t tππ= Which we wish to sample with a sampling frequency of 150s ωπ= to obtain a signal g(t) with Fourier transform ()G j ω.Determine the maximum value of 0ω for which it is guaranteed that0()75() ||G j X j for ωωωω=≤Where ()X j ω is the Fourier transform of x(t).Solution: 2sin(50)()t x t t ππ⎛⎫= ⎪⎝⎭))100cos(1(2122t t ππ-= ∴100M w π=But π150=s wthe figure about before-sampling and after-sampling of )(jw H isWe can see that only when π500≤w , the before-sampling and after-sampling of )(jw H have the same figure.So if 0..)..(75)(w w for jw X jw G ≤=The maximum value of 0w is π50.Chap 99.2 Consider the signal 5()(1)t x t e u t -=- and denote its Laplace transform by X(s).(a)Using eq.(9.3),evaluate X(s) and specify its region of convergence. (b)Determine the values of the finite numbers A and 0t such that the Laplace transform G(s) of 50()()t g t Ae u t t -=-- has the same algebraic form as X(s).what is the region of convergencecorresponding to G(s)?Solution:(a). According to eq.(9.3), we will getdt e t x s X st -∞∞-⎰=)()(dt e t u e st t --∞∞--=⎰)1(5dt e t s )5(1+-∞⎰=)5()5()5()5()5(1)5(+=+--=+-=+-+-∞+-s e s e s e s s t s ROC:Re{s}>-5 (b). )()(05t t u Ae t g t --=-−→←LT 0)5(5)(t s e s A s G ++-=, Re{s}<-5 ∴ If )()(s X s G =then it ’s obviously that A=-1, 10-=t , Re{s}<-5.9.5 For each of the following algebraic expressions for the Laplace transform of a signal, determine the number of zeros located in the finite s-plane and the number of zeros located at infinity: (a)1113s s +++ (b) 211s s +- (c) 3211s s s -++ Solution :(a).1, 1)3)(1(423111+++=+++s s s s s ∴ it has a zero in the finite s-plane, that is 2-=sAnd because the order of the denominator exceeds the order of the numerator by 1∴ X(s) has 1 zero at infinity.(b). 0, 111)1)(1(1112-=-++=-+s s s s s s ∴ it has no zero in the finite s-plane.And because the order of the denominator exceeds the order of the numerator by 1∴ X(s) has 1 zero at infinity.(c). 1, 011)1)(1(112223-=++++-=++-s s s s s s s s s ∴ it has a zero in the finite s-plane, that is 1=sAnd because the order of the denominator equals to the order of the numerator∴ X(s) has no zero at infinity.9.7 How many signals have a Laplace transform that may be expressed as 2(1)(2)(3)(1)s s s s s -++++ in its region of convergence?Solution:There are 4 poles in the expression, but only 3 of them have different real part.∴ The s-plane will be divided into 4 strips which parallel to the jw-axis and have no cut-across.∴ There are 4 signals having the same Laplace transform expression.9.8 Let x(t) be a signal that has a rational Laplace transform with exactly two poles located at s=-1 and s=-3. If2()() ()t g t e x t and G j ω=[ the Fourier transform of g(t)]converges, determine whether x(t) is left sided, right sided, or two sided.Solution:)()(2t x e t g t =∴)2()(-=s X s G ROC: R(x)+Re{2}And x(t) have three possible ROC strips:),1(),1,3(),3,(+∞-----∞∴g(t) have three possible ROC strips: ),1(),1,1(),1,(+∞---∞ IF jw s s G jw G ==|)()(Then the ROC of )(s G is (-1,1)∴)(t x is two sides. 9.9 Given that1(),{}Re{}sat e u t Re s a s a -↔>-+ Determine the inverse Laplace transform of22(2)(),Re{}3712s X s s s s +=>-++ Solution: It is obtained from the partial-fractional expansion:22(2)2(2)42()712(4)(3)43s s X s s s s s s s ++-===+++++++,Re{}3s >-We can get the inverse Laplace transform from given formula and linear property.43()4()2()t t x t e u t e u t --=-9.10 Using geometric evaluation of the magnitude of the Fourier transform from the corresponding pole-zero plot ,determine, for each of the following Laplace transforms, whether the magnitude of the corresponding Fourier transform is approximately lowpass, highpass, or bandpass. (a): 1}Re{,.........)3)(1(1)(1->++=s s s s H (b): 221(),{}12s H s e s s s =ℜ>-++(c): 232(),{}121s H s e s s s =ℜ>-++ Solution:(a). 1}Re{,.........)3)(1(1)(1->++=s s s s H It ’s lowpass.(b).21}Re{,.........1)(22->++=s s s s s H It ’s bandpass.(c). 1}Re{., (1)2)(223->++=s s s s s H It ’s highpass.9.13 Let ()()()g t x t x t α=+- ,Where ()()t x t e u t β-=. Andthe Laplace transform of g(t) is 2(),1{}11s G s e s s =-<ℜ<-. Determine the values of the constantsαand βSolution: ()()()g t x t x t α=+-,and ()()t x t e u t β-=The Laplace transform : ()()()G s X s X s α=+- and()1X s s β=+,Re{}1s >- From the scale property of Laplace transform, ()1X s s β-=-+,Re{}1s < So 2(1)(1)()()()111s G s X s X s s s s βαββαβαα--+=+-=+=+-+-,1Re{}1s -<< From given 2()1s G s s =-,1Re{}1s -<< We can determine : 11,2αβ=-=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 1.3 解:(a). 2401lim(),04Tt T TE x t dt e dt P ∞−∞∞→∞−====∫∫(b) dt t x TP T TT ∫−∞→∞=2)(21lim121lim ==∫−∞→dt TTTT∞===∫∫∞∞−−∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞−−∞∞→∞→∞−−===∞+===∫∫∫∫(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→−=∞→∞∑∑N N n x N P N N n n N NNn N 34)21()(lim202===∑∑−∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=−=−===++∑∑ (f) ∑−=∞→∞=+=NNn N n x N P 21)(121lim 2∑−=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的; c) 00007,,22m N N ωωππ=== d). 010;N = e). 非周期的; 1.12 解:∑∞=−−3)1(k k n δ对于4n ≥时,为1即4≥n 时,x(n)为0,其余n 值时,x(n)为1 易有:)3()(+−=n u n x , 01,3;M n =−=−1.15 解:(a)]3[21]2[][][222−+−==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+−, 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=−+−+−+−,1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =−+−+− 其中][n x 为系统输入。
(b) 交换级联次序后]2[4][2][][111−+==n x n x n y n y]4[2]3[]3[4]2[22222−+−+−+−=n x n x n x n x ]4[2]3[5]2[2−+−+−=n x n x n x 其中][n x 为系统输入通过比较可知,系统s 的输入-输出关系不改变 1.16 解:(a) 不是无记忆的,因为系统在某一时刻0n 的输出还与20−n 时刻的输入有关。
(b) 输出]2[][][−⋅=n A n A n y δδ0]2[][2=−=n n A δδ(c) 由(b)可得,不论A 为任意实数或者复数,系统的输出均为零,因此系统不可逆。
1.21.1.22和1.23画图均略 1.26 解:(a) 7320=πωΘ,为有理数,∴x[n]具有周期性,且周期N =7 (b) ππω16120=Θ,为无理数,∴x[n]无周期性 (c) 由周期性的定义,如果存在),8cos(])(2cos[,22n N n N ππ=+使得则函数有周期性,即:22812)(81n k N n πππ+=+ k nN N 1622=+∴,对全部n 成立取N 的最小值N =8,即为周期。
(d) )]41cos()43[cos(21)4cos()2cos(][n n n n n x ππππ+==,与(a)同理,x[n]具有周期性,对8)41cos(,8)43cos(21==N n N n 存在对存在ππ,8=∴N 基波周期(e) 与上题同理,4,16,8321===N N N 16N =周期∴ 1.27 a) 系统具有线性性与稳定性;e). 系统具有线性性, 时不变性与因果性与稳定性; 1.28 c) 系统是无记忆的,线性的,因果的;e) 系统是线性的,稳定的 g). 系统是线性的,稳定 1.31解: (a) 211211()()(2)()()(2)x t x t x t y t y t y t =−−∴=−−Q 如图PS2.17(a)所示。
(b) 311311()(1)()()(1)()x t x t x t y t y t y t =++∴=++Q如图PS2.17(b)所示。
1.331)正确。
设()x n 的周期为N 。
如果N 为偶数,则1()y n 的周期为/2N ;如果N 为奇数,则必须有022N N =,才能保证周期性,此时1()y n 的周期为0N N =。
2)不正确。
设()()()x n g n h n =+,其中()sin4ng n π=,对所有n ,1,()30,nn h n n ⎧⎛⎞⎪⎜⎟=⎨⎝⎠⎪⎩奇偶 显然()x n 是非周期的,但1()y n 是周期的。
3)正确。
若()x n 的周期为N ,则2()y n 的周期为2N 。
4)正确。
若2()y n 的周期为N ,则N 只能是偶数。
()x n 的周期为/2N 。
1.37 a) ()()()()xy yx t x t y d t φτττφ+∞−∞=+=−∫b) ()xx t φ=()xx t φ−, 奇部为零。
c). ()(),()()xy xx yy xx t t T t t φφφφ=−=1.42 解:(a) 结论正确。
设两线性时不变系统如下图所示级联。
当12()()()x t ax t bx t =+时,则有12()()()w t aw t bw t =+,于是12()()()y t ay t by t =+,因此整个系统是线性的。
若输入为0()x t t −,则由于时不变性可知系统1的输出为0()w t t −,这正是系统2的输入,因此总输出为0()y t t−。
即整个系统是时不变的。
)(b) 结论不对。
如系统1为()()3w t x t t =+,系统2为()()3y t w t t =−。
虽然两系统都不是线性的,但它们的级联()()y t x t =却是线性的。
c) 设系统1的输出为w(n), 系统2的输出为z(n).11()(2)(2)(21)(22)2411()(1)(2)24y n z n w n w n w n x n x n x n ==+−+−=+−+−1.46 解:a). ()(1)(1)y n n y n δ=−−−,n=0,y(n)=0,n=1,y(n)=1,n=2,y(n)=-1; 1()(1)(1)n y n u n −=−−b). ()(1)(1)y n u n y n =−−−,n=0,y(n)=0, n=1,y(n)=1,n=2,y(n)=0; n=3,y(n)=1,n=4,y(n)=0, n=5,y(n)=1……;1.47 解:a) {}{}111()()()y n S x n c L x n C =+=+,C 为系统的零输入响应。
{}{}{}{}111111()()()()()()()()}{()()()y n S x n x n y n L x n x n C y n L x n L x n C y n L x n =+−=++−=++−=c) 00/2,1,(),2,()(1)/2,n n eveny n n y n n n odd ⎧==⎨−⎩3. 非增量线性系统;4. ()()()/y t x t tdx t dt =+, 非增量线性系统5. 增量线性系统, 2()cos ()y n n π=Chapter 22.1解:(a) 1[][][][0][][1][1][3][3]y n x n h n x h n x h n x h n =∗=+−+−2[1]4[]2[1]2[2]2[4]n n n n n δδδδδ=+++−+−−−(图略)(b) 21[][2][][2]y n x n h n y n =+∗=+2[3]4[2]2[1]2[]2[2]n n n n n δδδδδ=++++++−−(图略)(c) 32[][][2][]y n x n h n y n =∗+=(图略)2.5解:9[][][]k y n x k h n k ==−∑,由[4]5y =可知:4N ≥由[14]0y =可知:9114N ++≤,即:4N ≤ 所以:4N =2.11解:(a) 3t ≤时,()0y t =35t <≤时,3()(3)()(3)()ty t u t h t u h t d τττ=−∗=−−∫3(3)3()313t tt e ed ττ−−−−−==∫5t >时,[]()63(5)53()31()(3)(5)()3t t e e y t t u t u h t ed ττ−−−−−−=−−−∗==∫因此:()3(3)63(5)0,31(),3531,53t t t e y t t e e t −−−−−⎧⎪≤⎪⎪−=<≤⎨⎪⎪−⎪>⎩(b )()(3)(5)dx t t t dtδδ=−−− 3(3)3(5)()()()(3)(5)(3)(5)t t dx t g t h t h t h t e u t e u t dt−−−−∴=∗=−−−=−−−(c) ()()dy t g t dt=2.13解:(a) 将1[][]5nh n u n ⎛⎞=⎜⎟⎝⎠代入式子得:111[][1][]55nn u n A u n n δ−⎛⎞⎛⎞−−=⎜⎟⎜⎟⎝⎠⎝⎠即:()1[]5[1][]5nu n Au n n δ⎛⎞−−=⎜⎟⎝⎠从而可得:51A =,即:15A = (b)由(a)可知:1[][1][]5h n h n n δ−−= 则1S 的逆系统2S 的单位脉冲响应为:11[][][1]5h n n n δδ=−− 2.16解:(a)对。
若21n N N −<,即:12n N N <+,则[]x k 与[]h n k −没有公共部分,显然有[][]0x n h n ∗=。
(b)错。
[1][][1][][1]k y n x k h n k x n h n +∞=−∞−=−−=∗−∑(c)对。
()()()y t x r h t r dr +∞−∞−=−−∫,令r λ=−,则: ()()()()()()()()y t x h t d x h t d x t h t λλλλλλ−∞+∞+∞−∞−=−−−=−−=−∗−∫∫(d)对。
若21t T T −>,则没有公共部分,故12t T T >+时,()()0x t h t ∗=。
2.19 a). ()(1)()y n y n w n αβ=−+, 1()()(1)w n y n y n αββ=+− 将w(n)代入后经比较可得:1,14αβ==。
