气体射流
流体力学第6章讲解

2、射孔的形状,圆孔口和方孔显然其扩张的情况不会相同。不同的射口形状有 不
同的实验值。用φ表示这个影响因素, 对圆断面射流 φ=3.4,长条缝射孔 φ=2.44。
圆孔综口合射这流两:个t影g响因素K:x k=Kφα 3.4a
x
R 1 3.4 as 3.4( as 0.294)
r0
vm
vm r0 1
1
v0 R
2
1
[(11.5 )2 ]2d
0
9
第二节圆断面射流的运动分析
1
n
1
n
[(1 1.5 )2 ] d Bn; [(1 1.5 )2 ] d Cn
0
0
n
1
1.5
2
2.5
3
Bn
0.0985
0.064
0.0464
0.0359
0.0286
第一节无限空间淹没紊流射流特性
二、紊流系数a及几何特征
其斜率即:tga=常数=k。 对于不同的条件,k值是不同的常数,也叫实验常数。 通过实验发现,k值的影响因素有两个主要的因素:
1、射孔出口截面上气流的紊流强度。 紊流强度的大小用紊流系数a(A)来表示:a大紊流的强度就大,因此,紊
流 系数的大小可以反映出射流的扩张能力,所以,a也叫表征射流流动结构的 特征系数。另一方面,由于a反映的是射流混合能力的大小,因此,a还可以反 映孔口出口截面上的速度均匀程度。a越小,则混合能力越差,说明流速越均匀 。
二、断面流量Q
R
微环面的流量表达式 Q 2vydy Q0 r02v0
0
主体段:
R
Q
v r 0
y
y
2 ( )( )d( )
(完整版)第六章气体射流

6.4 温差或浓差射流
温差(浓差)射流—本身温度(浓度)与周围有差异的射流 射流内边界层 温度内边界层
温度外边界层 射流外边界层
为简化,忽略温度(浓度)与射流速度边界的差
对于温差射流
出口截面与外界温差 轴心与外界温差
T0 T0 Te
Tm Tm Te
截面上某点与外界温差 T T Te
对于浓差射流
Q0v0 r02v02
任意截面动量
R
v2 ydyv
R 2v2 ydy
0
0
动量守恒
r02v02
R 2v2 ydy
0
6.2 圆断面射流的运动分析
根据紊流射流的特征来研究圆断面射流的速度、流量沿 射程的变化规律。
□ 6.2.1 轴心速度vm
方程两端同除 R2vm2 :
r02v02
喷嘴种类
带有收缩口的喷嘴 圆柱形管 带有导板的轴流式风机 带有导板的直角弯管 带有金属网的轴流式风机 收缩极好的平面喷口 平面壁上锐缘狭缝
具有导叶磨圆边口的风道纵向缝
a 0.066 0.08 0.12 0.20 0.24 0.108 0.118
0.155
2α 25o20' 29o00' 44o30' 68o30' 78o40' 29o30' 32o10'
41o20'
喷嘴上装置不同型式的风板栅栏,则出口截面上气流的扰动紊乱程度不同, 因而紊流系数 a 不同。扰动大的紊流系数 a 值增大,扩散角 α 也增大。
◇ 圆断面射流半径沿射程的变化规律
射流半径的沿程变化规律
R r0
3.4
as r0
0.294
流体力学第六章 气体射流

6.1 无限空间淹没紊流射流的特征
2.运动特征:速度分布具有相似性。 特留彼尔在轴对称射流主体段的实验结果,以及阿勃拉莫 维奇在起始段内的测定结果,见图6-2(a)及图6-3(a)。
6.1 无限空间淹没紊流射流的特征
6.1 无限空间淹没紊流射流的特征
3.动力特征 射流中的压强与周围流体中的压强相等。 可得各横截面上轴向动量相等——动量守恒,动量守 恒方程式为:
6.4 温差或浓度差射流
6.4 温差或浓度差射流
三.射流弯曲 温差射流或浓差射流由于密度与周围密度不同, 所受的重力与浮力不相平衡,使整个射流将发生向下或向上弯 曲。通过推导可得出无因次轨迹方程为
6.4 温差或浓度差射流
[例6-3]工作地点质量平均风速要求3m/s,工作面直径D=2.5m 送风温度为15℃,车间空气温度30 ℃,要求工作地点的质量 平均温度降到25 ℃ ,采用带导叶的轴流风机,紊流系数 = 0.12。求(1)风口的直径及速度;(2)风口到工作面的距离。 [解]温差 =15-30=-15 ℃
6 气体射流
6.1 无限空间淹没紊流射流的特征
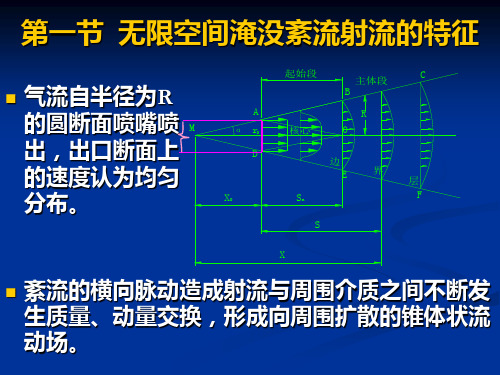
一.射流结构 出流到无限大空间中,流动不受固体边壁的限制,为无限 空间射流,又称自由射流。射流的流动特性及结构图:
6.1 无限空间淹没紊流射流的特征
二.射流的特性 1. 几何特性: 外边界线为一直线。tan a 紊流系数 a 是表征射流流动结构的特征系数。它与出口断 面上紊流强度有关,紊流强度越大。各种不同形状喷嘴的紊 流系数和扩散角的实测值列于表6-1。
一.特点:1.温度边界层与速度边界层不重合。 2.射流发生弯曲。
6.4 温差或浓度差射流
二.特性: 1.温差特性: 试验得出,截面上温差(浓度差分布)分布具有相 似性。 与速度分布关系如下:
《流体力学》第六章气体射流

.
射流参数的计算
段 名
参数名称
符号
圆断面射流
平面射流
扩散角 主
α tg3.4a tg2.44a
体
段 射流直径 或半高度
D b
D d0
6.8
as d0
0.147
b b0
2.44
0.095 as 0.147
d0
v1 0.492
v0
as 0.41
b0
v2
v2 v0
as
0.23 0.147
d0
v2 v0
0.833 as 0.41 b0
.
段名 参数名称
符 号
圆断面射流
平面射流
起
流量
Q
2
QQ0 10.76ar0s1.32ar0s
Q Q0
1 0.43 as b0
始
v 断面平均 流速
B0Kx
tgKxK3.4a
x
紊流系数
起始段
主体段
C
B
A
R
M
α r0
核心
0
D X0
边 E
界 层
Sn
F
S
X
射流结构
.
紊流系数与 出口断面上 紊流强度有 关,也与出 口断面上速 度分布的均 匀性有关。 (表6-1)
紊流系数
喷嘴种类 带有收缩口的喷嘴
a
0.066 0.071
圆柱形管
带有导风板的轴流式通风机 带导流板的直角弯管
已知射流直径D, v2,d0,a, 求S和Q0
气体射流混合反应器的作用

气体射流混合反应器的作用气体射流混合反应器的作用1. 引言气体射流混合反应器是一种常见的化学工程设备,广泛应用于各种工业领域,如化工、环保、能源等。
它的作用是通过引入射流来促进气体物质的混合和反应,提高反应效率和产物质量。
本文将以气体射流混合反应器为主题,探讨其作用、原理和应用。
2. 深度探讨2.1 气体混合作用气体射流混合反应器的核心作用之一是实现气体的混合。
在许多化学反应过程中,混合气体的均匀分布对于反应速率和产物选择至关重要。
气体射流混合反应器通过引入射流,能够有效地将不同组分的气体物质混合均匀,从而提供了良好的反应条件,促进反应的进行。
2.2 反应效率提高气体射流混合反应器在提高反应效率方面发挥着重要作用。
通过射流混合,反应物分子之间的碰撞频率可以大大增加,从而提高反应速率。
射流混合还能够提供更大的反应接触表面积,使得反应物与催化剂或吸附剂的接触更为充分,增强反应的效果。
气体射流混合反应器可以有效地提高反应效率,减少反应时间和废物产生。
2.3 选择性和产物质量控制气体射流混合反应器还可以通过适当的设计和操作控制反应的选择性和产物质量。
在反应过程中,通过调节射流速度、温度、压力等操作参数,可以实现对反应物的选择性控制,优化产物的选择性和纯度。
射流混合反应器还能够有效地控制反应物质的排放和废物产生,减少对环境的污染。
3. 应用领域3.1 化工工业在化工工业中,气体射流混合反应器被广泛应用于气体吸附、气体催化反应、气体分离等领域。
气体吸附是一种常见的气体处理技术,用于去除废气中的有害物质。
气体射流混合反应器可以通过引入适当的吸附剂和优化反应条件,高效去除废气中的有害物质,实现废气的净化和资源回收。
3.2 环保领域气体射流混合反应器在环保领域也具有重要意义。
在大气污染治理中,氧化反应是一种常见的处理方法。
气体射流混合反应器可以通过引入适当的氧化剂和调整反应条件,有效氧化污染物,降低大气污染程度。
气体动力学中的射流和喷射问题

气体动力学中的射流和喷射问题摘要:射流和喷射问题是气体动力学中的重要研究内容,对于理解气体的运动规律和应用于实际工程问题具有重要意义。
本论文将详细介绍射流和喷射问题的基本概念和原理,并以一些典型案例进行分析和讨论,最后总结出相应的结论。
引言:在气体动力学中,射流和喷射问题是研究流体力学的重要组成部分。
射流和喷射问题涉及到流体中的速度、压力、温度等物理量的变化,以及气体的流动特性和流场结构等方面。
射流和喷射问题的研究不仅有助于理解气体的运动规律,还具有广泛的实际应用价值,如喷射引擎、喷气式飞机等。
一、射流问题的基本概念和原理射流指的是气体在一个小孔或喷嘴中穿过后形成的高速流动。
射流可以是稳定的,也可以是非稳定的。
射流问题主要包括射流速度、射流的形状、射流的稳定性等方面。
1.1 射流速度射流速度是指射流中流体颗粒的速度大小。
根据连续介质假设,流体在射流过程中可以看作是连续的介质。
当气体从一个小孔或喷嘴中射流出来时,会受到压力的作用,从而形成高速流动。
射流速度与喷嘴的压强、射流口的几何形状、介质的物理性质等有关。
1.2 射流的形状射流的形状是指射流在空间中的空间分布情况。
根据射流所受到的作用力不同,射流可以呈现出不同的形状,如直线型、螺旋型、喷雾型等。
射流的形状与射流速度、密度、粘度等有关。
1.3 射流的稳定性射流的稳定性是指射流在运动过程中是否保持稳定的特性。
射流通常有一个稳定射流区域和一个不稳定射流区域,在稳定区域,射流流动平稳;而在不稳定区域,射流容易发生分离和湍流现象。
射流的稳定性与射流的速度、密度、湍流强度、流体介质等有关。
二、喷射问题的基本概念和原理喷射问题指的是将气体通过喷嘴或管道喷射到环境中形成的流动现象。
喷射问题涉及到喷射速度、喷射角度、气体与环境之间的相互作用等方面。
2.1 喷射速度喷射速度是指喷射气体的速度大小。
喷射速度与喷射口的压力、流量、喷嘴的几何形状等有关。
喷射速度的大小决定了喷射气体在空间中的传播范围和速度。
气射流原理

气射流原理气射流原理是指利用高速气体流动产生的动能来实现各种工程应用的原理。
气射流可以通过喷嘴、喷管等装置来产生,其应用领域涵盖了航空航天、化工、环保等多个领域。
在工程实践中,气射流原理被广泛应用于推进、混合、分离、加热、冷却等方面,具有重要的工程价值。
首先,气射流原理在推进领域具有重要应用。
通过喷嘴产生的高速气体流动,可以产生巨大的推力,被应用于航空航天领域的火箭、喷气发动机等推进装置中。
此外,在水下航行器、水下推进器等领域,气射流原理也被广泛应用,通过喷射高速气体来产生推进力,实现水下运动。
其次,气射流原理在混合领域也有重要应用。
在化工领域,气射流原理被应用于气固、气液、液固混合等反应过程中。
通过喷嘴产生的气体流动可以将不同物质混合均匀,实现化工反应过程的高效进行。
此外,在环保领域,气射流原理也被应用于废气处理、污水处理等工艺中,通过喷射高速气体来与污染物发生反应,实现污染物的分解和净化。
再次,气射流原理在分离领域也具有重要应用。
在化工、制药等领域,气射流原理被应用于气固、气液、液固分离过程中。
通过喷嘴产生的气体流动可以将混合物中的不同物质进行有效分离,实现物质的纯净提取和分离。
此外,气射流原理还被应用于加热、冷却等领域。
在工业生产中,通过喷射高速气体流动可以实现对物体的快速加热或冷却,提高生产效率和产品质量。
总之,气射流原理作为一种重要的工程原理,在航空航天、化工、环保等多个领域都具有重要的应用价值。
通过喷嘴、喷管等装置产生的高速气体流动,可以实现推进、混合、分离、加热、冷却等多种工程应用,为工程技术的发展和进步提供了重要支撑。
希望通过对气射流原理的深入研究和应用,可以进一步拓展其在工程领域的应用范围,为人类社会的发展做出更大的贡献。
第六章 气体射流要点

(2) 向含尘浓度高的车间吹送清洁空气以改善工作
环境;向高温火焰炉内喷吹燃料和助燃空气等属于浓 差射流的例子。
温差或浓差射流分析,主要 是研究温差或浓差场的分布规律, 同时讨论由温差或浓差引起的射 流弯曲的轴心轨迹。
第六章
气体射流
气体自孔口﹑管嘴或条缝向外喷射所形成的 流动,称为气体淹没射流,简称气体射流。当出
口速度较大,流动呈现紊流状态时,叫做紊流射
流。 射流在水泵、蒸汽泵、通风机、化工设备和 喷气式飞机等许多技术领域得到广泛应用。
第六章
气体射流
射流与孔口管嘴出流的研究对象不同,射流
主要研究的是出流后的流速场、温度场和浓度场。 后者仅讨论出口断面的流速和流量。 出流空间大小,对射流的流动影响很大。出
流到无限大空间中,流动不受固体边壁的限制,
为无限空间射流,又自由射流。反之为有限空间 射流
射流的分类方法:
1.按射流流体的流动状态不同,可分为层流射流 和紊流射流。一般按喷口直径和出口流速计算的雷诺 数大于30以后即为紊流射流。 2.按射流流体的流动速度大小不同,可分为亚音 速射流和超音速射流。
3.按射流流体在充满静止流体的空间内扩散流动
—湍流系数,由实验决定,是表示射流 流动结构的特征系数。 湍流系数与喷口断面的湍流强度 和速度分 布均匀性有关。
a
(三) 射流边界层的运动特征
图6-2 主体段速度分布图
图6-3 起始段速度分布
y 1 m R
1.5 2
1
(三)、射流轴线的弯曲
温差射流或浓差射流的密度与周围流体介质的密度不同, 致使作用于射流质点上的重力与浮力不平衡,造成整个射流 向上或向下弯曲,如图9-6所示。但这时整个射流仍可看作是 对称于轴线的,因此,只要了解射流轴线的弯曲情况,便可知 道整个射流的弯曲情况。一般热射流和含轻密度物质的射流 向上弯曲;而冷射流和含重密度物质的射流向下弯曲。
射流气浮原理

射流气浮原理射流气浮原理是指通过将气体以高速射流的形式注入液体中,使气液两相发生剧烈的相互作用,从而产生气泡并将液体推浮起来的一种物理现象。
这一原理在工程应用中具有广泛的应用,如废水处理、气浮沉淀、泡沫灭火等领域。
射流气浮原理的基本过程可以分为三个阶段:混合、增压和气泡上浮。
首先,在混合阶段,气体通过射流装置以高速射流的形式进入液体中,形成气液混合区域。
在这个区域内,气体与液体发生剧烈的混合,形成气泡。
接下来,气泡进入增压阶段,在增压阶段中,气泡受到周围液体的压力作用,气泡内部的压力增加,气泡体积减小,密度增大。
最后,在气泡上浮阶段,由于气泡的密度大于周围液体的密度,气泡受到浮力的作用,从而上浮至液体表面,将液体推浮起来。
射流气浮原理的物理机制主要有两个方面:液体的加速和气泡的上浮。
首先,当气体以高速射流的形式进入液体时,气体的动能转化为液体的动能,使液体发生加速运动。
这种加速运动会产生液体的剪切应力和涡旋流动,从而促进气液混合和气泡的形成。
其次,由于气泡在液体中具有较小的密度,所以受到浮力的作用,从而上浮至液体表面。
这种浮力是由于液体中的压力梯度引起的,即液体中的压力随深度的增加而增加,使气泡受到向上的浮力。
射流气浮原理的应用非常广泛。
在废水处理中,射流气浮技术可以将废水中的悬浮物和油脂等杂质从液体中分离出来,从而达到净化水质的目的。
在气浮沉淀中,射流气浮技术可以将气泡注入液体中,使悬浮物颗粒形成气团,从而增大颗粒的有效半径,提高沉降速度,加快固液分离的速度。
在泡沫灭火中,射流气浮技术可以通过射流装置将泡沫液和空气混合,形成致密的泡沫,从而有效地隔绝火源与氧气,达到灭火的目的。
射流气浮原理的优点是操作简单、效果好、投资成本低。
射流气浮技术不需要复杂的设备和高能耗,且工艺简单,易于实施。
同时,射流气浮技术具有较好的处理效果,可以有效地去除废水中的悬浮物和油脂等杂质,提高水质。
此外,射流气浮技术的投资成本相对较低,适用于各种规模的废水处理工程。
流体力学气体射流

3
起始段
主体段 B
A
M
核心
o
D x0
边 界
E s0
s
x
C
层 F
图 11—1 射流结构
以圆断面射流为例应用动量守恒原理
出口截面上动量流量为 Q00 r020,任意横截面上的动
量流量则需积分。
R
2ydy
R 2 2 ydy
0
0
列动量守恒式:
r0202
R 2 2 ydy
0
(11—1— 4) 10
y
12
dy
R
M
R r
y
y
y
yx
y
x0
s
x
12
图 11—2 射流计算式的推证
11
§11-3 圆断面射流的运动分析
m3/s
17
§11-4 平面射流
气体从狭长缝隙中外射运动时,射流只能在垂直条缝长度 的平面上扩散运动。如果条缝相当长,这种流动可视为平面运 动,故称为平面射流。
平面射流喷口高度以2b0(b0半高度)表示,a值见表11-1
后三项;j值为2.44,于是tan a=2.44a。而几何、运动、动力
特征则完全与圆断面射流相似。所以各运动参数规律的推导基 本与圆断面类似,这里不再推导,列公式于表11-3中。
温差或浓差射流分析,主要是研究射流温差、浓差分布场 的规律。同时讨论由温差、浓差引起射流弯曲的轴心轨迹。
在射流的形成过程中,会产生横向动量交换,旋涡的出现, 使之质量交换,热量交换,浓度交换。在这些交换中,热量扩 散比动量扩散要快些,因此温度边界比速度边界层发展要快些 厚些,如图11-3a所示。实线为速度边界层,虚线为温度边界 层的内外界线。
第六章 气体射流PPT课件

概述
横向动量交换,旋 涡的出现,使之质量交换, 热量交换,浓度交换。而 在这些交换中,由于热量 扩散比动量扩散要快些, 因此温度边界层比速度边 界层发展要快些厚些,如 图 6 一 6a 所示。实线 为速度边界层,虚线为温 度边界层的内外界线。
研究内容
浓度扩散与温度相似。在实 际应用中,为了简化起见,可以 认为,温度、浓度内外的边界与 速度内外的边界相同。于是参数 R 、 Q 、 vm 、 v1、 v2等可 使用前两节所述公式,仅对轴心 温差 △ Tm ,平均温差等沿射程 的变化规律进行讨论。
r0
r0
2、运动特征
轴心速度 最大,从轴心 向边界层边缘, 速度逐渐减小 至零。
距喷嘴距 离越远边界层 厚度越大,而 轴心速度则越 小,也就是速 度分布曲线不 断地扁平化了。
各参数定义
射流各截面上速度分布的 相似性。
3、动力特征
射流中任意点上的静压强均等于 周围气体的压强,即p=0。
各面上所受静压强均相等,x 轴 向外力之和为零。
为②边界层。 显然,射流边界层一方面不断地
向外扩散,带动周围介质进人边界层, 另一方面向射流中心扩展。
只有轴心点上速度为 u0的射流断
面 称为③ 过渡断面或转折断面。
以过渡断面分界,出口断面至 过渡断面称为射流④ 起始段。过 渡断面以后称为射流⑤ 主体段。
起始段射流轴心上速度都为
u0 ,而主体段轴心速度沿 x 方
三、紊流射流的特征
1、几何特征
射流半径和从极点起算的距离成正比, 即 BO =Kx。
扩散角α为一定值,其正切值
式中 K ― 试验系数,对圆断面射流 K=3.4a。
a ― 紊流系数,由实验决定,是表 示射流流动结构的特征系数。
第六章 气体射流

6-1 无限空间淹没紊流射流的特征
1、几何特征:射流按一定的扩散角α向前作扩散运动。 针对圆断面射流,有:
tg
任一断面的射流半径 R = k 3 .4 a 由极点算起的射程 x
(1)
k a
-试验系数(即外边界线的斜率) _紊流系数,取决于孔口的形状及孔口出流的紊流强度)
1
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
第三节 温差及浓差射流
一、定义 自孔口射出的流体的温度和浓度与周围气体存在差别的 射流。 二、温差、浓差射流的相似性 速度差→动量交换 这三种交换在机理上是相似的。这种相 似性反映在射流主体的速度分布和温度 温度差→热量交换 分布图结构非常相似。参看图 6- 6 浓度差→质量交换
温差或浓差射流研究的主要任务:射流温差、浓差分布场的规 律,并讨论由于温差、浓差的存在引起的射流轴心轨迹的偏移。
R R 3. 4ax r0 vm 0.96 v0 ax
R
又
R 3.4ax r0
代入上式,得:
vm 0.96 v0 ax
∴
利用射流的几何特征和运动特征:
∵
v v v m v0 vm v0 y y R r0 R r0
Q 0 . 96 2 2 3 . 4 a x 0 . 0985 Q0 ax
由
代入上式:
v r0 0 R vm
2
y 2 令 R
1 2 2 1 1.5 d 0
2
§ 6- 2 圆断面射流的运动分析
y 2 令 R
第六章 气体射流

由
T2 Te 0.23 as T0 Te 0.147 d0
0.23 as 0.147 d0
,可得
0.23 10 27 23.67 0 C 0.08 3 0.147 0.1
t 2 te
t0 te 27
从而有
a 3 2 0.51 s 0.35 s d 0 9.8 10 27 0.08 3 2 0.51 3 0.35 32 4.28m 2 273 27 0.1 y' g T0 2 0 Te
§6.4 温差射流与浓差射流
一、 温差与浓差射流的特征 2. 运动特征 由试验得出,截面上温差分布、浓差 分布与速度分布之间具有相似性,即:
T v y 1 1 1.5 Tm vm R
1 2 1.5
3. 热力学特征 在等压情况下,射流断面上相对焓值 流量不变。
cTdQ C
§6.4 温差射流与浓差射流
二、几个主要参数的计算公式 1. 轴心温差 Tm
Tm 0.35 T0 as 0.147 d0
2. 质量平均温差 T2
T2 0.23 as T0 0.147 d0
T2 .Qc 相对焓值流量
§6.4 温差射流与浓差射流
r0 tg 1.49a sn
【例】圆射流以 Q0=0.55m3/s,从 d0=0.3m 管嘴流出。试求 2.1m处射流半宽度R、轴心速度vm、断面平均速度v1 、质量 平均速度v2,并进行比较。 【解】查表得a=0.08。 先求核心长度 s n
r0 0.15 s n 0.672 0.672 1.26m a 0.08 sn s 2.1m ,所求截面在主体段内 。
气体射流
和浮力作用,推导轴心线弯曲轨迹公式。
y
A’
e g
y
d
A
A
y
xtg
m g
x
x
射流轴线的弯曲
eg
mg m j j
j:垂直向上的加速度
e m m
g
j
duy dt
d2y' dt 2
y ' uydt dt jdt
y'
dt
( e m
1)gdt
由气体状态方程式,在等压状态下,有:
T C
y
v1
v1 v0
0.095 as 0.147
d0
v1 0.492 v0 as 0.41
b0
v2
v2 v0
as
0.23 0.147
d0
v2 0.833 v0 as 0.41
b0
段名 参数名称
符 号
圆断面射流
平面射流
起
流量
QQ Q0
2
1
0.76
as r0
1.32
as r0
Q Q0
1 0.43 as b0
1 0.76 as r0
1
1.32
as r0
2
v2 v0
1 1 0.43 as
b0
段名 参数名称 符号 圆断面射流
起
核心长度
sn
sn
0.672
r0 a
平面射流
sn
1.03 b0 a
始 喷嘴至 极点距离
x0
x0
0.294
r0 a
x0
0.41b0 a
段 收缩角 tg 1.49a tg 0.97a
9 气体射流

Q ' + Q '' as as = 1 + 0.76 + 1.32( ) 2 Q0 r0 r0 11
9.2 圆断面射流的运动分析
9.2.7 起始断面平均流速v1 起始断面平均流速v
as as 2 1 + 0.76 + 1.32( ) r0 r0 v1 = v0 1 + 6.8 as + 11.56( as ) 2 r0 r0
ρ − ρm j= e ⋅g ρm
u y = ∫ jdt
d 2 y' j= = dt dt 2 du y
s
y ' = ∫ u y dt = ∫ dt ∫ jdt
y ' = ∫ dt ∫ (
ρe − 1) g ⋅ dt ρm
16
9.4 温差或浓差射流
9.4.4 射流弯曲
ρe − 1) g ⋅ dt ρm
0.73g ∆T0 ⋅ ∫ dt ∫ vm dt v0 Te ds vm = dt ⇓ 1 v0 1 v0 ds ∫ dt ∫ vm dt = ∫ sdt = v0 ∫ vm ⋅ vm sdt = v0 ∫ vm ⋅ dt ⋅ sdt y'=
17
9.4 温差或浓差射流
9.4.4 射流弯曲
y'=
0.73g ∆T0 ⋅ ∫ dt ∫ vm dt s v0 Te ds vm = dt ⇓ 1 v 1 v ds 1 v dt ∫ vm dt = ∫ sdt = ∫ 0 ⋅ vm sdt = ∫ 0 ⋅ ⋅ sdt = ∫ 0 ⋅ sds ∫ v0 vm v0 vm dt v0 vm
9.2 圆断面射流的运动分析
9.2.2 断面流量Q 断面流量Q
工程流体力学课件第六章 气体射流

几何特征: tg Kx K 3.4a x
K—试验系数,对圆断面射流K=3.4 a,平面射流K=2.44 a; a—紊流系数,由实验决定,是表示射流流动结构的特征系数。
紊流系数a确定,射流边界层的外边界线确定了,射流即按一定的扩散角 向前
作扩散运动,形成圆锥形流场,这就是圆形喷嘴紊流射流的几何特征。
动力特征
(1) 射流内部的压强是变化的,随射程的增大而增大,直至端头 末尾压强最大,达到稳定后数值比周围环境大气压强稍高一点。
(2) 射流中各横截面上的动量不再守恒,沿程逐渐减小,在第二 临界断面后,动量很快减小以至消失。
旋转射流
气体本身一面旋转,一面向周围介质中扩散前进, 其特征与自由射流和有限空间射流大不相同。
本章简要介绍无限空间射流和有限空间射流
一、自由湍流射流
右图为射流结构示意图
自由湍流射流特征
起始段和主体段
射流边界层从出口沿射程不断向外扩散,带动周围介质进入边界层,同时边界层也向 射流中心扩展,至出口如图的BOE面处,边界层扩展到射流轴心线,核心区域消失。
起始段:出口断面至过渡断面之间的部分称为射流起始段 主体段:过渡断面以后称为射流主体段
(2) 轴心流速 vm :
vm
0.965 as 0.294 v0
as
0.48 v0
0.147
r0
d0
(3) 断面平均流速v1 :
v1
Q A
as
0.19 0.294
v0
0.095 as 0.147
v0
r0
d0
(4) 质量平均流速 v2 :
Q 0.4545
0.23
v2
A
as
v0 0.294
流体力学第六章 气体射流

射流半径沿程的线形增长性。
R = 3.4a( x0 + s)
R
as
=ቤተ መጻሕፍቲ ባይዱ3.4( + 0.294)
r0
r0
2、运动特征
轴心速度 最大,从轴心 向边界层边缘, 速度逐渐减小 至零。
距喷嘴距 离越远边界层 厚度越大,而 轴心速度则越 小,也就是速 度分布曲线不 断地扁平化了。
在定义上根本不同,不可混淆。
矩形喷嘴运动参数
以上分析出圆断面射流主 体段内运动参数变化规律,这 些规律亦适用于矩形喷嘴。但 要将矩形换算成为流速当量直 径代人进行计算。换算公式按 第四章所述。
五、起始段核心长度 sn及核心 收缩角 θ
【例题6.3】圆射流以Q0=0.55m3/s,从d0=0.3m管嘴
BO 为圆断面射流截面的半径 R, R称为 ⑨ 射流半径。
三、紊流射流的特征
1、几何特征
射流半径和从极点起算的距离成正比, 即 BO =Kx。
扩散角α为一定值,其正切值
式中 K ― 试验系数,对圆断面射流 K = 3.4a 。
a ― 紊流系数,由实验决定,是表 示射流流动结构的特征系数。
紊流系数的影响因素
研究内容
浓度扩散与温度相似。在实 际应用中,为了简化起见,可以 认为,温度、浓度内外的边界与 速度内外的边界相同。于是参数 R 、 Q 、 vm 、 v1、 v2等可 使用前两节所述公式,仅对轴心 温差 △ Tm ,平均温差等沿射程 的变化规律进行讨论。
定义参数:以足标e表示周围气体的符号
截面上温差分布,浓差分布
第二节 圆断面射流的运动分析
一、轴心速度 vm
流体力学泵与风机-第6章-气体射流ppt课件

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.1
无限空间淹没紊流射流的特征
一、过渡断面(转折断面)、起始段、主体段
射流核心:u=u0 边界层: u<u0
主体段: 轴心u<u0 , u沿程下降 射流特征:几何?速度等?
出口截面动量流量
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
§6.2
圆断面射流的运动分析
一、主体段轴心速度vm
R
2v2ydyr02v02 0
两端同除以R2vm2 ,在一个断面上vm可视为常数进行计算
(r0)2(v 0)2 2R (v)2ydy () 21 (1 1 .5)4d 0 .09 Rv m 0 v m RR 0
r 0 3 .4 a 0 .15 3 .4 0 .08
(2)先求起始段核心长度sn
sn 0 .6r 7 a 0 1 0 .6 7 0 0 ..0 1 1 8 5 1 .2m 6 3 .8m 6所在求主断体面段内
v2 0.4545 0.4545 0.193
v0 as0.2940.0 83.860.294
三、运动特征
主 y--体-断速段面度:上分任布意: 点至vvm 轴心距[1离(R y问)1.题5]2:[1v m如1.5何]2确定?
R---该断面射流半径 v---y点的速度 vm---轴心速度
起始段:
y---断面上任意点 至核心边界的距离
R---同断面的边界层厚度 v---y点的速度 vm---核心速度v0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体射流1.圆射流以Q 0=0.55m³/s,从d 0=0.3m 管嘴流出。
试求2.1m 处射流半宽度R ,轴心速度m v ,断面平均流速1v ,质量平均2v ,并进行比较。
解:查表知:a =0.08 由m m ar S n 1.226.1672.00<== 在主体段r R =3.4⎪⎪⎭⎫⎝⎛+294.00r as∴R=3.4⎪⎭⎫⎝⎛+⨯294.015.01.208.0×0.15=0.72m 0v =A Q =23.0455.0⨯π=7.78m/s147.048.00+=d as v v m解得:s m v m /29.5= 147.0095.0001+=d as v v 解得:s m v /05.11= 147.023.002+=d as v v 解得:s m v /5.22=2.某体育馆的圆柱形送风口,d 0=0.6m ,风口至比赛区为60m ,要求比赛区风速(质量平均风速)不得超过0.3m/s ,求送风口送风量应不超过多少m³/s ? 解:查表知:a=0.08 由m m ar S n 6052.2672.00<==在主体段147.023.002+=d as v v (其中m s s m v 60,/3.02==) 解得:s m v d Q /3430200==π3.岗位送风所设风口向下,距地面4m 。
要求在工作区(距地面1.5米高范围)造成直径为1.5射流截面,限定轴心速度为2m/s ,求喷嘴直径及出口流量。
解:s m v a m S m /2,08.0,5.25.14===-=⎪⎪⎭⎫ ⎝⎛+=147.08.600d as d D∴d 0=0.14m 由m m ar S n 5.258.0672.00<==,在主体段147.048.00+=d as v v m 解出:s m v /56.60=s m v d Q /1.0430200==π4.收缩均匀的矩形孔口,截面为0.05×2m²,出口速度0v 为10m/s ,求距孔口2.0m 处,射流轴心速度m v ,质量平均速度2v 及流量Q 。
解: 此题为平面射流m b 205.00=∴查表:m m ab S m s a n 224.003.1,2,108.00<==== 在主体段2⎪⎪⎭⎫ ⎝⎛v v m=41.02.12+οb as∴m v =4m∕s202⎪⎪⎭⎫ ⎝⎛v v =41.0833.02+οb as∴s m v /78.22=0Q =0v A =10×0.05×2=1m³/sQ Q =41.02.10+b as∴Q =3.6 m³/s5 .8m/s 的速度从圆管喷出,d 为0.2m ,求距出口1.5m 处的m v ,2v 及D 。
解:查表知:a=0.08 由m m ar S n 5.184.0672.00<== 在主体段v v m =147.048.0+οd as∴m v =5.14 m/s2v v =147.023.0+οd as∴s m v /46.22=⎪⎪⎭⎫ ⎝⎛+=294.04.300r as d D∴D =1m6.室中灰尘的吹吸系统如题附图。
室长L=6m ,吹风口高1h =15cm ,宽为5m ,由于贴附底板,射流相当于半个平面射流。
底板即为轴心线。
问(1)吸风口高度2h 为多少?(2)若吸风口处速度为4m/s ,Q 。
应多少?(3)吸风口处风量为多少?解:查表得a =0.118,mb 15.00=(因为是贴附射流m cm b cm b 15.01515200==→=)m m ab S n 63.103.10<==在主体段 (1)2b h =2.44⎪⎪⎭⎫ ⎝⎛+41.00b as解得:m h 88.12=(2)v v m=147.0492.02+οb as∴s m v /4.180=s m A v Q /9.1315.054.18300=⨯⨯==(3)Q =Q 041.02.10+b as=37.9 m³/s 7.要求空气沐浴地带的宽度b=1m 。
周围空气中有害气体的浓度=e x 0.06mg/L 。
室外空气中浓度0x =0。
工作地带允的浓度为L mg x m /02.0=。
今用一平面喷嘴a =0.2,试求喷嘴b 0及工作地带距喷嘴的距离s 。
解:L mg x /06.006.000-=-=∆L mg x m /04.006.002.0-=-=∆假设射流工作地带处于主体带:=⎪⎪⎭⎫ ⎝⎛2x x m ∆∆94)06.004.0(41.0032.122=--=+οb as ∴4.241.00=+b as又∵b b =2.44⎪⎪⎭⎫ ⎝⎛+41.00b as 所以b 0=0.17ms =1.695m 校核:m m ab S n 695.188.003.10<==在主体段,假设成立8.温度为40℃的空气,以0v =3m/s ,从d 0=100mm 水平圆柱形喷嘴射入t 0=18℃的空气中。
求射流轨迹方程。
解:查表得 a =0.08 由轨迹方程Y =χtg α+Αr 20cos ⎪⎪⎭⎫ ⎝⎛αd X ⎪⎭⎫⎝⎛+35.0cos 51.0αX a 其中Αr=Tev T gd 2000∆ Te=18+273=291K ΔT 0=40-18=22K0v =3m/sd 0=100mm 0=α代入数据得 Y =0.0336X³+0.0288X²9.高出地面5m 处设一孔口d 0为0.1m ,以2m/s 速度向房间水平送风。
送风温度t 0=-10℃,室内温度t 0=27℃。
试求距出口3m 处的2v ,t 2及弯曲轴心坐标。
解:查表得a =0.08 m m ar S n 342.0672.00<== 在主体段由2v v =147.023.0+οd as 得:2v =0.18m/s 由02T T ∆∆ =147.023.0+οd as =2710272---t 得:t 2=23.7℃Y ′=⎪⎭⎫ ⎝⎛+2320035.051.0S S da Te v T g ∆=-4.89m 所以,轴心坐标为 x =3m y =–4.89m10.室外空气经过墙壁上H =6m 处的扁平窗口(b 0=0.3m )射入室内,室外温度t 0=0℃,室内温度t 0=25℃。
窗口处出口速度为2m/s ,问距壁面s =6m 处2v ,t 2及冷射流轴心坐标。
解:查表得a =0.108m m ab S n 686.203.10<== 在主体段22⎪⎪⎭⎫ ⎝⎛v v =41.0833.02+οb as2v =1m/s41.0833.025025202+=--=b ast T T ∆∆ ∴5.122=t ℃K T K T e 273,298252730==+=m T T a b xa Ab y e r 28.1)205.02(226.02022/500-=+⨯=(平面射流公式6-20a )轴心坐标为x =6m y =-1.28m11.喷出清洁空气的平面射流,射入含尘浓度为0.12mg/L 的静止空气中。
要求距喷口2m 处造成宽度为2b=1.2m 的射流区。
求设计喷口尺寸0b ,并求工作区轴心处灰尘浓度。
解:查表得a =0.118 假设在主体段 由0b b =2.44⎪⎪⎭⎫ ⎝⎛+41.00b as 得b 0=0.024m校核:m m ab S n 221.003.10<== 假设成立由0x x m ∆∆=12.0012.041.0032.10--=+m x b as解得:L mg x m /081.0=12.试验测得轴对称射流的0v =50m/s,某断面处=m v 5m/s ,试求在该断面上气体流量是初始流量的多少倍?解:由0v v m =147.048.0+οd as =1/10⎪⎪⎭⎫ ⎝⎛+147.00d as =4.8 0Q Q =4.4⎪⎪⎭⎫ ⎝⎛+147.00d as=21.213.有一圆形射流,在距出口处10m 的地方测得m v 为0v 的50%,试求其圆形喷嘴半径。
解:查表得 a=0.08 由0v v m =147.048.0+οd as =1/2得0d as +0.147=0.96得d o =0.98m 故r 0=m 49.014.试求0R =0.5m 的圆断面射流出口断面为20m ,距轴心距离y =1m 处的射流速度与出口速度之比。
解:查表得 a=0.08 由于m ar s n20672.00<=,所以在主体段 0R R=3.4⎪⎪⎭⎫⎝⎛+294.00R asm R 94.5=867.0)(125.1=⎥⎦⎤⎢⎣⎡-=R y v v m 0v v =239.0147.048.0867.00=+⨯=⨯d as v v v v m m 15.为保证距喷口中心x =20m ,y =2m 处的流速v =5m/s 及初始段长度S n =1m ,当a =0.07时,试求喷口出口处的初始量(m 3/h )。
解:a =0.07 S n =1m 由S n =0.672ar 0得r o =0.1mr R =3.4⎪⎪⎭⎫ ⎝⎛+294.00r asR =4.76529.0)(125.1=⎥⎦⎤⎢⎣⎡-=R y v v m 037.0147.048.0529.000=+⨯=⨯=d as v v v v v v m m s m vv /135037.00==h m d v Q /161003600432000=⨯=π16.由0R =75mm 的喷口中射出=0T 300K 的气体射流,周围介质温度为=Te 290K ,试求距喷口中心x=5m ,y=1m 处的气体温度(a=0.075)。
解:由R R =3.4⎪⎪⎭⎫ ⎝⎛+294.00R as R =m 35.15.1)(1290300290Ry T T T m -=--=∆∆ 解得:K T 6.293=17.绘制由R 0=75mm ,a =0.08的自由淹没紊流射流结构几何图。
解:tg α=3.4a =0.272 S n =0.627a R 0=0.5878 mX 0=0.294aR 0=0.276m (画法参照6-1的射流结构图)18.为什么用因次量研究射流运动?19.什么是质量平均流速v 2?为什么要引入这一流速?20.温差射流中,无因次温度分布线为什么在无因次速度线的外边?21.温差射流轨迹为什么弯曲?是怎样寻求轨迹方程的?22.旋转射流与自由淹没射流有那些不同点?试对比说明。
23.旋转强度说明什么物理意义?24.何谓受限射流?受限射流结构图如何?与自由射流对比有何异同?(18—24解略)。
