2016年4月浙江省普通高中学业水平考试(数学试题及答案)

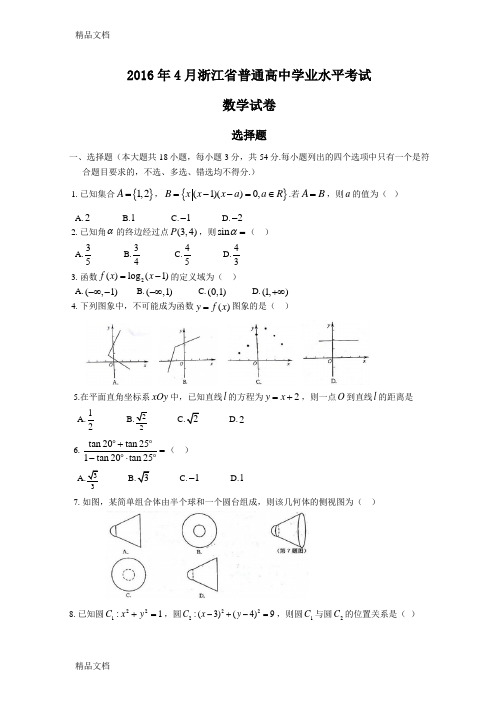
2016年4月浙江省普通高中学业水平考试

数学试题

一、选择题 （本大题共18小题，每小题3分，共54分。每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）

1. 已知集合A={1，2}，B={x|(x －1)(x －a)=0，a ∈R }。若A=B ，则a 的值为

A.2

B.1

C.－1

D.－2

2. 已知角α的终边经过点P （3，4），则sin α=

A.

3

5

B. 3

4

C. 4

5

D.

4

3

3. 函数f(x)=log 2(x －1)的定义域为

A. （－∞，－1）

B. （－∞，1）

C.（0，1）

D.（1，+∞）

4. 下列图象中，不可能．．．

成为函数y=f(x)图象的是 A. B. C. D.

5. 在平面直角坐标系xOy 中，已知直线l 的方程为y=x+2，则原点O 到直线l 的距离是

A.

1

2

B.

C.

D.2

6. tan 20tan 25

1tan 20tan 25+-⋅=

A.

B.

C.－1

D.1

7. 如图，某简单组合体由半个球和一个圆台组成，则该几何体的侧视图为

8. 已知圆C 1：x 2+y 2=1，圆C 2：(x －3)2+(y －4)2=9，则圆C 1与圆C 2的位置关系是

A.内含

B.外离

C.相交

D.相切

9. 对任意的正实数a 及m ，n ∈Q ，下列运算正确的是

A.(a m )n =a m+n

B. (a m )n =n

m a

C. (a m )n =a m －

n

D. (a m )n =a mn

10. 已知空间向量a =(2，－1，5)，b =(－4，2，x)(x ∈R )。若a ⊥b ，则x=

A.－10

B.－2

C.2

D.10

11. 在平面直角坐标系xOy 中，设a ∈R 。若不等式组,10,10y a x y x y ≤⎧⎪

-+≤⎨⎪+-≥⎩

所表示平面区域的边界为三角

形，则a 的取值范围为

A.(1，+∞)

B.(0，1)

C.(－∞，0)

D.(－∞，1)∪(1，+∞)

12. 已知数列{a n }(n ∈N *)满足a n+1=2,1,n n a n a n ⎧⎪⎨+⎪⎩为奇数，

为偶数。

设S n 是数列{a n }的前n 项和。若S 5=－20，

则a 1的值为

A. 23

9

-

B. 20

31-

C.－6

D.－2

13. 在空间中，设a ，b ，c 为三条不同的直线，α为一平面。现有： 命题p:若a α，b ⊂α，且a ∥b ，则a ∥α； 命题q ：若a ⊂α，b ⊂α，且c ⊥a ，c ⊥b ，则c ⊥α 则下列判断正确的是 A.p ，q 都是真命题

B. p ，q 都是假命题

C. p 是真命题，q 是假命题

D. p 是假命题，q 是真命题

14. 设n ∈N *，则“数列{a n }为等比数列”是“数列{2

1n a }为等比数列”的

A.充分不必要条件

B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

15. 在△ABC 中，已知∠A=30°，AB=3，BC=2，则△ABC 的形状是

A.钝角三角形

B.锐角三角形

C.直角三角形

D.不能确定

16. 如图所示，在侧棱垂直于底面的三棱柱ABC －A 1B 1C 1中， P 是棱BC 上的动点。记直线A 1P 与平面ABC 所成的角 为θ1，与直线BC 所成的角为θ2，则θ1，θ2的大小关系是

A. θ1=θ2

B. θ1>θ2

C. θ1<θ2

D.不能确定

17. 已知平面向量a ，b 满足|a

，b =e 1+λe 2(λ∈R )，其中e 1，e 2

为不共线的单位向量。若对符合

上述条件的任意向量a ，b 恒有|a －b |

≥e 1，e 2

夹角的最小值为

A. 6π

B. 3π

C. 23π

D.

56π 18. 设函数 f(x )=|2

x

－a x －b|(a ，b ∈R )。若对任意的正实数a 和实数b ，总存在x 0∈[1，2]，使得 f(x 0)≥m ，则实数m 的取值范围是

A.(－∞，0]

B.(－∞，

12

] C. (－∞，1]

D. (－∞，2]

二、填空题（本大题共4小题，每空3分，共15分） 19. 已知函数f(x)=2sin(x+

2

π)+3，x ∈R ，则f(x)的最小正周期是 ，而最小值为 。 20. 设函数f(x)=2x +a(a ∈R ).若函数f(x)的图象过点(3，18)，则a 的值为 。

21. 已知双曲线22

221(0,0)y x a b a b

-=>>。若存在圆心在双曲线 的一条渐近线上的圆，与另一条渐近线及x 轴均相切，则

双曲线的离心率为

22. 将棱长为1的正方体ABCD-EFGH 任意平移至A 1B 1C 1D 1-E 1F 1G 1H 1， 连接GH 1，CB 1。设M ， N 分别为GH 1，CB 1的中点，则MN 的长为